Analysis of Nodal Diameter Zero Blade Vibrations of a Radial Turbine †
Abstract
:1. Introduction
2. Experimental Investigations
2.1. Experimental Results ND0 Vibrations
2.2. Blade Vibration Analysis
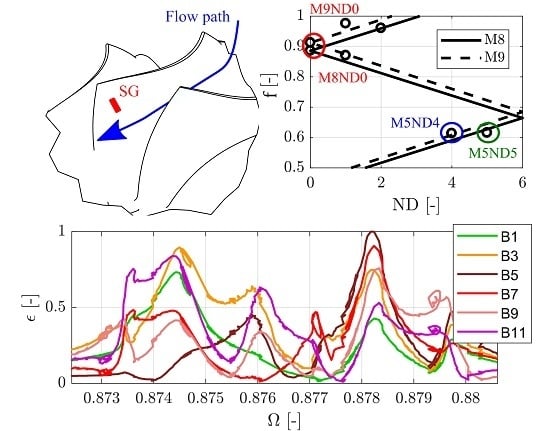
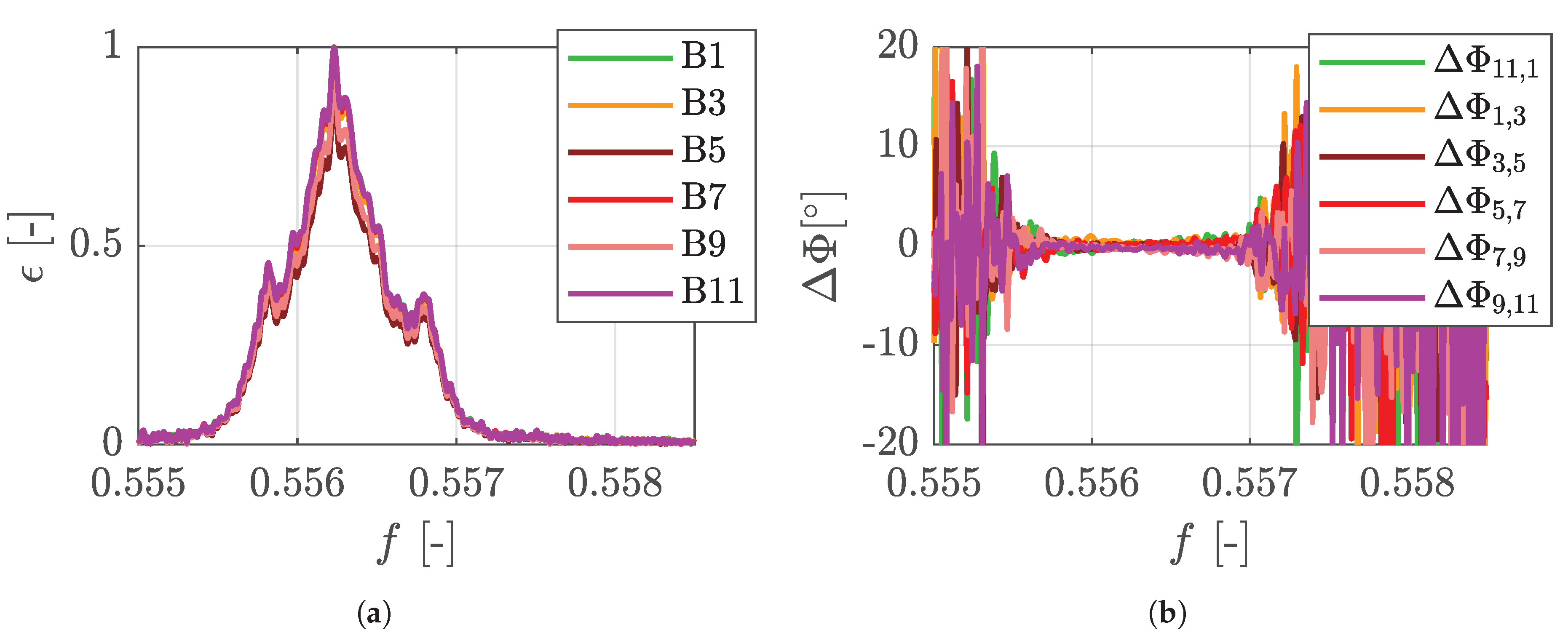
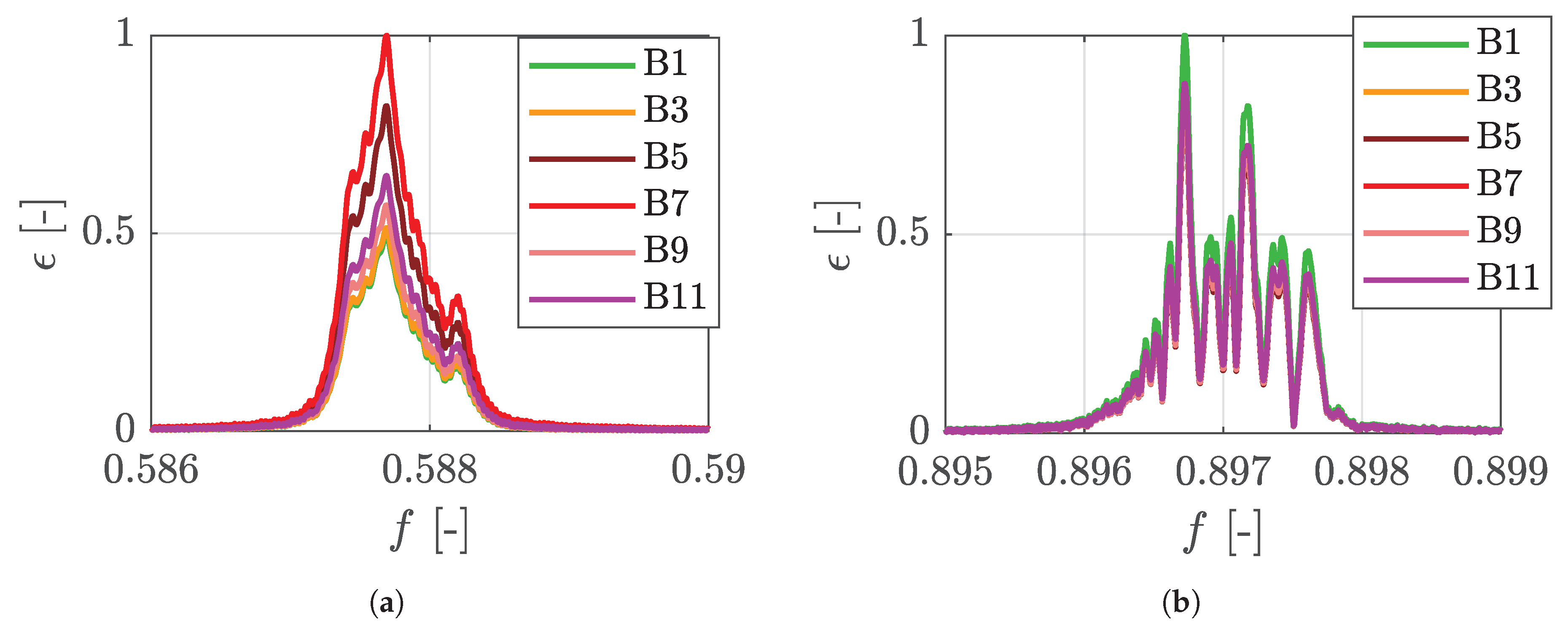
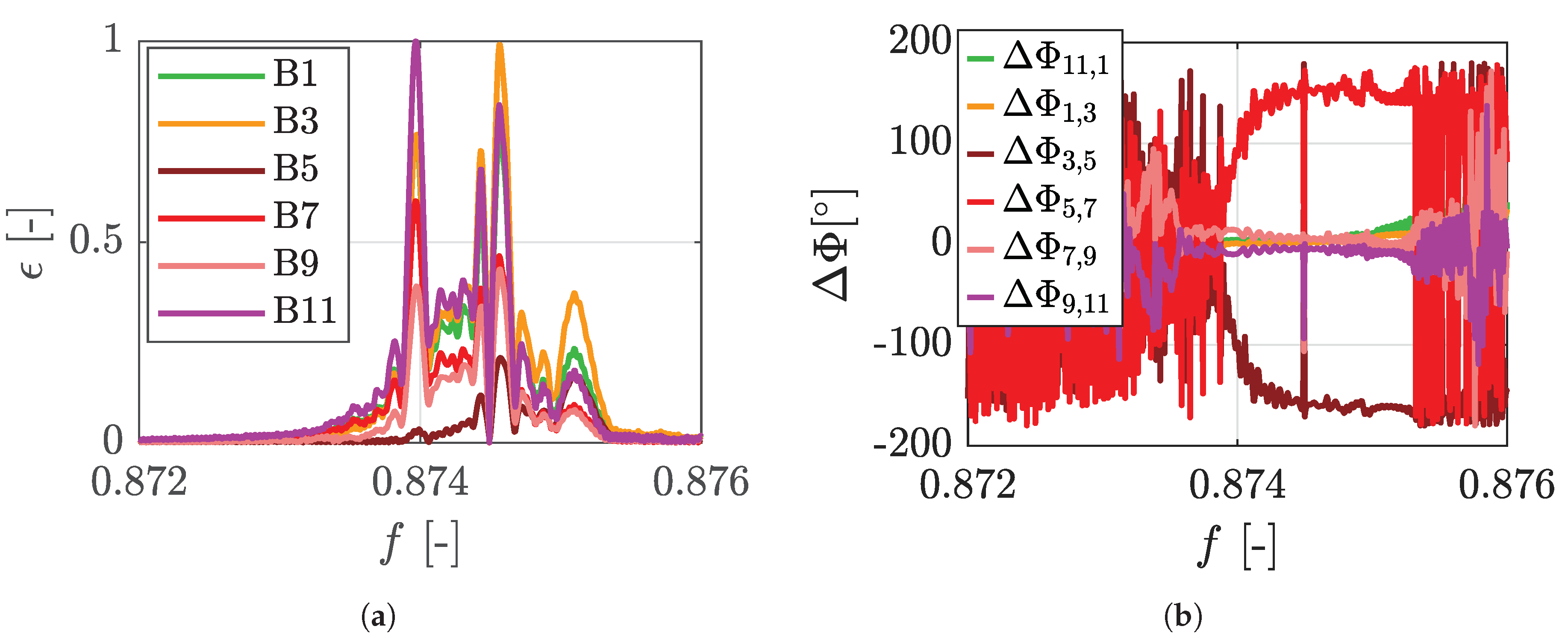
2.2.1. M5, M6, M9
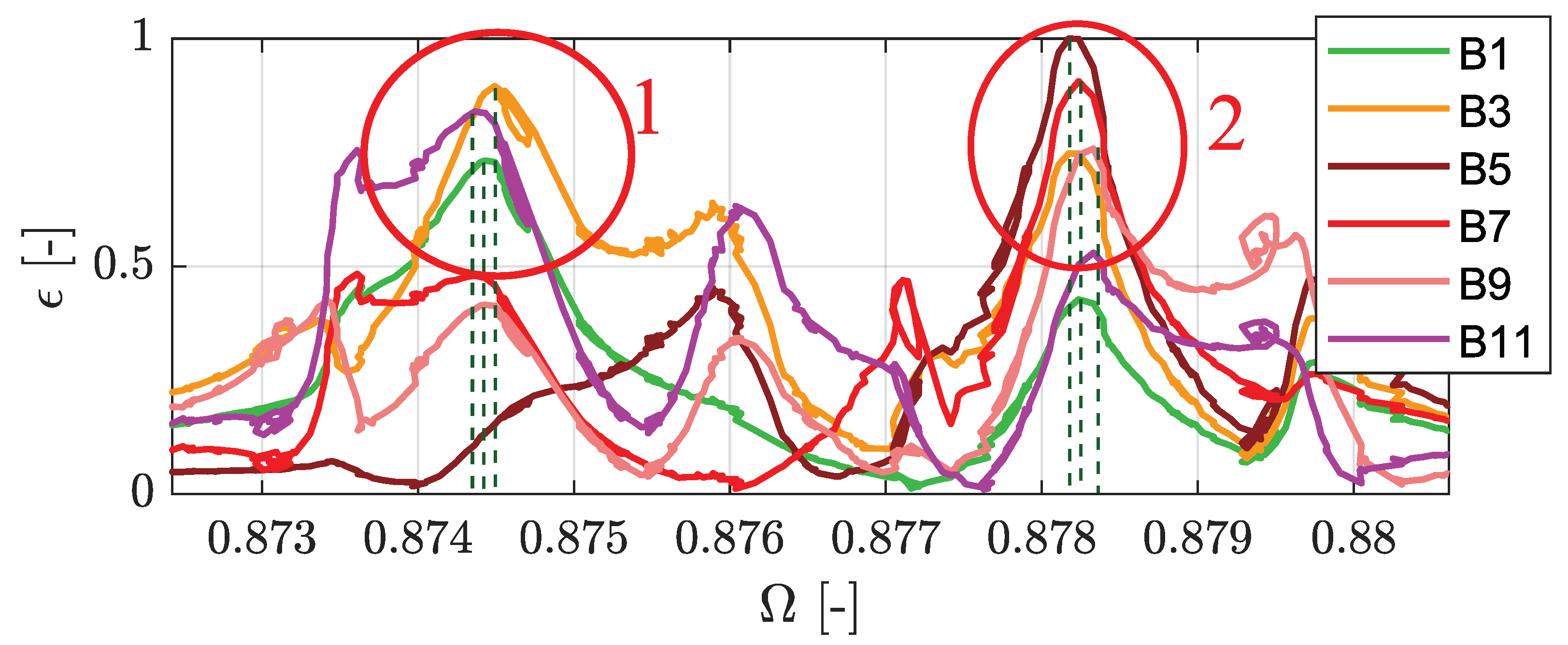
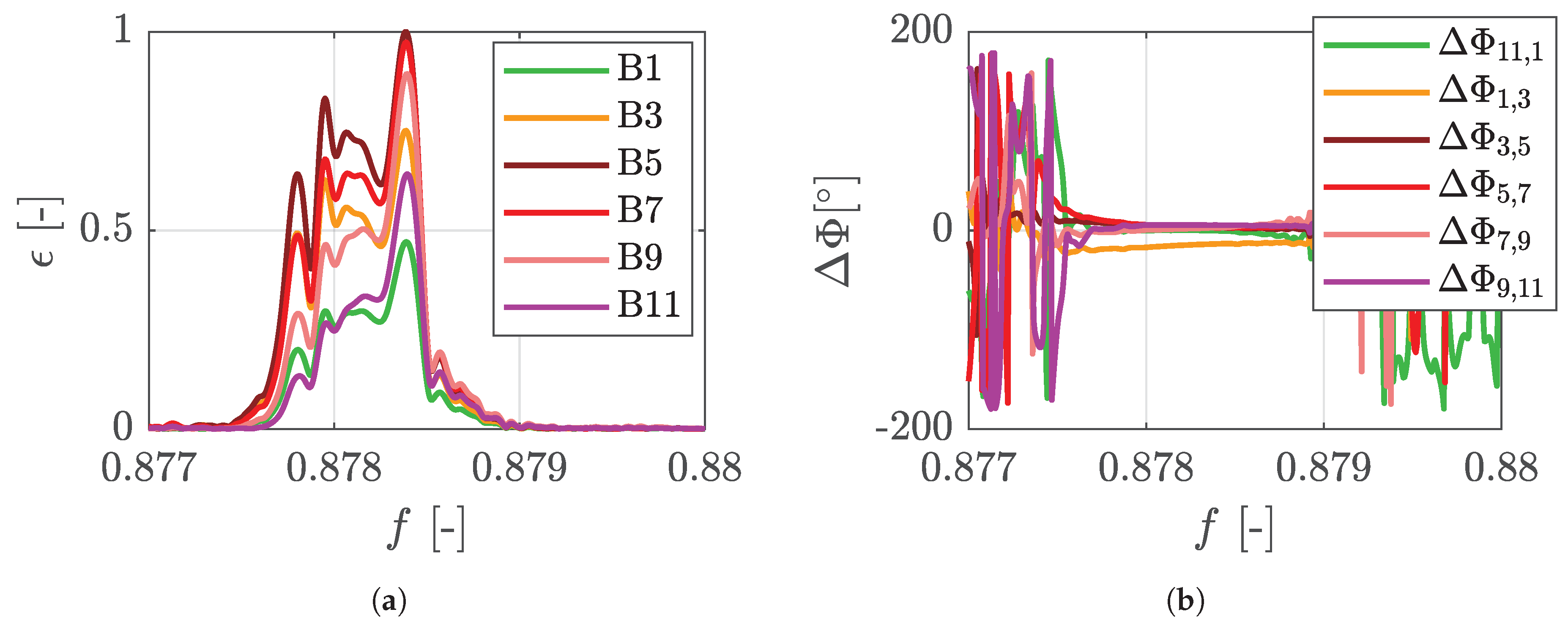
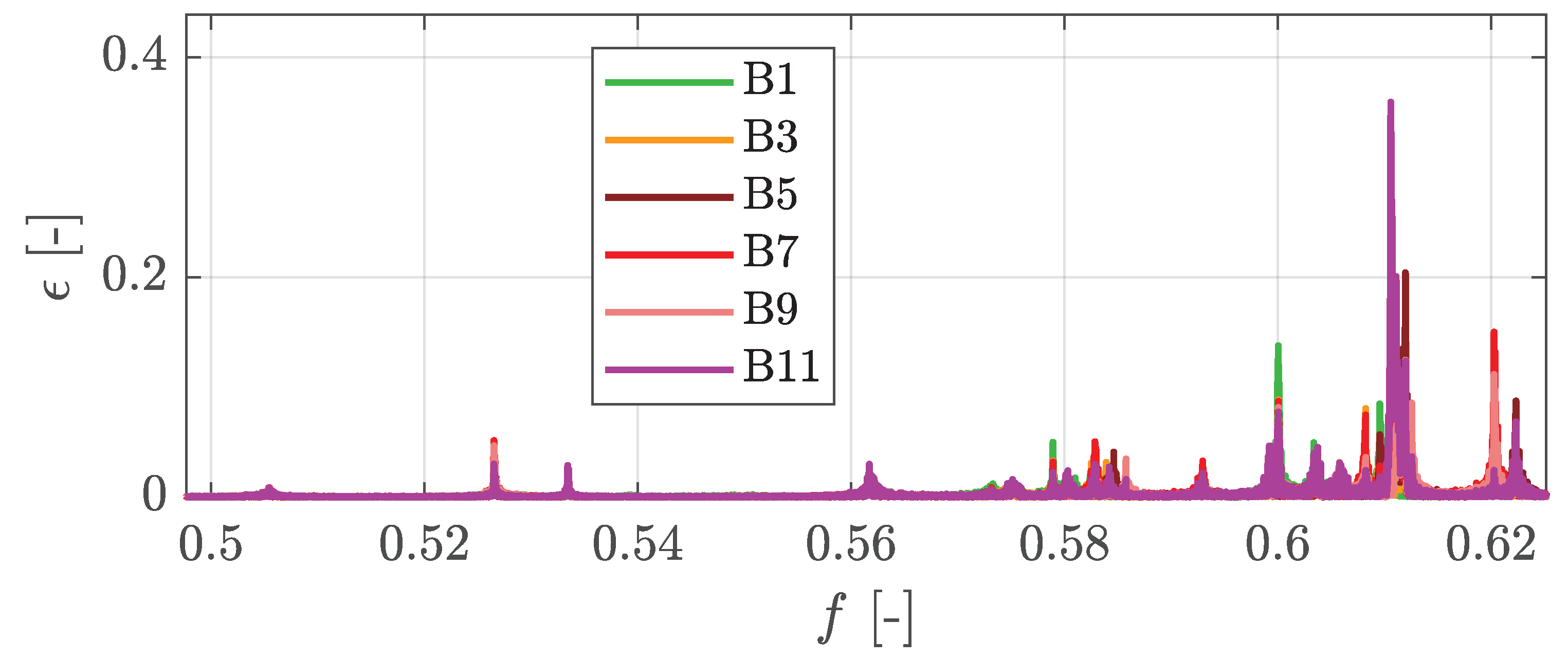
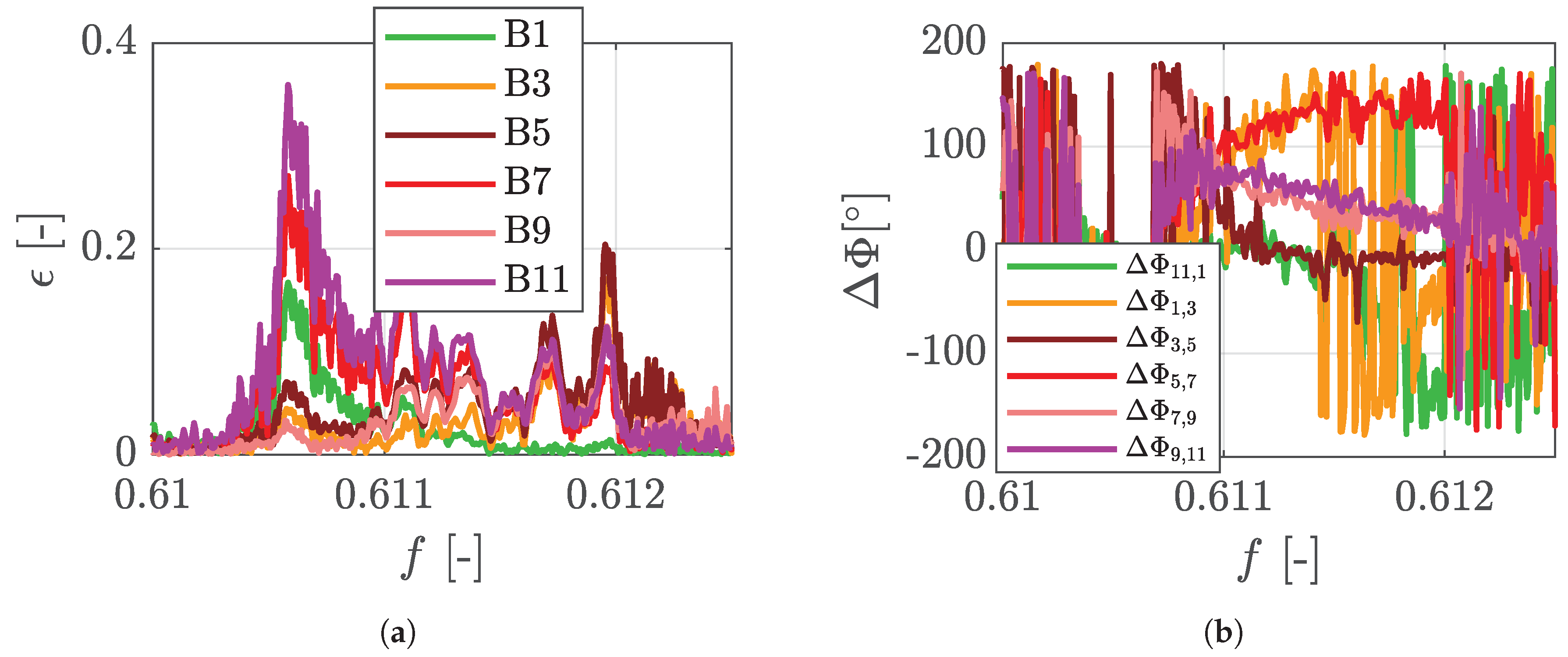
2.2.2. Mode 8
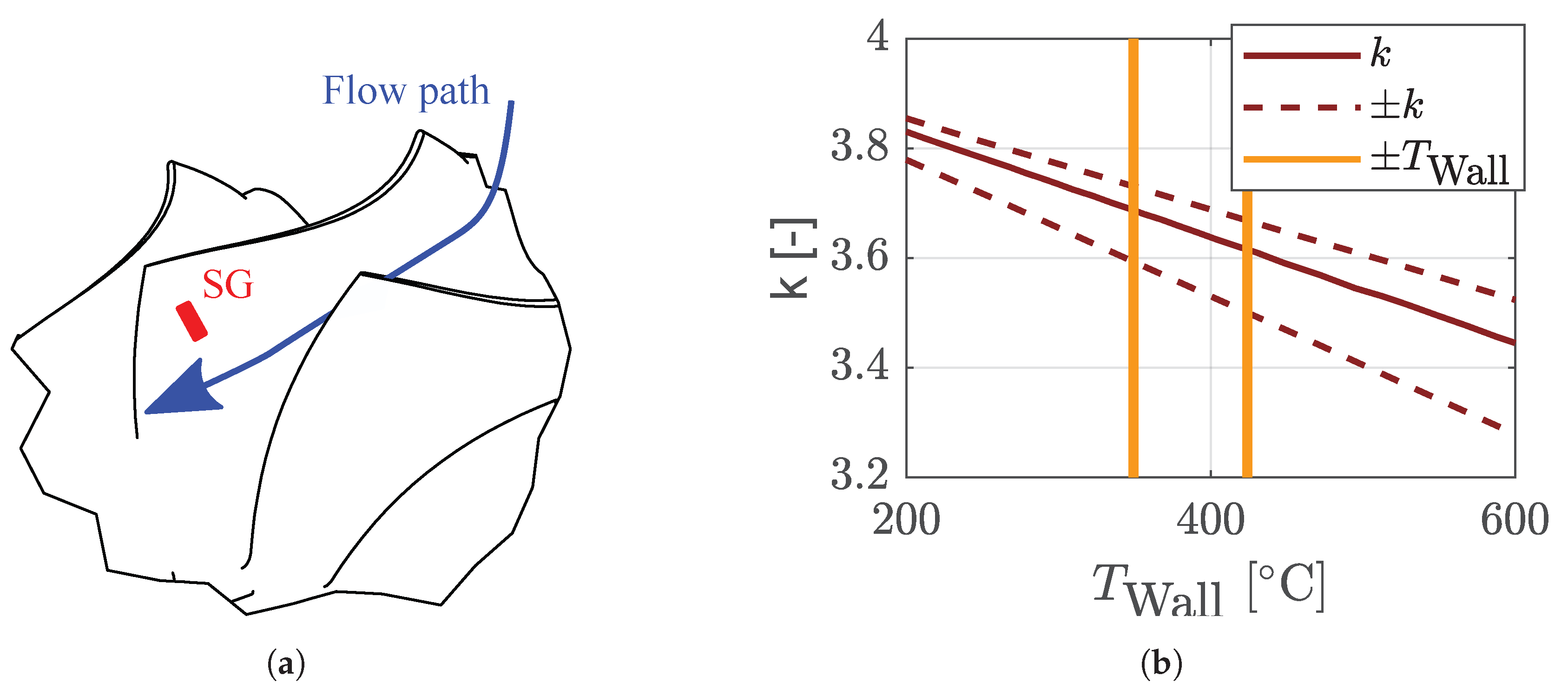
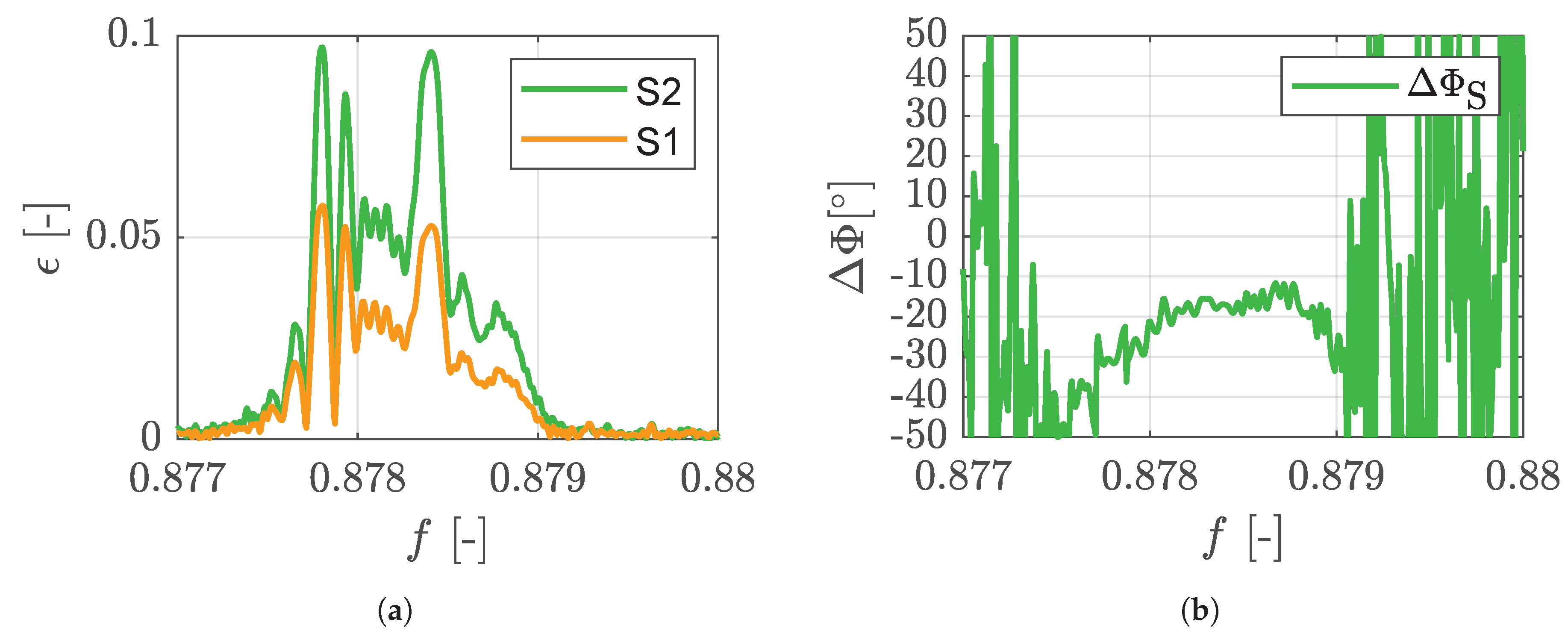
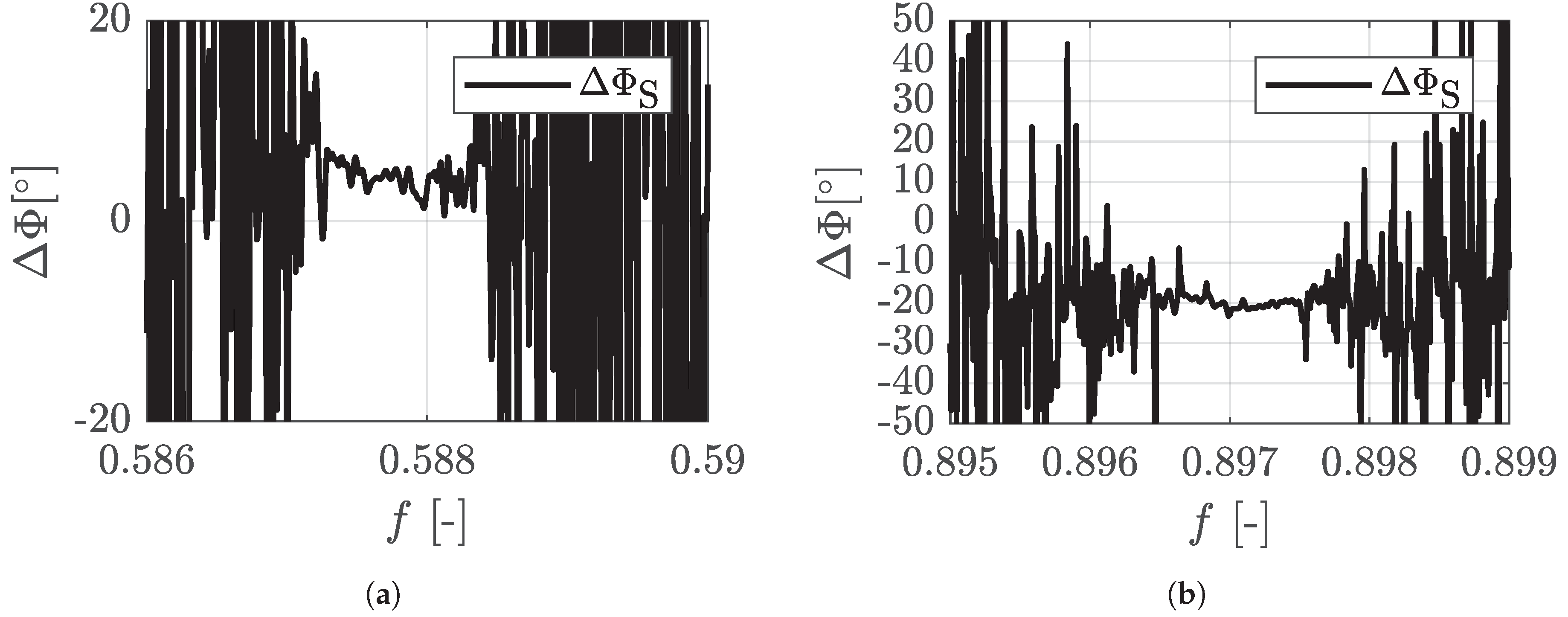
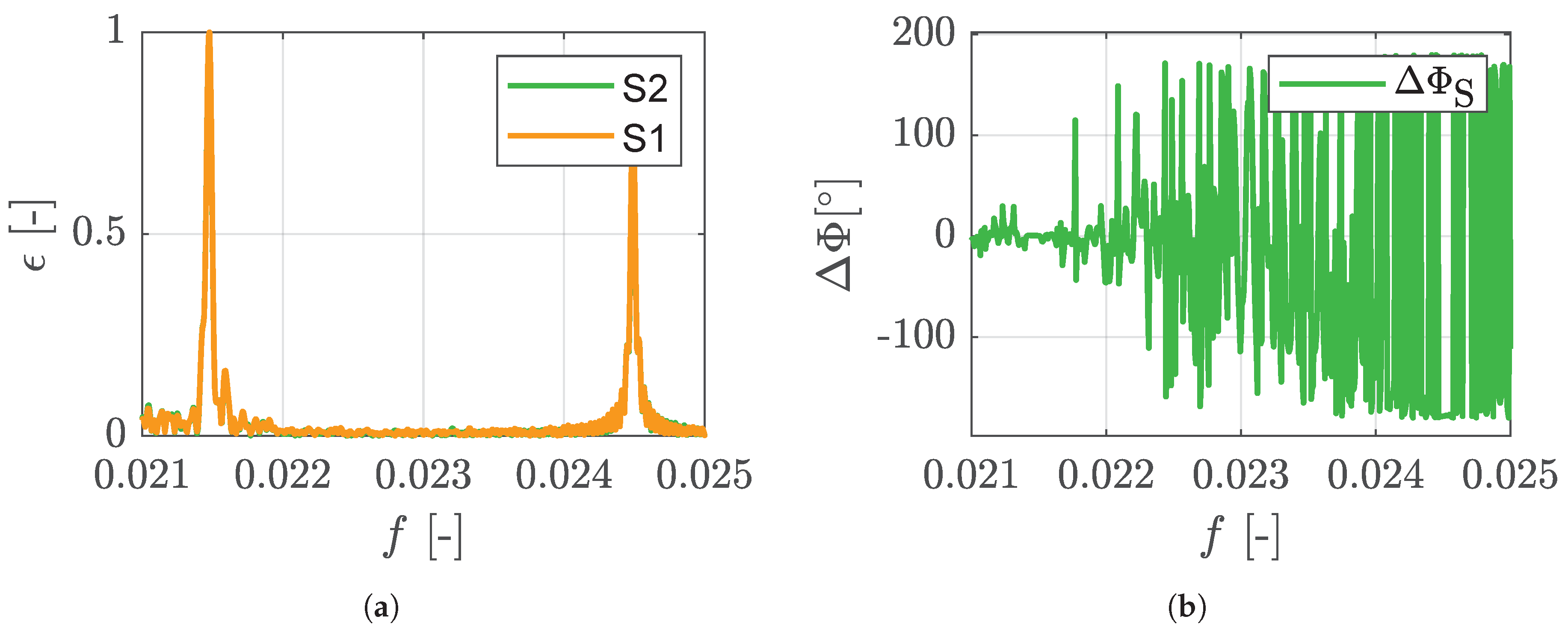
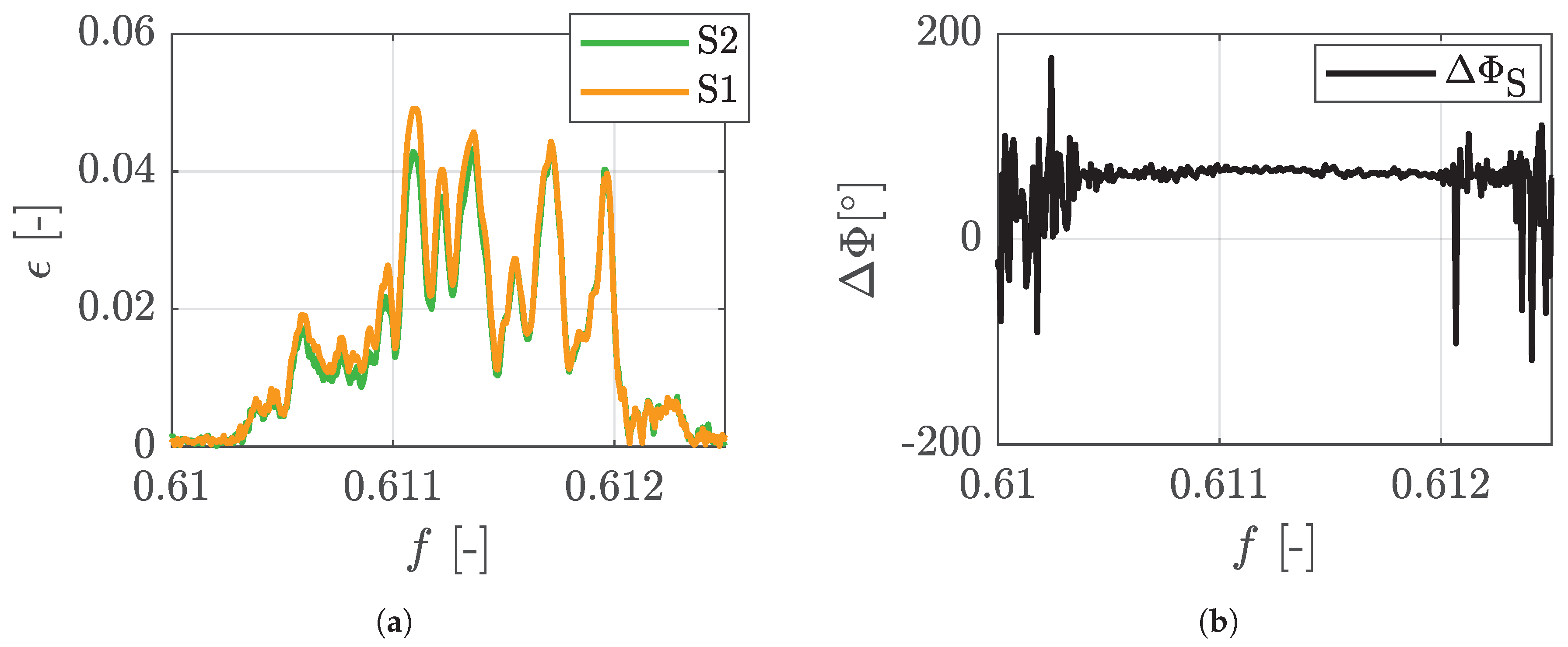
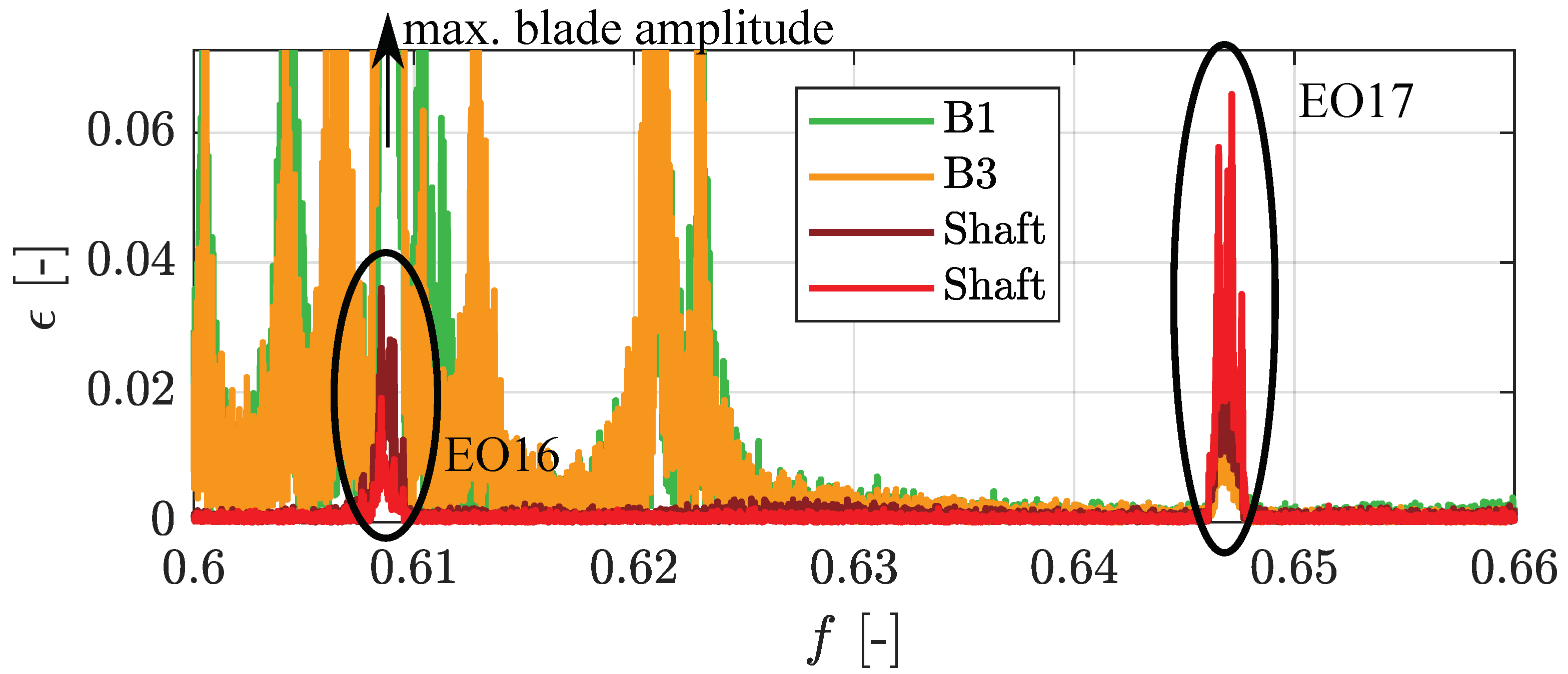
2.3. ND0 Shaft Oscillations
3. ND Vibrations
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| BLISK | blade integrated disk |
| Bi | strain signal of ith blade |
| EO | excitation order |
| phase lag of strain signals on ith and jth blade | |
| phase lag of strain signals on the shaft | |
| є | normalized strain |
| Fourier transform operator | |
| f | normalized frequency |
| FFT | fast Fourier transformation |
| resonance frequency kth Mode | |
| k | strain gauge sensitivity |
| ND | nodal diameter |
| N | rotational speed |
| Ω | normalized rotational speed |
| ω | rotational speed |
| S1,S2 | strain signal of shaft gauges |
| Tin | turbine inlet temperature |
| TWall | wall temperature (estimated by CFD) |
| IM, RE | imaginary and real part of a complex number |
| ζk | blade damping coefficient kth Mode |
References
- Kemp, N.H.; Sears, W.R. Aerodynamic Interference Between Moving Blade Rows. J. Aeronaut. Sci. 1953, 20, 585–597. [Google Scholar] [CrossRef]
- Kemp, N.H.; Sears, W.R. The Unsteady Forces Due to Viscous Wakes in Turbomachines. J. Aeronaut. Sci. 1955, 22, 478–483. [Google Scholar] [CrossRef]
- Klaus, M. Strömungsinduzierte Schaufelschwingungen in Radialturbinen mit beschaufeltem Spiralgehäuse: Zugl.: Karlsruhe, Univ., Diss, 2007; Forschungsberichte aus dem Institut für Thermische Strömungsmaschinen, Universität Karlsruhe (TH); Logos-Verl.: Berlin, Germany, 2007; Volume Bd. 33. [Google Scholar]
- Janicki, G.; Pezouvanis, A.; Mason, B.; Ebrahimi, M.K. Turbine Blade Vibration Measurement Methods for Turbocharges. Am. J. Sens. Technol. 2014, 2, 13–19. [Google Scholar]
- Beirow, B.; Kühhorn, A.; Nipkau, J. On the Influence of Strain Gauge Instrumentation on Blade Vibrations of Integral Blisk Compressor Rotors Applying a Discrete Model. In Proceedings of the ASME Turbo Expo 2009: Power for Land, Sea, and Air, Orlando, FL, USA, 8–12 June 2009; pp. 245–253. [Google Scholar]
- Kreuz-Ihli, T.; Filsinger, D.; Schulz, A.; Wittig, S. Numerical and Experimental Study of Unsteady Flow Field and Vibration in Radial Inflow Turbines. J. Turbomach. 2000, 122, 247–254. [Google Scholar] [CrossRef]
- Kreuz-Ihli, T. Strömungsinduzierte Schaufelschwingungen in Leitgitterlosen Radialturbinen. Ph.D. Thesis, TH Karlsruhe, Karlsruhe, Germany, 2001. [Google Scholar]
- Wilson, A.; Utengen, T. Turbine Blade Dynamics and Blade-Vane Interaction in a Radial Inflow Turbine. Agard Conf. Proc. 1994, 537, 35-1–35-11. [Google Scholar]
- Mueller, T.; Waldherr, C.; Kovachev, N.; Esper, A.; Wunderlich, M.; Lenzen, C. Blade Forces: FVV-Project No. 1189; Final Project Report BMWi/AiF 18568; FVV: Frankfurt am Main, Germany, 2018. [Google Scholar]
- Hackenberg, H.P.; Hartung, A. An Approach for Estimating the Effect of Transient Sweep Through a Resonance. J. Eng. Gas Turbines Power 2016, 138, 082502. [Google Scholar] [CrossRef]
- Kovachev, N.; Waldherr, C.U.; Mayer, J.F.; Vogt, D.M. Prediction of Aerodynamically Induced Blade Vibrations in a Radial Turbine Rotor Using the Nonlinear Harmonic Approach. J. Eng. Gas Turbines Power 2019, 141, 021007. [Google Scholar] [CrossRef]
- Waldherr, C.U.; Vogt, D.M. A Comparison of Two Reduced Order Methods for Probabilistic Mistuning Investigations. In Proceedings of the ASME 2017 Gas Turbine India Conference, Bangalore, India, 7–8 December 2017; p. V002T05A014. [Google Scholar] [CrossRef]
- Singh, P.M.; Vargo, J.; Schiffer, M.D.; Dello, D.J. SAFE Diagram—A Design and Reliability Tool for Turbine Blading; Turbomachinery Laboratories, Texas A&M University: College Station, TX, USA, 1988; Available online: http://hdl.handle.net/1969.1/163593 (accessed on 9 July 2020).
- Allport, J.M.; Jupp, M.L.; Pezouvanis, A.; Janicki, G.W.; Pierończyk, A.I.; Day, A.J.; Olley, P.; Mason, B.; Ebrahimi, M.K. Turbocharger blade vibration: Measurement and validation through laser tip-timing. In 10th International Conference on Turbochargers and Turbocharging; Elsevier: London, UK, 2012; pp. 173–181. [Google Scholar]
- Klauke, T. Schaufelschwingungen realer integraler Verdichterräder im Hinblick auf Verstimmung und Lokalisierung: Zugl.: Cottbus, Techn. Univ., Diss., 2007; Der Andere Verl.: Tönning, Germany, 2007. [Google Scholar]


| Turbine hub to tip ratio | 0.29 |
| Maximum rotational speed | 40,000 RPM |
| Turbine inlet temperature | |
| Maximum compressor volumetric flow rate | |
| Maximum compressor pressure ratio |
| ND | [°] | [°] | [°] | [°] |
|---|---|---|---|---|
| 1 | 30 | −30 | 60 | −60 |
| 2 | 60 | −60 | 120 | −120 |
| 3 | 90 | −90 | 180 | −180 |
| 4 | 120 | −120 | −120 | 120 |
| 5 | 150 | −150 | −60 | 60 |
| 6 | 180 | −180 | 0 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Wunderlich, M.; Esper, A.; Wirsum, M.; Buchmann, K. Analysis of Nodal Diameter Zero Blade Vibrations of a Radial Turbine. Int. J. Turbomach. Propuls. Power 2020, 5, 18. https://doi.org/10.3390/ijtpp5030018
Wunderlich M, Esper A, Wirsum M, Buchmann K. Analysis of Nodal Diameter Zero Blade Vibrations of a Radial Turbine. International Journal of Turbomachinery, Propulsion and Power. 2020; 5(3):18. https://doi.org/10.3390/ijtpp5030018
Chicago/Turabian StyleWunderlich, Markus, Alexander Esper, Manfred Wirsum, and Klaus Buchmann. 2020. "Analysis of Nodal Diameter Zero Blade Vibrations of a Radial Turbine" International Journal of Turbomachinery, Propulsion and Power 5, no. 3: 18. https://doi.org/10.3390/ijtpp5030018
APA StyleWunderlich, M., Esper, A., Wirsum, M., & Buchmann, K. (2020). Analysis of Nodal Diameter Zero Blade Vibrations of a Radial Turbine. International Journal of Turbomachinery, Propulsion and Power, 5(3), 18. https://doi.org/10.3390/ijtpp5030018