Parametric Study of a Turbofan Engine with an Auxiliary High-Pressure Bypass
Abstract
:1. Background and Introduction
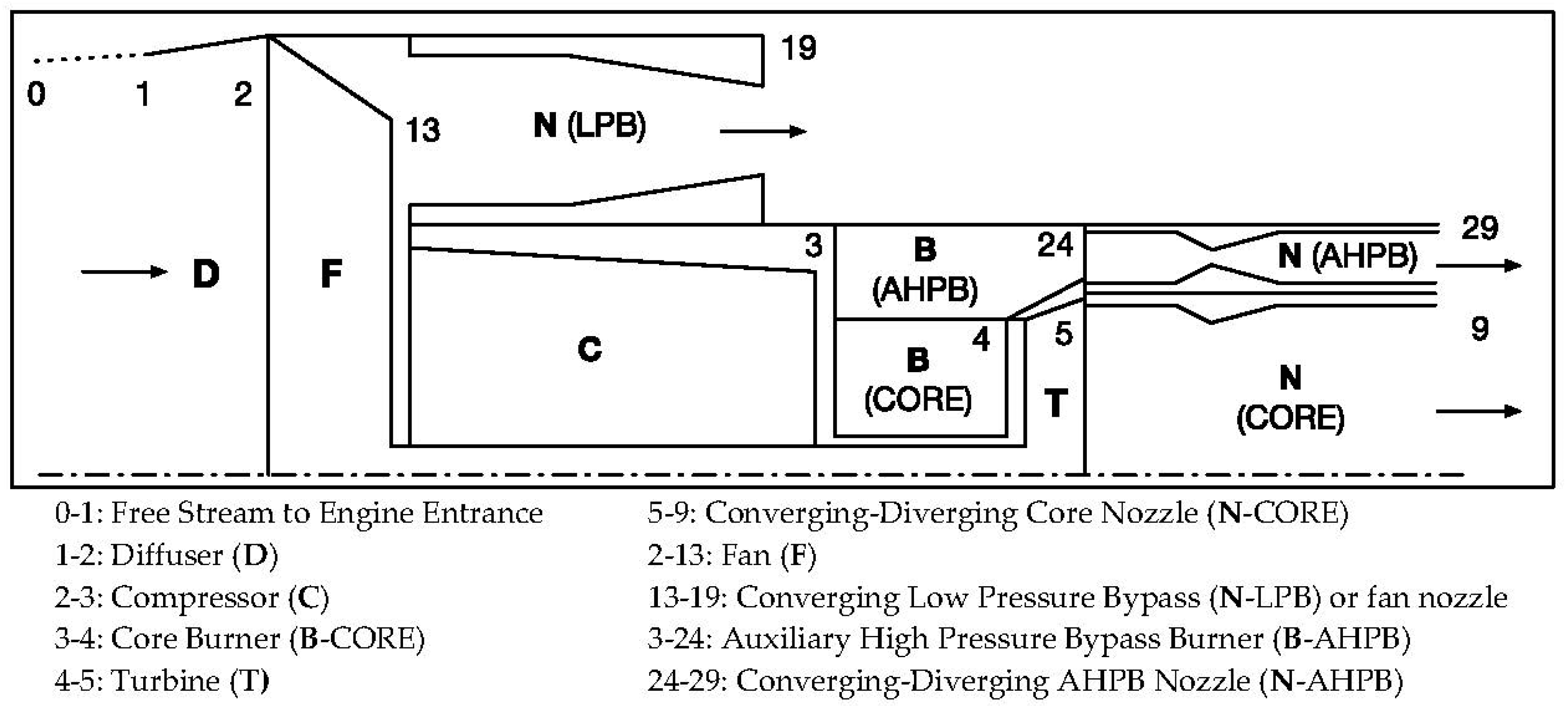
2. Configuration of the Turbofan Engine with an Auxiliary High-Pressure Bypass
3. Formulation of the Performance Parameters of the Turbofan Engine with an Auxiliary High-Pressure Bypass
- Isentropic flows without work are assumed through the diffuser and nozzles;
- Isentropic flows with work are assumed through the compressor, fan, and turbine;
- Constant-total-pressure flows are assumed in the core burner and AHPB burner;
- The core stream and AHPB stream exhaust through converging–diverging nozzles;
- The LPB stream exhausts through a converging nozzle.
3.1. Performance Parameters for Free Stream and Diffuser
3.2. Performance Parameters for Compressor, Core Burner, Fan, and Auxiliary High-Pressure Bypass Burner
- (a)
- Core stream—The compressor total pressure ratio was taken to be 50, () and constant-total-pressure combustion was assumed, i.e., . Based on these, the core stream values (Tt3, ht3, and ht4) were computed. The stagnation value of temperature, Tt3, was computed by substituting i = 2 and j = 3 into Equation (6).The total specific enthalpies, and , were computed by substituting i = 3 and i = 4, respectively, into Equation (3), and taking .
- (b)
- LPB stream—With the intent of obtaining maximum thrust and maximizing the overall efficiency [1], the fan total pressure ratio, , was varied between 1.78 and 6.10 for the LPB ratio varying from through . Also, . The stagnation value of temperature, , was computed by substituting i = 2, j = 13, and into Equation (6). The stagnation value of specific enthalpy, , was computed by substituting i = 13 into Equation (3). Additionally, and .
- (c)
- AHPB stream—The stagnation value of specific enthalpy, , was computed by substituting i = 24 and into Equation (3). Additionally, and .
3.3. Power Inputs and Outputs
3.4. Velocities and Mass Flow Rates
- (a)
- Core stream—The total pressure at station 5, , was computed by substituting i = 4 and j = 5 into Equation (6), and taking . It was also assumed that station 5 to station 9 was a perfectly expanded converging–diverging nozzle, i.e., . Additionally, as the flow was assumed to be isentropic. The temperature at the nozzle exit, , was computed by substituting i = 9 into Equation (2) and taking . The Mach number (), the speed of sound (), and the velocity of air () were computed using Equations (9)–(11). Since a perfectly expanded converging–diverging nozzle was assumed, .
- (b)
- Low-pressure bypass stream—It is to be noted that station 13 to station 19 was assumed to be a converging nozzle, i.e., M19 ≤ 1 (not perfectly expanded). Initially, was computed with the assumption that . However, if M19 ≥ 1, then M19 = 1; if not (i.e., M19 < 1), then M19 is taken to be the same as the computed value. At the LPB nozzle exit, the Mach number (M19), the speed of sound (a19), and the velocity of air (V19) were computed similarly to that in the core stream. Here, was computed as
- (c)
- AHPB stream—For the AHPB stream, station 24 to station 29 was assumed to be a perfectly expanded converging–diverging nozzle, i.e., . Additionally, , as the flow was assumed to be isentropic. The temperature at the nozzle exit, , was computed by substituting i = 29 into Equation (2) and taking . At the AHPB nozzle exit, the Mach number (M29), the speed of sound (a29), and the velocity of air (V29) were also computed similarly to the corresponding values in the core stream. Since a perfectly expanded converging–diverging nozzle was assumed, .
3.5. Thrusts, Fuel Consumption, and Efficiencies
- Thrust of the various streams—core thrust, LPB thrust, AHPB thrust, and total thrust.
- Thrust-specific fuel consumption (TSFC)
- Total specific thrust—specific thrust of the core, LPB stream, AHPB stream
- Rate of kinetic energy difference for the various streamsTotal rate of KE difference = sum of the rates of KE differences for the core, LPB, and AHPB streams.
- Efficiencies—thermal efficiency, propulsive efficiency, and overall efficiency
4. Simulation and Results
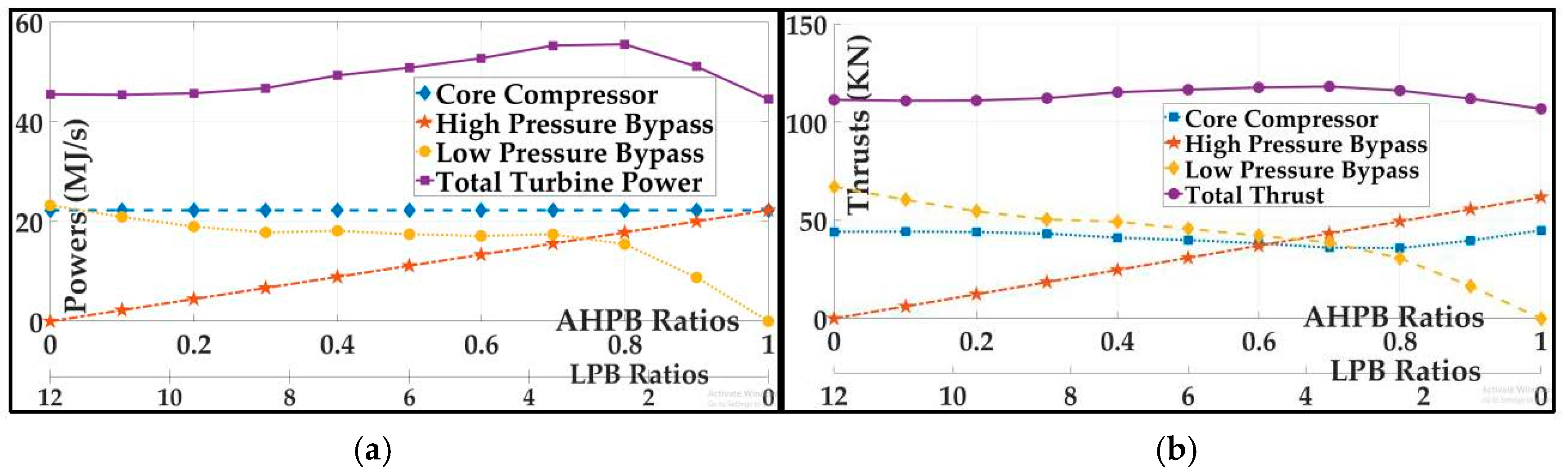
4.1. Varying Low-Pressure Bypass and Auxiliary High-Pressure Bypass Ratios for Maximizing Thrust and Overall Efficiency
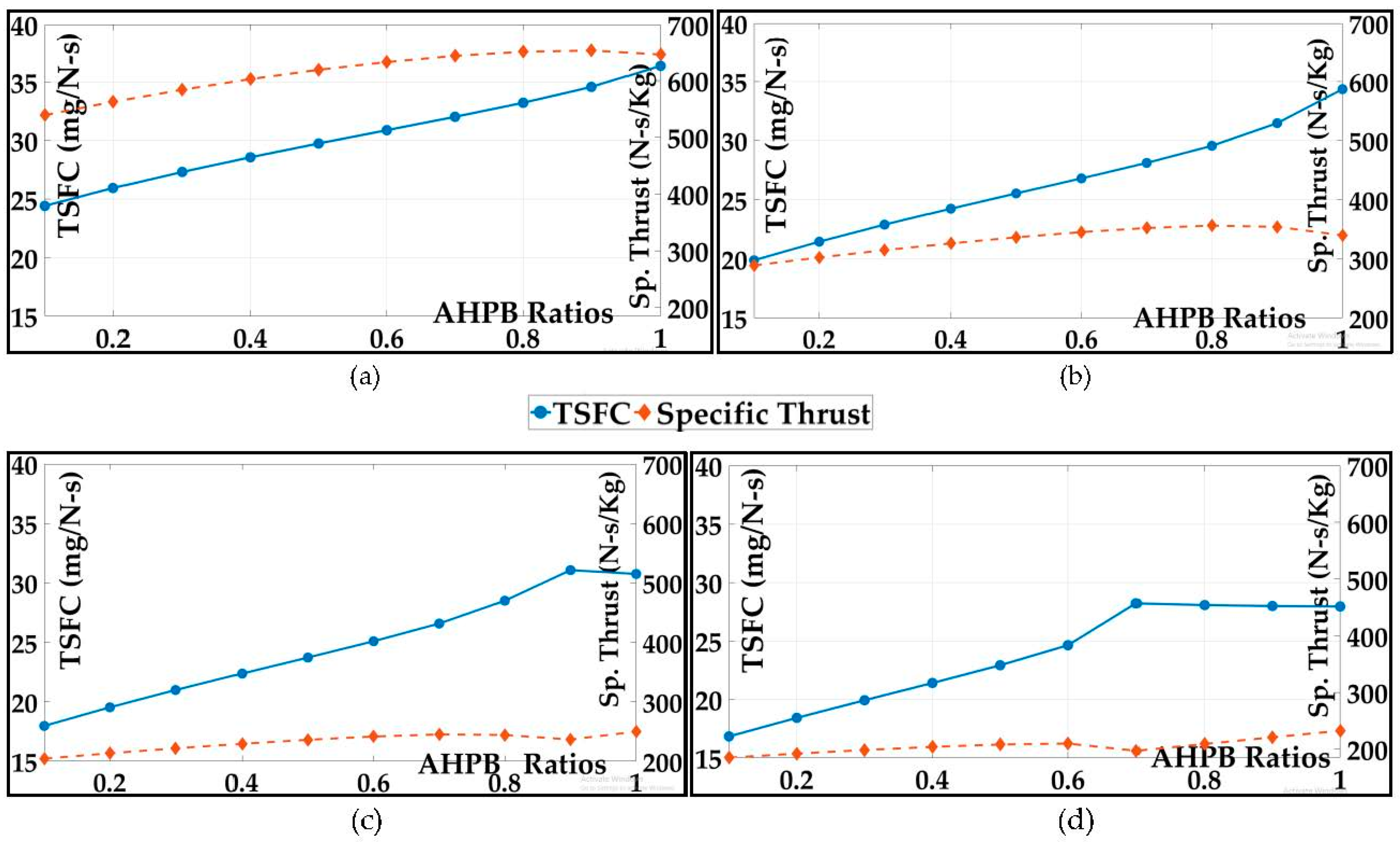
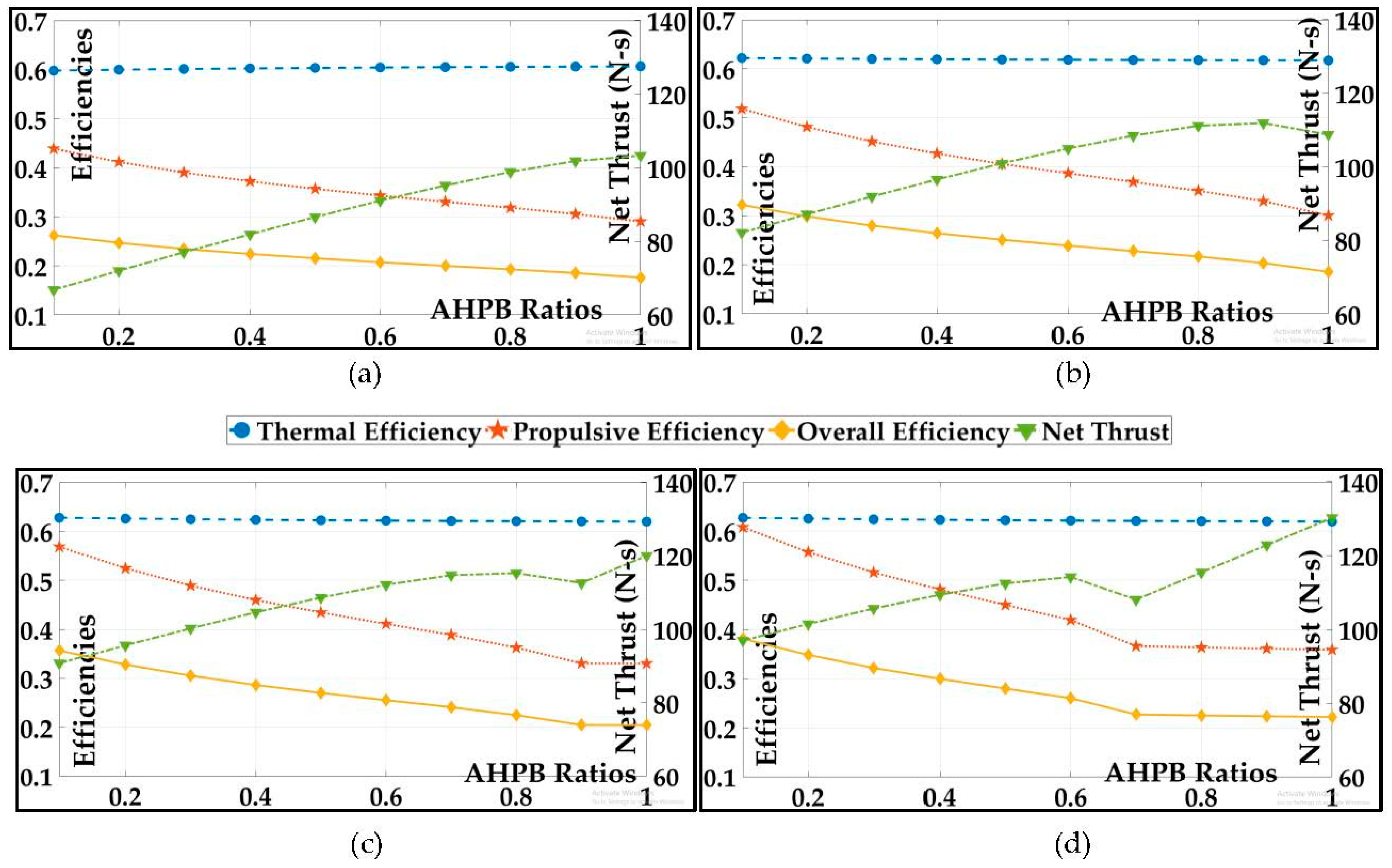
4.2. Constant Low-Pressure Bypass Ratio with Varying Auxiliary High-Pressure Bypass Ratios
4.2.1. Thrust-Specific Fuel Consumption vs. Specific Thrust
4.2.2. Efficiencies vs. Net Thrust
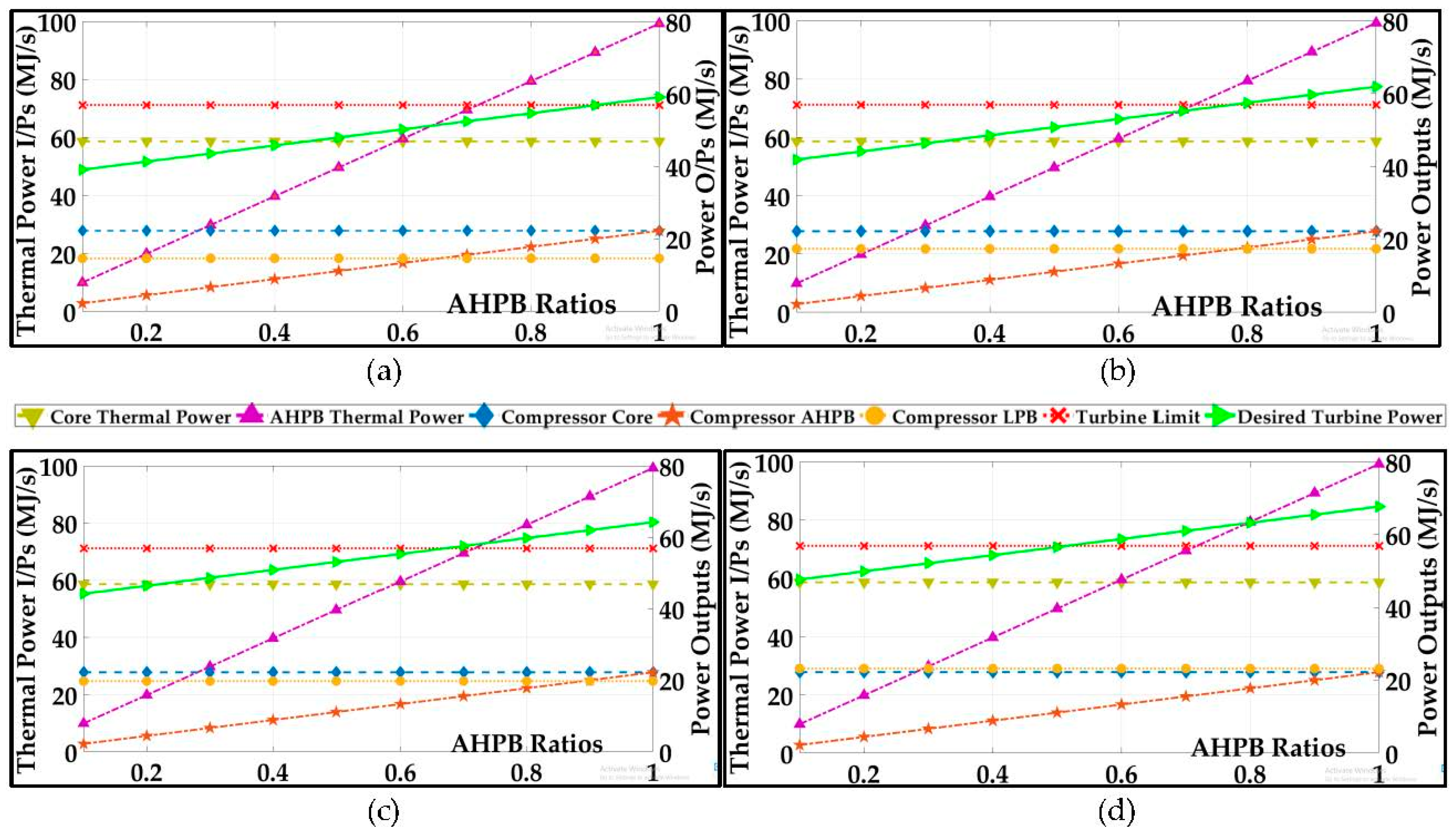
4.2.3. Power Input vs. Power Output
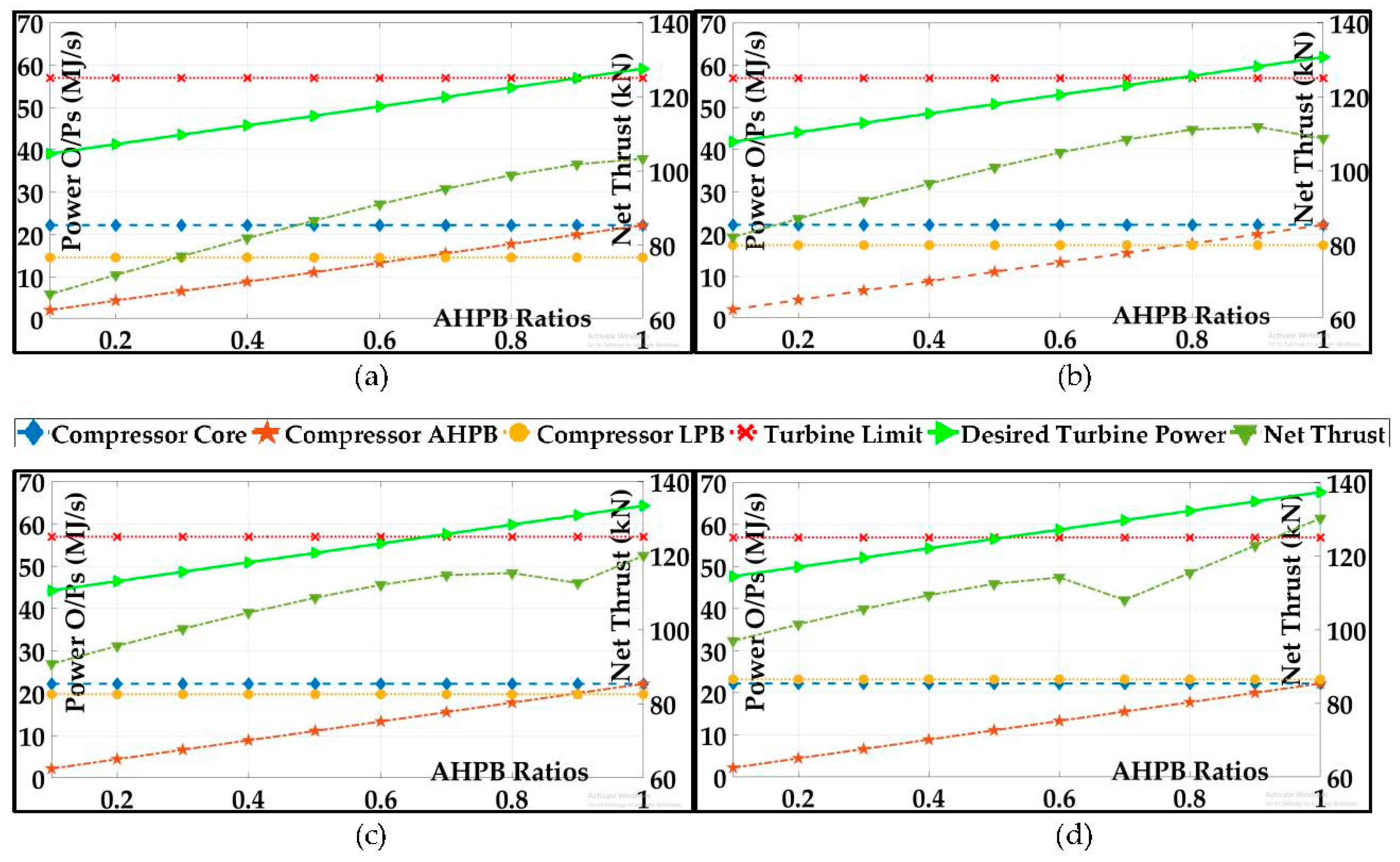
4.2.4. Power Output vs. Net Thrust
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| specific heat at constant pressure | |
| specific heat at constant volume | |
| ratio of specific heat at constant pressure to specific heat at constant volume | |
| perfect gas constant | |
| Mach number | |
| absolute pressure | |
| total (stagnation) pressure | |
| absolute temperature | |
| total (stagnation) temperature | |
| mass flow rate | |
| specific enthalpy | |
| total (stagnation) specific enthalpy | |
| low-pressure bypass ratio | |
| auxiliary high-pressure bypass ratio | |
| speed of sound | |
| flow velocity | |
| thrust | |
| efficiency | |
| calorific value | |
| compressor pressure ratio | |
| fan pressure ratio | |
| TSFC | thrust-specific fuel consumption |
| Subscripts | |
| i | station number |
| 1i | 1 corresponds to low-pressure bypass stream or fan stream |
| 2i | 2 corresponds to auxiliary high-pressure bypass stream |
| f | fuel |
| core | core stream |
| AHPB | auxiliary high-pressure stream |
| LPB | Low-pressure stream or fan stream |
| eff | effective |
References
- Mattingly, J.D.; Boyer, K.M. Elements of Propulsion: Gas Turbines and Rockets, 2nd ed.; AIAA Education Series; American Institute of Aeronautics & Astronautics: Reston, VA, USA, 2016. [Google Scholar]
- Raymer, D.P. Aircraft Design: A Conceptual Approach, 5th ed.; AIAA Education Series; American Institute of Aeronautics & Astronautics: Reston, VA, USA, 2012. [Google Scholar]
- Rutledge, J.L.; Polanka, M.D. Efficiency of an Ideal Brayton Cycle with a Constant-Volume Interturbine Burner. J. Propuls. Power 2015, 31, 970–976. [Google Scholar] [CrossRef]
- Lee, A.S.; Singh, R.; Probert, S.D. Two-combustor Engines’ Performances under Design and Off-design Conditions. In Proceedings of the 45th AIAA/ASME/ISAE/IASEE Joint Propulsion Conference & Exhibit, Denver, CO, USA, 2–5 August 2009; pp. 2009–4838. [Google Scholar] [CrossRef]
- Sirignano, W.A.; Liu, W. Performance Increases for Gas-Turbine Engines through Combustion Inside the Turbine. J. Propuls. Power 1999, 15, 111–118. [Google Scholar] [CrossRef]
- MacIsaac, B.; Langston, R. Gas Turbine Propulsion Systems, 1st ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Hadhazy, A. Fly the Electric Skies. AIAA Bulletin, Aerospace America. July/August 2017. Available online: https://aerospaceamerica.aiaa.org/features/fly-the-electric-skies/ (accessed on 25 October 2017).
- Daggett, D.L.; Brown, S.T.; Kawai, R.T. Ultra-Efficient Engine Diameter Study; NASA/CR-2003-003; Boeing Commercial Airplane Group; National Aeronautics and Space Administration: Seattle, WA, USA, May 2003. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20030061085.pdf (accessed on 13 January 2019).
- Farokhi, S. Aircraft Propulsion, 2nd ed.; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]

| Input parameters | |||||
| Air properties | |||||
| Gas properties | |||||
| Other parameters | K | K | kg/s | kg/s | |
| Units | Turbofan with LPB = 10 and AHPB = 0.2 | Turbofan with LPB = 6 and AHPB = 0.5 | Turbofan with LPB = 2 and AHPB = 0.8 | |
|---|---|---|---|---|
| Total air mass flow rate | kg·s−1 | 448 | 300 | 136 |
| AHPB ratio | 0.2 | 0.5 | 0.8 | |
| LPB ratio | 10 | 6 | 2 | |
| Total fuel mass flow rate | kg·s−1 | 2.1199 + 0.3148 (core + AHPB) | 2.1199 + 0.7871 (core + AHPB) | 2.1199 + 1.2594 (core + AHPB) |
| Core jet | m·s−1 | 543.0468 | 664.5678 | 1054.6523 |
| AHPB jet | m·s−1 | 1746.0344 | 1746.0344 | 1746.0344 |
| LPB jet | m·s−1 | 538.1605 | 589.4479 | 654.4585 |
| Net thrust | kN | 132.0586 | 124.9973 | 113.9338 |
| TSFC | mg·s−1·N−1 | 18.4370 | 23.2568 | 29.6603 |
| Specific thrust | N·s·kg−1 | 294.7736 | 416.6578 | 749.5648 |
| Thermal power input | Mega Watt (MW) | 102.2602 | 122.0956 | 141.9310 |
| Propulsive power output | MW | 35.5487 | 33.6479 | 30.6698 |
| KE rate difference | MW | 60.5767 | 71.8188 | 85.7482 |
| Thermal efficiency | 59.24% | 58.82% | 60.42% | |
| Propulsive efficiency | 58.68% | 46.86% | 35.77% | |
| Overall efficiency | 34.76% | 27.56% | 21.61% | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asundi, S.A.; Ali, S.F. Parametric Study of a Turbofan Engine with an Auxiliary High-Pressure Bypass. Int. J. Turbomach. Propuls. Power 2019, 4, 2. https://doi.org/10.3390/ijtpp4010002
Asundi SA, Ali SF. Parametric Study of a Turbofan Engine with an Auxiliary High-Pressure Bypass. International Journal of Turbomachinery, Propulsion and Power. 2019; 4(1):2. https://doi.org/10.3390/ijtpp4010002
Chicago/Turabian StyleAsundi, Sharanabasaweshwara A., and Syed Firasat Ali. 2019. "Parametric Study of a Turbofan Engine with an Auxiliary High-Pressure Bypass" International Journal of Turbomachinery, Propulsion and Power 4, no. 1: 2. https://doi.org/10.3390/ijtpp4010002
APA StyleAsundi, S. A., & Ali, S. F. (2019). Parametric Study of a Turbofan Engine with an Auxiliary High-Pressure Bypass. International Journal of Turbomachinery, Propulsion and Power, 4(1), 2. https://doi.org/10.3390/ijtpp4010002




