Optimization of the LS89 Axial Turbine Profile Using a CAD and Adjoint Based Approach †
Abstract
1. Introduction
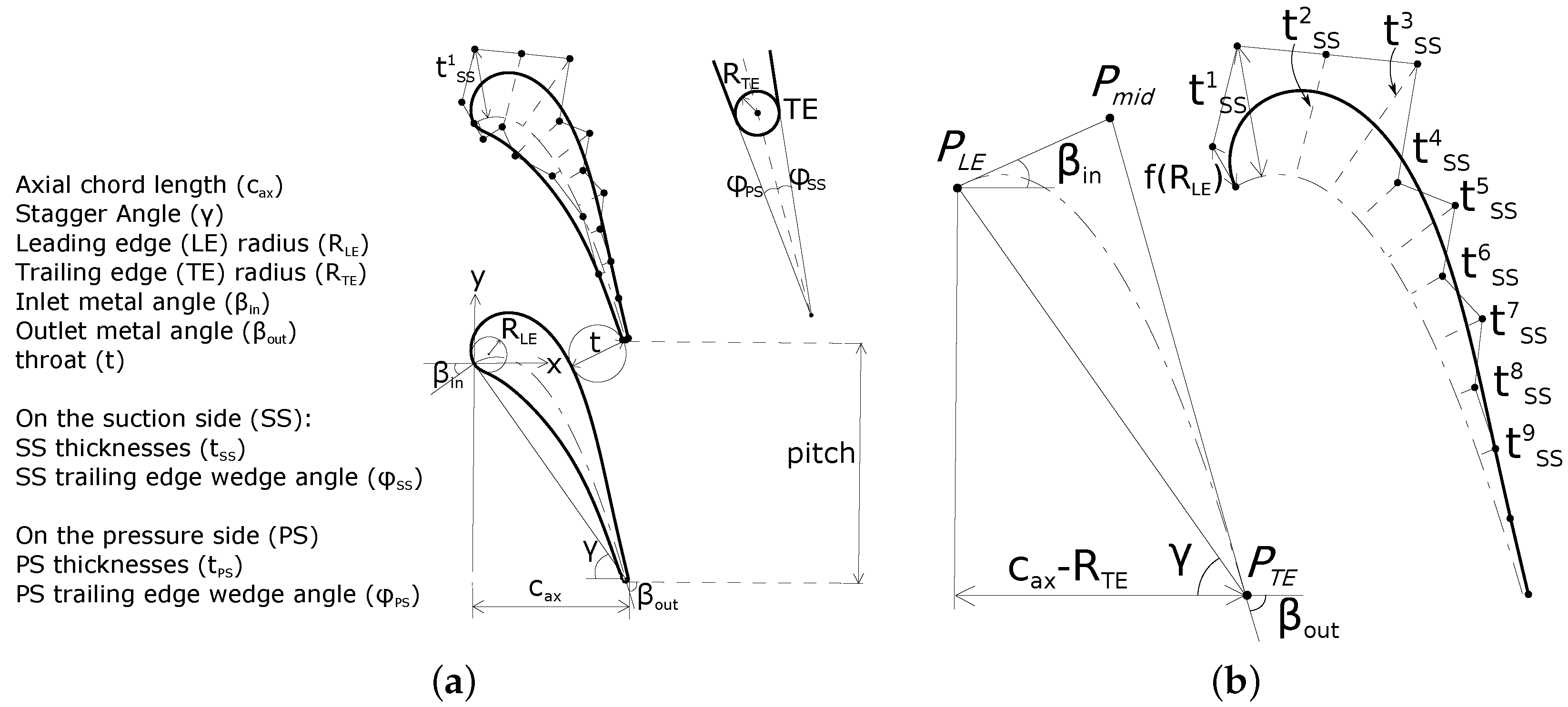
- The optimal shape remains defined within the CAD tool. The optimization problem herein is expressed by CAD parameters that are directly used in defining the CAD geometry by means of Bézier and B-spline curves.
- The in-house CAD and grid generation tools are automatically differentiated in forward mode to obtain the exact derivatives of the grid coordinates with respect to the CAD-based design parameters. This allows for an accurate prediction of the sensitivities and circumvention of the errors introduced by finite differences.
- The trailing edge thickness and axial chord length are kept fixed as manufacturing constraints and the exit flow angle is considered as an aerodynamic constraint.
2. Computer-Aided Design-Based Parametrization
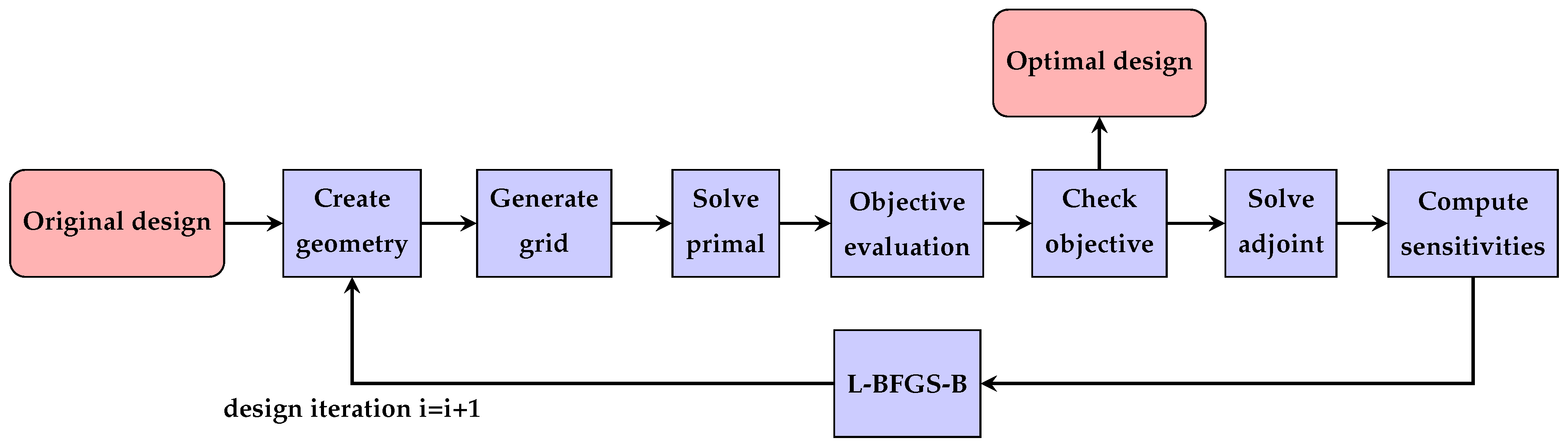
3. Optimization
3.1. Grid Generation
3.2. Flow and Adjoint Solvers
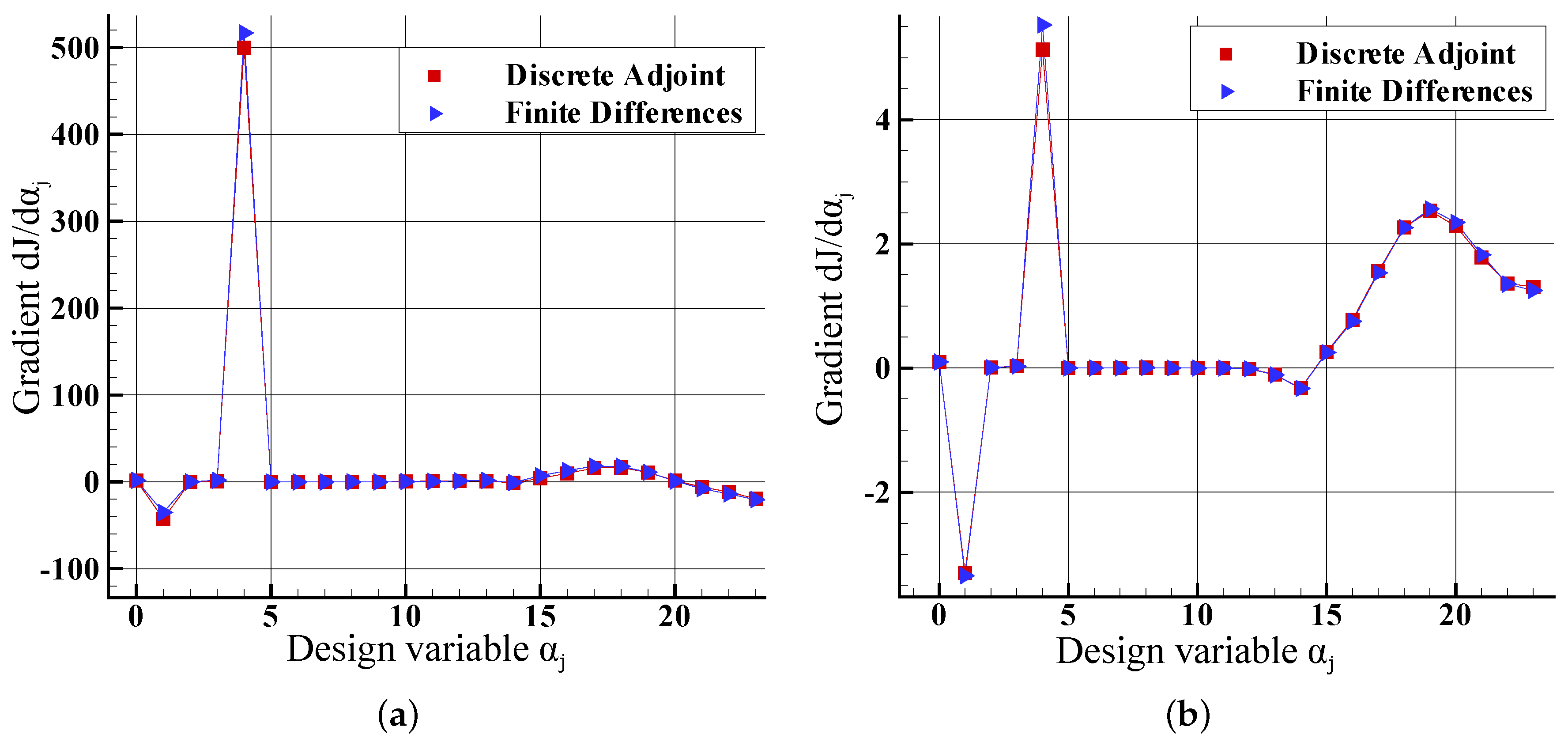
3.3. Gradient Computation
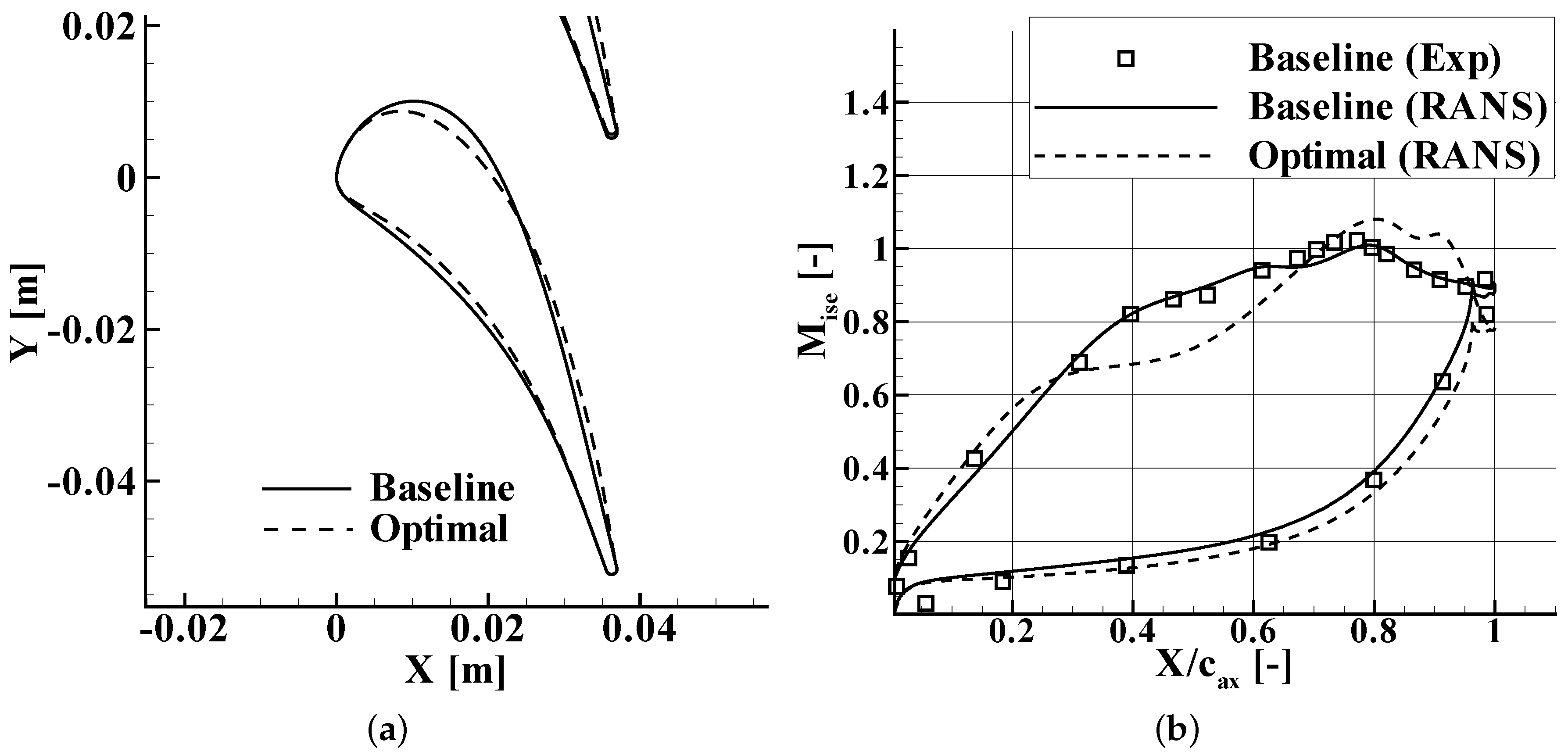
4. Results
4.1. Zweifel Loading Coefficient
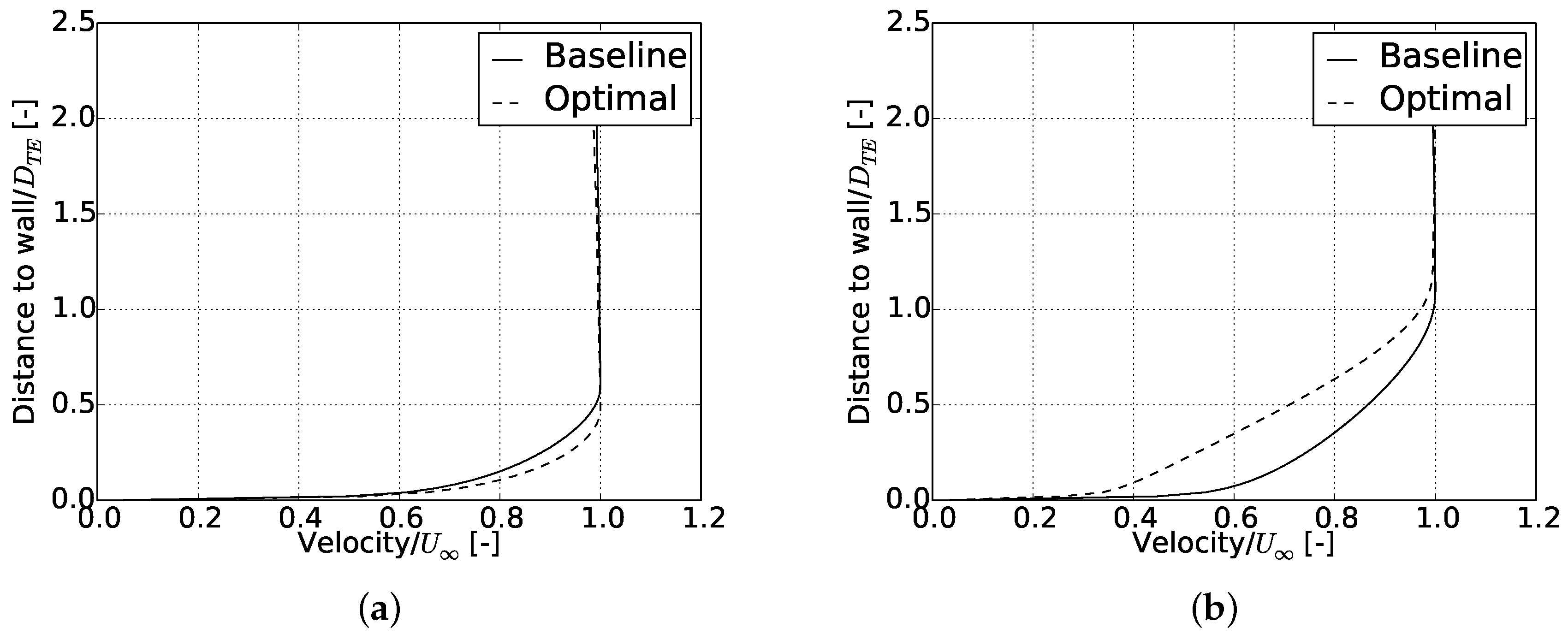
4.2. Boundary Layer Parameters
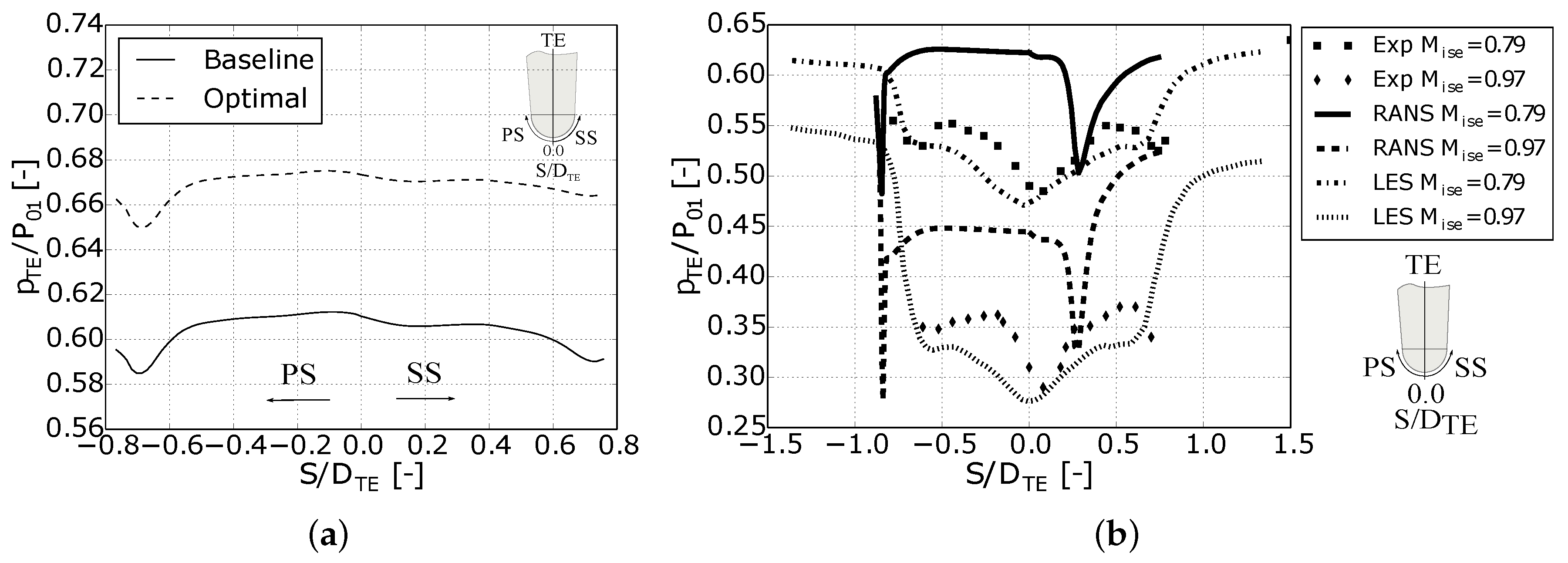
4.3. Base Pressure
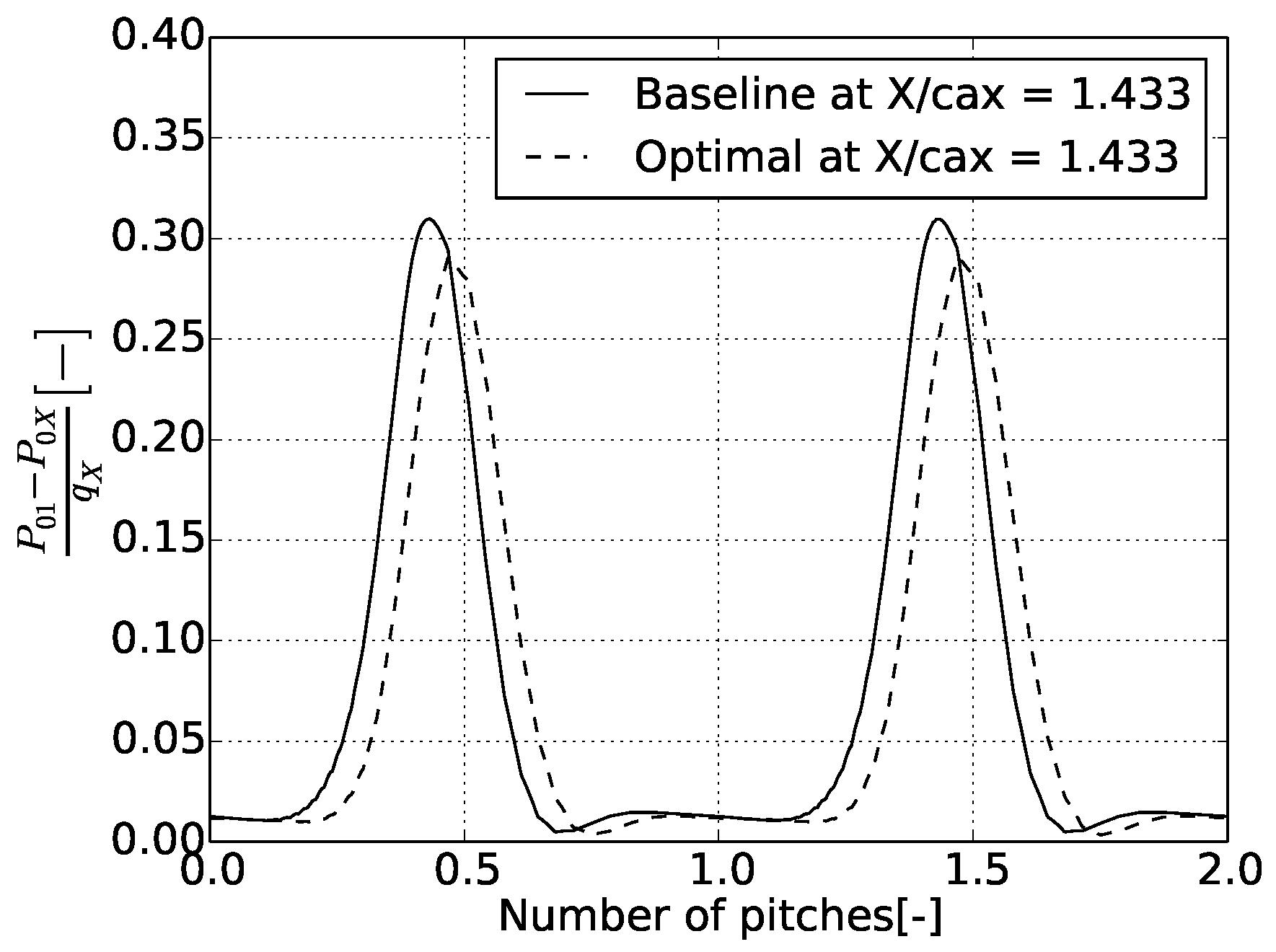
4.4. Profile Losses
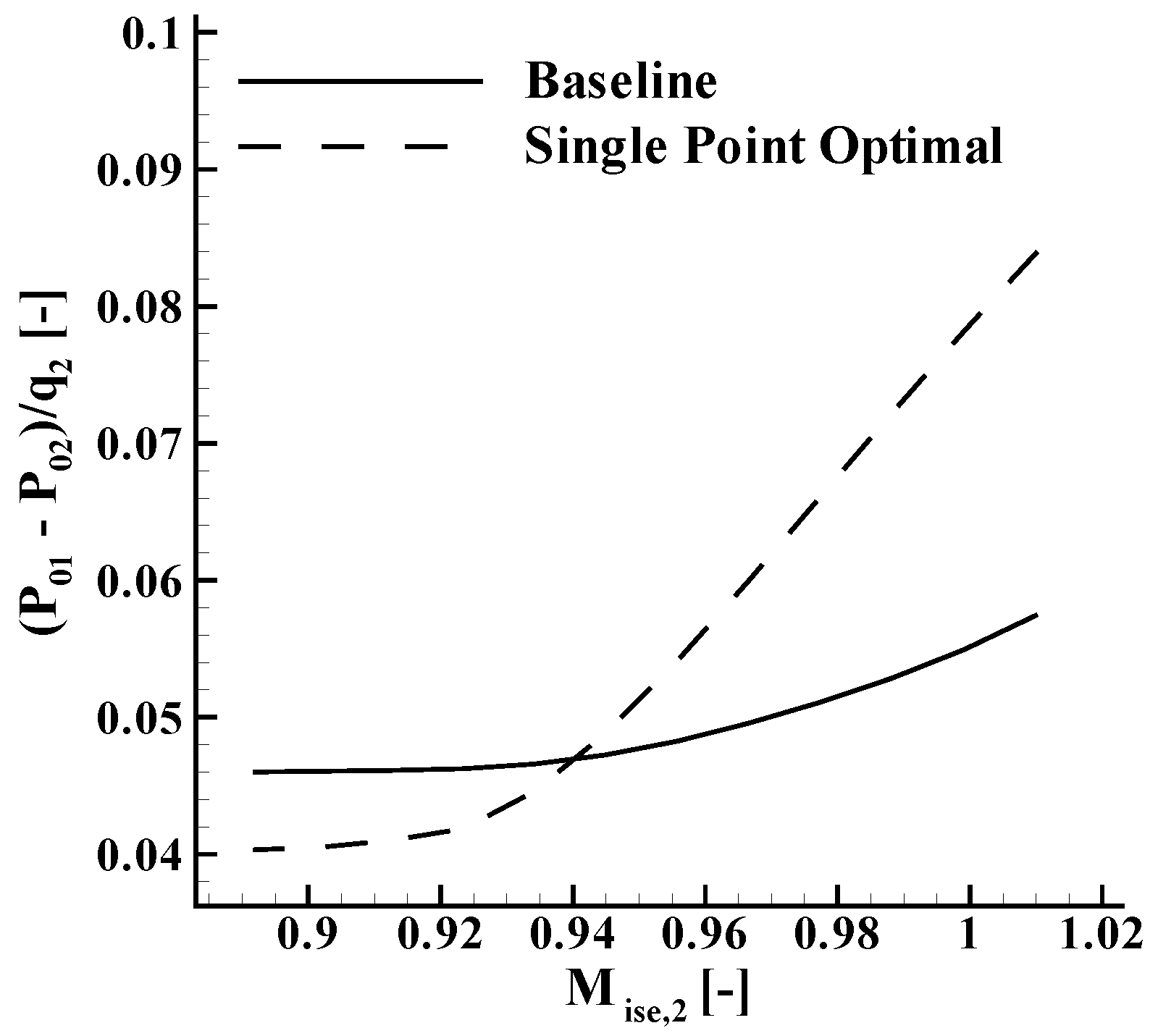
4.5. Off-Design Performance
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Roman Symbols | |
| Axial chord length | |
| Outlet (downstream) static pressure | |
| Base pressure coefficient | |
| Base pressure | |
| Trailing edge thickness | |
| Pressure side static pressure | |
| g | Pitch |
| Suction side static pressure | |
| H | Shape factor |
| dynamic head downstream at the X coord. plane | |
| Entropy generation | |
| Leading edge radius | |
| Exit flow angle | |
| Trailing edge radius | |
| Single point pseudo cost function | |
| t | Throat height |
| Mass flow | |
| PS thickness | |
| Isentropic Mach number | |
| SS thickness | |
| Inlet total pressure | |
| Grid x,y,z coordinates | |
| Outlet (downstream) total pressure | |
| Zweifel coefficient | |
| Greek Symbols | |
| Design vector | |
| Adjoint sensitivity vector | |
| Inlet angle | |
| Grid sensitivity vector | |
| Outlet angle | |
| Pressure side trailing edge wedge angle | |
| Boundary layer thickness | |
| Suction side trailing edge wedge angle | |
| Displacement thickness | |
| Solidity | |
| Distance to the inlet of the grid domain | |
| Momentum thickness | |
| distance to the outlet of the grid domain | |
| Downstream loss coefficient | |
| Stagger angle | |
| Profile losses | |
| Performance sensitivity vector | |
| Abbrevations | |
| AD | Algorithmic Differentiation |
| ADOL–C | Automatic Differentiation by OverLoading in C++ |
| CAD | Computer Aided Design |
| LES | Large Eddy Simulation |
| PS | Pressure Side |
| RANS | Reynolds–averaged Navier–Stokes |
| SS | Suction Side |
| TE | Trailing edge |
| URANS | Unsteady Reynolds-averaged Navier-Stokes |
References
- Peter, J.E.; Dwight, R.P. Numerical sensitivity analysis for aerodynamic optimization: A survey of approaches. Comput. Fluids 2011, 39, 373–391. [Google Scholar] [CrossRef]
- Jameson, A. Efficient aerodynamic shape optimization. In Proceedings of the 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Albany, NY, USA, 30 August–1 September 2004. AIAA Paper 4369. [Google Scholar]
- Becker, G.; Schäfer, M.; Jameson, A. An advanced NURBS fitting procedure for post-processing of grid-based shape optimizations. In Proceedings of the 49th AIAA Aerospace Sciences Meeting, Orlando, FL, USA, 4–7 January 2011. [Google Scholar]
- Leal, N.; Leal, E.; Branch, J.W. Simple method for constructing nurbs surfaces from unorganized points. In Proceedings of the 19th International Meshing Round Table, Chattanooga, TN, USA, 3–6 October 2010; Springer: Berlin, Germany, 2010; pp. 161–175. [Google Scholar]
- Samareh, J.A. Survey of shape parameterization techniques for high-fidelity multidisciplinary shape optimization. AIAA J. 2001, 39, 877–884. [Google Scholar] [CrossRef]
- Braibant, V.; Fleury, C. Shape optimal design using b-splines. Comput. Methods Appl. Mech. Eng. 1984, 44, 247–267. [Google Scholar] [CrossRef]
- Agarwal, D.; Robinson, T.; Armstrong, C.G.; Marques, S.; Vasilopoulos, I.; Meyer, M. Parametric design velocity computation for CAD-based design optimization using adjoint methods. Eng. Comput. 2018, 34, 225–239. [Google Scholar] [CrossRef]
- Griewank, A.; Walther, A. Evaluating: Principles and Techniques of Algorithmic Differentiation; SIAM: Philadelphia, PA, USA, 2008. [Google Scholar]
- Sanchez Torreguitart, I.; Verstraete, T.; Mueller, L. CAD kernel and grid generation algorithmic differentiation for turbomachinery adjoint optimization. In Proceedings of the 7th European Congress on Computational Methods in Applied Sciences and Engineering, Crete Island, Greece, 5–10 June 2016. [Google Scholar]
- Arts, T.; Lambert De Rouvroit, M.; Rutherford, A. Aero-thermal investigation of a highly loaded transonic linear turbine guide vane cascade. In A Test Case for Inviscid and Viscous Flow Computations; NASA STI/Recon Technical Report N 91; NASA: Washington, DC, USA, 1990; p. 23437. [Google Scholar]
- Van den Braembussche, R.; Leonard, O.; Nekmouche, L. Subsonic and transonic blade design by means of analysis codes. In Computational Methods for Aerodynamic Design (Inverse) and Optimization; AGARD: Paris, France, 1990; p. 463. [Google Scholar]
- Montanelli, H.; Montagnac, M.; Gallard, F. Gradient span analysis method: Application to the multipoint aerodynamic shape optimization of a turbine cascade. J. Turbomach. 2015, 137, 091006. [Google Scholar] [CrossRef]
- Verstraete, T. Cado: A computer aided design and optimization tool for turbomachinery applications. In Proceedings of the 2nd International Conference on Engineering Optimization, Lisbon, Portugal, 6–9 September 2010. [Google Scholar]
- Pierret, S. Designing Turbomachinery Blades by Means of the Function Approximation Concept Based on Artificial Neural Network, Genetic Algorithm, and the Navier-Stokes Equations. Ph.D. Thesis, Von Karman Institute for Fluid Dynamics, Sint-Genesius-Rode, Belgium, 1999; p. 12. [Google Scholar]
- Zhu, C.; Byrd, R.H.; Lu, P.; Nocedal, J. Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization. ACM Trans. Math. Softw. 1997, 23, 550–560. [Google Scholar] [CrossRef]
- Jones, E.; Oliphant, T.; Peterson, P. SciPy: Open Source Scientific Tools for Python. 2001. Available online: https://www.scipy.org/ (accessed on 8 February 2017).
- Roe, P.L. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Venkatakrishnan, V. On the accuracy of limiters and convergence to steady state solutions. In Proceedings of the 31st Aerospace Sciences Meeting, Reno, NV, USA, 11–14 January 1993. AIAA Paper 93-0880. [Google Scholar]
- Harten, A.; Hyman, J.M. Self-adjusting grid methods for one-dimensional hyperbolic conservation laws. J. Comput. Phys. 1983, 50, 235–269. [Google Scholar] [CrossRef]
- Allmaras, S.R.; Johnson, F.T.; Spalart, P.R. Modifications and clarifications for the implementation of the Spalart-Allmaras turbulence model. In Proceedings of the ICCFD7-1902, 7th International Conference on Computational Fluid Dynamics, Hawaii, HI, USA, 9–13 July 2012. [Google Scholar]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications, 2nd ed.; Elsevier Science Ltd.: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Xu, S.; Radford, D.; Meyer, M.; Müller, J.-D. Stabilisation of Discrete Steady Adjoint Solvers. J. Comput. Phys. 2015, 299, 175–195. [Google Scholar] [CrossRef]
- Walther, A.; Griewank, A. A Package for the Automatic Differentiation of Algorithms Written in C/C+. Available online: https://projects.coin-or.org/ADOL-C (accessed on 26 June 2017).
- Zweifel, O. The spacing of turbo-machine blading, especially with large angular deflection. Brown Boveri Rev. 1945, 32, 436–444. [Google Scholar]
- Xu, L.; Denton, J.D. The base pressure and loss of a family of four turbine blades. ASME J. Turbomach. 1988, 110, 9–17. [Google Scholar] [CrossRef]
- Sieverding, C.H.; Stanislas, M.; Snoek, J. The base pressure problem in transonic turbine cascades. In Proceedings of the ASME 1979 International Gas Turbine Conference and Exhibit and Solar Energy Conference, San Diego, CA, USA, 12–15 March 1979; American Society of Mechanical Engineers: New York, NY, USA, 1979; p. V01BT02A019. [Google Scholar]
- Sieverding, C.H.; Richard, H.; Desse, J.M. Turbine blade trailing edge flow characteristics at high subsonic outlet mach number. J. Turbomach. 2003, 125, 298–309. [Google Scholar] [CrossRef]
- Vagnoli, S.; Verstraete, T.; Mateos, B.; Sieverding, C.H. Prediction of the unsteady turbine trailing edge wake flow characteristics and comparison with experimental data. Proc. Inst. Mech. Eng. Part A 2015. [Google Scholar] [CrossRef]
- Denton, J.D. Loss mechanisms in turbomachines. In Proceedings of the ASME 1993 International Gas Turbine and Aeroengine Congress and Exposition, Cincinnati, OH, USA, 24–27 May 1993; American Society of Mechanical Engineers: New York, NY, USA, 1993; p. V002T14A001. [Google Scholar]
- Corriveau, D.; Sjolander, S.A. Influence of loading distribution on the performance of transonic high pressure turbine blades. In Proceedings of the ASME Turbo Expo 2003, Collocated with the 2003 International Joint Power Generation Conference, Atlanta, GA, USA, 16–19 June 2003; American Society of Mechanical Engineers: New York, NY, USA, 2003; pp. 125–135. [Google Scholar]
- Torreguitart, I.S.; Verstraete, T.; Mueller, L. CAD and Adjoint based Multipoint Optimization of an Axial Turbine Profile. In Proceedings of the 2017 International Conference on Evolutionary and Deterministic Methods for Design Optimization and Control with Applications to Industrial and Societal Problems (EUROGEN 2017), Madrid, Spain, 13–15 September 2017. [Google Scholar]
| Units | Baseline at | Optimal at | Baseline at | Optimal at | |
|---|---|---|---|---|---|
| [-] | 0.501 | 0.390 | 0.939 | 1.11 | |
| [-] | 0.104 | 0.079 | 0.206 | 0.346 | |
| [-] | 0.0557 | 0.0405 | 0.1186 | 0.1780 | |
| H | [-] | 1.86 | 1.96 | 1.74 | 1.95 |
| Units | Baseline | Optimal | Variation | |
|---|---|---|---|---|
| [-] | −0.0016 | −0.0065 | 302.2% | |
| [-] | 0.0066 | 0.0095 | 43.5% | |
| [-] | 0.0010 | 0.0012 | 21% | |
| [-] | 0.0060 | 0.0042 | −30% |
| Acronyms | Units | Baseline | Optimal | Variation | |
|---|---|---|---|---|---|
| Entropy generation | [Pa/(kg/m3)] | 826.7 | 731.0 | −11.6% | |
| Exit flow angle | [deg] | 74.89 | 74.89 | −0.01% | |
| Mass flow | [kg/s] | 0.008 | 0.009 | +1.2% | |
| Total pressure losses | [kPa] | 2.47 | 2.07 | −16.3% | |
| Downstream loss coeff | [-] | 0.02986 | 0.02500 | −16.3% | |
| Profile losses | [-] | 0.0060 | 0.0042 | −30% | |
| Zweifel coefficient | [-] | 0.67 | 0.81 | +21.2% | |
| Solidity | [-] | 1.118 | 1.108 | −0.9% | |
| Pitch | g | [m] | 0.0575 | 0.0580 | +0.9% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution NonCommercial NoDerivatives (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Sanchez Torreguitart, I.; Verstraete, T.; Mueller, L. Optimization of the LS89 Axial Turbine Profile Using a CAD and Adjoint Based Approach †. Int. J. Turbomach. Propuls. Power 2018, 3, 20. https://doi.org/10.3390/ijtpp3030020
Sanchez Torreguitart I, Verstraete T, Mueller L. Optimization of the LS89 Axial Turbine Profile Using a CAD and Adjoint Based Approach †. International Journal of Turbomachinery, Propulsion and Power. 2018; 3(3):20. https://doi.org/10.3390/ijtpp3030020
Chicago/Turabian StyleSanchez Torreguitart, Ismael, Tom Verstraete, and Lasse Mueller. 2018. "Optimization of the LS89 Axial Turbine Profile Using a CAD and Adjoint Based Approach †" International Journal of Turbomachinery, Propulsion and Power 3, no. 3: 20. https://doi.org/10.3390/ijtpp3030020
APA StyleSanchez Torreguitart, I., Verstraete, T., & Mueller, L. (2018). Optimization of the LS89 Axial Turbine Profile Using a CAD and Adjoint Based Approach †. International Journal of Turbomachinery, Propulsion and Power, 3(3), 20. https://doi.org/10.3390/ijtpp3030020





