Full Annulus Simulations of a Transonic Axial Compressor Stage with Distorted Inflow at Transonic and Subsonic Blade Tip Speed †
Abstract
:1. Introduction
2. Methods
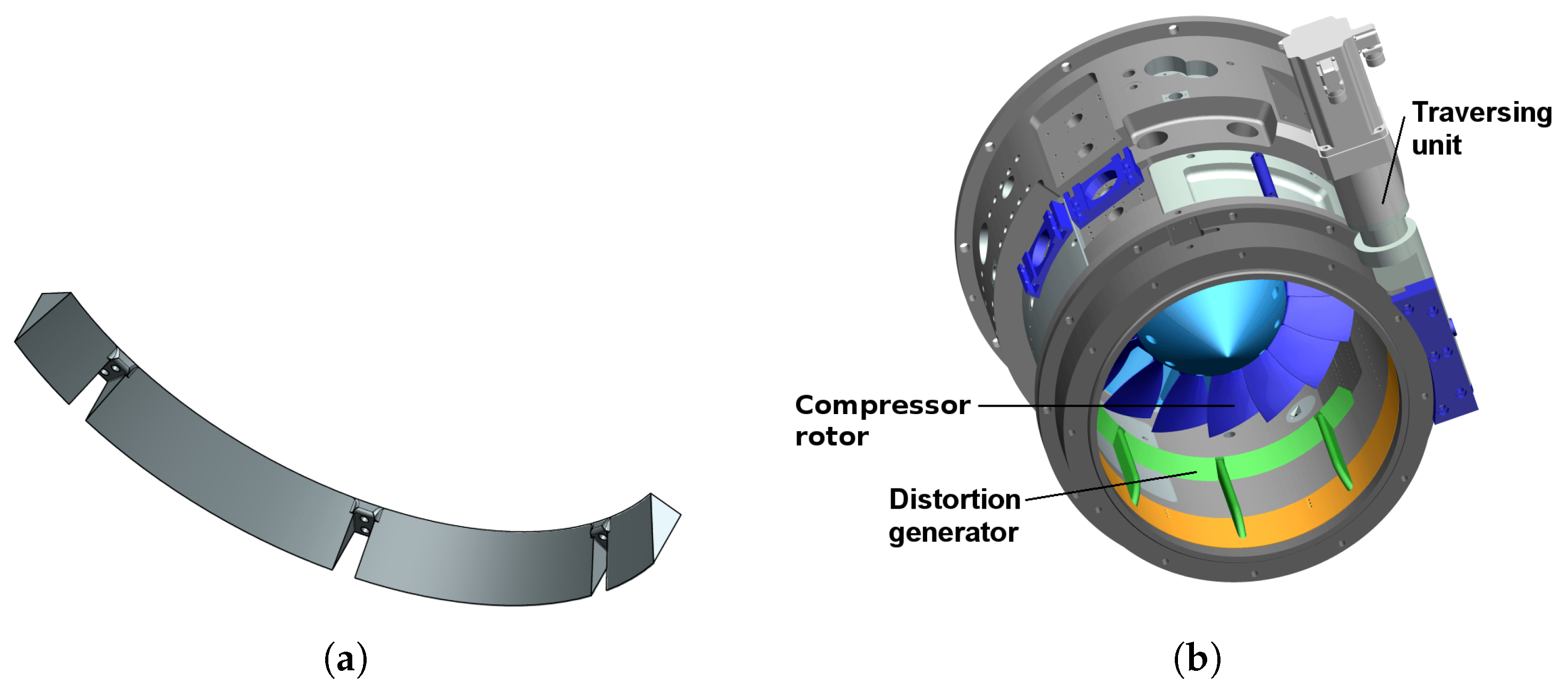
2.1. Compressor
2.2. Distortion Generator
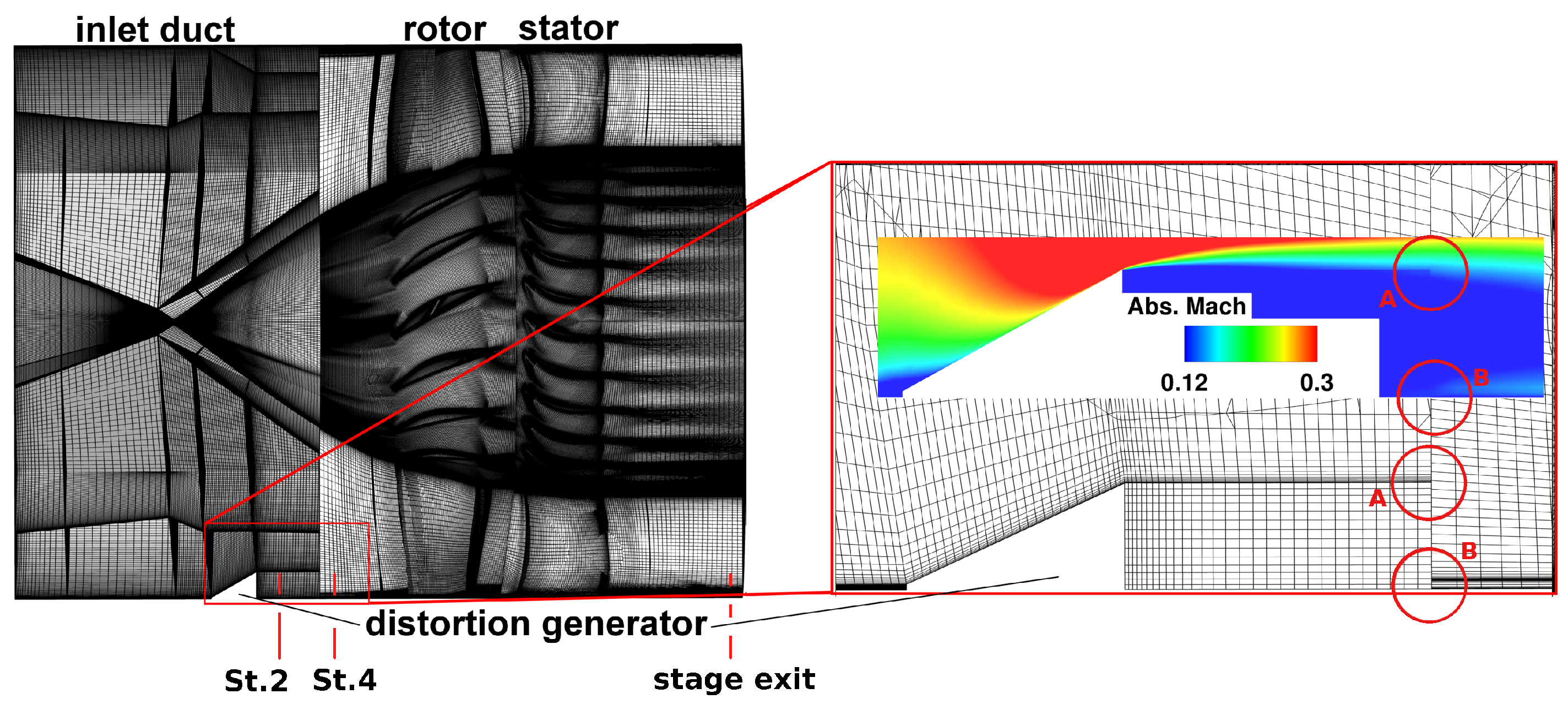
2.3. Meshing Procedures
2.4. Flow Solver
3. Results
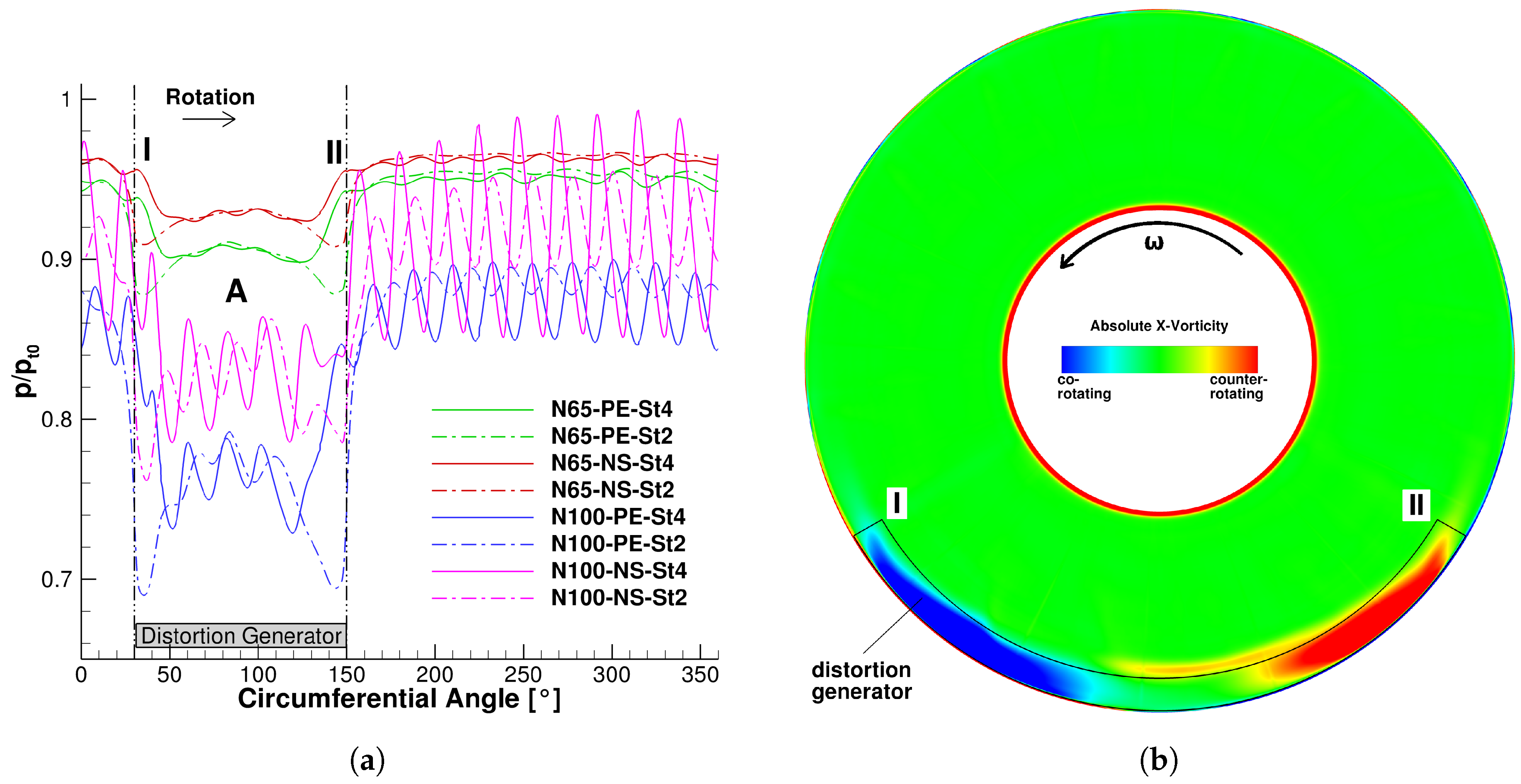
3.1. The Distortion in General
- Co-rotating swirl at the entry of the distortion
- Counter-rotating swirl at the exit of the distortion
- Alteration and change of shape of the distortion on its way downstream through the compressor
- Variation of incidence and blade loading
- Mass flow redistribution
3.2. Interaction of the Distorted Flow and the Rotor
Stretching and Transportation of the Distorted Flow in the Circumferential Direction
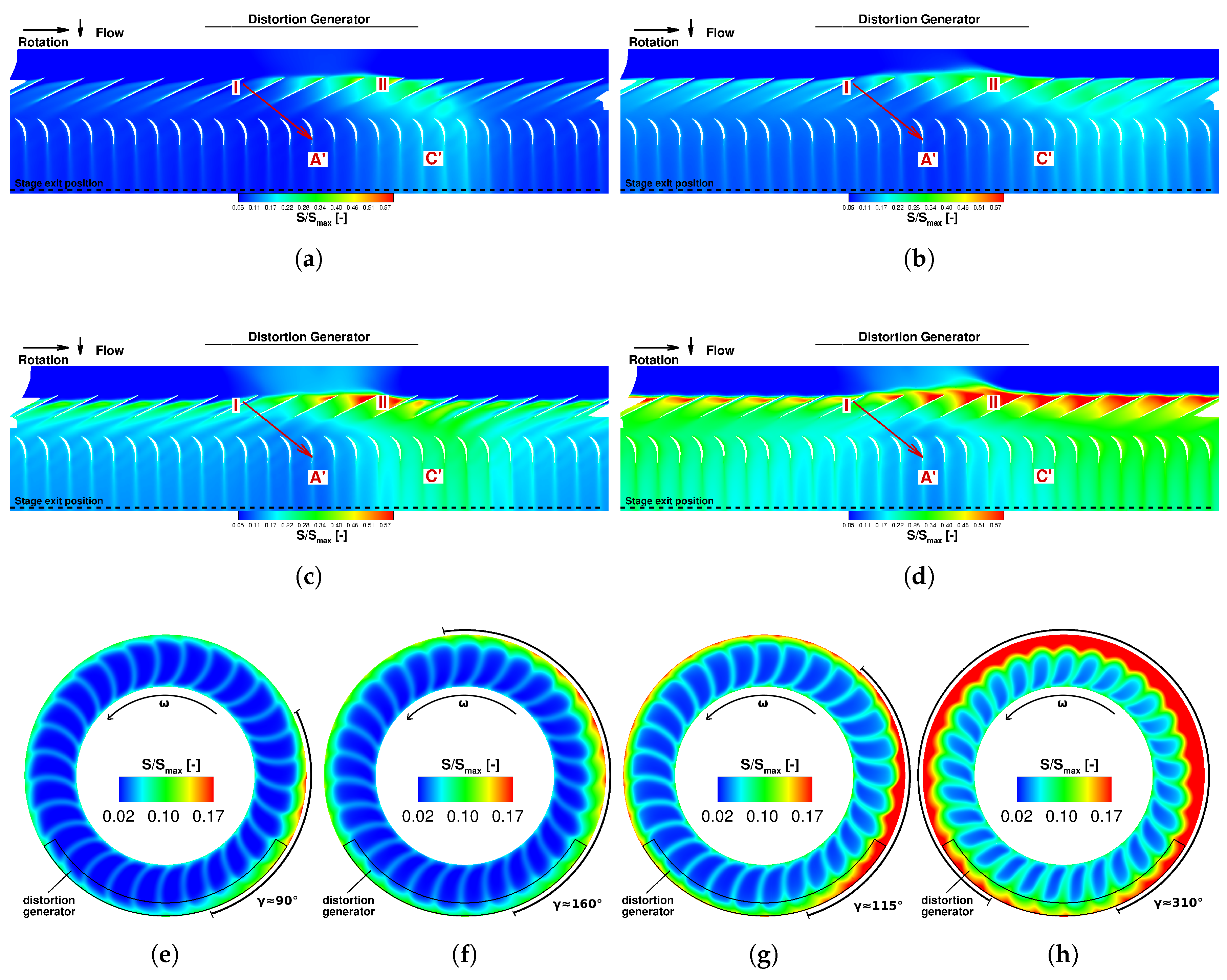
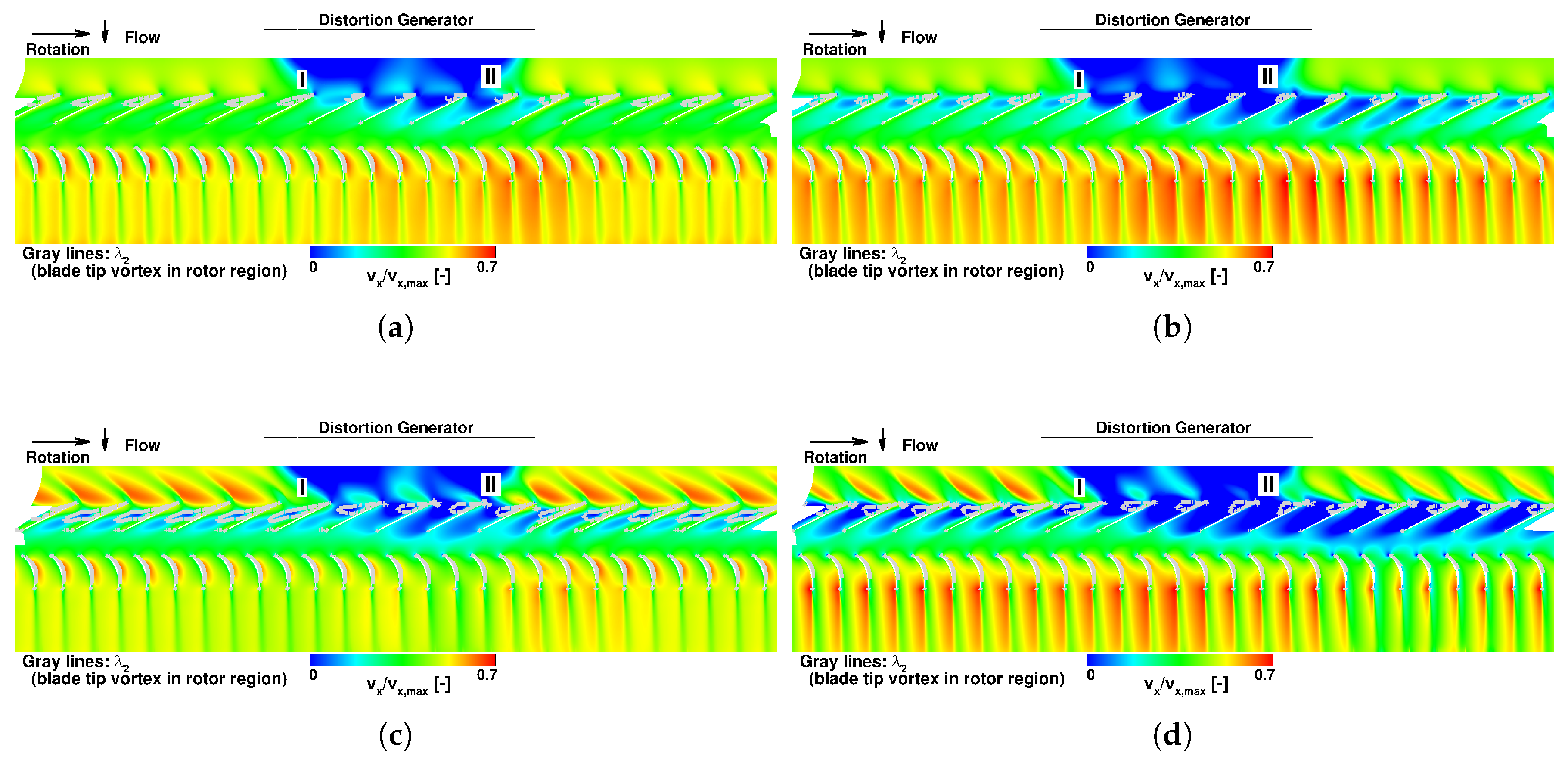
3.3. Blade Tip Vortices
3.3.1. Subsonic Blade Tip Speed
3.3.2. Transonic Blade Tip Speed
3.4. Radial Flow Redistribution
4. Conclusions
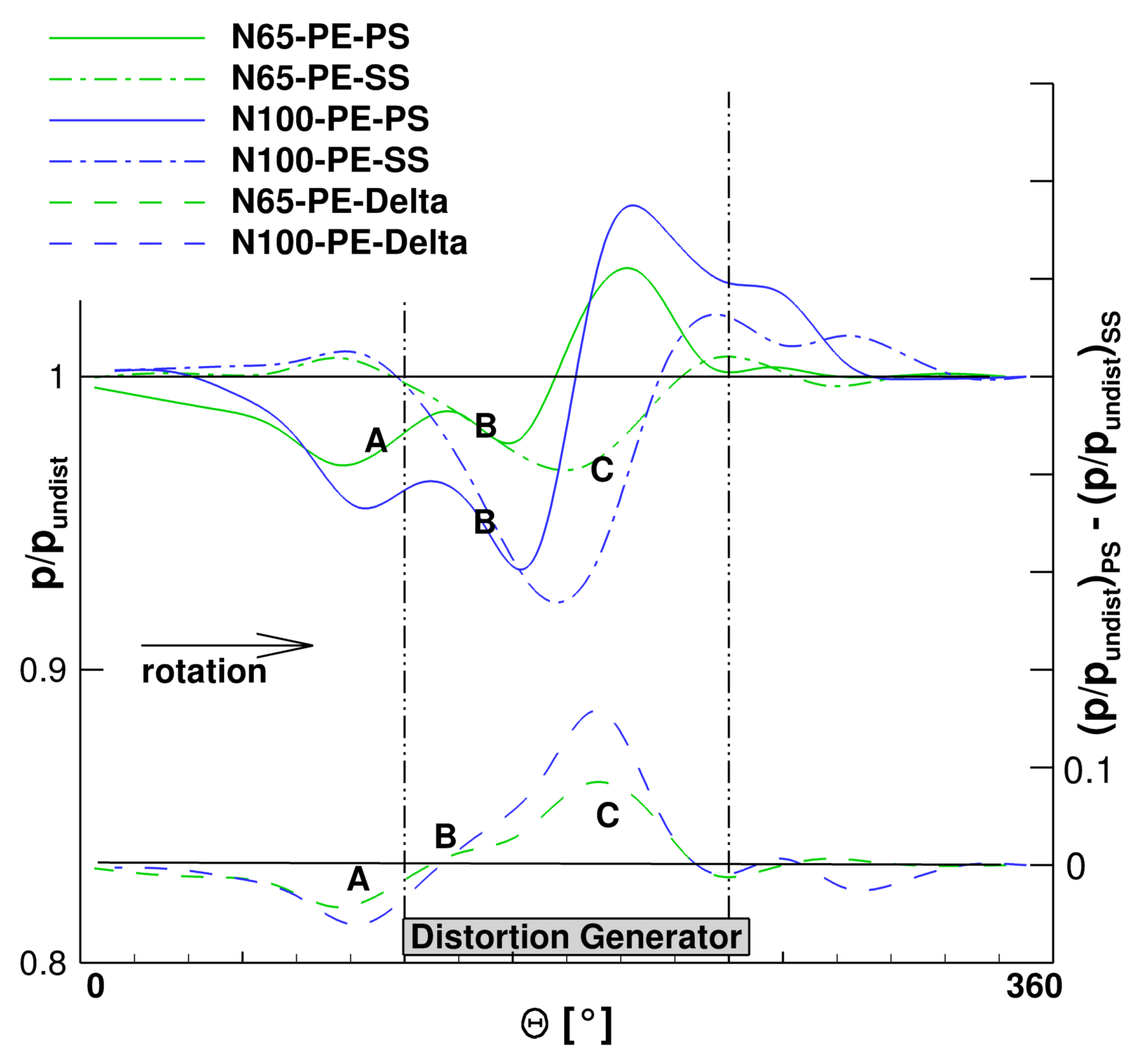
- While the shape of the distortion upstream of the rotor entry plane was neither influenced by the operating point nor the rotational speed of the rotor, the pressure drop inside the distorted flow sector strongly depended on the rotor rpm and showed a minor dependency on the operating point at the respective speedline.
- The degree of interaction between the distorted inflow and the rotor flow depended on the speedline as well as on the operating point on the respective speedline. Especially, the behaviour of the blade tip vortex varied with the rotational speed of the rotor when moving through the distorted flow sector. As the interaction of the distorted flow with the BTV had a strong impact on the compressor behaviour and performance, it can be considered as a important part of the interaction of the two flow regimes. At both speedlines, the BTV changed its shape soon after the blade entered the distorted flow, but characteristics and the recovery of the original shape of the BTVs depended on the speedline and operating point:
- -
- At N65, the BTV recovered quickly after the blades left the distorted flow. Additionally, the passage was not fully blocked in the tip region by low-energy fluid of the shortened or altered BTVs.
- -
- At N100, the interaction was stronger, as the BTV additionally interacted with the shock wave. Additionally, after break-down, the BTV recovered not as fast as at N65. The differences between PE and NS were higher than at N65, as the BTV regained its original shape much faster after leaving the distorted flow region at N100 PE than at N100 NS.
- The general trend of the variation of the blade loading showed similarities for the particular operating point on both speedlines, but the amplitude of the variations of the blade loading at one rotor revolution were higher at N100 than at N65.
- The radial flow redistribution depended on the speedline as well as on the operating point on each speedline, as it is driven by the mechanisms which are responsible for the interaction of the distorted flow and the rotor flow.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Abbreviations | |
| BTV | blade tip vortex |
| DG | distortion generator |
| DTC | Darmstadt Transonic Compressor |
| N65 | 65% design spool speed |
| N100 | 100% design spool speed |
| NS | near stall operating point |
| PE | peak efficiency operating point |
| PS | pressure side (of blade) |
| SS | suction side (of blade) |
| St. | station (see Figure 2) |
| Latin Symbols | |
| distortion coefficient | |
| p | pressure (Pa) |
| S | entropy (J/K) |
| V | velocity (m/s) |
| Greek Symbols | |
| difference | |
| angular extent of sector | |
| criterion for identifying vortices | |
| rotational speed | |
| Subscripts | |
| avg | averaged value |
| max | maximum value at respective case |
| t | total value |
| undist | undistorted |
| x | in x-direction |
References
- European Commission. Flightpath 2050—Europe’s Vision for Aviation; Publications Office of the European Union: Luxembourg, 2011. [Google Scholar]
- Schnell, R.; Schönweitz, D.; Theune, M.; Corroyer, J. Integration- and Intake-Induced Flow Distortions and their Impact on Aerodynamic Fan Performance. In Advances in Simulation of Wing and Nacelle Stall; Radespiel, R., Niehuis, R., Kroll, N., Behrends, K., Eds.; Notes on Numerical Fluid Mechanics and Multidisciplinary Design; Springer: Berlin/Heidelberg, Germany, 2015; Volume 131, pp. 251–269. [Google Scholar]
- Hah, C.; Rabe, D.; Sullivan, T.; Wadia, A. Effects of Inlet Distortion on the Flow Field in a Transonic Compressor Rotor. J. Turbomach. 1998, 120, 233–246. [Google Scholar] [CrossRef]
- Yao, J.; Gorrel, S.E.; Wadia, A.R. High-Fidelity Numerical Analysis of Per-Rev-Type Inlet Distortion Transfer in Multistage Fans—Part I: Simulations with Selected Blade Rows. J. Turbomach. 2010, 132, 041014. [Google Scholar] [CrossRef]
- Yao, J.; Gorrel, S.E.; Wadia, A.R. High-Fidelity Numerical Analysis of Per-Rev-Type Inlet Distortion Transfer in Multistage Fans—Part II: Entire Component Simulation and Investigation. J. Turbomach. 2010, 132, 11–17. [Google Scholar] [CrossRef]
- Lesser, A.; Niehuis, R. Transonic Axial Compressor with Total Pressure Inlet Flow Field Distortions. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. Paper No. GT2014-26627. [Google Scholar]
- Lesser, A. Numerische Untersuchung von Axialverdichtern mit Gestörter Zuströmung. Ph.D. Thesis, Universität der Bundeswehr München, Munich, Germany, 2015. [Google Scholar]
- Barthmes, S.; Haug, J.P.; Lesser, A.; Niehuis, R. Unsteady CFD Simulation of Transonic Axial Compressor Stages with Distorted Inflow. In Advances in Simulation of Wing and Nacelle Stall; Radespiel, R., Niehuis, R., Kroll, N., Behrends, K., Eds.; Notes on Numerical Fluid Mechanics and Multidisciplinary Design; Springer: Berlin/Heidelberg, Germany, 2015; Volume 131, pp. 303–321. [Google Scholar]
- Haug, J.P.; Barthmes, S.; Niehuis, R. Full Annulus Unsteady CFD Simulations on Effects of Inflow Distortions in a Transonic Axial Compressor Stage. In Proceedings of the International Gas Turbine Congress 2015, Tokyo, Japan, 15–20 November 2015; pp. 683–694. [Google Scholar]
- Schulze, G. Betriebsverhalten Eines Transsonischen Axialverdichters. Ph.D. Thesis, Technische Hochschule Darmstadt, Darmstadt, Germany, 1996. [Google Scholar]
- Bergner, J. Experimentelle Untersuchung der Strömung im Blattspitzenbereich Eines Transsonischen Axialverdichters Nahe der Stabilitätsgrenze. Ph.D. Thesis, Technische Universiät Darmstadt, Darmstadt, Germany, 2006. [Google Scholar]
- Biela, C.; Müller, M.W.; Schiffer, H.P.; Zscherp, C. Unsteady Pressure Measurement in a Single Stage Axial Transonic Compressor near the Stability Limit. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008. Paper No. GT2008-50245. [Google Scholar]
- Müller, M.W.; Biela, C.; Schiffer, H.P.; Hah, C. Interaction of Rotor and Casing Treatment Flow in an Axial Single-Stage Transonic Compressor with Circumferential Grooves. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008; pp. 2008–50135, Paper No. GT2008-50135. [Google Scholar]
- Niehuis, R.; Lesser, A.; Probst, A.; Radespiel, R.; Schulze, S.; Kähler, C.J.; Spiering, F.; Kroll, N.; Wartzek, F.; Schiffer, H.P. Simulation of Nacelle Stall and Engine Response. In Proceedings of the XXI International Symposium on Air Breathing Engines, Busan, Korea, 9–13 September 2013. Paper No. ISABE-2013-1402. [Google Scholar]
- Vunnam, K.; Hoover, R. Modeling of Inlet Distortion using a Combined Turbofan and Nacelle Inlet Model during Crosswind and Low Speed Forward Operation. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011. Paper No. GT2011-46466. [Google Scholar]
- Colin, Y.; Aupoix, B.; Boussuge, J.; Chanez, P. Numerical Simulation of the Distortion Generated by Crosswind Inlet Flows. In Proceedings of the 18th International Symposium on Air Breathing Engines, Beijing, China, 2–7 September 2007. ISABE-2007-1210. [Google Scholar]
- Hall, C.; Hynes, T. Measurements of Intake Separation Hysteresis in a Model Fan and Nacelle Rig. J. Propuls. Power 2006, 22, 872–879. [Google Scholar] [CrossRef]
- Reid, C. The Response of Axial Flow Compressor to Intake Flow Distortions. In Proceedings of the ASME 1969 Gas Turbine Conference and Products Show, Cleveland, OH, USA, 9–13 March 1969. Paper No. 69-GT-29. [Google Scholar]
- Wartzek, F.; Schiffer, H.P.; Haug, J.P.; Niehuis, R.; Bitter, M.; Kähler, C.J. Investigation of Engine Distortion Interaction. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Korea, 13–17 June 2016. Paper No. GT2016-56208. [Google Scholar]
- Ciorciari, R.; Lesser, A.; Blaim, F.; Niehuis, R. Numerical investigation of tip clearance effects in an axial transonic compressor. J. Therm. Sci. 2012, 21, 109–119. [Google Scholar] [CrossRef]
- Kozulovic, D.; Röber, T.; Kügeler, E.; Nürnberger, D. Modifications of a two-equation turbulence model for turbomachinery fluid flows. In Proceedings of the Deutscher Luft- und Raumfahrtkongress, Dresden, Germany, 20 September 2004. Paper No. DGLR-JT2004-229a. [Google Scholar]
- Marciniak, V.; Kügeler, E.; Funke, M. Predicting Transition on Low-Pressure Turbine Profiles. In Proceedings of the V European Conference on Computational Fluid Dynamics, Lisbon, Portugal, 14–17 June 2010. [Google Scholar]
- Wartzek, F.; Brandstetter, C.; Holzinger, F.; Schiffer, H.P. Response of a Transonic Compressor to a Massive Inlet Distortion. Proceedings of 1th European Conference on Turbomachinery Fluid dynamics and Thermodynamics, Madrid, Spain, 23–27 March 2015. Paper No. ETC2015-086. [Google Scholar]
- Gunn, E.J.; Tooze, S.E.; Hall, C.A.; Colin, Y. An Experimental Study of Loss Sources in a Fan Operating with Continuous Inlet Stagnation Pressure Distortion. J. Turbomach. 2012, 135, 051002. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Haug, J.P.; Niehuis, R. Full Annulus Simulations of a Transonic Axial Compressor Stage with Distorted Inflow at Transonic and Subsonic Blade Tip Speed. Int. J. Turbomach. Propuls. Power 2018, 3, 7. https://doi.org/10.3390/ijtpp3010007
Haug JP, Niehuis R. Full Annulus Simulations of a Transonic Axial Compressor Stage with Distorted Inflow at Transonic and Subsonic Blade Tip Speed. International Journal of Turbomachinery, Propulsion and Power. 2018; 3(1):7. https://doi.org/10.3390/ijtpp3010007
Chicago/Turabian StyleHaug, Jakob P., and Reinhard Niehuis. 2018. "Full Annulus Simulations of a Transonic Axial Compressor Stage with Distorted Inflow at Transonic and Subsonic Blade Tip Speed" International Journal of Turbomachinery, Propulsion and Power 3, no. 1: 7. https://doi.org/10.3390/ijtpp3010007
APA StyleHaug, J. P., & Niehuis, R. (2018). Full Annulus Simulations of a Transonic Axial Compressor Stage with Distorted Inflow at Transonic and Subsonic Blade Tip Speed. International Journal of Turbomachinery, Propulsion and Power, 3(1), 7. https://doi.org/10.3390/ijtpp3010007





