The determination of the settling time for pressure measurement systems has been the focus of study since quite early on in the history of wind tunnel testing. The settling time is important whenever there is a noticeable time lag between pressure changes at the measurement location and the actual measurement device. Sinclair and Robins [
3] developed an equation for the determination of settling time for laminar, incompressible flow measured by a manometer. The measured pressure at the measurement device—in the case of this reference, a manometer, but it can also be a pressure gauge—is a function of time
. At
, the system is in equilibrium at
. After a step change at the orifice of the measurement system (e.g., a probe tip) from
to
, the measured value will change. The settling time can be defined as time needed for the measured pressure to level 99.9% of the initial pressure difference
, i.e.,
In [
3], the settling time
is given as
with the natural logarithm ln, the total volume of the system
V and the displacement volume due to fluid level change in the manometer
. The equivalent length
is determined for a combination of different tube diameters
by
Larcombe and Peto [
4] derive the settling time for slip flow as
with
where
is equivalent to
in Equation (
2) and
f is the fraction of gas molecules diffusely reflected. In the reference,
f is suggested to be equal to 0.8 for air at 20
C. The equivalent length for a combination of various diameters is given as
In a recent publication, Grimshaw and Taylor [
1] use an electric circuit analogy to derive the set of differential equations for the determination of the pressure history. Though the results in their absolute values might differ from each other, altogether they show a strong dependency of the settling time from the absolute pressure level.
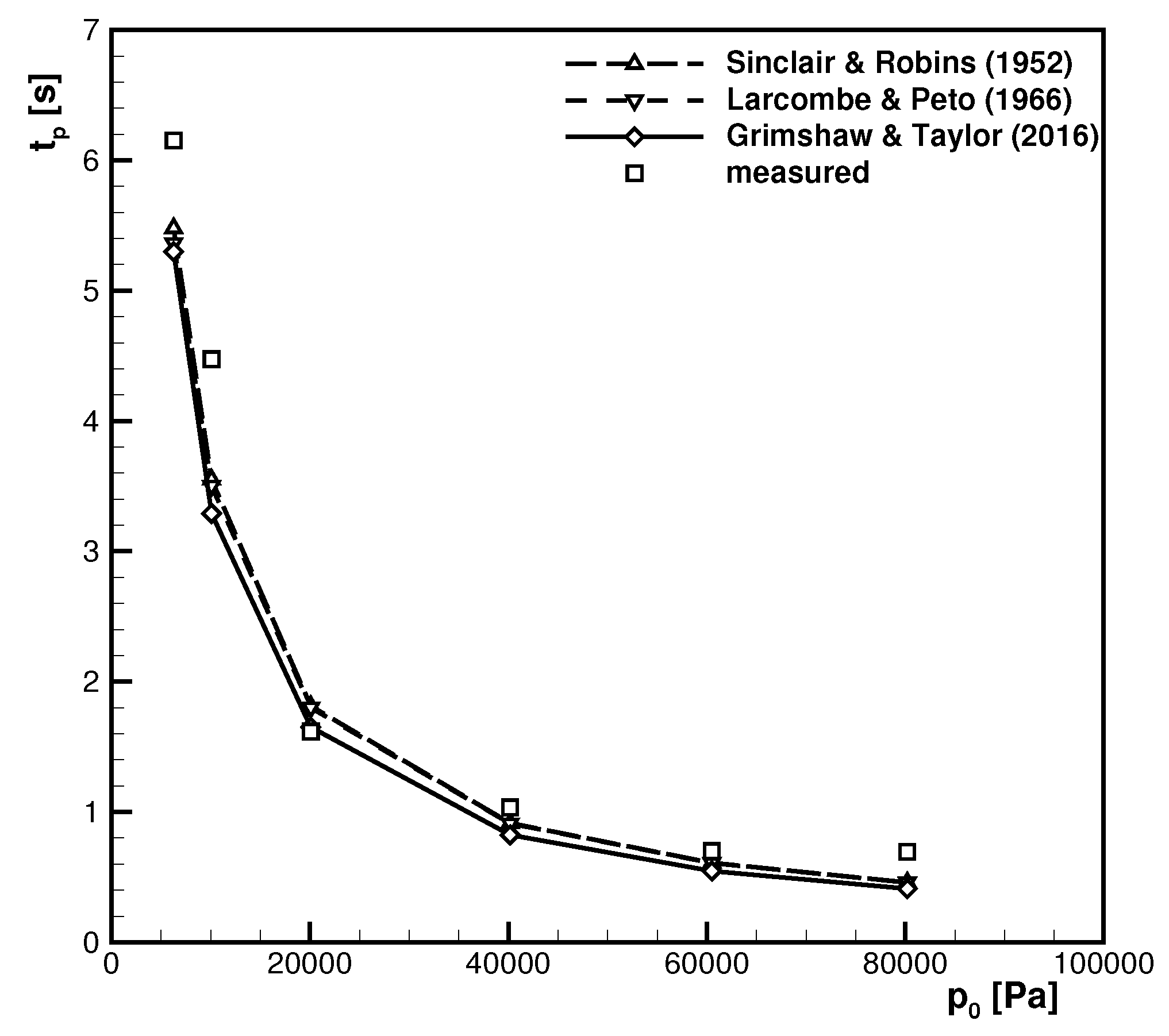
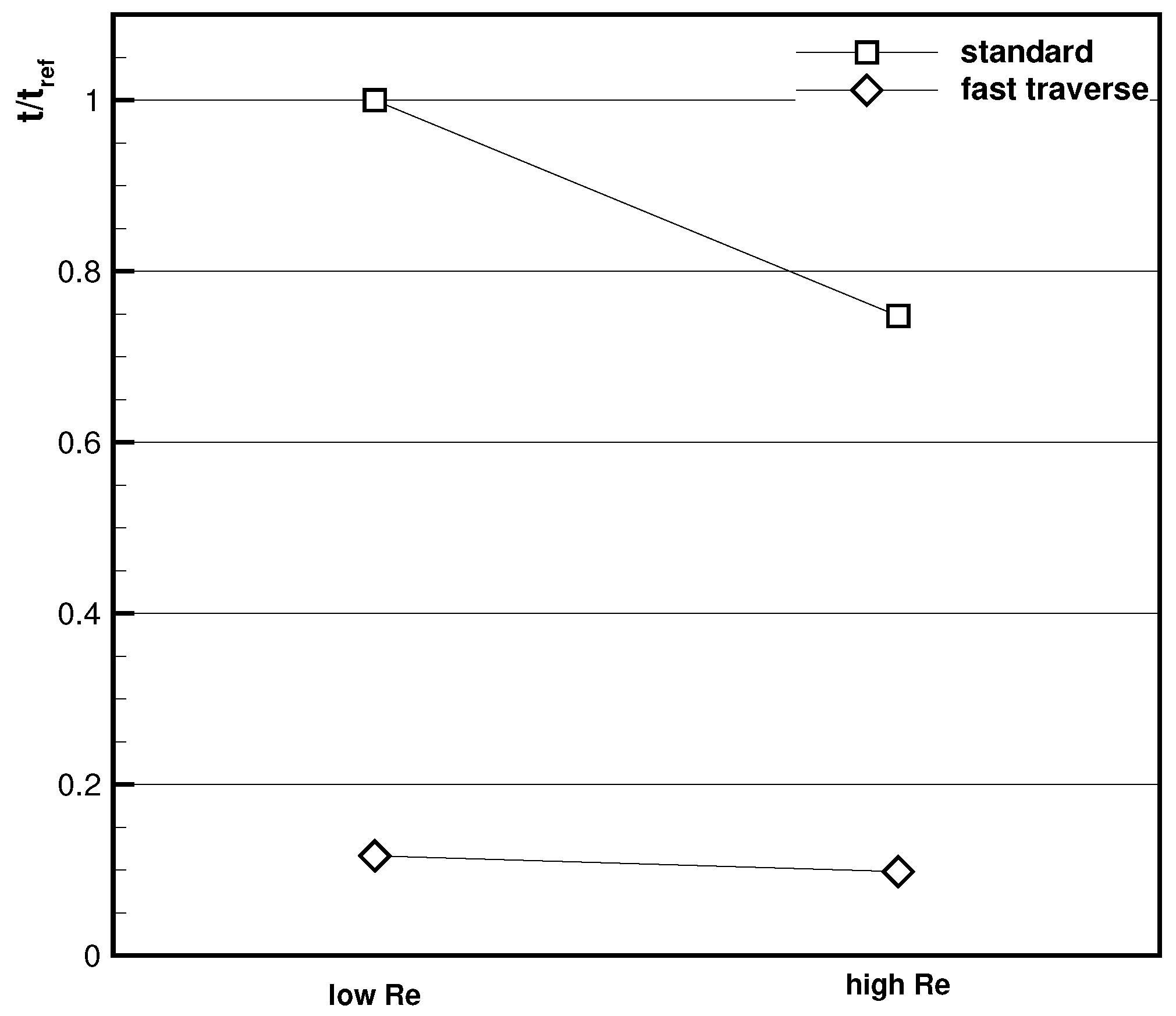
Figure 1 shows the settling time dependency on the overall pressure level
for a typical measurement configuration in a wind tunnel, applying the theories discussed so far. The strong increase of the settling time with decreasing pressure level seems evident. The configuration of the measurement set-up for a single pressure hole of the five-hole probe is explained in
Table 1, while the applied pressures are given in
Table 2. Overall, the probe head has a diameter of 2.5 mm.
Some validation measurements were carried out with a simple set-up and a manual valve to produce a sudden pressure increase from
to
at the five-hole probe tip. A Kulite (Leonia, NJ, USA) pressure sensor placed close to the probe tip is used as a reference signal to capture the actual pressure increase. The fast reacting pressure sensor is of the type
XCQ-062 and has a natural frequency of 150 kHz with a differential pressure range of 350 hPa. Overall, the measurements confirm the trend predicted by the cited authors as shown in
Figure 1. Viscous effects might be responsible for the slight increase in settling time in the experiments.
One may try to reduce the settling time as carried out, e.g., in [
3] or [
1] by optimizing the tube diameters, but physical limitations and constraints to the set-up will always lead to considerable time consumption of measurements with standard pneumatic probes, especially at low pressure levels.
2.1. Continuous Traverse Using Transfer Function
Paniagua and Dénos [
2] present a method using a transfer function to obtain the true pressure at the probe tip. Simplifying and neglecting any time delay between step change and pressure rise at the transducer, one can reconstruct the true pressure from the time history of the true pressure and the measured pressure. For a measurement at a sampling time instance
j, the true pressure
u is obtained by
with the order of the function
m and the measured pressure
y. A probe might then be traversed continuously through an inhomogeneous flow field and the actual pressure at each of the holes reconstructed by the measured pressure. For such an operation, one must know the coefficients
and
, which can be obtained by prior calibration, as shown by the same authors. However, if one is carrying out measurements at different pressure levels, this would imply a calibration for each pressure level, which would outweigh any time savings by this method.
A more suitable way for measurements under varying pressure conditions is to obtain the coefficients from the measurement itself, bypassing any calibration. Therefore, a method proposed by Bartsch et al. [
5] for optimization of the measurement point distribution for standard measurements is used here to determine the coefficients of the transfer function. In the publication from Bartsch et al. [
5], they perform two traverses in opposite directions downstream of an airfoil in order to determine the wake position and to enhance the measurement point distribution for a standard traverse.
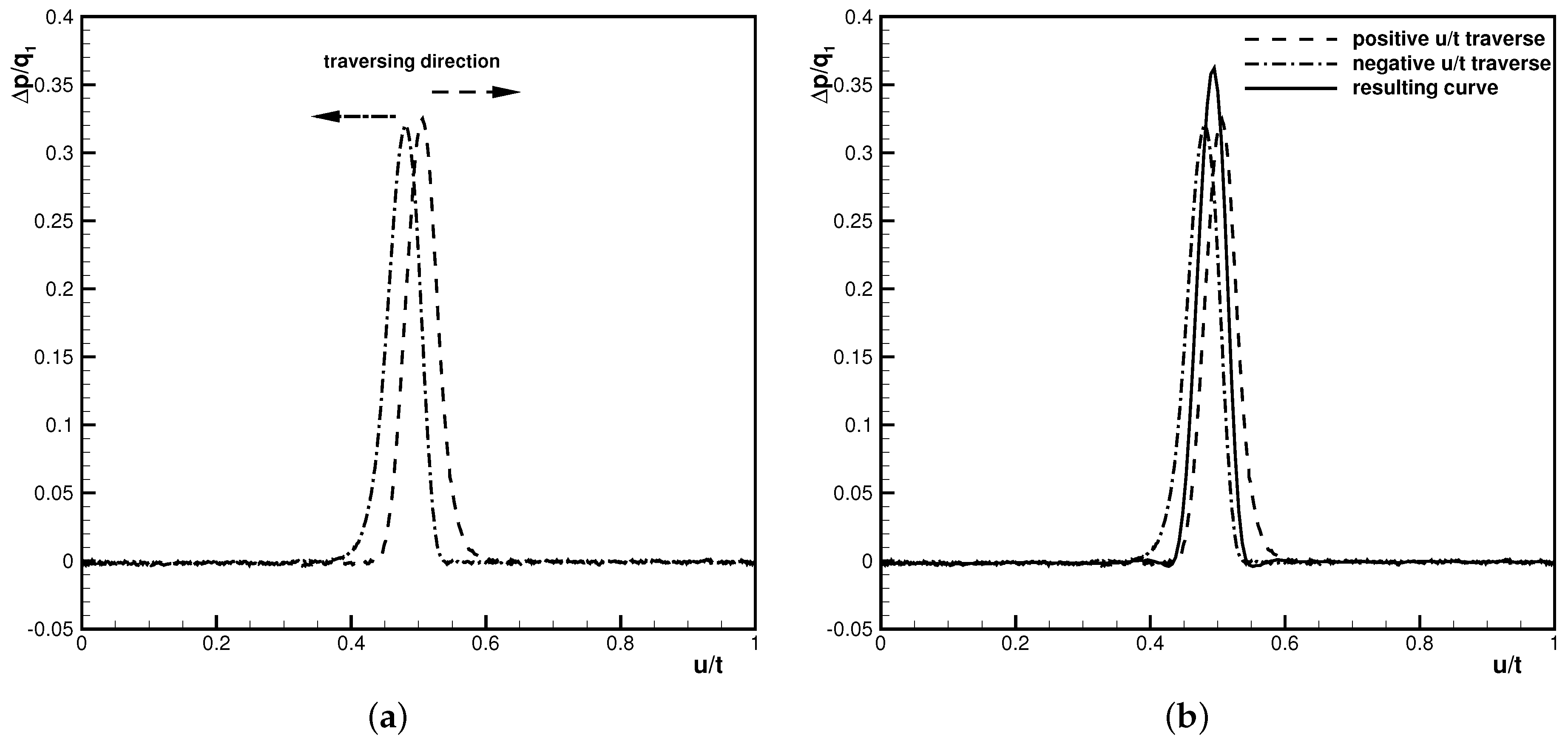
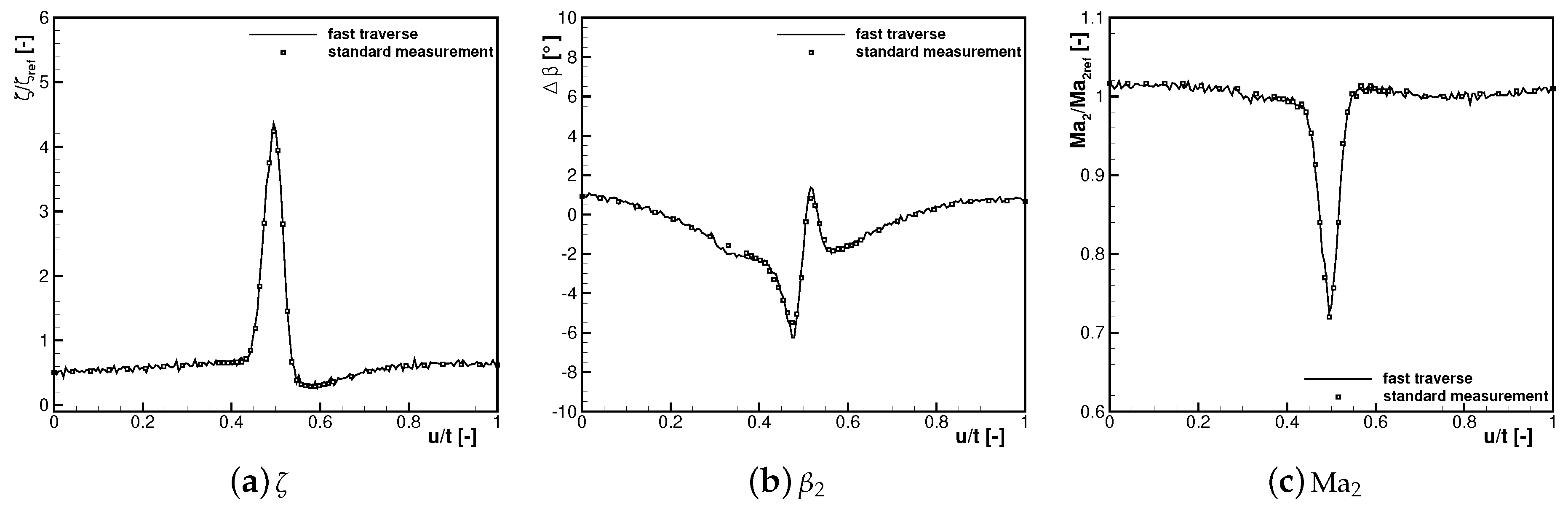
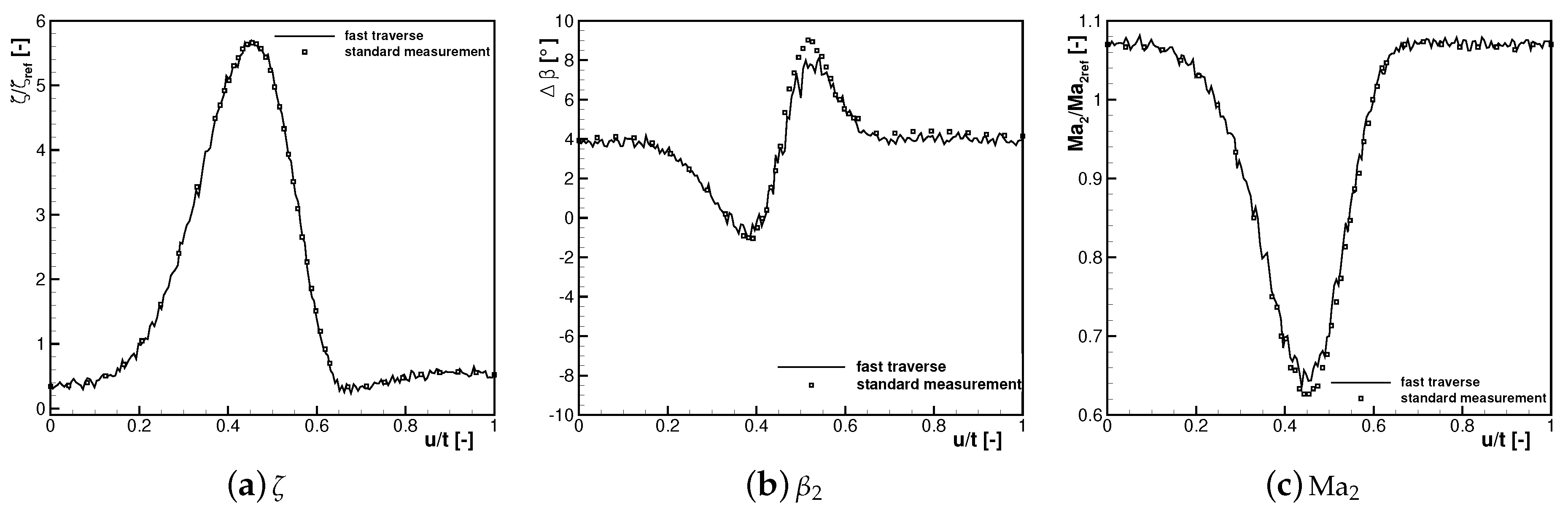
Such a dual traverse can also be used to directly obtain the actual pressure at each measurement location. In
Figure 2a, typical results for a dual traverse are plotted. The dashed line shows the measured pressure difference between total inlet pressure and the pressure at the centre hole of the probe normalized by a random stagnation pressure for a continuous traverse toward higher
values. The dashed–dotted line shows similar readings for a traverse in the same flowfield but moving in the opposite direction. It is evident that the time delay between actual pressure change and measured pressure leads to a phase lag of the measured pressure, seen in the different positions of the peak values. Additionally, the measured pressure difference is expected to be lower than the actual maximum. The coefficients for the transfer function in Equation (
7) can be evaluated iteratively and the function applied to both traverses must give the same result, or more precisely
with the vectors of the measured pressures
for
n measurement points and with the subscripts
f and
s for the first respectively second traverse. The vector
holds the coefficients of the transfer function while the matrix
is defined as
The coefficients of the vector
in Equation (
8) are iteratively searched to minimize the root mean square of the error vector
using the MatLab (MathWorks, Natick, MA, USA) function
fminsearch. The order of the function
m can be individually set for each experiment, but in our measurements an order higher than
did not change the results significantly.
Since the number of coefficients for
is in general higher than two, additional constraints are put into the algorithm for the iterative search: the resulting actual pressure history as a function of
has to cross all measured pressure difference peaks, i.e., maximum and minimum values, if this is the case. This is true, since the traversing velocity is moderate which results in macroscopic pressure changes, like the peaks in
Figure 2a, far below one Hertz. According to the works of Bergh and Tijdeman [
6] or Carolus [
7] at such low frequencies and since the system is overdamped, no noticeable phase lag is perceived for the pressure reverse at the tip of the probe. The resulting pressure line for the curves shown in
Figure 2a is plotted in
Figure 2b together with the measured curves.
Such an iterative search can be done for all the holes or measured pressure differences of the five-hole probe and the actual flow values can be computed. Additional smoothing of the obtained values by a moving average filter of window size equal to the order of the transfer function allows to decrease the wiggles due to overestimation of random variations in the pressure measurement.
2.1.1. Error Estimation
An error estimation is more difficult to conduct using the transfer function since every computed pressure difference relies on the history of the measured and reconstructed pressure values
. This means that every error in previous samples propagates to the following pressures. Using the linear error propagation technique, which is the more conservative approach, without any further analysis would very soon increase the uncertainty towards infinity, since
with
as the uncertainty of the pressure gauge, i.e.,
. However, one can overcome this problem if one separates the systematic from the random error with
The systematic error is constant for all samples; therefore, Equation (
10) can be rewritten as
The effect of such a method can be seen exemplary for a case of the order
for simplification. The first transformation is at the second sample
since at the first sample the probe is not in motion and the measured pressure can be seen as the actual pressure at the probe tip
. For the third reading, the result from Equation (
15) is set into the error estimation of Equation (
12)
Applying the same method into the fourth reading gives
Continuing the row, one can easily find the relation
The first summand of Equation (
17) can be brought to a geometric series for
with
Equation (
18) does not converge for
. It is therefore mandatory to find coefficients
where the sum of the absolute values is smaller than unity in order to maintain mathematically correctly the uncertainty at low levels. Otherwise, the uncertainty grows exponentially with the number of data points.
The fluctuating random error (second and third summand in Equation (
17)) is essentially due to noise and can, in general, be neglected for the average values, since the sum of the errors is equal to zero, see Equation (
11).
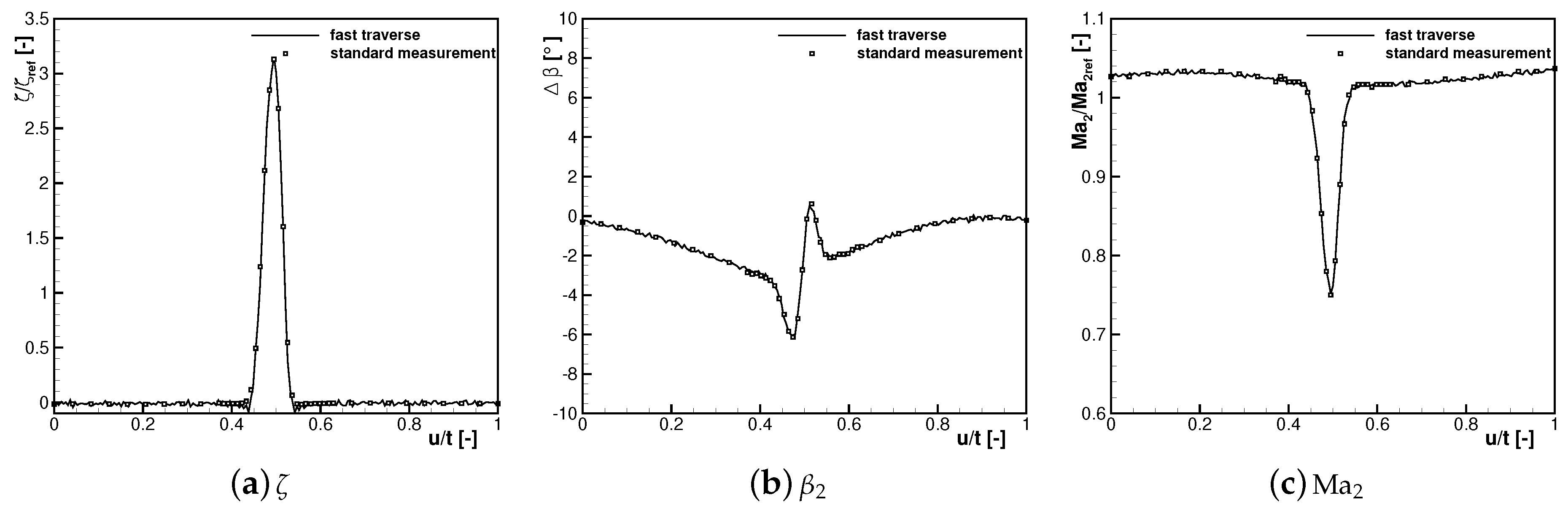
Doing so, the measurement accuracy for standard and new measurement techniques is 0.01 for the Mach number measured by the five-hole probe,
for the swirl
and approximately 10% of the total pressure loss coefficient
defined in Equation (
20).