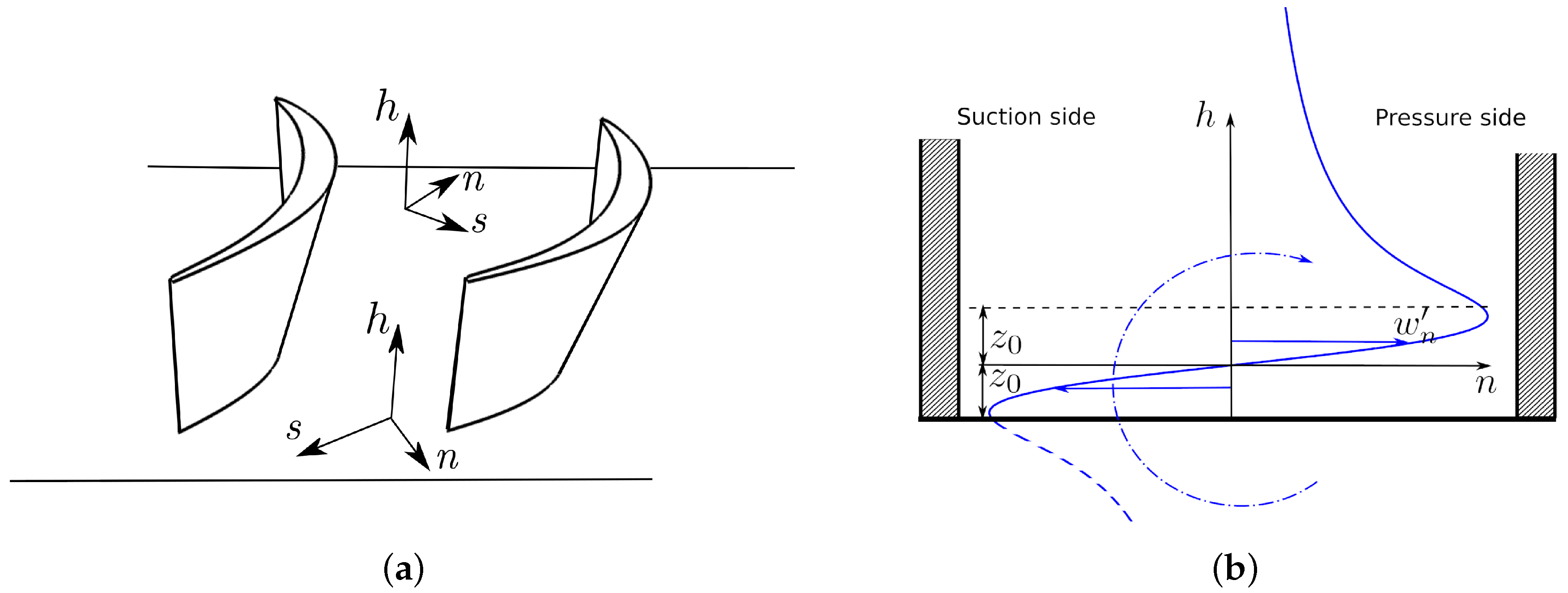
Secondary flows are modelled as additional 3D flow features associated with the vortices that are created when then non-uniform inlet flow is turned by the blade rows. They are accounted for in the throughflow procedure via a transverse velocity field and an additional loss distribution. When circumferentially averaged, the transverse velocity field is assumed to be represented by Lamb–Oseen-type vortices. The Lamb–Oseen vortex is an analytical solution of the Navier-Stokes equations with an axisymmetric distribution for the swirl velocity and zero radial and axial components. In polar coordinates, the tangential velocity as a function of the time
t and the distance from the vortex centre
r is expressed as:
One can overcome the explicit dependence on time by introducing a characteristic vortex core radius
which increases with time as a result of the diffusion of vorticity and shear stresses. In this work, the circumferentially averaged secondary velocity and vorticity are considered in the intrinsic relative coordinate system
(Hawtorne et al. [
12],
Figure 1a) and expressed as components
and
, respectively, given by:
where
, and
h is measured as the spanwise distance from the endwalls. The vortex characteristic length
(
Figure 1b) is estimated at the blade trailing edge as a fraction of the secondary flow penetration depth in the spanwise direction
Z:
. The value of
Z is estimated by using the Benner et al. correlation [
13]. A value of
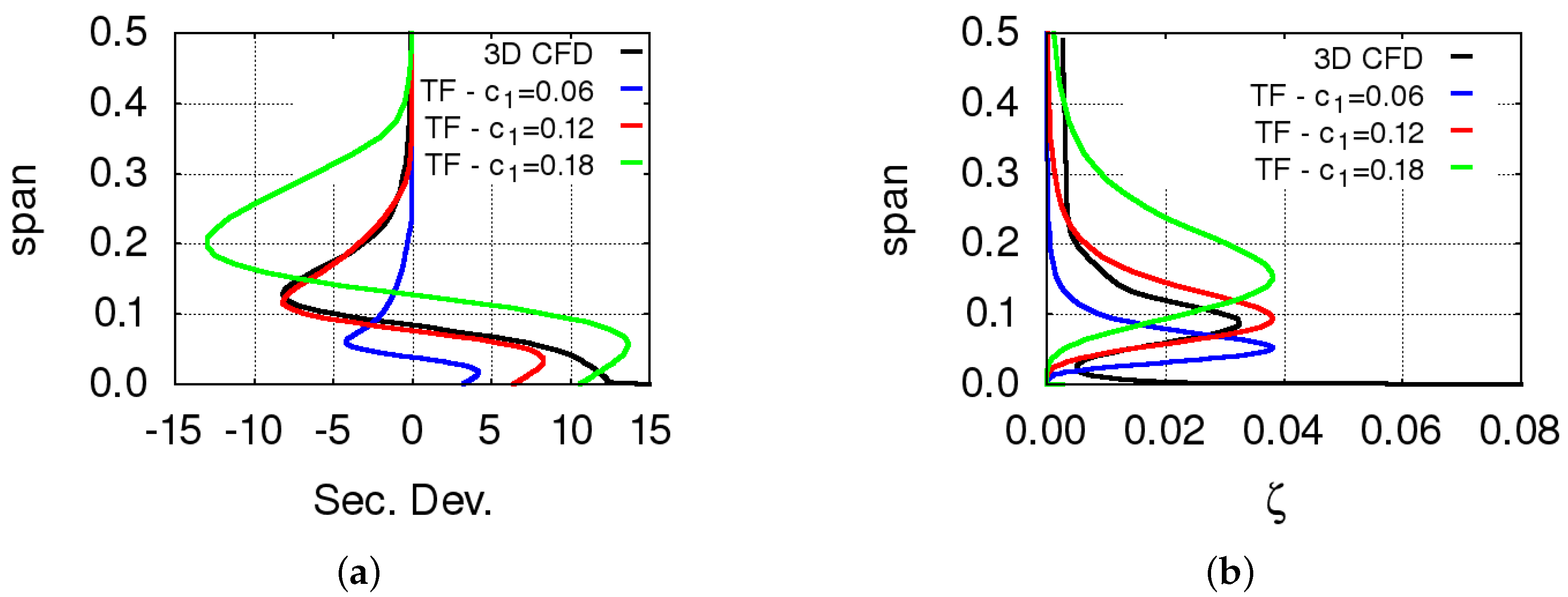
has been chosen for the constant
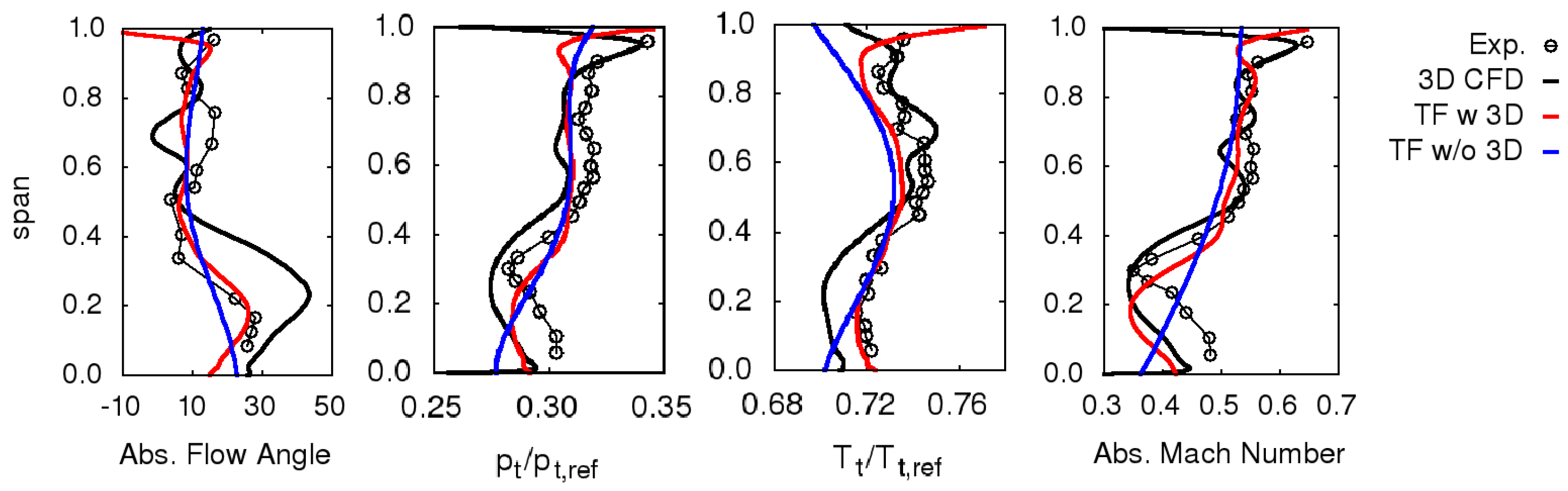
on the basis of numerical experiments and comparison with 3D CFD results (
Figure 2). Inside the blade passage, the characteristic length
is distributed linearly along the blade meridional length from the minimum blockage factor location up to the trailing edge. The circulation
can then be expressed in terms of the vorticity at the vortex centre
as:
. The vorticity component
is assumed to be coincident with the streamwise vorticity of the passage vortex. This is evaluated using the classical secondary flow theory (Hawthorne et al. [
12]). However, it must be noted that in this theory such a vorticity contribution is considered as distributed in the blade passage and not concentrated at the vortex centre, as in the present approach. The secondary velocity component given by Equation (
9) is finally projected in the tangential direction to obtain a tangential velocity
which is then used in Equation (
6) to generate an additional body force. This provides the secondary deviation distribution.
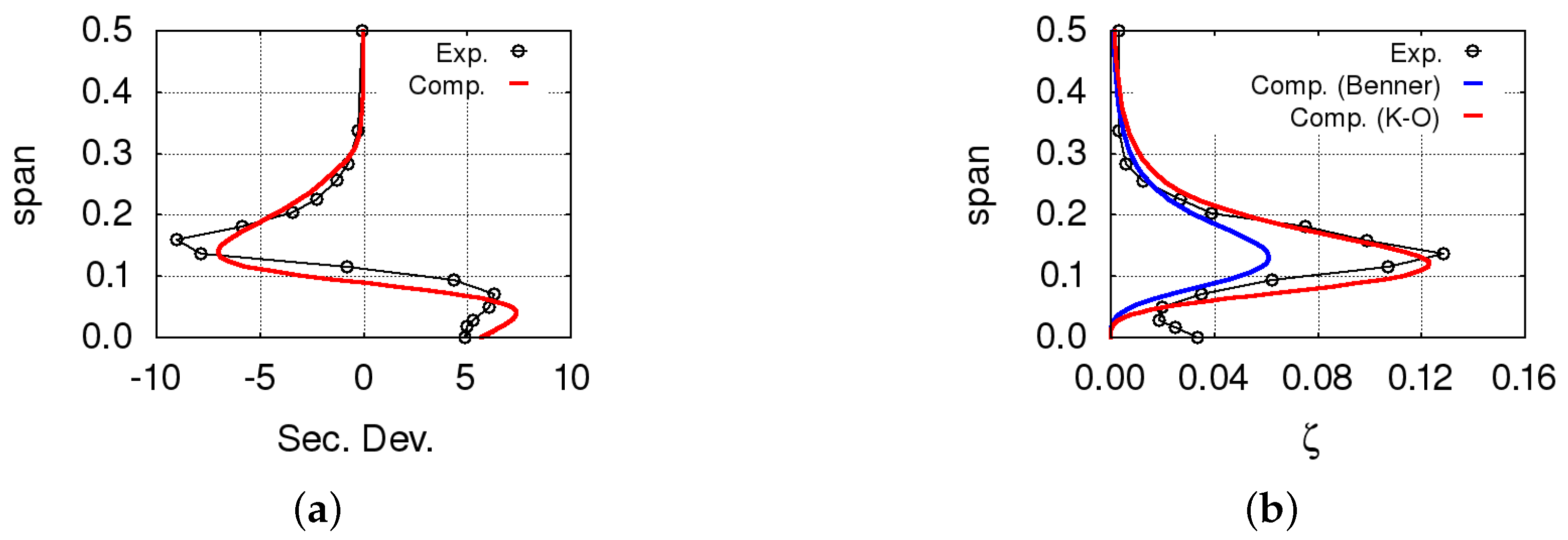
Secondary losses are estimated via correlations like the ones by Benner et al. [
13] or Kacker and Okapuu [
14]. Secondary loss coefficients are converted in entropy rise values
, where local flow conditions at the endwalls are used for this purpose. Such values are then distributed in the spanwise direction so that the integral average of the distribution corresponds to
, and the resulting entropy field is used for the distributed loss model. To this end, the following distribution function is used:
In practice, the function
is normalized with its integral value between the endwall and midspan and multiplied by
. It was found that Equation (
10)—which is suggested by the behaviour of the dissipation in a Lamb–Oseen vortex—closely matches the results of viscous three-dimensional CFD calculations. In fact, several parametric studies were carried out in order to check the behaviour of the function
and to determine the optimum value of the proportionality constant
between the vortex characteristic length
and the Benner et al. secondary flow penetration depth
Z [
13]. An example of these studies is summarized in
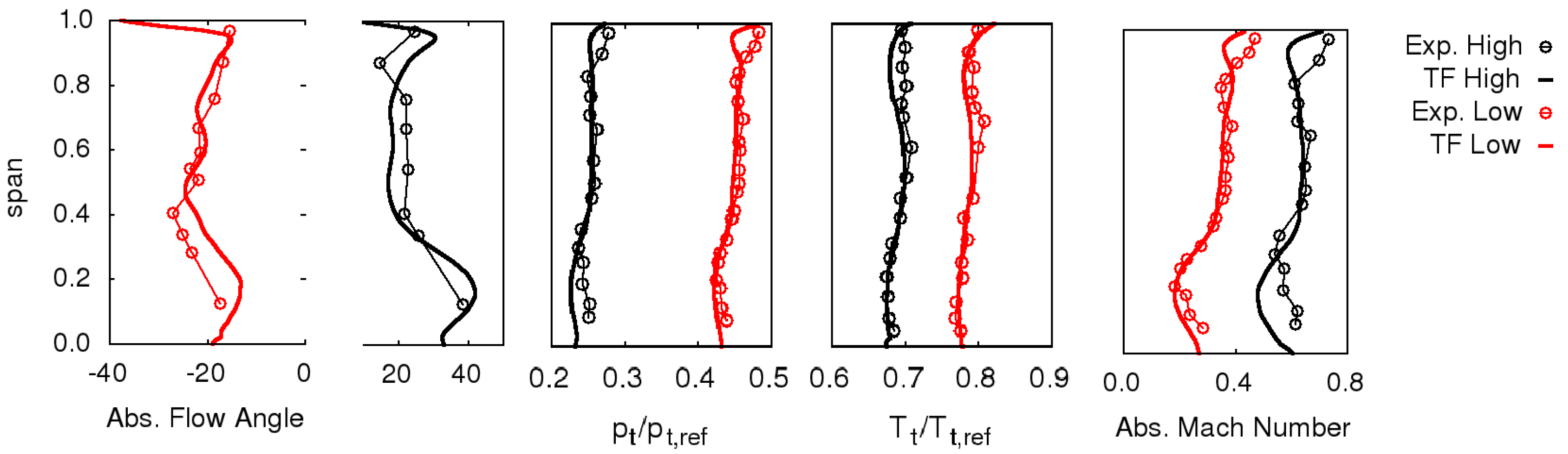
Figure 2, where 3D CFD results are compared to throughflow predictions in terms of secondary deviation angle and loss coefficient. These quantities are defined as the difference between the actual flow quantities and the corresponding ones that would be obtained without secondary flow effects. Secondary losses are estimated with the Kacker–Okapuu correlation [
14]. Results obtained with several values of the constant
are reported.