A Comparative Study of Varying Incidence Angle Effects on a Low-Reynolds-Number Compressor Cascade Based on Experiments and Low-Fidelity and High-Fidelity Numerical Simulations †
Abstract
1. Introduction
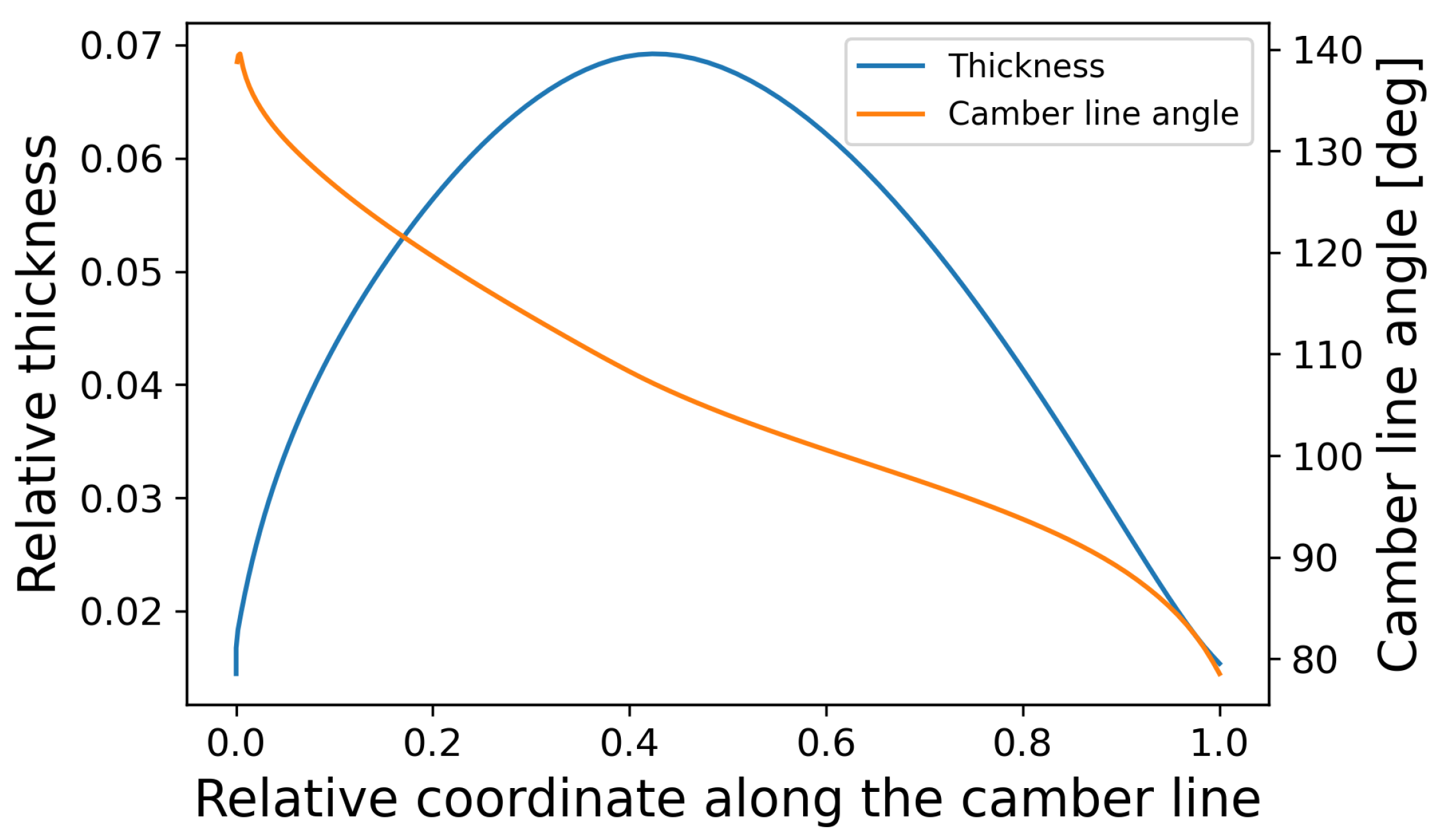
2. Cascade Description
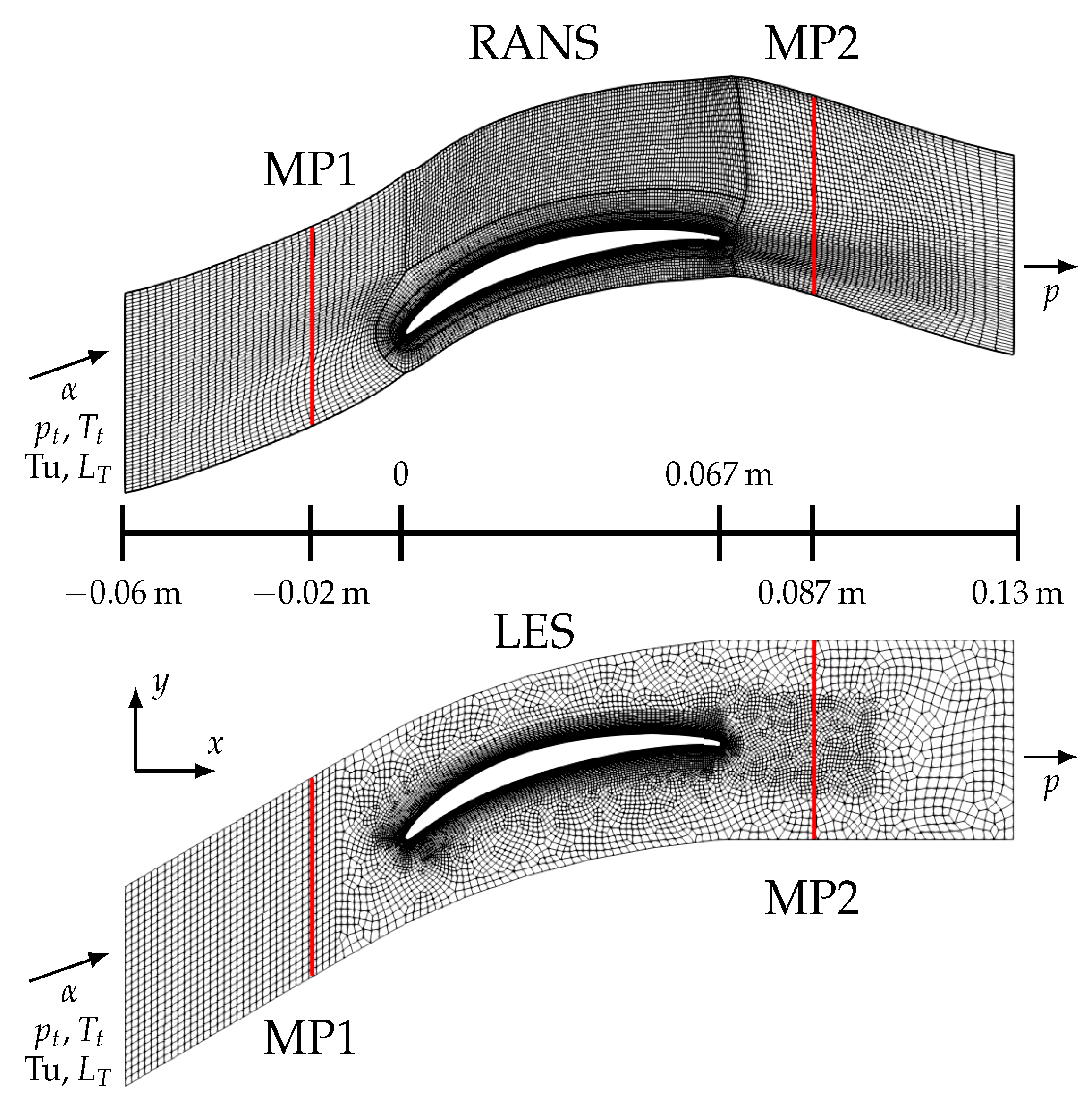
2.1. Experimental Setup
2.2. RANS Setup
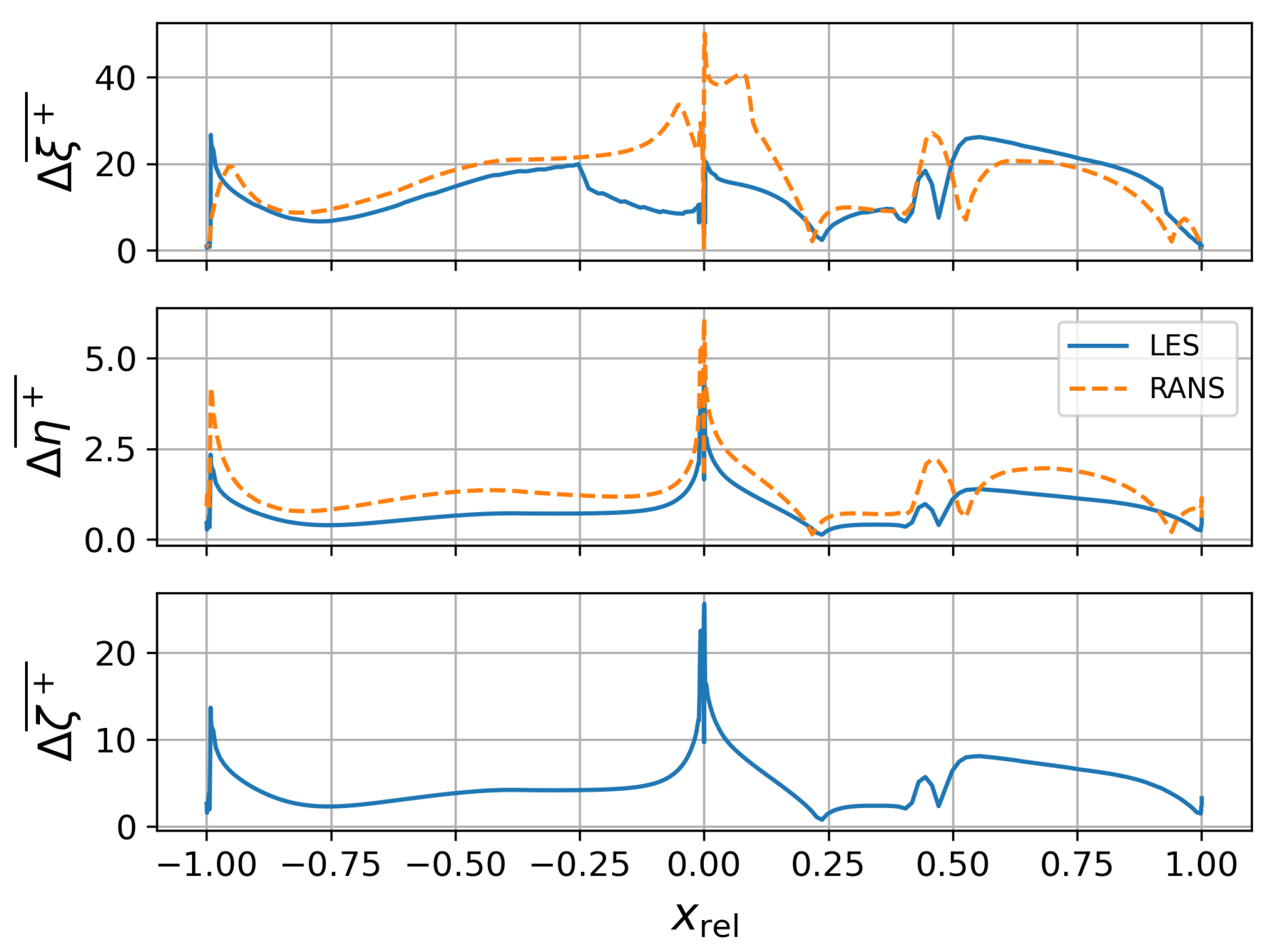
2.3. LES Setup
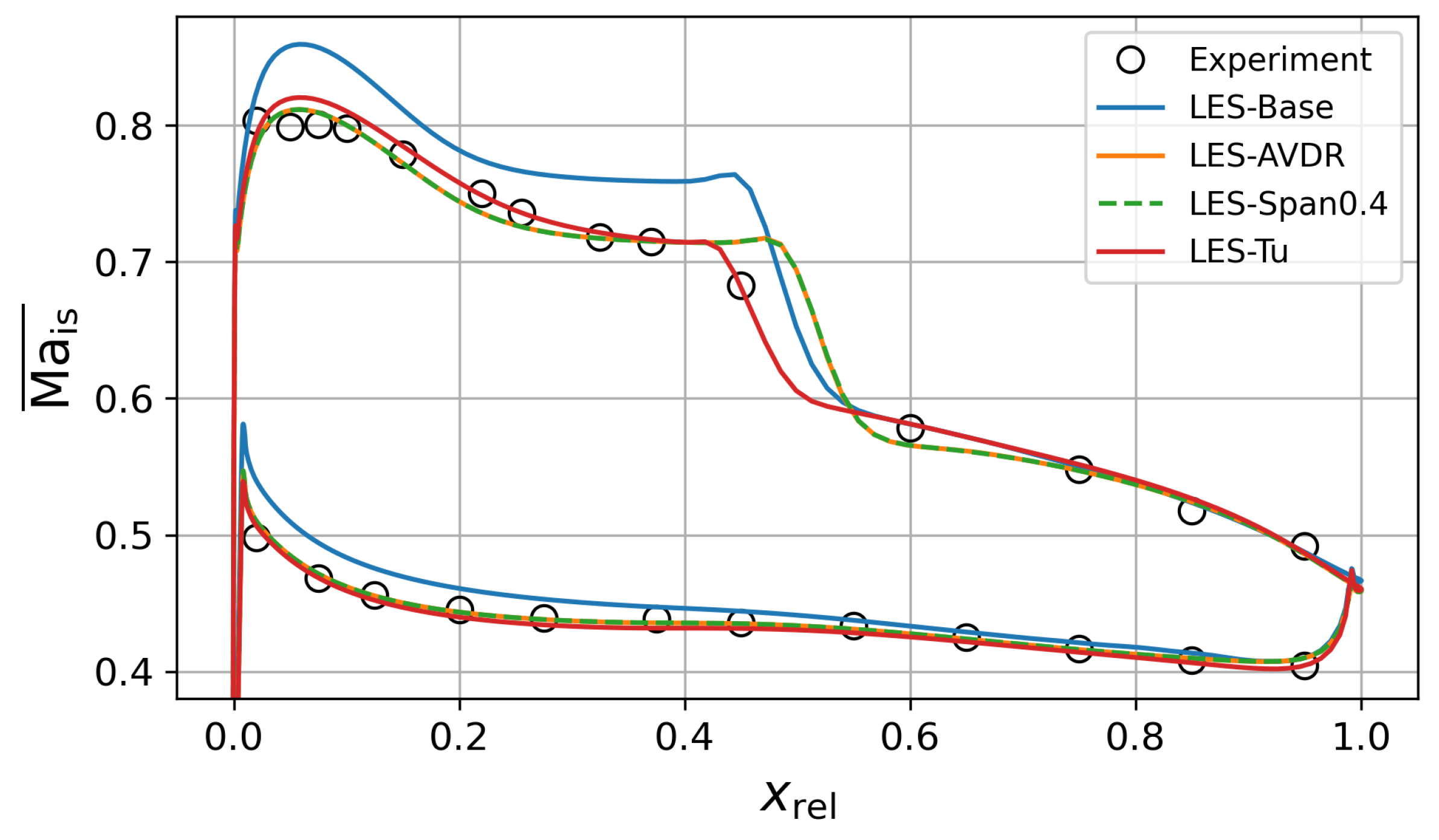
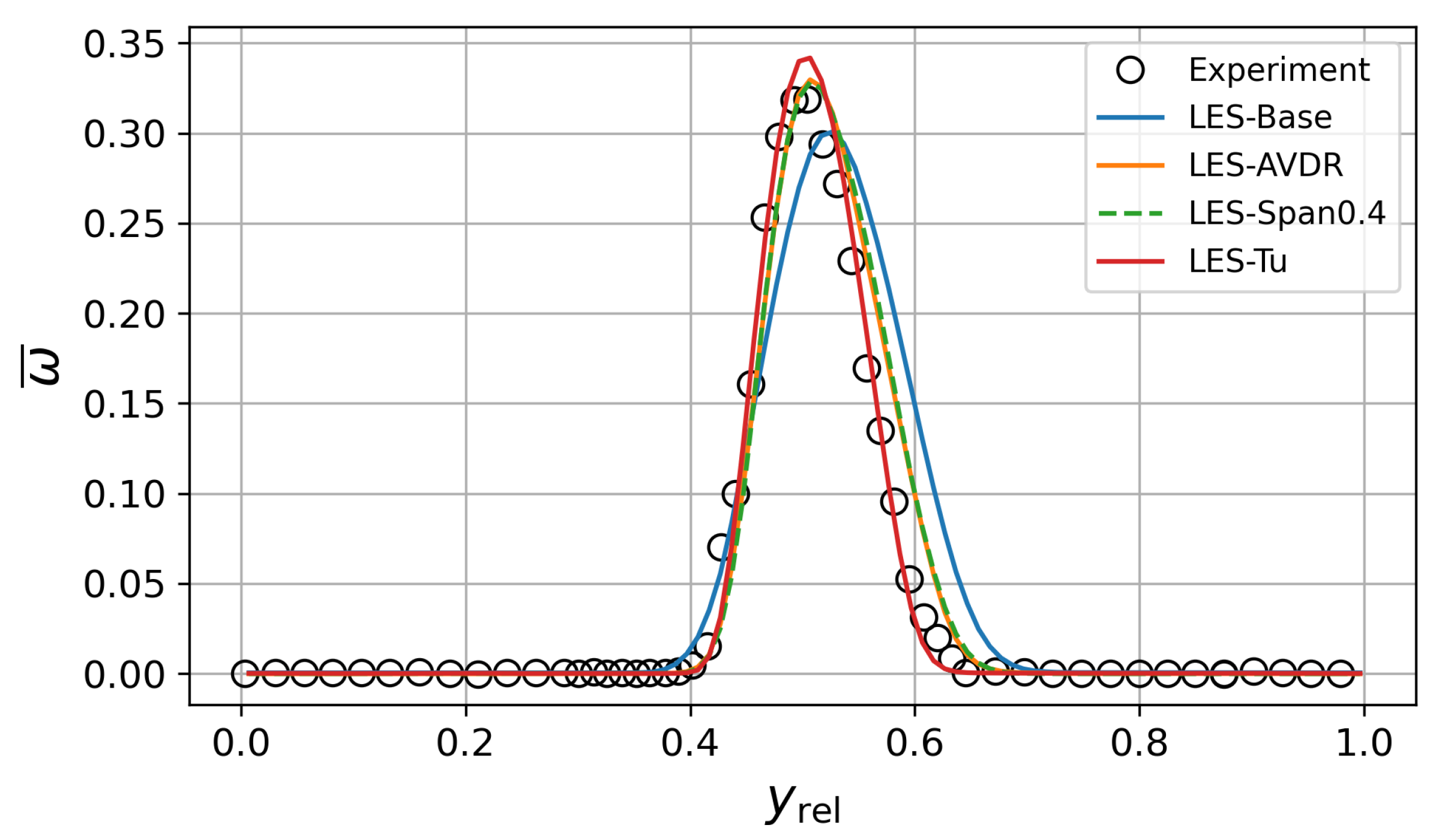
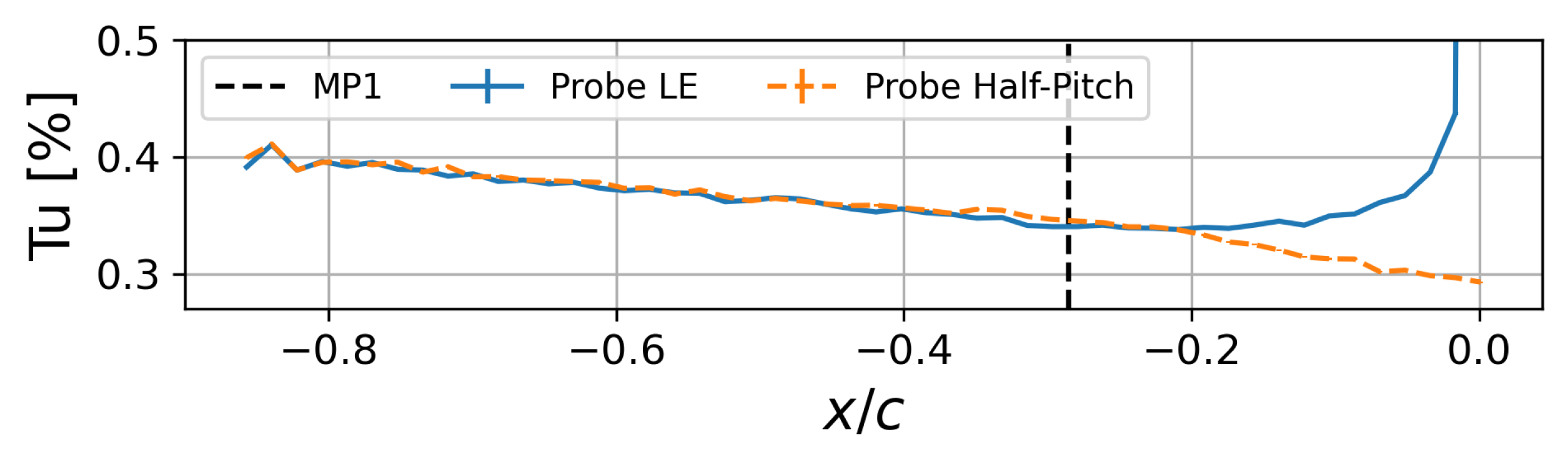
3. Analysis of the LES Setup for the Aerodynamic Design Point
4. Incidence Angle Variation
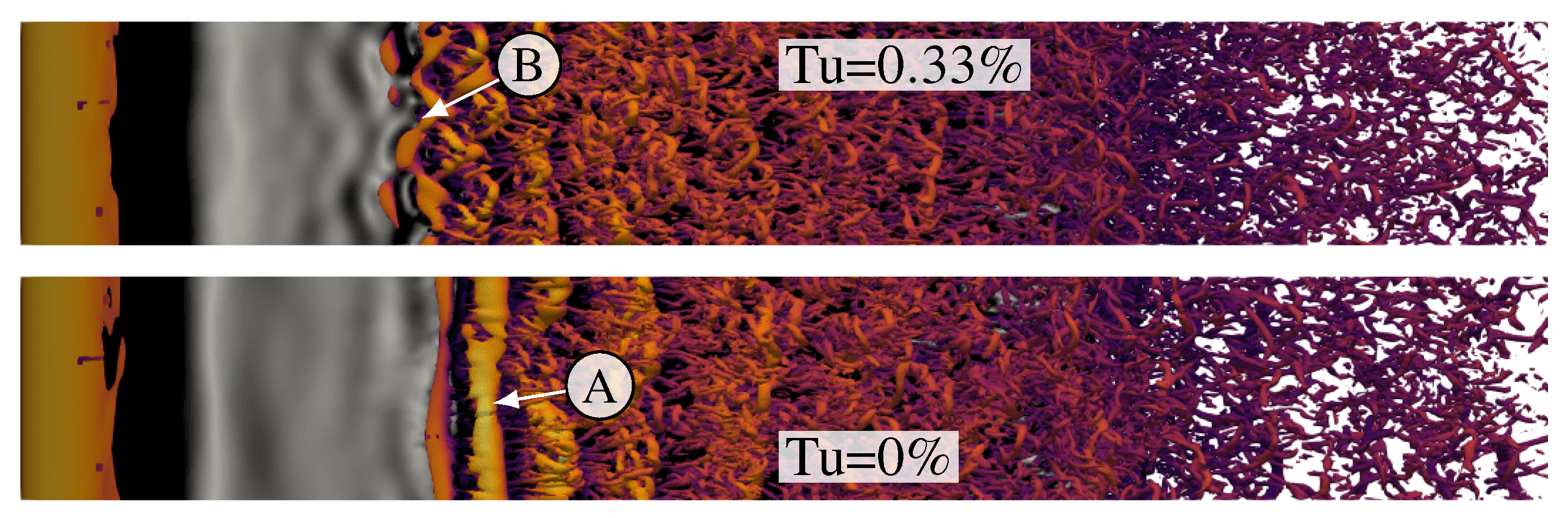
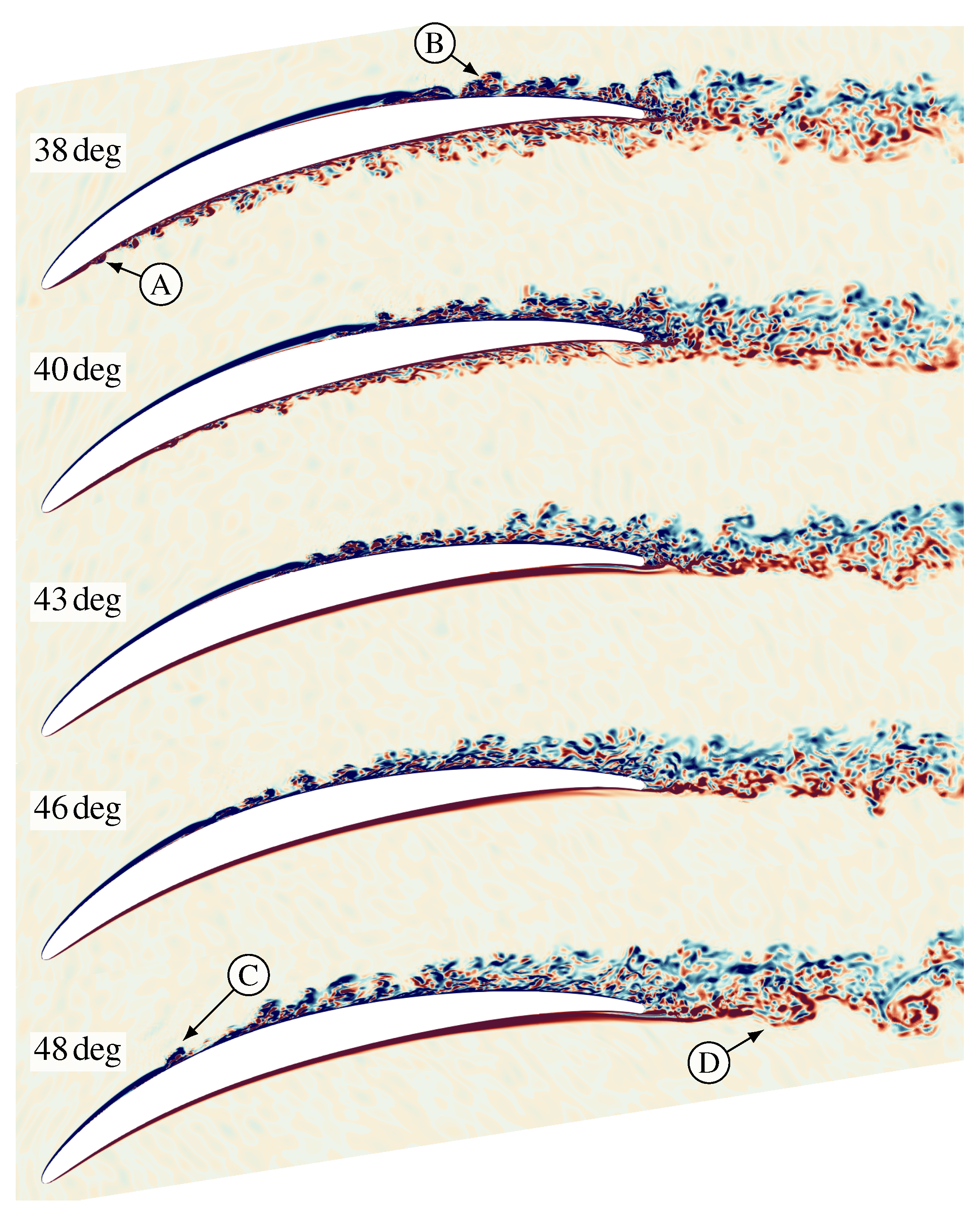
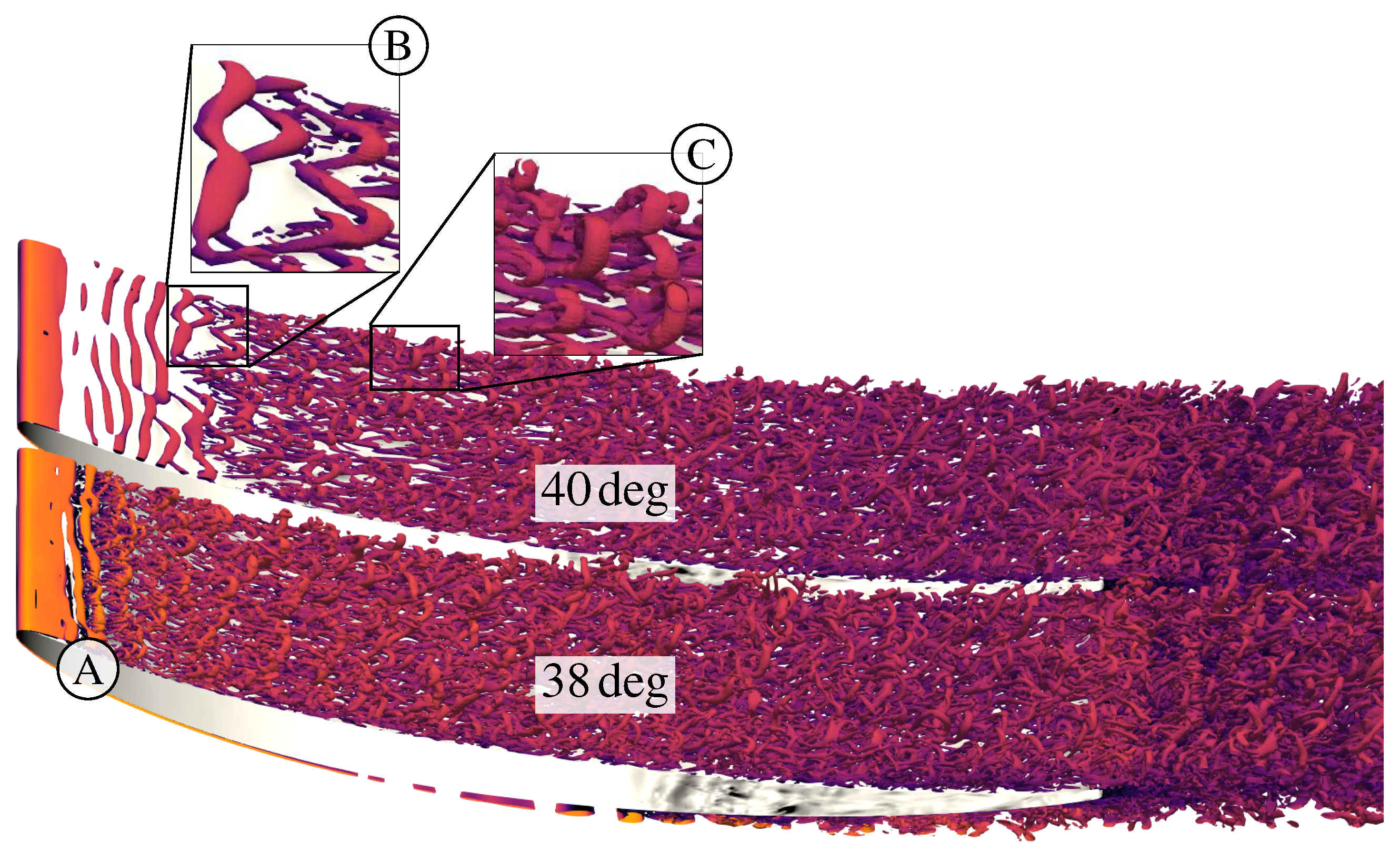
4.1. Instantaneous Flow Field
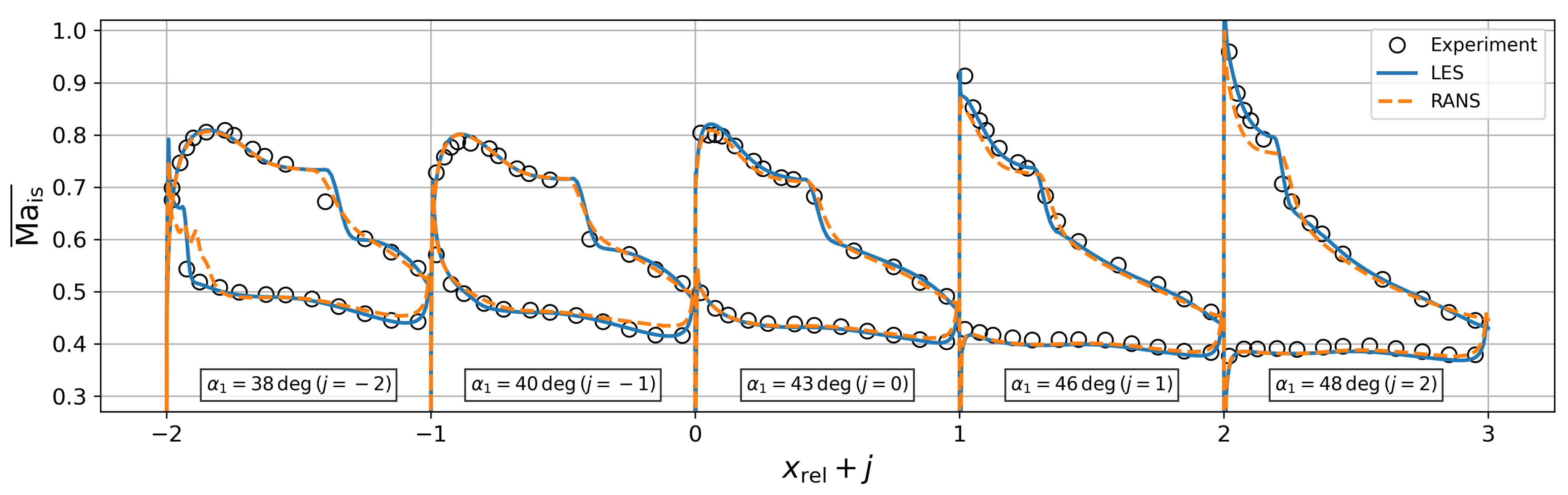
4.2. Blade Loading
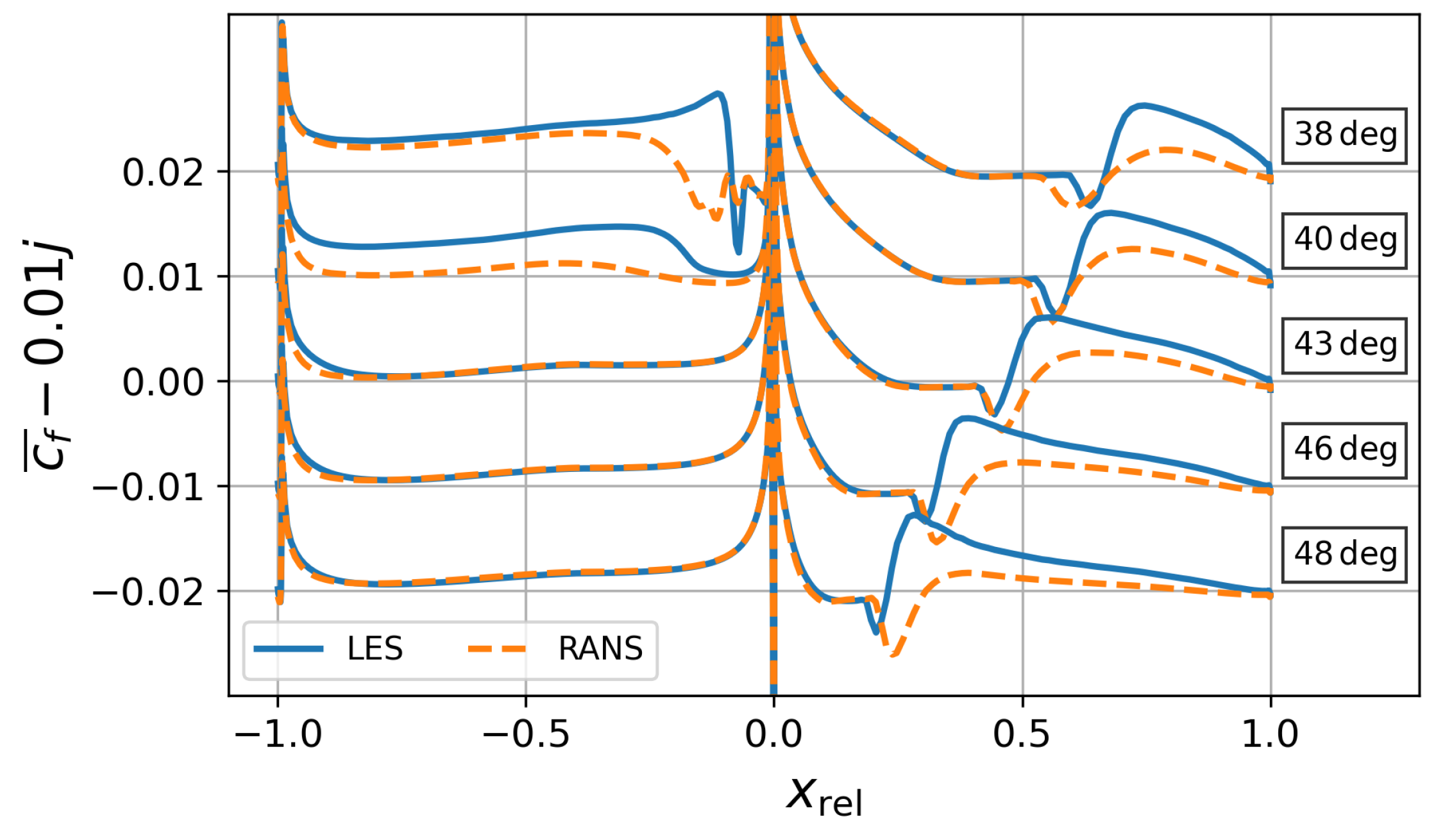
4.3. Skin Friction
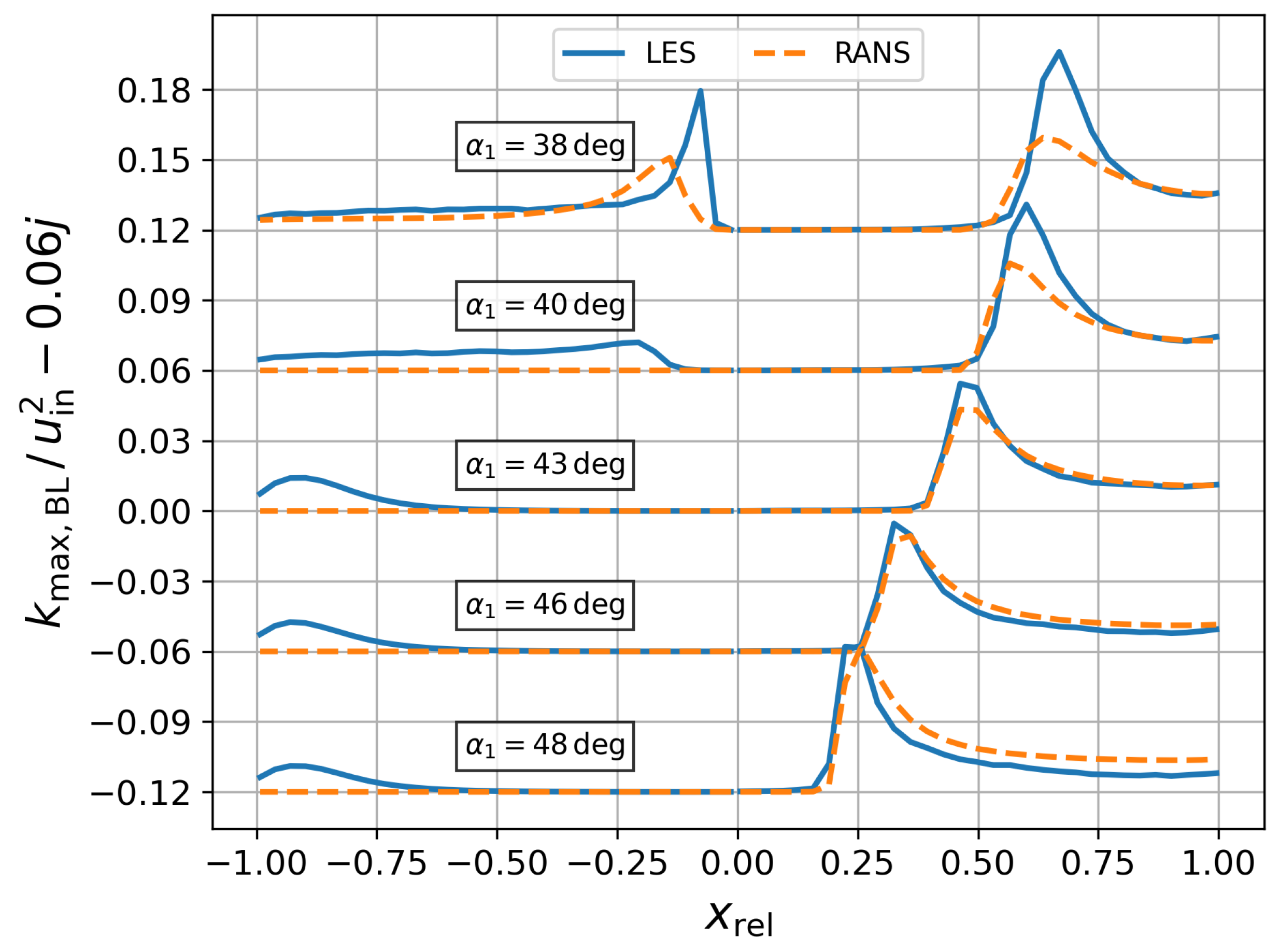
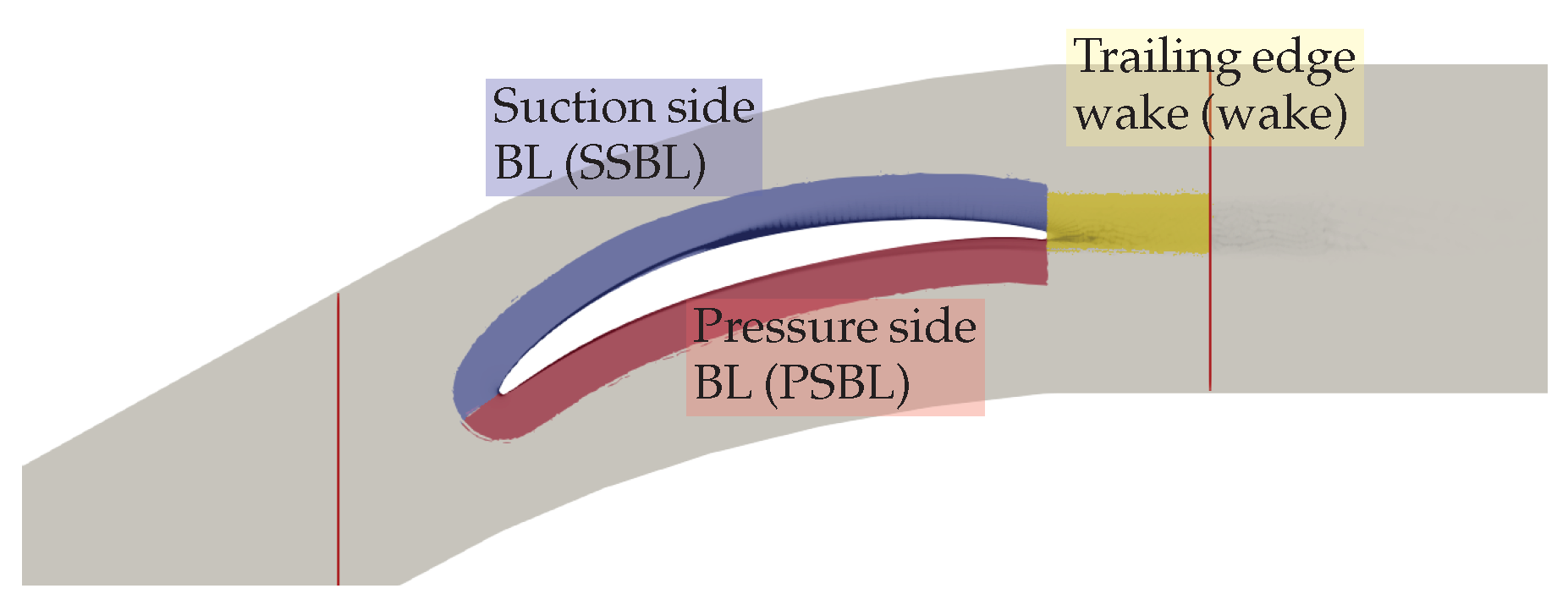
4.4. Boundary Layer Analysis
4.5. Conventional Wake Loss Analysis
4.6. Cascade Deflection Characteristics
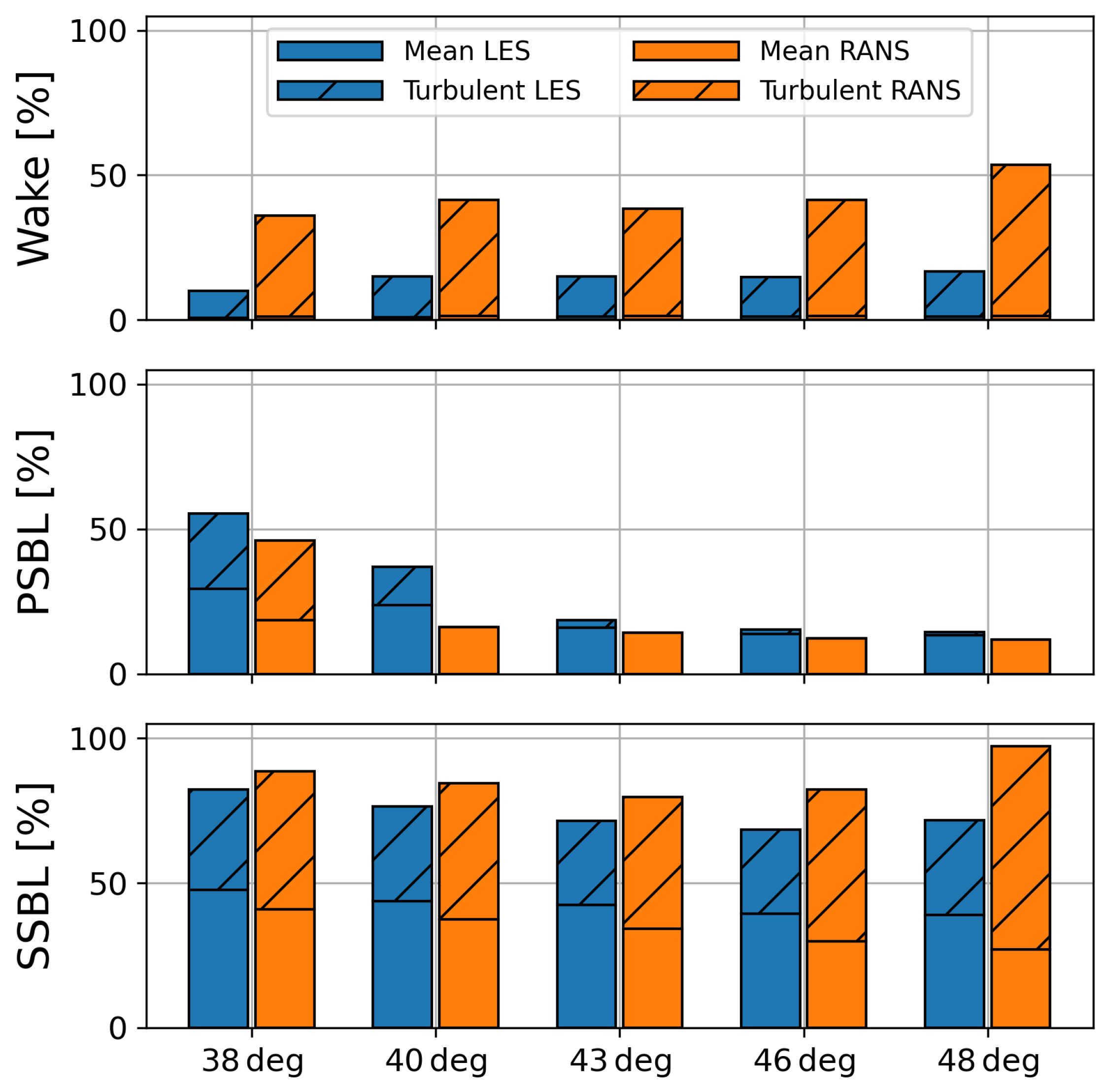
4.7. Entropy Generation Breakdown
- Suction-side boundary layer with and above the camber line;
- Pressure-side boundary layer with and below the camber line;
- Trailing edge wake with (), where is the vorticity vector and the prime coordinates represent the coordinate system aligned with the mean flow.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADP | Aerodynamic design point |
| AVDR | Axial velocity density ratio |
| DG | Discontinuous Galerkin |
| DGSEM | Discontinuous Galerkin Spectral Element Method |
| DOF | Degrees of freedom |
| DNS | Direct numerical simulation |
| LE | Leading edge |
| LES | Large-eddy simulation |
| MP | Measurement plane |
| MUSCL | Monotonic Upstream-centered Scheme for Conservation Laws |
| RANS | Reynolds-averaged Navier–Stokes |
| TE | Trailing edge |
| Variables | |
| b | Pitch |
| c | Chord length |
| Skin friction coefficient | |
| d | Distance |
| Sampling frequency | |
| g | Entropy generation |
| h | Channel height |
| j | Incidence |
| k | Turbulent kinetic energy |
| p | Static pressure |
| Convective time unit | |
| Reference velocity magnitude | |
| Cartesian coordinates | |
| F | Physical flux |
| T | Static temperature |
| V | Volume |
| Ma | Mach number |
| Re | Reynolds number |
| Tu | Turbulence intensity |
| Angle | |
| Deflection angle | |
| Turbulent dissipation rate | |
| Reference density | |
| Total pressure loss, vorticity | |
| Viscous stress | |
| Blade-aligned directions (streamwise, normal, spanwise) | |
| Subscripts | |
| 1 | Inflow conditions at MP1 |
| 2 | Outflow conditions at MP2 |
| in | Conditions at CFD inlet |
| out | Conditions at CFD outlet |
| t | Stagnation-point values |
| s | Stagger angle |
| adv | Advective component |
| rel | Relative |
References
- Hergt, A.; Pesch, M.; Grund, S.; Flamm, J. Low Reynolds Number Effects in Compressor Blade Design. Int. J. Gas Turbine Propuls. Power Syst. 2024, 15, v15n4tp08. [Google Scholar] [CrossRef]
- Diehl, M.; Schreiber, C.; Schiffmann, J. The Role of Reynolds Number Effect and Tip Leakage in Compressor Geometry Scaling at Low Turbulent Reynolds Numbers. J. Turbomach. 2020, 142, 031003. [Google Scholar] [CrossRef]
- Bennett, M.; Chapman, J.W.; Wells, D.P. An Approach to Evaluating the Impact of Small-core Turbofan Technologies on Engine and Aircraft Performance. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar] [CrossRef]
- Voß, C.; Aulich, M.; Kaplan, B.; Nicke, E. Automated Multiobjective Optimisation in Axial Compressor Blade Design. In Proceedings of the ASME Turbo Expo: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; Volume 6: Turbomachinery, Parts A and B, pp. 1289–1297. [Google Scholar] [CrossRef]
- Voß, C.; Hemmert-Pottmann, S.; Schmitz, A. Multi-fidelity optimization of a highly loaded low pressure compressor. In Proceedings of the Second European Workshop on MDO for Aeronautical Industrial Applications, Toulouse, France, 19–20 November 2019. [Google Scholar]
- Michelassi, V.; Chen, L.W.; Pichler, R.; Sandberg, R.D. Compressible Direct Numerical Simulation of Low-Pressure Turbines—Part II: Effect of Inflow Disturbances. J. Turbomach. 2015, 137, 071005. [Google Scholar] [CrossRef]
- Leggett, J.; Priebe, S.; Shabbir, A.; Michelassi, V.; Sandberg, R.; Richardson, E. Loss Prediction in an Axial Compressor Cascade at Off-Design Incidences with Free Stream Disturbances Using Large Eddy Simulation. J. Turbomach. 2018, 140, 071005. [Google Scholar] [CrossRef]
- Bergmann, M.; Morsbach, C.; Klose, B.F.; Ashcroft, G.; Kügeler, E. A Numerical Test Rig for Turbomachinery Flows Based on Large Eddy Simulations with a High-Order Discontinuous Galerkin Scheme—Part I: Sliding Interfaces and Unsteady Row Interactions. J. Turbomach. 2023, 146, 021005. [Google Scholar] [CrossRef]
- Morsbach, C.; Bergmann, M.; Tosun, A.; Klose, B.F.; Bechlars, P.; Kügeler, E. A Numerical Test Rig for Turbomachinery Flows Based on Large Eddy Simulations with a High-Order Discontinuous Galerkin Scheme—Part III: Secondary Flow Effects. J. Turbomach. 2023, 146, 021007. [Google Scholar] [CrossRef]
- Klose, B.F.; Morsbach, C.; Bergmann, M.; Munoz Lopez, E.J.; Hergt, A.; Kügeler, E. The Unsteady Shock–Boundary Layer Interaction in a Compressor Cascade—Part II: High-Fidelity Simulation. J. Turbomach. 2025, 147, 091002. [Google Scholar] [CrossRef]
- Choi, H.; Moin, P. Grid-point requirements for large eddy simulation: Chapman’s estimates revisited. Phys. Fluids 2012, 24, 011702. [Google Scholar] [CrossRef]
- Bergmann, M.; Gölden, R.; Morsbach, C. Numerical investigation of split form nodal discontinuous Galerkin schemes for the implicit LES of a turbulent channel flow. In Proceedings of the 7th European Conference on Computational Fluid Dynamics, Glasgow, UK, 11–15 June 2018. [Google Scholar]
- Bergmann, M. A Split-Form Discontinuous Galerkin Spectral Element Framework for Scale-Resolving Simulations of Turbomachinery Flows. Ph.D. Thesis, Universitätsbibliothek, Ruhr-Universität Bochum, Bochum, Germany, 2024. [Google Scholar] [CrossRef]
- Bergmann, M.; Morsbach, C.; Ashcroft, G. Assessment of Split Form Nodal Discontinuous Galerkin Schemes for the LES of a Low Pressure Turbine Profile. In Proceedings of the Direct and Large Eddy Simulation XII, Madrid, Spain, 5–7 June 2019; García-Villalba, M., Kuerten, H., Salvetti, M.V., Eds.; Springer: Cham, Switzerland, 2020; pp. 365–371. [Google Scholar]
- Klose, B.F.; Morsbach, C.; Bergmann, M.; Hergt, A.; Klinner, J.; Grund, S.; Kügeler, E. A Numerical Test Rig for Turbomachinery Flows Based on Large Eddy Simulations with a High-Order Discontinuous Galerkin Scheme—Part II: Shock Capturing and Transonic Flows. J. Turbomach. 2023, 146, 021006. [Google Scholar] [CrossRef]
- Bergmann, M.; Morsbach, C.; Möller, F.M.; Klose, B.F.; Hergt, A.; Goinis, G. A Comparative Study of Varying Incidence Angle Effects on a Low-Reynolds-Number Compressor Cascade Based on Experiments and Low-Fidelity and High-Fidelity Numerical Simulations. In Proceedings of the 16th European Turbomachinery Conference, Paper n. ETC2025-231. Hannover, Germany, 24–28 March 2025. [Google Scholar]
- Sonoda, T.; Yamaguchi, Y.; Arima, T.; Olhofer, M.; Sendhoff, B.; Schreiber, H.A. Advanced High Turning Compressor Airfoils for Low Reynolds Number Condition—Part I: Design and Optimization. J. Turbomach. 2004, 126, 350–359. [Google Scholar] [CrossRef]
- Schreiber, H.A.; Steinert, W.; Sonoda, T.; Arima, T. Advanced High-Turning Compressor Airfoils for Low Reynolds Number Condition—Part II: Experimental and Numerical Analysis. J. Turbomach. 2004, 126, 482–492. [Google Scholar] [CrossRef]
- Hergt, A.; Hage, W.; Grund, S.; Steinert, W.; Terhorst, M.; Schongen, F.; Wilke, Y. Riblet Application in Compressors: Toward Efficient Blade Design. J. Turbomach. 2015, 137, 111006. [Google Scholar] [CrossRef]
- Steinert, W.; Fuchs, R.; Starken, H. Inlet Flow Angle Determination of Transonic Compressor Cascades. J. Turbomach. 1992, 114, 487–493. [Google Scholar] [CrossRef]
- Hergt, A.; Klinner, J.; Grund, S.; Willert, C.; Steinert, W.; Beversdorff, M. On the Importance of Transition Control at Transonic Compressor Blades. J. Turbomach. 2021, 143, 031007. [Google Scholar] [CrossRef]
- Morsbach, C.; di Mare, F. Conservative segregated solution method for turbulence model equations in compressible flows. In Proceedings of the 6th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2012), Vienna, Austria, 10–14 September 2012. [Google Scholar]
- Menter, F.; Kuntz, M.; Langtry, R. Ten years of Industrial experience with the SST model. In Proceedings of the Turbulence, Heat and Mass Transfer 4, Antalya, Turkey, 12–17 October 2003; Hanjalić, K., Nagano, Y., Tummers, M., Eds.; Begell House, Inc.: Danbury, CT, USA, 2003; pp. 625–632. [Google Scholar]
- Kato, M.; Launder, B.E. The Modeling of Turbulent Flow Around Stationary and Vibrating Square Cylinders. In Proceedings of the 9th Symposium on Turbulent Shear Flows, Kyoto, Japan, 16–18 August 1993; pp. 10.4.1–10.4.6. [Google Scholar]
- Langtry, R.B.; Menter, F.R. Correlation-Based Transition Modeling for Unstructured Parallelized Computational Fluid Dynamics Codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Schlüß, D.; Frey, C.; Ashcroft, G. Consistent Non-reflecting Boundary Conditions for Both Steady and Unsteady Flow Simulations in Turbomachinery Applications. In Proceedings of the ECCOMAS Congress 2016 VII European Congress on Computational Methods in Applied Sciences and Engineering, Crete, Greece, 5–10 June 2016. [Google Scholar]
- Giles, M. UNSFLO: A Numerical Method for the Calculation of Unsteady Flow in Turobmachinery; Technical report, Gas Turbine Laboratory Report GTL 205; MIT Department of Aeronautics and Astronautics: Cambridge, MA, USA, 1991. [Google Scholar]
- Bolinches-Gisbert, M.; Robles, D.C.; Corral, R.; Gisbert, F. Prediction of Reynolds Number Effects on Low-Pressure Turbines Using a High-Order ILES Method. J. Turbomach. 2020, 142, 031002. [Google Scholar] [CrossRef]
- Weber, A.; Sauer, M. PyMesh—Template Documentation; Technical report DLR-IB-AT-KP-2016-34; Institute of Propulsion Technology, German Aerospace Center (DLR): Cologne, Germany, 2016. [Google Scholar]
- Bassi, F.; Rebay, S. A High-Order Accurate Discontinuous Finite Element Method for the Numerical Solution of the Compressible Navier–Stokes Equations. J. Comput. Phys. 1997, 131, 267–279. [Google Scholar] [CrossRef]
- Gassner, G.J.; Winters, A.R.; Kopriva, D.A. Split form nodal discontinuous Galerkin schemes with summation-by-parts property for the compressible Euler equations. J. Comput. Phys. 2016, 327, 39–66. [Google Scholar] [CrossRef]
- Kennedy, C.A.; Gruber, A. Reduced Aliasing Formulations of the Convective Terms Within the Navier-Stokes Equations for a Compressible Fluid. J. Comput. Phys. 2008, 227, 1676–1700. [Google Scholar] [CrossRef]
- Shu, C.W.; Osher, S. Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 1988, 77, 439–471. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. Synthetic Turbulence Generators for RANS-LES Interfaces in Zonal Simulations of Aerodynamic and Aeroacoustic Problems. Flow Turbul. Combus. 2014, 93, 63–92. [Google Scholar] [CrossRef]
- Morsbach, C.; Franke, M. Analysis of a Synthetic Turbulence Generation Method for Periodic Configurations. In Proceedings of the Direct and Large-Eddy Simulation XI; Salvetti, M.V., Armenio, V., Fröhlich, J., Geurts, B.J., Kuerten, H., Eds.; Springer: Cham, Switzerland, 2019; pp. 169–174. [Google Scholar]
- Leyh, S.; Morsbach, C. The Coupling of a Synthetic Turbulence Generator with Turbomachinery Boundary Conditions. In Proceedings of the Direct and Large Eddy Simulation XII; García-Villalba, M., Kuerten, H., Salvetti, M.V., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Georgiadis, N.J.; Rizzetta, D.P.; Fureby, C. Large-Eddy Simulation: Current Capabilities, Recommended Practices, and Future Research. AIAA J. 2012, 48, 1772–1784. [Google Scholar] [CrossRef]
- Bergmann, M.; Morsbach, C.; Ashcroft, G.; Kügeler, E. Statistical Error Estimation Methods for Engineering-Relevant Quantities From Scale-Resolving Simulations. J. Turbomach. 2021, 144, 031005. [Google Scholar] [CrossRef]
- Denton, J.D. Loss Mechanisms in Turbomachines. In Proceedings of the ASME 1993 International Gas Turbine and Aeroengine Congress and Exposition, Cincinnati, OH, USA, 24–27 May 1993; Volume 2: Combustion and Fuels; Oil and Gas Applications; Cycle Innovations; Heat Transfer; Electric Power; Industrial and Cogeneration; Ceramics; Structures and Dynamics; Controls, Diagnostics and Instrumentation. [Google Scholar] [CrossRef]
- Gassner, G.J.; Beck, A.D. On the accuracy of high-order discretizations for underresolved turbulence simulations. Theor. Comput. Fluid Dyn. 2012, 27, 221–237. [Google Scholar] [CrossRef]
- Muth, B.; Schwarze, M.; Niehuis, R.; Franke, M. Investigation of CFD Prediction Capabilities for Low Reynolds Turbine Aerodynamics. In Proceedings of the ASME Turbo Expo 2009: Power for Land, Sea, and Air, Orlando, FL, USA, 8–12 June 2009; ASMEDC: New York, NY, USA, 2009; Volume 7: Turbomachinery, Parts A and B, pp. 875–884. [Google Scholar] [CrossRef]
- Müller-Schindewolffs, C.; Baier, R.D.; Seume, J.R.; Herbst, F. Direct Numerical Simulation Based Analysis of RANS Predictions of a Low-Pressure Turbine Cascade. J. Turbomach. 2017, 139, 081006. [Google Scholar] [CrossRef]
- Morsbach, C.; Bergmann, M.; Tosun, A.; Klose, B.F.; Kügeler, E.; Franke, M. Large Eddy Simulation of a Low-Pressure Turbine Cascade with Turbulent End Wall Boundary Layers. Flow Turbul. Combust. 2024, 112, 165–190. [Google Scholar] [CrossRef]
- Cumpsty, N.A.; Horlock, J.H. Averaging Nonuniform Flow for a Purpose. J. Turbomach. 2005, 128, 120–129. [Google Scholar] [CrossRef]
- Kock, F. Bestimmung der Lokalen Entropieproduktion in Turbulenten Strömungen und Deren Nutzung zur Bewertung Konvektiver Transportprozesse. Ph.D. Thesis, TU Hamburg-Harburg, Hamburg, Germany, 2003. [Google Scholar]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]
- Zhao, Y.; Sandberg, R.D. Using a New Entropy Loss Analysis to Assess the Accuracy of RANS Predictions of an HPT Vane. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019; Volume 2C: Turbomachinery. [Google Scholar] [CrossRef]
- Borcherding, T.; Bode, C.; Rosenzweig, M.; Przytarski, P.J.; Leggett, J.; Sandberg, R.D. Entropy Loss Breakdown Comparison for LES and RANS of a Transonic Compressor Stage Midspan Section. In Proceedings of the ASME Turbo Expo 2023: Turbomachinery Technical Conference and Exposition, Boston, MA, USA, 26–30 June 2023; Volume 13A: Turbomachinery—Axial Flow Fan and Compressor Aerodynamics. [Google Scholar] [CrossRef]
- Wilcox, D. Turbulence Modeling for CFD; Number Bd. 1 in Turbulence Modeling for CFD; DCW Industries: Dhrangadhra, Gujarat, 2006. [Google Scholar]
- Raina, G.; Bousquet, Y.; Luquet, D.; Lippinois, E.; Binder, N. Loss Breakdown in Axial Turbines: A New Method for Vortex Loss and Wake Detection from 3D RANS Simulations. J. Turbomach. 2025, 147, 061006. [Google Scholar] [CrossRef]
- Goinis, G.; Satcunanathan, S.; Bergmann, M. Examining the Potential of High-Order SRS to Support RANS-Based Compressor Airfoil Optimization. In Proceedings of the ASME Turbo Expo 2025: Turbomachinery Technical Conference and Exposition, Memphis, TN, USA, 16–20 June 2025; Volume 11: Turbomachinery—Deposition, Erosion, Fouling, and Icing; Design Methods & CFD Modeling for Turbomachinery; Ducts, Noise & Component Interactions. [Google Scholar] [CrossRef]


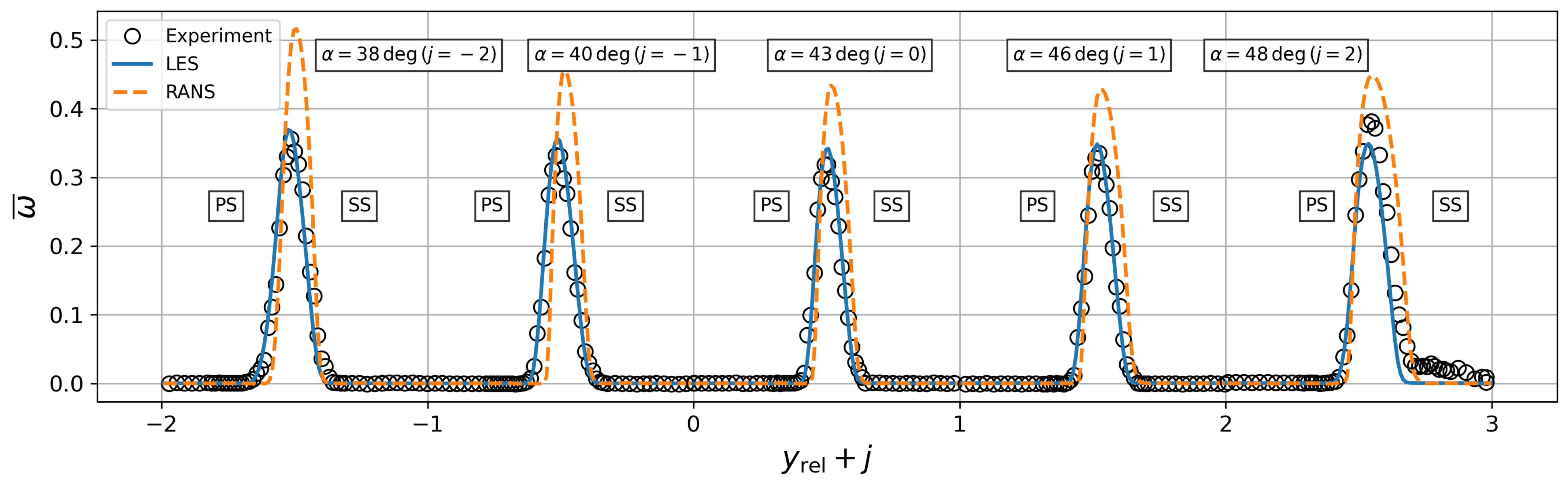
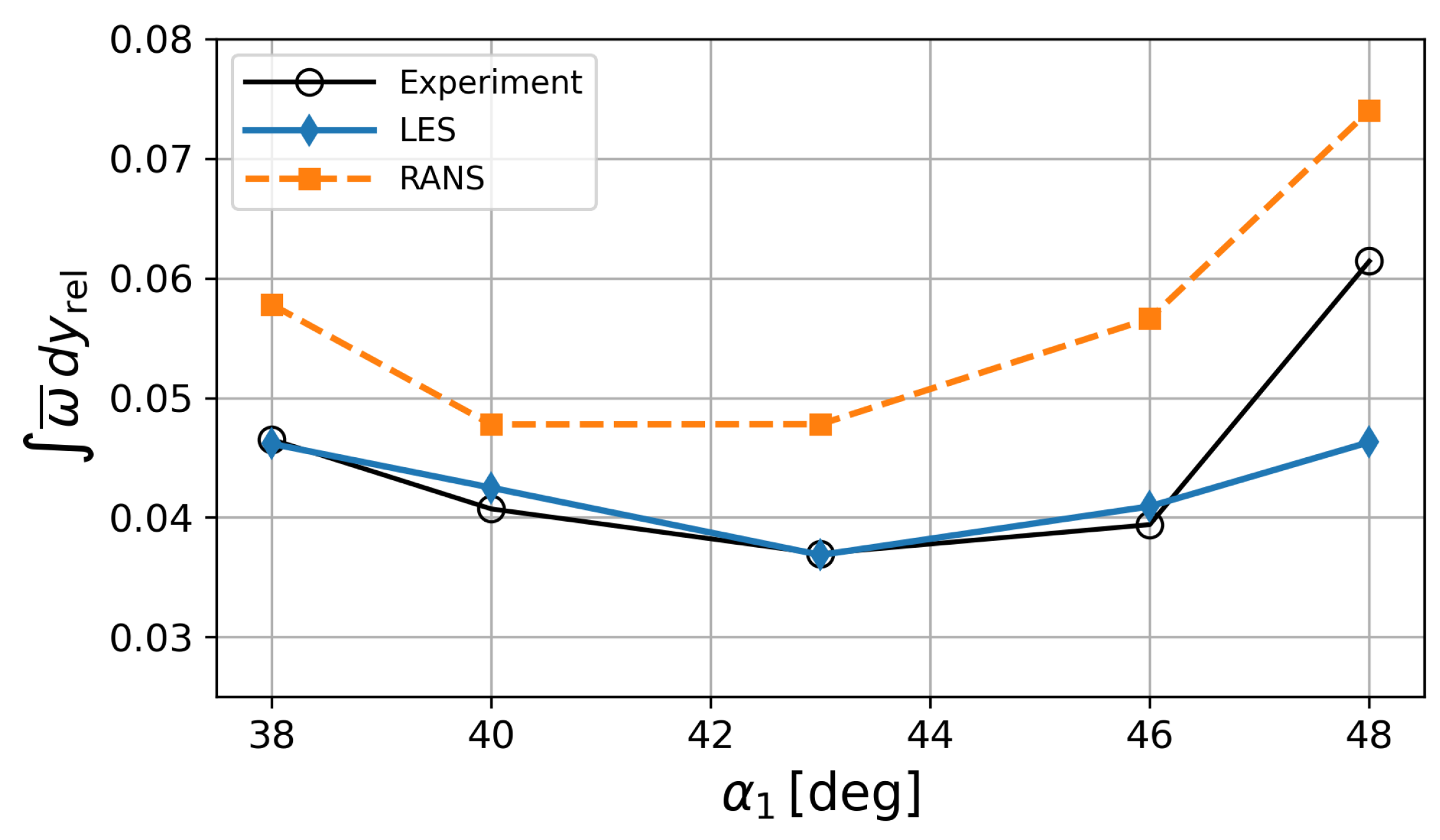

| Inflow Mach number | |
| Inflow Reynolds number | |
| Inflow angle | |
| Inflow turbulence intensity | |
| Chord length c | 70 mm |
| Pitch to chord ratio | |
| Height to chord ratio | |
| Stagger angle | |
| AVDR |
| Ma1 | Re1 | α1 [deg] | Tu1 [%] | LT/c | AVDR | Δz/c | DOF [106] | |
|---|---|---|---|---|---|---|---|---|
| Experiment | 0.603 | 150,791 | 43.0 | 0.3–0.5 | - | 1.0382 | 2.4 | |
| LES-Base | 0.630 | 155,377 | 43.0 | 0 | 0 | 1 | 0.2 | 63.7 |
| LES-AVDR | 0.600 | 150,294 | 43.0 | 0 | 0 | 1.0381 | 0.2 | 63.7 |
| LES-Span0.4 | 0.600 | 150,297 | 43.0 | 0 | 0 | 1.0380 | 0.4 | 127.5 |
| LES-Tu | 0.603 | 150,833 | 43.0 | 0.33 | 0.01429 | 1.0381 | 0.2 | 63.7 |
| Ma1 | Re1 | α1 [deg] | Tu1 [%] | AVDR | |
|---|---|---|---|---|---|
| , | |||||
| Exp | 0.603 | 160,361 | 38.0 | 0.3–0.5 | 1.035 |
| RANS | 0.598 | 159,290 | 38.0 | 0.35 | 1.035 |
| LES | 0.603 | 160,379 | 38.0 | 0.35 | 1.036 |
| , | |||||
| Exp | 0.602 | 151,992 | 40.0 | 0.3–0.5 | 1.024 |
| RANS | 0.595 | 151,127 | 40.0 | 0.36 | 1.024 |
| LES | 0.601 | 151,773 | 40.0 | 0.35 | 1.024 |
| , | |||||
| Exp | 0.603 | 150,791 | 43.0 | 0.3–0.5 | 1.038 |
| RANS | 0.595 | 149,443 | 43.0 | 0.35 | 1.038 |
| LES | 0.603 | 150,833 | 43.0 | 0.33 | 1.038 |
| , | |||||
| Exp | 0.600 | 147,764 | 46.0 | 0.3–0.5 | 1.032 |
| RANS | 0.590 | 145,862 | 46.0 | 0.35 | 1.032 |
| LES | 0.599 | 147,446 | 46.0 | 0.34 | 1.032 |
| , | |||||
| Exp | 0.593 | 149,447 | 48.0 | 0.3–0.5 | 1.024 |
| RANS | 0.593 | 149,259 | 48.0 | 0.35 | 1.024 |
| LES | 0.608 | 152,002 | 48.0 | 0.38 | 1.024 |
| RANS | 24.0% | 17.3% | 29.3% | 43.7% | 20.5% |
| LES | −0.8% | 4.4% | −0.3 % | 3.9% | −24.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the EUROTURBO. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Bergmann, M.; Morsbach, C.; Möller, F.M.; Klose, B.F.; Hergt, A.; Goinis, G. A Comparative Study of Varying Incidence Angle Effects on a Low-Reynolds-Number Compressor Cascade Based on Experiments and Low-Fidelity and High-Fidelity Numerical Simulations. Int. J. Turbomach. Propuls. Power 2025, 10, 42. https://doi.org/10.3390/ijtpp10040042
Bergmann M, Morsbach C, Möller FM, Klose BF, Hergt A, Goinis G. A Comparative Study of Varying Incidence Angle Effects on a Low-Reynolds-Number Compressor Cascade Based on Experiments and Low-Fidelity and High-Fidelity Numerical Simulations. International Journal of Turbomachinery, Propulsion and Power. 2025; 10(4):42. https://doi.org/10.3390/ijtpp10040042
Chicago/Turabian StyleBergmann, Michael, Christian Morsbach, Felix M. Möller, Björn F. Klose, Alexander Hergt, and Georgios Goinis. 2025. "A Comparative Study of Varying Incidence Angle Effects on a Low-Reynolds-Number Compressor Cascade Based on Experiments and Low-Fidelity and High-Fidelity Numerical Simulations" International Journal of Turbomachinery, Propulsion and Power 10, no. 4: 42. https://doi.org/10.3390/ijtpp10040042
APA StyleBergmann, M., Morsbach, C., Möller, F. M., Klose, B. F., Hergt, A., & Goinis, G. (2025). A Comparative Study of Varying Incidence Angle Effects on a Low-Reynolds-Number Compressor Cascade Based on Experiments and Low-Fidelity and High-Fidelity Numerical Simulations. International Journal of Turbomachinery, Propulsion and Power, 10(4), 42. https://doi.org/10.3390/ijtpp10040042






