Development of a Reduced Order Model for Turbine Blade Cooling Design †
Abstract
1. Introduction
2. One-Dimensional Cooling Model
3. One-Dimensional Analysis
3.1. Case Setup
3.2. Results
3.3. Sensitivity Analysis
4. CHT Analysis
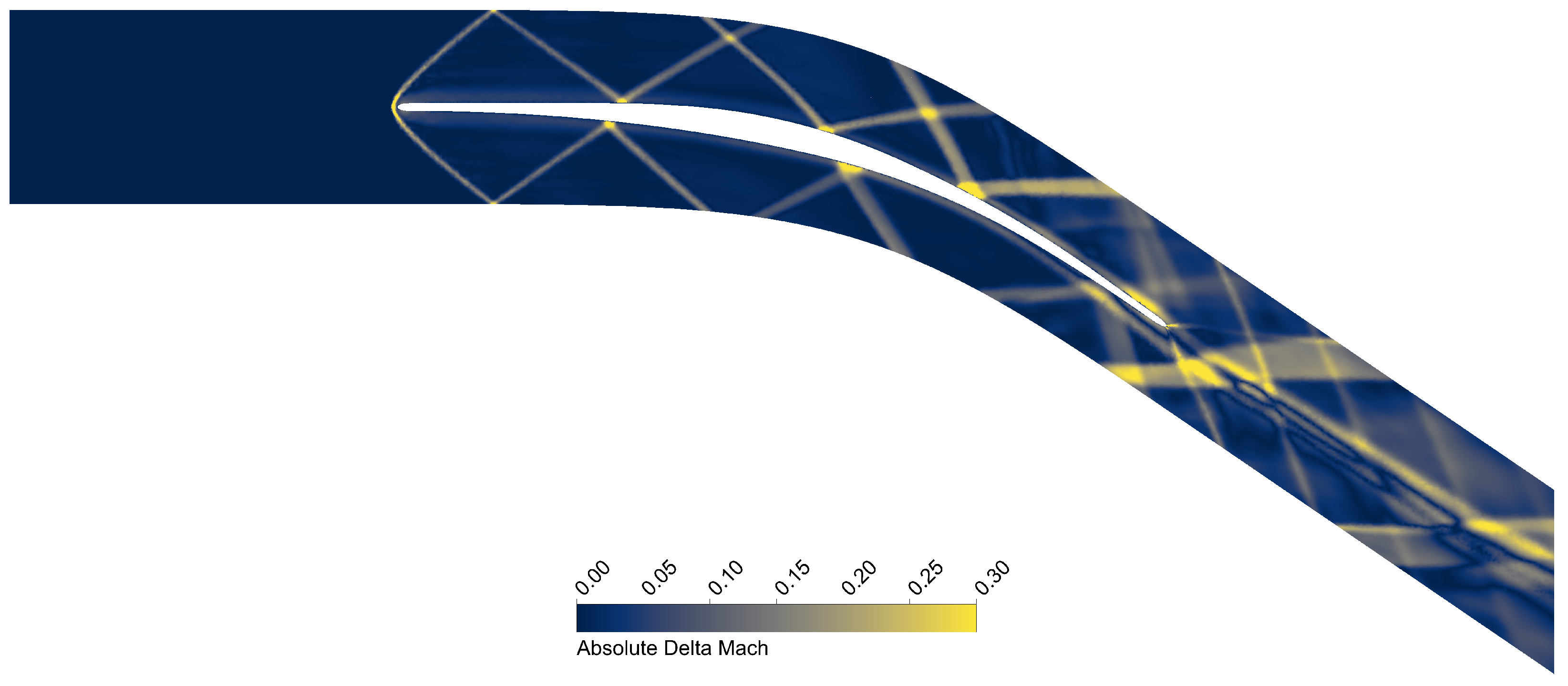
4.1. Validation
4.2. Case Setup
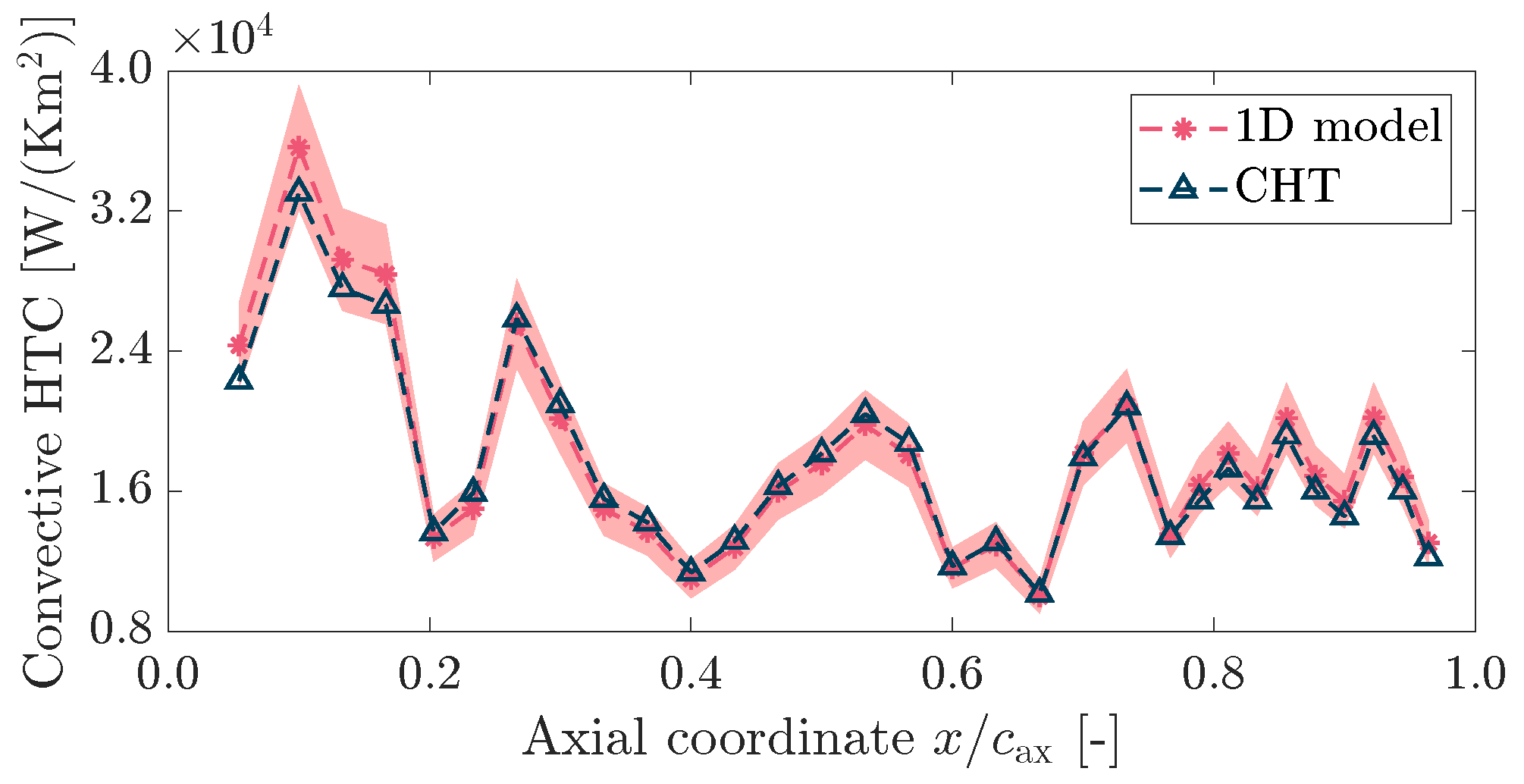
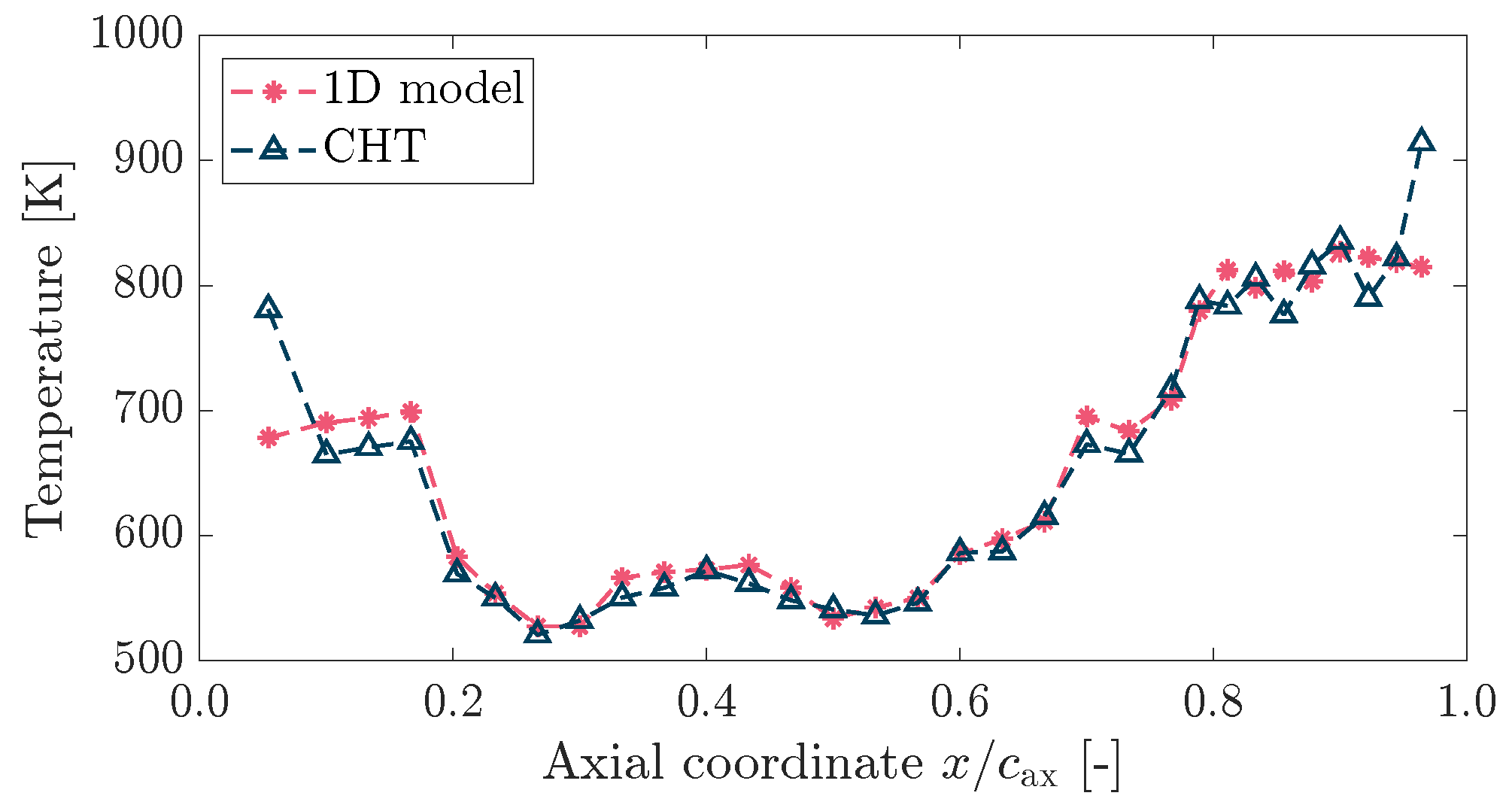
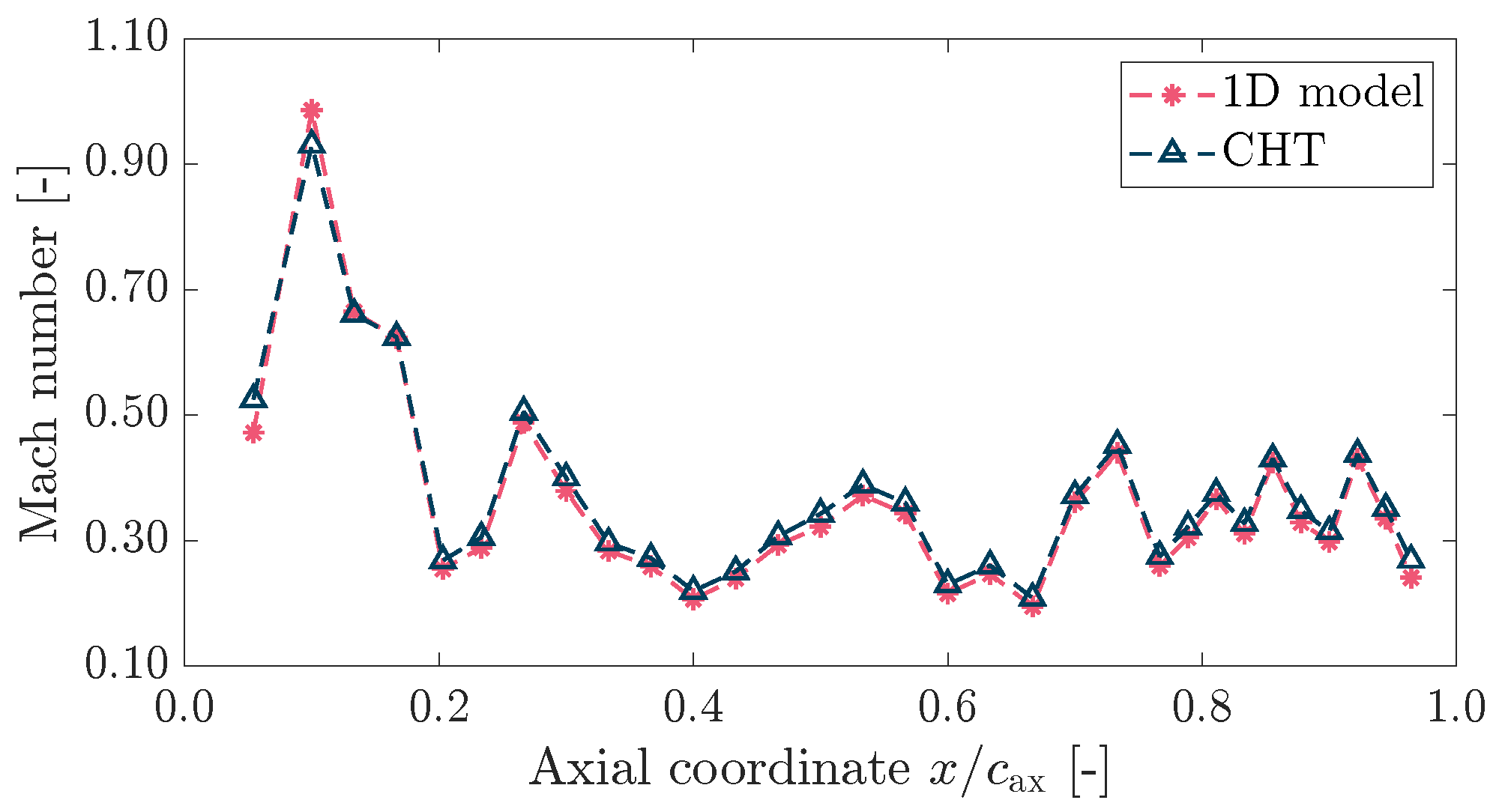
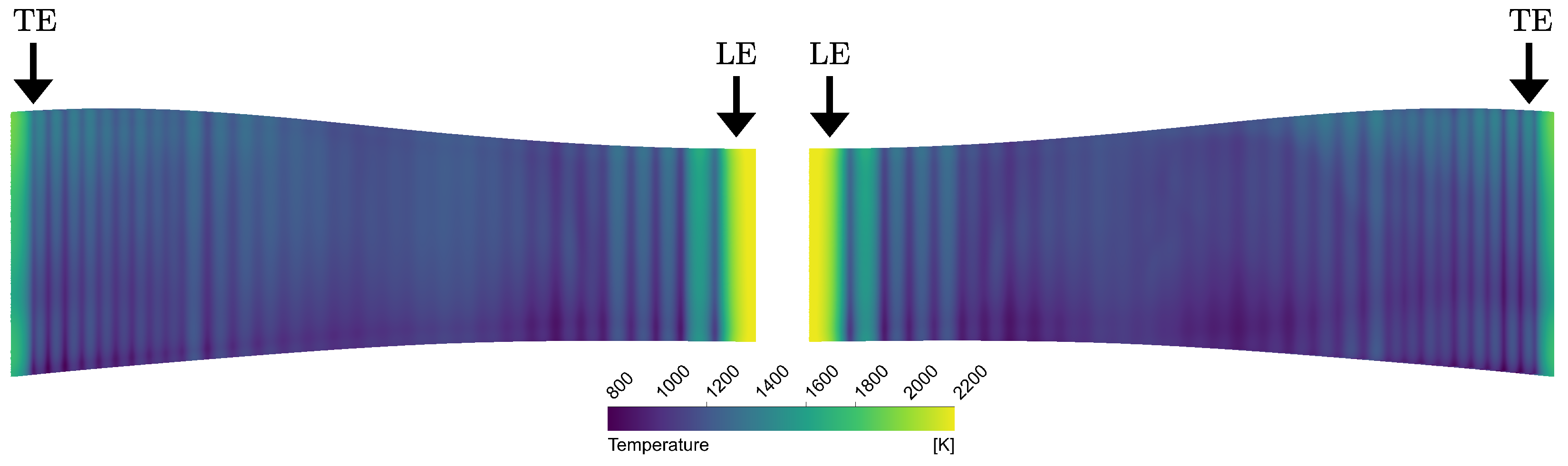
4.3. Results
5. Film Cooling
6. Feasibility Assessment
6.1. Finite Element Analysis
6.2. Cooling Power Requirements
- Option A, tailored for land-based turbine applications, involves the use of external compressors dedicated to supplying the coolant flow to the stator.
- Option B, suitable for both aeroengines and land-based applications, leverages the existing Joule–Brayton cycle compressor. To accommodate the elevated pressures required by the internal cooling flow, additional compression stages are introduced. These stages compensate for the pressure gain occurring in the rotating detonation combustor and ensure the coolant reaches the necessary high-pressure level required for internal cooling.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| blade channel outlet cross sectional area | m2 | |
| cooling channel lateral area | m2 | |
| b | blade height | m |
| axial chord | m | |
| specific heat at constant pressure | J/(kg K) | |
| hydraulic diameter | m | |
| turbulence heat transfer enhancement factor | ||
| f | Darcy friction factor | |
| h | convective heat transfer coefficient | W/(K m2) |
| specific enthalpy | J/kg | |
| K | error coefficient | |
| k | thermal conductivity | W/(m K) |
| Ma | Mach number | |
| mass flow rate | kg/s | |
| Pr | Prandtl number | |
| p | absolute pressure | Pa |
| thermal power | W | |
| linear thermal power | W/m | |
| heat flux | W/m2 | |
| specific gas constant | J/(kg K) | |
| average surface roughness | μm | |
| S | Sobol’ index | |
| St | Stanton number | |
| t | thickness | m |
| T | absolute temperature | K |
| x | axial coordinate | m |
| non-dimensional wall distance |
Greek Symbols
| blade metal angle | |
| cooling efficiency | |
| coolant-to-gas mass flow ratio | |
| dynamic viscosity | |
| density |
Subscripts
| b | blade |
| c | cooling channel |
| cool | coolant |
| ext | external (hot gas side) |
| g | gas |
| int | internal (coolant side) |
| rec | recovery |
| t | total quantity |
| w | wall |
Superscripts
| average value |
Acronyms
| CFD | computational fluid dynamics |
| CHT | conjugate heat transfer |
| GCI | grid convergence index |
| PCE | polynomial chaos expansion |
| RANS | Reynolds-averaged Navier–Stokes |
| RDE | rotating detonation engine |
| TBC | thermal barrier coating |
Appendix A. Pressure Drop Estimation
References
- Heiser, W.H.; Pratt, D.T. Thermodynamic cycle analysis of pulse detonation engines. J. Propuls. Power 2002, 18, 68–76. [Google Scholar] [CrossRef]
- Paxson, D.E.; Naples, A. Numerical and analytical assessment of a coupled rotating detonation engine and turbine experiment. In Proceedings of the AIAA SciTech Forum—55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; pp. 1–13. [Google Scholar] [CrossRef]
- Sousa, J.; Paniagua, G.; Collado-Morata, E. Analysis of the aerodynamic losses in a supersonic turbine. Am. Soc. Mech. Eng. Power Div. (Publication) POWER 2017, 1, 1–7. [Google Scholar] [CrossRef]
- Anand, V.; Gutmark, E. Rotating detonation combustors and their similarities to rocket instabilities. Prog. Energy Combust. Sci. 2019, 73, 182–234. [Google Scholar] [CrossRef]
- Schwer, D.; Kailasanath, K. Numerical Investigation of Rotating Detonation Engines. In Proceedings of the 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Nashville, TN, USA, 25–28 July 2010; Volume 33, pp. 2195–2202. [Google Scholar] [CrossRef]
- Paniagua, G.; Iorio, M.C.; Vinha, N.; Sousa, J. Design and analysis of pioneering high supersonic axial turbines. Int. J. Mech. Sci. 2014, 89, 65–77. [Google Scholar] [CrossRef]
- Sousa, J.; Paniagua, G. Entropy Minimization Design Approach of Supersonic Internal Passages. Entropy 2015, 17, 5593–5610. [Google Scholar] [CrossRef]
- Mushtaq, N.; Colella, G.; Gaetani, P. Design and Parametric Analysis of a Supersonic Turbine for Rotating Detonation Engine Applications. Int. J. Turbomach. Propuls. Power 2022, 7, 1. [Google Scholar] [CrossRef]
- Mushtaq, N.; Persico, G.; Gaetani, P. The role of endwall shape optimization in the design of supersonic turbines for rotating detonation engines. In Proceedings of the ASME Turbo Expo. American Society of Mechanical Engineers, Rotterdam, The Netherlands, 13–17 June 2022; Volume 10-B. [Google Scholar] [CrossRef]
- Grasa, S.; Paniagua, G. Design and Characterization of Highly Diffusive Turbine Vanes Suitable for Transonic Rotating Detonation Combustors. Int. J. Turbomach. Propuls. Power 2024, 9, 18. [Google Scholar] [CrossRef]
- Lozano, F.; Paniagua, G. Airfoil leading edge blowing to control bow shock waves. Sci. Rep. 2020, 10, 21922. [Google Scholar] [CrossRef] [PubMed]
- Nambiar, S.; Ananno, A.A.; Titus, H.; Wiberg, A.; Tarkian, M. Multidisciplinary Automation in Design of Turbine Vane Cooling Channels. Int. J. Turbomach. Propuls. Power 2024, 9, 7. [Google Scholar] [CrossRef]
- Filinov, E.; Kuz’michev, V.; Yu Tkachenko, A.; Ostapyuk, Y.; Krupenich, I. Estimation of cooling flow rate for conceptual design stage of a gas turbine engine. Proc. Inst. Mech. Eng. Part A J. Power Energy 2021, 235, 2014–2021. [Google Scholar] [CrossRef]
- Jordal, K. Gas Turbine Cooling Modeling–Thermodynamic Analysis and Cycle Simulations. Master’s Thesis, Lund Institute of Technology, Lund, Sweden, 1999. [Google Scholar]
- Ainley, D.G. Internal Air-Cooling for Turbine Blades. A General Design Survey; Technical Report; Aeronautical Research Council: London, UK, 1957. [Google Scholar]
- Horlock, J.H.; Torbidoni, L. Turbine Blade Cooling: The Blade Temperature Distribution. Proc. Inst. Mech. Eng. Part A J. Power Energy 2006, 220, 343–353. [Google Scholar] [CrossRef]
- Consonni, S. Performance Prediction of Gas/Steam Cycles for Power Generation. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1992. [Google Scholar]
- Sciubba, E. Air-cooled gas turbine cycles—Part 1: An analytical method for the preliminary assessment of blade cooling flow rates. Energy 2015, 83, 104–114. [Google Scholar] [CrossRef]
- Masci, R.; Sciubba, E. A Lumped Thermodynamic Model of Gas Turbine Blade Cooling: Prediction of First-Stage Blades Temperature and Cooling Flow Rates. J. Energy Resour. Technol. 2018, 140, 020901. [Google Scholar] [CrossRef]
- Torbidoni, L.; Horlock, J.H. A New Method to Calculate the Coolant Requirements of a High-Temperature Gas Turbine Blade. J. Turbomach. 2005, 127, 191–199. [Google Scholar] [CrossRef]
- Jordal, K.; Torbidoni, L.; Massardo, A.F. Convective Blade Cooling Modelling for the Analysis of Innovative Gas Turbine Cycles. In Proceedings of the Volume 2: Coal, Biomass and Alternative Fuels; Combustion and Fuels; Oil and Gas Applications; Cycle Innovations. American Society of Mechanical Engineers, New Orleans, LA, USA, 4–7 June 2001; Volume 2, pp. 1–8. [Google Scholar] [CrossRef]
- Torbidoni, L.; Massardo, A.F. Analytical Blade Row Cooling Model for Innovative Gas Turbine Cycle Evaluations Supported by Semi-Empirical Air-Cooled Blade Data. J. Eng. Gas Turbines Power 2004, 126, 498–506. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Gnielinski, V. On heat transfer in tubes. Int. J. Heat Mass Transf. 2013, 63, 134–140. [Google Scholar] [CrossRef]
- van de Noort, M.; Ireland, P.T. Genetic Algorithm-Based Optimisation of a Double-Wall Effusion Cooling System for a High-Pressure Turbine Nozzle Guide Vane. Int. J. Turbomach. Propuls. Power 2024, 9, 6. [Google Scholar] [CrossRef]
- Ansys® Fluent, Release 2023 R2; Ansys: Canonsburg, PA, USA, 2023.
- Chartrand, R. Numerical Differentiation of Noisy, Nonsmooth Data. ISRN Appl. Math. 2011, 2011, 1–11. [Google Scholar] [CrossRef]
- Pinardi, A.; Mushtaq, N.; Gaetani, P. Development of a reduced order model for turbine blade cooling design. In Proceedings of the 16th European Turbomachinery Conference, Hannover, Germany, 24–28 March 2025. paper n. ETC2025-226. [Google Scholar]
- Marelli, S.; Lüthen, N.; Sudret, B. UQLab User Manual—Polynomial Chaos Expansions; Technical Report; Chair of Risk, Safety and Uncertainty Quantification, ETH Zurich: Zurich, Switzerland, 2022. [Google Scholar]
- Marelli, S.; Lamas, C.; Konakli, K.; Mylonas, C.; Wiederkehr, P.; Sudret, B. UQLab User Manual—Sensitivity Analysis; Technical Report; Chair of Risk, Safety and Uncertainty Quantification, ETH Zurich: Zurich, Switzerland, 2022. [Google Scholar]
- Marelli, S.; Sudret, B. UQLab: A Framework for Uncertainty Quantification in Matlab. In Proceedings of the Vulnerability, Uncertainty, and Risk, Reston, VA, USA, 7 July 2014; pp. 2554–2563. [Google Scholar] [CrossRef]
- Hadigol, M.; Doostan, A. Least squares polynomial chaos expansion: A review of sampling strategies. Comput. Methods Appl. Mech. Eng. 2018, 332, 382–407. [Google Scholar] [CrossRef]
- Hylton, L.D.; Mihelc, M.S.; Turner, E.R.; Nealy, D.A.; York, R.E. Analytical and Experimental Evaluation of the Heat Transfer Distribution over the Surfaces of Turbine Vanes; Technical Report; NASA: Washington, DC, USA, 1983. [Google Scholar]
- Kumar, A.; Pathak, M. Conjugate heat transfer analysis of internally cooled superalloy turbine blades with grooved channels. Phys. Fluids 2023, 35, 095112. [Google Scholar] [CrossRef]
- Ansys® TurboGrid; Release 2023 R2; Ansys: Canonsburg, PA, USA, 2023.
- Facchini, B.; Magi, A.; Scotti Del Greco, A. Conjugate heat transfer simulation of a radially cooled gas turbine vane. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004; Volume 3, pp. 951–961. [Google Scholar] [CrossRef]
- Pinardi, A. Development of a Reduced Order Model for Turbine Cooling Design. Master’s Thesis, Politecnico di Milano, Milano, Italy, 2024. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. Trans. ASME 2008, 130, 0780011–0780014. [Google Scholar] [CrossRef]
- Gülen, S.C. Gas Turbines for Electric Power Generation; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Lima, R.S. Perspectives on Thermal Gradients in Porous ZrO2-7–8 wt.(YSZ) Thermal Barrier Coatings (TBCs) Manufactured by Air Plasma Spray (APS). Coatings 2020, 10, 812. [Google Scholar] [CrossRef]
- Han, J.C.; Park, J.S.; Lei, C.K. Heat Transfer Enhancement in Channels With Turbulence Promoters. J. Eng. Gas Turbines Power 1985, 107, 628–635. [Google Scholar] [CrossRef]
- Abaqus, release 2024; Dassault Systèmes: Vélizy-Villacoublay, France, 2024.
- INCO. Alloy IN-738 Technical Data—A Practical Guide To the Use of Nickel-Containing Alloys; Technical Report; Nickel Institute: Durham, NC, USA, 2020. [Google Scholar]
- Zhang, P.; Song, Y.; Xia, Z. Exact mathematical formulas for wall-heat flux in compressible turbulent channel flows. Acta Mech. Sin. 2022, 38, 321403. [Google Scholar] [CrossRef]
- Zaretsky, E.B.; Kanel, G.I.; Razorenov, S.V.; Baumung, K. Impact strength properties of nickel-based refractory superalloys at normal and elevated temperatures. Int. J. Impact Eng. 2005, 31, 41–54. [Google Scholar] [CrossRef]
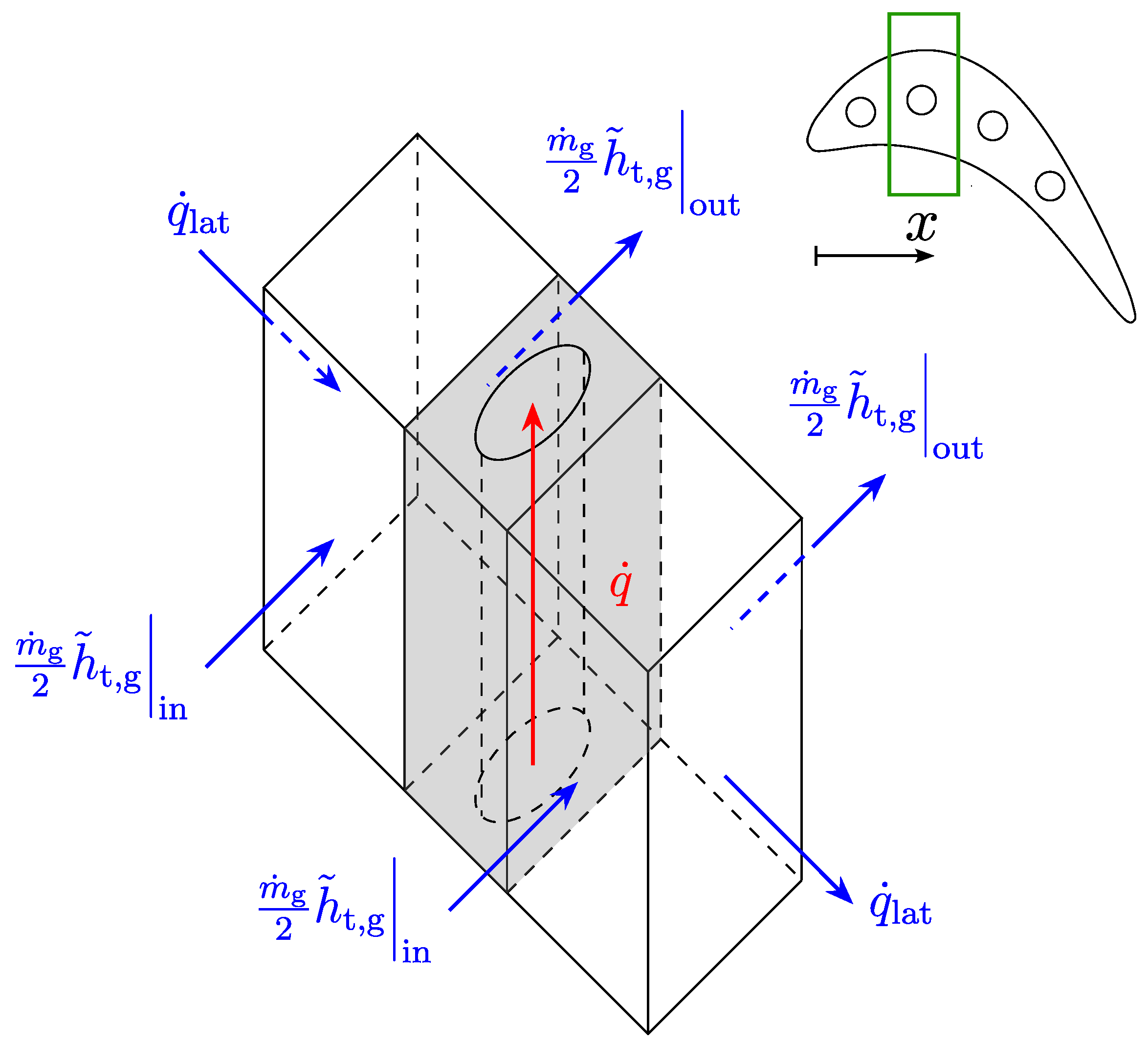
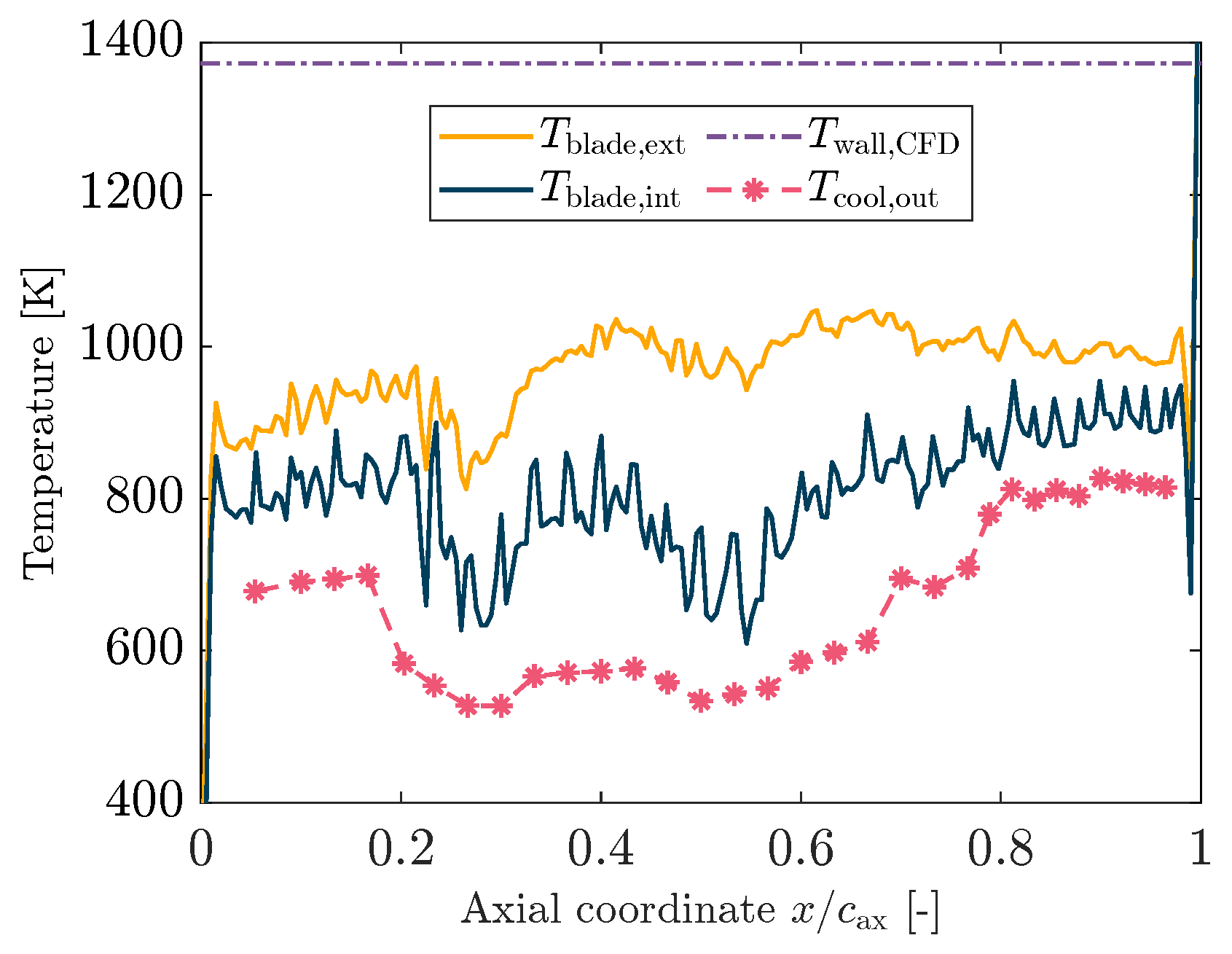
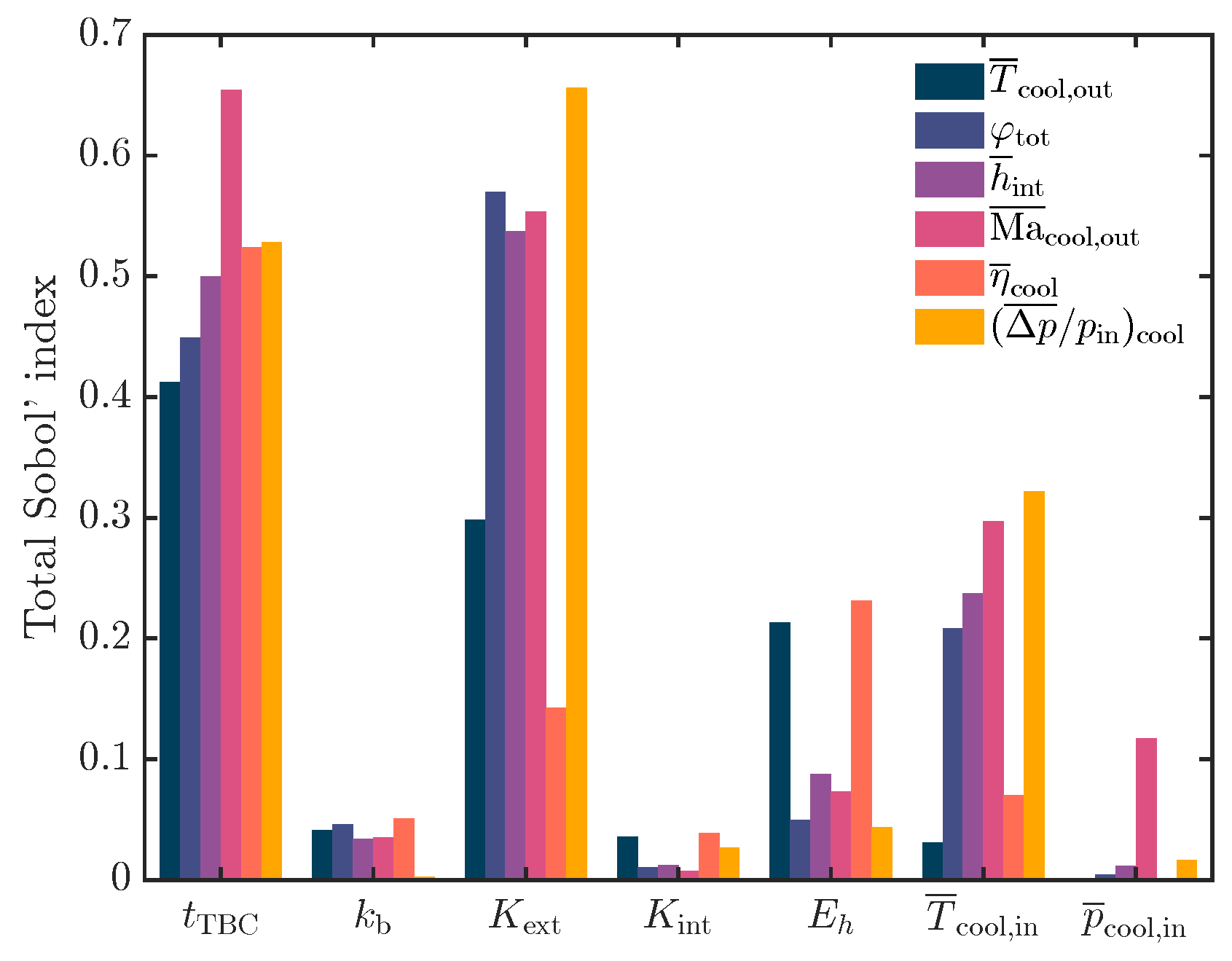
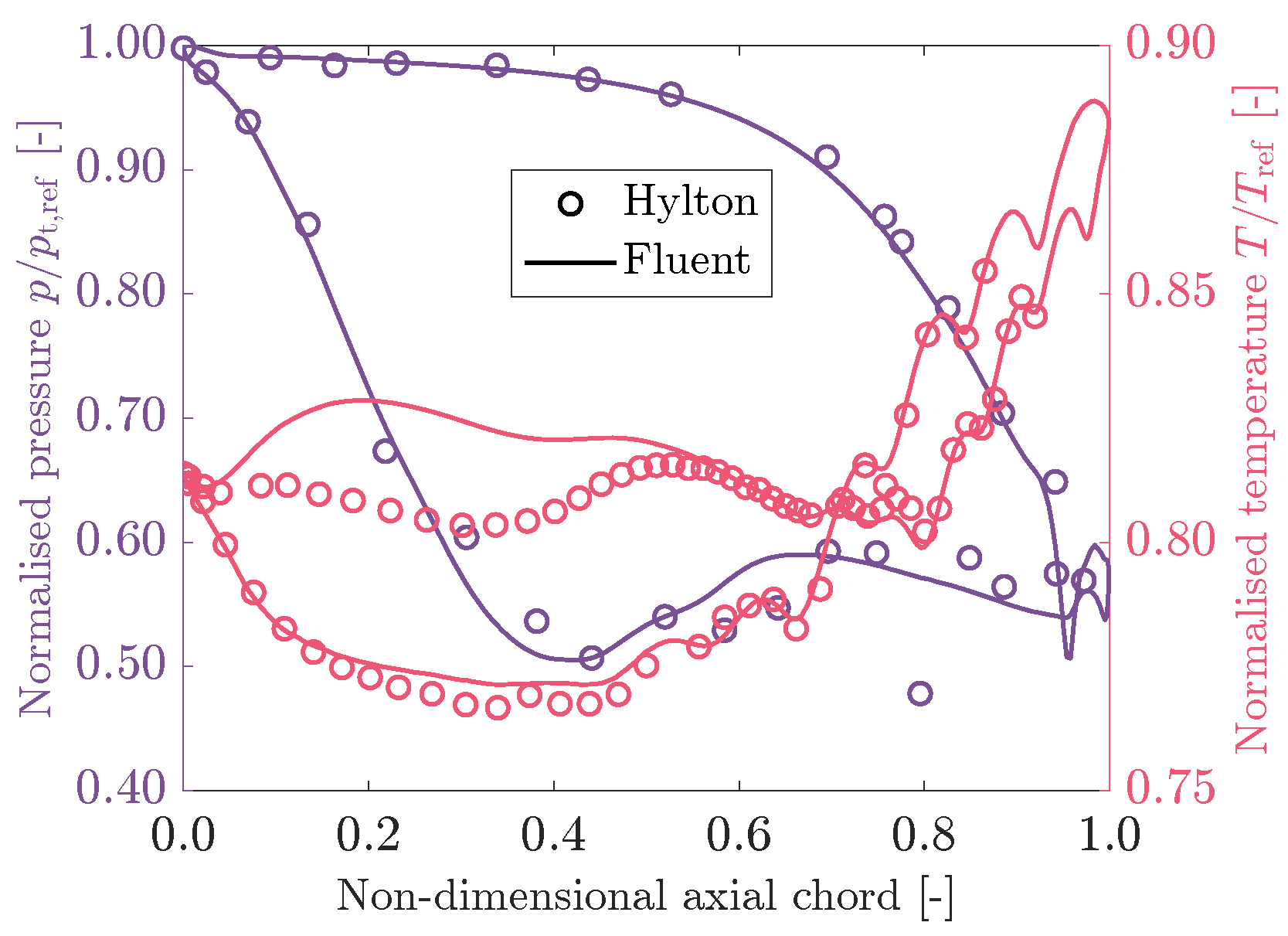

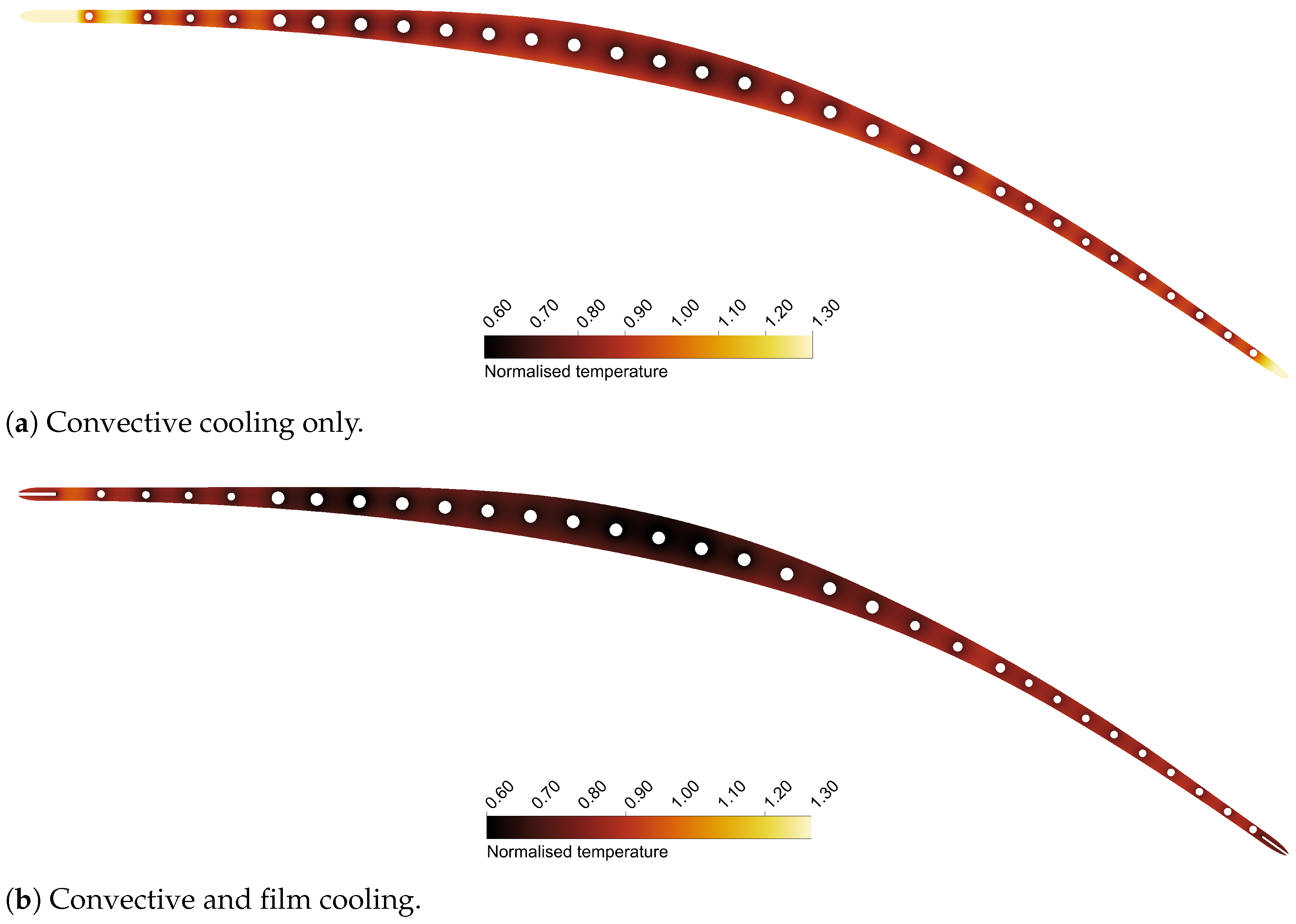
| Channel | |||||
|---|---|---|---|---|---|
| [mm] | [g/s] | [K] | [bar] | [%] | |
| 1 | 1.2 | 3.89 | 400 | 27.46 | 5 |
| 2 | 1.2 | 5.63 | 400 | 19.24 | 5 |
| 3 | 1.2 | 4.69 | 400 | 23.80 | 5 |
| 4 | 1.2 | 4.52 | 400 | 24.57 | 5 |
| 5 | 2.0 | 7.60 | 400 | 33.09 | 5 |
| 6 | 2.0 | 8.69 | 400 | 32.51 | 5 |
| 7 | 2.0 | 13.8 | 400 | 29.64 | 5 |
| 8 | 2.0 | 11.2 | 400 | 31.18 | 5 |
| 9 | 2.0 | 8.47 | 400 | 32.62 | 5 |
| 10 | 2.0 | 7.77 | 400 | 32.95 | 5 |
| 11 | 2.0 | 6.31 | 400 | 33.60 | 5 |
| 12 | 2.0 | 7.21 | 400 | 33.20 | 5 |
| 13 | 2.0 | 8.78 | 400 | 32.47 | 5 |
| 14 | 2.0 | 9.70 | 400 | 31.92 | 5 |
| 15 | 2.0 | 10.8 | 400 | 31.11 | 5 |
| 16 | 2.0 | 10.0 | 400 | 31.49 | 5 |
| 17 | 2.0 | 6.48 | 400 | 33.43 | 5 |
| 18 | 2.0 | 7.24 | 400 | 32.98 | 5 |
| 19 | 2.0 | 5.76 | 400 | 33.61 | 5 |
| 20 | 1.5 | 5.02 | 400 | 30.07 | 5 |
| 21 | 1.5 | 5.81 | 400 | 28.32 | 5 |
| 22 | 1.5 | 3.80 | 400 | 31.99 | 5 |
| 23 | 1.2 | 2.58 | 400 | 30.40 | 5 |
| 24 | 1.2 | 2.88 | 400 | 28.91 | 5 |
| 25 | 1.2 | 2.58 | 400 | 30.18 | 5 |
| 26 | 1.2 | 3.19 | 400 | 27.58 | 5 |
| 27 | 1.2 | 2.68 | 400 | 29.73 | 5 |
| 28 | 1.2 | 2.45 | 400 | 30.47 | 5 |
| 29 | 1.2 | 3.19 | 400 | 27.41 | 5 |
| 30 | 1.2 | 2.69 | 400 | 29.53 | 5 |
| 31 | 1.2 | 2.08 | 400 | 31.73 | 5 |
| Quantity | Symbol | Unit | Value | |
|---|---|---|---|---|
| 15 ch. | 31 ch. | |||
| Total coolant-to-gas | % | 11.85 | 10.74 | |
| mass flow ratio | ||||
| Coolant outlet | – | 1.04 | 0.292 | |
| Mach number | ||||
| Coolant outlet | K | 550 | 562 | |
| temperature | ||||
| Coolant percentage | % | 37.0 | 7.53 | |
| pressure drop | ||||
| Quantity | Unit | Range Studied |
|---|---|---|
| μm | 100–400 | |
| W/(K m) | 16–28 | |
| % | −25 to +25 | |
| % | −10 to +10 | |
| – | 1–3 | |
| K | 400–550 | |
| bar | 25–40 |
| Density | Specific Heat | Thermal Conductivity |
|---|---|---|
| [kg/m3] | [J/(kg K)] | [W/(K m)] |
| 7900 | 585.2 |
| Quantity | Unit | Law |
|---|---|---|
| Molecular weight | km/kmol | 28.96 |
| Specific heat | J/(kg K) | |
| Thermal conductivity | W/(K m) | |
| Dynamic viscosity | Pa·s |
| Quantity | Unit | Value |
|---|---|---|
| Inlet total pressure | bar | 3.22 |
| Inlet total temperature | K | 783 |
| Outlet static pressure | bar | 1.90 |
| Turbulent intensity | % | 8.30 |
| Turbulent length scale | mm | 0.782 |
| Channel | Diameter | Mass Flow Rate | Inlet Total Temperature |
|---|---|---|---|
| [mm] | [g/s] | [K] | |
| 1 | 6.30 | 7.79 | 393.3 |
| 2 | 6.30 | 6.58 | 393.1 |
| 3 | 6.30 | 6.34 | 375.2 |
| 4 | 6.30 | 6.66 | 381.0 |
| 5 | 6.30 | 6.52 | 359.2 |
| 6 | 6.30 | 6.72 | 419.1 |
| 7 | 6.30 | 6.33 | 373.0 |
| 8 | 3.10 | 2.26 | 371.6 |
| 9 | 3.10 | 1.38 | 426.9 |
| 10 | 1.98 | 0.68 | 451.4 |
| Material | Density | Specific Heat | Thermal Conductivity |
|---|---|---|---|
| [kg/m3] | [J/(kg K)] | [W/(K m)] | |
| Inconel 738 | 8110 | 650 | 22.5 |
| 7YSZ | 6000 | 470 | 1.50 |
| Quantity | Unit | Value |
|---|---|---|
| Inlet total pressure | bar | 15.0 |
| Inlet total temperature | K | 2340 |
| Inlet static pressure | bar | 1.94 |
| Turbulent intensity | % | 5 |
| Turbulent viscosity ratio | – | 5 |
| Stage | 1 | 2 | 3 | |
|---|---|---|---|---|
| Mass flow rate | kg/s | 9.2 | 9.2 | 8.8 |
| Inlet pressure | bar | 1 | 4.5 | 14.5 |
| Inlet temperature | K | 300 | 502 | 300 |
| Power | MW | 1.87 | 2.37 | 0.93 |
| Rotation speed | rpm | 30,000 | 56,700 | 56,700 |
| Outlet pressure | bar | 4.5 | 15 | 35 |
| Outlet temperature | K | 502 | 757 | 400 |
| Max diameter | m | 0.70 | 0.45 | 0.25 |
| Isentropic efficiency | % | 80 | 81 | 81 |
| Stage | 1 | 2 | |
|---|---|---|---|
| Mass flow rate | kg/s | 9.2 | 8.8 |
| Inlet pressure | bar | 13.6 | 14.5 |
| Inlet temperature | K | 690 | 300 |
| Power | MW | 0.21 | 0.93 |
| Rotation speed | rpm | 14,800 | 56,700 |
| Outlet pressure | bar | 15 | 35 |
| Outlet temperature | K | 715 | 400 |
| Max diameter | m | 0.50 | 0.25 |
| Isentropic efficiency | % | 85 | 81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the EUROTURBO. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Pinardi, A.; Mushtaq, N.; Gaetani, P. Development of a Reduced Order Model for Turbine Blade Cooling Design. Int. J. Turbomach. Propuls. Power 2025, 10, 37. https://doi.org/10.3390/ijtpp10040037
Pinardi A, Mushtaq N, Gaetani P. Development of a Reduced Order Model for Turbine Blade Cooling Design. International Journal of Turbomachinery, Propulsion and Power. 2025; 10(4):37. https://doi.org/10.3390/ijtpp10040037
Chicago/Turabian StylePinardi, Andrea, Noraiz Mushtaq, and Paolo Gaetani. 2025. "Development of a Reduced Order Model for Turbine Blade Cooling Design" International Journal of Turbomachinery, Propulsion and Power 10, no. 4: 37. https://doi.org/10.3390/ijtpp10040037
APA StylePinardi, A., Mushtaq, N., & Gaetani, P. (2025). Development of a Reduced Order Model for Turbine Blade Cooling Design. International Journal of Turbomachinery, Propulsion and Power, 10(4), 37. https://doi.org/10.3390/ijtpp10040037






