Experimental and Numerical Investigation of Suction-Side Fences for Turbine NGVs †
Abstract
1. Introduction
2. Fence Design
3. Experimental Campaign
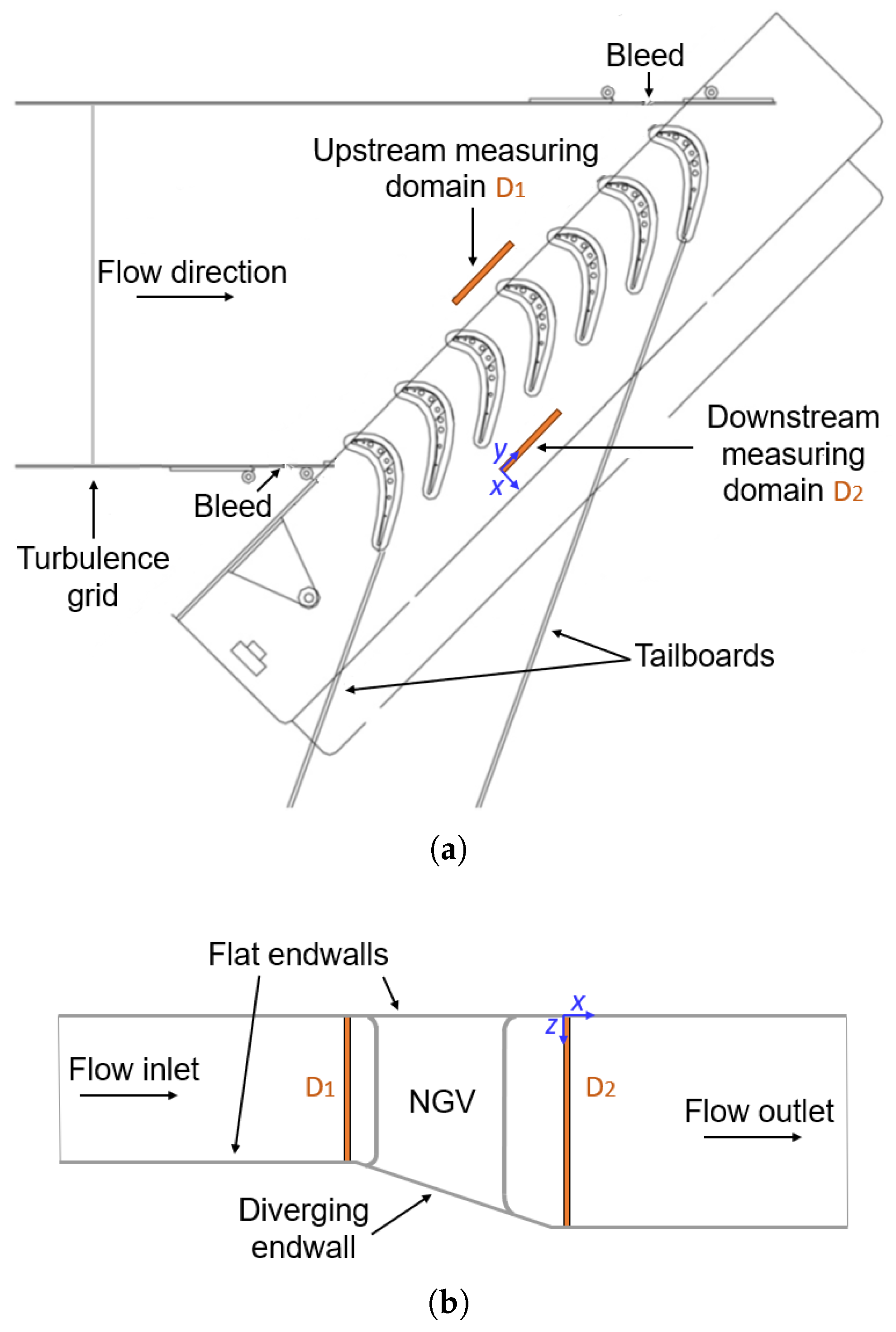
3.1. Experimental Setup
3.2. Measuring Technique
3.3. Fence Application
4. Numerical Campaign
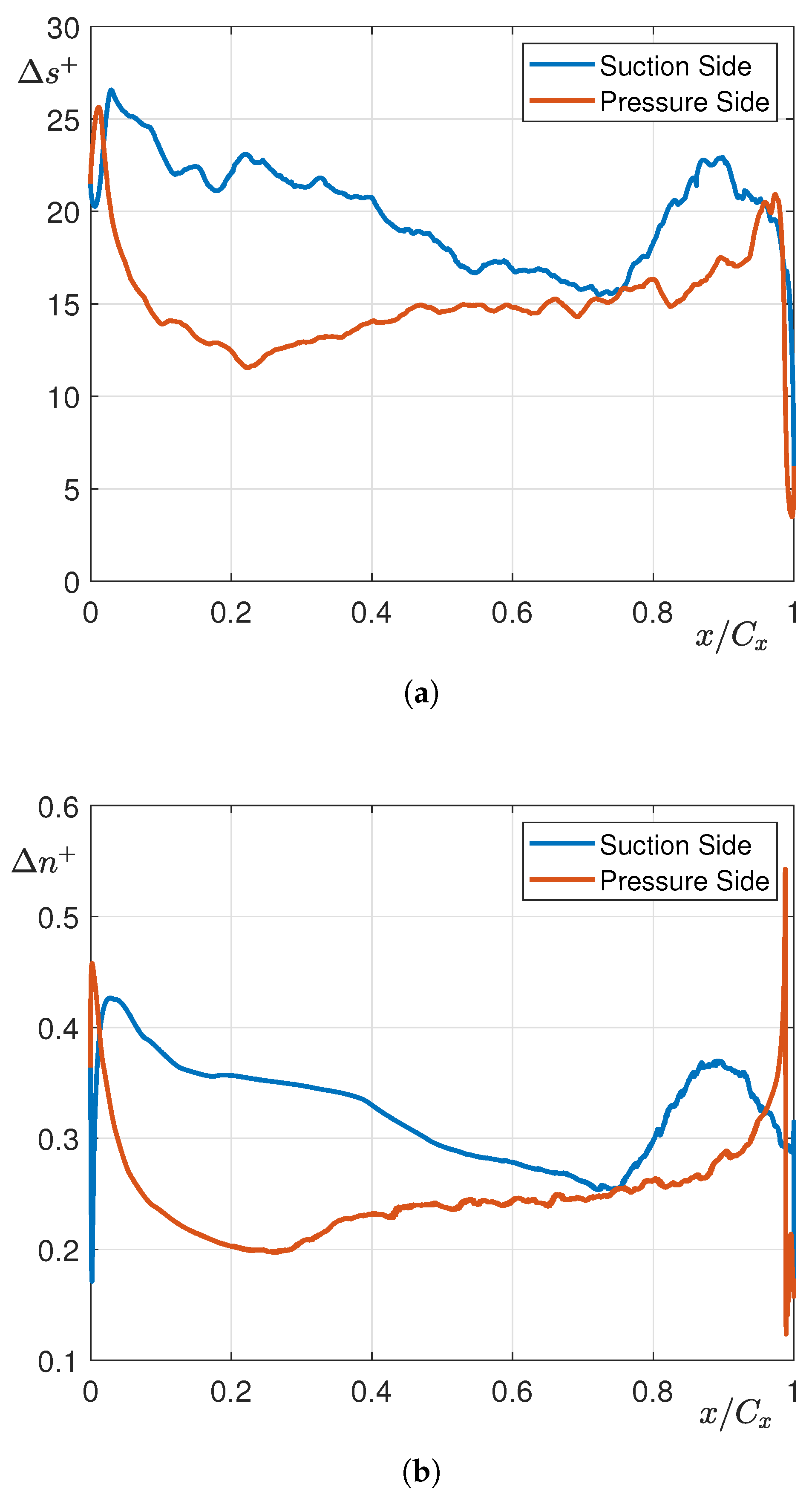
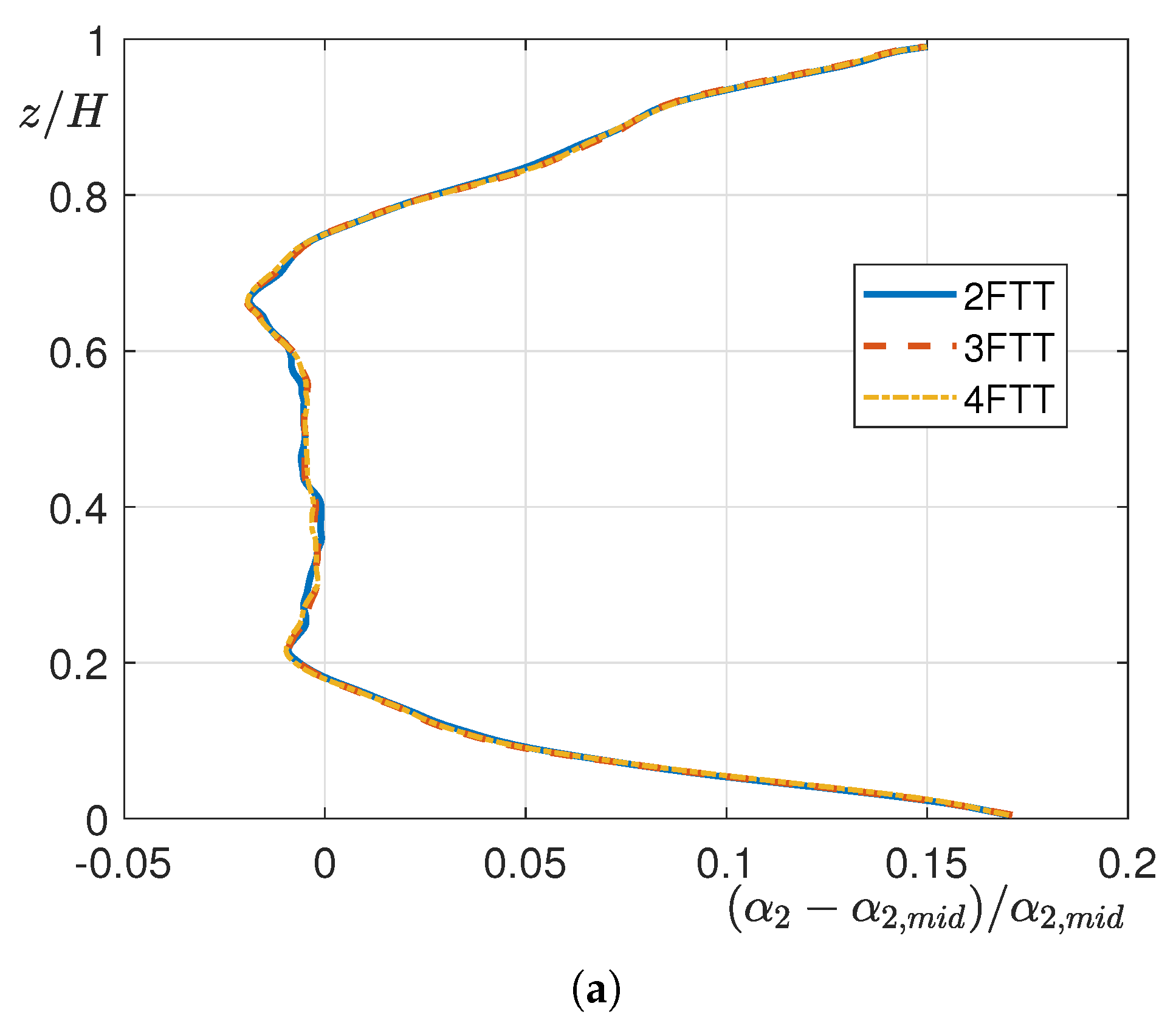
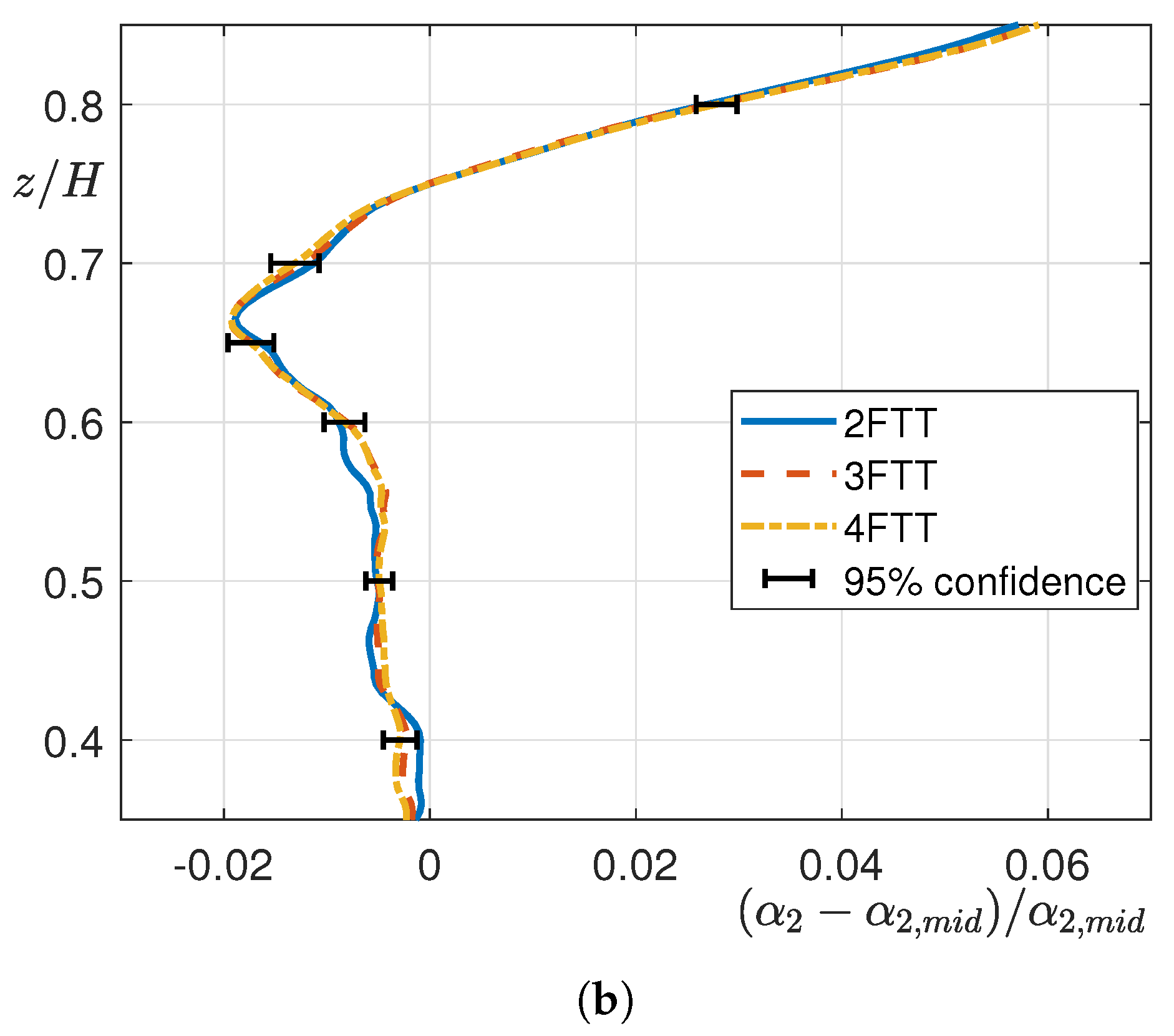
Numerical Setup
5. Results
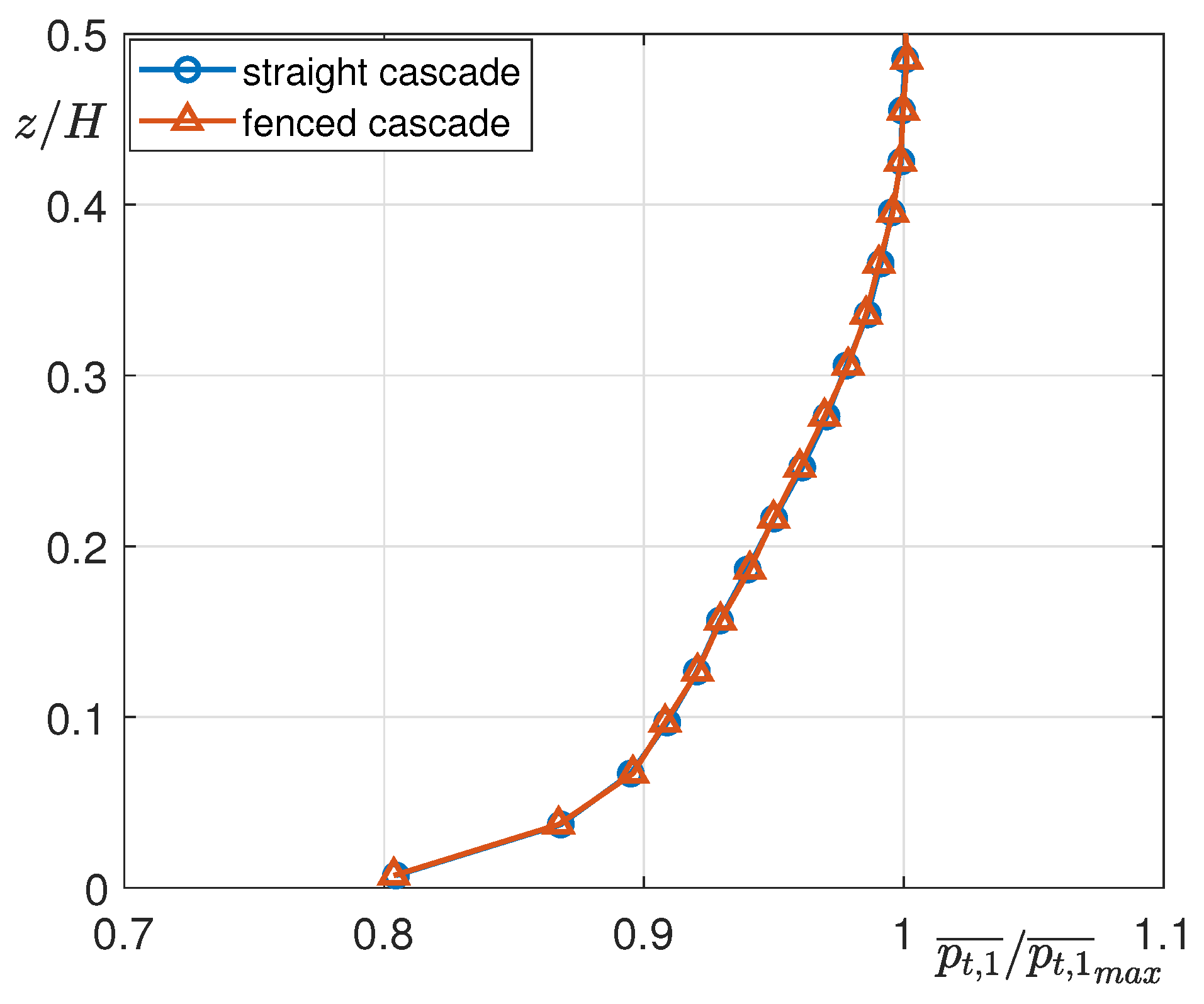
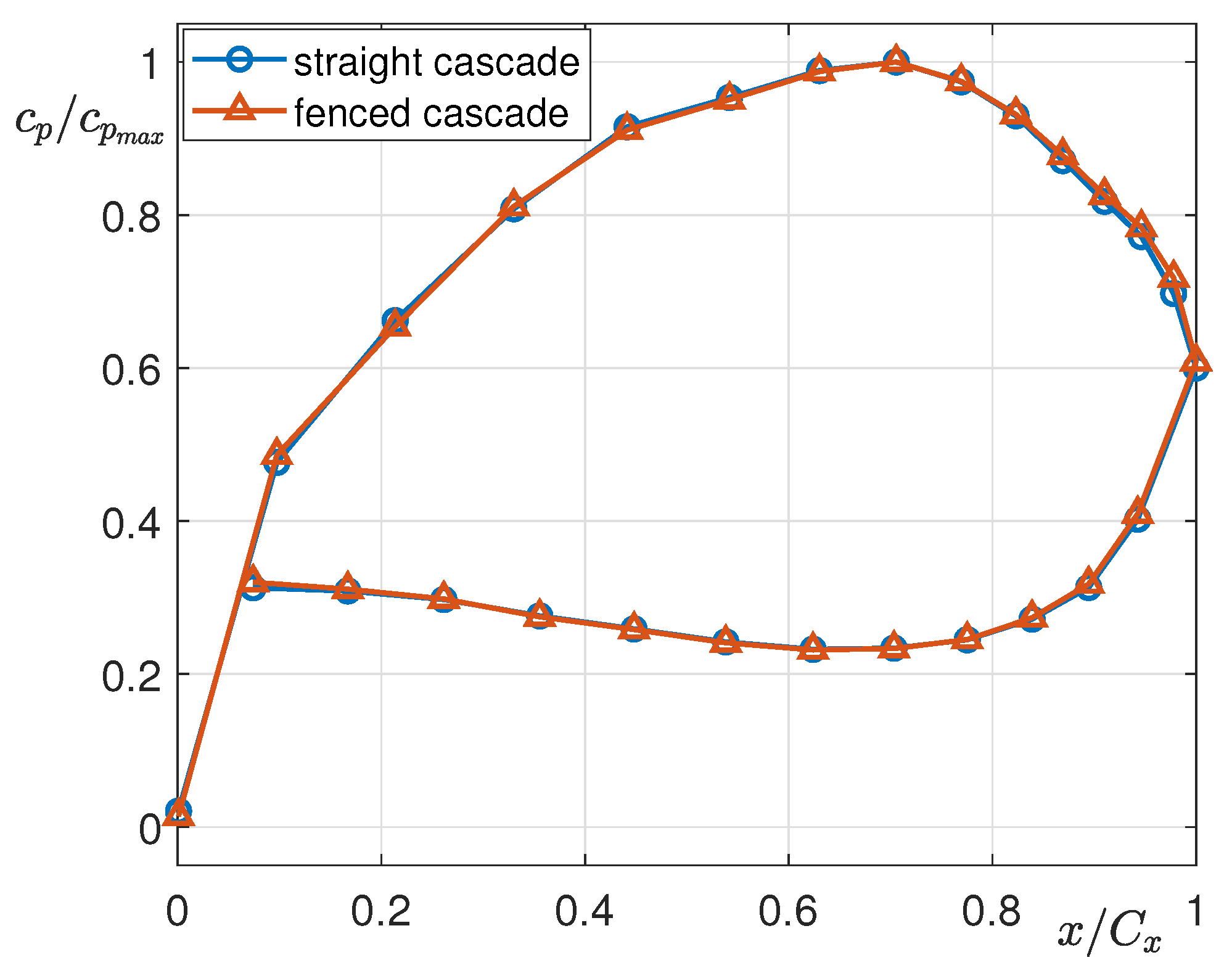
5.1. Inlet Boundary Layer and Aerodynamic Loading Distributions
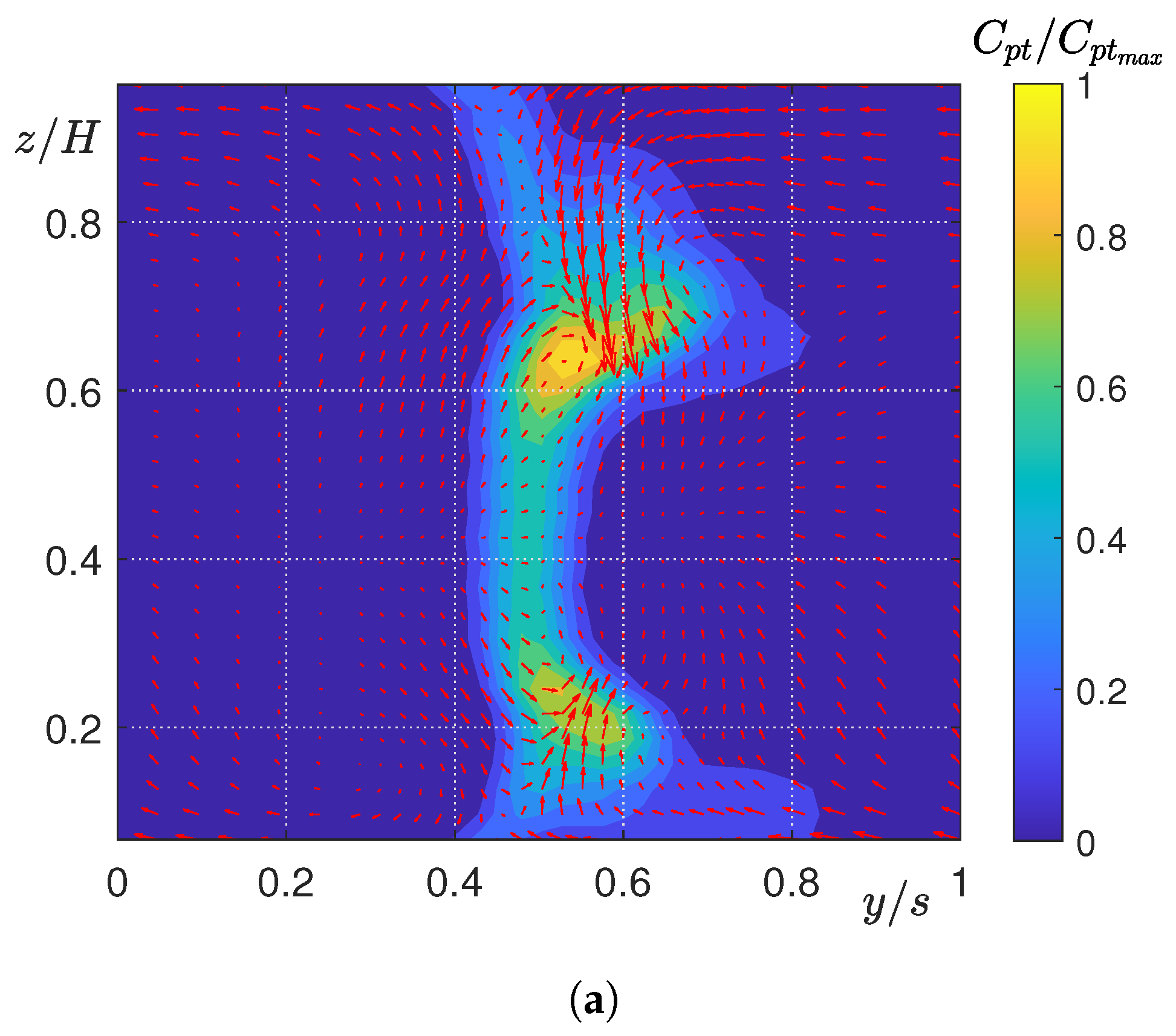
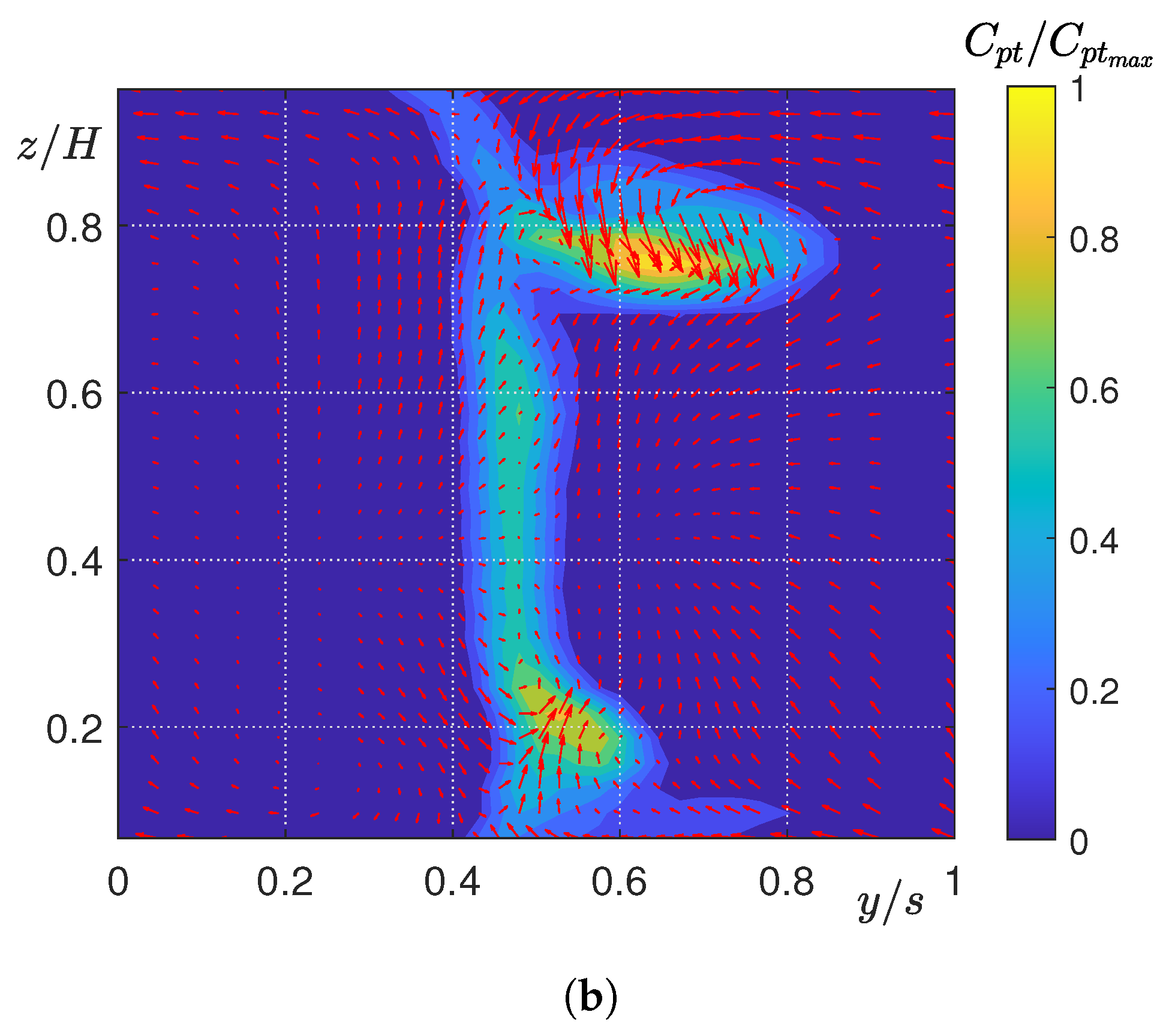
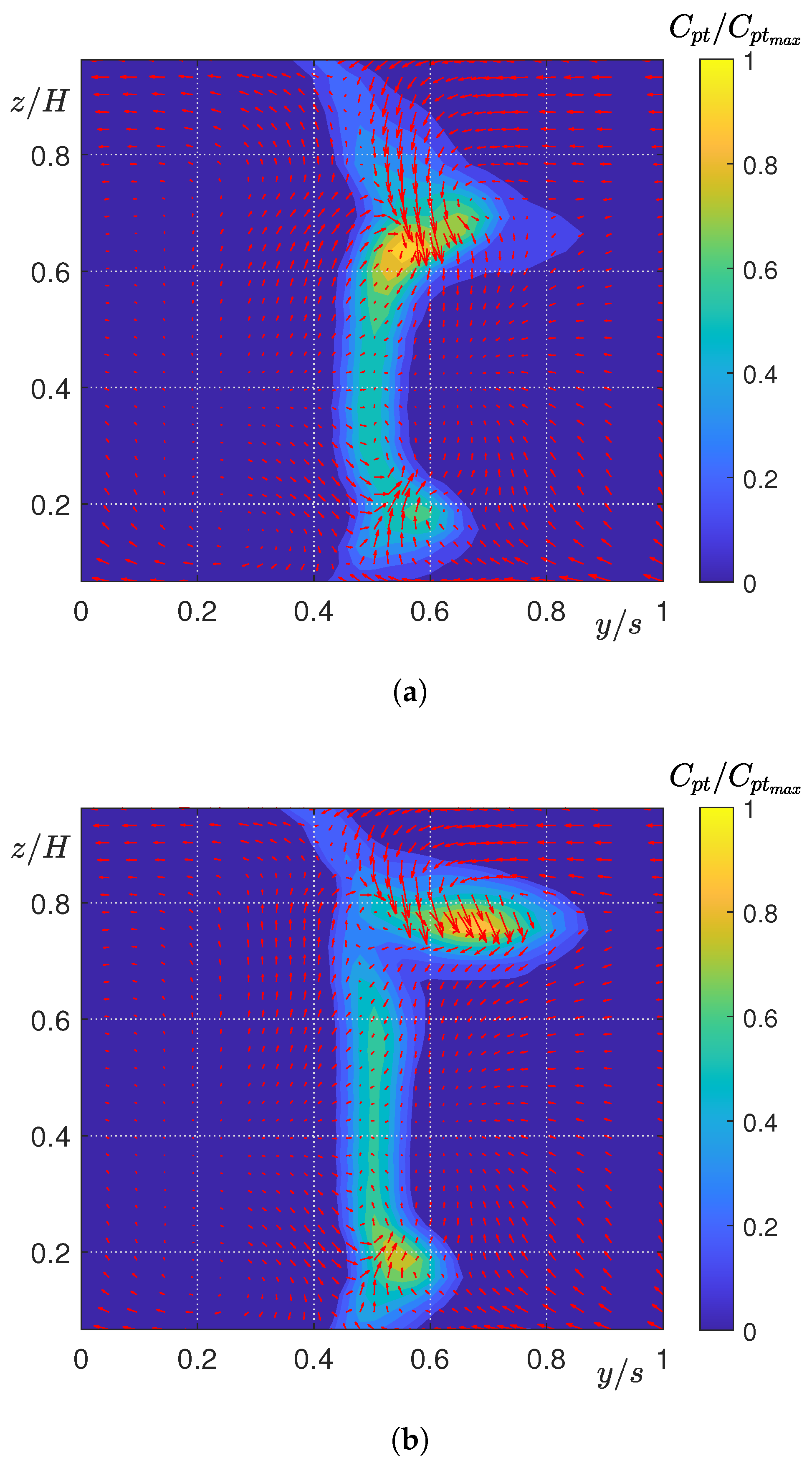
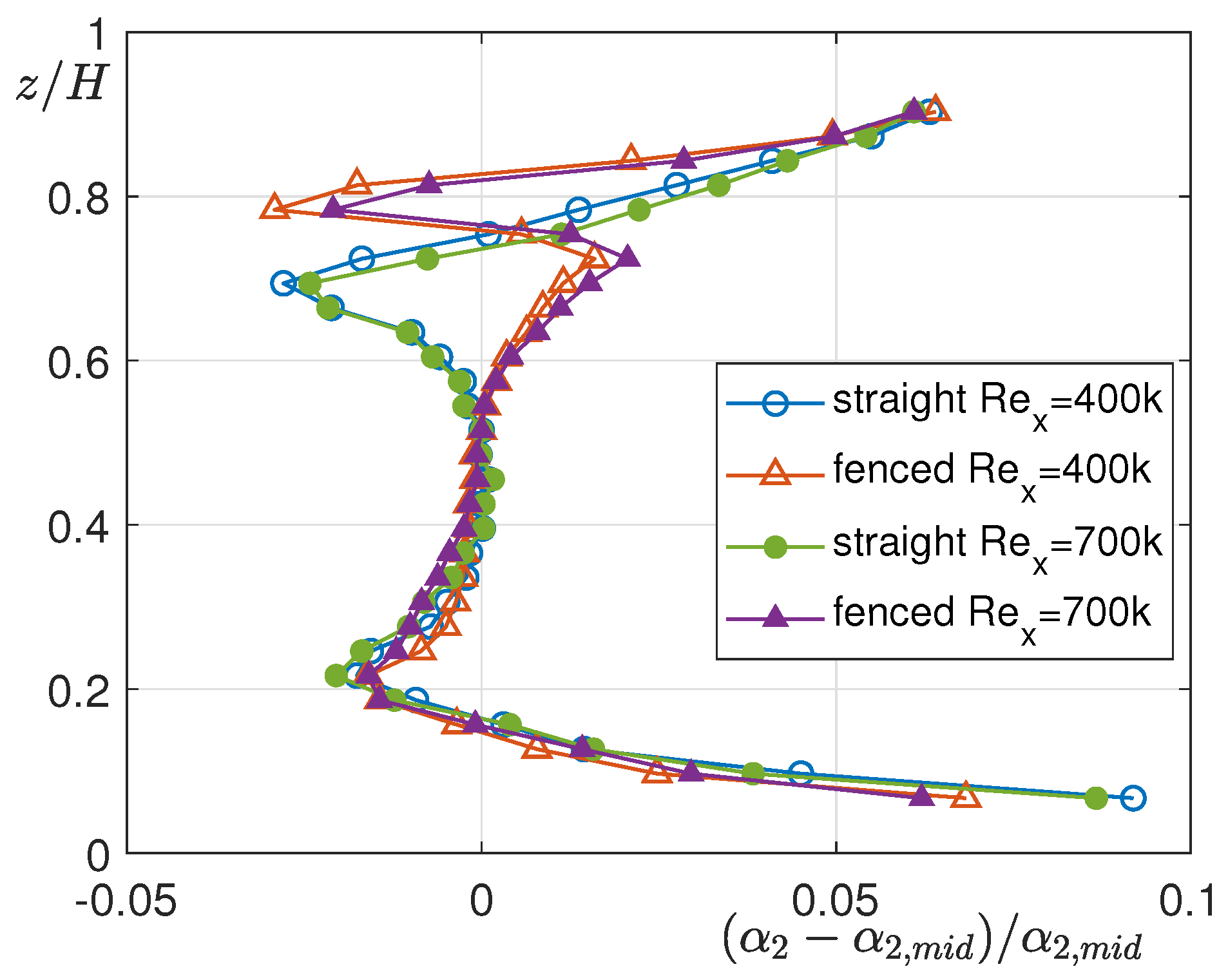
5.2. Experimental Analysis of Secondary Flows
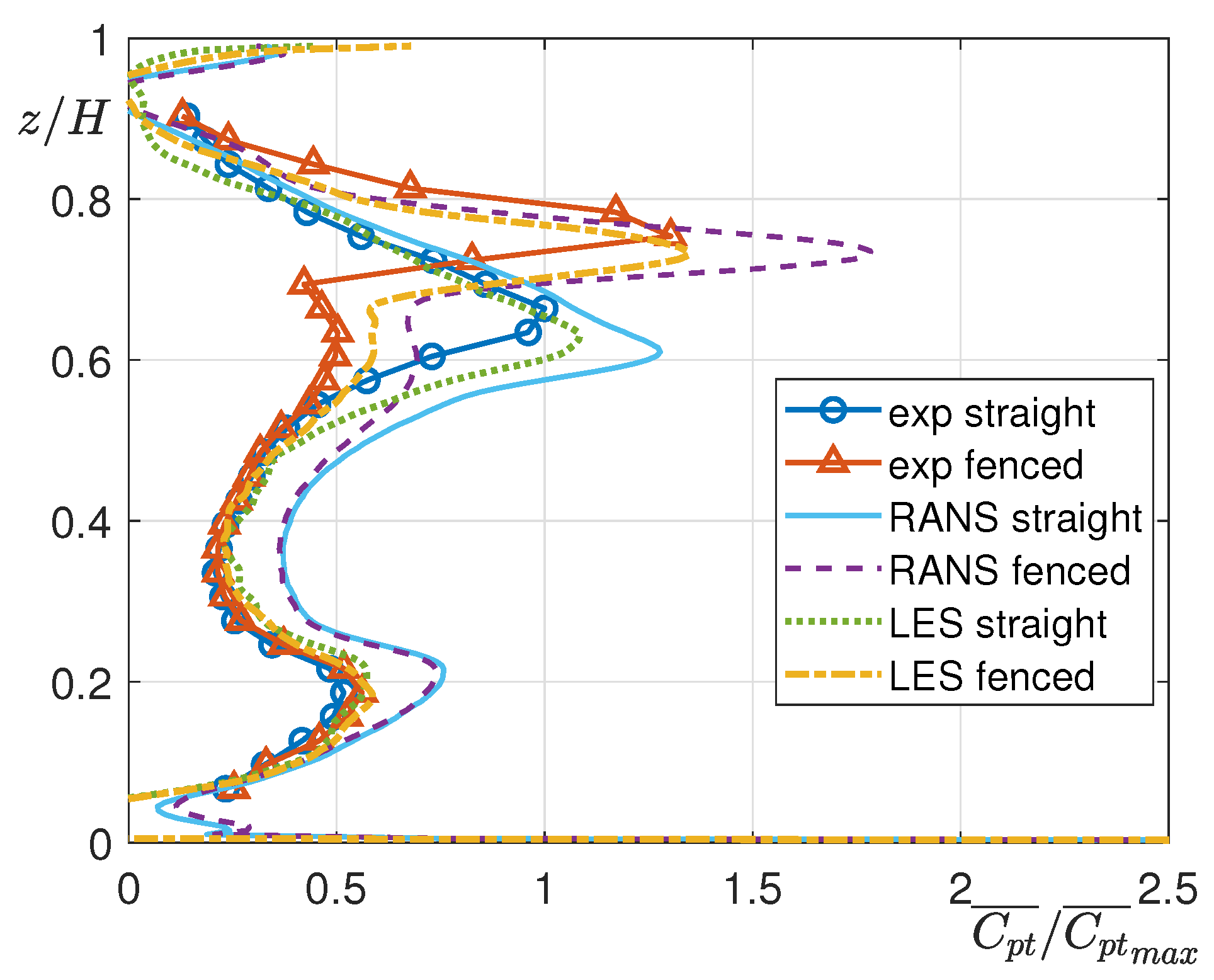
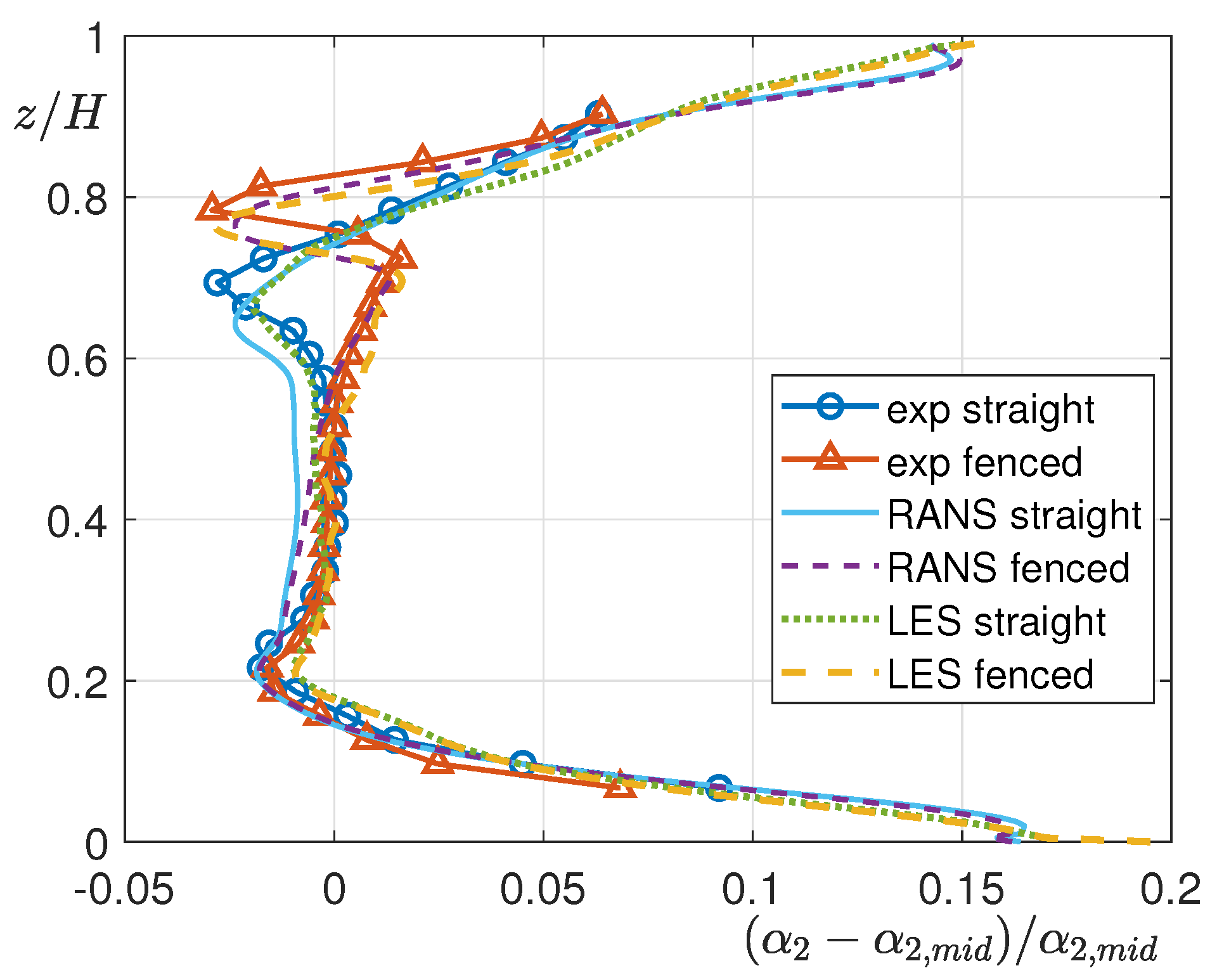
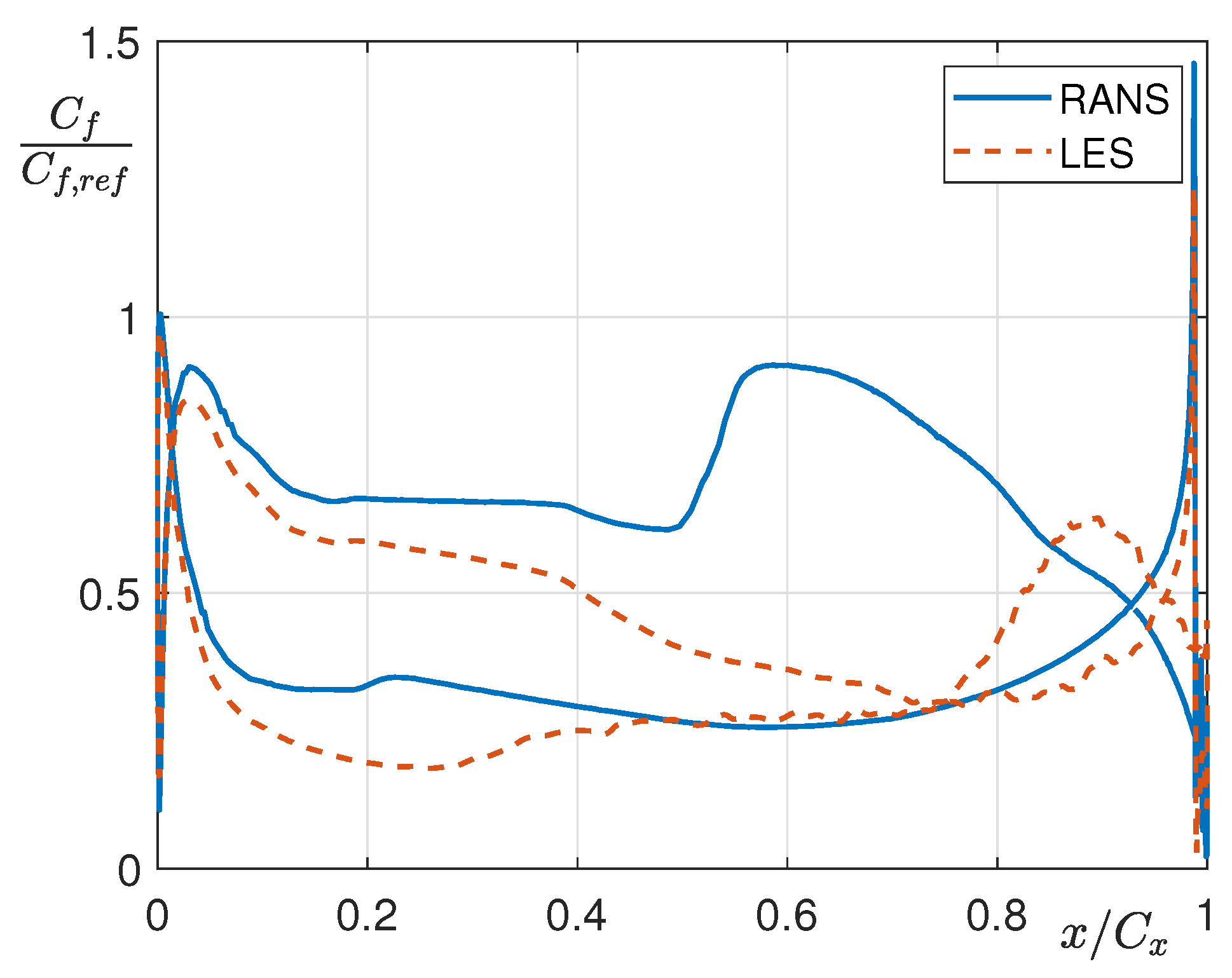
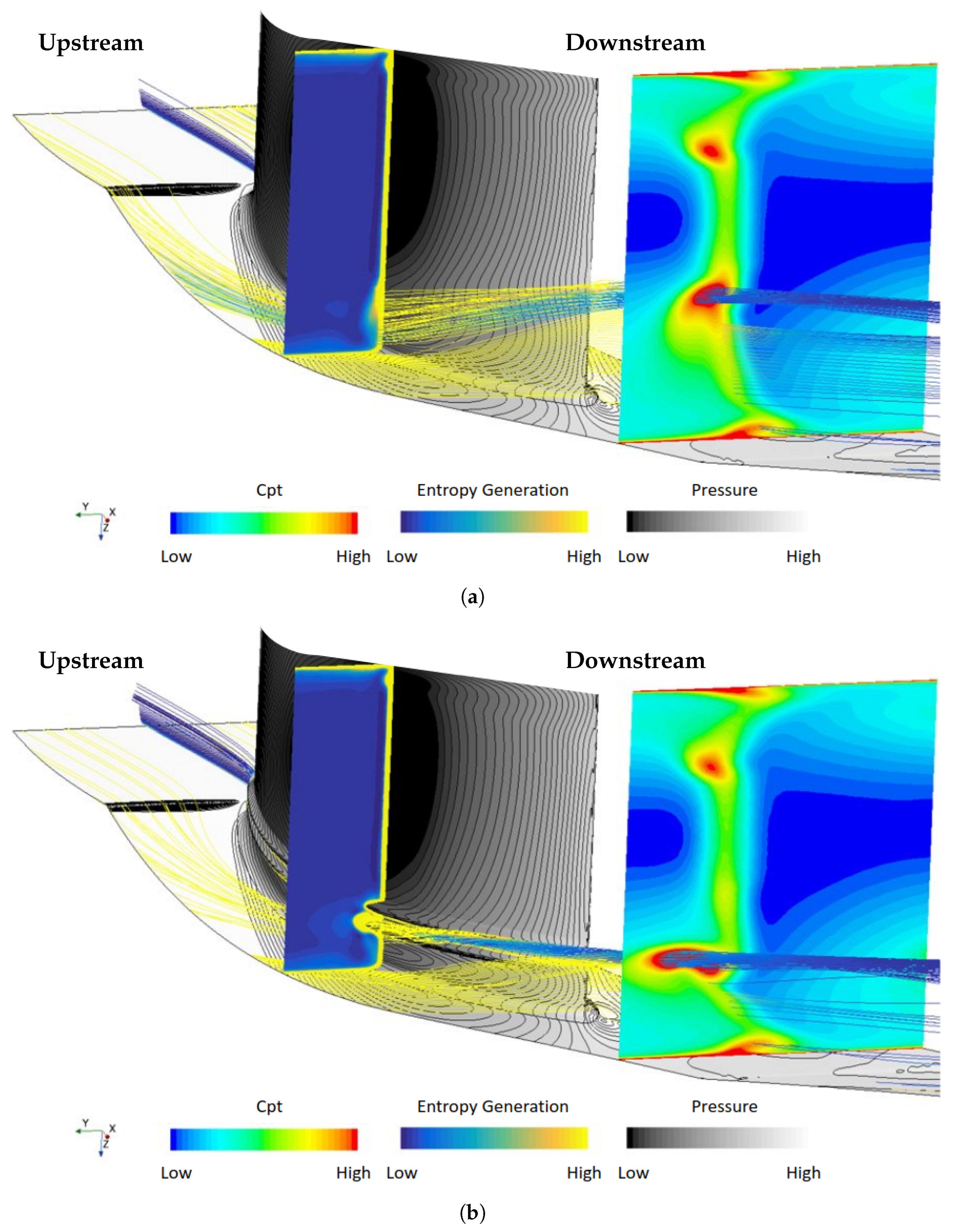
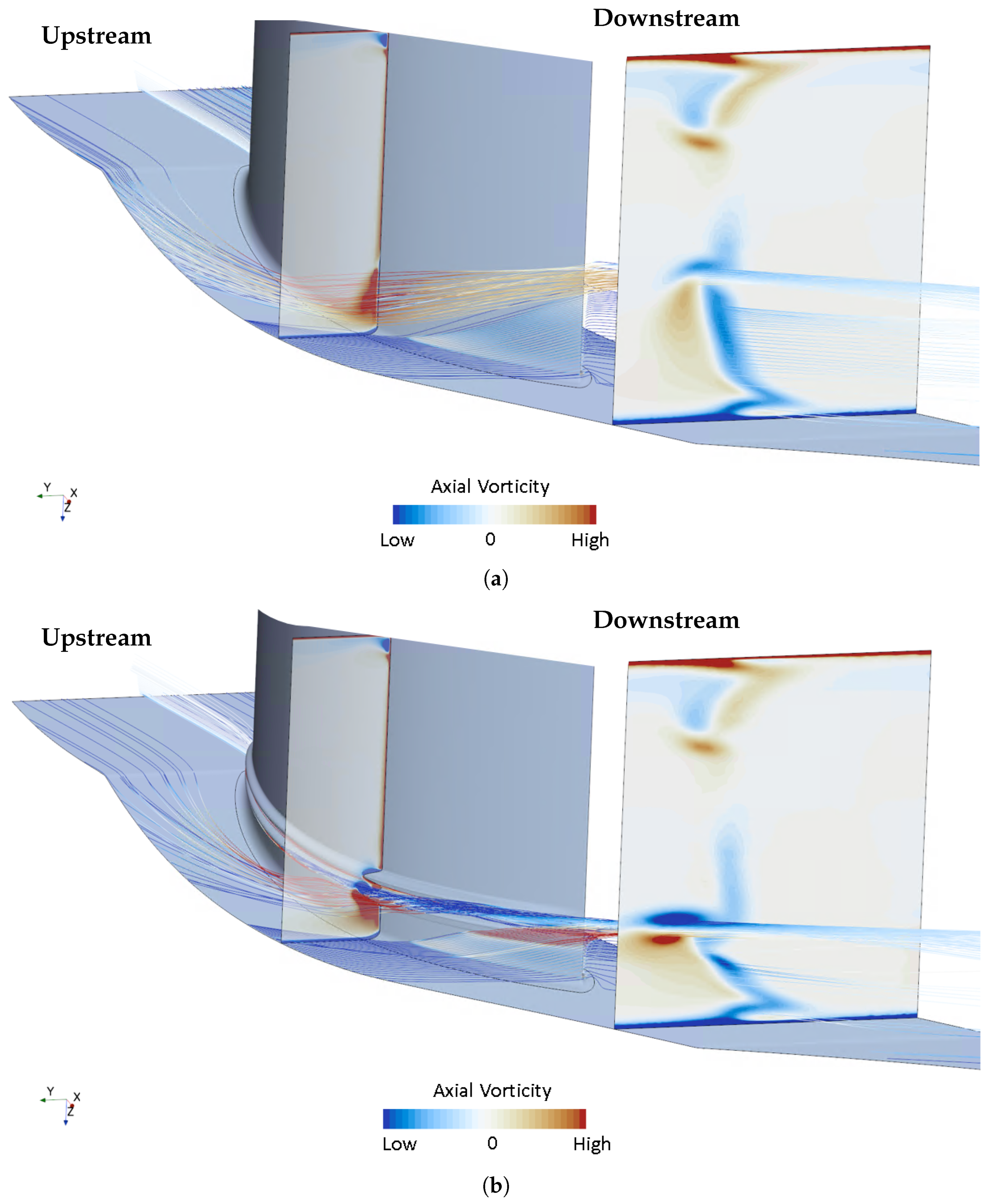
5.3. Numerical Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AR | Aspect Ratio |
| BC | Boundary Condition |
| BL | Boundary Layer |
| CFD | Computational Fluid Dynamics |
| FTT | Flow-Through Time |
| HPT | High Pressure Turbine |
| HSV | Horseshoe Vortex |
| IPT | Intermediate Pressure Turbine |
| LE | Leading Edge |
| LES | Large Eddy Simulation |
| LPT | Low Pressure Turbine |
| NGV | Nozzle Guide Vane |
| PS | Pressure Side |
| PV | Passage Vortex |
| RANS | Reynolds-Averaged Navier–Stokes |
| SKE | Secondary Kinetic Energy |
| SS | Suction Side |
| TE | Trailing Edge |
| TRL | Technology Readiness Level |
| 2D | Two-Dimensional |
| 3D | Three-Dimensional |
Nomenclature
| A | Channel area |
| c | Isentropic flow velocity |
| C | Blade chord |
| Blade loading = | |
| Total pressure loss coefficient = | |
| Maximum total pressure loss coefficient of the reference case (straight cascade | |
| and ) | |
| Inlet measuring domain | |
| Outlet measuring domain | |
| H | Blade height |
| p | Pressure |
| Downstream isentropic dynamic pressure = | |
| Reynolds number = | |
| s | Blade pitch |
| Free-stream turbulence intensity | |
| u | Flow velocity |
| y | Pitchwise direction |
| z | Spanwise direction |
| Zweifel number | |
| Greek symbols | |
| Yaw angle | |
| Exit yaw angle at blade midspan of the reference case (straight | |
| cascade and ) | |
| Pitch angle | |
| Mesh resolution along the blade surface normal direction | |
| Mesh resolution along the curvilinear abscissa | |
| Mesh resolution along the blade span | |
| Dynamic viscosity | |
| Fluid density | |
| Cascade solidity = | |
| Vorticity = | |
| Turning | |
| Total loss coefficient | |
| Profile loss coefficient | |
| Secondary loss coefficient | |
| Subscripts | |
| At midspan | |
| t | Total |
| x | Axial |
| 1 | Inlet |
| 2 | Outlet |
| Superscripts | |
| Pitchwise average | |
| Pitchwise and spanwise average |
References
- Göttlich, E. Research on the aerodynamics of intermediate turbine diffusers. Prog. Aerosp. Sci. 2011, 47, 249–279. [Google Scholar] [CrossRef]
- Norris, G.; Dominy, R.G.; Smith, A.D. Strut Influences Within a Diffusing Annular S-Shaped Duct; American Society of Mechanical Engineers: New York, NY, USA, 1998. [Google Scholar]
- Simon, P.; Andreas, P.; Albéniz, G.D.; Lucas, M.; Adrian, L.P.; Franz, H.; Andreas, M. The impact of inlet flow angle on turbine vane frame aerodynamic performance. In Proceedings of the ASME Turbo Expo: Power for Land, Sea, and Air, Rotterdam, The Netherlands, 13–17 June 2022; American Society of Mechanical Engineers: New York, NY, USA, 2022; Volume 86113. Paper No. V10CT33A001. [Google Scholar]
- Langston, L.S. Secondary flows in axial turbines—A review. Ann. N. Y. Acad. Sci. 2001, 934, 11–26. [Google Scholar] [CrossRef] [PubMed]
- Vinuesa, R.; Schlatter, P.; Nagib, H.M. Secondary flow in turbulent ducts with increasing aspect ratio. Phys. Rev. Fluids 2018, 3, 054606. [Google Scholar] [CrossRef]
- Wegener, D.; Quest, J.; Hoffmann, W. Secondary Flow in a Turbine Guide Vane with Low Aspect Ratio. Secondary Flows in Turbomachines. 1990; AGARD, SessionII-9-1. Available online: https://apps.dtic.mil/sti/tr/pdf/ADA220901.pdf (accessed on 20 June 2025).
- Bons, J.; Benton, S.; Bernardini, C.; Bloxham, M. Active flow control for low-pressure turbines. AIAA J. 2018, 56, 2687–2698. [Google Scholar] [CrossRef]
- Sullerey, R.K.; Pradeep, A.M. Secondary flow control using vortex generator jets. J. Fluids Eng. 2004, 126, 650–657. [Google Scholar] [CrossRef]
- Khan, Z.U.; Johnston, J.P. On vortex generating jets. Int. J. Heat Fluid Flow 2000, 21, 506–511. [Google Scholar] [CrossRef]
- Romero, S.; Gross, A. Numerical investigation of active flow control of low-pressure turbine endwall flow. J. Propuls. Power 2019, 35, 883–895. [Google Scholar] [CrossRef]
- Qu, X.; Li, L.; Zhang, Y.; Lu, X.; Zhu, J.; Zhang, Y. Controlling secondary flow in high-lift low-pressure turbine using boundary-layer slot suction. Chin. J. Aeronaut. 2024, 37, 21–33. [Google Scholar] [CrossRef]
- Volino, R.J. Passive flow control on low-pressure turbine airfoils. J. Turbomach. 2003, 125, 754–764. [Google Scholar] [CrossRef]
- Clark, C.J.; Pullan, G.; Curtis, E.; Goenaga, F. Secondary flow control in low aspect ratio vanes using splitters. J. Turbomach. 2017, 139, 091003. [Google Scholar] [CrossRef]
- Mingardo, G.; Kusano, K.; Pini, M.; Lettieri, C.; Kawata, Y. Secondary flow mitigation in turbine vanes using endwall fence optimization. In Proceedings of the Montreal 2018 Global Power and Propulsion Forum, Montreal, QC, Canada, 7–9 May 2018. GPPS-NA-2018-0058. [Google Scholar]
- Yuan, H.; Wu, Y.; Zhou, S.; Wang, M.; Lu, X.; Zhang, Y. Nonuniform height endwall fence optimization of a low-pressure turbine cascade. Int. J. Mech. Sci. 2023, 250, 108301. [Google Scholar] [CrossRef]
- Dossena, V.; Perdichizzi, A.; Savini, M. The Influence of Endwall Contouring on the Performance of a Turbine Nozzle Guide Vane; American Society of Mechanical Engineers: New York, NY, USA, 1999; Paper No. 99-GT-72; Volume 78620, p. V001T01A022. [Google Scholar]
- Kawai, T. Effect of combined boundary layer fences on turbine secondary flow and losses. JSME Int. J. Ser. B Fluids Therm. Eng. 1994, 37, 377–384. [Google Scholar] [CrossRef]
- Rubechini, F.; Giovannini, M.; Arnone, A.; Simoni, D.; Bertini, F. Reducing secondary flow losses in low-pressure turbines with blade fences: Part I—Design in an engine-like environment. In ASME Turbo Expo; American Society of Mechanical Engineers: New York, NY, USA, 2019; p. V02BT40A020. [Google Scholar] [CrossRef]
- Giovannini, M.; Rubechini, F.; Amato, G.; Arnone, A.; Simoni, D.; Yepmo, V.; Satta, F.; Bertini, F. Reducing secondary flow losses in low-pressure turbines with blade fences: Part II—Experimental validation on linear cascades. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 58561, p. V02BT40A021. [Google Scholar]
- Prümper, H. Application of boundary layer fences in turbomachinery. VDI-Berichte 1972, 311, 311–331. [Google Scholar]
- Kawai, T.; Adachi, T. Effects of blade boundary layer fences on secondary flow and losses in a turbine cascade. Nippon Kikai Gakkai Ronbunshu B Hen 1988, 54, 2484–2491. [Google Scholar] [CrossRef]
- Infantino, D.; Satta, F.; Simoni, D.; Ubaldi, M.; Zunino, P.; Bertini, F. Phase-locked investigation of secondary flows perturbed by passing wakes in a high-lift LPT turbine cascade. In ASME Turbo Expo; American Society of Mechanical Engineers: New York, NY, USA, 2015; p. V02CT44A008. [Google Scholar] [CrossRef]
- Bologna, V.; Petronio, D.; Satta, F.; De Vincentiis, L.; Giovannini, M.; Cattoli, G.; Gily, M.; Notaristefano, A. Experimental and Numerical Investigation of Suction-Side Fences for Turbine NGVs. In Proceedings of the 16th European Turbomachinery Conference, Hannover, Germany, 24–28 March 2025. Paper No. ETC2025-213. [Google Scholar]
- Satta, F.; Simoni, D.; Ubaldi, M.; Zunino, P.; Bertini, F. Profile and secondary flow losses in a high-lift LPT blade cascade at different Reynolds numbers under steady and unsteady inflow conditions. J. Therm. Sci. 2012, 21, 483–491. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Jarrin, N.; Benhamadouche, S.; Laurence, D.; Prosser, R. A synthetic-eddy-method for generating inflow conditions for large-eddy simulations. Int. J. Heat Fluid Flow 2006, 27, 585–593. [Google Scholar] [CrossRef]
- Bologna, V.; Paliotta, P.; Petronio, D.; Satta, F.; Simoni, D.; Giovannini, M.; Paccati, S.; De Vincentiis, L.; Gily, M. Detailed characterization of turbulence intensity and dissipation as boundary condition for 3D RANS simulations. In ASME Turbo Expo; American Society of Mechanical Engineers: New York, NY, USA, 2024; p. V12CT32A044. [Google Scholar] [CrossRef]
- Bergmann, M.; Morsbach, C.; Ashcroft, G.; Kügeler, E. Statistical error estimation methods for engineering-relevant quantities from scale-resolving simulations. J. Turbomach. 2021, 144, 031005. [Google Scholar] [CrossRef]
- Giovannini, M.; Rubechini, F.; Marconcini, M.; Simoni, D.; Yepmo, V.; Bertini, F. Secondary flows in low-pressure turbines cascades: Numerical and experimental investigation of the impact of the inner part of the boundary layer. J. Turbomach. 2018, 140, 111002. [Google Scholar] [CrossRef]
- Eckerle, W.A.; Awad, J.K. Effect of freestream velocity on the three-dimensional separated flow region in front of a cylinder. J. Fluids Eng. 1991, 113, 37–44. [Google Scholar] [CrossRef]
- Russo, M.; Carlucci, A.; Dellacasagr, M.; Petronio, D.; Lengani, D.; Simoni, D.; Bellucci, J.; Giovannini, M.; Granata, A.A.; Gily, M.; et al. Optimization of low-pressure turbine blade by means of fine inspection of loss production mechanisms. In ASME Turbo Expo; American Society of Mechanical Engineers: New York, NY, USA, 2024; p. V12DT36A023. [Google Scholar] [CrossRef]




| 400,000 | 700,000 | |||
| Cascade | straight | fenced | straight | fenced |
| 49 | 49 | 45 | 45 | |
| 51 | 56 | 46 | 51 | |
| 100 | 105 | 91 | 96 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the EUROTURBO. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Bologna, V.; Petronio, D.; Satta, F.; De Vincentiis, L.; Giovannini, M.; Cattoli, G.; Gily, M.; Notaristefano, A. Experimental and Numerical Investigation of Suction-Side Fences for Turbine NGVs. Int. J. Turbomach. Propuls. Power 2025, 10, 31. https://doi.org/10.3390/ijtpp10040031
Bologna V, Petronio D, Satta F, De Vincentiis L, Giovannini M, Cattoli G, Gily M, Notaristefano A. Experimental and Numerical Investigation of Suction-Side Fences for Turbine NGVs. International Journal of Turbomachinery, Propulsion and Power. 2025; 10(4):31. https://doi.org/10.3390/ijtpp10040031
Chicago/Turabian StyleBologna, Virginia, Daniele Petronio, Francesca Satta, Luca De Vincentiis, Matteo Giovannini, Gabriele Cattoli, Monica Gily, and Andrea Notaristefano. 2025. "Experimental and Numerical Investigation of Suction-Side Fences for Turbine NGVs" International Journal of Turbomachinery, Propulsion and Power 10, no. 4: 31. https://doi.org/10.3390/ijtpp10040031
APA StyleBologna, V., Petronio, D., Satta, F., De Vincentiis, L., Giovannini, M., Cattoli, G., Gily, M., & Notaristefano, A. (2025). Experimental and Numerical Investigation of Suction-Side Fences for Turbine NGVs. International Journal of Turbomachinery, Propulsion and Power, 10(4), 31. https://doi.org/10.3390/ijtpp10040031





