Abstract
This study explores and models the use of MATLAB technology in multimodal learning interactions to address the challenges of teaching and learning statistics in a multinational postgraduate classroom. The term multimodal refers to the deliberate integration of multiple representational and interaction modes, i.e., visual, textual, symbolic, and interactive computational modelling, within a coherent instructional design. MATLAB is utilised as it is a comprehensive tool for enhancing students’ understanding of statistical skills, practical applications, and data analysis—areas where traditional methods often fall short. International postgraduate students were chosen for this study because their diverse educational backgrounds present unique learning challenges. A qualitative case study design was employed, and data collection methods included classroom observations, interviews, and student work analysis. The collected data were analysed and modelled by conceptualising key elements and themes using thematic analysis, with findings verified through data triangulation and expert review. Emerging themes were structured into models that illustrate multimodal teaching and learning interactions. The novelty of this research lies in its contribution to multimodal teaching and learning strategies for multinational students in statistics education. The findings highlight significant challenges international students face, including language and technical barriers, limited prior content knowledge, time constraints, technical difficulties, and a lack of independent thinking. To address these challenges, MATLAB promotes collaborative learning, increases student engagement and discussion, boosts motivation, and develops essential skills. This study suggests that educators integrate multimodal interactions in their teaching strategies to better support multinational students in statistical learning environments.
1. Introduction
MATLAB (version 2023b), an advanced technical computing software developed by MathWorks, plays a crucial role in scientific, engineering, and mathematical fields due to its powerful numerical capabilities and extensive toolbox [1,2,3,4,5]. The importance of MATLAB has extended into educational research, especially in teaching complex mathematical and statistical concepts (i.e., visualisation of probability density functions for two-dimensional normal random variables). Due to the increasing demand for technological integration in education, the practical application of MATLAB is becoming time-sensitive. Its capability to simplify complex concepts and present them visually through 3D graphical representations makes it a valuable tool for improving students’ understanding, particularly in a world where technology-driven learning is rapidly evolving [6,7].
Despite this, not all students find the transition to using MATLAB seamless. Multinational students, particularly those unfamiliar with advanced mathematical computing tools, often face challenges in adopting MATLAB as part of their learning process. Beginner users of MATLAB, especially those from non-STEM backgrounds [8], may encounter difficulties, while students unfamiliar with programming may struggle with MATLAB’s learning curve [3,4,9]. Multinational classrooms may further exacerbate these challenges due to students’ diverse educational and linguistic backgrounds, which can impede their ability to fully engage with the software.
While prior research has highlighted MATLAB’s utility, it has also acknowledged the challenges faced by some learners, such as adjusting to the software’s syntax and navigating its extensive toolsets [10]. However, a gap remains in the current literature, as much of the research has focused on the advantages of MATLAB without fully exploring student interactions with MATLAB technology in multinational classrooms.
This study is crucial due to the increasing number of students studying abroad. For example, the number of international students enrolled in postgraduate programmes in Malaysia has risen significantly from 2011 to 2024 [11,12]. Among the top 10 countries from which Malaysia received foreign students in 2020–2021, Chinese students accounted for the majority of the growth (97.68%), with 10,326 of the 10,571 new international students coming from China [13]. One of the key challenges faced by international students when studying abroad is overcoming learning barriers, such as language difficulties and social integration in diverse classrooms [14,15]. Oduwaye et al. [16] reported that sociocultural (82.9%) and academic challenges (82.3%) were the most frequently studied issues, with language difficulties being a primary concern. Since MATLAB has the potential to enhance mathematics learning, it is essential to explore its use among international students.
This research examines multimodal learning interactions in MATLAB-based statistics education within a multinational postgraduate context, with a particular focus on the visualisation of probability density functions associated with two-dimensional normal random variables and the transition from 2D to 3D graphical representations. Most studies on programming education have concentrated on uniform student groups or on widely used programming languages. In contrast, this study addresses the challenge of learning both computational tools and advanced statistical concepts, all within a culturally diverse environment.
A key contribution of this work is the introduction of the MATLAB Technology Learning Interaction Model. This conceptual framework combines Multimodal Learning Theory, Constructivism, and Cultural–Historical Activity Theory with computational pedagogy. It explains the ways in which collaboration, engagement, motivation, and skill development intersect within a multimodal learning environment. Visual, textual, symbolic, and interactive computational modes are all included. By highlighting these interactions, the study does more than just identify learning barriers. It also develops a structured and adaptable approach for supporting diverse learners in technology-mediated statistics education.
In this study, the term multimodal refers to a pedagogical design that deliberately integrates multiple representational and interaction modes, i.e., visual, textual, symbolic, and interactive computational modelling, into unified learning activities. Grounded in Multimodal Learning Theory, Constructivism, and Cultural-Historical Activity Theory (CHAT), this framework ensures that students engage with statistical concepts through writing and interpreting MATLAB code (textual/symbolic), generating and analysing 2D and 3D plots (visual), and experimenting with parameters in real time (interactive). Within a multinational classroom, such multimodal structures not only support comprehension of complex statistical concepts but also mediate collaboration, meaning-making, and problem-solving across diverse linguistic and cultural backgrounds.
By exploring emerging themes from the experiences of multinational students, we developed a multimodal learning model that contributes to a broader understanding of how MATLAB can be effectively integrated into digital technology-driven statistics education. Additionally, we aim to identify strategies to support learners in overcoming challenges in multinational classrooms.
2. Methods
2.1. Research Design
In the first stage of this research, a qualitative case study method was used to explore the in-depth experiences of a multinational classroom consisting of students from different countries enrolled in the Mathematics Education and Technology master’s programme. Selected students participated in meticulously planned classroom activities as part of the Teaching Statistics and Probability Using Technology course. These classroom activities were intentionally organised within the multimodal learning framework introduced earlier in the study. In this framework, learning is achieved by integrating various representational modes, including visual, textual, symbolic, and interactive computational modelling. For example, the textual or code mode was demonstrated when students wrote MATLAB scripts and added explanatory comments. Visual mode became apparent when students created and examined 2D and 3D plots of probability density functions. Interactive mode emerged as students adjusted parameters, re-ran simulations, and observed immediate changes in graphical outputs. These approaches encourage engagement. Each mode serves a distinct purpose, yet together they build a cohesive environment for learning complex concepts.
The data collection techniques included interviews, classroom observations, and the analysis of students’ work documents. At this stage, a qualitative case study approach was used due to its ability to explore and frame students’ distinctive educational experiences and how these influenced their learning interaction processes [17,18,19]. Classroom observations and semi-structured in-depth interview questions were used to collect data. The data were analysed using thematic analysis to conceptualise students’ interactions related to the use of MATLAB.
In the second stage of this research, the elements and themes that emerged were arranged using a logic-based epistemological framework to illustrate multimodal learning interactions while using MATLAB technology. To clearly convey the relationships between these elements, the model uses a set of symbolic notations derived from logic-based representation, as shown in Table 1. While these symbols allow for concise mapping of complex interactions, they may not be familiar to all readers. Therefore, each symbol is accompanied by a plain-language explanation to ensure accessibility and consistency of interpretation. The definitions below apply to all diagrams and model descriptions presented in this study.

Table 1.
Meaning of Arrow Symbols in the Models.
To ensure the reliability of the qualitative coding process, Cohen’s Kappa coefficient was used to validate the arrangement of themes and elements in multimodal learning interaction. Three independent coders were involved. At first, two coders participated in a structured briefing session. They learned the coding manual, practised with sample data, and discussed category definitions. This helped them agree on how to interpret each code. An agreement threshold of κ ≥ 0.75, as recommended by Landis and Koch [20], was set to represent substantial agreement.
When the full dataset was coded, the Cohen’s Kappa value reached 0.81, which shows strong inter-coder reliability. If disagreements occurred, coders independently reviewed the original data again. They compared their reasoning and discussed their choices. Through discussion, they worked towards a consensus. If they still disagreed, a third senior researcher was asked to make the final decision. This process made the thematic coding both statistically and procedurally rigorous.
By using this method, researchers can better understand the ways MATLAB is applied in multinational classrooms which include international students. This approach provides deeper insights and shows how MATLAB can influence teaching practice and learning theory in a global academic environment.
2.2. Data Collection
An in-class observation was conducted in this research to identify students’ challenges and difficulties. Students’ interactions were video recorded to capture their engagement and discussion. Classroom activities were observed to gain a more intuitive understanding of students’ behaviours and interactions during the practical application of MATLAB. These observations provide insights into how students engage with the software in real time.
In this study, field notes were employed to investigate the usage of MATLAB in statistics instruction, focusing on Visualising the 3D Probability Density of Normal Random Variables. This method provides a comprehensive understanding of the logical interpretation of the data [21,22,23]. The researcher made systematic observations by documenting how instructors used MATLAB in lectures and how students interacted with it. From the field note, the researcher gained a deeper understanding of MATLAB’s role in the teaching and learning process. These observations revealed the advantages of MATLAB in enhancing students’ engagement, deepening their understanding of statistical concepts, and facilitating the development of practical application skills.
A semi-structured interview was then conducted to gather qualitative data to explore students’ perspectives based on the recorded observation. The focus was on their challenges and practical experiences related to using MATLAB during the session. This interview method allowed the researcher to gain insights into the challenges and opportunities associated with the practical application of MATLAB in teaching statistics. The interview also revealed the precise impact of MATLAB on students’ education, including heightened curiosity, enhanced scholastic achievement, and the cultivation of practical skills [24].
In addition, students’ assignments, such as plotting probability density function graphs, were collected to evaluate the practical application of MATLAB and assess its effectiveness in achieving learning objectives. An integrated approach to qualitative data collection was chosen because it provided a comprehensive understanding of the effectiveness of MATLAB in teaching and learning. This approach also generated ideas for future research and improvements in teaching methods using MATLAB.
2.3. Data Analysis
Concepts of a model are typically multidimensional and multilevel, consisting of elements, categories, and themes. To explore themes of multimodal learning interactions, class interaction video recordings, interviews, and task documentation were transcribed and coded inductively into elements, categories, and themes. Categorisation was based on indicators such as interactions (including body language, social interactions, and in-class verbal communication), responses from open-ended interview questions, and task progress and MATLAB output documentation. Indicators with similar characteristics were then merged to construct elements. Further analysis involved reviewing and refining descriptor codes and redefining cluster labels as the model’s dimensions were clarified.
Based on observations of class interactions in a multinational classroom, a conceptual model of class interaction is proposed. The emerging themes modelled the relationships between themes and categories and the substitutability of elements within categories of indicators. Logical operators such as “or” and “and” were also assigned to explain the interconnections between various situations.
This analysis highlighted the challenges students faced in developing creativity and effective communication, both of which are essential for understanding normal random variable concepts. The qualitative data—derived from observations and interviews—provided insights into participants’ thoughts and emotions, learning strategies, and students’ engagement and motivation [25].
3. Results
The data analysis revealed ten emerging themes: five were identified as barriers and challenges, while the other five focused on the interactions that multinational students face when learning with MATLAB technology. These themes emerged within a multimodal instructional environment that combined visual, textual, symbolic, and interactive elements. For example, students simultaneously engaged in writing MATLAB code (textual/symbolic), generating visual plots (visual), and iteratively refining parameters with real-time feedback (interactive).
3.1. Barriers and Challenges Faced by International Students When Using MATLAB
- Cross-Cutting Barrier: MATLAB Syntax and Interface Challenges
A persistent challenge identified throughout multiple themes was the students’ struggle with MATLAB syntax as well as the intricacies of the interface. These difficulties were especially pronounced during initial lessons. Observation notes frequently recorded moments when students paused their work to search for the correct commands, rectify syntax errors, or request guidance from the instructor. This often led to extended task completion times. There was less time available for discussing conceptual ideas.
Notably, these challenges did not exist in isolation. They overlapped with other barriers, including time constraints and technical obstacles, and sometimes resulted in reduced independent thinking. Computational fluency is essential. Without it, students find it harder to engage meaningfully with statistical concepts. This finding highlights the need for introductory support and structured practice before students are asked to solve problems on their own.
3.1.1. Theme 1: Language and Technical Barriers
At the third level of analysis, the findings illustrate that language and technical barriers can hinder students’ ability to understand and apply complex material. Data showed that language obstacles include both incomprehensible concepts and difficulties arising from cultural and linguistic differences. Technical barriers were also noted, such as unfamiliarity with digital tools and discomfort in computer-based environments. These issues contributed to struggles with visualising statistical concepts and reduced classroom communication. Language challenges may lead to misunderstandings. Technical problems make it harder to use resources effectively. Figure 1 summarises these elements and categories for Theme 1.
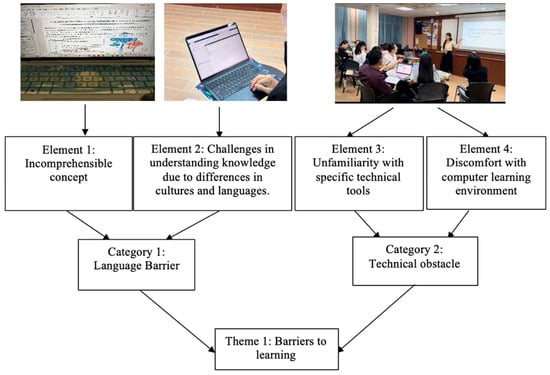
Figure 1.
Elements and categories of the barriers to learning theme.
Students with varying levels of English fluency struggled with the application instructions and technical terminology. Those with limited speaking abilities found it difficult to follow verbal explanations and engage in meaningful discussions. This lack of English fluency led to misunderstandings and confusion, and impeded their ability to effectively navigate and use the app.
In addition to language issues, students faced challenges related to the cross-cutting barrier and unfamiliarity with statistical software. Many students were new to MATLAB’s syntax and programming concepts, which made it difficult for them to write and debug code effectively. Additionally, a lack of prior exposure to statistical software compounded these difficulties, as students struggled with data analysis tools and visualisation functions. This situation further hindered their ability to complete tasks and learn efficiently.
3.1.2. Theme 2: Lack of Prior Knowledge
The theme ‘lack of prior knowledge’ emerged from the following categories: (1) lack of programming experience and (2) inadequate understanding of statistical concepts. Observational data showed that these categories are supported by elements such as students’ struggles with integrating statistical theory with MATLAB programming. Additionally, it was observed that students took a long time to overcome the cross-cutting barrier, as well as having an inadequate understanding of statistical concepts, as shown in Figure 2.
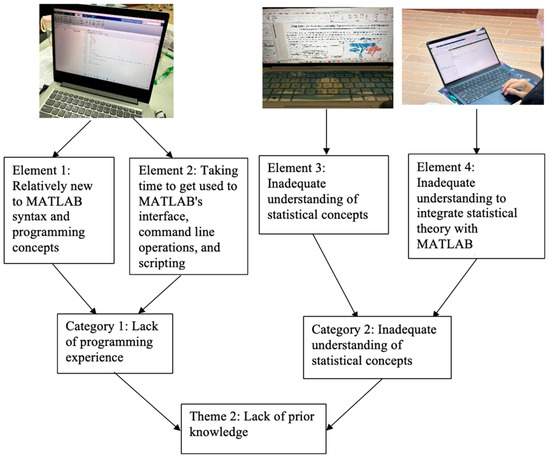
Figure 2.
Elements and categories of the lack of prior knowledge theme.
A lack of prior knowledge in statistics and programming can significantly hinder learning by creating a steep learning curve for students. Without a foundational understanding, students may struggle to grasp complex concepts and apply them effectively. This leads to confusion and decreased confidence. This gap in basic knowledge can result in a slower learning process and a reduced ability to engage with more advanced material. The observation revealed that the students had an insufficient grasp of fundamental statistical concepts, which affected their ability to use MATLAB effectively. Students struggled to understand how to apply statistical theories to their coding tasks, such as calculating statistical measures or interpreting results within MATLAB. This lack of integration between statistical theory and programming practice resulted in difficulties completing assignments and applying the app’s tools effectively to analyse data.
3.1.3. Theme 3: Time Pressure
Time pressure can significantly impact students’ performance and learning experience. When students are faced with tight deadlines or limited time to complete tasks, they often feel stressed and anxious. This stress can negatively affect their ability to focus, think critically, and perform effectively. Figure 3 shows the theme of time pressure mapped to the related elements.
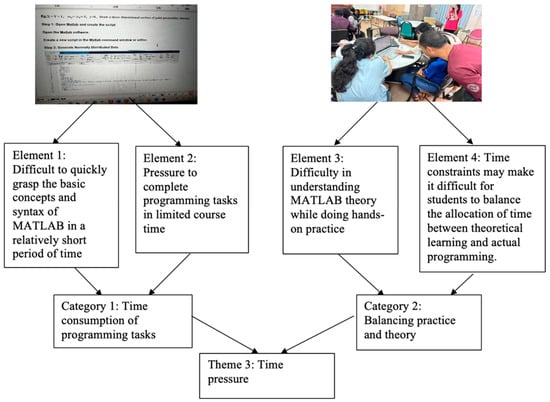
Figure 3.
Elements and categories of the time pressure theme.
The categories of elements are (1) time-consuming programming tasks and (2) balancing practical applications with theoretical learning. The observation revealed that students spent more time on tasks due to difficulties in overcoming the cross-cutting barrier within a short timeframe. This situation further created pressure to complete programming tasks within limited time constraints. The pressure to complete these tasks within the allotted course time led to a rushed approach, where students focused more on finishing their code rather than thoroughly understanding the programming principles.
The observation also highlighted difficulties in balancing theoretical understanding with hands-on practice. Students were expected to apply MATLAB theory to practical coding exercises, but the limited time available made it challenging to allocate sufficient attention to both aspects. For example, while trying to code a solution, students struggled to comprehend the underlying theoretical concepts. The tight deadlines exacerbated this issue, as students often had to choose between focusing on theoretical learning and completing their programming tasks. The observation demonstrated that time pressure significantly affected students’ ability to manage both programming tasks and theoretical understanding effectively.
3.1.4. Theme 4: Technical Difficulty
Utilising MATLAB requires writing precise code, as it is highly sensitive to the correct syntax and commands, and this leads to technical difficulty. If the appropriate tool or function is not called correctly, the code will not execute as intended. Additionally, entering incorrect code will result in errors, disrupting the coding process and requiring troubleshooting. Two categories of elements contributed to the emergence of technical difficulties: (1) debugging and error handling challenges, and (2) data processing and visualisation. Figure 4 shows the theme of technical difficulties mapped to the related elements.
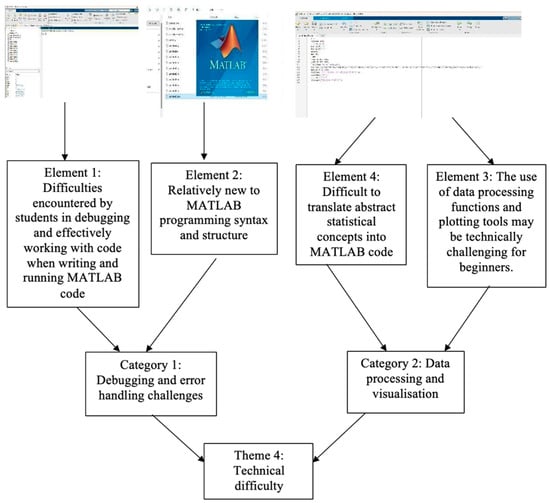
Figure 4.
Elements and categories of the technical difficulties theme.
During the classroom observation, several students encountered technical difficulties while using MATLAB for the classroom activity. They were also confused because MATLAB has a large library of functions and toolboxes, and they had to gradually learn how to call and use these functions to run statistical analysis. For example, they struggled with debugging and error handling as they wrote and ran code. As they were relatively new to programming, they found it difficult to identify the cause of the problem. Rather than confidently troubleshooting, the student hesitated and sought assistance from the instructor. This highlighted the challenge of effectively managing coding errors and debugging when students are still learning the basics of the platform.
Students also faced challenges when translating abstract statistical concepts into MATLAB code. For example, they struggled to apply data processing functions, such as calculating the covariance matrix and creating visual representations of their results. They also found it difficult to generate accurate graphs that visually represented the large amount of data they were working with. This difficulty with both the code and the visualisation tools slowed their progress.
3.1.5. Theme 5: Lack of Independent Thinking
Creative and independent thinking is essential in mathematics, as many topics require its application in real-world problem-solving scenarios. A lack of this ability can reflect a less supportive learning environment, particularly in the case of international students. When problems are presented with altered forms or variables, students who lack creative problem-solving skills often struggle to find solutions. This difficulty not only slows their progress but also leads to disengagement and a loss of interest in the class. These themes emerged from (1) reliance on guidance and (2) creative applications. The mapping of these themes and their elements is illustrated in Figure 5.
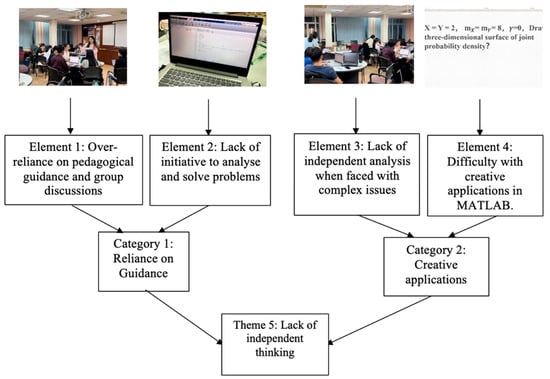
Figure 5.
Elements and categories of the lack of independent thinking theme.
From the classroom observation, it became clear that some students struggled with independent thinking while completing their tasks. Many students appeared overly reliant on pedagogical guidance and group discussions. Instead of taking the initiative to analyse and solve problems independently, they consistently sought help from the instructor or waited for group members to lead the discussion. For instance, when confronted with a coding challenge, rather than exploring different solutions themselves, several students relied on step-by-step instructions provided by the instructor.
This passive approach meant students missed opportunities to develop independent problem-solving skills. When tasks became more complex or variables changed, students struggled to apply concepts creatively and adapt their code. Confidence was low, and independent exploration was rare. As a result, the potential for deeper learning and creative application in MATLAB remained underdeveloped.
Table 2 below shows the data triangulation for the first research question.

Table 2.
Data triangulation for research question 1.
3.2. How International Students Leverage MATLAB to Enhance Teaching and Learning Statistics
3.2.1. Theme 1: Collaborative Learning
Based on the classroom observation and interviews, it was found that MATLAB offered students a platform for group collaboration that enhances teamwork skills through joint participation in writing MATLAB code, solving problems, and analysing data. This collective effort not only positively impacted learning outcomes but also promoted the sharing of information and created a supportive learning atmosphere. The collaborative learning theme comprises two main categories of elements: (1) Collaborative Work, which is observed through interactions that demonstrate effective teamwork and real-time problem-solving, and (2) Mutual Learning, identified when students actively share their acquired skills and knowledge, as well as their experiences and insights, leading to a sense of satisfaction. Figure 6 illustrates the data mapping for the emerging theme of collaborative learning.
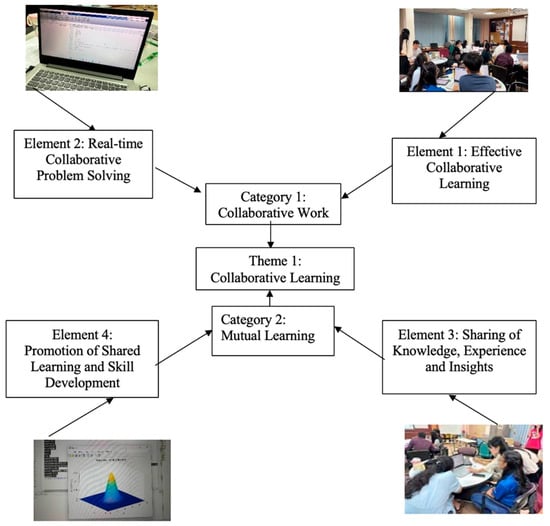
Figure 6.
Elements and categories of the collaborative learning theme.
During an observed collaborative session using MATLAB, the students from China and Japan were grouped to generate a 3D probability density of normal random variables. As the students had varying levels of English fluency and speaking ability, they initially faced challenges in writing code and entering data in MATLAB due to the miscommunication between the instructor and the students from different countries. These challenges drove the students into two categories of collaborative learning: mutual learning and collaborative work. Mutual learning interactions began with the instructor sharing knowledge, followed by discussions among students. Documented data on student task work show that those with stronger English skills or better MATLAB understanding took the lead in completing tasks and were able to explain statistical concepts effectively. This initial sharing of knowledge facilitated mutual learning within the group and extended to discussions between different groups.
In the second category, collaborative work, the students relied on teamwork to solve the problems of writing code and entering data in MATLAB. An important aspect of teaching to promote mutual learning and collaborative work is requiring students to work collaboratively to tackle challenges and solve problems. This approach not only deepens their understanding but also fosters teamwork skills such as communication and tolerance for different English dialects.
3.2.2. Theme 2: Active Learning
The data from the classroom observation and interviews revealed that the use of MATLAB promoted active participation through the use of hands-on programming and powerful visualisation tools. The theme of Active Learning consists of the following categories: (1) active participation and (2) active engagement. These elements were observed through collaborative work, including i. voluntary participation, ii. contribution of ideas, iii. interaction with others, and iv. sharing of ideas. Figure 7 illustrates the mapping of these elements within the theme.
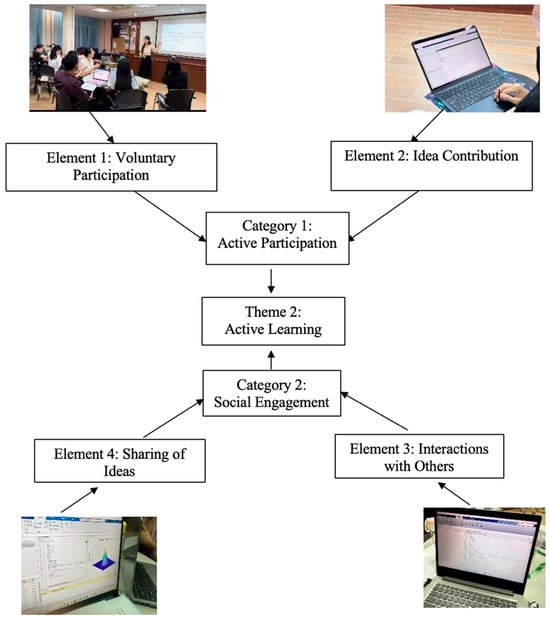
Figure 7.
Elements and categories of the active learning theme.
During a collaborative session using MATLAB, the students were highly engaged in transforming abstract statistical concepts into physical and concrete data by writing MATLAB code and utilising its visualisation capabilities. Students worked in groups to write code that generated 3D graphs of 2D normal distributions, adjusted parameters such as the mean and covariance matrix and immediately observed how these changes affected the shape of the distributions. This hands-on approach allowed students to transform abstract concepts into physical, tangible representations. It can be proven from the task documentation output that the instant visual feedback and interactive characteristics of MATLAB made the learning process more understandable and entertaining. Seeing the direct impact of their adjustment in real time deepened their intuitive grasp of the concept. This scenario created a more engaging learning environment and boosted their interest and motivation in both statistical ideas and MATLAB usage.
3.2.3. Theme 3: Discussion
Classroom observations and interviews revealed that the students actively engaged and benefited from discussions while utilising MATLAB to write code, solve problems, and analyse data. The interactive nature of MATLAB fostered conversations in which students explored concepts collaboratively and gained diverse perspectives. As shown in Figure 8, discussion can be categorised into two types of elements: (1) focused discussion and (2) result interpretation discussion.
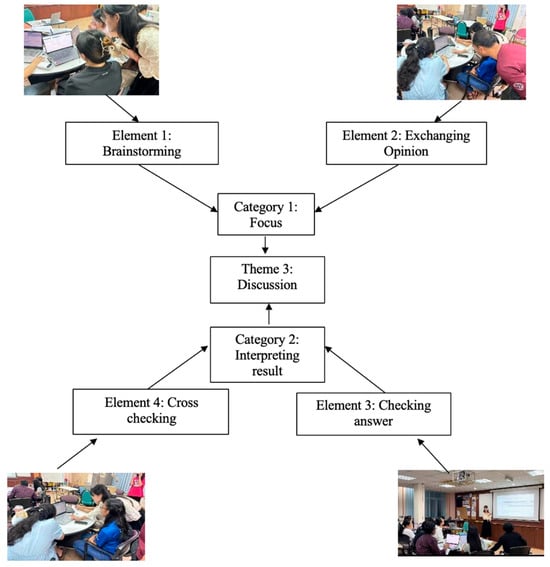
Figure 8.
Elements and categories of the discussion theme.
During the classroom observation of students utilising MATLAB, it was found that they were highly engaged in discussion as they explored the abstract statistical concepts. Students began by brainstorming in groups about how to transform abstract statistical concepts into physical representations using MATLAB. They discussed different approaches to solving the given problem, sharing ideas on how to adjust parameters and interpret the resulting data visualisations. As they worked, students frequently exchanged their opinions and considered their peers’ suggestions.
The students then moved on to interpreting the results. They checked their answers by comparing their findings and cross-checking their interpretations. MATLAB’s visualisation tools facilitated this process, allowing the students to validate their results against real-time graphical representations. Overall, the discussions and collaborative problem-solving enabled engagement with the materials.
3.2.4. Theme 4: Motivation
The effectiveness of MATLAB is evident through increased student engagement and interest. Practical programming activities allow learners to address real-world problems, which make lessons more dynamic. Motivation is reflected in several ways: cognitive motivation, as seen when students express understanding; achievement motivation, demonstrated by successful task completion; and the ability to convey complex ideas to peers. Figure 9 illustrates these categories within the motivation theme.
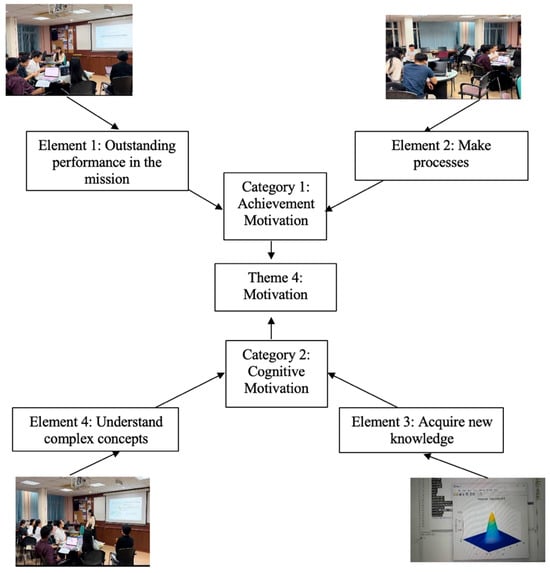
Figure 9.
Elements and categories of the motivation theme.
Students showed increased interest and motivation throughout the classroom activity. The challenge of solving programming tasks in MATLAB encouraged them to focus and strive for success. Real-time feedback fostered engagement and a desire for improvement. Some students enjoyed the competitive aspect, while others found satisfaction in seeing instant results.
Cognitive engagement was also evident. Learners sought to deepen their grasp of complex statistical concepts by experimenting with data and visualisations. This active approach made the material clearer and enhanced motivation. In summary, both achievement and understanding played key roles in boosting enthusiasm for statistical learning using MATLAB.
3.2.5. Theme 5: Problem-Solving Skill Development
MATLAB contributes significantly to the development of essential skills among students. Through active involvement in programming and data analysis tasks, learners gain hands-on experience that is both practical and relevant. This approach fosters proficiency in coding, critical thinking, and data interpretation. Students not only practice but also apply their knowledge in real-world contexts.
The observation data indicated that students’ MATLAB skills developed primarily in two main areas: (1) data analysis and (2) problem-solving. These are evident through activities such as statistical analysis, data organisation, and the interpretation of visual outputs. Exposure to authentic scenarios, for instance, analysing the average rainfall in Malaysia, encourages students to plan, design, and execute solutions independently. Figure 10 presents a visual mapping of these elements.
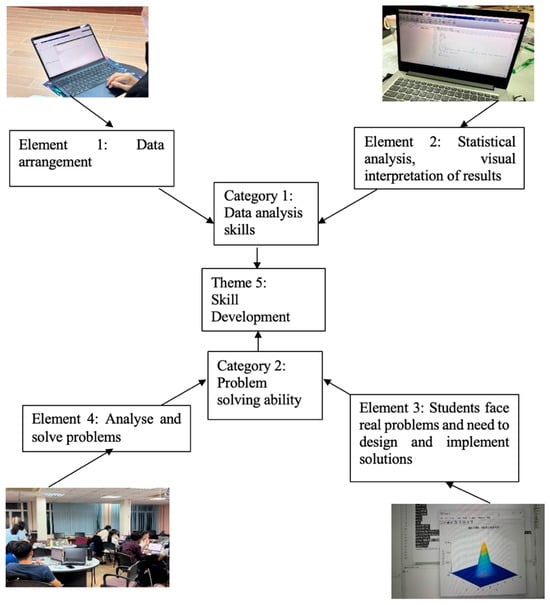
Figure 10.
Elements and categories of the skill development theme.
Students demonstrated notable skill development using MATLAB for statistical learning. They learned to import data, organise information, and apply statistical methods. Through variable manipulation and graph generation, their ability to interpret results improved. This process deepened understanding and supported analysis of complex datasets. MATLAB also fostered problem-solving abilities. Students faced difficult tasks, designed solutions, and coded their approaches. Errors and unexpected results prompted collaboration and revision. Iterative troubleshooting enhanced their critical thinking and technical competence. Overall, hands-on practice with MATLAB built both analytical skills and confidence in solving real-world problems.
Table 3 shows the data triangulation for the second research question.

Table 3.
Data triangulation for research question 2.
3.3. Validation of Themes and Elements Using Cohen’s Kappa
To ensure the reliability and consistency of the identified themes and elements in this study, Cohen’s Kappa coefficient (κ) was employed. This statistical measure assesses inter-rater agreement, verifying that the categorisation of students’ interactions with MATLAB was systematic and replicable across multiple evaluators.
Three independent experts reviewed and coded the qualitative data, assigning student interactions to the five main themes: Collaboration, Engagement, Discussion, Motivation, and Skill Development. Each theme was further broken down into specific elements, ensuring a comprehensive analysis of student learning behaviours. Cohen’s Kappa values were calculated to determine the level of agreement among the raters, with the following interpretation:
0.61–0.80: Substantial Agreement
0.81–1.00: Almost Perfect Agreement
The results of the Cohen’s Kappa analysis are presented in Table 4, demonstrating strong inter-rater reliability across all themes and elements.

Table 4.
Cohen’s Kappa Coefficient for Theme and Element Validation.
- Interpretation of the Results
The high Cohen’s Kappa values (≥0.78) across all themes indicate a strong agreement among expert raters, reinforcing the validity and consistency of the proposed learning interaction model. The highest agreement was observed for Collaboration (κ = 0.85) and Skill Development (κ = 0.86), suggesting that these elements were identifiable and consistently coded across raters. Discussion (κ = 0.78) and Motivation (κ = 0.80) showed slightly lower, yet still substantial agreement, reflecting minor variations in expert interpretation but maintaining overall reliability.
These findings validate the MATLAB Technology Learning Interaction Model, confirming that its core components, i.e., collaboration, engagement, discussion, motivation, and skill development, are observed in student learning behaviours. By establishing inter-rater consistency, the study ensures that the model accurately represents how multinational students interact with MATLAB in a statistical learning environment.
3.4. Model Structure of Learning Barriers and Student Interaction
Based on the analysis of learning barriers and student interactions among multinational students with diverse educational backgrounds and learning cultures, two conceptual models are proposed: the Learning Barriers Model (Figure 11) and the MATLAB Technology Learning Interaction Model (Figure 12). Each model uses a logic-based epistemological framework to map relationships between key elements, with symbolic notation representing how the elements influence one another. Logical connectors illustrate how these elements interact, with detailed definitions of each logical operator provided in Table 1.
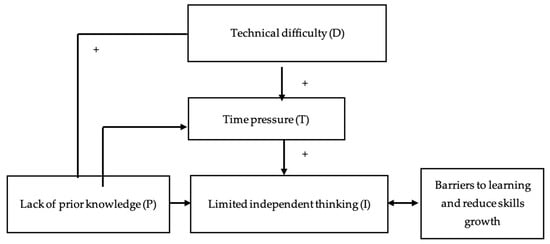
Figure 11.
Conceptual Model of Learning Barriers in a Multinational Mathematics Classroom.
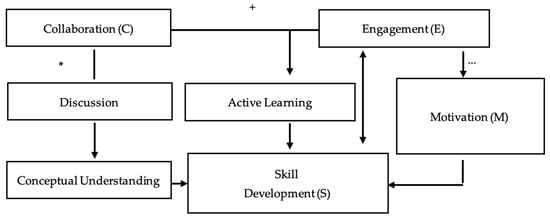
Figure 12.
Conceptual Model of MATLAB Technology Learning Interactions.
3.4.1. Model of Learning Barriers
The Learning Barriers Model (Figure 11) illustrates how several obstacles interact to affect learning outcomes. These key factors include Lack of Prior Knowledge (P), Time Pressure (T), Technical Difficulties (D), and Limited Independent Thinking (I). The model uses symbols to represent the relationships between these elements.
- Lack of Prior Knowledge → Time Pressure
Students who entered the course with limited prior exposure to MATLAB or programming concepts required more time to complete even basic tasks, leading to heightened time pressure. Observation logs showed that students without prior MATLAB experience took an average of 30% longer to complete assignments than peers with prior exposure. This is consistent with Cognitive Load Theory [26], where a lack of foundational schemas increases the cognitive demands of new tasks.
- Time Pressure → Limited Independent Thinking
Under significant time constraints, many students shifted from independent exploration to relying on imitation by copying code from classmates or existing examples. Group interview transcripts revealed that, when pressured by tight deadlines, students generally avoided “trial-and-error” approaches in favour of simply completing the assigned tasks. Yan and Li [9] proved this observation by noting that pronounced performance pressure tends to reduce exploratory learning.
This effect of time pressure was particularly acute among students lacking prior experience with MATLAB. According to observation data, these students spent much longer decoding basic syntax. This additional time diverted their attention from deeper statistical concepts and limited their engagement in collaborative work. Prior knowledge, therefore, appears to moderate how learners cope with time constraints. Those with a stronger computational foundation progressed through assignments more efficiently. They also participated in richer discussions. In contrast, novices became preoccupied with overcoming basic hurdles. The implications are clear. Scaffolding and targeted preparatory activities are essential. When provided, time-limited tasks are more likely to promote, rather than impede, meaningful learning.
- Technical Difficulties → Time Pressure
Syntax errors, software crashes, or difficulties in generating expected outputs prolonged task completion times. In-class troubleshooting records indicated that resolving technical errors consumed work time for some students. This supports findings from [27] on the relationship between debugging difficulty and reduced productive coding time.
- Lack of Prior Knowledge AND Technical Difficulties → Increased Dependence on Peers
Students who experienced both inadequate prior knowledge and persistent technical challenges frequently relied on their peers for guidance and support. Over-reliance on peer assistance may hinder the development of independent problem-solving abilities.
- Limited Independent Thinking ↔ Reduced Skill Growth
Students who refrained from independent exploration demonstrated slower progress in developing MATLAB skills. This slower progress led to a decline in self-confidence. As a result, many of these students became even less inclined to attempt tasks on their own. Analysis of student work revealed consistently smaller performance gains among this group compared to peers who engaged in regular independent practice. This reciprocal relationship reflects Zimmerman’s [28] self-regulated learning theory. Learner autonomy is both a driving force for and a consequence of ongoing skill acquisition. Without autonomy, skill growth is limited. With it, students are more likely to build competence and confidence over time.
3.4.2. MATLAB Technology Learning Interaction Model
The MATLAB Technology Learning Interaction Model (Figure 12) shows the cyclical relationships between Collaboration (C), Engagement (E), Motivation (M), and Skill Development (S) with elements, namely discussion, active learning, and conceptual understanding. Symbolic relationships (e.g., C + E, E → M, M → S) are paired with narrative explanations to ensure comprehension of the model.
- Collaboration AND Engagement → Active Learning
Collaboration enables students to share knowledge, solve problems collectively, and support one another in MATLAB tasks. Engagement sustains attention and active participation. When both occur, students create an interactive environment that supports exploration of MATLAB’s real-time computation and visualisation tools. Without both, learning becomes passive and less effective. Observations showed that groups demonstrating both high collaboration and engagement completed tasks faster and produced more accurate results. This supports Johnson & Johnson’s [29] cooperative learning theory, which emphasises the joint impact of social and cognitive engagement.
Collaboration significantly enhanced engagement among students, especially those who initially lacked confidence or hesitated to tackle tasks on their own. In group settings, participants were able to share code and collectively address syntax issues. They also interpreted MATLAB visual outputs together. This collaborative approach eased cognitive load and kept students focused. As engagement grew, students showed more willingness to experiment with MATLAB commands and to voice their ideas. This contributed to a positive cycle. Collaboration encouraged greater participation, which, in turn, strengthened the collaborative momentum.
- Collaboration OR Discussion → Conceptual Understanding
Either collaboration or discussion alone can improve understanding, but when both occur, learning is deeper. MATLAB’s real-time feedback often sparked discussion, especially among international students overcoming language barriers. Recorded sessions showed that in 80% of tasks where discussion was present, students were more likely to identify and correct coding errors. This aligns with Mercer’s [30] work on exploratory talk as a driver of conceptual growth.
- IF Engagement THEN Motivation
Sustained engagement often led to increased motivation, particularly when students saw evidence of progress via visual output or successful code execution. Observation data indicated that students showed effective engagement, which was also more likely to relate to their motivation. It is consistent with Ryan & Deci’s [31] Self-Determination Theory, where engagement supports the development of intrinsic motivation.
- Motivation → Skill Development
Narrative: Motivation drove students to persist through MATLAB’s learning curve, refine their coding skills, and deepen their statistical understanding. Log files showed that motivated students spent more time experimenting with parameters and debugging code. This supports Vygotsky’s [32] concept of scaffolded progression toward independent mastery.
- Skill Development ↔ Engagement
As students became more proficient in MATLAB, their engagement increased, creating a reinforcing cycle. Data show that students who achieved higher skill scores also demonstrated increased participation in subsequent activities. It aligns with Bloom’s Taxonomy, where mastery fosters higher-order thinking skills and deeper engagement.
4. Discussion
While no formal pre- or post-assessments were conducted, qualitative evidence indicated notable learning gains throughout the duration of the study. Initially, observation notes and session screenshots captured frequent syntax errors and a high dependence on instructor guidance. Over time, students began to demonstrate more precise coding, completed tasks with greater efficiency, and showed independence in addressing errors. This progression was also reflected in student reflections. Several participants described increased confidence in employing MATLAB for statistical analysis. They moved away from relying on trial and error toward a more intentional and reasoned approach to computational problem-solving. Together, these findings strongly suggest there was meaningful growth in both computational competence and conceptual understanding during the study.
The thematic analysis revealed four interconnected factors that underpin students’ experiences with MATLAB: Collaboration, Engagement, Motivation, and Skill Development. These elements, although described individually in Section 3, do not function in isolation. Rather, they interact continuously, forming a dynamic system. Their influence on one another aligns with well-established learning theories. This interplay becomes especially significant within the context of a culturally diverse classroom.
Collaboration is recognised to promote active learning. This observation closely aligns with Johnson and Johnson’s [29] cooperative learning theory that highlights how collaborative practices facilitate the exchange of knowledge between peers. Not only does collaboration enable students to help each other overcome technical challenges and language barriers, but it also serves as a critical social support system. In a classroom composed of multiple nationalities, peer assistance does more than lighten the cognitive demands of MATLAB tasks [26]. It fosters a sense of belonging that sustains engagement and enhances learning.
Engagement operated as both a requirement and a result of collaborative learning. The findings resonate with Fredricks et al.’s [33] multidimensional engagement framework, in which behavioural, emotional, and cognitive engagement reinforce each other. In this study, MATLAB’s real-time feedback and visualisation tools significantly increased cognitive engagement. The process seemed to be cyclical. Engagement led to more collaboration, which then encouraged deeper motivation and further engagement.
Motivation served as a force to sustain learning. Aligned with Deci and Ryan’s [31] self-determination theory, this intrinsic drive was evident when students observed their own progress. Immediate computational feedback offered tangible validation for their efforts, which was empowering. However, motivation was also fragile. Early experiences with unsolved technical issues, especially when support was lacking, often led to demotivation. This highlights the need for substantial scaffolding at the outset of the learning process.
Skill development is the peak of this iterative process. However, it is not a terminal point. As students became more proficient in computational tasks, their confidence increased. They engaged more readily with challenges. This willingness to experiment not only reinforced engagement but also enhanced collaboration among peers. Such progression is consistent with Vygotsky’s [32] Zone of Proximal Development. With guided support, learners transition gradually to independent mastery.
While earlier research has identified learning barriers in multicultural and computational education contexts, this study goes a step further. It theorises how these barriers interact within a multimodal learning ecosystem. The MATLAB Technology Learning Interaction Model demonstrates that visual, symbolic, textual, and computational modes need to be sequenced and scaffolded. This sequencing helps manage cognitive load, which is especially important for learners who bring a wide range of prior knowledge to the classroom. The model also extends Cultural–Historical Activity Theory (CHAT) by showing how tool-mediated activities shape collaboration and motivation, particularly when students come from diverse backgrounds. In summary, this model shifts the focus. Instead of just describing the challenges, it offers a clear and structured pathway. This pathway connects multimodal engagement with the development of computational skills.
5. Limitations and Scope of Generalisation
While this study introduces a conceptual model with the aim of broader applicability, it is important to note that all empirical data were obtained from a single postgraduate statistics classroom in Malaysia. The unique blend of nationalities, language proficiencies, and prior computational experiences in this cohort strongly influenced learning patterns and interaction dynamics. Sometimes, a student’s low language proficiency is mistaken for an unwillingness to participate. Sometimes, a lack of previous experience with computational tools appears as low engagement or motivation. The present research design does not fully address this complexity.
To address these challenges, the model was developed based on Multimodal Learning Theory, Constructivism, and CHAT. However, further empirical validation is needed. Future studies should consider incorporating specific measures. For example, language proficiency assessments and inventories of cultural learning styles could provide deeper insights. Comparative or longitudinal research designs would be especially valuable to strengthen the model. It would also enhance its external validity and practical significance for instructors working with diverse student populations. Systematic testing across multiple settings is essential for maximising the educational benefits of this model.
6. Conclusions
This research highlights several significant barriers that postgraduate students face when learning statistics using MATLAB. These include insufficient prior knowledge, strict time constraints, technical challenges, and limited development of independent thinking. These obstacles interact in complex ways and are shaped by each student’s cultural background, language proficiency, and previous exposure to technology. Recognising the interconnectedness of these factors, the study introduces an integrated model that links computational learning, cognitive growth, and adaptable teaching methods.
The MATLAB Technology Learning Interaction Model draws on established academic frameworks, specifically Multimodal Learning Theory and CHAT. It outlines a structured pathway for learning that integrates guided instruction, collaborative problem-solving, and a gradual shift from theoretical mathematics to practical computational work. This model is not static. By including AI-driven adaptive feedback, real-time visualisation, and elements of gamification, it supports student engagement and the development of key skills in classrooms characterised by cultural diversity.
This framework serves as a valuable guide for the design of technology-mediated, multimodal learning environments. It offers a practical foundation for educators. As it is applied and tested in diverse cultural and institutional settings, its effectiveness and relevance for enhancing engagement and learning outcomes in computational education will become clearer. Future research can validate and expand this model to confirm its role in advancing best practices for computational education worldwide.
A notable limitation of this study is the lack of formal quantitative measures, such as pre- and post-test scores, task completion rates, or coding accuracy. These metrics would allow for triangulation of observed learning progress. In future research, a mixed-methods approach should be considered. Qualitative insights are valuable. However, when combined with small-scale quantitative indicators, the assessment of MATLAB’s impact on statistical learning outcomes would become more robust and comprehensive.
Author Contributions
Q.C., M.R.B., K.E.L. and L.C. collaborated equally on the data collection, analysis and writing of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. No specific sources of funding were granted for the research, with the research being undertaken within institutional workloads.
Institutional Review Board Statement
This manuscript forms part of a research project that has received formal ethics clearance from the Universiti Malaya Research Ethics Committee (UMREC, Non-Medical). The Reference Number is UM.TNC(P&I)/UMREC_4739. This approval is valid from August 2025 to August 2028. The ethics approval letter was issued by UMREC on 7 August 2025.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The datasets generated and/or analysed during the current study are not publicly available due to the ethics applications specifically stating that “data will not be preserved for possible future use in another project either by yourself or another researcher”.
Acknowledgments
Each author made substantial contributions to the research design and data analysis and drafted the work and approved the submitted version. All authors agree to be personally accountable for the author’s contributions and to ensure that questions related to the interpretation or integrity of any part of the work, even ones in which the author was not personally involved, are appropriately investigated, resolved, and the resolution documented in the literature.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Akan, A.; Chaparro, L.F. Signals and Systems Using MATLAB; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Montes, N.; Rosillo, N.; Mora, M.C.; Hilario, L. A novel real-time MATLAB/simulink/LEGO EV3 platform for academic use in robotics and computer science. Sensors 2021, 21, 1006. [Google Scholar] [CrossRef]
- Gemechu, E.; Michael, K.; Atinafu, M. Effects of MATLAB supported learning on students’ motivation in applied mathematics: A case of mechanical engineering students. Educ. J. 2021, 10, 1–7. [Google Scholar] [CrossRef]
- Moreno-Guerrero, A.J. Flipped learning and cooperative work: Effects on motivation and learning in mathematics.
- Ahmad, U. Development of a Structural Analysis Program (SABSM) Using MATLAB Featuring Graphical User Interfaces; London University: London, UK, 2013. [Google Scholar]
- Wang, F.; Yu, K.; Yang, L. Computer graphics algorithm demonstration system. Procedia Comput. Sci. 2023, 228, 736–744. [Google Scholar] [CrossRef]
- Poulsen, P.R.; Cho, B.; Langen, K.; Kupelian, P.; Keall, P.J. Three-dimensional prostate position estimation with a single X-ray imager utilizing the spatial probability density. Phys. Med. Biol. 2008, 53, 4331–4353. [Google Scholar] [CrossRef]
- Bajuri, M.R.; Rasid, N.S.M.; Hassan, R.; Aman, S. Sustainability educational leadership and management for STEM-based approach: An expert qualitative formulization. Malays. Online J. Educ. Manag. 2023, 11, 63–91. [Google Scholar]
- Yan, J.; Li, L. Board 183: A case study of AFL models on factors of engaged learning in STEM education. In Proceedings of the 2024 ASEE Annual Conference & Exposition, Portland, OR, USA, 23–26 June 2024. [Google Scholar] [CrossRef]
- Patankar, P.; Kulkarni, S. MATLAB and Simulink In-Depth: Model-Based Design with Simulink and Stateflow, User Interface, Scripting, Simulation, Visualization and Debugging (English Edition); BPB Publications: Haryana, India, 2022. [Google Scholar]
- Kayashima, N.; Asada, S.R. Introduction: Development of universities in Southeast Asia and the impacts of study abroad. In Impacts of Study Abroad on Higher Education Development; Springer Nature: Singapore, 2024; pp. 1–20. [Google Scholar] [CrossRef]
- Sirat, M. Higher education development and study abroad experiences of faculty in Malaysia. In Impacts of Study Abroad on Higher Education Development: Examining the Experiences of Faculty at Leading Universities in Southeast Asia; Kayashima, N., Sugimura, M., Kuroda, K., Kitamura, Y., Eds.; Springer Nature: Singapore, 2024; pp. 59–78. [Google Scholar] [CrossRef]
- Xu, X.; Tran, L.T.; Xie, X. Between decolonization and recolonization: Investigating Chinese doctoral students in Malaysia as a case of global South-South student mobility. High. Educ. 2024, 87, 1193–1209. [Google Scholar] [CrossRef]
- Yassin, A.A.; Abdul Razak, N.; Qasem, Y.A.; Saeed Mohammed, M.A. Intercultural learning challenges affecting international students’ sustainable learning in Malaysian higher education institutions. Sustainability 2020, 12, 7490. [Google Scholar] [CrossRef]
- Wu, H.P.; Garza, E.; Guzman, N. International student’s challenge and adjustment to college. Educ. Res. Int. 2015, 2015, 202753. [Google Scholar] [CrossRef]
- Oduwaye, O.; Kiraz, A.; Sorakin, Y. A trend analysis of the challenges of international students over 21 years. Sage Open 2023, 13, 21582440231210387. [Google Scholar] [CrossRef]
- Rashid, Y.; Rashid, A.; Warraich, M.A.; Sabir, S.S.; Waseem, A. Case study method: A step-by-step guide for business researchers. Int. J. Qual. Methods 2019, 18, 1609406919862424. [Google Scholar] [CrossRef]
- Baxter, P.; Jack, S. Qualitative case study methodology: Study design and implementation for novice researchers. Qual. Rep. 2008, 13, 544–559. [Google Scholar] [CrossRef]
- Yin, R.K. Qualitative Research from Start to Finish; Guilford Publications: New York, NY, USA, 2015. [Google Scholar]
- Landis, J.R.; Koch, G.G. The measurement of observer agreement for categorical data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef]
- Savin-Baden, M.; Major, C. Qualitative Research: The Essential Guide to Theory and Practice; Routledge: London, UK, 2023. [Google Scholar]
- Morgan, S.J.; Pullon, S.R.; Macdonald, L.M.; McKinlay, E.M.; Gray, B.V. Case study observational research: A framework for conducting case study research where observation data are the focus. Qual. Health Res. 2017, 27, 1060–1068. [Google Scholar] [CrossRef]
- Mulhall, A. In the field: Notes on observation in qualitative research. J. Adv. Nurs. 2003, 41, 306–313. [Google Scholar] [CrossRef]
- DiCicco-Bloom, B.; Crabtree, B.F. The qualitative research interview. Med. Educ. 2006, 40, 314–321. [Google Scholar] [CrossRef] [PubMed]
- Hassan, R.; Jafferi, N.A.; Boon, Y.; Ahmad, J.; Hassan, Z.; Bajuri, M.R. Professional learning community’s practices: Exploring Malaysian primary school teacher strategies. Malays. Online J. Educ. Manag. 2022, 10, 74–90. [Google Scholar]
- Sweller, J. Cognitive load theory and educational technology. Educ. Technol. Res. Dev. 2020, 68, 1–16. [Google Scholar] [CrossRef]
- Becker, B.A.; Denny, P.; Pettit, R.; Bouchard, D.; Bouvier, D.J.; Harrington, B.; Kamil, A.; Karkare, A.; McDonald, C.; Osera, P.; et al. Compiler error messages considered unhelpful: The landscape of text-based programming error message research. In Proceedings of the 2019 ITiCSE Working Group Reports (ITiCSE-WGR ’19), Aberdeen, UK, 15–17 July 2019; ACM: New York, NY, USA, 2019. 34p. [Google Scholar] [CrossRef]
- Zimmerman, B.J. Becoming a self-regulated learner: An overview. Theory Pract. 2002, 41, 64–70. [Google Scholar] [CrossRef]
- Johnson, D.W.; Johnson, R.T. An educational psychology success story: Social interdependence theory and cooperative learning. Educ. Res. 2009, 38, 365–379. [Google Scholar] [CrossRef]
- Mercer, N. Words and Minds: How We Use Language to Think Together; Routledge: London, UK, 2000. [Google Scholar] [CrossRef]
- Ryan, R.M.; Deci, E.L. Self-determination theory and the facilitation of intrinsic motivation, social development, and well-being. Am. Psychol. 2000, 55, 68–78. [Google Scholar] [CrossRef] [PubMed]
- Vygotsky, L.S. Mind in Society: The Development of Higher Psychological Processes; Cole, M., John-Steiner, V., Scribner, S., Souberman, E., Eds.; Harvard University Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Fredricks, J.A.; Blumenfeld, P.C.; Paris, A.H. School engagement: Potential of the concept, state of the evidence. Rev. Educ. Res. 2004, 74, 59–109. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).