Designing Behavioural Artificial Intelligence to Record, Assess and Evaluate Human Behaviour
Abstract
:1. Introduction and Outline
1.1. Motivation
1.2. Context
1.3. Outline
1.4. Disclaimer
2. Behavioural Sciences
- (a)
- We elaborate on the claim that experts in psychology disagree on what affects behaviour (Section 2.1).
- (b)
- We argue that game theoretic models regularly fail to correctly predict human behaviour (Section 2.2).
- (c)
- We discuss the dilemma of competitive versus cooperative behaviour (Section 2.3) which our proof-of-concept behavioural artificial intelligence (cf. Section 6) was designed to face.
- (d)
- We introduce (Section 2.4) the model from behavioural psychology used for our formalization (Section 3).
2.1. Behavioural Psychology
2.2. Game Theory and Rational Choice
2.3. Cooperative/Competitive Behaviour
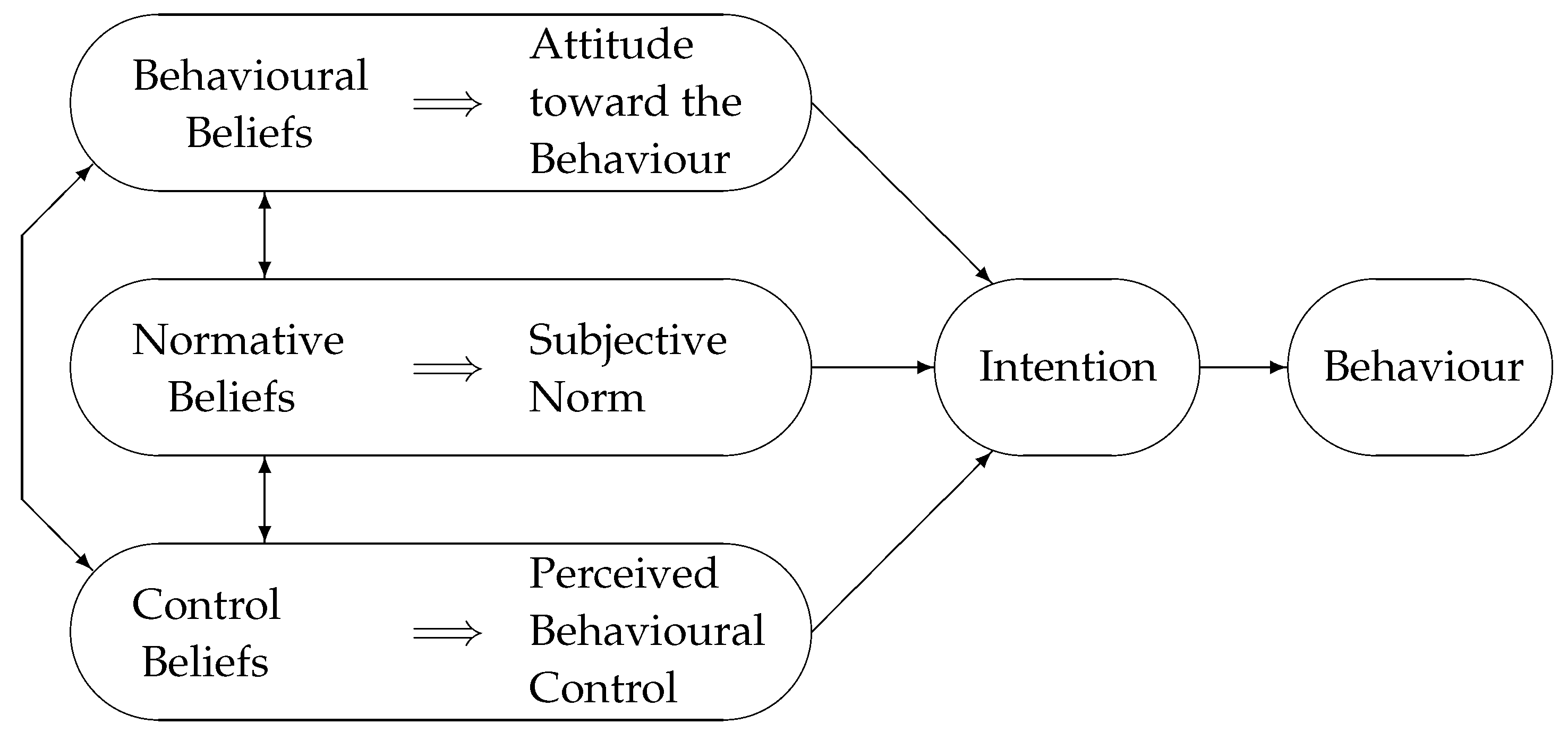
2.4. Modelling Behaviour
- Behavioural beliefs: Behavioural beliefs are someone’s expectations about the likely outcome of actions, paired with the subjective view of these outcomes.
- Normative beliefs: Normative beliefs are the opinion of others regarding the outcomes of actions, the personal intention to adhere to these peer standards as well as the desire of the individual to live up to the expectations of one’s peers.
- Control beliefs: Control beliefs are one’s level of confidence that they have control over all relevant factors required to bring about an outcome.
3. Formalisms
- (a)
- behavioural psychology (i.e., the TACT paradigm, Section 3.1) to formally describe behaviour;
- (b)
- philosophy and logic (i.e., classical propositional logic as well as modal logic, Section 3.2); and
- (c)
- game theory (i.e., game theory, utility theory and subjective expected utility theory, Section 3.3).
3.1. The TACT Paradigm
Examples
- Action: walking, exercising, working out
- Target: on a treadmill, on a stair master, on a walking machine
- Context: at home, in a physical fitness centre, in the gym
- Time: for at least 30 min each day in the forthcoming month
- (1)
- This summer, Person sells a boat to Person in Edinburgh.
- (2)
- Last year Person bought a boat from Person in Glasgow.
- (3)
- The next five months Person will not sail on the Clyde.
- Action: buy, sell, sail
- Target: Person , Person , Person
- Context: in Glasgow, in Edinburgh, on the Clyde
- Time: this summer, last year, the next five months
3.2. Propositional and Modal Logic
3.2.1. Propositional Logic
Syntax and Semantics
Syntactic Sugar
- (p ∨ q) is equivalent to ¬(¬p∧¬q)
- (p → q) is equivalent to ¬p∨ q
- (p ↔ q) is equivalent to (p →q) ∧ (q → p)
3.2.2. Modal Logic
Syntax
Semantics
3.3. Game Theory and Rational Choice
3.3.1. Game Theory
3.3.2. Utility Theory
3.3.3. Subjective Expected Utility (SEU) Theory
- A set of behaviours from which to choose
- A subset thereof to consider
- A set of possible futures, resulting from the different behaviours/actions
- A payoff function representing the utility
- A function to determine the outcome a certain action will bring about
- Some information about the probability of that particular outcome occurring
4. Games as a Discreet Environment for Controlled Behaviour Assessment
- (a)
- We open by mentioning the use of games in psychology and education in general.
- (b)
- We introduce a certain type of game which fits our purpose. The aim is to advocate the use of games as controllable environments where test subjects can be subjected to comparable decisions (with the obvious aim to then record and compare these choices).
- (c)
- The bulk of this section formally defines what we understand to be a game in Section 4.3.
- (d)
- The bulk of this section provides a formal model of games in Section 4.4. This model can then be used to interpret behavioural statements (which is defined in Section 5) when expressed in the formalism presented in Section 3.
4.1. Psychology and Computer Games
4.2. Resource-Management Games for Serious Games
- They are challenging due to restricted or limited resources, location and time, the need to plan ahead and the multitude of potentially conflicting objectives.
- They stimulate the fantasy by putting the player into an unfamiliar and imaginary position.
- They constantly require the player to control issues arising from the continuity of the game and from the actions of competing AI or human players. Choosing a behavioural strategy in response to actions of others is a substantial part of the game.
4.3. Defining a Game
- the set of players .
- the exhaustive set of histories .
- p
- a function mapping histories to individual payoffs for the n players.
4.4. Modelling a Game
4.4.1. Possible World Models (Kripke Semantics)
- the set of states .
- a set of rules .
- the set of states .
- a set of rules .
- a valuation
Practical Considerations
4.4.2. Potentially Infinite Games
4.4.3. Disjoint Submodels
4.4.4. Characterizing Submodels
Practical Considerations
4.4.5. Specific Instances of a Game
- 1.
- and with
- 2.
- and
- 3.
- and
4.4.6. Uncertainties
- ,
- :
5. Formalizing and Evaluating Human and Machine Behaviour
5.1. Formal Statements about Individual States of a Game
5.2. Formal Statements about Behaviour in Games
5.2.1. Behaviour in General
5.2.2. Behavioural Statements
5.2.3. Nested Statements
5.2.4. Complex Behavioural Statements
- Cooperative
- Player i is not bidding against any player this round
- Player i is not bidding against any player that has played cooperatively the last round
- Player i is not bidding against any player (that has played competitively against any player that has played cooperatively the last five rounds) this round
- Competitive
- Player i is bidding against another player this round
- Player i is bidding against all other players the next three rounds
- Player i is only bidding against players (that have bid on Player i the last round) this round
- Action: Player i is bidding
- Target: Player 1, Player 2, Player 3, Player 4
- Context: Player j has played ϕ (where is another TACT statement)
- Time: this round, last round, last five rounds, next three rounds
5.3. Automated Translation of Behaviour Statements
5.3.1. Formalism ⇔ Natural Language
- Translate atomic statements into their propositions.
- Replace occurrences of “it is not the case that” by ¬.
- Rewrite “statement1 and statement2” to (“statement1” ∧ “statement2”) and,correspondingly, “statement1 or statement2” to (“statement1” ∨ “statement2”).
- Sentences of the form “if statement1 then statement2” are replaced by (“statement1” → “statement2”).
- Finally, “statement1 if and only if statement2” is replaced by (“statement1” ↔ “statement2”).
5.3.2. Formalism ⇔ Normal Form
- (p ↔ q) becomes ¬(p∧¬q) ∧ ¬(¬p∧ q)
- (p → q) becomes ¬(p∧¬q)
- (p ∨ q) becomes ¬(¬p∧¬q)
- (p ↔ q) becomes ¬(¬(¬p ∨q) ∨ ¬(p ∨¬q))
- (p → q) becomes ¬p∨ q
- (p ∧ q) becomes ¬(¬p∨¬q)
5.4. Automated Behaviour Evaluation
5.5. Automated Generation of Consistent Behaviour Statements
5.6. Behavioural Artificial Intelligence
- the set of actions available to the player.
- the set of consequences of these actions.
- r
- the rules, i.e., a function mapping actions to consequences.
- a (subjective) strategy, i.e., a function mapping subsets of to an action a (, ).
- g
- a function mapping consequences to multi-valued goodness values representing specific aspects of these consequences (such as reaching the specific goal of, e.g., taking a pawn).
- u
- a function mapping goodness values to utility values (representing, for example, how taking that pawn will serve one of a number of strategic objectives, which ultimately lead to winning the game). The arity of u and that of its output may differ.
- an evaluation function , which maps a state to k boolean values. Each of these values indicates whether a formula ϕ is true in that state (i.e., whether the formula is valid, given the valuation (assignment of truth values to propositions) for that state). Each of these k formulae represents a behaviour which we want to support.
- a function , that combines the k boolean values calculated by and the m utility values. The output are m values which combine the utility as well as the behavioural preference of the action.
- ≻
- a preference relation over such that iff .
6. Proof of Concept Implementations
6.1. Aims and Objectives
- The formalism is suitable for controlled environments such as simulations and computer games (assuming that their data structures are designed appropriately). The evaluation and comparison of formally stated behaviours, as well as the translation thereof into their natural language equivalent, is straightforward and can be automated. The algorithms for doing so are computationally efficient and scale well.
- Using formal behaviour statements (expressed in our formalism), we can augment standard models for rational decision making from the literature to include behavioural stances. Using this model, we can design and implement a game-playing AI whose choices exhibit clear (and human-like) behavioural preferences.
6.2. Proof of Concept Game—Utility Tycoon
6.2.1. Objectives
6.2.2. Brief Description of the Game
6.2.3. Game Design and Implementation
Serious Game Principles
Implementation
6.2.4. Validation of Our Approach
Representation and Evaluation of Formalised Behaviour Statements
Computational Efficiency and Performance
6.3. Proof of Concept Game—SoxWars
6.3.1. Objectives
6.3.2. Brief Description of the Game
- The players initially start with a small amount of money (resource).
- Using that money they can purchase supplies of socks for stock (products).
- The shops where these socks can be sold are limited and there is a system in place that favours the supplier that has, in the past, supplied the respective shop.
- The game is turn-based, and turns consist of a number of phases, the order of which is fixed.
- The revenue from selling socks is fixed while the cost for restocking (i.e., the acquisition of socks) varies depending on the phase of the turn when it happens.
- During each phase, players make their choices simultaneously. These decisions, which can affect the outcome for all players, are being revealed directly afterwards (i.e., before the next phase).
- The game is designed to converge to situations where trade-offs are required. While a balanced and mutually fair distribution of opportunities is possible, any player can upset this balance and force the game into a series of conflicts (i.e., situations where players will compete for something).
6.3.3. Game Design
The Different Phases of a Turn
- RAC
- A limited number of new products can be acquired per round in three separate RAC phases:
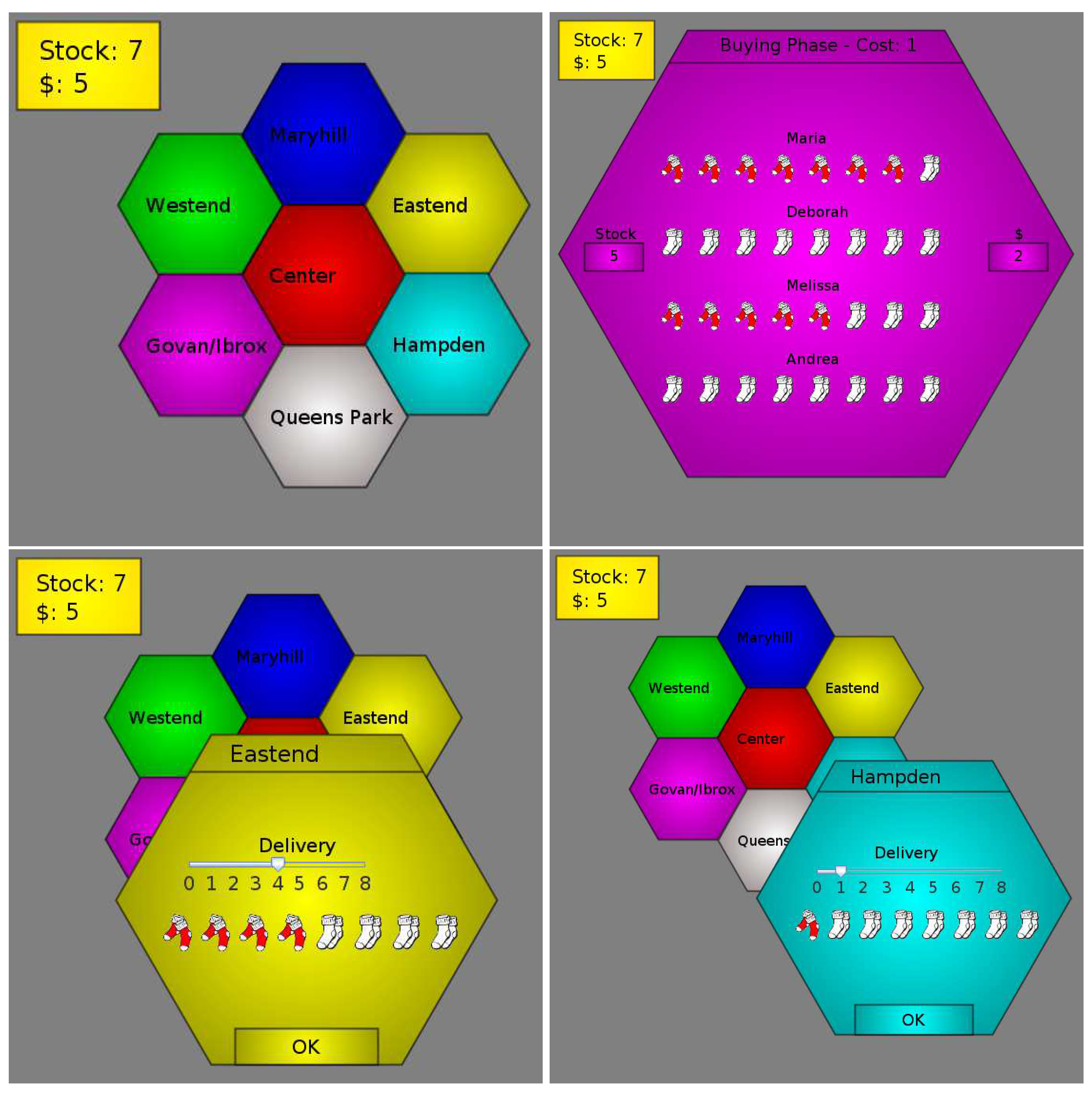
- RAC1 Buying: Each player is offered the same number of socks, for $1 per unit.
- RAC2 Bidding: The players are offered additional socks at a cost of $1.50 per product. Players can also choose to bid on the products offered to other players (at the inflated price of $2.50).
- RAC3 Trading: Players can offer remaining resources to other players for $2 (market value).
- RAS
- There are a number of territories, each with a number of shops where the resources are sold for $2 during RAL. Assignment happens in three phases and only to territories, not to specific shops:
- RAS1 Shops only accept resources from the player that delivered to them in the last round.
- RAS2 Shops that had a supplier last round only accept resources from that player.
- RAS3 Delivery to any remaining (not yet supplied) shop.
Conflicting deliveries are handled during the RAL part of a turn. - RAL
- There is a bias towards players who supplied shops in the last round, making it beneficial to reliably supply your shops. This is especially relevant since the number of shops is finite. Shops first accept delivery from players that supplied them in the last round but then accept supplies evenly from all supplying players (on a territory by territory basis). Conflicts are resolved by random allocation such that all players are favoured in turn. If a fair (but random) distribution is not mathematically possible, the human player is favoured (by design).Essentially, it is in the players’ interest to deliver (and keep delivering) to as many shops as possible. This will let the game converge to a state where all shops are loyal. At this stage, the game will produce only the number of resources required to satisfy the demand of all shops. Once this happens, the only way to acquire more territory is to bid on another player’s resources (at a loss) in the hope of keeping the shops this player can no longer deliver to in the next round.
Three Variations for the Order of Phases in a Turn
6.3.4. Modelling the Game
Modelling Resource-Acquisition
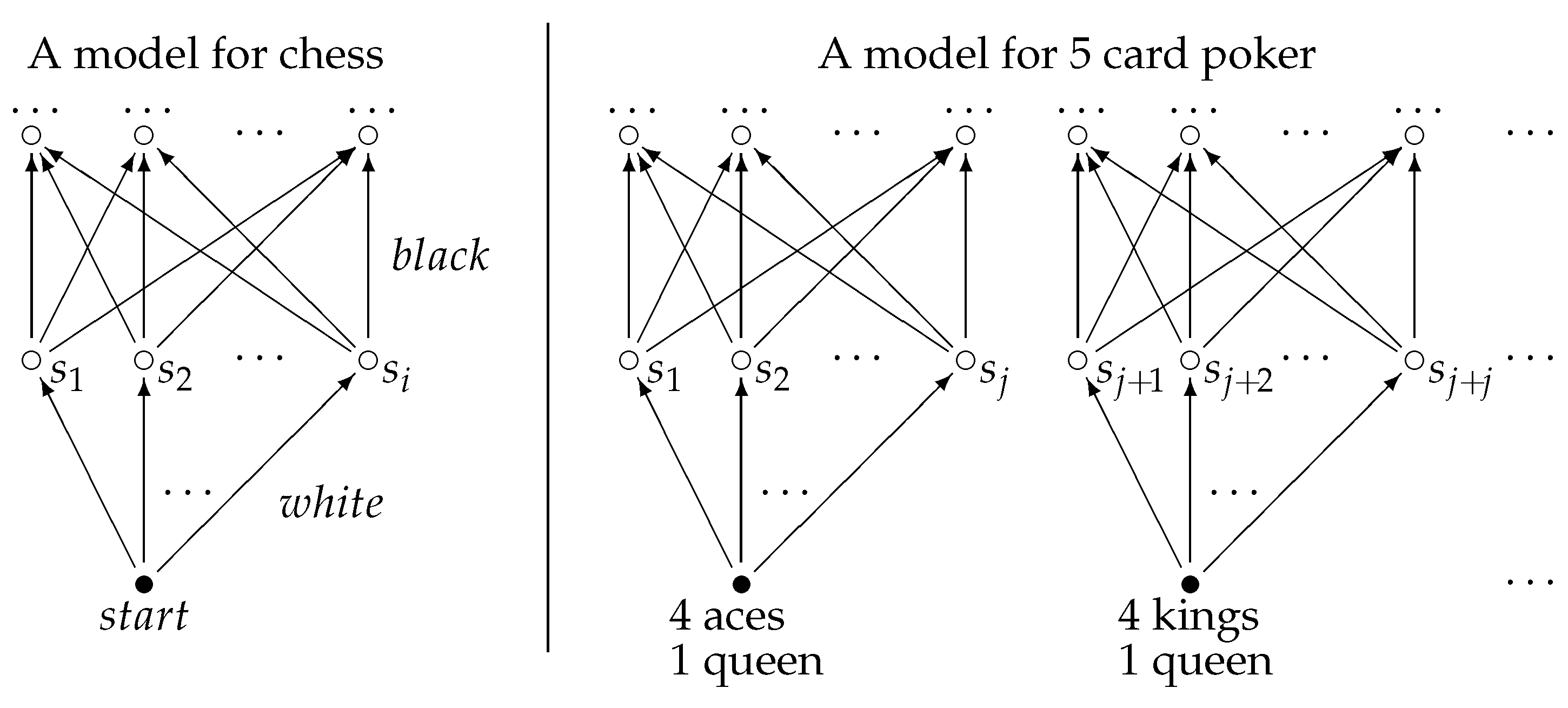
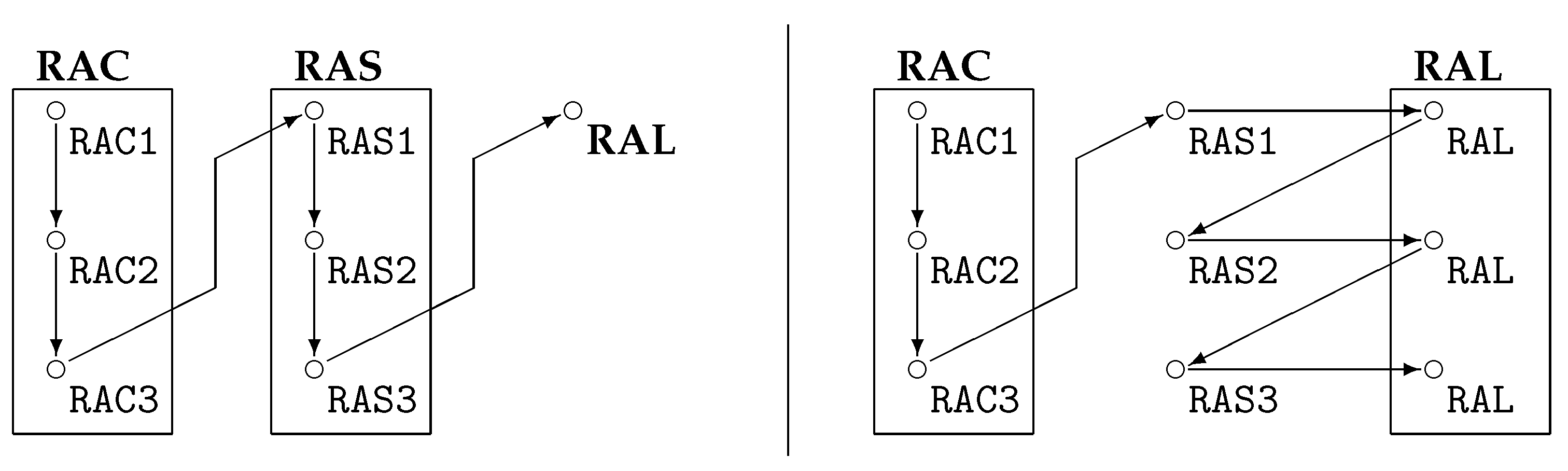
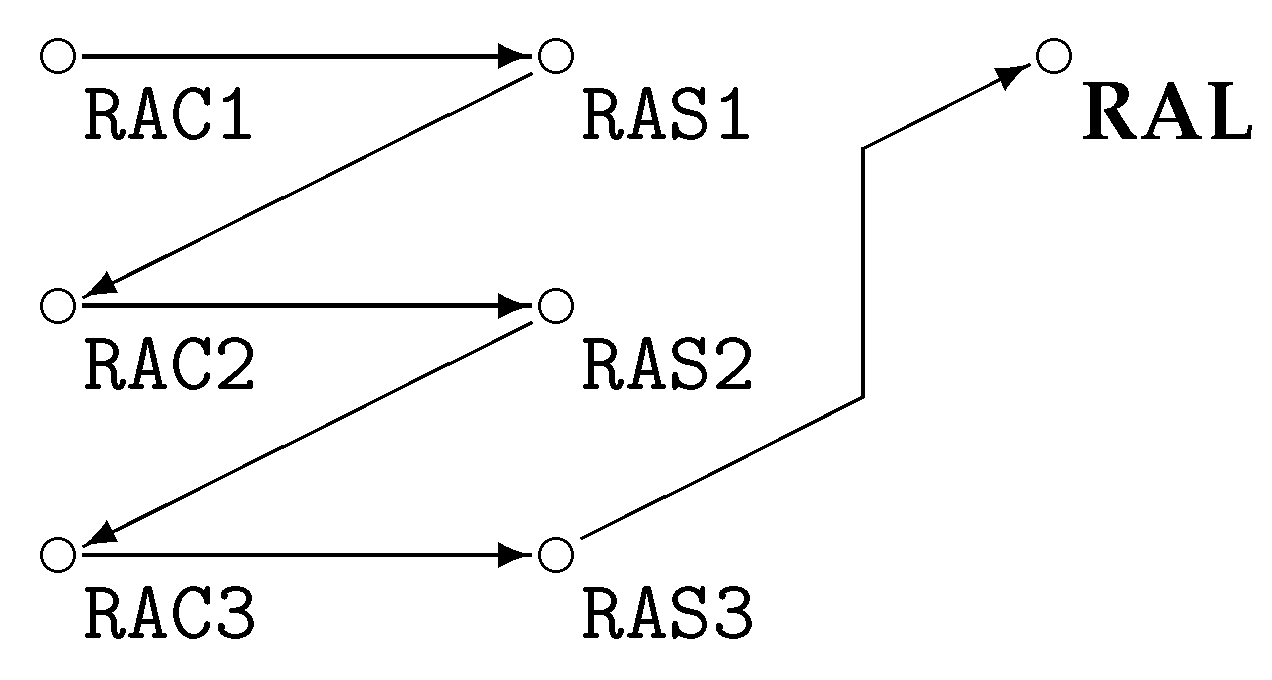
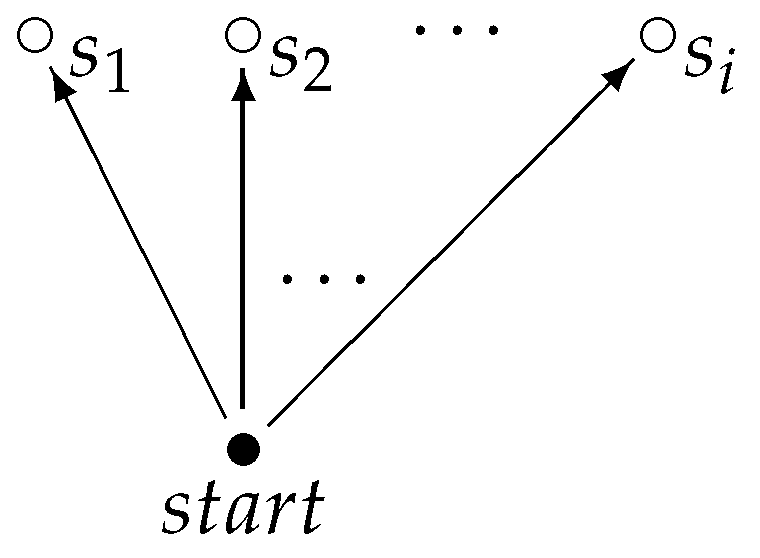
- Modelling RAC1: Phase one of the resource acquisition (RAC1) does not contain any behaviour of interest to us. Whether a player decides to purchase resources does not appear as part of the considered behavioural statements. Obviously, there are changes in the state of the game, but these can be represented as a single world in the model: if a specific player purchases resources, this only affects the propositions related to this player’s stock and funds. These propositions are disjoint with the propositions of the other players and thus we can express all the changes in within a single world. The only minor liberty taken in this approach is the fact that the globally available resources are of course decreasing every time a player purchases stock, which happens multiple times in the stage. However, global resources are not considered for our behavioural statements as they are not under the control of the player. Therefore, they are not included in .The difference in the frames (i.e., the models without the propositions assigned) for the stages is thus mainly in the number of possible future states (e.g., i in Figure 9: to .) This means that if the player can decide on the number of resources to purchase, and if there are exactly n products offered to each of the j players, there are different results for each player (allowing for zero products being purchased), resulting in in the model for RAC1. In our implementation, we included this information as it was relevant for the expression of the rational aspect of the AI; however, we restricted this decision to “buying” and “¬ buying”, so that in our implementation .
- Modelling RAC2: The second stage of the resource acquisition is the most important one for the behaviour analysis. Again, the model can be collapsed to the model shown in Figure 9. This time, however, we consider the actions of the individual players with regard to the other players as the bidding on resources happens by one player but targets the resources of a specific other player. As above for RAC1, we only allowed the bidding on resources and did not enable a quantification for this (i.e., it is not possible to bid on a few resources of a player, it is either bidding on all offered resources or bidding on none). We furthermore did not offer the option to “bid on all players”, forcing the player to select every opponent individually. We furthermore required that one bids on one’s own resources before bidding on those of other players. This is rational strategic behaviour and removes a number of complex behavioural constructions such as bidding on other players’ resources at the cost of not bidding on your own (which would be cheaper). This means that for j players there are other players to bid on, “bidding only on the resources offered to the player” and “not bidding at all”. Due to this, there are possible combinations, and thus in the model for RAC2 .
- Modelling RAC3: In the last stage where resources can be acquired, we ignored the decision to accept resources offered. The justification for this was that including this increases the complexity of the represented behaviour by allowing for sulking and other emotional responses. The main justification for being able to omit these more complex behaviours is that the AI players will make the decision to purchase such resources on a purely tactical basis. The idea is that the human player is aware that the opponents are played by a computer and it is assumed that emotional responses are not exhibited towards these players. The decisions in RAC3 are very similar to the one in RAC2, in that each player gets to decide whether to offer a fixed amount of stock to another player. Therefore, for model RAC3 as well.
Modelling Resource-Allocation
Modelling Resource-Assignment
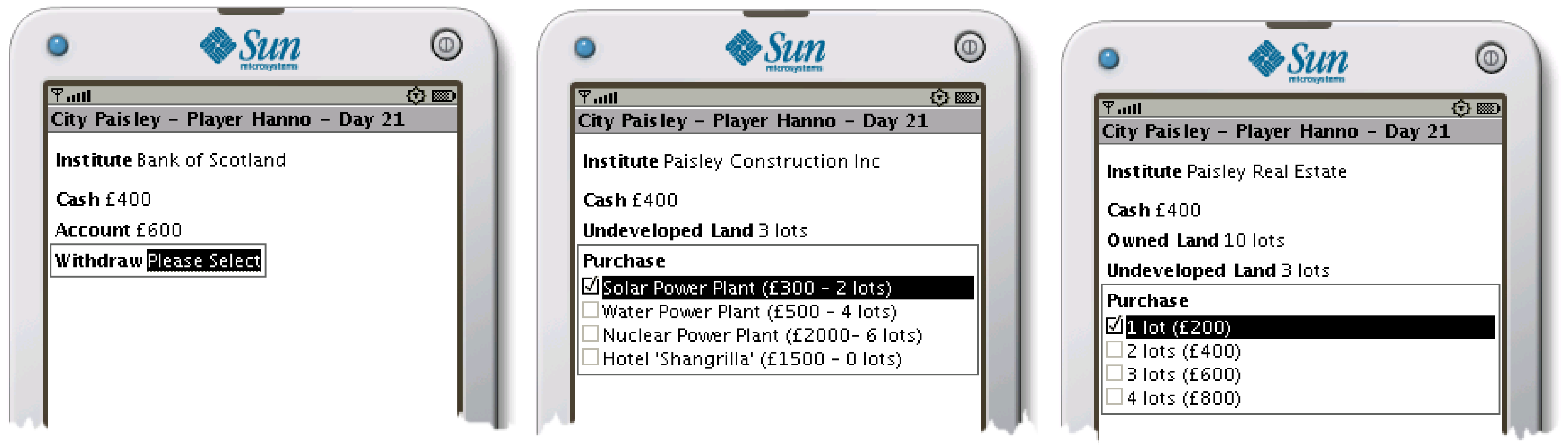
6.3.5. Implementation
Implementation: Cardboard Version
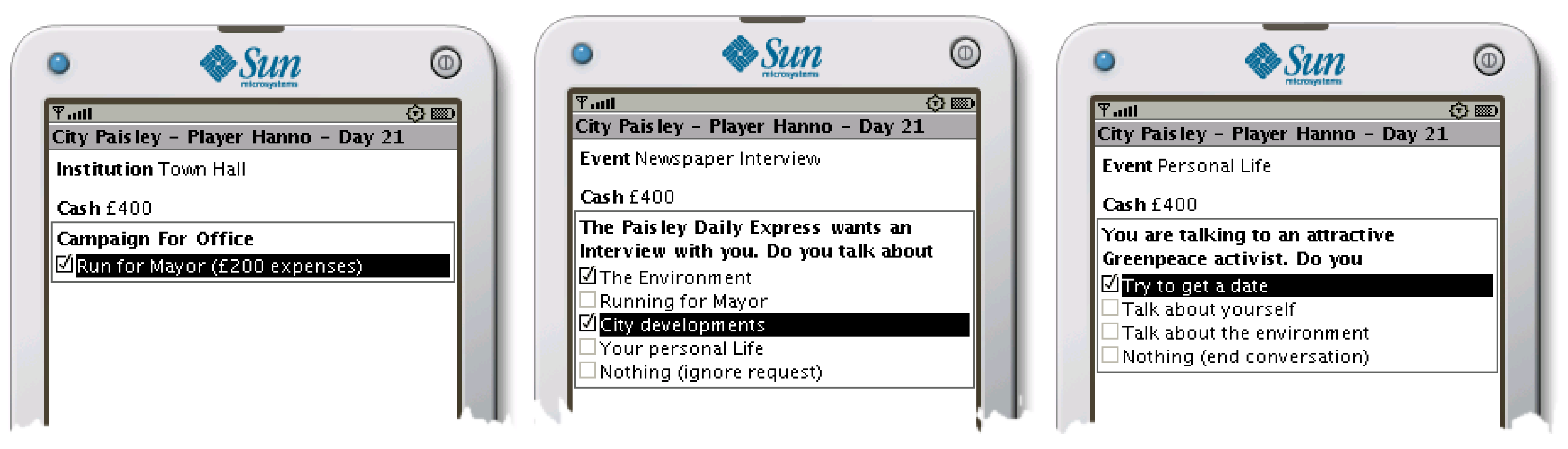
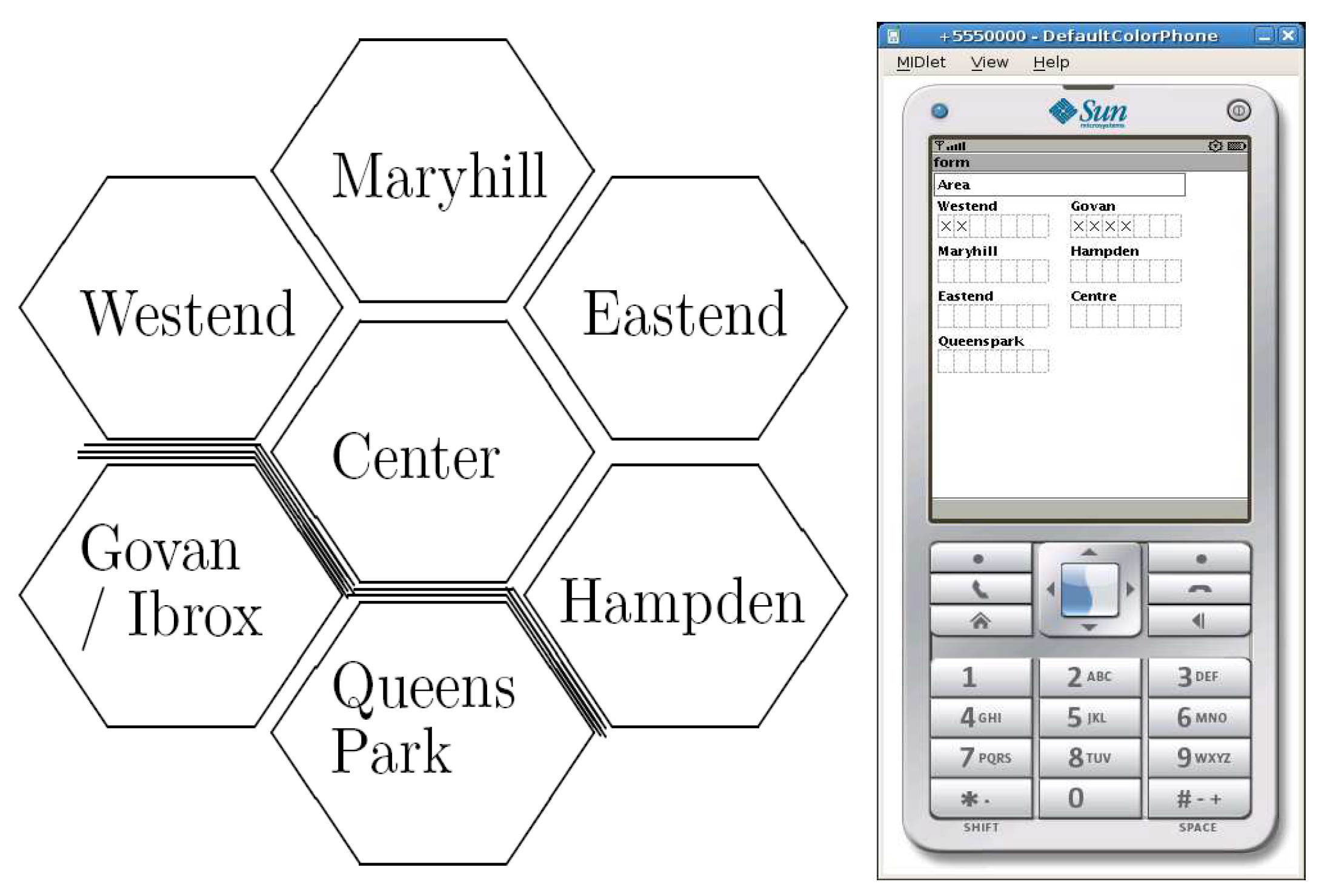
Implementation: Mobile Phone App
Implementation: Web-Based Game
6.3.6. Validation and Evaluation of Our Approach
Lessons Learned: Cardboard Version
Lessons Learned: Mobile Phone App
Lessons Learned: Web-Based Game
7. Summary and Conclusions
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence | |
| DOAJ | Directory of open access journals | |
| ToPB | Theory of Planned Behaviour | Section 2.4 |
| TACT | Target, Action, Context and Time | Section 3.1 |
| PL | Propositional Logic | Section 3.2.1 |
| ML | Modal Logic | Section 3.2.2 |
| SEU | Subjective Expected Utility | Section 3.3.3 |
| RMG | Resource-Management Games | Section 4.2 |
References
- Kitano, H. Intelligence in a changing world. Nature 2007, 447, 381–382. [Google Scholar] [CrossRef] [Green Version]
- Turing, A.M. Computing Machinery and Intelligence; Oxford University Press: Oxford, UK, 1950. [Google Scholar]
- Hildmann, H. Computer Games and Artificial Intelligence; Encyclopedia of Computer Graphics and Games; Springer International Publishing: Cham, Switzerland, 2018; Chapter 234. [Google Scholar]
- Hassabis, D. Artificial Intelligence: Chess match of the century. Nature 2017, 544, 413–414. [Google Scholar] [CrossRef] [Green Version]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of Go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Cho, A. ‘Huge leap forward’: Computer that mimics human brain beats professional at game of Go. Science 2016. [Google Scholar] [CrossRef]
- Silver, D.; Hubert, T.; Schrittwieser, J.; Antonoglou, I.; Lai, M.; Guez, A.; Lanctot, M.; Sifre, L.; Kumaran, D.; Graepel, T.; et al. Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm. ArXiv, 2017; arXiv:1712.01815. [Google Scholar]
- Frenkel, K.A. Schooling the Jeopardy! Champ: Far From Elementary. Science 2011, 331, 999. [Google Scholar] [CrossRef] [PubMed]
- Bowling, M.; Burch, N.; Johanson, M.; Tammelin, O. Heads-up limit hold’em poker is solved. Science 2015, 347, 145–149. [Google Scholar] [CrossRef] [PubMed]
- Riley, T. Artificial intelligence goes deep to beat humans at poker. Science 2017. [Google Scholar] [CrossRef]
- Moravčík, M.; Schmid, M.; Burch, N.; Lisý, V.; Morrill, D.; Bard, N.; Davis, T.; Waugh, K.; Johanson, M.; Bowling, M. DeepStack: Expert-level artificial intelligence in heads-up no-limit poker. Science 2017, 356, 508–513. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Simon, H.A. What Computers Mean for Man and Society. Science 1977, 195, 1186–1191. [Google Scholar] [CrossRef] [PubMed]
- Simon, H.A. The behavioral and social sciences. Science 1980, 209, 72–78. [Google Scholar] [CrossRef] [PubMed]
- Behrens, T.E.J.; Hunt, L.T.; Rushworth, M.F.S. The Computation of Social Behavior. Science 2009, 324, 1160–1164. [Google Scholar] [CrossRef] [PubMed]
- Simon, H.A. A Behavioral Model of Rational Choice. Q. J. Econ. 1955, 69, 99–118. [Google Scholar] [CrossRef]
- Henrich, J.; Heine, S.J.; Norenzayan, A. The weirdest people in the world? Behav. Brain Sci. 2010, 33, 61–83. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hildmann, H.; Uhlemann, A.; Livingstone, D. Simple mobile phone based games to adjust the player’s behaviour and social norms. Int. J. Mob. Learn. Organ. 2009, 3, 289–305. [Google Scholar] [CrossRef]
- Hildmann, H.; Hildmann, J. A critical reflection on the potential of mobile device based tools to assist in the professional evaluation and assessment of observable aspects of learning or (game) playing. In Proceedings of the 3rd European Conference on Games Based Learning (ECGBL09), Graz, Austria, 12–13 October 2009; API, Academic Publishing International: Graz, Austria, 2009. [Google Scholar]
- Hildmann, H. Mobile device based support to enrich initiative games and to facilitate in-game evaluation in experiential education. In Proceedings of Techniques and Applications for Mobile Commerce (TAMoCo09); IOS Press: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Hildmann, H.; Boyle, L. Evaluating player’s attitudes and behaviour through mobile device based serious games. In Proceedings of the IADIS International Conference on Mobile Learning 2009, Barcelona, Spain, 26–28 February 2009; IADIS Press: Florianopolis, Brazil, 2009. [Google Scholar]
- Hildmann, H.; Hirsch, B. Raising awareness for environmental issues through mobile device based serious games. In Proceedings of the 4th Microsoft Academic Days, Berlin, Germany, 19 November 2008. [Google Scholar]
- Hildmann, H.; Uhlemann, A.; Livingstone, D. A Mobile Phone Based Virtual Pet to Teach Social Norms and Behaviour to Children. In Proceedings of the DIGITEL ’08: Proceedings of the 2008 Second IEEE International Conference on Digital Game and Intelligent Toy Enhanced Learning, Banff, BC, Canada, 17–19 November 2008; IEEE Computer Society: Washington, DC, USA, 2008; pp. 15–17. [Google Scholar]
- Hildmann, H.; Guttmann, C. A formalism to recognise and monitor patient behaviour for intervention in intelligent collaborative care management. In Proceedings of the CARE Collaborative Agents—Research & Development Workshop at AAMAS 2011, Taibei, Taiwan, 2–6 May 2011. [Google Scholar]
- Bandura, A. Self-efficacy: Toward a unifying theory of behavioural change. Psychol. Rev. 1977, 84, 191–215. [Google Scholar] [CrossRef] [PubMed]
- Thorndike, E. The Fundamentals of Learning; Teachers College, Columbia University: New York, NY, USA, 1932. [Google Scholar]
- Skinner, B. The Behaviour of Organisms; D. Appleton & Company: New York, NY, USA, 1938. [Google Scholar]
- Skinner, B. Science and Human Behavior; Free Press Paperbacks; Macmillan: London, UK, 1953. [Google Scholar]
- Bogost, I. Persuasive Games: The Expressive Power of Videogames; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Chomsky, N. A Review of B. F. Skinner’s Verbal Behavior. Language 1959, 35, 26–58. [Google Scholar] [CrossRef]
- Holden, C. Carl Rogers: Giving People Permission to Be Themselves. Science 1977, 198, 31–35. [Google Scholar] [CrossRef] [PubMed]
- MacCorquodale, K. On Chomsky’s review of Skinner’s Verbal Behavior. J. Exp. Anal. Behav. 1970, 13, 83–99. [Google Scholar] [CrossRef]
- Chomsky, N. Language and Mind; Harcourt Brace & World: San Diego, CA, USA, 1968. [Google Scholar]
- Chomsky, N. A Review of Skinner’s Verbal Behavior. In Readings in the Psychology of Language; Jakobovits, L.A., Miron, M.S., Eds.; Prentice-Hall: Upper Saddle River, NJ, USA, 1967; pp. 142–143. [Google Scholar]
- Kahneman, D. Thinking, Fast and Slow; Farrar, Straus and Giroux: New York, NY, USA, 2011. [Google Scholar]
- Gigerenzer, G.; Goldstein, D.G. Reasoning the fast and frugal way: Models of bounded rationality. Psychol. Rev. 1996, 103, 650–669. [Google Scholar] [CrossRef] [PubMed]
- Gigerenzer, G.; Todd, P.; Group, A. Simple Heuristics that Make Us Smart; Evolution and Cognition; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Gigerenzer, G.; Selten, R. Bounded Rationality: The Adaptive Toolbox; Dahlem Konferenzen; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Minsky, M.; Lee, J. Society of Mind; Touchstone Book; Simon & Schuster: New York, NY, USA, 1988. [Google Scholar]
- Sanfey, A.G. Social Decision-Making: Insights from Game Theory and Neuroscience. Science 2007, 318, 598–602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nash, J. Non-Cooperative Games (PhD Thesis). In The Essential John Nash; Kuhn, H., Nasar, S., Eds.; Princeton University Press: Princeton, NJ, USA, 2001; p. 244. [Google Scholar]
- Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behaviour, 3rd ed.; Princeton University Press: Princeton, NJ, USA, 1974. [Google Scholar]
- Friedman, M. Essays in Positive Economics; Phoenix Bks; University of Chicago Press: Chicago, IL, USA, 1953. [Google Scholar]
- Shapley, D. Game Theorist Morgenstern Dies. Science 1977, 197, 649. [Google Scholar] [CrossRef] [PubMed]
- Dreber, A.; Rand, D.G.; Fudenberg, D.; Nowak, M.A. Winners don’t punish. Nature 2008, 452, 348–351. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nowak, M.A. Five Rules for the Evolution of Cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Von Hippel, W.; Trivers, R. The evolution and psychology of self-deception. Behav. Brain Sci. 2011, 34, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Fehr, E.; Gächter, S. Altruistic punishment in humans. Nature 2002, 415, 137–140. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; Page, K.M.; Sigmund, K. Fairness Versus Reason in the Ultimatum Game. Science 2000, 289, 1773–1775. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Axelrod, R.; Hamilton, W. The evolution of cooperation. Science 1981, 211, 1390–1396. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; Sigmund, K. Evolutionary Dynamics of Biological Games. Science 2004, 303, 793–799. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ball, P. When does punishment work? Nature 2009. [Google Scholar] [CrossRef]
- Gass, S.; Assad, A. An Annotated Timeline of Operations Research: An Informal History; International Series in Operations Research & Management Science; Kluwer Academic Publishers: Alphen aan den Rijn, The Netherlands, 2005. [Google Scholar]
- Poundstone, W. Prisoner’s Dilemma; Anchor Books; Knopf Doubleday: New York, NY, USA, 1992. [Google Scholar]
- Axelrod, R. The Evolution of Cooperation; Basic Books: New York, NY, USA, 2006. [Google Scholar]
- Nowak, M.A.; Sigmund, K. Game-dynamical aspects of the prisoner’s dilemma. Appl. Math. Comput. 1989, 30, 191–213. [Google Scholar] [CrossRef]
- Nowak, M.A.; May, R.M. Evolutionary games and spatial chaos. Nature 1992, 359, 826–829. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sigmund, K. A strategy of win-stay, lose-shift that outperforms tit-for-tat in the Prisoner’s Dilemma game. Nature 1993, 364, 56–58. [Google Scholar] [CrossRef] [PubMed]
- Ai, G.; Deng, Y. An overview of prospect theory in travel choice behavior under risk. In Proceedings of the 2017 4th International Conference on Transportation Information and Safety (ICTIS), Edmonton, AB, Canada, 8–10 August 2017; pp. 1128–1133. [Google Scholar]
- Dörner, D. The Logic of Failure: Recognizing and Avoiding Error in Complex Situations; Merloyd Lawrence Book; Basic Books: New York, NY, USA, 1996. [Google Scholar]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–292. [Google Scholar] [CrossRef]
- Kahnemann, D. Voice—10 Questions with... Daniel Kahneman on Humans and Decision Making. J. Financ. Plan. 2004, 17, 1013. [Google Scholar]
- Gratch, J.; Marsella, S. A domain-independent framework for modeling emotion. Cogn. Syst. Res. 2004, 5, 269–306. [Google Scholar] [CrossRef]
- Marsella, S.C.; Gratch, J.; Petta, P. Computational Models of Emotion. In A Blueprint for an Affectively Competent Agent: Cross-Fertilization between Emotion Psychology, Affective Neuroscience, and Affective Computing; Marsella, S., Gratch, J., Petta, P., Eds.; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Smith, A.M.; Lewis, C.; Hullet, K.; Smith, G.; Sullivan, A. An Inclusive View of Player Modeling. In Proceedings of the 6th FDG ’11—International Conference on Foundations of Digital Games, Bordeaux, France, 28 June–1 July 2011; ACM: New York, NY, USA, 2011; pp. 301–303. [Google Scholar]
- Yannakakis, G.N.; Spronck, P.; Loiacono, D.; André, E. Player Modeling. In Artificial and Computational Intelligence in Games; Lucas, S.M., Mateas, M., Preuss, M., Spronck, P., Togelius, J., Eds.; Dagstuhl Follow-Ups; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2013; Volume 6, pp. 45–59. [Google Scholar]
- Gow, J.; Baumgarten, R.; Cairns, P.; Colton, S.; Miller, P. Unsupervised Modeling of Player Style with LDA. IEEE Trans. Comput. Intell. AI Games 2012, 4, 152–166. [Google Scholar] [CrossRef]
- Simon, H.A. Motivational and Emotional Controls of Cognition. Psychol. Rev. 1967, 74, 29–39. [Google Scholar] [CrossRef] [PubMed]
- Tversky, A.; Kahneman, D. The framing of decisions and the psychology of choice. Science 1981, 211, 453–458. [Google Scholar] [CrossRef] [PubMed]
- De Martino, B.; Kumaran, D.; Seymour, B.; Dolan, R.J. Frames, Biases, and Rational Decision-Making in the Human Brain. Science 2006, 313, 684–687. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ajzen, I. From intentions to actions: A theory of planned behavior. In Action Control; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Ajzen, I. The theory of planned behavior. Organ. Behav. Hum. Decis. Process. 1991, 50, 179–211. [Google Scholar] [CrossRef]
- Ajzen, I. Constructing a ToPB Questionnaire: Conceptual and Methodological Considerations. 2002. Available online: http://www.unix.oit.umass.edu/tpb.measurement.pdf (accessed on 13 March 2018).
- Adamson, R. Short History of Logic; Forgotten Books: London, UK, 2009. [Google Scholar]
- Restall, G. Logic: An Introduction; Routledge: Abingdon, UK, 1969. [Google Scholar]
- Towell, A. The Psychology of Rational Thought: A Critical Estimate of Current Views and an Hypothesis Concerning the Role of Language in the Structure of Human Reason. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 1931. [Google Scholar]
- Hastie, R.; Dawes, R. Rational Choice in an Uncertain World: The Psychology of Judgment and Decision Making; Sage: Newcastle upon Tyne, UK, 2009. [Google Scholar]
- Hamilton, W.; Mansel, H.; Vietch, J. Lectures on Metaphysics and Logic; Number v. 1 in Lectures on Metaphysics and Logic; Gould & Lincoln: Boston, MA, USA, 1859. [Google Scholar]
- Cohen, M.; Nagel, E.; Corcoran, J. An Introduction to Logic; Hackett Publishing Company: Indianapolis, IN, USA, 1993. [Google Scholar]
- Kant, I. Logic; W. Simpkin and R. Marshall: London, UK, 1819. [Google Scholar]
- Anderson, J. Cognitive Psychology and Its Implications; A Series of Books in Psychology; W.H. Freeman: New York, NY, USA, 1990. [Google Scholar]
- Van Benthem, J.; van Ditmarsch, H.; Ketting, J.; Meyer-Viol, W. Logica voor Informatici; Addison-Wesley Nederland: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Parry, W.T.; Hacker, E.A. Aristotelian Logic; State University of New York Press: Albany, NY, USA, 1991. [Google Scholar]
- Priest, G. Logic: A Very Short Introduction; Very Short Introductions; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Blackburn, P.; deRijke, M.; Venema, Y. Modal Logic; Cambridge U. Press: Cambridge, UK, 2001. [Google Scholar]
- Hamilton, A. Logic for Mathematicians; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Joyner, D. Adventures in Group Theory: Rubik’s Cube, Merlin’s Machine, and Other Mathematical Toys; Adventures in Group Theory; Johns Hopkins University Press: Baltimore, MD, USA, 2008. [Google Scholar]
- Goldblatt, R. Mathematical modal logic: A view of its evolution. J. Appl. Logic 2003, 1, 309–392. [Google Scholar] [CrossRef]
- Kripke, S.A. A Completeness Theorem in Modal Logic. J. Symb. Logic 1959, 24, 1–14. [Google Scholar] [CrossRef]
- Hansson, S.O. Semantics for more plausible deontic logics. J. Appl. Logic 2004, 2, 3–18. [Google Scholar] [CrossRef]
- Post, E.L. Introduction to a General Theory of Elementary Propositions. Am. J. Math. 1921, 43, 163–185. [Google Scholar] [CrossRef]
- Gilbert, D. Buried by bad decisions. Nature 2011, 474, 275–277. [Google Scholar] [CrossRef] [PubMed]
- Davis, M. Game Theory: A Nontechnical Introduction; Dover Books on Mathematics; Dover Publications: Mineola, NY, USA, 1997. [Google Scholar]
- Osborne, M.J.; Rubenstein, A. A Course in Game Theory; The MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Hilbe, C.; Traulsen, A. Emergence of responsible sanctions without second order free riders, antisocial punishment or spite. Sci. Rep. 2012, 2, 458. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tversky, A.; Kahneman, D. Advances in prospect theory: Cumulative representation of uncertainty. J. Risk Uncert. 1992, 5, 297–323. [Google Scholar] [CrossRef] [Green Version]
- Gibson, D.R. Nuclear deterrence: Decisions at the brink. Nature 2012, 487, 27–29. [Google Scholar] [CrossRef] [PubMed]
- Sagan, S.D. Policy: A call for global nuclear disarmament. Nature 2012, 487, 30–32. [Google Scholar] [CrossRef] [PubMed]
- Schopenhauer, A. Die Welt als Wille und Vorstellung; Number 1 in DieWelt alsWille und Vorstellung, Brockhaus; Library of Alexandria: Alexandria, Egypt, 1844. [Google Scholar]
- Kahneman, D. Maps of Bounded Rationality: Psychology for Behavioral Economics. Am. Econ. Rev. 2003, 93, 1449–1475. [Google Scholar] [CrossRef]
- Edwards, W. The theory of decision making. Psychol. Bull. 1954, 41, 380–417. [Google Scholar] [CrossRef]
- Edwards, W.; Shanteau, J.; Mellers, B.; Schum, D. Decision Science and Technology: Reflections on the Contributions of Ward Edwards; Klumer Academic: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Luce, R.; Raïffa, H. Games and Decisions: Introduction and Critical Survey; Dover Books on Mathematics; Dover Publications: Mineola, NY, USA, 1989. [Google Scholar]
- Luce, R. Utility of Gains and Losses: Measurement-Theoretical and Experimental Approaches; Scientific Psychology Series; Lawrence Erlbaum: Mahwah, NJ, USA, 2000. [Google Scholar]
- Barberis, N.C. Thirty Years of Prospect Theory in Economics: A Review and Assessment. J. Econ. Perspect. 2013, 27, 173–196. [Google Scholar] [CrossRef]
- Hey, J.D.; Lotito, G.; Maffioletti, A. The Descriptive and Predictive Adequacy of Theories of Decision Making under Uncertainty/Ambiguity; Discussion Papers 08/04; Department of Economics, University of York: York, UK, 2008. [Google Scholar]
- Luce, R.D. Where Does Subjective Expected Utility Fail Descriptively? J. Risk Uncert. 1992, 5, 5–27. [Google Scholar]
- Brown, S. Play as an Organizing Principle: Clinical Evidence and Personal Observations; Cambridge University Press: Cambridge, UK, 1998; Chapter 12; pp. 243–260. [Google Scholar]
- Bruce, T. Developing Learning in Early Childhood; 0–8 Series; Paul Chapman: London, UK, 2004. [Google Scholar]
- Pasin, F.; Giroux, H. The impact of a simulation game on operations management education. Comput. Educ. 2011, 57, 1240–1254. [Google Scholar] [CrossRef]
- Christoph, N. The Role of Metacognitive Skills in Learning to Solve Problems. Ph.D. Thesis, Universiteit van Amsterdam, Amsterdam, The Netherlands, 2006. [Google Scholar]
- Pee, N.C. Computer Games Use in an Educational System. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2011. [Google Scholar]
- Sandberg, J.; Christoph, N.; Emans, B. Tutor training: A systematic investigation of tutor requirements and an evaluation of a training. Br. J. Educ. Technol. 2001, 32, 69–90. [Google Scholar] [CrossRef]
- Warren, S.J.; Jones, G.; Trombley, A. Skipping Pong and moving straight to World of Warcraft: The challenge of research with complex games used for learning. Int. J. Web Based Communities 2011, 7, 218–233. [Google Scholar] [CrossRef]
- Malone, T.; Lepper, M.R. Making learning fun: A Taxonomy of Intrinsic Motivations for Learning. Aptit. Learn. Instruct. 1987, 3, 223–235. [Google Scholar]
- Schneider, M.; Carley, K.M.; Moon, I.C. Detailed Comparison of America’s Army Game and Unit of Action Experiments; Technical Report; Carnegie Mellon University: Pittsburgh, PA, USA, 2005. [Google Scholar]
- Habgood, M.P.J. The Effective Integration of Digital Games and Learning Content. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2007. [Google Scholar]
- Squire, K.; Barnett, M.; Grant, J.M.; Higginbotham, T. Electromagnetism supercharged!: Learning physics with digital simulation games. In Proceedings of the 6th International Conference on Learning Sciences, Santa Monica, CA, USA, 22–26 June 2004; ACM Press: New York, NY, USA, 2004; pp. 513–520. [Google Scholar]
- Young, J.; Upitis, R. The microworld of Phoenix Quest: Social and cognitive considerations. Educ. Inf. Technol. 1999, 4, 391–408. [Google Scholar] [CrossRef]
- Ford, C.W., Jr.; Minsker, S. TREEZ—An educational data structures game. J. Comput. Sci. Coll. 2003, 18, 180–185. [Google Scholar]
- Zhu, Q.; Wang, T.; Tan, S. Adapting Game Technology to Support Software Engineering Process Teaching: From SimSE to MO-SEProcess. In Proceedings of the ICNC ’07 Third International Conference on Natural Computation, Haikou, China, 24–27 August 2007; IEEE Computer Society: Washington, DC, USA, 2007; Volume 5, pp. 777–780. [Google Scholar]
- Beale, I.L.; Kato, P.M.; Marin-Bowling, V.M.; Guthrie, N.; Cole, S.W. Improvement in Cancer-Related Knowledge Following Use of a Psychoeducational Video Game for Adolescents and Young Adults with Cancer. J. Adolesc. Health 2007, 41, 263–270. [Google Scholar] [CrossRef] [PubMed]
- Lennon, J.L. Debriefings of web-based malaria games. Simul. Gaming 2006, 37, 350–356. [Google Scholar] [CrossRef]
- Roubidoux, M.A. Breast cancer detective: A computer game to teach breast cancer screening to Native American patients. J. Cancer Educ. 2005, 20, 87–91. [Google Scholar] [CrossRef] [PubMed]
- Connolly, T.; Boyle, E.; Stansfield, M.; Hainey, T. A Survey of Students’ computer game playing habits. J. Adv. Technol. Learn. 2007, 4, 218–223. [Google Scholar] [CrossRef]
- Connolly, T.; Boyle, E.; Hainey, T. A Survey of Students’ Motivations for Playing Computer Games: A Comparative Analysis. In Proceedings of the 1st European Conference on Games-Based Learning (ECGBL), Scotland, UK, 25–26 October 2007. [Google Scholar]
- Puschel, T.; Lang, F.; Bodenstein, C.; Neumann, D. A Service Request Acceptance Model for Revenue Optimization—Evaluating Policies Using a Web Based Resource Management Game. In Proceedings of the HICSS ’10 2010 43rd Hawaii International Conference on System Sciences, Kauai, HI, USA, 1–8 January 2010; IEEE Computer Society: Washington, DC, USA, 2010; pp. 1–10. [Google Scholar]
- Babb, E.M.; Leslie, M.A.; Slyke, M.D.V. The Potential of Business-Gaming Methods in Research. J. Bus. 1966, 39, 465–472. [Google Scholar] [CrossRef]
- Rowland, K.M.; Gardner, D.M. The Uses of Business Gaming in Education and Laboratory Research; Vol. BEBR No. 10; Education, Gaming; University of Illinois: Champaign, IL, USA, 1971. [Google Scholar]
- Connolly, T.; Stansfield, M.; Josephson, J.; L’azaro, N.; Rubio, G.; Ortiz, C.; Tsvetkova, N.; Tsvetanova, S. Using Alternate Reality Games to Support Language Learning. In Proceedings of the Web-Based Education WBE 2008, Innsbruck, Austria, 17–19 March 2008. [Google Scholar]
- Peschon, J.; Isaksen, L.; Tyler, B. The growth, accretion, and decay of cities. In Proceedings of the 1996 International Symposium on Technology and Society Technical Expertise and Public Decisions, Princeton, NJ, USA, 21–22 June 1996; pp. 301–310. [Google Scholar]
- Kuemmerle, W. Launching a High-Risk Business—An Interactive Simulation. Developed by High Performance Systems, Inc., based on the work of William A. Sahlman and Michael J. Roberts. Small Bus. Econ. 2000, 15, 243–245. [Google Scholar] [CrossRef]
- Gee, J.P. What Video Games Have to Teach Us About Learning and Literacy; Palgrave Macmillan: Basingstoke, UK, 2003. [Google Scholar]
- Genesereth, M.; Love, N. General game playing: Overview of the AAAI competition. AI Mag. 2005, 26, 62–72. [Google Scholar]
- Love, N.; Hinrichs, T.; Haley, D.; Schkufza, E.; Genesereth, M. General Game Playing: Game Description Language Specification; Technical Report; Stanford Logic Group: Stanford, CA, USA, 2008. [Google Scholar]
- Blackburn, P.; van Benthem, J.; Wolter, F. Handbook of Modal Logic; Elsevier: New York, NY, USA, 2005. [Google Scholar]
- Fagin, R.; Halpern, J.Y.; Moses, Y.; Vardi, M.Y. Reasoning about Knowledge; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Hildmann, H.; Hildmann, J. A formalism to define, assess and evaluate player behaviour in mobile device based serious games. In Serious Games and Edutainment Applications; Springer: London, UK, 2012; Chapter 6. [Google Scholar]
- Shankar, N. Cambridge Tracts in Theoretical Computer Science 38: Metamathematics, Machines, and Gödel’s Proof; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Pizzi, D.; Cavazza, M.; Whittaker, A.; Lugrin, J.L. Automatic Generation of Game Level Solutions as Storyboards. In Proceedings of the Fourth Artificial Intelligence and Interactive Digital Entertainment Conference (AIIDE), Stanford, CA, USA, 22–24 October 2008; The AAAI Press: Palo Alto, CA, USA, 2008. [Google Scholar]
- Ochert, A. Nature versus nurture at 60 MHz. Nature 1997, 385, 499. [Google Scholar] [CrossRef]
- Fishbein, M.; Ajzen, I.; Albarracín, D.; Hornik, R. Prediction and Change of Health Behavior: Applying the Reasoned Action Approach; L. Erlbaum Associates: Mahwah, NJ, USA, 2007. [Google Scholar]
- Cowley, B.; Charles, D.; Black, M.; Hickey, R. Analyzing player behavior in pacman using feature-driven decision theoretic predictive modeling. In Proceedings of the CIG’09 5th international conference on Computational Intelligence and Games, Milano, Italy, 7–10 September 2009; IEEE Press: Piscataway, NJ, USA, 2009; pp. 170–177. [Google Scholar]
- Hildmann, H. Behavioural game AI—A theoretical approach. In Proceedings of the 2011 International Conference for Internet Technology and Secured Transactions (ICITST), Abu Dhabi, UAE, 11–14 December 2011; pp. 550–555. [Google Scholar]
- Bitterberg, T.; Hildmann, H.; Branki, C. Using resource management games for mobile phones to teach social behaviour. In Proceeding of 2008 Conference on Techniques and Applications for Mobile Commerce; IOS Press: Amsterdam, The Netherlands, 2008; pp. 77–84. [Google Scholar]
- Hildmann, J.; Hildmann, H. Computer Games in Education; Encyclopedia of Computer Graphics and Games; Springer International Publishing: Cham, Switzerland, 2018; Chapter 278. [Google Scholar]
- Hildmann, H.; Livingstone, D. A Formal Approach to Represent, Implement and Assess Learning Targets in Computer Games. In Proceedings of the 1st European Conference on Games-Based Learning (ECGBL), Scotland, UK, 25–26 October 2007; Academic Conferences, Limited: Paisley, UK, 2007. [Google Scholar]
- Hildmann, H.; Hainey, T.; Livingstone, D. Psychology and logic: Design considerations for a customisable educational resource management game. In Proceedings of the 5th Annual International Conference in Computer Game Design and Technology, Liverpool, UK, 2007; Available online: https://s3.amazonaws.com/academia.edu.documents/30800375/SP1.pdf?AWSAccessKeyId=AKIAIWOWYYGZ2Y53UL3A&Expires=1537866177&Signature=4JAas10rDHnfMz98vA30nDFNyPI%3D&response-content-disposition=inline%3B%20filename%3DPsychology_and_logic_design_consideratio.pdf (accessed on 25 September 2018).
- Hildmann, H.; Branki, C.; Pardavila, C.; Livingstone, D. A framework for the development, design and deployment of customisable mobile and hand held device based serious games. In Proceedings of the 2nd European Conference on Games Based Learning (ECGBL08), Barcelona, Spain, 16 October 2008; API, Academic Publishing International: Barcelona, Spain, 2008. [Google Scholar]
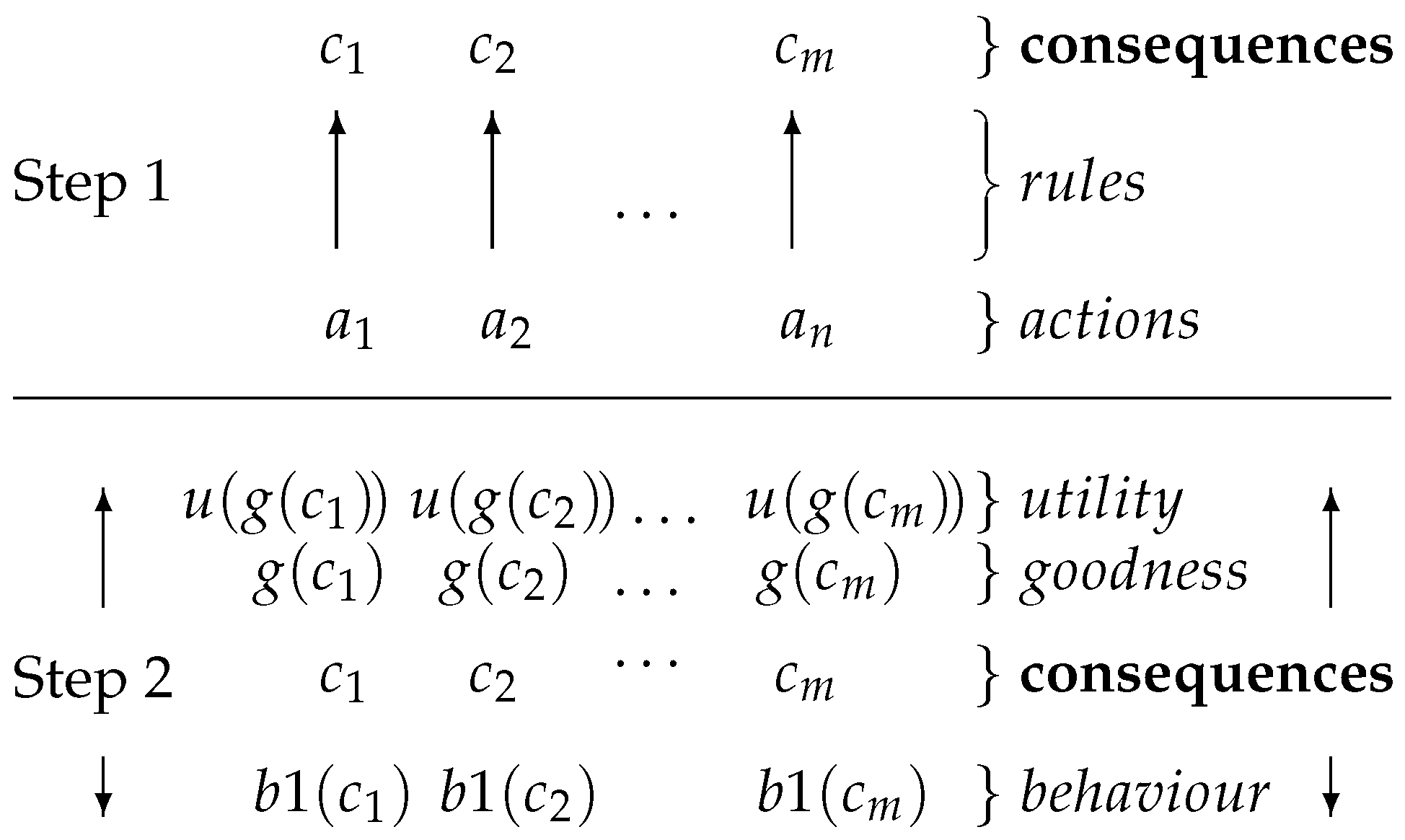



| Cooperate Player 1 | Defect Player 1 | |
|---|---|---|
| Cooperate Player 2 | (B, B) | (A, D) |
| Defect Player 2 | (D, A) | (C, C) |
| p | ¬p |
| T | F |
| F | T |
| p | q | (p ∧ q) |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
| Connector | Usage | Operator | Usage | Rewritten | |
|---|---|---|---|---|---|
| not | “it is not the case that statement’ | ¬ | |||
| or | “statement1 or statement2’ | ∨ | |||
| and | “statement1 and statement2’ | ∧ | ≡ | ||
| if ... then | “if statement1 then statement2’ | → | ≡ | ||
| if and only if | “statement1 if (and only if) statement2’ | ↔ | ≡ |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hildmann, H. Designing Behavioural Artificial Intelligence to Record, Assess and Evaluate Human Behaviour. Multimodal Technol. Interact. 2018, 2, 63. https://doi.org/10.3390/mti2040063
Hildmann H. Designing Behavioural Artificial Intelligence to Record, Assess and Evaluate Human Behaviour. Multimodal Technologies and Interaction. 2018; 2(4):63. https://doi.org/10.3390/mti2040063
Chicago/Turabian StyleHildmann, Hanno. 2018. "Designing Behavioural Artificial Intelligence to Record, Assess and Evaluate Human Behaviour" Multimodal Technologies and Interaction 2, no. 4: 63. https://doi.org/10.3390/mti2040063
APA StyleHildmann, H. (2018). Designing Behavioural Artificial Intelligence to Record, Assess and Evaluate Human Behaviour. Multimodal Technologies and Interaction, 2(4), 63. https://doi.org/10.3390/mti2040063