Abstract
In the realm of urban geotechnical infrastructure development, accurate estimation of the California Bearing Ratio (CBR), a key indicator of the strength of unbound granular material and subgrade soil, is paramount for pavement design. Traditional laboratory methods for obtaining CBR values are time-consuming and labor-intensive, prompting the exploration of novel computational strategies. This paper illustrates the development and application of machine learning techniques—multivariate linear regression (MLR), artificial neural networks (ANN), and the adaptive neuro-fuzzy inference system (ANFIS)—to indirectly predict the CBR based on the soil type, plasticity index (PI), and maximum dry density (MDD). Our study analyzed 2191 soil samples for parameters including PI, MDD, particle size distribution, and CBR, leveraging theoretical calculations and big data analysis. The ANFIS demonstrated superior performance in CBR prediction with an R2 value of 0.81, surpassing both MLR and ANN. Sensitivity analysis revealed the PI as the most significant parameter affecting the CBR, carrying a relative importance of 46%. The findings underscore the potent potential of machine learning and neuro-fuzzy inference systems in the sustainable management of non-renewable urban resources and provide crucial insights for urban planning, construction materials selection, and infrastructure development. This study bridges the gap between computational techniques and geotechnical engineering, heralding a new era of intelligent urban resource management.
1. Introduction
The sweeping global phenomenon of urbanization is molding the face of our planet, with increasingly more of the world’s population calling cities their home. This transformative trend is full of challenges as cities worldwide grapple with a growing urban populace’s environmental and infrastructural implications [1]. The urban landscape requires continuous adaptation and expansion, necessitating substantial resource consumption and putting immense pressure on our planet’s finite natural assets. The urbanization trend’s exponential trajectory and the resulting resource demands have inevitably altered urban relationships with the environment [2]. Amidst this unprecedented consumption rate, the challenge is finding new resources to sustain urban growth and enhancing how we utilize current resources to support urban lifestyles. This task involves refining our strategies to generate more value and a higher quality of life with less input or, in other words, transitioning towards more sustainable cities [3]. Cities have always functioned akin to living organisms, drawing in resources and energy to survive. Yet, the increasing urban inflows catalyzed by technological advancements and population growth necessitate more systematic and sustainable resource management [4]. A critical area of this discourse is the development of new, sustainable materials suitable for urban cities, with particular emphasis on the construction sector—a significant consumer of resources and a substantial contributor to environmental degradation.
In particular, soil, extensively used in construction activities, especially for roads and pavements, is under immense pressure. Thus, understanding soil properties and behavior is paramount for the sector’s sustainability. A key soil parameter utilized in road and pavement design is the California Bearing Ratio (CBR), which measures the highest density of soil’s penetration resistance [5]. This ratio is significant in designing the thickness of pavement and sub-base layers, and it can be represented as follows:
The ‘Test Load’ refers to the force penetrating a soil sample. At the same time, the ‘Standard Load’ denotes the resistance provided by a standard crushed aggregate sample with a CBR of 100% against equivalent penetration. The CBR values are estimated at 2.5 mm and 5 mm penetrations, with the higher value used in the design [5].
Devised in the 1920s by the California State Highway Division, the CBR test was widely adopted, even by the United States Corps of Engineers, for military airfields during the 1940s [6]. Traditionally, CBR testing involves compacting soil samples to their maximum dry density in the lab and subjecting them to either a 2.5 or 5 mm penetration depth. In situ, the CBR is indirectly measured using experimental methods, such as the Dynamic Cone Penetration (DCP) test performed in an excavated test pit at the subgrade level [7]. Although laboratory CBR testing provides critical insights, it is time-consuming and susceptible to human errors and data collection issues, potentially invaliding test results. The CBR value can also vary significantly depending on the soil type and properties [8,9]. Therefore, indirect methods to estimate CBR values swiftly and accurately are essential for mitigating project delays and ensuring consistent construction quality [10]. The importance of efficient CBR value predictions cannot be overstated, especially considering the environmental implications of unsustainable construction practices. Innovative approaches are necessary to improve the accuracy of CBR value predictions and, thus, the sustainability of urban construction activities [11]. Fortunately, emerging technologies offer promising solutions. In recent years, machine learning (ML) techniques and theoretical simulations have proven effective in solving complex problems across various sectors [12]. Incorporating ML techniques into soil classification and characterization could provide a rapid, cost-effective, and accurate means of estimating soil properties, such as the CBR value. This prospect is essential for the sustainability of construction activities and constitutes an opportunity to navigate the urban resource challenge by improving construction efficiency and reducing waste [13]. Moreover, we can find a deep connection between urban resources and ecosystems. As cities depend on imported external resources, they also benefit from internal resources and ecosystem services [14]. For example, studying soil properties such as CBR values plays a crucial role in urban planning and infrastructure development, thus interlinking urban resources, the environment, and machine learning methodologies.
Recent developments have witnessed a growing adoption of predictive modeling exercises employing a diverse range of machine learning techniques, such as artificial neural networks (ANN), Ensemble Piecewise Regression (EPR) models, Multivariate Adaptive Regression Splines, Random Forests, Gradient Boosting Machines, and Gene Expression Programming (GEP), to infer California Bearing Ratio (CBR) values indirectly [15,16,17,18,19]. This emerging trend holds the promise of substantially reducing the time and resources expended in traditional laboratory-based CBR testing, thus elevating the efficiency of urban resource management and planning, contributing to the advancement of more sustainable cities. However, it is vital to consider the various ML techniques available and their suitability for different applications [20]. For instance, the prediction of CBR values has been attempted using techniques such as Support Vector Machines (SVM) and artificial neural networks (ANN). While both techniques have shown promise, each has its strengths and limitations, and their performance can be context-dependent [21].
As we continue to deepen our understanding of soil properties and their predictive modeling, we also expand our toolkit for tackling the resource challenges that rapidly urbanizing cities worldwide face. There needs to be more understanding regarding using ML techniques and theoretical simulations in predicting soil properties, particularly CBR values. Additionally, the existing literature predominantly focuses on conventional methods, which, while helpful, may be more resource-intensive and less accurate than newer, more innovative approaches [22]. Table 1 summarizes the notable literature that has developed models for predicting the CBR of fine-grained soils using various methodologies, including regression analysis, artificial neural networks (ANN), and adaptive neuro-fuzzy inference systems (ANFIS). While these studies have contributed to the field, most of them were limited by small data sizes, limiting themselves to a particular type of soil and hindering the generalizability and applicability of their models. In contrast, the present study benefits from a substantial number of data points with various soil types, enhancing the reliability and robustness of the developed models. Addressing these gaps in knowledge and practice is critical for advancing toward sustainable cities, emphasizing the importance of this study. This study, therefore, contributes to the literature by exploring the use of machine learning techniques and theoretical simulations for CBR value prediction. The primary objective is to determine whether these approaches can improve the accuracy and efficiency of CBR value prediction, thus contributing to more sustainable construction practices in urban environments. This investigation aligns with the Special Issue’s theme, offering a novel perspective on urban resource management and the role of technology in promoting sustainability [23].

Table 1.
Summary of the notable literature to predict the CBR.
This study’s significance lies in its potential to improve the accuracy of CBR value prediction and its broader implications for urban resource management. By demonstrating the feasibility and effectiveness of using machine learning techniques and theoretical simulations in soil property prediction, this research may encourage their wider adoption in the construction sector, promoting more efficient resource use and contributing to the sustainability of cities worldwide [33].
The study aims to develop MLR, ANN, and ANFIS models for predicting the soil CBR based on the collected dataset. A comprehensive dataset of 2191 CBR test results from subgrade soils representing a wide range of soil types were collected. The dataset includes various soil parameters such as the plasticity index (PI), maximum dry density (MDD), and particle size distribution. These parameters were selected based on their known influence on CBR values and availability in standard soil testing protocols [34,35,36].
The developed models will be compared in terms of their predictive efficacy, as assessed by metrics such as the root mean square error (RMSE) and the coefficient of determination (R2). The ANFIS model, with its ability to handle complex relationships and non-linear data, is expected to outperform the traditional MLR models and potentially rival the predictive performance of ANN models. This study contributes to advancing sustainable urban resource management by utilizing machine learning techniques and theoretical simulations. The findings will improve our understanding of the factors influencing CBR values and provide valuable insights for decision-makers and engineers involved in urban infrastructure development. Applying these predictive models can optimize the design and construction of urban geotechnical infrastructure, leading to more sustainable and efficient urban development practices.
2. Soil Database and Laboratory Testing
The current research examines soil properties in Andhra Pradesh state, specifically focusing on samples collected from core and non-core road networks, as shown in Figure 1. A comprehensive range of critical parameters was collected to generate robust and reliable data models, such as particle size distribution, Atterberg limits, maximum dry density, optimum moisture content (OMC), and CBR values. To mitigate the negative impacts of multicollinearity on data quality, data preprocessing was conducted, involving the exercise of a multicollinearity check to comprehend the interdependencies among independent variables. In particular, the Karl Pearson Correlation was applied in conjunction with the variance inflation factor (VIF) for each independent variable, where the VIF indicates how much the variance of the estimated regression coefficient is inflated due to multicollinearity. A VIF value exceeding five suggests the presence of multicollinearity. The soil type, PI, and MDD parameters were selected for input into the data modeling phase, as they exhibited no multicollinearity. Additionally, box plots were developed to eliminate any outliers for the input and output parameters of interest. This led to the selection of 2191 samples for CBR value modeling after removing outliers from the CBR results of 2469 subgrade samples used in the study. The collected soil samples were of coarse- and fine-grained varieties and were classified according to the Indian Standard Soil Classification System, falling into eight distinct soil types (SW, SP, SM, SC, GP, GM, CL, CI), as illustrated in Figure 2. The laboratory-based determination of CBR values for each sample was performed using a soil compaction method by the ASTM D1883-16 Standard Test Procedure [34]. Statistically descriptive analyses of the soil properties collected in the database are detailed in Table 2, with accompanying frequency histograms presented in Figure 3.
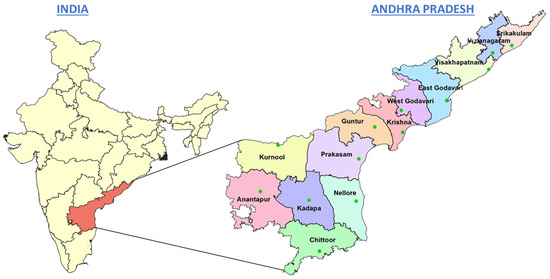
Figure 1.
Study Location.
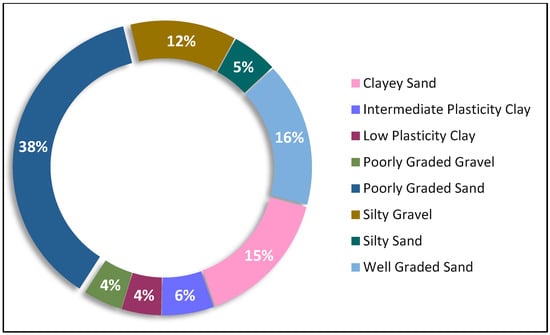
Figure 2.
Distribution of different Soil types.

Table 2.
Descriptive statistics of the data.
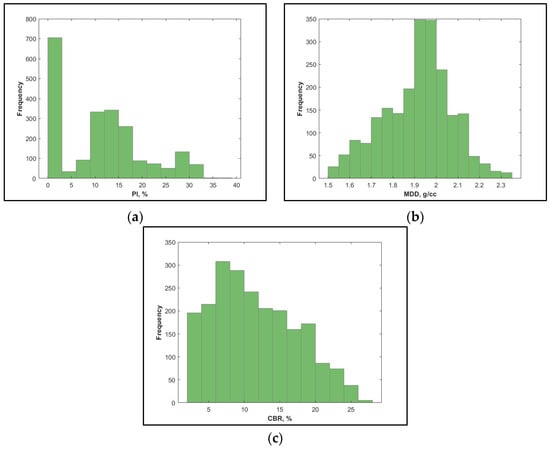
Figure 3.
Frequency histograms of (a) PI, (b) MDD, and (c) CBR.
Upon examining Table 2 and Figure 3, it is evident that the skew values of 0.44 for both PI and CBR signify a slight right skewness in the distribution. This implies that more data points are located on the right side of the distribution, which leads to a positively skewed distribution. Moreover, the kurtosis values of −0.68 for both PI and CBR indicate that the distribution is platykurtic, which means it is flatter than a normal distribution. This suggests that the data are less concentrated around the mean than a normal distribution, with a more extensive and dispersed shape. Additionally, the MDD distribution has a negative skew value of −0.30 and kurtosis of −0.16, signifying a slight left skewness and flatter profile than a normal distribution, with fewer extreme values.
As the variable “Soil type” was represented in characters, it was necessary to encode it as numerical values to analyze it using the MLR and ANFIS methods, which do not consider string values. This encoding was completed using the Statistical Package for the Social Sciences (SPSS) version 28. Table 3 presents the laboratory data from soil testing utilized in this study.

Table 3.
Sample laboratory test results.
3. Data Analysis
3.1. MLR Analysis
Multivariate linear regression analysis (MLR) is a statistical method with broad applicability in various fields, such as engineering, economics, and the social sciences, to investigate the relationship between multiple independent variables and a single dependent variable. The main objective of MLR is to establish a connection between the predictor or independent variable and a dependent variable to predict future outcomes accurately. In this study, the observed CBR value was linked to three soil parameters: soil type, plasticity index, and MDD, using MLR analysis in IBM SPSS version 28. The CBR test value served as the dependent variable. At the same time, the soil type, plasticity index, and MDD were independent factors in the study Equation (2). MLR analysis has several advantages, including its ability to identify the most significant independent variables that influence the dependent variable. This is beneficial for understanding the relationships between different variables and developing more accurate predictive models. However, MLR has some limitations, such as the assumption of linearity between the independent and dependent variables, which may need to be validated in complex systems. Despite these limitations, MLR is a valuable and widely used method for analyzing the relationships between variables, and its results can provide valuable insights for decision-making and forecasting.
Yi = α0 + α1 × xi1 + α2 × xi2 + … + αp × xip+ E
Yi = The dependent variable
xi = Independent variables
α0 = intercept on the y-axis
αp = coefficients of slopes of independent variables
E = Error or Residual
The results of the correlation coefficient and t-test were examined to determine the statistical significance of the model.
3.2. Artificial Neural Network
An artificial neural network (ANN) is a machine-learning algorithm that mimics the structure and function of the human brain. It comprises layers of interconnected nodes, or neurons, that process input data and generate output. During training, the weights of the connections between neurons are adjusted using backpropagation to minimize error. ANNs effectively handle complex and noisy data, as they can learn to extract features from raw data and make accurate predictions. However, they can be computationally expensive and require much-labeled training data to perform well. Additionally, the internal workings of ANNs can be difficult to interpret, making it challenging to understand how they arrive at their decisions.
ANN has been used to address technical challenges by researchers working on complicated technical problems over the past decade. The ANN model may be built in a variety of forms, all of which are based on the same fundamental structure. A collection of input nodes, a single layer or layers of hidden nodes, and a collection of output nodes are all included in this [37]. A multilayer network with multiple transfer functions was used to determine the best ANN model to predict the CBR. The model’s accuracy in predicting the output is governed by the training function, transfer function, number of hidden layers, and number of neurons inside the hidden layers. A Multi-Layered Perception (MLP) Feed-Forward Back-Propagation mechanism, a log-sig (log-sigmoid) activation function, and a Levenberg–Marquardt (trainlm) learning function were incorporated to develop a suitable ANN model for predicting the CBR of the soil. Different combinations of the number of hidden layers and the corresponding number of neurons were tried to obtain a model with a higher R2 value and lower RMS error. One hidden layer with five neurons offered the optimum network structure for the inputs such as soil type, PI, MDD, and CBR as an output (3-5-1). Of the total data points, 70% were used to train the model, 15% were used to test the model, and the remaining 15% were validated using MATLAB r2022a software. The suggested ANN model architecture is shown in Figure 3.
3.3. Adaptive Neuro-Fuzzy Inference System (ANFIS)
An adaptive neuro-fuzzy inference system (ANFIS) is a machine learning model that combines the strengths of artificial neural networks (ANN) and fuzzy logic. It uses a hybrid learning algorithm to build a system to learn and make decisions based on input data. ANFIS models consist of fuzzy rules that can be adjusted using neural network techniques, making them highly adaptable to different data types. In 1965, Lofti Zahed invented fuzzy set theory, a method for dealing with imprecision in decision-making using a set of fuzzy linguistic rules. ANFIS models are used in various applications, including pattern recognition, time-series prediction, and control. The model comprises a set of fuzzy rules extracted from the input data by fuzzy clustering and a set of neural networks trained using backpropagation. The fuzzy rules and neural networks work together to make accurate predictions based on input data. An ANFIS can handle complex data and learn from large datasets, making it suitable for various applications. ANFIS models are more accurate than ANN models in some cases due to the incorporation of fuzzy logic, which allows for more human-like decision-making. This is particularly advantageous when dealing with complex, ill-defined problems where traditional rule-based systems may need to be improved. An ANFIS can be more robust to noisy data, as the fuzzy logic components can help to smooth out the effects of outliers and other anomalies. ANFIS models also can explain their decision-making process, making them more transparent than ANN models. Additionally, ANFIS models require less training data than ANN models, which can save time and resources.
One of the key components of an ANFIS is the membership function, which represents the degree of membership of an input to a particular fuzzy set. The membership function determines how much influence an input has on a specific output. The shape of the membership function can be adjusted to fit the data, and different types of membership functions can be used, such as Gaussian, triangular, and trapezoidal. ANFIS membership functions are typically characterized by a set of parameters that are optimized during the learning process. These parameters determine the membership function’s shape, spread, and center. The parameters can be tuned using gradient descent or other optimization algorithms to minimize errors between the system’s predictions and output. ANFIS membership functions are powerful because they can model complex and non-linear relationships between input and output variables, making them useful for various applications.
The membership functions are named after the curve’s geometry, such as triangular, bell-shaped, trapezoidal, and Gaussian membership functions [Equation (3)]. The developed ANFIS model was evaluated with all membership functions, and the trapezoidal membership function (trapmf) was found to give the best results with the lowest RMSE value and was therefore used in the research. With four scalar parameters to define its curve: a, b for feet and c, d for shoulders, trapmf forms the shape of a truncated triangle, as shown in Figure 4.
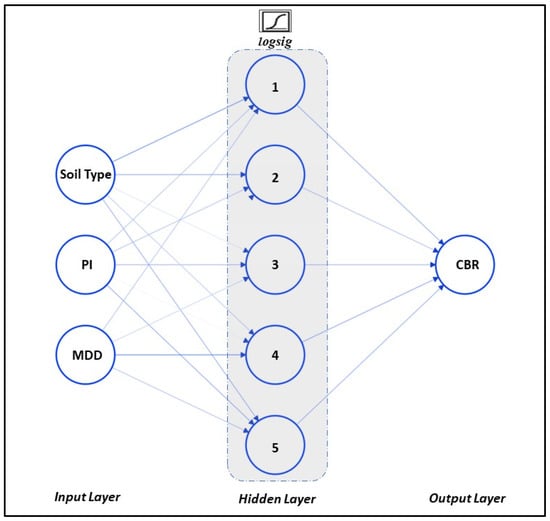
Figure 4.
The architecture of the proposed ANN model (3-5-1).
It is mathematically represented by
A five-layer architecture usually depicts a typical ANFIS network, as represented in Figure 5. In references such as Jang [38], extensive documentation for ANFIS is available (1993). The adaptive neuro-fuzzy inference system considers three inputs, soil type, PI, and MDD, and an output, CBR. Below is a brief description of each layer’s functions in the ANFIS.
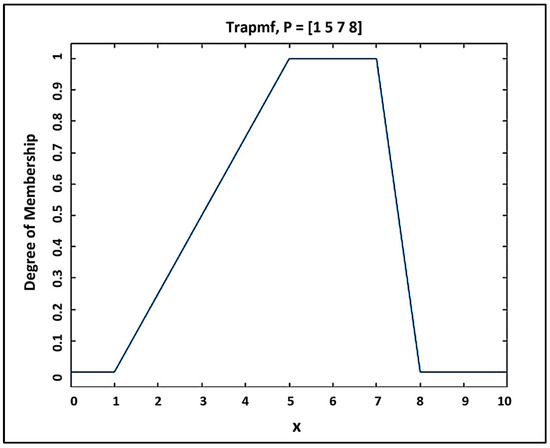
Figure 5.
Trapezoidal MF.
Layer 1 is an adaptive node fuzzy layer with three trapezoidal membership functions for each input variable. Soil type, PI, and MDD are inputs to the system. T1,i is the target output of the nth node of layer l. A square node represents the adaptive nodes.
The adaptive functions can be mathematically expressed as
where µAn, µBn−3, and µCn−6 represent the trapezoidal membership functions.
T1,n = µAn (Soil Type) for n = 1, 2, 3
T1,n = µBn−3 (PI) for n = 4, 5, 6
T1,n = µCn−6 (MDD) for n = 7, 8, 9
Layer 2 has fixed nodes and performs the ‘AND’ function, multiplying outputs from layer 1 to give the Firing strength (wn).
T2,n = wn = μAn(Soil Type) × μBn(PI) × μCn(MDD) for n = 1, 2, 3.
Layer 3 also has fixed nodes. This layer normalizes the firing strength of all rules by computing the ratio of the nth rule’s firing strength to the sum of all rules’ firing strength.
Layer 4 has adaptive nodes, and they perform the function of defuzzification.
The parameters in this layer (pn, qn, rn, and sn) are adjustable parameters called consequent parameters.
Layer 5 has a single fixed node. The output is given by the addition of all signals received.
For the ANFIS analysis, the trapezoidal membership function (Trapmf) was used with the different number of epochs to obtain a model with the least RMSE value. A Takagi-Sugeno-type ANFIS model was used in the study (Figure 6 and Figure 7). The grid partitioning technique was used to generate the FIS. Further, the generated FIS was trained using a hybrid learning algorithm with 70% of the data. The model was tested on 15% of the data and was validated on the remaining 15% of the data using MATLAB r2022a.
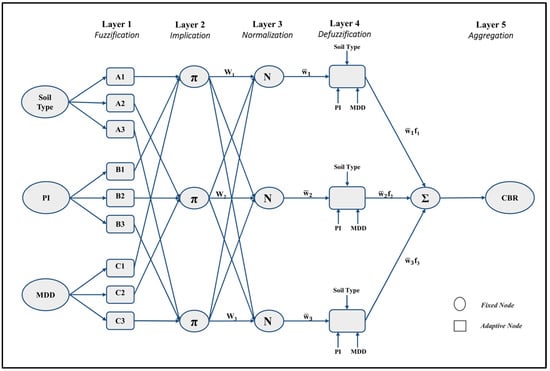
Figure 6.
The architecture of the ANFIS with 3 inputs, 1 output, and 3 membership functions.
Figure 7.
Sugeno-type FIS used in the ANFIS model.
3.4. Performance Criteria
The potential of the MLR, ANN, and ANFIS models was assessed statistically by computing the RMSE and R2 values. These criteria are defined by the equations below.
E = Predicted Value
A = Observed Value
= Average of A values
n = Number of Observations
4. Results and Discussion
4.1. MLRA Results
The obtained model for the CBR from multivariate linear regression analysis is as follows:
CBR = 2.13 + 1.24 × (Soil Type) − 0.25 × (PI) − 2.67 × (MDD)

Table 4.
Model Performance Metrics.

Table 5.
Coefficients and Significance Test.
A statistical analysis was conducted to assess the suitability of the suggested model. The hypotheses considered are
H0 = CBR is not related to Soil Type, PI, and MDD,
H1 = CBR is related to Soil Type, PI, and MDD.
Based on the statistical results, a significance level (p-value) of less than 0.05 was used as the threshold to determine statistical significance. Consequently, the null hypothesis (H0) was rejected, indicating a favorable relationship between the CBR and the variables soil type, PI, and MDD.
4.2. ANN Results
The following passage discusses the development and validation of an artificial neural network (ANN) model for predicting the California Bearing Ratio (CBR) based on three inputs: soil type, plasticity index (PI), and maximum dry density (MDD). The model consisted of a single hidden layer with five neurons, and the log-sig transfer function was used for this layer. The model’s performance was evaluated by determining the R2 (coefficient of determination) and RMSE (root mean square error) values for the training, testing, and validation data sets. The data was split into three sets to validate the accuracy of the ANN model for predicting the CBR: training, testing, and validation. The model was trained on 70 percent of the data, and the R2 value obtained for this training data set was 0.67, indicating that the model explains 67% of the variation in the CBR (Figure 8). The RMSE value was 2.63, indicating the average difference between the predicted and actual CBR values. Similarly, the R2 and RMSE values were calculated for the testing and validation data sets. For the testing data set, the R2 value was 0.65, and the RMSE value was 2.70. The R2 and RMSE values for the validation data set were 0.66 and 2.64, respectively. The results of the ANN model were compared to those obtained from a Multiple Linear Regression Analysis (MLRA), which is a traditional statistical method used for predicting the CBR. The results showed that the ANN model outperformed the MLRA analysis in predicting the CBR value [25,28,31]. The success of the ANN model can be attributed to its ability to process complex networks and establish the connection between input and output parameters, resulting in more accurate results. The scatterplot in Figure 9 compares the predicted CBR values by the ANN model and the actual CBR values.
Figure 8.
Depiction of obtained ANFIS structure.
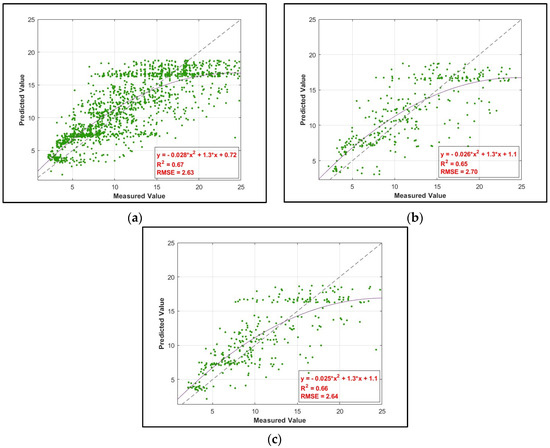
Figure 9.
Measured versus predicted CBR values obtained from the ANN model for (a) training data, (b) testing data, and (c) validation data.
4.3. ANFIS Results
An adaptive neuro-fuzzy inference system (ANFIS) analysis using the trapmf method, which involved three membership functions for each input variable, was developed. The ANFIS model was used to indirectly predict soil California Bearing Ratio (CBR) values. To evaluate the accuracy of the ANFIS model, the predicted CBR values were compared with the actual CBR values using scatterplots, and the correlation coefficient was determined. Additionally, the mean square error was calculated for the ANFIS model. The results of the ANFIS analysis were promising, with an R2 value of 0.81 and an RMSE of 2.26 for the training data set, indicating that the model explains 81% of the variation in the CBR. Similarly, for the testing data set, the R2 value was 0.82, and the RMSE value was 2.29. The R2 and RMSE values for the validation data set were 0.82 and 2.23, respectively. These results suggest that the ANFIS model could predict soil CBR values with high accuracy, as evidenced by the high correlation coefficient and low mean square error.
In summary, the ANFIS analysis using the trapmf method with three membership functions for each input variable showed promising results in predicting soil CBR values. The high R2 values and low RMSE values obtained from the training, testing, and validation data sets indicate the model’s high degree of accuracy [30,31]. The use of ANFIS models in soil analysis can provide valuable insights into the behavior of soil properties, which can be useful in designing geotechnical structures and infrastructure projects.
Figure 10a depicts that the predicted CBR value with a PI value between 0 and 10 is highest for soil types SP and SW (7 and 8) and lowest for the soil types CI and CL (1 and 2) with high PI values and a moderate CBR for GM, GP, SC and SM (3, 4, 5 and 6). A further increase in the PI value reduces the CBR value significantly. From the Figure 10b it can be observed that soil type SP and SW with higher MDD have the highest CBR value. Whereas soil types CI and CL (1 and 2) and GM, GP, SC, and SM (3, 4, 5, and 6) provided the lowest and moderate CBR values, respectively, the MDD value was reduced. The combined result can be observed in Figure 10c, wherein the highest CBR value is obtained for a lesser PI value and a higher MDD value. Figure 11 represents variation of the CBR with changes in (a) soil type and PI, (b) soil type and MDD, and (c) PI and MDD.
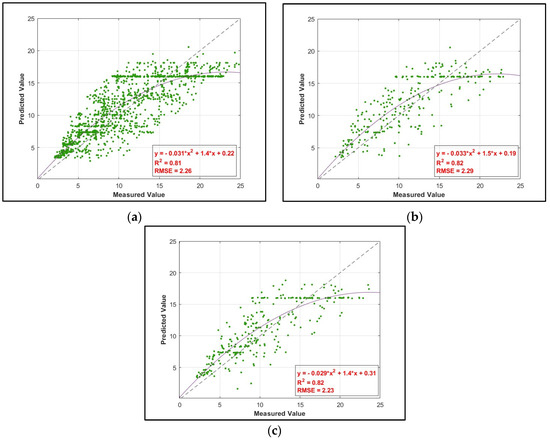
Figure 10.
Measured versus predicted CBR values obtained from the ANFIS model for (a) training data, (b) testing data, and (c) validation.
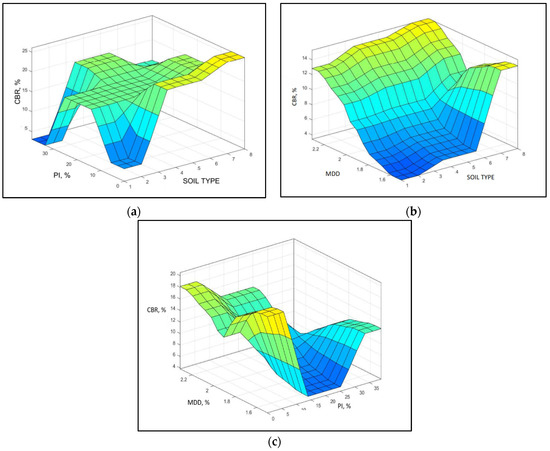
Figure 11.
Variation of the CBR with changes in (a) soil type and PI, (b) soil type and MDD, and (c) PI and MDD.
The summary of the prediction metrics of the obtained model is compared in Table 6. The previous works in the literature showcased R2 values ranging from 0.80 to 0.93 for MLRA, 0.78 to 0.97 for ANN, and 0.98 for ANFIS, respectively, for the CBR prediction with smaller datasets comprising 124 to 264 samples [25,26,28,29,30,31]. In contrast, our investigation employed a more extensive dataset consisting of 2191 samples, encompassing diverse soil types. Consequently, the variability in R2 values might be attributed to the larger dataset. Nonetheless, our study aligns with the observed trend of higher prediction efficacy achieved by the ANFIS model, followed by the ANN and MLRA models. Table 7 compares the predicted CBR values from the developed model with the actual laboratory data.

Table 6.
Comparative analysis of the developed models.

Table 7.
Comparison of the predicted CBR obtained from different techniques.
4.4. Sensitivity Analysis
Sensitivity analysis is a critical tool that can determine the most influential parameters affecting the California Bearing Ratio (CBR) value. Its primary purpose is to investigate the importance of imprecision or uncertainty in model inputs, thereby enabling decision-makers and modelers to identify key variables that can substantially influence the values of a particular output variable. By measuring the effect of changes in model input values on model output values, sensitivity analysis can help to improve the accuracy and robustness of CBR predictions. In practice, it is commonly observed that only a relatively small number of input variables significantly affect the values of a particular output variable. As such, sensitivity analysis techniques can be used to calculate a parameter known to be of input importance. The input importance of each parameter can then be evaluated and ranked to identify which variables are most significant. In this study, multivariate sensitivity analysis was carried out based on Principal Component Analysis [39]. Figure 12 shows the input importance of different parameters. The results of the analysis suggest that the PI changes are a highly significant factor and play a major role in affecting the CBR, with a relative importance of 46% [40]. Soil type is ranked second at 34%, while maximum dry density (MDD) is ranked last with a relative importance of 20%. The low impact of MDD on the CBR suggests that it is less influential than other parameters and should be given less weight in CBR predictions [41].
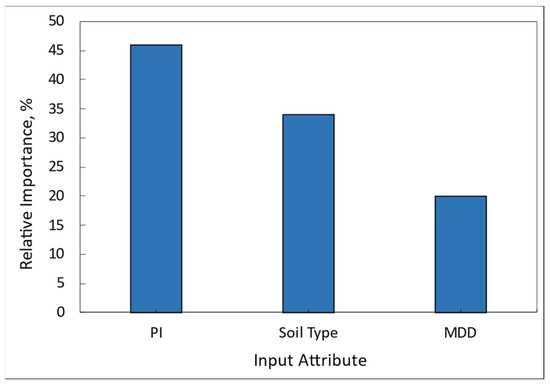
Figure 12.
Input Variable Importance.
5. Conclusions
In conclusion, this study focused on investigating the impact of soil type, plasticity index (PI), and maximum dry density (MDD) on the California Bearing Ratio (CBR) of subgrade soils. The objective was to develop predictive CBR models using statistical and soft computing techniques. A multivariate linear regression (MLR) analysis was initially employed, but its limited capacity to accurately predict the CBR, as indicated by the low R2 value of 0.45, prompted the exploration of advanced methods. The artificial neural network (ANN) and adaptive neuro-fuzzy inference system (ANFIS) models were developed and compared, with promising results. The ANN model improved predictive ability, achieving R2 values of 0.67, 0.65, and 0.66 for training, testing, and validation, respectively. The ANFIS model, outperforming the MLR model, yielded higher predictive accuracy with R2 values of 0.81, 0.82, and 0.82 for training, testing, and validation data, respectively. While the use of a larger dataset (2191 data points with a variety of soil types) resulted in lower R2 values compared to the previous literature, which utilized smaller data samples. However, the trend of prediction efficiency remained consistent, showing the ANFIS model outperforming both the ANN and MLRA models in estimating the CBR, which aligns with previous studies. The results confirm the efficacy of soft computing techniques, particularly the ANFIS model, in predicting the CBR based on soil type, PI, and MDD values, providing more accurate and efficient CBR estimation. These models offer a viable alternative to traditional statistical analysis methods and contribute to the sustainable management of urban resources. Accurate CBR prediction is crucial for optimizing the design and construction of urban infrastructure, promoting efficient resource utilization, and ensuring the long-term sustainability of cities. The combination of machine learning techniques and theoretical simulations demonstrated by the ANN and ANFIS models offers a powerful approach to CBR prediction. The developed models provide valuable insights into the factors influencing the CBR and can assist engineers and decision-makers in making informed choices for urban infrastructure development. Further research can explore incorporating additional soil parameters and examining the applicability of these models in different geotechnical contexts.
Author Contributions
Conceptualization, S.G. and V.K.; methodology, V.K.; software, A.G.; validation, S.G., V.K. and B.K.S.; formal analysis, G.K.; investigation, V.K.; resources, B.K.S.; data curation, A.G.; writing—original draft preparation, V.K.; writing—review and editing, S.G.; visualization, P.S.; supervision, S.G.; project administration, G.K.; funding acquisition, S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are available on request from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- United Nations. The World’s Cities in 2018; United Nations, Department of Economic and Social Affairs, Population Division: San Franciso, CA, USA, 2018. [Google Scholar]
- Bulkeley, H.; Betsill, M. Rethinking sustainable cities: Multilevel governance and the ‘urban’ politics of climate change. Environ. Politics 2005, 14, 42–63. [Google Scholar] [CrossRef]
- Beatley, T. Green Urbanism: Learning from European Cities; Island Press: Washington, DC, USA, 2000. [Google Scholar]
- Kennedy, C.; Cuddihy, J.; Engel-Yan, J. The changing metabolism of cities. J. Ind. Ecol. 2007, 11, 43–59. [Google Scholar] [CrossRef]
- California Department of Transportation. California Bearing Ratio (CBR) Test Procedure; California Department of Transportation: Sacramento, CA, USA, 2019.
- Irwin, L.H. The Pressuremeter and Foundation Engineering; Elsevier Science & Technology: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Farrar, M.J.; Al-Taher, A.H.; Wood, R.M. Comparison of Clegg Impact Test and California Bearing Ratio for Subgrade Strength. Geotech. Geol. Eng. 2013, 31, 1191–1201. [Google Scholar]
- Bharti, G.; Hurukadli, P.; Shukla, B.K.; Sihag, P.; Jagudi, S.; Tripathi, A. Environmental impact analysis and utilization of copper slag for stabilising black cotton soil. Mater. Today Proc. 2023, in press. [Google Scholar] [CrossRef]
- Arya, P.; Patel, S.B.; Bharti, G.; Shukla, B.K.; Hurukadli, P. Impact of using a blend of bagasse ash and polyester fiber in black cotton soil for improvement of mechanical and geotechnical properties of soil. Mater. Today Proc. 2023, 78, 738–743. [Google Scholar] [CrossRef]
- Vichare, P.; Deo, M. Soft computing approach for soil classification and its impact on the bearing capacity of soil. In Soft Computing for Problem Solving; Springer: Singapore, 2016; pp. 611–620. [Google Scholar]
- Mair, P.; Wilcox, R.; Degeneffe, D. Predicting California Bearing Ratio (CBR) of Fine-Grained Soils for Airfields Using the DCP. Geotech. Geol. Eng. 2016, 34, 835–848. [Google Scholar]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Taillard, E.; Waelti, P.; Zufferey, N. An efficient simulated annealing procedure for the fleet size and mix vehicle routing problem with time windows. Transp. Sci. 2007, 41, 206–218. [Google Scholar]
- Pickett, S.T.; Cadenasso, M.L.; McGrath, B.P. (Eds.) Resilience in Ecology and Urban Design: Linking Theory and Practice for Sustainable Cities; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Erzin, Y.; Turkoz, D. Use of neural networks for the prediction of the CBR value of some Aegean sands. Neural Comput. Appl. 2016, 27, 1415–1426. [Google Scholar] [CrossRef]
- Chao, Z.; Ma, G.; Zhang, Y.; Zhu, Y.; Hu, H. The application of artificial neural network in geotechnical engineering. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2018; Volume 189, p. 022054. [Google Scholar]
- Ghorbani, A.; Hasanzadehshooiili, H. Prediction of UCS and CBR of microsilica-lime stabilized sulfate silty sand using ANN and EPR models; application to the deep soil mixing. Soils Found. 2018, 58, 34–49. [Google Scholar] [CrossRef]
- Ikeagwuani, C.C. Estimation of modified expansive soil CBR with multivariate adaptive regression splines, random forest and gradient boosting machine. Innov. Infrastruct. Solut. 2021, 6, 199. [Google Scholar] [CrossRef]
- Bakri, M.; Aldhari, I.; Alfawzan, M.S. Prediction of California Bearing Ratio of Granular Soil by Multivariate Regression and Gene Expression Programming. Adv. Civ. Eng. 2022, 2022, 7426962. [Google Scholar] [CrossRef]
- Kelleher, J.D.; Mac Namee, B.; D’Arcy, A. Fundamentals of Machine Learning for Predictive Data Analytics: Algorithms, Worked Examples, and Case Studies; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Coduto, D.P.; Yeung, M.R.; Kitch, W.A. Geotechnical Engineering: Principles & Practices; Pearson: London, UK, 2020. [Google Scholar]
- Burton, E. The use of urban resources for adaptation to climate change. Local Environ. 2010, 15, 591–603. [Google Scholar]
- Taskiran, T. Prediction of California bearing ratio (CBR) of fine grained soils by AI methods. Adv. Eng. Softw. 2010, 41, 886–892. [Google Scholar] [CrossRef]
- Yildirim, B.; Gunaydin, O. Estimation of California bearing ratio by using soft computing systems. Expert Syst. Appl. 2011, 38, 6381–6391. [Google Scholar] [CrossRef]
- Suthar, M.; Aggarwal, P. Predicting CBR value of stabilized pond ash with lime and lime sludge using ANN and MR models. Int. J. Geosynth. Ground Eng. 2018, 4, 6. [Google Scholar] [CrossRef]
- Kurnaz, T.F.; Kaya, Y. Prediction of the California bearing ratio (CBR) of compacted soils by using GMDH-type neural network. Eur. Phys. J. Plus 2019, 134, 326. [Google Scholar] [CrossRef]
- Taha, S.; Gabr, A.; El-Badawy, S. Regression and neural network models for California bearing ratio prediction of typical granular materials in Egypt. Arab. J. Sci. Eng. 2019, 44, 8691–8705. [Google Scholar] [CrossRef]
- Al-Busultan, S.; Aswed, G.K.; Almuhanna, R.R.; Rasheed, S.E. Application of artificial neural networks in predicting subbase CBR values using soil indices data. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; Volume 671, p. 012106. [Google Scholar]
- Iqbal, M.; Onyelowe, K.C.; Jalal, F.E. Smart computing models of California bearing ratio, unconfined compressive strength, and resistance value of activated ash-modified soft clay soil with adaptive neuro-fuzzy inference system and ensemble random forest regression techniques. Multiscale Multidiscip. Model. Exp. Des. 2021, 4, 207–225. [Google Scholar] [CrossRef]
- Varol, T.; Ozel, H.B.; Ertugrul, M.; Emir, T.; Tunay, M.; Cetin, M.; Sevik, H. Prediction of soil-bearing capacity on forest roads by statistical approaches. Environ. Monit. Assess. 2021, 193, 1–13. [Google Scholar] [CrossRef]
- Nagaraju, T.V.; Bahrami, A.; Prasad, C.D.; Mantena, S.; Biswal, M.; Islam, R. Predicting California Bearing Ratio of Lateritic Soils Using Hybrid Machine Learning Technique. Buildings 2023, 13, 255. [Google Scholar] [CrossRef]
- Duan, H.; Li, W. Research on urban resource circulation and urban sustainable development. Procedia Environ. Sci. 2011, 5, 193–200. [Google Scholar]
- ASTM D1883-15; Standard Test Method for California Bearing Ratio (CBR) of Laboratory-Compacted Soils. ASTM International: West Conshohocken, PA, USA, 2016.
- ASTM D4318-10; Standard Test Methods for Liquid Limit, Plastic Limit, and Plasticity Index of Soils. ASTM International: West Conshohocken, PA, USA, 2015.
- ASTM D4253-14; Standard Test Method for Maximum Index Density and Unit Weight of Soils Using a Vibratory Table. ASTM International: West Conshohocken, PA, USA, 2015.
- Gunaydin, O.; Gokoglu, A.; Fener, M. Prediction of artificial soil’s unconfined compression strength test using statistical analyses and artificial neural networks. Adv. Eng. Softw. 2010, 41, 1115–1123. [Google Scholar] [CrossRef]
- Jang, J.-S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Xiao, S.; Lu, Z.; Xu, L. Multivariate sensitivity analysis based on the direction of eigenspace through principal component analysis. Reliab. Eng. Syst. Saf. 2017, 165, 1–10. [Google Scholar] [CrossRef]
- National Cooperative Highway Research Program (NCHRP). Guide for Mechanistic and Empirical-Design for New and Rehabilitated Pavement Structures, Final Document; Appendix CC-1: Correlation of CBR Values with Soil Index Properties; Ara, Inc.: Champaign, IL, USA, 2021. [Google Scholar]
- Bassey, O.B.; Attah, I.C.; Ambrose, E.E.; Etim, R.K. Correlation between CBR Values and Index Properties of Soils: A Case Study of Ibiono, Oron, and Onna in Akwa Ibom State. Resour. Environ. 2017, 7, 94–102. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).