Towards a Model of Urban Evolution—Part III: Rules of Evolution

Abstract

This paper develops a formal model of urban evolution in terms of (1) sources of variations; (2) principles of selection; and (3) mechanisms of retention. More specifically, regarding (1) it defines local and environmental sources of variation and identifies some of their generative processes, such as recombination, migration, mutation, extinction, and transcription errors. Regarding (2), it outlines a series of selection processes as part of an evolutionary ecology of urban forms, including density dependence, scope dependence, distance dependence, content dependence, and frequency dependence. Regarding (3), it characterizes retention as a combination of absorption and restriction of novel variants, defines mechanisms by which these can occur, including longevity, fidelity, and fecundity, and specifies how these processes issue in trajectories define by properties such as stability, pace, convergence, and divergence. A conclusion reviews the effort and looks forward to computer simulation and data-driven applications, as well as focused theoretical extensions of parts of the model. This paper builds on Parts I and II and is part of the Urban Genome Project, about which more information can be found here.

1. Introduction

This paper builds on Parts I [1,2] of “Towards a Model of Urban Evolution”. It develops a formal model of urban evolution in terms of (1) sources of variations; (2) principles of selection; and (3) mechanisms of retention. More specifically, after reviewing key definitions and functions from Part II, regarding (1) it defines local and environmental sources of variation and identifies some of their generative processes, such as recombination, migration, mutation, extinction, and transcription errors. Regarding (2), it outlines a series of selection processes as part of an evolutionary ecology of urban forms, including density dependence, scope dependence, distance dependence, content dependence, and frequency dependence. Regarding (3), it characterizes retention as a combination of absorption and restriction of novel variants, defines mechanisms by which these can occur, including longevity, fidelity, and fecundity, and specifies how these processes issue in trajectories define by properties such as stability, pace, convergence, and divergence. A conclusion reviews the effort and looks forward to computer simulation and data-driven applications, as well as focused theoretical extensions of parts of the model.

2. Formal Model Review

This section summarizes key aspects of the formal model introduced in Part II [2].

At the core of the model is the spatial area that is being modelled.

• C: the set of all spatial areas in the domain.

Members of C can be spatially related using standard geo-spatial or administrative primitives. A model can be created for any member of C, allowing for the modelling of an urban area at different levels of aggregation and alternative spatial boundaries.

Our model of a spatial area c is comprised of three “components”:

• P: the set of all possible types of physical Forms.
• A: the set of all possible types of Activities (uses).
• G: the set of all possible types of Groups (users).

Any member of a component is referred to as an element (e). For example, a warehouse is an element of the component P. The elements of each component determine how expressive the model will be.

Central to our model is the recognition that P, A and G are interdependent. Forms enable activities performed by groups. However, the relationship is not uni-directional. Groups enact their own interpretation of forms in order to carry out activities for which the forms may not have been designed.

To capture the relationship among elements of P, A and G, we introduce the concept of Formeme. Formemes constitute the information encoded in a space, enabling features of urban form to be replicated elsewhere, maintained into the future, or recoding into new configurations. A Formeme f is defined to be a triple composed of elements of P, A and G.

f = <f[p], f[a], f[g]> where f[p] ⊆ P ∧ f[g] ⊆ G ∧ f[a] ⊆ A.

f[p] can be understood as an idea or script for how to encode space with a physical design, which we might summarize “be made out of this stuff arranged in this way”.

The Genome of a spatial area captures the set of formemes engendered by its physical forms: the local conceptions about how to organize space for some groups to do some activities on offer. The genome codifies the result of evolution of a spatial area at some time t.

We define a genome U as a set of formemes:

U = {u| Formeme(u)}

where Formeme(f) is true if f[p] ⊆ P ∧ f[g] ⊆ G ∧ f[a] ⊆ A.

We define

• u_i: the i^th formeme in U
• u_i [p]: the set of forms in the i^th formeme in U
• u_i [a]: the set of activities in the i^th formeme in U
• u_i [g]: the set of groups in the i^th formeme in U

We define the Urban Genome as tying a specific genome U to a spatial location c, at time t:

We define

• Genome (c, t, U, w) where
  • c: denotes a spatial area
  • t: denotes the time at which the genome describes c
  • w: denotes the world in which U exists. [In most cases, we will omit this parameter, but when we need to compare alternative scenarios for the same space c and time t, w will be used to distinguish them (i.e., alter native worlds)].

In this document we sometimes use the function UG:

UG(c, t) = U = {u| Formeme(u)}

In other words c and t uniquely identify a specific genome.

The genome describes information regarding the way a space is organized physically and for certain uses and users. Human users may or may not share these conceptions. Hence, we refer to Hunome H: the human actors who utilize and frequent a spatial area. This introduces the beginning of a dynamic component to the model. Where U is the information encoded in an area’s physical forms, H is the information encoded in its human users’ customs, practices, routines, and modes of interpretation. U is what the space expects from its users; H is what the users expect from their spaces.

H = {h| Formeme(h)}

Expressed another way, the Hunome H is a subset of the powerset of formemes: H ⊆ 𝓕

We define

• h_i: the i^th formeme in H
• h_i [p]: the set of physical forms in the i^th formeme in H
• h_i [a]: the set of activities in the i^th formeme in H
• h_i [g]: the set of groups in the i^th formeme in H

and

• H[p] = ⨆_i h_i[p] → set of all forms in H
• H[a] = ⨆_i h_i[a] → set of all activities in H
• H[g] = ⨆_i h_i[g] → set of all groups in H

We can now define the function HG:

HG(c, t) = H = {h_i| Formeme(h_i)} for some space c at time t

Signals are crucial in our urban evolutionary model. Any code must be communicated via some mechanism and we call that mechanism the Signal (S). We define S to be a set of signals, where each signal is composed of a

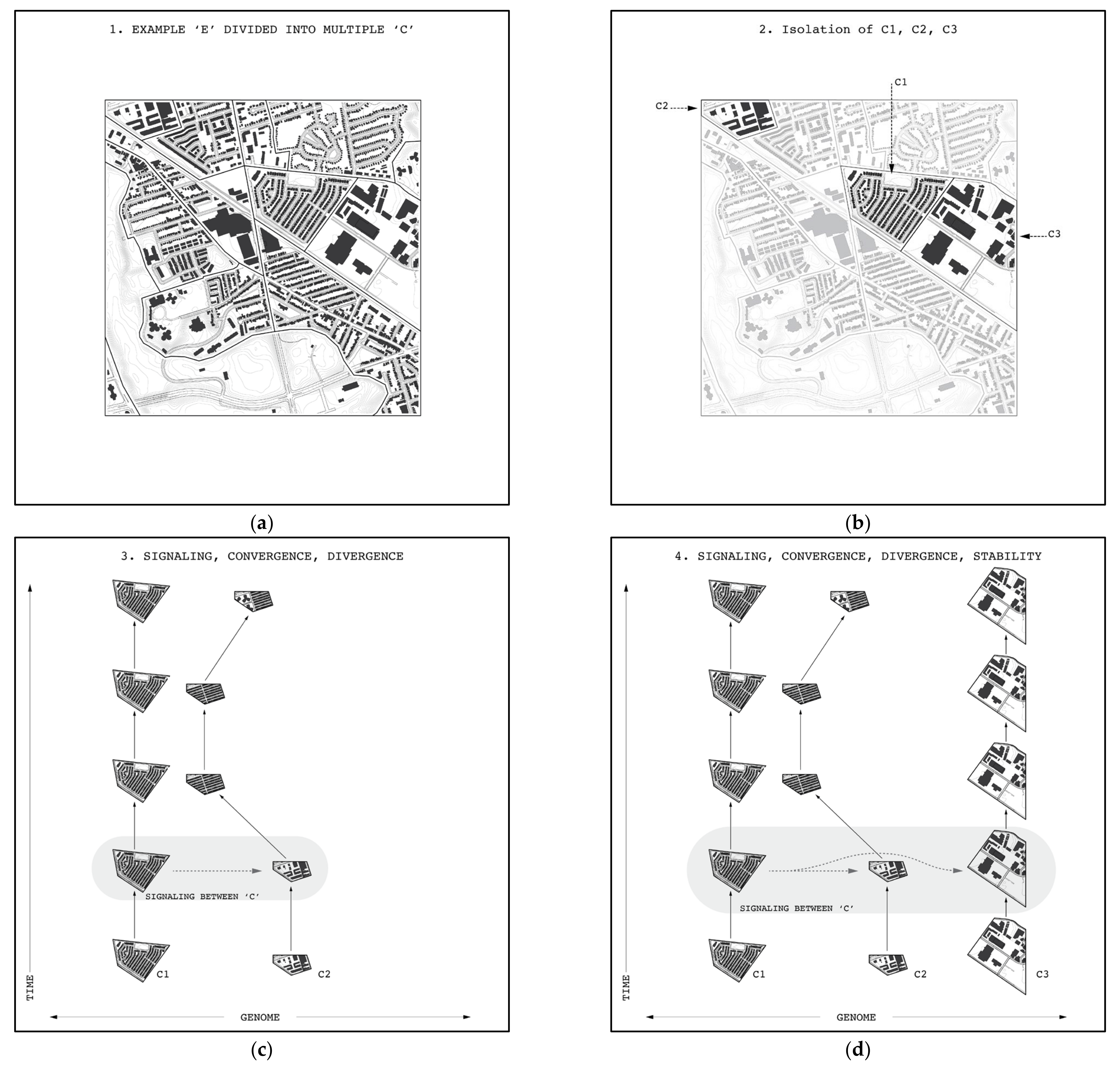
• formeme that communicates a fragment of a genome. This fragment may be assimilated by another spatial area, first as a change to hunome H, and if it survives, eventually as a change to U;
• the source of the signal a spatial area receives. Where a signal comes from affects how it is received;
• method of communication. A formeme may be communicated in more than one way, and depending on the method of communication, the signal may travel only within c (intra-spatial signal), or between c’s (inter-spatial signal), or both (bi-spatial signal);
• the capacity of a signal to alter the recoding costs in the area that receives the signal; and
• the number of times the signal has been received. A signal that is received with a high frequency may have a higher probability of assimilation in H.

S = {s_i|s_i = <f, r, c, SF, cm, n>}

where

• f is a formeme that is being signalled
• r is a function that transforms the recoding cost function R in the receiving signature
• c is a spatial area from which the signal originates
• SF is a set of formemes in c
• cm is a communication methods
• n is the number of times s_i has been received from c during the time span of the signature

We define:

• s_i: the i^th signal in S
• s_i[f]: is the formeme f of the i^th signal
• s_i[r]: is the recoding cost transform
• s_i[c]: is the spatial area from which the signal originates
• s_i[sf]: is the formeme sf that is the source of the i^th signal
• s_i[cm]: is the communication methods of the i^th signal
• s_i,[n]: is the frequency of the i^th signal from c during the time span of the signature

and

S[p] = ⨆_i s_i[f][p] → set of all forms in S

S[a] = ⨆_i s_i[f][a] → set of all activities in S

S[g] = ⨆_i s_i[f][g] → set of all groups in S

S[f] = ⨆_i s_i[f] → set of all formemes in S

To complete the definition of our model, we introduce a spatial area’s Signature. A signature combines the aforementioned concepts to provide a complete representation of a spatial area at some time t. It tells us what information is available in the spatial area, i.e., the genome (U), the conceptions about urban form held by its users (H), and the formemes received as signals (S). In addition, a Signature includes a recoding cost function R which captures the cost of recoding/transforming a formeme into another.

Signature(c, t, U, H, S, R, w)

We can now define the function:

SIG(c, t, w) = <U, H, S, R>

in other words, the complete signature for space c at time t.

Based on the model, we introduce the following functions:

• Size(c, t, e): is a function that returns the quantity of instances of element e at spatial location c at time t, where e ∈ P ∪ A ∪ G. If e is an activity, it can represent the number of occurrences of that activity up to time t. If e is a group, it can represent the number of people in the group at time t.
• Usize(c, t, e): is size(c, t, e) for e ∈ U[p] ∪ U[a] ∪ U[g]
• Value(c, t, e): is a function that returns the value of element e at spatial location c at time t where e ∈ P ∪ A ∪ G. The value of a building, parcel of land, the assets of a group, or the value associated with the ability to perform an activity.
• ActivityCost(F, a): the cost of performing activity a in the context of the set of formemes F.

3. Sources of Variation in Urban Evolution

In this section, we use our model to discuss variation: how do novel formeme variants appear in an area, which in turn could be differentially selected or retained? In our model, novel formeme variants represent potential modifications to the genome U. Therefore, they must arise from other components of the Signature SIG, namely human uses/users (Hunome H) or signals (S). We refer to variant formemes that arise from changes in the local population of activities or groups as “local variation”. We call variant formemes that emerge from changes in signals “environmental variation” because this source of variation introduces potential novelty into the genome indirectly, from S through H.

While one might imagine elaborating any number of detailed accounts of variation, our intention is to illustrate the general principles involved, opening the door to further specialization of these two types of variation. In the course of the discussion, we identify key mechanisms involved in generating urban variation that are broadly analogous to similar mechanisms in biological evolution. These include mutation, migration/gene flow, recombinatorial seedbeds, transcription error, and extinction events.

3.1. Local Variation (LV)

Local Variation (LV) refers to variant formemes that arise from changes in the local population of uses or users, H, which introduces novel formeme variants to the spatial area (c) in question. We can define LV as follows:

• LV: the introduction of new users, usages and forms in the hunome (H), which may or may not result in the modification of the genome (U).

LV plays an important role in urban evolution, akin to quasi-random mutations. People try out new things. Most of the time these will not go anywhere, and U will remain relatively unchanged. Sometimes they might prove deleterious. Sometimes they can catch on.

In order for them to do so, however, these new variants need to appear. Juval Portugali [3] provides a useful example of how this can occur. As he recounts, sometime in the 1950s, a Tel Aviv resident had the idea to enlarge their apartment by enclosing their balcony, making it into a kind of “half room”. Thus a novel formeme appeared. Encoding this formeme in physical space was likely somewhat costly for this user, but was nevertheless not so costly as adding a new full room. Thus at t = 1, we can assume that the existing signature did not foreclose this usage, even if it imposed enough costs so that it was an initially unusual occurrence.

Omitting Signals in this example, we could represent this situation using the following Signature:

Signature(c1, t = 1,
     U[p] = {openAirBalcony}, U[a] = {outdoor}, U[g] = {residents, guests},
     H[p] = {openAirBalcony, enclosedBalcony}, H[a] = {indoor, outdoor},
     H[g] = {residents, guests})

At t = 1, the activityCost of the indoor activity is less than the resources (value of their assets) available to the group,

activityCost(c1, 1, outdoor) < activityCost(c1, 1, indoor) < value(c1, 1, {residents, guests})

thereby allowing them to perform the activity. This difference between genome activity (U[a]) and hunome activity (H[a]) is highlighted above in bold. We have a novel formeme, embedded in a human activity, which has neither propagated more widely nor been retained in the genome.

The enclosed balcony is a fairly singular innovation, yet many novel variants emerge as recombinations of existing formemes within a given area more open to such experimentation. Recombination is akin to biological variation introduced through sexual reproduction, though it admits of more combinations. We call particularly fertile areas seedbeds. It is a recurrent observation that some cities are crucibles for creativity and unconventionality [4,5,6,7,8], such that some locales are more likely to generate variation than others. A feature of such spaces is that they connect diverse people and activities to one another, allowing each to learn and adapt from the other. Exposure to information about a critical mass of various groups and activities tends to increased opportunities to recombine and reconstitute them in new ways.

In our model, the creativity of an urban area becomes its formetic fecundity. Where a great diversity of formetic information is available, new combinations of formemes should appear at greater rates. If we adopt the view that innovation involves recombining features of extant forms into new forms, then the ‘newest innovations’ will be those that draw on the widest diversity of forms. This fecundity clearly depends upon the richness and heterogeneity of the Signals circulating in an area, suggesting the importance of Signals as sources of formetic variation, which we refer to as Environmental Variation.

3.2. Environmental Variation (EV)

The notion of Environmental Variation describes an indirect process through which variant formemes arise from Signals which in turn introduce new conceptions regarding uses, users and forms to an area. Change in the environment makes it more likely that different ideas about uses, users and forms will appear, which in turn become candidates for selection and retention in the local spatial area.

To illustrate, let us imagine a simple scenario, in which an industrial warehouse has been entrenched over an extended period of time.

Signature (c2, t = 100,
U[p] = {industrialBuilding, machinery, signs, fences},
U[a] = {industrialZone, securityGuard}, U[g] = {industrialists},
H[p] = {industrialBuilding, machinery, signs, fences}, H[a] = {industrial},
H[g] = {industrialists})

In this representation, securityGuard functions to enforce expected uses of the area; at the same time, the security guards could become a distinct group, whose presence and whose group objectives and organizational culture in turn comes to independently influence the way the space is defined, beyond the narrow purpose of enforcing its functional boundaries. These sorts of complex feedbacks arising from the introduction of new elements in formemes are a very fertile area for additional investigation.

Setting aside such complexities for the moment, in the present scenario, c2 refers to the space occupied by a building. U[p] refers to the fact that the space has been encoded with a certain physical form, which imposes some costs on potential users who wish to interact with it. We can imagine that it is a brick building with much open space and an ample supply of loading machinery so that using it for industrial purposes will be less costly than, for example, residential uses. U[g] and U[a] refer to who and what the building is for. Fencing, security guards, “employees only” signs and zoning rules help to define it as a space for industrial uses and users.

Let us now imagine that from t = 100 to t = 200, the environment changes in two major ways: first, the macro-economy changes from “industrial” to “post-industrial”. Second, the broader culture changes toward valuing personal self-expression and active leisure. “Post-industrialization” is a massive simplification involving numerous overlapping processes, but from the point of view of our industrial warehouse (at least at this location, let us say), it means a gradual increase in costs, requiring a correspondingly large increase in resources necessary to continually maintain it.

These changes in the environment are communicated as change in the Signals (S) received at c2, communicating information to the effect that industrial uses are less viable and more costly in the area. The signal S not only specifies a different activity, postIndustrial, but also includes cost transformation function r150 (For convenience, the cost transformation function name includes the time point it was communicated, e.g., r150.) that changes the cost of performing both industrial and non-industrial activities.

Thus at t = 150 the situation could be represented as:

Signature (c2, t = 150,
U[p] = {building, machinery, signs, fences}, U[a] = {industrial, securityGuard},
U[g] = {industrialists},
H[p] = {building, machinery, signs, fences}, H[g] = {industrialists}, H[a] = {industrial},
S[a] = {postIndustrial}, S[r] = r150)

This does not mean that industrial activities immediately cease, but the ActivityCosts for some activities in U[a] have increased; security may increase and hours of industrial operation may be reduced, thus incurring greater cost.

While the warehouse could be maintained for some time by expending greater resources, let us say that eventually these resources are spent. The factory closes by t = 200.

Signature (c2, t = 200,
U[p] = {building, machinery, signs, fences}, U[a] = {industrial, security},
U[g] = {industrialists},
H[p] = {building, machinery, signs, fences}, H[g] = {¬industrialists}, H[a] = {¬industrial},
S[a] = {postIndustrial}, S[r] = r200)

At t = 200, activities at this location have basically ceased, a situation indicated by the negation (¬) of industrialists being the users H[g] and industrial usage the activities H[a]. The use of negation in this signature captures the situation where we know that no industrial activities are taking place, but we do not know what activities are taking place. The change in the Signal has resulted in a c2 that is open to new uses and users. It is an urban analogue to an extinction event in biological evolution: industrialist and industrial elements of the formemes have disappeared.

The second change in the environment is a Signal communicating to groups the value in expending significant resources to participate in self-expressive night life activities such as dancing. At t = 210 this will be costly: one might get hurt jumping the fence; the guard might still be patrolling; city inspectors may impose a fine; the old machines strewn around the warehouse could get in the way of dancing. Still, these costs are much lower than at previous periods, leaving room for novel formeme variants to thrive.

Signature (c2, t = 210,
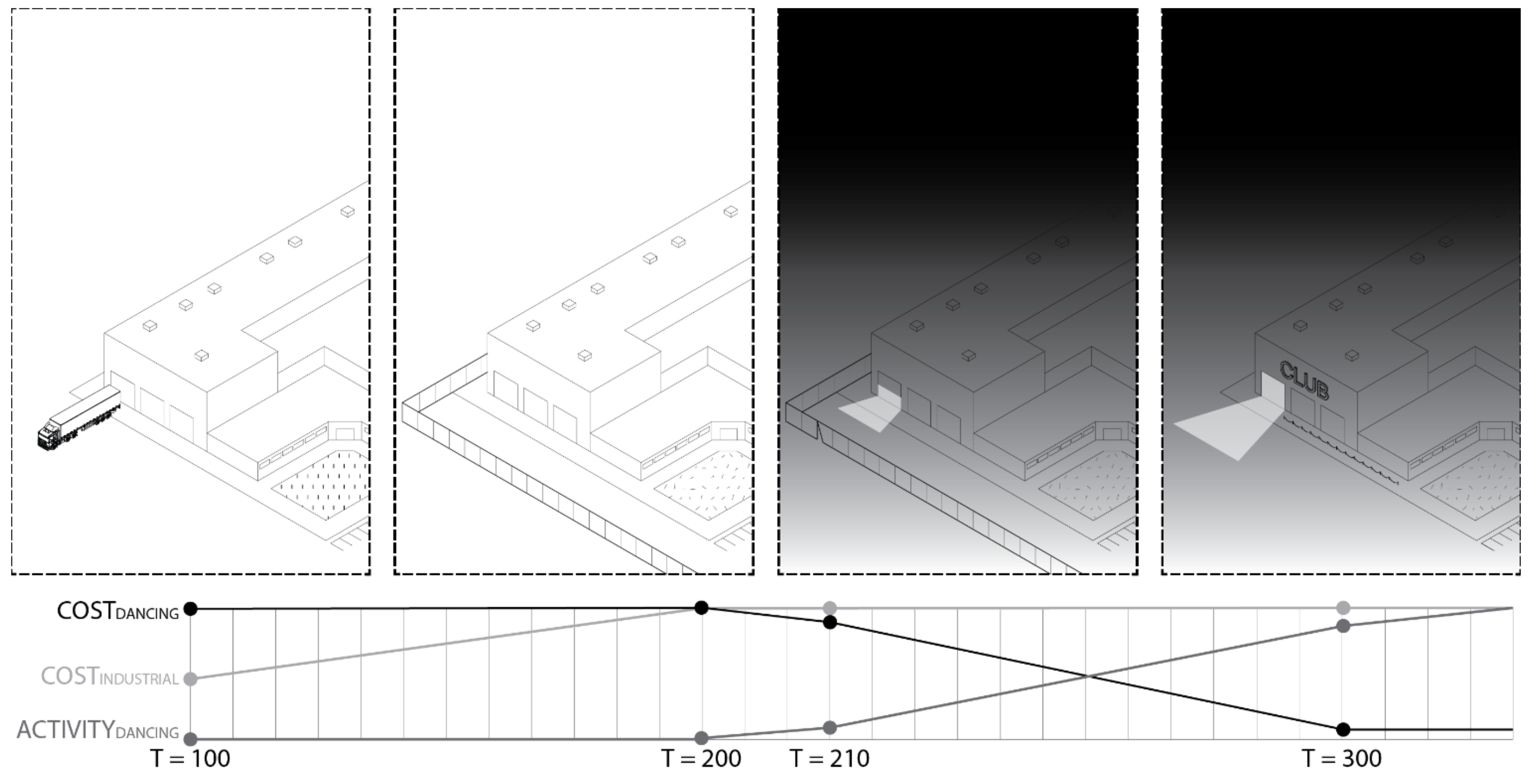
U[p] = {building, machinery, signs, fences}, U[a] = {industrial, security},
U[g] = {industrialists},
H[p] = {building, machinery, signs, fences}, H[g] = {dancers}, H[a] = {dancing},
S[a] = {postIndustrialExpressiveCulture}, S[r] = r210)

H now includes dancers and dancing (illicitly), even though U is relatively unchanged. This process of migration or formeme flow bringing new formemes into an area is akin to gene flow in biological evolution.

Environmental Variation arises not only from changes in Signals regarding types of appropriate activities (S[a]). Change in communication method (cm) also can impact formeme variation. Consider the warehouse at a later time, when it has become an underground dance club. H includes a dance floor, sound proofing, and an expectation that the space is for dancing, enforced through a dress code and bouncers. The primary method by which this information is received by others is through word-of-mouth: users personally tell other users when events are happening, for example.

Signature (c2, t = 300
U[p] = {building, machinery, signs, fences}, U[a] = {industrial, security},
U[g] = {industrialists},
H[p] = {building, danceFloor, soundproof}, H[g] = {dancers}, H[a] = {dancing, dressCode},
S[cm] = {wordOfMouth}, S[a] = {postIndustrialExpressiveCulture}, S[r] = r300)

Here, knowledge about the warehouse is the ultimate ‘insider’ resource, it primarily reaches (socially) nearby audiences, which are small in size, and more (socially) distant audiences barely register it.

A change in the communication method will tend to introduce variation among the formemes into the area, often through reaching new users and in turn sparking migration or formeme flow. For example, the dance club acquires a webpage, listing an event schedule. Users add it to Yelp, reviews accumulate, and as the Yelp profile fills in, other information is transmitted about cost, ambiance, assumed users (“good for kids?”), and more. The cost of receiving this information has dramatically decreased: anybody with an internet connection can access it, without much new noise being introduced.

Signature (c2, t = 310,
U[p] = {building, machinery, signs, fences}, U[a] = {industrial, security},
U[g] = {industrialists},
H[p] = {building, danceFloor, soundproof}, H[g] = {uncoolDancers}, H[a] = {dancing},
S[cm] = {wordOfMouth, yelp, website}, S[a] = {postIndustrialExpressiveCulture},
S[r] = r310)

Here the communication method transmits information about the dance club more widely, such that more potential users can access it. If we define two signals that convey the same information but by different communication methods:

s₁ = <f₁, {wordOfMouth}>
s₂ = <f₂, {yelp}>

We can then use the signal characteristics elaborated in Fox et al. (2022a) to define that the reach, i.e., % of population within c that receive and can process the signal, of wordOfMouth is less than yelp:

reach(s₁, c2, 310) < reach(s₂, c2, 310)

Given that these new users were not part of the tight social circles reachable by word of mouth, they will tend to represent an alteration in users, who in turn are likely to carry divergent formemes. This process illustrates the role of Signals in formeme flow. People (H[g]) from areas outside of c2 carry information from elsewhere, which introduces new variants of form into a focal c2.

Finally, we note that some Environmental Variations will likely appear through a process akin to “transcription errors”. Transcription errors happen when a formeme is not reproduced precisely. This failure to faithfully transcribe the formeme introduces novel variants. For example, civil engineers in China may attempt to implement urban design ideas from the US, but in the process make subtle changes, due to language differences that unintentionally produce a new formeme variant.

Formally, transcription errors occur when a signal’s formeme, s[f], is modified during transmission or interpretation in the receiving spatial area c. We represent the degree to which a signal is subject to transcription errors by the signal characteristic noise:

noise(s, c1, t1, c2, t2): percentage of the signal s formemes
that mutate in transmission from spatial area c1 at time
t1 to spatial area c2 at time t2

As a result of noise in signal transmission between two areas, novel formeme variants appear and become candidates for selection or retention, as they do through migration, recombination, or other sources of variation such as individual experimentation. Whether a novel variant becomes a formeme that survives at high rates or is retained over time in U is a different question, however, clearly related to many other factors, of the sort outlined in Section 4 (selection) and Section 5 (retention).

4. Principles of Selection in Urban Evolution

This section elaborates some key principles of selection in urban evolution. These principles generate differential rates of replication among populations of formemes. Differential rates of replication are a function of many processes. To formulate propositions about these processes, we adapt some basic principles from evolutionary ecology. In general, evolutionary ecology seeks to “complete Darwin’s mission by providing a theory or theories of what selection favours under different ecological conditions” [9]. See [9] for a comparison of evolutionary ecology to population genetics and metabolic ecology. (The former includes reference to the ecological environment, but in a generic, under-specified way; the latter is closer to the approach taken by West and colleagues in studying urban dynamics.) In this view, the surrounding ecological environment “enables and constrains what can evolve” there [9]. Given that we are interested in features whose relative rates of reproduction vary across locations depending on characteristics of those locations, this approach is a useful way to formulate propositions about the survival rates of formemes.

A central feature of evolutionary ecology is that it does not posit a single type of selection. Rather, it constitutes a theory of how selection functions under different scenarios. In this spirit, we formulate some propositions about how various types of selection might operate in the urban evolutionary process. These propositions are not exhaustive but rather illustrative, and an important further direction is to collect, codify, and evaluate a host of such propositions. Nor are they necessarily true: the point is to demonstrate how to use our model in order to formulate relatively precise hypotheses that may or may not find empirical support, but which can guide and give meaning to research.

In this section we highlight five types of selection in urban evolution: density dependence, scope dependence, distance dependence, content dependence, and frequency dependence. These selection processes change the probability of some formemes surviving among the human actors within a set of locations (H), in turn increasing or decreasing the similarity of those locations. The principles by which these changes in H are retained to various degrees in the urban genome (U) is the topic of Section 5.

4.1. Density Dependence

Density dependence is arguably the central type of selection envisioned in biological theories of evolutionary ecology. While its elements and predictions can be elaborated in great detail and have been controversial, the basic intuition is simple. It holds that different strategies tend to be more or less successful depending on the density of competitors and resources. “R strategies” are strategies that yield rapid reproduction of numerous offspring, generally of “low” quality. These tend to thrive in lower densities, which makes it possible to rapidly fill the space. “K strategies” are strategies that yield slower reproduction of fewer offspring, generally of “higher” quality. These strategies tend to thrive in higher densities, which favor “digesting”, synthesizing, or otherwise “elevating” features of the existing population.

The proliferation of pizza restaurants provides an illustration of how these processes can contribute to the evolution of urban space. Pizza first emerged in Naples in the late 19th century and has spread rapidly since via a multitude of R strategies: pizza on a bagel, on potato chips, in military meal kits, in space. As it has been copied to new environments, it has tended to proliferate widely, unconstrained by any enforceable rules on its spread. However, beginning in the 1980s, a different strategy appeared, represented by the AVPN, a trade group. The group imposes strict guidelines which are supposed to ensure that the modern chef can recreate the original version. The association has helped to spark a renaissance of Neapolitan pizza, even among restauranteurs who do not strictly adhere to the guidelines. The pizza revival movement represents a K-type strategy—it insists on higher fidelity copies, and it thrives in an environment where there are an abundance of pizza and restaurant forms. (An early finding of our research is that certified restaurants have propagated steadily since the 1980s, but slowly enough that we can know where all of them are.).

The problem we face is how to formalize the intuitive notions of density dependence using our model. We illustrate general principles via the specific example of pizza. First, we distinguish between two types of pizza making activities within a signature:

AVPNPizzaMaking ∈ H[a] and otherPizzaMaking ∈ H[a]

Next we have to operationalize the concept of density. To do this we first have to identify what other activities a particular activity is in competition with. Is an AVPNPizzaMaking activity only in competition with other AVPNPizzaMaking activities, or with otherPizzaMaking activities too? Or with restaurants in general? Or with some other set or subsets of consumption activities? We define the set of competing types of activities as follows:

competingActivities(c, t, a) = {a′|CompetesWith(a, a′) ∧ a′ ∈ H[a]}

where CompetesWith is a predicate that determines whether two types of activities compete

competitionSize(c, t, a) = 𝜮 _{a′ ∈ competingActivities(c, t, a)} size(c, t, a′)

where competitionSize sums the number of actual competing activities across all types of competing activities

competitionDensity(c, t, a) = size(c, t, a)/competitionSize(c, t, a)

where competitionDensity is the ratio of the number of activities of type a, divided by the number of competing activities

Assuming the replication strategies that can be applied to the genome include R-replication ∈ 𝓡, and K-replication ∈ 𝓡, we next propose the conditions under which each strategy will succeed.

Proposition 1. 

There exists a competition density threshold d_r below which the application of R-replication results in a survival rate greater than 1.

ActivitySurvivalStrategy(c, a, t, t′, R-replication, d_r):
MIN_t, MAX _t′ t < t′ ⋀ HG(c, t′) = replicate(c, t, R-replication)
⋀ competitionDensity(c, t, a) < d_r ⋀ activitySurvivalRate(c, a, t, t′) > 1.

Proposition 2. 

There exists a competition density threshold d_k above which the application of K-replication results in a survival rate greater than 1.

ActivitySurvivalStrategy(c, a, t, t′, K-replication, d_k):
MIN_t, MAX _t′ t < t′ ⋀ HG(c, t’) = replicate(c, t, K-replication)
⋀ competitionDensity(c, t, a) > d_k ⋀ activitySurvivalRate(c, a, t, t′) > 1.

We refine our definition of these two strategies by introducing the notion of “saturation”: the point of diminishing returns for selection due to the population of c, i.e., H[g], not being able to sustain the replicated activities in U[a].

Proposition 3. 

Activity saturation occurs when there exists a density k at some time t where the survival rate of some activity a is less than 1.

Saturation(c, a, t, t′, k):
∃k, t, t′ t < t′ ⋀ (activitySurvivalRate(c, a, t, t′) < 1) ⋀ (size(c, t, a)/populationSize(c, t)) > k

where populationSize is the sum of the sizes of all groups in H[g]:

populationSize(c, t) = 𝜮 _{g′ ∈ H[g]} size(c, t, g′)

4.2. Scope Dependence

Density dependence propositions hold spatial area constant. However, the number of spatial areas in which a formeme exists will vary, which in turn shapes their survival rates. We describe scope in terms of niche width [10], where niche is understood as the physical area over which an entity thrives. For example, a formeme with a wide niche width exists across a very large spatial area (numerous c’s); a formeme with a narrow niche width exists in a smaller spatial area (fewer c’s).

We can define the width of a set of formemes F:

formemeWidth(t, C, F) = formemeCount(C, t, F)/|C|

Niche-width may drive urban evolution in a few ways, as summarized by Popielarz and Neal [10]. The first associates niche width with the size and pace of formemes; the second with their survival rates under varying conditions of stability. The first suggests the proposition that, generally, formemes with high niche width are likely to be connected to larger institutions, such as corporations or governments, and should change relatively slowly. They are adapted to thrive in many different locations. Fast-food restaurants such as McDonalds could be an example. By contrast, formemes with low niche width should be smaller, independent, and change more rapidly. Independent art galleries could be an example. The second suggests the proposition that in a relatively stable environment, formemes with narrow niche widths should thrive: they are adapted to a specialized function in a narrow range of areas. However, in times of relatively rapid change, generalists should be favored, since their success is not dependent on being located in any specific location, enabling them to “weather the storm”.

Our model helps formulate such propositions from existing literature. The notion that high formeme width is associated with larger institutions can be represented directly in our model as a formeme that ties the organization to specific groups and activities, and has a large formemeWidth within a set of spatial areas. Formulating the proposition that survival rates for specialist and generalist formemes (narrow vs. wide niche widths) depends on the stability of the environment can be formulated using the Estable predicate defined in Part II.

4.3. Distance Dependence

Density and scope dependence presume that physical distance does not affect survival rates. However, some formemes are more likely to proliferate in some locations than others solely due to those locations’ physical distance from its other instances. We can describe this type of selection as distance dependence.

Using the spatial distance functions introduced in Part II, we can define these dependence propositions. For instance, let us imagine that HG(c1, t) and HG(c2, t) have very similar formemes, but that HG(c2, t) is located near HG(c3, t) and HG(c1, t) is far from HG(c3, t).

distanceB(c1, c3, t) > distanceB(c2, c3, t)

Proposition 4. 

Spatial areas that are close become more similar over time.

If distanceB(c1, c3) > distanceB(c2, c3) Then probability that
Fdist(HG(c2, t + n), HG(c3, t + n)) < Fdist(HG(c2, t), HG(c3, t))
is greater than the probability that
Fdist(HG(c1, t + n), HG(c3, t + n)) < Fdist(HG(c1, t), HG(c3, t)).

This proposition states that the closer the spatial boundaries of two genomes are, the higher the probability that they become more similar over time. Even if internally HG(c1, t) and HG (c2, t) may be quite similar, their differential proximities to HG(c3, t) mean that features associated HG (c3, t) are more likely to proliferate in HG(c2, t). HG(c2, t) is better-positioned to recruit new ideas about uses and users from HG(c3, t) than is HG(c1, t). Extending our example of the industrial warehouse above, HG(c3, t) could be an artsy café where hip youth hang out, while HG(c1, t) and HG(c2, t) would be industrial warehouses of varying distances from HG(c3, t). The proposition then says that HG(c2, t) should be more likely to host hip entertainment venues than HG(c1, t).

A possible explanation for distance dependence lies in signals. The closer two spatial areas are, the higher the frequency of signals between the two areas and the higher the quality of the signal. For example, there may be more movement of people between the areas, leading to greater frequency of word-of-mouth with higher accuracy.

Of course, minimizing distance is not always beneficial for a given formeme. Mostly for reasons of competitive advantage, sometimes maximizing distance between competitors can be more effective, especially within the area within which resources like markets and land may be accessed. The twin strategies to cluster among resources and away from competitors create complicated equilibrium conditions that have long been studied in urban economics, and that often are established iteratively. In one of the most discussed such studies [11], the physical distance between agents ends up fully minimized only after competitors have taken turns locating themselves between the market and their competitor.

4.4. Content Dependence

Physical distance is only one form of distance. The spread of some formemes will likely depend upon the similarity/distance of their socio-cultural content. Accordingly, content dependence refers to the fact that aspects of the urban environment will reproduce at higher rates in locations where there are concentrations of groups with a preference for similar types of forms, including forms geared toward similar activities or groups.

This proposition states that the more similar the groups present in two locations, the more likely are formemes associated with one to propagate in the other. An example could be restaurants devoted to ethnic cuisine being more likely to make up higher shares of formemes in areas where members of that ethnicity live. Another example could be physical features like gated communities spreading to areas with high concentrations of high-income residents.

gdist and adist measure the similarity between two groups and activities, respectively. The smaller the distance, the more similar they are. We can recast content dependence as:

Proposition 5. 

The smaller the gdist(H[g], H[g]’), then the smaller the adist(H[a], H[a]’).

If gdist(H[g], H[g]’) < gdist(H[g], H[g]’’) then adist(H[a], H[a]’) < adist(H[a], H[a]’’).

4.5. Frequency Dependence

The frequency with which information about a formeme is received can alter its survival rate. Frequency dependence indicates that formemes that comprise large shares of the Signals received in a given location are more likely to be reproduced. In other words, once a formeme passes a given frequency threshold within the set of Signals received by a given area, it becomes more likely than not to propagate there. The sheer quantity of repeated references to the formeme can make it into an urban feature that any area is expected to have.

The following proposition states that if the frequency of a formeme received by an area c exceeds some threshold k, then the distance between the signalled formeme and H decreases over time.

Proposition 6. 

Given HG(c, t) = H1 and HG(c, t’) =H2 and formeme(f) and t < t’.

If formemeSignalFrequency(c, t, t’, f) > k Then Fdist(F1, f) > Fdist(F2, f).

For example, a coffeehouse a-la Starbucks was not always as ubiquitous as it is in the modern American city. However, between the time the first Starbucks opened in 1971 and today when there are over 28,000 locations, the sheer quantity of signals concerning coffeehouse formemes dramatically increased. We can hypothesize that the introduction of Starbucks into new areas is to some degree an instance of Environmental Variation, discussed in Section 3. Think about two adjacent neighborhoods, one with a Starbucks and one without. Now think of all the Starbucks signals—the signs, the takeout coffee cups, the word-of-mouth—transmitted from one side of the invisible neighborhood line to another to customers who inhabit the other neighborhood. The activities of residents in the next neighborhood might begin to change (‘I should check that out’). Additionally, if they bring enough of their own signals to the home neighborhood, there may eventually be demand for a Starbucks of their own. In this scenario, neighborhood change starts with the coffee cup. The word-of-mouth-led transmission of Starbucks would be an example of what is known as endogenous transmission of an innovation. It is possible or perhaps even likely that many Starbucks are spread via some exogeneous mechanism like the schedule of a corporate office, or that exogenous and exogeneous mechanisms interact. To that extent that local signals matter, frequency dependence may play a role.

In any case, the accumulation of Starbucks Signals likely added more information to the Signals circulating in many areas, such that the very ubiquity of Starbucks was an advantage to newer forms like “single source” coffeehouses such as Blue Bottle or Intelligentsia. Operators of these catered to a market for whom the global abundance of Starbucks might have been stifling. For customers and operators of these smaller establishments, the high frequency of Starbucks signals creates the conditions for potentially being on the lookout for relatively rare signals, another form of frequency dependence in which minority rather than majority formemes are reproduced. (On this hypothesis, boutique ‘third wave’ coffee shops would be relatively more likely to be found where ‘second wave’ Starbucks type signals have accumulated).

The notion of frequency dependence can be extended to cover propositions in which not just the quantity but the quality of the formeme is part of the Signal. We can think of this as a way to capture the fact that since socio-cultural evolution proceeds through a social learning process, the survival rate of socio-cultural items will often depend upon their prestige or renown. In other words, some formemes reproduce at higher rates because they are prestigious. Examples of success dependence are abundant. For instance, the Burnham Plan became a model for many cities, and its prestige helped to spread urban forms associated with the City Beautiful movement. More recently, the artistic prestige of Williamsburg has provided a model adopted in small and mid-sized towns, where artisanal ice cream shops and sophisticated cocktail bars now proliferate.

To articulate this intuition more formally, we formulate the proposition that formemes that broadcast more positive representations via their Signals will propagated more widely (by contrast, negative representations will tend to reduce survival rates).

Proposition 7. 

Given HG(c, t) = F and HG(c, t’) = F’ and Signal formemes s1[f] and s2[f].

If prestige(s1[f]) > prestige(s2[f]) Then Fdist(s1[f], F’) < Fdist(s [2], F’).

In other words, higher prestige signal formemes will be adopted by a usage genome over time.

Table 1. Principles Governing the Evolution of Urban Form.

Type of Dependence	Summary	Example
Principles Related to Form Features
Scope	Formemes with wider niches will tend to attract more resources Formemes with wider niche width will have a relativity higher probability of survival when the environment is changing, specialized forms will be favored under stable conditions	McDonalds has a wider niche width than a vegan, organic hamburger stand. McDonalds is more likely to survive a 30% increase in the local minimum wage or a pandemic than the local hamburger stand.
Content	The viability of a formeme will be influenced by its proximity to groups with a preference for or against the substantive content of its activities or the group affiliation it affirms.	Ethnic shops will tend to proliferate in areas where members of that ethnicity reside; satanic book stores will have low survival rates nearby Evangelical Christian populations.
Distance	Propagation of a formeme depends on how physically close it is to other iterations of the same formeme.	The franchise of a successful operation will be more viable at some ideal physical distance from the original
Principles related to environmental features
Density	Propagation of a formeme depends on density of competitors in the environment	Neopolitan pizza thrives when there is a glut of pizza restaurants
Frequency	Propagation of a formeme depends on the size of the formeme’s population	The 28,000th Starbucks location propagates at a different rate and in different places than the first.

summarizes the key elements of the above propositions and organizes them in terms of principles related to features of urban forms or their environments. These propositions provide general guidance, but each may be elaborated and specified when pursued to identify key mechanisms. For example, signal frequency dependence might operate through intellectual champions of specific types of forms, such as Jane Jacobs’ writings about the virtues of Greenwich Village, old buildings, and dense street networks. Formemes that acquire such champions are more likely to become models, and in turn be copied. The propositions moreover need not operate in isolation, and complex interactions are possible and likely.

5. Retention in Urban Evolution

Various formemes survive at different rates. For evolution to occur, however, characteristics of survivors need to be retained through time. Retention makes it possible for existing configurations of urban life to be preserved and passed on into the future. In our model, retention is a duality with two sides: on one side, it is a conservative force that restricts what additional variations are possible, much like the inherited features of organisms restrict what variations they can undergo; on the other side, it determines what formemes are absorbed by the urban genome (U). In the former, the urban genome U constrains the selections introduced into H, in the latter, selected formemes in H are introduced into the urban genome U.

Restriction and absorption are the same process seen from two points of view. From the restriction side, the urban genome U constrains the selection process, thus reducing variability in H and the probability of absorption. In a sense, U imposes a cost on introducing variations into H that are inconsistent with U; we call these costs “recoding costs”. Relatively high recoding costs increase the chances that a given U will be retained by imposing restrictions on what can be absorbed. Relatively low recoding costs allow the introduction of greater variability in the selection of new formemes in H, thereby making retention of the existing U less likely and opening the door for other formemes in H to become absorbed in U. From the absorption side, the recoding of U occurs when restriction is overcome. This occurs when there is significant deviation between the formemes held by local human actors H and those embedded in the existing forms (U). New formemes are introduced into H, resulting in an increasing distance between U and H. As the distance increases, so does the probability of absorption increase, just as the capacity to restrict absorption decreases. Restriction constrains absorption; absorption overcomes restriction. Retention is the result of this dual process.

Retention means that tomorrow’s city resemble today’s—but not exactly. As differences in what is retained accumulate, lineages emerge. As part of a lineage, current areas exist within a sequence of ancestors from which their characteristics have descended. For example, elements of medieval and Roman cities—such as road width and street design—have been retained in many European cities, just as features of threshold spaces such as porches and verandas have been retained in many North American cities. These urban inheritances continue to place constraints on the way subsequent spaces can be programmed in the future. They make the city into a vast memory bank, a storehouse of information retained from the past. This aspect of our model is especially important to note, given Mehmood’s [12] critique of Marshall’s [13] exclusion of memory from his model of urban evolution: “I consider that this normative exercise disbalances Marshall’s whole argument about the process of evolution, as memory function happens to be a key element of evolutionary metaphors in various forms [12] (p. 22)”. In this light, the study of retention thus naturally moves us toward questions of descent and taxonomy, central to the historicist aspect of evolutionary theory.

To elaborate these ideas more precisely, we proceed as follows. We first illustrate the notion of retention by returning to the example of the industrial warehouse from Section 3. We then provide examples of retention hypotheses, describing conditions when formemes encoded in a given U are more or less likely to be inherited in future iterations. Following Dawkins and Hull [14,15,16], these retention hypotheses feature the concepts of longevity, fecundity, and fidelity. Finally, we discuss the concept of evolutionary trajectories, and define some of their key characteristics.

5.1. Illustrating Recoding and Retention

Returning to the example of the industrial warehouse from Section 3 helps to provide an initial description of recoding and retention. For SIG(c, t = 310), selection has modified H to be quite distant from U, triggering the absorption process of retention. SIG(c, t = 325) depicts the absorption process resulting in a recoding of U, in particular the elements related to the use of the space as a dance floor, including soundproof, uncoolDancers, bouncers, etc.

Signature (c, t = 325,
U[p] = {building, danceFloor, soundproof},
U[a] = {EntertainmentZone, dressCode}, U[g] = {uncoolDancers, bouncers},
H[p] = {building, danceFloor, soundproof, fenceWithHoles},
H[g] = {uncoolDancers}, H[a] = {dancing},
S[cm] = {wordOfMouth, yelp, website} >, S[a] = {postIndustrialExpressiveCulture})

In this example, elements of UG (t = 310) disappear in UG(c, t = 325), and elements of HG(c, t = 310) appear in UG(c, t = 325), marking the absorption aspect of retention.

At t = 325, U no longer constrains groups and activities to those of an industrial zone, imperiling the survival chances of industrial formemes. There is little cost to recoding the space away from industrial uses, though the physical form of the building restricts the range of alternative uses, thereby creating a lineage to past iterations of the space that inherits some information from ancestral formemes. Interaction with the physical environment in which formemes are embedded affects their survival and retention. Concurrently, the absorption of new users with more mainstream expectations for the space has reduced the costs of recoding the space toward relatively conventional groups and activities. More formally, for some non industrialZone activity, niza, the cost of recoding the space c at some time t > 325 is less than the cost of recoding at some time t < 325:

recodeCost(HG(c, t₁), H′) > recodeCost(HG(c, t₂), H′)

where t₁ < 325, t₂ > 325 and H′[a] = HG[a] ∪ {niza}

As recoding costs change, U fails to retain exact replicas from previous time periods. The degree of retention can be represented with the Fdist function, introduced earlier:

retention(F, F′) = 1-Fdist(F, F′)

Retention varies from 0 to 1. A retention of 1 would indicate a perfect replica. A retention of 0 would indicate that two genomes share no elements, which implies a state of total volatility, where the future bears no relation to the past. Neither extreme is realistic, nor would either result in any form of evolution.

In the present example, the retention of the U from t = 310 to t = 325 would be represented as follows:

retention(UG(c, t = 310), UG(c, t = 325))

The result of this process is that the U for this location begins to incorporate characteristics of selected formeme variants introduced in H. For instance, U[p] changes to accommodate more users and uses: a condominium is built atop the warehouse, and the area is rezoned for entertainment uses. This process is represented in Figure 1.

5.2. Retention Hypotheses

The previous section described retention as a variable outcome relative to restriction and absorption processes. We now illustrate how to formulate propositions about the conditions under which retention should vary. The general form of such propositions are similar to what Stinchcombe [17] characterizes as “historicist causal imagery”. Sorenson’s [18] discussion of the process of generating path dependence is also relevant. We describe conditions which make the costs of maintaining a given U lower than changing it, even under pressure to do so.

A classic example is language: once a language is established, each new member of a society is under strong pressure to learn it, in order to participate in the common culture and commerce. Hence, patterns of culture and commerce tend to be retained from one generation to the next. Stinchcombe observes that a similar process occurs with respect to urban infrastructure: “There are resources which, in order to be used at all must be maintained [such as] [roads, railroads, harbors, canals, water supply systems… housin [When] the cost of regenerating such a resource is smaller than the cost of investing in a new pattern activity, the resource will tend to be maintained [17] (p. 121)”. Our propositions indicate how to generalize and formalize this insight within our model of urban evolution. We identify four general classes of retention hypotheses: longevity, fidelity, fecundity, and co-evolution.

Longevity. A first type of retention proposition concerns longevity. Longevity refers to the durability of the physical form in which a formeme is encoded [14]. The proposition states that

• Retention will be higher the more durable the physical material in which a formeme is encoded, and lower the less durable.

In terms of our model, we represent this proposition by comparing the aggregate cost of activities with and without the form e, where the activities include the cost of removing/replacing e.

Given e ∊ F[p] and e ∉ F′[p]
if aggregateActivityCost(F) ≤ aggregateActivityCost(F′)
then it costs more to remove e, leading to greater retention.

Graded beds for roads illustrate this proposition. Graded beds are extremely durable, making it very costly to alter the basic pattern of transit activity in the city. A region c where its physical form U[p] is encoded with “graded beds” is unlikely to suddenly change to a different usage than “road use”. For similar reasons, many political and religious movements have sought to encode their ideas in durable material, such as marble. By contrast, less durable materials can be more easily recoded, and so formemes encoded in them are less likely to be retained, and in general such areas should show greater degrees of volatility.

Fidelity. Retention varies with the degree of fidelity at which a formeme is reproduced. More faithful maintenance of past forms increases the retention rate. Hence, fidelity propositions state:

Retention will be higher the more faithfully a given formeme is maintained between two times.

In terms of our model, we can represent this proposition by focusing on the activities that lead to retention. In particular, we can define an activity e as having a positive impact on the fidelity of a formeme f if the removal of the activity (possibly) leads to the disappearance of the formeme:

Given UG(c, t₁) = U₁, and UG(c, t₂) = U₂, and t₁ < t₂, and e ∊ U₁[a], f ∊ U₁:

if e ∉ U₂[a] and f ∉ U₂ then the activity e possibly contributes to the fidelity of f, leading to greater retention.

Fidelity can be generated through many mechanisms. Consider three examples. First, fidelity, and hence retention, will be higher when a particular formeme is legally required by planning or building codes, and lower when there is less formal regulation of space. This is more likely to occur when the groups associated with that space (U[g]) are relatively powerful, and hence able to impose costs on alternative users and uses. For instance, in Toronto’s Greektown, while the number of Greek residents has declined over recent decades, Greek business leaders continue to control the local Business Improvement Association, which supports Greek-themed festivals and [19]. By contrast, if more powerful groups appear in an area who are guided by different formemes (H[g]), the formal codes could change, and less of the past U would be retained.

Second, fidelity will be higher where users and uses correspond more closely to what a form is for. This occurs where U is more similar to H. In this situation, users of a space have expectations for a space that correspond to its expected uses. They are therefore more likely to maintain the pattern of past usages. This could be exemplified by a traditional ethnic neighbourhood, where for instance numerous Italian residents regenerate similar Italian restaurants and Roman Catholic churches over time. By contrast, as new groups enter with greater formetic distance from existing groups (for instance by processes of migration illustrated in Section 3), tension between U and H is likely to increase. The existing set of formemes encoded in U are more likely to be retained if the amount of corresponding activity of local users increases enough to counteract the (different) expectations of new users.

Third, fidelity will be lower when existing formemes embedded in a U are challenged by formemes originating in groups with reputations for reducing the risk of change. A major cause of maintaining past forms faithfully is fear of change, rooted in the inability to predict the future. Science and technology reduce risk by enhancing the control of the future. Therefore, the recoding costs of formemes arising from scientists and engineers are likely to be lower than that coming from different groups.

Fecundity. A third class of retention hypotheses involve fecundity. Fecundity refers to the number of copies of itself that a formeme generates. The general form of fecundity proposition is:

• Retention will be higher when more copies of a given formeme are generated, wherever they are located.

Stated formally in terms of our model, we write this proposition as follows:

Proposition 8. 

The retention of formeme f is proportional to the number of signatures it appears in:

retention(f) ∝ formemeWidth(t, C, {f}) for some set of spatial areas C

Proposition 9. 

The retention of formeme f is proportional to the frequency of outbound signals containing f:

retention(f) ∝ formemeSentSignalFrequency(c, t, t′, f)

Fecundity in our model operates via Signals and indirectly through increasing or decreasing fidelity. In general, when a formeme moves from H to U, the reach of its signals increase. For example, as hipster lifestyle became encoded in the cafes, lofts, and cultural venues of Williamsburg, NY, this style in turn could be communicated in newspaper articles and glossy magazine spreads. Yet, signal properties (elaborated in Part II) still vary across Us, in turn affecting their chances of retention. Consider three examples, which illustrate processes by which particular bits of formetic information become more or less heritable.

First, as reach increases, more instances of a formeme circulate more widely. This increases the probability that more instances of a formeme appear in more Hs. It also means an increase in the popular support for a formeme, thereby increasing the chances it will be maintained faithfully.

Second, if reach increases along with clarity, it will also reduce the likelihood of transcription errors occurring. It does so by creating more environments similar to the original one, as more people consume more similar signals that they understand in a similar way. For example, the widespread knowledge of English in many countries increases the retention of formemes embedded in a U located in an Anglophone region.

Third, retention will vary depending on the communication method. When formemes are communicated by mass media and through well-developed educational systems the retention rates of the urban genomes in which they are encoded are likely to be higher. For example, recoding costs for architectural styles featured in the New York Times and taught in architectural schools will be relatively high. By contrast, a style known to only a few via word of mouth and banished from curricula will be much more fragile, and its retention will be lower.

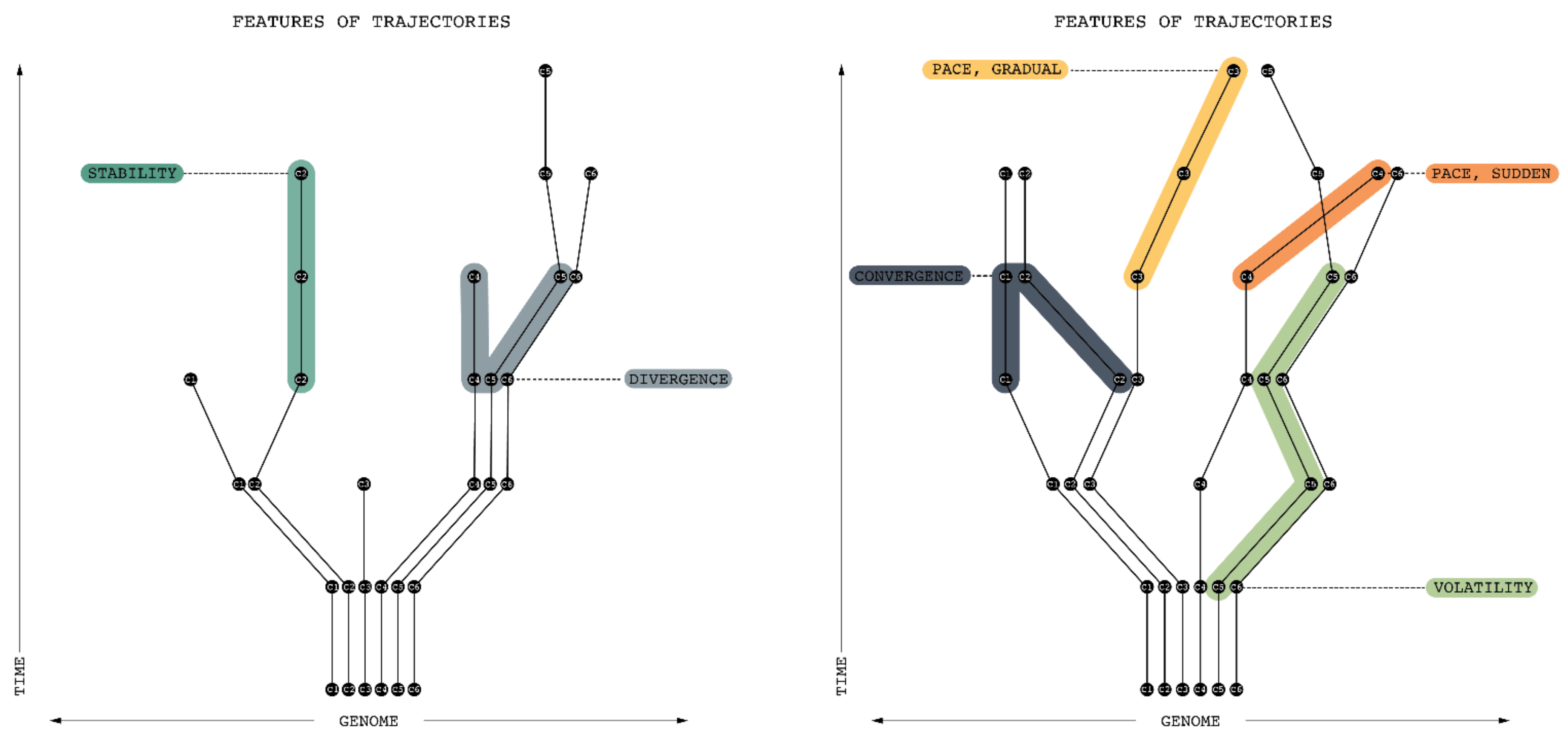
5.3. Trajectories

Depending on retention, forms of urban life exhibit trajectories. They come from somewhere and are on their way to somewhere else. Examining trajectories is central to the historicist dimension of an evolutionary approach to cities. This aspect of our approach is akin to the Darwinian notion of taxonomy. In simple terms, Darwinian classification adds a historical dimension to the form of classification developed by Darwin’s predecessors, such as Linnaeus. Linnaeus’ taxonomies of organisms were based on their similar attributes. Darwin rejected the idea that there is a fixed set of species, and instead argued that species are more similar if they are more closely related, and that their relatedness arises from sharing common ancestors. More recent versions of this approach look to shared genetics.

In the context of a model of urban evolution, this means making lineages themselves our units of analysis. The challenge is to develop concepts to: (a) characterize trajectories as a whole, (b) define breakpoints in trajectories that lead to branchings, that is to say, speciation events, and (c) classify particular urban genomes by their positions within trajectories. The result is methods for classifying forms of urban life phylogenetically, by their shared lineage, and not only by their common attributes.

Properties of urban trajectories. First, we can characterize some key features of trajectories in our model as a result of retention. The stability, pace, divergence, and convergence of trajectories all arise from their degrees of retention.

• Stability/volatility: where retention is very high, a trajectory is relatively stable; where retention is low, a trajectory is volatile
• Pace: where retention is high but changes by a small amount at every time step, a trajectory exhibits a gradual pace; where retention drops suddenly at a given point in time, a trajectory exhibits a sudden pace.
• Divergence: where later versions differ substantially from prior versions, a form is on a divergent trajectory. Divergence can involve any number of branchings.
• Convergence: where multiple, initially different genomes become more similar over time, they exhibit convergence.

Figure 2 visualizes these features of trajectories.

We can define trajectory stability with respect to some time interval by restricting the increase in distance between temporally adjacent Us or Hs. UStable is a predicate that determines if a trajectory with respect to a spatial area c, has temporally pair-wise genomes whose differences in distance is less than 𝝰.

UStable(c, t_b, t_e, t_u, 𝝰) is True iff
∀ t₁, t₂ t_b < t₁ < t₂ < t_e, ∧ t₁ − t₂ < t_u, ∧ Fdist(UG(c, t₁), UG(c, t₂)) ≤ 𝝰

where c is the spatial area, t_b, t_e, are the start and end times of the time interval, t_u, is the maximum temporal distance between t₁ and t₂, and 𝝰 is the maximum distance between the two temporally adjacent genomes. HStable is defined similarity.

Pace, Divergence and Convergence can be defined in a similar manner.

Speciation events. Evolution is generally a gradual process, but at some point it produces genomes so different from their predecessors that they might well be considered a different type. When this happens, we can speak of speciation. As in the natural world, speciation is a continuum with many shades in between; if it has occurred, it only becomes clear after the fact [20]. This makes defining speciation difficult. At what point does the degree of similarity become small enough to warrant recognition of a new species? We define the predicate SpeciationEvent as an event that occurs when the distance between the genome UG(c₂, t′) and a preceding genome UG(c₁, t) exceeds 𝜃:

SpeciationEvent(c₂, t′): ∃c₁, t (t < t′) ∧ DPath(c₁, t, c₂, t′) ∧ Fdist(UG(c₁, t), UG(c₂, t′)) > 𝜃

An open question is what is the value of 𝜃. Is there only one value? Or are there gradations of speciation? Or are they location dependent?

Urban evolutionary taxonomy. Just as we can characterize trajectories as such, we can also characterize genomes and formemes in terms of their positions within trajectories. For example:

• Emergent: genomes that occur at later but not earlier points in a trajectory
• Extinct: genomes that occur at earlier but not later points in a trajectory
• “Sourceness”: a genome has more “sourceness” when it contributes a greater share of the formemes of later genomes
• “Sinkness”: a genome has more “sinkness” when a higher proportion of the formemes from earlier genomes converge on it.

Each of these types of formemes can be defined using the DPath predicate. Identifying trajectories and taxonomizing urban genomes in terms of their positions in larger temporal sequences is one important direction for research in urban evolution. These concepts provide guidance for that effort.

Consider Figure 3. A city can be divided into multiple spatial areas ‘C’ (See Figure 3a). This division could follow political boundaries, physical edges, or some imposed logic such as a grid (See Figure 3b). For the sake of simplicity, three ‘C’s are isolated from the larger set (See Figure 3c). The changes in these ‘C’s can be plotted in terms of the similarity or differentiation of their genomes over time. As a simple example, note how two moments of significant change in the physical form of C2 lead to changes in its genome—first, through the re-planning of the area as long blocks of single family homes, and next, through the addition of some high density housing. Yet, each ‘C’ does not develop in isolation: signaling between ‘C’s can drive urban change. Here, for example, C1 acts as a template for the first redevelopment of C2. Furthermore, each change in the ‘C’s genomes leads to convergences or divergences over time, as they become more or less similar. While the recoding of C2 by C1 yields a convergence, the later recoding of C2 leads to a divergence between them (See Figure 3d). Although signaling between different ‘C’s can lead to urban change, it need not necessarily do so. For example, even if C3 is subject to the same signaling as C2, its current genome might persist if it is highly stable or the conditions which led to change in C2 are not present. Although this set of figures relies on significant urban redevelopments of ‘C2’ to illustrate an evolutionary trajectory, it is important to keep in mind that the genome can change over time in many ways without such explicit physical evidence.

6. Discussion and Conclusions

This paper constitutes a conceptual attempt to formulate the central elements of a model of urban evolution. Inspired by a growing urban literature turning to evolutionary concepts to build a “new science of cities”, we adapt the central algorithm of “generalized Darwinism”–variation, selection, retention–for the domain of urban life. In this view, life itself is an experimental process whereby forms of life emerge, grow, spread, and pass away. We have sought to extend this experimentalist orientation to urban life, by developing a model capable of formally and precisely characterizing how variant forms of urban life emerge, survive at differential rates, and are retained. We have shown that the model provides tools for explaining a host of urban phenomena. It can be extended to cover additional topics.

This capacity to formally decompose key urbanist intuitions to their constituent elements is a critical contribution of our model. In fact, the identification of a new theoretically defined entity—the formeme—that enables this decomposition is perhaps its most profound aspect. This entity makes it possible to formulate an urban evolutionary theory at all. Indeed, without this concept it would be difficult to conceptualize how aspects of urban life vary, disseminate, are inherited, and survive at different rates. It is for this reason, we suspect, that prior efforts to develop a formal theory of urban evolution have not been able to move beyond identifying variables in systems dynamics [21] or cellular automata models in which seeds grow to maturity [22]. Just as the identification of the concept of the atom or of the gene paved the way for advances in physical and biological theory, we believe that the concept of the formeme is the crucial basis for a next wave of advances in urban theory.

More generally, the model synthesizes components from multiple urban literatures. Joining and subsuming them under the broader umbrella of single conceptual framework in our view constitutes a substantial theoretical contribution in its own right. It provides a set of conceptual tools for explaining where and why cities have the forms they do, and how these change. Nevertheless, our model is only a first step, and significant additional work is necessary to realize its potential. Indeed, a critical virtue of the model is that it projects forward a series of tasks for extending and validating it, theoretically and empirically.

In terms of theoretical extensions, many components of the model can and should be expanded and refined. For example, the notion of value can be more formally elaborated to define multiple types of resources (economic, cultural, social) and how they interact with different types of costs (activity and group), along the lines with how we refined the concept of Signals to include key notions from information theory and semiotics, such as audience, noise, clarity, and reach. Likewise, we can extend the model to define more precisely how formemes agglomerate into larger clusters that in turn become part of their selective environments, an urban variant of niche construction. This is a way to recover notions of distinct local environments with their own particular identities—the genius loci of vitalist streams of evolutionary thought [12]—on the basis of the micro-mechanisms identified in Darwinian terms. Similarly, co-evolutionary concepts can help to elaborate how symbiotic relations among formemes affect their survival rates—for example, mutual (both benefit), commensal (one benefits, neutral to the other) and parasitic (helps one hurts the other). This is a way to build out from Darwinian concepts to meet with those theories that stress “organic” metaphors of mutual constitution (Mehmood 2010), but again to set these on the micro-foundations from which they emerge without committing to any concept of cities as self-balancing, self-equilibriating organisms. Instead, from the point of view of our model, the question is about the conditions under which “cooperative” relations arise, where and why they diffuse, how they are sustained, and what would threaten to dissolve them.

Another important direction involves using our theoretical model to build computer simulations. These allow us to test propositions about how urban evolution can unfold in a controlled environment. In these models, we can define strategies in terms of the physical forms, orientations to groups and activities, and types of signals encoded throughout a hypothetical city. The simulation permits us to observe which strategies survive and spread and which die out in a complex interacting system. Moreover, extending existing work on “the evolution or cooperation” [23] allows us to examine conditions under which “selfish” formemes adopt “cooperative” strategies in which each becomes dependent on the success of the other. This approach we believe can both offer substantial insights into the conditions under which distinct type of neighborhoods form as well as methodological contributions to traditions of evolutionary simulation work on various solutions to the prisoner’s dilemma.

Just as important are efforts to develop empirical applications of our model. This can proceed on a number of fronts. The various propositions we have articulated provide clear tools for empirical studies into the conditions under which diverse spatial forms diffuse and survive at different rates. In particular, studies can seek to determine for a number of urban forms some of the threshold parameters we have defined—for instance density thresholds or saturation points at which different strategies appear. Related work can aim to identify and observe mechanisms by which formemes and genomes survive at differential rates, such as the intellectuals whose writings formulate, redefine, and spread urban formetic information to locations and the planners and architects who adopt and implement these ideas, to varying degrees of fidelity. More generally, simply identifying the most recurrent formemes across time and space, as well as their typical patterns of co-occurrence, constitutes an important empirical project that can determine what in fact are the basic constituents of urban genomes. Another direction for empirical validation of the model involves building taxonomies. Here, the goal is to identify the basic structures of long-term trajectories in terms of concepts such as paths, divergence, convergence, stability, and volatility. This in turn will yield new substantial insights that can inform how we classify cities and neighbourhoods in terms of their family resemblances and shared lineage.

We are working in many of these directions already, and periodically reporting on results at our website, https://urbangenome.utoronto.ca. Nevertheless, data without theory is blind. This paper constitutes an attempt to illuminate the way forward toward a theory of urban evolution.