Abstract
Hydraulic properties (such as soil–water characteristic curves (SWCC) and hydraulic conductivity function (HCF)) play an important role in evaluating the stability of unsaturated soil slopes. Loess soils are widely distributed in Gansu Province in China, and most of them are in unsaturated conditions due to the deep groundwater table (G.W.T). In this study, twenty-eight sets of data published in the literature were analyzed to develop the upper and lower bounds of the SWCC for loess soil in Gansu. The variation of HCF for the loess soil was estimated from the upper and lower bounds curve developed in this study. Subsequently, numerical analyses incorporating scenarios considering different SWCCs, HCFs, and rainfall conditions were conducted for investigating the effects of those factors on the rainfall-induced slope stability. The results of analyses indicate that the infiltration plays an important role in the rainfall-induced slope stability. Higher permeable soil leads to a larger infiltration amount, which, in turn, results in a lower safety factor. In addition, the effect of the hydraulic property on the rainfall-induced slope stability decreases with the increase in slope angle.
1. Introduction
Loess soils are widely distributed in northwest China, and most of them are situated in unsaturated conditions due to the deep ground water table. Numerous steep slopes are stable in nature. However, the stability of these slopes is affected by climatic conditions. Rahardjo et al. [1] indicate that rainfall is commonly considered as the major factor resulting in shallow landslides. Brand [2], Kristo et al. [3], Rahardjo et al. [4], and Rahardjo et al. [1] indicate that the infiltration of rainwater is commonly recognized as the main factor leading to rainfall-induced slope failure. The works of Crosta [5], Basile et al. [6], and Ost et al. [7] indicate that several factors such as climatic conditions, geological features, topography, vegetation, or a combination of these factors, could result in the failure of slopes under rainfall conditions. Fredlund et al. [8] indicate that the shear strength function (SSF) of unsaturated soil is a function of soil suction that is sensitive to the infiltrated rainwater. Climatic conditions are gradually changing due to global warming. From a sustainability perspective, it is good to understand the effects of factors, such as those mentioned above, on the variation of the stability of the loess soil slopes. Therefore, in this paper, a parametric study is conducted to investigate the effects of factors such as variation in soil properties (considering different soil–water characteristic curves or SWCCs, hydraulic conductivity functions or HCFs, and SSFs), geometric profile, and variation in rainfall conditions on the stability of loess soil slopes. The safety factor (Fs) for loess soil slopes with different slope angles, soil properties, and rainfall conditions were primarily computed. Subsequently, the infiltration rates near the ground surfaces of the slopes were computed. Consequently, the normalized Fs was re-produced from the computed Fs. It is observed that the Fs for the high permeable soil drops drastically during rainfall. The rate of dropping in Fs decreases with an increase in slope angle.
2. Mathematical Models for SWCC, HFC, and SSF
Various continuous mathematical models, such as Gardner [9], Brooks and Corey [10], van Genuchten [11], and Fredlund and Xing [12] have been proposed for the representation of the SWCC. Fredlund and Xing’s equation [12], as illustrated in Equation (1), is one of most popular models, widely used by geotechnical engineers. Therefore, this study adopts Fredlund and Xing’s equation [12] for the representation of the SWCC of loess soil.
where af, nf, and mf are fitting parameters, and Cr is the input parameter for the rough estimation of the residual suction. Zhai and Rahardjo [13] and Zhai et al. [14] recommend that Cr = 1500 kPa for most cases. The work from Wang et al. [15] indicates that Cr should be larger than the air-entry value (AEV) for the soil with AEV greater than 1500 kPa; θs is the saturated volume water content; ψ is soil suction; θ is the volumetric water content.
Many models have been proposed for the estimation of the HCF for the unsaturated soil. Mualem [16] categorized the models into three groups: empirical (such as Richards [17], Winds [18], and Gardner [9]), macroscopic (such as Averjanov [19] and Yuster [20]), and statistical (such as Childs and Collis-George [21] and Mualem [16]) models. Recently, Fredlund et al. [12] and Zhai and Rahardjo [22] proposed integration form and summation form for the statistical model, respectively. D.G. Fredlund and M.D. Fredlund [23] indicate that Zhai and Rahardjo’s equation [22] is workable using Microsoft Excel, which provides convenience for the engineers. Therefore, Zhai and Rahardjo’s [22] equation (Equation (2)) is adopted for predicting the HCF of the loess soil in this study.
where S(ψk) is the saturation of soil when the soil suction is equal to ψk,; S(ψi) is the saturation of soil when the soil suction is equal to ψi; k(ψk) is the permeability coefficient when the soil suction is equal to ψk; and k(ψref) is the permeability coefficient when the soil suction at the reference point is equal to ψref.
The correlation between S(ψ) and ψ is defined using Fredlund and Xing’s equation [12] in this study. Fredlund et al. [8] proposed the model for estimating the SSF for the unsaturated soil with two independent variables. Vanapalli et al. [24] and Zhai et al. [25] further improved this model. Zhai et al. [26] conducted stress analysis on the soil structure where the meniscus is created between soil particles. It is observed that meniscus results in two types of action on the soil, including isotropic compression to the soil structure and capillary bonding between soil particles. In addition, Zhai et al. [25] also indicate that hydroscopic water attached to the individual soil particle does not result in any action on the soil structure. The hydroscopic water should not be included in the estimation of the SSF for the unsaturated soil. Zhai et al. [26] indicate that the fourth term in the original Zhai et al. [25] equation has an insignificant effect on the estimated results, and this term can be ignored for most cases. As a result, the simplified equation from Zhai et al. [25], as shown in Equation (3), is adopted to estimate SSF for the loess soil in this paper.
where S is saturation; S′ is the saturation corresponding to 3100 kPa soil suction; and S(ψi) is the saturation corresponding to soil suction ψi.
3. Hydraulic Properties of the Loess
Loess soils are widely distributed in northwest China. A large number of high and steep loess slopes maintain long-term stability under natural conditions. Twenty-eight sets of SWCC data for the loess soil were collected from different sources in the published literature, and are illustrated in Table 1. Some of the index properties for the soils were not reported from the referring literature and are marked as “-“ in Table 1. Both upper and lower bounds for the determined SWCC of loess soil are estimated from the collected data based on the confidence level of 95%, as shown in Figure 1. Subsequently, the HCF were estimated from the best-fitted curve, upper and lower bounds, and shown in Figure 2.

Table 1.
Index properties of loess soil collected from the different literature.
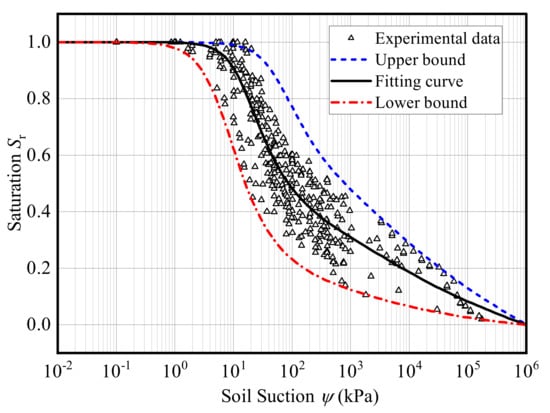
Figure 1.
Illustration of best-fitted SWCC, upper and lower bounds for the loess.
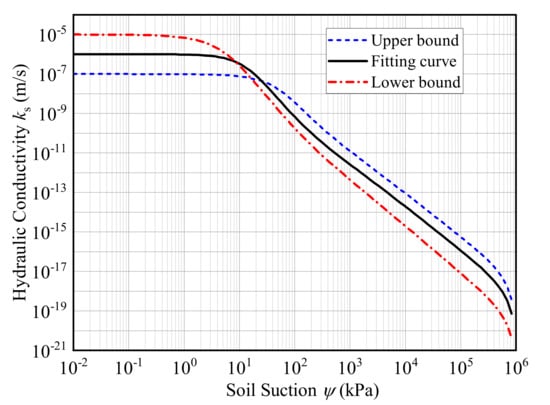
Figure 2.
Illustrated the estimated HCF from best-fitted SWCC, upper and lower bounds.
4. Evaluation of the Rainfall-Induced Slope Stability
The Seep/W is formulated based on the assumption that water flow in the soil (either saturated or unsaturated soil) follows Darcy’s law. Richard [17]’s equation, as shown in Equation (4), is commonly used to solve the problems related to the seepage in unsaturated soil.
where H is the total water head; kx and ky are the hydraulic conductivity in x and y directions, respectively; mw is the storage capacity of soil; γw is the unit weight of water; and Q is the applied boundary condition.
The seepage analyses were conducted using Seep/W, and the results from the seepage analyses were subsequently incorporated in the slope stability analyses using Slope/w. Equation (3) was adopted for estimating SSF of the loess soil from different SWCCs. The schematic diagram of the seepage model and the boundary conditions are illustrated in Figure 3. Various scenarios considering different soil properties, geometric profile, and rainfall conditions are illustrated in Table 2.
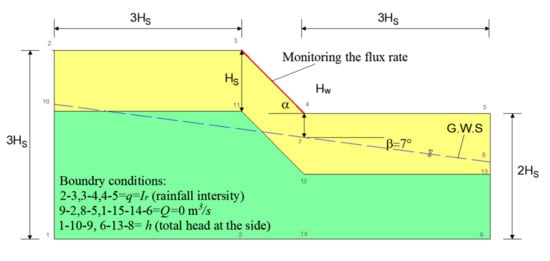
Figure 3.
Schematic diagram and the boundary conditions for the seepage model.

Table 2.
Shear strength properties of soil.
Azarafza et al. [54] reviewed discontinuous rock slope stability analysis using the limit equilibrium approaches. Chen et al. [55] conducted numerical analyses on the slope stability by considering the interaction of rainfall and earthquakes. Zhang et al. [56] conducted slope stability analyses for cracked soil under the rainfall conditions. Deliveris et al. [57] investigated the effect of the rainwater infiltration on the stability of the deep excavation. Azadi et al. [58] conducted slope stability analyses under rainfall, considering the rapid drawdown conditions. In this paper, the parametric study on the rainfall-induced slope stability was conducted by considering the variation in the hydraulic properties of soil, geometrical profile, and rainfall intensity. The pore-water pressure profile was computed from the Seep/w, and subsequently coupled into the Slope/w for the stability analysis. The Fs was computed using the Morgenstern and Price [59] method, which satisfies both force equilibrium and moment equilibrium, as illustrated in Equations (5) and (6), respectively.
where Ff is the factor of safety that satisfies the force equilibrium and Fm is the factor of safety that satisfies the moment equilibrium; c’ is the effective cohesion; φ’ is the effective internal friction angle; l is the base length of the slice; and α is the angle between the base and the horizontal line; uw is the pore-water pressure; P is the component of weight of slice that is perpendicular to the base; tan(φb) defines the rate increase in shear strength of unsaturated soil with an increase in soil suction; W is the summation of the weight of slices; x and f are the arm of force W and P with respect to the rotation point O, respectively; and R is the radius of the arc for the rotation.
Three slope heights Hs = 10 m was selected in the parametric studies. Four slope angles α (15°, 30°, 45°, and 60°) were utilized in the parametric studies. The initial depth Hw and the inclination of the groundwater table (G.W.T) at the slope toe is 4 m and 7°, respectively. Three different soil types were adopted in the parametric studies, namely S1, S2, and S3, illustrated in Table 3. Three types of rainfall intensity including Ir = 8.45 mm/h, 80 mm/h, and ks with duration of 24 h were set in the study, as shown in Table 4. A series of numerical analyses were carried out to evaluate the influence of soil properties on the coefficient of saturated permeability, and the influence of slope angle on the stability of soil slope under different rainfall conditions.

Table 3.
Fitting parameters of SWCC and saturated hydraulic conductivity.

Table 4.
Parameter design of influencing factors of slope stability under constant rainfall.
The analyzed results for scenario A are illustrated in Figure 4 for the soil type S1, in Figure 5 for the soil type S2, and in Figure 6 for the soil type S3.
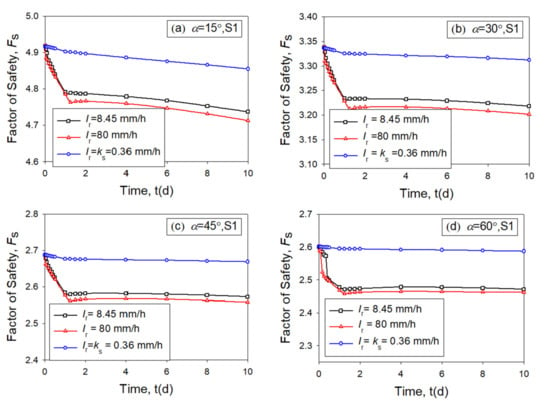
Figure 4.
Variation diagram of Fs of soil S1 for the slope with different slope angles, (a) α = 15°; (b) α = 30°; (c) α = 45°; (d) α = 60°.
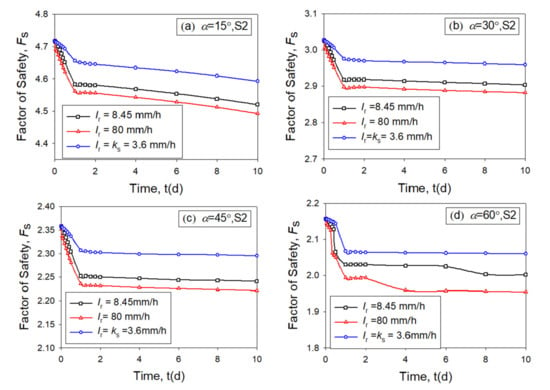
Figure 5.
Variation diagram of Fs of soil S2 for the slope with different slope angles, (a) α = 15°; (b) α = 30°; (c) α = 45°; (d) α = 60°.
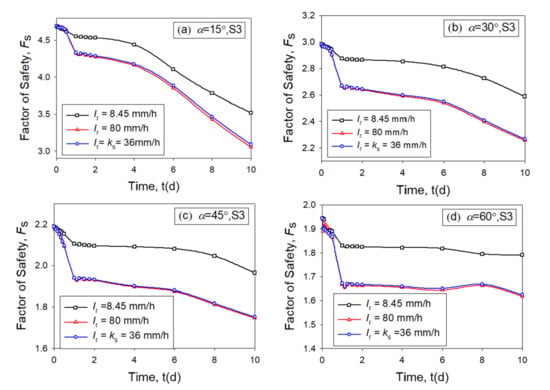
Figure 6.
Variation diagram of Fs of soil S3 for the slope with different slope angles, (a) α = 15°; (b) α = 30°; (c) α = 45°; (d) α = 60°.
Figure 4, Figure 5 and Figure 6 show that the factors of safety (Fs) drops dramatically during the rainfall period, and decreases slowly after the rainfall stops. It is different from the observation from Rahardjo et al. [60]. The authors conducted a separate analysis, and observe that when the groundwater table is near the ground surface, which is the condition reported in Rahardjo et al. [60], the Fs gradually restores after the rainfall stops. When the initial groundwater table is deep, the Fs decreases slowly after the rainfall stops. Figure 4, Figure 5, and Figure 6indicate that higher rainfall intensity results in lower Fs. It is interesting to note low Fs results from the large amount of rainwater infiltration. It is commonly believed that the saturated coefficient of permeability ks is the threshold of the infiltration rate. However, Figure 4, Figure 5, and Figure 6show that the infiltration rate can be higher than the ks. Therefore, the flux rate around the ground surface at 24 h (when rainfall stops) is monitored and shown in Figure 7.
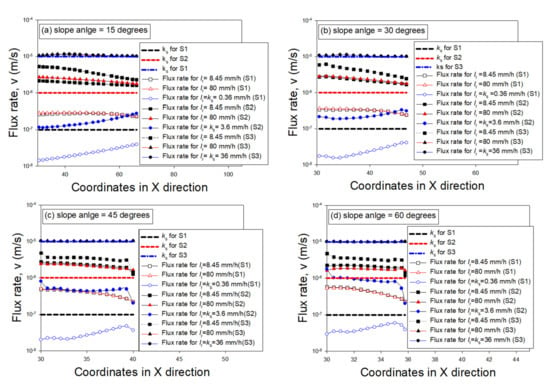
Figure 7.
The flux rate near the slope surface, (a) α = 15°; (b) α = 30°; (c) α = 45°; (d) α = 60°.
Figure 7 indicates under the same rainfall condition, higher HCF results in a higher infiltration rate. When the rainfall intensity is higher than the ks of the slope soil, the infiltration rate is higher than ks. When the rainfall intensity Ir is higher than ks, the infiltration rate on the section near the crest is larger than that near the toe. For this case, the soil near the ground surface is saturated, water drains out of soil near the toe, and results in a lower infiltration rate near the toe. When the rainfall intensity Ir is lower than ks, the infiltration rate on the section near the crest is less than that near the toe. For this case, the soil near the ground surface is still unsaturated, and the suction near the toe is lower than that near the crest. As a result, the infiltration rate on the section near the toe is larger than that near the crest for the scenario that Ir is lower than ks.
For a better comparison, the normalized Fs, which defines the ratio between the factor of safety and the maximum factor of safety at the initial state, is adopted. The results in Figure 4, Figure 5 and Figure 6 were reproduced using the normalized Fs, and illustrated in Figure 8.
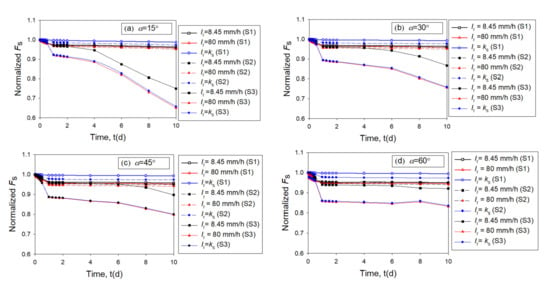
Figure 8.
The normalized Fs for different slopes under different conditions, (a) α = 15°; (b) α = 30°; (c) α = 45°; (d) α =60°.
It is observed that Fs drops 1% to 5% for the slope with different slope angles under 10 days rainfall for S1; drops 2% to 10% for the slope with different slope angles under 10 days rainfall for S2; and drops 8% to 35% for the slope with different slope angles under 10 days rainfall for S3. The magnitude of dropping in Fs for the three types of soil agrees with the infiltration rates shown in Figure 7. A higher infiltration rate results in a large dropping in Fs. Therefore, the effect of the variation in the hydraulic properties of soil (i.e., the differences between S1, S2, and S3) on the rainfall-induced slope stability is significant. Figure 8 also indicates that the magnitude of the decrease in the normalized Fs decreases with an increase in slope angle. It indicates that the significance of the effect of hydraulic properties on the rainfall-induced slope stability deceases with an increase in the slope angle.
5. Conclusions and Recommendations
The rate of infiltration into the slope soil is much dependent on the hydraulic conductivity of the soil. Higher hydraulic conductivity leads to a larger amount of infiltration (e.g., S3 > S2 > S1 in this study). It is also observed that the slope stability of the higher permeable soil is more sensitive to the rainfall than that of the lower permeable soil. The normalized Fs for S3 drops 8% to 35% under a specific rainfall condition, while those for S1 and S2 drop 1% to 5% and 2% to 10%, respectively. It is also observed that the magnitude of dropping in normalized Fs is 35% for the slope angle of 15°, while it is 18% for the slope angle of 60%. It indicates that the significance of the effect of hydraulic properties on the rainfall-induced slope stability decreases with an increase in the slope angle. As the infiltration plays an important role in the rainfall-induced slope stability, field instruments are recommended to be installed in the loess soil slopes to monitor the variation of pore-water pressure under rainfall conditions.
Author Contributions
Conceptualization, Q.Z. and Y.L.; methodology, G.T.; software, G.T.; validation, all authors; formal analysis, G.T.; investigation, S.W.; resources, S.W.; data curation, S.W.; writing—original draft preparation, Y.L., G.T., A.S., and Q.Z.; writing—review and editing, A.S. and Q.Z.; visualization, S.W.; supervision; project administration, S.W.; funding acquisition, S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China, grant number (No. 52078128), China Huaneng Group Co. Ltd. (No. HNKJ19-H17).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rahardjo, H.; Satyanaga, A.; Leong, E.C. Effects of rainfall characteristics on the stability of tropical residual soil slope. E3S Web Conf. 2016, 9, 15004. [Google Scholar] [CrossRef] [Green Version]
- Brand, E.W. Landslides in Southeast Asia, A State-of the Art Report; Proc. 4th Int. Symp. Landslides: Toronto, ON, Canada, 1984. [Google Scholar]
- Kristo, C.; Rahardjo, H.; Satyanaga, A. Effect of Hysteresis on The Stability of Residual Soil Slope. Int. Soil Water Conserv. Res. 2019, 7, 226–238. [Google Scholar] [CrossRef]
- Rahardjo, H.; Satyanaga, A.; Harnas, F.R.; Leong, E.C. Use of Dual Capillary Barrier as Cover System for a Sanitary Landfill in Singapore. Indian Geotech. J. 2016, 46, 228–238. [Google Scholar] [CrossRef]
- Crosta, G. Regionalization of rainfall thresholds: An aid to landslide hazard evaluation. Environ. Geol. 1998, 35, 131–145. [Google Scholar] [CrossRef]
- Basile, A.; Mele, G.; Terribile, F. Soil hydraulic behaviour of a selected benchmark soil involved in the landslide of Sarno 1998. Geoderma 2003, 117, 331–346. [Google Scholar] [CrossRef]
- Ost, L.; Van Den Eeckhaut, M.; Poesen, J.; Vanmaercke-Gottigny, M.C. Characteristics and spatial distribution of large landslides in the Flemish Ardennes (Belgium). Z. Für Geomorphol. 2003, 47, 329–350. [Google Scholar] [CrossRef]
- Fredlund, D.; Morgenstern, N.R.; Widger, R. The shear strength of unsaturated soils. Can. Geotech. J. 1978, 15, 313–321. [Google Scholar] [CrossRef]
- Gardner, W. Mathematics of isothermal water conduction in unsaturated soils. Highw. Res. Board Spec. Rep. 1958, 40, 78–87. [Google Scholar]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media; Colorado State University: Fort Collins, CO, USA, 1965. [Google Scholar]
- Van Genuchten, M. A close form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Amer. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Fredlund, D.; Xing, A.; Huang, S. Predicting the permeability function for unsaturated soils using the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 533–546. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H. Determination of soil–water characteristic curve variables. Comput. Geotech. 2012, 42, 37–43. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A. Effects of residual suction and residual water content on the estimation of permeability function. Geoderma 2017, 303, 165–177. [Google Scholar] [CrossRef]
- Wang, S.; Li, W.; Chen, Z.; Tian, G.; Dai, G.; Zhai, Q.; Rahardjo, H. Effect of Cr on the performance of Fredlund and Xing (1994)’s equation in best fitting soil-water characteristic curve data. Results Eng. 2022, 13, 100373. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Wind, G. A field experiment concerning capillary rise of moisture in a heavy clay soil. Neth. J. Agri-Cult. Sci. 1955, 3, 60–69. [Google Scholar] [CrossRef]
- Averjanov, S. About permeability of surface soils in case of incomplete saturation. Engl. Collect. 1950, 7, 19–21. [Google Scholar]
- Yuster, S. Theoretical considerations of multiphase flow in idealized capillary systems. In Proceedings of the 3rd World Petroleum Congress, The Hague, The Netherlands, 4–6 June 1951. [Google Scholar]
- Childs, E.C.; Collis-George, N. The permeability of porous materials. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1950, 201, 392–405. [Google Scholar]
- Zhai, Q.; Rahardjo, H. Estimation of permeability function from the soil–water characteristic curve. Eng. Geol. 2015, 199, 148–156. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Fredlund, M.D. Application of ‘estimation procedures’ in unsaturated soil mechanics. Geoscience 2020, 10, 364. [Google Scholar] [CrossRef]
- Vanapalli, S.; Fredlund, D.; Pufahl, D.; Clifton, A. Model for the prediction of shear strength with respect to soil suction. Can. Geotech. J. 1996, 33, 379–392. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A.; Dai, G. Estimation of unsaturated shear strength from soil–water character-istic curve. Acta Geotech. 2019, 14, 1977–1990. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A.; Dai, G. Estimation of tensile strength of sandy soil from soil–water charac-teristic curve. Acta Geotech. 2020, 15, 3371–3381. [Google Scholar] [CrossRef]
- Li, X.; Liu, A.; Liu, L.; Liu, Y.; WU, Y. A rapid method for determining the soil-water characteristic curves in the full suction range. Rock Soil Mech. 2021, 43, 299–306. [Google Scholar]
- Zhang, Z.; Liu, L.F.; Zhao, X.; Zhou, D. A soil water characteristic curve model considering void ratio variation with stress. J. Hydraul. Eng. 2013, 44, 578–585. [Google Scholar]
- Chen, W.; Bi, J.; Ma, Y.; Liu, W.; Jiang, Y. Fitted and predicted equations of MK model for soil-water characteristic curve and their parametric analysis. Rock Soil Mech. 2016, 37, 3208–3214. [Google Scholar]
- Jiang, Y. Study on the Relationship between Structural Properties and Unsaturated Characteristics of Loess. Ph.D Thesis, Jilin University, Changchun, China, 2020. [Google Scholar]
- Liu, P. Study on the Instability Mechanism of Unsaturated Loess Landslide. Ph.D Thesis, Changan University, Xi’an, China, 16 April 2013. [Google Scholar]
- Li, H.; Li, T.; Jiang, R.; Wang, Y.; Zhang, Y. A new method to simultaneously measure the soil-water characteristic curve and hydraulic conductivity function using filter paper. Geotech. Test. J. 2020, 43, 1541–1551. [Google Scholar] [CrossRef]
- Huang, M.; Fredlund, D.; Fredlund, M. Comparison of measured and PTF predictions of SWCCs for loess soils in China. Geotech. Geol. Eng. 2010, 28, 105–117. [Google Scholar] [CrossRef]
- Li, L.; Li, X.-A.; Wang, L.; Hong, B.; Shi, J.; Sun, J. The effects of soil shrinkage during centrifuge tests on SWCC and soil microstructure measurements. Bull. Eng. Geol. Environ. 2020, 79, 3879–3895. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, W.; Wang, G.; Sun, G.; Zhang, F. Influence of initial dry density and water content on the soil–water characteristic curve and suction stress of a reconstituted loess soil. Bull. Eng. Geol. Env. -Ment 2017, 76, 1085–1095. [Google Scholar] [CrossRef]
- Xie, X.; Li, P.; Hou, X.; Li, T.; Zhang, G. Microstructure of compacted loess and its influence on the soil-water characteristic curve. Adv. Mater. Sci. Eng. 2020. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Xiang, W.; Bi, R. Experimental study of influence of matric suction on disintegration of unsaturated remolded loess. Rock Soil Mech. 2011, 32, 3258–3262. [Google Scholar]
- Li, H.; Li, T.; Jiang, R.; Fan, J. Measurement of unsaturated permeability curve using filter paper method. Rock Soil Mech. 2020, 41, 895–904. [Google Scholar]
- Sun, S.; Chen, Z.; Zhu, Y.; Liu, Y.; Wang, L. Coordinated Ceremic Plate Extractors and Some Problems of SWCC Test. J. Logist. Eng. Univ. 2006, 22, 1–5. [Google Scholar]
- Cai, G.; Han, B.; Yang, Y.; Liu, Y.; Zhao, C. Experimental study on soil-water characteristic curves of sandy loess. Chin. J. Geotech. Eng. 2020, 42, 11–15. [Google Scholar]
- Hu, Z.; Liang, Z.; Guo, J.; Feng, Z.; Wang, K.; She, H. Prediction of permeability coefficient of unsaturated lime-improved loess. Chin. J. Geotech. Eng. 2020, 42, 26–31. [Google Scholar]
- Nie, Y.; Ni, W.; Li, X.; Wang, H.; Yuan, K.; Guo, Y.; Tuo, W. The influence of drying-wetting cycles on the suc-tion stress of compacted loess and the associated microscopic mechanism. Water 2021, 13, 1809. [Google Scholar] [CrossRef]
- Wang, H.; Ni, W.; Li, X.; Li, L.; Yuan, K.; Nie, Y. Predicting the pore size distribution curve based on the evolu-tion mechanism of soil–water characteristic curve. Environ. Earth Sci. 2022, 81, 1–10. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, A.; Ren, W.; Niu, L. Study on the soil water characteristic curve and its fitting model of Ili loess with high level of soluble salts. J. Hydrol. 2019, 578, 124067. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, Z.; Weng, X.; Xie, Y. A new soil-water characteristic curve model for unsaturated loess based on wetting-induced pore deformation. Geofluids 2019, 2019, 1672418. [Google Scholar] [CrossRef]
- Zheng, F.; Shao, S.; She, F.; Yuan, H. True triaxial shear tests of remolded loess under different matrix suctions. Rock Soil Mech. 2020, 41, 156–162. [Google Scholar]
- Fu, Y.; Liao, H.; Chai, X.; Li, Y.; Lv, L. A Hysteretic Model Considering Contact Angle Hysteresis for Fitting Soil-Water Characteristic Curves. Water Resour. Res. 2021, 57. [Google Scholar] [CrossRef]
- Xing, Y.; Li, Z.; An, P. Shear Strength Properties of Loess on South Bank of Crossing the Yellow River Project in the Middle Route of South-to-North Water Diversion Project. South North Water Transf. Water Sci. Technol. 2014, 12, 129–132. [Google Scholar]
- Jian, W.; Xu, Q.; Wu, H.; Tong, L. Study of unsaturated hydraulic parameters of Huangtupo landslide in Three Gorges reservoir area. Rock Soil Mech. 2014, 35, 3517–3522. [Google Scholar]
- Zhang, D.; Chen, C.; Yang, J.; Wang, J.; Zhang, W. Deformation and water retention behaviour of collapsible loess during wetting under lateral confinement. Chin. J. Rock Mech. Eng. 2016, 35, 604–612. [Google Scholar]
- Mu, Q.; Dang, Y.; Dong, Q.; Liao, H.; Dong, H. Water-retention characteristics and collapsibity behaviors: Com-parison between intact and compacted loesses. Chin. J. Geotech. Eng. 2019, 41, 1496–1504. [Google Scholar]
- Xing, Y.; Luo, Y.; Li, Z. The Rupture Failure Strength of Loess. J. Hydroelectr. Eng. 1999, 4, 36–44. [Google Scholar]
- Wang, Z.; Luo, Y.; Xiao, H.; Yao, Z. Experimental study on suction characteristic s of loess in Yuncheng Region. Rock Soil Mech. 2002, 23, 51–54. [Google Scholar]
- Azarafza, M.; Akgün, H.; Ghazifard, A.; Asghari-Kaljahi, E.; Rahnamarad, J.; Derakhshani, R. Discontinuous rock slope stability analysis by limit equilibrium approaches–a review. Int. J. Digit. Earth 2021, 14, 1918–1941. [Google Scholar] [CrossRef]
- Chen, C.Y.; Chen, H.W.; Wu, W.C. Numerical modeling of interactions of rainfall and earthquakes on slope stability analysis. Environ. Earth Sci. 2021, 80, 1–11. [Google Scholar] [CrossRef]
- Zhang, Z.; Fu, X.; Sheng, Q.; Du, Y.; Zhou, Y.; Huang, J. Stability of cracking deposit slope considering parameter deterioration subjected to rainfall. Int. J. Geomech. 2021, 21, 05021001. [Google Scholar] [CrossRef]
- Deliveris, A.V.; Theocharis, A.I.; Koukouzas, N.C.; Zevgolis, I.E. Numerical Slope Stability Analysis of Deep Excavations Under Rainfall Infiltration. Geotech. Geol. Eng. 2022, 40, 4023–4039. [Google Scholar] [CrossRef]
- Azadi, A.; Esmatkhah Irani, A.; Azarafza, M.; Hajialilue Bonab, M.; Sarand, F.B.; Derakhshani, R. Coupled Numerical and Analytical Stability Analysis Charts for an Earth-Fill Dam under Rapid Drawdown Conditions. Appl. Sci. 2022, 12, 4550. [Google Scholar] [CrossRef]
- Morgenstern, N.R.; Price, V.E. The analysis of the stability of general slip surfaces. Geotech. 1965, 15, 79–93. [Google Scholar]
- Rahardjo, H.; Santoso, V.A.; Leong, E.C.; Ng, Y.S.; Hua, C.J. Numerical Analyses and Monitoring Performance of Residual Soil Slopes. Soils Found. 2011, 51, 471–482. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).