Effects of Neighboring Units on the Estimation of Particle Penetration Factor in a Modeled Indoor Environment
Abstract
1. Introduction
2. Materials and Methods
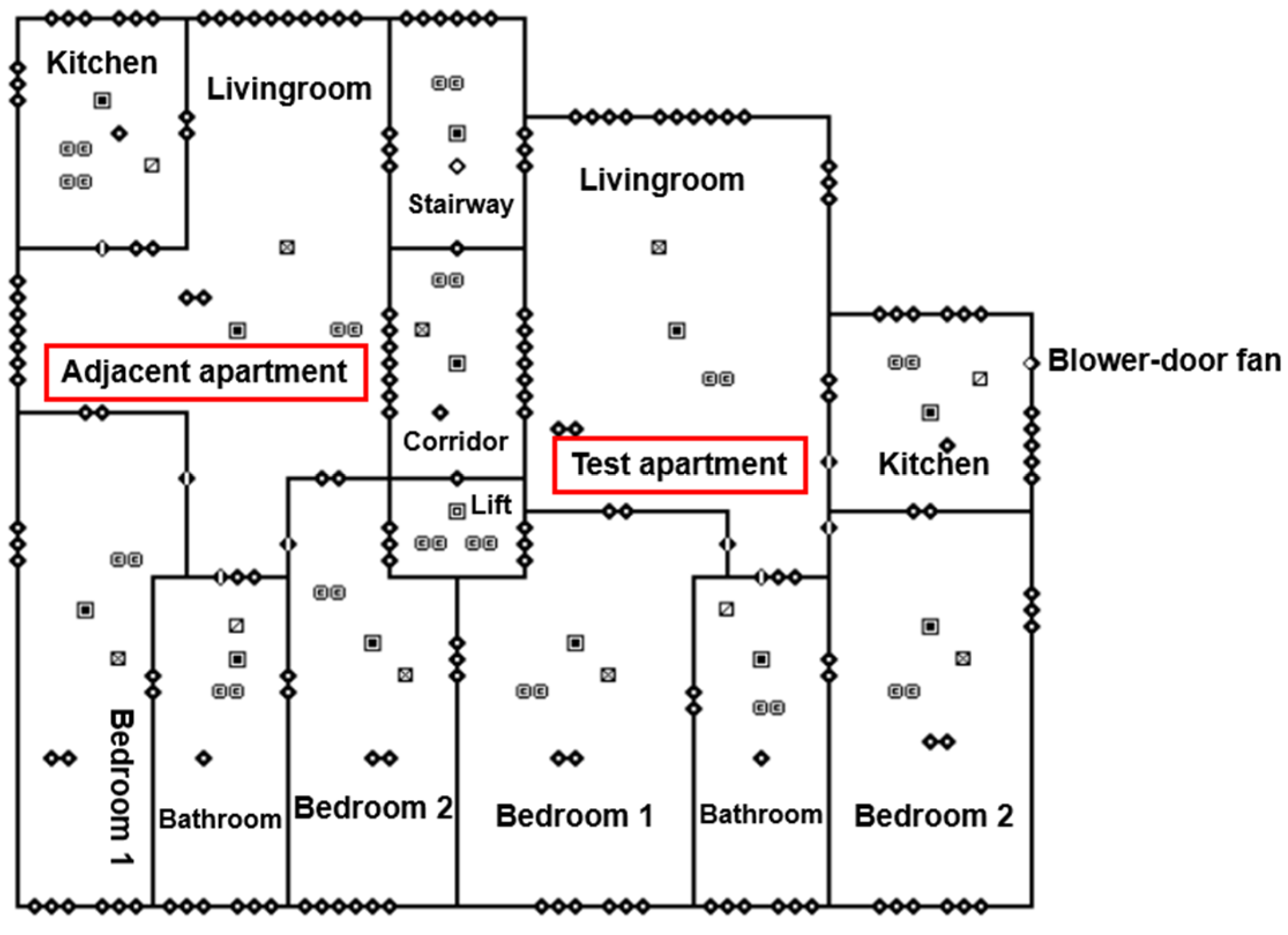
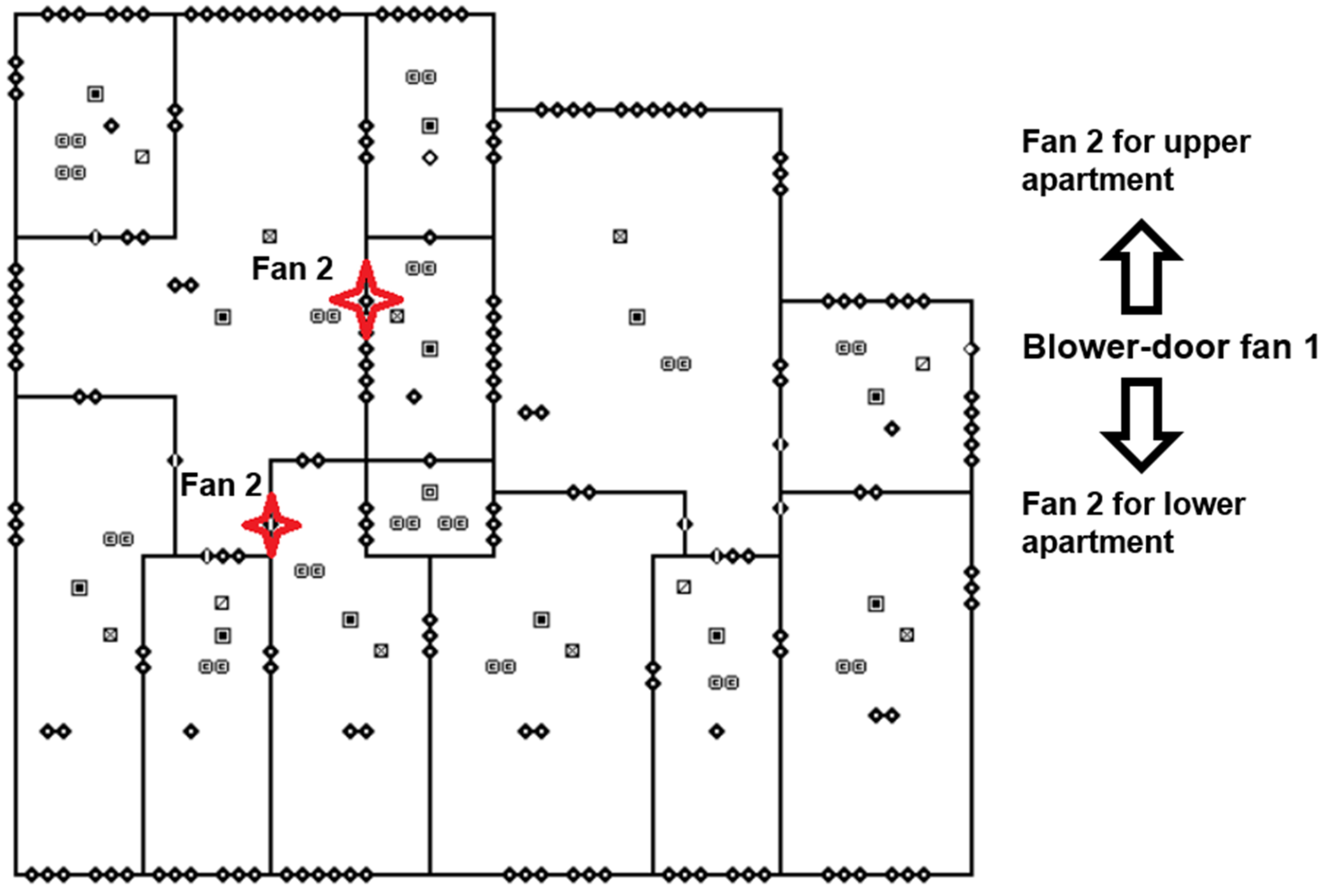
2.1. Building Description
2.2. Field Measurements
2.3. Mass Balance Model
2.4. Multi-Zone Simulation
2.5. Statistical Analysis
- (1)
- The correlation coefficient (R) ≥ 0.9;
- (2)
- The regression line between measurements and simulations should have a slope (M) between 0.75 and 1.25;
- (3)
- An intercept (b) should less than 25% of the average measured concentration;
- (4)
- The normalized mean square error (NMSE) ≤ 0.25;
- (5)
- Absolute values of normalized or fractional bias (FB) ≤ 0.25;
- (6)
- Absolute value of fractional bias based on the variance (FS) ≤ 0.50.
3. Results and Discussion
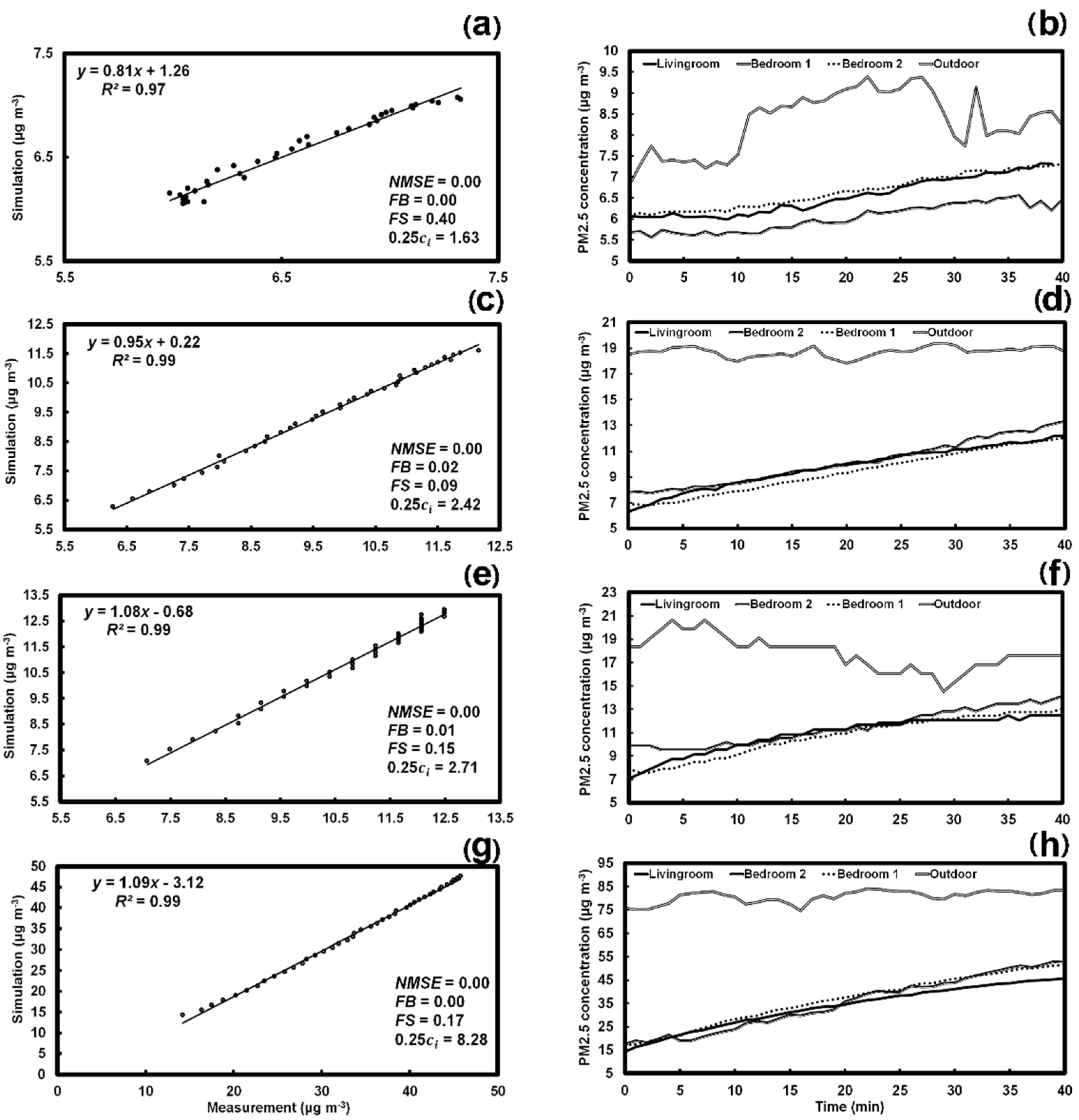
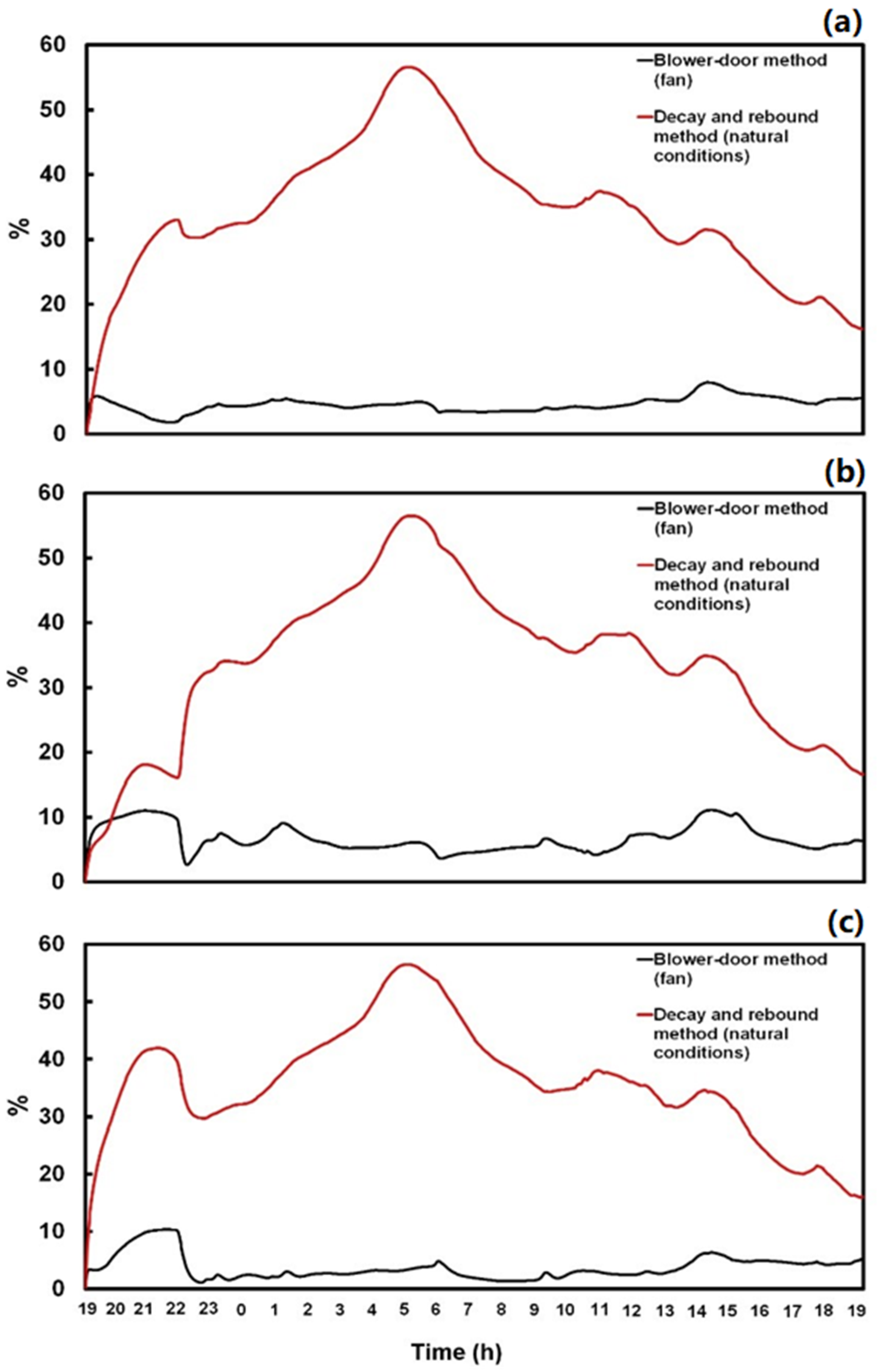
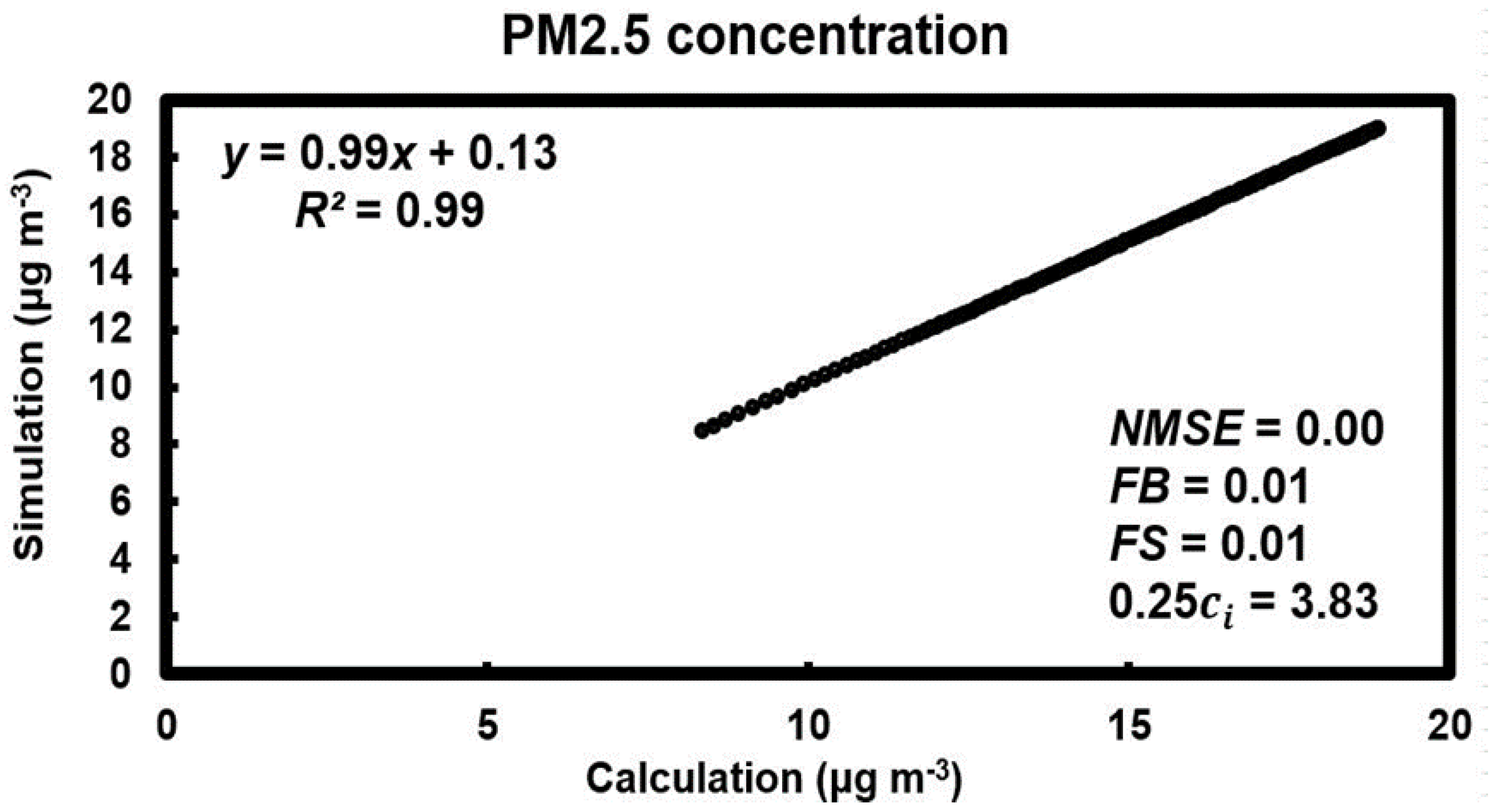
3.1. Indoor PM2.5 Concentration: Simulation and Measurements
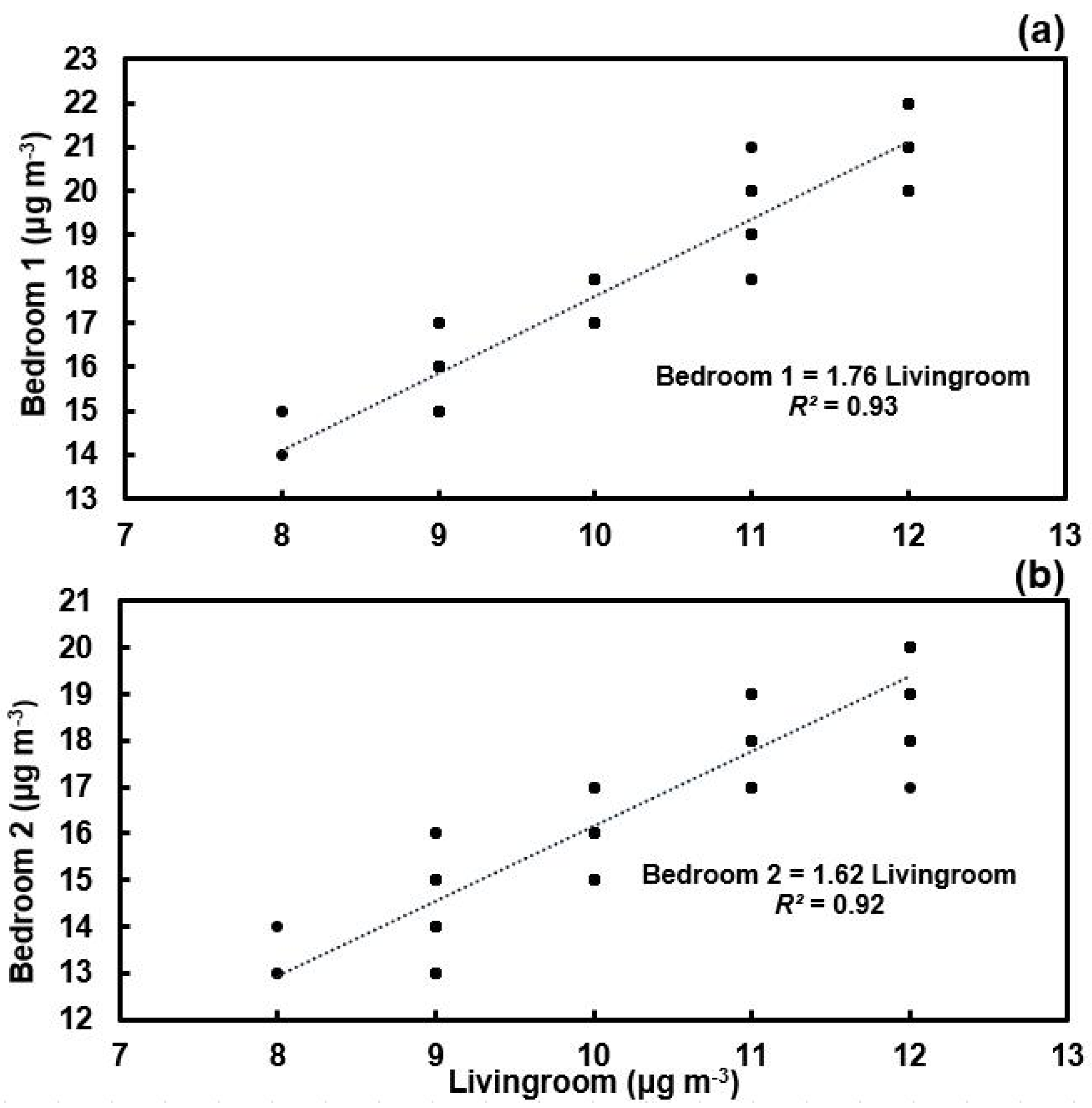
3.2. Simulating Variability
3.3. Effect of Emissions from Adjacent Apartments
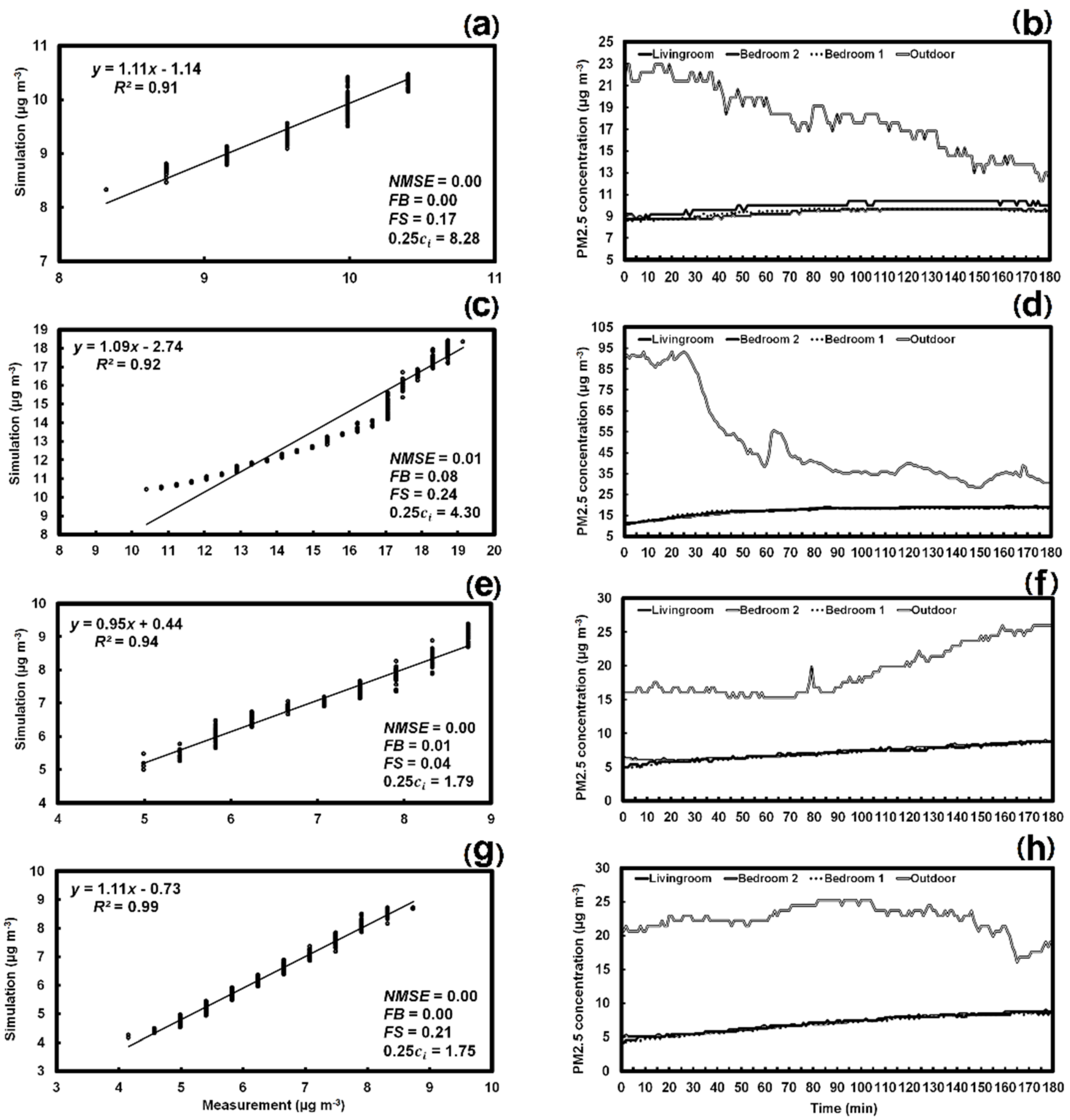
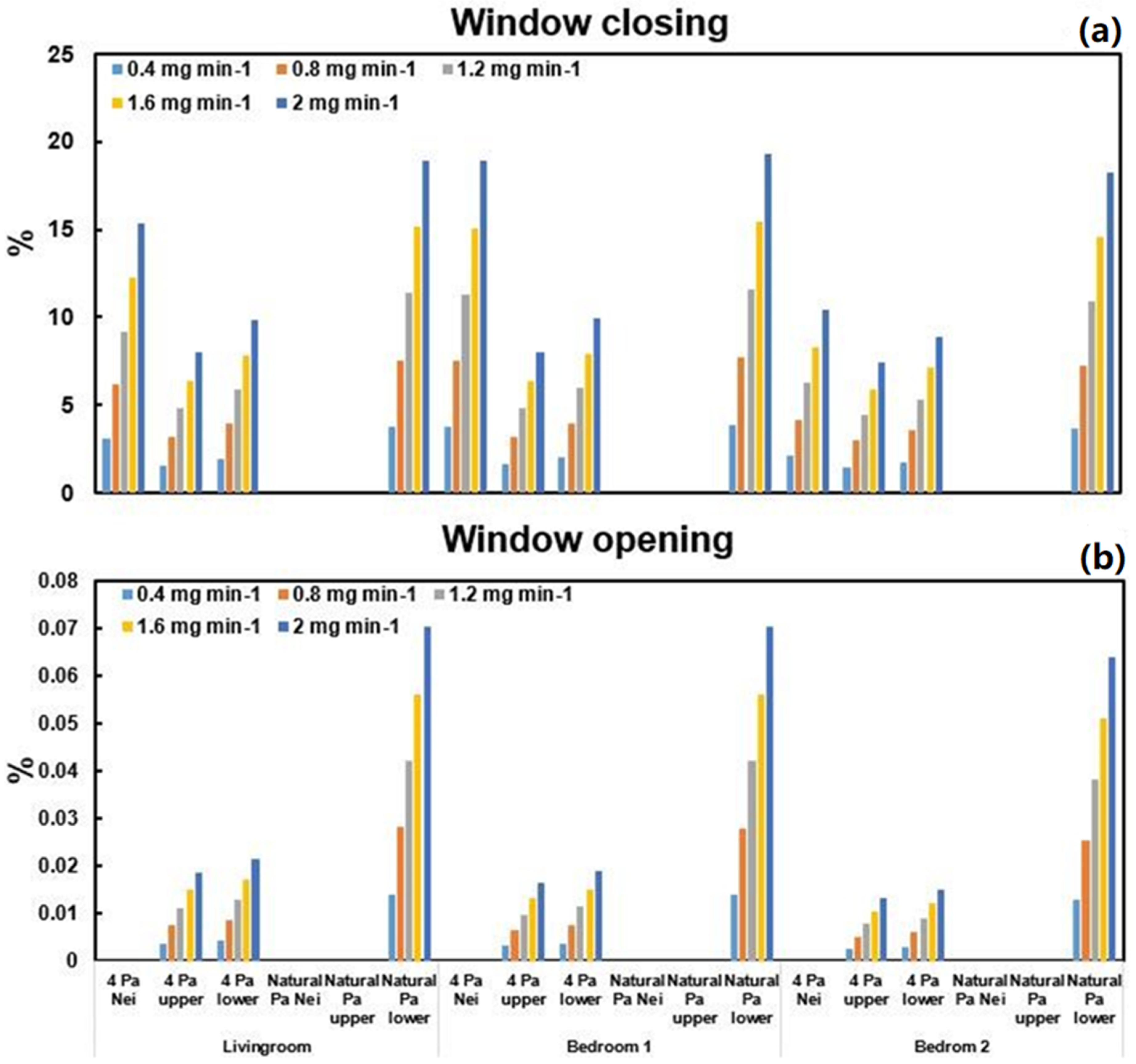
3.3.1. PM2.5 Accumulation, Error of Penetration Factor and Window Closure
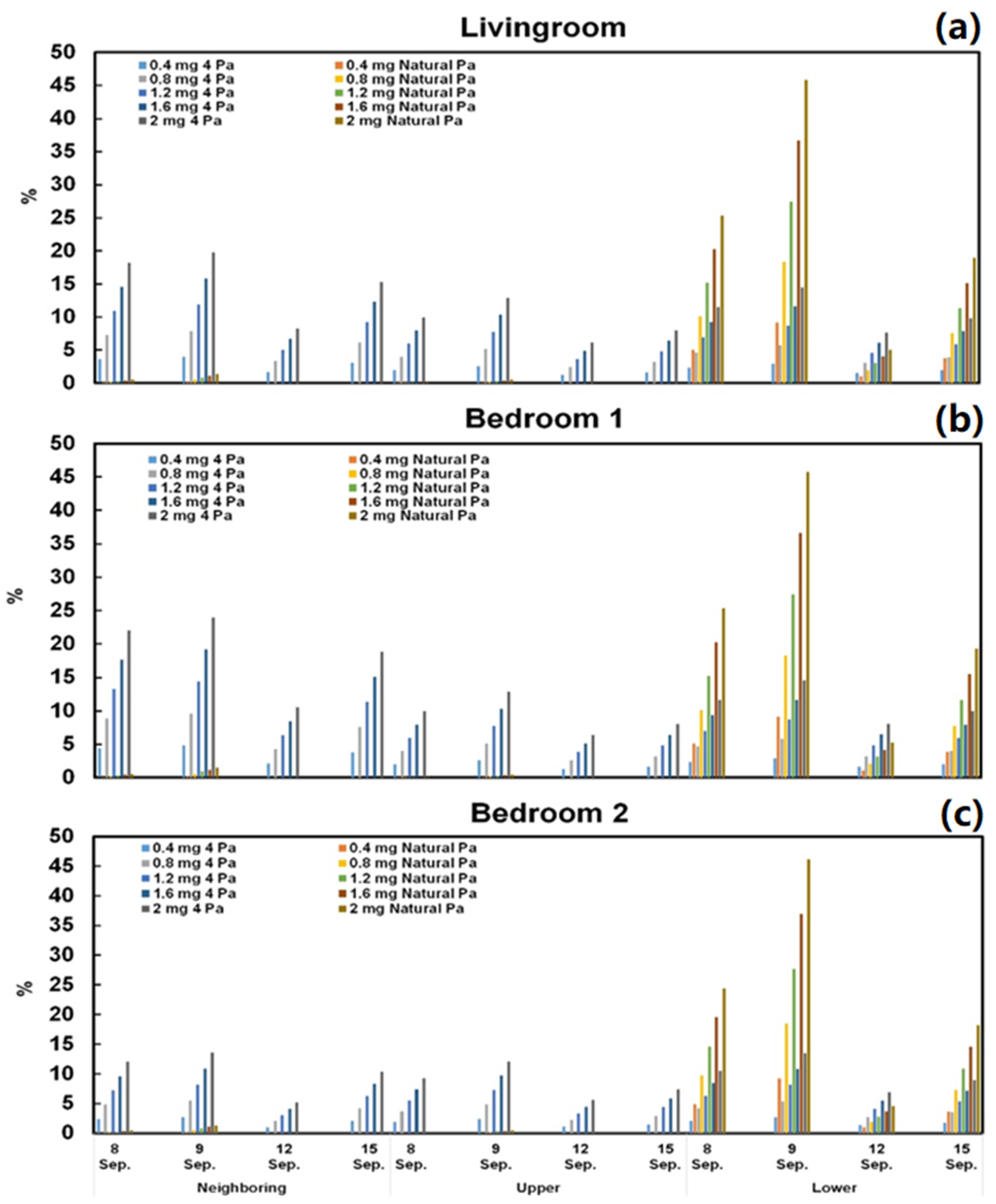
3.3.2. PM2.5 Accumulation and the Error of Penetration Factor on Different Days
3.4. A Proposed Experimental Method for Estimating the Distribution of Airflow Paths
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Klepeis, N.E.; Neilson, W.C.; Ott, W.R.; Robinson, J.P.; Tsang, A.M.; Switzer, P.; Behar, J.V.; Hern, S.C.; Englemann, W.H. The national human activity pattern survey (NHAPS): A resource for assessing exposure to environmental pollutants. J. Exp. Anal. Environ. Epidemiol. 2001, 11, 231–252. [Google Scholar] [CrossRef] [PubMed]
- Samuel, A.A.; Strachan, P. An Integrated Approach to Indoor Contaminant Modeling. HVAC&R Res. 2006, 12 (Suppl. S1), 599–619. [Google Scholar]
- ASHRAE. ASHRAE Handbook—2009 Fundamentals; ASHRAE: Atlanta, GA, USA, 2009. [Google Scholar]
- Lai, Y.; Ridley, I.A.; Brimblecombe, P. Air Change in Low and High-Rise Apartments. Urban Sci. 2020, 4, 25. [Google Scholar] [CrossRef]
- Mao, J.C.; Gao, N.P. The airborne transmission of infection between flats in high-rise residential buildings: A review. Build. Environ. 2005, 94, 516–531. [Google Scholar] [CrossRef] [PubMed]
- Yu, I.T.; Li, Y.; Wong, T.W.; Tam, W.; Chan, A.T.; Lee, J.H.; Ho, T. Evidence of airborne transmission of the severe acute respiratory syndrome virus. N. Engl. J. Med. 2004, 350, 1731–1739. [Google Scholar] [CrossRef] [PubMed]
- Yeung, K.H.; Yu, I.T.S. Possible meteorological influence on the severe acute respiratory syndrome (SARS) community outbreak at Amoy Gardens. J. Environ. Health 2007, 70, 39–46. [Google Scholar]
- Health, Welfare & Food Bureau. SARS Bulletin 28 May 2003. In Government of the Hong Kong Special Administrative Region; 2012. Available online: http://www.info.gov.hk/info/sars/bulletin/bulletin0528e.pdf (accessed on 24 December 2020).
- Liu, X.P.; Niu, J.L.; Perino, M.; Heiselberg, P. Numerical simulation of inter-flat air cross contamination under the condition of single-sided natural ventilation. J. Build. Perform. Simul. 2008, 1, 133–147. [Google Scholar] [CrossRef]
- Wu, Y.; Niu, J.L. Assessment of mechanical exhaust in preventing vertical cross-household infections associated with single-sided ventilation. Build. Environ. 2016, 105, 307–316. [Google Scholar] [CrossRef]
- Wang, J.H.; Wang, S.G.; Zhang, T.F.; Battaglia, F. Assessment of single-sided natural ventilation driven by buoyancy forces through variable window configurations. Energy Build. 2017, 139, 762–779. [Google Scholar] [CrossRef]
- Mu, D.; Gao, N.P.; Zhu, T. Wind tunnel tests of inter-flat pollutant transmission characteristics in a rectangular multi-storey residential building, part A: Effect of wind direction. Build. Environ. 2016, 108, 159–170. [Google Scholar] [CrossRef]
- Mu, D.; Gao, N.P.; Zhu, T. Wind tunnel tests of inter-flat pollutant transmission characteristics in a rectangular multi-storey residential building, part B: Effect of source location. Build. Environ. 2017, 114, 281–292. [Google Scholar] [CrossRef] [PubMed]
- Mao, J.C.; Yang, W.W.; Gao, N.P. The transport of gaseous pollutants due to stack and wind effect in high-rise residential buildings. Build. Environ. 2015, 94, 543–557. [Google Scholar] [CrossRef]
- Wang, L.; Dols, W.S.; Chen, Q. Using CFD Capabilities of CONTAM 3.0 for Simulating Airflow and Contaminant Transport in and around Buildings. HVAC&R Res. 2010, 16, 749–763. [Google Scholar]
- Argyropoulos, C.D.; Hassan, H.; Kumar, P.; Kakosimos, K.E. Measurements and modelling of particulate matter building ingress during a severe dust storm event. Build. Environ. 2020, 167, 106441. [Google Scholar] [CrossRef]
- Underhill, J.; Dols, W.S.; Lee, S.K.; Fabian, M.P.; Levy, J.I. Quantifying the impact of housing interventions on indoor air quality and energy consumption using coupled simulation models. J. Expo. Sci. Environ. Epidemiol. 2020, 30, 436–447. [Google Scholar] [CrossRef]
- Zhu, S.; Jenkins, S.; Addo, K.; Heidarinejad, M.; Romo, S.A.; Layne, A.; Ehizibolo, J.; Dalgo, D.; Mattise, N.W.; Hong, F.; et al. Ventilation and laboratory confirmed acute respiratory infection (ARI) rates in college residence halls in College Park, Maryland. Environ. Int. 2020, 137, 105537. [Google Scholar] [CrossRef]
- Lai, Y.; Brimblecombe, P.; Ridley, I.A. Estimating PM2.5 penetration factors and deposition rates in a dwelling using a combined blower-door test. In Proceedings of the Indoor Air 2018—15th International Conference of the Society of Indoor Air Quality and Climate, Philadelphia, PA, USA, 22 July–27 July 2018. Paper No. 165. [Google Scholar]
- Nabinger, S.; Persily, A. Impacts of airtightening retrofits on ventilation rates and energy consumption in a manufactured home. Energy Build. 2011, 43, 3059–3067. [Google Scholar] [CrossRef]
- Sherman, M.H.; Chan, R. Building air tightness: Research and practice. In Lawrence Berkeley National Laboratory Report No. LBNL 53356; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2004. [Google Scholar]
- Zhu, Y.; Smith, T.J.; Davis, M.E.; Levy, J.I.; Herrick, R.; Jiang, J. Comparing Gravimetric and Real-Time Sampling of PM2.5 Concentrations inside Truck Cabins. J. Occup. Environ. Hyg. 2011, 8, 662–672. [Google Scholar] [CrossRef]
- Lai, Y.; Ridley, I.A.; Brimblecombe, P. Blower-door estimates of PM2.5 deposition rates and penetration factors in an idealised room. Indoor Built Environ. 2020. [Google Scholar] [CrossRef]
- Thatcher, T.L.; Lunden, M.M.; Revzan, K.L.; Sextro, R.G.; Brown, N.J. A concentration rebound method for measuring particle penetration and deposition in the indoor environment. Aerosol Sci. Technol. 2003, 37, 847–864. [Google Scholar] [CrossRef]
- Rim, D.; Wallace, L.; Persily, A. Infiltration of outdoor ultrafine particles into a test house. Environ. Sci. Technol. 2010, 44, 5908–5913. [Google Scholar] [CrossRef] [PubMed]
- Stephens, B.; Siegel, J.A. Penetration of ambient submicron particles into single-family residences and associations with building characteristics. Indoor Air. 2012, 22, 501–513. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; Freihaut, J.D.; Bahnfleth, W.P.; Aumpansub, P.; Thran, B. Modeling Particle Dispersion under Human Activity Disturbance in a Multizone Indoor Environment. J. Architect. Eng. 2007, 13, 187. [Google Scholar] [CrossRef]
- Rim, D.; Persily, A.; Emmerich, S.; Dols, W.S.; Wallace, L. Multi-zone modeling of size-resolved outdoor ultrafine particle entry into a test house. Atmos. Environ. 2013, 69, 219–230. [Google Scholar] [CrossRef]
- Dols, W.S.; Emmerich, S.J.; Polidoro, B.J. Coupling the multizone airflow and contaminant transport software CONTAM with EnergyPlus using co-simulation. Build. Simul. 2016, 9, 469–479. [Google Scholar] [CrossRef] [PubMed]
- Dols, W.S.; Polidoro, B.J. NIST Technical Note 1887: CONTAM User Guide and Program Documentation; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015. [Google Scholar]
- Liu, F.; Gong, N.; Yan, Z.J. Opening Flow Coefficient and its Effect on Fire Smoke Flow. J. Chongqing Jianzhu Univ. 2000, 22, 86–92. [Google Scholar]
- Swami, M.V.; Chandra, S. Procedures for calculating natural ventilation airflow rates in buildings. In Work Performed for ASHRAE Research Project 448-RP; Florida Solar Energy Center: Cocoa, FL, USA, 1987. [Google Scholar]
- Ng, L.; Musser, A.; Persily, A.K.; Emmerich, S.J. Multizone airflow models for calculating infiltration rates in commercial reference buildings. Energy Build. 2013, 58, 11–18. [Google Scholar] [CrossRef]
- Abt, E.; Suh, H.H.; Catalano, P.; Koutrakis, P. Relative contribution of outdoor and indoor particle sources to indoor concentrations. Environ. Sci. Technol. 2000, 34, 3579–3587. [Google Scholar] [CrossRef]
- Wallace, L.; Emmerich, S.J.; Howard-Reed, C. Effect of central fans and in-duct filters on deposition rates of ultrafine and fine particles in an occupied townhouse. Atmos. Environ. 2004, 38, 405–413. [Google Scholar] [CrossRef]
- He, C.; Morawska, L.; Gilbert, D. Particle deposition rates in residential houses. Atmos. Environ. 2005, 39, 3891–3899. [Google Scholar] [CrossRef]
- Long, C.M.; Suh, H.H.; Catalano, P.J.; Koutrakis, P. Using time- and size-resolved particulate data to quantify indoor penetration and deposition behaviour. Environ. Sci. Technol. 2001, 35, 2089–2099. [Google Scholar] [CrossRef] [PubMed]
- ASHRAE. ASHRAE Handbook—2005 Fundamentals; ASHRAE: Atlanta, GA, USA, 2005. [Google Scholar]
- ASTM D5157-19; Standard Guide for Statistical Evaluation of Indoor Air Quality Models; ASTM International: West Conshohocken, PA, USA, 2019.
- Hu, T.; Singer, B.C.; Logue, J.M. Compilation of published PM2.5 Emission Rates for cooking, candles and incense for use in Modeling of exposures in residences. In Lawrence Berkeley National Lab (LBNL) Report No. LBNL 53356; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2012. [Google Scholar]
- Lai, A.C.K. Particle deposition indoors: A review. Indoor Air 2002, 12, 211–214. [Google Scholar] [CrossRef] [PubMed]

| Setting | Test Date | Indoor T (SDa) °C | Air Change Rate h−1 | Outdoor Conditions | |||
|---|---|---|---|---|---|---|---|
| Living Room | Bedroom 1 | Bedroom 2 | T (SD) °C | W (SD) m s−1 | |||
| Blower-door fan | 8 September 2017 | 30.36 (0.32) | 30.27 (0.27) | 30.28 (0.30) | 0.71 | 27.58 (4.46) | 1.41 (1.69) |
| 9 September 2017 | 30.69 (0.15) | 30.53 (0.15) | 30.57 (0.17) | 0.69 | 28.59 (2.00) | 1.33 (1.10) | |
| 15 September 2017 | 31.77 (0.26) | 31.60 (0.22) | 30.64 (0.13) | 0.70 | 26.94 (3.54) | 0.83 (0.72) | |
| 16 September 2017 | 32.01 (0.34) | 31.83 (0.32) | 30.79 (0.10) | 0.71 | 26.89 (2.42) | 1.32 (0.84) | |
| Natural condition | 11 September 2017 | 31.36 (0.36) | 31.19 (0.34) | 30.22 (0.27) | 0.23 | 27.79 (4.48) | 0.77 (0.88) |
| 12 September 2017 | 31.78 (0.19) | 31.65 (0.22) | 30.71 (0.16) | 0.29 | 27.50 (5.46) | 0.95 (0.81) | |
| 13 September 2017 | 31.82 (0.42) | 31.71 (0.30) | 30.90 (0.20) | 0.12 | 25.85 (5.56) | 0.49 (0.88) | |
| 15 September 2017 | 31.77 (0.26) | 31.60 (0.22) | 30.64 (0.13) | 0.25 | 26.94 (3.54) | 0.83 (0.72) | |
| Method | Test Date | Deposition Loss Rate (v) h−1 | Penetration Factor (P) |
|---|---|---|---|
| Blower-door | 8 September 2017 | 0.14 | 0.89 |
| 9 September 2017 | 0.12 | 0.86 | |
| 15 September 2017 | 0.12 | 0.91 | |
| 16 September 2017 | 0.13 | 0.90 | |
| Average (Cv) | 0.13 (8%) | 0.89 (2%) | |
| Decay-rebound | 11 September 2017 | 0.14 | 0.85 |
| 12 September 2017 | 0.01 | 0.81 | |
| 13 September 2017 | 0.18 | 0.87 | |
| 15 September 2017 | 0.14 | 0.83 | |
| Average (Cv) | 0.12 (63%) | 0.84 (3%) |
| Time | Sources Location | Neighboring Window Condition | Emission Rate (mg min−1) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.4 | 0.8 | 1.2 | 1.6 | 2.0 | Mean | Cv (%) | |||
| Three hours | Adjacent apartment | Closing | 0.86 | 1.07 | 1.28 | 1.49 | 1.70 | 1.91 | 1.39 | 28.37 |
| Opening | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0 | ||
| Upper apartment | Closing | 0.86 | 1.00 | 1.14 | 1.28 | 1.42 | 1.56 | 1.21 | 21.65 | |
| Opening | 0.89 | 0.89 | 0.89 | 0.89 | 0.89 | 0.89 | 0.89 | 0 | ||
| Lower apartment | Closing | 0.86 | 1.02 | 1.19 | 1.36 | 1.53 | 1.69 | 1.28 | 24.53 | |
| Opening | 0.89 | 0.89 | 0.89 | 0.89 | 0.89 | 0.89 | 0.89 | 0 | ||
| Mean | 0.88 | 0.96 | 1.05 | 1.14 | 1.22 | 1.31 | ||||
| Cv (%) | 2.43 | 7.98 | 16.57 | 23.88 | 30.15 | 35.52 | ||||
| 24 h | Adjacent apartment | Closing | 0.87 | 0.88 | 0.89 | 0.9 | 0.91 | 0.92 | 0.90 | 2.09 |
| Opening | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0 | ||
| Upper apartment | Closing | 0.87 | 0.87 | 0.88 | 0.88 | 0.89 | 0.89 | 0.88 | 1.02 | |
| Opening | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 | 0 | ||
| Lower apartment | Closing | 0.87 | 0.88 | 0.88 | 0.89 | 0.89 | 0.9 | 0.89 | 1.19 | |
| Opening | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 0 | ||
| Mean | 0.90 | 0.90 | 0.91 | 0.91 | 0.91 | 0.92 | ||||
| Cv (%) | 3.75 | 3.39 | 3.03 | 2.73 | 2.44 | 2.27 |
| Time | Sources Location | Emission Rate (mg min−1) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.4 | 0.8 | 1.2 | 1.6 | 2.0 | Mean | Cv (%) | |||
| Three hours | Adjacent apartment | Mean | 0.85 | 1.05 | 1.25 | 1.45 | 1.65 | 1.86 | 1.35 | 27.96 |
| Cv (%) | 2.95 | 6.94 | 9.28 | 11.42 | 12.95 | 14.01 | ||||
| Upper apartment | Mean | 0.85 | 0.99 | 1.14 | 1.29 | 1.43 | 1.58 | 1.21 | 22.62 | |
| Cv (%) | 2.95 | 3.62 | 4.21 | 4.94 | 5.01 | 5.59 | ||||
| Lower apartment | Mean | 0.85 | 1.01 | 1.18 | 1.35 | 1.52 | 1.69 | 1.27 | 24.86 | |
| Cv (%) | 2.95 | 2.84 | 3.04 | 3.22 | 3.31 | 3.43 | ||||
| 24 h | Adjacent apartment | Mean | 0.87 | 0.88 | 0.89 | 0.91 | 0.92 | 0.92 | 0.90 | 2.15 |
| Cv (%) | 1.44 | 1.43 | 1.41 | 0.64 | 0.63 | 0.54 | ||||
| Upper apartment | Mean | 0.87 | 0.88 | 0.88 | 0.89 | 0.90 | 0.90 | 0.89 | 1.20 | |
| Cv (%) | 1.44 | 1.61 | 1.43 | 1.59 | 1.07 | 1.28 | ||||
| Lower apartment | Mean | 0.87 | 0.88 | 0.89 | 0.90 | 0.90 | 0.91 | 0.89 | 1.49 | |
| Cv (%) | 1.44 | 1.43 | 1.08 | 1.44 | 1.28 | 1.27 |
| Isolated Zone | Air Change Rate Proportion (m) | Absolute Difference | Percentage (%) (100x Absolute Difference/Calculated Value) | |
|---|---|---|---|---|
| Calculated Value | Simulated Value | |||
| Horizontal adjacent apartment | 0.068 | 0.064 | 0.004 | 6 |
| Upper floor apartment | 0.065 | 0.062 | 0.003 | 5 |
| Lower floor apartment | 0.053 | 0.056 | 0.003 | 6 |
| Corridor area | 0.105 | 0.105 | 0.000 | 0 |
| Outside | 0.709 | 0.713 | 0.003 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, Y.; Ridley, I.A.; Brimblecombe, P. Effects of Neighboring Units on the Estimation of Particle Penetration Factor in a Modeled Indoor Environment. Urban Sci. 2021, 5, 2. https://doi.org/10.3390/urbansci5010002
Lai Y, Ridley IA, Brimblecombe P. Effects of Neighboring Units on the Estimation of Particle Penetration Factor in a Modeled Indoor Environment. Urban Science. 2021; 5(1):2. https://doi.org/10.3390/urbansci5010002
Chicago/Turabian StyleLai, Yonghang, Ian A. Ridley, and Peter Brimblecombe. 2021. "Effects of Neighboring Units on the Estimation of Particle Penetration Factor in a Modeled Indoor Environment" Urban Science 5, no. 1: 2. https://doi.org/10.3390/urbansci5010002
APA StyleLai, Y., Ridley, I. A., & Brimblecombe, P. (2021). Effects of Neighboring Units on the Estimation of Particle Penetration Factor in a Modeled Indoor Environment. Urban Science, 5(1), 2. https://doi.org/10.3390/urbansci5010002






