Finite Element Method for the Estimation of Insertion Loss of Noise Barriers: Comparison with Various Formulae (2D)
Abstract
:1. Introduction
1.1. Mathematical Formulation, Exact Solutions and Approximate Analytical Solutions
1.2. Formulae of Insertion Loss
1.3. FEM, Other Numerical Methods and Noise Barriers
1.4. Aims and Novelties
- Validate of the accuracy of FEM for calculation of insertion loss of noise barriers.
- Present a simple and applicable methodology for the accurate calculation of insertion loss utilizing commercial software which can be extended to various cases (e.g., predict the behavior of noise barriers with various shapes, with a profile which absorbs or disperses sound, in 3D space, etc.).
- Lay the groundwork for application of FEM for urban acoustic microscale modeling.
- To the best of our knowledge this is the first study that extensively compares insertion loss results of FEM with Kurze–Anderson, ISO 9316-2/Tatge and Menounou formulae results.
- This is the first study to present the accuracy of FEM for the calculation of insertion loss of noise barriers especially in the cases where the receiver is near the barrier or in the shadow border and when both source and receiver are near the barrier.
2. Methods
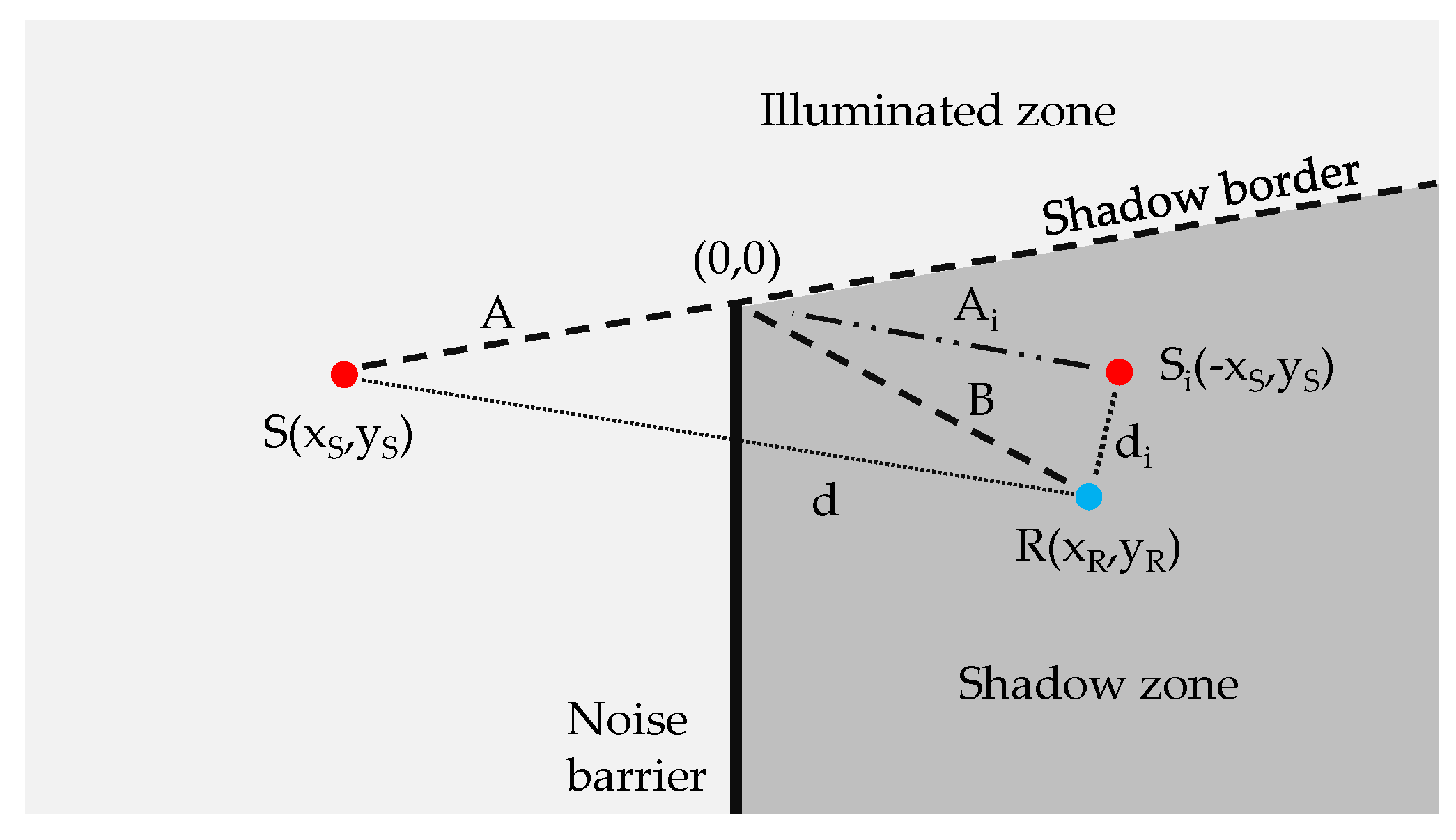
2.1. Elements Regarding Insertion Loss
2.2. Formulae for the Calculation of Insertion Loss
2.2.1. Kurze–Anderson Formula
2.2.2. ISO 9613-2/Tatge Formulae
2.2.3. Menounou Formula
2.3. FEM Setup and Methodology for the Calculation of Insertion Loss
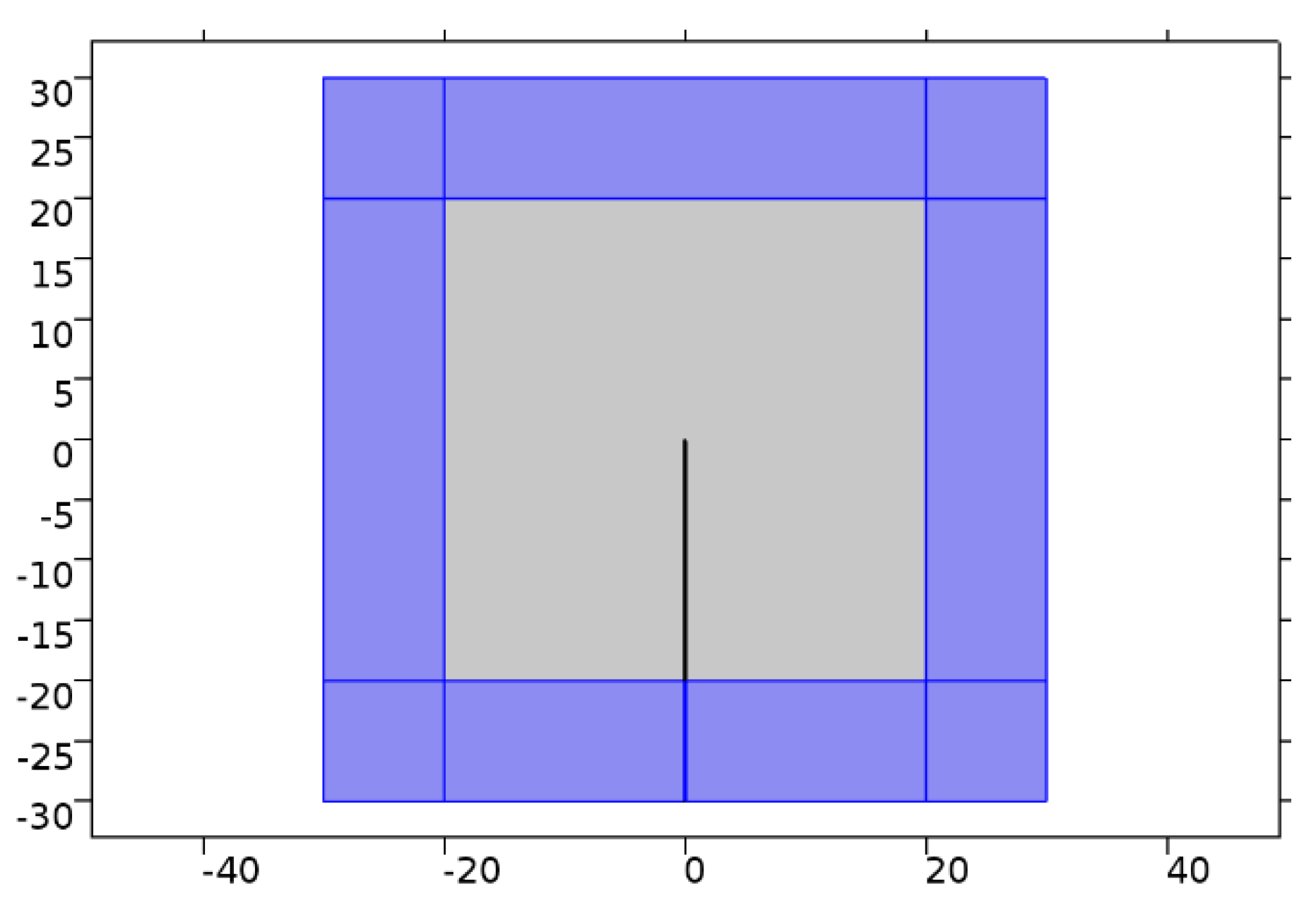
2.3.1. FEM Models
2.3.2. FEM Formulation
3. Results
3.1. Sound Pressure Levels and Acoustic Pressures of the Domain via FEM
3.2. Calculation of Insertion Loss via FEM and Various Formulae
- S1: source in medium distance from the barrier (4 m)
- S2: source in long distance from the barrier (16 m)
- S3: source in short distance from the barrier (0.2 m)
- S4: source above the barrier (6 m)
- RSZ: receiver in the shadow zone
- RSB: receiver near the shadow border
- RNB: receiver near the barrier
3.2.1. Receiver in the Shadow Zone
3.2.2. Receiver near Barrier (0.1 m)
3.2.3. Receiver in Increasing Distance from the Barrier (0.1 m–5 m)
3.2.4. Receiver near the Shadow Border (0.1 m)
3.2.5. Receiver in Increasing Distance from the Shadow Border (0.1 m–5 m)
4. Discussion
- FEM and various formulae insertion loss calculations.
- Future work and further applications of FEM for noise barriers and microscale urban acoustic modeling.
4.1. FEM and Various Formulae Insertion Loss Calculations
4.2. Future Work and Further Applications of FEM for Noise Barriers and Microscale Urban Acoustic Modeling
- Accuracy
- Availability
- Low cost
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ABC | Absorbing Boundary Condition |
| BEM | Boundary Element Method |
| CAD | Computer-Aided Design |
| FDTD | Finite-Difference Time-Domain |
| FEM | Finite Element Method |
| GPU | Graphics Processing Unit |
| IL | Insertion Loss |
| PML | Perfectly Matched Layer |
| PSTD | Pseudo-Spectral Time-Domain |
| RNB | Receiver Near the Barrier |
| RSB | Receiver in the Shadow Border (near) |
| RSZ | Receiver in the Shadow Zone |
| SPL | Sound Pressure Levels |
| WHO | World Health Organization |
Appendix A
| Receiver Area | Distance d(m) | Source Positions (x,y) | |||
|---|---|---|---|---|---|
| S1(−4.00, −4.00) | S2(−16.00, −10.00) | S3(−0.20, −5.00) | S4(−6.00, 6.00) | ||
| Receiver Positions (x,y) | |||||
| Shadow zone | RSZ1(4.00, −4.00) | RSZ2(10.00, −9.00) | RSZ3(5.00, −4.00) | RSZ4(3.00, −8.00) | |
| Shadow border (0.10 m in the shadow zone) | RSB11(4.07, 3.93) | RSB21(12.05, 7.42) | RSB31(0.50, 10.00) | RSB41(8.93, −9.07) | |
| Near barrier | RNB1(0.10, −3.00) | RNB2(0.10, −8.00) | RNB3(0.10, −5.00) | RNB4(0.10, −7.00) | |
| Varying distance d from shadow border (in the shadow zone) | 0.10 | RSB11(4.07, 3.93) | RSB21(12.05, 7.42) | RSB31(0.50, 10.00) | RSB41(8.93, −9.07) |
| 0.20 | RSB12(4.14, 3.86) | RSB22(12.11, 7.33) | RSB32(0.60, 9.99) | RSB42(8.86, −9.14) | |
| 0.30 | RSB13(4.21, 3.79) | RSB23(12.16, 7.25) | RSB33(0.70, 9.99) | RSB43(8.79, −9.21) | |
| 0.40 | RSB14(4.28, 3.71) | RSB24(12.21, 7.16) | RSB34(0.80, 9.98) | RSB44(8.72, −9.28) | |
| 0.50 | RSB15(4.35, 3.65) | RSB25(12.27, 7.08) | RSB35(0.90, 9.98) | RSB45(8.65, −9.35) | |
| 0.75 | RSB16(4.53, 3.47) | RSB26(12.40, 6.86) | RSB36(1.15, 9.97) | RSB46(8.47, −9.53) | |
| 1.00 | RSB17(4.71, 3.29) | RSB27(12.53, 6.65) | RSB37(1.40, 9.96) | RSB47(8.29, −9.71) | |
| 1.50 | RSB18(5.06, 2.94) | RSB28(12.80, 6.23) | RSB38(1.90, 9.94) | RSB48(7.94, −10.06) | |
| 2.00 | RSB19(5.41, 2.59) | RSB29(13.06, 5.80) | RSB39(2.40, 9.92) | RSB49(7.59, −10.41) | |
| 3.00 | RSB110(6.12, 1.88) | RSB210(13.59, 4.96) | RSB310(3.40, 9.88) | RSB410(6.88, −11.12) | |
| 4.00 | RSB111(6.83, 1.17) | RSB211(14.12, 4.11) | RSB311(4.40, 9.84) | RSB411(6.17, −11.83) | |
| 5.00 | RSB112(7.54, 0.46) | RSB212(14.65, 3.26) | RSB312(5.40, 9.80) | RSB412(5.46, −12.54) | |
| Varying distance d near barrier (in the shadow zone) | 0.10 | RNB11(0.10, −5.00) | RNB21(0.10, −7.00) | RNB31(0.10, −7.00) | RNB41(0.10, −12.00) |
| 0.20 | RNB12(0.20, −5.00) | RNB22(0.20, −7.00) | RNB32(0.20, −7.00) | RNB42(0.20, −12.00) | |
| 0.30 | RNB13(0.30, −5.00) | RNB23(0.30, −7.00) | RNB33(0.30, −7.00) | RNB43(0.30, −12.00) | |
| 0.40 | RNB14(0.40, −5.00) | RNB24(0.40, −7.00) | RNB34(0.40, −7.00) | RNB44(0.40, −12.00) | |
| 0.50 | RNB15(0.50, −5.00) | RNB25(0.50, −7.00) | RNB35(0.50, −7.00) | RNB45(0.50, −12.00) | |
| 0.75 | RNB16(0.75, −5.00) | RNB26(0.75, −7.00) | RNB36(0.75, −7.00) | RNB46(0.75, −12.00) | |
| 1.00 | RNB17(1.00, −5.00) | RNB27(1.00, −7.00) | RNB37(1.00, −7.00) | RNB47(1.00, −12.00) | |
| 1.50 | RNB18(1.50, −5.00) | RNB28(1.50, −7.00) | RNB38(1.50, −7.00) | RNB48(1.50, −12.00) | |
| 2.00 | RNB19(2.00, −5.00) | RNB29(2.00, −7.00) | RNB39(2.00, −7.00) | RNB49(2.00, −12.00) | |
| 3.00 | RNB110(3.00, −5.00) | RNB210(3.00, −7.00) | RNB310(3.00, −7.00) | RNB410(3.00, −12.00) | |
| 4.00 | RNB111(4.00, −5.00) | RNB211(4.00, −7.00) | RNB311(4.00, −7.00) | RNB411(4.00, −12.00) | |
| 5.00 | RNB112(5.00, −5.00) | RNB212(5.00, −7.00) | RNB312(5.00, −7.00) | RNB412(5.00, −12.00) | |
| Shadow border line equations | y = x | y = 0.625x | y = 25x | y = −x | |
| Perpendicular line equations (for varying distance from the shadow border points) | y = 8 − x | y = 26.7 − 8x/5 | y = 1252/125 –x/25 | y = −18 + x | |
| Points of intersection of the above lines (x,y) | (4.00, 4.00) | (12.00, 7.50) | (0.40, 10.00) | (9.00, −9.00) | |
References
- Kang, J. Urban Sound Environment; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Berglund, B.; Lindvall, T.; Schwela, D.H. Guidel. Community Noise; Stockholm University and Karolinska Institute: Stockholm, Sweden, 1999. [Google Scholar]
- Hothersall, D.; Crombie, D.; Chandler-Wilde, S. The performance of T-profile and associated noise barriers. Appl. Acoust. 1991, 32, 269–287. [Google Scholar] [CrossRef]
- Watts, G. Acoustic performance of a multiple edge noise barrier profile at motorway sites. Appl. Acoust. 1996, 47, 47–66. [Google Scholar] [CrossRef]
- Shima, H.; Watanabe, T.; Mizuno, K.; Iida, K.; Matsumoto, K. Noise reduction of a multiple edge noise barrier. In Proceedings of the Inter-Noise 96 (Noise control: The next 25 years), Liverpool, UK, 30 July–2 August 1996; pp. 791–794. [Google Scholar]
- Fujiwara, K.; Furuta, N. SDound shielding efficiency of a barrier with a cylinder at the edge. Noise Control Eng. J. 1991, 37, 5–11. [Google Scholar] [CrossRef]
- Alfredson, R.; Du, X. Special shapes and treatments for noise barriers. In Proceedings of the Inter-Noise 95, Newport Beach, CA, USA, 10–12 July 1995; pp. 381–384. [Google Scholar]
- Iida, K.; Kondoh, Y.; Okado, Y. Research on a device for reducing noise. Transp. Res. Rec. 1984, 983, 51–54. [Google Scholar]
- Fujiwara, K.; Ohkubo, T.; Omoto, A. A note on the noise shielding efficiency of a barrier with absorbing obstacle at the edge. In INTER-NOISE and NOISE-CON Congress and Conference Proceedings; Institute of Noise Control Engineering: San Diego, CA, USA, 1995; pp. 393–396. [Google Scholar]
- Huang, X.; Zou, H.; Qiu, X. Effects of the Top Edge Impedance on Sound Barrier Diffraction. Appl. Sci. 2020, 10, 6042. [Google Scholar] [CrossRef]
- Hutchins, D.; Jones, H.; Russell, L. Model studies of barrier performance in the presence of ground surfaces. Part II—Different shapes. J. Acoust. Soc. Am. 1984, 75, 1817–1826. [Google Scholar] [CrossRef]
- Jin, B.-J.; Kim, H.-S.; Kang, H.-J.; Kim, J.-S. Sound diffraction by a partially inclined noise barrier. Appl. Acoust. 2001, 62, 1107–1121. [Google Scholar] [CrossRef]
- Wirt, L. The control of diffracted sound by means of thnadners (shaped noise barriers). Acta Acust. United Acust. 1979, 42, 73–88. [Google Scholar]
- Watts, G.R.; Hothersall, D.; Horoshenkov, K.V. Measured and predicted acoustic performance of vertically louvred noise barriers. Appl. Acoust. 2001, 62, 1287–1311. [Google Scholar] [CrossRef]
- Slutsky, S.; Bertoni, H.L. Analysis and programs for assessment of absorptive and tilted parallel barriers. Transp. Res. Rec. 1998, 1176, 13–22. [Google Scholar]
- May, D.N.; Osman, N. Highway noise barriers: New shapes. J. Sound Vib. 1980, 71, 73–101. [Google Scholar] [CrossRef]
- Kotzen, B.; English, C. Environmental Noise Barriers: A Guide to Their Acoustic and Visual Design; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Martínez-Sala, R.; Sancho, J.; Sánchez, J.V.; Gómez, V.; Llinares, J.; Meseguer, F. Sound attenuation by sculpture. Nature 1995, 378, 241. [Google Scholar] [CrossRef]
- Guo, J.; Pan, J. Increasing the insertion loss of noise barriers using an active-control system. J. Acoust. Soc. Am. 1998, 104, 3408–3416. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, X.; Zhang, T.; Bano, S.; Pan, H.; Qi, L.; Zhang, Z.; Yuan, Y. A renewable low-frequency acoustic energy harvesting noise barrier for high-speed railways using a Helmholtz resonator and a PVDF film. Appl. Energy 2018, 230, 52–61. [Google Scholar] [CrossRef]
- Voropayev, S.I.; Ovenden, N.C.; Fernando, H.J.; Donovan, P.R. Finding optimal geometries for noise barrier tops using scaled experiments. J. Acoust. Soc. Am. 2017, 141, 722–736. [Google Scholar] [CrossRef] [Green Version]
- Baulac, M.; Defrance, J.; Jean, P. Optimisation with genetic algorithm of the acoustic performance of T-shaped noise barriers with a reactive top surface. Appl. Acoust. 2008, 69, 332–342. [Google Scholar] [CrossRef]
- Zhao, W.; Chen, L.; Zheng, C.; Liu, C.; Chen, H. Design of absorbing material distribution for sound barrier using topology optimization. Struct. Multidiscip. Optim. 2017, 56, 315–329. [Google Scholar] [CrossRef]
- Kook, J.; Koo, K.; Hyun, J.; Jensen, J.S.; Wang, S. Acoustical topology optimization for Zwicker’s loudness model–Application to noise barriers. Comput. Methods Appl. Mech. Eng. 2012, 237, 130–151. [Google Scholar] [CrossRef]
- Zannin, P.H.T.; Do Nascimento, E.O.; Da Paz, E.C.; Do Valle, F. Application of artificial neural networks for noise barrier optimization. Environments 2018, 5, 135. [Google Scholar] [CrossRef] [Green Version]
- Ekici, I.; Bougdah, H. A review of research on environmental noise barriers. Build. Acoust. 2003, 10, 289–323. [Google Scholar] [CrossRef]
- Lau, S.; Tang, S. Performance of a noise barrier within an enclosed space. Appl. Acoust. 2009, 70, 50–57. [Google Scholar] [CrossRef]
- Wang, C.; Bradley, J. A mathematical model for a single screen barrier in open-plan offices. Appl. Acoust. 2002, 63, 849–866. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Zou, H.; Qiu, X. A preliminary study on the performance of indoor active noise barriers based on 2D simulations. Build. Environ. 2015, 94, 891–899. [Google Scholar] [CrossRef] [Green Version]
- ISO 9613-2:1996. Acoustics—Attenuation of Sound during Propagation Outdoors—Part 2: General Method of Calculation; International Organization for Standardization (ISO): Geneva, Switzerland, 1996. [Google Scholar]
- Maffei, L.; Masullo, M.; Aletta, F.; Di Gabriele, M. The influence of visual characteristics of barriers on railway noise perception. Sci. Total Environ. 2013, 445, 41–47. [Google Scholar] [CrossRef] [PubMed]
- Joynt, J.L.; Kang, J. The influence of preconceptions on perceived sound reduction by environmental noise barriers. Sci. Total Environ. 2010, 408, 4368–4375. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sommerfeld, A. Mathematische Theorie der Diffraction. Math. Ann. 1896, 47, 317–374. [Google Scholar] [CrossRef]
- Macdonald, H. A class of diffraction problems. Proc. Lond. Math. Soc. 1915, 2, 410–427. [Google Scholar] [CrossRef] [Green Version]
- Bowman, J.J.; Senior, T.B.A.; Uslenghi, P.L.E. Electromagnetic and Acoustic Scattering by Simple Shapes; Wiley-Interscience: New York, NY, USA, 1969; Volume 154, pp. 1085–1090. [Google Scholar]
- Hadden, W.J., Jr.; Pierce, A.D. Sound diffraction around screens and wedges for arbitrary point source locations. J. Acoust. Soc. Am. 1981, 69, 1266–1276. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Rubinowicz, A.; Skudrzyk, E. The Foundations of Acoustics; Springer: New York, NY, USA, 1971. [Google Scholar]
- Embleton, T.F. Line integral theory of barrier attenuation in the presence of the ground. J. Acoust. Soc. Am. 1980, 67, 42–45. [Google Scholar] [CrossRef]
- Li, K.; Wong, H. A review of commonly used analytical and empirical formulae for predicting sound diffracted by a thin screen. Appl. Acoust. 2005, 66, 45–76. [Google Scholar] [CrossRef]
- Redfearn, S. XX. Some acoustical source-observer problems. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1940, 30, 223–236. [Google Scholar] [CrossRef]
- Maekawa, Z. Noise reduction by screens. Appl. Acoust. 1968, 1, 157–173. [Google Scholar] [CrossRef]
- Rathe, E. Note on two common problems of sound propagation. J. Sound Vib. 1969, 10, 472–479. [Google Scholar] [CrossRef]
- Kurze, U.; Anderson, G. Sound attenuation by barriers. Appl. Acoust. 1971, 4, 35–53. [Google Scholar] [CrossRef]
- Kurze, U.J. Noise reduction by barriers. J. Acoust. Soc. Am. 1974, 55, 504–518. [Google Scholar] [CrossRef]
- Tatge, R. Barrier-wall attenuation with a finite-sized source. J. Acoust. Soc. Am. 1973, 53, 1317–1319. [Google Scholar] [CrossRef]
- Menounou, P. A correction to Maekawa’s curve for the insertion loss behind barriers. J. Acoust. Soc. Am. 2001, 110, 1828–1838. [Google Scholar] [CrossRef]
- Kawai, T.; Fujimoto, K.; Itow, T. Noise propagation around a thin half-plane. Acta Acust. United Acust. 1977, 38, 313–323. [Google Scholar]
- Hu, Z.; Wong, R.L. Barrier insertion loss versus Fresnel number and secondary parameters. NCE 1983, 20, 31–36. [Google Scholar] [CrossRef]
- Reiter, P.; Wehr, R.; Ziegelwanger, H. Simulation and measurement of noise barrier sound-reflection properties. Appl. Acoust. 2017, 123, 133–142. [Google Scholar] [CrossRef]
- Morandi, F.; Miniaci, M.; Marzani, A.; Barbaresi, L.; Garai, M. Standardised acoustic characterisation of sonic crystals noise barriers: Sound insulation and reflection properties. Appl. Acoust. 2016, 114, 294–306. [Google Scholar] [CrossRef]
- Krynkin, A.; Umnova, O.; Chong, A.; Taherzadeh, S.; Attenborough, K. Sonic crystal noise barriers made of resonant elements. In Proceedings of the 20th International Congress on Acoustics (ICA), Sydney, Australia, 23–27 August 2010. [Google Scholar]
- Fredianelli, L.; Del Pizzo, A.; Licitra, G. Recent developments in sonic crystals as barriers for road traffic noise mitigation. Environments 2019, 6, 14. [Google Scholar] [CrossRef] [Green Version]
- Sigmund, O.; Schevenels, M.; Lazarov, B.S.; Lombaert, G. Topology optimization of two-dimensional elastic wave barriers. J. Sound Vib. 2016, 376, 95–111. [Google Scholar]
- Schevenels, M.; Lombaert, G. Topology Optimization of Elastic Wave Barriers Using a Two-and-A-Half Dimensional Finite Element Methodology. In Proceedings of the World Congress of Structural and Multidisciplinary Optimisation, Braunschweig, Germany, 5–9 June 2017; pp. 1906–1922. [Google Scholar]
- Daee, B.; El Naggar, H. 3D finite element analysis of composite noise barrier constructed of polyurethane products. Front. Struct. Civ. Eng. 2017, 11, 100–110. [Google Scholar] [CrossRef]
- Papadakis, N.M.; Stavroulakis, G.E. Estimation Of Insertion Loss of Sound Barriers via Finite Element Method. In Proceedings of the 9th GRACM International Congress on Computational Mechanics, Chania, Greece, 4–6 June 2018. [Google Scholar]
- Ishizuka, T.; Fujiwara, K. Performance of noise barriers with various edge shapes and acoustical conditions. Appl. Acoust. 2004, 65, 125–141. [Google Scholar] [CrossRef]
- Egan, C.; Chilekwa, V.; Oldham, D. An investigation of the use of the top edge treatments to enhance the performance of a noise barrier using boundary element method. In Proceedings of the 13th International Congress on Sound and Vibration, Vienna, Austria, 2–6 July 2006. [Google Scholar]
- Forssén, J.; Mauriz, L.E.; Torehammar, C.; Jean, P.; Axelsson, Ö. Performance of a Low-Height Acoustic Screen for Urban Roads: Field Measurement and Numerical Study. Acta Acust. United Acust. 2019, 105, 1026–1034. [Google Scholar] [CrossRef]
- Baulac, M.; Defrance, J.; Jean, P.; Minard, F. Efficiency of noise protections in urban areas: Predictions and scale model measurements. Acta Acust. United Acust. 2006, 92, 530–539. [Google Scholar]
- Fard, S.; Peters, H.; Marburg, S.; Kessissoglou, N. Acoustic performance of a barrier embedded with Helmholtz resonators using a quasi-periodic boundary element technique. Acta Acust. United Acust. 2017, 103, 444–450. [Google Scholar] [CrossRef]
- Oldham, D.J.; Egan, C.A. A parametric investigation of the performance of multiple edge highway noise barriers and proposals for design guidance. Appl. Acoust. 2015, 96, 139–152. [Google Scholar] [CrossRef]
- Li, Q.; Duhamel, D.; Luo, Y.; Yin, H. Analysing the acoustic performance of a nearly-enclosed noise barrier using scale model experiments and a 2.5-D BEM approach. Appl. Acoust. 2020, 158, 107079. [Google Scholar] [CrossRef]
- Koussa, F.; Defrance, J.; Jean, P.; Blanc-Benon, P. Acoustic performance of gabions noise barriers: Numerical and experimental approaches. Appl. Acoust. 2013, 74, 189–197. [Google Scholar] [CrossRef]
- Greiner, D.; Aznárez, J.J.; Maeso, O.; Winter, G. Single-and multi-objective shape design of Y-noise barriers using evolutionary computation and boundary elements. Adv. Eng. Softw. 2010, 41, 368–378. [Google Scholar] [CrossRef]
- Grubeša, S.; Jambrošić, K.; Domitrović, H. Noise barriers with varying cross-section optimized by genetic algorithms. Appl. Acoust. 2012, 73, 1129–1137. [Google Scholar] [CrossRef]
- Toledo, R.; Aznárez, J.; Maeso, O.; Greiner, D. Optimization of thin noise barrier designs using Evolutionary Algorithms and a Dual BEM Formulation. J. Sound Vib. 2015, 334, 219–238. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Chen, L.; Zhao, W.; Chen, H. Shape optimization of sound barrier using an isogeometric fast multipole boundary element method in two dimensions. Eng. Anal. Bound. Elem. 2017, 85, 142–157. [Google Scholar] [CrossRef]
- Sakamoto, S.; Seimiya, T.; Tachibana, H. Visualization of sound reflection and diffraction using finite difference time domain method. Acoust. Sci. Technol. 2002, 23, 34–39. [Google Scholar] [CrossRef] [Green Version]
- Yokota, T.; Hirao, Y.; Yamamoto, K. Efficient calculation on outdoor sound propagation by FDTD and PE methods. Acoust. Sci. Technol. 2006, 27, 177–179. [Google Scholar] [CrossRef] [Green Version]
- Van Renterghem, T.; Botteldooren, D. Numerical simulation of the effect of trees on downwind noise barrier performance. Acta Acust. United Acust. 2003, 89, 764–778. [Google Scholar]
- Heimann, D. On the efficiency of noise barriers near sloped terrain–a numerical study. Acta Acust. United Acust. 2010, 96, 1003–1011. [Google Scholar] [CrossRef]
- Hornikx, M.; Forssén, J. Modelling of sound propagation to three-dimensional urban courtyards using the extended Fourier PSTD method. Appl. Acoust. 2011, 72, 665–676. [Google Scholar] [CrossRef]
- Van Renterghem, T.; Hornikx, M.; Smyrnova, Y.; Jean, P.; Kang, J.; Botteldooren, D.; Defrance, J. Road traffic noise reduction by vegetated low noise barriers in urban streets. In Proceedings of the 9th European Conference on Noise Control (Euronoise 2012), Prague, Czech Republic, 10–13 June 2012. [Google Scholar]
- Okuzono, T.; Otsuru, T.; Tomiku, R.; Okamoto, N. Fundamental accuracy of time domain finite element method for sound-field analysis of rooms. Appl. Acoust. 2010, 71, 940–946. [Google Scholar] [CrossRef] [Green Version]
- Papadakis, N.; Stavroulakis, G.E. Time domain finite element method for the calculation of impulse response of enclosed spaces. Room acoustics application. In Proceedings of the Mechanics of Hearing: Protein to Perception: 12th International Workshop on the Mechanics of Hearing, Cape Sounio, Greece, 23–29 June 2015; AIP Publishing LLC: Melville, NY, USA, 2015; p. 100002. [Google Scholar]
- Harari, I.; Hughes, T.J. A cost comparison of boundary element and finite element methods for problems of time-harmonic acoustics. Comput. Methods Appl. Mech. Eng. 1992, 97, 77–102. [Google Scholar] [CrossRef]
- Bolejko, R.; Dobrucki, A. FEM amd BEM computing costs for acoustical problems. Arch. Acoust. 2006, 31, 193–212. [Google Scholar]
- Möser, M. Engineering Acoustics: An Introduction to Noise Control; Springer Science & Business Media: Berlin, Germany, 2009; p. 184. [Google Scholar]
- Ihlenburg, F. Finite Element Analysis of Acoustic Scattering; Springer Science & Business Media: Berlin, Germany, 2006; Volume 132. [Google Scholar]
- Papadakis, N.M.; Stavroulakis, G.E. Effect of Mesh Size for Modeling Impulse Responses of Acoustic Spaces via Finite Element Method in the Time Domain. In Proceedings of the Euronoise 2018 Heraclion, Crete, Greece, 27–31 May 2018. [Google Scholar]
- Delaunay, B. Sur la sphere vide. Izv. Akad. Nauk SSSR Otd. Mat. Estestv. Nauk 1934, 7, 1–2. [Google Scholar]
- Sommerfeld, A. Die Greensche Funktion der Schwingungsgleichung. J. Ber. Dtsch. Math. Ver. 1912, 21, 309–353. [Google Scholar]
- Thompson, L.L. A review of finite-element methods for time-harmonic acoustics. J. Acoust. Soc. Am. 2006, 119, 1315–1330. [Google Scholar] [CrossRef] [Green Version]
- Shirron, J.J.; Babuška, I. A comparison of approximate boundary conditions and infinite element methods for exterior Helmholtz problems. Comput. Methods Appl. Mech. Eng. 1998, 164, 121–139. [Google Scholar] [CrossRef]
- Berenger, J.-P. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Liu, Q.-H.; Tao, J. The perfectly matched layer for acoustic waves in absorptive media. J. Acoust. Soc. Am. 1997, 102, 2072–2082. [Google Scholar] [CrossRef]
- Zampolli, M.; Malm, N.; Tesei, A. Improved perfectly matched layers for acoustic radiation and scattering problems. In Proceedings of the 2008 COMSOL Conference, Hannover, Germany, 4–6 November 2008. [Google Scholar]
- Papadakis, N.M. Application of Finite Element Method for Estimation of Acoustic Parameters. Ph.D. Thesis, Technical Univeristy of Crete, Chania, Greece, 2018. Available online: https://www.didaktorika.gr/eadd/handle/10442/42505 (accessed on 18 December 2020).
- Bermúdez, A.; Hervella-Nieto, L.; Prieto, A.; Rodrı, R. An optimal perfectly matched layer with unbounded absorbing function for time-harmonic acoustic scattering problems. J. Comput. Phys. 2007, 223, 469–488. [Google Scholar] [CrossRef]
- Marburg, S.; Nolte, B. Computational Acoustics of Noise Propagation in Fluids: Finite and Boundary Element Methods; Springer: Berlin/Heidelberg, Germany, 2008; Volume 578. [Google Scholar]
- Arenas, J.P. Potential problems with environmental sound barriers when used in mitigating surface transportation noise. Sci. Total Environ. 2008, 405, 173–179. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Kang, J. Combined acoustical and visual performance of noise barriers in mitigating the environmental impact of motorways. Sci. Total Environ. 2016, 543, 52–60. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, J. Urban Acoustics. Appl. Acoust. 2005, 66, 121–243. [Google Scholar] [CrossRef]
- FEniCS FEM Software Documentation. Available online: https://fenicsproject.org/documentation/ (accessed on 23 June 2020).
- Chango, J.F.; Navarro, C.A.; González-Montenegro, M.A. GPU-accelerated rectangular decomposition for sound propagation modeling in 2D. In Proceedings of the 2019 38th International Conference of the Chilean Computer Science Society (SCCC), Concepcion, Chile, 4–9 November 2019; pp. 1–7. [Google Scholar]
- Mehra, R.; Raghuvanshi, N.; Savioja, L.; Lin, M.C.; Manocha, D. An efficient GPU-based time domain solver for the acoustic wave equation. Appl. Acoust. 2012, 73, 83–94. [Google Scholar] [CrossRef] [Green Version]
- Papadakis, N.; Stavroulakis, G.E. Validation of Time Domain Finite Element method via calculations of acoustic parameters in a reverberant space. In Proceedings of the 10th HSTAM International Congress on Mechanics, Chania, Greece, 25–27 May 2013. [Google Scholar]
- Attenborough, K.; Bashir, I.; Taherzadeh, S. Outdoor ground impedance models. J. Acoust. Soc. Am. 2011, 129, 2806–2819. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yudin, M. Comparison of FDM and FEM models for a 2D gravity current in the atmosphere over a valley. Bull. Novos. Comput. Cent. 2012, 13, 95–101. [Google Scholar]
- Nomura, T.; Takagi, K.; Sato, S. Finite element simulation of sound propagation concerning meteorological conditions. Int. J. Numer. Methods Fluids 2010, 64, 1296–1318. [Google Scholar] [CrossRef]
- Hornikx, M. Ten questions concerning computational urban acoustics. Build. Environ. 2016, 106, 409–421. [Google Scholar] [CrossRef] [Green Version]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papadakis, N.M.; Stavroulakis, G.E. Finite Element Method for the Estimation of Insertion Loss of Noise Barriers: Comparison with Various Formulae (2D). Urban Sci. 2020, 4, 77. https://doi.org/10.3390/urbansci4040077
Papadakis NM, Stavroulakis GE. Finite Element Method for the Estimation of Insertion Loss of Noise Barriers: Comparison with Various Formulae (2D). Urban Science. 2020; 4(4):77. https://doi.org/10.3390/urbansci4040077
Chicago/Turabian StylePapadakis, Nikolaos M., and Georgios E. Stavroulakis. 2020. "Finite Element Method for the Estimation of Insertion Loss of Noise Barriers: Comparison with Various Formulae (2D)" Urban Science 4, no. 4: 77. https://doi.org/10.3390/urbansci4040077
APA StylePapadakis, N. M., & Stavroulakis, G. E. (2020). Finite Element Method for the Estimation of Insertion Loss of Noise Barriers: Comparison with Various Formulae (2D). Urban Science, 4(4), 77. https://doi.org/10.3390/urbansci4040077






