Surface Urban Heat Island in Middle City: Spatial and Temporal Characteristics
Abstract
:1. Introduction
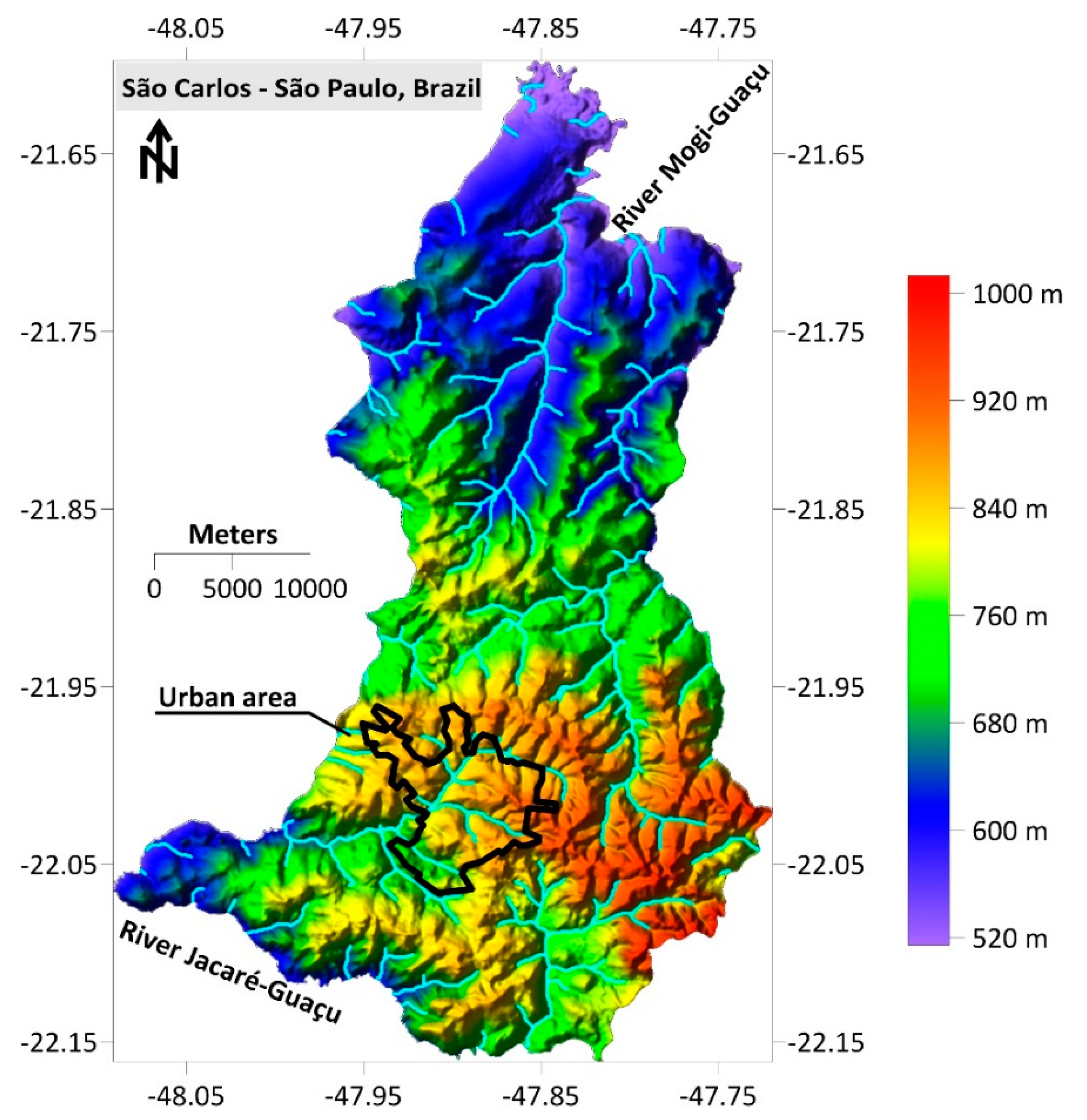
Study Area
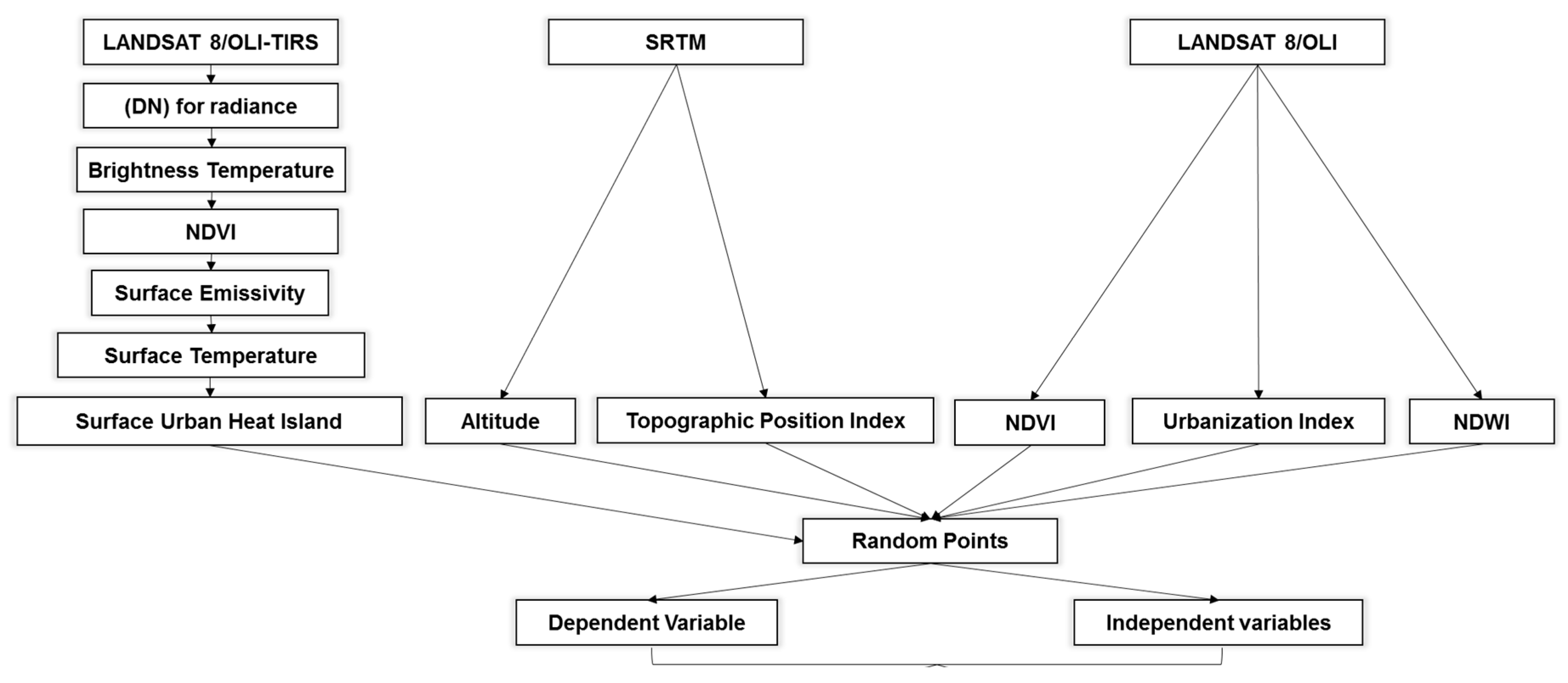
2. Materials and Methods
2.1. Dependent Variable
Procedures for Calculation of the SUHI
Step 1: Digital Numbers (DN) for Radiance
Step 2: Brightness Temperature
Step 3: NDVI Calculation
Step 4: Determination of Earth’s Surface Emissivity
Step 5: Surface Temperature Correction
Step 6: Surface Temperature Transformation into SUHI
2.2. Independent Variables
2.2.1. Altitude
2.2.2. Topographical Position Index
2.2.3. Urbanization Index
2.2.4. Normalized Difference Water Index
3. Results and Discussion
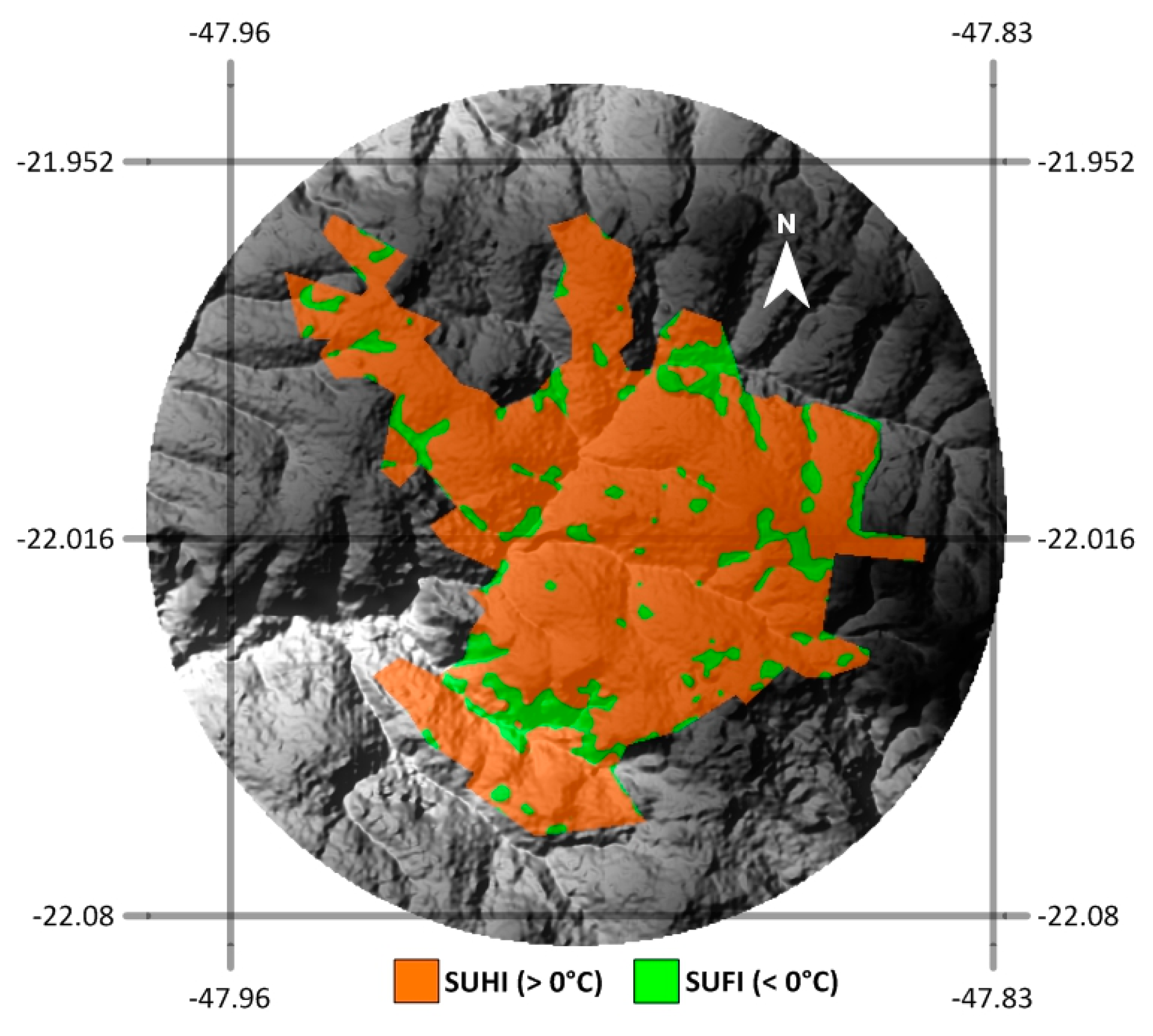
3.1. SUHI in São Carlos
3.2. Seasonality of Urban Surface Heat Islands
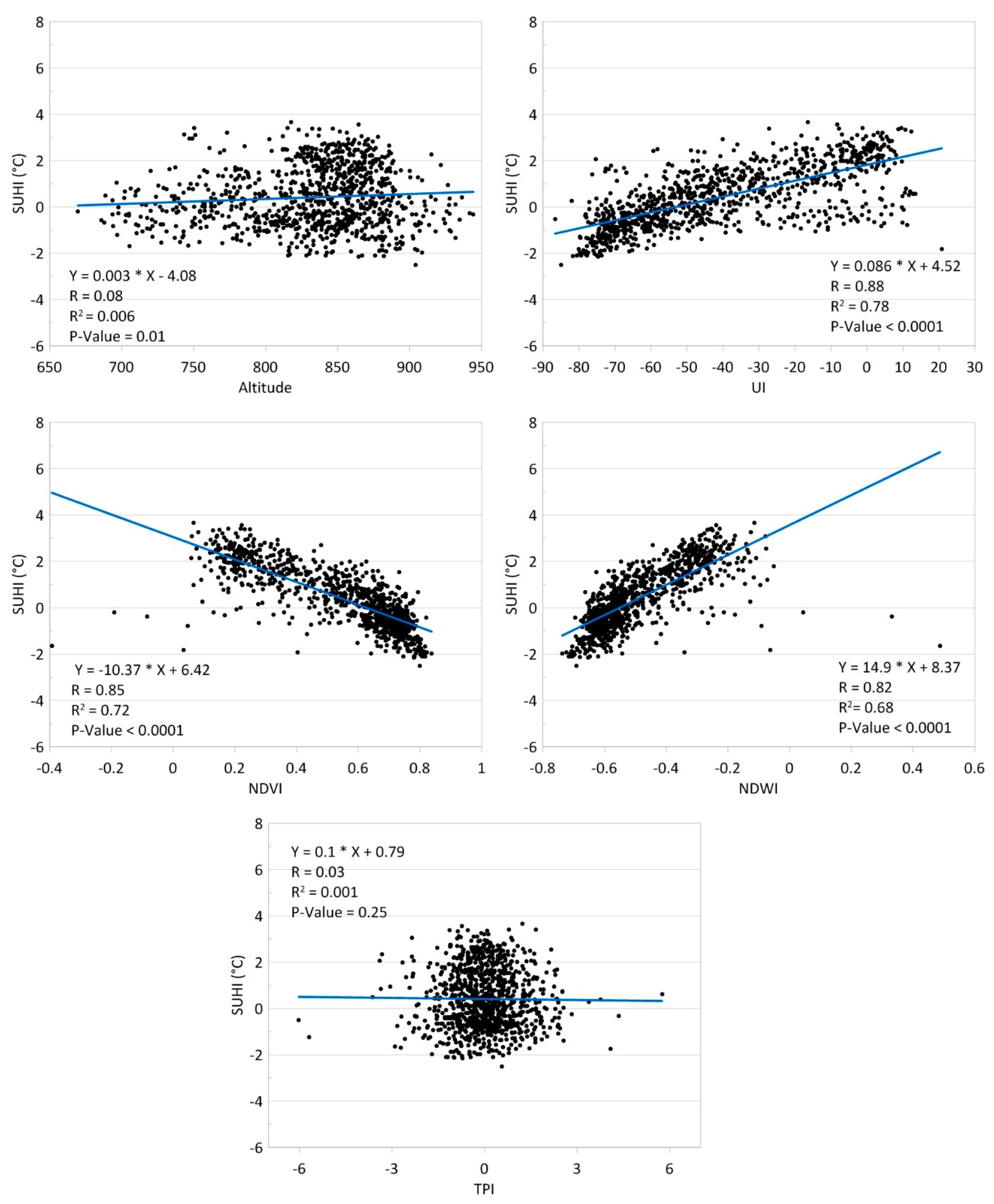
3.3. Relationship between SUHI, UI, NDVI, NDWI and TPI
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oke, T.R. Canyon geometry and the nocturnal urban heat island: Comparison of scale model and field observations. J. Climatol. 1981, 1, 237–254. [Google Scholar] [CrossRef]
- Souch, C.; Grimmond, S. Applied climatology: Urban climate. Prog. Phys. Geogr. 2006, 30, 270–279. [Google Scholar] [CrossRef]
- Coutts, A.M.; Beringer, J.; Tapper, N.J. Characteristics influencing the variability of urban CO2 fluxes in Melbourne, Australia. Atmos. Environ. 2007, 41, 51–62. [Google Scholar] [CrossRef]
- Alcoforado, M.-J.; Andrade, H.; Lopes, A.; Vasconcelos, J. Application of climatic guidelines to urban planning. Landsc. Urban Plan. 2009, 90, 56–65. [Google Scholar] [CrossRef]
- Zoulia, I.; Santamouris, M.; Dimoudi, A. Monitoring the effect of urban green areas on the heat island in Athens. Environ. Monit. Assess. 2009, 156, 275–292. [Google Scholar] [CrossRef] [PubMed]
- Tarifa, J.R.; de Azevedo, T.R. Os Climas na Cidade de São Paulo: Teoria e Prática; GEOUSP—Coleção Novos Caminhos: São Paulo, Brazil, 2001; Volume 4. [Google Scholar]
- Amorim, M.; Dubreuil, V.; Cardoso, R. Modelagem espacial da ilha de calor urbana em Presidente Prudente (SP)—Brasil. Rev. Bras. Climatol. 2015, 16, 29–45. [Google Scholar] [CrossRef] [Green Version]
- Lombardo, M.A. Ilhas de Calor nas Metrópoles: O exemplo de São Paulo; HUCITEC: São Paulo, Brazil, 1985. [Google Scholar]
- Alves, E.; Lopes, A. The Urban Heat Island Effect and the Role of Vegetation to Address the Negative Impacts of Local Climate Changes in a Small Brazilian City. Atmosphere 2017, 8, 18. [Google Scholar] [CrossRef] [Green Version]
- De Monteiro, C.A.F. Teoria e Clima Urbano; Universidade de São Paulo: São Paulo, Brazil, 1976. [Google Scholar]
- Alves, E.D.L.; Biudes, M.S. Análise da temperatura do ar e da umidade relativa: Estudo de microclimas. Interthesis 2012, 9, 139–156. [Google Scholar] [CrossRef] [Green Version]
- Alves, E.; Anjos, M.; Lopes, A. Multitemporalidade das anomalias da temperatura de superfície: O caso da cidade de Iporá, Brasil. GOT J. Geogr. Spat. Plan. 2017, 5–21. [Google Scholar] [CrossRef]
- Gartland, L. Heat Islands: Understanding and Mitigating Heat in Urban Areas; Routledge: London, UK, 2012. [Google Scholar]
- Oke, T.R.; Mills, G.; Christen, A.; Voogt, J.A. Urban Climates; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Ma, Y.; Kuang, Y.; Huang, N. Coupling urbanization analyses for studying urban thermal environment and its interplay with biophysical parameters based on TM/ETM+ imagery. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 110–118. [Google Scholar] [CrossRef]
- Gémes, O.; Tobak, Z.; van Leeuwen, B. Satellite Based Analysis of Surface Urban Heat Island Intensity. J. Environ. Geogr. 2016, 9, 23–30. [Google Scholar] [CrossRef] [Green Version]
- Bala, R.; Prasad, R.; Yadav, V.P.; Sharma, J. A comparative study of land surface temperature with different indices on heterogeneous land cover using Landsat 8 data. In The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; International Society of Photogrammetry and Remote Sensing: Hannover, Germany, 2018; Volume 42, pp. 20–23. [Google Scholar]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Minaki, C.; Amorim, M.C.C.T. Análise da temperatura e da umidade relativa do ar na primavera-verão em Araçatuba/SP. Rev. Bras. Climatol. 2014, 13, 236–247. [Google Scholar] [CrossRef] [Green Version]
- Stewart, I.D.; Oke, T.R. Local Climate Zones for Urban Temperature Studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
- Alves, E.D.L.; Biudes, M.S. Method for determining the footprint area of air temperature and relative humidity. Acta Sci. Technol. 2013, 35, 187–194. [Google Scholar] [CrossRef] [Green Version]
- Lopes, A.; Alves, E.; Alcoforado, M.J.; Machete, R. Lisbon Urban Heat Island Updated: New Highlights about the Relationships between Thermal Patterns and Wind Regimes. Adv. Meteorol. 2013, 1–11. [Google Scholar] [CrossRef]
- Alves, E. Seasonal and Spatial Variation of Surface Urban Heat Island Intensity in a Small Urban Agglomerate in Brazil. Climate 2016, 4, 61. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Qin, Z.; Wan, H. Spatial and Temporal Dynamics of Urban Heat Island and Their Relationship with Land Cover Changes in Urbanization Process: A Case Study in Suzhou, China. J. Indian Soc. Remote Sens. 2010, 38, 654–663. [Google Scholar] [CrossRef]
- Nichol, J.E. Visualisation of urban surface temperatures derived from satellite images. Int. J. Remote Sens. 1998, 19, 1639–1649. [Google Scholar] [CrossRef]
- Xu, S. An approach to analyzing the intensity of the daytime surface urban heat island effect at a local scale. Environ. Monit. Assess. 2009, 151, 289–300. [Google Scholar] [CrossRef]
- Abreu-Harbich, L.V.; Labaki, L.C.; Matzarakis, A. Thermal bioclimate in idealized urban street canyons in Campinas, Brazil. Theor. Appl. Climatol. 2013. [Google Scholar] [CrossRef]
- Ali-toudert, F.; Djenane, M.; Bensalem, R.; Mayer, H. Outdoor thermal comfort in the old desert city of Beni-Isguen, Algeria. Clim. Res. 2005, 28, 243–256. [Google Scholar] [CrossRef] [Green Version]
- Gabriel, K.M.A.; Endlicher, W.R. Urban and rural mortality rates during heat waves in Berlin and Brandenburg, Germany. Environ. Pollut. 2011, 159, 2044–2050. [Google Scholar] [CrossRef]
- Tan, J.; Zheng, Y.; Tang, X.; Guo, C.; Li, L.; Song, G.; Zhen, X.; Yuan, D.; Kalkstein, A.J.; Li, F.; et al. The urban heat island and its impact on heat waves and human health in Shanghai. Int. J. Biometeorol. 2010, 54, 75–84. [Google Scholar] [CrossRef] [PubMed]
- Lima, M.S.; Anjos, M.W.B.; Ramos, P.H.; Alves, E.D.L. Temperatura do ar no meio urbano: primeiros experimentos em Ceres – Goiás. Rev. Bras. Climatol. 2020, 26, 286–295. [Google Scholar] [CrossRef]
- Mihalakakou, G.; Flocas, H.; Santamouris, M.; Helmis, C.G. Application of Neural Networks to the Simulation of the Heat Island over Athens, Greece, Using Synoptic Types as a Predictor. J. Appl. Meteorol. 2002, 41, 519–527. [Google Scholar] [CrossRef]
- Saitoh, T.S.; Shimada, T.; Hoshi, H. Modeling and simulation of the Tokyo urban heat island. Atmos. Environ. 1996, 30, 3431–3442. [Google Scholar] [CrossRef]
- Stewart, I.D.; Oke, T.R.; Krayenhoff, E.S. Evaluation of the ‘local climate zone’ scheme using temperature observations and model simulations. Int. J. Climatol. 2013, 34, 1062–1080. [Google Scholar] [CrossRef]
- Amorim, M.C.D.C.T.; Junior, J.C.U. Os climas das cidades e as relações Sociedade/Natureza. Rev. Anpege 2016, 12, 252–278. [Google Scholar] [CrossRef]
- Oke, T. City size and the urban heat island. Atmos. Environ. 1973, 7, 769–779. [Google Scholar] [CrossRef]
- Coseo, P.; Larsen, L. How factors of land use/land cover, building configuration, and adjacent heat sources and sinks explain Urban Heat Islands in Chicago. Landsc. Urban Plan. 2014, 125, 117–129. [Google Scholar] [CrossRef]
- Tan, M.; Li, X. Quantifying the effects of settlement size on urban heat islands in fairly uniform geographic areas. Habitat Int. 2015, 49, 100–106. [Google Scholar] [CrossRef]
- Monteiro, C. A Dinâmica Climática e as Chuvas no Estado de São Paulo : Estudo Geográfico Sob Forma de Atlas; Instituto de Geografia: São Paulo, Brazil, 1973. [Google Scholar]
- Embrapa, Banco de Dados Climáticos do Brasil. 2019. Available online: https://www.cnpm.embrapa.br/projetos/bdclima/balanco/resultados/sp/451/balanco.html (accessed on 17 January 2019).
- Zen, G.; de Figueiredo Neves, G.Z.; Alves, E.D.L.; dos Santos, B.C.; Vecchia, F.A.S. Variabilidade e mudanças climáticas: Análise da tendência da precipitação na estação climatológica do CRHEA/USP em Itirapina-SP. In Proceedings of the XII Simpósio Brasileiro de Climatologia Geográfica, Goiania, Brazil, 25–29 October 2016; pp. 2673–2683. Available online: http://www.abclima.ggf.br/sbcg2016/anais/arquivos/eixo_6/trabalho(34).pdf (accessed on 21 April 2020).
- Barbosa, R.V.R. Estudo do Campo Térmico Urbano de São Carlos (SP): Análise da Intensidade da Ilha de Calor Urbano em Episódio Climático de Verão; Universidade de São Paulo: São Paulo, Brazil, 2009. [Google Scholar]
- IBGE, Cidades. 2018. Available online: http://www.cidades.ibge.gov.br/ (accessed on 1 May 2020).
- Bere, T.; Tundisi, J.G. Epipsammic Diatoms in Streams Influenced by Urban Pollution, São Carlos, SP, Brazil. Braz. J. Biol. 2010, 70, 920–930. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barbosa, R.V.R.; Vecchia, F. Estudos de ilha de calor urbana por meio de imagens do Landsat 7 ETM + : Estudo de caso em São Carlos (SP). Minerva 1996, 6, 273–278. Available online: http://www.fipai.org.br/Minerva06(03)07.pdf (accessed on 6 May 2020).
- USGS, Earth Explorer. 2016. Available online: http://earthexplorer.usgs.gov/ (accessed on 1 August 2016).
- Ndossi, M.I.; Avdan, U. Application of Open Source Coding Technologies in the Production of Land Surface Temperature (LST) Maps from Landsat: A PyQGIS Plugin. Remote Sens. 2016, 8, 431. [Google Scholar] [CrossRef] [Green Version]
- Ndossi, M.I.; Avdan, U. “Inversion of Land Surface Temperature (LST) Using Terra ASTER Data: A Comparison of Three Algorithms. Remote Sens. 2016, 8, 993. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhong, T.; Feng, X.; Wang, K. Estimation of the relationship between vegetation patches and urban land surface temperature with remote sensing. Int. J. Remote Sens. 2009, 30, 2105–2118. [Google Scholar] [CrossRef]
- USGS, Using the USGS Landsat 8 Product. Available online: http://landsat.usgs.gov/Landsat8_Using_php (accessed on 1 May 2020).
- Srivastava, P.K.; Han, D.; Rico-Ramirez, M.A.; Bray, M.; Islam, T.; Gupta, M.; Dai, Q. Estimation of land surface temperature from atmospherically corrected LANDSAT TM image using 6S and NCEP global reanalysis product. Environ. Earth Sci. 2014, 72, 5183–5196. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Foody, G.M. Geographical weighting as a further refinement to regression modelling: An example focused on the NDVI-rainfall relationship. Remote Sens. Environ. 2003, 88, 283–293. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Li, Y. A C++ program for retrieving land surface temperature from the data of Landsat TM/ETM+ band6. Comput. Geosci. 2006, 32, 1796–1805. [Google Scholar] [CrossRef]
- Artis, D.A.; Carnahan, W.H. Survey of emissivity variability in thermography of urban areas. Remote Sens. Environ. 1982, 12, 313–329. [Google Scholar] [CrossRef]
- Sinha, S.; Pandey, P.C.; Sharma, L.K.; Nathawat, M.S.; Kumar, P.; Kanga, S. Remote Estimation of Land Surface Temperature for Different LULC Features of a Moist Deciduous Tropical Forest Region; Springer: Berlin, Germany, 2014; pp. 57–68. [Google Scholar]
- Cao, X.; Onishi, A.; Chen, J.; Imura, H. Quantifying the cool island intensity of urban parks using ASTER and IKONOS data. Landsc. Urban Plan. 2010, 96, 224–231. [Google Scholar] [CrossRef]
- Li, S.; Mo, H.; Dai, Y. Spatio-temporal Pattern of Urban Cool Island Intensity and Its Eco-environmental Response in Chang-Zhu-Tan Urban Agglomeration. Commun. Inf. Sci. Manag. Eng. 2011, 1, 1–6. [Google Scholar]
- Rasul, A.; Balzter, H.; Smith, C. Spatial variation of the daytime Surface Urban Cool Island during the dry season in Erbil, Iraqi Kurdistan, from Landsat 8. Urban Clim. 2015, 14, 176–186. [Google Scholar] [CrossRef] [Green Version]
- Cheval, S.; Dumitrescu, A. The summer surface urban heat island of Bucharest (Romania) retrieved from MODIS images. Theor. Appl. Climatol. 2014, 121, 631–640. [Google Scholar] [CrossRef]
- Debbage, N.; Shepherd, J.M. The urban heat island effect and city contiguity. Comput. Environ. Urban Syst. 2015, 54, 181–194. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Z.; Miaomiao, X.; Wang, Y. Investigating spatial non-stationary and scale-dependent relationships between urban surface temperature and environmental factors using geographically weighted regression. Environ. Model. Softw. 2010, 25, 1789–1800. [Google Scholar] [CrossRef]
- INPE, TOPODATA. Available online: http://www.webmapit.com.br/inpe/topodata/ (accessed on 21 May 2020).
- Trentin, R.; Robaina, L.E.D.S.; Baratto, D.D.S. Análise de elementos do relevo através do Topographic Position Index (TPI) da bacia hidrográfica do arroio Puitã—Oeste do Rio Grande do Sul/Brasil. Rev. Dep. Geogr. 2016, 31, 14–25. [Google Scholar] [CrossRef] [Green Version]
- Ivajnšič, D.; Kaligarič, M.; Žiberna, I. Geographically weighted regression of the urban heat island of a small city. Appl. Geogr. 2014, 53, 341–353. [Google Scholar] [CrossRef]
- Paszynski, J. Mapping urban topoclimates. Energy Build. 1991, 16, 1059–1062. [Google Scholar] [CrossRef]
- Kawamura, M.; Jayamanna, S.; Tsujiko, Y. Relation Between Social and Environmental Conditions in Colombo, Sri Lanka and the Urban Index Estimated by Satellite Remote Sensing Data. Int. Arch. Photogramm. Remote Sens. 1996, XXXI, 321–326. Available online: http://scholar.google.com/scholar?hl=en&btnG=Search&q=intitle:Relation+Between+social+and+environmental+conditions+in+Colombo,+Sri+Lanka+and+the+urban+index+estimated+by+satellite+remote+sensing+data#0 (accessed on 13 June 2020).
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Alves, E.D.L. Quantifying the effect of waterways and green areas on the surface temperature. Acta Sci. Technol. 2017, 39, 89. [Google Scholar] [CrossRef]
- Carfan, A.C.; Galvani, E.; Nery, J.T. Study of the microclimate effect in the urban vertical structure in Ourinhos, São Paulo State. Acta Sci. Technol. 2012, 34, 313–320. [Google Scholar] [CrossRef] [Green Version]
- Skoulika, F.; Santamouris, M.; Kolokotsa, D.; Boemi, N. On the thermal characteristics and the mitigation potential of a medium size urban park in Athens, Greece. Landsc. Urban Plan. 2014, 123, 73–86. [Google Scholar] [CrossRef]
- Mendonça, F.; Dubreuil, V. Termografia de superfície e temperatura do ar na RMC (Região Metropolitana de Curitiba/PR). RaegaO Espaço Geográfico em Análise 2005, 9, 25–35. [Google Scholar] [CrossRef] [Green Version]
- Jauregui, E. Influence of a large urban park on temperature and convective precipitation in a tropical city. Energy Build. 1990, 15, 457–463. [Google Scholar] [CrossRef]
- Anjos, M.; Lopes, A.; Alves, E.D.L.; de Lucena, A.J. Rede climatológica urbana aplicada ao estudo da ilha de calor em Aracaju-SE. Caminhos Geogr. 2017, 18, 203–216. [Google Scholar] [CrossRef] [Green Version]
- Junior, J.C.U.; Amorim, M.C.C.T. Clima urbano em Jales/SP: Características da temperatura e da umidade relativa em episódios de inverno. Rev. Geográfica América Cent. 2011, 2, 1–25. [Google Scholar]
- Alves, E.D.L. Ilha de calor urbana em cidade de pequeno porte e a influência de variáveis geourbanas. Rev. Bras. Climatol. 2017, 20, 97–116. [Google Scholar] [CrossRef] [Green Version]
- Alves, E.D.L.; Vecchia, F.A.S.; De Lima, E.A.; Anjos, M.; Mariano, Z.D.F. A temperatura do ar e umidade absoluta em cidade de pequeno porte: Características espaciais e temporais. Acta Sci. Hum. Soc. Sci. 2016, 38, 219. [Google Scholar] [CrossRef] [Green Version]
- Lopes, A. Drenagem e acumulação de ar frio em noites de arrefecimento radiativo. Um exemplo no vale de Barcarena (Oeiras). Finisterra 2012, 30, 149–164. [Google Scholar] [CrossRef]
- Buyantuyev, A.; Wu, J. Urban heat islands and landscape heterogeneity: Linking spatiotemporal variations in surface temperatures to land-cover and socioeconomic patterns. Landsc. Ecol. 2009, 25, 17–33. [Google Scholar] [CrossRef]
- Haashemi, S.; Weng, Q.; Darvishi, A.; Alavipanah, S.K. Seasonal Variations of the Surface Urban Heat Island in a Semi-Arid City. Remote Sens. 2016, 8, 352. [Google Scholar] [CrossRef] [Green Version]
- Lazzarini, M.; Marpu, P.R.; Ghedira, H. Remote Sensing of Environment Temperature-land cover interactions: The inversion of urban heat island phenomenon in desert city areas. Remote Sens. Environ. 2013, 130, 136–152. [Google Scholar] [CrossRef]
- Becerra, J.A.B.; Shimabukuro, Y.E.; Alvalá, R.C.D.S. Relação do padrão sazonal da vegetação com a precipitação na região de cerrado da Amazônia Legal, usando índices espectrais de vegetação. Rev. Bras. Meteorol. 2009, 24, 125–134. [Google Scholar] [CrossRef] [Green Version]
- Bernatzky, A. The contribution of tress and green spaces to a town climate. Energy Build. 1982, 5, 1–10. [Google Scholar] [CrossRef]
- Oliveira, S.; Andrade, H.; Vaz, T. The cooling effect of green spaces as a contribution to the mitigation of urban heat: A case study in Lisbon. Build. Environ. 2011, 46, 2186–2194. [Google Scholar] [CrossRef]
- Altman, D.G.; Bland, J.M. Absence of evidence is not evidence of absence. BMJ 1995, 311, 485. [Google Scholar] [CrossRef] [Green Version]
- Deilami, K.; Kamruzzaman; Hayes, J.F. Correlation or Causality between Land Cover Patterns and the Urban Heat Island Effect? Evidence from Brisbane, Australia. Remote Sens. 2016, 8, 716. [Google Scholar] [CrossRef] [Green Version]
- Lee, L.; Chen, L.; Wang, X.; Zhao, J. Use of Landsat TM/ETM+ Data to Analyze Urban Heat Island and Its Relationship with Land Use/Cover Change. In Proceedings of the 2011 International Conference on Remote Sensing, Environment and Transportation Engineering, Nanjing, China, 24–26 June 2011; pp. 922–927. [Google Scholar] [CrossRef]
- Tyubee, B.T.; Anyadike, R.N.C. Investigating the Effect of Land Use/Land Cover on Urban Surface Temperature in Makurdi, Nigeria. In Proceedings of the ICUC9—9th International Conference on Urban Climate Jointly with 12th Symposium on the Urban Environment, Toulouse, France, 20–24 July 2015; pp. 1–15. [Google Scholar]
- Chen, X.; Zhang, Y. Impacts of urban surface characteristics on spatiotemporal pattern of land surface temperature in Kunming of China. Sustain. Cities Soc. 2017, 32, 87–99. [Google Scholar] [CrossRef] [Green Version]
- Flores, R.J.L.; Filho, A.J.P.; Karam, H.A. Estimation of long term low resolution surface urban heat island intensities for tropical cities using MODIS remote sensing data. Urban Clim. 2016, 17, 32–66. [Google Scholar] [CrossRef]
- Rasul, A.; Balzter, H.; Smith, C.L. Diurnal and Seasonal Variation of Surface Urban Cool and Heat Islands in the Semi-Arid City of Erbil, Iraq. Climate 2016, 4, 42. [Google Scholar] [CrossRef] [Green Version]
- Sun, D.; Kafatos, M. Note on the NDVI-LST relationship and the use of temperature-related drought indices over North America. Geophys. Res. Lett. 2007, 34, 24406. [Google Scholar] [CrossRef] [Green Version]



| Image | Date | Time (UTC) | Cloud Cover (%) | Image Quality | Path/Raw | Spatial Resolution (m) |
|---|---|---|---|---|---|---|
| 1 | 23 April 2015 | 13:09:12 | 10.46 | 9 | 220/075 | 30 OLI/100 TIRS |
| 2 | 9 May 2015 | 13:08:57 | 0.10 | 9 | 220/075 | 30 OLI/100 TIRS |
| 3 | 10 June 2015 | 13:09:07 | 0.01 | 9 | 220/075 | 30 OLI/100 TIRS |
| 4 | 28 July 2015 | 13:09:29 | 0.07 | 9 | 220/075 | 30 OLI/100 TIRS |
| 5 | 13 August 2015 | 13:09:34 | 0.01 | 9 | 220/075 | 30 OLI/100 TIRS |
| 6 | 29 September 2015 | 13:09:40 | 0.01 | 9 | 220/075 | 30 OLI/100 TIRS |
| 7 | 16 October 2015 | 13:09:53 | 1.95 | 9 | 220/075 | 30 OLI/100 TIRS |
| 8 | 9 April 2016 | 13:09:29 | 0.00 | 9 | 220/075 | 30 OLI/100 TIRS |
| 9 | 14 July 2016 | 13:09:49 | 0.01 | 9 | 220/075 | 30 OLI/100 TIRS |
| 10 | 30 July 2016 | 13:09:53 | 1.06 | 9 | 220/075 | 30 OLI/100 TIRS |
| 11 | 2 October 2016 | 13:10:07 | 1.57 | 9 | 220/075 | 30 OLI/100 TIRS |
| 12 | 23 February 2017 | 13:09:46 | 0.10 | 9 | 220/075 | 30 OLI/100 TIRS |
| 13 | 3 September 2017 | 13:09:59 | 0.04 | 9 | 220/075 | 30 OLI/100 TIRS |
| 14 | 19 September 2017 | 13:10:01 | 0.52 | 9 | 220/075 | 30 OLI/100 TIRS |
| 15 | 5 October 2017 | 13:10:07 | 0.00 | 9 | 220/075 | 30 OLI/100 TIRS |
| Date | Air Temperature (°C) | Relative Humidity (%) | Wind Speed (m/s) | Atmospheric Pressure (hPa) | Solar Radiation (W/m2/day) |
|---|---|---|---|---|---|
| 23 April 2015 | 23.2 | 87.3 | 2.50 | 927.2 | 493.69 |
| 9 May 2015 | 21.0 | 76.0 | 1.18 | 930.2 | 325.71 |
| 10 June 2015 | 21.1 | 71.8 | 0.63 | 929.2 | 304.55 |
| 28 July 2015 | 19.7 | 67.0 | 1.48 | 930.1 | 314.79 |
| 13 August 2015 | 20.7 | 55.5 | 3.22 | 931.7 | 367.37 |
| 29 September 2015 | 20.9 | 73.3 | 3.54 | 932.4 | 417.01 |
| 16 October 2015 | 28.4 | 54.0 | 3.05 | 929.4 | 440.34 |
| 9 April 2016 | 27.0 | 66.8 | 2.97 | 925.1 | 385.18 |
| 14 July 2016 | 20.9 | 86.5 | 3.03 | 925.4 | 302.54 |
| 30 July 2016 | 17.7 | 66.8 | 2.84 | 930.9 | 300.92 |
| 2 October 2016 | 22.7 | 57.3 | 7.23 | 929.6 | 521.31 |
| 23 February 2017 | 26.4 | 63.8 | 3.00 | 927.6 | 499.75 |
| 3 September 2017 | 21.8 | 40.8 | 4.67 | 934.1 | 456.64 |
| 19 September 2017 | 23.8 | 45.0 | 4.50 | 929.8 | 420.57 |
| 5 October 2017 | 27.2 | 51.5 | 3.26 | 928.4 | 426.64 |
| Land Surface Emissivity (LSE) | |
|---|---|
| 0.995 | |
| 0.985 | |
| 0.990 |
| Summer | Autumn | Winter | Spring | Variation | |
|---|---|---|---|---|---|
| SUHI | SUHI | SUHI | SUHI | SUHI | |
| Altitude | −0.08 | 0.08 * | −0.10 | 0.01 | −0.18 |
| UI | 0.88 * | 0.69 * | 0.35 * | 0.33 * | 0.55 |
| NDVI | −0.85 * | −0.84 * | −0.69 * | −0.73 * | −0.12 |
| NDWI | 0.82 * | 0.83 * | 0.59 * | 0.67 * | 0.23 |
| TPI | 0.04 | 0.04 | 0.02 | 0.04 | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alves, E.; Anjos, M.; Galvani, E. Surface Urban Heat Island in Middle City: Spatial and Temporal Characteristics. Urban Sci. 2020, 4, 54. https://doi.org/10.3390/urbansci4040054
Alves E, Anjos M, Galvani E. Surface Urban Heat Island in Middle City: Spatial and Temporal Characteristics. Urban Science. 2020; 4(4):54. https://doi.org/10.3390/urbansci4040054
Chicago/Turabian StyleAlves, Elis, Max Anjos, and Emerson Galvani. 2020. "Surface Urban Heat Island in Middle City: Spatial and Temporal Characteristics" Urban Science 4, no. 4: 54. https://doi.org/10.3390/urbansci4040054
APA StyleAlves, E., Anjos, M., & Galvani, E. (2020). Surface Urban Heat Island in Middle City: Spatial and Temporal Characteristics. Urban Science, 4(4), 54. https://doi.org/10.3390/urbansci4040054






