1. Introduction
Across the Global North, “shrinking cities” [
1], alternatively termed legacy cities or cities in transition [
2,
3], are a cohort of older urban settlements that once played prominent roles in the industrial economy but, in the second half of the 20th century, experienced persistent, prevalent, and severe depopulation, economic contraction, and undesirable physical change [
1,
4,
5,
6,
7,
8]. In the American experience, post-World War II federal highway and mortgage lending policies enabled mass suburbanization by pushing relatively affluent residents from central cities toward rapidly developing adjacent suburbs [
9,
10]. Happening at and around the same time was a massive drop-off in local manufacturing and industrial production that saw factories, mills, and warehouses close, leaving scores of urban residents without jobs [
8]. Many former workers left industrial cities and regions altogether to seek employment elsewhere. The cumulative results of these and connected push-and-pull forces, in addition to natural demographic change [
5], have left American cities such as Buffalo, NY; Cleveland, OH; Detroit, MI; Pittsburgh, PA; and St. Louis, MO; among others, with less than half of their peak populations [
4].
One consequence of massive population loss is that the built environments of shrinking cities, which were constructed for multiples of their current (post-shrinkage) commercial and residential populations, become dotted with ever-increasing inventories of vacant and abandoned structures [
11]. Vacant and abandoned properties are significant obstacles to neighborhood and city stabilization, reinvestment, and revitalization [
12], insofar as they tend to reduce nearby property values and contribute to the geographic diffusion of blight [
13]. As such, vacancy and abandonment are popular, and necessary, targets for public policy intervention in shrinking cities [
14]. At least in the United States, however, decision-makers in shrinking cities regularly conceptualize these phenomena as relatively static in nature, and, for that reason, largely eradicable through public spending on structural demolitions and public policies that are friendly to economic development and oriented toward re-growth (e.g., [
15]). Yet, as ample scholarship on shrinking cities tends to agree: (1) the problems related to urban shrinkage and decline are manifold and complex (e.g., [
16,
17,
18]), which suggests that simply demolishing existing vacant and abandoned structures is unlikely to correct the issue; (2) demand for housing in shrinking cities is often very weak and highly spatially uneven, such that neighborhoods with excessive vacant housing stocks and related conditions of urban decline rarely benefit from the limited growth or development that does occur in shrinking cities [
3,
19]; and, (3) at bottom, the pro-growth mental model underlying many policy programs in shrinking cities rests on assumptions of re-growth that are rarely grounded in the reality of the cities’ current circumstances or near-term prospects [
15].
While there are certainly counter-examples pushing against the broad strokes painted in the preceding paragraph (e.g., [
20,
21,
22]), the literature and recent historical record suggest that pro-examples are much more numerous (e.g., [
8,
15,
16,
23,
24,
25]). In one case that is relatively popular among American shrinking cities researchers (e.g., [
15,
26,
27,
28,
29,
30,
31,
32,
33]), the “5 in 5” demolition program enacted in 2007 in Buffalo, NY, USA, famously sought to demolish 5000 vacant and abandoned properties over five years, in an attempt to bring the city’s overall “vacancy rate … closer to five percent”, down from the estimated citywide vacancy rate of 15 percent at the policy’s inception [
34] (pp. 1–2). Ultimately, the city fell short of its ambitious 5000 demolition target due to financial constraints, which calls the program’s efficacy into question [
15] (p. 9). Crucially, though, we argue that it was the city’s logic, especially the assumption that demolishing a specific quota of vacant and abandoned properties can materially and unilaterally affect a shrinking city’s overall vacancy rate, and not financial infeasibility per se that was the fatal flaw of the “5 in 5” program. We make the case that similar logic will continue to undermine any vacancy management strategy that fails to grapple with the complexity and dynamism of urban shrinkage and decline (see related arguments in [
8,
11,
15,
27]). To aid us in building that case, we undertake an empirical evaluation of Buffalo’s “5 in 5” program directed at the following questions:
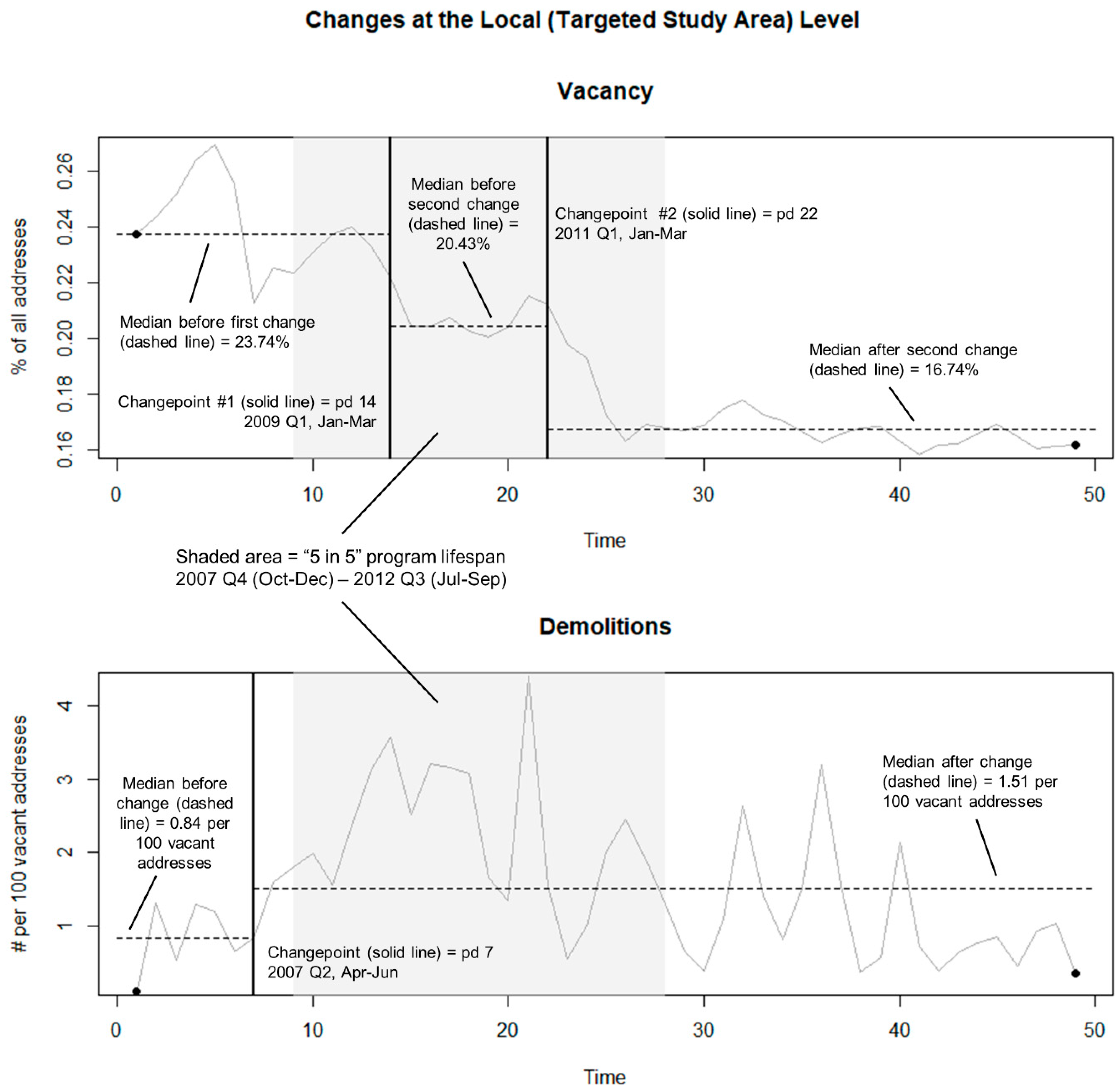
Where did demolitions occur around the time of the “5 in 5” program, and was Buffalo’s demolition activity spatiotemporally clustered in any subareas of the city? (NB: if clusters are detected, then we will seek to answer questions #2–4, below, at both the citywide/global and cluster-area/local levels of analysis. This multi-scalar approach will be taken to account for the possibility that the program’s efficacy might look different in the subarea(s) where it was most active relative to the city as a whole.)
Did vacancy in the study area(s) appear to change significantly around or since the time of the “5 in 5” program?
Did demolition activity in the study area(s) appear to change significantly around the time of the “5 in 5” program?
Does demolition activity in the study area(s) Granger-cause changes in vacancy? (where Granger causality describes a statistical test used to detect the extent to which one time series influences [“Granger-causes”] a second time series). For this question, we are interested in knowing whether the “5 in 5” program’s foundational premise—that more demolitions can cause change to Buffalo’s vacancy stock—holds up when placed under an empirical microscope. Null findings here would support our contention that demolition alone does not offer a simple solution to complex vacancy problems in shrinking cities. As such, this fourth question is the one in which we are most interested. Answers to questions #1–3 guide our approach to answering this core question, as well as inform our interpretation of results.
Prior to describing the materials and methods used to answer these questions, the remainder of this section frames our intervention and briefly characterizes its place in the shrinking cities literature. In doing so, we start from the foundation that problems related to urban decline are interdependent and multi-causal [
16]. For that reason, to more effectively manage these problems, political decision-makers must replace simple, event-oriented thinking (e.g., “if we demolish more structures, then the vacancy rate will necessarily fall”) with more complex,
systems thinking that appreciates feedback effects and opens the door for comparatively proactive strategies that are grounded in real world circumstances, patterns, trends, and possible futures. With respect to the case under investigation—Buffalo’s “5 in 5” demolition program—we produce empirical evidence to suggest that demolition by itself has limited efficacy for substantively changing vacancy in a shrinking city. These results buttress the argument that cities ought to avoid using demolition as a standalone vacancy management strategy, and must instead incorporate it into longer-term, multi-pronged, holistic approaches [
2,
14,
35,
36,
37]. Importantly, in framing the empirical analyses, we draw heavily from the toolbox of systems thinking. Employing these tools allows us to interpret our results in a way that offers several important lessons for practitioners in shrinking cities. Above all, our discussion challenges decision-makers to enumerate the relevant (known) sources of change that affect a given variable (e.g., vacancy) prior to designing an intervention aimed at altering that variable. Part of that exercise, as we illustrate, must involve identifying and critically engaging with the core assumptions, or “mental models”, that underlie the desired intervention.
1.1. On Shrinkage, Decline, and Their Causes and Symptoms: A Brief Introduction
Cities are complex systems made up of untold numbers of interacting parts [
38]. When a shock affects one or more of those parts in space and time, the interconnectivity of the system’s parts and subsystems implies that consequences can be many orders of magnitude greater than the original shock [
39]. That is, changes in any part of an interconnected urban system can give rise to powerful self-reinforcing feedback processes.
Prior to World War II, these feedback processes almost unanimously pointed to a
virtuous cycle of urbanization. Simply put, cities grew. The world over, prewar industrialized cities enjoyed steady, positive inflows of people, jobs, aggregate income, and built structures [
40]. Indeed, the field of urban planning emerged largely from the need to control and manage these widespread, seemingly unabating patterns of city growth [
9]. While urban growth did not stop after World War II (in fact, the urban share of global population has increased in every decade since 1940 [
41]), by 1950 the phenomenon became far narrower in its geographical scope. That is, whereas prewar urbanization was mostly
distributive, in that it seemingly applied to all cities, postwar urbanization has been comparably
parasitic, fueling growth in some cities while contributing to stagnation, shrinkage, and/or decline in others [
4].
Acknowledging that there is no universally accepted definition of the concept [
6], elsewhere in our work [
8] we have interpreted
shrinkage as sustained, downward,
quantitative adjustments to the population of a geographic community (also see [
27]). Stated another way, urban shrinkage involves long-term, “persistent” decreases in the total number of people living in an affected, shrinking area [
40]. Frequently, this sort of sustained population loss is accompanied, preceded, and/or succeeded by downward quantitative adjustments (shrinkage) in the size of the economy and built environment of the depopulating community. In other words, population loss tends to be highly correlated with both (1) job loss and (2) vacancy and property abandonment, the latter of which precedes property demolition [
8]. While the precise chain of causality involved in this complex relationship remains unresolved [
5], most researchers and practitioners agree that these linkages between population, the economy, and the built environment mean that shrinkage, decline, and their many manifestations cannot possibly have simple, standalone policy fixes [
16,
17].
On that backdrop, unlike the predominantly virtuous cycles of prewar distributive urbanization, the contemporary era of parasitic urbanization has placed numerous shrinking communities across the world into vicious cycles of harmful, self-reinforcing demographic, economic, and physical change. These quantitative decreases are much more than accounting matters. As American urban scholar Lewis Mumford observed in
The City in History [
42] (p. 486), these changes often lead to a “breakup of the old urban form”. That is, parasitic urbanization tends to have deleterious effects on a shrinking city’s existing urban functions. Through that lens, distinct from quantitative shrinkage, we interpret
decline as negative
qualitative change to the fabric and form of a given geographic community. Following basic dictionary definitions of the words “fabric” and “form”, urban fabric is taken to mean the comprehensive collection of a community’s social and physical elements and their spatial arrangement in relation to each other. Furthermore, urban form is interpreted to be the novel structures, such as neighborhoods and patterns of positive or negative social relations, that emerge from localized interactions between elements in the urban fabric (see [
43]). In this vein, urban decline is a downgrading in the quality of the urban fabric that can lead to, in the spirit of Mumford’s observation, “breakup” of the existing urban form (e.g., neighborhood abandonment; see [
44]).
Based on the foregoing definitions, urban shrinkage can be understood as a sufficient, but not a necessary, condition for urban decline. While the quantitative adjustments related to shrinkage invariably coincide with qualitative change in the urban fabric or form of an affected place [
45] (pp. 9–10), the latter phenomena can occur in the absence of the former. That is, decline can take shape in all varieties of communities, regardless of whether their populations are growing, shrinking, or stable. Decline, it follows, has been operating in cities since long before the notion of urban shrinkage came to the attention of academic researchers and planners (e.g., [
3]). The significance of this point lies in the fact that shrinkage and decline tend to be conflated in both theory and practice (see [
8]). As such, widely adopted policy strategies crafted in response to
decline in otherwise growing or stable city contexts, such as government-funded blight removal via structural demolition, followed by opening cleared spaces to private reinvestment [
12], are regularly taken up by cities where decline is exacerbated by
shrinkage and vice versa [
8]. The problem with this approach is that many such policies rest on assumptions about private market demand that do not hold in shrinking cities [
3]. More precisely, the problem lies in simplistic event-oriented thinking of the form: “if you clear it (the land), they will come (the real estate developers)”. Thinking more systemically about shrinkage and decline ought to better illuminate the weakness with this type of reasoning. It is on this note that we present and employ two systems thinking tools that the shrinking cities research and practice communities might find valuable for framing problems and crafting solutions.
1.2. Two Systems Thinking Tools for Planning and Decision-Making in Shrinking Cities
1.2.1. The Iceberg Model
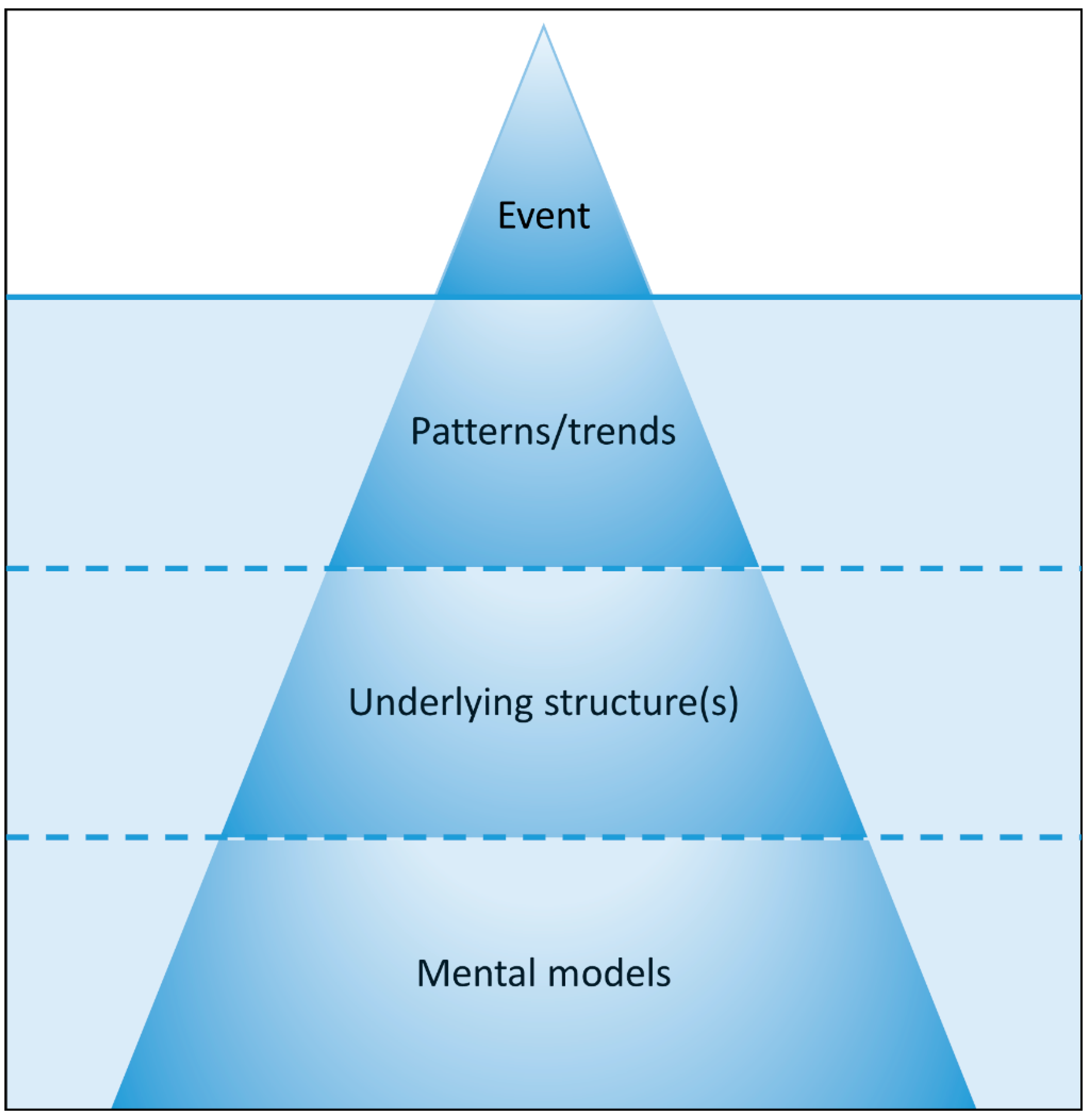
Systems thinking is an inquiry-based approach to explaining the relationships between the structures and behaviors of a system [
46]. Effective systems thinking requires one to ask probing questions about how the many parts of a system interact and influence one another, and how those part-level interactions have consequences at the level of the whole. In this way, systems thinking endeavors to go “below the surface” to uncover systemic (e.g., structural, cultural, and political) attributes that produce certain patterns and events. One tool for systems thinking is the popular iceberg model [
47] depicted in
Figure 1.
The iceberg model is a tool for contextualizing a given (observable) problem or event (e.g., vacancy and abandonment) as part of a whole system (e.g., the political economy and prevailing cultural norms of a shrinking city). Like an iceberg, the model imparts that what we see is only a small fraction of the system that produces the observable outcome. The majority of what we would like to know lies beneath the surface [
47]. Immediately below the surface, then, is where we might find patterns of behavior in space or time. These patterns or trends in behavior would suggest that the observable problem or event of interest might be part of some larger scope or longer-term tendency. Underlying all patterns or trends is a
structure or set of structures from which the observable behavioral patterns are generated. Structures include, among other variables, institutions of governance, their interrelationships, laws and regulations, and, especially, the market-based allocation, production, and consumption mechanisms that prevail in developed nations. Finally, below the structural level are the
mental models, i.e., the attitudes, values, beliefs, norms, and conventions, that keep the existing structure(s) in place.
As a tool for facilitating systems thinking, the iceberg model equips its users with at least some capacity to identify leverage points in the system under investigation. Leverage points are places to intervene in the system, where making some sort of strategic modification could nudge the system toward a different, preferably more desirable state [
46]. Two generic types of leverage points and interventions implicated by the iceberg model are: (1)
redesigning the structure(s) of the system; and (2)
transforming mental model(s) in the system [
48]. Within the shrinking cities literature, there have been numerous recent calls for decision-makers to supplant growth-oriented goals and their attendant pro-growth policies [
9,
10,
23] with visions of “smart shrinkage” or “right-sizing” [
8,
9,
10,
11,
27]. In interpreting our results, we suggest that heeding these calls is tantamount to
transforming the [pro-growth]
mental models that help to create and reinforce patterns of parasitic urbanization [
8].
1.2.2. Stock and Flow Diagramming and Feedback Loops
In systems,
stocks are inventories that exist at a particular point in time. The sizes of inventories change as a result of
flows, or the rates at which units are added to (
inflow) and subtracted from (
outflow) the stocks over time [
46]. The classic example of a stock with one principal inflow and one principal outflow is an unoccupied bathtub. The quantity of water present in the bathtub is the available stock. The water entering the tub through the activated faucet is the inflow that adds to the stock over time, and the quantity of water leaving the tub through an unplugged drain is the outflow that subtracts from the stock. If the inflow and outflow per unit time are equal, then the stock of water remains the same. Discrepancies between the two flows cause the water stock to either increase (when inflow > outflow) or decrease (when inflow < outflow) over time.
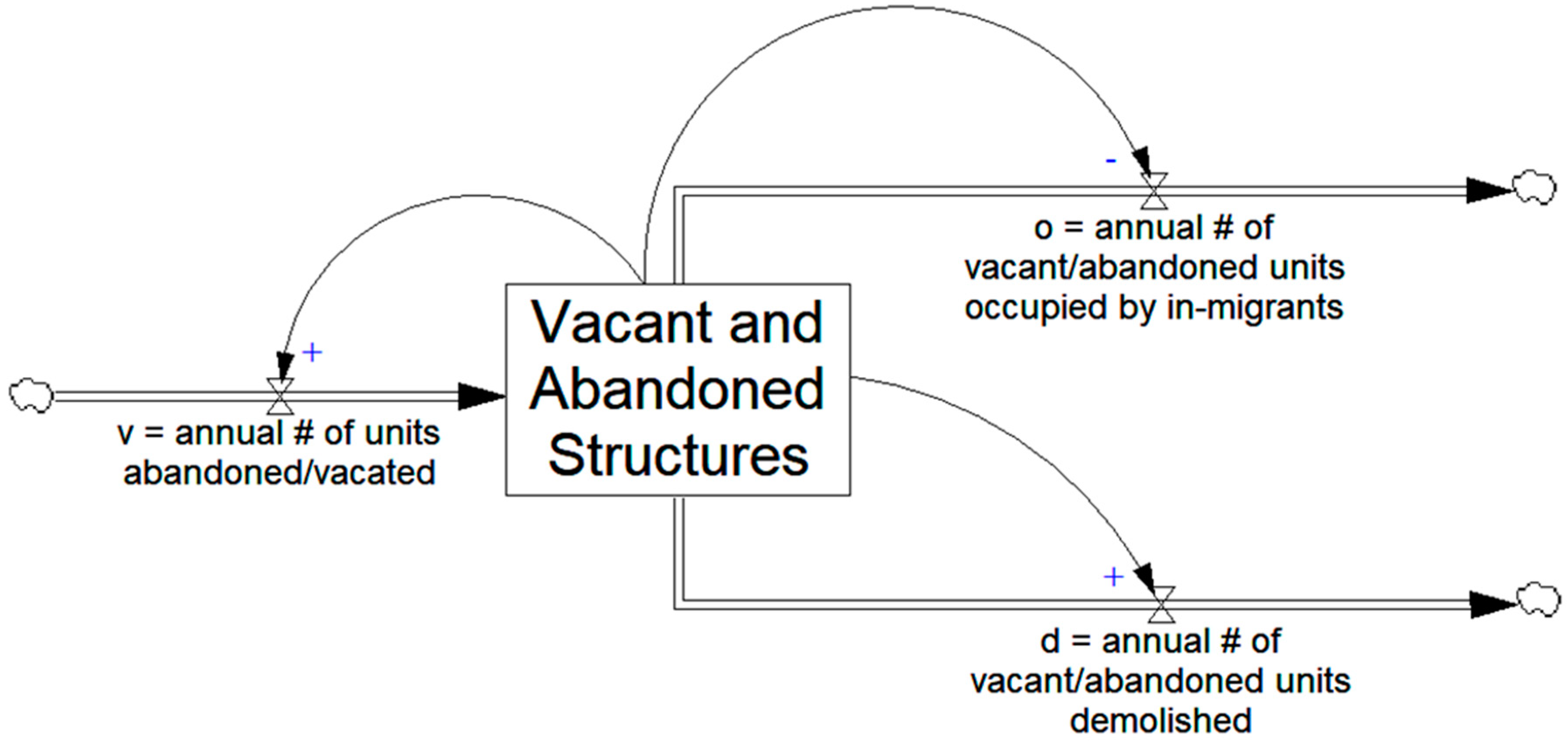
For planning and decision-making purposes, we claim that there is utility in visualizing stocks and flows prior to implementing an intervention that seeks to change one or more of them. Visualizing stocks and flows is called diagramming.
Figure 2 presents a simplified stock and flow diagram that considers annual changes to the inventory of vacant and abandoned properties in a city. The large rectangle at the center of the diagram represents the stock of vacant and abandoned properties. Adding to the stock is the annual rate at which properties are vacated and/or abandoned in the city (labeled v in the diagram). Subtracting from the stock are two outflows. First is the annual rate at which vacant and abandoned properties are occupied by in-migrants or otherwise reused (labeled o). Second is the annual rate at which vacant and abandoned properties are demolished or otherwise torn down (d). From year to year, the net effects of these inflows and outflows are responsible for changes measured in the stock of vacant and abandoned structures. When inflows exceed outflows, the vacancy problem worsens. Balanced flows result in a stable or constant stock of vacant and abandoned properties. Furthermore, citywide vacancy is lessened when outflows are collectively larger in magnitude than inflows.
Three feedback loops are depicted in the simplified diagram above. First, research has shown that the more vacant, abandoned, and blighted properties there are in an area, the more likely it is that additional properties fall into disrepair and become abandoned over time (e.g., [
13,
49]). Stated another way, larger stocks of vacant and abandoned properties often strengthen their own inflow (v). Second, the higher the stock of abandoned or blighted structures in a given area, the lower is the demand for property therein (e.g., [
3]). As such, the size of stock shown in
Figure 2 affects the rate at which properties are occupied or otherwise reused over time (o). Third, considering evidence that policies aimed at reducing blight are largely reactive [
33,
37], it is likely the case that larger stocks of vacant and abandoned properties are met with more aggressive levels of publicly funded demolitions (d). Indeed, such a reaction was arguably one of the driving forces behind Buffalo’s “5 in 5” demolition program.
While we turn next to the specifics of that program, it is worth observing here that the stock and flow diagram from
Figure 2 provides convenient framing for our empirical analyses, and the iceberg model from
Figure 1 provides a medium through which we can interpret our results. Explicitly,
Figure 2 makes it clear that the demolition outflow (d) is only one source of change affecting vacant property stocks. Thus, in the absence of complementary policies to balance the remaining two flows (v and o), demolition should not be expected to substantively reduce vacancy (hence our fourth and primary research question from above). With respect to
Figure 1, the reason that standalone demolition programs continue to endure as vacancy management strategies in shrinking cities [
8,
11], despite the logic against such a practice (
Figure 2), is perhaps that decision-makers subscribe to pro-growth mental models [
9,
23] that assume growth is the “natural” urban tendency [
5], and that clearing land will necessarily bring new development (and, with it, new demand for urban housing) [
8,
23].
1.3. The “5 in 5” Demolition Program in Buffalo, NY, USA
In the summer of 2007, facing public and political backlash on the issue of vacancy following life-threatening injuries to a firefighter during a structure fire at an abandoned property, newly-elected Mayor Byron Brown and his administration hurriedly put together a demolition program. In August of that year, a policy brief introduced the program as “Mayor Brown’s ‘5 in 5’ Demolition Plan” [
34]. Calling vacancy “one of the most important issues facing our community,” the Mayor’s plan was a highly aggressive program aimed at demolishing 5,000 structures over a five-year period. An explicit goal of the plan was to reduce the number of vacant structures in the city and get the vacancy rate “closer to 5%”, down from the estimated 15% at the time of the policy brief [
34]. Past research has criticized the seemingly arbitrary nature of this target [
8], as well as the fact that the program mainly functioned outside of larger planning contexts [
3,
11]. More specifically, while the city’s adopted comprehensive plan included a Vacant Property Asset Management Strategy, the “5 in 5” program conspicuously was not linked to it, calling into question its potential to be successful [
27]. Additionally, Yin and Silverman [
33] and Silverman et al. [
15] have discussed the reactionary nature of the program, arguing that its detachment from proactive and comprehensive planning efforts undermined its efficacy.
In this context, the present paper is not breaking entirely new ground in critiquing the “5 in 5” program. What we add to the discussion, though, is a systems thinking perspective along with novel empirical results. Concerning the former, as expanded on in the next subsection, both the framework of systems thinking and the contents of its toolbox that were introduced above allow us to expose flaws in the program in a way that offers a broad lesson for vacancy management in shrinking cities. In particular, we demonstrate that demolition alone cannot cure vacancy. Whereas existing literature has drawn on observational data and professional insights to make a similar case [
3], our approach illustrates, logically, why demolition can only ever be a partial solution to vacancy problems. With respect to the latter contribution, we rely on that same systems thinking framing to guide an empirical evaluation of the “5 in 5” program that moves our critique beyond dialogue (e.g., [
11,
27]) and into the realm of quantitative evidence.
Challenging the “5 in 5” Program’s Event-Oriented Thinking
Conventional or “event-oriented” thinking assumes that problems are “well bounded, clearly defined, relatively simple and linear with respect to cause and effect”, such that they are solved either “through control of the processes that lead to [them]…or through amelioration of the problem after it occurs” [
50] (p. 78). In this sense, problems, or observed events, are the tips of the iceberg from the model shown in
Figure 1. Solutions proposed from an event-oriented perspective rarely dig below this surface to reveal the structures or mental models that exist in the system. Instead, the world is thought to function at or near the water line. The “5 in 5” program arguably falls into this trap.
For the “5 in 5” program, the surface-level problem identified by decision-makers was a large stock of vacant and abandoned properties; around 15% of all structures were thought to be vacant, and the city viewed 5% vacancy as a more desirable number. In event-oriented fashion, the city’s proposed solution to the problem was “amelioration” (see [
50]) in the form of structural demolitions. The city reasoned that by increasing a known
outflow of vacant and abandoned property (
Figure 2), the “5 in 5” program would necessarily reduce the stock targeted by the policy. As an example, assume that a city contains 50,000 total structures. With a 15% vacancy rate, the stock of vacant properties in the city would therefore consist of 7500 structures. If 5000 of these structures were demolished
and no other changes were made, then the city would be left with 45,000 total structures, 2500 of which would still be vacant, for a 5.6% vacancy rate. In this hypothetical scenario, the “5 in 5” program accomplishes its goal: through aggressive demolition activity, the city’s vacancy rate gets “closer to 5%” from where it was at the inception of the program.
The problem, of course, is that this way of thinking ignores the other flows affecting vacancy (
Figure 2). In reality, the social, political, and economic structures of shrinking cities are such that communities become locked into downward spirals, whereby the “spatial-economic” attributes, “social-cultural fabric”, and “image aspects” of cities deteriorate seemingly unabated [
16] (p. 1519). In such scenarios, wherein “the young and talented tend to migrate, leaving the elderly and underprivileged behind” [
16] (p. 1511), the possibility that annual property abandonment rates and annual reuse/new occupancy rates are fixed to zero or otherwise perfectly counterbalanced (see
Figure 2) is far-fetched. Real estate demand in such spaces tends to be weak or non-existent [
3], while “push factors”, such as urban blight, inadequate public service provision, and concentrated poverty, continue to incentivize outmigration [
16].
On that note, the “5 in 5” program’s key premise—that demolition can unilaterally reduce vacancy stocks—is vastly oversimplified. Without designing additional instruments to influence, at minimum, the city’s rate of property abandonment (v in
Figure 2) and/or the rate of property reuse (o in
Figure 2), there is no reason to expect relatively non-strategic demolition programs [
11,
27], no matter how aggressive or large in scope [
12], to meaningfully decrease vacant property stocks in shrinking cities. This broad, systems thinking lesson for shrinking cities echoes the chorus of scholars and practitioners who call for demolition programs to be grounded in and guided by comprehensive planning efforts [
2,
13,
35,
36,
37].
To add empirical support to the claim, below we build up to a test of the null hypothesis that demolition activity does not Granger-cause vacancy rates; in other words, that demolition rates do not influence vacancy over time. We expect this null hypothesis to hold up against the alternative that demolition does in fact influence vacancy on its own. Prior to performing this analytical operation, however, it is worth briefly engaging with the iceberg model of systems thinking (
Figure 1) to consider what
mental models underlie efforts like the “5 in 5” program, which appears to be guided by unrealistic assumptions.
While we encourage readers to look elsewhere in the literature for deeper dives into the mental models that persist in many shrinking cities (e.g., [
16,
51]), here it is worth highlighting one. Specifically, as prior research has already pointed out [
15], demolition programs are regularly crafted with a pro-growth bias, whereby growth is seen as “success” and shrinkage and decline are framed as “failure” [
15] (also see [
8,
16,
23]). Within this mental model, vacant and abandoned properties are typically considered blighting factors and, consequently, hindrances to growth and development (and therefore obstacles to success) [
15]. Thus, the logic goes that eradicating blighting factors via structural demolition will remove barriers to growth and development, thereby, seemingly automatically, triggering new development [
8]. In other words, based on past urban growth scenarios [
4], decision-makers often hold onto the notion that there is an assumed demand for developable land in all cities, including shrinking ones [
23]. Once again, this reasoning ignores structural issues that lie below the surface of the problem. Namely, recall that real estate demand in shrinking cities tends to be critically low in most places [
3], which implies that blight removal (via demolition) by itself is a poor economic development strategy [
8].
1.4. Recap
In summary, urban researchers uniformly agree that shrinkage and decline are complex phenomena with multiple interdependent causes and multiple interdependent consequences (e.g., [
5,
8,
16,
39]). As such, an observable problem like a high stock of vacant and abandoned properties cannot be fixed by a single, independent policy instrument such as structural demolition. A systems thinking perspective makes the reason for this outcome clear. Simply put, demolition is only one outflow from a vacant property stock that is affected by at least two other dynamic flows (
Figure 2). Without designing programs to account for those other sources of flow, expectations about the capacity for large-scale demolition programs to reduce vacancy stocks should be kept in check.
Related to this point, scholars have critiqued large-scale demolition programs in general [
8], and Buffalo’s “5 in 5” demolition program in particular [
15], on the grounds that they are typically reactive, disconnected from larger comprehensive planning efforts, and built on a pro-growth mental model containing unrealistic expectations about development potential in shrinking communities [
11,
15,
23,
27]. What is still lacking to date, though, is an empirical test of the foundational premise from the “5 in 5” and related programs that demolition alone can decrease vacant property stocks in a shrinking city. While our systems thinking framework casts severe doubt on this proposition, it is important to add empirical weight to the argument. Such is the cause taken up herein.
4. Discussion
The introduction to this paper laid out four interconnected research questions aimed at challenging a key, event-oriented-thinking assumption that frequently underwrites large-scale demolition programs in shrinking cities—explicitly, that demolishing vacant properties necessarily decreases vacancy stocks. Our first challenge to this notion was purely conceptual, and in that way its implications extended to shrinking cities beyond Buffalo, NY, USA. More precisely, by filtering the assumption through the toolbox of systems thinking, we pinpointed two non-mutually exclusive issues with it. First, vacant and abandoned property stocks were affected by at least two dynamic flows
other than demolition activity. Thus, and second, to believe that demolition will decrease vacancy in shrinking cities requires
at least one of the following accompanying assumptions/beliefs: (1) the
inflow of vacant and abandoned properties will be strictly less than the
outflow created by demolitions, in which case the outflow related to property reuse and in-migration is immaterial (i.e., even if the rate is zero, the stock will decrease); and/or (2) the
inflow of vacant and abandoned properties will be less than the combined
outflow of demolition coupled with property reuse and/or in-migration (
Figure 2). We argued that both of these accompanying beliefs were consistent with a
mental model (
Figure 1) in which growth, economic development, and high real estate demand were presumed to be the “normal” urban condition (e.g., [
5,
8]). The response to urban shrinkage and its many symptoms from within such a mental model is typically to “trivialize” it [
16] (p. 1511), and to put faith in growth-oriented policies (e.g., [
9]). These policies are commonly detached from the real-world circumstances and prospects of shrinking cities [
8]. Indeed, the literature is quite clear in suggesting that cities experiencing persistent, prevalent, and severe urban shrinkage tend to be caught in downward spirals [
16,
17,
18], escape from which will require new, decline-oriented [
22], or “right-sizing”, programs and policy instruments that break conspicuously from the assumption that urban growth is the norm [
5,
8,
9,
10,
11,
22,
27,
28]. In other words, planning and decision-making in shrinking cities will benefit from new
mental models (
Figure 1).
Our second challenge to the notion that aggressive demolition could unilaterally decrease vacancy stocks came in the form of a multi-phase empirical evaluation of the “5 in 5” program conducted in the shrinking city of Buffalo, NY. While other scholars have critiqued this program on the grounds that it was not connected to larger planning frameworks [
11,
27], it was reactive [
33], and that it did not complete its targeted (“aggressive”) number of demolitions [
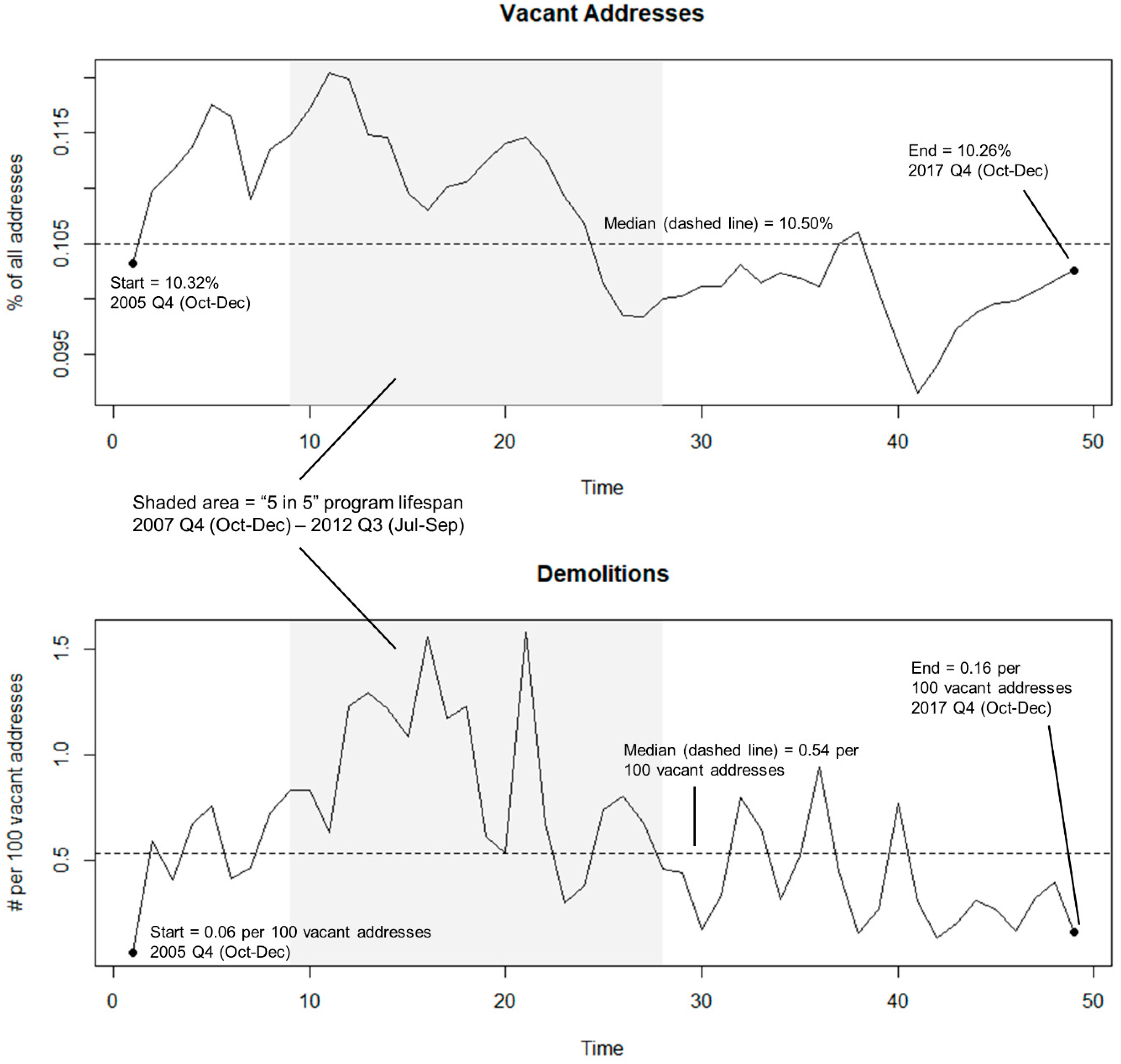
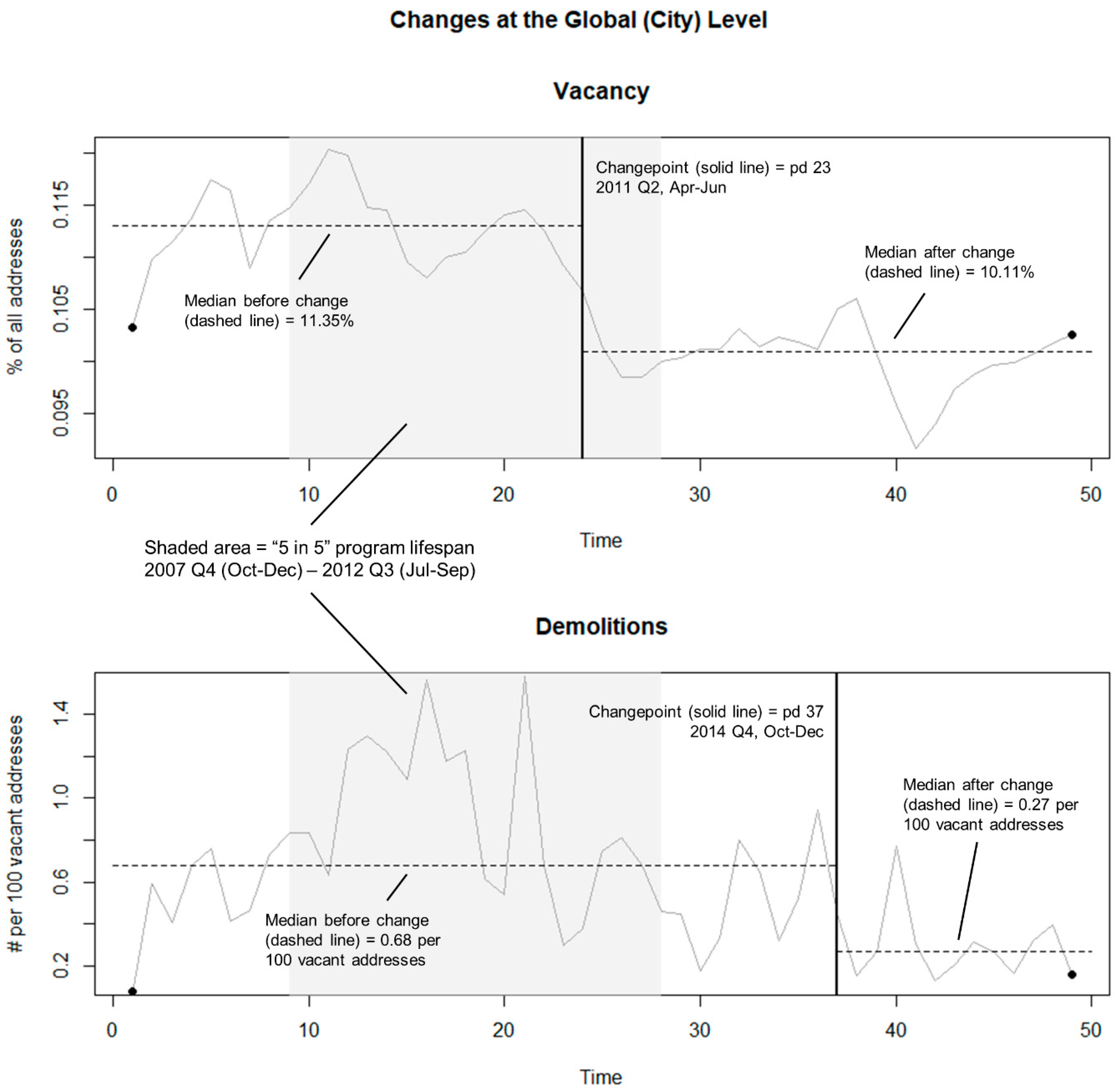
15], we sought to add some empirical weight to this conversation. In particular, we put the foundational assumption—that demolition lowers vacancy—to the test. First, we used spatiotemporal cluster analysis to better understand the spatial footprint of the program. From there, we performed both global (citywide) and local (demolition cluster) changepoint analyses on HUD/USPS vacancy data and city of Buffalo demolition data to establish the optics of the policy. We observed that, in a key administrative dataset used to track vacancy at regular temporal intervals [
15], Buffalo appeared to experience a significant drop in vacancy around the time of the “5 in 5” program. While there was no corresponding (statistically significant) uptick in demolition activity despite the aggressive rhetoric of the “5 in 5” program [
34], it was still tempting to claim that the city’s seemingly swift response to vacancy (refer to
Section 1.3) brought about change. The temptation to reach this conclusion was strongly reinforced when one monitors the same data in the subarea of Buffalo where demolition activity was spatiotemporally clustered. Indeed, in the east-central part of the city, vacancy experienced two significant
negative changepoints during the “5 in 5” program, all while demolition experienced a significant
increase.
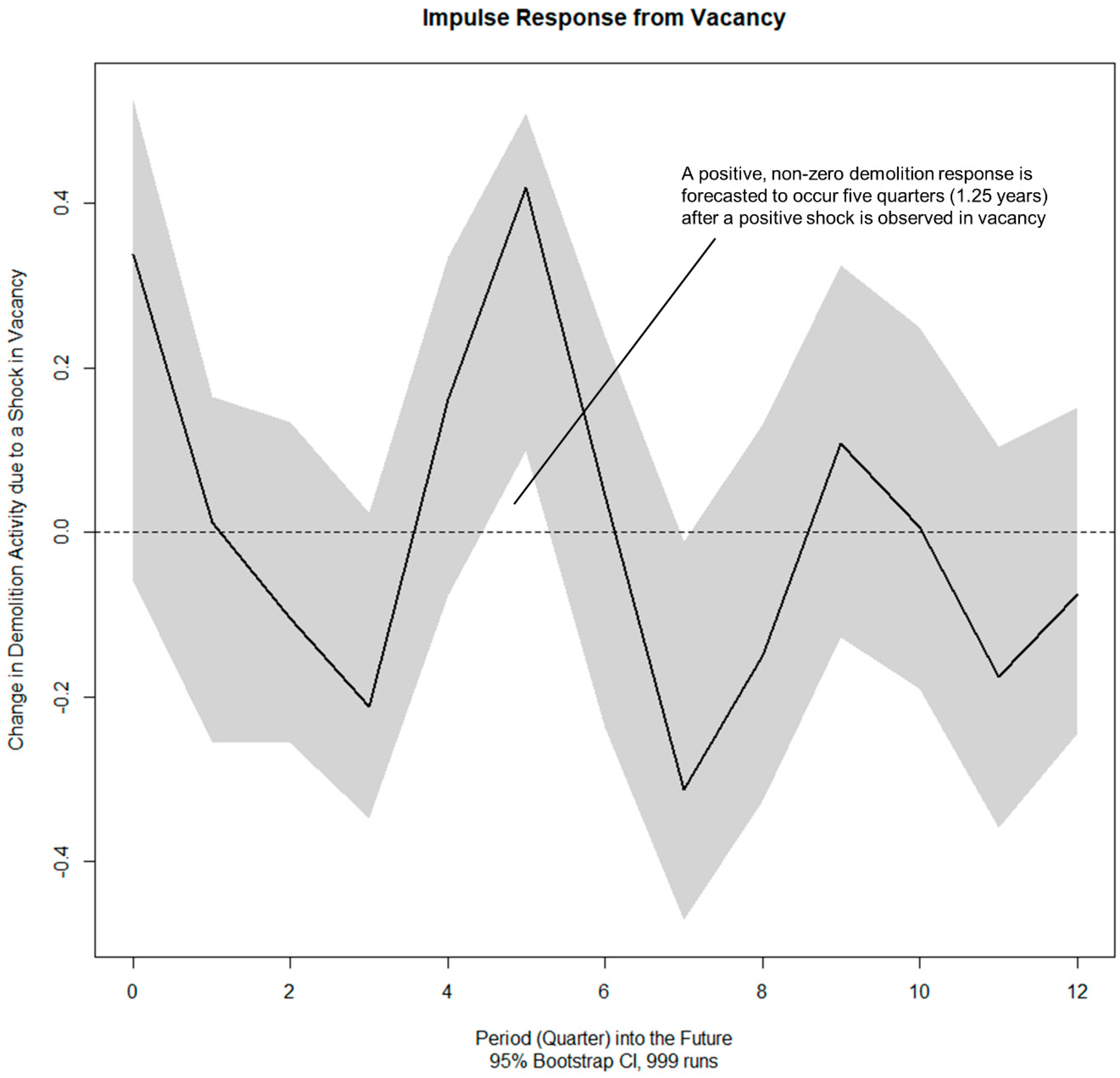
Together, these two sets of results built a strong circumstantial case in favor of Buffalo’s signature demolition program. They also pushed hard against the grain of the systems thinking reasoning described in the preceding paragraph. For that reason, in the final phase of empirical analysis, we directly tested the null hypothesis that the city’s demolition activity caused change in vacancy. Granger-causality tests failed to reject the null hypothesis of no influence, i.e., demolition does
not Granger-cause changes in vacancy stocks, at both the citywide and cluster-wide levels of analysis. At the same time, in the local demolition cluster, we found evidence to support the alternative hypothesis of causality in the opposite direction—that vacancy Granger-causes change in demolition activity. This finding supported speculations that “5 in 5” program was reactive, and, as such, used demolition as a tool in areas perceived to be most affected by vacancy rather than grounding demolition activity in a proactive, comprehensive planning strategy [
11,
15].
In total, then, the flaw with the “5 in 5” program was not that it was underfunded or that it failed to complete its targeted number (5000) of demolitions. Instead, to the extent that the program was ineffective in its goal of moving the city’s vacancy rate [
34], event-oriented thinking atop of a pro-growth mental model were to blame. The city failed to adequately engage with the complexity and dynamics of urban shrinkage and decline (and their many interrelated causes and consequences), preferring to design a “surface-level” solution to a much deeper problem (
Figure 1). The hard lesson for shrinking cities is, as many researchers have rightly observed (e.g., [
9,
11,
16,
27]), that decision-makers must face the realities of shrinkage and break free from growth-oriented mental models and the toolboxes that those models endorse. Planners and policymakers in shrinking cities will have to embrace context and begin to design innovative instruments aimed at stabilization and improving local quality of life for the residents and buildings who remain “after abandonment” [
11,
13,
22,
63].
5. Conclusions
Demolition is a necessary implement in the toolbox of shrinking cities [
2,
14]. When rolled out in standalone form, however, our study suggests that it is not an effective vacancy management strategy. The built-in demand for developable land that tends to exist in growing cities is generally not part of the structure (
Figure 1) of shrinking cities [
3]. As such, demolition must be part of broader, comprehensive planning and policy strategies [
9,
14,
35,
36,
37]. At minimum, complementary efforts are needed (1) to slow or stall the ongoing inflow of property abandonment, and/or (2) to increase the rate at which extant vacant or abandoned properties are reused (
Figure 2). In the absence of these efforts, large-scale demolition programs in shrinking cities are destined to remain faith-based vacancy management strategies. Namely, faith is placed in pro-growth mental models (
Figure 1) which assume that (1) increasing the supply of vacant land will increase developers’ demand for that land, and (2) the resultant development will create new demand for urban housing. The glaring lack of real world evidence to support these beliefs [
3] suggests that decision-makers in shrinking cities must
transform their mental models (see
Section 1.2.1 and [
48]). Strategies built atop these new “right-sizing” [
27] or “smart shrinkage” [
10] mental models should be informed by dynamic analyses of neighborhood change processes and make use of systems thinking. Seeking to develop better, more systemic understandings of neighborhood dynamics will allow for more proactive and predictive policymaking, as opposed to the reactive trap in which many shrinking cities currently find themselves (e.g., [
15];
Figure 7).