Dynamical Modeling and Active Vibration Control Analysis of a Double-Layer Cylindrical Thin Shell with Active Actuators
Abstract
1. Introduction
2. Dynamic Modeling of Double-Layer Cylindrical Thin Shell
2.1. Admittance Analysis of Cylindrical Thin Shell Subsystems
2.2. Support System
2.3. Integrated Solution of Coupled System
- (1)
- is an order square matrix, which describes the transitive relation between the vibration displacement response at the excitation point (along the direction of the vibration source excitation) of the vibration source excitation on the shell A. The point of action of the excitation force from each vibration source is , and the direction of action is ; , and are the angles between and the base vectors , , and . Then, Equation (8) can be used to obtain
- (2)
- is an order matrix, which describes the transitive relation between the vibration displacement response at the point of excitation (along the direction of excitation) of the vibration source on the support excitation of shell A. Given that the installation position of each support on shell A and shell B are and , the excitation force acting on shell A is along the direction
- (3)
- is an order matrix, which describes the transitive relation between the vibration displacement response at the support installation position (along the support direction) and the excitation on shell A. Note that the displacement response at the installation position of each support on the A shell should be in the positive direction of the direction, so according to Equation (8), we can obtain
- (4)
- is an order square matrix, which describes the transitive relation between the vibration source excitation on the A shell and the vibration displacement response at the support installation position (along the support direction). The prescribed positive direction (along direction) of the support excitation acting on shell A is opposite to the prescribed positive direction (along direction) of the displacement response at its position of action, so according to Equation (8), it can be obtained as
- (5)
- In Equation (20), is an order square matrix composed of directional displacement admittance , which is the displacement response along the direction on the B shell to the directional displacement admittance of the support excitation along the direction
2.4. Vibration Power Flow
3. Simulation Analysis of Active Vibration Control
3.1. Simulation Model Establishment
3.2. Definition of Active Feedback Parameters
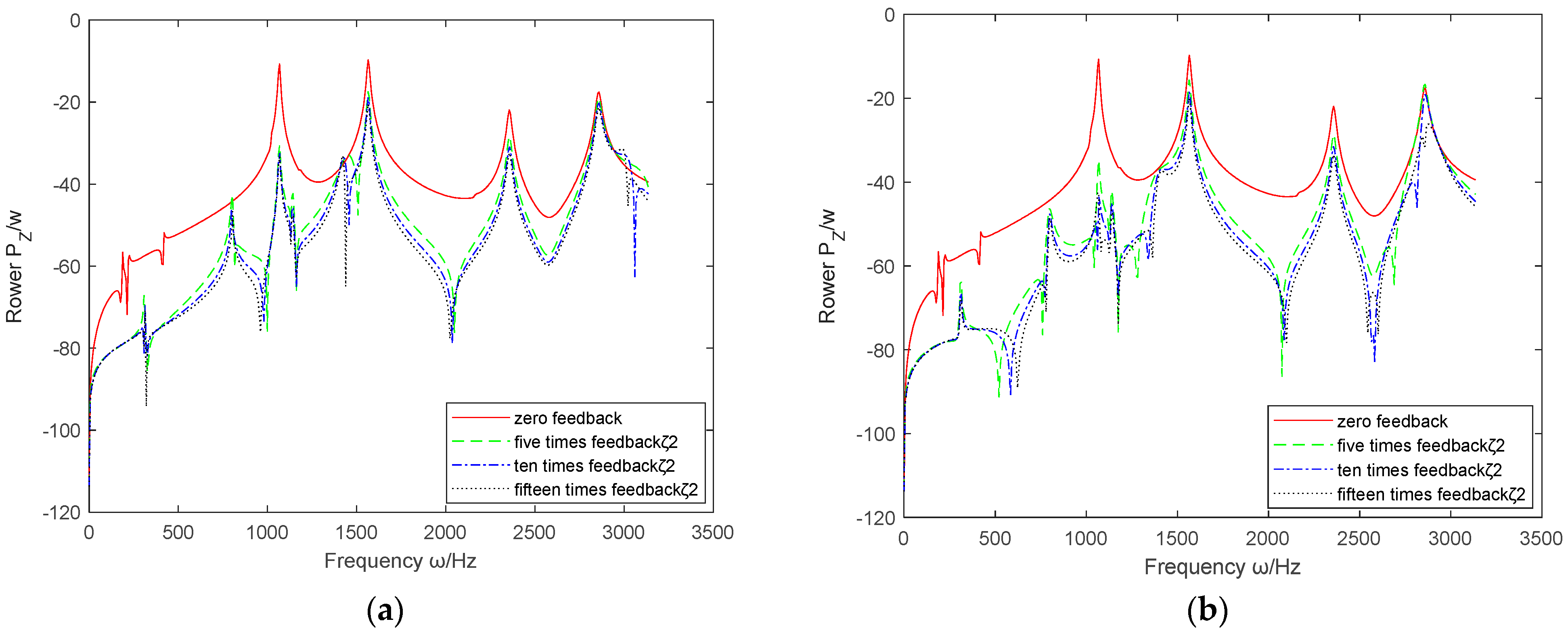
3.3. Analysis and Discussion of Different Feedback Control Methods
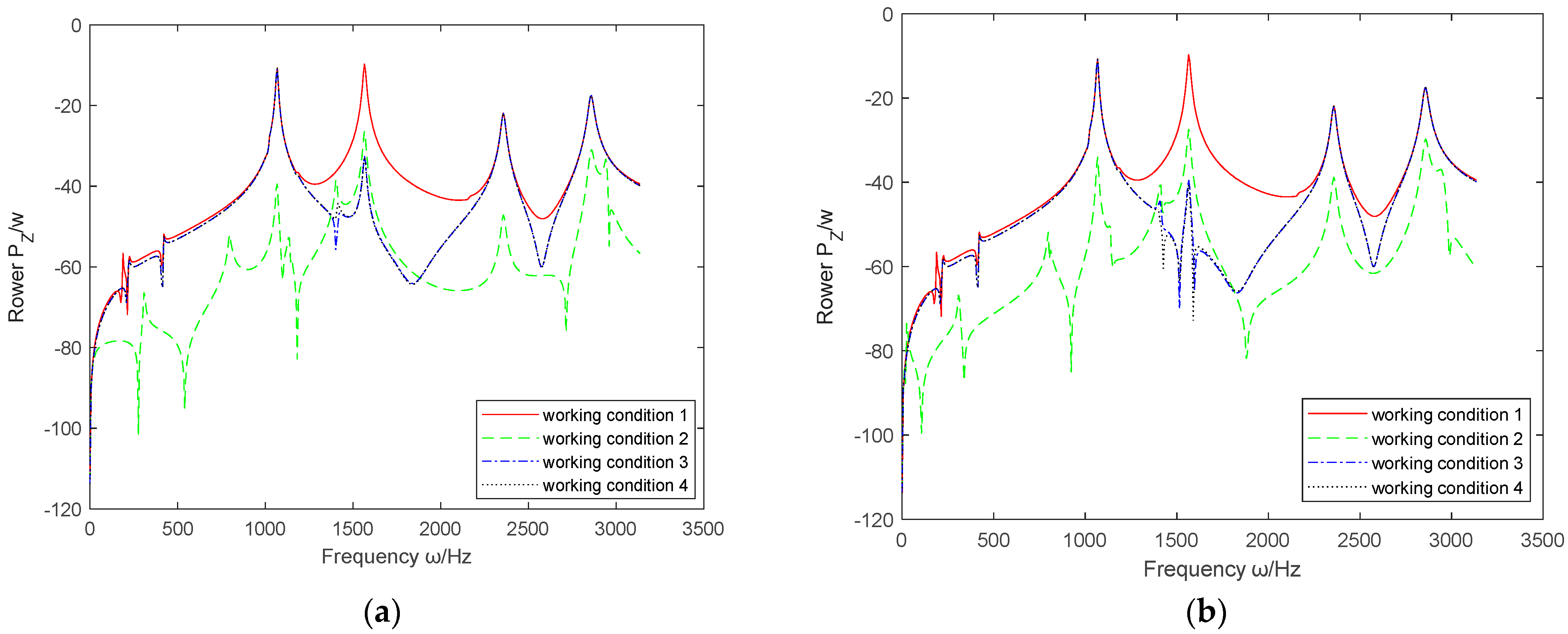
3.3.1. The Influence of Non-Cross Feedback Control Method on the Effectiveness of Active Vibration Control
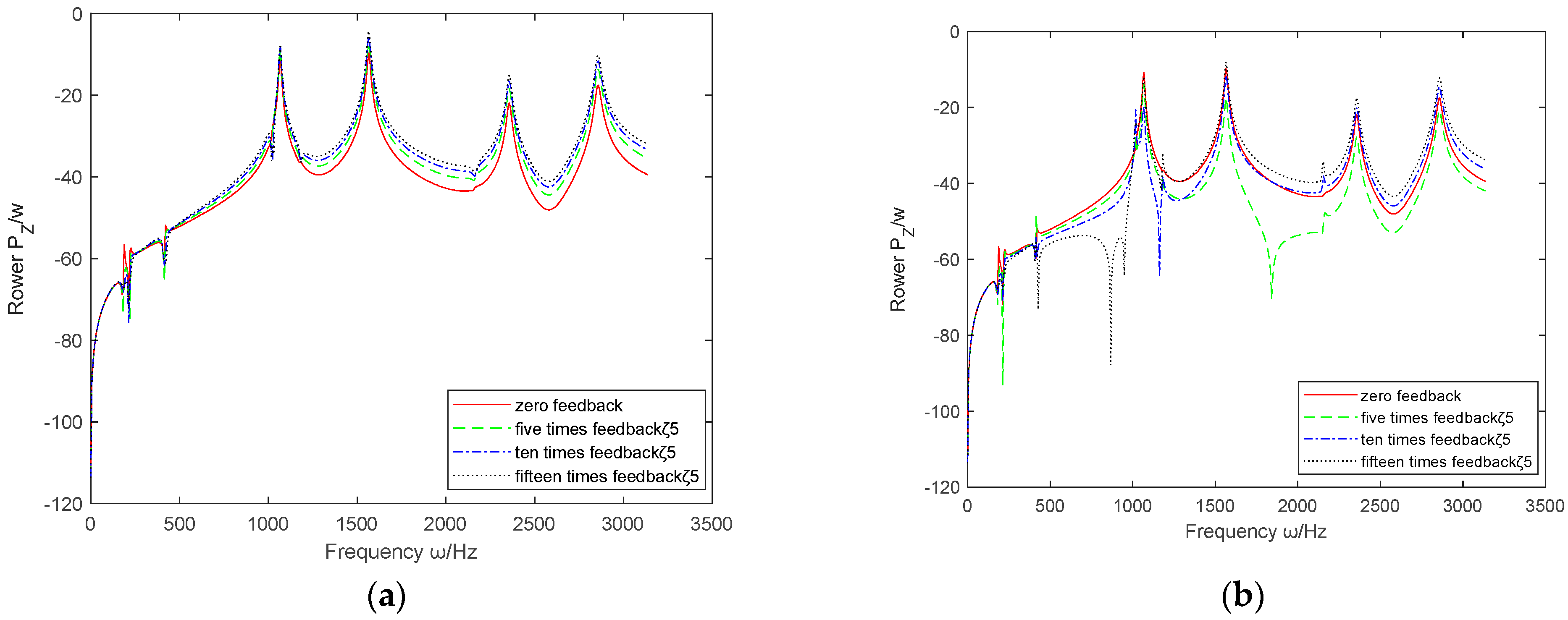
- 1.
- The influence of absolute displacement feedback parameters
- 2.
- The influence of absolute velocity feedback parameters
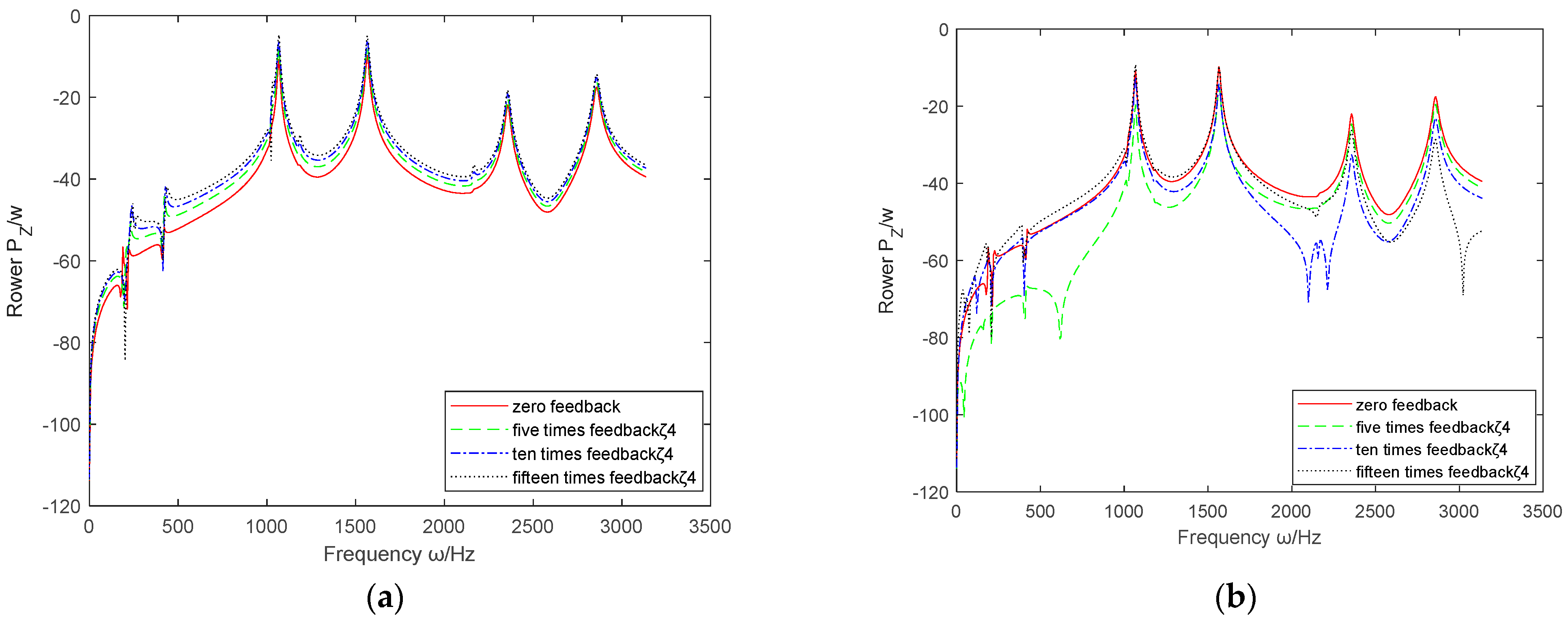
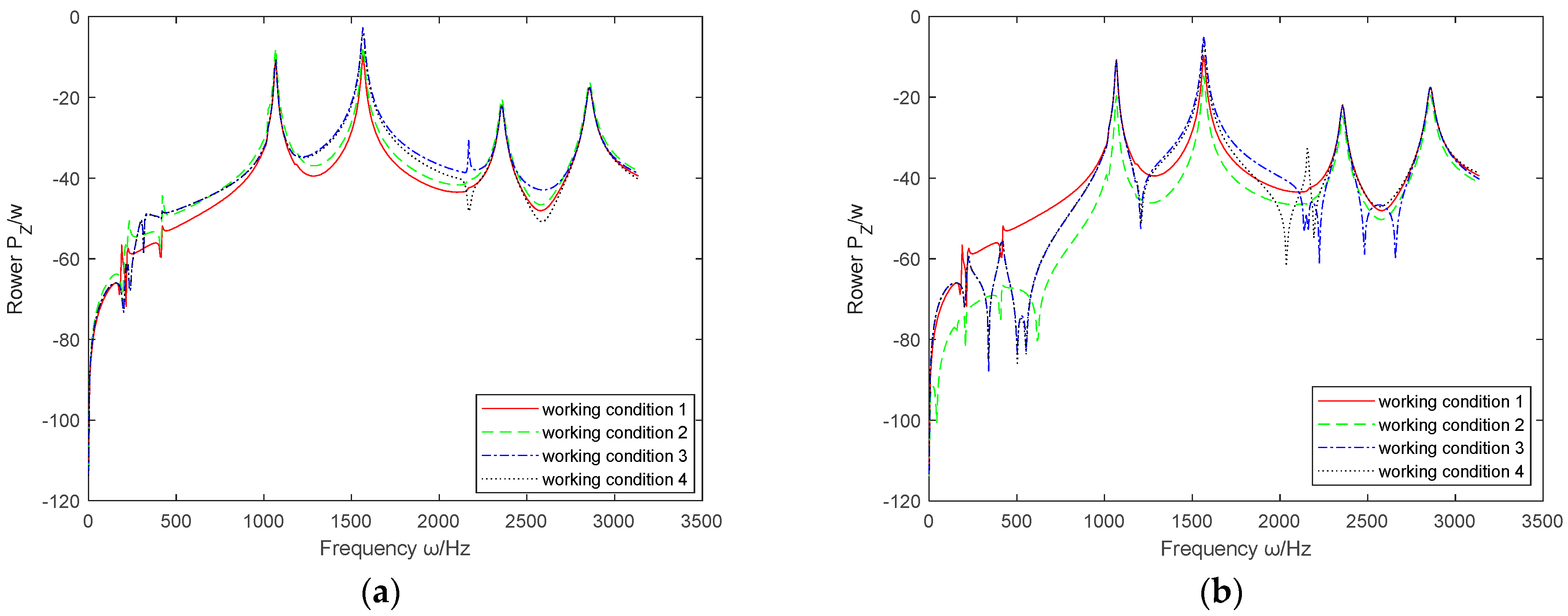
- 3.
- The influence of absolute acceleration feedback parameters .
- 4.
- The influence of relative displacement feedback parameters .
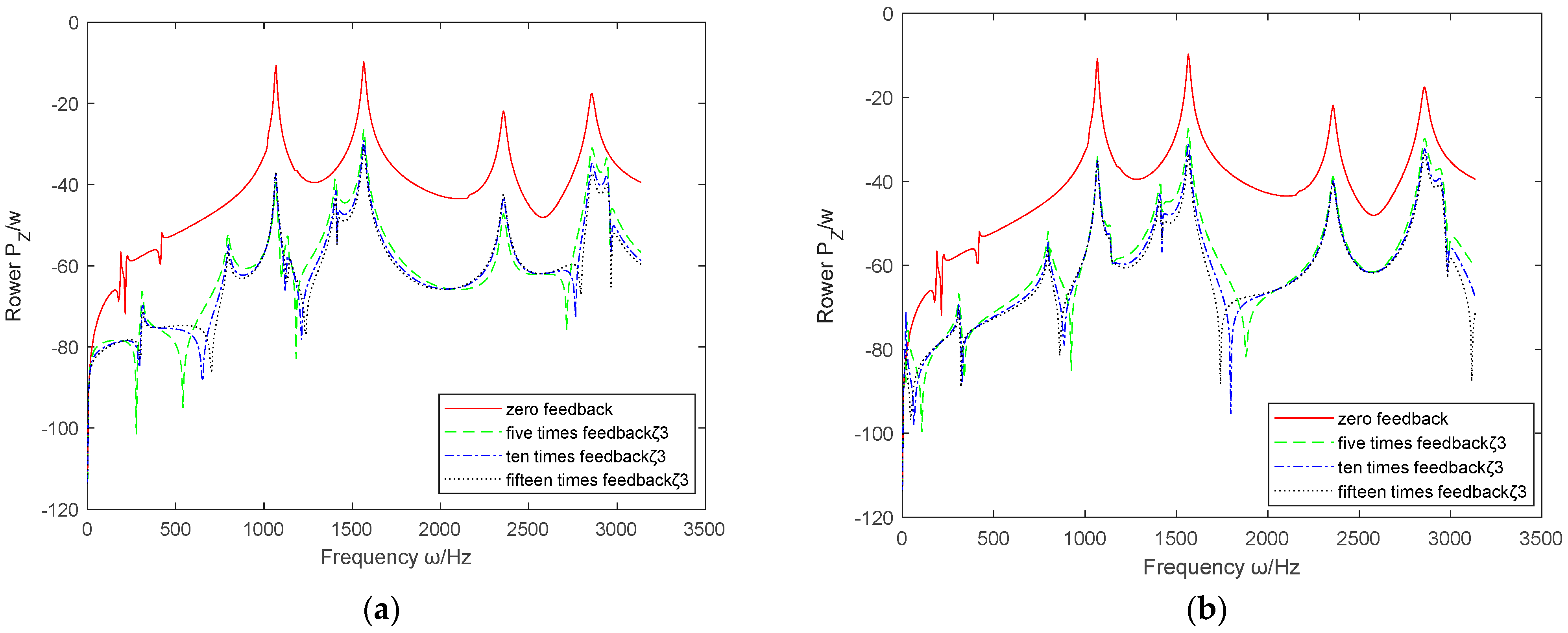
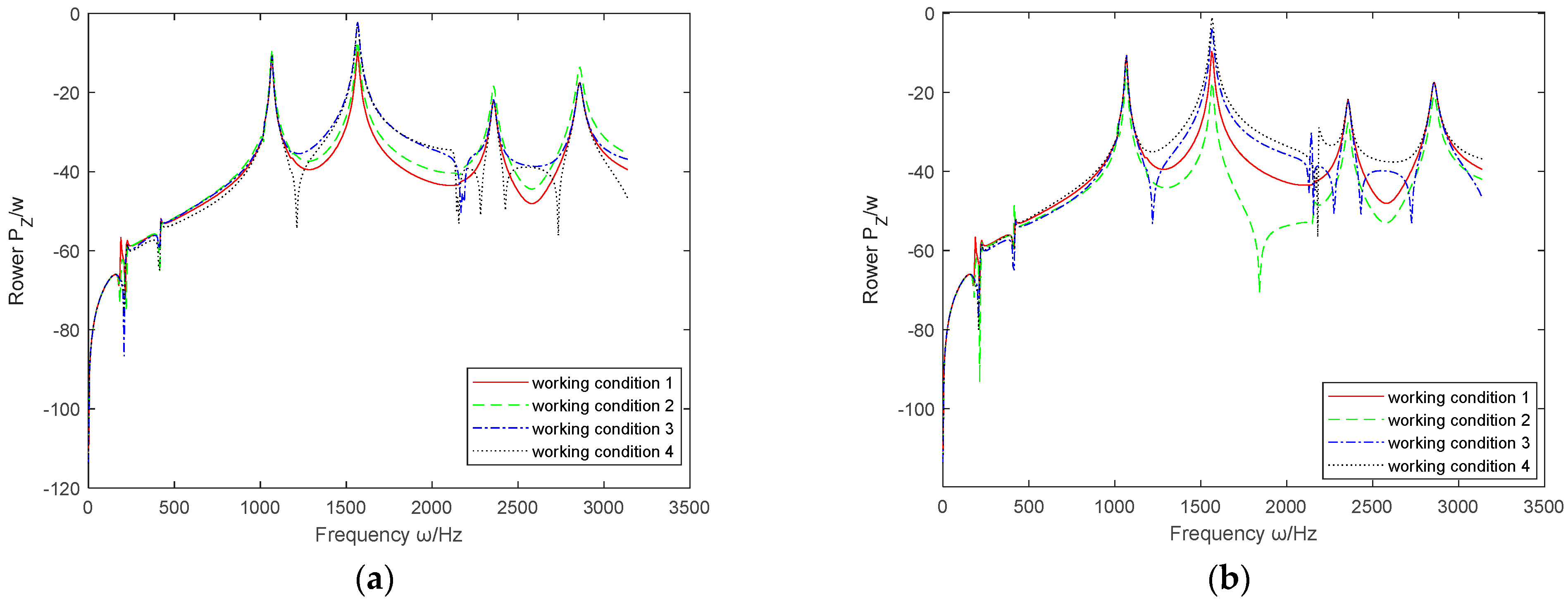
- 5.
- The influence of relative velocity feedback parameters
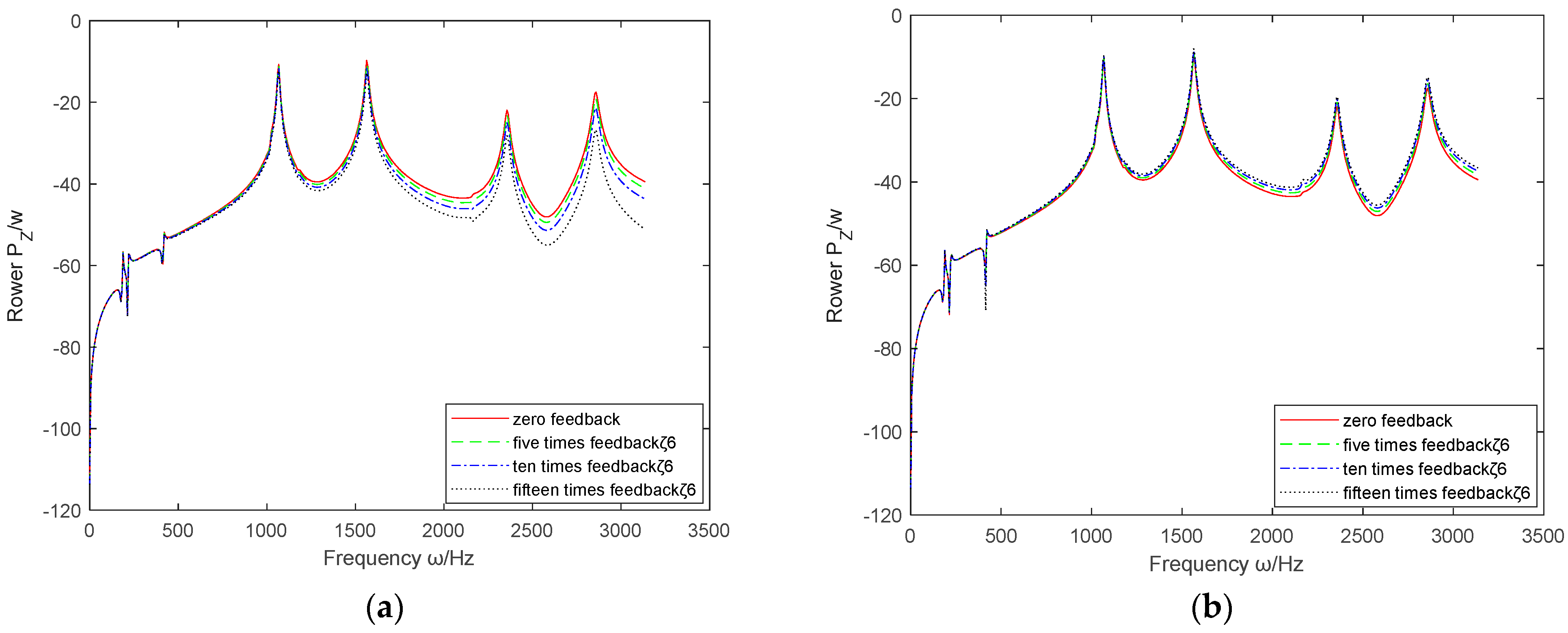
- 6.
- The influence of relative acceleration feedback parameters
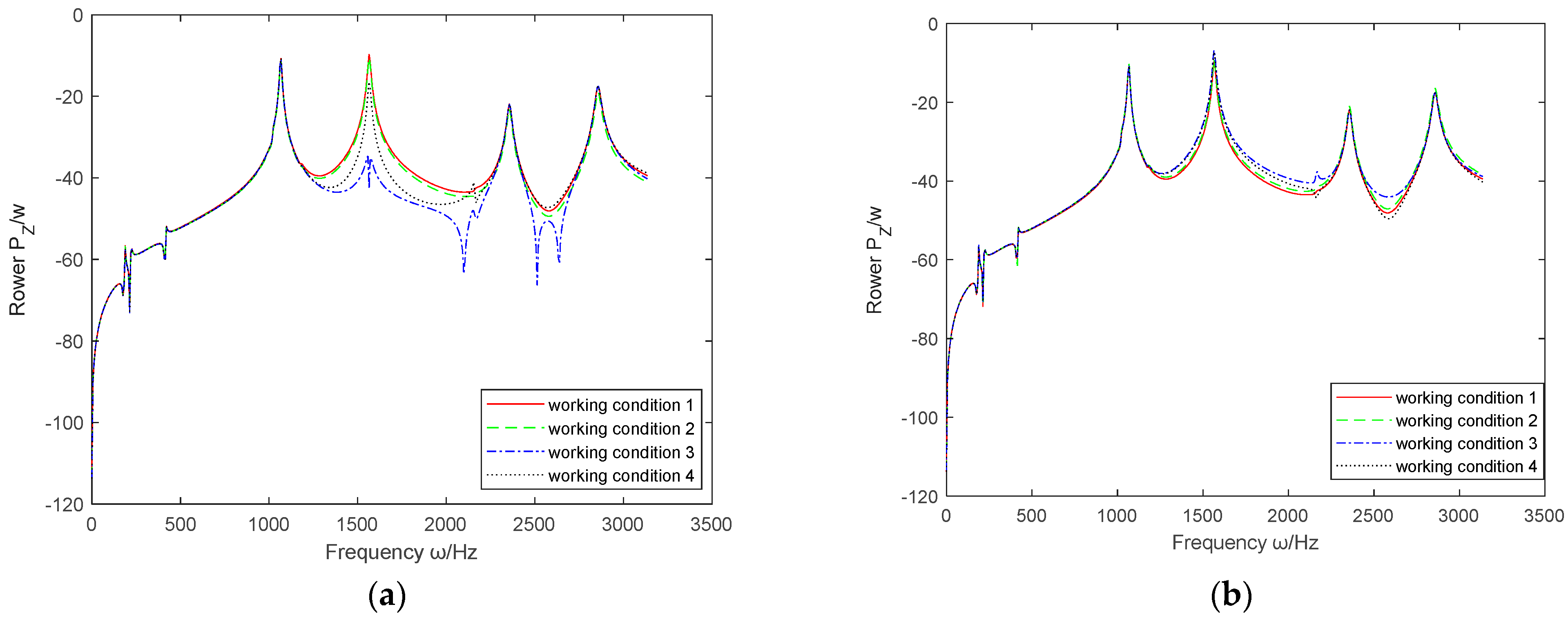
- 7.
- Comparison results of six cases without cross feedback parameters
- (1)
- By comparing the absolute and relative feedback parameters of displacement, velocity, and acceleration, it can be concluded that , , and are generally superior to , , and in vibration control of the coupled system.
- (2)
- Based on the above six sets of images, it can be seen that the effective range controlled by and is the largest, covering the entire working range. The effects of and are not significant and may even cause deterioration.
- (3)
- has improved the active control effect of the coupling system in the middle and low frequencies, but the control effect in the high frequency part is not ideal; on the contrary, has almost no control effect at low frequencies, but when it is positive, the control effect in the mid to high frequency range is also improved, although compared to and , the control effect is not as prominent.
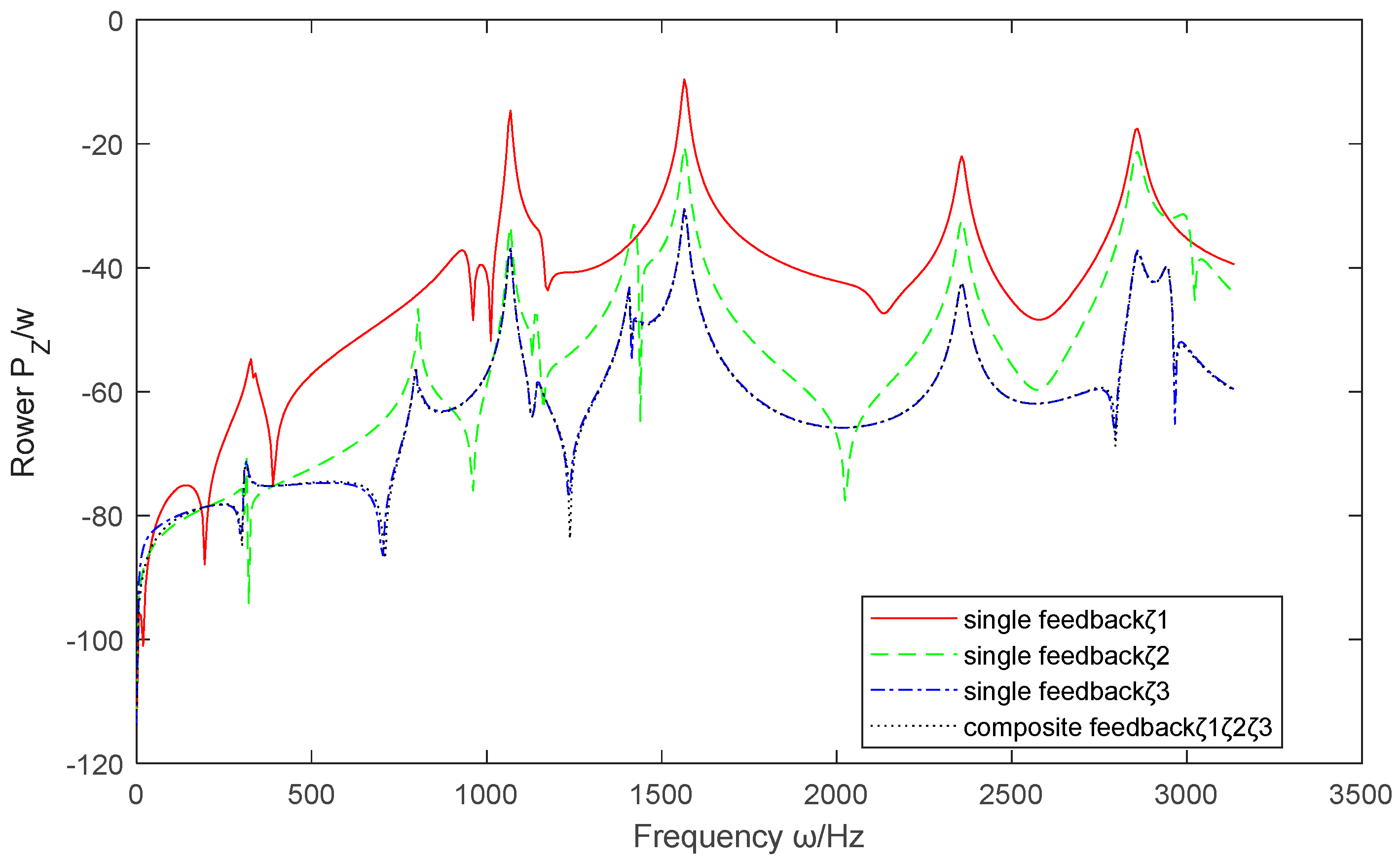
3.3.2. Composite Case Without Cross Feedback Parameters
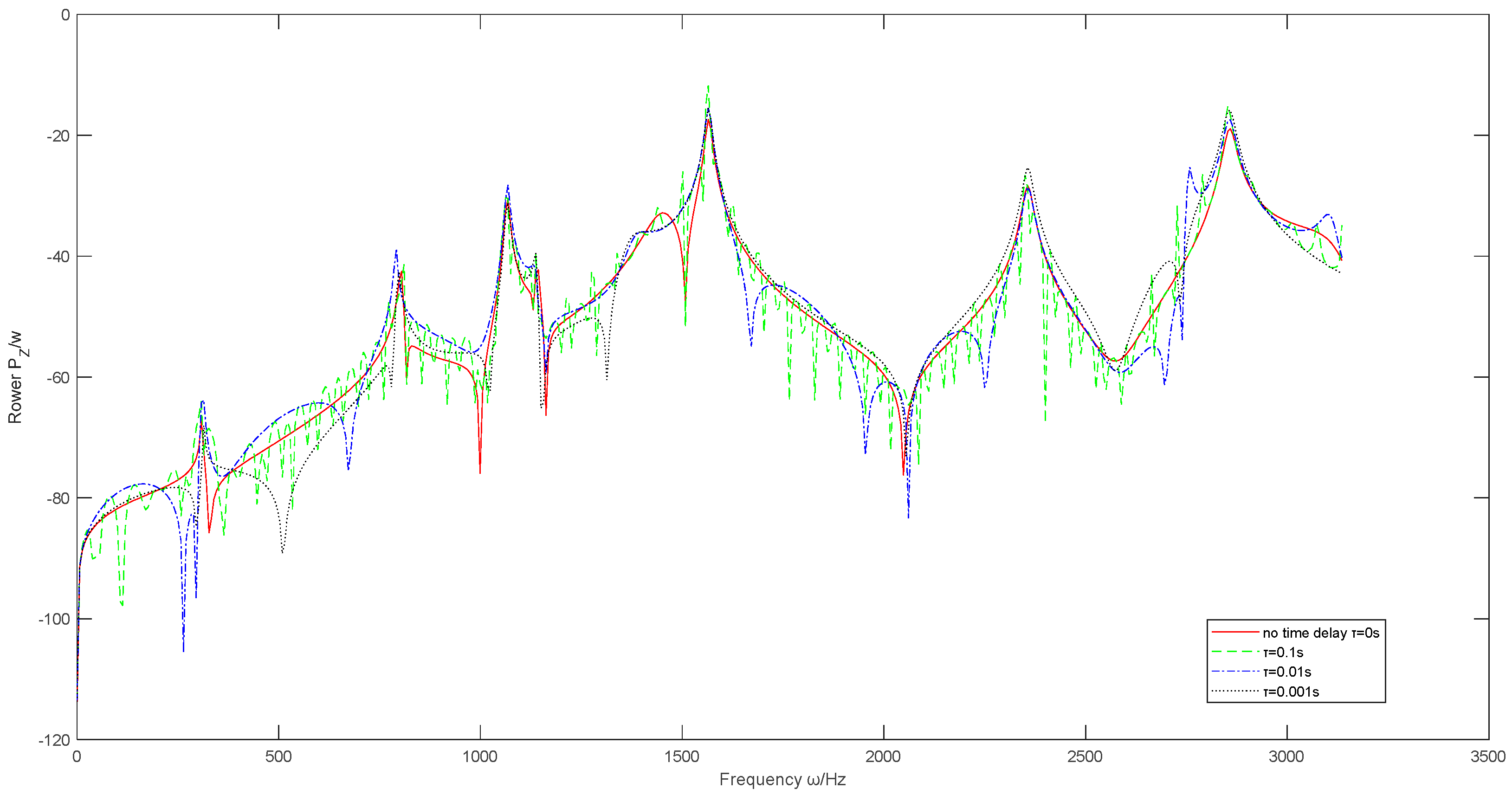
3.3.3. The Influence of Time Delay of Active Actuators on the Effectiveness of Active Vibration Control
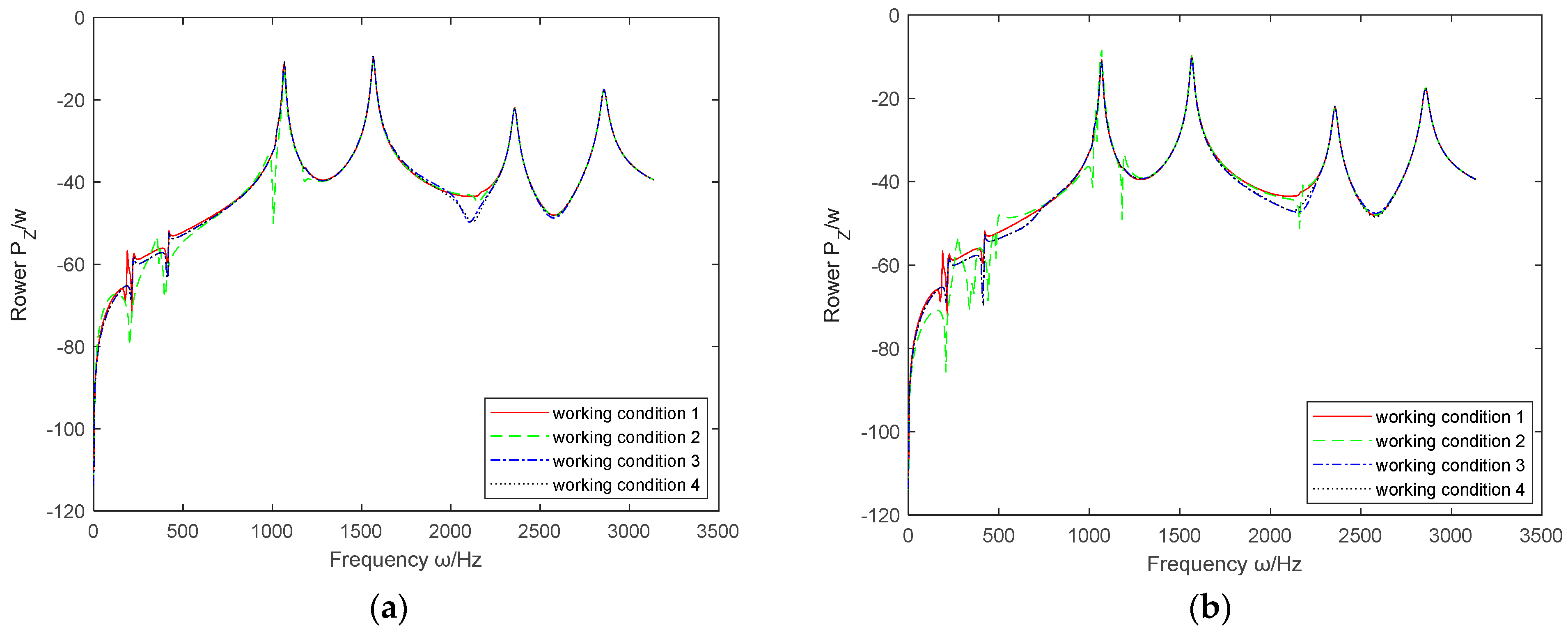
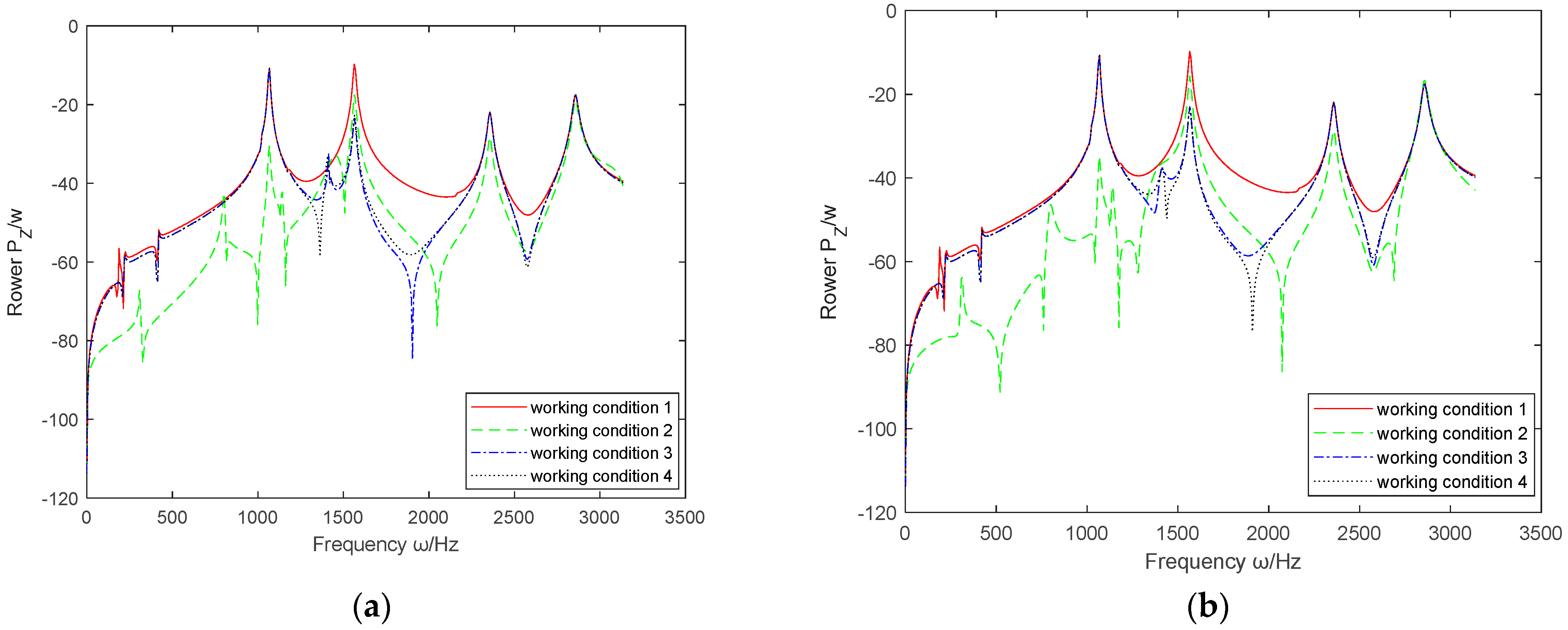
3.3.4. The Influence of Cross Feedback Control Method on the Effectiveness of Active Vibration Control
4. Conclusions
- (1)
- In the non-cross feedback control method, the absolute feedback parameter has a better overall vibration control effect on the coupled system than the relative feedback parameter. In addition, the absolute velocity and acceleration feedback parameters have the largest effective range and the most obvious effect on improving vibration control. Compared with the vibration control effect of the relative velocity and acceleration feedback process, the power flow curve is smoother and more stable. The absolute displacement feedback parameter improves the control effect of the coupling system’s mid low frequency vibration, while the control effect of the high frequency part is no ideal. However, when the controlled gain is positive, the relative acceleration feedback parameter improves the control effect in the mid high frequency.
- (2)
- In the non-cross feedback control method, the relative displacement and velocity feedback control when the controlled gain is positive, as well as the relative acceleration feedback control when the controlled gain is negative, have a deteriorating effect on the control performance of the system. Thus, for absolute feedback control parameters, the control effect of relative feedback control parameters is unstable, and if the controlled gain is not selected appropriately, it will have the opposite effect.
- (3)
- In the non-cross feedback control method, except for the relative acceleration feedback control parameter, all other feedback parameters have a certain low frequency control effect, especially the control effect of the three absolute feedback control parameters is the most prominent. If the influence of time delay is considered, the low frequency control effect will be more obvious.
- (4)
- Appropriately increasing the delay compensation of the active actuator can improve the mid low frequency control effect of the coupled system, but it has little impact on the high frequency region, and excessive delay compensation can make the power flow curve of the coupled system extremely unstable.
- (5)
- When the absolute displacement feedback parameter is applied, considering factors such as cross feedback control and time delay, the difference in its image is not significant. According to (1), the working range of absolute velocity and acceleration feedback control is very wide, but considering the cross feedback control method, its improvement degree is suppressed over a large area. The relative acceleration feedback parameter has little effect at low frequencies, regardless of whether cross feedback or time delay is considered. However, at medium to high frequencies, cross feedback control enhances the effect of no cross feedback, while time delay suppresses the effect of cross feedback control. Among the three relative feedback control parameters, the role of the cross feedback control method is actually to amplify the vibration control effect of the non-cross feedback control method, whether this effect is improved or deteriorated.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Deduction of Vibration Differential Equations for Cylindrical Thin Shells
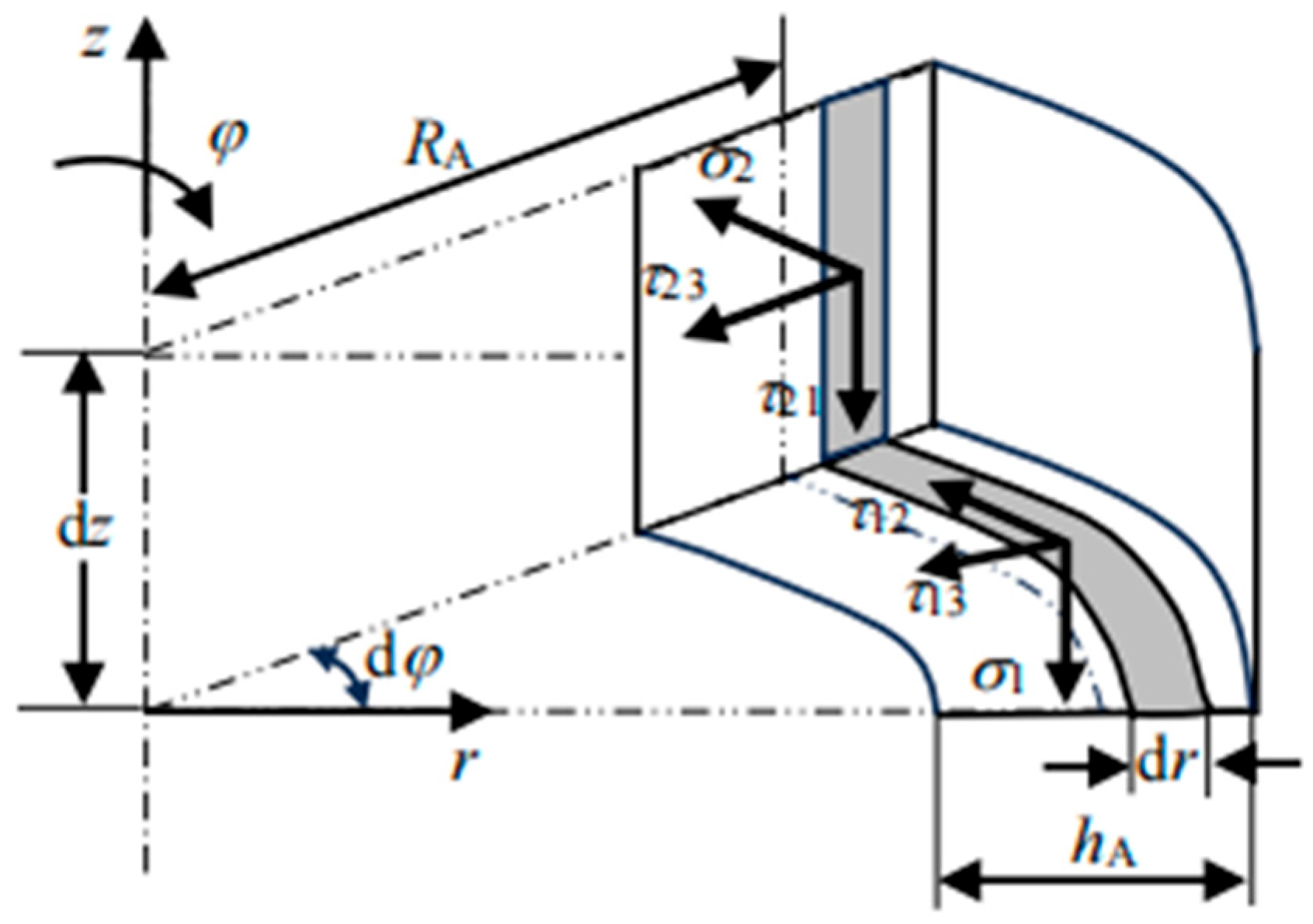
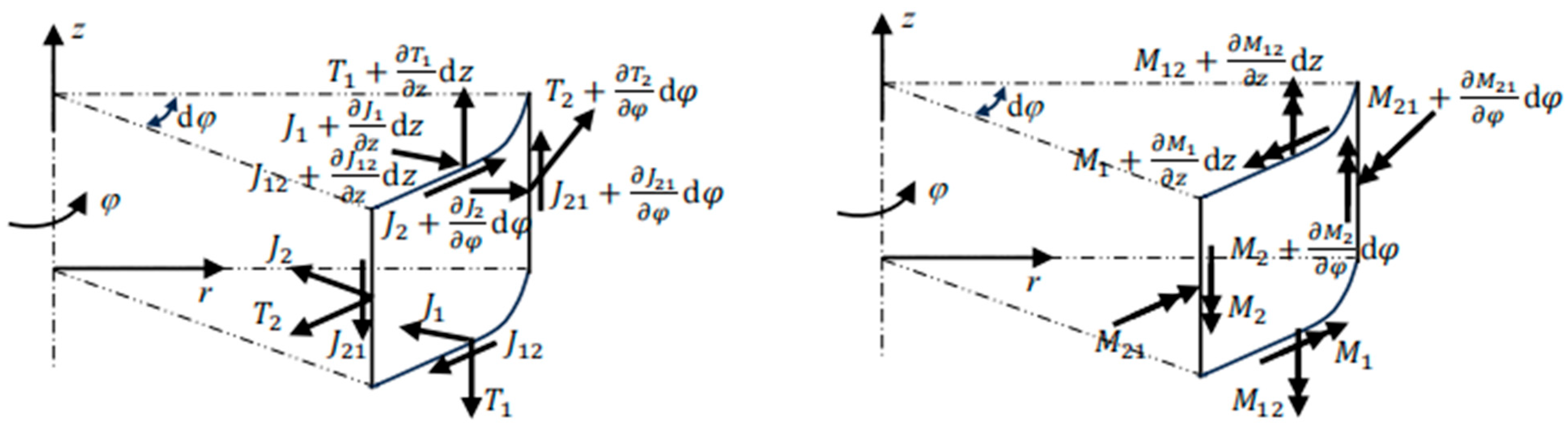
Appendix B. Admittance Function Form of Double-Layer Cylindrical Thin Shell Based on Simply Supported Boundary
Appendix C. Summary of Results from Various Discussions in Part Three
| Large Branch Situation | Specific Situation | Feedback Control (+,−) | Low Frequency | Intermediate Frequency | High Frequency | Overall Control Effect |
|---|---|---|---|---|---|---|
| No cross feedback control | Absolute displacement | + | improve | improve instability | no | medium |
| − | ||||||
| Absolute velocity | + | improve | improve | improve | high | |
| − | ||||||
| Absolute acceleration | + | improve | improve | improve | high | |
| − | ||||||
| Relative displacement | + | deteriorate | deteriorate | deteriorate | negative | |
| − | improve | improve | improve | high | ||
| Relative velocity | + | deteriorate | deteriorate | deteriorate | negative | |
| − | improve | improve instability | deteriorate | low | ||
| Relative acceleration | + | improve a bit | improve a bit | improve a bit | medium | |
| − | no | deteriorate a bit | deteriorate a bit | negative | ||
| Composite case without cross feedback parameters | Absolute comparison | improve | improve | improve | appropriate combination control results in improved performance | |
| Relative comparison | deteriorate | deteriorate | deteriorate | |||
| All comparison | improve | improve | improve | |||
| Non-cross feedback control | Consider the case of time delay | improve | improve a bit | improve a bit | high | |
| Cross feedback control | Absolute displacement | improve instability | improve a bit | no | medium | |
| Absolute velocity | improve instability | improve instability | improve instability | medium | ||
| Absolute acceleration | improve instability | improve instability | improve instability | medium | ||
| Relative displacement | deteriorate | deteriorate | deteriorate | negative | ||
| improve | improve | improve | high | |||
| Relative velocity | improve a bit | unstable control effect | unstable control effect | low | ||
| Relative acceleration | no | improve | improve | medium | ||
| deteriorate | deteriorate | negative |
References
- Zhang, L.; Zhao, L.; Pan, L. Research progress of composite cylindrical shells. Polym. Compos. 2023, 44, 7298–7316. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, H.; Li, P. Axisymmetric finite element boundary element coupling calculation method for vibration of cylindrical shells with sealing plates in dynamic water. J. Vib. Eng. 2025, 38, 687–696. [Google Scholar]
- Nie, L. Study on the buckling behavior of double-layer cylindrical shells under uniform axial compression. Jiangsu Univ. Sci. Technol. 2023. [Google Scholar]
- Liu, W.; Pang, L.; Lv, Z. Free Vibration Analysis of Functionally Graded Piezoelectric Porous Microcylinder Shell with Elastic Support. J. Appl. Mech. 2024, 41, 411–421. [Google Scholar]
- Wang, T.; Tan, D.; Hou, Y. Analytical and experimental investigation of vibration response for the cracked fluid-filled thin cylindrical shell under transport condition. Appl. Math. Model. 2025, 142, 115969. [Google Scholar] [CrossRef]
- Liu, X.; Sun, W.; Liu, H. An investigation of vibration responses for bolted composite flanged-cylindrical shells considering material and joint nonlinearity. Thin Walled Struct. 2024, 204, 112335. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, X.; Kong, J. Preparation process and vibration characteristics analysis of composite cylindrical shell with co cured damping film embedded. J. Weapon Equip. Eng. 2024, 45, 254–261. [Google Scholar]
- Lv, Z.; Liu, W.; Liu, C. The influence of thermal environment on the modal frequency of functionally graded thin-walled cylindrical shells. Noise Vib. Control. 2022, 42, 28–33. [Google Scholar]
- Hu, Z.; Li, S.; Liu, Z. Analysis of Bearing Capacity and Explosion Resistance of Double layer Pressure resistant Reinforced Cylindrical Shell Structure. Chin. Ship Res. 2024, 19, 205–216. [Google Scholar]
- Tang, Q.; Li, B.; Ding, Z. Optimization of buckling bearing capacity of sandwich cylindrical shell structure under axial compression load. Mech. Des. Manuf. 2020, 80–84. [Google Scholar]
- Li, S.; Zhu, S.; He, W. Optimization design characteristics analysis of titanium alloy double-layer reinforced cylindrical shell under different design requirements. Chin. Ship Res. 2025, 20, 317–328. [Google Scholar] [CrossRef]
- Liu, S.; Huo, R.; Wang, L. Vibroacoustic Transfer Characteristics of Underwater Cylindrical Shells Containing Complex Internal Elastic Coupled Systems. Appl. Sci. 2023, 13, 3994. [Google Scholar] [CrossRef]
- Wang, L.; Huo, R. Effect of Support Stiffness Nonlinearity on the Low-Frequency Vibro-Acoustic Characteristics for a Mechanical. Inventions 2023, 8, 118. [Google Scholar] [CrossRef]
- Wang, R.; Huang, J. Research on the Relationship between Structural Parameters and Instability Modes of Ring Ribbed Cylindrical Shells. Equip. Environ. Eng. 2025, 22, 77–86. [Google Scholar]
- Liu, W.; Wang, X.; Tang, Y. Research on the control effect of irregular spacing between large ribs on vibration transmission of cylindrical shells. Ship Sci. Technol. 2023, 45, 7–13. [Google Scholar]
- Liu, J.; Li, S. Research on Vibration Characteristics of Viscoelastic Damping Cylindrical Shell Based on GHM Model. Dalian Univ. Technol. 2021, 931–943. [Google Scholar] [CrossRef]
- Zhang, J. Optimization analysis of cylindrical shell vibration control based on dynamic absorbe. Key Laboratory of Ship Vibration and Noise, Hubei Acoustic Society. In Proceedings of the 2016 Acoustic Technology Academic Conference China Shipbuilding Research and Design Center, Key Laboratory of Ship Vibration and Noise, Wuhan, China, October 2016; pp. 26–29. [Google Scholar]
- Wang, L.; Huo, R.; Liu, S.; Li, Y.; He, D. Average Energy Transfer Characteristics and Control Strategy of Active Feedback Sound Insulation for Water-Filled Acoustic System Based on Double-layer Piate Structure. Appl. Sci. 2022, 12, 11482. [Google Scholar] [CrossRef]
- Li, X. Research on piezoelectric energy harvesting and active vibration control of cylindrical shells. Master’s Thesis, Zhejiang University, Hangzhou, China, 2012. [Google Scholar]
- Geng, X.; Yin, S.; Zhou, J. Optimization method for active control actuator position of cylindrical shell vibration. J. Underw. Unmanned Syst. 2020, 28, 650–656. [Google Scholar]
- Liu, T.; Wang, C.; Liu, Q. Dynamics and Active Vibration Control Analysis of Piezoelectric Functionally Graded Plates Based on Isogeometric Method. Eng. Mech. 2020, 37, 228–242. [Google Scholar]
- Tang, B.; Li, Y.; Zhang, Z. Research progress on vibration and sound radiation problems of composite multi-layer cylindrical shells. Mater. Introd. 2023, 37, 256–263. [Google Scholar]
- Wang, F.; He, L.; Weng, Z. Modeling of underwater vibration of double-layer ribbed cylindrical shell based on neural network. China Shipbuilding Engineering Society, Key Laboratory of Ship Vibration and Noise. In Proceedings of the 15th Symposium on Underwater Noise of Ships Key Laboratory of Ship Vibration and Noise, Zhengzhou, China, 1 August 2015; pp. 123–129. [Google Scholar]
- Chai, K.; Liu, J.; Lou, J. Vibration characteristics of cylindrical shells with discontinuous connections based on the spectral element method. Int. J. Solids Struct. 2025, 308, 113148. [Google Scholar] [CrossRef]
- Wu, J.; Yan, B.; Wu, W. Vibration Characteristics Analysis of Ribbed Cylindrical Shell Based on Spectral Element Method. China Shipbuild. 2025, 1–11. Available online: http://kns.cnki.net/kcms/detail/31.1497.U.20250217.1616.002.html (accessed on 18 February 2025).
- Xu, Z. Elasticity; Higher Education Press: Beijing, China, 2016; pp. 28–33. [Google Scholar]
- Yu, A.; Zhao, Y.; Hou, J. Study on Vibration Transmission Characteristics of Double layered Shells with Elastic Connections and Interlayer Fluid. Vib. Shock 2023, 42, 167–176+205. [Google Scholar] [CrossRef]




| Structural Parameters | Symbols | Units | Values | Remarks |
|---|---|---|---|---|
| Cylinder height | L | m | 2 | |
| Inner shell thickness | m | 0.015 | ||
| Inner shell thickness | m | 0.01 | ||
| Inner shell thickness intermediate radius | m | 0.35 | ||
| Inner shell thickness intermediate radius | m | 0.4 |
| Material Characteristic Parameter | Symbols | Units | Values | Remarks |
|---|---|---|---|---|
| Poisson’s ratio | non | |||
| Elastic modulus | Pa | |||
| Material density |
| Characteristic Parameters | Symbols | Units | Values | Remarks |
|---|---|---|---|---|
| Drive circuit resistance | ||||
| Electrical time constant | ||||
| Control force output coefficient | 1.1 | |||
| Time delay | s | |||
| Controlled gain | ||||
| Support stiffness | ||||
| Structural damping loss factor | 0.01 |
| Controller Gain Values | k = 1 | k = 2 | k = 3 | k = 4 | k = 5 | k = 6 |
|---|---|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Huo, R. Dynamical Modeling and Active Vibration Control Analysis of a Double-Layer Cylindrical Thin Shell with Active Actuators. Sci 2025, 7, 78. https://doi.org/10.3390/sci7020078
Wu Y, Huo R. Dynamical Modeling and Active Vibration Control Analysis of a Double-Layer Cylindrical Thin Shell with Active Actuators. Sci. 2025; 7(2):78. https://doi.org/10.3390/sci7020078
Chicago/Turabian StyleWu, Yu, and Rui Huo. 2025. "Dynamical Modeling and Active Vibration Control Analysis of a Double-Layer Cylindrical Thin Shell with Active Actuators" Sci 7, no. 2: 78. https://doi.org/10.3390/sci7020078
APA StyleWu, Y., & Huo, R. (2025). Dynamical Modeling and Active Vibration Control Analysis of a Double-Layer Cylindrical Thin Shell with Active Actuators. Sci, 7(2), 78. https://doi.org/10.3390/sci7020078





