Japanese Sword Studies Using Neutron Bragg-Edge Transmission and Computed Tomography
Abstract
1. Introduction
2. Japanese Swords
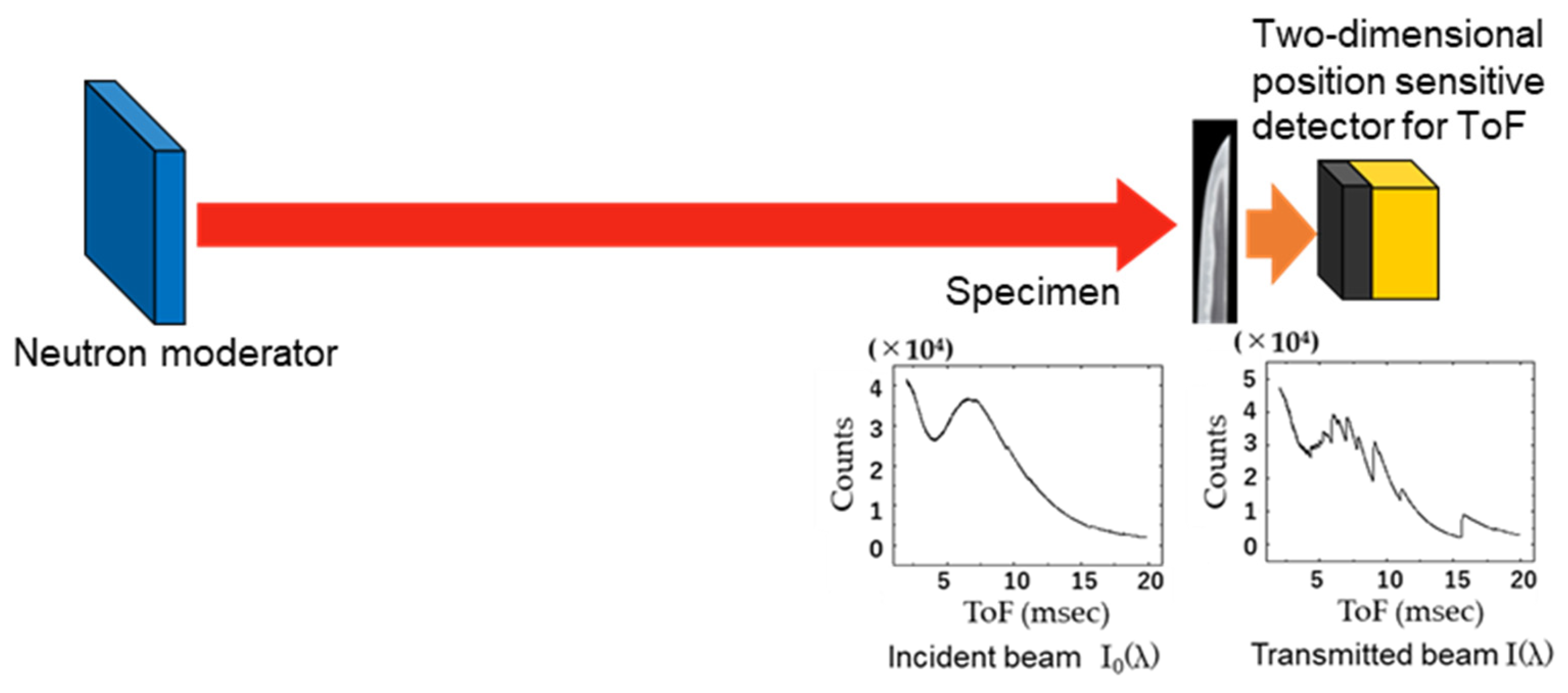
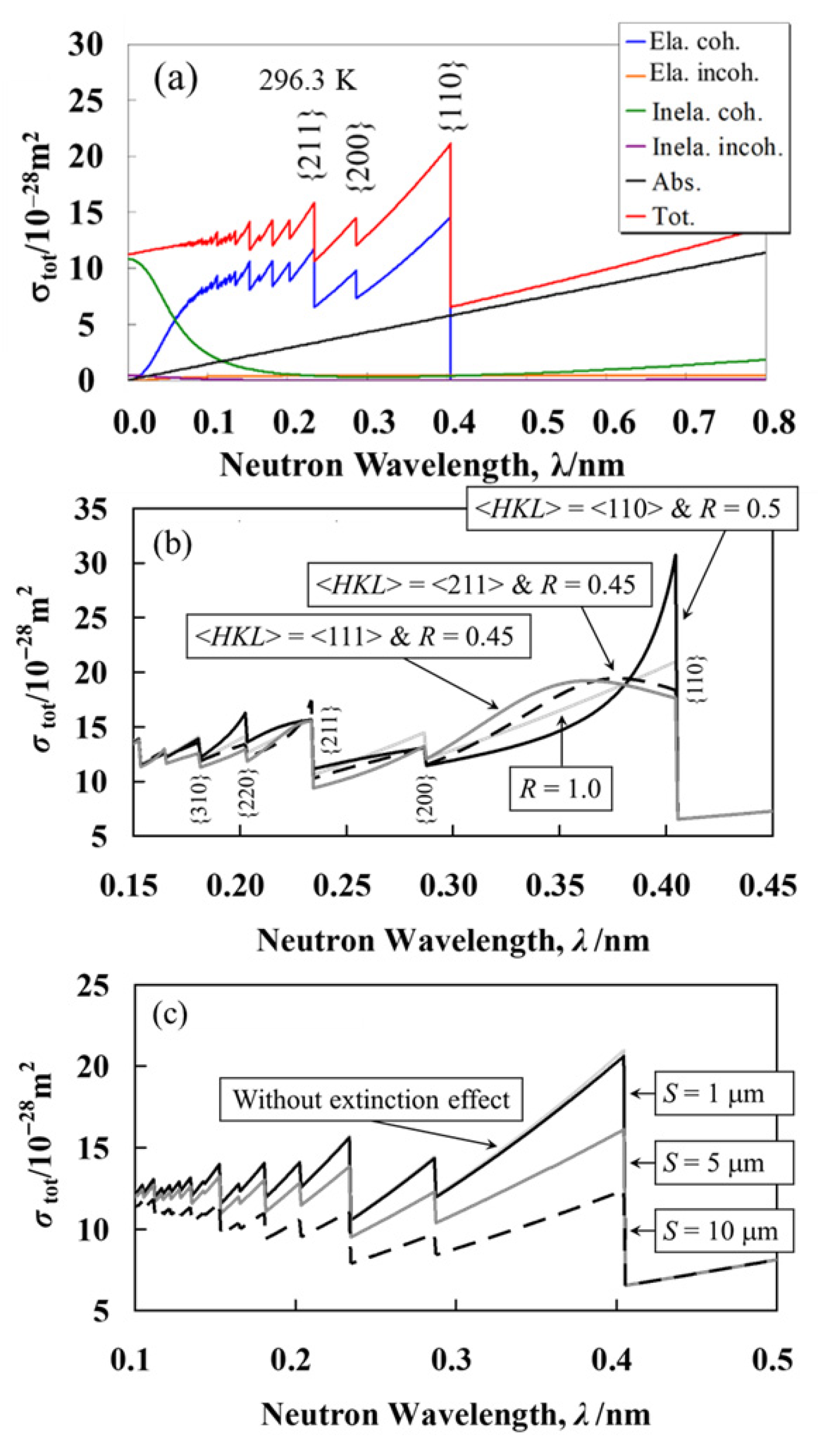
3. Experimental Methods
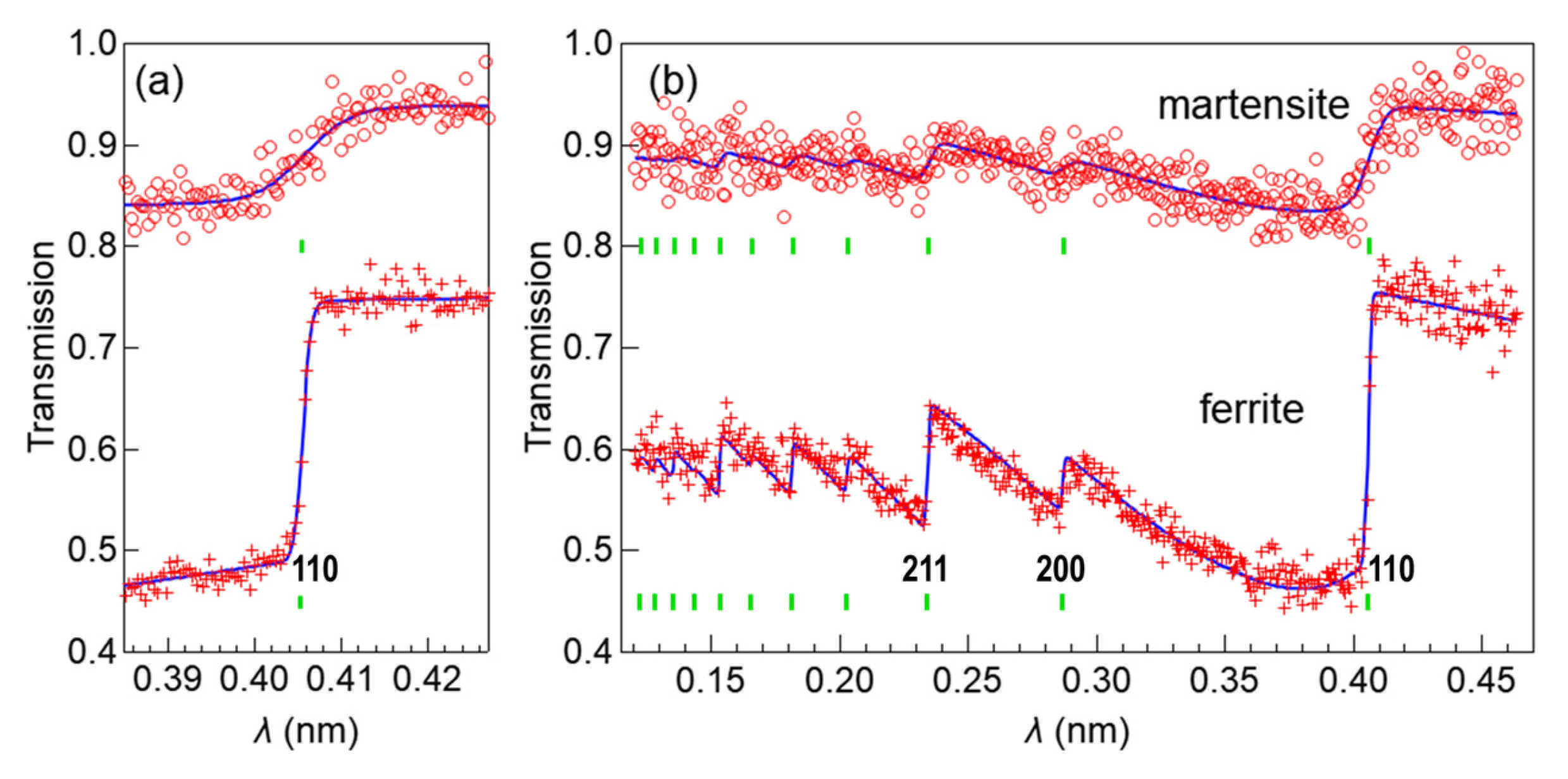
4. Comparison of Neutron Imaging Results
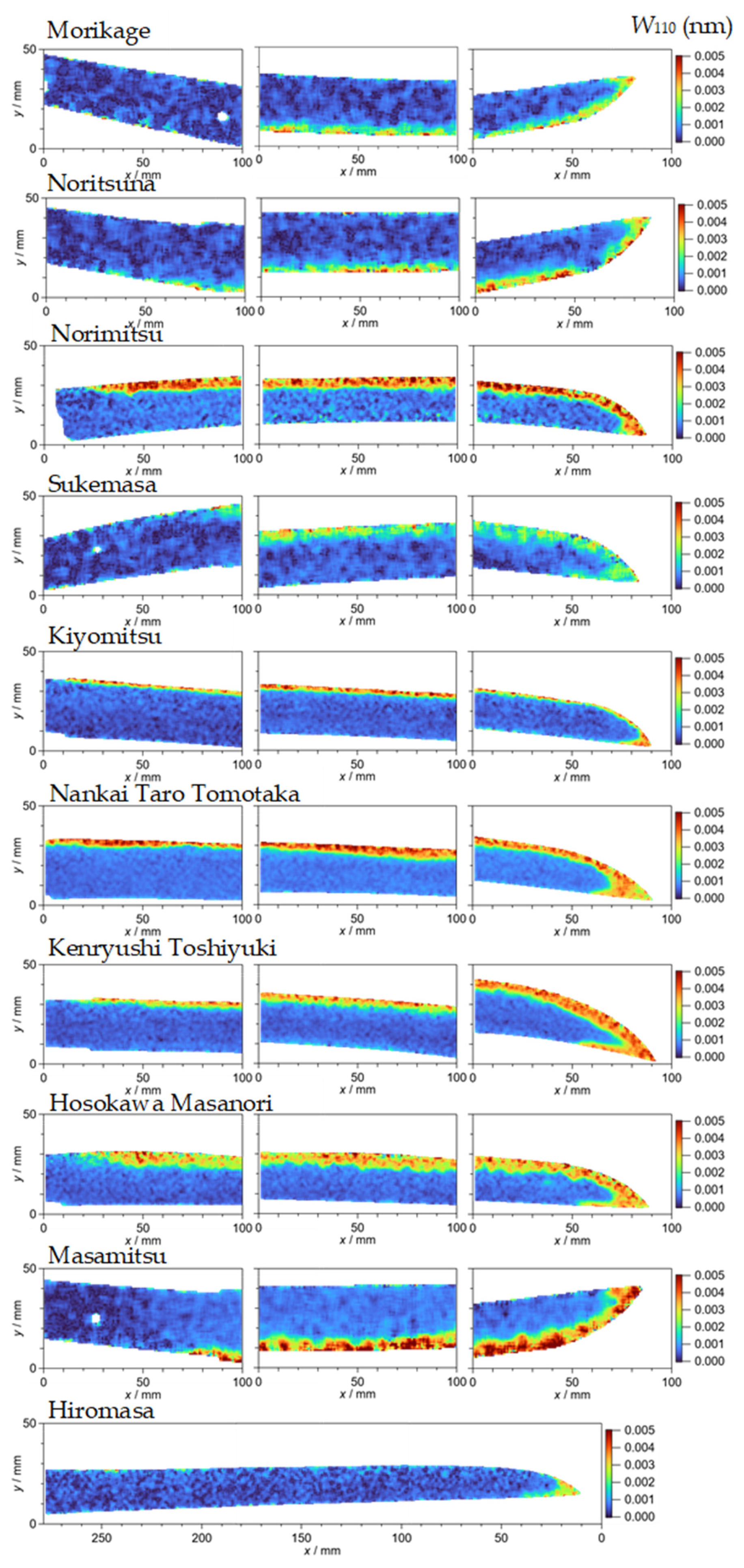
4.1. Edge Broadening W110 (Quenching Region)
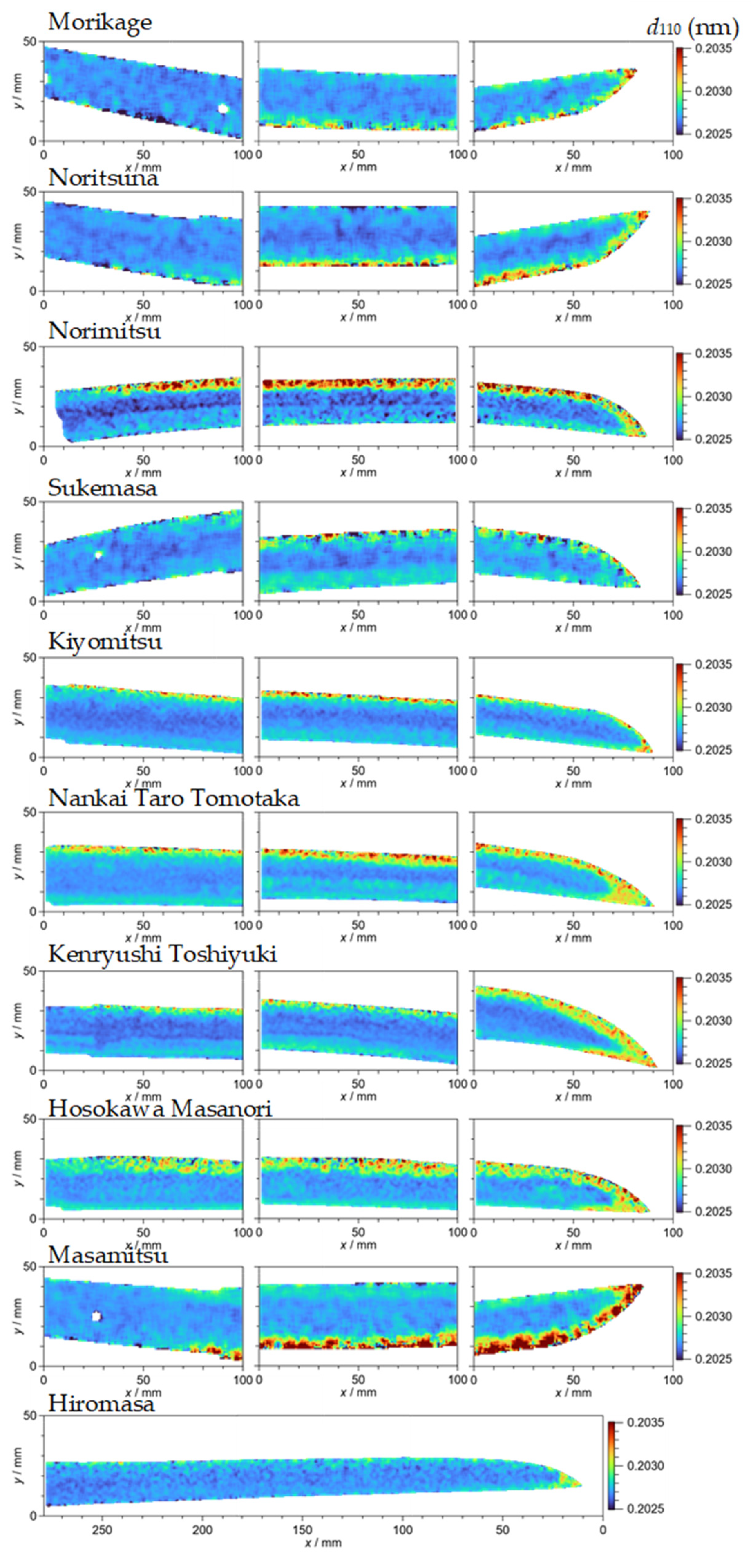
4.2. Lattice Plane Spacing d110
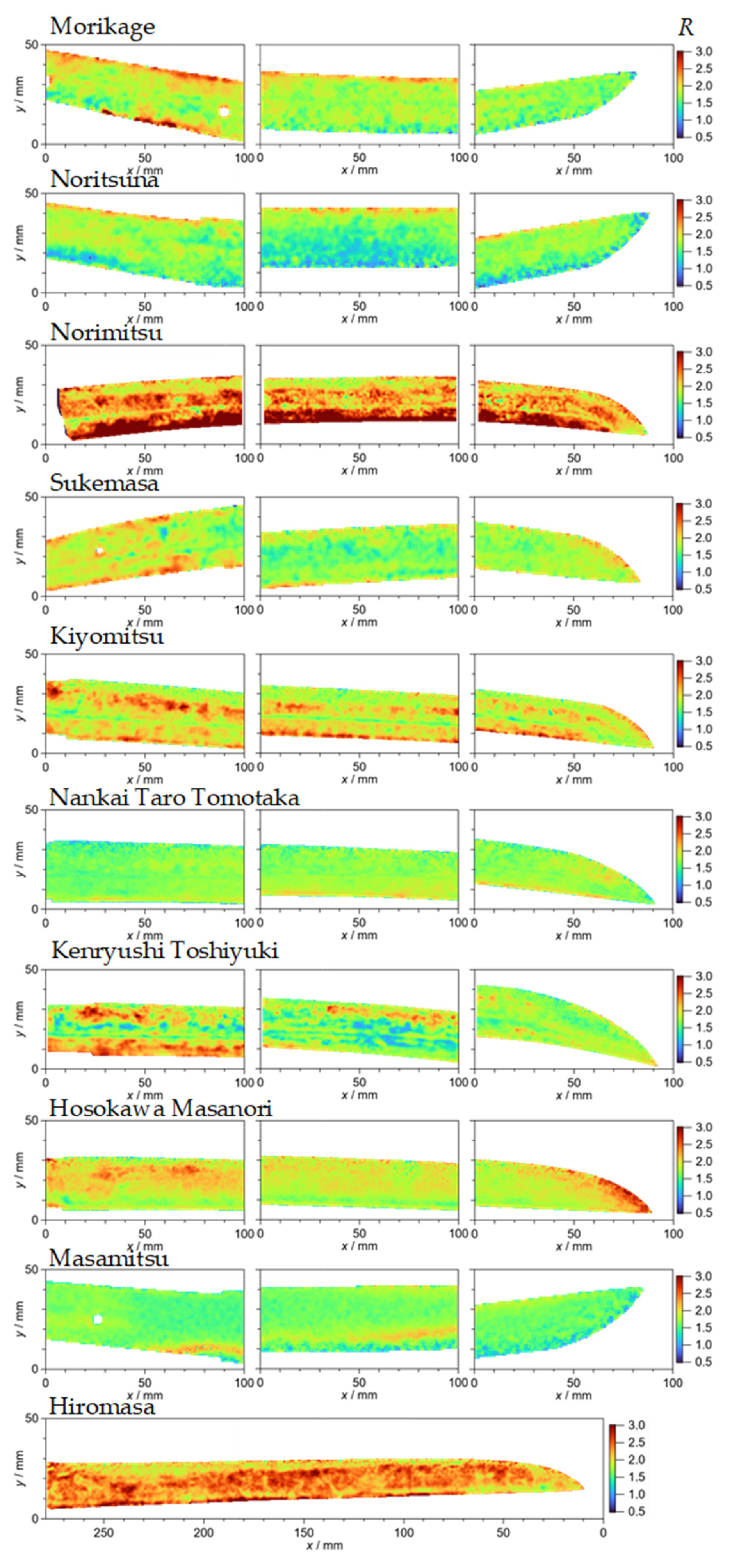
4.3. Degree of Anisotropy (Texture)
4.4. Crystallite Size
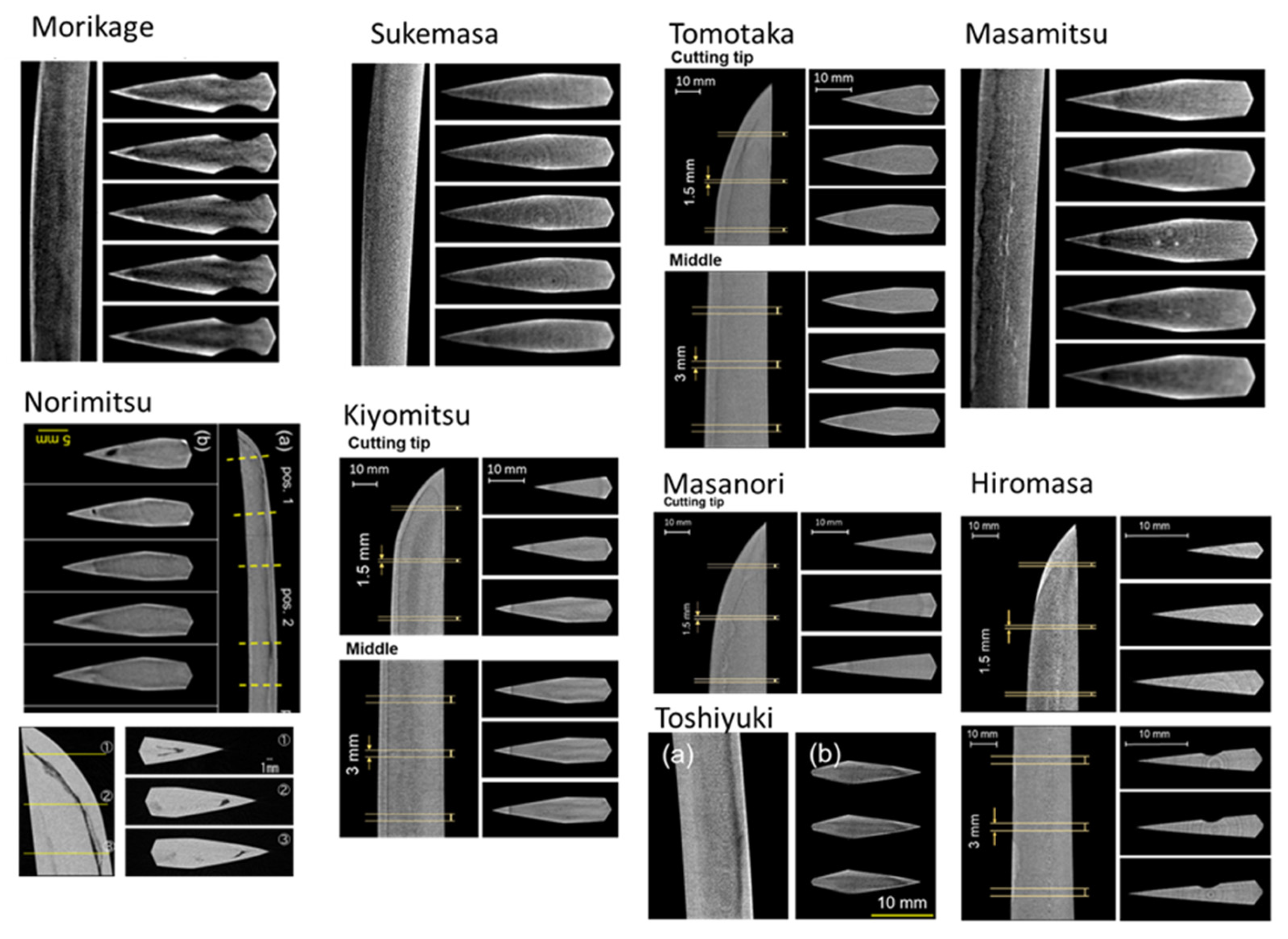
4.5. CT Images
5. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tawara, K. Nihontoh no Kagakuteki Kenkyu (Scientific Research of Japanese Swords); Hitachi Hyoronsha: Tokyo, Japan, 1953; pp. 6–77. (In Japanese) [Google Scholar]
- Tanimura, H. Development of the Japanese Sword. JOM 1980, 32, 63–73. Available online: https://link.springer.com/article/10.1007/BF03354549 (accessed on 18 November 2025). [CrossRef]
- Notis, M.R. The history of the metallographic study of the Japanese sword. Mater. Char. 2000, 45, 253–258. [Google Scholar] [CrossRef]
- Inoue, T. Tatara and the Japanese sword: The science and technology. Acta Mech. 2010, 214, 17–30. [Google Scholar] [CrossRef]
- Yaso, M.; Takaiwa, T.; Minagi, Y.; Kubota, K.; Morito, S.; Ohba, T.; Das, A.K. Study of Microstructures on Cross Section of JAPANESE SWORD. ESOMAT 2009, 2009, 07018. [Google Scholar] [CrossRef]
- Das, A.K.; Ohba, T.; Morito, S.; Yaso, M. Evidence of lath martensite in high-C Japanese sword produced from tamahagane steel by tatara process. Mater. Sci. Forum. 2010, 654–656, 138–141. [Google Scholar] [CrossRef]
- Matsumoto, C.; Das, A.K.; Ohba, T.; Morito, S.; Hayashi, T.; Takami, G. Characteristics of Japanese sword produced from tatara steel. J. Alloys Compd. 2013, 577S, S673–S677. [Google Scholar] [CrossRef]
- Pham, A.H.; Ohba, T.; Morito, S.; Hayashi, T. Automatic reconstruction approach to characterization of prior-austenite microstructure in various Japanese swords. Mater. Trans. 2015, 56, 1639–1647. [Google Scholar] [CrossRef]
- Inoue, T. The Japanese Sword: The material, manufacturing and computer simulation of quenching process. Mater. Sci. Res. Int. 1997, 3, 193–203. [Google Scholar] [CrossRef]
- Deschler-Erb, E.; Lehmann, E.H.; Pernet, L.; Vontobel, P.; Hartmann, S. The complementary use of neurons and X-rays for the non-destructive investigation of archaeological objects from Swiss collections. Archaeometry 2004, 46, 647–661. [Google Scholar] [CrossRef]
- Grazzi, F.; Civita, F.; Williams, A.; Scherillo, A.; Barzagli, E.; Bartoli, L.; Edge, D.; Zoppi, M. Ancient and historic steel in Japan, India and Europe, a non-invasive comparative study using thermal neutron diffraction. Anal. Bioanal. Chem. 2011, 400, 1493–1500. [Google Scholar] [CrossRef]
- Grazzi, F.; Bartoli, L.; Civita, F.; Franci, R.; Paradowska, A.; Scherillo, A.; Zoppi, M. From Koto age to modern times: Quantitative characterization of Japanese swords with Time of Flight Neutron Diffraction. J. Anal. At. Spectrom. 2011, 26, 1030–1039. [Google Scholar] [CrossRef]
- Barzagli, E.; Grazzi, F.; Scherillo, A.; Civita, F.; Zoppi, M. Determination of the metallurgical properties of six ferrous Japanese arrow tips through time-of-flight neutron diffraction. Acta Crystallogr. A 2011, 67, C525–C526. [Google Scholar] [CrossRef]
- Salvemini, F.; Luzin, V.; Grazzi, F.; Gatenby, S.; Kim, M.J. Structural characterization of ancient Japanese swords from MAAS using neutron strain scanning measurements. Mater. Res. Proc. 2017, 2, 443–448. [Google Scholar] [CrossRef]
- Salvemini, F.; Luzin, V.; Avdeev, M.; Tremsin, A.; Sokolova, A.; Gregg, A.; Wensrich, C.M.; Gatenby, S.; Kim, M.J.; Grazzi, F. Samurai’s swords, a non-invasive investigation by neutron techniques. Materials Science Forum. 2020, 983, 15–23. [Google Scholar] [CrossRef]
- Harjo, S.; Kawasaki, T.; Grazzi, F.; Shinohara, T.; Tanaka, M. Neutron diffraction study on full-shape Japanese sword. Materialia 2019, 7, 100377. [Google Scholar] [CrossRef]
- Sato, H.; Kamiyama, T.; Kiyanagi, Y. A Rietveld-type analysis code for pulsed neutron Bragg-edge transmission imaging and quantitative evaluation of texture and microstructure of a welded α-iron plate. Mater. Trans. 2011, 52, 1294–1302. [Google Scholar] [CrossRef]
- Sato, H.; Sato, T.; Shiota, Y.; Kamiyama, T.; Tremsin, A.S.; Ohnuma, M.; Kiyanagi, Y. Relation between Vickers hardness and Bragg-edge broadening in quenched steel rods observed by pulsed neutron transmission imaging. Mater. Trans. 2015, 56, 1147–1152. [Google Scholar] [CrossRef]
- Bunge, H.J. Advantages of neutron diffraction in texture analysis. Textures Micro Struct. 1989, 10, 265–307. [Google Scholar] [CrossRef]
- Brokmeier, H.G.; Gan, W.M.; Randau, C.; Völler, M.; Rebelo-Kornmeier, J.; Hofmann, M. Texture analysis at neutron diffractometer STRESS-SPEC. Nucl. Instrum. Methods Phys. Res. A 2011, 642, 87–92. [Google Scholar] [CrossRef]
- Matthies, S.; Pehl, J.; Wenk, H.-R.; Lutterotti, L.; Vogel, S.C. Quantitative texture analysis with the HIPPO neutron TOF diffractometer. J. Appl. Cryst. 2005, 38, 462–475. [Google Scholar] [CrossRef]
- Kockelmann, W.; Chapon, L.C.; Radaelli, P.G. Neutron texture analysis on GEM at ISIS. Phys. B 2006, 385–386, 639–643. [Google Scholar] [CrossRef]
- Xu, P.G.; Harjo, S.; Ojima, M.; Suzuki, H.; Ito, T.; Gong, W.; Vogel, S.C.; Inoue, J.; Tomota, Y.; Aizawa, K.; et al. High stereographic resolution texture and residual stress evaluation using time-of-flight neutron diffraction. J. Appl. Crystallogr. 2018, 51, 746–760. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.G.; Liss, K.D. Multiple wavelengths texture measurement using angle dispersive neutron diffraction at WOMBAT. Quantum Beam Sci. 2021, 5, 11. [Google Scholar] [CrossRef]
- Xu, P.G.; Tomota, Y.; Arakaki, Y.; Harjo, S.; Sueyoshi, S. Evaluation of austenite volume fraction in TRIP steel sheets using neutron diffraction. Mater. Charact. 2017, 127, 104–110. [Google Scholar] [CrossRef]
- Oikawa, K.; Kiyanagi, Y.; Sato, H.K.; Ohmae, K.; Pham, A.H.; Watanabe, K.; Matsumoto, Y.; Shinohara, T.; Kai, T.; Harjo, S.; et al. Pulsed neutron imaging based crystallographic structure study of a Japanese sword made by Sukemasa in the Muromachi period. Mater. Res. Proc. 2020, 15, 207–213. [Google Scholar] [CrossRef]
- Sato, H.; Kiyanagi, Y.; Oikawa, K.; Ohmae, K.; Pham, A.H.; Watanabe, K.; Matsumoto, Y.; Shinohara, T.; Kai, T.; Harjo, S.; et al. Crystallographic microstructure study of a Japanese sword made by Noritsuna in the Muromachi period by pulsed neutron Bragg-edge transmission imaging. Mater. Res. Proc. 2020, 15, 214–220. [Google Scholar] [CrossRef]
- Matsumoto, Y.; Watanabe, K.; Ohmae, K.; Uritani, A.; Kiyanagi, Y.; Sato, H.; Ohnuma, M.; Pham, A.H.; Morito, S.; Ohba, T.; et al. Comparative study of ancient and modern Japanese swords using neutron tomography. Mater. Res. Proc. 2020, 15, 221–226. [Google Scholar] [CrossRef]
- Ohmae, K.; Kiyanagi, Y.; Sato, H.; Oikawa, K.; Pham, A.H.; Watanabe, K.; Matsumoto, Y.; Shinohara, T.; Kai, T.; Harjo, S.; et al. Crystallographic structure study of a Japanese sword Masamitsu made in the 1969 using pulsed neutron imaging. Mater. Res. Proc. 2020, 15, 227–232. [Google Scholar] [CrossRef]
- Matsumoto, Y.; Oikawa, K.; Watanabe, K.; Sato, H.; Parker, J.D.; Shinohara, T.; Kiyanagi, Y. Nondestructive analysis of internal crystallographic structures of Japanese swords using neutron imaging. J. Archaeol. Sci. Rep. 2024, 58, 104729. [Google Scholar] [CrossRef]
- Oikawa, K.; Matsumoto, Y.; Watanabe, K.; Sato, H.; Parker, J.D.; Shinohara, T.; Kiyanagi, Y. Energy-resolved neutron imaging study of a Japanese sword signed by Bishu Osafune Norimitsu. Sci. Rep. 2024, 14, 27990. [Google Scholar] [CrossRef]
- Kiyanagi, Y.; Oikawa, K.; Ninomiya, K.; Watanabe, K.; Pham, A.H.; Tampo, M.; Kubo, K.M.; Sato, H.; Matsumoto, Y.; Shinohara, T.; et al. Metallurgical study of Japanese swords made in Bizen in the Muromachi period by using pulsed neutron imaging and muon lifetime measurements. JPS Conf. Proc. 2025. accepted. [Google Scholar]
- Oikawa, K.; Matsumoto, Y.; Sato, H.; Watanabe, K.; Parker, J.D.; Sshinohara, T.; Kiyanagi, Y. Pulsed-Neutron imaging study of a naginata from the Edo period and spears from the Muromachi period. JPS Conf. Proc. 2025. accepted. [Google Scholar]
- Shinohara, T.; Kai, T.; Oikawa, K.; Nakatani, T.; Segawa, M.; Hiroi, K.; Su, Y.; Ooi, M.; Harada, M.; Iikura, H.; et al. The energy-resolved neutron imaging system. RADEN. Rev. Sci. Instrum. 2020, 91, 043302. [Google Scholar] [CrossRef] [PubMed]
- Fermi, E.; Sturm, W.J.; Sachs, R.G. The Transmission of Slow Neutrons through Microcrystalline Materials. Phys. Rev. 1947, 71, 589–594. [Google Scholar] [CrossRef]
- Dollase, W.A. Correction of intensities for preferred orientation in powder diffractometry: Application of the March model. J. Appl. Cryst. 1986, 19, 267–272. [Google Scholar] [CrossRef]
- Larson, A.C.; Von Dreele, R.B. General Structure Analysis System (GSAS); Los Alamos National Laboratory Report LAUR 86-748; Los Alamos National Laboratory: Los Alamos, NM, USA, 2004.
- Sabine, T.M. A reconciliation of extinction theories. Acta Crystallogr. Sec. A 1988, 44, 368–373. [Google Scholar] [CrossRef]
- Sabine, T.M.; Von Dreele, R.B.; Jørgensen, J.-E. Extinction in time-of-flight neutron powder diffractometry. Acta Cryst. 1988, A44, 374–379. [Google Scholar] [CrossRef]
- Kropff, F.; Granada, J.R. CRIPO: A Fast Computer Code for the Evaluation of σT in Polycrystalline Materials; Unpublished Report CAB-1977; Institute Balseiro: Bariloche, Argentina, 1977. [Google Scholar]
- Kitada, M. Microstructure of Japanese Swords in the Muromachi Period, Uchida Rokakuho, Japan; Uchida Rokakuho: Tokyo, Japan, 2008; Chapter 3-1; pp. 13–17. (In Japanese) [Google Scholar]
- Ninomiya, K.; Kubo, M.K.; Inagaki, M.; Yoshida, G.; Chiu, I.; Kudo, T.; Asari, S.; Sentoku, S.; Takeshita, S.; Shimomura, K.; et al. Development of a non-destructive depth-selective quantification method for sub-percent carbon contents in steel using negative muon lifetime analysis. Sci. Rep. 2024, 14, 1797. [Google Scholar] [CrossRef]
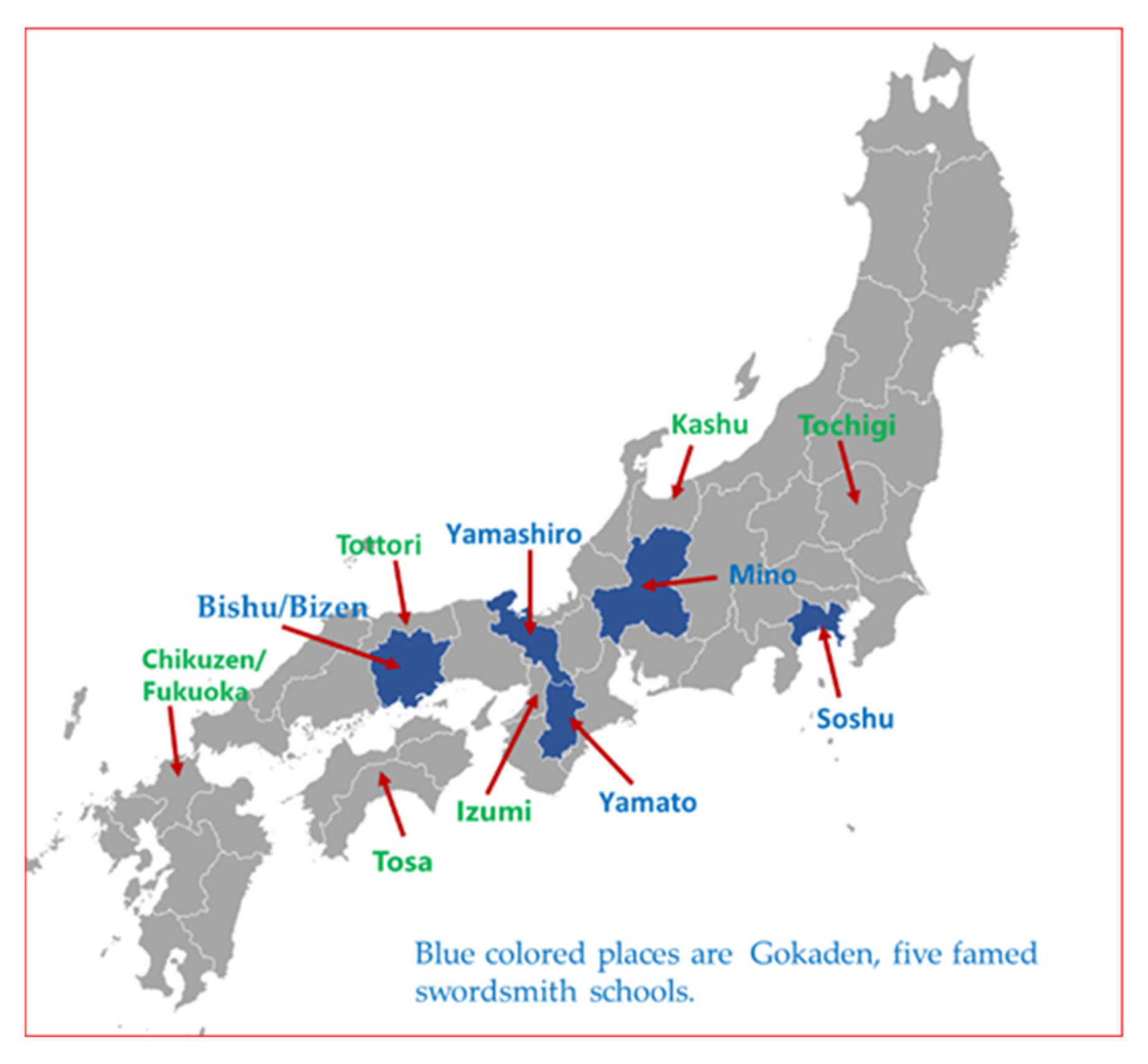


| No. | Swordsmith | Production Age | Type | Production Area (Present-Day Prefecture) | Blade Length (cm) |
|---|---|---|---|---|---|
| 1 | Morikage | South and North Courts period (1356–1361) | Long sword (Old sword) | Bishu (Okayama) | 80.3 |
| 2 | Noritsuna | Muromachi period (1405) | Long sword (Old sword) | Bishu (Okayama) | 75.0 |
| 3 | Norimitsu | Muromachi period (~15th century) | Wakizashi (Old sword) | Bishu (Okayama) | 45.4 |
| 4 | Sukemasa | Latter period of Muromachi | Sword (Old sword) | Izumi (Osaka) | 64.0 |
| 5 | Kiyomitsu | Edo period | Sword (New-new sword) | Kashu (Ishikawa) | 69.6 |
| 6 | Nankai Taro Tomotaka | Edo period (1836) | Sword (New-new sword) | Tosa (Kochi)/ Yamashiro(Kyoto) | 70.8 |
| 7 | Hosokawa Masanori | Edo to Meiji period | Wakizashi (New-new sword) | (Tochigi) | 31.3 |
| 8 | Masamitsu | Showa period (1969) | Long sword (Modern sword) | (Fukuoka) | 74.2 |
| 9 | Kenryushi Toshiyuki | Edo period (1846) | Naginata (New-new sword) | Tottori (Tottori) | 39.1 |
| 10 | Hiromasa | Beginning of Muromachi period | Short sword (Old sword) | Soshu (Kanagawa) | 26.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiyanagi, Y.; Oikawa, K.; Matsumoto, Y.; Parker, J.D.; Watanabe, K.; Sato, H.; Shinohara, T. Japanese Sword Studies Using Neutron Bragg-Edge Transmission and Computed Tomography. Quantum Beam Sci. 2025, 9, 33. https://doi.org/10.3390/qubs9040033
Kiyanagi Y, Oikawa K, Matsumoto Y, Parker JD, Watanabe K, Sato H, Shinohara T. Japanese Sword Studies Using Neutron Bragg-Edge Transmission and Computed Tomography. Quantum Beam Science. 2025; 9(4):33. https://doi.org/10.3390/qubs9040033
Chicago/Turabian StyleKiyanagi, Yoshiaki, Kenichi Oikawa, Yoshihiro Matsumoto, Joseph Don Parker, Kenichi Watanabe, Hirotaka Sato, and Takenao Shinohara. 2025. "Japanese Sword Studies Using Neutron Bragg-Edge Transmission and Computed Tomography" Quantum Beam Science 9, no. 4: 33. https://doi.org/10.3390/qubs9040033
APA StyleKiyanagi, Y., Oikawa, K., Matsumoto, Y., Parker, J. D., Watanabe, K., Sato, H., & Shinohara, T. (2025). Japanese Sword Studies Using Neutron Bragg-Edge Transmission and Computed Tomography. Quantum Beam Science, 9(4), 33. https://doi.org/10.3390/qubs9040033