Quantum Beam Scattering—Beam’s Coherence Length, Which-Path Information and Weak Values

Abstract

The conventional theory of neutron beams interacting with many-body systems treats the beam as a classical system, i.e., with its dynamical variables appearing in the quantum dynamics of the scattering process not as operators but only as c-numbers. Moreover, neutrons are described with plane waves, i.e., the concept of a neutron’s (finite) coherence length is here irrelevant. The same holds for electron, atom or X-ray scattering. This simplification results in the full decoupling of the probe particle’s dynamics from the quantum dynamics of the scatterer—a well-known fact also reflected in the standard formalism of time-correlation functions (see textbooks). Making contact with modern quantum-theoretical approaches (e.g., quantum entanglement, “which-path information” versus interference, von Neumann measurement, Weak Values (WV), etc.), new observable effects of non-relativistic quantum beam scattering may be exposed and/or predicted, for instance, a momentum-transfer deficit and an intensity deficit in neutron scattering from protons of hydrogen-containing samples. A new WV-theoretical treatment is provided, which explains both these “deficit effects” from first principles and on equal footing.

1. Introduction

The well-known particle-wave dual nature of a quantum object, known as complementarity, allows for various (often strange appearing) quantum correlation and interference phenomena, like, e.g., the delocalization and self-interference of very large organic molecules [1], and the “bomb detection” method in a Mach–Zehnder interferometer (MZI) with the aid of the so-called interaction-free-measurement (IFM) method discovered by Elitzur and Vaidman [2]. The most striking of these non-classical phenomena is quantum entanglement (QE), which has been the most debated element of quantum mechanics ever since the theory was formulated about 100 years ago. QE (see e.g., [3]) is the phenomenon that two or more particles can exist in a shared quantum state, regardless of how far apart they are. Einstein criticized QE as a “spooky action at a distance” and Schrödinger said it was quantum mechanics’ most important trait; see, e.g., [4,5]. “The Nobel prize in physics 2022” statement of grounds refers to QE as quantum mechanics’ most important resource [5], which also pioneered quantum information science and the associated emerging new quantum technologies; cf. [6,7,8,9,10].

In this paper, all the considerations and results are specifically focused on non-relativistic scattering of particles off many-body (or condensed matter) systems, with a particular emphasis on incoherent neutron scattering (INS). When we say “incoherent”, we mean that a neutron (or any other particle such as a photon, electron or atom) collides and scatters from a single particle, such as a nucleus, atom or molecule. When neutrons scatter from protons (commonly referred to as H atoms), the scattering is predominantly incoherent due to the neutron–proton spin-flip mechanism involved in the collision process. Details about this spin-flip mechanism can be found in textbooks such as [11,12].

Essentially, this means that the scattering process provides “which-path information”, as, e.g., described in the texbook [13], allowing us to identify and isolate the scattering proton from all other potential scatterers. Consequently, this destroys any possible interferences between different paths that the neutron could take during the scattering process.

A clear first-principles explanation of this effect, and of coherent versus incoherent scattering, may be found in the Feynman Lectures [14], in particular Section 3.3 of [14]. Consider neutron scattering from a crystal consisting of atoms with nuclear spin 1/2 (as the neutron, too), in particular the case where the neutron has spin-up and the crystal nuclei have spin-down (before scattering), in which case spin-exchange (or -flip) can happen. This causes the incoherent part of the scattering process which produces no sharp interference peaks in the scattered neutron beam (the latter being characteristic of coherent scattering). This spin-flip corresponds to “which-path knowledge”—the specific spin-flip scattering nucleus (now having spin-up) is singled out; i.e., which-path information concerning the neutron does exist. This constitutes a generally valid quantum-mechanical feature that suppresses quantum interference phenomena. Moreover, Feynman emphasizes this phenomenon as follows:

• “You may argue, “I don’t care which atom is up.” Perhaps you don’t, but nature knows; and the probability is, in fact, what we gave above—there isn’t any interference.”; [14], page 3–9.

This quotation is strongly related to the intrinsic physical connections between the basic quantum-mechanical concepts of wave-particle duality, complementarity, uncertainty principle and which-path knowledge versus interference. These have attracted great interest and are still under vivid theoretical and experimental investigations; see Refs. [13,15,16,17,18,19,20,21,22] and references cited therein.

The presentation below is organized as follows. Section 2 considers in some detail the fact that conventional (neutron) scattering theory treats the neutron beam as a classical system and even as a plane wave. In the light of modern quantum mechanics, this has certain severe theoretical and experimental consequences, which are examined in the following sections. The introductory Section 3 about the “neutron beam as a quantum object” gives an introduction to the specific topics of impulsive (von Neumann or strong) measurement and creation of QE caused by the scattering. Section 4 introduces (very) shortly the basic concepts of Weak Value (WV) and Two-State Vector Formalism (TSCF).

The next two sections discuss real neutron-scattering experiments. In Section 5 the theory is further developed with respect to the experimental field of incoherent and inelastic neutron scattering (INS) with thermal neutrons [23]. Section 6 extends the theoretical investigation towards the field of epithermal neutron scattering (i.e., in the energy transfer range 1–100 eV) which is known as neutron Compton scattering (NCS) [24,25,26]. Both Section 5 and Section 6 contain subsections dealing explicitly with concrete experiments and their theoretical interpretations, which also include examples of effects that have no interpretation within conventional theory.

The last section, Section 7, provides some additional discussion of the main aspects and succinct features of scattering of a quantum beam from a quantum scattering system. Here, as well as in appropriate places during the preceding presentations, the theoretical connection of our investigations with modern quantum-theoretical approaches and concepts is stressed (e.g., quantum entanglement, ‘which-path detection’ versus quantum interference, complementarity and weak values).

2. Conventional Theory: Neutron Beam as a Classical Object

In the conventional non-relativistic neutron-scattering theory, the concept of quantum entanglement (QE) is not explicitly mentioned, leaving uncertainty about its role in the theory [11,12,23]. Although a neutron is a quantum object and would generally be expected to become entangled with a colliding nucleus or atom (see Section 3), this process is not considered in this theory. Specifically, the neutron’s quantum degrees of freedom are not properly incorporated into the fundamental scattering formulas of the theory, such as the equation for the partial differential cross-section or the van Hove correlation functions. Instead, these formulas only involve classical values (c-numbers) associated with the neutron.

To illustrate this point, let us examine the basic formulas of the theory, including the expression for the partial differential cross-section.

$$\frac{d^2{\sigma }_A}{d\mathrm{\Omega }d\omega }=\frac{k_f}{k_i}{\sigma }_{A}S(\mathbf{K},\omega )$$

(1)

($E=\hslash \omega$. $d\mathrm{\Omega }$: solid angle measured/covered by the detector. ${\mathbf{k}}_i$ and ${\mathbf{k}}_f$: initial and final wavevectors of the scattered neutron. $k_a$: absolute value of ${\mathbf{k}}_a$. $\mathbf{K}$: momentum transfer from the neutron to the system due to the collision, $\mathbf{K}={\mathbf{k}}_i-{\mathbf{k}}_f$. ${\sigma }_A$: scattering cross-section of scattering system A).

$S(\mathbf{K},\omega )$ is the dynamic structure factor of the scattering system A (also known as scattering function of A), which contains dynamical variables of A only. (In simpler terms, the wavefunction of the complete neutron-A system contains dynamical variables referring to the scatterer only, but not to the neutron). Thus, the neutron is “downgraded” to a classical object. That is, no operator quantity appears here, only c-numbers referring to the neutron: the scattering cross-section ${\sigma }_A$ of the neutron-A collision process and the initial ($k_i$) and final ($k_i$) wavevectors of the impinging and scattered neutron.

This is related to properties of the first Born approximation and the so-called Fermi’s Golden Rule which the conventional theory is based on [11,12,24,25]. As a consequence, the complete dynamics of the two systems (neutron and scattering system) become decoupled—the neutron dynamics do not appear in Equation (1), since it contains only c-numbers of neutron quantities, i.e., only the quantum dynamics of the system A captured with the dynamical structure factor $S(\mathbf{K},\omega )$.

This imposed classicality for the neutron has as a consequence that the typical quantum concept of the particle’s (or beam’s) coherence length, $l_{coh}$, is also absent in the frame of conventional neutron-scattering theory. As a matter of fact, the main Equation (1) contains the values of the initial and final wavevectors only, which are considered as plane waves—another basic element of conventional theory.

In other terms, the scattering process describes the scattering probability from an infinitely well-defined state ${\mathbf{k}}_i$ to an accordingly precise final state ${\mathbf{k}}_f$. Of course, the actually observed quantity is the (double) average over the finite distributions of ${\mathbf{k}}_i$ and ${\mathbf{k}}_f$ associated with a real experimental setup.

Now the following crucial point made by conventional theory should be considered: According to standard quantum mechanics, there are no quantum interference effects between incoming particles (or photons) with different wavenumbers. Thus, it seems natural to argue that there is no experimentally detectable difference between (a) a wave packet with a given finite coherence length (i.e., a coherent superposition of waves with different wavenumbers) and (b) an incoherent classical ensemble of plane waves, i.e., waves with infinitely well-defined wavenumbers (which means that their coherence lengths are infinite) and with no definite phase relations between them.

This is because every observable scattering quantity is expected to only depend on the square ${|a(\mathbf{k})|}^2$ of the $\mathbf{k}$-component of the incoming beam and not on products $|a({\mathbf{k}}_{\mathbf{1}})a^{*}({\mathbf{k}}_{\mathbf{2}})|$ of components with different wavenumbers (${\mathbf{k}}_1\ne {\mathbf{k}}_2$), where the asterisk indicates complex conjugation. This is consistent with Dirac’s famous remark in his textbook: “Each photon then interferes only with itself. Interference between two different photons never occurs.” See (p. 9, [27]).

In summary, standard scattering theory holds that an experimental problem is completely characterized by the classical wavenumber distributions of the incoming and outgoing particle (or photon) beams; structural details of the wavefunctions of the beam particles are irrelevant and thus also the coherence properties of these wavefunctions. Impinging and scattered neutrons are described by plane waves.

Further Explanatory Remarks on the Basic Formula Equation (1)

Some additional remarks on the validity of Equation (1) are in order. In conventional theory, the following holds

$$S(\mathbf{K},\omega )=\frac{1}{2\pi \hslash }{\int }_{-\infty }^{\infty }exp(-i\omega t)F(\mathbf{K},t)dt$$

(2)

where $F(\mathbf{K},t)$ is the intermediate correlation function

$$F(\mathbf{K},t)=\frac{1}{N}\sum _{j,k}^N\langle exp(-i\mathbf{K}·{\widehat{\mathbf{r}}}_j(0))exp(i\mathbf{K}·{\widehat{\mathbf{r}}}_k(t))\rangle$$

(3)

Operators ${\mathbf{r}}_j(t)$, with $j=1,...N$, represent the spatial positions (in the Heisenberg representation) of the particles of the N-body scattering system A with Hamiltonian $H_A$, A being assumed to be isolated. $\langle ...\rangle$ represents an appropriate average over all N particles.

However, note that the complete neutron–system Hamiltonian is

$$H=H_A+H_n+H_{nA}$$

The unitary time evolution operator

$$U_A(t)=exp(-\frac{i}{\hslash }{H}_{A}t)$$

(4)

which defines the Heisenberg operators

$${\widehat{\mathbf{r}}}_j(t)=U_A^{†}(t){\widehat{\mathbf{r}}}_j{U}_A(t)$$

(5)

($j=1,\dots N$) refers to the complete N-body system A, but not to the neutron [11,12]. That is, the neutron–system interaction Hamiltonian $H_{nA}$ and the Hamiltonian of the free neutron $H_n$ play no role here.

The Heisenberg operators ${\widehat{\mathbf{r}}}_j(t)$ in Equations (3) and (5), if “interpreted” in classical terms, represent the particles’ positions. Obviously this is a crude oversimplification, because the unitary operator $U_A(t)$ is an N-body operator depending on the N-body Hamiltonian $H_A$ of the scattering system—and so any operator ${\widehat{\mathbf{r}}}_j(t)$ is (for $t\ne t_0$) an N-body quantity, too. (The pathological limiting case of A consisting on N non-interacting atoms is irrelevant for the present paper.)

3. Neutron Beam as a Quantum Object—Introductory Considerations

As already pointed out, the above considerations refer to conventional neutron scattering theory, but the situation in neutron interferometry theory is totally different. Here, wavepackets with finite coherence length for the initial and final neutron states represent the standard situation in real experiments.

Perhaps the most important fact to stress from the beginning is the following. After scattering of a neutron n from a particle (say, H, as in the experiments considered below), the neutron and the particle are in an entangled state, in general. This always happens if the scattering interaction is strong enough, so that an initial not entangled two-body product state evolves into a linear superposition of final two-body states

$$|{\psi }_n\rangle \otimes |{\varphi }_H\rangle ⟶\sum _j{c}_j|{\psi }_{n,j}\rangle \otimes |{\varphi }_{H,j}\rangle$$

(6)

with amplitudes $c_j$ ($j=1,2,...$) and $\sum |c_j{|}^2=1$. In general, this final state is entangled. Trivially, this basic quantum-theoretical fact is not captured within conventional theory since there is no QE of a quantum with a classical (here: neutron) object. Parenthetically, QE between indistinguishable (identical) particles belonging to a many-particle scattering system may exist, in principle, also within conventional theory; see, e.g., [28]).

Let us emphasize here again that the QE shown in Equation (6) is impossible within the frame of conventional neutron-scattering theory.

An important feature in the following investigations is that here the scattering is mainly incoherent; cf. the Introduction. Moreover, Feynman’s citation given in the Introduction appears to play a decisive role in the theoretical analysis and interpretation of the neutron-scattering experimental results considered below. Interestingly, the fundamental point stressed by Feynman is intimately related with several basic concepts of quantum theory, e.g., which-path information versus interference, complementarity and uncertainty principle.

The neutron (and, more generally, the incoming beam of particles or photons) is assumed to be a quantum system and so, in this respect, it has to be treated on an equal footing with the quantum scatterer. That is, the dynamical variables of the neutron (or at least some of them) have to be represented by operators (instead of c-numbers) and should appear explicitly in the theoretical derivations and results. Obviously, when the above requirements are fulfilled, then the obtained results may be expected to be beyond the reach of conventional theory.

The simplest and best known theoretical model of the interaction between two quantum systems is given by the von Neumann interaction Hamiltonian [29]

$$H_{int}=g(t)\widehat{A}\otimes \widehat{M}$$

(7)

which also plays a central role in the theoretical derivations below. Operator $\widehat{A}$ refers to the first system and $\widehat{M}$ to the second one. $g(t)$ is a real function describing the interaction strength and it is assumed to be nonzero only for a very short time interval. As an example, $\widehat{M}$ may correspond to a neutron (electron, atom, etc), i.e., it is associated with the quantum beam of a scattering process as considered below; $\widehat{A}$ represents an observable of the (many-body) scattering system. In the case of neutron scattering, $g(t)$ is proportional to the delta-like Fermi pseudo-potential; see textbooks, e.g., [11,12].

Parenthetically, the following investigations will appear to have a strong similarity with well-established theoretical approaches in the field of so-called quantum optics, quantum circuits theory and quantum information theory; e.g., see [6,7,13].

4. On Weak Values, Two-State-Vector Formalism and Impulsive Weak Measurements

Some introductory remarks about the theory of WV and TSVF (in short also denoted as TV-TSVF) [30,31] are in order. Consider the standard expression of the expectation value

$$\langle A\rangle =\langle {\psi }_i|\widehat{A}|{\psi }_i\rangle$$

(8)

$\widehat{A}$ is the operator representing an observable A and $|{\psi }_i\rangle$ is the state of the system just before the measurement interaction, which is assumed to be of short duration. $\widehat{A}$ is hermitian and $\langle A\rangle$ is a real number.

Now one defines

$$A^w\equiv \frac{\langle {\psi }_f|\widehat{A}|{\psi }_i\rangle }{\langle {\psi }_f|{\psi }_i\rangle }$$

(9)

in which appears the final state $|{\psi }_f\rangle$ of the system, i.e., the system’s state after the interaction is turned off. Note that this number, $A^w$, is a complex in general. $A^w$ is called the weak value (WV) of $\widehat{A}$. $|{\psi }_i\rangle$ is called the initial, or pre-selected, state and $|{\psi }_f\rangle$ is called the final or post-selected state. ($H_{int}$ is assumed to be sufficiently weak; see below.) Note that these two states are assumed to be experimentally accessible [30]. Hence, the real and the imaginary parts of $A^w$ are experimentally accessible quantities. For some examples, see the review article [32].

Obviously, the following holds

$$\mathrm{if}|{\psi }_i\rangle =|{\psi }_f\rangle \mathrm{then}\langle A\rangle =A^w$$

(10)

Hence, Equation (9) represents a generalization of the common expectation value, Equation (8). Note that, for sufficiently weak measurements, the denominator in Equation (9) does not vanish, $\langle {\psi }_f|{\psi }_i\rangle \ne 0$ [30].

Now we consider once more the expectation value of $\widehat{A}$, Equation (8), and presume the expansion $|{\psi }_i\rangle ={\sum }_j{c}_j|j\rangle$. The set of kets $\{|j\rangle \}$ denote an orthogonal basis of the Hilbert space associated with the considered system. Now we may assume that we carry out a measurement of the observable $\widehat{A}$ with respect to this basis and, additionally, also make a post-selection of the results associated with the final state $|j\rangle$. In other terms, we envisage a strong (called projective or von Neumann) measurement associated with the projector $|j\rangle \langle j|$. Hence, in this case we are interested in determining the average of the measuring results; we obtain:

$$\langle A\rangle =\langle {\psi }_i|\widehat{A}|{\psi }_i\rangle =\sum _j{c}_j^{*}\langle j|\widehat{A}|{\psi }_i\rangle =\sum _j|c_j{|}^2\frac{\langle j|\widehat{A}|{\psi }_i\rangle }{\langle j|{\psi }_i\rangle }\equiv \sum _j{|c_j|}^2{A}_{j,{\psi }_i}^w$$

(11)

As defined above, $A_{j,{\psi }_i}^w$ is the WV of $\widehat{A}$ with respect to the pre- and post-selected states $|{\psi }_i\rangle$ and $|j\rangle$, respectively. $|c_j{|}^2$ is the probability of the appearance of $|j\rangle$; cf. [30,33,34]. Thus, we see that possibly existing experimental features associated with the experimentally accessible quantity $A_{j,{\psi }_i}^w$ become “smeared out” in the common expectation value $\langle {\psi }_i|\widehat{A}|{\psi }_i\rangle$.

Indeed, Aharonov, Vaidman and collaborators have demonstrated the basic physical significance of Equation (9). Namely, in well-defined and properly designed experimental setups, WVs become measurable quantities [30]. As WVs are unknown in standard quantum mechanics (see textbooks), their existence and experimental accessibility should be considered to represent a novelty and/or discovery.

Further physical insight into the basic quantum nature of the concept of WV may be provided by the following consideration by Pati and Wu [35].

To start with, one notices the formula

$$\widehat{A}|{\psi }_i\rangle =\langle \widehat{A}\rangle |{\psi }_i\rangle +\Delta \widehat{A}|{\overline{\psi }}_i\rangle$$

(12)

which may be found in the textbook [30], p. 39, or in Ref. [35]. $|{\overline{\psi }}_i\rangle$ is a state orthogonal to $|{\psi }_i\rangle$, $\widehat{A}$ represents an observable, and $\langle \widehat{A}\rangle =\langle {\psi }_i|\widehat{A}|{\psi }_i\rangle$. Further, $\Delta \widehat{A}$ denotes the uncertainty of the observable A when the system is in the state $|{\psi }_i\rangle$; that is, ${(\Delta \widehat{A})}^2=\langle {\psi }_i|{(\widehat{A}-\langle \widehat{A}\rangle )}^2|{\psi }_i\rangle$. Taking the scalar product of $\langle {\psi }_f|$ with both sides of Equation (12) we obtain

$$A^w=\langle \widehat{A}\rangle +\Delta \widehat{A}\frac{\langle {\psi }_f|{\overline{\psi }}_i\rangle }{\langle {\psi }_f|{\psi }_i\rangle }\equiv \langle \widehat{A}\rangle +\delta A^w$$

(13)

Hence, we may say that $\delta A^w$ is the WV-correction to the conventional-theoretical expectation value $\langle \widehat{A}\rangle$.

This simple derivation shows the crucial reason for the term $\delta A^w$, which represents the difference between the common quantity $\langle \widehat{A}\rangle$ and the WV $A^w$. This difference is caused (1) by a non-vanishing uncertainty $\Delta \widehat{A}>0$ and (b) by an accompanying non-vanishing scalar product $\langle {\psi }_f|{\overline{\psi }}_i\rangle \ne 0$. Obviously, the latter relation means that the two states $|{\psi }_f\rangle$ and $|{\overline{\psi }}_i\rangle$ are capable of producing quantum interferences.

It should be emphasized that the aforementioned condition $\langle {\psi }_f|{\overline{\psi }}_i\rangle \ne 0$ is fully unknown in conventional quantum dynamics (exact or perturbative). Or, in simpler terms, this condition appears nowhere in conventional-theoretical treatments and/or interpretations of experimental observations or results. This also demonstrates the novelty of the two-state vector formalism (TSVF) which is an indispensable part of the general WV-theory [30,31].

In summary, the remarkably short derivation presented in Equations (12) and (13) shows that the new effects interpretable within WV-TSVF are caused by the quantum interference of the post-selected state with a quantum state being orthogonal to the pre-selected state of the system [35].

Impulsive von Neumann Measurement and WV-TSVF Theory

In WV-TSVF theory, the measurement process is characterized by an impulsive von Neumann interaction Hamiltonian [29]; see below. This incorporates an observable for a pointer or measuring apparatus, whose wavefunction is denoted by $|\mathrm{\Phi }\rangle$. That is, the pointer itself is also a quantum object.

The implementation of the von Neumann model, which describes an ideal case, is modeled by the two-body interaction Hamiltonian

$$H_{int}=g(t)\widehat{A}\otimes \widehat{M}\mathrm{with}g(t)=g\delta (t-t_0)$$

(14)

where $\widehat{M}$ is a dynamical variable of the pointer and $\widehat{A}$ is the system’s operator representing the physical quantity to be measured. $g(t)$ is a (small and real) coupling function, and $t_0$ specifies the time of the impulsive two-body collision. In an ideal measurement, $g(t)$ is nonzero only during a very short time interval—formally captured with the delta function— and thus the free Hamiltonians of the participating systems during this time period can be neglected.

The von Neumann measurement, also known as a strong measurement, provides the eigenvalues of the measured observable. However, it simultaneously disturbs the measured system, resulting in a change in its initial state. The final state corresponds to an eigenstate of the operator representing the observable. Alternatively, by weakly coupling a measuring device to the system, a technique known as Weak Measurement (WM), it becomes possible to extract specific information while limiting the disturbance induced by the measurement on the system. As initially proposed by Aharonov and collaborators [36,37], additional physical insights are unveiled when one selectively post-selects a specific outcome of the experiment.

Let the initial system-apparatus state, i.e., for $t<t_0$ be ${\psi }_i\otimes {\mathrm{\Phi }}_i$. Due to the interaction, this evolves as follows:

$${\psi }_i\otimes {\mathrm{\Phi }}_i\to e^{-ig\widehat{A}\otimes \widehat{M}}{\psi }_i\otimes {\mathrm{\Phi }}_i$$

(15)

For convenience and as often done in theoretical papers, in the following derivations we temporarily put $\hslash =1$. We also may write g instead of $g(t)$.

Then one post-selects (with a strong measurement) a specific final state of the system, say ${\psi }_f$. The experimental result is associated with the corresponding apparatus’ final state, ${\mathrm{\Phi }}_f$, from which the measurement’s result is determined. ${\mathrm{\Phi }}_f$ is obtained by tracing out the dynamical variables of the system, i.e.,

$${\mathrm{\Phi }}_f=\langle {\psi }_f|e^{-ig\widehat{A}\otimes \widehat{M}}|{\psi }_i\rangle {\mathrm{\Phi }}_i$$

(16)

In the following, one considers the weak interaction limit (i.e., small g) and obtains through power expansion of the exponent:

$${\mathrm{\Phi }}_f\approx \langle {\psi }_f|1-ig\widehat{A}\otimes \widehat{M}|{\psi }_i\rangle {\mathrm{\Phi }}_i=\langle {\psi }_f|{\psi }_i\rangle (1-ig{A}^w\widehat{M}){\mathrm{\Phi }}_i\approx \langle {\psi }_f|{\psi }_i\rangle e^{-ig{A}^w\widehat{M}}{\mathrm{\Phi }}_i$$

(17)

$A^w$ is the WV of the system’s observable $\widehat{A}$. It is assumed that $\langle {\psi }_f|{\psi }_i\rangle \ne 0$. Thus, the state of the measuring device evolves with an effective one-body Hamiltonian ${\widehat{H}}_M=g{A}^w\widehat{M}$, i.e.,

$${\mathrm{\Phi }}_i\to e^{-ig{A}^w\widehat{M}}{\mathrm{\Phi }}_i$$

(18)

Hence the following interesting result is obtained: The pointer’s dynamics displays information about the system only through the single complex number $A^w$.

For the following theoretical derivations we will make the specific choice

$$\widehat{M}=\widehat{p}$$

(19)

In other words, the pointer’s variable in the interation Hamiltonian will be its momentum. We will also need the variance of $\widehat{p}$ in its initial pointer state

$$Va{r}_p=\langle {\mathrm{\Phi }}_i|{\widehat{p}}^2|{\mathrm{\Phi }}_i\rangle -\langle {\mathrm{\Phi }}_i|\widehat{p}{|{\mathrm{\Phi }}_i\rangle }^2$$

(20)

In the theoretical treatment of the experimental neutron-scattering results presented below, it will be shown that the imaginary part $Im\left[A^w\right]$ of $A^w$ is of particular interest. According to the general WV-TSVF theory, the pointer momentum after the interaction changes from ${\langle p\rangle }_i$ (its initial value) to

$${\langle p\rangle }_f={\langle p\rangle }_i+2gIm\left[A^w\right]Va{r}_p$$

(21)

(its final value). Note that $Va{r}_p$ refers to the apparatus (or pointer). Moreover, the real part of the weak value, $Re\left[A^w\right]$, is determined by the shifted position (x-shift) of the pointer, i.e.,

$${\langle x\rangle }_f={\langle x\rangle }_i+gRe\left[A^w\right]$$

(22)

For full derivations and further explanations, see, e.g., [33,38]. It will be shown that, in our investigations, the relevant WV entering the scattering process is purely imaginary. The physical significance of an imaginary WV was analyzed by Dressel and Jordan [39].

5. Momentum-Transfer Deficit in the INS Scattering in the Frame of WV Theory

Let us point out already here, for clarity, that the following derivations refer to a possible correction to a conventionally expected measurement outcome, as predicted by Weak Values (WM) and Two-State Vector Formalism (TSVF); see, e.g., Equation (29) below.

For simplicity of notation, we take the direction of momentum-transfer vector, $K_A$, due to scattering of a neutron with initial momentum, $p_n$, to be parallel to the x-axis of the laboratory system. Now we consider the von Neumann-type interaction Hamiltonian

$$H_{int}=g\widehat{p}\otimes \widehat{X}$$

(23)

(g: small coupling constant, as discussed above), with the understanding that $H_{int}$ should theoretically describe a (possibly existing) deviation from the conventional momentum transfer due to the neutron–system collision. $\widehat{X}$ is the position operator of the system (or a system’s part, e.g., a nucleus) being hit by the neutron, which has the momentum operator $\widehat{p}$. The sign of g is not specified yet.

Now one has to calculate the WV of the system variable $\widehat{x}\equiv \widehat{X}$, according to Equation (9)

$$X^w\equiv \frac{\langle {\psi }_f|\widehat{X}|{\psi }_i\rangle }{\langle {\psi }_f|{\psi }_i\rangle }$$

(24)

Clearly, the explicit forms of the state vectors in configuration space are very complicated (and time-dependent even over a short time interval around the time $t_0$ of collision). So we may be able to perform a part of the calculation in the momentum space—as done in our earlier works [40,41]. To do so, one may use the replacement

$$\widehat{X}\to -\frac{1}{i}\frac{\partial }{\partial \widehat{P}}$$

(25)

(recall the aforementioned convention $\hslash =1$), where $\widehat{P}$ is the associated momentum variable of the quantum system. (Note that the fundamental commutation relation $[\widehat{P},\widehat{X}]=1/i$ is fulfilled.)

Let us now calculate $X^w$ in the momentum representation, causing the usual assumption of the wavefunctions of initial and final states to be approximated by Gaussians (i.e., of the form $G(P)=exp(-P^2/2{\sigma }_P^2)$). This gives for the nominator

$$\begin{array}{ccc}\hfill \langle {\psi }_f|\widehat{X}|{\psi }_i\rangle & =& (-1/i)\langle {\psi }_f|\frac{\partial }{\partial \widehat{P}}|{\psi }_i\rangle =(-1/i)\langle G(P-K_A)|\frac{\partial }{\partial \widehat{P}}|G(P)\rangle \hfill \\ & =& (-1/i)(-1/{\sigma }_P^2)\langle G(P-K_A)|\widehat{P}|G(P)\rangle \hfill \\ & =& -i1/{\sigma }_P^2\langle {\psi }_f|\widehat{P}|{\psi }_i\rangle \hfill \end{array}$$

(26)

The integral $\langle {\psi }_f|\widehat{P}|{\psi }_i\rangle$ is exactly the same as the one that appeared in the calculation of the WV of momentum P in the treatment of INS [40,41]. Those calculations showed that $P^w$ is real and positive. Thus, we immediately arrive at the interesting result that $X^w$ is purely imaginary.

It is in order to repeat the short calculation of $P^w$ here, see [40,41], that

$$\begin{array}{ccc}\hfill P^w& =& \frac{\langle G_f|\widehat{P}|G_i\rangle }{\langle G_f|G_i\rangle }=\frac{\int dPG{(P-K_A)}_{f}PG{(P)}_i}{\int dPG{(P-K_A)}_{f}G{(P)}_i}\hfill \\ & =& +\frac{K_A}{2}\equiv +\frac{K}{2}\hfill \end{array}$$

(27)

In Equations (26) and (27) holds by definition $K_A\equiv K$. The value of the integral in the numerator follows immediately from the following facts: $(a)$ the two functions G are positioned symmetrically around the middle point $\overline{P}=K_A/2$—one function is centered at 0, the other at $K_A$; and $(b)$ in this integral, P is a linear factor. Note also that this result is independent of the width of the Gaussian G.

Of course, this integral, and thus $P^w$, should change with variations of the assumed shape (and width) of the final state $G_f$. See the discussion of this issue given in [40].

Thus, we obtain from Equations (26) and (27)

$$X^w=-ig1/{\sigma }_P^2\frac{K}{2}$$

(28)

which is a negative imaginary number (if the smallness parameter g is positive). It may be noted that an imaginary WV is associated with the back-action of one system on the second, due to the interaction [39].

We apply now the main result (21) of the WV-TSVF theory [33,38]. By re-introducing explicitly the factor ℏ in the expression for momentum transfer, $K\to \hslash K$, we obtain for the WV-correction to the conventionally expected pointer momentum,

$${\left[{\langle \widehat{p}\rangle }_f-{\langle \widehat{p}\rangle }_i\right]}_{\mathrm{WV-correction}}=-2g/{\sigma }_P^2\frac{\hslash K}{2}Va{r}_p=-g\hslash K\frac{Va{r}_p}{Va{r}_P}$$

(29)

using the definition $Va{r}_P={\sigma }_P^2$. Note that $K>0$ since the neutron impinges on the system (initially at rest) along the x-axis “from the left” and thus the momentum transfer $\hslash K$ on the scatterer is positive, $\hslash K>0$. This result contains the variances of both quantum participants (i.e., neutron and scatterer) in the collisional process. Moreover, Equation (29) constitutes the main result of our derivation.

5.1. Physical Significance of the Main Result Equation (29)

We make now the following crucial observations:

(I) This concise theoretical result predicts the vanishing of the correction term caused by the WV-TSVF theory when considering the limiting case of a perfect plane wave neutron beam, where the variance of momentum ($Va{r}_p$) equals zero. This outcome is highly satisfactory as it accurately reproduces the conventional results found in textbooks [11,12].

(II) Additionally, if the scatterer is composed of quantum objects with well-defined positions, the uncertainty principle dictates that the variance of their momenta becomes infinite, denoted as $1/Va{r}_P\to 0$. Consequently, the correction term (29) disappears. Thus, this limit also aligns with the expected outcomes according to conventional theory [11,12].

Moreover, these observations yield the following noteworthy conclusions:

(III) Specifically for the mentioned hydrogenous materials, which exhibit an unusual deficiency in momentum transfer from the neutron to the impacted hydrogen atom, the coupling factor g in the model Hamiltonian (23) must be positive ($g>0$). It is important to note that there is no inherent restriction on g being positive beforehand. This finding introduces a novel quantum characteristic associated with the overall dynamics of neutron–matter interactions, as uncovered by the WV-TSVF theory.

(IV) The preceding effect of momentum-transfer deficit and the intensity-deficit effect are presented below; both are absent in the above limiting or idealized cases Iand II which are crucial for the validity of the conventional theory [11,12].

In summary, the above results provide new insights into the consequences following from the nature of quantum beams (here: neutron beam) and also further evidence of the novel character of WV-TSVF theory. The new experimental field of applicability of WV-TSVF (i.e., neutron scattering) may be pointed out.

5.2. Momentum-Transfer Deficit in INS from H${}_2$ Molecules in C-Nanotubes

In this subsection, we examine an incoherent (and inelastic) neutron-scattering (INS) experiment in order to illustrate the preceding theoretical findings. The theoretical basis and experimental method of INS are thoroughly explained in the textbook [23].

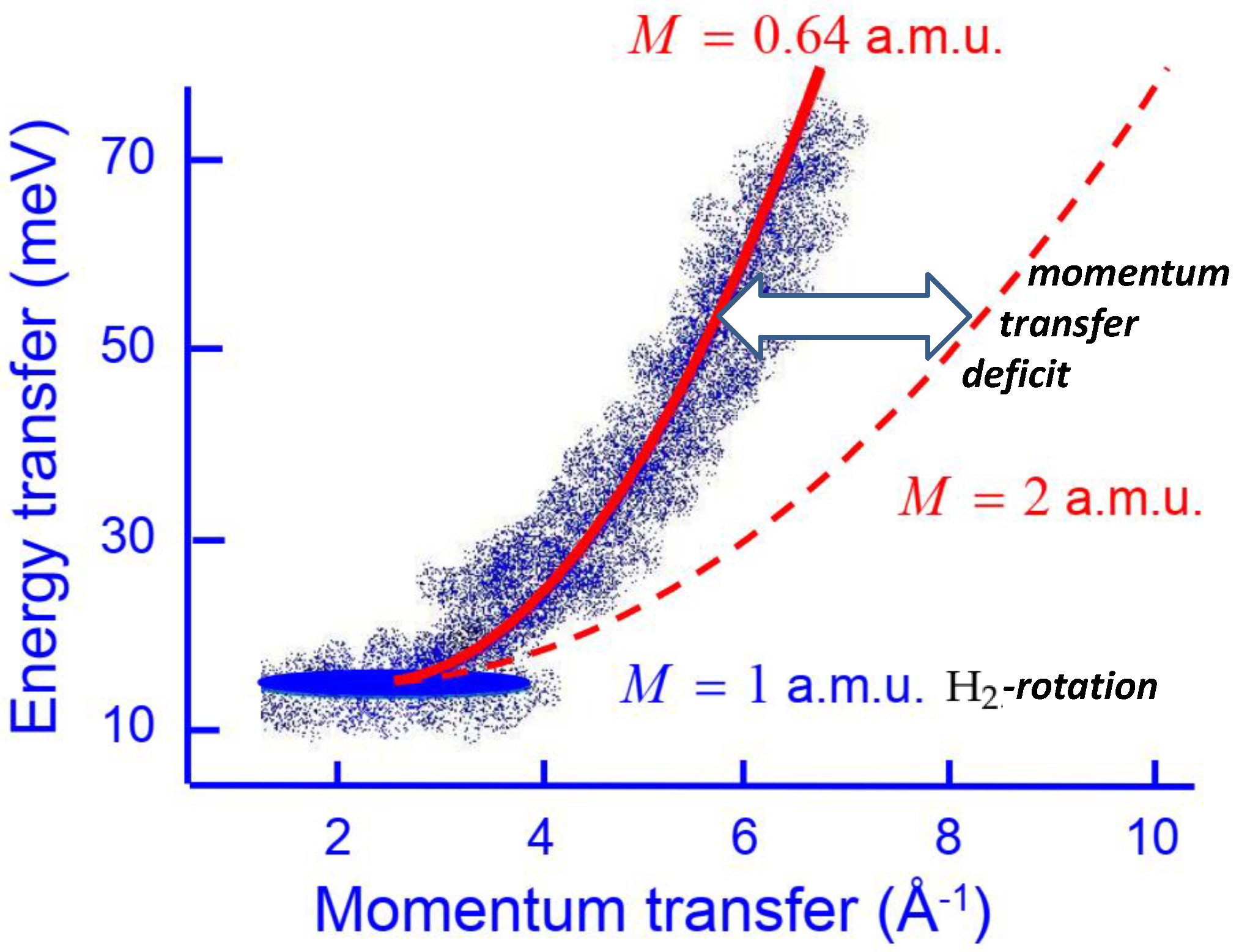
The experiment of Olsen et al. [42] focuses on INS involving individual hydrogen molecules adsorbed in carbon nanotubes. The measurements were conducted at the Oak Ridge National Laboratory’s new generation spallation neutron source (SNS) in the United States. Detailed information about the experiment and a comprehensive data analysis can be found in the original publication [42]. The primary outcomes of this INS experiment are depicted in Figure 1.

Figure 1 illustrates the primary outcomes of the INS experiment. In the realm of WV-TSVF theory, it is crucial to emphasize that achieving the post-selected state of H (or H${}_2$) is easily accomplished by orienting the axis of the C-nanotube in relation to the momentum transfer. This can be observed in the following two extreme scenarios:

(1) When the C-nanotube axis is perpendicular to $\mathbf{K}$, the trapped H (or H${}_2$) experiences a strong potential due to the repulsive nature of the C-nanotube wall.

(2) When the C-nanotube axis is parallel to $\mathbf{K}$, the trapped H (or H${}_2$) encounters a weak potential since it is only lightly adsorbed on the C-nanotube wall. As a result, it can undergo translational motion.

Evidently, the INS experimental results in scenario (2), specifically regarding the roto-translation motion of H${}_2$, exhibit a significant WV-correction. This correction deviates from the conventionally expected momentum transfer value and is even apparent upon visual examination.

To the best of our knowledge, no first-principles conventional (quantum or classical) theoretical explanation of this effect existed until now.

6. Intensity Deficit in Neutron Compton Scattering from H-Containing Materials

In this section, we consider exclusively the experimental method of neutron Compton scattering (NCS) and in particular an effect known as intensity deficit in the scattering from protons of H-containing materials. Here, it will be of crucial importance to take into account the value of some NCS characteristic parameters, i.e., the collisional time window and the energy and momentum transfers involved.

6.1. Characteristic Parameters of NCS

In the context of NCS, which applies so-called epithermal neutrons, the achieved momentum and energy transfers are large, i.e.,

$$\Delta E\approx 1-100\mathrm{eV}\mathrm{and}|\mathbf{K}|\sim 20-200{\AA }^{-1}$$

(30)

As a consequence, here the so-called Impulse Approximation (IA) applies [24,25]. Moreover, the time scale—often called “scattering time”, ${\tau }_{sc}$—characterizing the neutron–proton scattering dynamics is very short [24], i.e., about

$${\tau }_{sc}\sim 100-1000\mathrm{as}$$

(31)

(as: attosecond, ${10}^{-18}$ s). These physical parameters are provided at the eVS-Vesuvio instrument of the ISIS facility, Rutherford Appleton Laboratory, UK. These parameters are related as described by the theoretical result of IA [24,25]

$${\tau }_{sc}|\mathbf{K}|\langle v_0\rangle \approx 1$$

(32)

In this formula, $\langle v_0\rangle$ is the root-mean-square velocity of the nucleus (here, proton) before collision, which of course depends on the system (material) under investigation. $\hslash \mathbf{K}$ is the momentum transfer as already defined in the previous sections. Furthermore, it holds that ${\tau }_{sc}$ equals the t-width of the intermediate correlation function $F(K,t)$ (see Section 2) [24,25].

In the IA, the scattering is assumed to be essentially incoherent, essentially meaning that each neutron scatters from a single nucleus—a single proton, in our case. Indeed, experimental determination of the energy transfer associated with the measured H-recoil peak shows that the mass of the struck H atom of the benzene sample (see below) is equal to 1 a.m.u. (atomic mass unit)—i.e., the neutron collides with a single proton.

For these reasons, the NCS method is applied to explore single-particle properties, and especially the momentum distribution of an atom in its initial state. Furthermore, this is supposed to reflect structural details of the Born–Oppenheimer potential $V_{BO}$ surrounding the struck atom before collision [24].

The original motivation to establish the NCS experimental method was the possibility to measure the momentum distributions $n(p)$ of He atoms in the normal liquid state of helium, and also in its superfluid state [24,25]; see the original proposal by Hohenberg and Platzman [26].

6.2. WV-TSVF Interpretation of the Intensity-Deficit Effect

A surprisingly straightforward consequence based on the preceding theoretical derivations predicts, from first principles, the so-called intensity-deficit effect for hydrogen, earlier observed in several neutron Compton scattering (NCS) experiments from various H-containing materials; see [43,44,45,46,47] and papers cited therein.

To show this, it suffices to refer to the preceding general WV-theoretical result, Equation (18), stated here again for convenience:

$${\mathrm{\Phi }}_i\to {\mathrm{\Phi }}_f=e^{-ig{A}^w\widehat{M}}{\mathrm{\Phi }}_i$$

(33)

Namely, for the case of an imaginary and negative, $A^w=-i|Im\left[A^w\right]|$, we obtain

$${\mathrm{\Phi }}_i\to {\mathrm{\Phi }}_f=e^{-g|Im\left[A^w\right]|\widehat{M}}{\mathrm{\Phi }}_i$$

(34)

The exponential factor, which now is a real negative number, reduces the norm of the pointer-state wavefunction,

$$||{\mathrm{\Phi }}_f||<||{\mathrm{\Phi }}_i||$$

(35)

In other terms, here the time evolution is non-unitary.

Now, in our case (see below) we are interested in the scattering intensity from protons (or H). On physical ground, it is obvious that $\langle {\mathrm{\Phi }}_f|{\mathrm{\Phi }}_f\rangle$ is proportional to the scattering intensity ($I_H$) as measured by the pointer:

$$\langle {\mathrm{\Phi }}_f|{\mathrm{\Phi }}_f\rangle \propto I_H$$

(36)

Finding (35) is sometimes criticized as being an artifact of the post-selection and not a true quantum dynamical effect, due to the fact that here the pointer operator $\widehat{p}$ commutes with the interaction Hamiltonian $H_{int}$. However, it must be emphasized that there is no arbitrariness or any “improper approximation” involved in the preceding derivation of the imaginary weak value $X^w$ and the associated non-unitary evolution Equation (34). In this context, note also that the choice of the final state of the system (i.e., a displaced Gaussian in momentum space) is common in theoretical investigations. Moreover, the fact that here $X^w$ has a vanishing real part implies that the associated pointer’s position remains invariant, i.e.,

$${\langle \widehat{x}\rangle }_f={\langle \widehat{x}\rangle }_i$$

This is fully consistent with the impulsive, $\delta$-like, nature of $H_{int}$. In simple terms, the hit system has no time to change its position just after the interaction is turned off.

6.3. Experiment: H-Intensity Deficit in NCS from Liquid Benzene

In short, the experimental NCS procedure is as follows. From a measured time-of-flight (TOF) spectrum with an individual detector, the data analysis routine determines the relevant peak areas $A_X$ or intensities $I_X$ (where X = H, C, Nb) from the measured partial differential cross-section $d^2\sigma /d\omega d\mathrm{\Omega }$; see Section 2. Thus, one determines by standard numerical analysis the ratio

$$R_{exp}\equiv \frac{I_H}{I_X}$$

(37)

Standard NCS theory [24] predicts that the expected value $R_{conv}$ of this ratio is

$$R_{conv}=\frac{N_H{\sigma }_H}{N_X{\sigma }_X}.$$

(38)

$N_X$ is the number density of atom X and ${\sigma }_X$ is the tabulated cross-section of the nucleus of X.

Here we are interested in the ratio $I_H/I_C$ for benzene—which is achieved by the data analysis after subtraction of the “overlapping” Nb-peak of the metallic nyobium container (see Figure 2A). Surprisingly, the experimental results presented below (and many others, too) exhibit a striking intensity deviation, i.e.,

$${(I_H/I_C)}_{exp}\approx 0.75{(I_H/I_C)}_{conv}$$

(39)

This effect has found no conventional interpretation thus far.

Assuming approximately that the heavier C atoms behave “conventionally”, we may attribute this effect to the H atoms (i.e., the protons) and speak of the H-intensity deficit effect.

Parenthetically, some accompanying NCS measurements on deuterated benzene (C${}_6$D${}_6$) were performed, which showed a considerably smaller (although discernible) D-intensity deficit relative to the C-intensity. Moreover, similar electron Compton-like scattering (ECS) experiments from H${}_2$ and D${}_2$ in the gas phase reveal an intensity-deficit effect, too [46].

6.4. Which-Path Information and Impossibility of Neutron Beam Interferences in NCS from Several Entangled Protons

Earlier [28], a theoretical interpretation of the NCS-intensity-deficit effect was proposed, based on the hypothesis that two (or more) entangled protons may exist in the characteristic coherence volume of the neutron beam—a few Å${}^3$, in the short time-window of NCS, see relation (31). It was argued that this QE concerns spatial and spin degrees of freedom, due to the identity of the involved protons [28]. Consequently, the measured cross-section should be due to scattering by such an entangled protonic system of two (or more) protons. It was theoretically derived that the assumed QE should reduce the scattering intensity of the system. This reduction is tantamount to a destructive quantum interference of the various participating, possible neutron paths. Clearly, this physical view goes beyond the standard one [24], which considers NCS (or, equivalently, DINS) essentially as a two-body scattering process.

However, this theoretical proposal appears highly questionable in the light of modern quantum mechanics, in which the aforementioned phenomenon of impossibility of interference in the case of which-path information plays a central role. Indeed, the high energy transfer (say, e.g., 5–50 eV—which even breaks the chemical C-H bond) on a scattering proton makes it distinguishable from the other H atoms of the scattering system, independently of whether QE effects are present or not. In other terms, this large energy transfer is equivalent to full which-path information, which rules out the aforementioned proposed interpretation of the intensity-deficit effect: namely, the path of the scattered neutron is here fully known, because the scattering proton is easily distinguishable from the non-hit protons in the aforementioned coherence volume.

To put it differently, the NCS-intensity deficit effect can be attributed to the collision of a neutron with a single hydrogen atom (which interacts with its environment). That is, this effect is unrelated to any assumed quantum interference of several neutron paths originating from different protons. This is in line with the conventional viewpoint that NCS scattering is incoherent [24,25].

The conceptual similarity to the common quantum two-slit experiment should be obvious: when we have information about which path a particle (such as a neutron, atom or photon) takes, this cancels the interference pattern on the screen (i.e., the measurement device). Moreover, having partial knowledge about the path reduces the visibility of the interference fringes accordingly; see [13,15,16,17,18,19,20,21,22].

The above remarks are fully in line with Feynman’s statement stressed in the Introduction, which, in the present case, may be rephrased as follows: You may argue, “I don’t care which specific proton has scattered the neutron”. Perhaps you don’t, but nature knows; and neutron’s scattering amplitude behaves, in fact, as we just discussed—there isn’t any interference.

7. Discussion

In order to facilitate a bit more the understanding of the preceding results, here we provide some additional remarks and explanations.

In some cases, the quantum character of the beam particles (i.e., neutrons in the cases considered above) enforces the need to go “beyond” the conventional scattering theory. E.g., the neutrons have to be considered as quantum objects with finite coherence length; the duration of the neutron–nucleus collision has to be specified; the neutron–nucleus colliding system is an open quantum system, which in general may have a non-unitary time evolution. These remarks clearly contrast the conventional theory, where (1) the neutrons are plane waves, (2) the concept of duration of the collision plays no role in the interpretation of experimental scattering results, (3) the quantum dynamics of the scattering system (assumed to be isolated) is unitary and (4) where the neutron is described by c-numbers (and not by operators).

The novel theory of weak values (WV) and two-state vector formalism (TSVF) introduces a fresh perspective by explicitly considering the quantum nature of the probe beam. This approach uncovers various counter-intuitive effects that might appear “strange” or even “wrong” when compared to conventional theory. For example, the momentum-transfer deficit effect may seem to violate the fundamental laws of energy and momentum conservation. However, these objections stem from the incorrect (often tacit) assumption that the scattering particle A is an isolated quantum system. In other words, the quantum dynamics of the “environment” of A actively participate in the neutron-A scattering process and thus play an indispensable role in understanding the new WV-TSVF effects mentioned earlier. Therefore, it is beneficial to highlight the accurate conservation relations in the following manner:

$$\Delta E_{H+env}=-\Delta E_n\mathrm{and}\Delta \hslash {\mathbf{K}}_{H+env}=-\Delta \hslash {\mathbf{K}}_n$$

(40)

$\Delta X_Y$ represents the change of quantity $X_Y$ due to the collision. The participating environmental degrees of freedom are indicated by the subscript env; n refers to the neutron and H refers to the system—here, the (proton of the) struck H atom.

Here, a note of caution should be introduced. In most experimental situations, the environment of a quantum system A disturbs its dynamics. Hence, the environment referred to here could be alternatively called ancilla—as in the theory of quantum computing [6]—because it plays a constructive role in the dynamics, i.e., preserves the unitarity of the whole “A + ancilla” system. Note that ancillas are present in the overwhelming majority of quantum circuits designed to carry out various well-known algorithms in quantum computers [6].

Additionally, considering these comments, a straightforward corollary arises that is highly perplexing for conventional theory: the short-time evolution of any elementary neutron-H scattering process in INS or NCS, where H is a component of a hydrogenous condensed material (or a molecule), is non-unitary.

In conventional NCS theory, an approximation is made where the complete Hamiltonian is replaced “by hand” using intuitive justifications, such as the extremely short scattering time ${\tau }_{sc}$. Instead of the complete Hamiltonian, one introduces an effective one-particle Hamiltonian (i.e., that of a H) residing in a Born–Oppenheimer (BO) potential; cf. [24]. Clearly, the mentioned BO potential plays only a passive role in the microscopic scattering dynamics, since it has no dynamical variables. This theoretical framework suggests that any dynamical non-unitary process, such as decoherence, is here impossible. This implies that the validity of various investigations claiming to “directly measure the ab initio BO potential” should be critically reconsidered.

In our theoretical models concerning neutron scattering (INS and NCS), the interaction Hamiltonian in Equation (14) involves two distinct quantum systems, namely a neutron and a proton. The operators $\widehat{p}$ and $\widehat{X}$ within this Hamiltonian pertain to these individual systems. Consequently, as clarified by Vaidman [48], the concept of WV emerges in this context due to the interference of an entangled quantum wave and thus it lacks an equivalent counterpart in classical wave interference or classical physics. This highlights that WV is a fundamentally quantum concept, rather than an approximation. It is important to remember that there is no quantum entanglement between a classical system and a quantum system.

All the preceding derivations and considerations are related to (or based on) the concept of weak measurement, which usually is not believed to be generally applicable to “real experiments”. However, it has been shown that weak measurements are universal [49]. In essence, this holds because any projective (strong) measurement can be decomposed into a sequence of weak measurements, which cause only small changes to the system’s state. Further analysis showed that this result holds even in the broader case of so-called generalized measurements [49].

The theoretical results we derived showed that the WV of the coupling system variable $\widehat{X}$ is purely imaginary, Equation (26). The physical significance of imaginary WVs has been analyzed in detail in Ref. [39]. It was argued that the imaginary WV provides direct information about how the initial state would be unitarily disturbed by the observable operator. Furthermore, as the imaginary part constitutes a shift in the pointer momentum, this latter effect is a reflection of the back-action of a measurement on the particle (scatterer).

Moreover, our analysis of the intensity-deficit effect provides a new insight into, or a new aspect of, the physical meaning of an imaginary WV. Furthermore, note that a positive imaginary WV, together with a positive coupling g, would theoretically predict an intensity surplus instead of a deficit. However, as of now, we are not aware of a related experimental observation in another quantum beam-scattering context.

Here, let us mention some additional references [50,51,52,53], which provide further evidence for the predictive power of, and newer physical insights into, the theory of WV and TSVF.

It should be helpful to emphasize the connection of the above NCS and INS investigations with the vivid scientific debate about complementarity, which-path experiments and the uncertainty principle. This is a topic of considerable activity (and controversy) over the past three decades. In simple terms, the NCS-intensity deficit effect is a “single H atom effect”, and it has nothing to do with quantum interference of all possible paths of a neutron originating from many protons of the scattering material. This is due to the fact that the struck proton (which receives several tens of eVs by the NCS-collision) is distinguishable from the adjacent non-struck protons. E.g. in the case of the measured H-intensity in NCS from benzene, only one proton is struck. (This is experimentally proven by the H-peak position in the measured time-of-flight spectra, as calculated in standard NCS theory). That is, the struck proton is the scattering “system” A and the remaining five protons, the six C-nuclei and all the electrons of the molecule constitute the “environment” or ancilla.

To conclude these discussions about NCS quantum dynamics and in the spirit of Feynman’s quotation (see the Introduction), we can state that “nature knows”, and therefore there is no interference between the amplitudes of the six potential n-H scattering trajectories from C${}_6$H${}_6$ to the H-recoil peak shown in Figure 2A. Hence, the above-considered surprising NCS effect appears to have a true quantum dynamical origin based on the open-system quantum dynamics of specific few-body interactions. These involve the struck system (proton or H), which is coupled with its quantum environment (or ancilla), and the impinging quantum particle, i.e., the neutron.

8. Conclusions

Since the preceding discussion section is rather long and considers diverse issues, let us conclude by pointing out the main findings and results of the paper.

We provided theoretical and experimental evidence that certain assumptions of the conventional neutron-scattering theory cannot explain the experimental INS and NCS results considered above. Certain questionable assumptions of conventional theory have been discussed in considerable detail. Among these are:

(1) The plane-waves approximation for the neutron beam;

(2) The missing concept of scattering time by the interpretation of experimental results;

(3) The assumptions that the scattering system is an isolated quantum system and that the short-time neutron-particle scattering dynamics is unitary;

(4) The dynamical observables (operators) of the neutron beam are “replaced” by c-numbers.

The latter also implies that QE between a neutron and the scatterer (i.e., protons, in the discussed experiments) does not exist in conventional theory.

The novel quantum-theoretical approach of WV and TSVF overcomes these weaknesses (1–4) and makes a novel approach to quantum beam scattering possible. This theoretical formalism provides a theoretical interpretation of both the momentum-deficit and the intensity-deficit effects “from first principles” and on equal footing.

The presented discussions of the considered INS and NCS processes demonstrated that the scatterers (i.e., protons, in the examples) cannot be considered as isolated systems. That is, their interactions with the environment must be taken into account by the formulation of the basic energy- and momentum-conservation laws; see Equation (40). In simple terms, discarding the environment would lead to the wrong conclusion that these basic conservation laws could be violated in the experiments under consideration.

The presented theoretical analysis also makes contact with the widely used concept of (effective) Born–Oppenheimer potential, $V_{BO}$, which also appears in NCS investigations; cf. [24]. Also, it holds here that no dynamical quantities (operators) are associated with the environmental particles participating to the $V_{BO}$. One may say that the BO potential is a static concept, rather than a dynamical one.

In the presented theoretical derivations and discussions, the fundamental concept of which-path information [13,15,16,17,18,19,20,21,22] (also called which-way information, or welcher Weg detection in [15]) plays a crucial role. This concept is very well known in the field of quantum optics, but not in neutron-scattering theory. The basic physics of this concept is already stressed, in a slightly different wording, in the textbook [14] by Feynman, which we repeatedly cited above in various appropriated places (e.g., in the Introduction and the Discussion sections). Furthermore, it plays a decisive role in the critical analysis of the NCS-theoretical model of the intensity-deficit effect presented in Section 6.4.

Finally, here we may stress the novelty of the derived main WV-theoretical results, Equations (29) and (34), which provide, for the first time, a unified theoretical interpretation of the momentum-transfer deficit observed with INS and the intensity-deficit effect observed with NCS. Among various limiting cases (see Section 5.1), this result demonstrates an important point: in the limit of the plane-waves approximation for the neutron beam, the momentum-transfer deficit of INS disappears and thus the corresponding predictions of conventional theory concerning momentum transfer are re-derived. This result provides further evidence for the experimental relevance and predictive power of the novel theory of WV and TSVF; see Section 4 and references cited therein.