On the Schott Term in the Lorentz-Abraham-Dirac Equation
Abstract
:1. Introduction
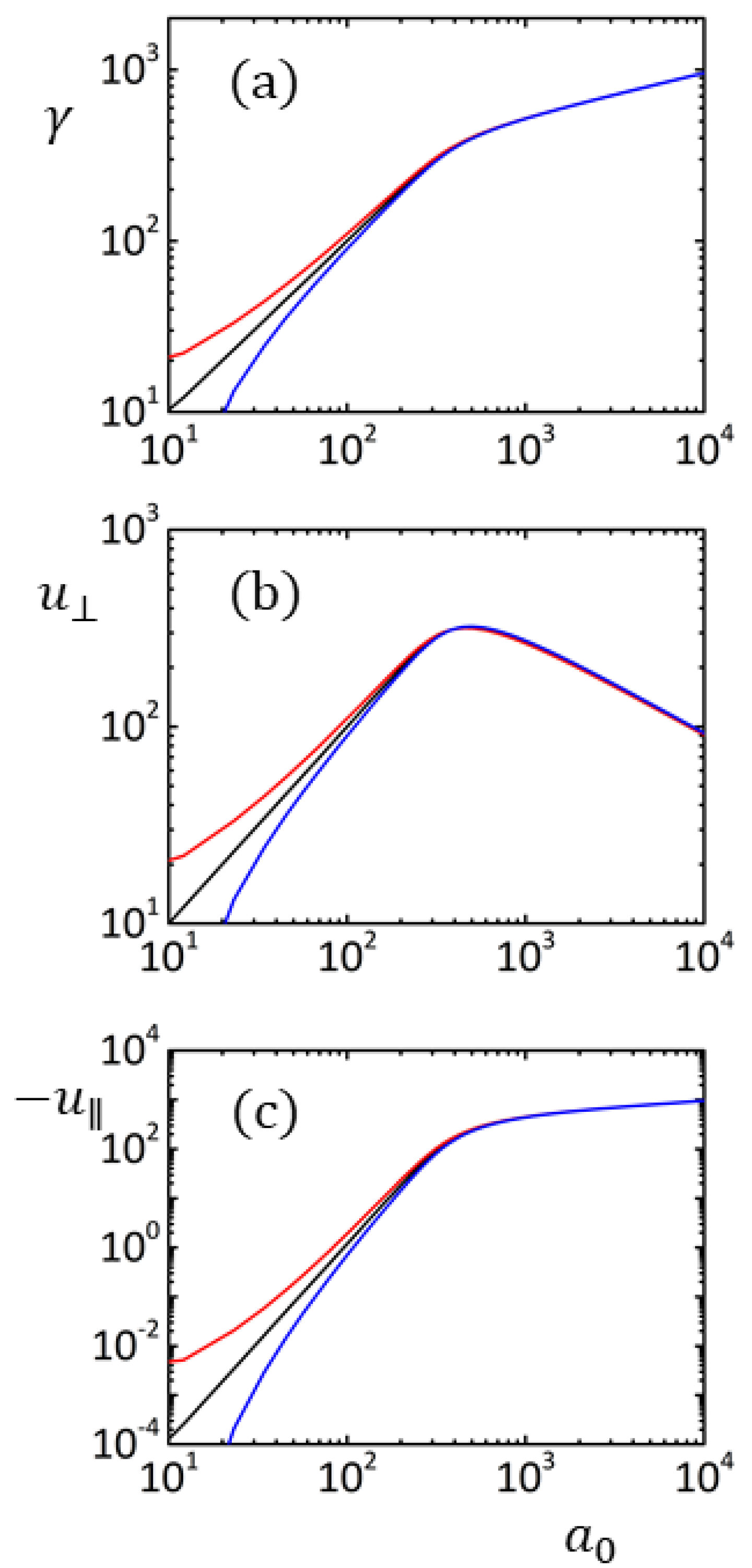
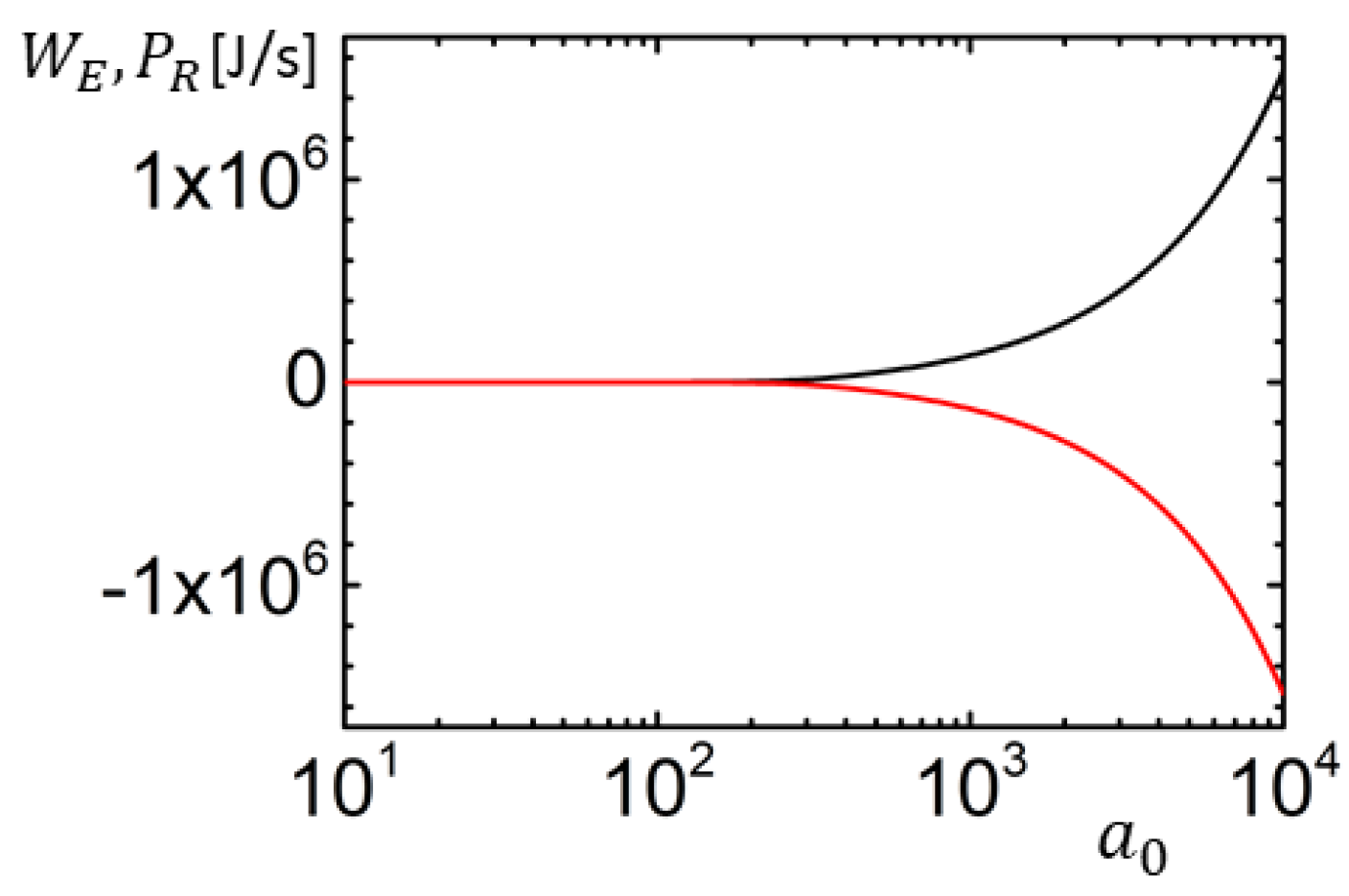
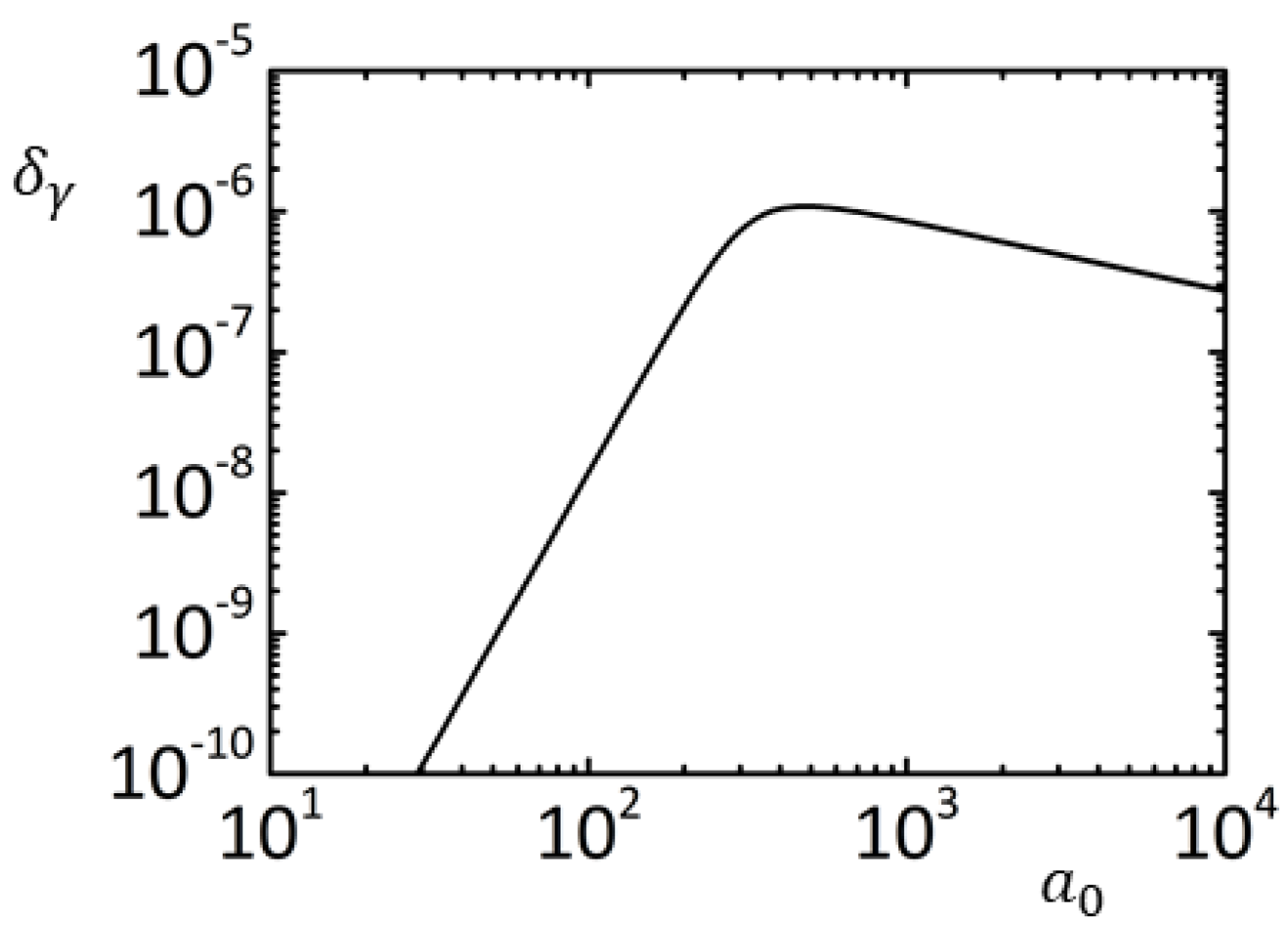
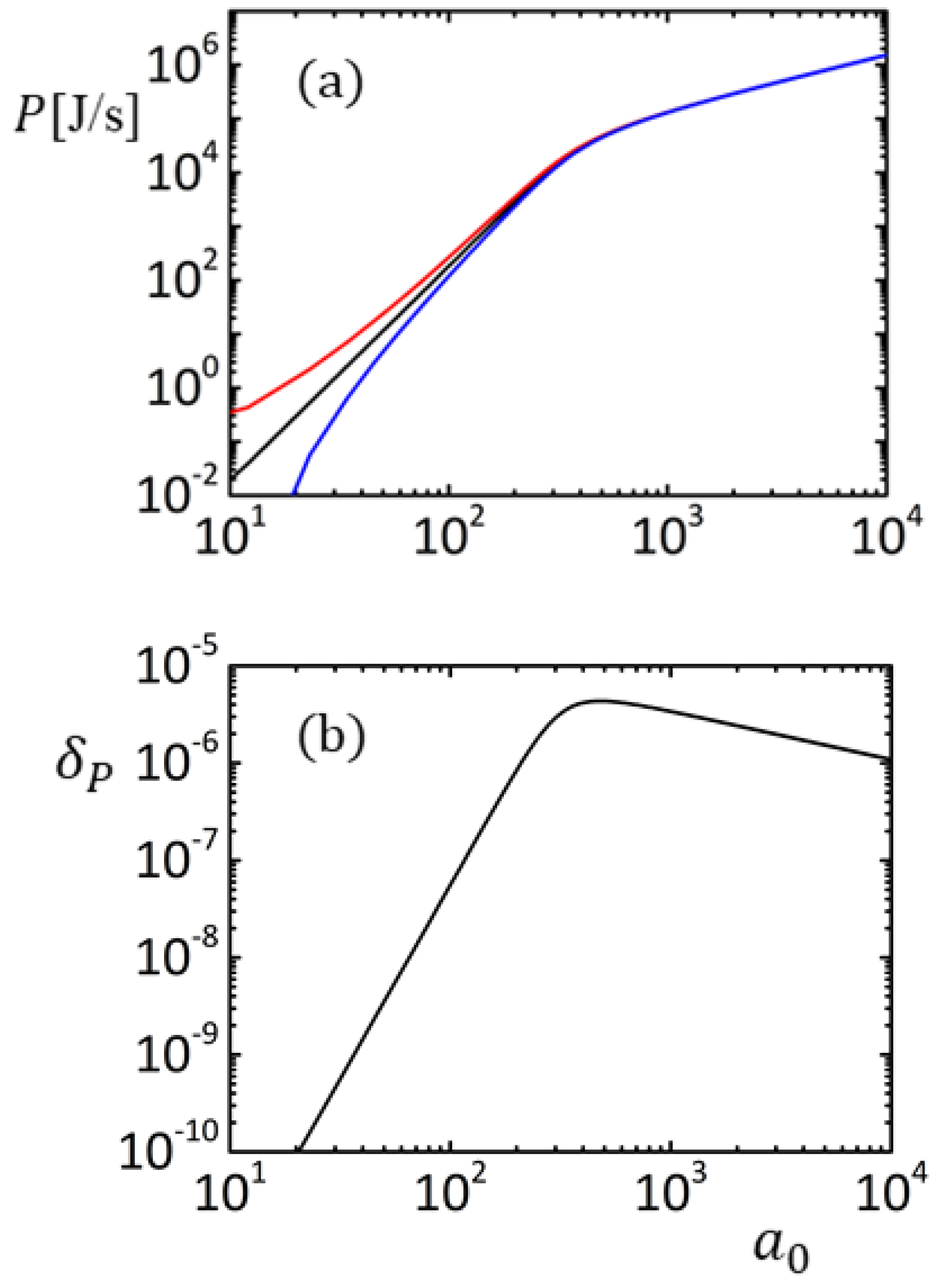
2. The Schott Term for a Stationary Motion
3. Stationary Solution of LAD Equation Without the Schott Term
4. Conclusions
Funding
Conflicts of Interest
References
- Extreme Light Infrastructure (ELI). Available online: https://eli-laser.eu/ (accessed on 3 August 2020).
- Ain, Q.; Li, S.; Miraie, M.; Harz, N.A.M. Generation of GeV electron beam from a laser-plasma accelerator and its prospect as a desktop source of energetic positrons and gamma rays for applications. IEEE Trans. Nucl. Res. 2018, 65, 2671. [Google Scholar] [CrossRef]
- Sharma, A.; Lamperidis, C. High energy proton micro-bunches from a laser plasma accelerator. Sci. Rep. 2019, 9, 13840. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nakamura, T.; Hayakwa, T. Quasi-monoenergetic positron beam generation from ultra-intense laser-matter interactions. Phys. Plasmas 2016, 23, 103109. [Google Scholar] [CrossRef]
- Nakamura, T.; Koga, J.; Esirkepov, T.Z.; Kando, M.; Korn, G.; Bulanov, S.V. High energy ions from near-critical density plasmas via magnetic vortex acceleration. Phys. Rev. Lett. 2012, 108, 195001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rigers, C.P.; Brady, C.S.; Duclous, R.; Kirk, J.G.; Bennet, K.; Arber, T.D.; Robinson, A.P.L.; Bell, A.R. Dense electron-positron plasmas and ultraintense γ rays from laser-irradiated solids. Phys. Rev. Lett. 2012, 108, 165006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lorentz, H. The Theory of Electrons and Its Applications to the Phenomenon of Light and Radiant Heat; B.G.Teubner: Leipzig, Germany, 1909. [Google Scholar]
- Abraham, M. Theorie der Elektrizitat; B.G.Teubner: Leipzig, Germany, 1905. [Google Scholar]
- Von Laue, M. Die wellenstrahlung einer bewegten punktladung nach dem relativitatsprinzip. Ann. Phys. 1909, 28, 436. [Google Scholar] [CrossRef] [Green Version]
- Dirac, P.A.M. Classical theory of radiating electrons. Proc. R. Soc. A 1938, 167, 148–169. [Google Scholar]
- Pauli, W. Theory of Relativity; Pergamon Press: New York, NY, USA, 1958. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; Wiley: New York, NY, USA, 1975. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Pergamon Press: Oxford, UK, 1994. [Google Scholar]
- Rohlich, R. Classical Charged Particle; World Scientific: Singapore, 2007. [Google Scholar]
- Yaghjian, A.D. Relativistic Dynamics of a Charged Sphere; Springer: New York, NY, USA, 1992. [Google Scholar]
- Mo, T.C.; Papas, C.H. New equation of motion for classical charged particles. Phys. Rev. D 1971, 4, 3566. [Google Scholar] [CrossRef] [Green Version]
- Ford, G.W.; O’Connell, R.F. Radiation reaction in electrodynamics and the elimination of runaway solutions. Phys. Lett. A 1991, 157, 217. [Google Scholar] [CrossRef]
- Ilderton, A.; Torgrimsson, G. Radiation reaction in strong field QED. Phys. Rev. D 2013, 88, 025021. [Google Scholar] [CrossRef] [Green Version]
- Cremaschini, C.; Tessarotto, M. Exact solution of the EM radiation-reaction problem for classical finite-size and Lorentzian charged particles. Eur. Phys. J. Plus 2011, 126, 42. [Google Scholar] [CrossRef] [Green Version]
- Steane, A.M. The fields and self-force of a constantly accelerating spherical shell. Proc. Roy. Soc. A 2014, 470, 20130480. [Google Scholar] [CrossRef] [Green Version]
- Seto, K. Radiation reaction in quantum vacuum. Prog. Theor. Exp. Phys. 2015, 2015, 023A01. [Google Scholar] [CrossRef] [Green Version]
- Faci, S.; Helayel-Neto, J.A.; Satheeshkumar, V.H. Physical and Mathematical Aspects of Symmetries; Duarte, S., Gazeau, J.-P., Faci, S., Micklitz, T., Scherer, R., Eds.; Springer International Publishing AG: Gewerbestrasse, Switzerland, 2017; p. 177. [Google Scholar]
- Schott, G.A. Electromagnetic Radiation and the Mechanical Reactions Arising from It; Cambridge University Press: Cambridge, UK, 1912. [Google Scholar]
- Teitelboim, C. Splitting of the Maxwell tensor: Radiation reaction without advanced fields. Phys. Rev. D 1970, 1, 1572. [Google Scholar] [CrossRef]
- Eriksen, E.; Grøn, Ø. Electrodynamics of hyperbolically accelerated charges IV. Energy-momentum conservation of radiating charged particles. Ann. Phys. 2002, 297, 243. [Google Scholar] [CrossRef]
- Grøn, Ø. The significance of the Schott energy for energy-momentum conservation of a radiating charge obeying the Lorentz-Abraham-Dirac equation. Am. J. Phys. 2011, 79, 115. [Google Scholar]
- Hofmann, A. The Physics of Synchrotron Radiation; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Sokolov, I.V. Renormalization of the Lorentz-Abraham-Dirac equation for radiation reaction force in classical electrodynamics. J. Exp. Theor. Phys. 2009, 109, 207. [Google Scholar] [CrossRef] [Green Version]
- Capdessus, R.; Noble, A.; McKenna, P.; Jaroszynski, D.A. Role of momentum and velocity for radiating electrons. Phys. Rev. D 2016, 93, 045034. [Google Scholar] [CrossRef] [Green Version]
- Rivera, R.; Villaroel, D. Exact solutions to the Mo-Papas and Landau-Lifshitz equations. Phys. Rev. E 2002, 66, 046618. [Google Scholar] [CrossRef] [PubMed]
- Bulanov, S.V.; Esirkepov, T.Z.; Kando, M.; Koga, J.K.; Bulanov, S.S. Lorentz-Abraham-Dirac versus Landau-Lifshitz radiation friction force in the ultrarelativistic electron interaction with electromagnetic wave (exact solutions). Phys. Rev. E 2011, 84, 056605. [Google Scholar] [CrossRef] [PubMed] [Green Version]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakamura, T. On the Schott Term in the Lorentz-Abraham-Dirac Equation. Quantum Beam Sci. 2020, 4, 34. https://doi.org/10.3390/qubs4040034
Nakamura T. On the Schott Term in the Lorentz-Abraham-Dirac Equation. Quantum Beam Science. 2020; 4(4):34. https://doi.org/10.3390/qubs4040034
Chicago/Turabian StyleNakamura, Tatsufumi. 2020. "On the Schott Term in the Lorentz-Abraham-Dirac Equation" Quantum Beam Science 4, no. 4: 34. https://doi.org/10.3390/qubs4040034
APA StyleNakamura, T. (2020). On the Schott Term in the Lorentz-Abraham-Dirac Equation. Quantum Beam Science, 4(4), 34. https://doi.org/10.3390/qubs4040034



