Laser Requirements for High-Order Harmonic Generation by Relativistic Plasma Singularities †
Abstract
1. Introduction
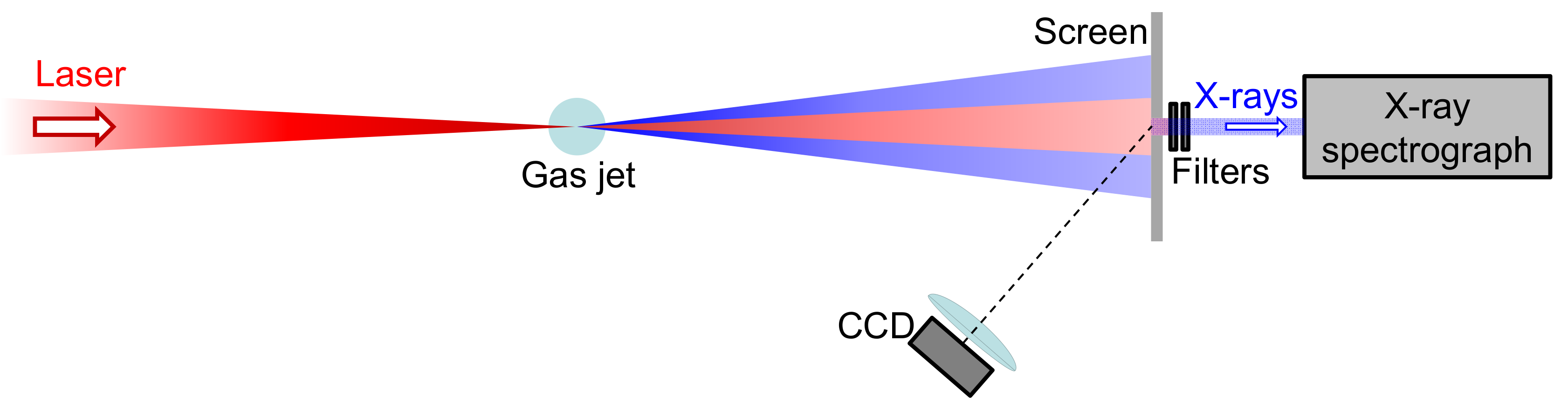
2. Materials and Methods
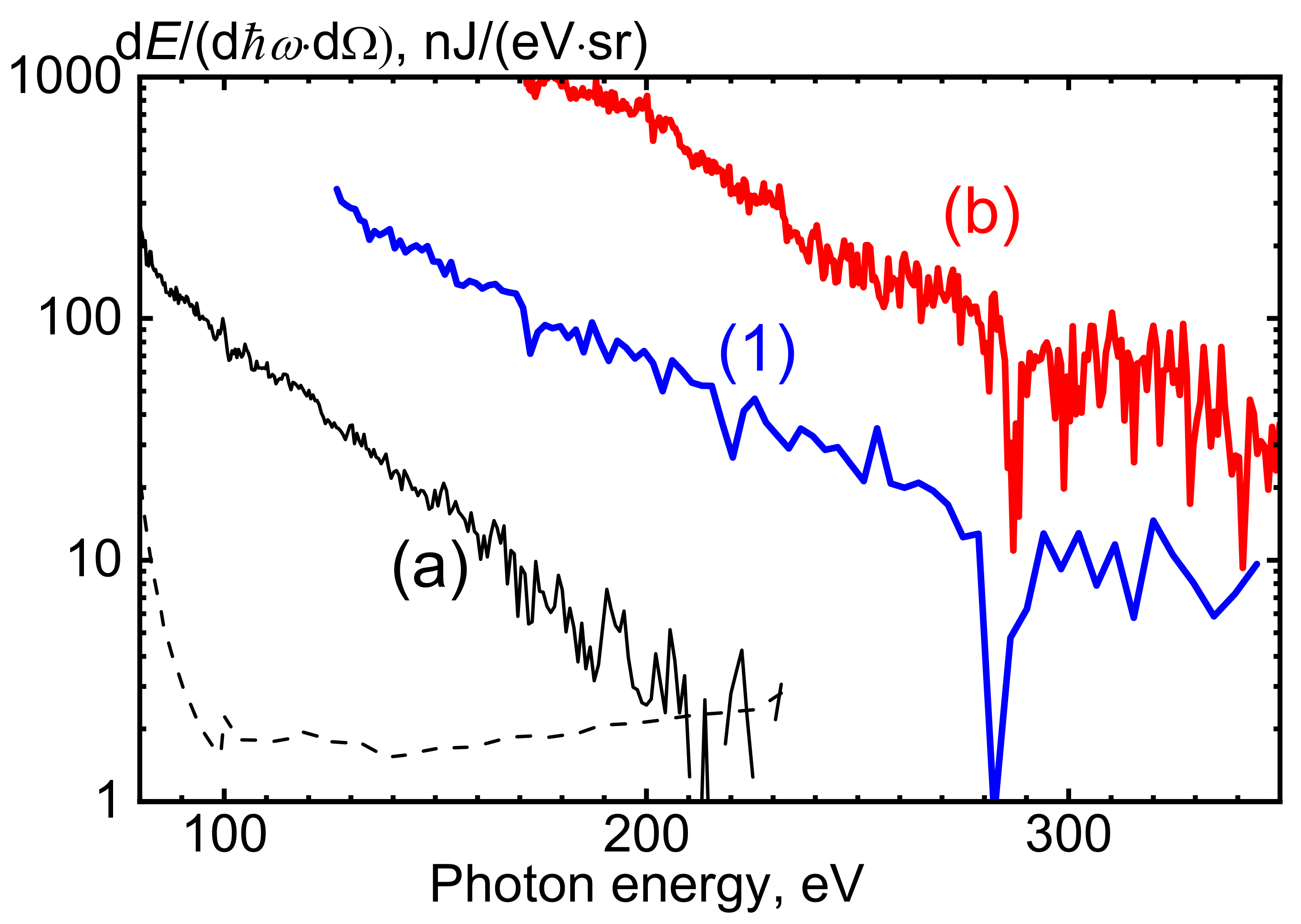
3. Results
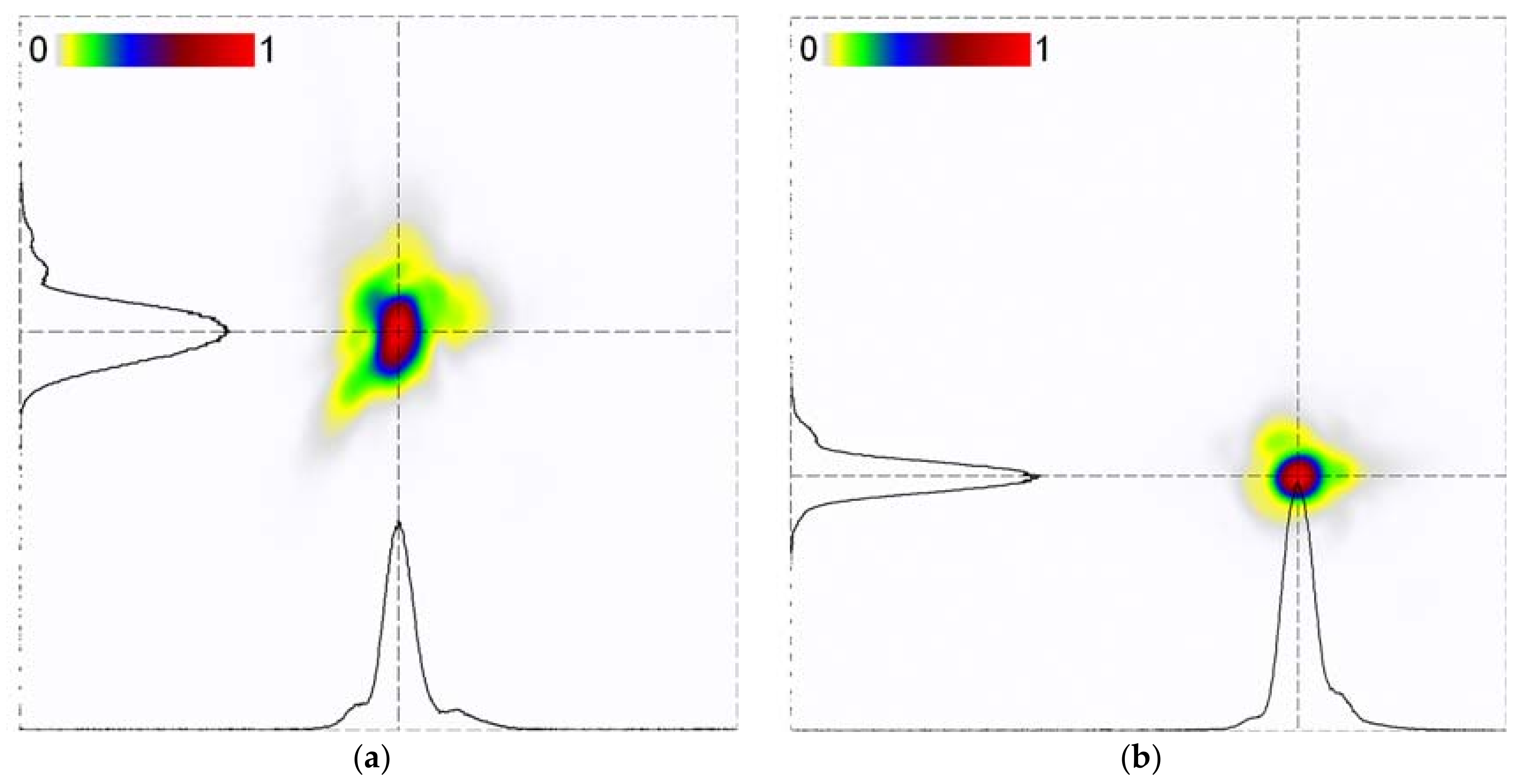
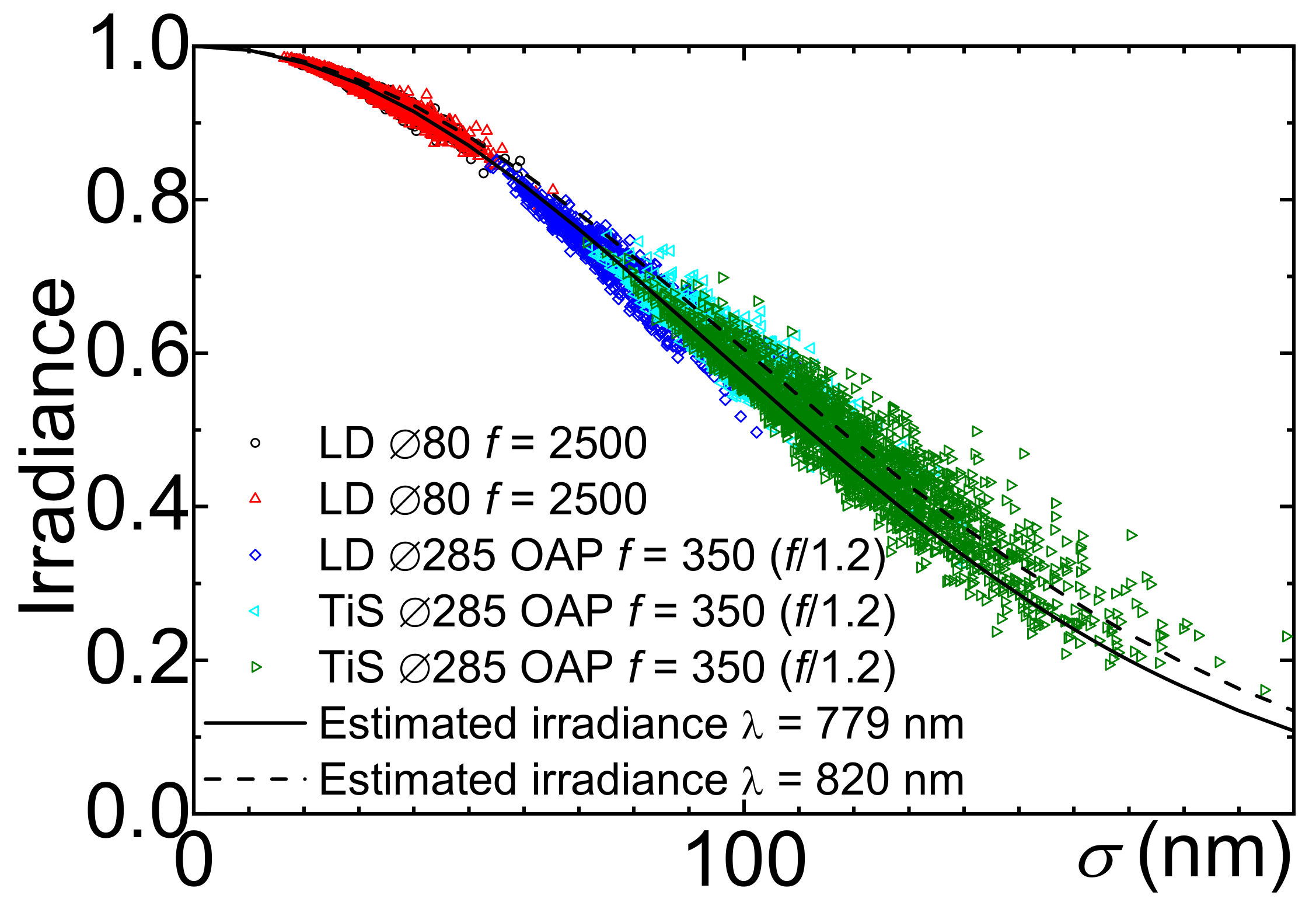
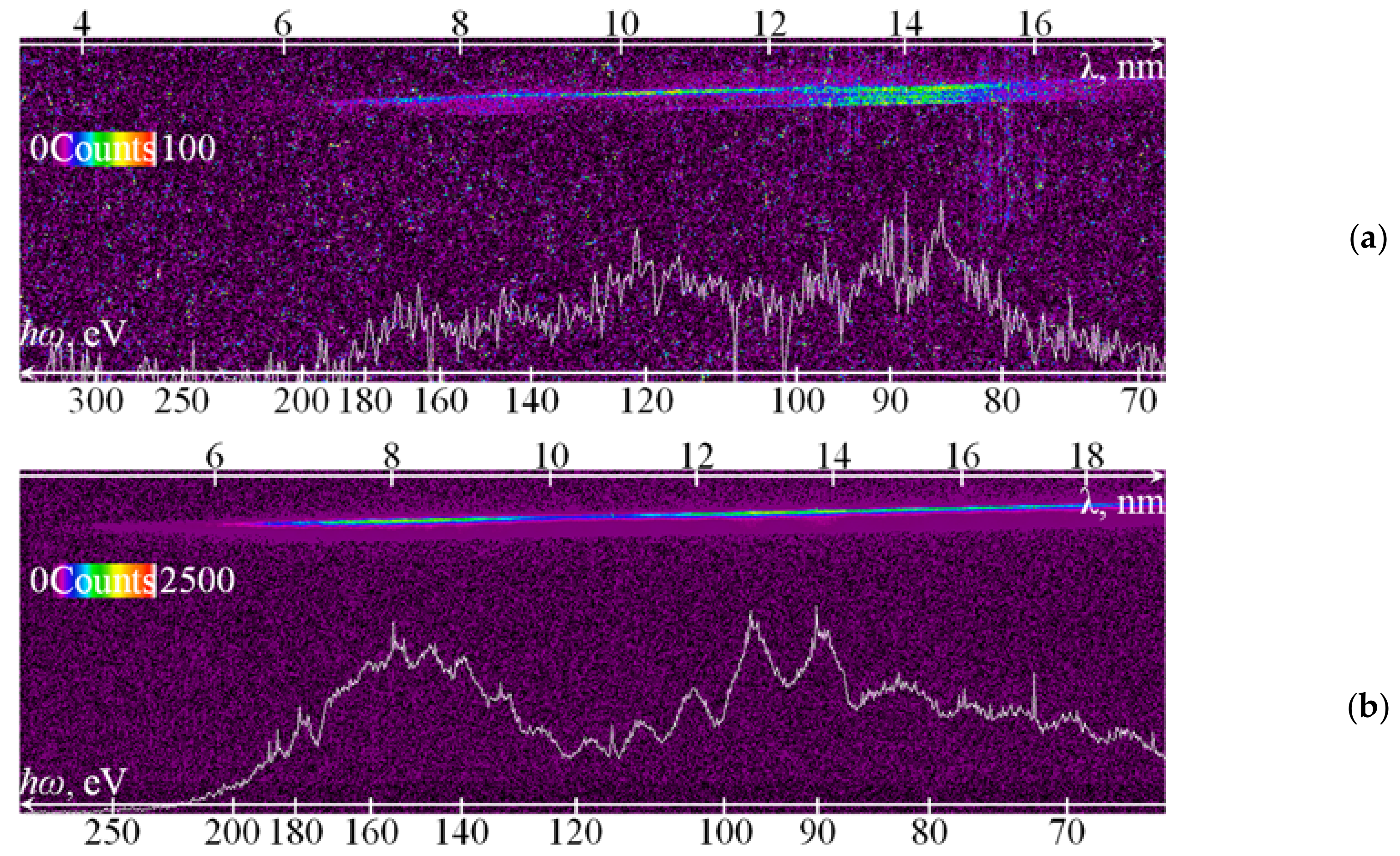
3.1. Dependence on the Irradiance
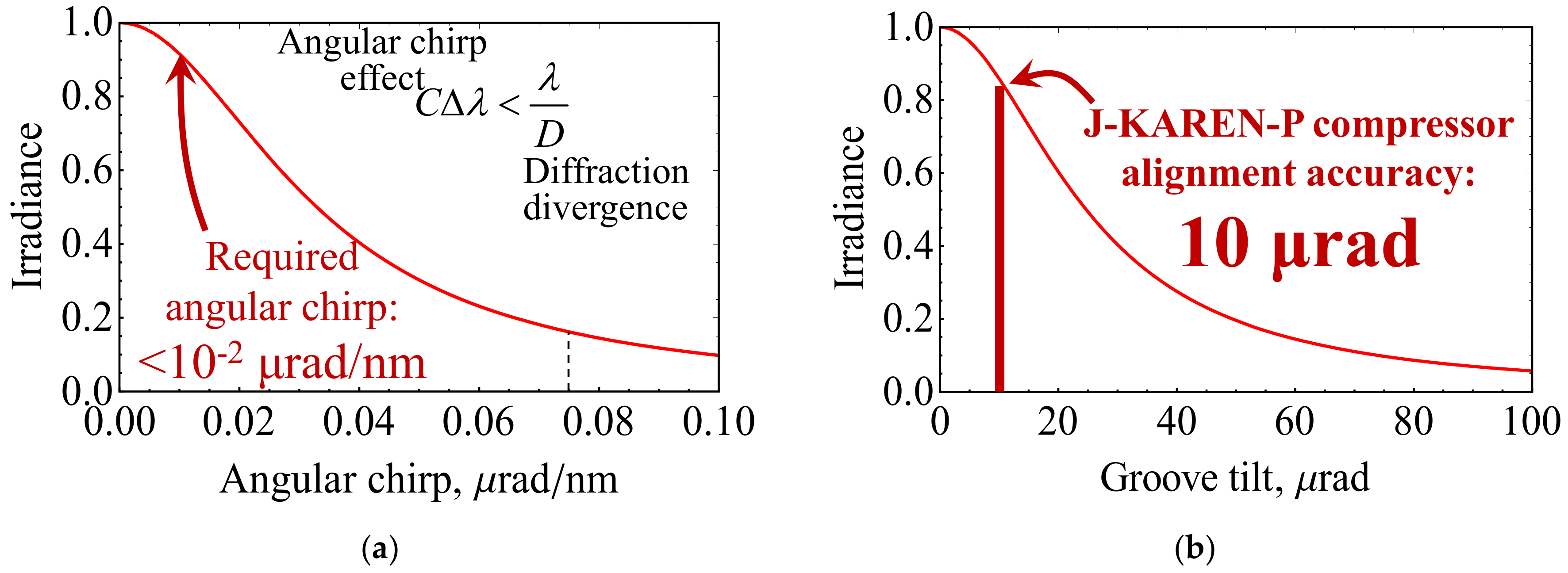
3.2. Driving Laser Requirements
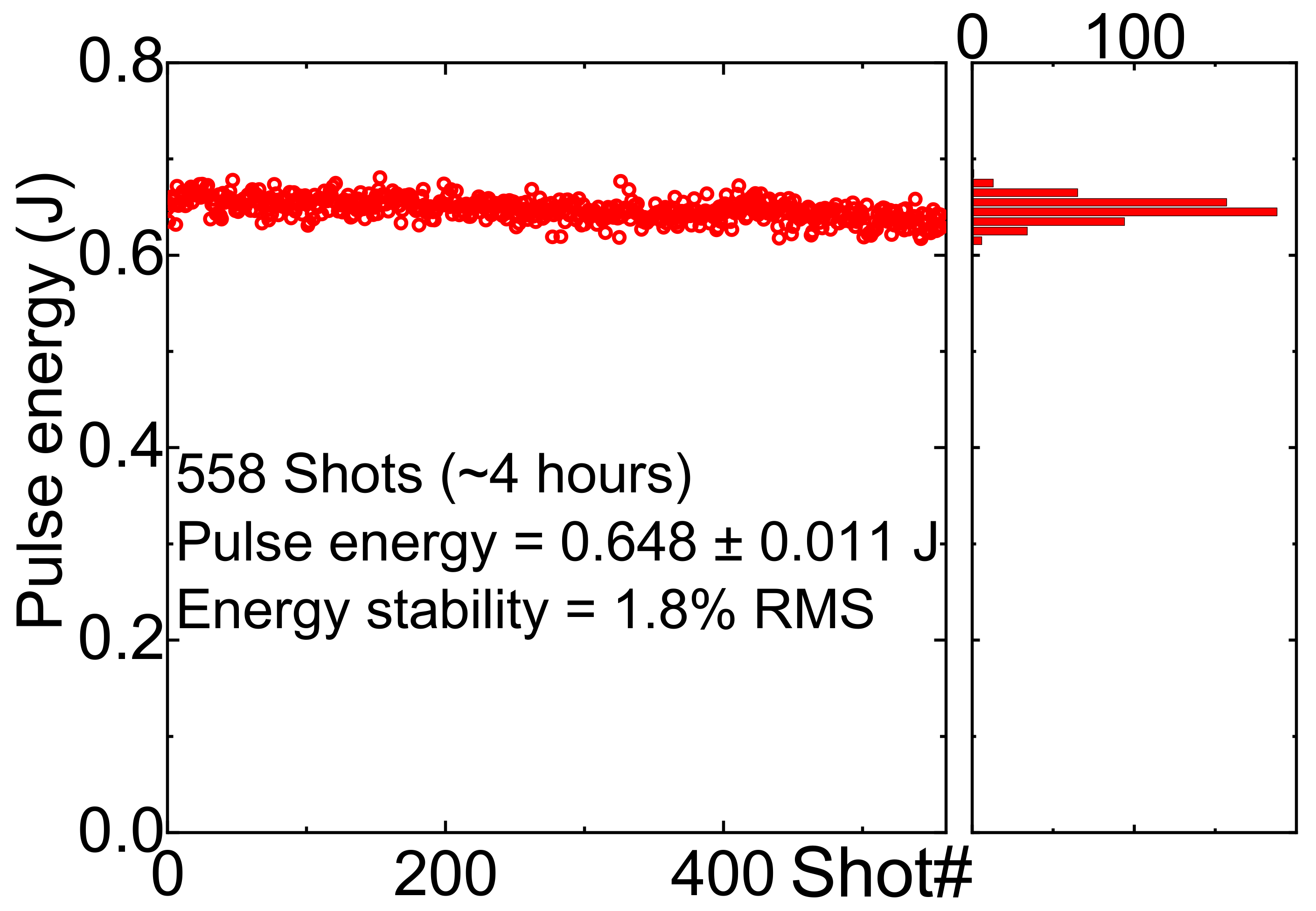
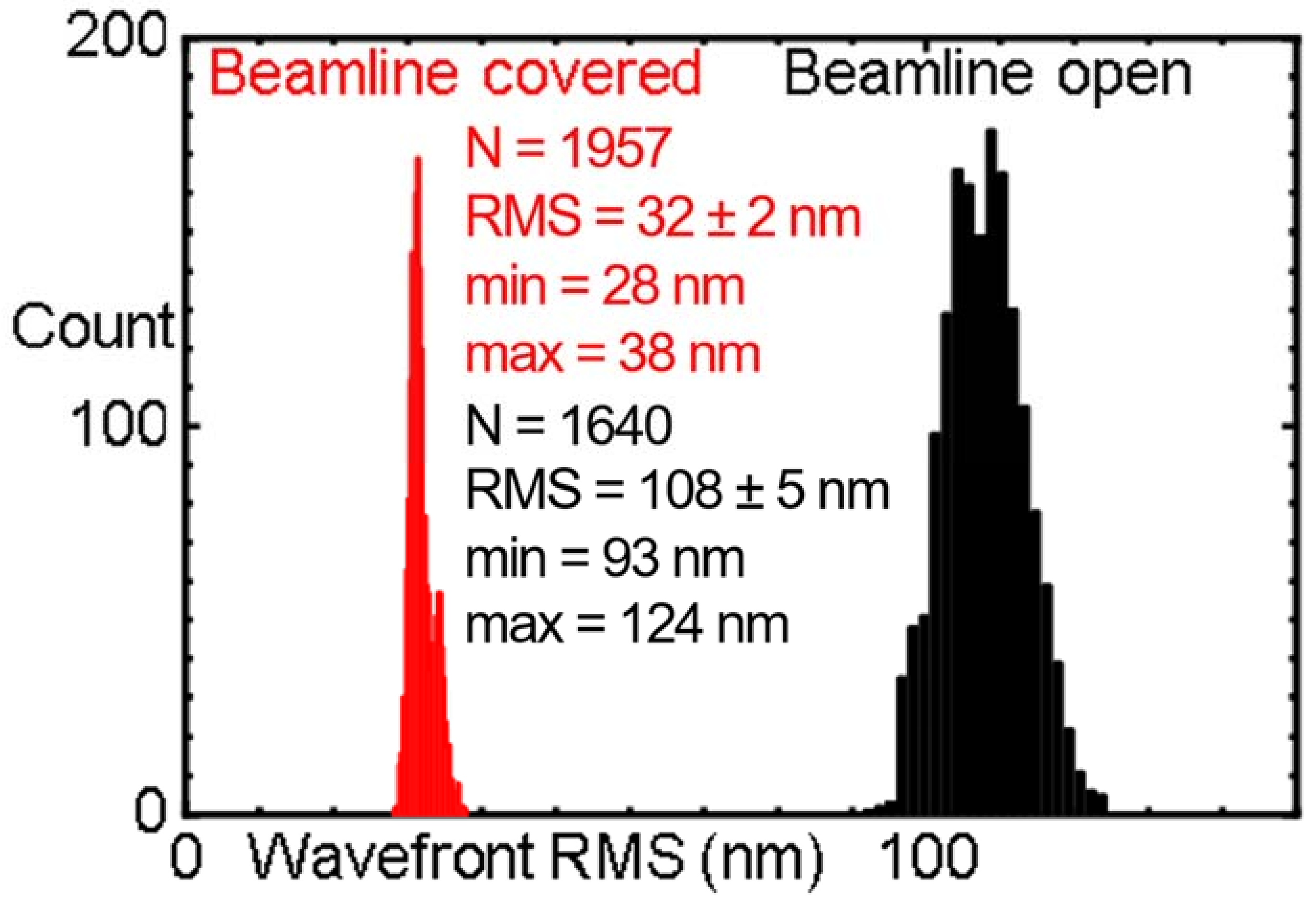
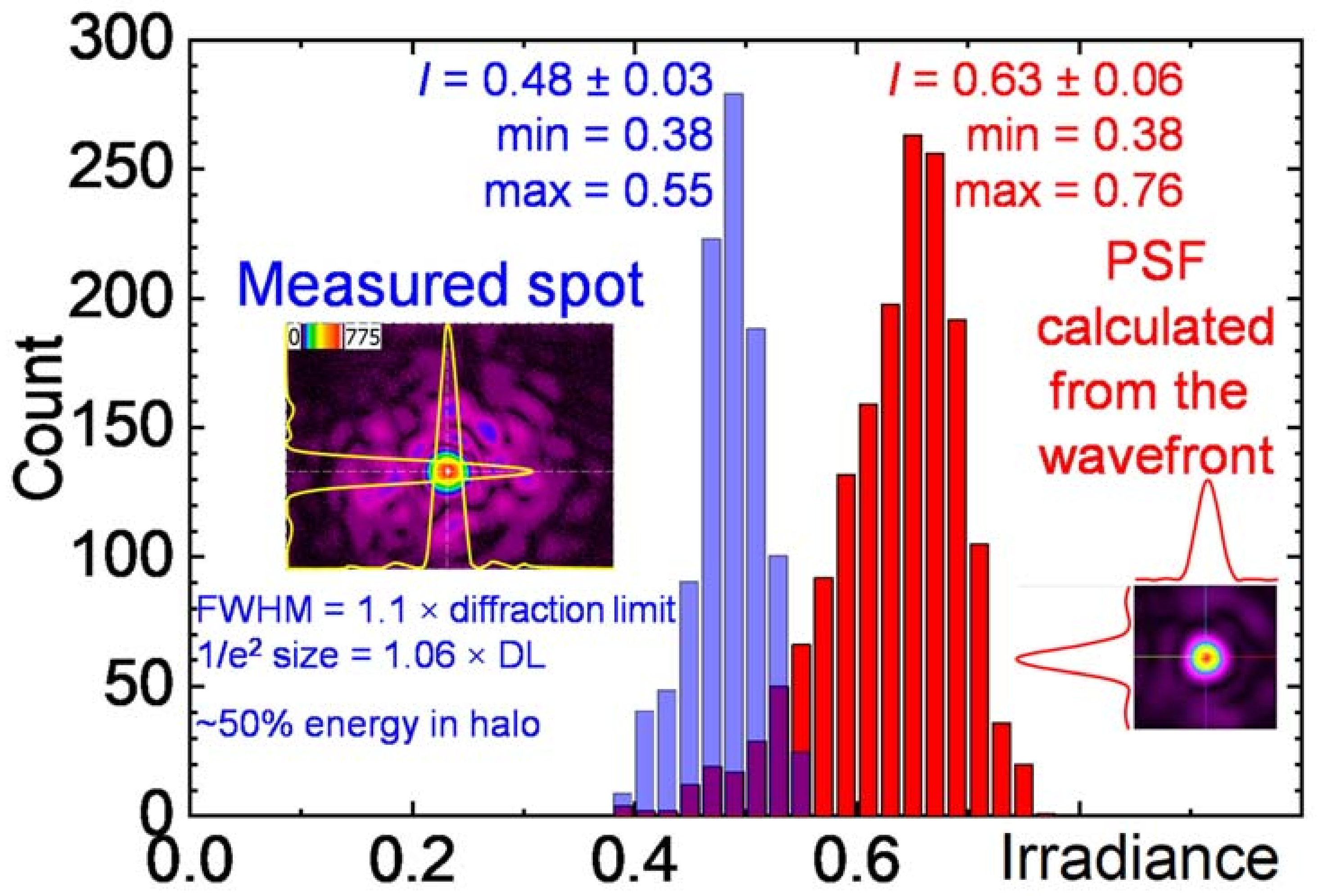
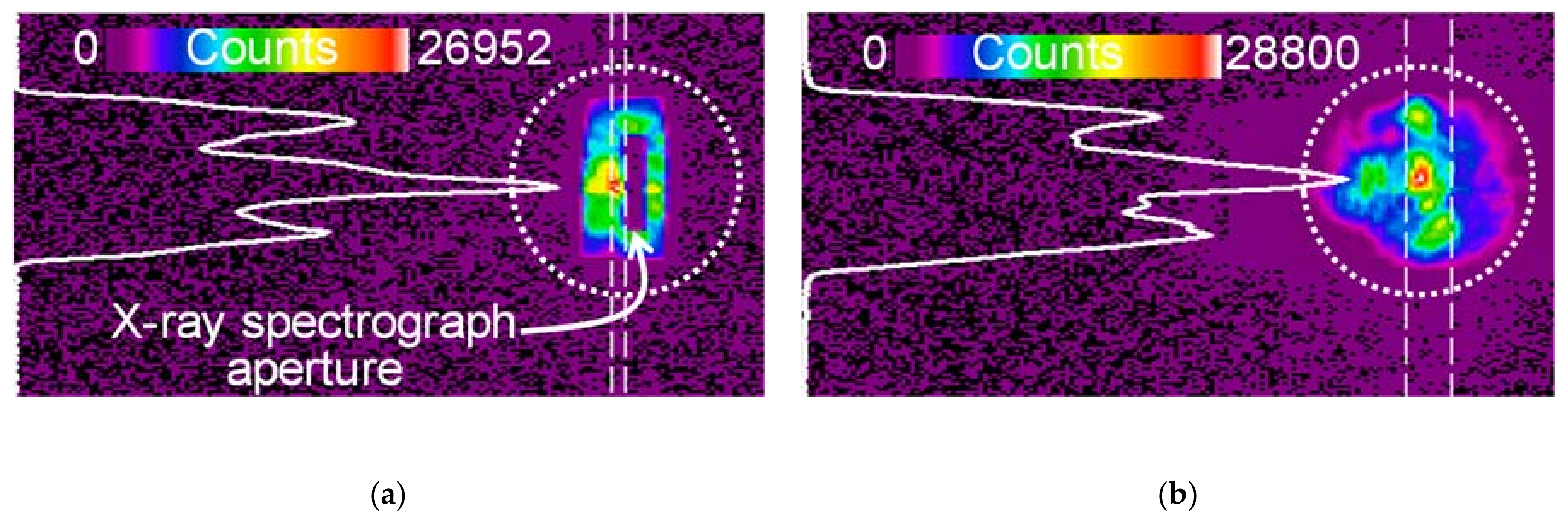
3.3. J-KAREN-P Laser Preparation
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pirozhkov, A.S.; Kando, M.; Esirkepov, T.Zh.; Gallegos, P.; Ahmed, H.; Ragozin, E.N.; Faenov, A.Ya.; Pikuz, T.A.; Kawachi, T.; Sagisaka, A.; et al. Soft-X-Ray harmonic comb from relativistic electron spikes. Phys. Rev. Lett. 2012, 108, 135004. [Google Scholar] [CrossRef] [PubMed]
- Pirozhkov, A.S.; Kando, M.; Esirkepov, T.Zh.; Gallegos, P.; Ahmed, H.; Ragozin, E.N.; Faenov, A.Ya.; Pikuz, T.A.; Kawachi, T.; Sagisaka, A.; et al. High order harmonics from relativistic electron spikes. New J. Phys. 2014, 16, 093003. [Google Scholar] [CrossRef]
- Esirkepov, T.Zh.; Kato, Y.; Bulanov, S.V. Bow wave from ultraintense electromagnetic pulses in plasmas. Phys. Rev. Lett. 2008, 101, 265001. [Google Scholar] [CrossRef] [PubMed]
- Arnold, V.I. Catastrophe Theory, 3rd ed.; Springer: Berlin/Heidelberg/New York, 1992. [Google Scholar]
- Poston, T.; Stewart, I. Catastrophe Theory and its Applications; Dover Pubns: Mineola, NY, USA, 1996. [Google Scholar]
- Pirozhkov, A.S.; Esirkepov, T.Zh.; Pikuz, T.A.; Faenov, A.Ya.; Ogura, K.; Hayashi, Y.; Kotaki, H.; Ragozin, E.N.; Neely, D.; Kiriyama, H.; et al. Burst intensification by singularity emitting radiation in multi-stream flows. Sci. Rep. 2017, 7, 17968. [Google Scholar] [CrossRef] [PubMed]
- Kiriyama, H.; Shimomura, T.; Sasao, H.; Nakai, Y.; Tanoue, M.; Kondo, S.; Kanazawa, S.; Pirozhkov, A.S.; Mori, M.; Fukuda, Y.; et al. Temporal contrast enhancement of petawatt-class laser pulses. Opt. Lett. 2012, 37, 3363–3365. [Google Scholar] [CrossRef] [PubMed]
- Pretzler, G.; Kasper, A.; Witte, K.J. Angular chirp and tilted light pulses in CPA lasers. Appl. Phys. B 2000, 70, 1–9. [Google Scholar] [CrossRef]
- Akturk, S.; Gu, X.; Gabolde, P.; Trebino, R. The general theory of first-order spatio-temporal distortions of Gaussian pulses and beams. Opt. Express 2005, 13, 8642–8661. [Google Scholar] [CrossRef] [PubMed]
- Pariente, G.; Gallet, V.; Borot, A.; Gobert, O.; Quéré, F. Space–time characterization of ultra-intense femtosecond laser beams. Nat. Photonics 2016, 10, 547–553. [Google Scholar] [CrossRef]
- Kiriyama, H.; Mori, M.; Pirozhkov, A.S.; Ogura, K.; Sagisaka, A.; Kon, A.; Esirkepov, T.Zh.; Hayashi, Y.; Kotaki, H.; Kanasaki, M.; et al. High-Contrast, high-intensity petawatt-class laser and applications. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 1601118. [Google Scholar] [CrossRef]
- Pirozhkov, A.S.; Fukuda, Y.; Nishiuchi, M.; Kiriyama, H.; Sagisaka, A.; Ogura, K.; Mori, M.; Kishimoto, M.; Sakaki, H.; Dover, N.P.; et al. Approaching the diffraction-limited, bandwidth-limited Petawatt. Opt. Express 2017, 25, 20486–20501. [Google Scholar] [CrossRef] [PubMed]
- Volodin, B.A.; Gusev, S.A.; Drozdov, M.N.; Zuev, S.Y.; Klyuenkov, E.B.; Lopatin, A.Y.; Luchin, V.I.; Pestov, A.E.; Salashchenko, N.N.; Tsybin, N.N.; et al. Multilayer thin-film filters of extreme ultraviolet and soft X-ray spectral regions. Bull. Rus. Ac. Sci. Phys. 2010, 74, 46–49. [Google Scholar] [CrossRef]
- Koike, M.; Yamazaki, T.; Harada, Y. Design of holographic gratings recorded with aspheric wave-front recording optics for soft X-ray flat-field spectrographs. J. Electron Spectrosc. Rel. Phen. 1999, 101–103, 913–918. [Google Scholar] [CrossRef]
- Wenz, J.; Schleede, S.; Khrennikov, K.; Bech, M.; Thibault, P.; Heigoldt, M.; Pfeiffer, F.; Karsch, S. Quantitative X-ray phase-contrast microtomography from a compact laser-driven betatron source. Nat. Commun. 2015, 6, 7568. [Google Scholar] [CrossRef] [PubMed]
- Ruze, J. The effect of aperture errors on the antenna radiation pattern. Il Nuovo Cimento (1943–1954) 1952, 9, 364–380. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pirozhkov, A.S.; Esirkepov, T.Z.; Pikuz, T.A.; Faenov, A.Y.; Sagisaka, A.; Ogura, K.; Hayashi, Y.; Kotaki, H.; Ragozin, E.N.; Neely, D.; et al. Laser Requirements for High-Order Harmonic Generation by Relativistic Plasma Singularities. Quantum Beam Sci. 2018, 2, 7. https://doi.org/10.3390/qubs2010007
Pirozhkov AS, Esirkepov TZ, Pikuz TA, Faenov AY, Sagisaka A, Ogura K, Hayashi Y, Kotaki H, Ragozin EN, Neely D, et al. Laser Requirements for High-Order Harmonic Generation by Relativistic Plasma Singularities. Quantum Beam Science. 2018; 2(1):7. https://doi.org/10.3390/qubs2010007
Chicago/Turabian StylePirozhkov, Alexander S., Timur Zh. Esirkepov, Tatiana A. Pikuz, Anatoly Ya. Faenov, Akito Sagisaka, Koichi Ogura, Yukio Hayashi, Hideyuki Kotaki, Eugene N. Ragozin, David Neely, and et al. 2018. "Laser Requirements for High-Order Harmonic Generation by Relativistic Plasma Singularities" Quantum Beam Science 2, no. 1: 7. https://doi.org/10.3390/qubs2010007
APA StylePirozhkov, A. S., Esirkepov, T. Z., Pikuz, T. A., Faenov, A. Y., Sagisaka, A., Ogura, K., Hayashi, Y., Kotaki, H., Ragozin, E. N., Neely, D., Koga, J. K., Fukuda, Y., Nishikino, M., Imazono, T., Hasegawa, N., Kawachi, T., Daido, H., Kato, Y., Bulanov, S. V., ... Kando, M. (2018). Laser Requirements for High-Order Harmonic Generation by Relativistic Plasma Singularities. Quantum Beam Science, 2(1), 7. https://doi.org/10.3390/qubs2010007






