Coherent Resonant Soft X-ray Scattering Study of Magnetic Textures in FeGe
Abstract
1. Introduction
2. Materials and Methods
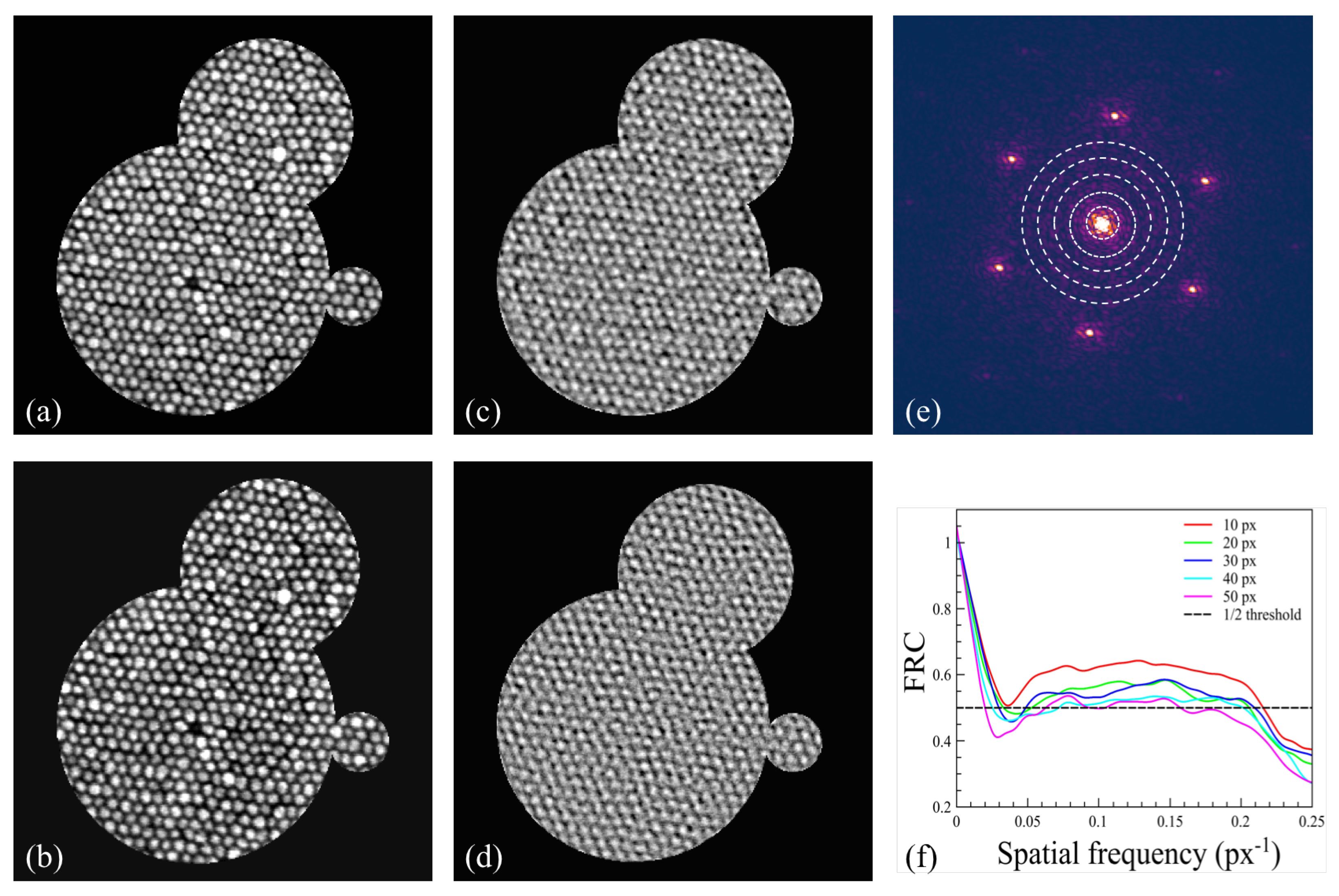
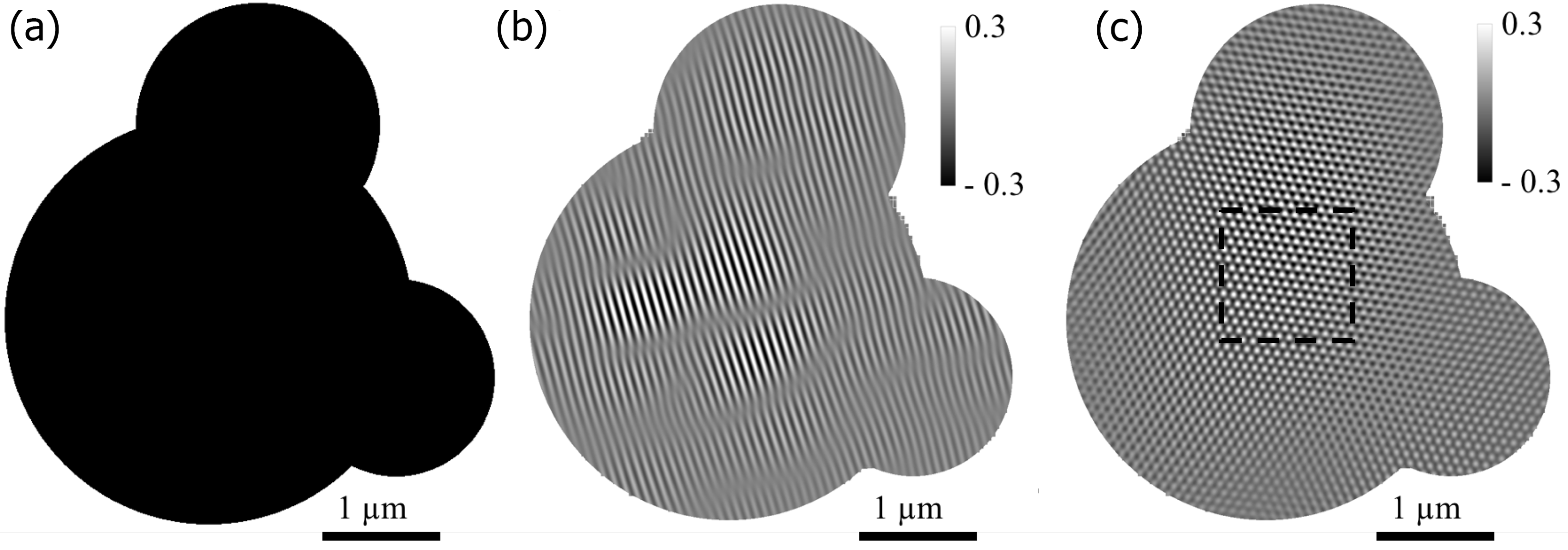
2.1. Simulation of the Noise and Beamstop Effect on the Phase Retrieval Reliability
2.2. Experiment
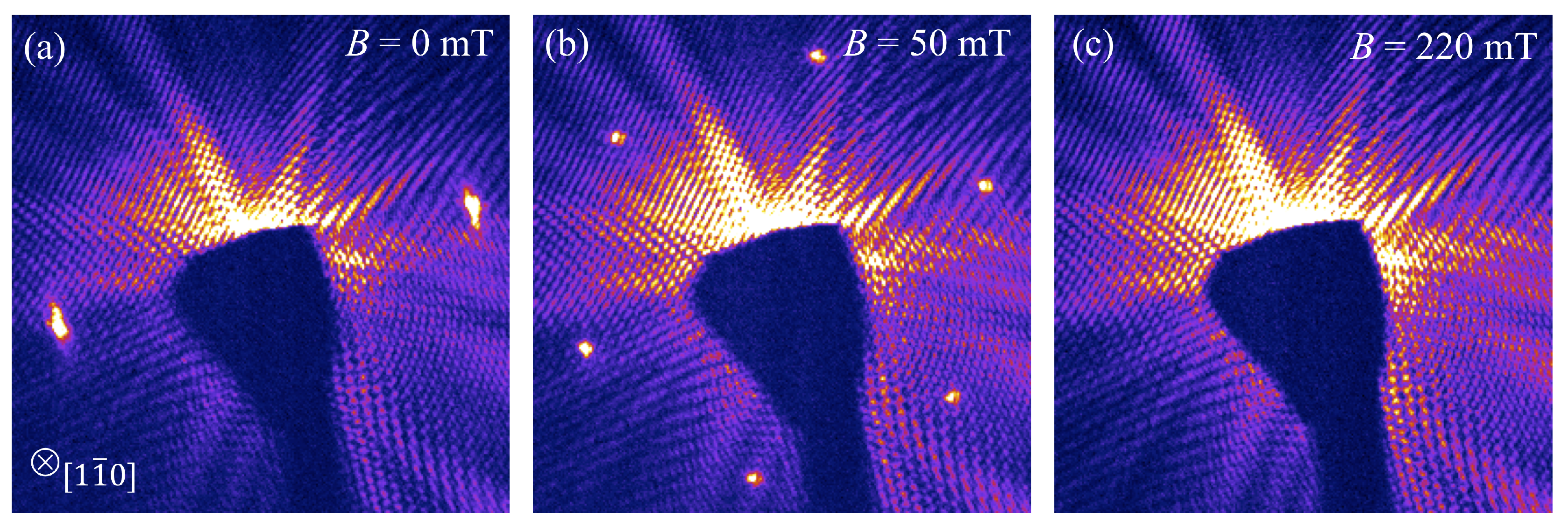
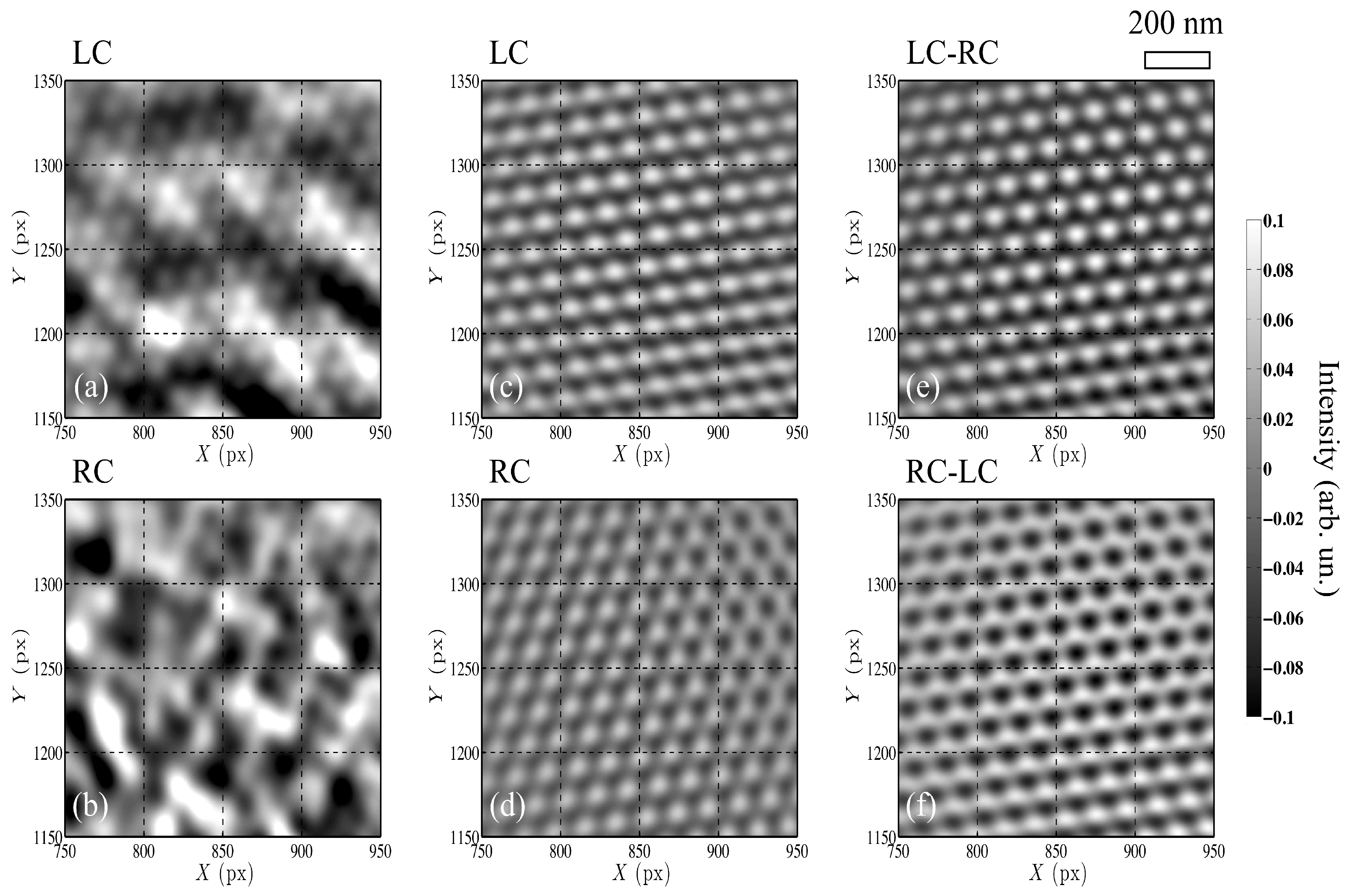
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Miao, J.; Ishikawa, T.; Robinson, I.K.; Murnane, M.M. Beyond crystallography: Diffractive imaging using coherent X-ray light sources. Science 2015, 348, 530–535. [Google Scholar] [CrossRef] [PubMed]
- Miao, J.; Charalambous, P.; Kirz, J.; Sayre, D. Extending the methodology of X-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens. Nature 1999, 400, 342–344. [Google Scholar] [CrossRef]
- Tuchin, V.V. Handbook of coherent-domain optical methods. In Handbook of Coherent-Domain Optical Methods: Biomedical Diagnostics, Environmental Monitoring, and Materials Science; Springer Science+Business Media: New York, NY, USA, 2013; ISBN 978-1-4614-5175-4. [Google Scholar]
- Chapman, H.N.; Nugent, K.A. Coherent lensless X-ray imaging. Nat. Photonics 2010, 4, 833–839. [Google Scholar] [CrossRef]
- Gulden, J.; Yefanov, O.; Mancuso, A.; Abramova, V.; Hilhorst, J.; Byelov, D.; Snigireva, I.; Snigirev, A.; Petukhov, A.; Vartanyants, I. Coherent x-ray imaging of defects in colloidal crystals. Phys. Rev. B 2010, 81, 224105. [Google Scholar] [CrossRef]
- Gulden, J.; Yefanov, O.; Mancuso, A.; Dronyak, R.; Singer, A.; Bernátová, V.; Burkhardt, A.; Polozhentsev, O.; Soldatov, A.; Sprung, M.; et al. Three-dimensional structure of a single colloidal crystal grain studied by coherent X-ray diffraction. Opt. Express 2012, 20, 4039–4049. [Google Scholar] [CrossRef] [PubMed]
- Fischer, P. X-ray imaging of magnetic structures. IEEE Trans. Magn. 2015, 51, 1–31. [Google Scholar] [CrossRef]
- Wilkins, S.; Hatton, P.; Roper, M.; Prabhakaran, D.; Boothroyd, A. Soft X-ray resonant magnetic diffraction. Phys. Rev. Lett. 2003, 90, 187201. [Google Scholar] [CrossRef] [PubMed]
- Langner, M.; Roy, S.; Mishra, S.; Lee, J.; Shi, X.; Hossain, M.; Chuang, Y.D.; Seki, S.; Tokura, Y.; Kevan, S.; et al. Coupled skyrmion sublattices in Cu2OSeO3. Phys. Rev. Lett. 2014, 112, 167202. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Bauer, A.; Burn, D.M.; Milde, P.; Neuber, E.; Eng, L.M.; Berger, H.; Pfleiderer, C.; van der Laan, G.; Hesjedal, T. Multidomain Skyrmion Lattice State in Cu2OSeO3. Nano Lett. 2016, 16, 3285–3291. [Google Scholar] [CrossRef] [PubMed]
- Tonnerre, J.; Seve, L.; Raoux, D.; Soullié, G.; Rodmacq, B.; Wolfers, P. Soft X-ray resonant magnetic scattering from a magnetically coupled Ag/Ni multilayer. Phys. Rev. Lett. 1995, 75, 740. [Google Scholar] [CrossRef] [PubMed]
- Gutt, C.; Streit-Nierobisch, S.; Stadler, L.M.; Pfau, B.; Günther, C.; Könnecke, R.; Frömter, R.; Kobs, A.; Stickler, D.; Oepen, H.; et al. Single-pulse resonant magnetic scattering using a soft X-ray free-electron laser. Phys. Rev. B 2010, 81, 100401. [Google Scholar] [CrossRef]
- Kortright, J.B.; Kim, S.K.; Denbeaux, G.P.; Zeltzer, G.; Takano, K.; Fullerton, E.E. Soft-X-ray small-angle scattering as a sensitive probe of magnetic and charge heterogeneity. Phys. Rev. B 2001, 64, 092401. [Google Scholar] [CrossRef]
- Yamasaki, Y.; Morikawa, D.; Honda, T.; Nakao, H.; Murakami, Y.; Kanazawa, N.; Kawasaki, M.; Arima, T.; Tokura, Y. Dynamical process of skyrmion-helical magnetic transformation of the chiral-lattice magnet FeGe probed by small-angle resonant soft X-ray scattering. Phys. Rev. B 2015, 92, 220421. [Google Scholar] [CrossRef]
- Okamura, Y.; Yamasaki, Y.; Morikawa, D.; Honda, T.; Ukleev, V.; Nakao, H.; Murakami, Y.; Shibata, K.; Kagawa, F.; Seki, S.; et al. Directional electric-field induced transformation from skyrmion lattice to distinct helices in multiferroic Cu2OSeO3. Phys. Rev. B 2017, 95, 184411. [Google Scholar] [CrossRef]
- Zhang, S.; Van Der Laan, G.; Hesjedal, T. Direct experimental determination of the topological winding number of skyrmions in Cu2OSeO3. Nat. Commun. 2017, 8. [Google Scholar] [CrossRef] [PubMed]
- Turner, J.J.; Huang, X.; Krupin, O.; Seu, K.A.; Parks, D.; Kevan, S.; Lima, E.; Kisslinger, K.; McNulty, I.; Gambino, R.; et al. X-ray diffraction microscopy of magnetic structures. Phys. Rev. Lett. 2011, 107, 033904. [Google Scholar] [CrossRef] [PubMed]
- Flewett, S.; Schaffert, S.; Mohanty, J.; Guehrs, E.; Geilhufe, J.; Günther, C.M.; Pfau, B.; Eisebitt, S. Method for single-shot coherent diffractive imaging of magnetic domains. Phys. Rev. Lett. 2012, 108, 223902. [Google Scholar] [CrossRef] [PubMed]
- Flewett, S.; Günther, C.; von Korff Schmising, C.; Pfau, B.; Mohanty, J.; Büttner, F.; Riemeier, M.; Hantschmann, M.; Kläui, M.; Eisebitt, S. Holographically aided iterative phase retrieval. Opt. Express 2012, 20, 29210–29216. [Google Scholar] [CrossRef] [PubMed]
- Eisebitt, S.; Lüning, J.; Schlotter, W.; Lörgen, M.; Hellwig, O.; Eberhardt, W.; Stöhr, J. Lensless imaging of magnetic nanostructures by X-ray spectro-holography. Nature 2004, 432, 885–888. [Google Scholar] [CrossRef] [PubMed]
- Scherz, A.; Schlotter, W.; Chen, K.; Rick, R.; Stöhr, J.; Lüning, J.; McNulty, I.; Günther, C.; Radu, F.; Eberhardt, W.; et al. Phase imaging of magnetic nanostructures using resonant soft X-ray holography. Phys. Rev. B 2007, 76, 214410. [Google Scholar] [CrossRef]
- Pfau, B.; Günther, C.M.; Könnecke, R.; Guehrs, E.; Hellwig, O.; Schlotter, W.F.; Eisebitt, S. Magnetic imaging at linearly polarized x-ray sources. Opt. Express 2010, 18, 13608–13615. [Google Scholar] [CrossRef] [PubMed]
- Duckworth, T.A.; Ogrin, F.; Dhesi, S.S.; Langridge, S.; Whiteside, A.; Moore, T.; Beutier, G.; Van Der Laan, G. Magnetic imaging by X-ray holography using extended references. Opt. Express 2011, 19, 16223–16228. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, A.; Mohanty, J.; Dietze, S.H.; Shpyrko, O.G.; Shipton, E.; Fullerton, E.E.; Kim, S.S.; McNulty, I. Dichroic coherent diffractive imaging. Proc. Natl. Acad. Sci. USA 2011, 108, 13393–13398. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Fischer, P.; Neu, V.; Elefant, D.; Lee, J.; Shapiro, D.; Farmand, M.; Tyliszczak, T.; Shiu, H.W.; Marchesini, S.; et al. Soft x-ray ptychography studies of nanoscale magnetic and structural correlations in thin SmCo5 films. Appl. Phys. Lett. 2016, 108, 094103. [Google Scholar] [CrossRef]
- Huang, X.; Nelson, J.; Steinbrener, J.; Kirz, J.; Turner, J.J.; Jacobsen, C. Incorrect support and missing center tolerances of phasing algorithms. Opt. Express 2010, 18, 26441–26449. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, A.; Shpyrko, O.; McNulty, I.; McNulty, I.; Eyberger, C.; Lai, B. Influence of Noise and Missing Data on Reconstruction Quality in Coherent X-ray Diffractive Imaging. In AIP Conference Proceedings; AIP: New York, NY, USA, 2011; Volume 1365, pp. 305–308. [Google Scholar]
- Fienup, J.; Wackerman, C. Phase-retrieval stagnation problems and solutions. JOSA A 1986, 3, 1897–1907. [Google Scholar] [CrossRef]
- Marchesini, S. Invited article: A unified evaluation of iterative projection algorithms for phase retrieval. Rev. Sci. Instrum. 2007, 78, 011301. [Google Scholar] [CrossRef] [PubMed]
- Fienup, J.R. Phase retrieval algorithms: A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef] [PubMed]
- Marchesini, S.; He, H.; Chapman, H.N.; Hau-Riege, S.P.; Noy, A.; Howells, M.R.; Weierstall, U.; Spence, J.C. X-ray image reconstruction from a diffraction pattern alone. Phys. Rev. B 2003, 68, 140101. [Google Scholar] [CrossRef]
- Wilhelm, H.; Baenitz, M.; Schmidt, M.; Rößler, U.; Leonov, A.; Bogdanov, A. Precursor phenomena at the magnetic ordering of the cubic helimagnet FeGe. Phys. Rev. Lett. 2011, 107, 127203. [Google Scholar] [CrossRef] [PubMed]
- Moskvin, E.; Grigoriev, S.; Dyadkin, V.; Eckerlebe, H.; Baenitz, M.; Schmidt, M.; Wilhelm, H. Complex chiral modulations in FeGe close to magnetic ordering. Phys. Rev. Lett. 2013, 110, 077207. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.Z.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W.; Ishiwata, S.; Matsui, Y.; Tokura, Y. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 2011, 10, 106–109. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Chien, C. Extended skyrmion phase in epitaxial FeGe (111) thin films. Phys. Rev. Lett. 2012, 108, 267201. [Google Scholar] [CrossRef] [PubMed]
- Kanazawa, N.; Kubota, M.; Tsukazaki, A.; Kozuka, Y.; Takahashi, K.; Kawasaki, M.; Ichikawa, M.; Kagawa, F.; Tokura, Y. Discretized topological Hall effect emerging from skyrmions in constricted geometry. Phys. Rev. B 2015, 91, 041122. [Google Scholar] [CrossRef]
- Kanazawa, N.; White, J.; Rønnow, H.M.; Dewhurst, C.; Fujishiro, Y.; Tsukazaki, A.; Kozuka, Y.; Kawasaki, M.; Ichikawa, M.; Kagawa, F.; et al. Direct observation of anisotropic magnetic field response of the spin helix in FeGe thin films. Phys. Rev. B 2016, 94, 184432. [Google Scholar] [CrossRef]
- Zhang, S.; Stasinopoulos, I.; Lancaster, T.; Xiao, F.; Bauer, A.; Rucker, F.; Baker, A.; Figueroa, A.; Salman, Z.; Pratt, F.; et al. Room-temperature helimagnetism in FeGe thin films. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, A.S.; Rowland, J.; Esser, B.D.; Dunsiger, S.; McComb, D.W.; Randeria, M.; Kawakami, R.K. Chiral Bobber Formation in Epitaxial FeGe/Si (111) Films. arXiv, 2017; arXiv:1706.08248. [Google Scholar]
- Gallagher, J.; Meng, K.; Brangham, J.; Wang, H.; Esser, B.; McComb, D.; Yang, F. Robust Zero-Field Skyrmion Formation in FeGe Epitaxial Thin Films. Phys. Rev. Lett. 2017, 118, 027201. [Google Scholar] [CrossRef] [PubMed]
- Bak, P.; Jensen, M.H. Theory of helical magnetic structures and phase transitions in MnSi and FeGe. J. Phys. C Solid State Phys. 1980, 13, L881. [Google Scholar] [CrossRef]
- Adams, T.; Mühlbauer, S.; Pfleiderer, C.; Jonietz, F.; Bauer, A.; Neubauer, A.; Georgii, R.; Böni, P.; Keiderling, U.; Everschor, K.; et al. Long-range crystalline nature of the skyrmion lattice in MnSi. Phys. Rev. Lett. 2011, 107, 217206. [Google Scholar] [CrossRef] [PubMed]
- Seki, S.; Kim, J.H.; Inosov, D.; Georgii, R.; Keimer, B.; Ishiwata, S.; Tokura, Y. Formation and rotation of skyrmion crystal in the chiral-lattice insulator Cu2OSeO3. Phys. Rev. B 2012, 85, 220406. [Google Scholar] [CrossRef]
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.; Han, J.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef] [PubMed]
- Chapman, J. The investigation of magnetic domain structures in thin foils by electron microscopy. J. Phys. D Appl. Phys. 1984, 17, 623. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, W.; Yu, G.; Jungfleisch, M.B.; Upadhyaya, P.; Somaily, H.; Pearson, J.E.; Tserkovnyak, Y.; Wang, K.L.; Heinonen, O.; et al. Mobile Néel skyrmions at room temperature: Status and future. AIP Adv. 2016, 6, 055602. [Google Scholar] [CrossRef]
- Pollard, S.D.; Garlow, J.A.; Yu, J.; Wang, Z.; Zhu, Y.; Yang, H. Observation of stable Néel skyrmions in cobalt/palladium multilayers with Lorentz transmission electron microscopy. Nat. Commun. 2017, 8. [Google Scholar] [CrossRef] [PubMed]
- Romming, N.; Hanneken, C.; Menzel, M.; Bickel, J.E.; Wolter, B.; von Bergmann, K.; Kubetzka, A.; Wiesendanger, R. Writing and deleting single magnetic skyrmions. Science 2013, 341, 636–639. [Google Scholar] [CrossRef] [PubMed]
- Fert, A.; Cros, V.; Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 2013, 8, 152–156. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Mascaraque, A.; N’Diaye, A.T.; Schmid, A.K. Room temperature skyrmion ground state stabilized through interlayer exchange coupling. Appl. Phys. Lett. 2015, 106, 242404. [Google Scholar] [CrossRef]
- Kézsmárki, I.; Bordács, S.; Milde, P.; Neuber, E.; Eng, L.; White, J.; Rønnow, H.M.; Dewhurst, C.; Mochizuki, M.; Yanai, K.; et al. Néel-type skyrmion lattice with confined orientation in the polar magnetic semiconductor GaV4S8. Nat. Mater. 2015, 14, 1116–1122. [Google Scholar] [CrossRef] [PubMed]
- Fujima, Y.; Abe, N.; Tokunaga, Y.; Arima, T. Thermodynamically stable skyrmion lattice at low temperatures in a bulk crystal of lacunar spinel GaV4Se8. Phys. Rev. B 2017, 95, 180410. [Google Scholar] [CrossRef]
- Bordács, S.; Butykai, A.; Szigeti, B.; White, J.; Cubitt, R.; Leonov, A.; Widmann, S.; Ehlers, D.; von Nidda, H.A.K.; Tsurkan, V.; et al. Equilibrium Skyrmion Lattice Ground State in a Polar Easy-plane Magnet. Sci. Rep. 2017, 7, 7584. [Google Scholar] [CrossRef] [PubMed]
- Kurumaji, T.; Nakajima, T.; Ukleev, V.; Feoktystov, A.; Arima, T.H.; Kakurai, K.; Tokura, Y. Néel-Type Skyrmion Lattice in the Tetragonal Polar Magnet VOSe2O5. Phys. Rev. Lett. 2017, 119, 237201. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Xu, Z.; Zhang, X.; Wu, Y.; Guo, Z.; Tai, R. Effects of missing low-frequency information on ptychographic and plane-wave coherent diffraction imaging. Appl. Opt. 2013, 52, 2416–2427. [Google Scholar] [CrossRef] [PubMed]
- Van Heel, M.; Schatz, M. Fourier shell correlation threshold criteria. J. Struct. Biol. 2005, 151, 250–262. [Google Scholar] [CrossRef] [PubMed]
- Banterle, N.; Bui, K.H.; Lemke, E.A.; Beck, M. Fourier ring correlation as a resolution criterion for super-resolution microscopy. J. Struct. Biol. 2013, 183, 363–367. [Google Scholar] [CrossRef] [PubMed]
- Steinbrener, J.; Nelson, J.; Huang, X.; Marchesini, S.; Shapiro, D.; Turner, J.J.; Jacobsen, C. Data preparation and evaluation techniques for x-ray diffraction microscopy. Opt. Express 2010, 18, 18598–18614. [Google Scholar] [CrossRef] [PubMed]
- Wilke, R.; Vassholz, M.; Salditt, T. Semi-transparent central stop in high-resolution X-ray ptychography using Kirkpatrick–Baez focusing. Acta Crystallogr. Sect. A Found. Crystallogr. 2013, 69, 490–497. [Google Scholar] [CrossRef]
- He, H.; Marchesini, S.; Howells, M.; Weierstall, U.; Hembree, G.; Spence, J.C. Experimental lensless soft-X-ray imaging using iterative algorithms: Phasing diffuse scattering. Acta Crystallogr. Sect. A Found. Crystallogr. 2003, 59, 143–152. [Google Scholar] [CrossRef]
- Yamasaki, Y.; Sudayama, T.; Okamoto, J.; Nakao, H.; Kubota, M.; Murakami, Y. Diffractometer for small angle resonant soft X-ray scattering under magnetic field. J. Phys. Conf. Ser. 2013, 425, 132012. [Google Scholar] [CrossRef]
- Hannon, J.; Trammell, G.; Blume, M.; Gibbs, D. X-ray resonance exchange scattering. Phys. Rev. Lett. 1988, 61, 1245. [Google Scholar] [CrossRef] [PubMed]
- Shibata, K.; Iwasaki, J.; Kanazawa, N.; Aizawa, S.; Tanigaki, T.; Shirai, M.; Nakajima, T.; Kubota, M.; Kawasaki, M.; Park, H.; et al. Large anisotropic deformation of skyrmions in strained crystal. Nat. Nanotechnol. 2015, 10, 589–592. [Google Scholar] [CrossRef] [PubMed]
- Eisebitt, S.; Lörgen, M.; Eberhardt, W.; Lüning, J.; Stöhr, J.; Rettner, C.; Hellwig, O.; Fullerton, E.; Denbeaux, G. Polarization effects in coherent scattering from magnetic specimen: Implications for X-ray holography, lensless imaging, and correlation spectroscopy. Phys. Rev. B 2003, 68, 104419. [Google Scholar] [CrossRef]
- Martin, A.V.; Wang, F.; Loh, N.; Ekeberg, T.; Maia, F.R.; Hantke, M.; van der Schot, G.; Hampton, C.Y.; Sierra, R.G.; Aquila, A.; et al. Noise-robust coherent diffractive imaging with a single diffraction pattern. Opt. Express 2012, 20, 16650–16661. [Google Scholar] [CrossRef]
- Lewis, J. Fast normalized cross-correlation. In Vision Interface; Canadian Image Processing and Pattern Recognition Society: Quebec, QC, Canada, 1995; Volume 10, pp. 120–123. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ukleev, V.; Yamasaki, Y.; Morikawa, D.; Kanazawa, N.; Okamura, Y.; Nakao, H.; Tokura, Y.; Arima, T.-h. Coherent Resonant Soft X-ray Scattering Study of Magnetic Textures in FeGe. Quantum Beam Sci. 2018, 2, 3. https://doi.org/10.3390/qubs2010003
Ukleev V, Yamasaki Y, Morikawa D, Kanazawa N, Okamura Y, Nakao H, Tokura Y, Arima T-h. Coherent Resonant Soft X-ray Scattering Study of Magnetic Textures in FeGe. Quantum Beam Science. 2018; 2(1):3. https://doi.org/10.3390/qubs2010003
Chicago/Turabian StyleUkleev, Victor, Yuichi Yamasaki, Daisuke Morikawa, Naoya Kanazawa, Yoshihiro Okamura, Hironori Nakao, Yoshinori Tokura, and Taka-hisa Arima. 2018. "Coherent Resonant Soft X-ray Scattering Study of Magnetic Textures in FeGe" Quantum Beam Science 2, no. 1: 3. https://doi.org/10.3390/qubs2010003
APA StyleUkleev, V., Yamasaki, Y., Morikawa, D., Kanazawa, N., Okamura, Y., Nakao, H., Tokura, Y., & Arima, T.-h. (2018). Coherent Resonant Soft X-ray Scattering Study of Magnetic Textures in FeGe. Quantum Beam Science, 2(1), 3. https://doi.org/10.3390/qubs2010003



