Explosive Nucleosynthesis Study Using Laser Driven γ-ray Pulses
Abstract
:1. Introduction
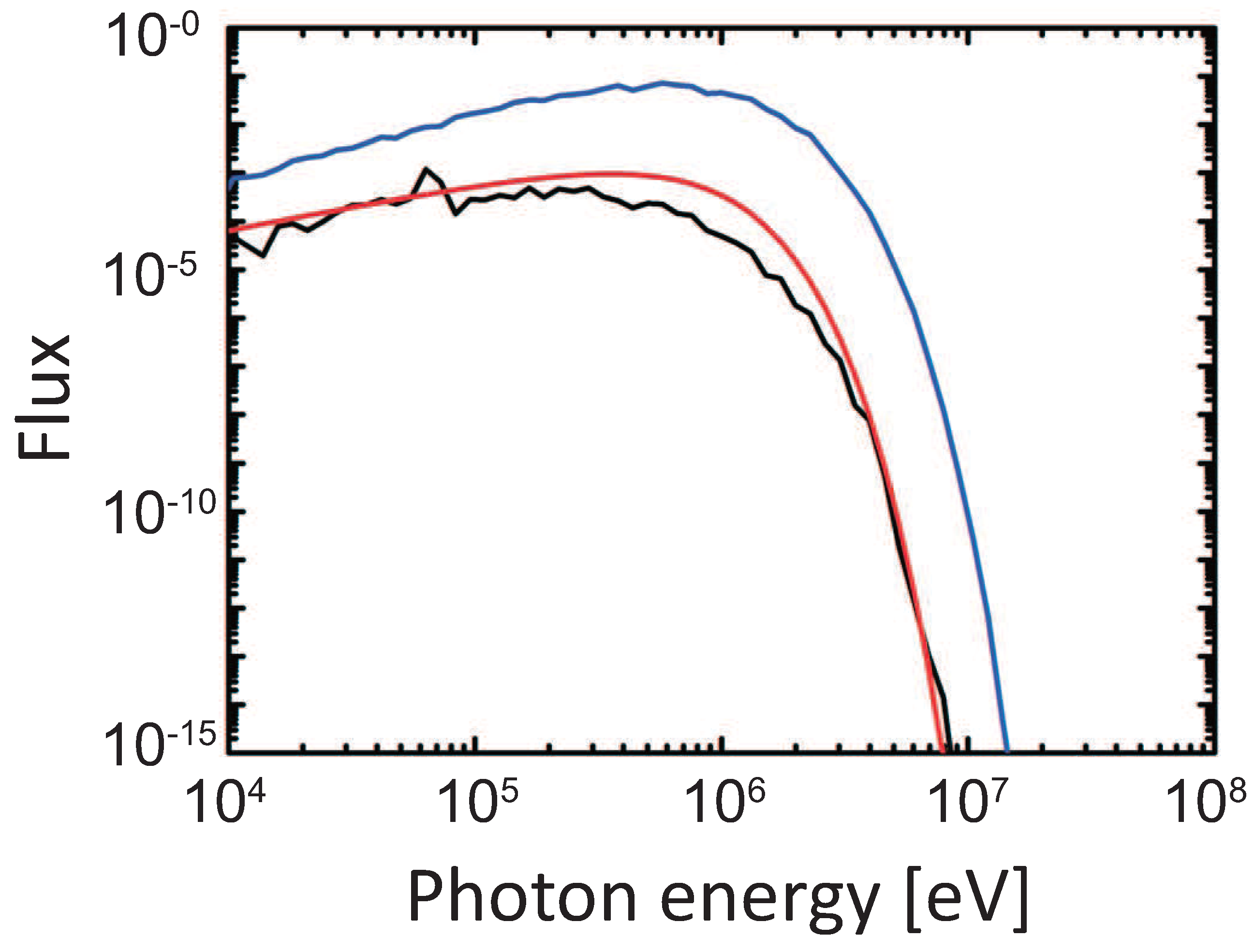
2. Calculation Method and Results
3. Discussion
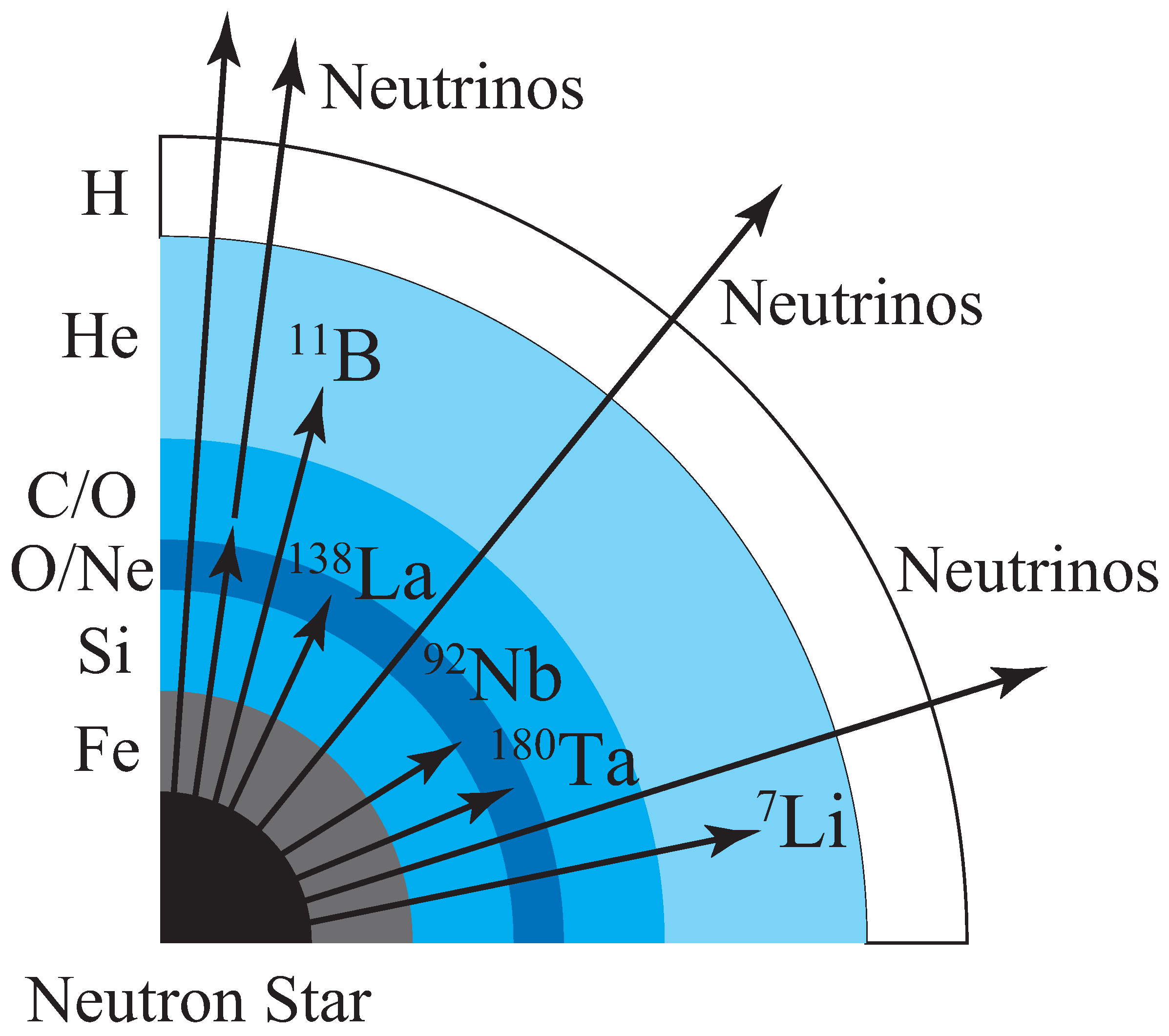
3.1. Role of Photons in Explosive Nucleosynthesis
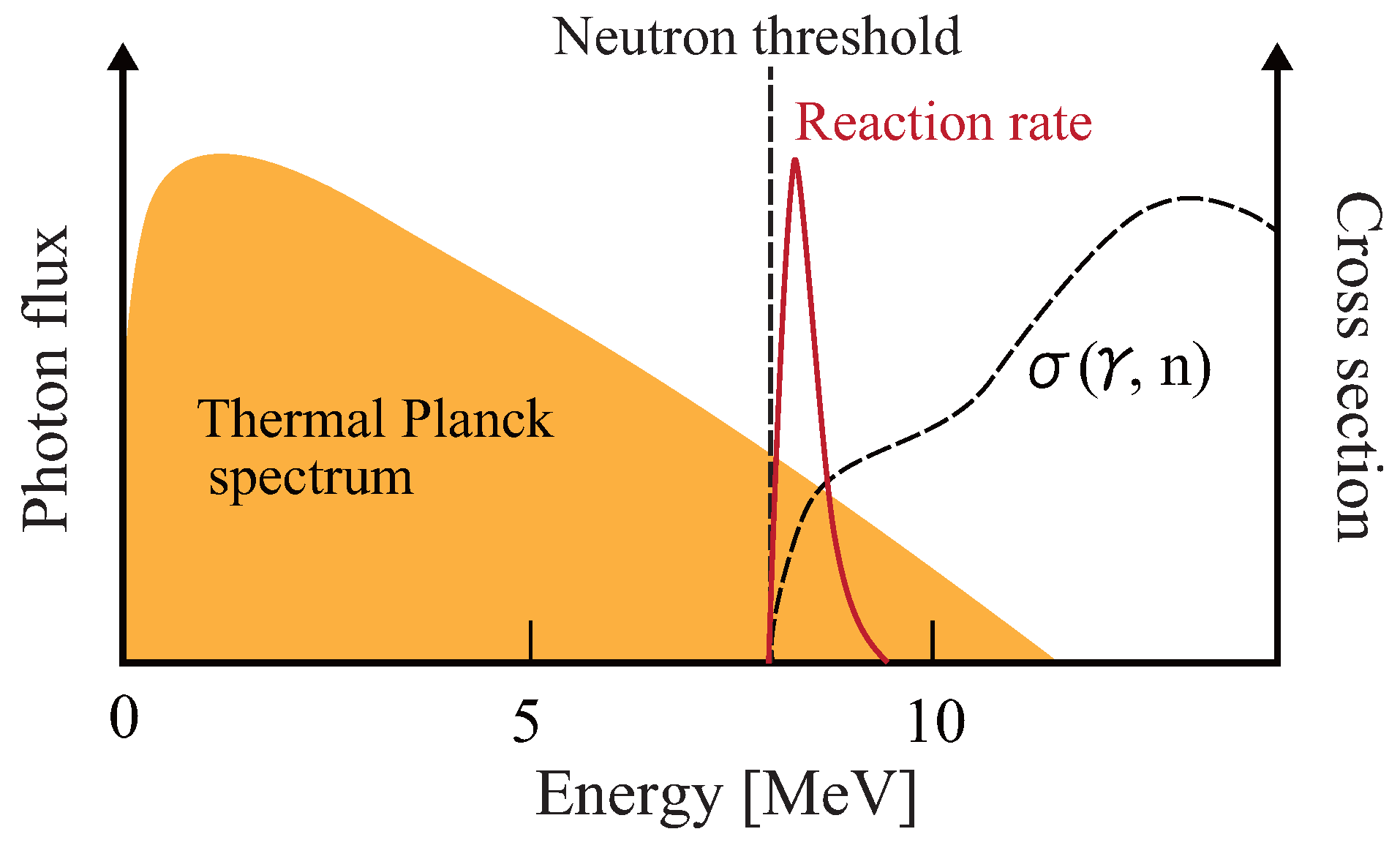
3.2. Direct Measurement of Stellar Nuclear Reaction Rate on the Ground State
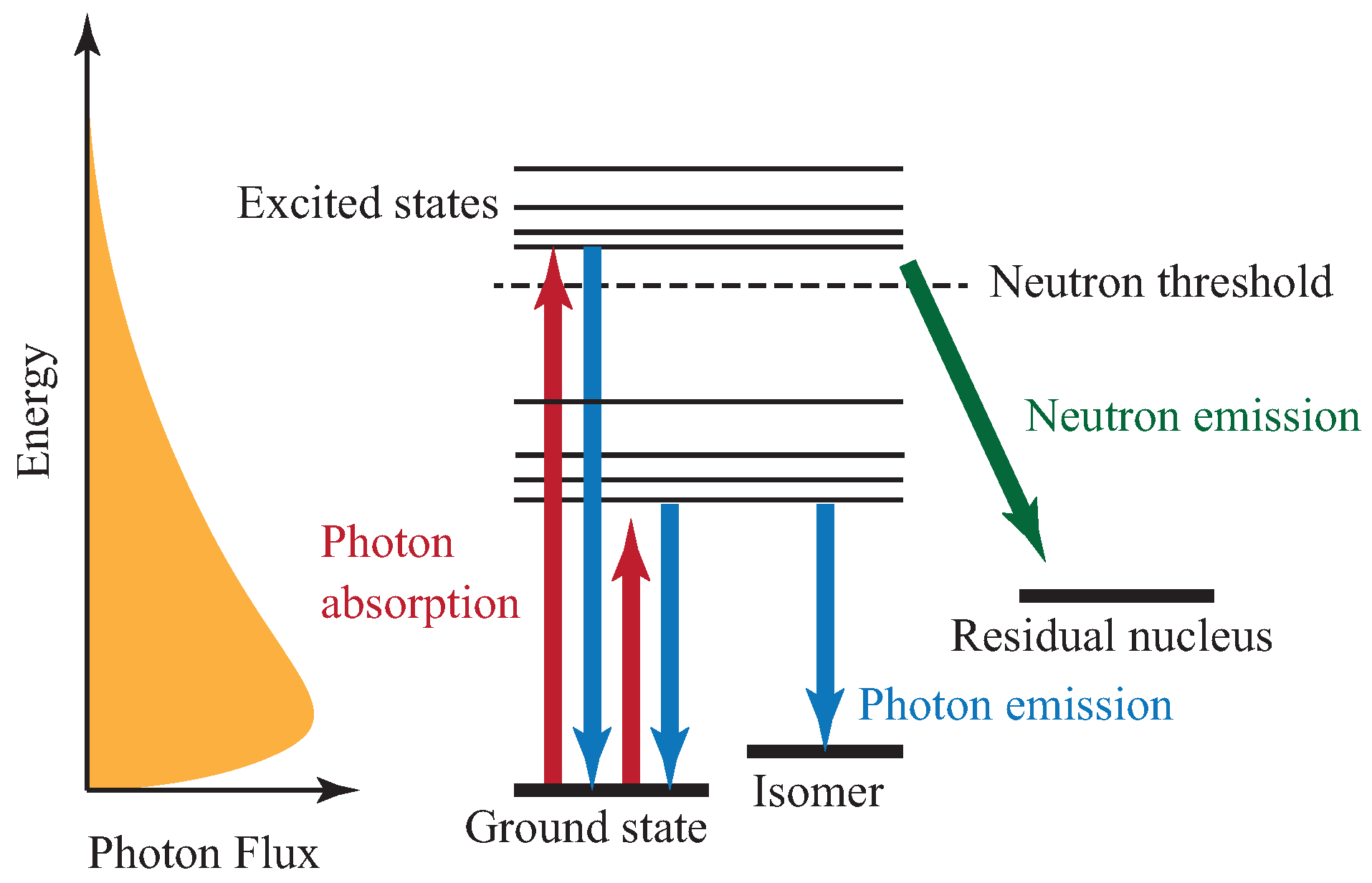
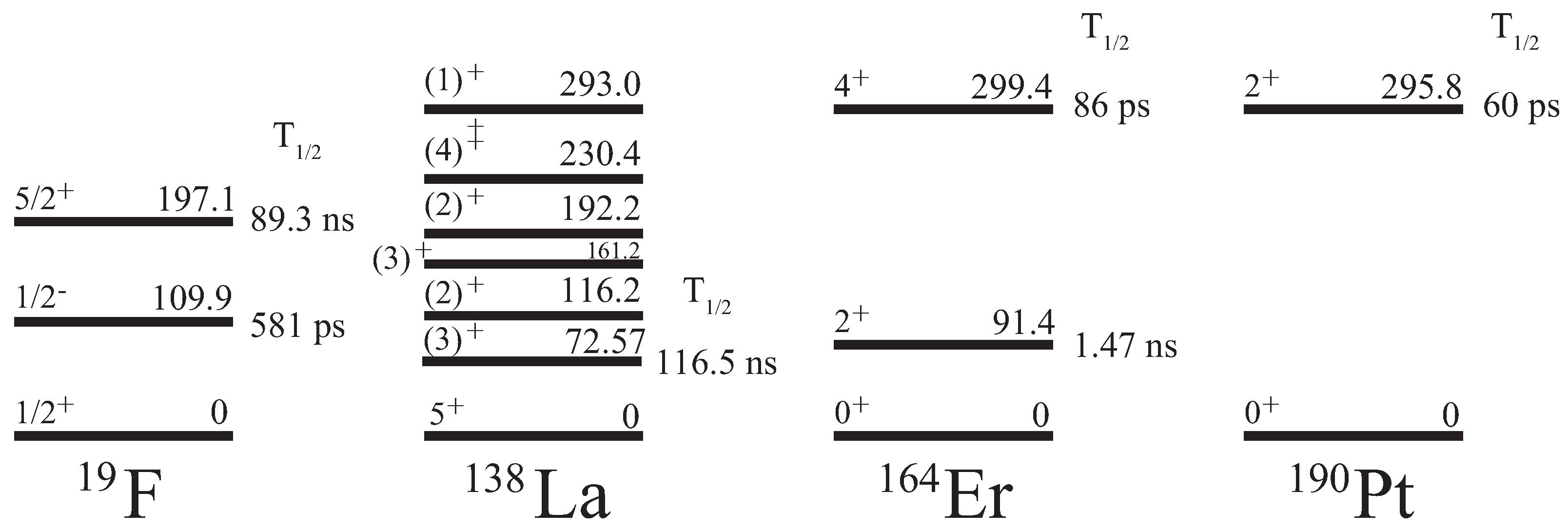
3.3. Direct Measurements of Nuclear Reactions on Excited States
3.4. Measurements of Isomer Transition Probability
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mourou, G.; Tajima, T. More Intense, Shorter Pulses. Science 2011, 331, 41–42. [Google Scholar] [CrossRef] [PubMed]
- Habs, D.; Thirolf, P.G.; Gross, M.; Allinger, K.; Bin, J.; Henig, A.; Kiefer, D.; Ma, W.; Schreiber, J. Introducing the fission-fusion reaction process: Using a laser-accelerated Th beam to produce neutron-rich nuclei towards the N = 126 waiting point of the r-process. Appl. Phys. B 2011, 103, 471–484. [Google Scholar] [CrossRef]
- Berstein, L.A.; Bleuel, D.L.; Caggiano, J.A.; Cerjan, C.; Fortner, R.J.; Gostic, J.; Grant, P.M.; Gharibyan, N.; Hagmann, C.; Hatarik, R.; et al. Low Energy Neutron Measurements in High Energy Density Plasmas using the National Ignition Facility. Plasma Fusion Res. 2014, 9, 4404101. [Google Scholar] [CrossRef]
- Barbui, M.; Bang, W.; Bonasera, A.; Hagel, K.; Schmidt, K.; Natowitz, J. B.; Burch, R.; Giuliani, G.; Barbarino, M.; Zheng, H.; et al. Measurement of the Plasma Astrophysical S Factor for the 3He(d, p)4He Reaction in Exploding Molecular Clusters. Phys. Rev. Lett. 2013, 111, 082502. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, T.; Hayakawa, T. Numerical modeling of quantum beam generation from ultra-intense laser-matter interactions. Laser Part. Beams 2015, 33, 151–155. [Google Scholar] [CrossRef]
- Nakamura, T.; Hayakawa, T. Laser-driven c-ray, positron, and neutron source from ultra-intense laser-matter interactions. Phys. Plasmas 2015, 22, 083113. [Google Scholar] [CrossRef]
- Hendersona, A.; Lianga, E.; Rileyb, N.; Yepesa, P.; Dyerb, G.; Serrattob, K.; Shagina, P. Ultra-intense gamma-rays created using the Texas Petawatt Laser. High Energy Density Phys. 2014, 12, 46–56. [Google Scholar] [CrossRef]
- Joen, J.H.; Nakajima, K.; Kim, H.T.; Rhee, Y.J.; Pathak, V.B.; Cho, M.H.; Shin, J.H.; Yoo, B.J.; Hojbota, C.; Jo, S.H.; et al. A broadband gamma-ray spectrometry using novel unfolding algorithms for characterization of laser wakefield-generated betatron radiation. Rev. Sci. Instrum. 2015, 86, 123116. [Google Scholar] [CrossRef] [PubMed]
- Kojima, S.; Ikenouchi, T.; Arikawa, Y.; Sakata, S.; Zhang, Z.; Abe, Y.; Nakai, M.; Nishimura, H.; Shiraga, H.; Ozaki, T.; et al. Development of Compton X-ray spectrometer for high energy resolution single-shot high-flux hard X-ray spectroscopy. Rev. Sci. Instrum. 2016, 87, 043502. [Google Scholar] [CrossRef] [PubMed]
- Sato, T.; Niita, K.; Matsuda, N.; Hashimoto, S.; Iwamoto, Y.; Noda, S.; Ogawa, T.; Iwase, H.; Nakashima, H.; Fukahori, T.; et al. Particle and Heavy Ion Transport Code System PHITS, Version 2.52. J. Nucl. Sci. Technol. 2013, 50, 913–923. [Google Scholar] [CrossRef]
- Schnürer, M.; Kalashnikov, M.P.; Nickles, P.V.; Schlegel, Th.; Sander, W. Hard X-ray emission from intense short pulse laser plasmas. Phys. Plasm. 1995, 2, 3106–3110. [Google Scholar] [CrossRef]
- Beg, F.N.; Bell, A.R.; Dangor, A.E.; Danson, C.N.; Fews, A.P.; Glinsky, M.E.; Hammel, B.A.; Lee, P.; Tatarakis, M. A study of picosecond laser-solid interactions up to 1019 Wcm−2. Phys. Plasm. 1997, 4, 447–457. [Google Scholar] [CrossRef]
- Woosley, S.E.; Howard, W.M. The p-process in supernovae. Astrophys. J. Supp. 1978, 36, 285–304. [Google Scholar] [CrossRef]
- Hayakawa, T.; Iwamoto, N.; Kajino, T.; Shizuma, T.; Umeda, H.; Nomoto, K. Empirical abundance scaling laws and implications for the gamma process in core-collapse supernovae. Astrophys. J. 2008, 685, 1089–1102. [Google Scholar] [CrossRef]
- Dillmann, I.; Käppeler, F.; Rauscher, T.; Thielemann, F.-K.; Gallino, R.; Bisterzo, S. Are there only 30 p nuclei? In Proceedings of the 10th Symposium on Nuclei in the Cosmos, Mackinac Island, MI, USA, 27 July–1 August 2008.
- Woosley, S.E.; Hartmann, D.H.; Hoffman, R.D.; Haxton, W.C. The ν-process. Astrophys. J. 1990, 356, 272–301. [Google Scholar] [CrossRef]
- Heger, A.; Kolbe, E.; Haxton, W.C.; Langanke, K.; Martinez-Pinedo, G.; Woosley, S.E. Neutrino nucleosynthesis. Phys. Lett. B 2005, 606, 258–264. [Google Scholar] [CrossRef]
- Hayakawa, T.; Nakamura, K.; Kajino, T.; Chiba, S.; Iwamoto, N.; Cheoun, M.K.; Mathews, G. J. Supernova neutrino nucleosynthesis of the radioactive 92Nb observed in primitive meteorites. Astrophy. J. Lett. 2013, 779, L9–L12. [Google Scholar] [CrossRef]
- Lugaro, M.; Pignatari, M.; Ott, U.; Zuber, K.; Travaglio, C.; Gyurky, G.; Fulop, Z. Origin of the p-process radionuclides 92Nb and 146Sm in the early solar system and inferences on the birth of the Sun. Proc. Natl. Acad. Sci. USA 2016, 113, 907–912. [Google Scholar] [CrossRef] [PubMed]
- Mohr, P. Nucleosynthesis of 92Nb and the relevance of the low-lying isomer at 135.5 keV. Phys. Rev. C 2016, 93, 065804. [Google Scholar] [CrossRef]
- Mohr, P.; Vogt, K.; Babilon, M.; Enders, J.; Hartmann, T.; Hutter, C.; Rauscher, T.; Volz, S.; Zilges, A. Experimental simulation of a stellar photon bath by bremsstrahlung: The astrophysical γ-process. Phys. Lett. B 2000, 488, 127–130. [Google Scholar] [CrossRef]
- Beer, H.; Käppeler, F. Neutron capture cross sections on 138Ba, 140,142Ce, 175,176Lu, and 181Ta at 30 keV: Prerequisite for investigation of the 176Lu cosmic clock. Astrophys. J. 1980, 21, 534–544. [Google Scholar]
- Lederer, C.; Käppeler, F.; Mosconi, M.; Nolte, R.; Heil, M.; Reifarth, R.; Schmidt, S.; Dillmann, I.; Giesen, U.; Mengoni, A.; et al. Definition of a standard neutron field with the 7Li(p, n)7Be reaction. Phys. Rev. C 2012, 85, 055809. [Google Scholar] [CrossRef]
- Käppeler, F.; Naqvi, A.A.; Al-Ohali, M. Stellar krypton cross sections at kT=25 and 52 keV. Phys. Rev. C 1987, 35, 936–941. [Google Scholar] [CrossRef]
- Heil, M.; Dababneh, S.; Juseviciute, A.; Kappeler, F.; Plag, R.; Reifarth, R.; O’Brien, S. Quasistellar spectrum for neutron activation measurements at kT = 5 keV. Phys. Rev. C 2005, 71, 025803. [Google Scholar] [CrossRef]
- Vogt, K.; Mohr, P.; Babilon, M.; Enders, J.; Hartmann, T.; Hutter, C.; Rauscher, T.; Volz, S.; Zilges, A. Measurement of the (γ, n) reaction rates of the nuclides 190Pt, 192Pt, and 198Pt in the astrophysical γ process. Phys. Rev. C 2001, 63, 055802. [Google Scholar] [CrossRef]
- Utsunomiya, H.; Akimune, H.; Goko, S.; Ohta, M.; Ueda, H.; Yamagata, T.; Yamasaki, K.; Ohgaki, H.; Toyokawa, H.; Lui, Y.-W.; et al. Cross section measurements of the 181Ta(γ, n)180Ta reaction near neutron threshold and the p-process nucleosynthesis. Phys. Rev. C 2003, 67, 015807. [Google Scholar] [CrossRef]
- Nakamura, T.; Koda, J.; Esikepov, T.Z.; Kando, M.; Korn, G.; Bulanov, S.V. High-Power γ-Ray Flash Generation in Ultraintense Laser-Plasma Interactions. Phys. Rev. Lett. 2012, 108, 195001. [Google Scholar] [CrossRef] [PubMed]
- Edwards, R.D.; Sinclair, M.A.; Goldsack, T.J.; Krushelnick, K.; Beg, F.N.; Clark, E.L.; Dangor, A.E.; Najmudin, Z.; Tatarakis, M.; Walton, B.; et al. Characterization of a gamma-ray source based on a laser-plasma accelerator with applications to radiography. Appl. Phys. Lett. 2002, 80, 2129–2131. [Google Scholar] [CrossRef]
- Granja, C.; Kubab, J.; Hidukb, A.; Renner, O. Survey of nuclei for low-energy nuclear excitation in laser-produced plasma. Nucl. Phys. A 2007, 784, 1–12. [Google Scholar] [CrossRef]
- Hayakawa, T.; Nakamura, T. Proceedings of the 14th Nuclei in Cosmos. JPS Conf. Proc. 2017, 14, 021103. [Google Scholar]
- Kando, M.; Fukuda, Y.; Pirozhkov, A.S.; Ma, J.; Daito, I.; Chen, L.-M.; Esirkepov, T.Z.; Ogura, K.; Homma, T.; Hayashi, Y.; et al. Demonstration of Laser-Frequency Upshift by Electron-Density Modulations in a Plasma Wakefield. Phys. Rev. Lett. 2007, 99, 135001. [Google Scholar] [CrossRef] [PubMed]
- Edwards, M.J.; Patel, P.K.; Lindl, J.D.; Atherton, L.J.; Glenzer, S.H.; Haan, S.W.; Kilkenny, J.D.; Landen, O.L.; Moses, E.I.; Nikroo, A.; et al. Progress towards ignition on the National Ignition Facility. Phys. Plasma 2013, 20, 070501. [Google Scholar] [CrossRef]
- Habara, H.; Xu, G.; Jitsuno, T.; Kodama, R.; Suzuki, K.; Sawai, K.; Kondo, K.; Miyanaga, N.; Tanaka, K.A.; Mima, K.; et al. Pulse compression and beam focusing with segmented diffraction gratings in a high-power chirped-pulse amplification glass laser system. Opt. Lett. 2010, 35, 1783–1785. [Google Scholar] [CrossRef] [PubMed]
- Hayakawa, T.; Kajino, T.; Chiba, S.; Mathews, G.J. New estimate for the time-dependent thermal nucleosynthesis of 180Tam. Phys. Rev. C 2010, 81, 052801(R). [Google Scholar] [CrossRef]
- Diehl, R.; Halloin, H.; Kretschme, K.; Lichti, G.G.; Schönfelder, V.; Strong, A.W.; von Kienlin, A.; Wang, W.; Jean, P.; Knödlseder, J.; et al. Radioactive 26Al from massive stars in the Galaxy. Nature 2006, 439, 45–47. [Google Scholar] [CrossRef] [PubMed]
- Mohr, P.; Käppeler, F.; Gallino, R. Survival of nature’s rarest isotope 180Ta under stellar conditions. Phys. Rev. C. 2007, 75, 012802(R). [Google Scholar] [CrossRef]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayakawa, T.; Nakamura, T.; Kotaki, H.; Kando, M.; Kajino, T. Explosive Nucleosynthesis Study Using Laser Driven γ-ray Pulses. Quantum Beam Sci. 2017, 1, 3. https://doi.org/10.3390/qubs1010003
Hayakawa T, Nakamura T, Kotaki H, Kando M, Kajino T. Explosive Nucleosynthesis Study Using Laser Driven γ-ray Pulses. Quantum Beam Science. 2017; 1(1):3. https://doi.org/10.3390/qubs1010003
Chicago/Turabian StyleHayakawa, Takehito, Tatsufumi Nakamura, Hideyuki Kotaki, Masaki Kando, and Toshitaka Kajino. 2017. "Explosive Nucleosynthesis Study Using Laser Driven γ-ray Pulses" Quantum Beam Science 1, no. 1: 3. https://doi.org/10.3390/qubs1010003
APA StyleHayakawa, T., Nakamura, T., Kotaki, H., Kando, M., & Kajino, T. (2017). Explosive Nucleosynthesis Study Using Laser Driven γ-ray Pulses. Quantum Beam Science, 1(1), 3. https://doi.org/10.3390/qubs1010003






