Effect of the Particle Size Distribution of the Ballast on the Lateral Resistance of Continuously Welded Rail Tracks
Abstract
1. Introduction
2. Specifications of Material and DEM Simulations
2.1. Geometry of the Model
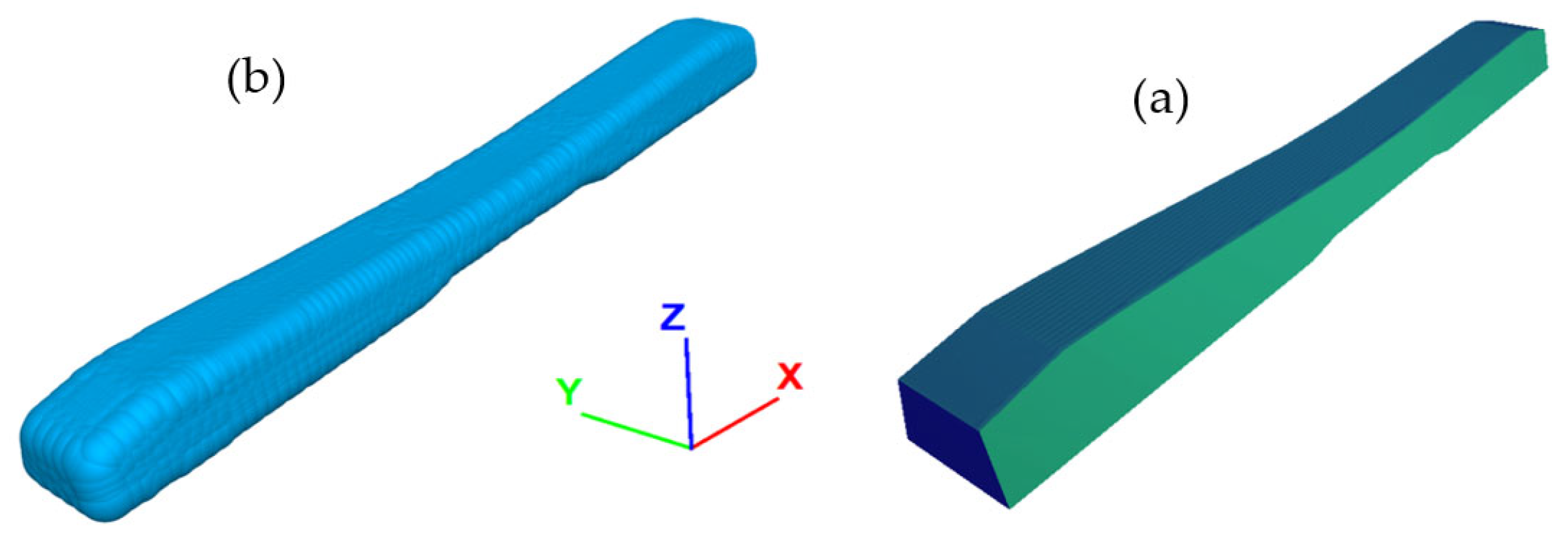
2.2. Sleeper’s Simulation
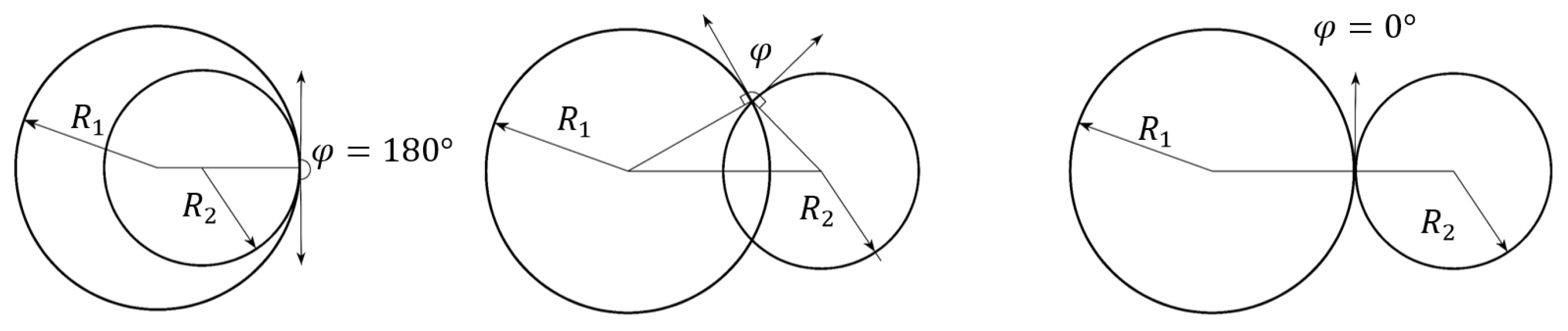
2.3. Simulation of Ballast Particles
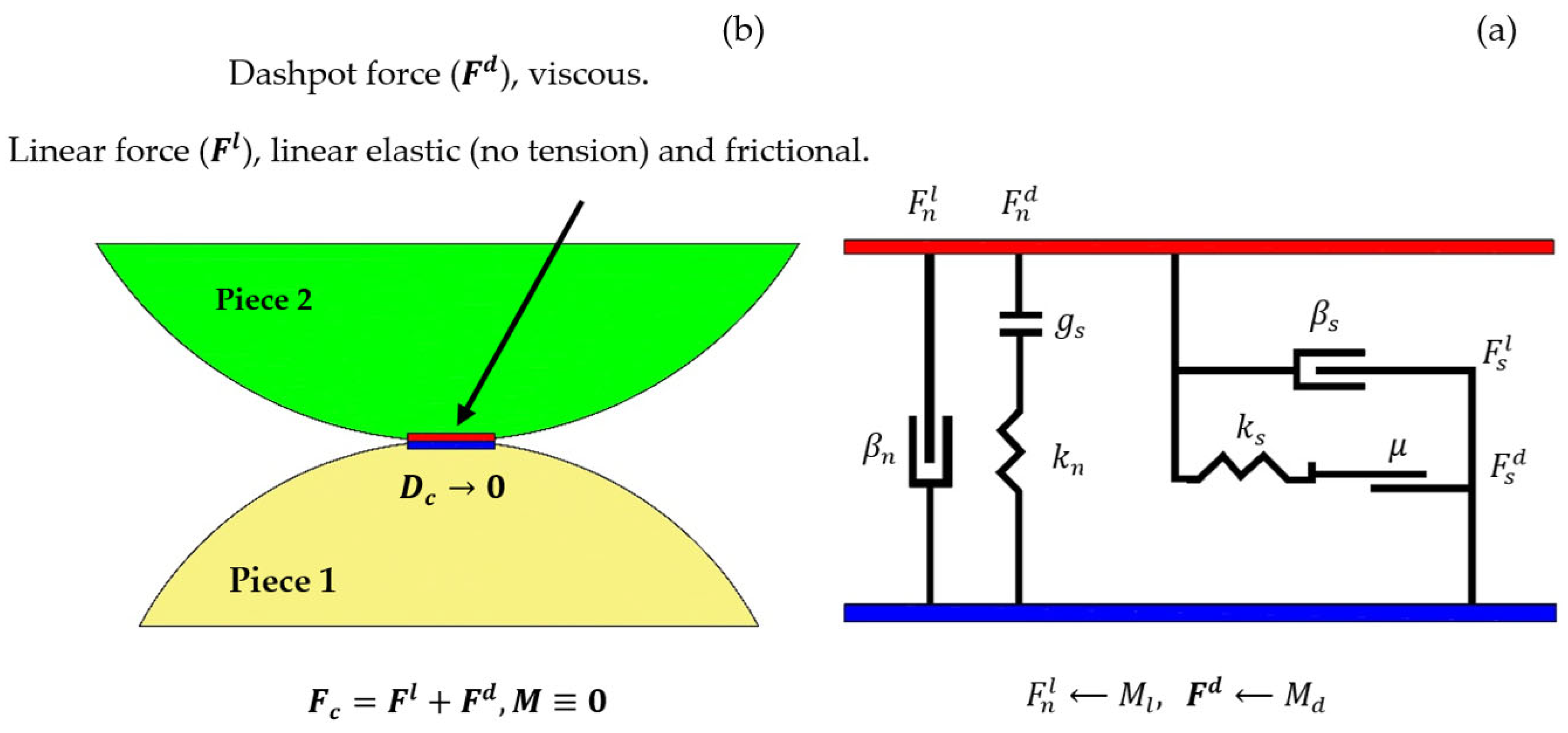
2.4. Contact Model
2.5. The STPT Process’s Simulation
3. Results
4. Conclusions
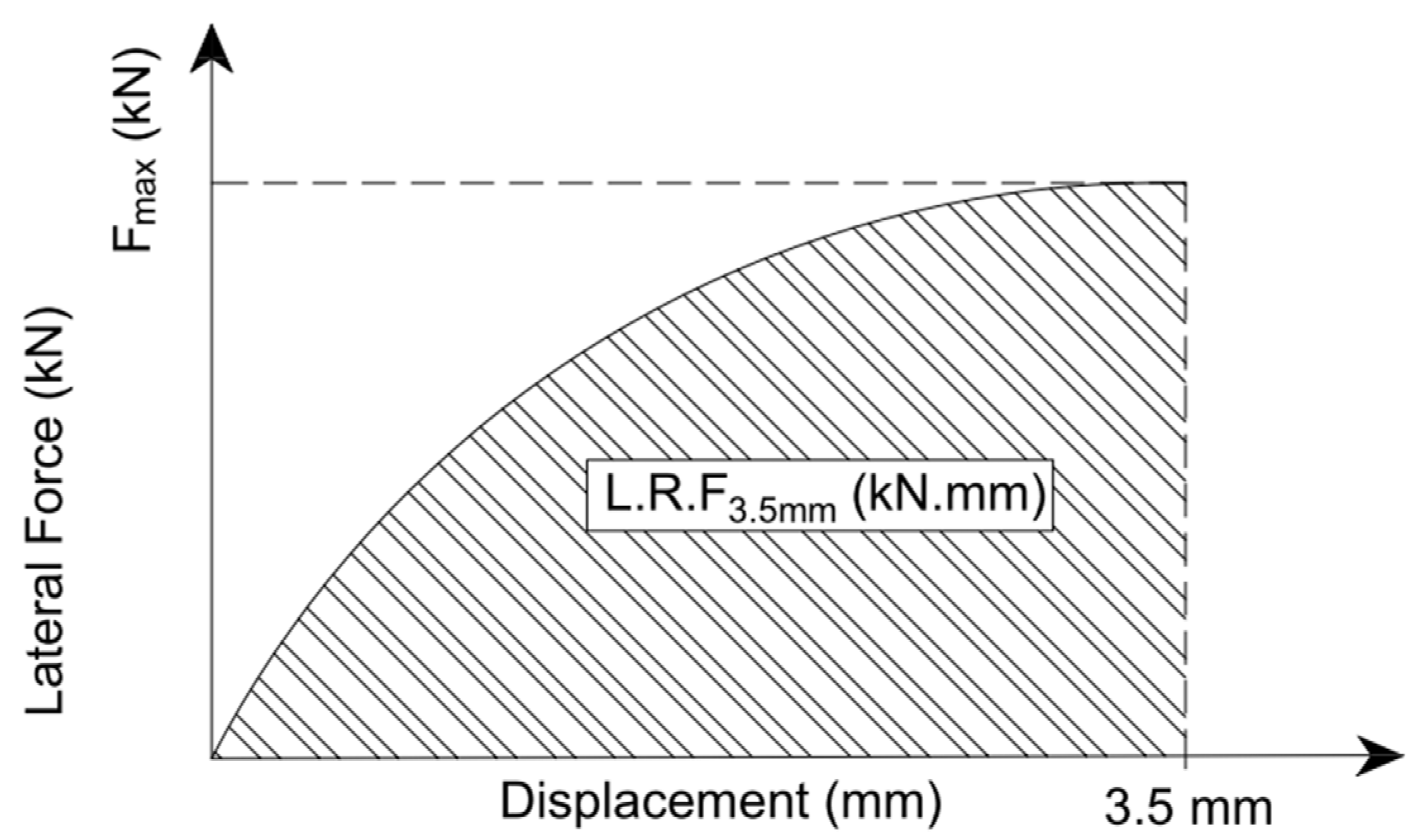
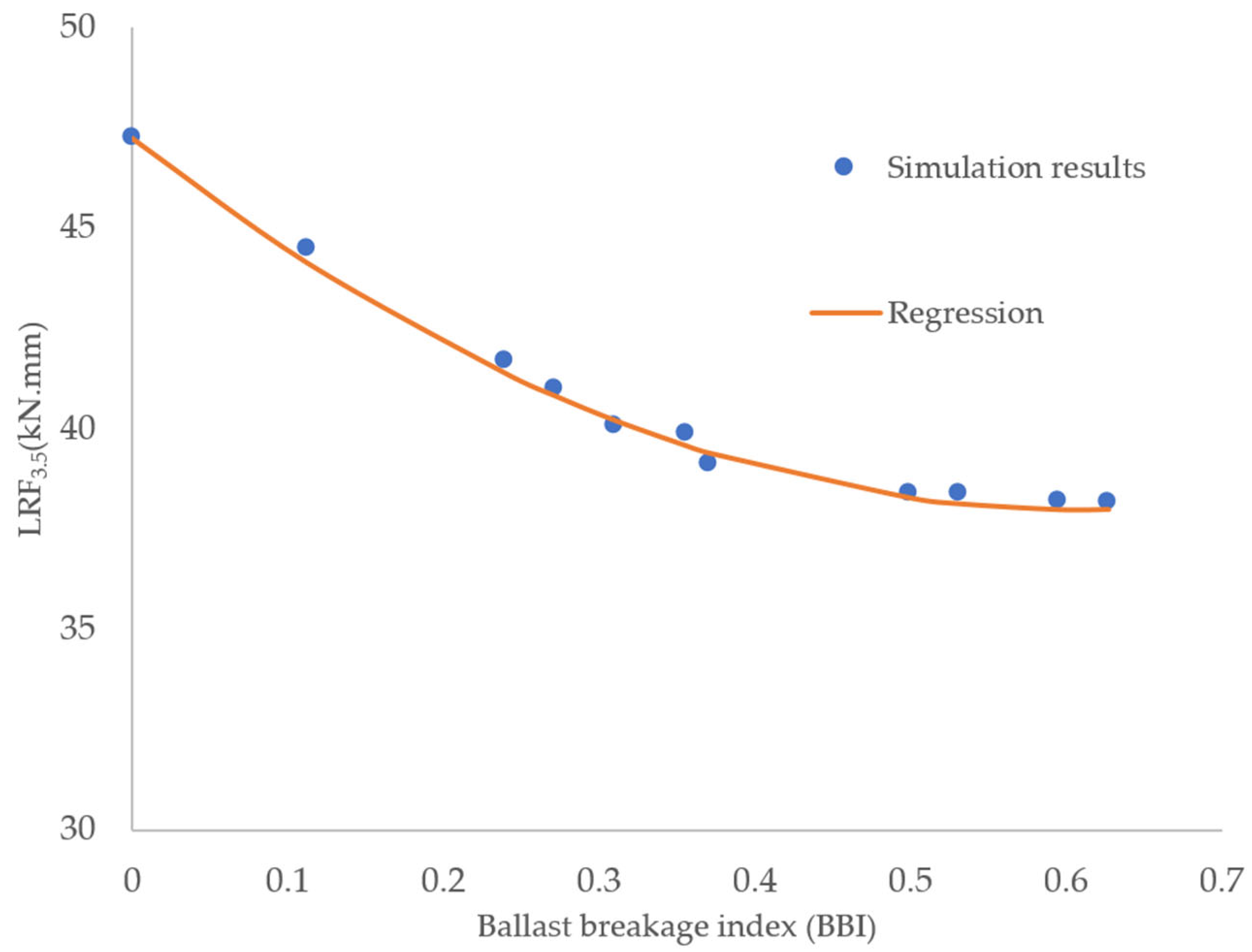
- The DEM results demonstrate satisfactory agreement with experimental data regarding lateral resistance displacement for a 3.5 mm displacement. However, a gap was observed in the graph, attributed to inherent differences in ballast and sleeper shapes, as well as variations in the loading process and conditions;
- According to Equation (5), the LRF3.5 value decreases with an increase in BBI, but the rate of decrease continues until it reaches zero at BBI = 0.6. This implies that lateral resistance decreases up to a specific value of ballast breakage, and after that point, it remains constant.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
List of Abbreviations
| Abbreviation | Definition |
| CWR | Continuous Welded Rail |
| 3DEC | Three-Dimensional Distinct Element Code |
| AREMA | American Railway Engineering and Maintenance-of-Way Association |
| ASTM | American Society for Testing Materials |
| DEM | Discrete Element Modeling |
| EHL | Elastohydrodynamically lubricated |
| FEM | Finite Element Method |
| ISRM | International Society for Rock Mechanics |
| PFC | Particle Flow Code |
| PSD | Particle Size Distribution |
| STL | Standard Triangle Language |
| STPTs | Single Sleeper (Tie) Push Tests |
| UDEC | Universal Distinct Element Code |
| WILAC | Water-Induced Low-Adhesion Creep force model |
List of Symbols
| Symbols and Indexes | Units in SI System | Definition |
| N | Contact force | |
| N | The normal components of the dashpot force | |
| N | The normal components of the linear force | |
| N | The shear components of the dashpot force | |
| N | The shear components of the linear force | |
| Pa | Shear modulus | |
| N/m | Normal stiffnesses | |
| N/m | Shear stiffnesses | |
| Nm | Lateral resistance factor | |
| [−] | Dashpot mode | |
| [−] | Normal-force update mode | |
| m | Particle radius | |
| [−] | The friction coefficient for the base wall boundary | |
| [−] | Side wall friction coefficient | |
| m | A surface gap | |
| [−] | The normal critical damping ratio | |
| [−] | The shear critical damping ratio | |
| kg/m3 | Ballast particle density | |
| kg/m3 | Sleeper clump density | |
| m | Particle overlaps | |
| [−] | Ballast Breakage Index | |
| [−] | The interparticle friction coefficient | |
| [−] | Contact moment | |
| [−] | Coefficient of friction | |
| [−] | Friction coefficient | |
| [−] | Poisson’s ratio | |
| degrees | The angle of pebbles of a clump particle |
References
- Vitković, N.; Marinković, D.; Stan, S.-D.; Simonović, M.; Miltenović, A.; Tomić, M.; Barać, M. Decision Support System for Managing Marshalling Yard Deviations. Acta Polytech. Hung. 2024, 21, 121–134. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Gao, S. Current Collection Quality of High-speed Rail Pantograph-catenary Considering Geometry Deviation at 400 km/h and above. In IEEE Transactions on Vehicular Technology; IEEE: Piscataway, NJ, USA, 2024. [Google Scholar] [CrossRef]
- Jovanović, V.; Janošević, D.; Marinković, D.; Petrović, N.; Pavlović, J. Railway Load Analysis During the Operation of an Excavator Resting on the Railway Track. Acta Polytech. Hung. 2023, 20, 79–93. [Google Scholar] [CrossRef]
- Jovanović, V.; Marinković, D.; Janošević, D.; Petrović, N. Influential Factors in the Loading of the Axial Bearing of the Slewing Platform Drive in Hydraulic Excavators. Teh. Vjesn. 2023, 30, 158–168. [Google Scholar] [CrossRef]
- Volkov, V.; Taran, I.; Volkova, T.; Pavlenko, O.; Berezhnaja, N. Determining the Efficient Management System for a Specialized Transport Enterprise. Nauk. Visnyk Natsionalnoho Hirnychoho Univ. 2020, 2020, 185–191. [Google Scholar] [CrossRef]
- Saukenova, I.; Oliskevych, M.; Taran, I.; Toktamyssova, A.; Aliakbarkyzy, D.; Pelo, R. Optimization of Schedules for Early Garbage Collection and Disposal in the Megapolis. East.-Eur. J. Enterp. Technol. 2022, 1, 13–23. [Google Scholar] [CrossRef]
- Ézsiás, L.; Tompa, R.; Fischer, S. Investigation of the Possible Correlations Between Specific Characteristics of Crushed Stone Aggregates. Spectr. Mech. Eng. Oper. Res. 2024, 1, 10–26. [Google Scholar] [CrossRef]
- Fischer, S. Evaluation of inner shear resistance of layers from mineral granular materials. Facta Univ. Ser. Mech. Eng. 2023, 12155. [Google Scholar] [CrossRef]
- Nagy, R.; Horvát, F.; Fischer, S. Innovative Approaches in Railway Management: Leveraging Big Data and Artificial Intelligence for Predictive Maintenance of Track Geometry. Teh. Vjesn. 2024, 31, 1245–1259. [Google Scholar] [CrossRef]
- Kuchak, A.T.J.; Marinkovic, D.; Zehn, M. Finite Element Model Updating—Case Study of a Rail Damper. Struct. Eng. Mech. 2020, 73, 27–35. [Google Scholar] [CrossRef]
- Kuchak, A.T.J.; Marinkovic, D.; Zehn, M. Parametric Investigation of a Rail Damper Design Based on a Lab-Scaled Model. J. Vib. Eng. Technol. 2021, 9, 51–60. [Google Scholar] [CrossRef]
- Brautigam, A.; Szalai, S.; Fischer, S. Investigation of the application of austenitic filler metals in paved tracks for the repair of the running surface defects of rails considering field tests. Facta Univ. Ser. Mech. Eng. 2023, 12081. [Google Scholar] [CrossRef]
- Fischer, S.; Harangozó, D.; Németh, D.; Kocsis, B.; Sysyn, M.; Kurhan, D.; Brautigam, A. Investigation of Heat-Affected Zones of Thermite Rail Weldings. Facta Univ. Ser. Mech. Eng. 2023, 11420. [Google Scholar] [CrossRef]
- Németh, A.; Fischer, S. Investigation of glued insulated rail joints applied to CWR tracks. Facta Univ. Ser. Mech. Eng. 2021, 19, 681–704. [Google Scholar] [CrossRef]
- Monek, G.D.; Fischer, S. Expert Twin: A Digital Twin with an Integrated Fuzzy-Based Decision-Making Module. Decis. Mak. Appl. Manag. Eng. 2024, 8, 1–21. [Google Scholar] [CrossRef]
- Szalai, S.; Szívós, B.; Kocsis, D.; Sysyn, M.; Liu, J.; Fischer, S. The Application of DIC in Criminology Analysis Procedures to Measure Skin Deformation. J. Appl. Comput. Mech. 2024. [Google Scholar] [CrossRef]
- Oslakovic, I.S.; ter Maat, H.; Hartmann, A.; Dewulf, G. Risk Assessment of Climate Change Impacts on Railway Infrastructure. In Proceedings of the Engineering Project Organization Conference, Tabernash, CO, USA, 9–11 July 2013. [Google Scholar]
- Quinn, A.; Unión Internacional de Ferrocarriles. RAIL Adapt: Adapting the Railway for the Future. In Proceedings of the 7th Transport Research Arena TRA 2018, Vienna, Austria, 16–19 April 2018; A Report for the International Union of Railways (UIC); Railway Technical Publications (ETF): Paris, France, 2017; ISBN 9782746126800. [Google Scholar]
- Ngamkhanong, C.; Kaewunruen, S.; Afonso Costa, B.J. State-of-the-Art Review of Railway Track Resilience Monitoring. Infrastructures 2018, 3, 3. [Google Scholar] [CrossRef]
- Dindar, S.; Kaewunruen, S.; An, M.; Osman, M.H. Natural Hazard Risks on Railway Turnout Systems. Procedia Eng. 2016, 161, 1254–1259. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Wang, Y.; Ngamkhanong, C. Derailment-Resistant Performance of Modular Composite Rail Track Slabs. Eng. Struct. 2018, 160, 1–11. [Google Scholar] [CrossRef]
- Zakeri, J.A.; Mirfattahi, B.; Fakhari, M. Lateral Resistance of Railway Track with Frictional Sleepers. Proc. Inst. Civ. Eng. Transp. 2012, 165, 151–155. [Google Scholar] [CrossRef]
- Fang, C.; Jaafar, S.A.; Zhou, W.; Yan, H.; Chen, J.; Meng, X. Wheel-Rail Contact and Friction Models: A Review of Recent Advances. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2023, 237, 1245–1259. [Google Scholar] [CrossRef]
- Anbazhagan, P.; Bharatha, T.P.; Amarajeevi, G. Study of Ballast Fouling in Railway Track Formations. Indian Geotech. J. 2012, 42, 87–99. [Google Scholar] [CrossRef]
- Sussmann, T.R.; Ruel, M.; Chrismer, S.M. Source of Ballast Fouling and Influence Considerations for Condition Assessment Criteria. Transp. Res. Rec. 2012, 2289, 87–94. [Google Scholar] [CrossRef]
- Lei, X.; Feng, Q. Analysis of Stability of Continuously Welded Rail Track with Finite Elements. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2004, 218, 225–233. [Google Scholar] [CrossRef]
- Carvalho, J.; Delgado, J.; Calçada, R.; Delgado, R. A New Methodology for Evaluating the Safe Temperature in Continuous Welded Rail Tracks. Int. J. Struct. Stab. Dyn. 2013, 13, 1350016. [Google Scholar] [CrossRef]
- Ngamkhanong, C.; Wey, C.M.; Kaewunruen, S. Buckling Analysis of Interspersed Railway Tracks. Appl. Sci. 2020, 10, 3091. [Google Scholar] [CrossRef]
- Esveld, C. Improved Knowledge of CWR Track. In Interactive Conference on Cost Effectiveness and Safety Aspects of Railway Track; UIC/ERRI: Paris, France, 1998; pp. 8–9. [Google Scholar]
- Kish, A. On the fundamentals of track lateral resistance. In Proceedings of the AREMA 2011 Annual Conference, Minneapolis, MN, USA, 18–21 September 2011. [Google Scholar]
- AREMA. Manual for Railway Engineering. Man. Railw. Eng. 2010, 1. [Google Scholar]
- Kabo, E. A Numerical Study of the Lateral Ballast Resistance in Railway Tracks. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2006, 220, 425–433. [Google Scholar] [CrossRef]
- Ali Zakeri, J.; Esmaeili, M.; Kasraei, A.; Bakhtiary, A. A Numerical Investigation on the Lateral Resistance of Frictional Sleepers in Ballasted Railway Tracks. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 440–449. [Google Scholar] [CrossRef]
- Ngamkhanong, C.; Kaewunruen, S.; Baniotopoulos, C. A Review on Modelling and Monitoring of Railway Ballast. Struct. Monit. Maint. 2017, 4, 195–220. [Google Scholar] [CrossRef]
- Cundall, P.A. A Computer Model for Simulating Progressive Large-Scale Movements in Blocky Rock Systems. In Proceedings of the Symposium of the International Society of Rock Mechanics, Nancy, France, 4–6 October 1971; Volume 8, pp. 129–136. [Google Scholar]
- Irazábal González Supervisor, J. Numerical Analysis of Railway Ballast Behaviour Using the Discrete Element Method. Ph.D. Thesis, Departament d’Enginyeria Civil i Ambiental, Universitat Politècnica de Catalunya, Barcelona, Spain, 2017. [Google Scholar] [CrossRef]
- Jing, G.Q.; Aela, P.; Fu, H.; Yin, H. Numerical and Experimental Analysis of Single Tie Push Tests on Different Shapes of Concrete Sleepers in Ballasted Tracks. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2019, 233, 666–677. [Google Scholar] [CrossRef]
- Guo, Y.; Fu, H.; Qian, Y.; Markine, V.; Jing, G. Effect of Sleeper Bottom Texture on Lateral Resistance with Discrete Element Modelling. Constr. Build. Mater. 2020, 250, 118770. [Google Scholar] [CrossRef]
- Khatibi, F.; Esmaeili, M.; Mohammadzadeh, S. DEM Analysis of Railway Track Lateral Resistance. Soils Found. 2017, 57, 587–602. [Google Scholar] [CrossRef]
- Irazábal González, J.; Salazar González, F. Numerical Modelling of Railway Ballast Using the Discrete Element Method. Master’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2015. [Google Scholar] [CrossRef]
- Jing, G.; Aela, P.; Fu, H. The Contribution of Ballast Layer Components to the Lateral Resistance of Ladder Sleeper Track. Constr. Build. Mater. 2019, 202, 796–805. [Google Scholar] [CrossRef]
- Xiao, H.; Ling, X. Experiment and DEM Analysis of Lateral Resistance of Glued Ballast. Xinan Jiaotong Daxue Xuebao/J. Southwest Jiaotong Univ. 2017, 52, 1046–1054. [Google Scholar] [CrossRef]
- Jing, G.; Zhang, X.; Jia, W. Lateral Resistance of Polyurethane-Reinforced Ballast with the Application of New Bonding Schemes: Laboratory Tests and Discrete Element Simulations. Constr. Build. Mater. 2019, 221, 627–636. [Google Scholar] [CrossRef]
- Tutumluer, E.; Huang, H.; Hashash, Y.; Ghaboussi, J. Aggregate Shape Effects on Ballast Tamping and Railroad Track Lateral Stability. In Proceedings of the AREMA Annual Conference, Louisville, KY, USA, 17–20 September 2006; pp. 17–20. [Google Scholar]
- Guo, Y.; Markine, V.; Song, J.; Jing, G. Ballast Degradation: Effect of Particle Size and Shape Using Los Angeles Abrasion Test and Image Analysis. Constr. Build. Mater. 2018, 169, 414–424. [Google Scholar] [CrossRef]
- Lichtberger, B. Track Compendium, 1st ed.; Eurailpress: Hamburg, Germany, 2005. [Google Scholar]
- Chalabii, J.; Movahedi Rad, M.; Hadizadeh Raisi, E.; Esfandiari Mehni, R. Effect of Sleeper-Ballast Particle Contact on Lateral Resistance of Concrete Sleepers in Ballasted Railway Tracks. Materials 2022, 15, 7508. [Google Scholar] [CrossRef]
- Feng, B.; Hou, W.; Tutumluer, E. Implications of Field Loading Patterns on Different Tie Support Conditions Using Discrete Element Modeling: Dynamic Responses. Transp. Res. Rec. 2019, 2673, 509–520. [Google Scholar] [CrossRef]
- Ngamkhanong, C.; Feng, B.; Tutumluer, E.; Hashash, Y.M.A.; Kaewunruen, S. Evaluation of Lateral Stability of Railway Tracks Due to Ballast Degradation. Constr. Build. Mater. 2021, 278, 122342. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, L.; Zhang, Y.R.; Yin, H.; Cai, X.P. Discrete Element Method Analysis of Lateral Resistance of Fouled Ballast Bed. J. Cent. South Univ. 2016, 23, 2373–2381. [Google Scholar] [CrossRef]
- Lim, N.H.; Kim, K.J.; Bae, H.U.; Kim, S. DEM Analysis of Track Ballast for Track Ballast-Wheel Interaction Simulation. Appl. Sci. 2020, 10, 2717. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A Discrete Numerical Model for Granular Assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- CGI Itasca. PFC3D (Particle Flow Code in Three Dimensions); CGI Itasca: Grand Rapids, MN, USA, 2021. [Google Scholar]
- Taghavi, R. Automatic Clump Generation Based on Mid-Surface. In Proceedings of the 2nd international FLAC/DEM Symposium, Melbourne, Australia, 14–16 February 2011; pp. 791–797. [Google Scholar]
- Irazábal, J.; Salazar, F.; Oñate, E. Numerical Modelling of Granular Materials with Spherical Discrete Particles and the Bounded Rolling Friction Model. Application to Railway Ballast. Comput. Geotech. 2017, 85, 220–229. [Google Scholar] [CrossRef]
- Chen, C.; McDowell, G.R.; Thom, N.H. Discrete Element Modelling of Cyclic Loads of Geogrid-Reinforced Ballast under Confined and Unconfined Conditions. Geotext. Geomembr. 2012, 35, 76–86. [Google Scholar] [CrossRef]
- Laryea, S.; Safari Baghsorkhi, M.; Ferellec, J.F.; McDowell, G.R.; Chen, C. Comparison of Performance of Concrete and Steel Sleepers Using Experimental and Discrete Element Methods. Transp. Geotech. 2014, 1, 225–240. [Google Scholar] [CrossRef]
- Yimsiri, S.; Soga, K. DEM Analysis of Soil Fabric Effects on Behaviour of Sand. Geotechnique 2010, 60, 483–495. [Google Scholar] [CrossRef]
- Lin, X.; Ng, T.T. A Three-Dimensional Discrete Element Model Using Arrays of Ellipsoids. Geotechnique 1997, 47, 319–329. [Google Scholar] [CrossRef]
- Chen, Y.C.; Hung, H.Y. Evolution of Shear Modulus and Fabric during Shear Deformation. Soils Found. 1991, 31, 148–160. [Google Scholar] [CrossRef][Green Version]
- Sitharam, T.G.; Vinod, J.S.; Ravishankar, B.V. Evaluation of Undrained Response from Drained Triaxial Shear Tests: DEM Simulations and Experiments. Geotechnique 2008, 58, 605–608. [Google Scholar] [CrossRef]
- Chalabii, J.; Movahedi Rad, M.; Hosseini, S. Optimal Shape Design of Concrete Sleepers under Lateral Loading Using DEM. Buildings 2023, 13, 1574. [Google Scholar] [CrossRef]
- Indraratna, B.; Lackenby, J.; Christie, D. Effect of Confining Pressure on the Degradation of Ballast under Cyclic Loading. Geotechnique 2005, 55, 325–328. [Google Scholar] [CrossRef]
- Koyama, E.; Ito, K.; Hayano, K.; Momoya, Y. A New Approach for Evaluating Lateral Resistance of Railway Ballast Associated with Extended Sleeper Spacing. Soils Found. 2021, 61, 1565–1580. [Google Scholar] [CrossRef]
- Esmaeili, M.; Khodaverdian, A.; Neyestanaki, H.K.; Nazari, S. Investigating the Effect of Nailed Sleepers on Increasing the Lateral Resistance of Ballasted Track. Comput. Geotech. 2016, 71, 1–11. [Google Scholar] [CrossRef]





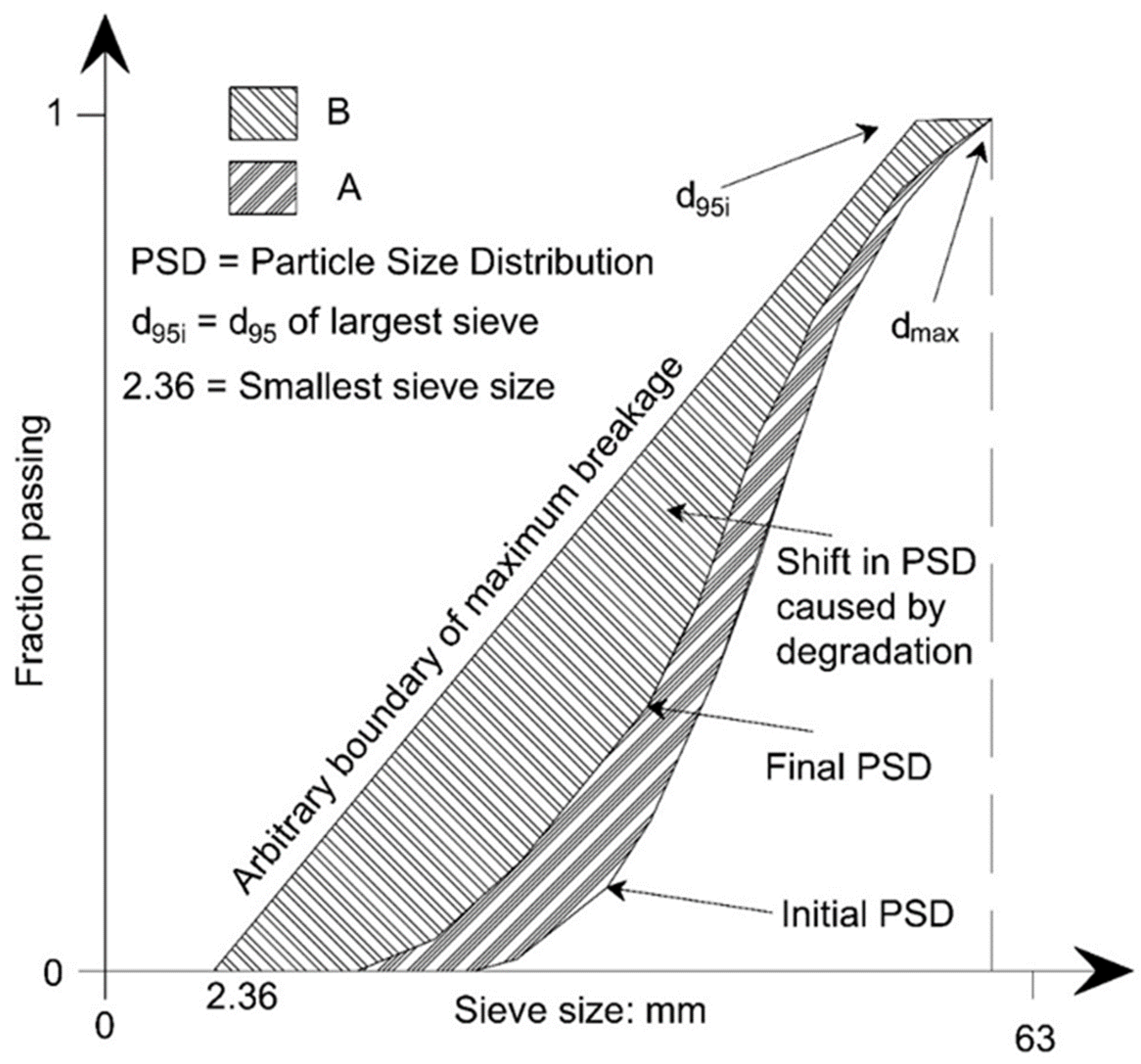

| Kind of PSD | Percentage of Passing (%) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sieve Size (mm) | No. 24 | No. 25 | No. 57 | No. 5 | No. 4A | No. 4 | No. 3 | #5 | #4 | #3 | #2 | #1 | |
| 75 | 100 | 100 | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | |
| 63 | 90 | 80 | --- | --- | 100 | --- | 100 | 100 | --- | --- | --- | --- | |
| 50 | --- | 60 | --- | --- | 90 | 50 | 95 | 90 | 100 | 100 | 100 | --- | |
| 38.1 | --- | --- | --- | --- | --- | --- | --- | 35 | 90 | 90 | 90 | 100 | |
| 37.5 | 25 | 50 | 100 | 100 | 60 | 90 | 35 | --- | --- | --- | --- | --- | |
| 25 | --- | 15 | 95 | 90 | 10 | 20 | 15 | 5 | 20 | 70 | 70 | 90 | |
| 19.05 | 0 | --- | --- | 75 | --- | 15 | --- | 0 | 5 | 30 | 50 | 70 | |
| 12.5 | --- | 5 | 60 | 35 | --- | 5 | 5 | --- | 0 | 20 | 25 | 40 | |
| 9.5 | --- | 0 | --- | 15 | 3 | --- | 0 | --- | --- | 0 | 10 | 20 | |
| 4.75 | --- | --- | 10 | 0 | 0 | 0 | --- | --- | --- | --- | 0 | 0 | |
| 2.36 | --- | --- | 5 | --- | --- | --- | --- | --- | --- | --- | --- | --- | |
| Parameters of Contact | Symbol | Units | Value in Simulation | Experimental Value [39] |
|---|---|---|---|---|
| Shear elastic modulus | -- | |||
| Poisson’s ratio of ballast | -- | -- | ||
| Ballast particle density | ||||
| Sleeper clump density | ||||
| Interparticle friction coefficient | -- | |||
| Side wall friction coefficient | -- | -- | ||
| Base wall friction coefficient (subgrade) | -- | -- | ||
| Wall’s normal and shear stiffness | -- |
| PSD | Diameter of Particles (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (Pa) | (Pa) |
|---|---|---|---|---|---|---|---|---|
| No. 24 | 63.4, 38.1, 19 | 31.7 | 19.05 | 23.8 | 17 | |||
| 9.5 | 19.05 | 12.7 | 0.85 | |||||
| 31.7 | 9.5 | 14.6 | ||||||
| 38.1, 25.4, 19.05 | 19.05 | 12.7 | 15.24 | 12.13 | ||||
| #4 | 19.05 | 9.52 | 12.7 | 0.6 | ||||
| 12.7 | 6.35 | 8.5 | ||||||
| No. 3 | 38.1, 25.4, 19.05, 12.7 | 19.05 | 12.7 | 15.24 | 10.74 | |||
| 19.05 | 9.52 | 12.7 | ||||||
| 19.05 | 6.35 | 9.52 | ||||||
| 12.7 | 9.52 | 10.88 | 0.54 | |||||
| 12.7 | 6.35 | 8.5 | ||||||
| 9.52 | 6.35 | 7.62 | ||||||
| #3 | 50, 37.5, 25, 12.5 | 25 | 18.75 | 21.43 | 13.47 | |||
| 25 | 12.5 | 16.7 | ||||||
| 25 | 6.25 | 10 | 0.67 | |||||
| 18.75 | 12.5 | 15 | ||||||
| 18.75 | 6.25 | 9.37 | ||||||
| 12.5 | 6.25 | 8.3 | ||||||
| No. 4A | 50, 37.5, 25, 9.5 | 25 | 18.75 | 21.4 | 12.59 | |||
| 25 | 12.5 | 16.7 | ||||||
| 25 | 4.75 | 8 | 0.63 | |||||
| 18.75 | 12.5 | 15 | ||||||
| 18.75 | 12.5 | 7.6 | ||||||
| 18.75 | 6.25 | 6.9 | ||||||
| #2 | 38.1, 25.4, 19.05, 12.7 | 19.05 | 12.7 | 15.2 | 10.74 | |||
| 19.05 | 9.525 | 12.7 | ||||||
| 19.05 | 6.35 | 9.52 | 0.54 | |||||
| 12.7 | 9.525 | 10.88 | ||||||
| 12.7 | 6.35 | 8.47 | ||||||
| 9.525 | 6.35 | 7.62 | ||||||
| No. 4 | 37.5, 25, 19 | 18.75 | 12.5 | 15 | 11.98 | |||
| 18.75 | 9.5 | 12.6 | 0.6 | |||||
| 12.5 | 6.25 | 8.3 | ||||||
| No. 5 | 25, 19, 12.5, 9.5 | 12.5 | 9.5 | 10.79 | 7.54 | |||
| 12.5 | 6.25 | 8.3 | ||||||
| 12.5 | 4.75 | 6.9 | 0.38 | |||||
| 9.5 | 6.25 | 7.5 | ||||||
| 9.5 | 4.75 | 6.3 | ||||||
| 6.25 | 4.75 | 5.4 | ||||||
| No. 57 | 25, 12.5, 4.75 | 12.5 | 6.25 | 8.3 | 5.25 | |||
| 12.5 | 2.375 | 4 | 0.26 | |||||
| 6.25 | 2.375 | 3.4 | ||||||
| #1 | 25.4, 19.05, 12.7, 9.25 | 12.7 | 9.525 | 10.9 | 7.01 | |||
| 12.7 | 6.35 | 8.47 | ||||||
| 12.7 | 4.625 | 6.78 | 0.35 | |||||
| 9.525 | 6.35 | 7.62 | ||||||
| 9.525 | 4.625 | 6.23 | ||||||
| 6.35 | 4.625 | 5.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chalabii, J.; Esmaeili, M.; Gosztola, D.; Fischer, S.; Movahedi Rad, M. Effect of the Particle Size Distribution of the Ballast on the Lateral Resistance of Continuously Welded Rail Tracks. Infrastructures 2024, 9, 129. https://doi.org/10.3390/infrastructures9080129
Chalabii J, Esmaeili M, Gosztola D, Fischer S, Movahedi Rad M. Effect of the Particle Size Distribution of the Ballast on the Lateral Resistance of Continuously Welded Rail Tracks. Infrastructures. 2024; 9(8):129. https://doi.org/10.3390/infrastructures9080129
Chicago/Turabian StyleChalabii, Jafar, Morteza Esmaeili, Dániel Gosztola, Szabolcs Fischer, and Majid Movahedi Rad. 2024. "Effect of the Particle Size Distribution of the Ballast on the Lateral Resistance of Continuously Welded Rail Tracks" Infrastructures 9, no. 8: 129. https://doi.org/10.3390/infrastructures9080129
APA StyleChalabii, J., Esmaeili, M., Gosztola, D., Fischer, S., & Movahedi Rad, M. (2024). Effect of the Particle Size Distribution of the Ballast on the Lateral Resistance of Continuously Welded Rail Tracks. Infrastructures, 9(8), 129. https://doi.org/10.3390/infrastructures9080129









