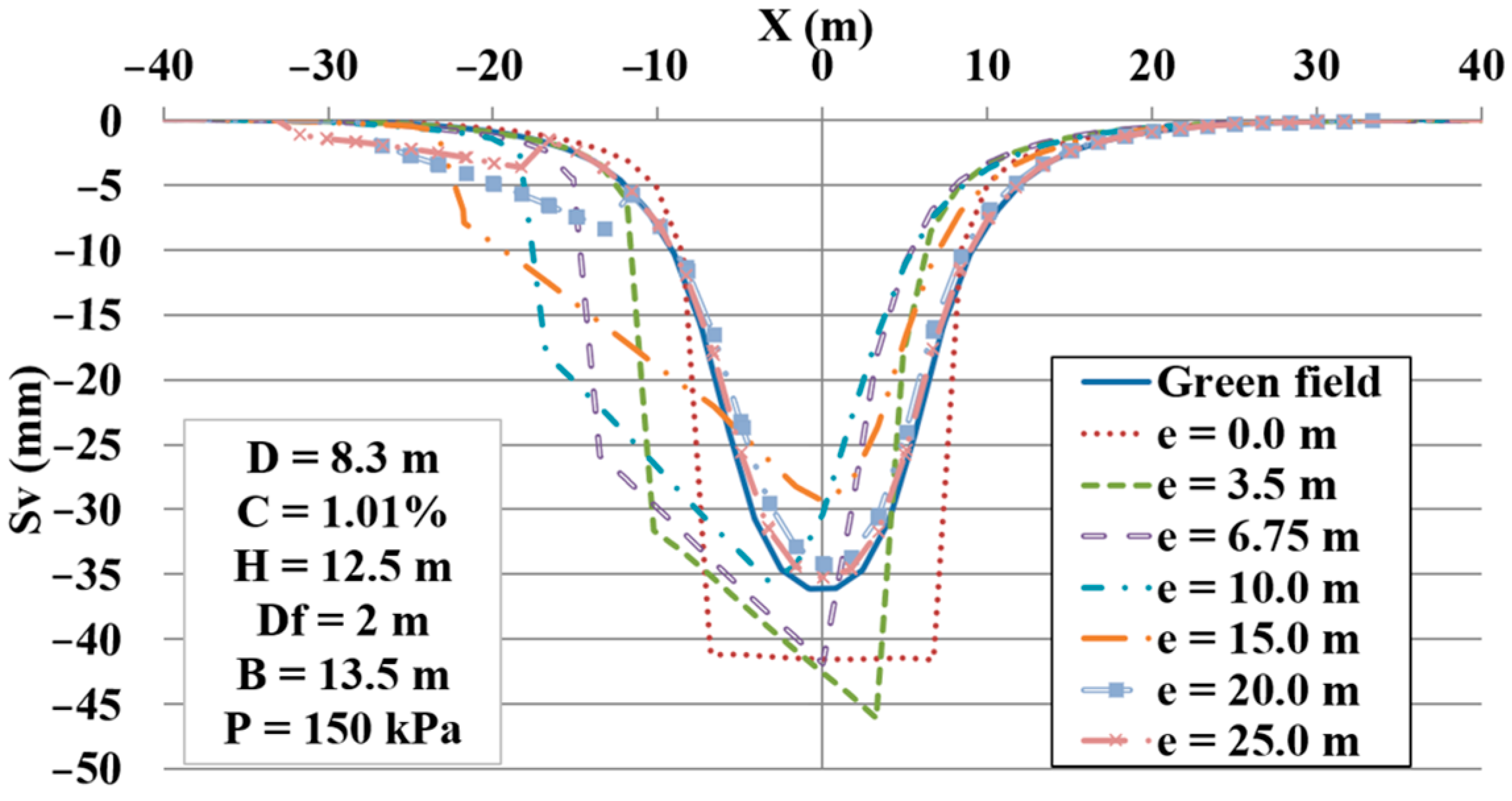
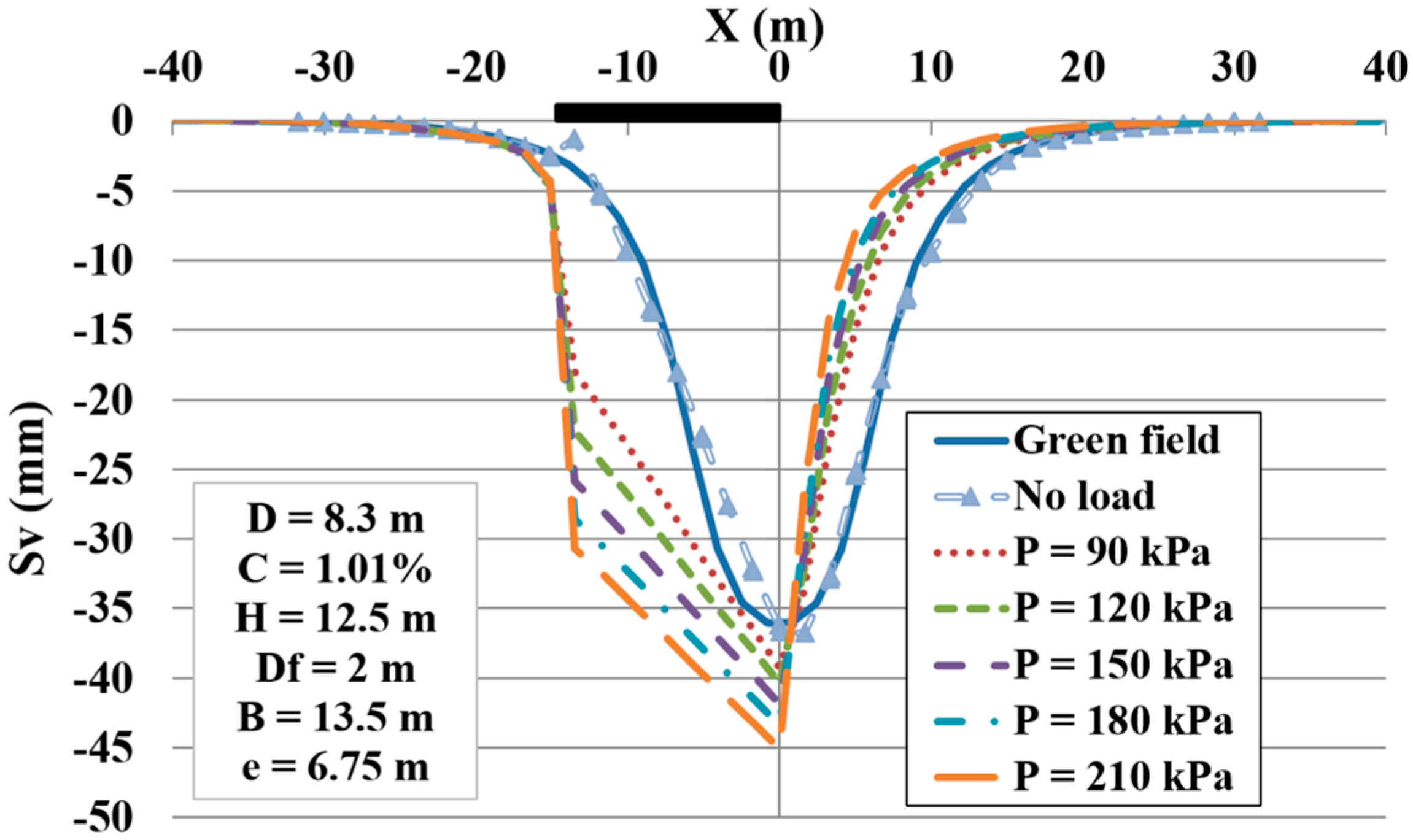
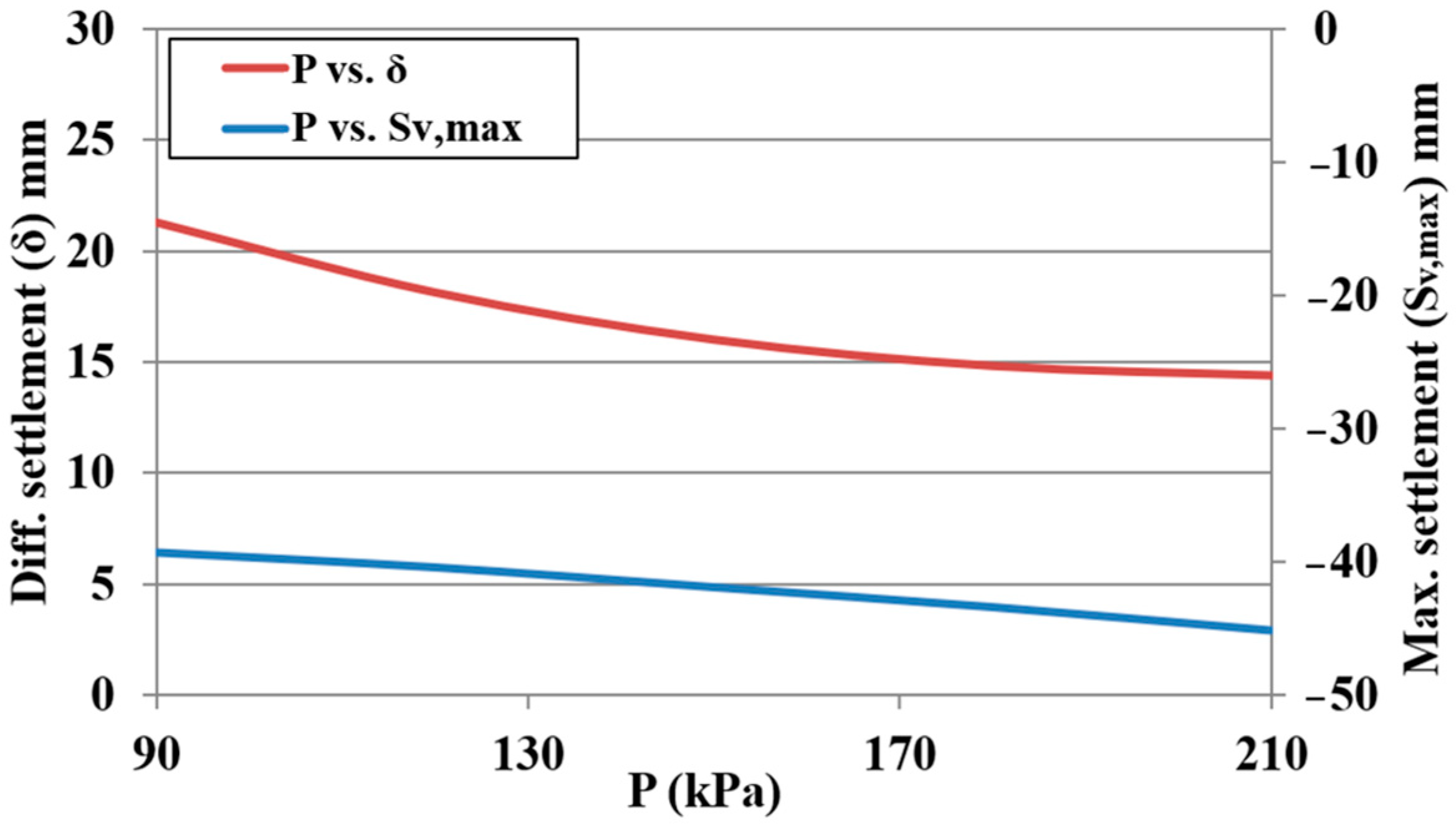
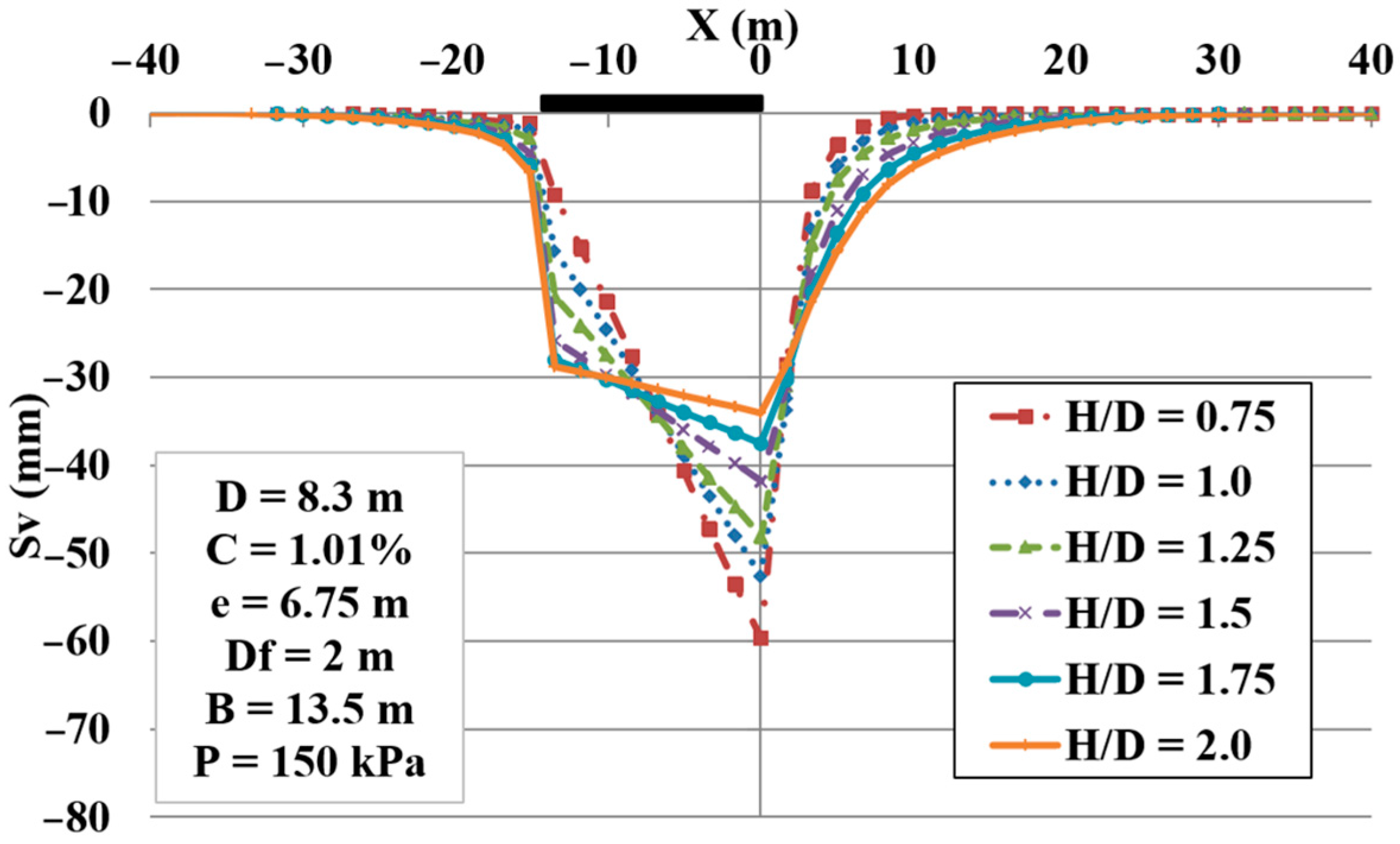
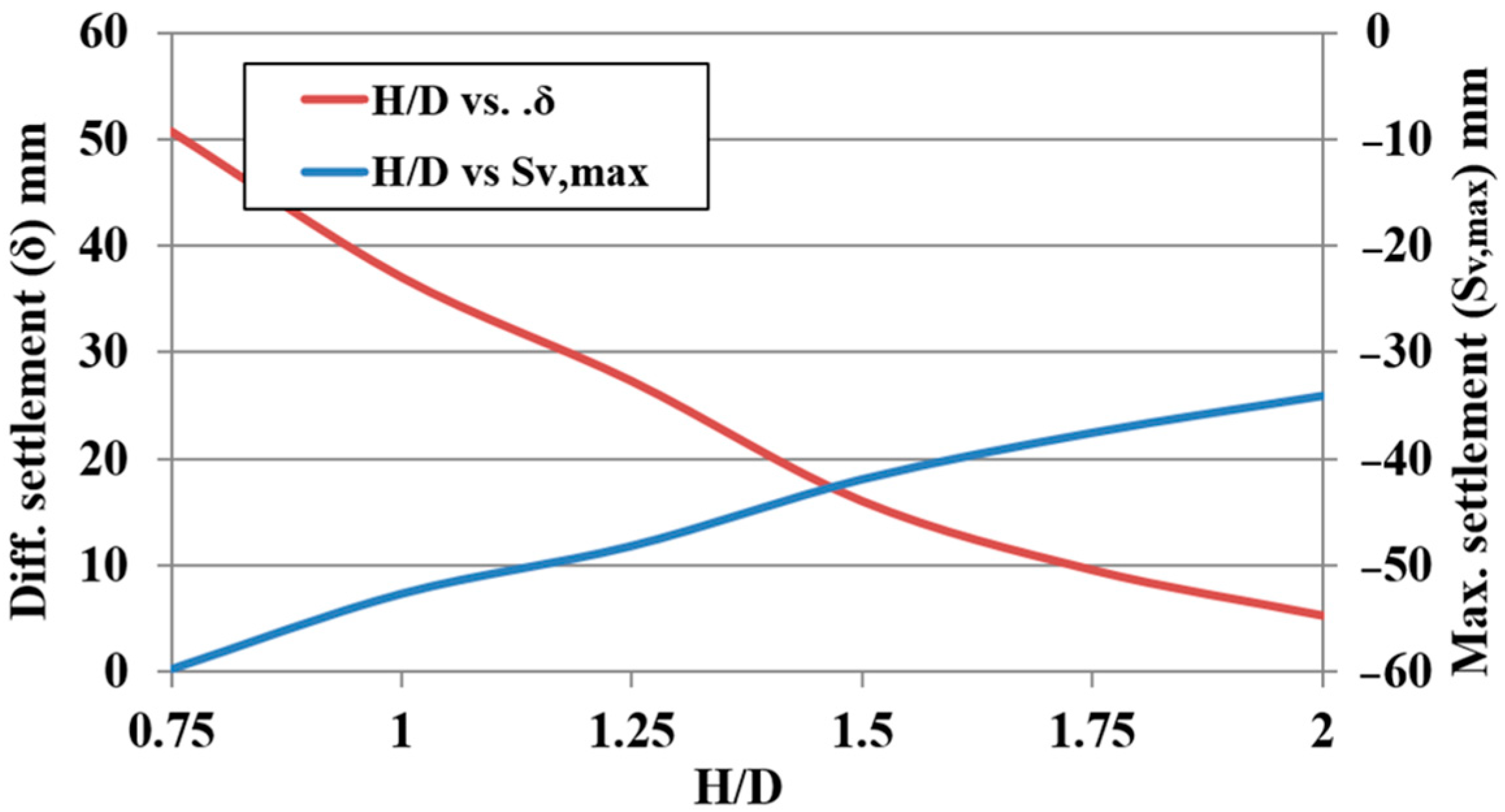
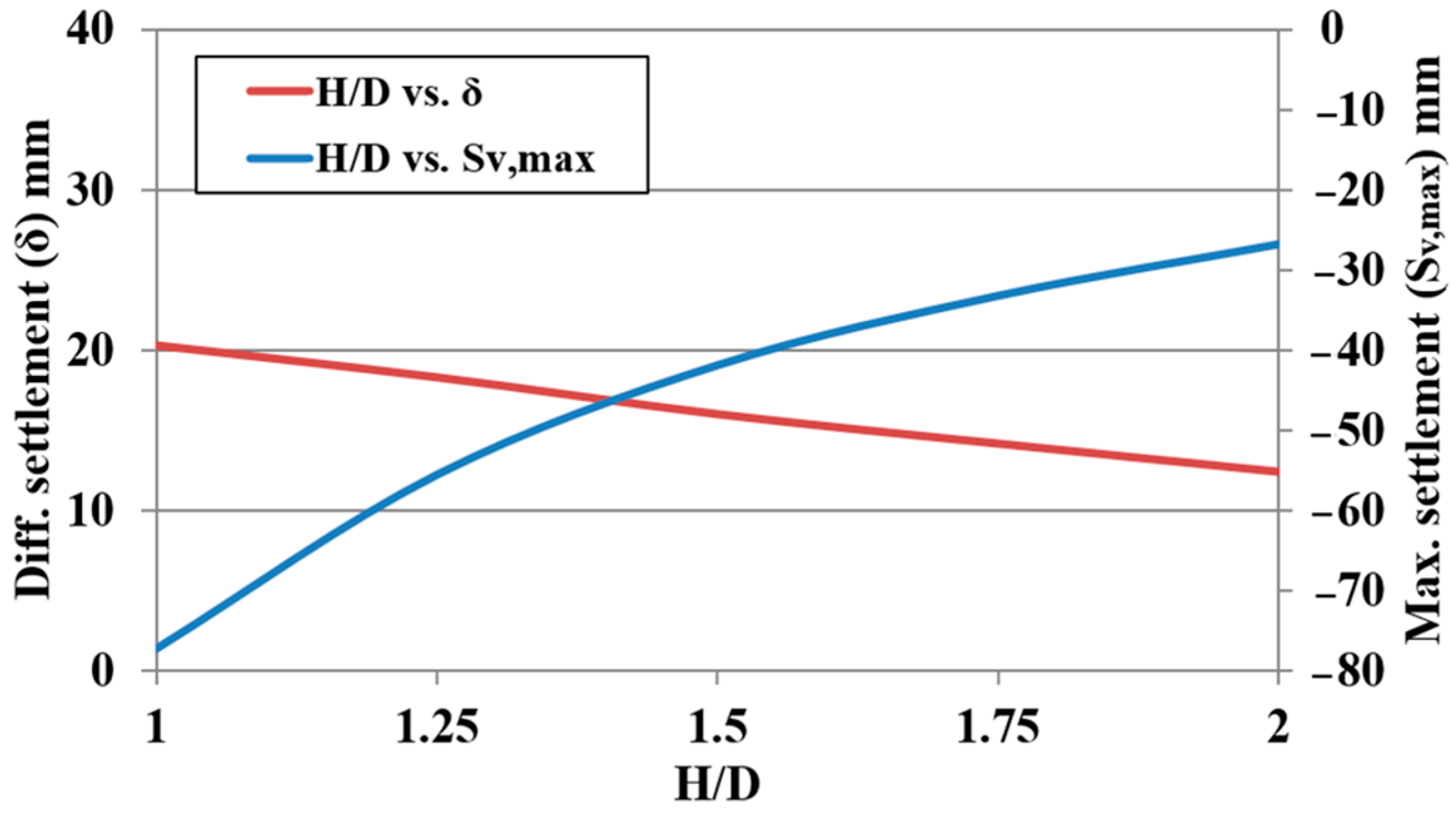
A sensitivity analysis was conducted to demonstrate the influence of the various parameters on the settlements.
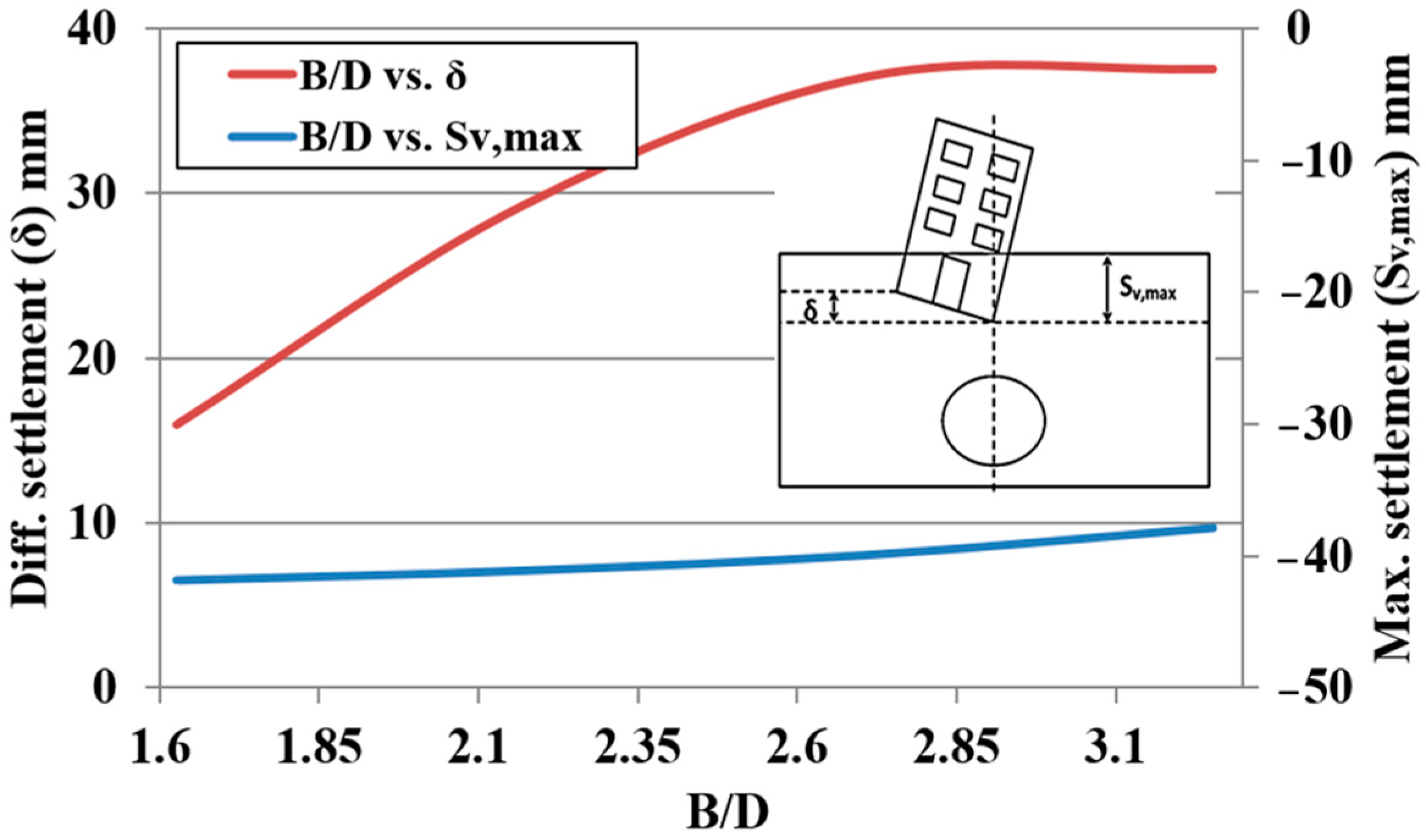
Table 6 shows this influence through an increase of 20 % of each parameter. It is clear that the most effective parameters on the maximum settlement of the adjacent structure are the following: the tunnel diameter (
D), the foundation eccentricity (
e), and the overburden depth (
H).
Dc, means that the diameter of the tunnel is constant. Similarly,
Hc means that the overburden depth is constant, and
E represents the elastic modulus of the equivalent soil layer surrounding the tunnel.
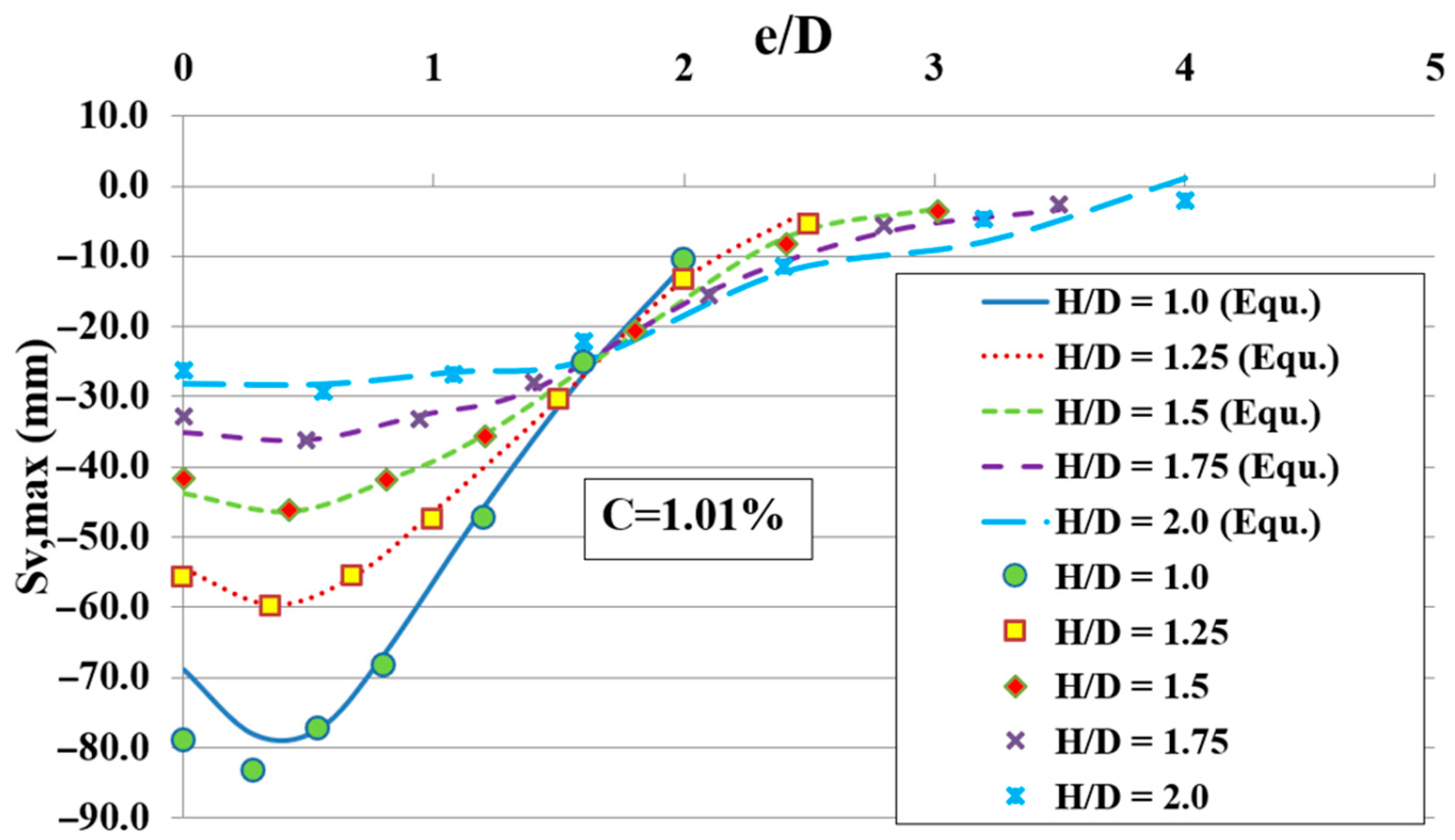
In this part, a newly proposed equation was developed based on the validated model of the tunnel. An extended parametric study of the independent variables (
D,
e,
H,
C), where
C% denotes the contraction coefficient, was conducted using a total of 392 observations to derive the equation for maximum settlement (i.e., dependent variable). The presumptive values of the independent variables are listed in
Table 7. The contraction method was adopted to derive the equation for the reasons explained above in
Section 4.1. The EUREQA Version 1.2 software [
30] was applied to find the mathematical connections between the dependent and the independent variables, based on the available database. This equation is recommended for usein the elementary analysis of tunnels.
Many fundamental issues should be considered with the use of this equation. This equation can be considered eligible for subsurface tunnels with the following constraints: H/D ≤ 2, the values of the contraction coefficient should range between (0.2–1.6) %, the shallow foundation of the structure should be rigid, and the angles should be in radians.
Validation of the Proposed Equation
This paper utilized three cases to validate the proposed equation: (i) the Second Heinenoord Tunnel: a comparison between the numerical analysis outputs of the validated model and the equation solutions; (ii) the Milan Twin Tunnel: a validated model is adopted for the comparison with equation solutions; and (iii) three case studies (the Thessaloniki subway, the Naples tunnel, and centrifuge tests) are used to compare the real measurements and the equation solutions.
The Validated Model of the Second Heinenoord Tunnel [
18]
A parametric study was conducted in terms of
e⁄D and
H⁄D to validate the proposed equation.
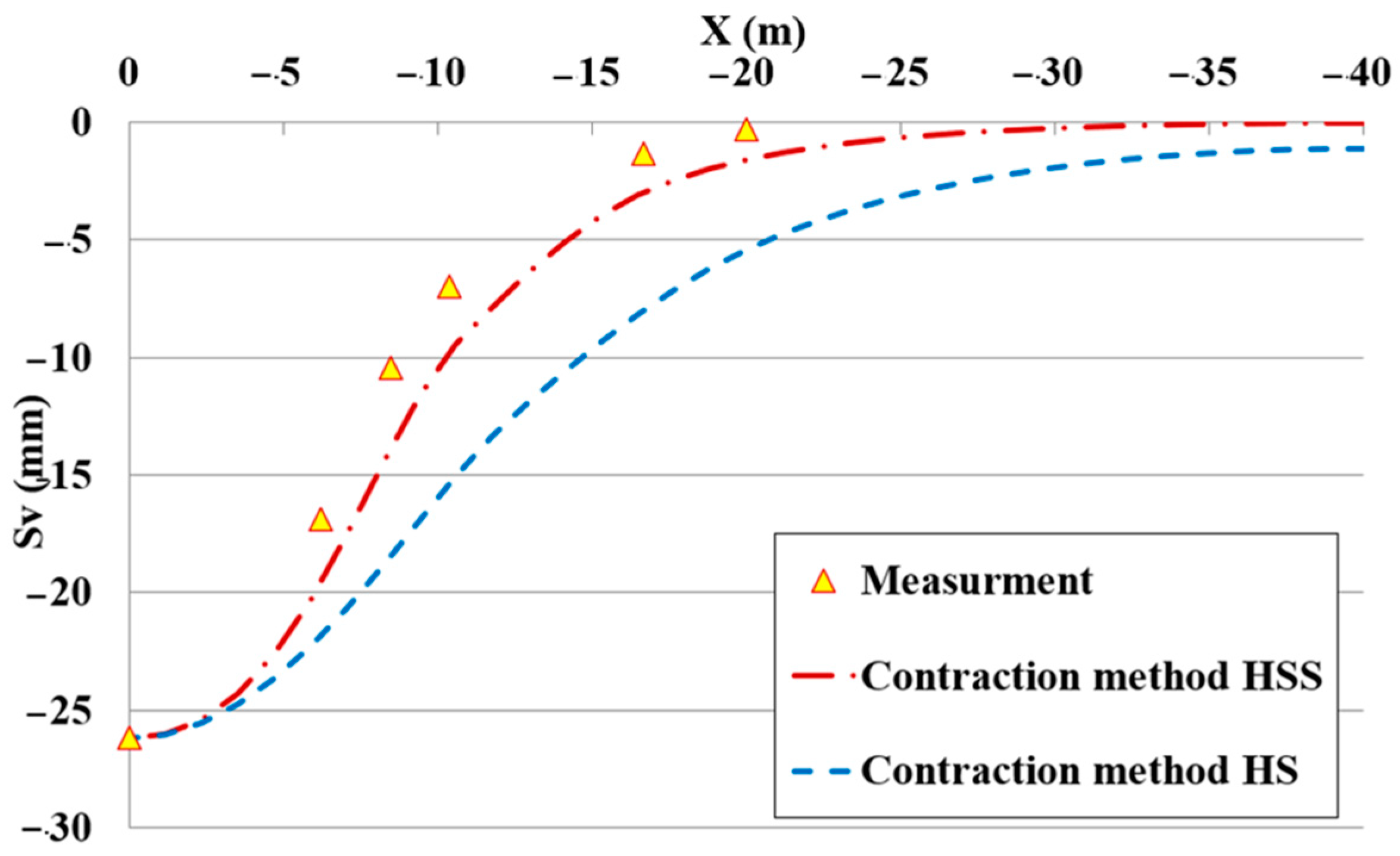
Figure 20 shows a consistent comparison between the numerical model results and the equation solutions.
With an overall distance of 12.6 km, the metro-line 5 in Italy is composed of a twin tunnel with an outer diameter (
D) = 6.7 m, and it stretches between the north and the west of Milan [
31]. The twin tunnel height (
H) = 11.65 m and the span between tunnel axes is 15 m. The tunnels were excavated in a gravely sand soil, whose properties are illustrated in
Table 8. The groundwater level is 15 m, which means that the tunnels were constructed partially underneath the water table. An EPB shield was used on site to reduce the ground movements in these highly inhabited regions. The tunnel lining was modeled as a beam element with linear elastic behavior, and the properties of the lining are listed in
Table 9.
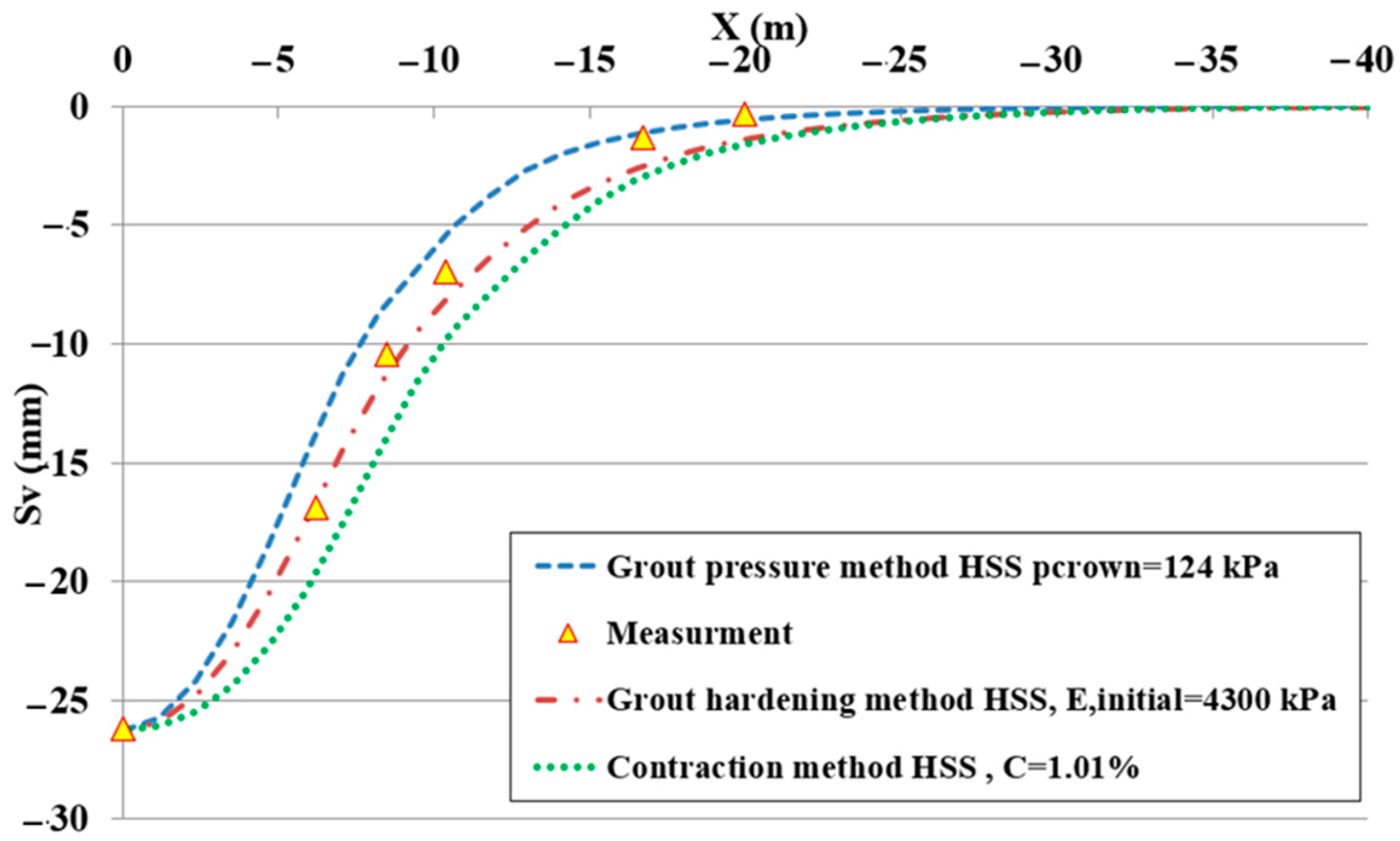
The field measurements of settlements of the transversal ground section S16 under the greenfield conditions were conducted after the excavation of the first tunnel and both tunnels, respectively. Plaxis 2D software was adopted in this study to validate the twin tunnel (for additional information, see [
31]).
HSS was employed to simulate the behavior of the surrounding soil of the twin tunnel. The contraction coefficients are depicted in
Figure 21. This study [
31] targeted the ground surface settlements that resulted from the excavation of the first tunnel.
Based on the back analysis method, a comparison was performed between the measured surface subsidence in the field and those predicted by the
HSS model. The field measurements were performed in two stages: (1) after the complete excavation of the first tunnel, and (2) after the excavation of the second tunnel.
Figure 21 indicates a good agreement between the field data and the
HSS results.
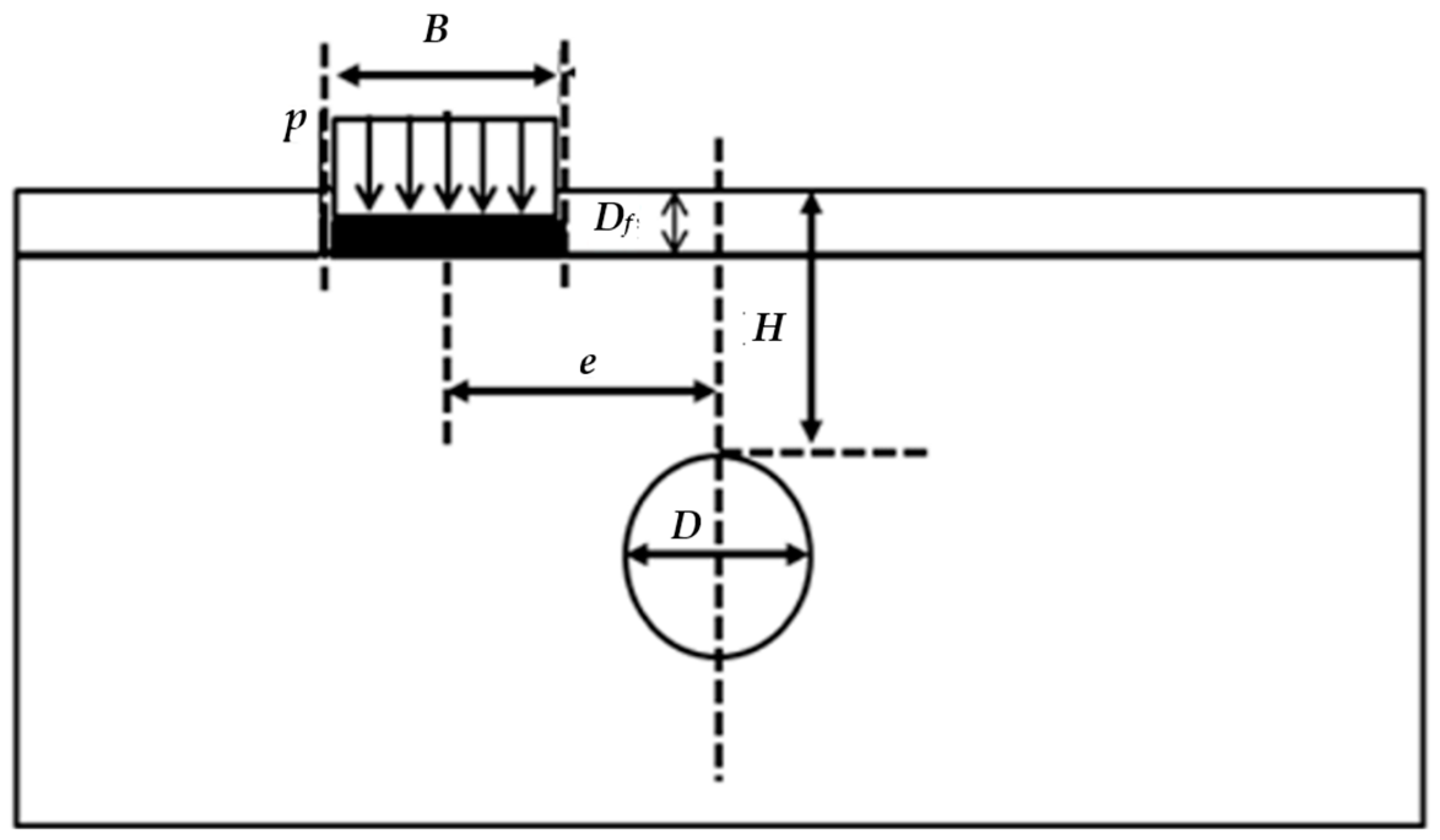
After the validation of this model, a structure represented by a distributed load (
P) of 150 kPa was added to the model, where the foundation width (
B) was 13.5 m and the foundation depth (
Df) was 2 m.
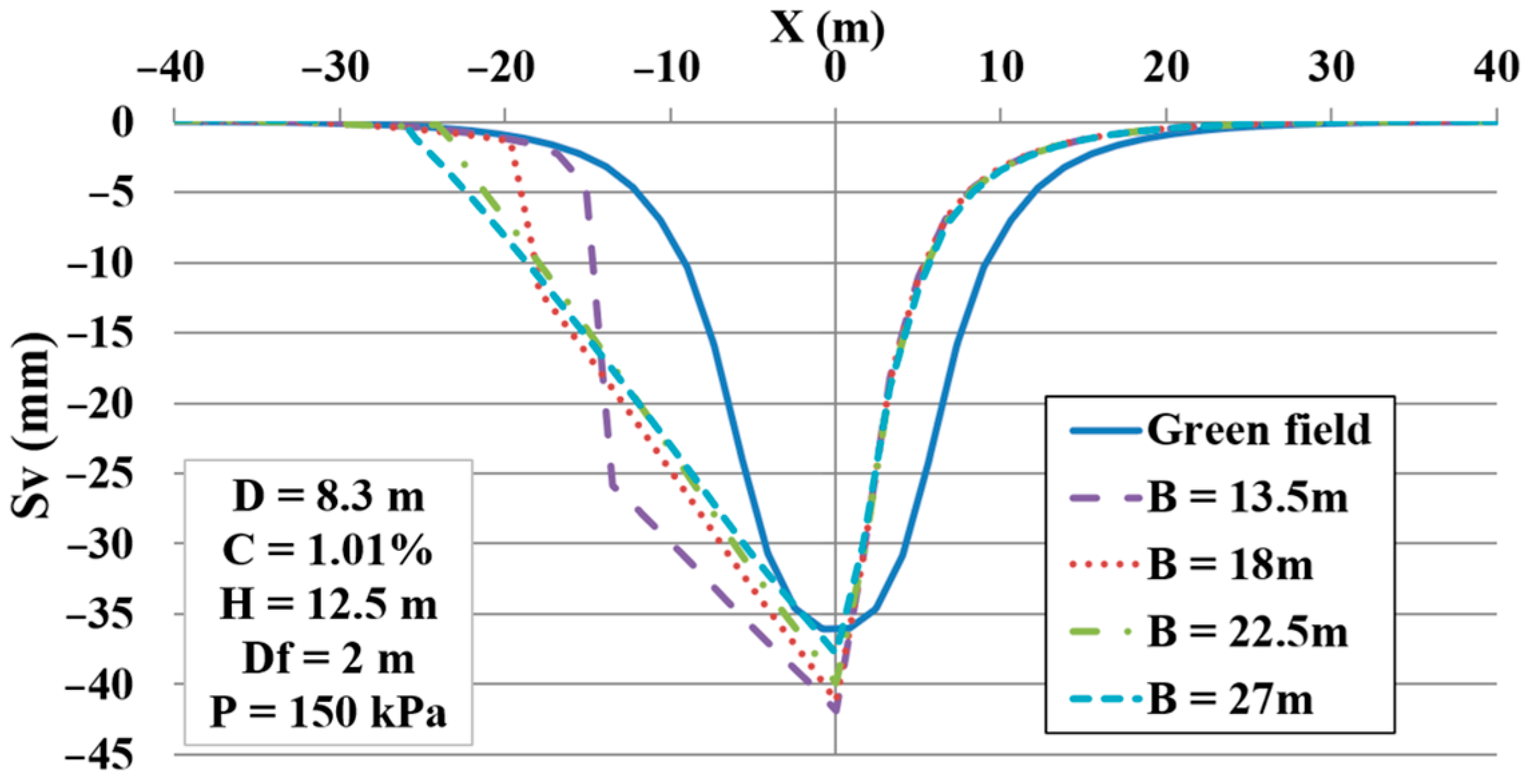
Figure 22 illustrates the comparison between the proposed equation results and the numerical model outputs for the maximum settlements of the structure. The presented equation results are relatively compatible with those of FEM.
Case Studies
- -
The Thessaloniki subway, Greece
The northbound and southbound lines are the designations of the twin tunnels that make up the Thessaloniki city subway in Greece [
32]. The two lines pass through densely populated areas at relatively shallow depths, ranging from 8 to 20 m, and are in proximity to adjacent structures. Two TBM-EPBs were utilized to decrease the surface settlements when the excavation passed through a sandy clay deposit. The groundwater table is located 5 meters beneath the ground surface. Settlements of the stiff raft foundation of the adjacent structure D91 were measured after the excavation of the southbound tunnel (first executed tunnel), which consists of seven stories. The site conditions and the design parameters are as follows: the tunnel diameter (
D) = 6.2 m, the overburden depth (
H) = 14.5m, the eccentricity (
e) = 22.5 m, the raft width (
B) = 11 m, the over excavation (20 mm), and the contraction coefficient (
C) = 0.65%.
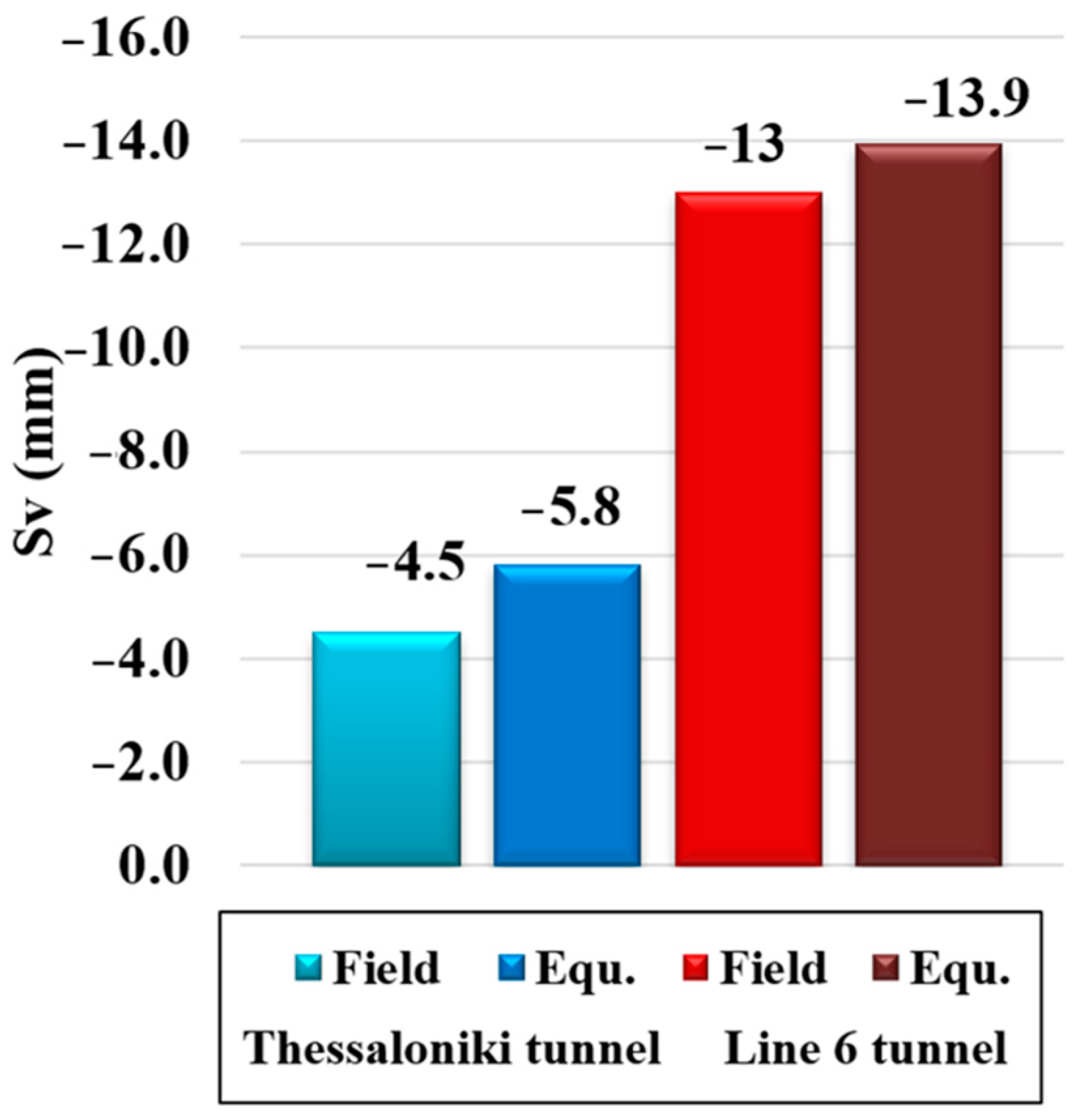
Figure 23 shows a comparison between the proposed equation and the field measurements for the maximum settlements of the structure raft foundation. The result of the present equation is somewhat consistent with the measured settlement.
- -
Line 6 of the Naples Underground
The Naples Underground Line 6 is a part of the public railway network provided by the Municipal Plan of Transportation for the Metropolitan Area of Naples (Italy) [
33]. The Santa Maria Della Vittoria church with a width of 17.3 m is located next to the path of the Line 6 tunnel, which was excavated between 2009 and 2011. Field measurements were conducted on the front façade of the church. The overburden depth (
H) = 13.225 m, the tunnel diameter (
D) = 8.15 m, and the eccentricity (
e) = 12.6 m, while the contraction coefficient was (
C) = 0.3%. The equation gives a result that is fairly close to the field measurements of the maximum settlement of the church, see
Figure 23.
- -
Comparison Based on the Centrifuge Tests
The results of the centrifuge test series for the tunnel in regular dense dry silica sand performed by Ritter et al. [
34,
35], at 75 g, were considered. A structure on strip footings affected by tunneling was tested in 1/75th scale models. The dimensions corresponding to the prototype scale (1/75th) are as follows: the tunnel diameter (
D) = 6.2 m, the cover-to-diameter ratio (
H/D) = 1.3, and the overburden depth (
H) = 8.2 m. The contraction coefficient is (
C) = 1% [
36].
Table 10 shows the parameters used for each test.
Figure 24 confirms that the equation results are in good agreement with the results of the centrifuge test.