Shear Behavior of Recycled Coarse Aggregates Concrete Dry Joints Keys Using Digital Image Correlation Technique
Abstract
1. Introduction
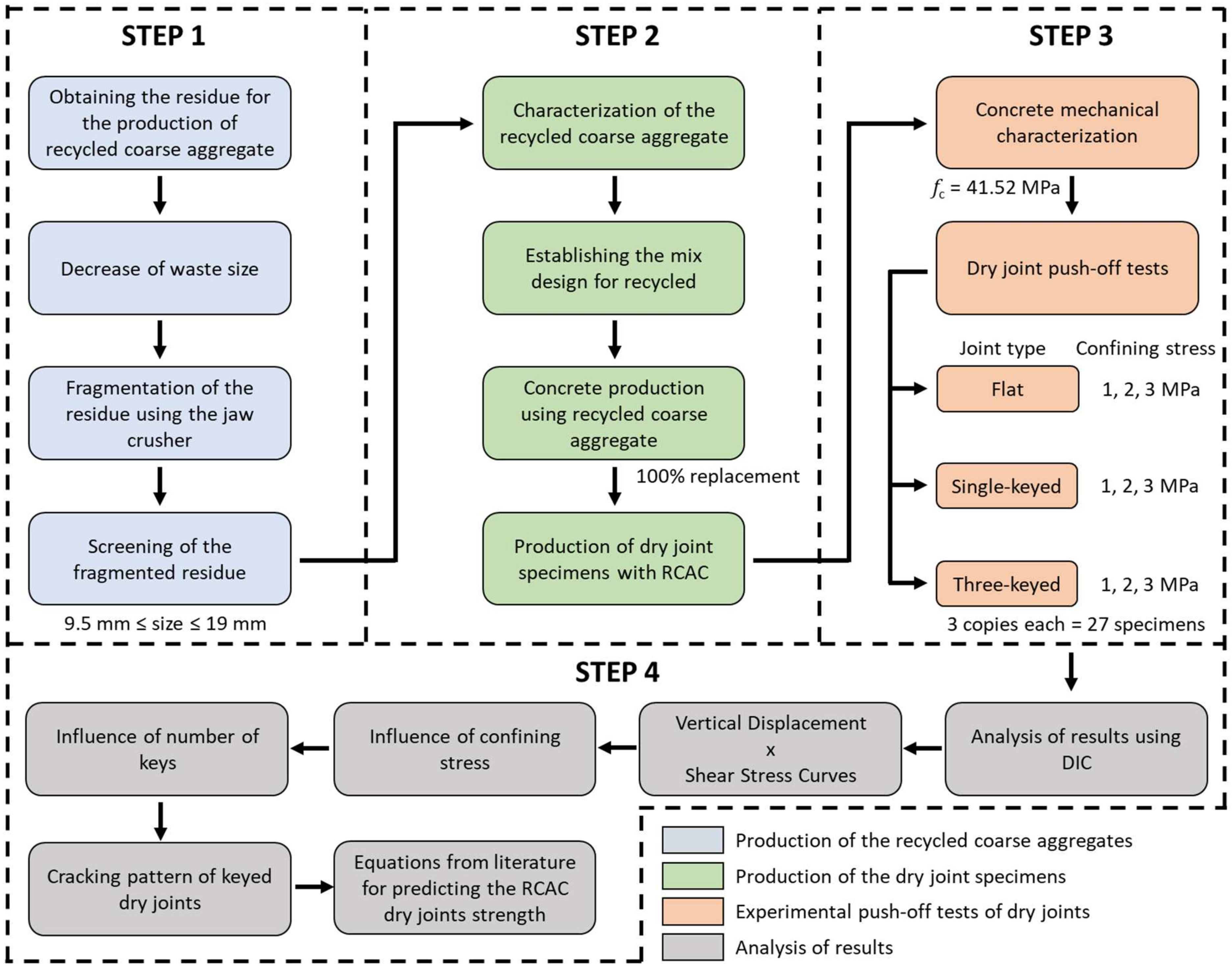
2. Materials and Methods
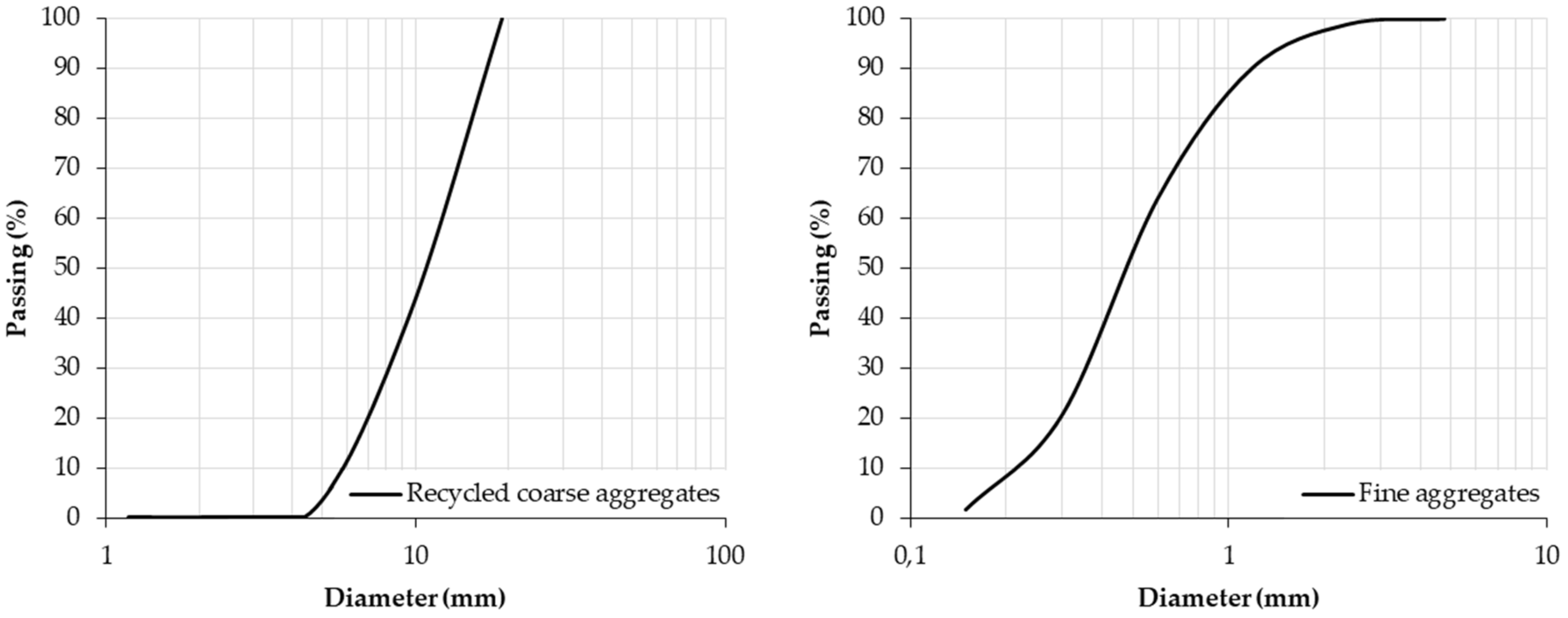
2.1. Materials
2.2. Concrete Proportioning
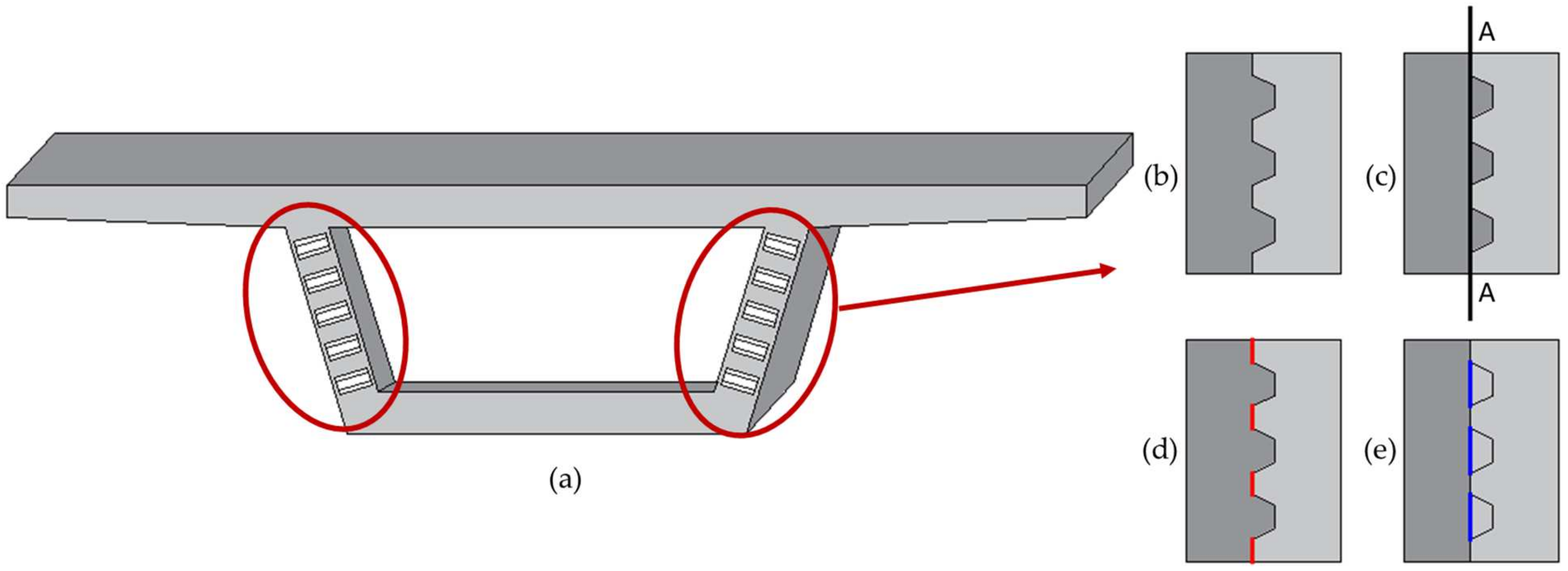
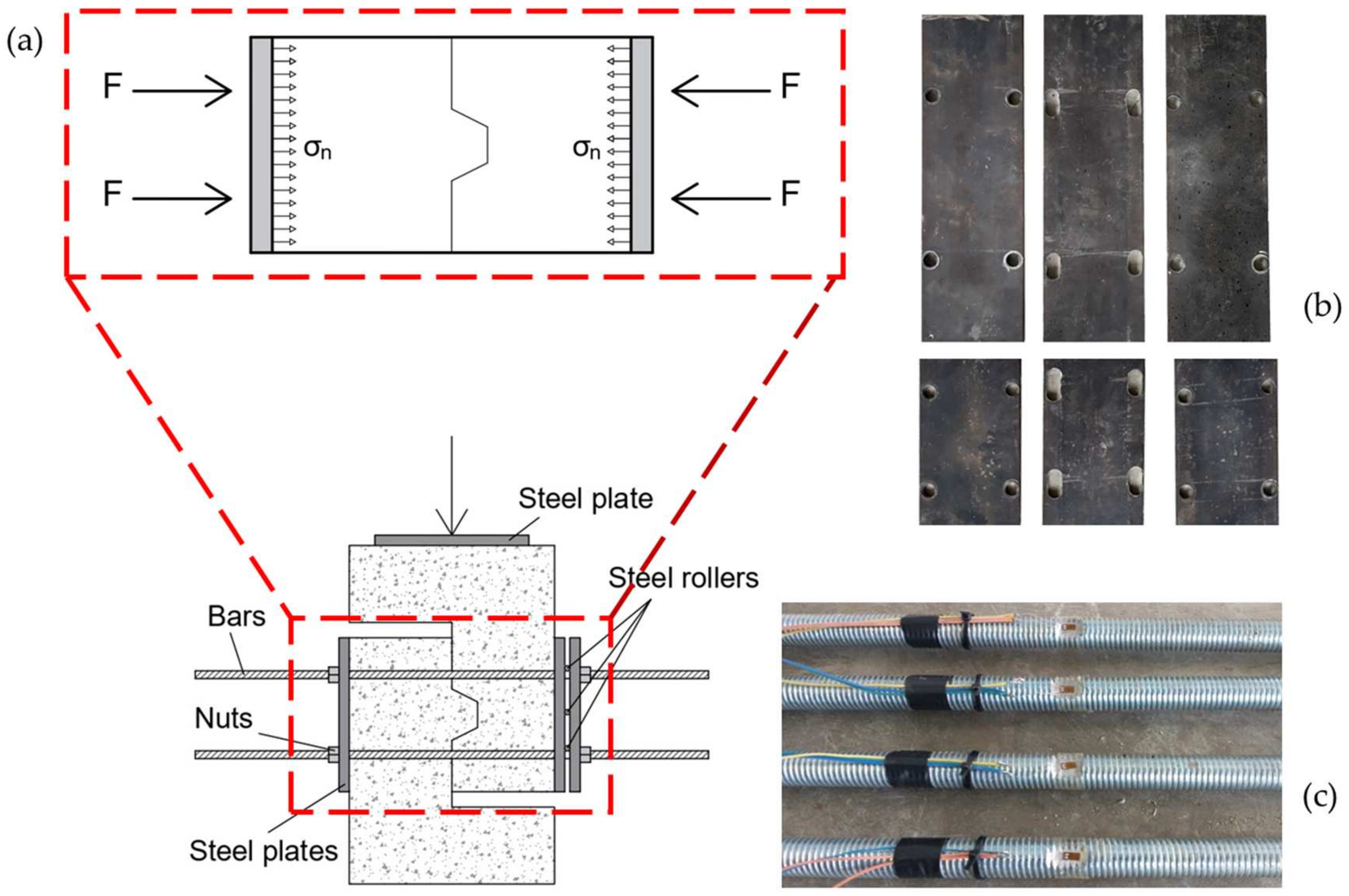
2.3. Details of Specimens
2.4. Details of Specimens
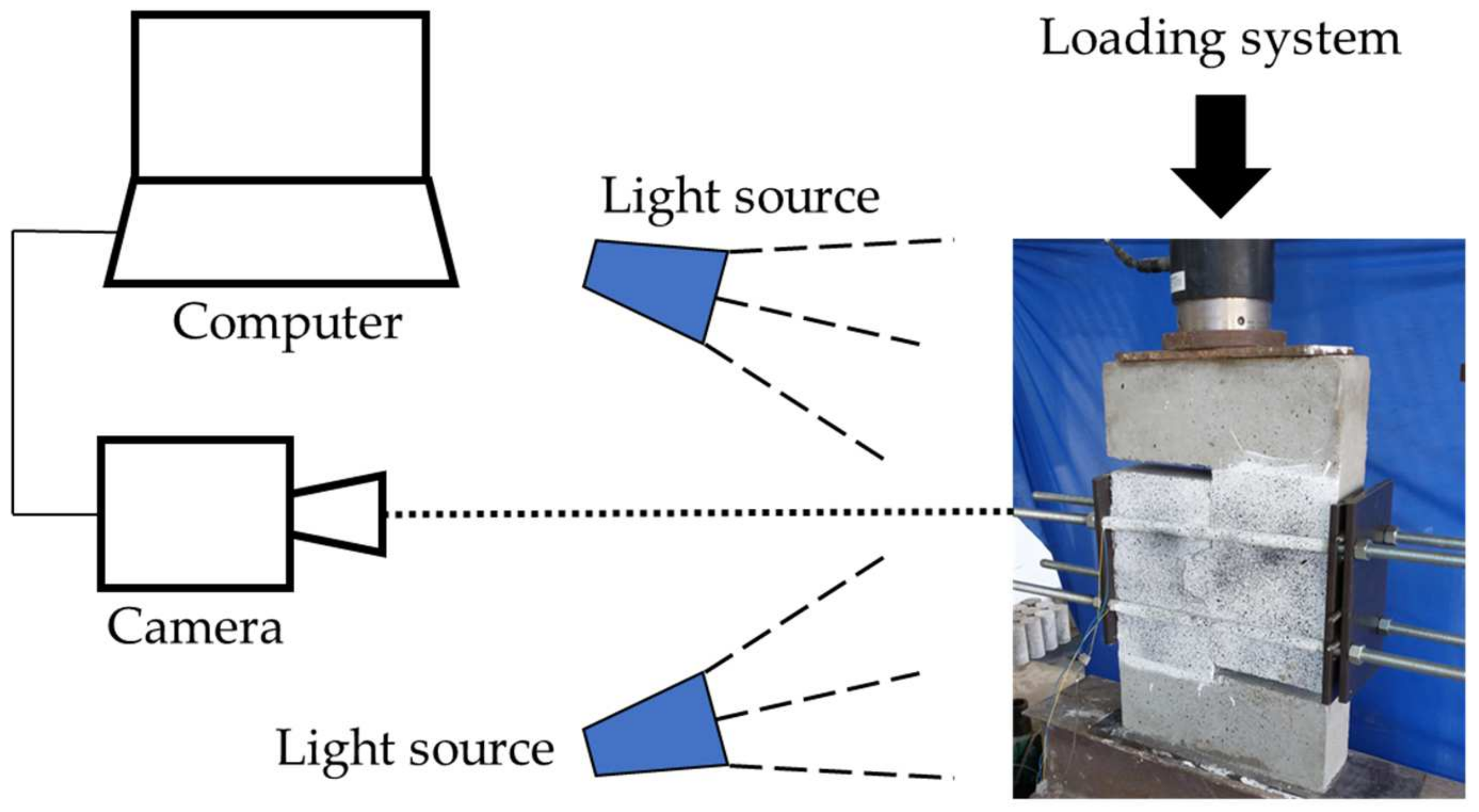
2.5. Setup and Instrumentation
2.6. Digital Image Correlation Technique
3. Results and Discussion
3.1. Shear Strength of RAC Dry Joints
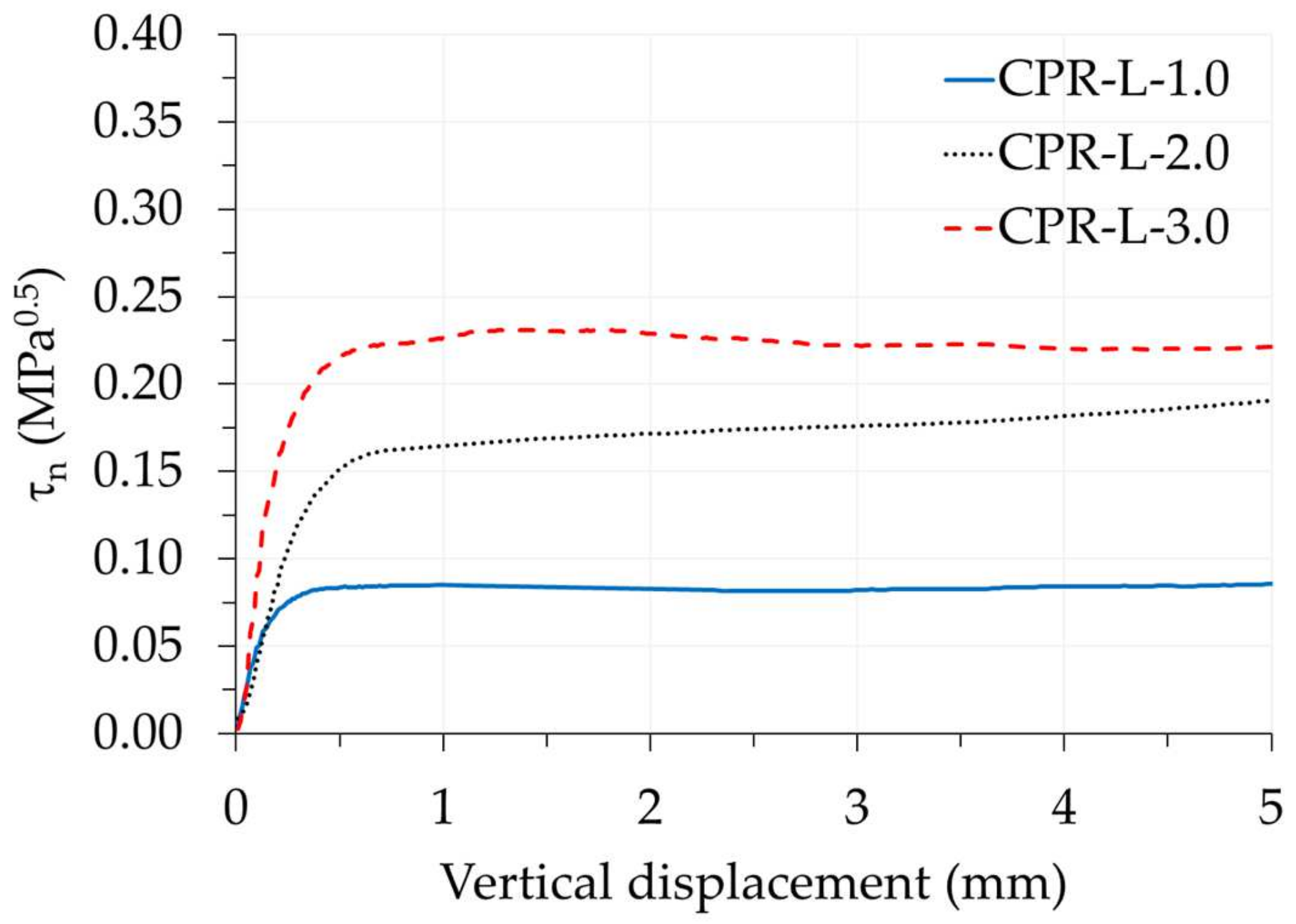
3.1.1. Flat Dry Joints
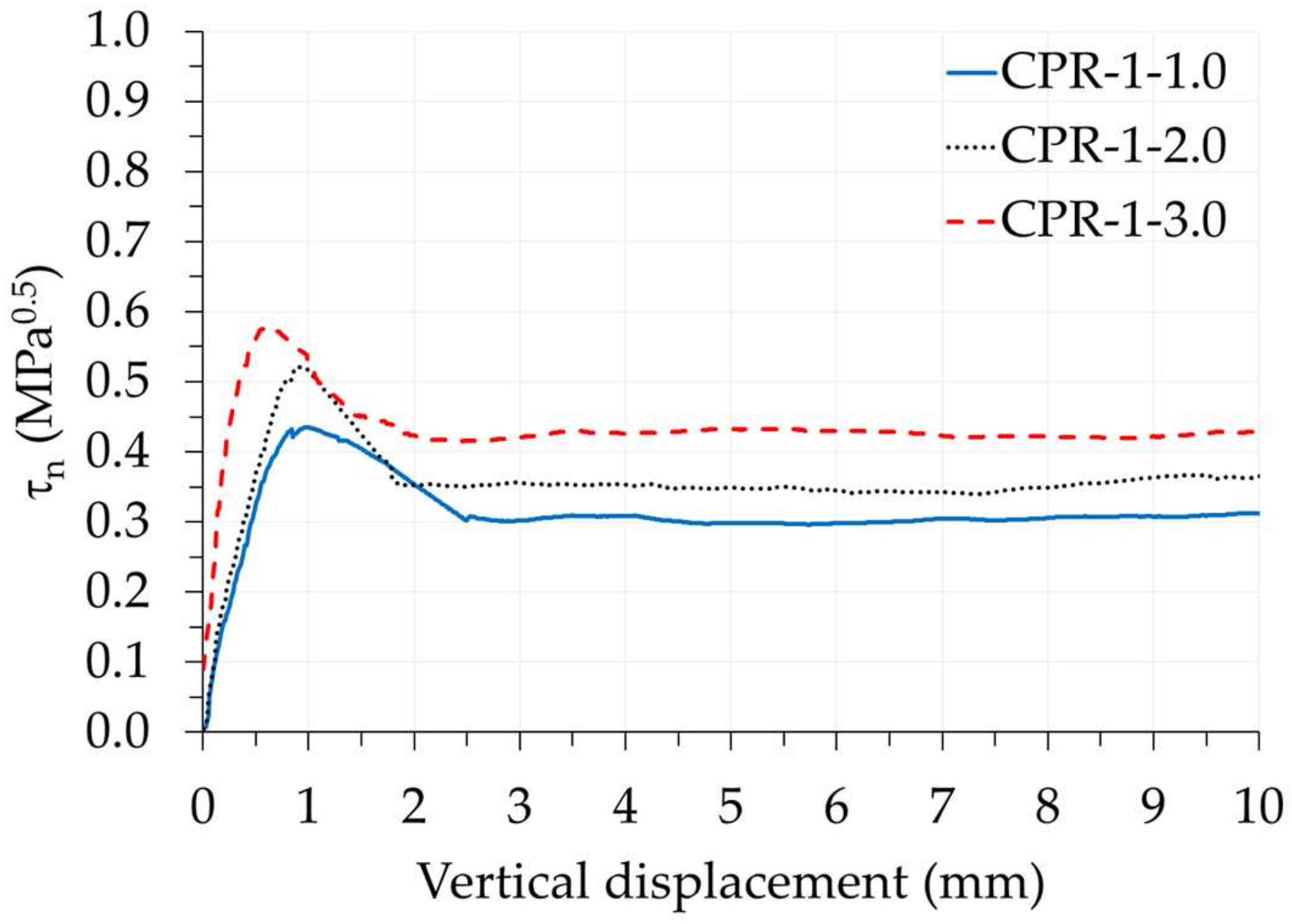
3.1.2. Single-Keyed Dry Joints
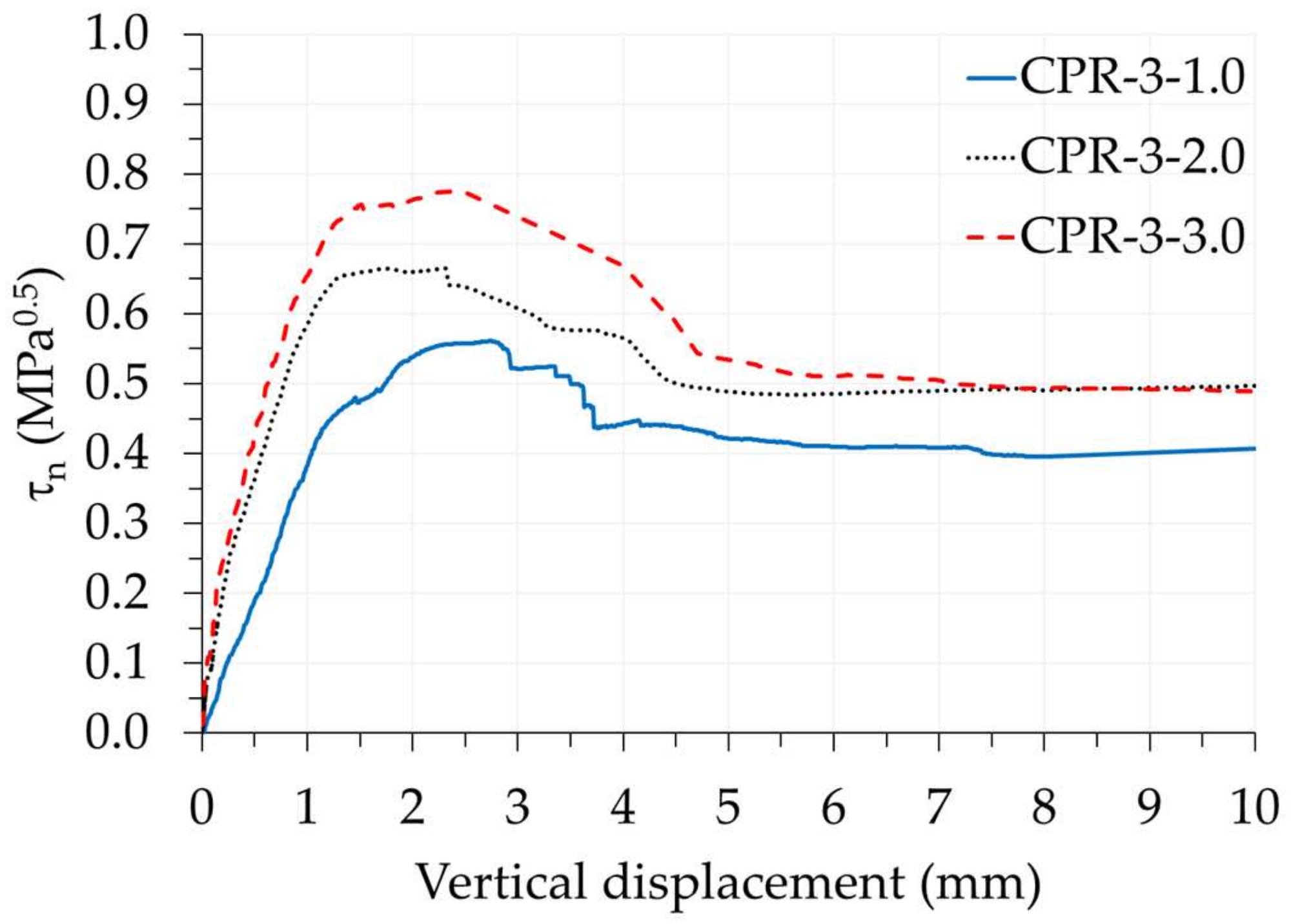
3.1.3. Three-Keyed Dry Joints
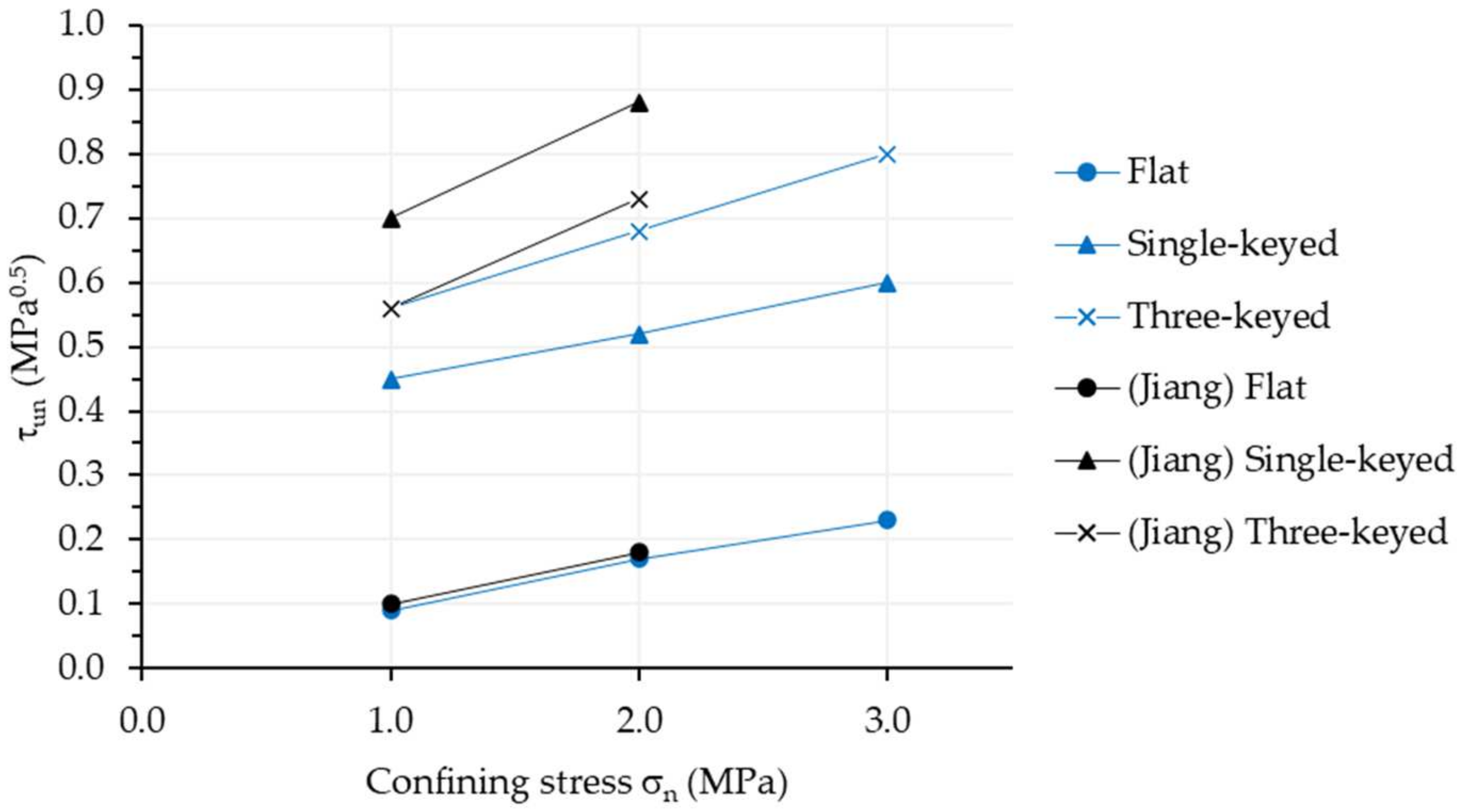
3.2. Influence of the Confining Stress
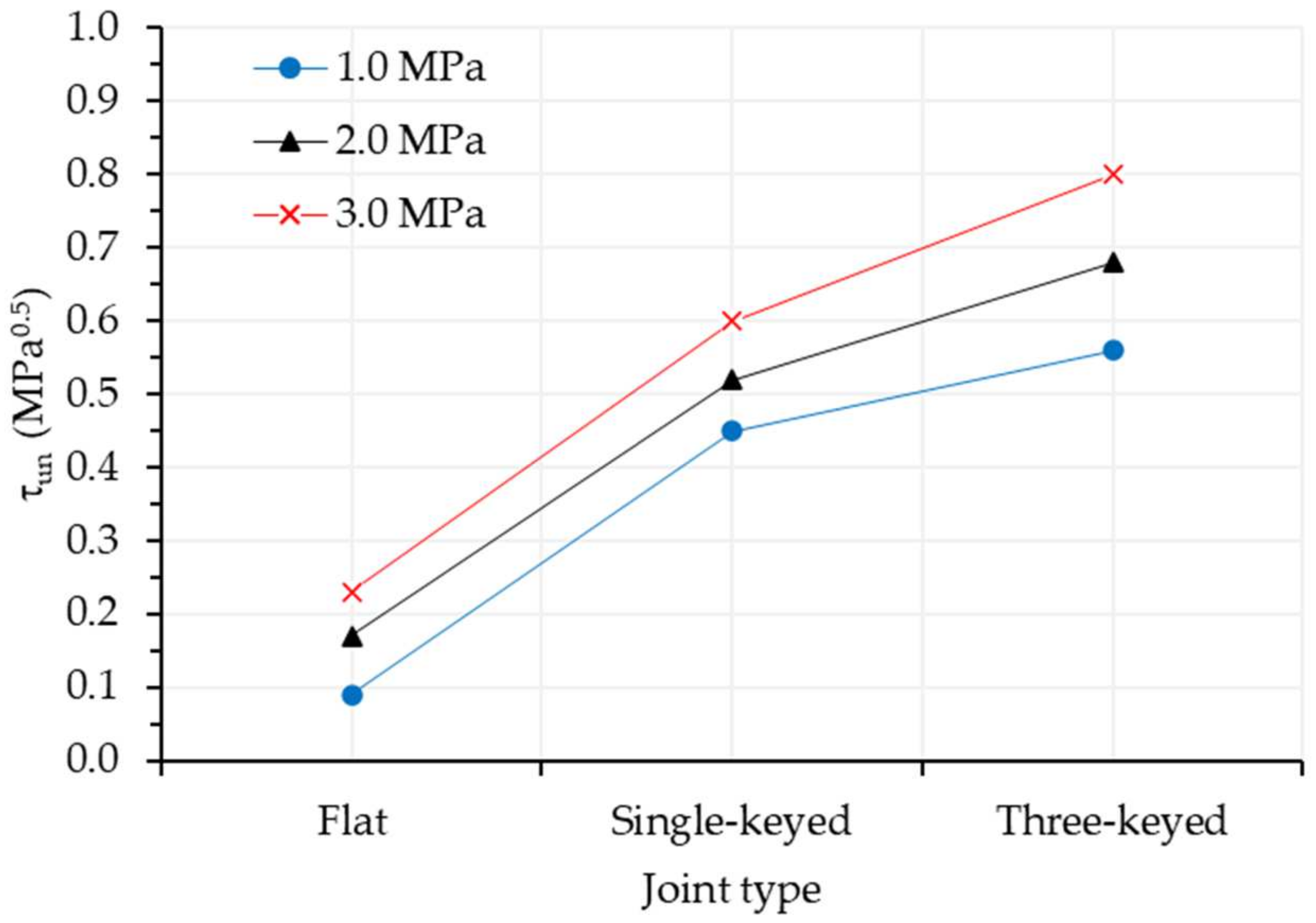
3.3. Influence of the Number of Keys
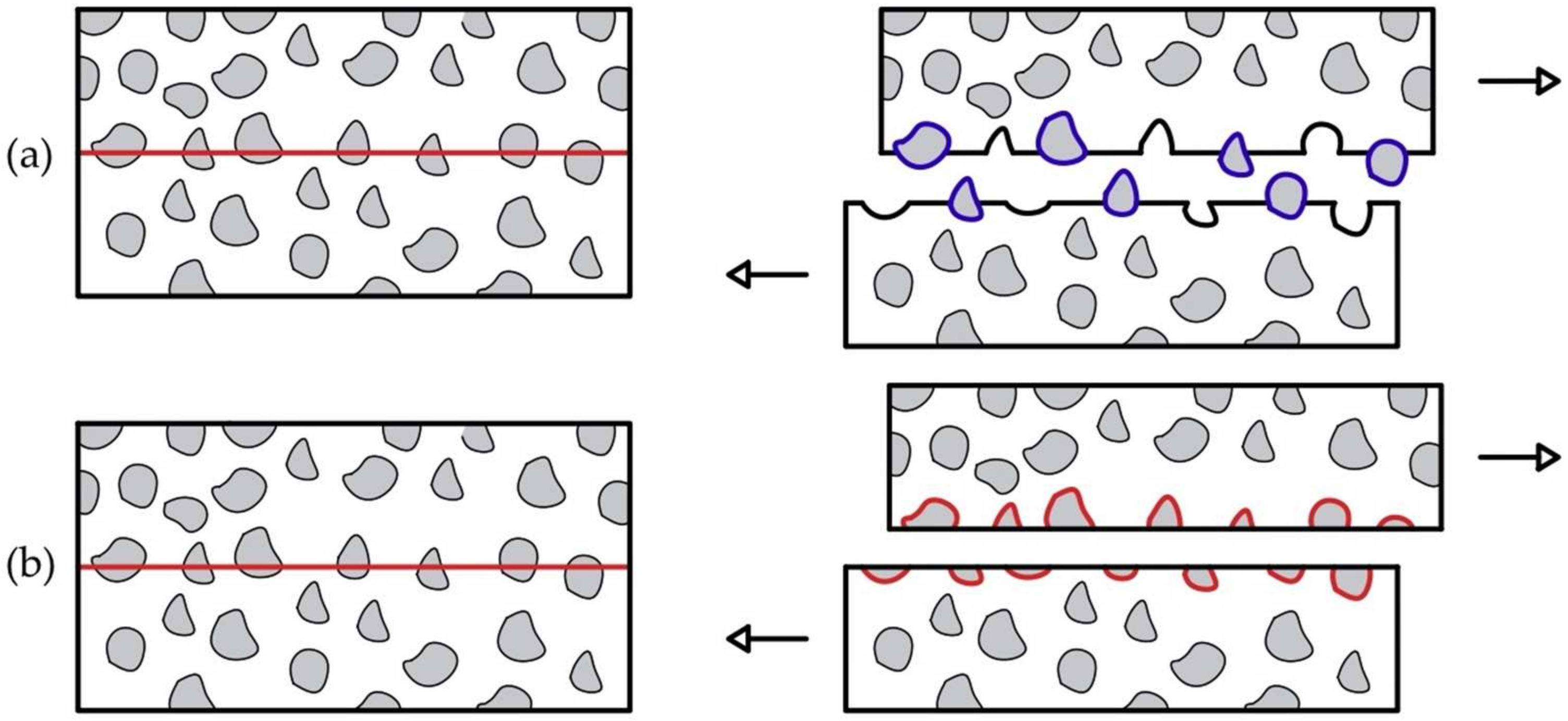
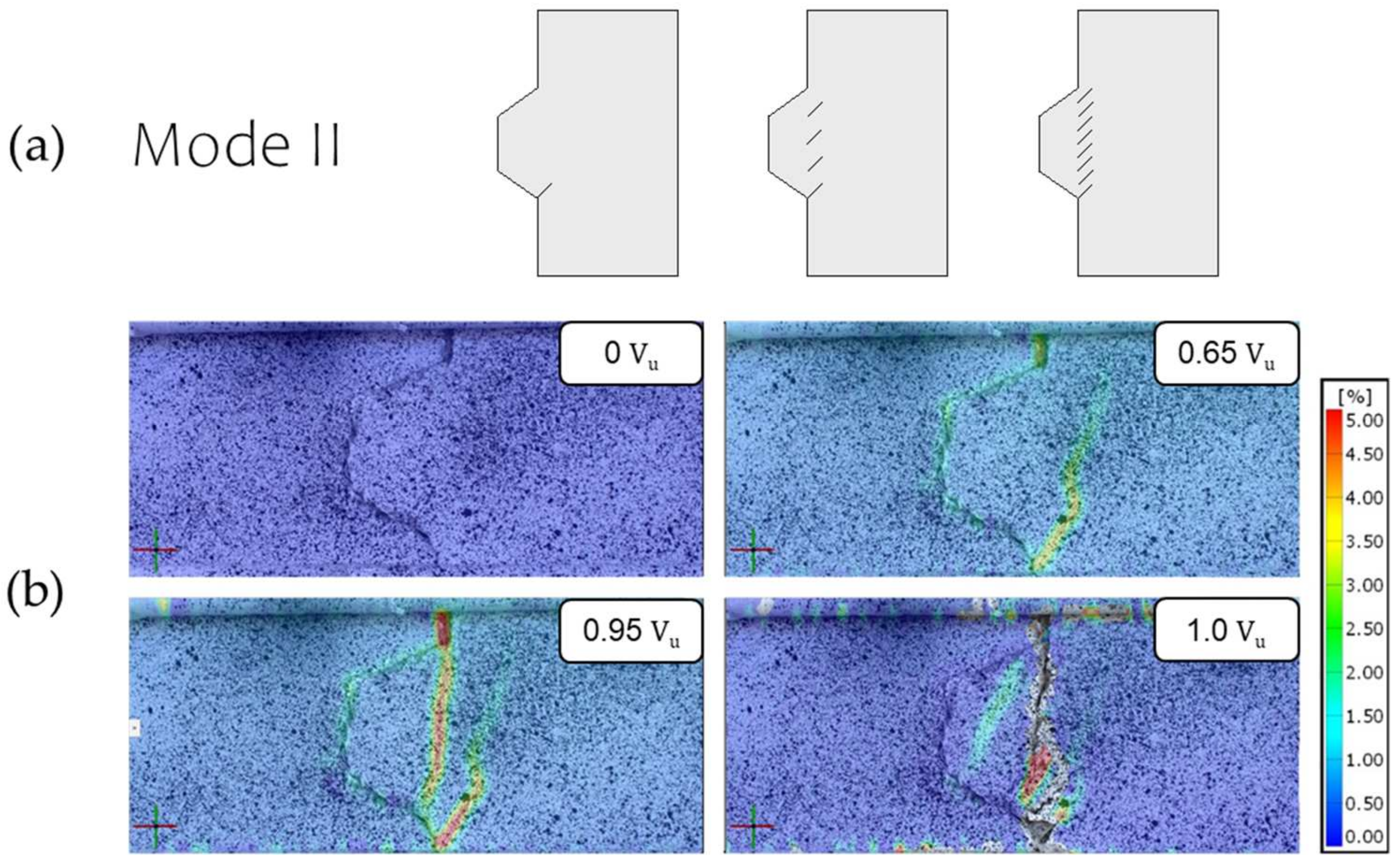
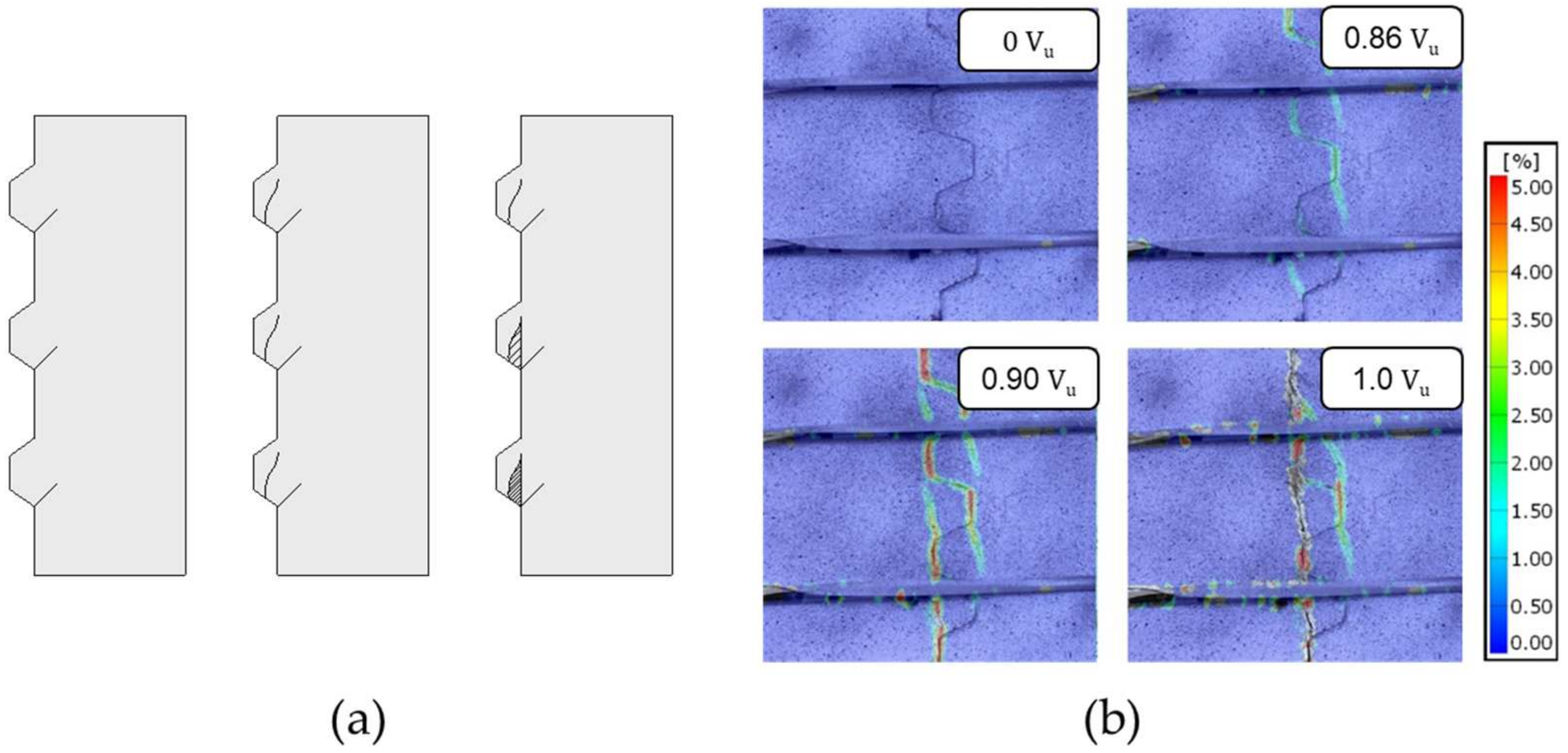
3.4. Cracking Pattern of Keyed Dry Joints Specimens
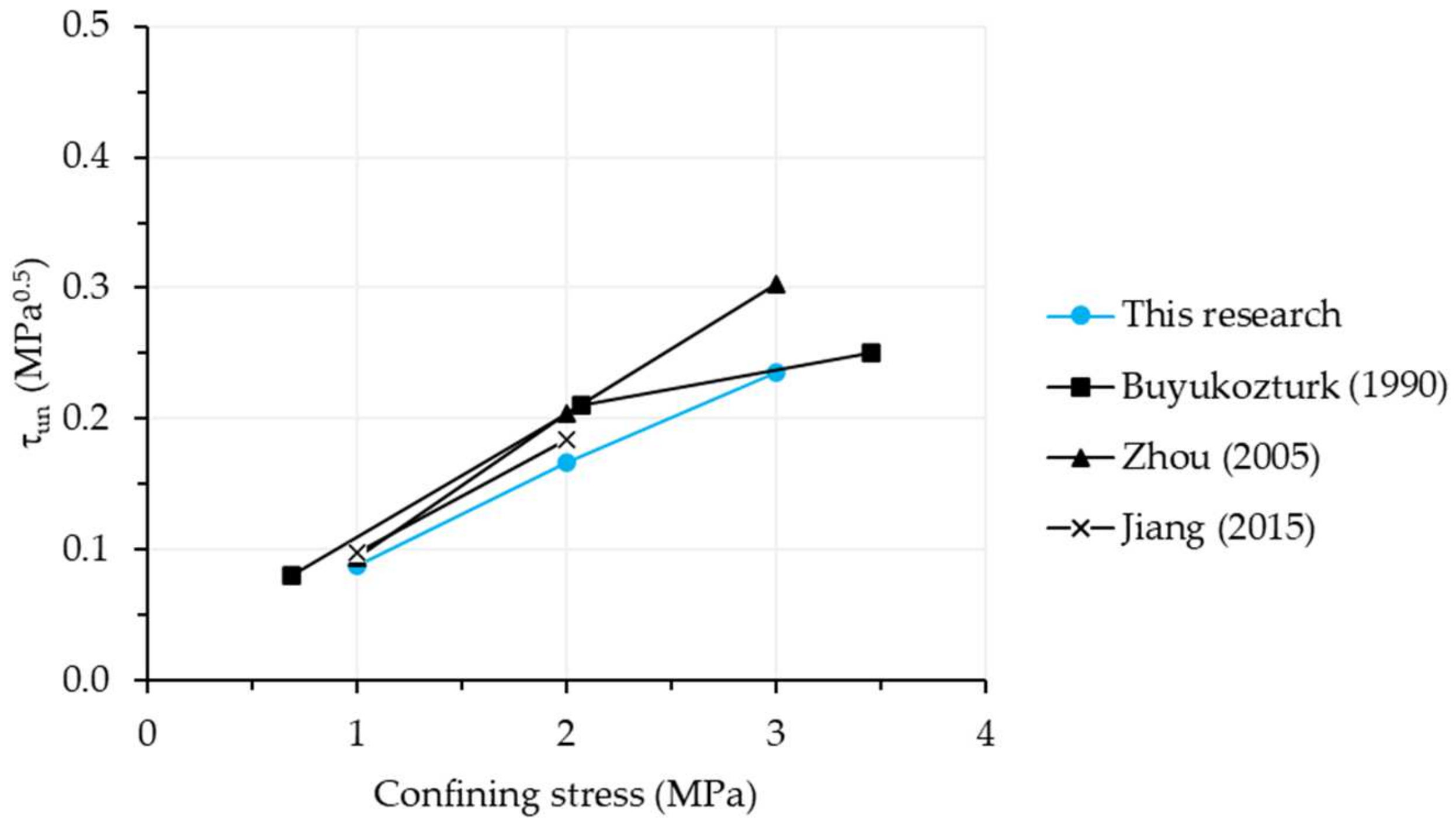
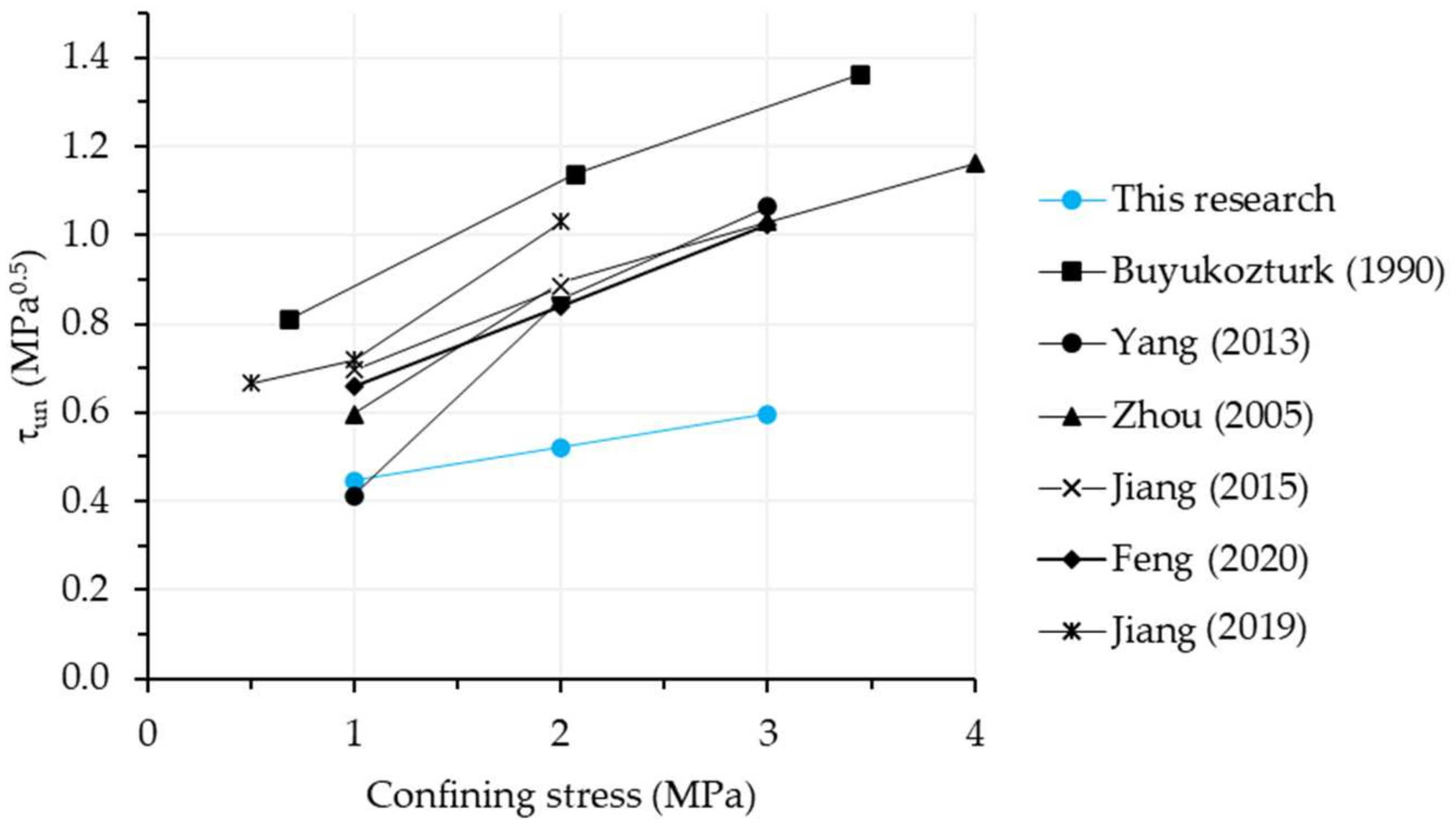
3.5. Comparison between the Results of This Research with Those of Other Researchers
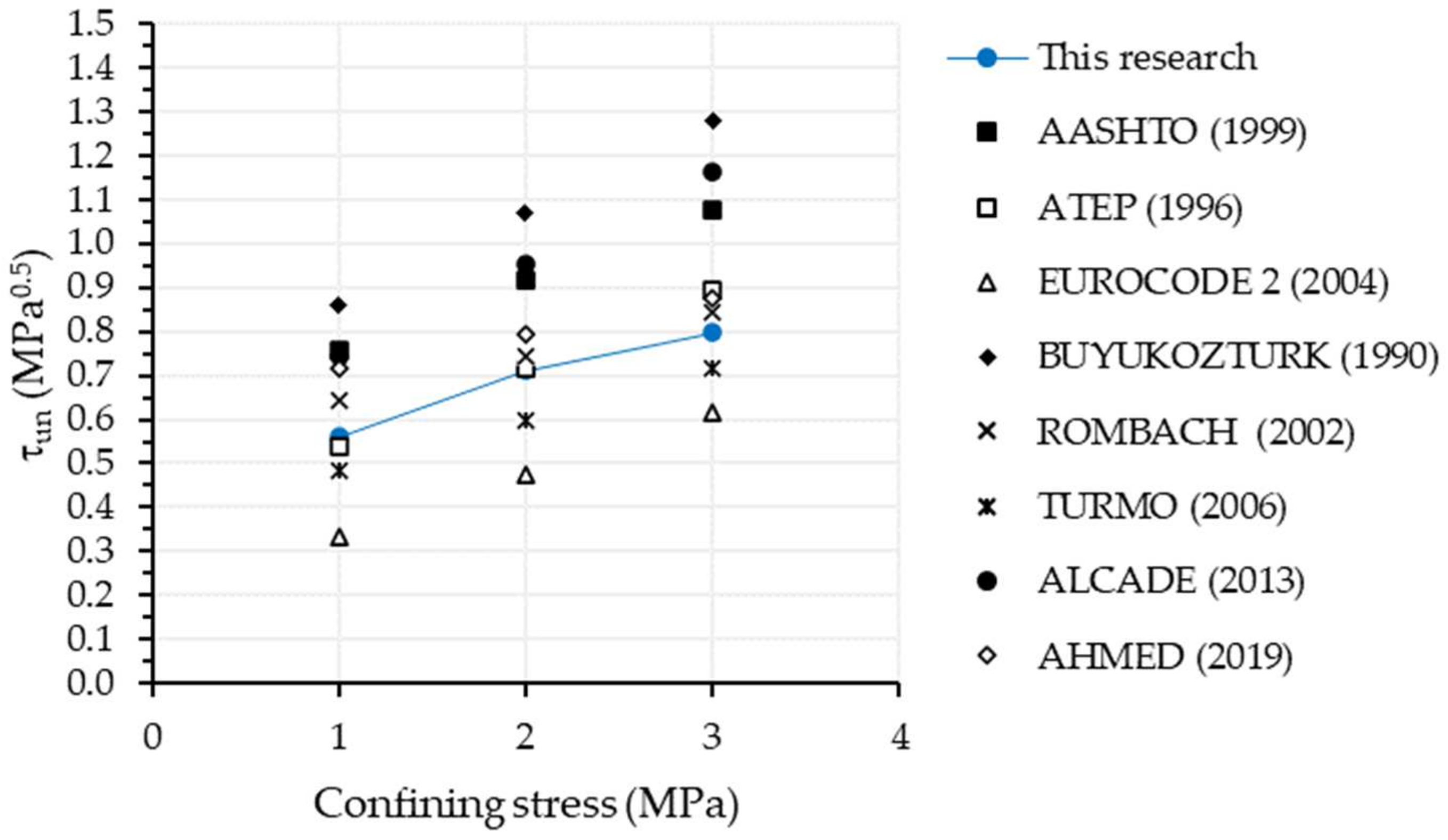
3.6. Equations for Predicting the Strength of RAC Dry Joints
4. Conclusions
- The dry joints produced with recycled coarse aggregates concrete showed similar behavior during the push-off test as those produced with conventional concrete. The failure of RAC joints was caused by the formation of a crack at the base of the shear keys, at an angle of approximately 45 degrees to the horizontal plane. With increasing load, additional cracks appeared in the shear plane of the keys, leading to the ultimate rupture when the cracks cut through the key. The cracking of single-keyed dry joint specimens with recycled coarse aggregates concrete followed model 2 as presented by Jiang et al. [30]. The cracking of the three-keyed dry joint specimens with recycled coarse aggregates concrete showed the cracking pattern in a sequence of the shear keys, as seen in previous work;
- The normalized shear strength of dry joints with recycled coarse aggregates concrete was lower when compared to the results of other researchers obtained with conventional concrete. The results of this study indicate that, although RAC concrete is less resistant than conventional concrete, its load versus vertical slip curves display similar trends. Furthermore, a reduction in the normalized shear stress was observed for smooth joints, with decreases of 10%, 18%, and 22% for the confining stresses of 1.0, 2.0, and 3.0 MPa, respectively. Single-key joints exhibited a greater reduction, with decreases of 38%, 49%, and 44%. The three-keys joints showed the least difference between results, with reductions of 6% and 8% for the confining stresses of 1.0 and 2.0 MPa, respectively. This is likely due to the rupture effect in sequence of the keys, which does not permit the full strength of the keys in the joint;
- The confining stress proved an essential resistance mechanism for dry joints with recycled coarse aggregate concrete. When the confinement stress of the smooth joints was increased from 1.0 MPa to 2.0 MPa, the strength gain was 88.89%, and from 2.0 MPa to 3.0 MPa, it was 35.29%. For the joint with keys, when the confinement stress was increased from 1.0 MPa to 2.0 MPa, the strength gain was 15.56% for one key and 21.43% for three keys. Furthermore, when the confinement stress increased from 2.0 MPa to 3.0 MPa, the strength gain was 15.38% for one key and 17.65% for three keys;
- The number of keys influenced the resistance of the dry joints, and its increase was beneficial for the final resistance of the joint. When the number of keys increased from none to single-keyed, the strength gain was 400%, 205.88%, and 160.87% for the confining stresses of 1.0, 2.0, and 3.0 MPa, respectively. When the number of keys increased from single-keyed to three-keyed, the strength gain was 24.44%, 30.77%, and 33.33% for the confining stresses of 1.0, 2.0, and 3.0 MPa, respectively;
- Equations of the literature used to predict the maximum load on dry joints with recycled coarse aggregates concrete showed safe values. The results showed that for single-keyed RAC dry joints, the equations of Turmo et al. [20], Rombach and Specker [19], and EUROCODE 2 [24] provided conservative values, while for the three-keyed RAC dry joints were those of Turmo et al. [20] and EUROCODE 2 [24];
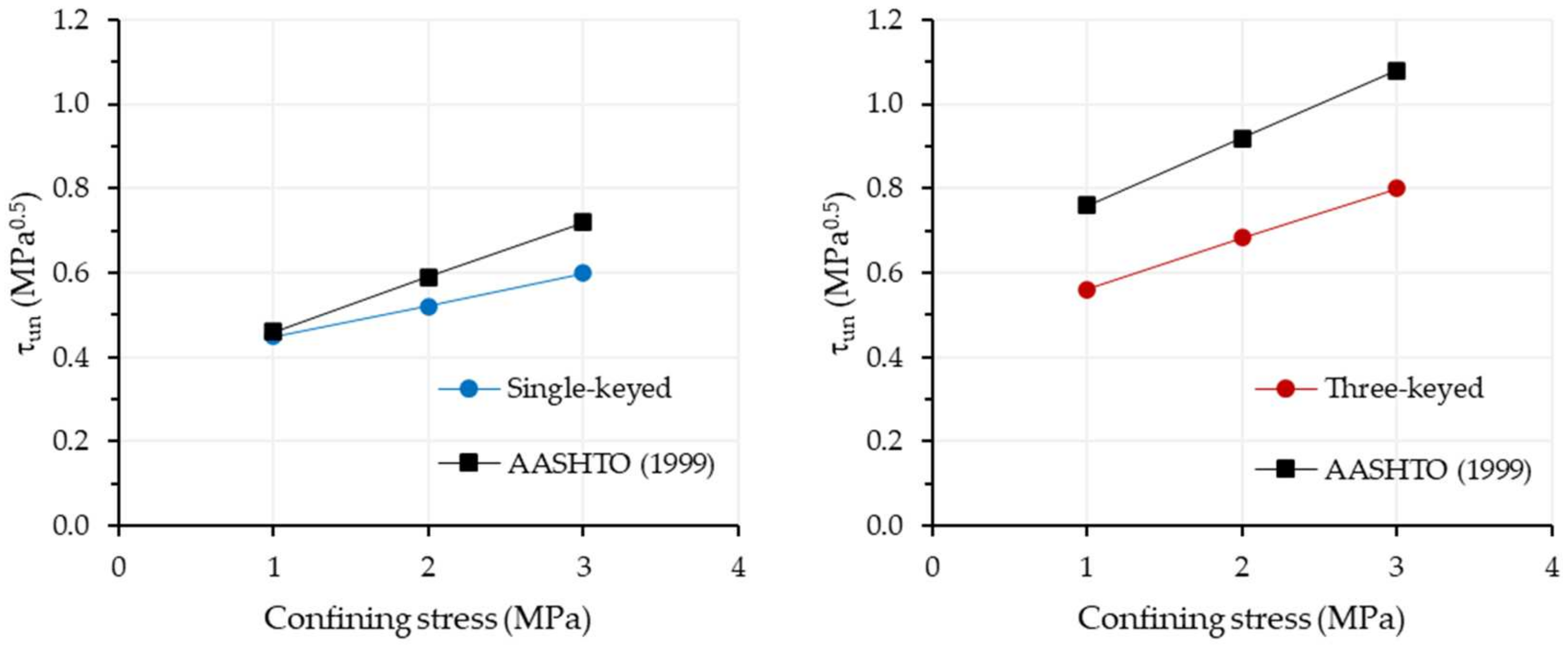
- The normative equation of AASHTO [21] satisfactorily predicted the strength of the single-keyed dry joint with recycled coarse aggregates concrete for the confining stress of 1.0 MPa; however, as the confining stress increased, the experimental results deviated from the forecast. For joints with three keys, the experimental results showed values far from the normative prediction;
- The authors recommend the consideration of a minimization coefficient in the AASHTO [21] normative equation in the value of 0.7 for the prediction of recycled coarse aggregates concrete dry joints.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cantero, B.; Bravo, M.; Brito, J.; Sáez del Bosque, I.F.; Medina, C. Mechanical Behaviour of Structural Concrete with Ground Recycled Concrete Cement and Mixed Recycled Aggregate. J. Clean. Prod. 2020, 275, 122913. [Google Scholar] [CrossRef]
- Pani, L.; Francesconi, L.; Rombi, J.; Mistretta, F.; Sassu, M.; Stochino, F. Effect of Parent Concrete on the Performance of Recycled Aggregate Concrete. Sustainability 2020, 12, 9399. [Google Scholar] [CrossRef]
- Naouaoui, K.; Bouyahyaoui, A.; Cherradi, T. Experimental Characterization of Recycled Aggregate Concrete. MATEC Web Conf. 2019, 303, 05004. [Google Scholar] [CrossRef]
- Liu, B.; Feng, C.; Deng, Z. Shear Behavior of Three Types of Recycled Aggregate Concrete. Constr. Build. Mater. 2019, 217, 557–572. [Google Scholar] [CrossRef]
- Patil, S.V.; Rao, K.B.; Nayak, G. Influence of Silica Fume on Mechanical Properties and Microhardness of Interfacial Transition Zone of Different Recycled Aggregate Concretes. Adv. Civ. Eng. Mater. 2021, 10, 412–426. [Google Scholar] [CrossRef]
- Silva, R.V.; Brito, J. Reinforced Recycled Aggregate Concrete Slabs: Structural Design Based on Eurocode 2. Eng. Struct. 2020, 204, 110047. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, Y.; Yin, F. A Practical Equation for the Elastic Modulus of Recycled Aggregate Concrete. Buildings 2022, 12, 187. [Google Scholar] [CrossRef]
- Khatab, M.A.T.; Altmami, M. Correlation between Different Properties of Recycled Aggregate and Recycled Aggregate Concrete. AIP Conf. Proc. 2019, 2146, 020005. [Google Scholar] [CrossRef]
- Meddah, M.S.; Al-Harthy, A.; Ismail, M.A. Recycled Concrete Aggregates and Their Influences on Performances of Low and Normal Strength Concretes. Buildings 2020, 10, 167. [Google Scholar] [CrossRef]
- Lavado, J.; Bogas, J.; de Brito, J.; Hawreen, A. Fresh Properties of Recycled Aggregate Concrete. Constr. Build. Mater. 2020, 233, 117322. [Google Scholar] [CrossRef]
- Feng, W.; Tang, Y.; Yang, Y.; Cheng, Y.; Qiu, J.; Zhang, H.; Isleem, H.F.; Tayeh, B.A.; Namdar, A. Mechanical Behavior and Constitutive Model of Sustainable Concrete: Seawater and Sea-Sand Recycled Aggregate Concrete. Constr. Build. Mater. 2023, 364, 130010. [Google Scholar] [CrossRef]
- Birkeland, P.W.; Birkeland, H.W. Connections in Precast Concrete Construction. ACI J. Proc. 1966, 63, 345–368. [Google Scholar] [CrossRef]
- Buyukozturk, O.; Bakhoum, M.M.; Beattie, S.M. Shear Behavior of Joints in Precast Concrete Segmental Bridfes. J. Struct. Eng. 1990, 116, 3380–3401. [Google Scholar] [CrossRef]
- Xiao, J.; Sun, C.; Lange, D.A. Effect of Joint Interface Conditions on Shear Transfer Behavior of Recycled Aggregate Concrete. Constr. Build. Mater. 2016, 105, 343–355. [Google Scholar] [CrossRef]
- ACI 213R–03; Guide for Structural Lightweight-Aggregate Concrete. ACI Concrete Institute: Farmington Hills, MI, USA, 2014.
- Greene, G.; Graybeal, B. Lightweight Concrete: Mechanical Properties; Report No. Federal Highway Administration-HRT-13-062; McLean: Washington, DC, USA, 2013. [Google Scholar]
- Greene, G.; Graybeal, B. Lightweight Concrete: Shear Performance; Report No. Federal Highway Administration-HRT-15-022; McLean: Washington, DC, USA, 2015. [Google Scholar]
- Ahmed, G.H.; Aziz, O.Q. Shear Strength of Joints in Precast Posttensioned Segmental Bridges during 1959–2019, Review and Analysis. Structures 2019, 20, 527–542. [Google Scholar] [CrossRef]
- Rombach, G.; Specker, A. Design of Joints in Segmental Hollow Box Girder Bridges. In Proceedings of the 1st FIB Kongress, Osaka, Japan, 13–19 October 2002; pp. 1–6. [Google Scholar]
- Turmo, J.; Ramos, G.; Aparicio, A.C. Resistencia de Juntas Secas Conjugadas de Puentes de Dovelas Prefabricadas de Hormigón: Propuesta Para El Eurocódigo 2. Mater. Constr. 2006, 56, 45–52. [Google Scholar] [CrossRef]
- AASHTO. Guide Specifications for Design and Construction of Segmental Concrete Bridges; AASHTO GSCB: Washington, DC, USA, 1999. [Google Scholar]
- Alcalde, M.; Cifuentes, H.; Medina, F. Influencia Del Número de Llaves En La Resistencia a Cortante de Juntas Secas Postensadas. Mater. Constr. 2013, 63, 297–307. [Google Scholar] [CrossRef]
- ATEP Proyecto y Construcción de Puentes y Estructuras Con Pretensado Exterior. Col. Ing. Caminos, Canales y Puertos, Madrid. 1996. H.P.10-96 vol E-6. Available online: https://books.google.co.jp/books/about/Proyecto_y_construcci%C3%B3n_de_puentes_y_es.html?id=l_QDPgAACAAJ&redir_esc=y (accessed on 1 March 2023).
- EN 1992-1-1:2004; EUROCODE 2 Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Commission: Brussels, Belgium, 2004.
- Fonteboa, G.; Martínez, F.; Carro, D.; Eiras, J. Cortante-Fricción de Los Hormigones Reciclados. Mater. Constr. 2010, 60, 53–67. [Google Scholar] [CrossRef]
- Xiao, J.; Xie, H.; Yang, Z. Shear Transfer across a Crack in Recycled Aggregate Concrete. Cem. Concr. Res. 2012, 42, 700–709. [Google Scholar] [CrossRef]
- Rahal, K. Shear Strength of Recycled Aggregates Concrete. Procedia Eng. 2017, 210, 105–108. [Google Scholar] [CrossRef]
- Trindade, J.; Garcia, S.; Fonseca, G. Experimental Study of Direct Shear in Concrete with Recycled Aggregate. ACI Struct. J. 2020, 17, 233–243. [Google Scholar]
- Trindade, J.; Garcia, S.L.; Torres, H. Shear Strength of Concrete with Recycled Aggregates Reinforced with Steel Fibers. ACI Mater. J. 2021, 118, 185–198. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, L.; Ma, Z.J.; Feng, W. Shear Behavior of Dry Joints with Castellated Keys in Precast Concrete Segmental Bridges. J. Bridg. Eng. 2015, 20, 1–12. [Google Scholar] [CrossRef]
- ABNT NBR 11578:1991; Cimento Portland Composto. ABNT: São Paulo, Brazil, 1991.
- ABNT NBR NM 52; Agregado Miúdo—Determinação Da Massa Específica e Massa Específica Aparente. ABNT: São Paulo, Brazil, 2003.
- ABNT NBR NM 53; Agregado Graúdo—Determinação de Massa Específica, Massa Específica Aparente e Absorção de Água. ABNT: São Paulo, Brazil, 2002.
- EN 1097-1:2011; Ensayos Para Determinar Las Propriedades Mecánicas y Físicas de Los Áridos. Asociación Española de Normalización y Certificación: Madrid, Spain, 2011.
- Bazuco, R.S. Utilização de Agregados Reciclados de Concreto Para a Produção de Novos Concretos. Master’s Thesis, Universidade Federal de Santa Catarina, Florianópolis, Brazil, 1999. [Google Scholar]
- ABNT NBR 5739; Concreto—Ensaio de Compressão de Corpos de Prova Cilíndricos. ABNT: São Paulo, Brazil, 2018.
- ABNT NBR 7222; Concreto e Argamassa—Determinação Da Resistência à Tração Por Compressão Diametral de Corpos de Prova Cilíndricos. ABNT: São Paulo, Brazil, 2011.
- ABNT NBR 8522; Concreto—Determinação Dos Módulos Estáticos de Elasticidade e de Deformação à Compressão. ABNT: São Paulo, Brazil, 2017.
- ABNT NBR 9778; Argamassa e Concreto Endurecidos—Determinação Da Absorção de Água, Índice de Vazios e Massa Específica. ABNT: São Paulo, Brazil, 2009.
- Zhou, X.; Mickleborough, N.; Li, Z. Shear Strength of Joints in Precast Concrete Segmental Bridges. ACI Struct. J. 2005, 102, 901–904. [Google Scholar]
- Yang, I.H.; Kim, K.C.; Kim, Y.J. Shear Strength of Dry Joints in Precast Concrete Modules. In Proceedings of the 13th East Asia-Pacific Conference on Structural Engineering and Construction, EASEC-13, Sapporo, Japan, 11–13 September 2013. [Google Scholar]
- Liu, T.; Wang, Z.; Guo, J.; Wang, J. Shear Strength of Dry Joints in Precast UHPC Segmental Bridges: Experimental and Theoretical Research. J. Bridg. Eng. 2019, 24, 04018100. [Google Scholar] [CrossRef]
- Feng, J.; Liang, W.; Jiang, H.; Huang, C.; Zhang, J. Shear Performance of Single-Keyed Dry Joints between Reactive Power Concrete and High Strength Concrete in Push-off Tests. Sci. Prog. 2020, 103, 1–27. [Google Scholar] [CrossRef]
- Jiang, H.; Feng, J.; Liu, A.; Liang, W.; Tan, Y.; Liang, H. Effect of Specimen Thickness and Coarse Aggregate Size on Shear Strength of Single-Keyed Dry Joints in Precast Concrete Segmental Bridges. Struct. Concr. 2019, 20, 955–970. [Google Scholar] [CrossRef]
- 3D Metrology GOM Correlate 2020; Precise Industrial: Rockwood, TN, USA, 2020.
- Tang, Y.; Huang, Z.; Chen, Z.; Chen, M.; Zhou, H.; Zhang, H.; Sun, J. Novel Visual Crack Width Measurement Based on Backbone Double-Scale Features for Improved Detection Automation. Eng. Struct. 2023, 274, 115158. [Google Scholar] [CrossRef]
- Que, Y.; Dai, Y.; Ji, X.; Kwan Leung, A.; Chen, Z.; Tang, Y.; Jiang, Z. Automatic Classification of Asphalt Pavement Cracks Using a Novel Integrated Generative Adversarial Networks and Improved VGG Model. Eng. Struct. 2023, 277, 115406. [Google Scholar] [CrossRef]








| Author/Standard | Equation | |
|---|---|---|
| AASHTO (1999) [21] | (1) | |
| ATEP (1996) [23] | (2) | |
| EUROCODE 2 [24] | (3) | |
| Buyukozturk et al. (1990) [13] | (4) | |
| Rombach and Specker (2002) [19] | (5) | |
| Turmo et al. (2006) [20] | (6) | |
| Alcade et al. (2013) [22] | (7) | |
| Ahmed and Aziz (2019) [18] | (8) | |
| Variable | Notation | Description |
|---|---|---|
| Design Parameters | Maximum shear force (kN) | |
| Confining Stress (MPa) | ||
| Characteristic compressive strength of concrete (MPa) | ||
| Concrete compressive strength (MPa) | ||
| Design concrete compressive strength (MPa) | ||
| Concrete tensile strength (MPa) | ||
| Geometric characteristics | Total joint area (mm2) | |
| Area relative to the joint keys (mm2) | ||
| Area related to the flat part of the joint (mm2) | ||
| Number of keys | ||
| The factor relating to the key’s cutout equal to 0.14 |
| Specific Mass (g/cm3) [33] | Water Absorption (%) [33] | Abrasion Micro-Deval (%) [34] | Adhered Mortar (%) (Adapted from [35]) |
|---|---|---|---|
| 2.31 | 5.55 | 13.97 | 40.0 |
| Material | Quantities/m3 |
|---|---|
| Portland Cement CP2-E-32 | 513.59 kg |
| Fine aggregate | 735.85 kg |
| Recycled coarse aggregate | 904 kg |
| Water | 236.25 L |
| w/c | 0.46 |
| RAC Properties | Values | Standard Deviation | Coefficient of Variation (%) |
|---|---|---|---|
| Compressive strength [36] | 41.52 MPa | 6.00 MPa | 14.45 |
| Tensile strength [37] | 2.71 MPa | 0.21 MPa | 7.75 |
| Modulus of Elasticity [38] | 34.65 GPa | 5.34 GPa | 15.41 |
| Density [39] | 2450 kg/m3 | 20 kg/m3 | 0.82 |
| Water absorption [39] | 7.38% | 0.63% | 8.54 |
| Specimen | Joint Type | Shear Area (mm2) | Confining Stress (MPa) |
|---|---|---|---|
| CPR-L-1.0 | Flat | 30,000 | 1.0 |
| CPR-L-2.0 | 2.0 | ||
| CPR-L-3.0 | 3.0 | ||
| CPR-1-1.0 | Single-keyed | 30,000 | 1.0 |
| CPR-1-2.0 | 2.0 | ||
| CPR-1-3.0 | 3.0 | ||
| CPR-3-1.0 | Three-keyed | 50,000 | 1.0 |
| CPR-3-2.0 | 2.0 | ||
| CPR-3-3.0 | 3.0 |
| Confinement Stress (MPa) | Deformation in the Bar (με) | Reaction Force (kN) |
|---|---|---|
| 1.0 | 114.71/191.18 | 7.50/12.5 |
| 2.0 | 229.41/382.35 | 15.0/25.0 |
| 3.0 | 344.12/573.53 | 22.5/37.5 |
| Specimens | Failure Load Vu (kN) | Maximum Shear Stress τu (MPa) | Normalized Cracking Shear Stress τnf (MPa0.5) | Maximum Normalized Shear Stress τun (MPa0.5) | Standard Deviation (MPa) | Maximum Normalized Shear Stress τun,J (MPa0.5) |
|---|---|---|---|---|---|---|
| CPR-L-1.0 | 16.98 | 0.57 | - | 0.09 | 0.01 | 0.10 |
| CPR-L-2.0 | 32.01 | 1.07 | - | 0.17 | 0.02 | 0.18 |
| CPR-L-3.0 | 45.31 | 1.51 | - | 0.23 | 0.02 | - |
| CPR-1-1.0 | 86.18 | 2.87 | 0.20 | 0.45 | 0.03 | 0.70 |
| CPR-1-2.0 | 104.89 | 3.50 | 0.28 | 0.52 | 0.01 | 0.88 |
| CPR-1-3.0 | 115.11 | 3.84 | 0.35 | 0.60 | 0.01 | - |
| CPR-3-1.0 | 180.34 | 3.61 | 0.45 | 0.56 | 0.03 | 0.56 |
| CPR-3-2.0 | 228.89 | 4.58 | 0.62 | 0.68 | 0.04 | 0.73 |
| CPR-3-3.0 | 256.60 | 5.13 | 0.72 | 0.80 | 0.07 | - |
| Joint | σn (MPa) | τun/τun,J |
|---|---|---|
| Flat | 1 | 0.90 |
| 2 | 0.94 | |
| Single-keyed | 1 | 0.64 |
| 2 | 0.59 | |
| Three-keyed | 1 | 1.00 |
| 2 | 0.93 |
| Paper | Joint Type | Concrete Strength Resistance (MPa) | Joint Width (mm) | Total Smooth Joint Area (mm2) | Total Monolithic Joint Area (mm2) | Total Joint Area (mm2) |
|---|---|---|---|---|---|---|
| Buyukozturk [13] | Flat | 47.37 | 76.2 | 5806.44 | - | 5806.44 |
| Single-keyed | 47.37 | 76.2 | 3992.9 | 7620 | 11,612.9 | |
| Zhou [40] | Flat | 52.2–52.8 | 250 | 50,000 | - | 50,000 |
| Single-keyed | 37.1–56.2 | 250 | 25,000 | 25,000 | 50,000 | |
| Three-keyed | 30.2–63.7 | 250 | 50,000 | 75,000 | 125,000 | |
| Yang [41] | Single-keyed | 60 | 100 | 10,000 | 7000 | 17,000 |
| Jiang [30] | Flat | 40.49 | 100 | 20,000 | - | 20,000 |
| Single-keyed | 41.51 | 100 | 10,000 | 10,000 | 20,000 | |
| Three-keyed | 41.82 | 100 | 20,000 | 30,000 | 50,000 | |
| Jiang [44] | Single-keyed | 41.03 | 100 | 10,000 | 10,000 | 20,000 |
| Liu [42] | Flat | 123.9–125.59 | 150 | 45,000 | - | 45,000 |
| Single-keyed | 123.9–125.59 | 150 | 30,000 | 15,000 | 45,000 | |
| Three-keyed | 123.6–124.66 | 150 | 30,000 | 45,000 | 75,000 | |
| Feng [43] | Single-keyed | 64.21 | 100 | 10,000 | 10,000 | 20,000 |
| Specimens | AASHTO 1 | ATEP 2 | EUR 3 | BUYU 4 | ROMB 5 | TURM 6 | ALCA 7 | AHMD 8 |
|---|---|---|---|---|---|---|---|---|
| CPR-1-1.0 | 1.04 | 1.21 | 0.75 | 1.92 | 0.90 | 0.70 | 1.41 | 1.09 |
| CPR-1-2.0 | 1.09 | 1.32 | 0.88 | 1.97 | 0.93 | 0.77 | 1.68 | 1.14 |
| CPR-1-3.0 | 1.21 | 1.50 | 1.03 | 2.15 | 1.01 | 0.88 | 2.01 | 1.26 |
| CPR-3-1.0 | 1.35 | 0.97 | 0.60 | 1.53 | 1.15 | 0.86 | 1.33 | 1.28 |
| CPR-3-2.0 | 1.29 | 1.01 | 0.67 | 1.50 | 1.05 | 0.84 | 1.34 | 1.12 |
| CPR-3-3.0 | 1.35 | 1.12 | 0.77 | 1.61 | 1.06 | 0.90 | 1.46 | 1.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sousa, J.B.; Garcia, S.L.G.; Pierott, R.M.R. Shear Behavior of Recycled Coarse Aggregates Concrete Dry Joints Keys Using Digital Image Correlation Technique. Infrastructures 2023, 8, 60. https://doi.org/10.3390/infrastructures8030060
Sousa JB, Garcia SLG, Pierott RMR. Shear Behavior of Recycled Coarse Aggregates Concrete Dry Joints Keys Using Digital Image Correlation Technique. Infrastructures. 2023; 8(3):60. https://doi.org/10.3390/infrastructures8030060
Chicago/Turabian StyleSousa, Jedson Batista, Sergio Luis Gonzalez Garcia, and Rodrigo Moulin Ribeiro Pierott. 2023. "Shear Behavior of Recycled Coarse Aggregates Concrete Dry Joints Keys Using Digital Image Correlation Technique" Infrastructures 8, no. 3: 60. https://doi.org/10.3390/infrastructures8030060
APA StyleSousa, J. B., Garcia, S. L. G., & Pierott, R. M. R. (2023). Shear Behavior of Recycled Coarse Aggregates Concrete Dry Joints Keys Using Digital Image Correlation Technique. Infrastructures, 8(3), 60. https://doi.org/10.3390/infrastructures8030060





