Numerical Study of the Influence of the Interaction Distance, the Polymeric Strips Pre-Tensioning, and the Soil–Polymeric Interaction on the Performance of Back-to-Back Reinforced Soil Walls
Abstract
:1. Introduction
- ○
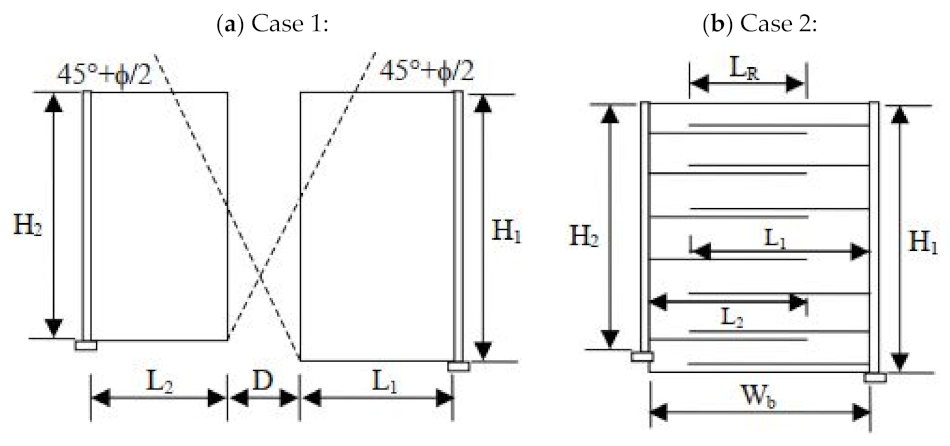
- Case 1: if the interaction distance Di between the back of the reinforced soil zone for opposite walls is less than the active zone:
- ○
- Case 2: there is an overlapping of the reinforcement layers such that the two walls interact with each other. When the overlap length (LR) is greater than 0.3H2, where H2 is the shorter of the walls, no active earth thrust from the backfill needs to be considered for external stability calculations.
- ○
- For intermediate geometries between cases 1 and 2, when:
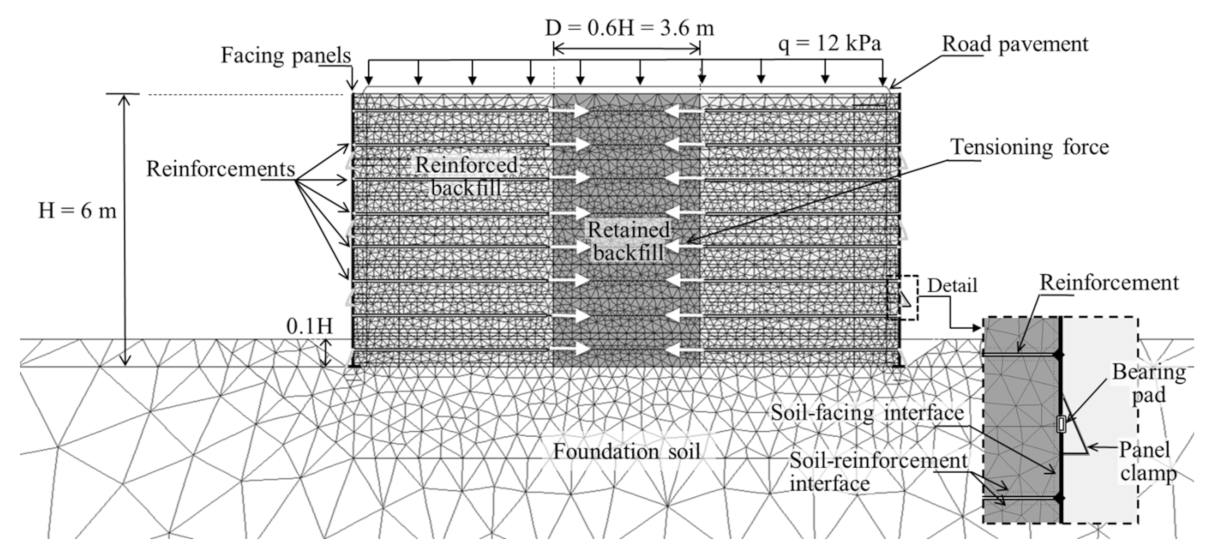
2. Finite Element Modeling
2.1. General
2.2. Soil and Road Pavement
2.3. Facing: Precast Panels and Bearing Pads
2.4. Reinforcement
2.5. Interface Properties and Boundary Conditions
2.6. Numerical Modeling Verification
3. Numerical Results and Discussion
3.1. General
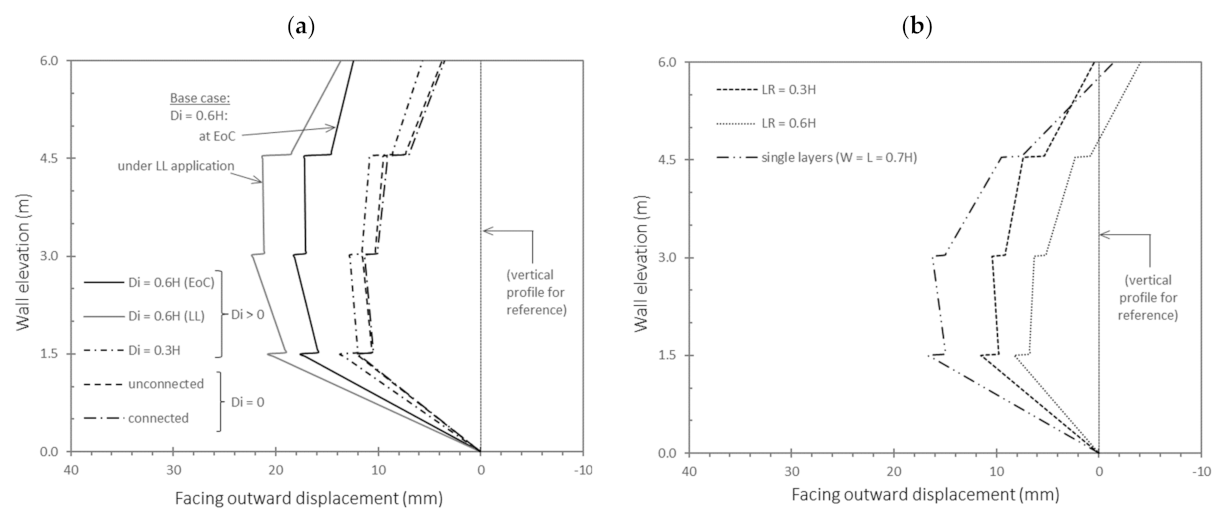
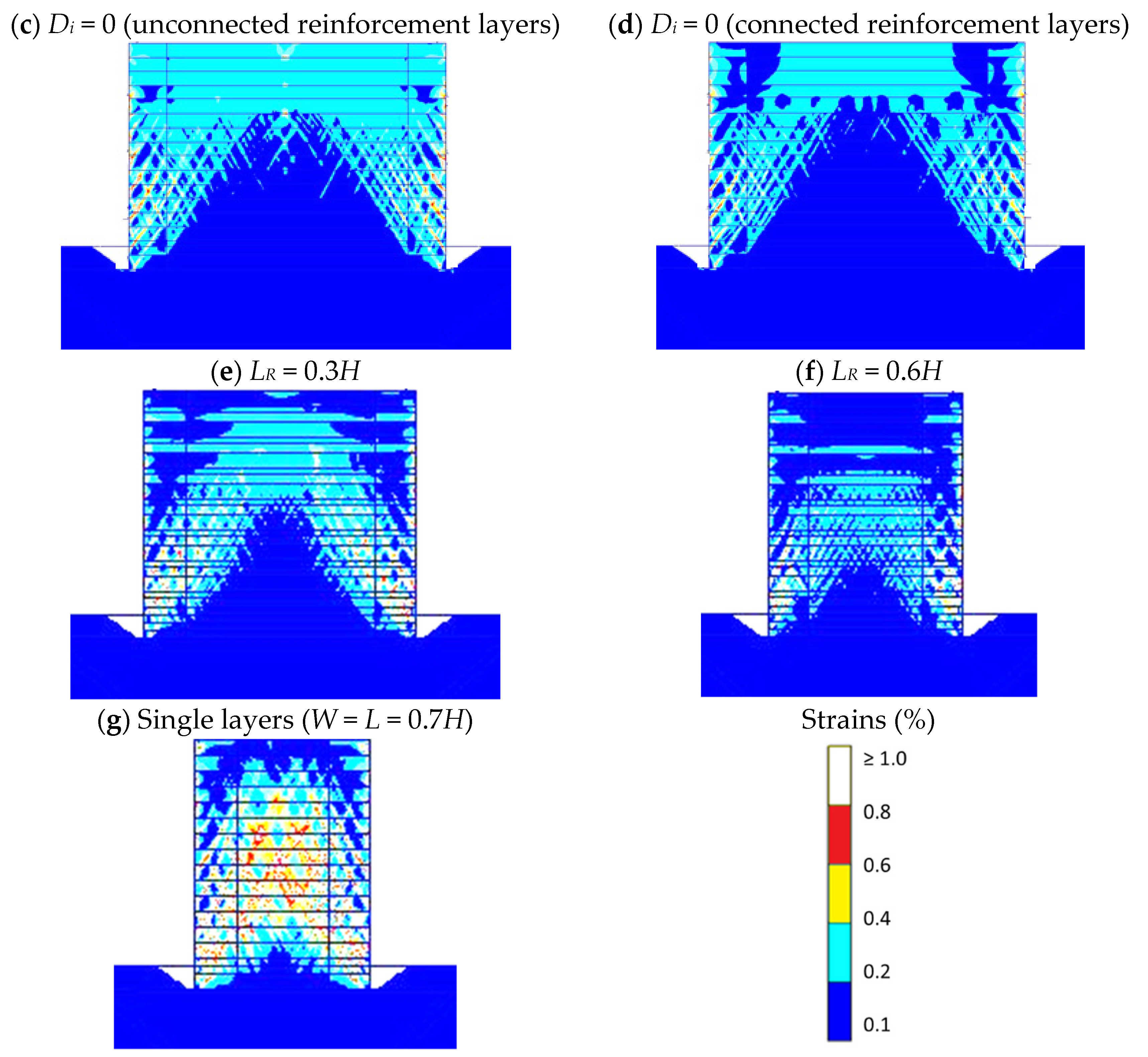
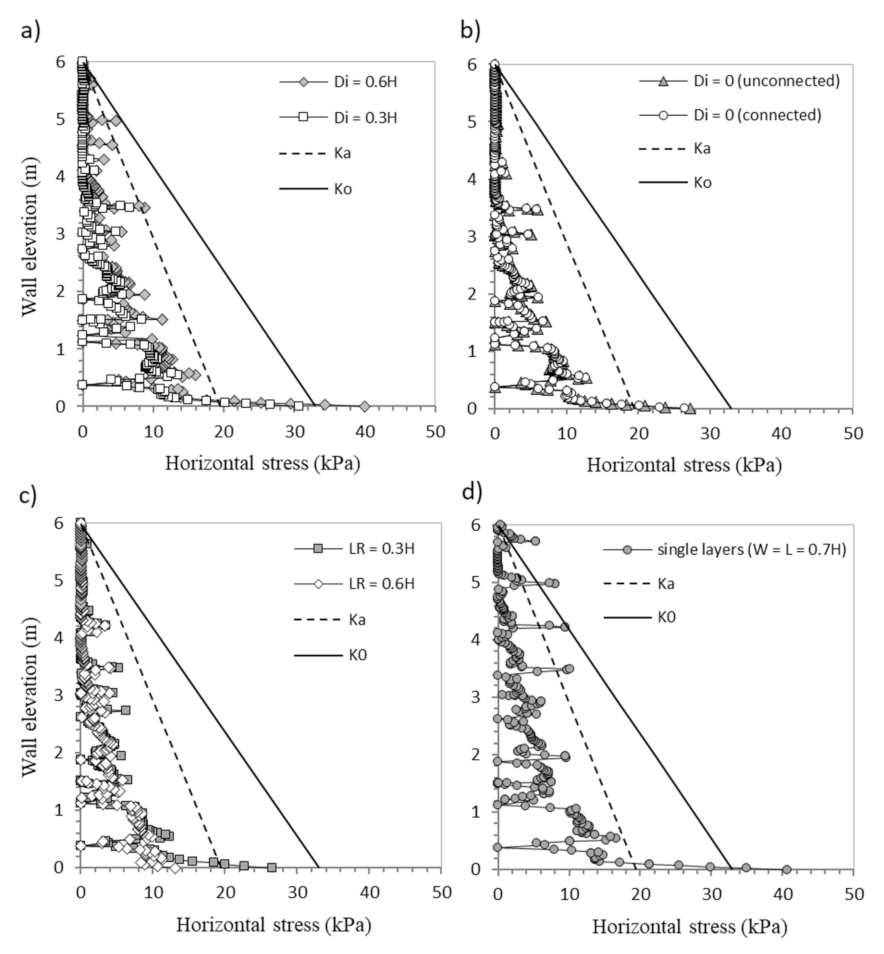
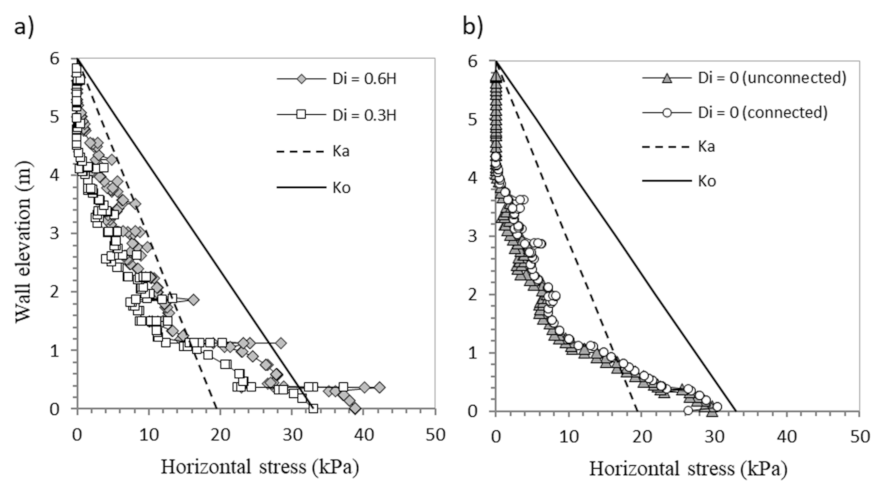
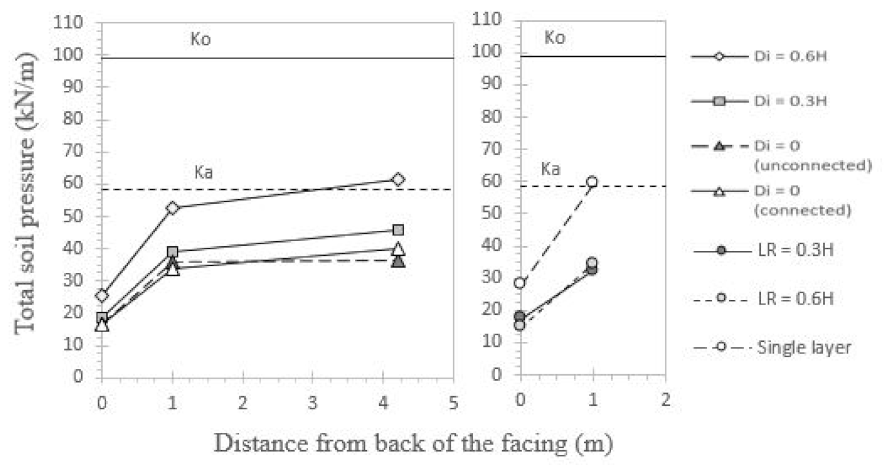
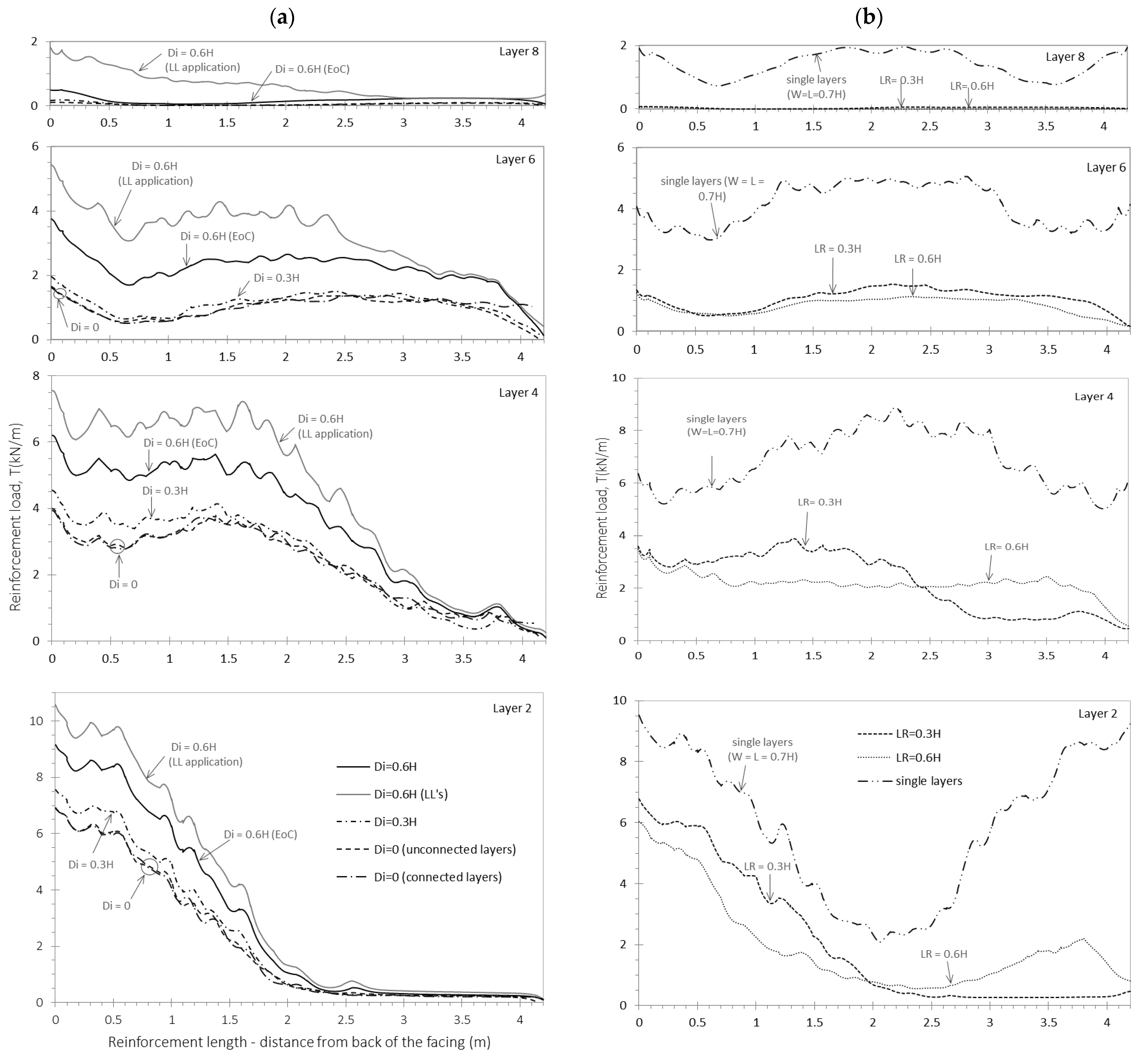
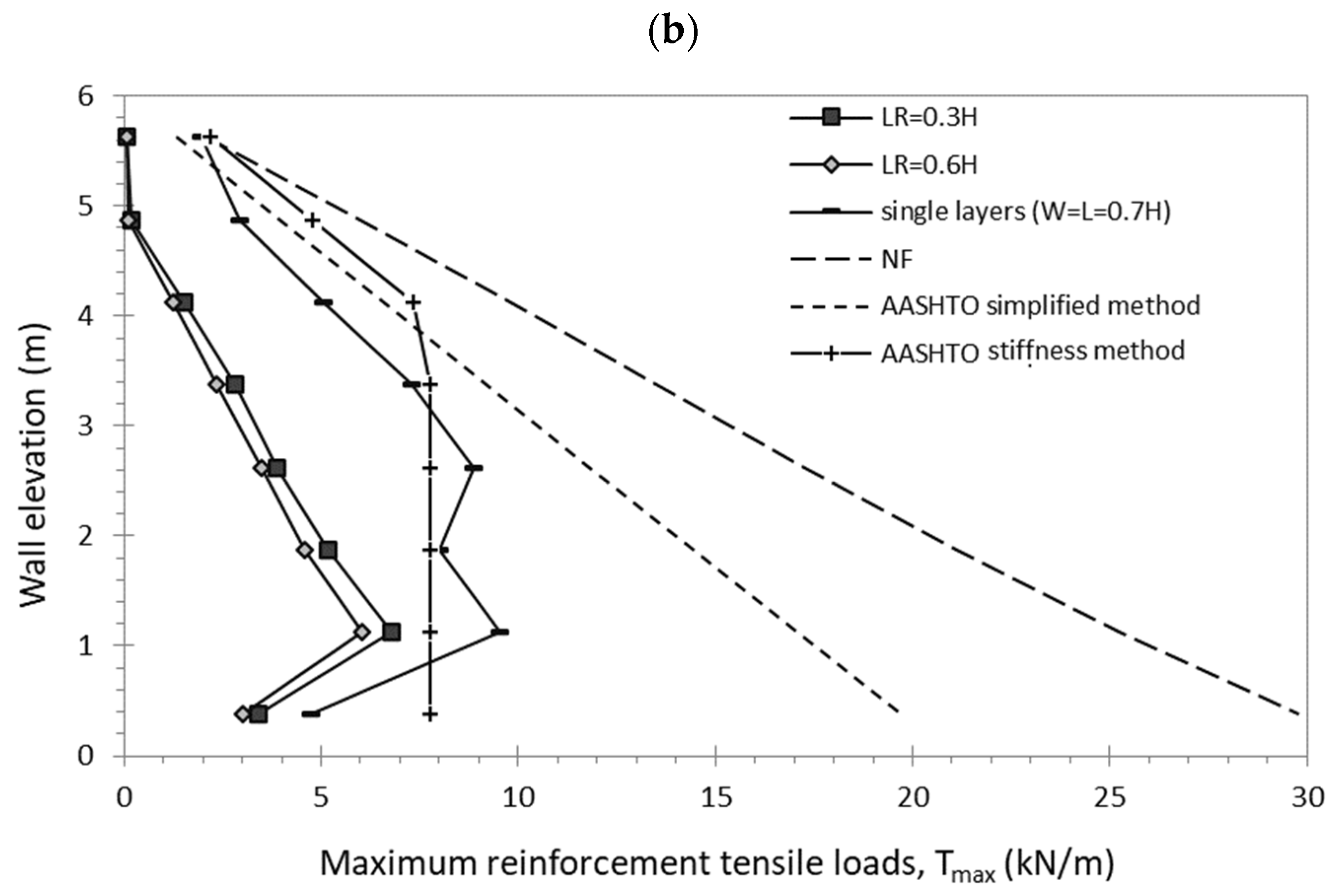
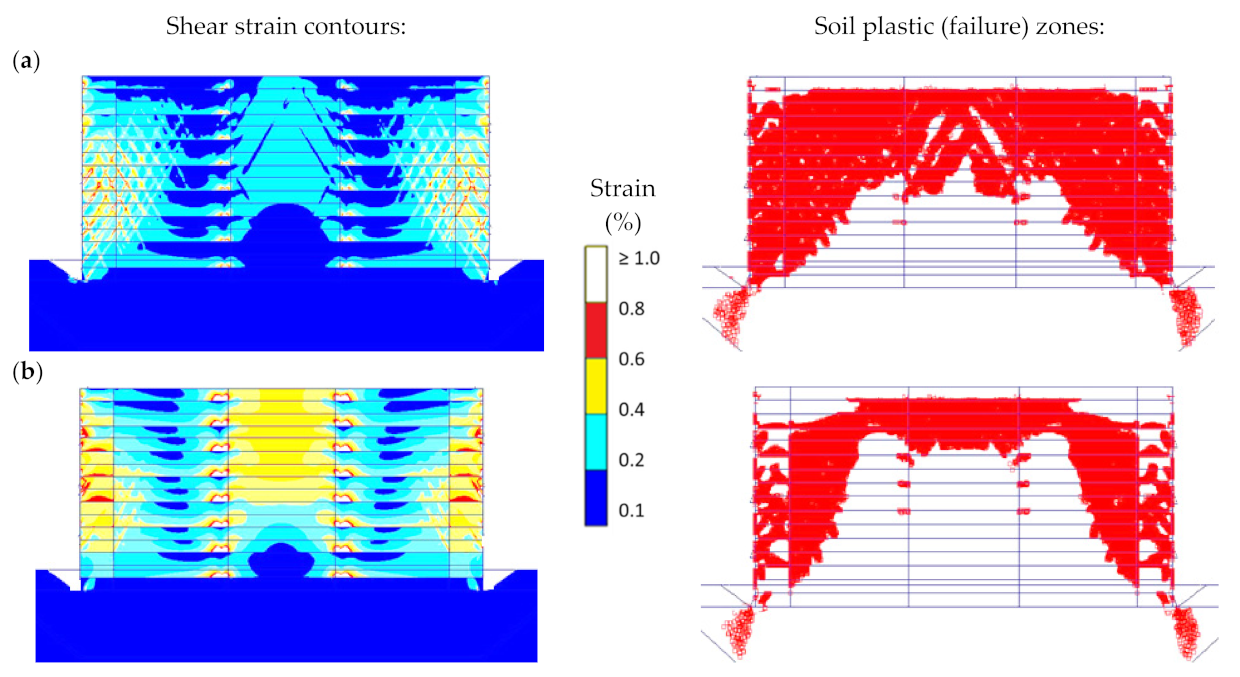
3.2. Effect of the Interaction Distance (Di) between Back-to-Back Walls
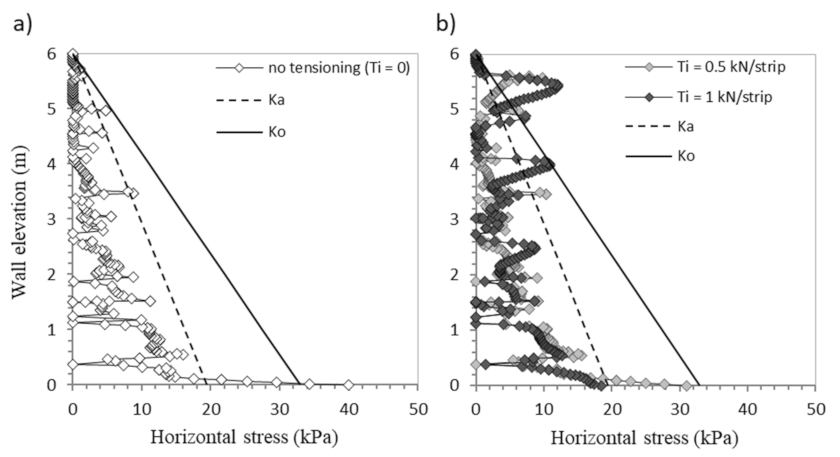
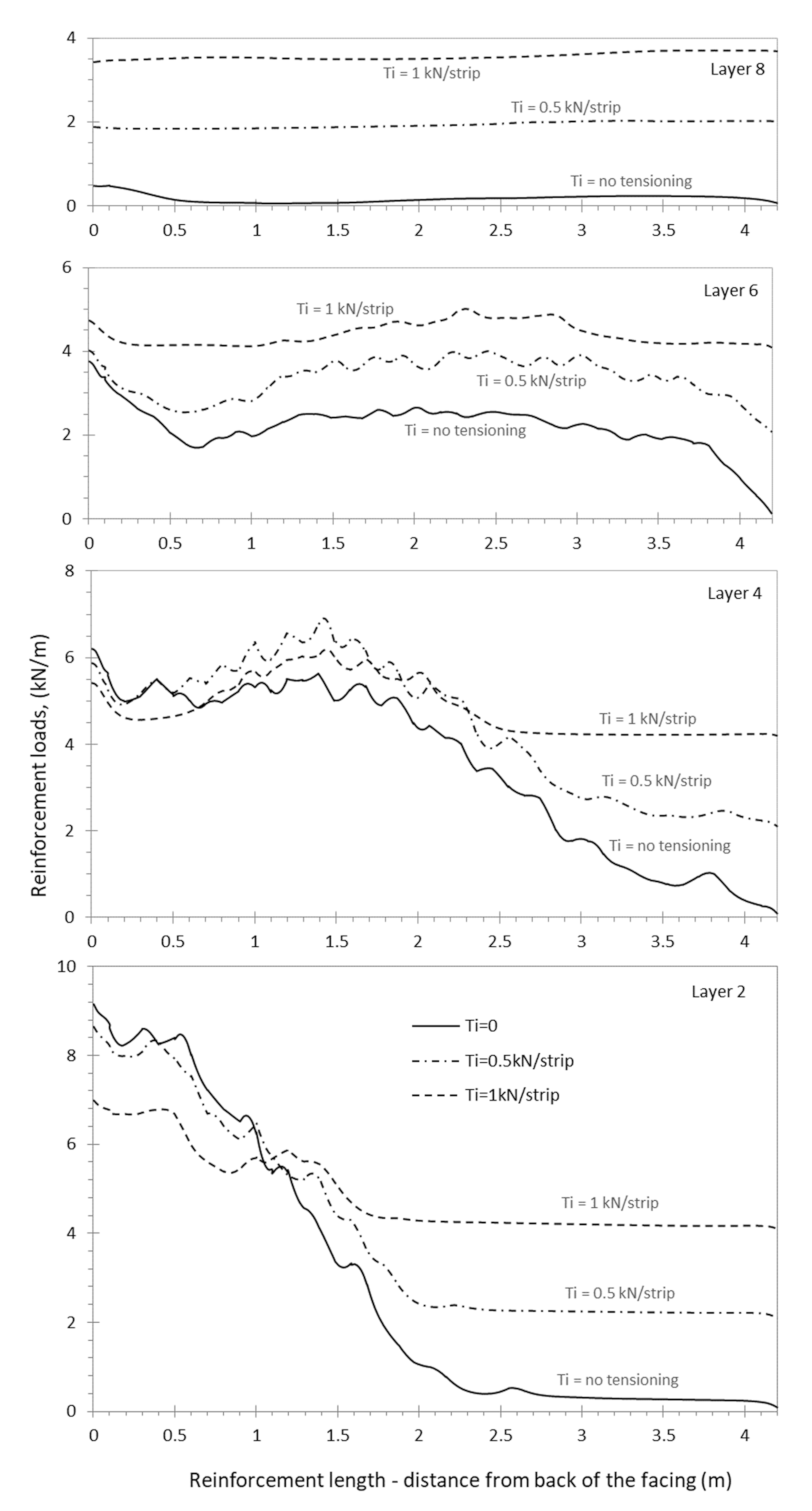
3.3. Effect of the Pre-Tensioning (Ti)
3.4. Effect of the Soil–Polymeric Interaction (Ri)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Damians, I.P.; Bathurst, R.J.; Adroguer, E.; Josa, A.; Lloret, A. Sustainability assessment of earth retaining wall structures. ICE Environ. Geotech. 2018, 5, 187–203. [Google Scholar] [CrossRef]
- Berg, R.R.; Christopher, B.R.; Samtani, N.C. Design of Mechanically Stabilized Earth Walls and Reinforced Soil Slopes, No. FHWA-NHI-10-024; National Highway Institute, Federal Highway Administration: Washington, DC, USA, 2009. [Google Scholar]
- Han, J.; Leshchinsky, D. Analysis of back-to-back mechanically stabilized earth. Geotext. Geomembr. 2010, 28, 262–267. [Google Scholar] [CrossRef]
- El-Sherbiny, R.; Ibrahim, E.; Salem, A. Stability of back-to-back mechanically stabilized earth walls. In Geo-Congress Stability and Performance of Slopes and Embankments III; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2013; pp. 555–565. [Google Scholar]
- Benmebarek, S.; Attallaoui, S.; Benmebarek, N. Interaction analysis of back-to-back mechanically stabilized earth walls. J Rock Mech. Geotech. Eng. 2016, 8, 697–702. [Google Scholar] [CrossRef] [Green Version]
- Benmebarek, S.; Djabri, M. FEM to investigate the effect of overlapping-reinforcement on the performance of back-to-back embankment bridge approaches under self-weight. Transp. Geotech. 2017, 11, 17–26. [Google Scholar] [CrossRef]
- Sravanam, S.M.; Balunaini, U.; Madhira, R.M. Behavior of Connected and Unconnected Back-to-Back Walls for Bridge Approaches. Int. J. Geomech. 2020, 20, 06020013. [Google Scholar] [CrossRef]
- Dram, A.; Balunaini, U.; Benmebarek, S.; Mouli, S. Earthquake response of connected and unconnected back-to-back geosynthetic-reinforced soil walls. ASCE Int. J. Geom. 2021, 21, 04021223. [Google Scholar] [CrossRef]
- Samee, A.A.; Yazdandoust, M.; Ghalandarzadesh, A. Performance of back-to-back MSE walls reinforced with steel strips under seismic conditions. Transp. Geot. 2021, 30, 100540. [Google Scholar] [CrossRef]
- EN 14475. Execution of Special Geotechnical Works—Reinforced Fill; European Committee for Standardization (CEN): Brussels, Belgium, 2006. [Google Scholar]
- VSL Construction Systems—VSoL® Retained Earth System. Available online: www.vsl.com (accessed on 9 February 2022).
- PLAXIS. PLAXIS 2D Reference Manual Version 9, PLAXIS; Delft University of Technology: Delft, The Netherlands, 2008. [Google Scholar]
- LRFD Bridge Design Specifications, American Association of State Highway and Transportation Officials (AASHTO), 9th ed.; AASHTO: Washington, DC, USA, 2020.
- BS8006-1 2010+A1. Code of Practice for Strengthened/Reinforced Soil and Other Fills; British Standards Institution (BSI): Milton Keynes, UK, 2010. [Google Scholar]
- Damians, I.P.; Bathurst, R.J.; Lima, J.; Lloret, A.; Josa, A. Numerical study of the use of actively-tensioned polymeric strips for reinforced soil walls. In Proceedings of the XVI European Conference on Soil Mechanics and Geotechnical Engineering, Geotechnical Engineering for Infrastructure and Development, Edinburgh, UK, 13–17 September 2015; pp. 3834–3838. [Google Scholar]
- Brouthen, A.; Damians, I.P.; Bathurst, R.J.; Houhou, M.N. FE analysis of the effect of soil-reinforcement interaction and reinforcement pre-tensioning on the behaviour of back-to-back polymeric strip reinforced soil walls. In Proceedings of the 7th European Geos Conference (EuroGeo7), Warsaw, Poland, 4–7 September 2022. [Google Scholar]
- Damians, I.P.; Bathurst, R.J.; Josa, A.; Lloret, A. Vertical facing panel-joint gap analysis for steel-reinforced soil walls. Int. J. Geomech. 2016, 16, 04015103. [Google Scholar] [CrossRef] [Green Version]
- Damians, I.P.; Bathurst, R.J.; Josa, A.; Lloret, A.; Albuquerque, P.J.R. Vertical facing loads in steel reinforced soil walls. J. Geotech. Geoenviron. Eng. 2013, 139, 1419–1432. [Google Scholar] [CrossRef]
- Damians, I.P.; Bathurst, R.J.; Josa, A.; Lloret, A. Numerical study of the influence of foundation compressibility and reinforcement stiffness on the behavior of reinforced soil walls. Int. J. Geotech. Eng. 2014, 8, 247–259. [Google Scholar] [CrossRef]
- GECO Industrial Co. Ltd. Available online: http://gecoind.com/en/product/fasten.php (accessed on 9 February 2022).
- Runser, D.J.; Fox, P.J.; Bourdeau, P.L. Field performance of a 17 m-high reinforced soil retaining wall. Geosynth. Int. 2001, 8, 367–391. [Google Scholar] [CrossRef]
- Damians, I.P.; Bathurst, R.J.; Josa, A.; Lloret, A. Numerical analysis of an instrumented steel reinforced soil wall. Int. J. Geomech. 2015, 15, 04014037. [Google Scholar] [CrossRef]
- Yu, Y.; Bathurst, R.J.; Miyata, Y. Numerical analysis of a mechanically stabilized earth wall reinforced with steel strips. Soils Found 2015, 55, 536–547. [Google Scholar] [CrossRef]
- Jayakrishnan, P.V. Report on Full Scale Instrumented MacRes Wall at Jundiai-Brazil; Officine Maccaferri S.p.A.: Bologna, Italy, 2013. [Google Scholar]
- Capilleri, P.P.; Ferraiolo, F.; Motta, E.; Scotto, M.; Todaro, M. Static and dynamic analysis of two mechanically stabilized earth walls. Geosynth. Int. 2019, 26, 26–41. [Google Scholar] [CrossRef]
- Miyata, Y.; Bathurst, R.J.; Allen, T.M. Evaluation of tensile load model accuracy for PET strap MSE walls. Geosynth. Int. 2018, 25, 656–671. [Google Scholar] [CrossRef]
- Won, M.S.; Kim, Y.S. Internal deformation behavior of geosynthetic-reinforced soil walls. Geotex. Geomem. 2007, 25, 10–22. [Google Scholar] [CrossRef]
- Huang, B.; Bathurst, R.J.; Hatami, K.; Allen, T.M. Influence of toe restraint on reinforced soil segmental walls. Cana. Geotech. J. 2010, 47, 885–904. [Google Scholar] [CrossRef]
- NF P 94-270. Calcul Géotechnique: Ouvrages de Soustènement. Remblais Renforcés et Massifs en Soil Cloué; Norme française, Association Française de Normalisation (AFNOR): La Plaine Saint-Denis, France, 2009. [Google Scholar]





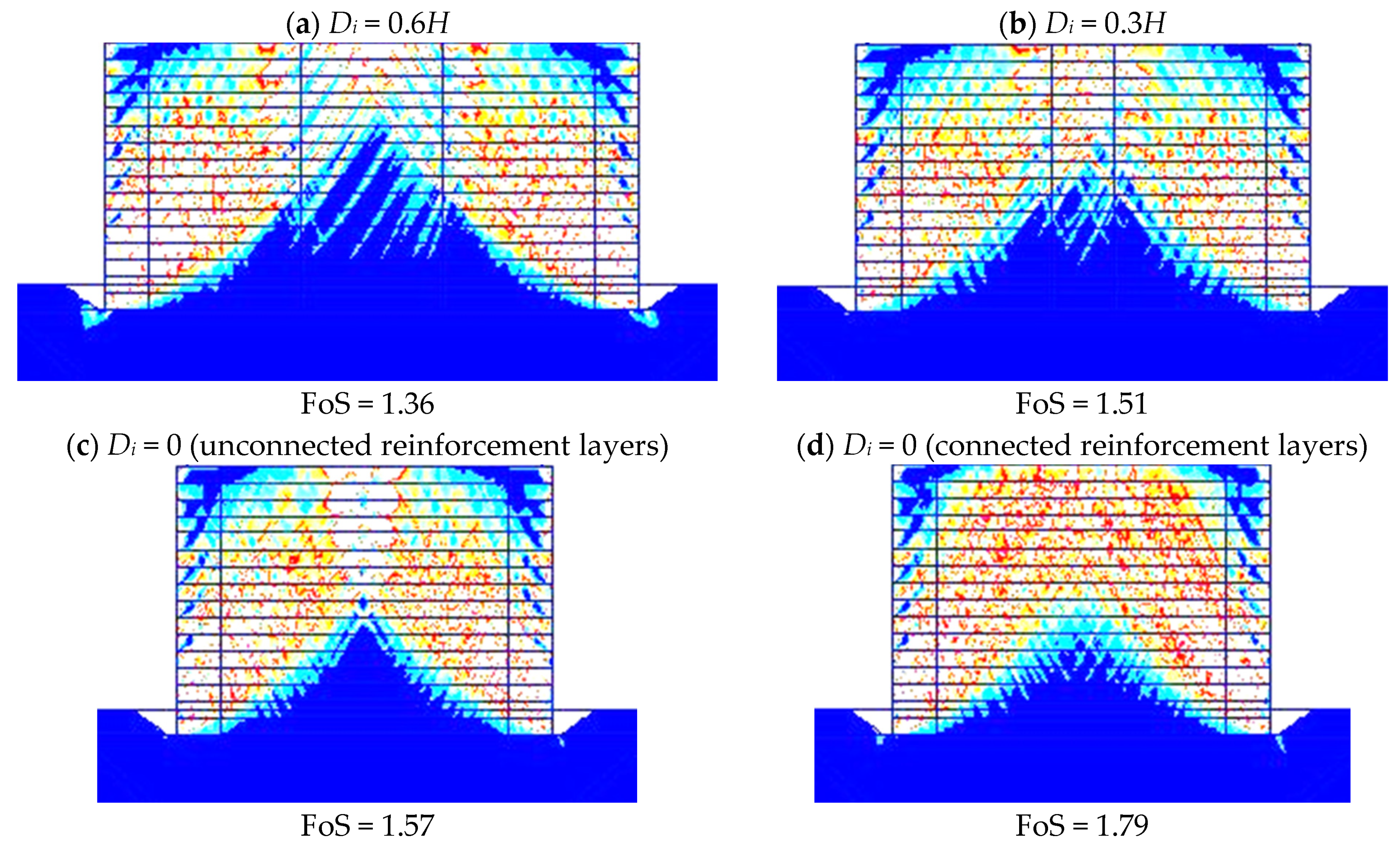
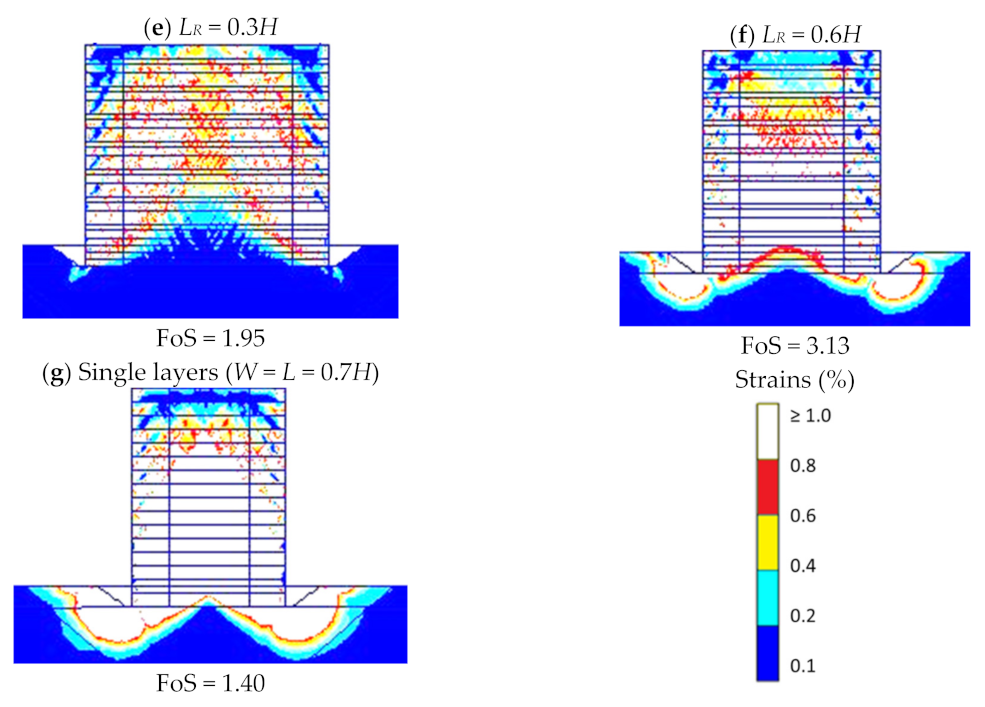
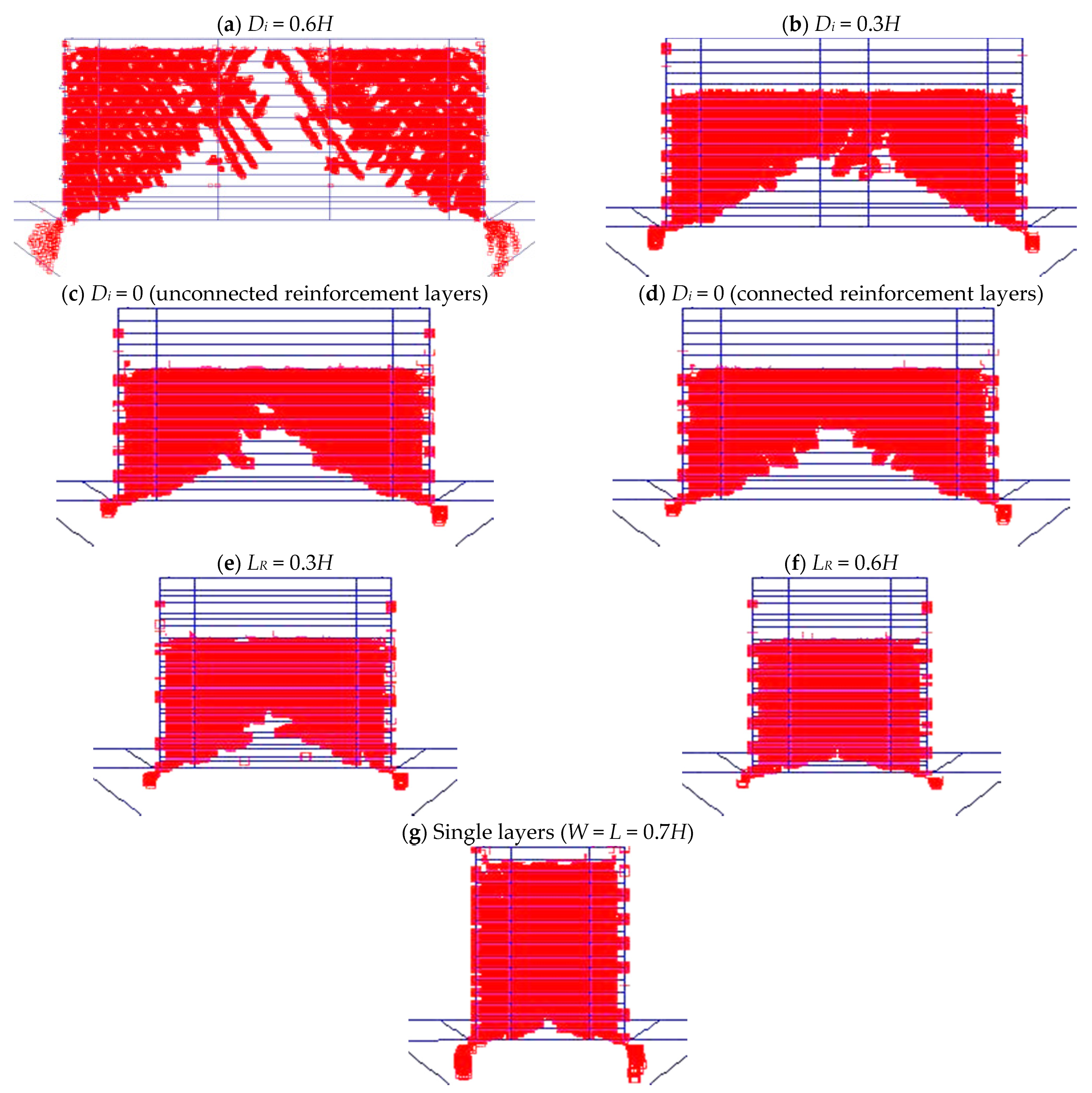
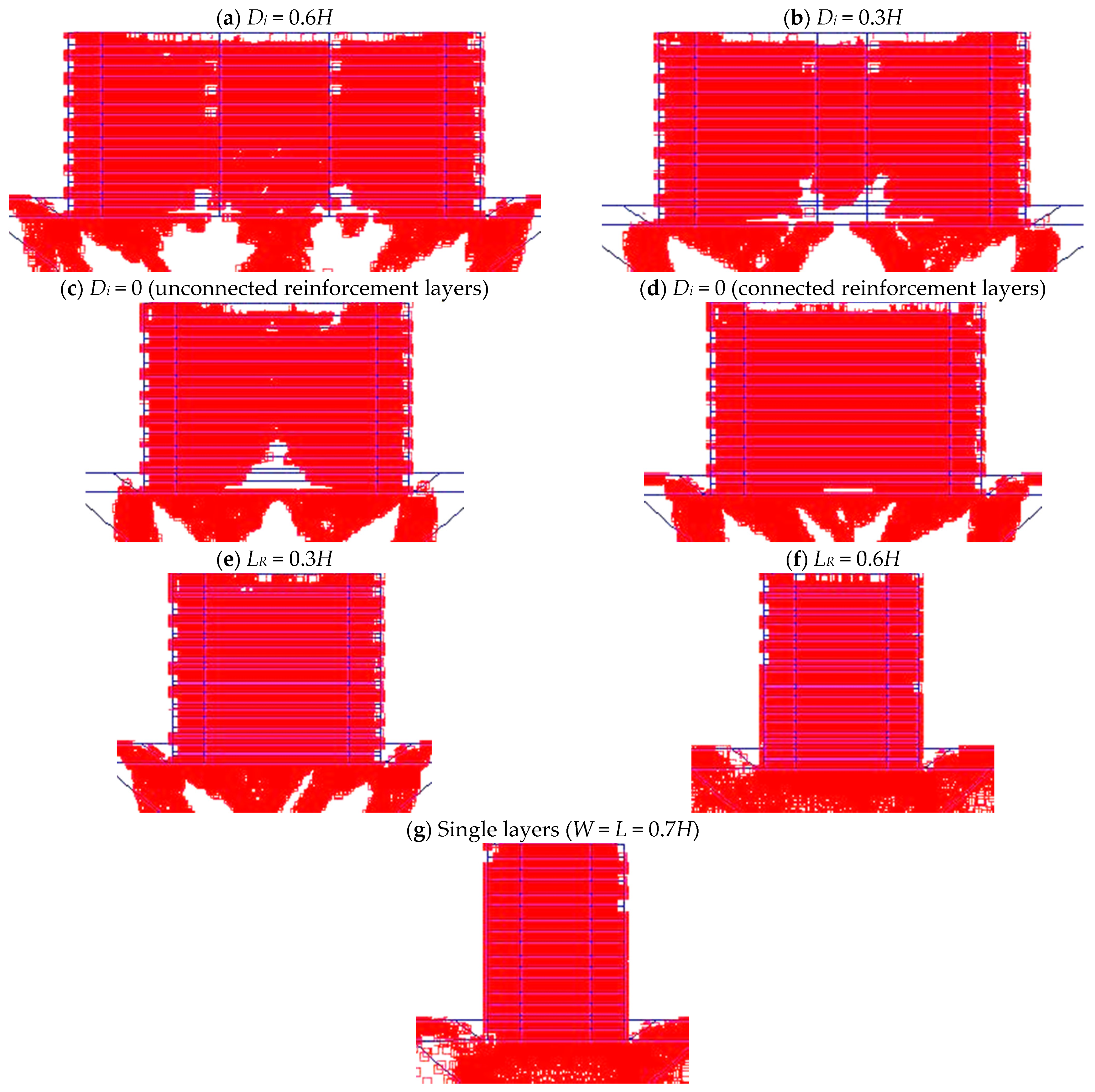



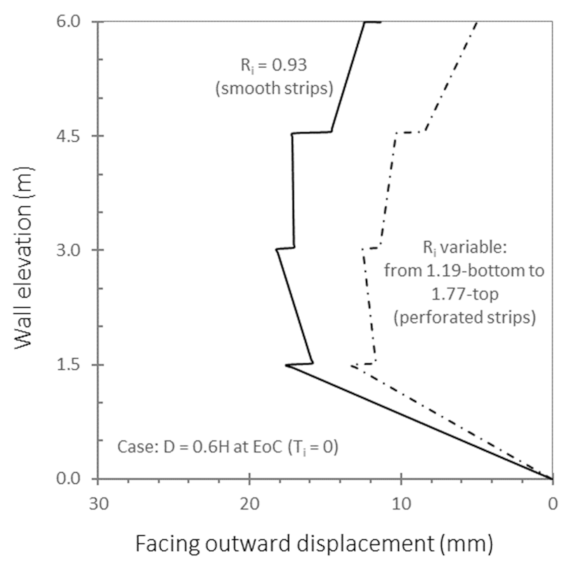
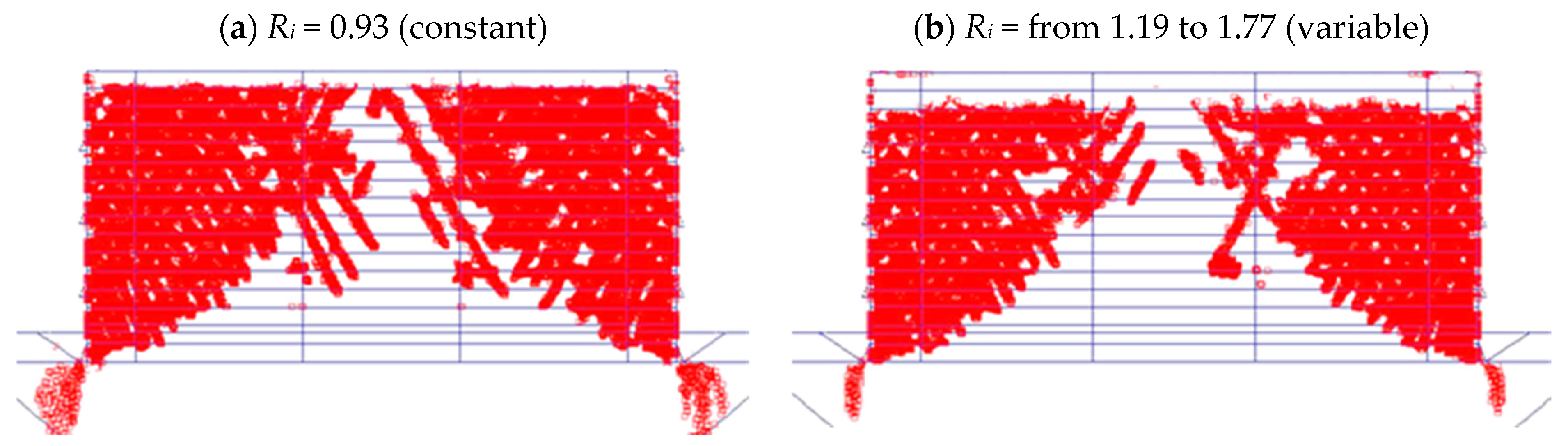
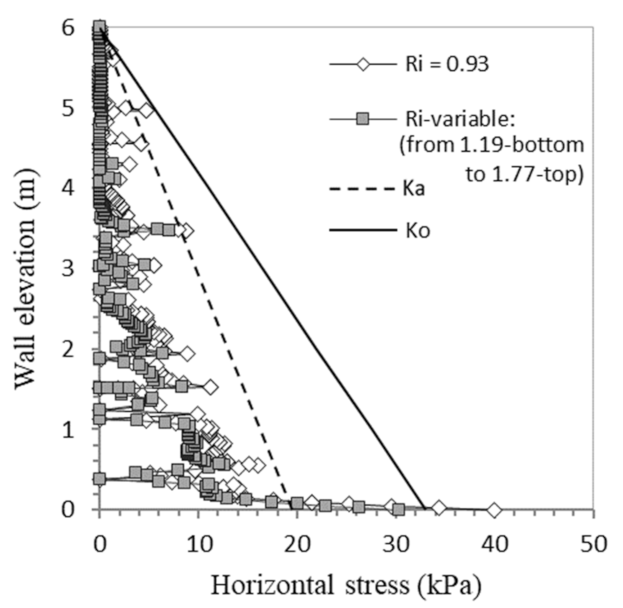

| Parameter | Backfill | Foundation | Road Pavement (20 cm Thick) | |
|---|---|---|---|---|
| (Distance from Face (a)): | ||||
| >1 m | <1 m | |||
| Unit weight, γ (kN/m3) | 18 | 20 | 23 | |
| Friction angle (b), ϕ (°) | 44 | 40 | - | |
| Dilatancy angle, ψ (°) | 14 | 10 | - | |
| Cohesion, c (kPa) | 1 | 10 | - | |
| Elastic modulus, E (MPa) | 50 | 25 | 1000 (c) | 3500 |
| Poisson’s ratio, ν (-) | 0.3 | 0.3 | 0.35 | |
| Parameter | Facing Panels (Concrete) | Bearing Pads (HPDE) |
|---|---|---|
| Axial stiffness, EA (MN/m) | 6000 | 1.1 |
| Bearing stiffness, EI (kN/m2/m) | 11,000 | 2.1 |
| Weight, w (kN/m/m) | 4.5 | 0.1 |
| Poisson’s ratio, ν (-) | 0.15 | 0.40 |
| Parameters | Soil-Facing Interface | Soil-Reinforcement Interface: | |||
|---|---|---|---|---|---|
| Smooth Strip | Perforated Strip | ||||
| (Distance from Back of the Facing): | |||||
| >1 m | <1 m | >1 m | <1 m | ||
| Cohesion, ci (kPa) | 0.3 | 0.93 | 1.19 to 1.77 | ||
| Friction angle, ϕi (°) | 16 | 42 | 49 to 60 | ||
| Dilatancy angle, ψi (°) | 0 | 0 | 14 | ||
| Shear modulus, Gi (MPa) | 0.9 | 8.4 | 16.7 | 27.0–60.4 | 13.5–30.2 |
| Elastic modulus, Ei (MPa) | 2.5 | 24 | 48 | 78.3–175.2 | 39.2–87.6 |
| Interface strength–stiffness reduction factor, Ri (Equation (7)) | 0.3 | 0.93 | variable: from 1.19 (bottom) to 1.77 (top) | ||
| Parameter | Sandy Backfill | Soil below and behind the Wall |
|---|---|---|
| Material model | Mohr–Coulomb | Mohr–Coulomb |
| Unit weight, γ (kN/m3) | 17 | 18.5 |
| Elastic modulus, E (MPa) | 50 | 60 |
| Poisson’s ratio, ν (-) | 0.3 | 0.3 |
| Cohesion, c (kPa) | 0 | 20 |
| Friction angle, ϕ (°) | 42 | 38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brouthen, A.; Houhou, M.N.; Damians, I.P. Numerical Study of the Influence of the Interaction Distance, the Polymeric Strips Pre-Tensioning, and the Soil–Polymeric Interaction on the Performance of Back-to-Back Reinforced Soil Walls. Infrastructures 2022, 7, 22. https://doi.org/10.3390/infrastructures7020022
Brouthen A, Houhou MN, Damians IP. Numerical Study of the Influence of the Interaction Distance, the Polymeric Strips Pre-Tensioning, and the Soil–Polymeric Interaction on the Performance of Back-to-Back Reinforced Soil Walls. Infrastructures. 2022; 7(2):22. https://doi.org/10.3390/infrastructures7020022
Chicago/Turabian StyleBrouthen, Abdelaziz, Mohamed Nabil Houhou, and Ivan Puig Damians. 2022. "Numerical Study of the Influence of the Interaction Distance, the Polymeric Strips Pre-Tensioning, and the Soil–Polymeric Interaction on the Performance of Back-to-Back Reinforced Soil Walls" Infrastructures 7, no. 2: 22. https://doi.org/10.3390/infrastructures7020022
APA StyleBrouthen, A., Houhou, M. N., & Damians, I. P. (2022). Numerical Study of the Influence of the Interaction Distance, the Polymeric Strips Pre-Tensioning, and the Soil–Polymeric Interaction on the Performance of Back-to-Back Reinforced Soil Walls. Infrastructures, 7(2), 22. https://doi.org/10.3390/infrastructures7020022







