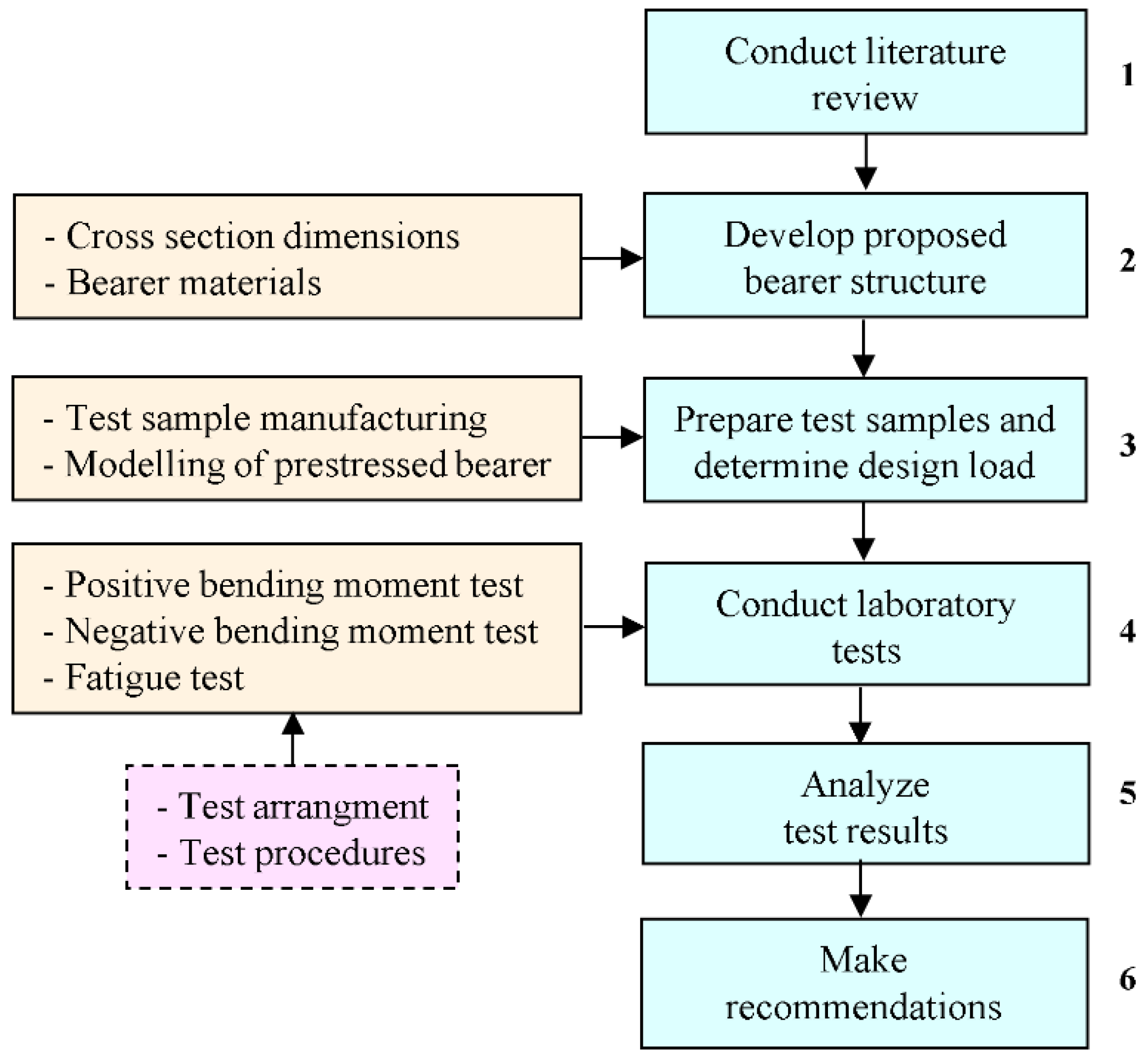
Performance Evaluation of Carrying Capacity of Prestressed Bearers for Railway Turnouts Using Laboratory Experiments in Vietnam
Abstract
1. Introduction
2. Proposed Bearer Structure
2.1. Cross-Section Dimensions
2.2. Bearer Materials
3. Test Sample Preparation and Design Load
3.1. Test Sample Manufacturing
- The initial stage of bearer production was to create the ready molds. Steel molds were used in the casting of the bearers. The molds were made following the bearers’ shape and size requirements. The bearers were cast in steel molds that could be changed in length by the steel plates at both ends. First, the ready molds used for the casting of concrete were cleaned. Then, lubrication was performed on the inner sides of the molds to reduce or avoid sticky action of the concrete toward the molds.
- After cleaning and lubricating the molds, the strands were cut into the required shape and inserted into the molds. These strands were fixed at both ends using anchors. Then, the strands were tensioned with P0 = 530 kN using a hydraulic jack, and the anchors were tightened.
- The concrete was premixed and poured into the molds. Then, needle vibrators were used to compact the concrete properly and fill the required shape with an even mix distribution. When the concrete filled and began to overflow onto the mold’s surface, a table vibrator compactor was used to flatten the surface.
- After the completion of concrete casting, the molds with concrete were cured naturally for about 16–20 h. When the concrete reached the strength of 30.1 N/mm2, the tension force was removed, and the strands were cut. Then, the molds were carefully removed using machinery. The molds can be reused for manufacturing purposes. After being checked to ensure quality, the production samples were transferred to the yard with a 3-ton forklift.
3.2. Modelling of Narrow Prestressed Bearers
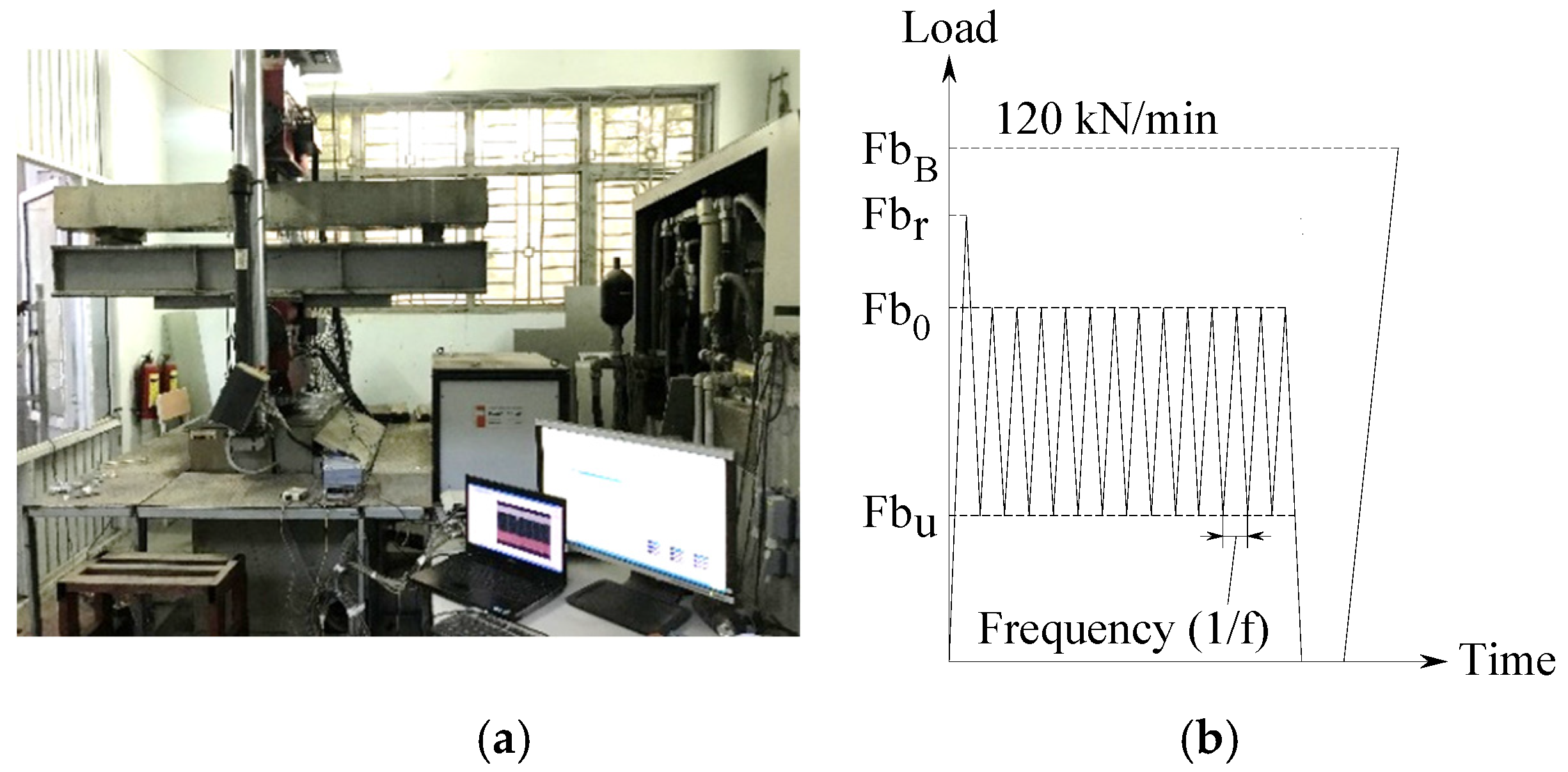
4. Laboratory Testing
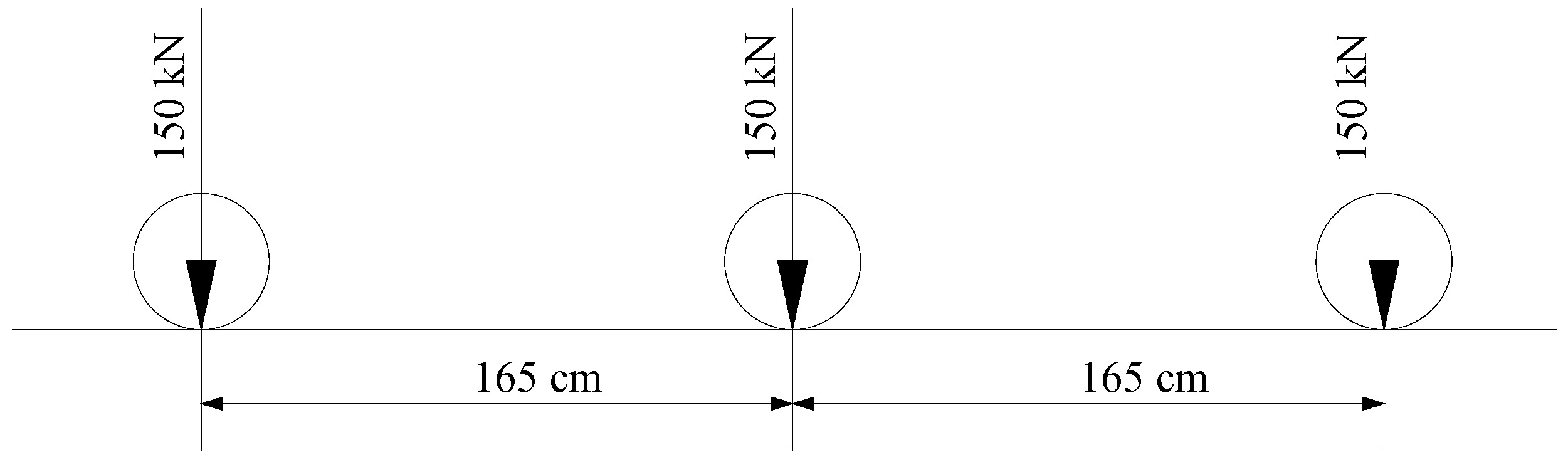
4.1. Test Arrangement
4.2. Test Procedures
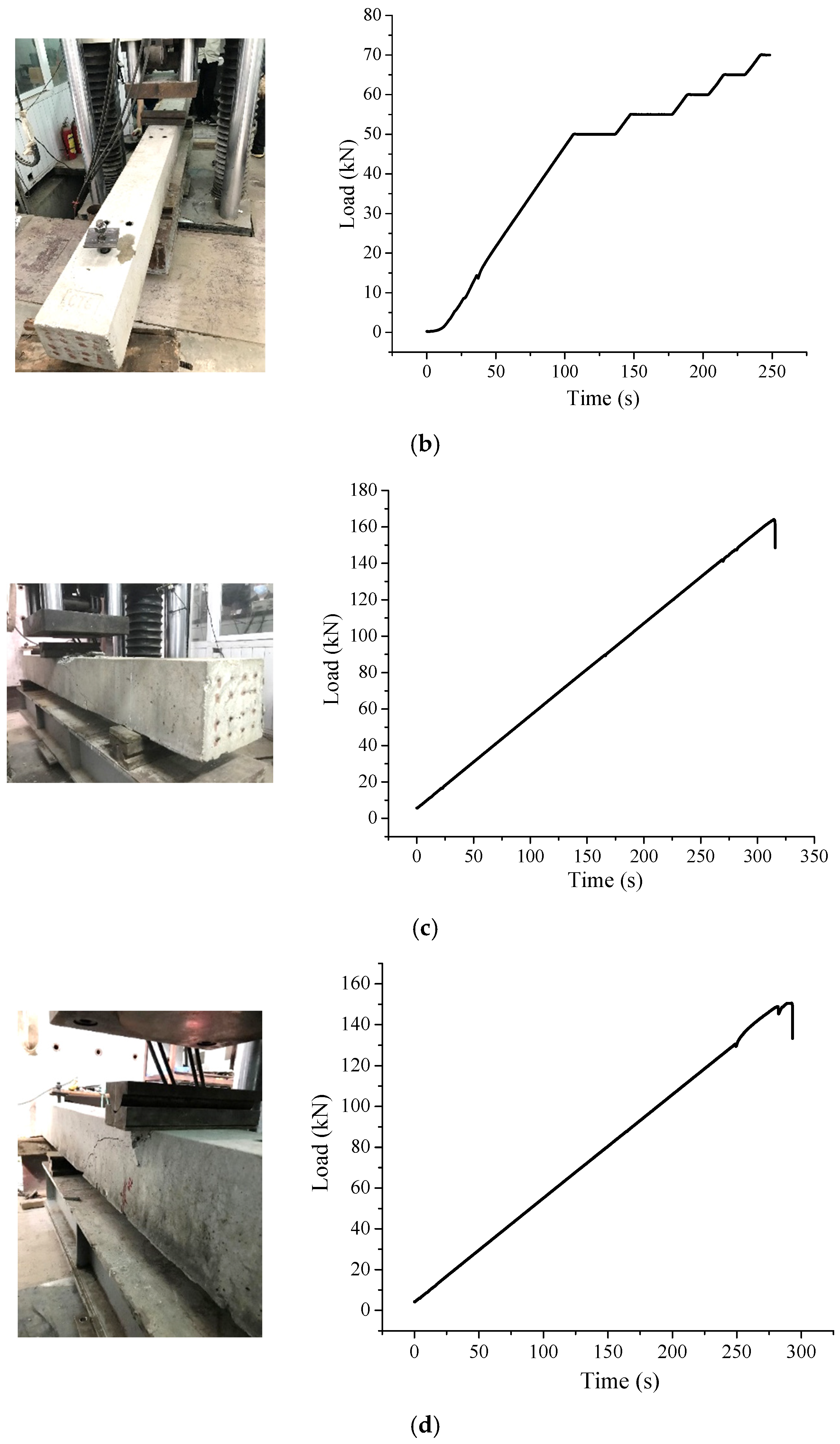
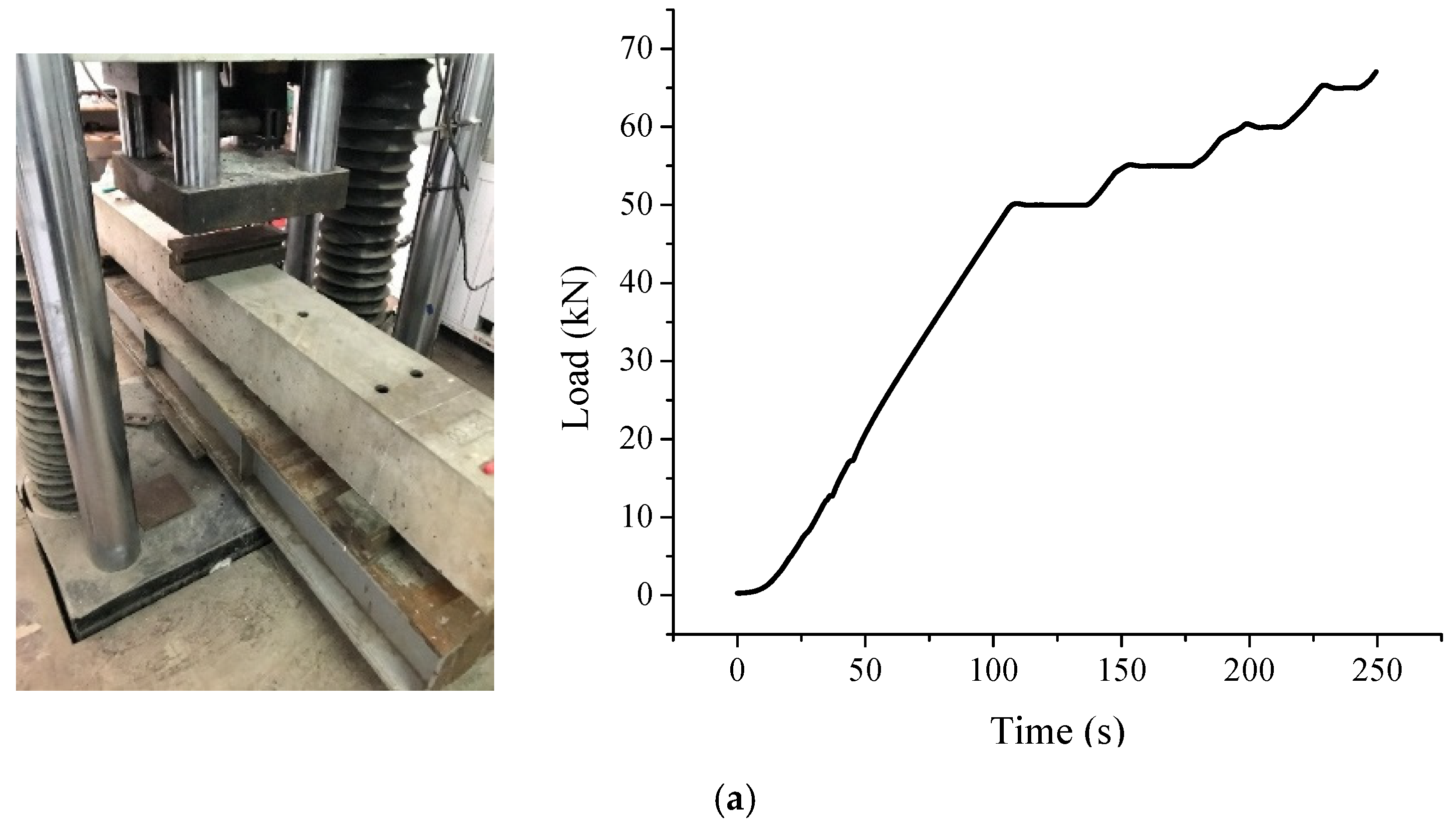
4.2.1. Positive Bending Moment Test
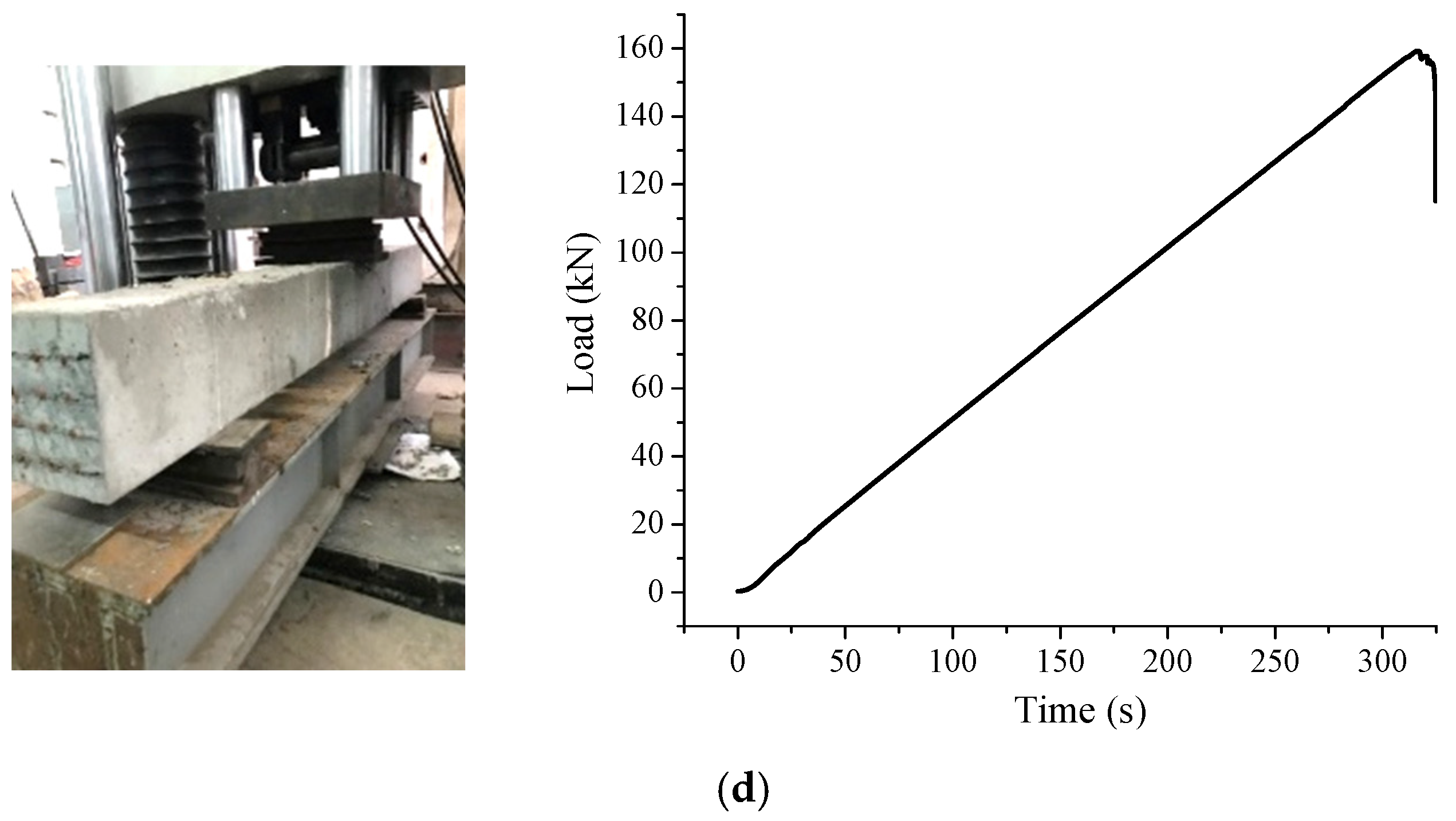
4.2.2. Negative Bending Moment Test
4.2.3. Fatigue Test
5. Results
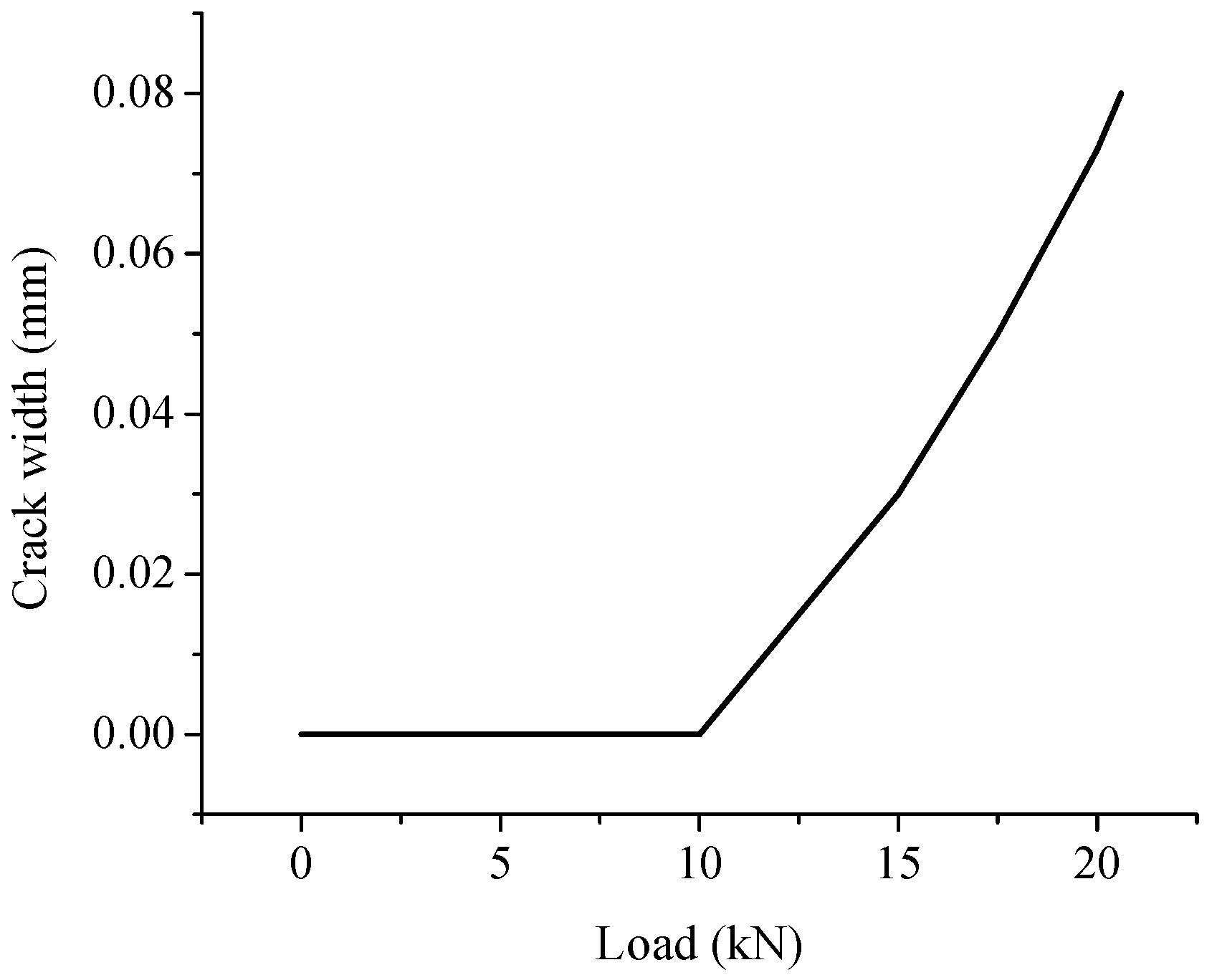
5.1. Results of Positive Bending Moment Test
5.2. Results of Negative Bending Moment Test
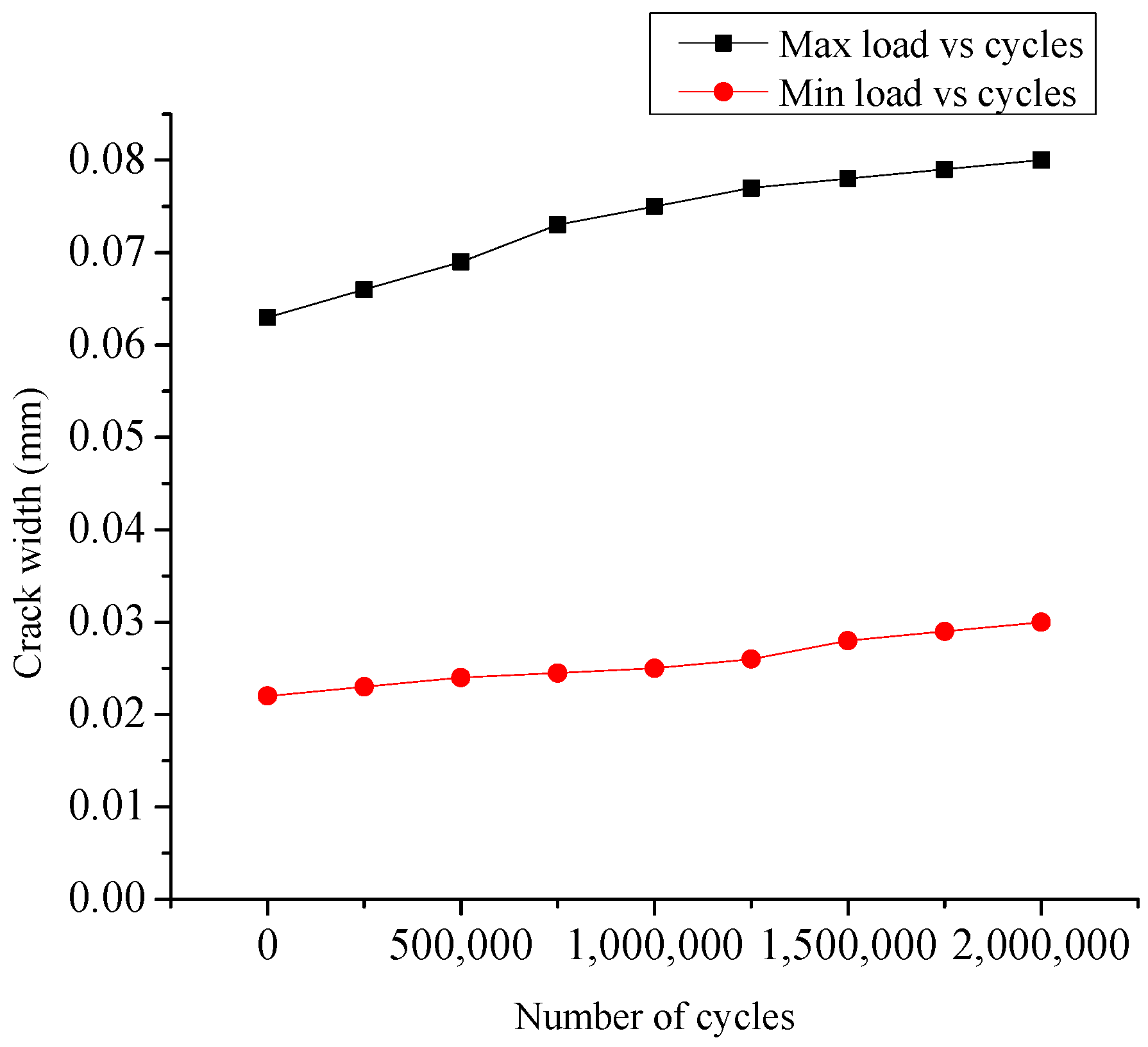
5.3. Results of Fatigue Test
6. Discussion
7. Conclusions
- Bearers for turnouts were manufactured in a factory and tested in the laboratory. Based on a detailed analysis of the static and fatigue test results and the requirements of the standards [20], the proposed bearers for turnouts meet the requirements set for assessing the behaviour of the tested bearers subjected to static and fatigue loads. These bearers can replace the wooden sleepers at turnouts.
- The results of static and fatigue tests of the bearers for turnouts show that there is a considerable reserve in the cross-section capacity, which means that the existing reserve can be used with a greater locomotive axle, and the bearer design can be optimized by arranging the prestressed strands and changing the geometric dimensions of the bearer cross-section.
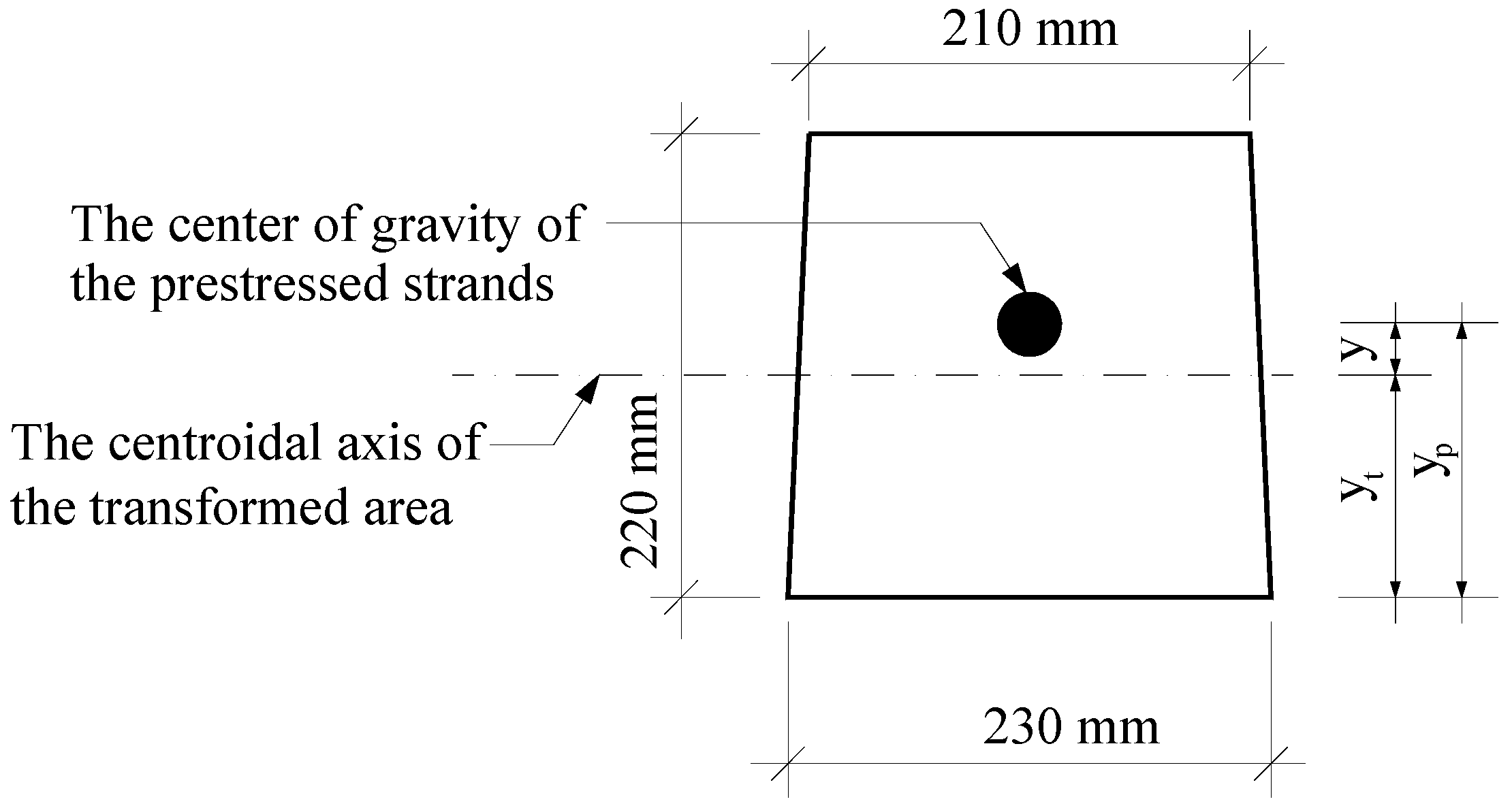
- Concrete cracking due to the prestressed force can be limited by arranging the strands appropriately. The eccentricity of the centroid of the prestressed force should be close to zero.
- The new bearer minimises maintenance costs, provides longer service life, and is environmentally friendly compared with traditional wooden bearers. The concrete bearers are more durable (service life is up to 50 years, compared to 12–15 years for wooden bearers), more economical, easier to manufacture, and not susceptible to vermin attack, fire, or weather. It is expected that concrete bearers will dominate in Vietnam in the coming years.
- The new bearer structure proposed in this study was evaluated using only laboratory experiments. Future research will focus on evaluating the performance of the new bearer structure in the field to fully assess PSB behaviour.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, P. Design of High-Speed Railway Turnout; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Weiping, Y. Technical characteristics of French high-speed railway turnouts. China Railw. 2006, 8, 40–41. [Google Scholar]
- Weizhou, F. Major technical characteristics of high-speed turnout in France. J. Railw. Eng. Soc. 2009, 9, 18–35. [Google Scholar]
- Andersson, C.; Dahlberg, T. Wheel/rail impacts at a railway turnout crossing. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 1998, 212, 123–134. [Google Scholar] [CrossRef]
- Kassa, E.; Andersson, C.; Nielsen, J.C.O. Simulation of dynamic interaction between train and railway turnout. Veh. Syst. Dyn. 2006, 44, 247–258. [Google Scholar] [CrossRef]
- Kassa, E.; Nielsen, J.C.O. Stochastic analysis of dynamic interaction between train and railway turnout. Veh. Syst. Dyn. 2008, 46, 429–449. [Google Scholar] [CrossRef]
- Kassa, E.; Nielsen, J.C.O. Dynamic train-turnout interaction in an extended frequency range using a detailed model of track dynamics. J. Sound Vib. 2009, 320, 893–914. [Google Scholar] [CrossRef]
- Rong-shan, Y.; Xue-yi, L.; Ping, W. Research on longitudinal force computation theory and experiment of welded turnout on bridge. J. China Railw. Soc. 2010, 32, 135–142. [Google Scholar]
- Wang, P.; Chen, R.; Quan, S. Development and application of wheel-set lateral displacement test system in high speed railway turnout zone. Prz. Elektrothchniczny Electr. Rev. 2012, 88, 69–73. [Google Scholar]
- Xu, J.; Wang, P.; Chen, R.; Xu, H. Mechanical properties of high-speed turnout switching and locking device. J. Southwest Jiaotong Univ. 2013, 48, 702–707. [Google Scholar]
- Gao, Z.; Qian, Y.; Dersch, M.S.; Edwards, J.R. Compressive stress distribution in prestressed concrete and its effect on railroad crosstie design. Constr. Build. Mater. 2017, 151, 147–157. [Google Scholar] [CrossRef]
- Blanco-Saura, A.E.; Velarte-González, J.L.; Ribes-Llario, F.; Real-Herráiz, J.I. Study of the dynamic vehicle-track interaction in a railway turnout. Multibody Syst. Dyn. 2018, 43, 21–36. [Google Scholar] [CrossRef]
- Silva, R.; Silva, W.V.; Farias, J.Y.; Santos, M.A.A.; Neiva, L.O. Experimental and Numerical Analyses of the Failure of Prestressed Concrete Railway Sleepers. Materials 2020, 13, 1704. [Google Scholar] [CrossRef]
- Ferdous, W.; Manalo, A. Failures of mainline railway sleepers and suggested remedies—Review of current practice. Eng. Fail. Anal. 2014, 44, 17–35. [Google Scholar] [CrossRef]
- JIS E 1201; Japanese Industrial Standard: Prestressed concrete sleepers—Pretensioning type. Standard Japan: Tokyo, Japan, 1997.
- Code of International Union of Railways (UIC Code). Design of Monoblock Concrete Sleepers; UIC CODE 713 R.; UIC Code: Paris, France, 2004. [Google Scholar]
- Manufacturing Process of Vietnam. Concrete Sleepers and Bearers Manufacturing Process; Construction Joint Stock Company No.6: Hanoi, Vietnam, 2022. [Google Scholar]
- EN 13230–6; Railway Applications. Track. Concrete Sleepers and Bearers. Part 6: Design. CEN: Brussels, Belgium, 2016.
- EN 1992-1-1:2004; Eurocode 2: Design of Concrete Structures-Part 1-1: General Rules and Rules for Buildings. CEN: Brussels, Belgium, 2004.
- EN 13230–4; Railway Applications. Track. Concrete Sleepers and Bearers. Part 4: Prestressed Bearers for Switches and Crossings. CEN: Brussels, Belgium, 2016.
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 12, 159–164. [Google Scholar] [CrossRef]
- Curíc, E.; Dreníc, D.; Grdíc, Z. Analysis of carrying capacity of concrete sleepers for switches and crossings under static and dynamic load. Građevinar 2014, 12, 1117–1124. [Google Scholar]
- ABNT NBR 11709; Concrete Sleepers—Design, Materials and Components. The Brazilian Association of Technical Standards: Rio de Janeiro, Brasil, 2015.
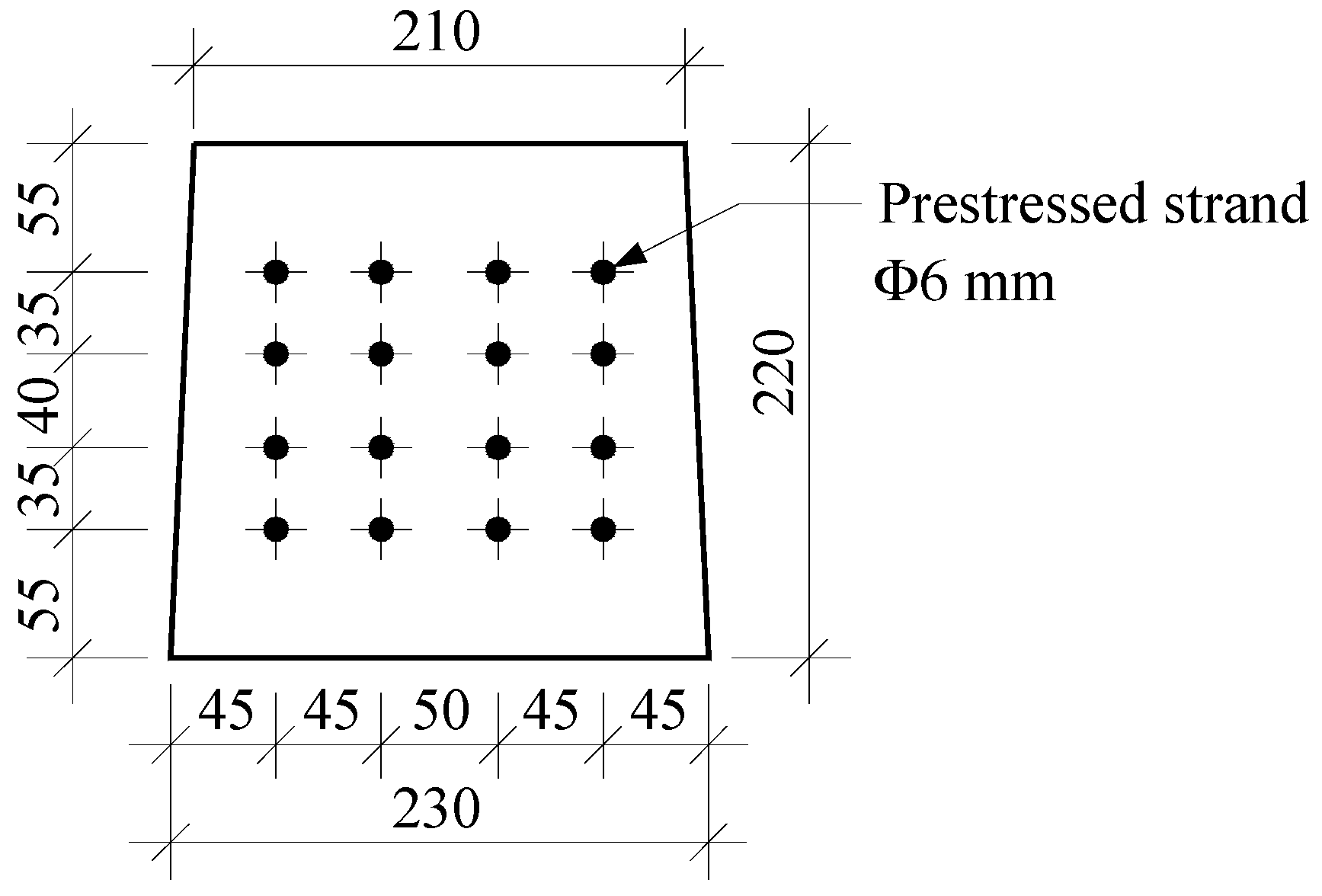


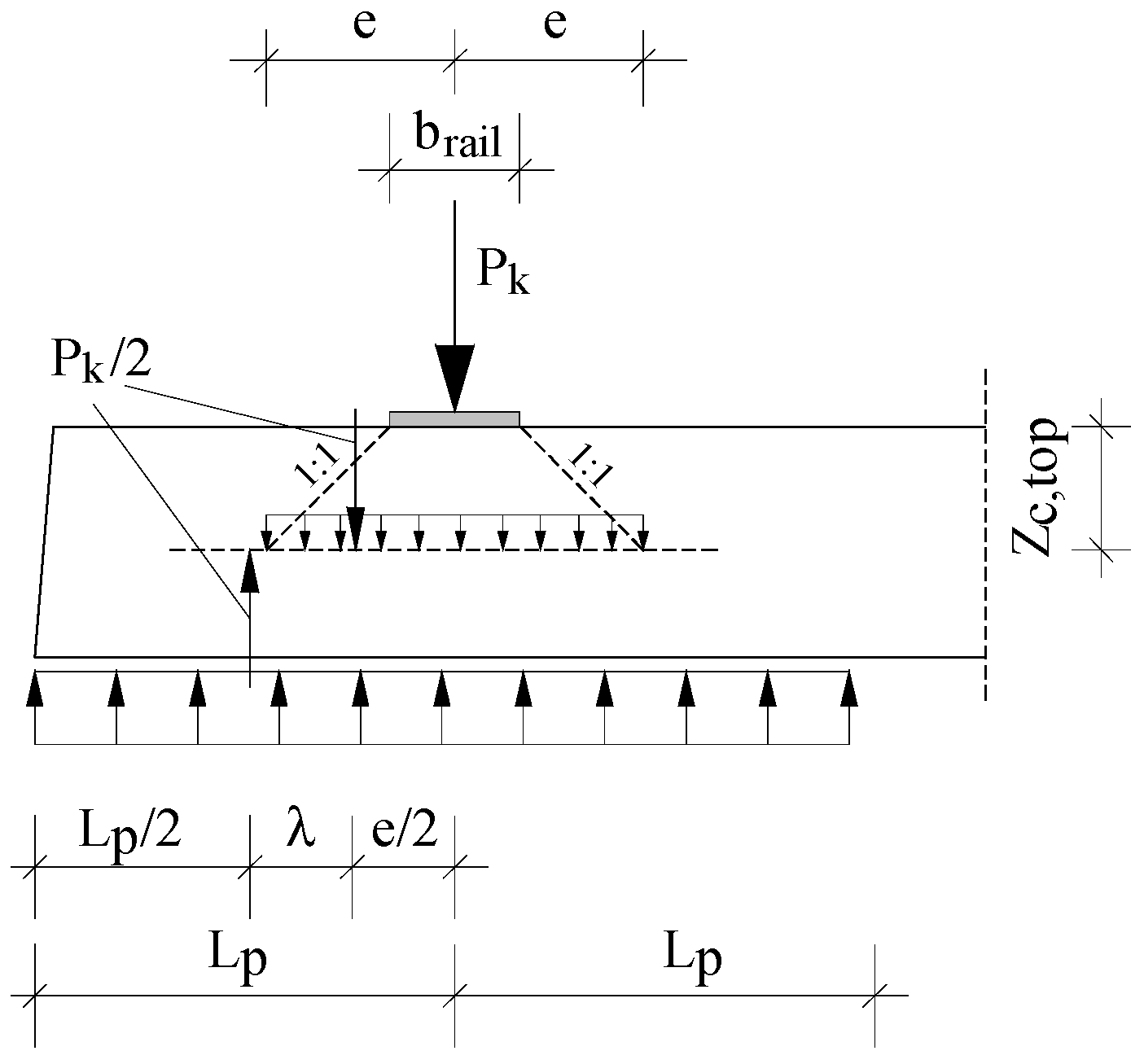
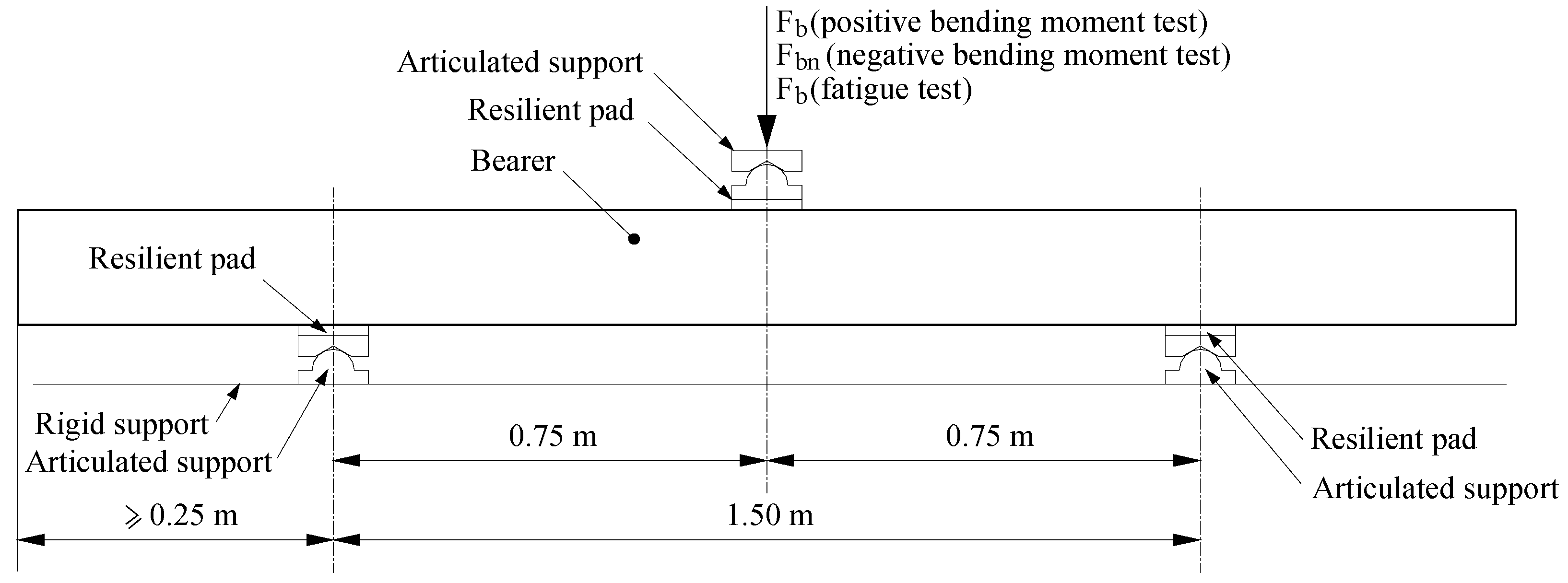
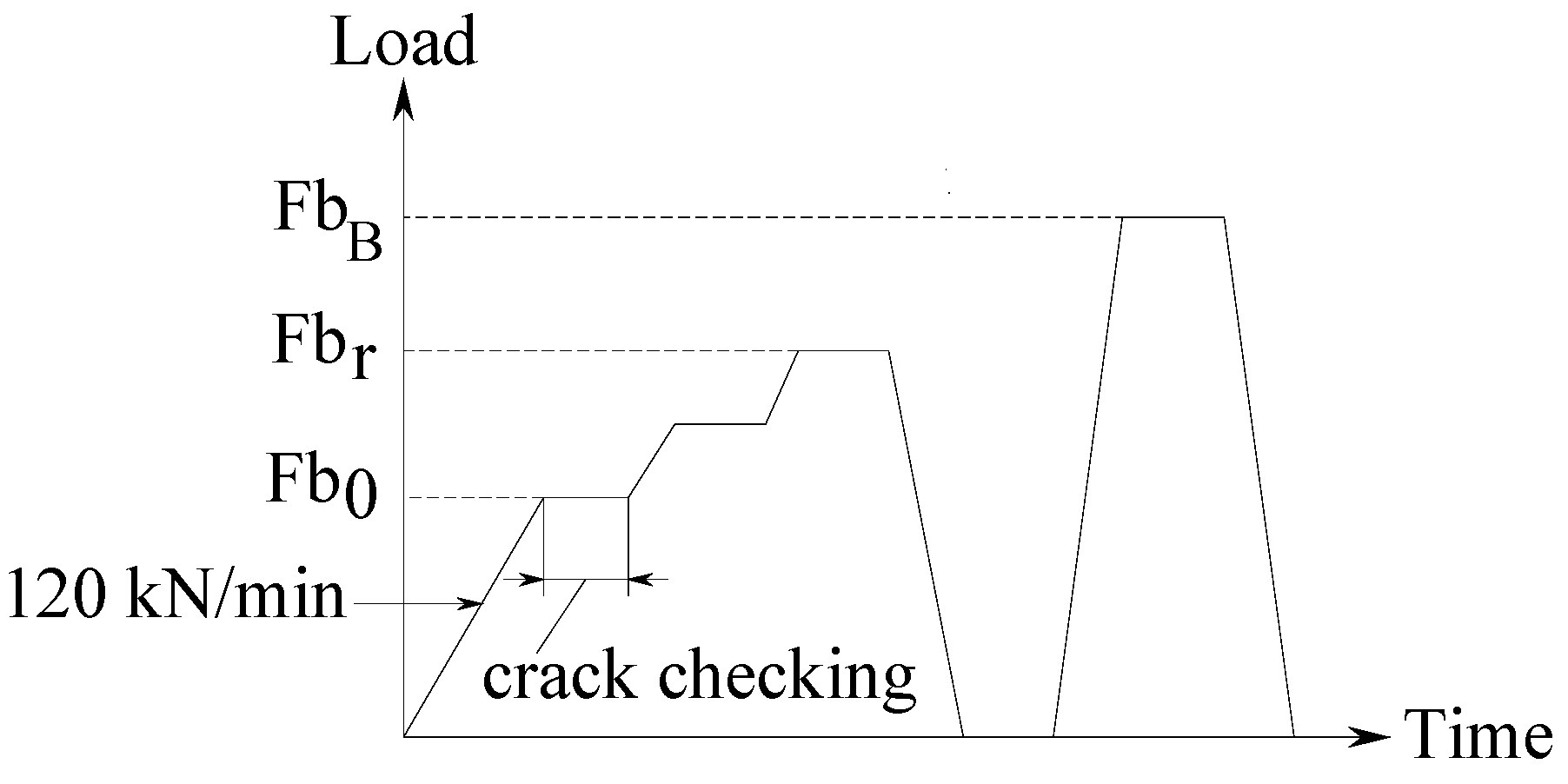
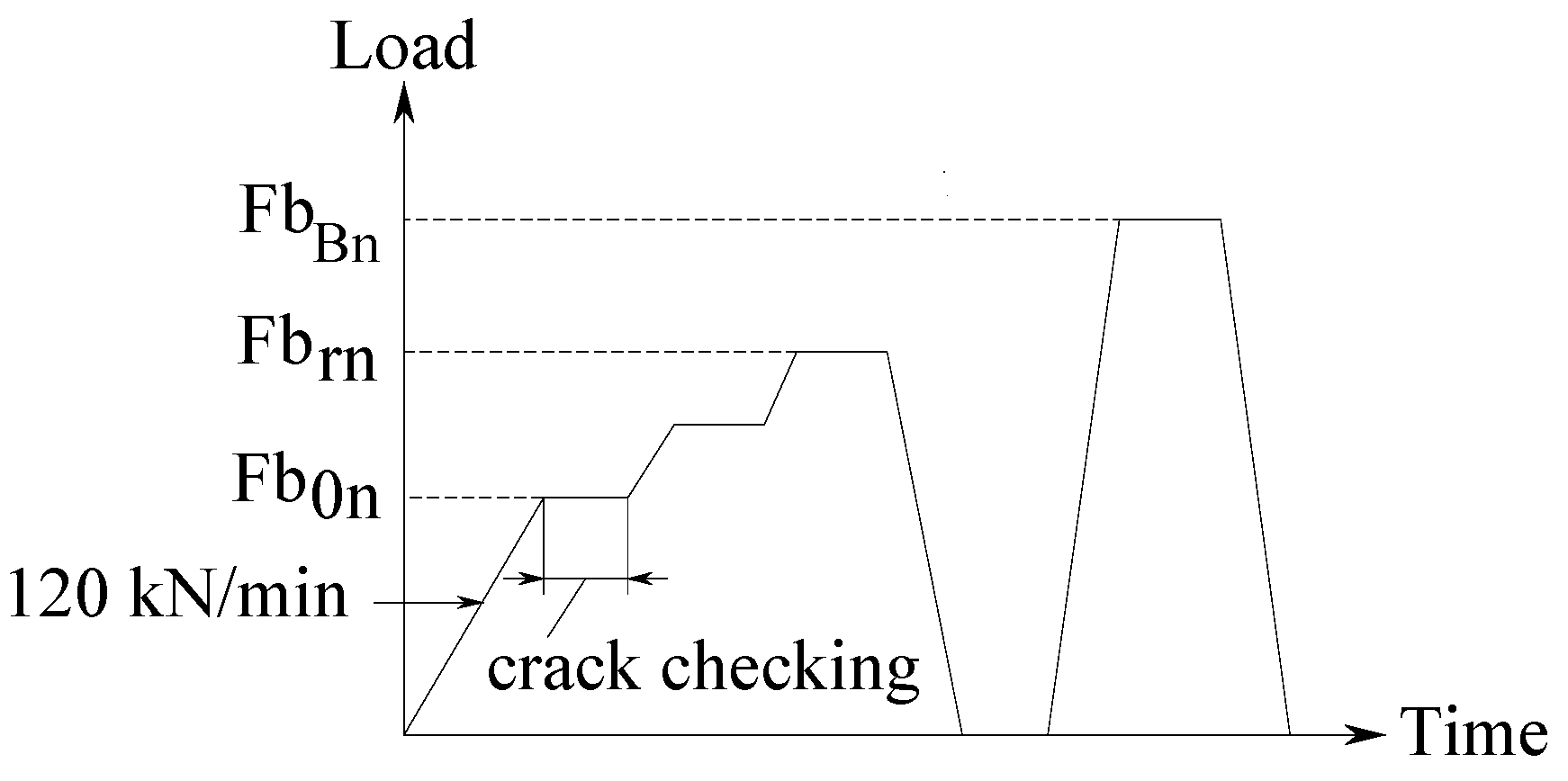




| Parameter | Symbol | Dimension |
|---|---|---|
| Height of bearers | hpsb | 220 mm |
| Width of the bearer’s top | btpsb | 210 mm |
| Width of the bearer’s bottom | bbpsb | 230 mm |
| Area of a single strand | Aps | 28.2743 mm2 |
| Number of strands | n | 16 |
| Modulus of elasticity of strand | Ep | 205,000 MPa |
| Modulus of elasticity of concrete | Ecm | 36,000 MPa |
| Area of the concrete section | Ac | 48,400 mm2 |
| Distance from the bottom of the bearer to the center of gravity of the concrete | yc | 108.4 mm |
| Distance from the bottom of the bearer to the center of gravity of the strands | yp | 110.0 mm |
| Property | Variable | Symbol | Value |
|---|---|---|---|
| Concrete properties | Concrete class C45/55 | fck | 45 MPa |
| Average compressive strength | fcm | 53 Mpa | |
| Modulus of elasticity of concrete | Ecm | 36,000 Mpa | |
| Strand properties | Diameter | φ | 6 mm |
| Characteristic tensile strength | fPk | 1670 Mpa | |
| Characteristic 0.1% absorption | fP0,1k | 1389 MPa | |
| Modulus of elasticity of strand | Ep | 205,000 MPa |
| No. | Bearer Length (m) | Number of Bearers |
|---|---|---|
| 1 | 1.8 | 3 |
| 2 | 3.4 | 2 |
| 3 | 2.0 | 6 |
| 4 | 2.2 | 5 |
| 5 | 2.4 | 4 |
| 6 | 2.6 | 3 |
| 7 | 2.8 | 3 |
| 8 | 3.0 | 3 |
| 9 | 3.1 | 2 |
| 10 | 3.3 | 4 |
| No. | Specimen ID | Acceptance Criteria | Results | Conclusion |
|---|---|---|---|---|
| 1 | PSB1 | Fbr1 > kt1 × Fb0 | Fbr1 = 67.6 kN > kt1 × Fb0 = 21.30 kN | Passes |
| FbB1 > kb × Fb0 | FbB1 = 164.03 kN > kb × Fb0 = 52.41 kN | Passes | ||
| 2 | PSB2 | Fbr2 > kt1 × Fb0 | Fbr2 = 70.1 kN > kt1 × Fb0 = 21.30 kN | Passes |
| FbB2 > kb × Fb0 | FbB2 = 150.54 kN > kb × Fb0 = 52.41 kN | Passes |
| No. | Specimen ID | Acceptance Criteria | Results | Conclusion |
|---|---|---|---|---|
| 1 | PSB3 | Fbrn3 > kt2 × Fb0n | Fbrn3 = 90.4 kN > kt2 × Fb0n = 10.41 kN | Passes |
| FbBn3 > kbn × Fb0n | FbBn3 = 180.24 kN > kbn × Fb0n = 24.76 kN | Passes | ||
| 2 | PSB4 | Fbrn4 > kt2 × Fb0n | Fbrn4 = 80.0 kN > kt2 × Fb0n = 10.41 kN | Passes |
| FbBn4 > kbn × Fb0n | FbBn4 = 159.25 kN > kbn × Fb0n = 24.76 kN | Passes |
| References | Country | Standard | Crack Load (kN) | Failure Load (kN) | Distance between AS a (m) | Number of Prestressed Strands | Concrete Cross-Section Area (mm2) |
|---|---|---|---|---|---|---|---|
| Silva et al. [13] | Brazil | ABNT NRB, 11709 [23] | 210.5 | 490 | 0.746 | 13 | 52,185 |
| Curíc et al. [22] | Serbia | EN 13230 [18,20] | 70.0 | 210 | 1.50 | 18 | 63,800 |
| Present study | Vietnam | EN 13230 [18,20] | 67.6 | 164 | 1.50 | 16 | 48,400 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dung, T.A.; Easa, S.M. Performance Evaluation of Carrying Capacity of Prestressed Bearers for Railway Turnouts Using Laboratory Experiments in Vietnam. Infrastructures 2022, 7, 151. https://doi.org/10.3390/infrastructures7110151
Dung TA, Easa SM. Performance Evaluation of Carrying Capacity of Prestressed Bearers for Railway Turnouts Using Laboratory Experiments in Vietnam. Infrastructures. 2022; 7(11):151. https://doi.org/10.3390/infrastructures7110151
Chicago/Turabian StyleDung, Tran Anh, and Said M. Easa. 2022. "Performance Evaluation of Carrying Capacity of Prestressed Bearers for Railway Turnouts Using Laboratory Experiments in Vietnam" Infrastructures 7, no. 11: 151. https://doi.org/10.3390/infrastructures7110151
APA StyleDung, T. A., & Easa, S. M. (2022). Performance Evaluation of Carrying Capacity of Prestressed Bearers for Railway Turnouts Using Laboratory Experiments in Vietnam. Infrastructures, 7(11), 151. https://doi.org/10.3390/infrastructures7110151







