Digital Image Correlation for Evaluation of Cracks in Reinforced Concrete Bridge Slabs
Abstract
:1. Introduction
1.1. Danish Capacity Evaluation Program
1.2. The Danish Classification System
1.3. Monitoring and Stop Criteria
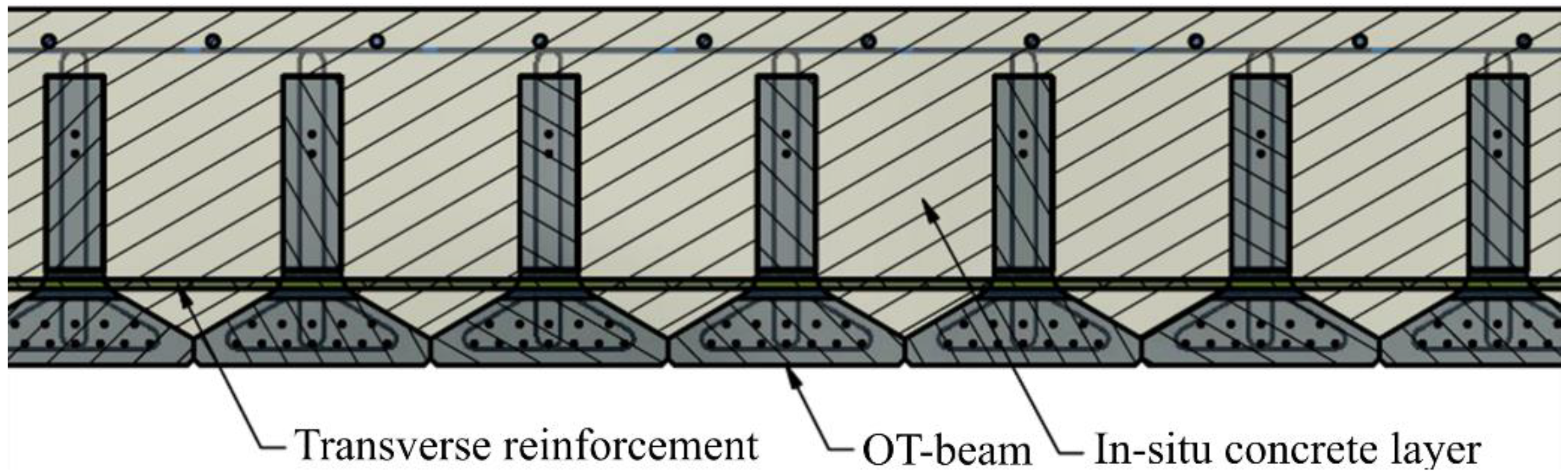
2. Structural Composition and Test Series
2.1. Full-Scale Bridge Tests
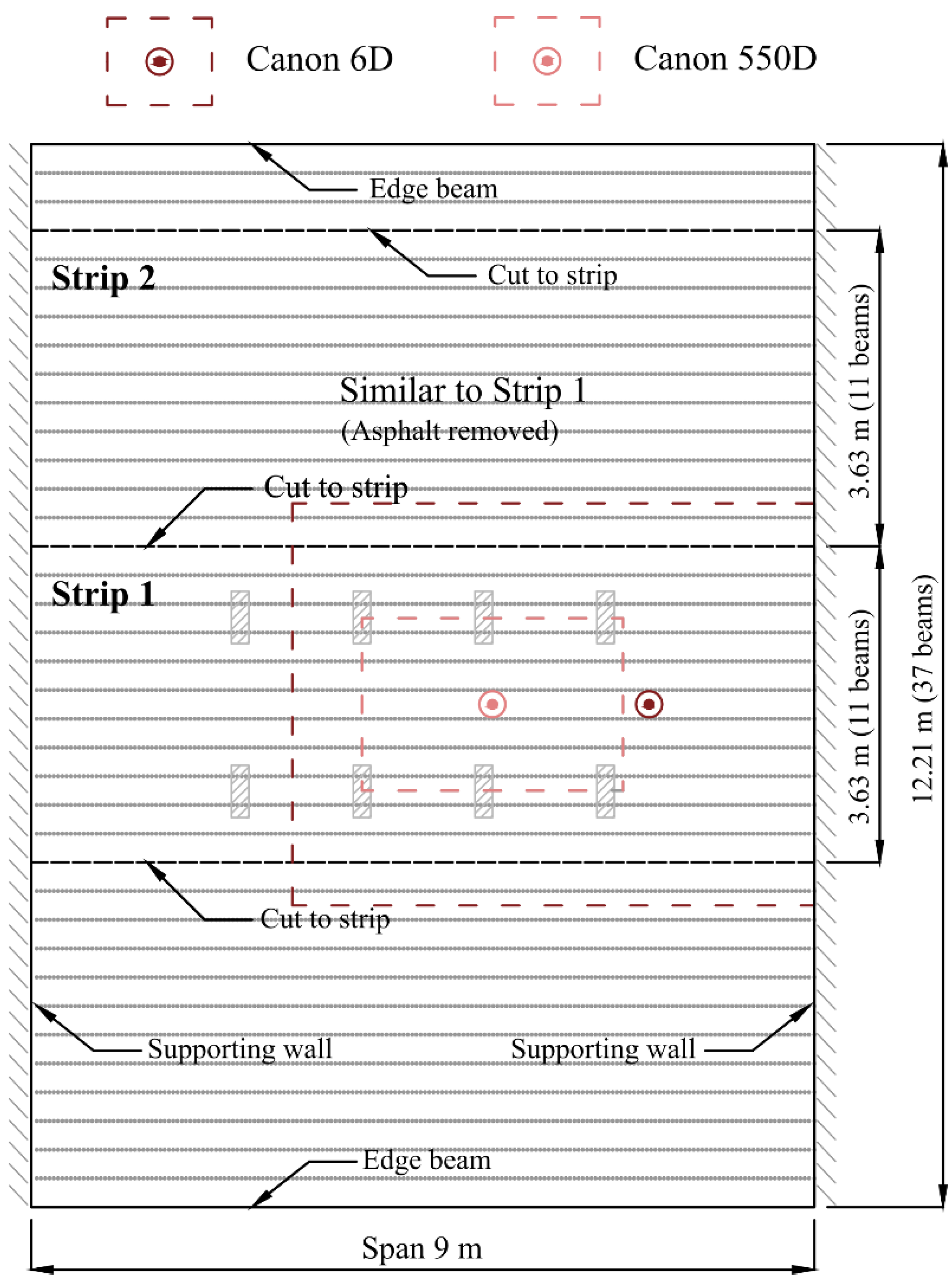
2.2. Strip Tests 1 and 2
2.3. Scaled Laboratory Tests
- To investigate the transverse shear transfer of load between OT-beam elements.
- To evaluate crack initiation threshold in situ and compare these to results gained in laboratory conditions.
- Provide experience with testing and monitoring for future application in in situ tests.
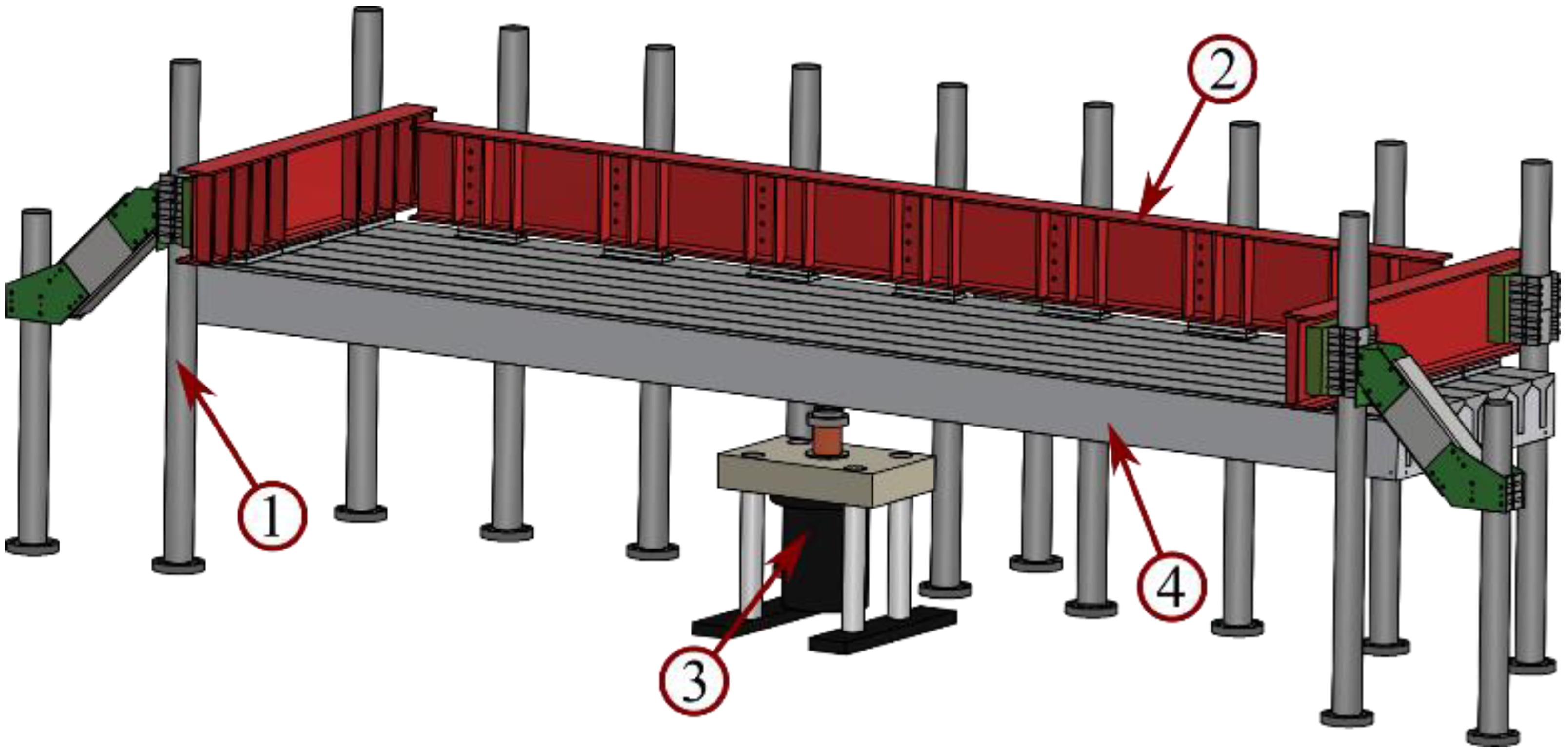
2.3.1. Laboratory Test Specimen
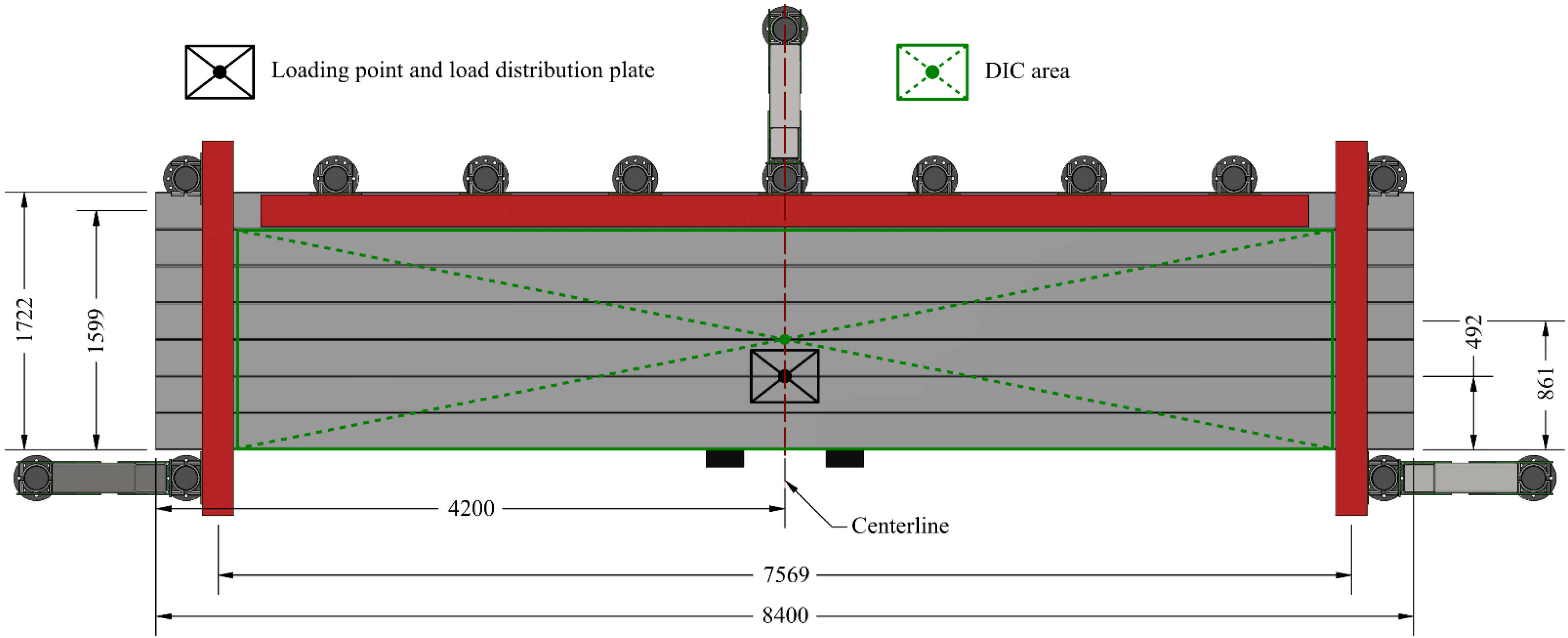
2.3.2. Laboratory Test Setup
2.3.3. Laboratory Test Monitoring
2.4. DIC Monitoring Setup Comparison
3. Experimental Results and Analysis
3.1. Laboratory Test
3.1.1. Laboratory Test Pattern Recognition
- Whether a speckle pattern is applied;
- Whether the grey level distribution within the pattern is sufficient [43];
- Undesirable lighting and reflections on the surface affect the above points;
- Changes in lighting or reflections during testing affects the algorithm’s ability to match the image patterns.
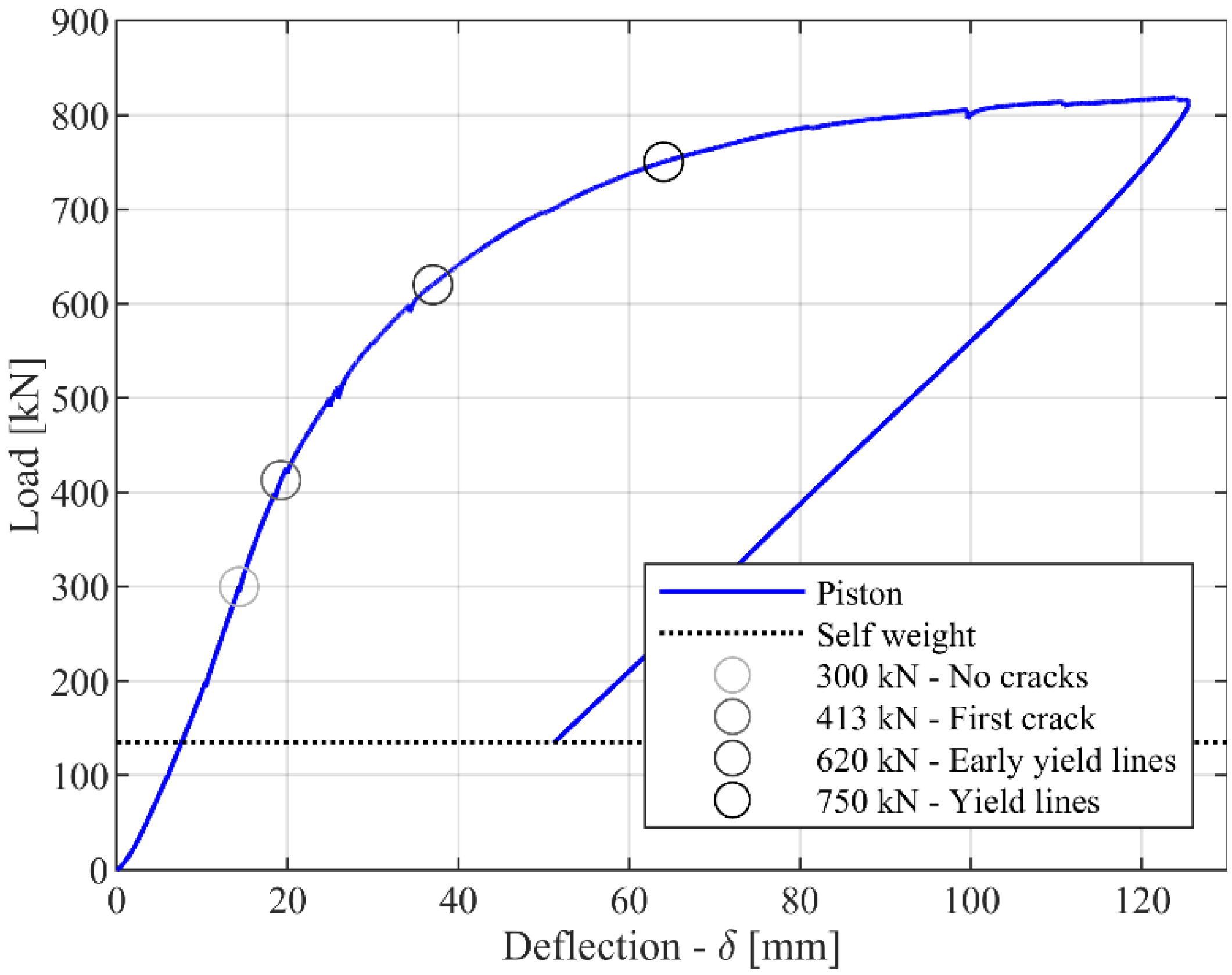
3.1.2. Laboratory Test Crack Detection
3.1.3. Laboratory Crack Width Measurements
3.2. Strip Tests
3.2.1. Strip Test Pattern Recognition and Optimization
- The parameters of the grey level stretch may be varied, but the exact same parameters were applied to all images in the image series;
- Images with larger bit-depth are preferred because of the additional information stored in the image;
- Camera noise is also stretched, which may increase the overall noise in the results. It is therefore a balance between the additional information gained and the noise level;
- Contour is not changed.
3.2.2. Strip Test Crack Detection
3.2.3. Strip Test Crack Widths
4. Evaluation of Results towards Proof-Loading
Future Probabilistic Application of Test Results
5. Conclusions
- The laboratory slab surface with speckle pattern was well identified by the DIC software.
- The in situ specimen surfaces with no speckle patterns and only concrete surface texture showed larger areas with good readability, but in some areas, the surface was not read well by the DIC software.
- Enhancing the in situ images using linear grey level transformation resulted in images that were identified well.
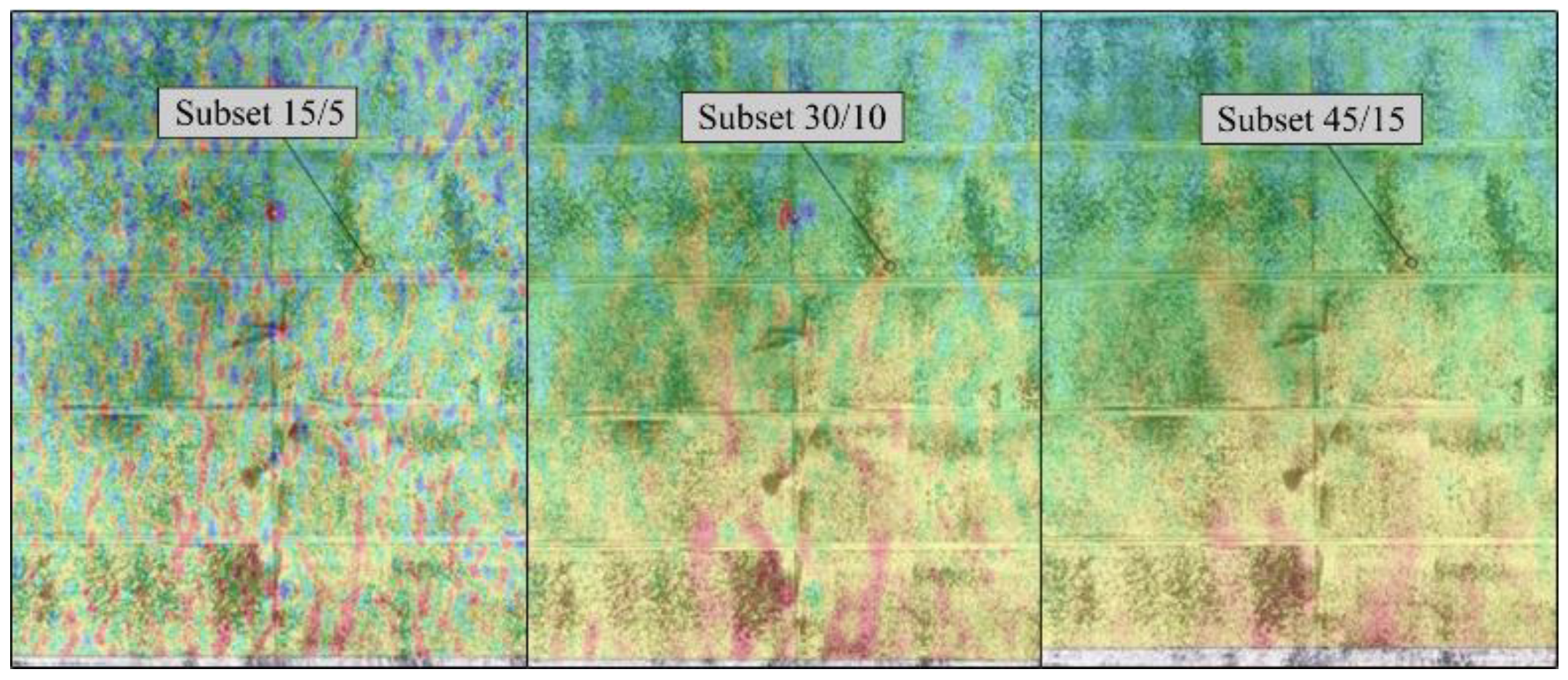
- The successful enhancement resulted in a good surface identification, thus enabling the use of different subset configurations (15/5, 30/10, 45/15).
- Subset 15/5 worked well in the laboratory test, where the cracks were detected in the elastic stage of the load/deflection curve.
- Larger subset configurations smoothen the strain intensities and might only show indications of cracking.
- In the strip tests, subset 15/5 did not work well for crack detection due to noise, but subset 30/10 detected the crack formation well and at an acceptable stage in the load/deflection curve.
- The strip test results also showed that crack indications by the use of multiple cameras for confirmation of cracking can be beneficial.
- Crack widths measured at the time of crack detection and corrected for out-of-plane movement showed values of 0.080 mm to 0.132 mm in the laboratory tests.
- The same procedure resulted in crack width values from 0.104 mm to 0.332 mm in the strip tests.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lantsoght, E.; van der Veen, C.; de Boer, A.; Hordijk, D.A. Proof Load Testing of Reinforced Concrete Slab Bridges in the Netherlands. Struct. Concr. 2017, 18, 597–606. [Google Scholar] [CrossRef] [Green Version]
- Bagge, N.; Popescu, C.; Elfgren, L. Failure Tests on Concrete Bridges: Have We Learnt the Lessons? Struct. Infrastruct. Eng. 2018, 2479, 292–319. [Google Scholar] [CrossRef]
- Schmidt, J.W.; Halding, P.S.; Jensen, T.W.; Engelund, S. High Magnitude Loading of Concrete Bridges. ACI Struct. J. 2018, 323, 9.1–9.20. [Google Scholar]
- Jensen, T.W.; Poulsen, P.N.; Hoang, L.C. Limit Analysis of Reinforced Concrete Slabs with Construction Joints. Eng. Struct. 2020, 205, 110062. [Google Scholar] [CrossRef]
- Anonymous. Destruction of the Prestressed Concrete Footbridge at the South Bank. Civ. Eng. Rev. 1952, 6, 330–334. [Google Scholar]
- Gosbell, K.B.; Stevens, L.K. Test Loading of a Full Scale Bridge. In Proceedings of the Australian Road Research Board; 1968; Volume 4, pp. 2018–2041. Available online: https://trid.trb.org/view/103665 (accessed on 6 July 2021).
- Goodpasture, D.W.; Burdette, E.G. Full Scale Tests to Failure of Four Highway Bridges. Am. Railw. Eng. Assoc. 1973, 74, 454–473. [Google Scholar]
- Isaksen, H.R.; Kanstad, T.; Olsen, P.-E. Prøvebelastning Av Bru Nr 02-1234 Smedstua Bru; Statens Vegvesen: Vegdirektoratet, Norway, 1998. [Google Scholar]
- Zhang, J.; Peng, H.; Cai, C.S. Field Study of Overload Behavior of an Existing Reinforced Concrete Bridge under Simulated Vehicle Loads. J. Bridg. Eng. 2011, 16, 226–237. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, H.; Cai, C.S. Destructive Testing of a Decommissioned Reinforced Concrete Bridge. J. Bridg. Eng. 2013, 18, 564–569. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L. Shear in Reinforced Concrete Slabs under Concentrated Loads Close to Supports; Uitgeverij BOXPress: North Brabant, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Elmont, V.J. Test-Loading until Breaking Point of a 100-Foot Arch Bridge. Can. Eng. 1913, 24, 739–744. [Google Scholar]
- Rösli, A. Die Versuche an Der Glattbrücke in Opfikon. Eidgenössische Mater. Und Versuchsanstalt Für Ind. Bauwes. Und Gew. 1963, 192, 7–24. [Google Scholar]
- Bergström, M.; Täljsten, B.; Carolin, A. Failure Load Test of a CFRP Strengthened Railway Bridge in Örnsköldsvik, Sweden. J. Bridg. Eng. 2009, 14, 300–308. [Google Scholar] [CrossRef]
- Köppel, S.; Vogel, T. Feldversuch Steilerbachbrücke. In Institut für Baustatik und Konstruktion, Eidgenössische Technische Hochschule Zürich; ETH Library: Zürich, Switzerland, 1997. [Google Scholar] [CrossRef]
- Plos, M. Application of Fracture Mechanics to Concrete Bridges, Chalmers Tekniska Högskola. Avdelningen för Betongbyggnad. 1995. Available online: https://research.chalmers.se/en/publication/1158 (accessed on 6 July 2021).
- Song, H.-W.; You, D.-W.; Byun, K.-J.; Maekawa, K. Finite Element Failure Analysis of Reinforced Concrete T-Girder Bridges. Eng. Struct. 2002, 24, 151–162. [Google Scholar] [CrossRef]
- Jorgenson, J.L.; Larson, W. Field Testing of a Reinforced Concrete HIghway Bridge to Collapse. Transp. Res. Rec. 1976, 66–71. [Google Scholar]
- Azizinamini, A. Old Concrete Slab Bridges.1. Experimental Investigations. J. Struct. Eng. 1994, 120, 3284–3304. [Google Scholar] [CrossRef]
- Nanni, A.; Alkhrdaji, T.; Chen, G.; Barker, M.; Yang, X.; Mayo, R. Overview of Testing to Failure of a Highway Bridge Strengthened with FRP Composites. In Proceedings of the 4th International Symposium on FRP for Reinforcement of Concrete Structures (FRPRCS4), Baltimore, MD, USA, 31 October–5 November 1999; pp. 69–80. [Google Scholar]
- Alkhrdaji, T.; Barker, M.; Chen, G.; Mu, H.; Nanni, A.; Yang, X. Destructive and Non-Destructive Testing of Bridge J857, Phelps County, Missouri. Volume 1—Strengthening and Testing to Failure of Bridge Decks; Springfield: Washington, DC, USA, 2001. [Google Scholar]
- Halding, P.S.; Schmidt, J.W.; Jensen, T.W.; Henriksen, A.H. Structural Response of Full-Scale Concrete Bridges Subjected to High Load Magnitudes. In Proceedings of the SMAR, Zürich, Switzerland, 13–15 September 2017. [Google Scholar]
- Jensen, T.W.; Poulsen, P.N.; Hoang, L.C. Finite Element Limit Analysis of Slabs Including Limitations on Shear Forces. Eng. Struct. 2018, 174, 896–905. [Google Scholar] [CrossRef]
- Jensen, T.W.; Poulsen, P.N.; Hoang, L.C. Layer Model for Finite Element Limit Analysis of Concrete Slabs with Shear Reinforcement. Eng. Struct. 2019, 195, 51–61. [Google Scholar] [CrossRef]
- Vejdirektoratet (The Danish Road Directorate). Vejledning Til Belastnings Og Beregningsgrundlag; Vejregelrådet: Denmark, 2010; Available online: http://vejregler.lovportaler.dk/ShowDoc.aspx?q=Vejledning+til+Belastnings+beregningsgrundlag+for+vej-+stibroer+Vejdirektoratet+-+Vejregelr%C3%A5det%2C+juli+2010&docId=vd-20101203132049684-full (accessed on 6 July 2021).
- Vejdirektoratet (The Danish Road Directorate). Annex A: Lastmodeller for Klassificering Og Bæreevnevurdering (Models of Special Vehicles for Road Bridges); Vejregelrådet: Denmark, 2017; Available online: http://vejregler.lovportaler.dk/searchresult.aspx?texttype=&t=%2fV1%2fNavigation%2fTillidsmandssystemer%2fVejregler%2fAnlaegsplanlaegning%2fBygvaerker%2f (accessed on 6 July 2021).
- Vejdirektoratet (The Danish Road Directorate). Strategic Road Map. Available online: https://www.vejdirektoratet.dk/api/drupal/sites/default/files/2020-03/00-Tungvognsvejnet_Danmark_wcag (accessed on 5 March 2020).
- DafStb. DAfStb-Guideline: Load Tests on Concrete Structures; Deutscher Ausschuss für Stahlbeton: Berlin, Germany, 2000. [Google Scholar]
- ACI Commitee 437. Code Requirements for Load Testing of Existing Concrete Structures (ACI 437.2M-13); American Concrete Institute: Farmington Hills, MI, USA, 2013. [Google Scholar]
- Lantsoght, E.O.L.; Yang, Y.; Van Der Veen, C.; Hordijk, D.A. Stop Criteria for Flexure for Proof Load Testing of Reinforced Concrete Structures. Front. Built Environ. 2019, 5, 47. [Google Scholar] [CrossRef] [Green Version]
- Lantsoght, E.O.L.; Yang, Y.; Tersteeg, R.H.D.; Van Der Veen, C.; De Boer, A. Development of Stop Criteria for Proof Loading. In Proceedings of the Life-Cycle of Engineering Systems: Emphasis on Sustainable Civil Infrastructure—5th International Symposium on Life-Cycle Engineering, IALCCE 2016, Delft, The Netherlands, 16–20 October 2016. [Google Scholar]
- Lantsoght, E.O.L.; Yang, Y.; Van Der Veen, C.; De Boer, A.; Hordijk, D.A. Beam Experiments on Acceptance Criteria for Bridge Load Tests. ACI Struct. J. 2017, 114, 1031–1041. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L.; van der Veen, C.; Hordijk, D.A. Proposed Stop Criteria for Proof Load Testing of Concrete Bridges and Verification. In Proceedings of the Life-Cycle Analysis and Assessment in Civil Engineering: Towards an Integrated Vision—Proceedings of the 6th International Symposium on Life-Cycle Civil Engineering, IALCCE 2018, Ghent, Belgium, 28–31 October 2018. [Google Scholar]
- Lantsoght, E.; Yang, Y.; Tersteeg, R.H.D.; van der Veen, C.; de Boer, A. Stop Criteria for Proof Loading. Life Cycle Eng. Syst. Emphas. Sustain. Civ. Infrastruct. 2016. Available online: https://www.frontiersin.org/articles/10.3389/fbuil.2019.00047/full (accessed on 6 July 2021).
- Lantsoght, E.O.L.; Yang, Y.; Van Der Veen, C.; De Boer, A.; Hordijk, D.A. Determination of Loading Protocol and Stop Criteria for Proof Loading with Beam Tests. In Proceedings of the High Tech Concrete: Where Technology and Engineering Meet—Proceedings of the 2017 Fib Symposium, Maastricht, The Netherlands, 12–14 June 2017. [Google Scholar]
- Lantsoght, E.O.L.; Yang, Y.; Van Der Veen, C.; Hordijk, D.A. Stop Criteria for Proof Load Tests Verified with Field and Laboratory Testing of the Ruytenschildt Bridge Ruytenschildt Field Test. In Proceedings of the IABSE Conference, Copenhagen, Denmark, 25–27 June 2018; pp. 1–8. [Google Scholar]
- Tan, X.; Abu-Obeidah, A.; Bao, Y.; Nassif, H.; Nasreddine, W. Measurement and Visualization of Strains and Cracks in CFRP Post-Tensioned Fiber Reinforced Concrete Beams Using Distributed Fiber Optic Sensors. Autom. Constr. 2021, 124, 103604. [Google Scholar] [CrossRef]
- Halding, P.S.; Schmidt, J.W.; Christensen, C.O. DIC-Monitoring of Full-Scale Concrete Bridge Using High-Resolution Wideangle Lens Camera. In Proceedings of the Maintenance, Safety, Risk, Management and Life-Cycle Performance of Bridges—9th International Conference on Bridge Maintenance, Safety and Management, IABMAS 2018, Melbourne, Australia, 9–13 July 2018. [Google Scholar]
- Christensen, C.O.; Lantsoght, E.O.L.; Schmidt, J.W. Quantification of Digital Image Correlation Applicability Related to In-Situ Proof Load Testing of Bridges. In Proceedings of the SMAR 2019—Fifth Conference on Smart Monitoring, Assessment and Rehabilitation of Civil Structures, Potsdam, Germany, 27–29 August 2019; pp. 1–8. [Google Scholar]
- Halding, P.S.; Christensen, C.O.; Schmidt, J.W. Surface Rotation Correction and Strain Precision of Wide-Angle 2D DIC for Field Use. J. Bridg. Eng. 2019, 24, 04019008. [Google Scholar] [CrossRef] [Green Version]
- European Committee for Standardization EN 1992-1-1, Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings 2008. Available online: https://webshop.ds.dk/en-gb/subjects/standard/ds-en-1992-1-1-ac2008 (accessed on 6 July 2021).
- GOM. GOM Correlate Professional 2018. Available online: https://www.gom.com/ (accessed on 19 November 2020).
- Triconnet, K.; Derrien, K.; Hild, F.; Baptiste, D. Parameter Choice for Optimized Digital Image Correlation. Opt. Lasers Eng. 2009, 47, 728–737. [Google Scholar] [CrossRef] [Green Version]
- Sutton, M.A.; Matta, F.; Rizos, D.; Ghorbani, R.; Rajan, S.; Mollenhauer, D.H.; Schreier, H.W.; Lasprilla, A.O. Recent Progress in Digital Image Correlation: Background and Developments since the 2013 W M Murray Lecture. Exp. Mech. 2017, 57, 1–30. [Google Scholar] [CrossRef]
- Kapoor, M.; Schmidt, J.W.; Sørensen, J.D.; Thöns, S. A Decision Theoretic Approach towards Planning of Proof Load Tests. In Proceedings of the 13th International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP13), Seoul, Korea, 26–30 May 2019. [Google Scholar]
- Kapoor, M.; Thöns, S.; Schmidt, J.W.; Sørensen, J.D.; Christensen, C.O. Decision Analytic Approach for Using Elastic Limit Information from Proof Loading in Bridge Reclassification. Struct. Infrastruct. Eng. Under Rev. Currenly Under Review.
- Schmidt, J.W.; Thöns, S.; Kapoor, M.; Christensen, C.O.; Engelund, S.; Sørensen, J.D. Challenges Related to Probabilistic Decision Analysis for Bridge Testing and Reclassification. Front. Built Environ. 2020, 6, 14. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Mahadevan, S. Fatigue Reliability Analysis Using Nondestructive Inspection. J. Struct. Eng. 2001, 127, 957–965. [Google Scholar] [CrossRef]
- Wall, M.; Burch, S.; Lilley, J. Human Factors in POD Modelling and Use of Trial Data. Insight Non Destr. Test. Cond. Monit. 2009, 51, 553–561. [Google Scholar] [CrossRef]














| Comparison Parameter | Strip 1 | Strip 2 | Lab Test |
|---|---|---|---|
| Camera position | Centered transversely covering along mid-span towards one support | Centered transversely covering along mid-span towards one support | Centered |
| Camera distance | 3.8 m, 2.6 m | 3.8 m, 2.6 m | 3.8 m |
| Speckle pattern | No | No | Yes |
| Variation in lighting over the covered surface | Slight | Slight | No |
| Variation in lighting during testing | Slight | Slight | No |
| Image capture interval | 3 min | 3 min | 10 s |
| Crack Width No. | Measured Value (mm) | Correction (mm) | Corrected Value (mm) |
|---|---|---|---|
| 1 | 0.221 | 0.100 | 0.121 |
| 2 | 0.249 | 0.132 | 0.117 |
| 3 | 0.232 | 0.152 | 0.080 |
| 4 | 0.25 | 0.118 | 0.132 |
| 5 | 0.207 | 0.125 | 0.082 |
| 6 | 0.287 | 0.179 | 0.108 |
| Crack No. | Strip No. | Camera Model | Load Level (kN) | Measured Value (mm) | Correction (mm) | Corrected Value (mm) |
|---|---|---|---|---|---|---|
| 1 | 1 | 550D | 2632 | 0.309 | 0.118 | 0.191 |
| 1 | 1 | 550D | 3280 | 0.509 | 0.218 | 0.291 |
| 2 | 1 | 550D | 2632 | 0.263 | 0.099 | 0.164 |
| 2 | 1 | 550D | 3280 | 0.456 | 0.182 | 0.274 |
| 3 | 1 | 550D | 2632 | 0.256 | 0.103 | 0.153 |
| 3 | 1 | 550D | 3280 | 0.496 | 0.191 | 0.305 |
| 3 | 1 | 6D | 3280 | 0.468 | 0.136 | 0.332 |
| 4 | 1 | 550D | 2632 | 0.196 | 0.092 | 0.104 |
| 4 | 1 | 550D | 3280 | 0.389 | 0.170 | 0.219 |
| 4 | 1 | 6D | 3280 | 0.477 | 0.179 | 0.298 |
| 5 | 1 | 550D | 3280 | 0.373 | 0.155 | 0.218 |
| 5 | 1 | 6D | 3280 | 0.423 | 0.142 | 0.281 |
| Crack No. | Strip No. | Camera Model | Measured Value (mm) | Correction (mm) | Corrected Value (mm) |
|---|---|---|---|---|---|
| 6 | 2 | 550D | 0.335 | 0.160 | 0.175 |
| 6 | 2 | 6D | 0.535 | 0.207 | 0.328 |
| 7 | 2 | 550D | 0.361 | 0.173 | 0.188 |
| 7 | 2 | 6D | 0.508 | 0.241 | 0.267 |
| 8 | 2 | 550D | 0.413 | 0.190 | 0.223 |
| 8 | 2 | 6D | 0.53 | 0.252 | 0.278 |
| 9 | 2 | 550D | 0.457 | 0.217 | 0.240 |
| 9 | 2 | 6D | 0.431 | 0.195 | 0.236 |
| 10 | 2 | 550D | 0.413 | 0.177 | 0.236 |
| 10 | 2 | 6D | 0.493 | 0.229 | 0.264 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Christensen, C.O.; Schmidt, J.W.; Halding, P.S.; Kapoor, M.; Goltermann, P. Digital Image Correlation for Evaluation of Cracks in Reinforced Concrete Bridge Slabs. Infrastructures 2021, 6, 99. https://doi.org/10.3390/infrastructures6070099
Christensen CO, Schmidt JW, Halding PS, Kapoor M, Goltermann P. Digital Image Correlation for Evaluation of Cracks in Reinforced Concrete Bridge Slabs. Infrastructures. 2021; 6(7):99. https://doi.org/10.3390/infrastructures6070099
Chicago/Turabian StyleChristensen, Christian Overgaard, Jacob Wittrup Schmidt, Philip Skov Halding, Medha Kapoor, and Per Goltermann. 2021. "Digital Image Correlation for Evaluation of Cracks in Reinforced Concrete Bridge Slabs" Infrastructures 6, no. 7: 99. https://doi.org/10.3390/infrastructures6070099
APA StyleChristensen, C. O., Schmidt, J. W., Halding, P. S., Kapoor, M., & Goltermann, P. (2021). Digital Image Correlation for Evaluation of Cracks in Reinforced Concrete Bridge Slabs. Infrastructures, 6(7), 99. https://doi.org/10.3390/infrastructures6070099






