Abstract
Deteriorated concrete cover, e.g., spalling or delamination, especially when it occurs at the web of a reinforced concrete (RC) beam within the shear span, can reduce the shear capacity of the beam. Patching of this deteriorated area may be the best option to recover the shear capacity of the beam affected. For this purpose, unsaturated polyester resin mortar (UPR mortar) has been formulated. This research aims to investigate the efficacy of UPR mortar in limiting the shear cracking and so restoring the shear capacity of the deteriorated RC beam. The investigation is carried out by an experimental and numerical study. Two types of beams with a size of 150 × 250 × 1000 mm were prepared. The first type of beams was assigned as a normal beam. The other was a beam with a cut off in the non-stirrup shear span, which was eventually patched with UPR mortar. Two reinforcement ratios were assigned for each type of beams. The results show that UPR mortar is effective to hamper the propagation of diagonal cracks leading to increase the shear failure load by 15–20% compared to the reference (normal) beam. The increase of shear strength with the use of UPR mortar is consistently confirmed at various reinforcement ratios.
1. Introduction
Shear failure of reinforced concrete is characterised in a brittle manner. For safety reasons, the reinforced concrete beam is designed in such a way as to ensure that the shear capacity exceeds the flexural capacity at all points in the beam. This is reflected in the design codes by providing a more conservative reduction factor of shear strength than that of flexural strength [,]. It is also expected that this safety condition is maintained throughout its service life. However, an insufficient shear capacity may arise in the future when deterioration of the concrete occurs in the shear span. In such a situation, repair and strengthening are needed to recover the shear strength of the beam [,,,,,,,,,].
The deterioration of concrete can appear in various forms: cracking, spalling, delamination of concrete cover, etc. Various types of repair system and materials have been developed and applied to remedy the deteriorations. In the case of spalling or delamination, the most common method to repair such damages is by a patching system. This system requires a patch repair material that must be compatible with the concrete being repaired [,,,,,]. ACI 546R-04 [] and EN 1504-9 [] set out basic considerations and properties to select appropriate repair materials to ensure compliance with the parent concrete. However, it is noted that the main goal of the patch repair system is to replace the damaged concrete by new concrete or mortar, without strengthening the deficient strength of the parent concrete []. Patch repair only serves to restore the dimension of the damaged concrete and protect it from further deterioration. To regain or strengthen the deficient strength of the damaged concrete elements, another strengthening system is usually needed. For the case of deterioration that causes a strength reduction, it would be beneficial if the patching material is capable not only to restore the size of the damaged concrete section, but it would also be able to recover the strength of the concrete element being repaired. In this respect, the repair material must sufficiently adhere to the parent concrete so that the two materials, as a composite system, resist internal stresses induced by an external load that equals or exceeds the corresponding failure load of the original beam [,,,]. Survey of literatures shows that there are several repair materials which indicate their capability to restore the structural performance of patched RC elements. However, most of the repair materials were applied to recover the flexural performance of the damaged RC beams, even though some of the beams were repaired in their shear zone [,,,]. Among the scanty literatures on the shear strengthening of RC beams using cementitious based materials, none of them has been utilized for the patching system. Instead, these materials, reinforced with fibre, were used to strengthen the shear strength of RC beams by method of surface jacketing or wrapping [,,,,,,].
The efficacy of the repair material used to restore the shear strength of a reinforced concrete beam can be traced from the influence of this material in altering the development of a diagonal shear crack. There are many mechanisms by which a diagonal shear crack can be formed, depending mainly on the ratio of the shear span to the effective depth of the beam (a/d). A beam with a/d less than 1 indicates an inclined compression crack pattern, where the crack extends directly from the load to the reaction (arch action). On the contrary, a beam with a/d more than 3 shows an inclined tension crack pattern. The crack is initiated by a vertical flexural crack and then inclined toward the load due to the diagonal tension stress induced by the combined flexure and shear stress. For a beam with a/d in the range of 1–3, the formation of a diagonal crack arises from the shear–compression failure pattern [,,,].
The shear strength of a reinforced concrete beam can be deduced from the equilibrium of forces acting on a diagonally cracked beam. In this respect, the shear strength (Vc) of a reinforced concrete beam consists of the shear provided by the uncracked portion of concrete (Vcz), the vertical component of the aggregate interlock force at the surface of the diagonal crack (Viy), and the dowel action of the longitudinal reinforcement (Vd) [,,,]. The presence of the repair material can alter the development of the diagonal crack, redistribute a portion of the shear strength components, and eventually affect the ultimate shear strength of the reinforced concrete beam.
This paper investigates the efficacy of unsaturated polyester resin (UPR) mortar as a patch repair material to recover the shear strength of reinforced concrete beams. A series of investigations have been carried out by authors which showed that UPR mortar has good characteristics in term of mechanical and dimensional related performance [,,,,,,], and so this material is promising to be used for shear recovery of damaged RC beam. Previous investigation confirmed the capability of this material to regain the shear deficient of the damaged RC beam []. However, the study was limited to one longitudinal reinforcement ratio and without any attempt to reveal the mechanism of shear recovery of the patched RC beam. The current study is an extension of the previous study to cover other reinforcement ratios. The investigation is confined to a shear span without stirrups. Both experimental and numerical simulations are presented to reveal the mechanism by which UPR mortar can regain the shear strength of the reinforced concrete beam. The simulation is expanded to investigate the influence of UPR mortar on the shear strength of a beam with various longitudinal reinforcement ratios.
2. Materials and Methods
2.1. Materials
The concrete used for this investigation was a conventional (normal) concrete. Its mixture was proportioned following the Indonesian Standard [] to achieve an average strength of 25 MPa. The obtained mix composition per m3 of concrete was as follows: 388 kg of cement, 771 kg of sand, 941 kg of coarse aggregate, and 225 kg of water. The actual strength of the concrete was determined by the testing of cylinder specimens of 150 × 300 mm. The compressive strength obtained at 28 days was 23.80 MPa and 25.29 MPa for batch 1 and 2, respectively. Meanwhile, the repair material used for patching the reinforced concrete beam was a UPR mortar. It was made from the following constituents per m3: 950 kg of sand, 808 kg of cement, 143 kg of fly ash, 475 kg of UPR, and 24 kg of hardener. The compressive strength of the UPR mortar was determined following the ASTM C 579-01 []. The average compressive strength obtained at 1 day was 73.67 MPa.
2.2. Beam Specimens
Two types of reinforced concrete beam were made, i.e., repair beam (BR) and normal beam (BN). BR was formed with a cut-off at one face of the web. The cut-off was located in the shear span where the diagonal shear crack could be expected to cross over it. After 90 days of ageing, the cut-off was eventually patched with UPR mortar. Figure 1 shows the two types of beams with their reinforcement layout. Two longitudinal reinforcements (i.e., either 2D19 or 2D22) were inserted in the tensile zone along the beam span. In addition, two other longitudinal reinforcements (2D8) were embedded along the compression zone. Vertical stirrups (D6-150) were introduced along one of the shear spans, while the other shear span was assigned with no stirrup. The one with no stirrup was designed to ensure that the beam would fail in shear at this particular span. Table 1 summarizes the beam specimens prepared for the investigation.
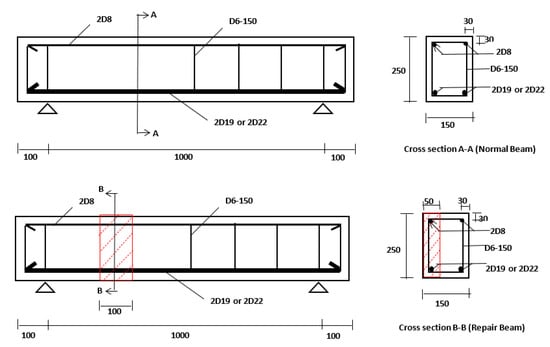
Figure 1.
Two types of beam with their reinforcement layout.

Table 1.
Description of beam specimens.
2.3. Testing Beam Specimens
The beams were tested under a concentrated load which was applied at the mid-span (Figure 2). The load was incrementally imposed at 2kN for each step of loading. This rate of loading was maintained until the beams failed. The shear failure mode of the beams was observed from the initiation, propagation, and final development of the crack patterns. Particular attention was paid to the formation of diagonal cracks, since this type of crack is exclusive to the shear failure mode. The span to depth ratio (a/d) of the tested beams was 2.38, and so the investigation was limited to observe only one type of shear failure. According to [], the a/d of 2.38 is thought to be a transitional value between very short and slender shear spans. The shear transfer mechanism in this type of beam comprises the arch action and beam action, which can be investigated through experimental work and numerical analysis.
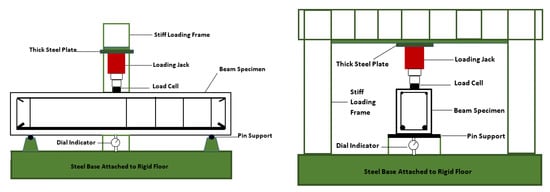
Figure 2.
Setting up the beam testing.
2.4. Numerical Modelling
Numerical modelling was performed using 3D ATENA Engineering software. Both concrete and UPR-mortar were modelled as 3D nonlinear cementitious material 2, where the complete equivalent stress-strain diagram of this model can be seen in Figure 3. Constitutive model for steel follows an elastic-perfectly plastic behavior and the software provided this definition through the option of reinforcement bilinear model. Steel plate was used as a medium to transfer the load at either the loading point or the supports. In this way, the concentration of loads that might affect the fracture of concrete was eliminated. The steel plate was modelled as 3D elastic isotropic, where the steel behaves as an elastic material with unlimited strength.
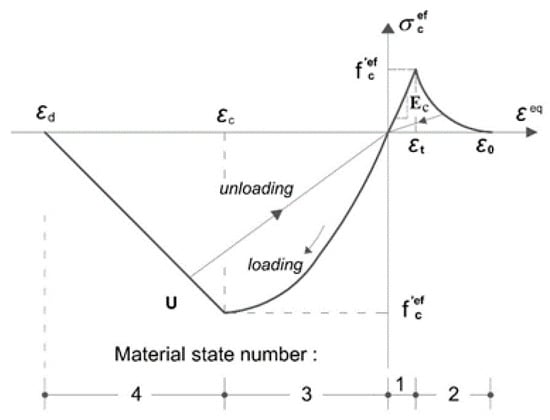
Figure 3.
Equivalent uniaxial stress-strain of concrete.
Meshes of solid 3D finite element generated for both normal and repair beam are shown in Figure 4. A linear brick element type was used for generating these meshes. In the real experiment, the beam was laid on top of pin supports. These supports provided a vertical restraint for the downward movement, but no restraint for the upward movement. The horizontal movement was partially restrained. For these reasons, the supports were modelled as nonlinear spring with a massive stiffness to resist the downward movement and a light stiffness to slightly restrain the upward movement. In addition, a linear elastic spring was defined to partially restrain the horizontal movement. Table 2 summarizes properties of materials and their corresponding constitutive models used in this investigation. Numerical simulation was performed by testing the beam models with a force at specified joint, i.e., at the top centre of the beam. The load was incrementally applied at 200 N until failure. The rate of loading was definitely lower, i.e., about one-tenth of the experimental loading. The smaller rate of loading in this simulation was intended to capture more details of the development of the cracks. The numerical simulation was expanded on similar beams but with various reinforcement ratios.
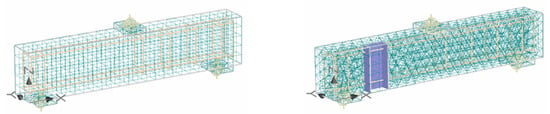
Figure 4.
Finite element model of normal beam (left) and repair beam (right).

Table 2.
Properties of materials and their corresponding constitutive model.
3. Results and Discussion
3.1. Load-Deflection Behaviour
Figure 5 shows the observed load-deflection behaviour of the beams. Generally, all beams exhibit linear behaviour up to at least 50% of their corresponding peak load; after which they show a slight increase in deformation under an increment loading. The beams show a sudden collapse when the loads reach their respective peak value. The influence of patching can be identified as follows: UPR mortar can recover the stiffness of the damaged beams as demonstrated by the similar stiffness of the repair beams to those of undamaged (normal) beams. UPR mortar also restores the shear strength of the damaged beams; even their strengths are greater than the corresponding strengths of the undamaged beams. An increase of strength by 15–20% can be expected when the UPR mortar is used to patch repair the damaged beams. This level of increase is comparable to the shear strengthening of undamaged RC beams using ultra-high performance fibre reinforced concrete (UHPC) jacketing, which gives an increase of 25–28% at ratio a/d of 2.0 [], and 16% at a ratio of a/d 2.5 []. The increase is greater compared to shear strengthening using ferrocement jacketing which provides an increase of only 1.5–5.8% when the strengthening was applied after beam cracking []. Other cement-based fibre composite material indicates that the increase in shear capacity can be achieved only if an adequate strengthening configuration is adopted. When discontinuous U-wrapped strips are applied, they will not be effective to increase the shear strength []. All of these comparisons suggest that patching using UPR mortar is a good alternative to repair shear deficient beam.
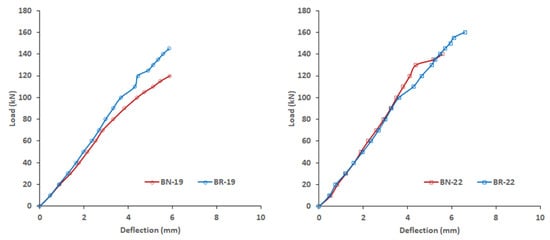
Figure 5.
Load-deflection behaviour.
Figure 6 shows comparisons of the experiment versus numerical simulation of load-deflection behaviours. The similarity between the numerical curves with the experimental load-deflection behaviours indicates the capability of the numerical simulation to capture the behaviour of the investigated beams.
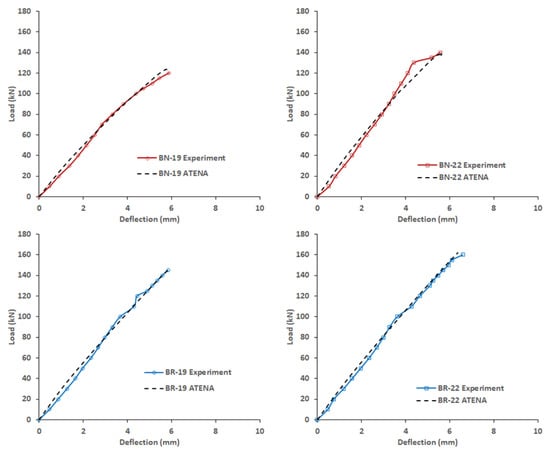
Figure 6.
Experimental vs. numerical load-deflection.
3.2. Shear Cracking Failure
The failure mode of the reinforced concrete beams can be observed from the initiation, propagation, and final formation of cracks leading to the failure of the beams. Typical shear failure modes of reinforced concrete beams are presented in Figure 7. The first crack to appear is a vertical crack, i.e., a typical flexural crack occurs at the mid-span of the beam corresponding to the existence of the maximum bending moment. When the load is increased, more flexural cracks are observed adjacent to the middle span of the normal beams. After a certain load level, some of the vertical cracks propagate in length, directed toward the loading point to form diagonal cracks. The final formation of cracks at the peak load indicates that one of the diagonal cracks (i.e., the one within the shear span without stirrup) has widened significantly, dictating the failure mode of the beam. In all cases of beams, diagonal crack causing beam failure traverses along the point of loading and support.
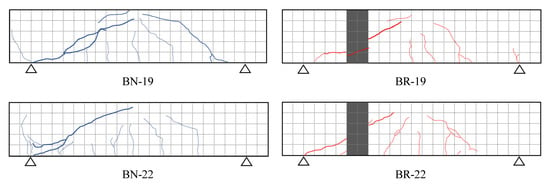
Figure 7.
Shear cracking observed from experimental investigation.
The influence of the UPR mortar on the shear failure mode can be studied from the comparison of the crack development in the normal and repair beams (Figure 7). In both beams, flexural cracks begin at a similar load (about 30 kN). With regard to the diagonal crack formation, the presence of UPR mortar disrupts the continuity of diagonal crack. Even in the BR-22 specimen, diagonal crack does not cross over the UPR-mortar. The lower modulus of elasticity of the UPR mortar compared to the parent concrete could cause the stresses are more concentrated in the concrete section; and so that although the UPR mortar remains solid, on the contrary, the parent concrete section may suffer intense cracks. The observation of crack patterns on the opposite side of the beams confirmed this. The final formation of shear crack that dictates the failure mode of the repair beams occur at higher loads compared to the corresponding failure loads of the normal beams. The UPR mortar can increase the shear strength of reinforced concrete beams around 15–20%.
3.3. Stress Distribution in Concrete Beam
Stresses in the beam induced by an external load can cause cracks in the concrete if the stresses attain the tensile capacity of the concrete. Once the beam is cracked, the stresses are redistributed in such a way that the beam reaches a new equilibrium state of forces. Further increase of the load will intensify the stresses, resulting in the formation of new cracks and expanding the preceding cracks in both length and width. Hence, the initiation, propagation, and formation of cracks are related to the distribution and redistribution of stresses in the beam. Of course, the properties of the materials involved will considerably influence that behaviour. In this section, examples of stresses distribution in the normal and repair beams at various stages of loading are presented (Figure 8 and Figure 9) in order to highlight the cause of cracks formation in the two beams.
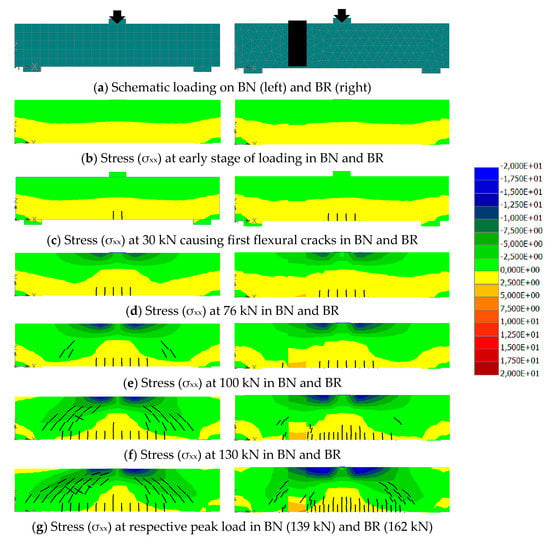
Figure 8.
Normal stress (σxx) distribution and cracks formation at various stages of loading.
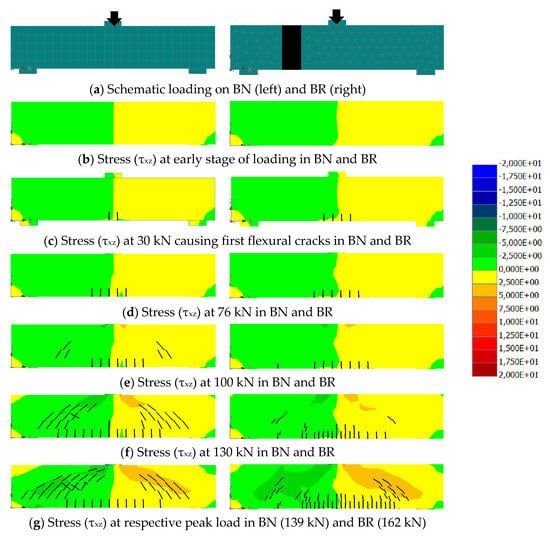
Figure 9.
Shear stress (τxx) distribution and cracks formation at various stages of loading.
At the early stage of loading, negative and positive normal stresses (σxx) due to flexural moment can be identified above and below the neutral axis, respectively. Similarly, negative and positive shear stresses (τxx) due to the shear force can be observed at the left and right shear span, respectively. At this early stage of loading, no crack is found. Therefore, the normal stresses are distributed proportionately in the compression and tension zones. In the same way, a fairly equal distribution of shear stresses can be seen in the left and right shear span.
The first flexural crack appears at about the mid-span of the beam. The load corresponding to the first appearance of flexural cracks is about 30 kN. These cracks cause some redistribution of stresses. The most noticeable influence of these cracks is to alter the neutral axis above the cracks. As a consequence, the depth of the compression zone at this site is decreased. Hence, this zone tends to take higher compressive stresses. An increase of load after the first flexural cracks generates more flexural cracks around the mid-span and intensifies the stresses in the compression zone (Figure 8d). Meanwhile, the formation of flexural cracks seems not to influence the proportionate distribution of shear stresses. However, the stress distribution is significantly altered after the formation of the first diagonal crack. At this load level (about 100 kN and 130 kN for BN and BR, respectively), the depth of the compression zone at around the mid-span is further decreased. On the other hand, at about a half of the shear spans, the depth of the compression zone is increased. The depth of compression zone is greater where a diagonal crack is present in the particular shear span. At the final stage of loading, inclined compression zones develop in directions from the loading point toward the supports. A high concentration of compression and shear stresses can be observed near the loading point at this final stage before failure.
The influence of the UPR mortar in the distribution of stresses can be identified as follows: at early stage of loading up to the first formation of flexural cracks, there is a little influence of UPR mortar. The stresses distributions in the BN and BR are fairly similar. After the formation of the first diagonal cracks in BN, i.e., at a load of 100 kN, the UPR mortar seems to produce a discontinuity of the normal stress distribution (Figure 8e). In addition, the UPR mortar increases the load that initiates the first appearance of diagonal cracks from 100 kN to 130 kN (Figure 8f). At this load level, the repair beam undergoes less intense stresses compared to the normal beam; an incident that can be related to the diagonal crack intensity. A similar case is also observed with respect to the shear stress (Figure 9f). The behaviour may be explained by the fact that the UPR mortar has high tensile strength. Therefore, it can take a higher stress before cracking. Its presence in the shear span provides a means to hinder the development of diagonal shear cracks. Hence, the cracks in this shear span of the BR are less intense and narrower than those of the BN. All of these factors affect the redistribution of stresses. The repair beam with a smaller crack intensity undergoes little stress concentration at the inclined compression zones. At final stage of loading, both beams undergo considerable normal (σxx) and shear (τxz) stress at the inclined compression zone, leading to the development of diagonal cracks that cause beams failure.
3.4. Reinforcement Strain
The evolution of longitudinal reinforcement strain (ϵxx) is presented in Figure 10. At the early stages of loading, the tensile strain along the longitudinal reinforcement follows the bending moment, where the maximum value occurs at the mid-span (strain#6). After flexural cracks occur at a load of 30 kN, the tensile strain of the longitudinal reinforcement at the mid-span (strain #6) start to deviate from the original straight line. Further increase of load up to about 50 kN will cause the strains at around the mid-span (strain #3–6) start to increase sharply. At a loading stage corresponding to the first diagonal cracks (i.e., 100 kN for BN and 130 kN for BR), an increase of tensile reinforcement strain can be observed in a wider zone (strain #1–6). This wider zone of tensile reinforcement strain is related to widespread cracking zone at this load level (see Figure 8 and Figure 9). It can be noted that the presence of UPR mortar tends to conserve the development of strains in the tensile reinforcement to the left of UPR mortar. Even the reinforcement strain #1 of BR is hardly increased. On the other hand, reinforcement strains to the right of UPR mortar (strain #4–6) exhibit higher values; it is interesting to note that strains #4–6 develop similar magnitude. This behaviour indicates that more stresses are distributed to the right of the UPR mortar. At the final stage of loading, high tensile strain extends almost along the whole of the longitudinal reinforcement, with the exception of strain #1 in BR. Examining Figure 8, Figure 9 and Figure 10 and especially the evolution of stress and strain distribution from the first diagonal cracks formation to the final stage of loading, one can see that there is a transition of the shear resistance mechanism from beam action into arch action.
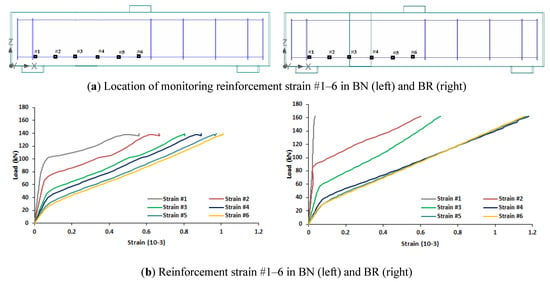
Figure 10.
Reinforcement strain (ϵxx) in BN (left) and BR (right) at various stages of loading.
3.5. Shear Strength
It has been shown that the use of UPR mortar as a patch repair material can alter the initiation, propagation, and final formation of primary diagonal cracks, leading to shear failure of the reinforced concrete beam. The alteration of diagonal cracks development results in an increase of shear strength. The experimental investigation confirms that the shear strength of repair beam is increased by 15–20% compared to the normal beam. In this section, numerical simulation is carried out to show the influence of UPR mortar on shear strength at expanded reinforcement ratio. The results are presented in Figure 11. The increase of shear strength with respect to the use of UPR mortar as a patch repair material can be observed consistently at an extended reinforcement ratio. The level of increase is slightly greater at a higher reinforcement ratio.
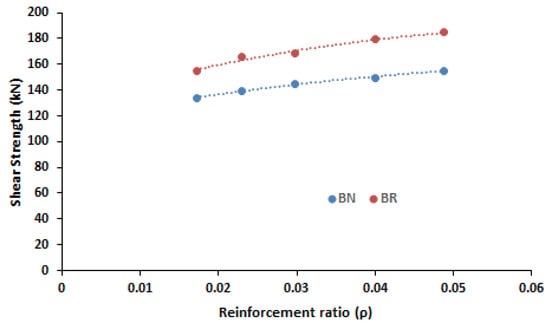
Figure 11.
Influence of UPR mortar on shear strength of RC beam at various reinforcement ratios (numerical simulation).
4. Conclusions
The influence of UPR mortar as a patch repair material on the shear failure of a reinforced concrete beam without stirrup can be identified as follows:
- It causes the first diagonal crack appearing at a higher load compared to that of normal beam.
- The high tensile strength of UPR is beneficial to hamper the propagation of the diagonal cracks.
- It alters the stress distribution in such a way to cause the stresses in the span between support and UPR mortar decrease. On the other hand, the stresses in the span between UPR mortar and loading point increase.
- UPR mortar can increase the shear strength of the reinforced concrete beam about 15–20% at a variety of reinforcement ratios.
Based on the above findings and considering an easy of its application, UPR mortar can be a good alternative to repair shear deficient of the damaged RC beams. The level of shear recovery can be expected comparable to other method of shear strengthening, i.e., jacketing or wrapping using various cementitious based repair materials.
Author Contributions
Conceptualization, S.A.K.; methodology, S.A.K. and A.S.; simulation, S.A.K.; validation, S.A.K. and H.A.S.; formal analysis, S.A.K.; investigation, S.A.K. and A.S.; resources, S.A.K.; data curation, S.A.K.; writing—original draft preparation, S.A.K.; writing—review and editing, H.A.S. and A.S.; visualization, S.A.K.; supervision, S.A.K.; project administration, A.S.; funding acquisition, S.A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by UNIVERSITAS SEBELAS MARET, grant number 516/UN27.21/PP/2019.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
Authors would like to acknowledge student (Hapsara B Wicaksana) and laboratory technical assistance (Mas Topo) at the Civil Engineering Department, Universitas Sebelas Maret for their support during laboratory investigation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- ACI Committee. ACI Committee 318, “Building Code Requirements for Structural Concrete (ACI 318-14)”; ACI Committee: Farmington Hills, MI, USA, 2019. [Google Scholar]
- Badan Standarisasi Nasional. SNI 03-2847, “Persyaratan Beton Struktural Untuk Bangunan Gedung”; Badan Standarisasi Nasional: Jakarta, Indonesia, 2019; pp. 1–695.
- Kristiawan, S.; Supriyadi, A.; Sangadji, S.; Wicaksono, H.B. Shear failure of patched reinforced concrete beam without web reinforcements. Key Eng. Mater. 2017, 737, 441–447. [Google Scholar] [CrossRef]
- Belarbi, A.; Bae, S.W.; Brancaccio, A. Behavior of full-scale RC T-beams strengthened in shear with externally bonded FRP sheets. Constr. Build. Mater. 2012, 32, 27–40. [Google Scholar] [CrossRef]
- Shahbazpanahi, S.; Ali, A.A.A.; Kamgar, A.; Farzadnia, N. Fracture mechanic modeling of fiber reinforced polymer shear-strengthened reinforced concrete beam. Compos. Part B Eng. 2015, 68, 113–120. [Google Scholar] [CrossRef]
- Alam, M.A.; Al Riyami, K. Shear strengthening of reinforced concrete beam using natural fibre reinforced polymer laminates. Constr. Build. Mater. 2018, 162, 683–696. [Google Scholar] [CrossRef]
- Nguyen-Minh, L.; Rovňák, M. Size effect in uncracked and pre-cracked reinforced concrete beams shear-strengthened with composite jackets. Compos. Part B Eng. 2015, 78, 361–376. [Google Scholar] [CrossRef]
- Contamine, R.; Larbi, A.S.; Hamelin, P. Identifying the contributing mechanisms of textile reinforced concrete (TRC) in the case of shear repairing damaged and reinforced concrete beams. Eng. Struct. 2013, 46, 447–458. [Google Scholar] [CrossRef]
- Larbi, A.S.; Contamine, R.; Ferrier, E.; Hamelin, P. Shear strengthening of RC beams with textile reinforced concrete (TRC) plate. Constr. Build. Mater. 2010, 24, 1928–1936. [Google Scholar] [CrossRef]
- Täljsten, B.; Orosz, K.; Blanksvärd, T. Strengthening of concrete beams in shear with mineral based composites laboratory tests and theory. In Proceedings of the International Conference on FRP Composites in Civil Engineering, Miami, FL, USA, 13–15 December 2006; pp. 609–612. [Google Scholar]
- Ombres, L. Structural performances of reinforced concrete beams strengthened in shear with a cement based fiber composite material. Compos. Struct. 2015, 122, 316–329. [Google Scholar] [CrossRef]
- Triantafillou, T.C. Shear strengthening of reinforced concrete beams using epoxy-bonded FRP composites. ACI Struct. J. 1998, 95, 107–115. [Google Scholar]
- Matthews, S. CONREPNET: Performance-based approach to the remediation of reinforced concrete structures: Achieving durable repaired concrete structures. J. Build. Apprais. 2007, 3, 6–20. [Google Scholar] [CrossRef] [Green Version]
- Courard, L.; Garbacz, A. FAILURE OF CONCRETE REPAIR: HOW TO AVOID IT? In Proceedings of the 2nd International Symposium on Advances in Concrete through Science and Engineering, Quebec City, QC, Canada, 11–13 September 2006; pp. 167–191. [Google Scholar]
- Lukovic, M.; Ye, G.; van Breugel, K. Reliable concrete repair: A critical review. In Proceedings of the 14th International Conference on Structural Faults and Repair, Edinburgh, UK, 3–5 July 2012. [Google Scholar]
- Kiani, B.; Liang, R.Y.; Gross, J. Material selection for repair of structural concrete using VIKOR method. Case Stud. Constr. Mater. 2018, 8, 489–497. [Google Scholar] [CrossRef]
- Vaysburd, A.M.; Bissonnette, B.; von Fay, K.F. Compatibility Issues in Design and Implementation of Concrete Repairs and Overlays; US Department of the Interior, Bureau of Reclamation, Technical Service Center, Materials Engineering and Research Laboratory: Denver, CO, USA, 2014; Volume 385, pp. 1–136. [Google Scholar]
- Vaysburd, A.M. DURABILITY OF REPAIRED CONCRETE STRUCTURES—THE BATTLE FOR SURVIVAL. In Proceedings of the 2nd International Symposium on Advances in Concrete through Science and Engineering, Quebec City, QC, Canada, 11–13 September 2006; pp. 207–224. [Google Scholar]
- ACI Committee. ACI Committee 546, “Concrete Repair Guide (ACI 546R-04)”; ACI Committee: Montreal, QC, Canada, 2004. [Google Scholar]
- British Standard Institution. BS EN 1504-9:2008 Products and Systems for the Protection and Repair of Concrete Structures—Definitions, Requirements, Quality Control and Evaluation of Conformity—Part 9: General Principles for Use of Products and Systems; British Standard Institution: London, UK, 2008. [Google Scholar]
- Raupach, M.; Büttner, T. Concrete Repair to EN 1504; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2014. [Google Scholar]
- Bhikshma, V.; Reddy, M.K.; Sunitha, K. Experimental study on rehabilitation of RC beams using epoxy resins. Asian J. Civ. Eng. 2010, 11, 533–542. [Google Scholar]
- Pattanaik, S.C. Structural strengthening of damaged RCC Structures with polymer modified concrete. In Proceedings of the Workshop 2009 on Rehabilitation and Retrofitting of Structures, Mumbai, India, 28–30 August 2009. [Google Scholar]
- Morgan, D.R. Compatibility of concrete repair materials and systems. Constr. Build. Mater. 1996, 10, 57–67. [Google Scholar] [CrossRef]
- Venkiteela, G.; Klein, M.; Najm, H.; Balaguru, P.N. Evaluation of the Compatibility of Repair Materials for Concrete Structures. Int. J. Concr. Struct. Mater. 2017, 11, 435–445. [Google Scholar] [CrossRef] [Green Version]
- Park, S.K.; Yang, D.S. Flexural behavior of reinforced concrete beams with cementitious repair materials. Mater. Struct. Constr. 2005, 38, 329–334. [Google Scholar] [CrossRef]
- Jumaat, M.Z.B.; Kabir, M.H.; Obaydullah, M. Structural performance of reinforced concrete beams repairing from spalling. Eur. J. Sci. Res. 2010, 45, 89–102. [Google Scholar]
- Mansour, W.; Tayeh, B.A. Shear Behaviour of RC Beams Strengthened by Various Ultrahigh Performance Fibre-Reinforced Concrete Systems. Adv. Civ. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Rafeeqi, S.; Lodi, S.; Wadalawala, Z. Behaviour of Reinforced Concrete Beams Strengthened in Shear. J. Ferrocem. 2005, 35, 479–489. [Google Scholar]
- Bahraq, A.A.; Al-Osta, M.A.; Ahmad, S.; Al-Zahrani, M.M.; Al-Dulaijan, S.O.; Rahman, M.K. Experimental and Numerical Investigation of Shear Behavior of RC Beams Strengthened by Ultra-High Performance Concrete. Int. J. Concr. Struct. Mater. 2019, 13, 1–19. [Google Scholar] [CrossRef]
- Collins, M.P.; Bentz, E.C.; Sherwood, E.G.; Xie, L. Adequate theory for the shear strength of reinforced concrete structures. In Proceedings of the Morley Symposium on Concrete Plasticity and Its Application, Cambridge, UK, 23 July 2007; pp. 75–94. [Google Scholar]
- Yang, Y.; van der Veen, C.; Hordijk, D.; de Boer, A. The shear capacity of reinforced concrete members with plain bars. In Proceedings of the 16th International Conference on Structural Fault and Repair, Edinburg, UK, 17–19 May 2016. [Google Scholar]
- Jeong, J.P.; Kim, W. Shear Resistant Mechanism into Base Components: Beam Action and Arch Action in Shear-Critical RC Members. Int. J. Concr. Struct. Mater. 2014, 8, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Birgisson, S.R. Shear Resistance of Reinforced Concrete Beams without Stirrups; Reykjavik University: Reykjavik, Iceland, 2011. [Google Scholar]
- Nilson, A.; Darwin, D.; Dolan, C. Design of Concrete Structures, 14th ed.; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- MacGregor, J.G. Reinforced Concrete Mechanics & Design, 3rd ed.; Prentice Hall: Hoboken, NJ, USA, 1997. [Google Scholar]
- Budi, A.S.; Safitri, E.; Sangadji, S.; Kristiawan, S.A. Shear Strength of HVFA-SCC Beams without Stirrups. Buildings 2021, 11, 177. [Google Scholar] [CrossRef]
- Kristiawan, S.A.; Fitrianto, R.S. Comparison of shrinkage related properties of various patch repair materials. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Bali, Indonesia, 19–20 March 2016; Volume 176, p. 012017. [Google Scholar]
- Kristiawan, S.A.; Utomo, V.P. Shrinkage cracking tendency of repair materials made from unsaturated polyester resin (UPR) mortar. In Proceedings of the 6th International Conference of Asian Concrete Federation, Seoul, Korea, 21–24 September 2014; pp. 1438–1441. [Google Scholar]
- Kristiawan, S.; Supriyadi, A.; Pradana, D.R.; Azhim, M.R.N. Flexural behaviour of one-way patched reinforced concrete (RC) slab under concentrated load. Asian J. Civ. Eng. 2018, 19, 157–164. [Google Scholar] [CrossRef]
- Kristiawan, S.A.; Prakoso, A.B. Flexural Behaviour of Patch-Repair Material Made from Unsaturated Polyester Resin (UPR)-Mortar. Mater. Sci. Forum 2016, 857, 426–430. [Google Scholar] [CrossRef]
- Kristiawan, S.; Supriyadi, A.; Sangadji, S.; Santosa, D. Cracking behaviour and its effect on the deflection of patched-reinforced concrete beam under flexural loading. In Proceedings of the MATEC Web of Conferences, Seoul, Korea, 22–25 August 2017; Volume 138. [Google Scholar]
- Stefanus, K.; Agus, S.; Ageng, B.P.; Siti, R. Mechanical properties of unsaturated polyester resin (UPR)—Mortar and its potential application to restore the strength and serviceability of patched reinforced concrete slab. Key Eng. Mater. 2017, 737, 560–566. [Google Scholar]
- Badan Standarisasi Nasional. SNI 7656:2012, "Tata Cara Pemilihan Campuran Untuk Beton Normal, Beton Berat Dan Beton Massa"; Badan Standarisasi Nasional: Jakarta, Indonesia, 2012.
- American Society of Testing and Materials. C579-01: Standard Test Methods for Compressive Strength of Chemical—Resistance Mortars, Grouts and Monolithic Surfacings and Polymer Concretes; ASTM Int.: West Conshohocken, PA, USA, 2013. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).