Vision-Based Methodology for Characterizing the Flow of a High-Density Crowd on Footbridges: Strategy and Application
Abstract
1. Introduction
1.1. Related Work
1.2. Contribution of the Present Study
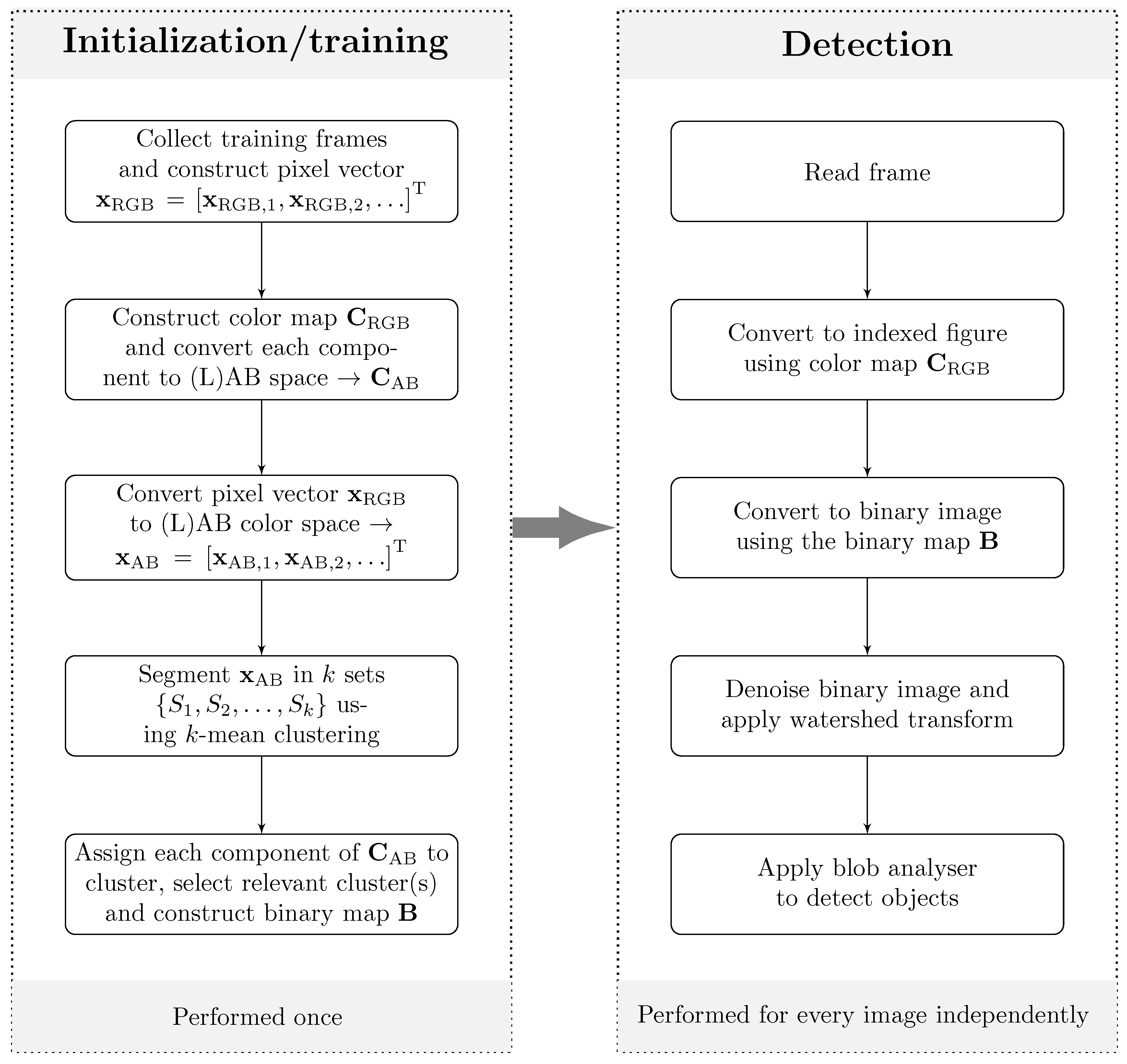
- A computationally efficient approach to detect the pedestrians is proposed employing image indexing by a limited number of colors. A detection map for the colors corresponding to the detection is only initialized a single time using a vector quantization algorithm which greatly enhances the processing speed.
- An approach is proposed to minimize the influence of the random measurement noise. To this extent, a Kalman filter and smoother are applied thereby maximally exploiting the fact that the results are processed offline instead of online. Its optimal characteristics are determined using an expectation maximizing algorithm. The methodology in [42] only used a Kalman filter where its parameters were chosen using engineering judgment.
- An overview of the present systematic measurement errors in the envisaged scope of applications is presented and its effect on the obtained trajectories is evaluated.
- The methodology is applied on a benchmark data set yielding the time-variant positions of all the participants which constitutes an indispensable quantity for the benchmark data set. Moreover, the time duration is now much longer (>2 h instead of 10 min).
- The considered activities now comprise both walking and jogging events instead of only walking events.
- Besides a static camera setup, additional footage captured by a drone is now considered as well.
2. Large-Scale Measurement Campaign
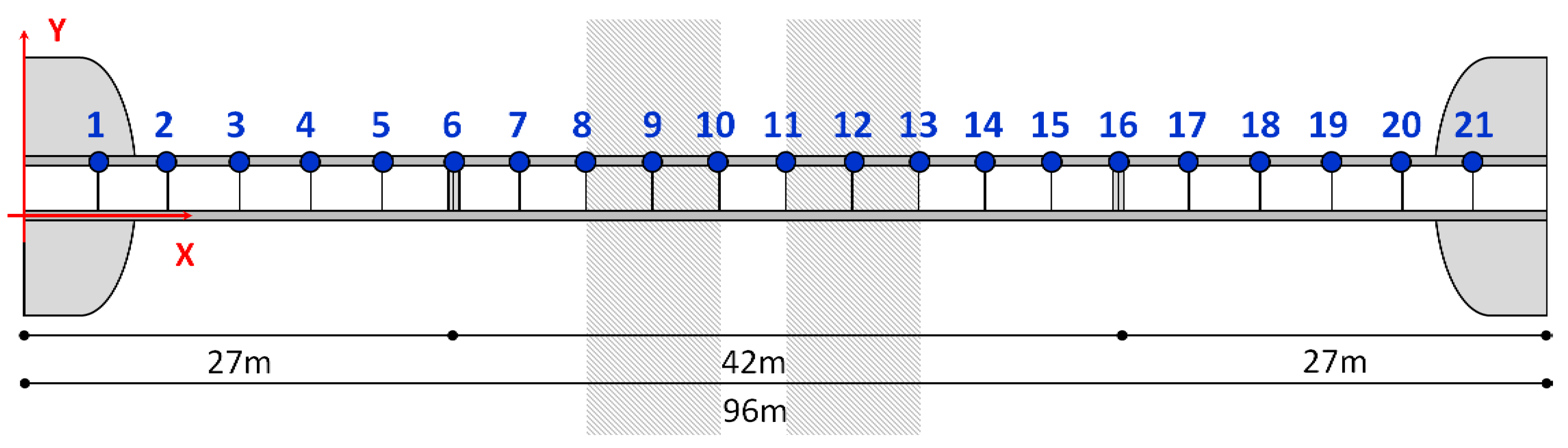
2.1. Camera Setup
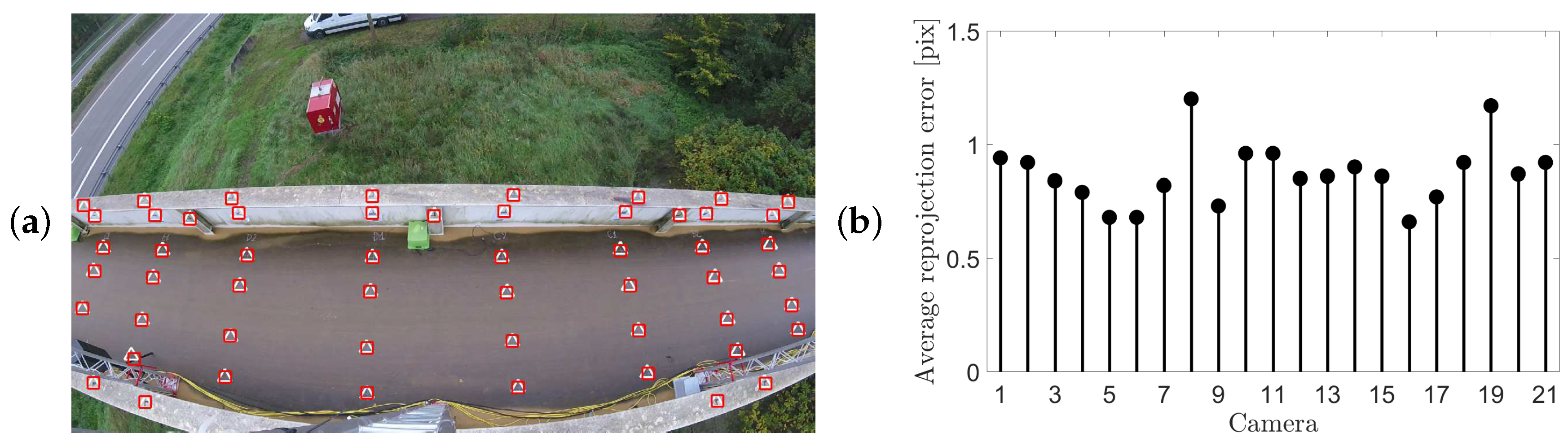
2.2. Calibration Points
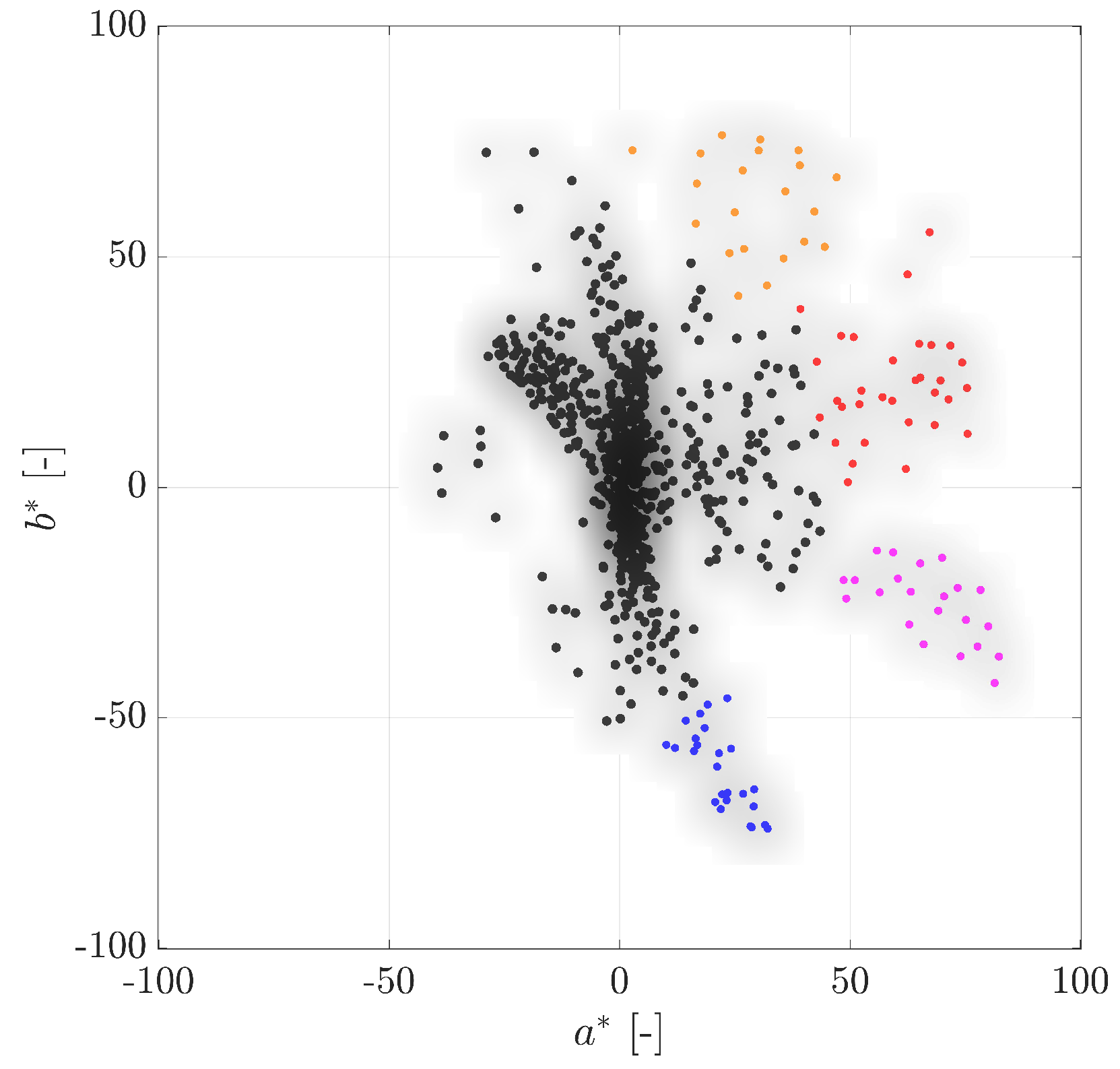
2.3. Colored Hats
3. Pedestrian Detection
4. Pedestrian Trajectory Reconstruction
4.1. Transformation of 2D Image Coordinates to 3D World Coordinates
4.1.1. Camera Model
4.1.2. Camera Calibration
4.1.3. Position and Orientation Estimation of the Drone
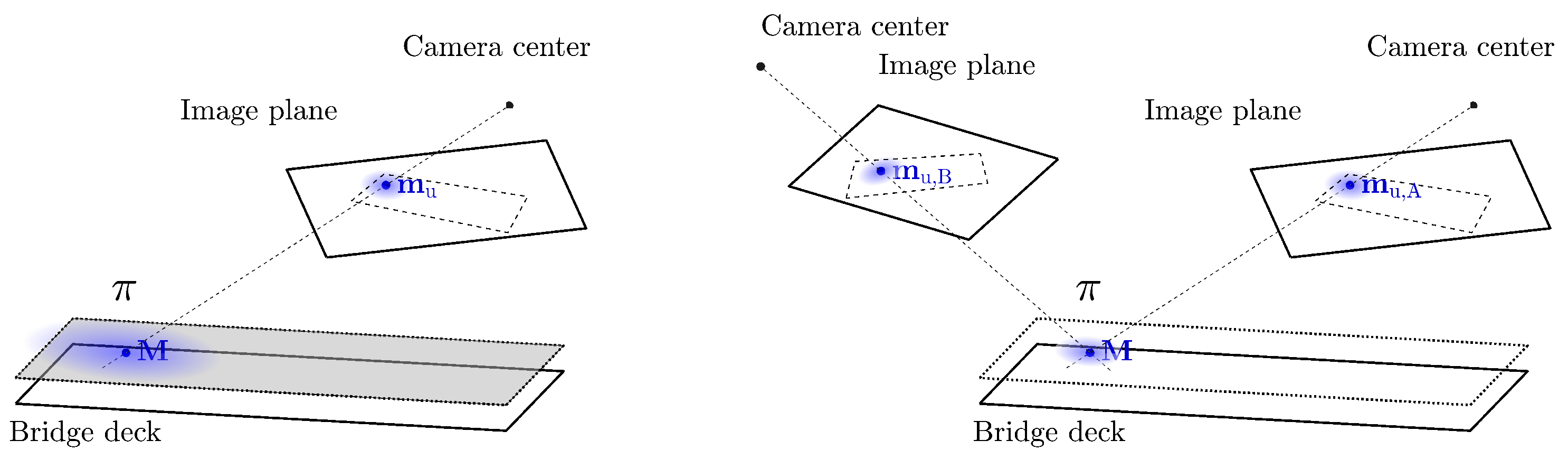
4.1.4. Retrieving the 3D Position Using Stereo-View Geometry: Triangulation
4.1.5. Retrieving the 3D Position Using Mono-View Geometry: Homography
4.2. Trajectory Reconstruction Using a Kalman Filter
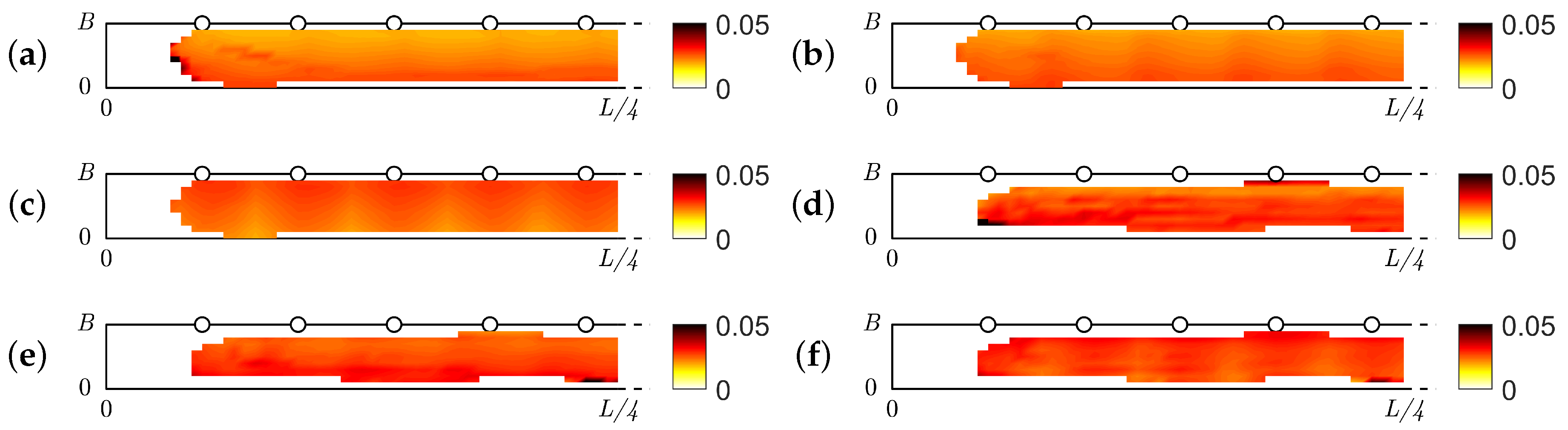
5. Results and Discussion
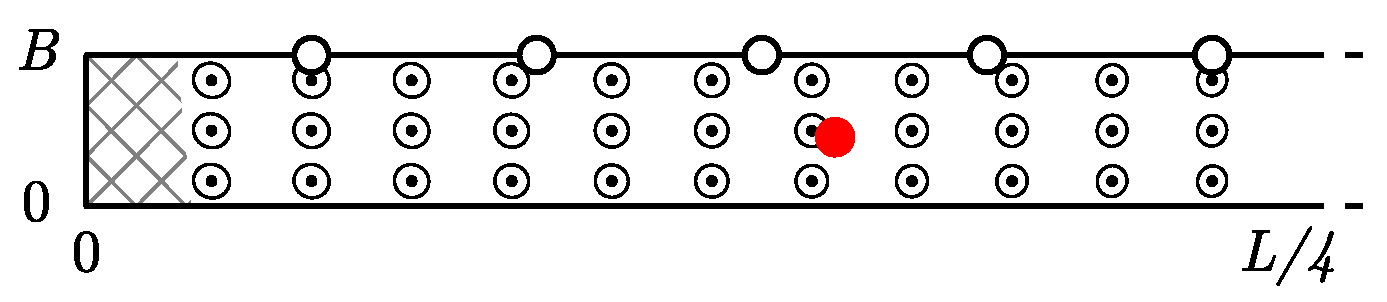
5.1. Theoretical Example to Evaluate the Effect of the Systematic Measurement Errors
5.1.1. Effect of the Shape of the Hat
5.1.2. Effect of the Vertical Sway of the Head
5.2. Experimental Results
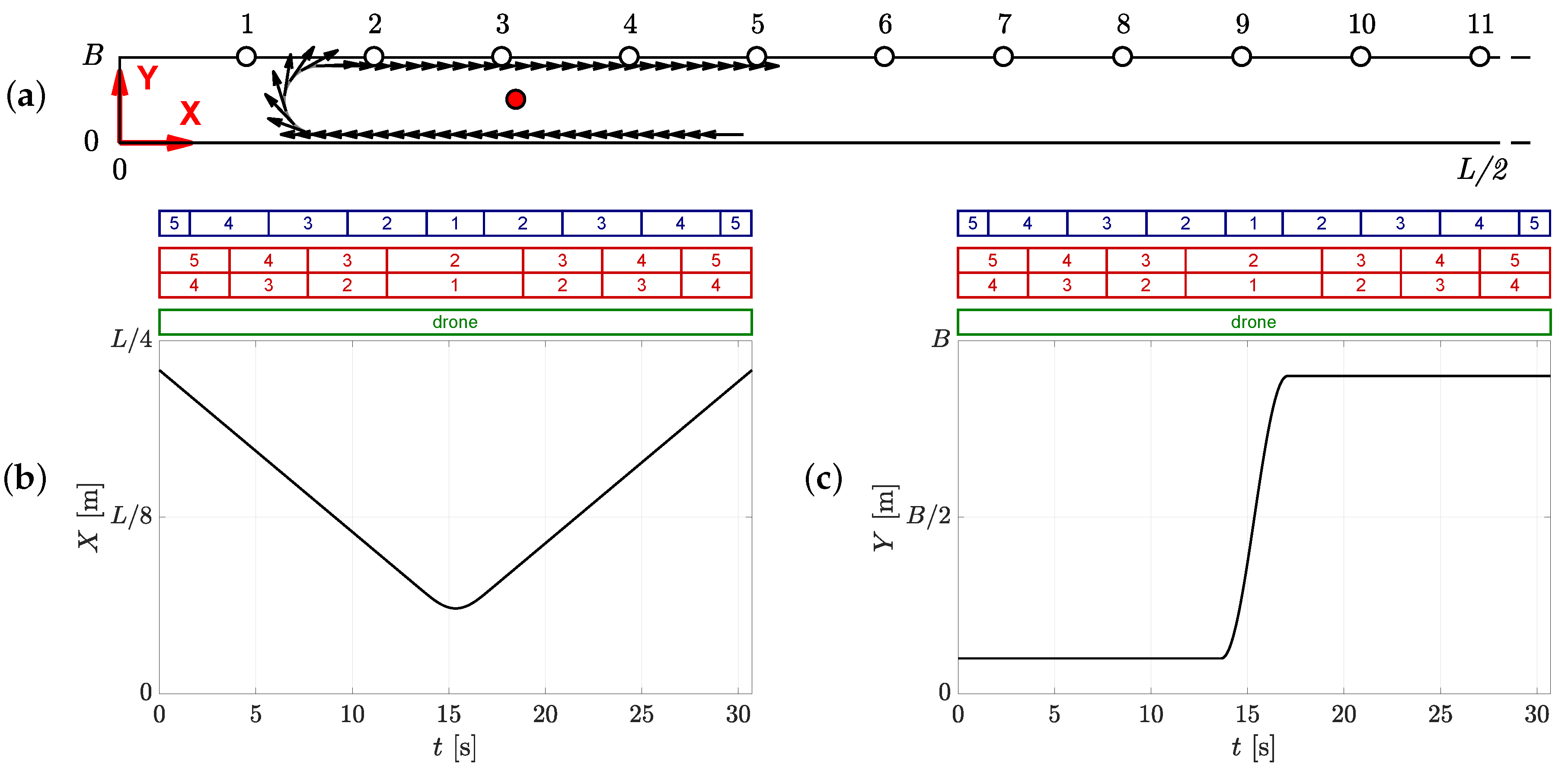
5.2.1. Obtained Trajectories
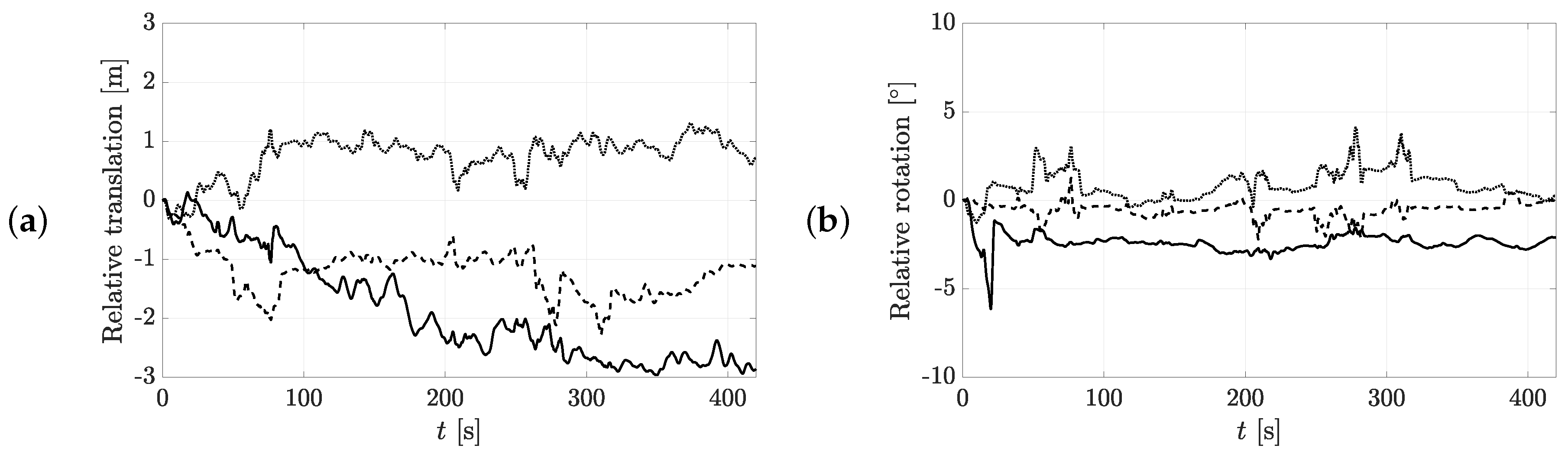
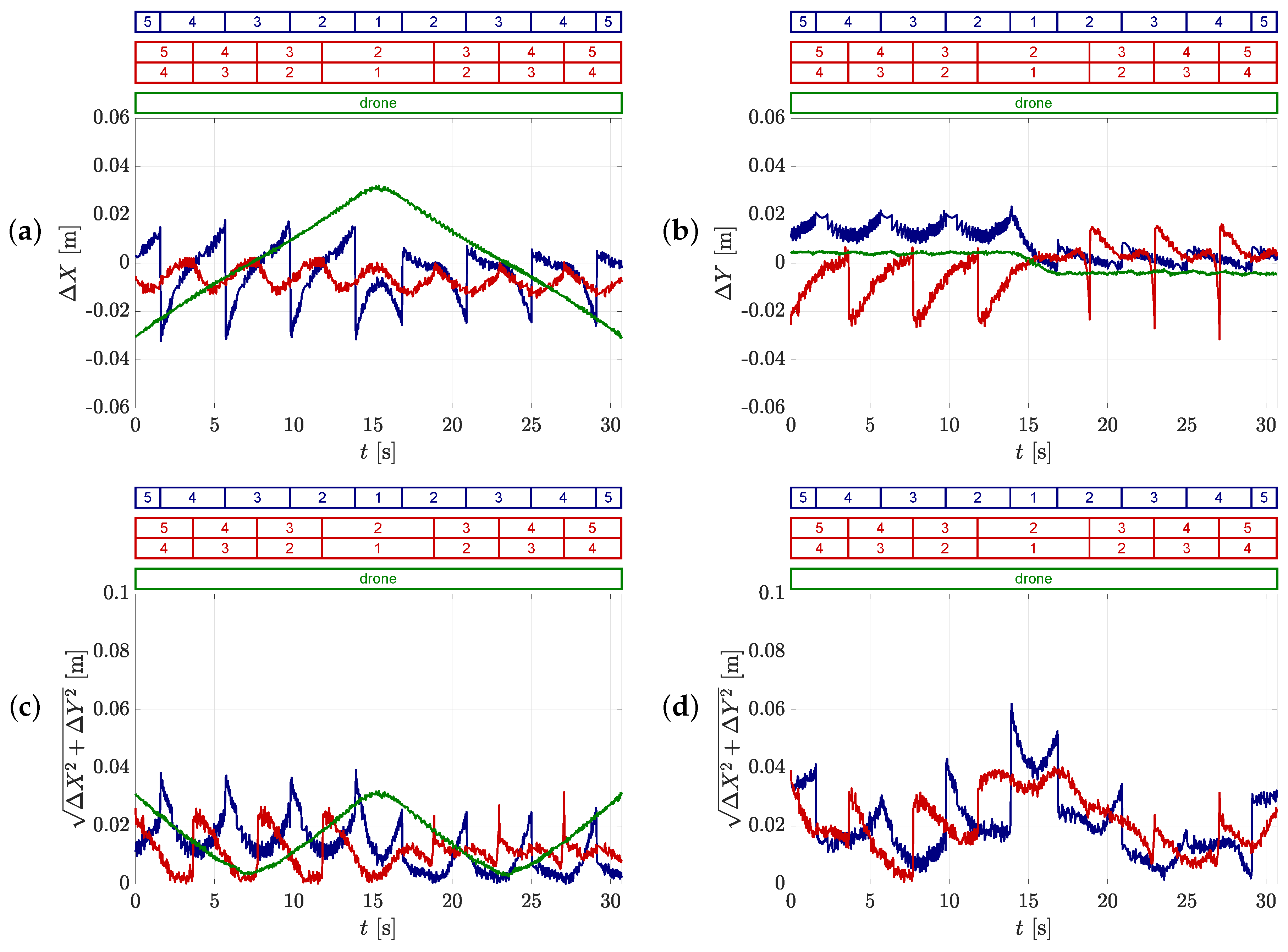
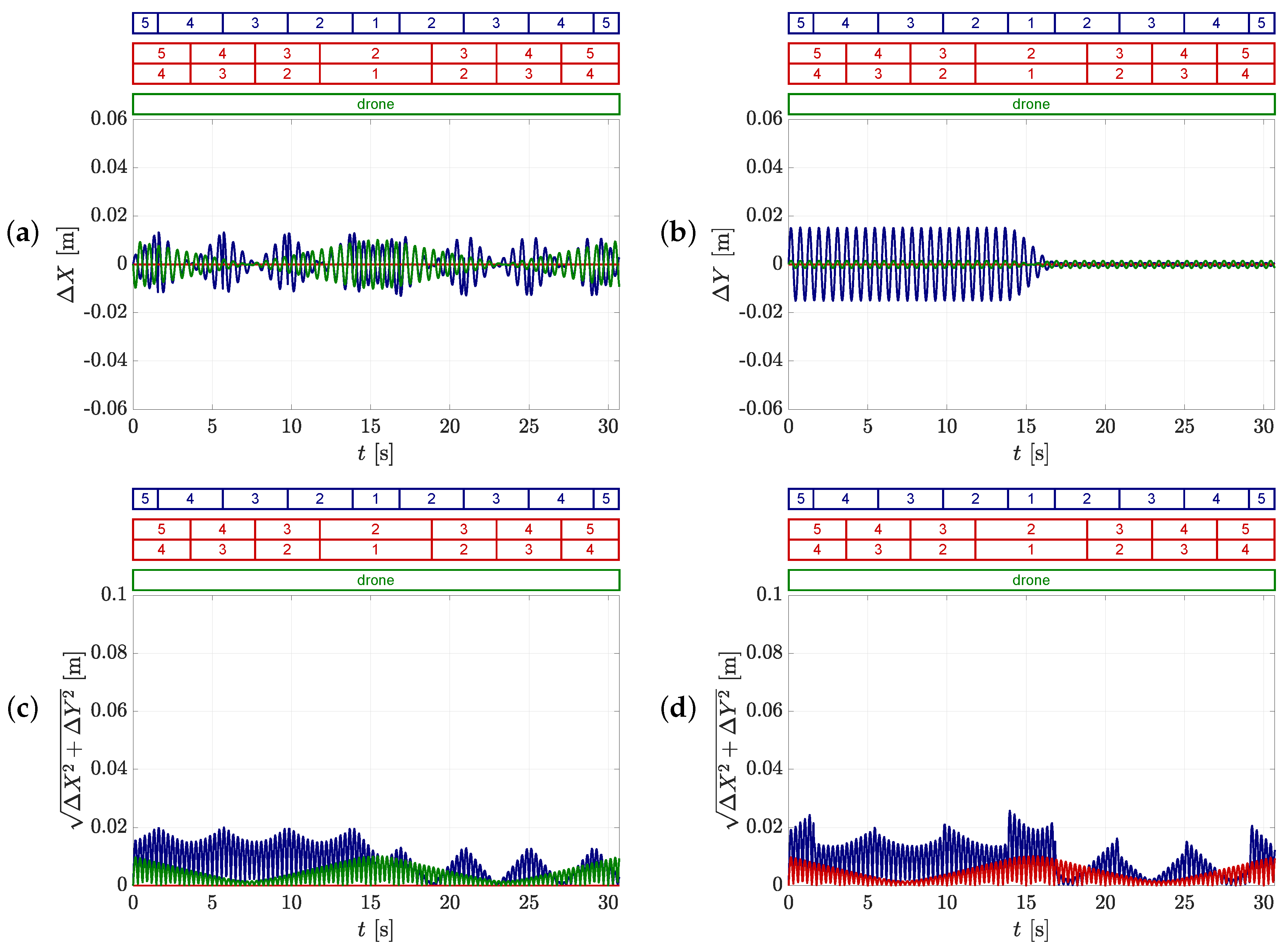
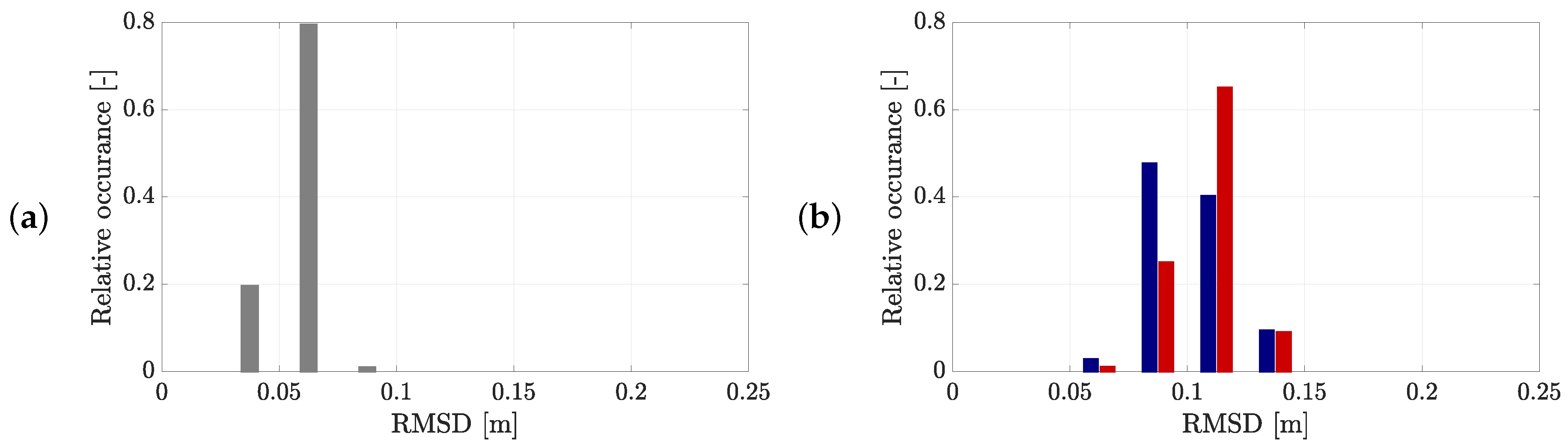
5.2.2. Uncertainty of the Obtained Trajectories by the Static Camera Setup
5.2.3. Uncertainty of the Obtained Trajectories with the Drone
5.2.4. Comparison of the Different Camera Setups
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FOV | Field of View |
| KLT | Kanade-Lucas-Tomasi |
| KF | Kalman Filter |
| RTS | Rauch-Tung-Striebel |
| EKF | Extended Kalman Filter |
| RMSD | Root Mean Squared Difference |
Appendix A. Derivation of the Homography Based on Plane Equation and Camera Projection Matrix
References
- Brunetti, A.; Buongiorno, D.; Trotta, G.F.; Bevilacqua, V. Computer vision and deep learning techniques for pedestrian detection and tracking: A survey. Neurocomputing 2018, 300, 17–33. [Google Scholar] [CrossRef]
- Cao, Y.; Guan, D.; Huang, W.; Yang, J.; Cao, Y.; Qiao, Y. Pedestrian detection with unsupervised multispectral feature learning using deep neural networks. Inf. Fusion 2019, 46, 206–217. [Google Scholar] [CrossRef]
- Khalifa, A.F.; Badr, E.; Elmahdy, H.N. A survey on human detection surveillance systems for Raspberry Pi. Image Vis. Comput. 2019, 85, 1–13. [Google Scholar] [CrossRef]
- Hou, Y.L.; Song, Y.; Hao, X.; Shen, Y.; Qian, M.; Chen, H. Multispectral pedestrian detection based on deep convolutional neural networks. Infrared Phys. Technol. 2018, 94, 69–77. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, D.; Lv, L.; Zhang, Q. Multi-task learning for dangerous object detection in autonomous driving. Inf. Sci. 2018, 432, 559–571. [Google Scholar] [CrossRef]
- Campmany, V.; Silva, S.; Espinosa, A.; Moure, J.; Vázquez, D.; López, A. GPU-based pedestrian detection for autonomous driving. Procedia Comput. Sci. 2016, 80, 2377–2381. [Google Scholar] [CrossRef]
- Bruno, L.; Corbetta, A. Uncertainties in crowd dynamic loading of footbridges: A novel multi-scale model of pedestrian traffic. Eng. Struct. 2017, 147, 545–566. [Google Scholar] [CrossRef]
- Ahmadi, E.; Caprani, C.; Heidarpour, A. An equivalent moving force model for consideration of human-structure interaction. Appl. Math. Model. 2017, 51, 526–545. [Google Scholar] [CrossRef]
- Ahmadi, E.; Caprani, C.; Živanović, S.; Heidarpour, A. Vertical ground reaction forces on rigid and vibrating surfaces for vibration serviceability assessment of structures. Eng. Struct. 2018, 172, 723–738. [Google Scholar] [CrossRef]
- Georgakis, C.T.; Ingólfsson, E. Recent advances in our understanding of vertical and lateral footbridge vibrations. In Proceedings of the 5th International Footbridge Conference, Crete, Greece, 22–27 June 2014. [Google Scholar]
- Živanović, S. Benchmark Footbridge for Vibration Serviceability Assessment under Vertical Component of Pedestrian Load. J. Struct. Eng. 2012, 138, 1193–1202. [Google Scholar] [CrossRef]
- Wei, X.; Van den Broeck, P.; De Roeck, G.; Van Nimmen, K. A simplified method to account for the effect of human-human interaction on the pedestrian-induced vibrations of footbridges. In Proceedings of the 10th International Conference on Structural Dynamics, EURODYN 2017, Rome, Italy, 10–13 September 2017. [Google Scholar]
- Van Hauwermeiren, J.; Van Nimmen, K.; Van den Broeck, P. The effect of the spatial distribution of crowds on the structural response to pedestrian excitation. In Proceedings of the 13th International Conference on Recent Advances in Structural Dynamics, Lyon, France, 15–17 April 2019. [Google Scholar]
- Helbing, D.; Molnar, P. Social force model for pedestrian dynamics. Phys. Rev. 1995, 51, 4282–4286. [Google Scholar] [CrossRef] [PubMed]
- Haghani, M.; Sarvi, M.; Shahhoseini, Z.; Boltes, M. Dynamics of social groups’ decision-making in evacuations. Transp. Res. Part C Emerg. Technol. 2019, 104, 135–157. [Google Scholar] [CrossRef]
- Von Krüchten, C.; Schadschneider, A. Empirical study on social groups in pedestrian evacuation dynamics. Phys. A Stat. Mech. Its Appl. 2017, 475, 129–141. [Google Scholar] [CrossRef]
- Karamouzas, I.; Heil, P.; van Beek, P.; Overmars, M.H. A Predictive Collision Avoidance Model for Pedestrian Simulation. In Motion in Games; Egges, A., Geraerts, R., Overmars, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 41–52. [Google Scholar]
- Van den Berg, J.; Guy, S.; Lin, M.; Manocha, D. Reciprocal n-Body Collision Avoidance. Springer Tracts Adv. Robot. 2011, 70, 3–19. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, Herds and Schools: A Distributed Behavioral Model. In SIGGRAPH Computer Graphics; Association for Computing Machinery: New York, NY, USA, 1987; pp. 25–34. [Google Scholar]
- Helbing, D.; Buzna, L.; Johansson, A.; Werner, T. Self-Organized Pedestrian Crowd Dynamics: Experiments, Simulations, and Design Solutions. Transp. Sci. 2005, 39, 1–24. [Google Scholar] [CrossRef]
- Fujino, Y.; Pacheco, B.; Nakamura, S.I.; Warnitchai, P. Synchronization of human walking observed during lateral vibration of a congested pedestrian bridge. Earthq. Eng. Struct. Dyn. 1993, 22, 741–758. [Google Scholar] [CrossRef]
- Dallard, P.; Fitzpatrick, A.J.; Flint, A.; Le Bourva, S.; Low, A.; Ridsdill Smith, R.M.; Willford, M. The London Millennium Footbridge. Struct. Eng. 2001, 79, 17–33. [Google Scholar]
- Setareh, M. Study of Verrazano-Narrows Bridge Movements during a New York City Marathon. J. Bridge Eng. 2011, 16, 127–138. [Google Scholar] [CrossRef]
- Macdonald, J.H.G. Pedestrian-induced vibrations of the Clifton Suspension Bridge, UK. Proc. Inst. Civ. Eng. Bridge Eng. 2008, 161, 69–77. [Google Scholar] [CrossRef]
- Dang, H.V.; SŽivanović, S. Experimental characterisation of walking locomotion on rigid level surfaces using motion capture system. Eng. Struct. 2015, 91, 141–154. [Google Scholar] [CrossRef]
- McDonald, M.G.; Živanović, S. Measuring Ground Reaction Force and Quantifying Variability in Jumping and Bobbing Actions. J. Struct. Eng. 2017, 143. [Google Scholar] [CrossRef]
- Dang, H.V.; Živanović, S. Influence of Low-Frequency Vertical Vibration on Walking Locomotion. J. Struct. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Racic, V.; Brownjohn, J.; Pavic, A. Reproduction and application of human bouncing and jumping forces from visual marker data. J. Sound Vib. 2010, 329, 3397–3416. [Google Scholar] [CrossRef]
- Carroll, S.; Owen, J.; Hussein, M. Reproduction of lateral ground reaction forces from visual marker data and analysis of balance response while walking on a laterally oscillating deck. Eng. Struct. 2013, 49, 1034–1047. [Google Scholar] [CrossRef]
- Bocian, M.; Brownjohn, J.; Racic, V.; Hester, D.; Quattrone, A.; Monnickendam, R. A framework for experimental determination of localised vertical pedestrian forces on full-scale structures using wireless attitude and heading reference systems. J. Sound Vib. 2016, 376, 217–243. [Google Scholar] [CrossRef]
- Neges, M.; Koch, C.; König, M.; Abramovici, M. Combining visual natural markers and IMU for improved AR based indoor navigation. Adv. Eng. Inform. 2017, 31, 18–31. [Google Scholar] [CrossRef]
- Kang, W.; Han, Y. SmartPDR: Smartphone-based pedestrian dead reckoning for indoor localization. IEEE Sens. J. 2015, 15, 2906–2916. [Google Scholar] [CrossRef]
- Tian, Q.; Salcic, Z.; Wang, K.I.; Pan, Y. A Multi-Mode Dead Reckoning System for Pedestrian Tracking Using Smartphones. IEEE Sens. J. 2016, 16, 2079–2093. [Google Scholar] [CrossRef]
- Poulose, A.; Han, D.S. Hybrid indoor localization using IMU sensors and smartphone camera. Sensors 2019, 19, 5084. [Google Scholar] [CrossRef]
- Xing, B.; Zhu, Q.; Pan, F.; Feng, X. Marker-based multi-sensor fusion indoor localization system for micro air vehicles. Sensors 2018, 18, 1706. [Google Scholar] [CrossRef]
- Mirshekari, M.; Pan, S.; Fagert, J.; Schooler, E.M.; Zhang, P.; Noh, H.Y. Occupant localization using footstep-induced structural vibration. Mech. Syst. Signal Process. 2018, 112, 77–97. [Google Scholar] [CrossRef]
- Boltes, M.; Seyfried, A. Collecting pedestrian trajectories. Neurocomputing 2013, 100, 127–133. [Google Scholar] [CrossRef]
- Haghani, M.; Sarvi, M. Herding in direction choice-making during collective escape of crowds: How likely is it and what moderates it? Saf. Sci. 2019, 115, 362–375. [Google Scholar] [CrossRef]
- Shahhoseini, Z.; Sarvi, M. Pedestrian crowd flows in shared spaces: Investigating the impact of geometry based on micro and macro scale measures. Transp. Res. Part B Methodol. 2019, 122, 57–87. [Google Scholar] [CrossRef]
- Feliciani, C.; Nishinari, K. Measurement of congestion and intrinsic risk in pedestrian crowds. Transp. Res. Part C Emerg. Technol. 2018, 91, 124–155. [Google Scholar] [CrossRef]
- Shi, X.; Ye, Z.; Shiwakoti, N.; Tang, D.; Lin, J. Examining effect of architectural adjustment on pedestrian crowd flow at bottleneck. Phys. A Stat. Mech. Its Appl. 2019, 522, 350–364. [Google Scholar] [CrossRef]
- Van Hauwermeiren, J.; Van den Broeck, P.; Van Nimmen, K.; Vergauwen, M. Vision-based methodology for characterizing the flow of a high-density crowd. In Proceedings of the 9th International Conference on Bridge Maintenance, Safety and Management, Melbourne, Australia, 9–13 July 2018; Taylor and Francis Group, CRC Press: Melbourne, Australia, 2018. [Google Scholar]
- Van Nimmen, K.; Lombaert, G.; Jonkers, I.; De Roeck, G.; Van den Broeck, P. Characterisation of walking loads by 3D inertial motion tracking. J. Sound Vib. 2014, 333, 5212–5226. [Google Scholar] [CrossRef]
- Triggs, B.; McLauchlan, P.F.; Hartley, R.I.; Fitzgibbon, A.W. Bundle Adjustment: A Modern Synthesis. In Proceedings of the ICCV 99 Proceedings of the International Workshop on Vision Algorithms: Theory and Practice, Corfu, Greece, 21–22 September 1999. [Google Scholar]
- Berns, R.; Billmeyer, F.; Saltzman, M. Billmeyer and Saltzman’s Principles of Color Technology; Wiley-Interscience, Wiley: Hoboken, NJ, USA, 2000; ISBN 9780471194590. [Google Scholar]
- MATLAB Version 9.1.0.441655 (R2016b); The Mathworks, Inc.: Natick, MA, USA, 2017.
- Thomas, S.W. Efficient inverse color map computation. Graph. Gems II 1991, 116–125. [Google Scholar] [CrossRef]
- Lloyd, S.P. Least Squares Quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Meyer, F. Topographic distance and watershed lines. Signal Process. 1994, 38, 113–125. [Google Scholar] [CrossRef]
- Maurer, C.R., Jr.; Qi, R.; Raghavan, V. A Linear Time Algorithm for Computing Exact Euclidean Distance Transforms of Binary Images in Arbitrary Dimensions. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 265–270. [Google Scholar] [CrossRef]
- Moons, T.; Gool, L.J.V.; Vergauwen, M. 3D Reconstruction from Multiple Images: Part 1—Principles. Found. Trends Comput. Graph. Vis. 2009, 4, 287–404. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge Books Online; Cambridge University Press: Cambridge, UK, 2003; ISBN 9780521540513. [Google Scholar]
- Lucas, B.D.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of the 7th International Joint Conference on Artificial Intelligence, Vancouver, BC, Canada, 24–28 August 1981. [Google Scholar]
- Shi, J.; Tomasi, C. Good features to track. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 21–23 June 1994. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering And Prediction Problems. ASME J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Bertsekas, D.; Tsitsiklis, J. Introduction to Probability; Athena Scientific Books; Athena Scientific: Nashua, NH, USA, 2002; ISBN 9781886529403. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–38. [Google Scholar]













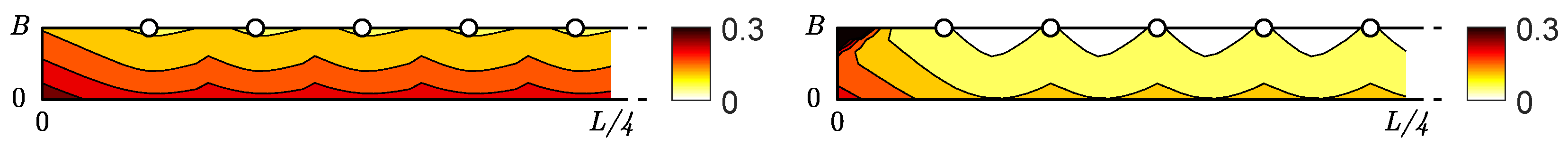

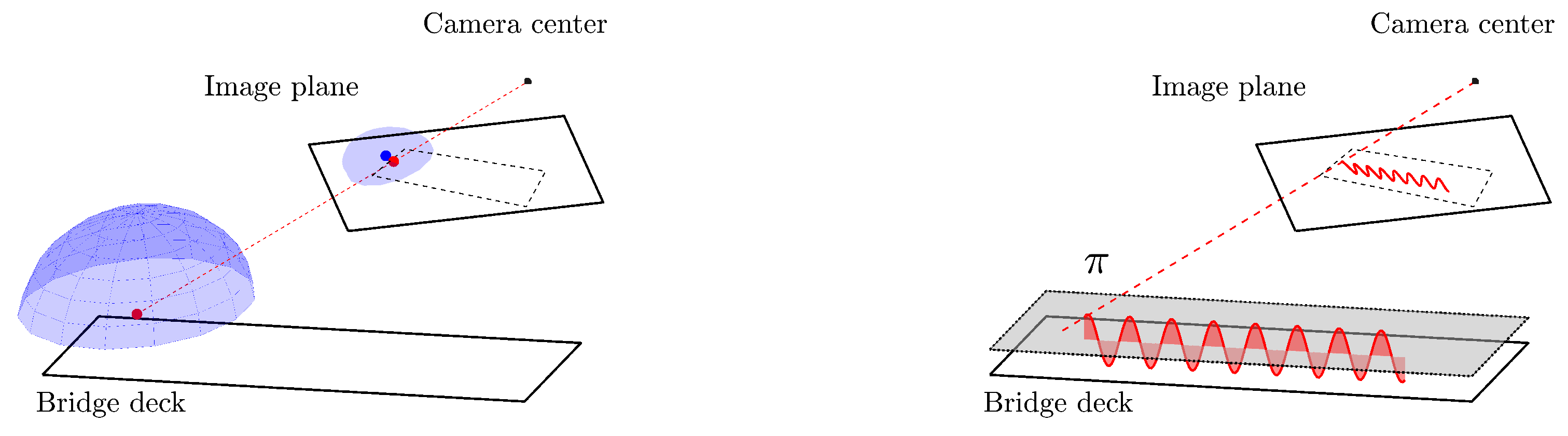

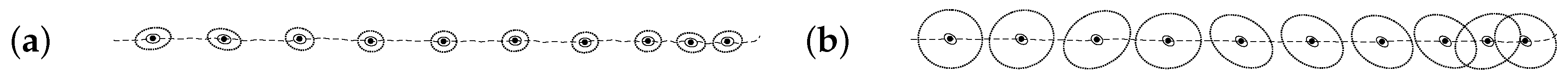

| Test Number | Activity | Number of Participants [-] | Duration [s] | No. of Frames [K] |
|---|---|---|---|---|
| 1 | Jogging | 15 | 800 | 504 |
| 2 | Jogging | 15 | 900 | 567 |
| 3 | Jogging | 15 | 300 | 189 |
| 4 | Walking | 73 | 720 | 454 |
| 5 | Walking | 73 | 315 | 199 |
| 6 | Walking | 73 | 660 | 416 |
| 7 | Walking | 73 | 649 | 409 |
| 8 | Walking | 72 | 1860 | 1172 |
| 9 | Walking | 148 | 1200 | 756 |
| 10 | Walking | 148 | 1200 | 756 |
| 11 | Walking | 148 | 950 | 599 |
| 12 | Walking | 148 | 300 | 189 |
| 13 | Jogging | 74 | 400 | 252 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Hauwermeiren, J.; Van Nimmen, K.; Van den Broeck, P.; Vergauwen, M. Vision-Based Methodology for Characterizing the Flow of a High-Density Crowd on Footbridges: Strategy and Application. Infrastructures 2020, 5, 51. https://doi.org/10.3390/infrastructures5060051
Van Hauwermeiren J, Van Nimmen K, Van den Broeck P, Vergauwen M. Vision-Based Methodology for Characterizing the Flow of a High-Density Crowd on Footbridges: Strategy and Application. Infrastructures. 2020; 5(6):51. https://doi.org/10.3390/infrastructures5060051
Chicago/Turabian StyleVan Hauwermeiren, Jeroen, Katrien Van Nimmen, Peter Van den Broeck, and Maarten Vergauwen. 2020. "Vision-Based Methodology for Characterizing the Flow of a High-Density Crowd on Footbridges: Strategy and Application" Infrastructures 5, no. 6: 51. https://doi.org/10.3390/infrastructures5060051
APA StyleVan Hauwermeiren, J., Van Nimmen, K., Van den Broeck, P., & Vergauwen, M. (2020). Vision-Based Methodology for Characterizing the Flow of a High-Density Crowd on Footbridges: Strategy and Application. Infrastructures, 5(6), 51. https://doi.org/10.3390/infrastructures5060051






