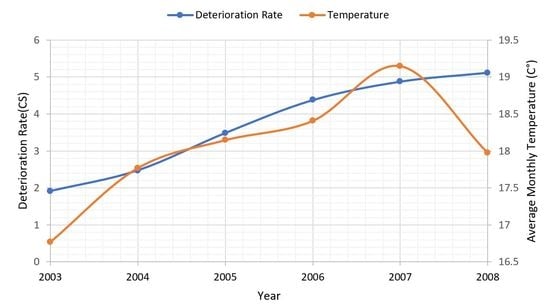
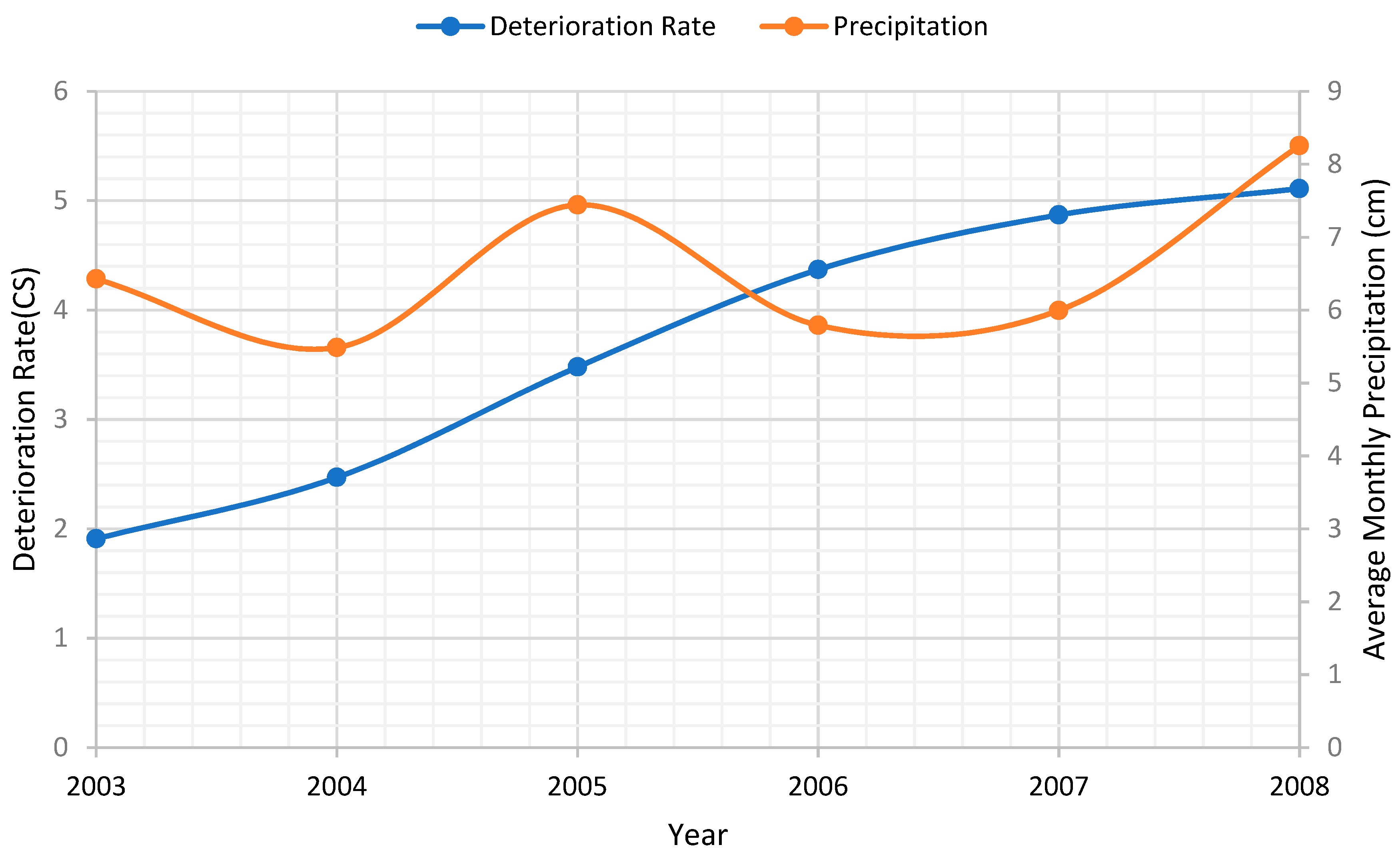
Impacts of Seasonal and Annual Weather Variations on Network-Level Pavement Performance
Abstract
:1. Introduction
2. Methodology
3. Case Study
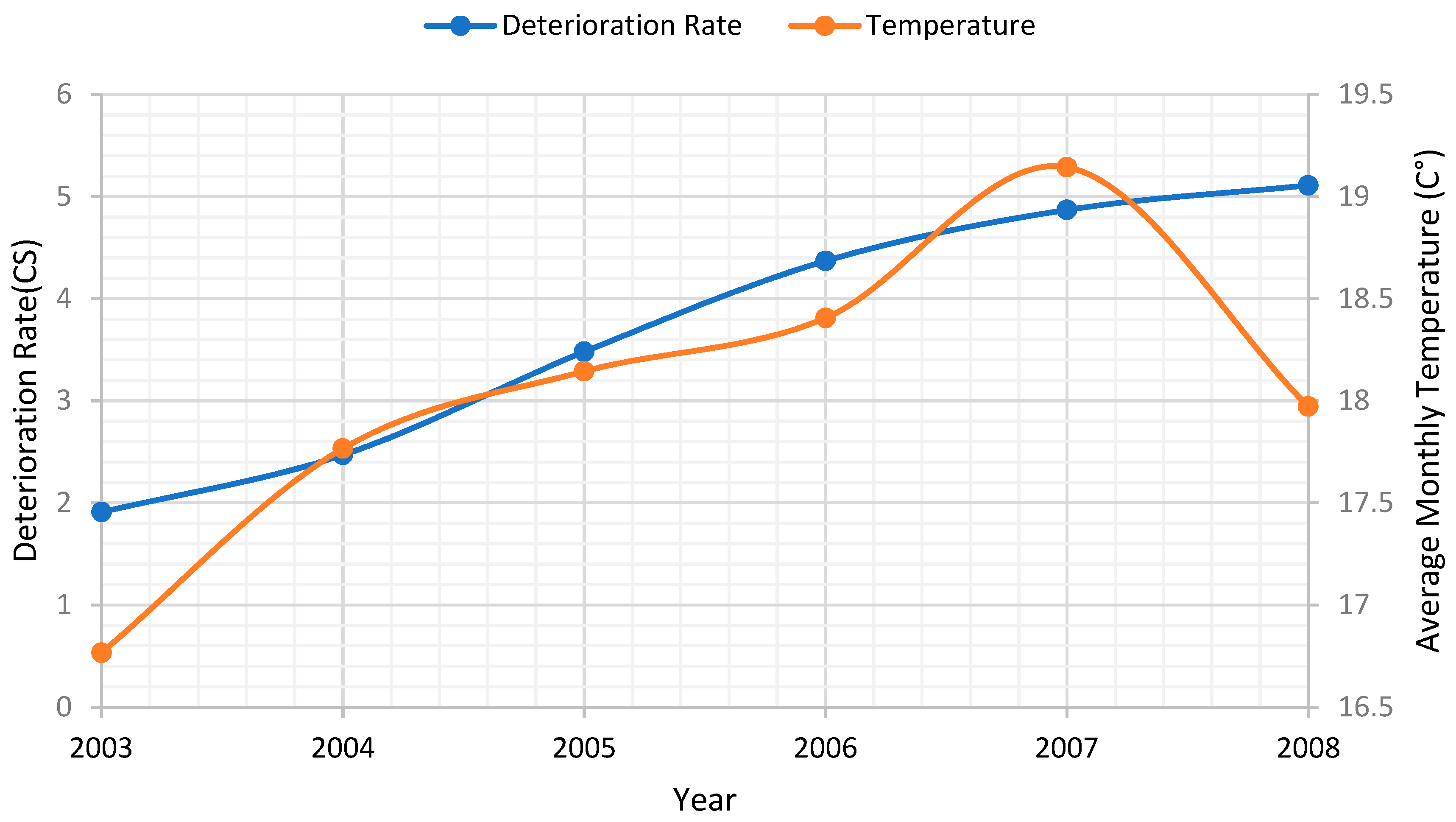
Dataset
4. Estimation Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Variables | Explanation |
| Index for pavement sections | |
| Index for inspection time periods | |
| The ith pavement section’s condition at inspection time period t | |
| Covariates of the ith pavement section at inspection time period t | |
| Unobserved specific factor of the ith pavement section | |
| Error term | |
| , and | Regression Coefficients |
| Vector of values | |
| Vector of values | |
| Vector of values | |
| Vector of values | |
| Block diagonal matrix | |
| Instrument Variables Matrix | |
| First-difference operator |
References
- Anastasopoulos, P.C.; Mannering, F.L. Analysis of pavement overlay and replacement performance using random parameters hazard-based duration models. J. Infrastruct. Syst. 2014, 21, 04014024. [Google Scholar] [CrossRef]
- Arellano, M.; Bond, S. Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations. Rev. Econ. Stud. 1991, 58, 277–297. [Google Scholar] [CrossRef]
- Bäckström, M. Ground temperature in porous pavement during freezing and thawing. J. Transp. Eng. 2000, 126, 375–381. [Google Scholar] [CrossRef]
- Bazlamit, S.M.; Reza, F. Changes in asphalt pavement friction components and adjustment of skid number for temperature. J. Transp. Eng. 2005, 131, 470–476. [Google Scholar] [CrossRef]
- Bosscher, P.J.; Bahia, H.U.; Thomas, S.; Russell, J.S. Relationship between pavement temperature and weather data: Wisconsin field study to verify superpave algorithm. Transp. Res. Rec. 1998, 1609, 1–11. [Google Scholar] [CrossRef]
- Burke, E.J.; Brown, S.J.; Christidis, N. Modeling the recent evolution of global drought and projections for the twenty-first century with the Hadley Centre climate model. J. Hydrometeorol. 2006, 7, 1113–1125. [Google Scholar] [CrossRef]
- Cechet, B. Climate Change Impact on the Pavement Maintenance and Rehabilitation Costs associated with the Australian National Highway Network. In Proceedings of the MODSIM 2005 International Congress on Modelling and Simulation; Modelling and Simulation Society of Australia and New Zealand Inc.: Canberra, Australia, December 2005; pp. 489–496. [Google Scholar]
- Chu, C.Y.; Durango-Cohen, P.L. Estimation of dynamic performance models for transportation infrastructure using panel data. Transp. Res. Part B Methodol. 2008, 42, 57–81. [Google Scholar] [CrossRef]
- Dong, Q.; Huang, B. Evaluation of influence factors on crack initiation of LTPP resurfaced-asphalt pavements using parametric survival analysis. J. Perform. Constr. Facil. 2012, 28, 412–421. [Google Scholar] [CrossRef]
- Gao, L.; Aguiar-Moya, J.P.; Zhang, Z. Bayesian Analysis of Heterogeneity in Modeling of Pavement Fatigue Cracking. J. Comput. Civ. Eng. 2011, 26, 37–43. [Google Scholar] [CrossRef]
- Hong, F.; Prozzi, J.A. Estimation of pavement performance deterioration using Bayesian approach. J. Infrastruct. Syst. 2006, 12, 77–86. [Google Scholar] [CrossRef]
- Hong, F.; Prozzi, J.A. Roughness model accounting for heterogeneity based on in-service pavement performance data. J. Transp. Eng. 2010, 136, 205–213. [Google Scholar] [CrossRef]
- Jayawickrama, P.W.; Thomas, B. Correction of field skid measurements for seasonal variations in Texas. Transp. Res. Rec. J. Transp. Res. Board 1998, 1639, 147–154. [Google Scholar] [CrossRef]
- Ker, H.W.; Lee, Y.H. Preliminary Analysis of Flexible Pavement Serviceability Index Data Using Linear Mixed Effects Models. 2011. Available online: http://mail.tku.edu.tw/yinghaur/lee/papers/TRB2011-PSI-rev.pdf (accessed on 15 May 2019).
- Lee, D.G. Dynamic prediction model of as-built roughness in asphaltic concrete pavement construction. J. Transp. Eng. 2007, 133, 90–95. [Google Scholar] [CrossRef]
- Lee, D.; Russell, J.S. Panel data analysis of factor affecting as-built roughness in highway pavement construction. J. Transp. Eng. ASCE 2004, 130, 479–485. [Google Scholar] [CrossRef]
- Lethanh, N.; Kaito, K.; Kobayashi, K. Infrastructure Deterioration Prediction with a Poisson Hidden Markov Model on Time Series Data. J. Infrastruct. Syst. 2014, 21, 04014051. [Google Scholar] [CrossRef]
- Li, Q.; Mills, L.; McNeil, S. The Implications of Climate Change on Pavement Performance and Design; University of Delaware University Transportation Center: Newark, DE, USA, 2011. [Google Scholar]
- Loizos, A.; Karlaftis, M. Prediction of pavement crack initiation from in-service pavements: A duration model approach. Transp. Res. Rec. J. Transp. Res. Board 2005, 1940, 38–42. [Google Scholar] [CrossRef]
- Madanat, S.M.; Nakat, Z.E.; Sathaye, N. Development of Empirical-Mechanistic Pavement Performance Models Using Data from the Washington State PMS Database; Institute of Transportation Studies: California, CA, USA, 2005. [Google Scholar]
- Marasteanu, M.O.; Li, X.; Clyne, T.R.; Voller, V.; Timm, D.H.; Newcomb, D. Low Temperature Cracking of Asphalt Concrete Pavement; Minnesota Department of Transportation: Dakota, DA, USA, 2004. [Google Scholar]
- Meagher, W.; Daniel, J.S.; Jacobs, J.; Linder, E. Method for Evaluating Implications of Climate Change for Design and Performance of Flexible Pavements. Transp. Res. Rec. J. Transp. Res. Board 2012, 2305, 111–120. [Google Scholar] [CrossRef]
- Mills, B.N.; Tighe, S.L.; Andrey, J.; Smith, J.T.; Huen, K. Climate change implications for flexible pavement design and performance in southern Canada. J. Transp. Eng. 2009, 135, 773–782. [Google Scholar] [CrossRef]
- Mohamed, A.R.; Hansen, W. Effect of nonlinear temperature gradient on curling stress in concrete pavements. Transp. Res. Rec. 1997, 1568, 65–71. [Google Scholar] [CrossRef]
- Mohd Hasan, M.R.; Hiller, J.E.; You, Z. Effects of mean annual temperature and mean annual precipitation on the performance of flexible pavement using ME design. Int. J. Pavement Eng. 2016, 17, 647–658. [Google Scholar] [CrossRef]
- Nakat, Z.S.; Madanat, S.M. Stochastic duration modeling of pavement overlay crack initiation. J. Infrastruct. Syst. 2008, 14, 185–192. [Google Scholar] [CrossRef]
- Nielsen-Gammon, J.W. The Changing Climate of Texas. The Impact of Global Warming on Texas; University of Texas Press: Austin, TX, USA, 2011; pp. 39–68. [Google Scholar]
- Oh, S.M.; Madanat, S.M.; Ragland, D.R.; Chan, C.Y. Evaluation of Traffic and Environment Effects on Skid Resistance in California. Safe Transportation Research and Education Center, 2010. Available online: https://pdfs.semanticscholar.org/2a9d/6c51ee97375850f7fd90999834bfb1e3aab2.pdf (accessed on 15 May 2019).
- Ongel, A.; Harvey, J. Analysis of 30 Years of Pavement Temperatures Using the Enhanced Integrated Climate Model (EICM); Pavement Research Centre, University of California Davis: California, CA, USA, 2004. [Google Scholar]
- Qiao, Y.; Flintsch, G.W.; Dawson, A.R.; Parry, T. Examining effects of climatic factors on flexible pavement performance and service life. Transp. Res. Rec. 2013, 2349, 100–107. [Google Scholar] [CrossRef]
- Reger, D.; Christofa, E.; Guler, I.; Madanat, S. Estimation of pavement crack initiation models by combining experimental and field data. J. Infrastruct. Syst. 2013, 19, 434–441. [Google Scholar] [CrossRef]
- Song, W.; Chen, X.; Smith, T.; Hedfi, A. Investigation of hot mix asphalt surfaced pavements skid resistance in Maryland state highway network system. In Proceedings of the Transportation Research Board 85th Annual Meeting Compendium of Papers CD-ROM, Washington, DC, USA, 21 January 2007–25 January 2007. [Google Scholar]
- Stampley, B.E.; Miller, B.; Smith, R.E.; Scullion, T. Pavement Management Information System Concepts, Equations, and Analysis Models. TRID the TRIS and ITRD database, revised. 1985. Available online: https://trid.trb.org/view/460629 (accessed on 15 May 2019).
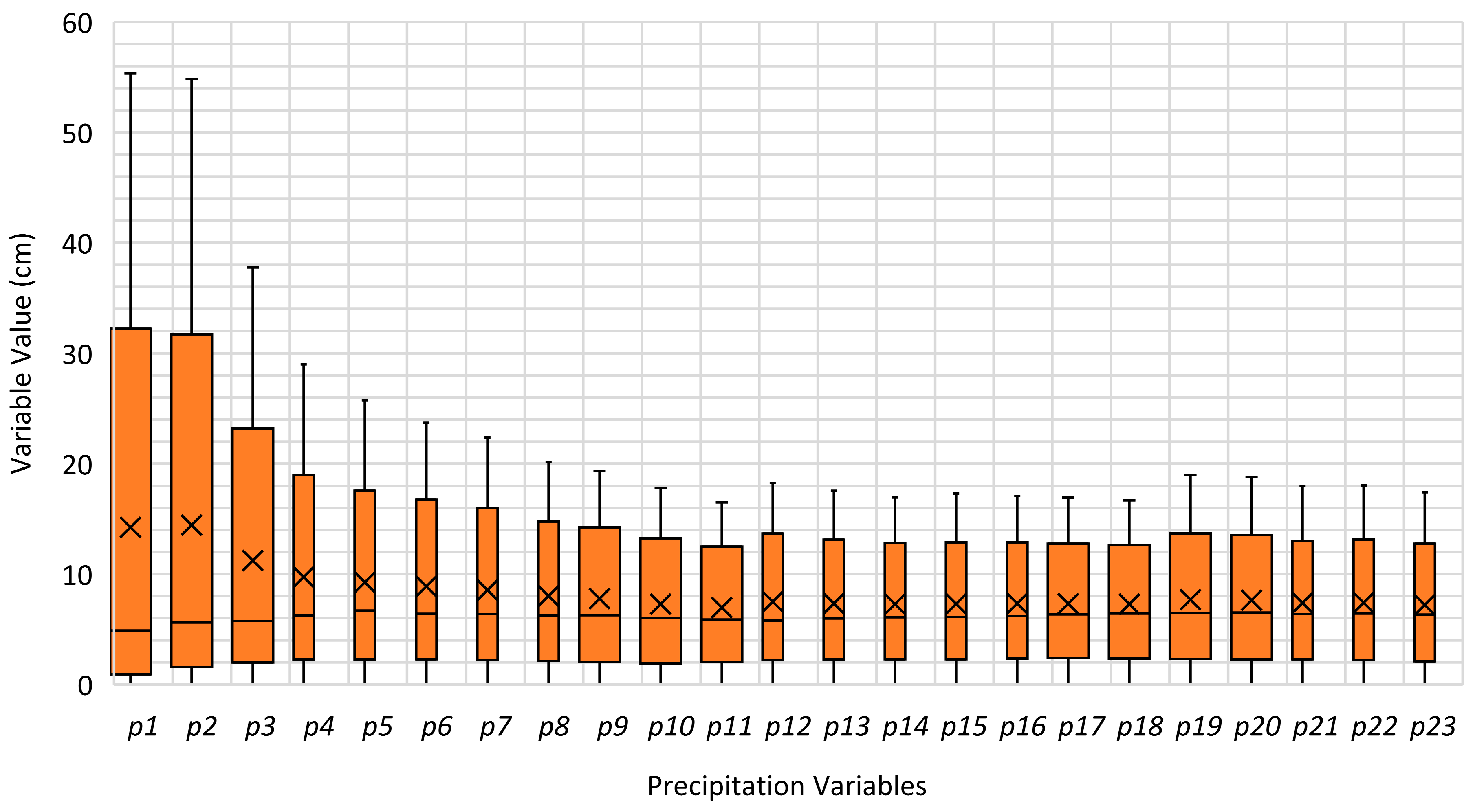
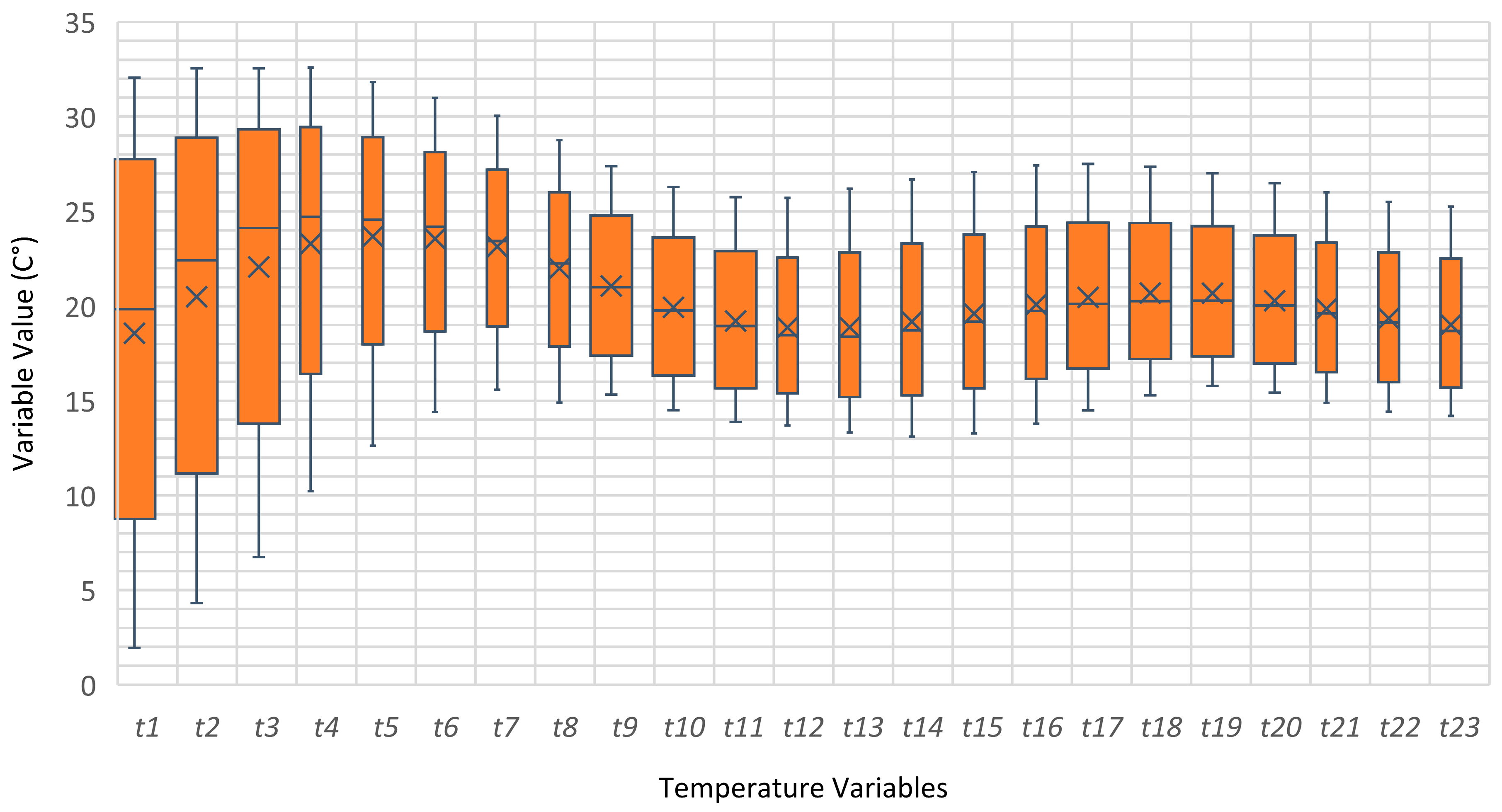
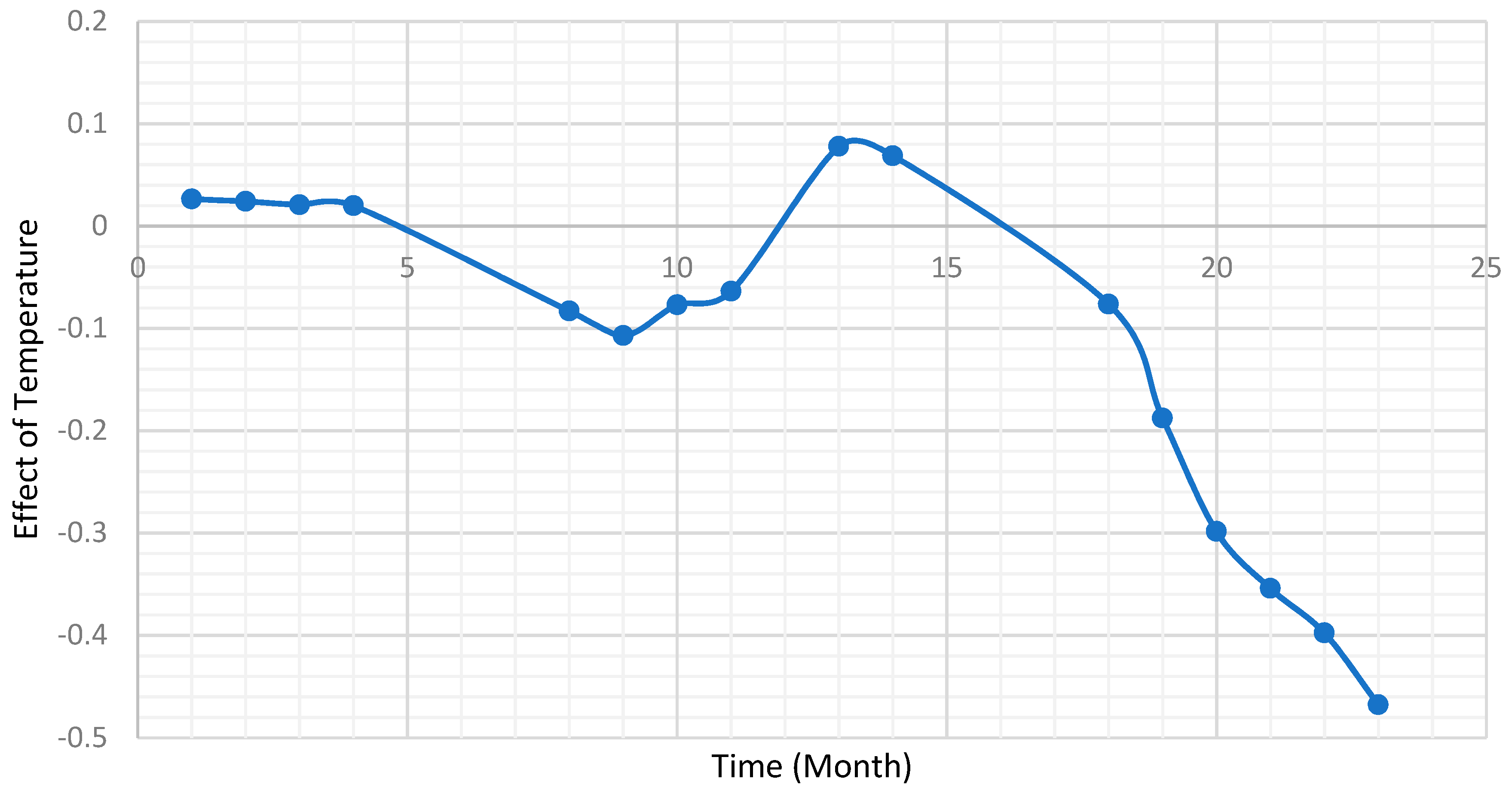
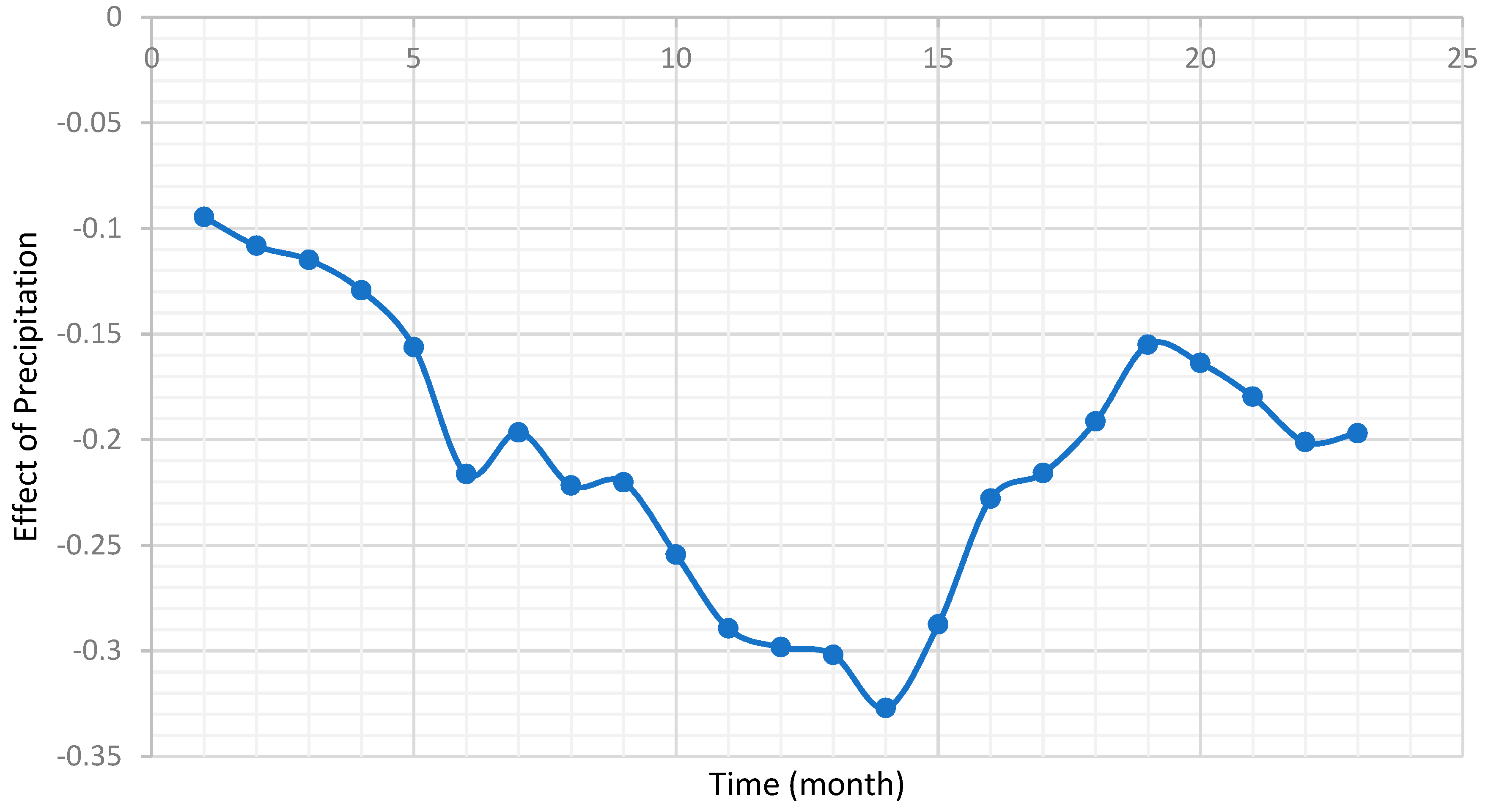
| Specification | Time Variable | Lag Variable | Weather Variable | ||||
|---|---|---|---|---|---|---|---|
| 1 | −1.5175 | (0.0) | 0.7043 | (0.0) | t1 | 0.0265 | (0.0) |
| 2 | −1.5185 | (0.0) | 0.7042 | (0.0) | t2 | 0.0241 | (0.0002) |
| 3 | −1.516 | (0.0) | 0.7042 | (0.0) | t3 | 0.0208 | (0.0038) |
| 4 | −1.5149 | (0.0) | 0.7041 | (0.0) | t4 | 0.0198 | (0.0246) |
| 5 | −1.5127 | (0.0) | 0.704 | (0.0) | t5 | 0.0192 | (0.0831) |
| 6 | −1.5073 | (0.0) | 0.704 | (0.0) | t6 | 0.0064 | (0.3685) |
| 7 | −1.4978 | (0.0) | 0.7042 | (0.0) | t7 | -0.0362 | (0.0851) |
| 8 | −1.4852 | (0.0) | 0.7046 | (0.0) | t8 | -0.0831 | (0.0025) |
| 9 | −1.4828 | (0.0) | 0.7047 | (0.0) | t9 | −0.1071 | (0.0001) |
| 10 | −1.4935 | (0.0) | 0.7045 | (0.0) | t10 | −0.077 | (0.0046) |
| 11 | −1.4946 | (0.0) | 0.7045 | (0.0) | t11 | −0.0638 | (0.0293) |
| 12 | −1.5074 | (0.0) | 0.704 | (0.0) | t12 | 0.01 | (0.403) |
| 13 | −1.5199 | (0.0) | 0.7037 | (0.0) | t13 | 0.0778 | (0.0221) |
| 14 | −1.5181 | (0.0) | 0.7038 | (0.0) | t14 | 0.0687 | (0.0241) |
| 15 | −1.5151 | (0.0) | 0.704 | (0.0) | t15 | 0.0448 | (0.0853) |
| 16 | −1.51 | (0.0) | 0.704 | (0.0) | t16 | 0.018 | (0.2966) |
| 17 | −1.5029 | (0.0) | 0.704 | (0.0) | t17 | −0.011 | (0.3871) |
| 18 | −1.4872 | (0.0) | 0.704 | (0.0) | t18 | −0.0763 | (0.049) |
| 19 | −1.459 | (0.0) | 0.7041 | (0.0) | t19 | −0.1878 | (0.0003) |
| 20 | −1.4262 | (0.0) | 0.7042 | (0.0) | t20 | −0.2985 | (0.0) |
| 21 | −1.407 | (0.0) | 0.7043 | (0.0) | t21 | −0.3542 | (0.0) |
| 22 | −1.3925 | (0.0) | 0.7045 | (0.0) | t22 | −0.3977 | (0.0) |
| 23 | −1.3779 | (0.0) | 0.7042 | (0.0) | t23 | −0.4679 | (0.0) |
| Specification | Time Variable | Lag Variable | Weather Variable | ||||
|---|---|---|---|---|---|---|---|
| 1 | −1.5048 | (0.0) | 0.7031 | (0.0) | p1 | −0.0946 | (0.0) |
| 2 | −1.4956 | (0.0) | 0.7031 | (0.0) | p2 | −0.1082 | (0.0) |
| 3 | −1.4951 | (0.0) | 0.703 | (0.0) | p3 | −0.1149 | (0.0) |
| 4 | −1.4952 | (0.0) | 0.7025 | (0.0) | p4 | −0.1293 | (0.0) |
| 5 | −1.4828 | (0.0) | 0.7022 | (0.0) | p5 | −0.1562 | (0.0) |
| 6 | −1.4691 | (0.0) | 0.701 | (0.0) | p6 | −0.2163 | (0.0) |
| 7 | −1.4637 | (0.0) | 0.7014 | (0.0) | p7 | −0.1966 | (0.0) |
| 8 | −1.4616 | (0.0) | 0.7014 | (0.0) | p8 | −0.2218 | (0.0) |
| 9 | −1.4653 | (0.0) | 0.7014 | (0.0) | p9 | −0.2203 | (0.0) |
| 10 | −1.4644 | (0.0) | 0.7012 | (0.0) | p10 | −0.2545 | (0.0) |
| 11 | −1.4622 | (0.0) | 0.7008 | (0.0) | p11 | −0.2895 | (0.0) |
| 12 | −1.4718 | (0.0) | 0.7002 | (0.0) | p12 | −0.2983 | (0.0) |
| 13 | −1.4736 | (0.0) | 0.7 | (0.0) | p13 | −0.3019 | (0.0) |
| 14 | −1.4693 | (0.0) | 0.6999 | (0.0) | p14 | −0.3271 | (0.0) |
| 15 | −1.4776 | (0.0) | 0.7009 | (0.0) | p15 | −0.2875 | (0.0) |
| 16 | −1.4894 | (0.0) | 0.7018 | (0.0) | p16 | −0.2279 | (0.0) |
| 17 | −1.4936 | (0.0) | 0.7021 | (0.0) | p17 | −0.2159 | (0.0002) |
| 18 | −1.4959 | (0.0) | 0.7025 | (0.0) | p18 | −0.1914 | (0.0016) |
| 19 | −1.4991 | (0.0) | 0.703 | (0.0) | p19 | −0.1551 | (0.0103) |
| 20 | −1.4998 | (0.0) | 0.703 | (0.0) | p20 | −0.1637 | (0.0085) |
| 21 | −1.4983 | (0.0) | 0.7029 | (0.0) | p21 | −0.1797 | (0.0056) |
| 22 | −1.4997 | (0.0) | 0.7028 | (0.0) | p22 | −0.2011 | (0.0035) |
| 23 | −1.5019 | (0.0) | 0.703 | (0.0) | p23 | −0.197 | (0.0089) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Hong, F.; Ren, Y.-H. Impacts of Seasonal and Annual Weather Variations on Network-Level Pavement Performance. Infrastructures 2019, 4, 27. https://doi.org/10.3390/infrastructures4020027
Gao L, Hong F, Ren Y-H. Impacts of Seasonal and Annual Weather Variations on Network-Level Pavement Performance. Infrastructures. 2019; 4(2):27. https://doi.org/10.3390/infrastructures4020027
Chicago/Turabian StyleGao, Lu, Feng Hong, and Yi-Hao (Wilson) Ren. 2019. "Impacts of Seasonal and Annual Weather Variations on Network-Level Pavement Performance" Infrastructures 4, no. 2: 27. https://doi.org/10.3390/infrastructures4020027
APA StyleGao, L., Hong, F., & Ren, Y.-H. (2019). Impacts of Seasonal and Annual Weather Variations on Network-Level Pavement Performance. Infrastructures, 4(2), 27. https://doi.org/10.3390/infrastructures4020027