Seismic Response of a Cylindrical Liquid Storage Tank with Elastomeric Bearing Isolations Resting on a Soil Foundation
Abstract
1. Introduction
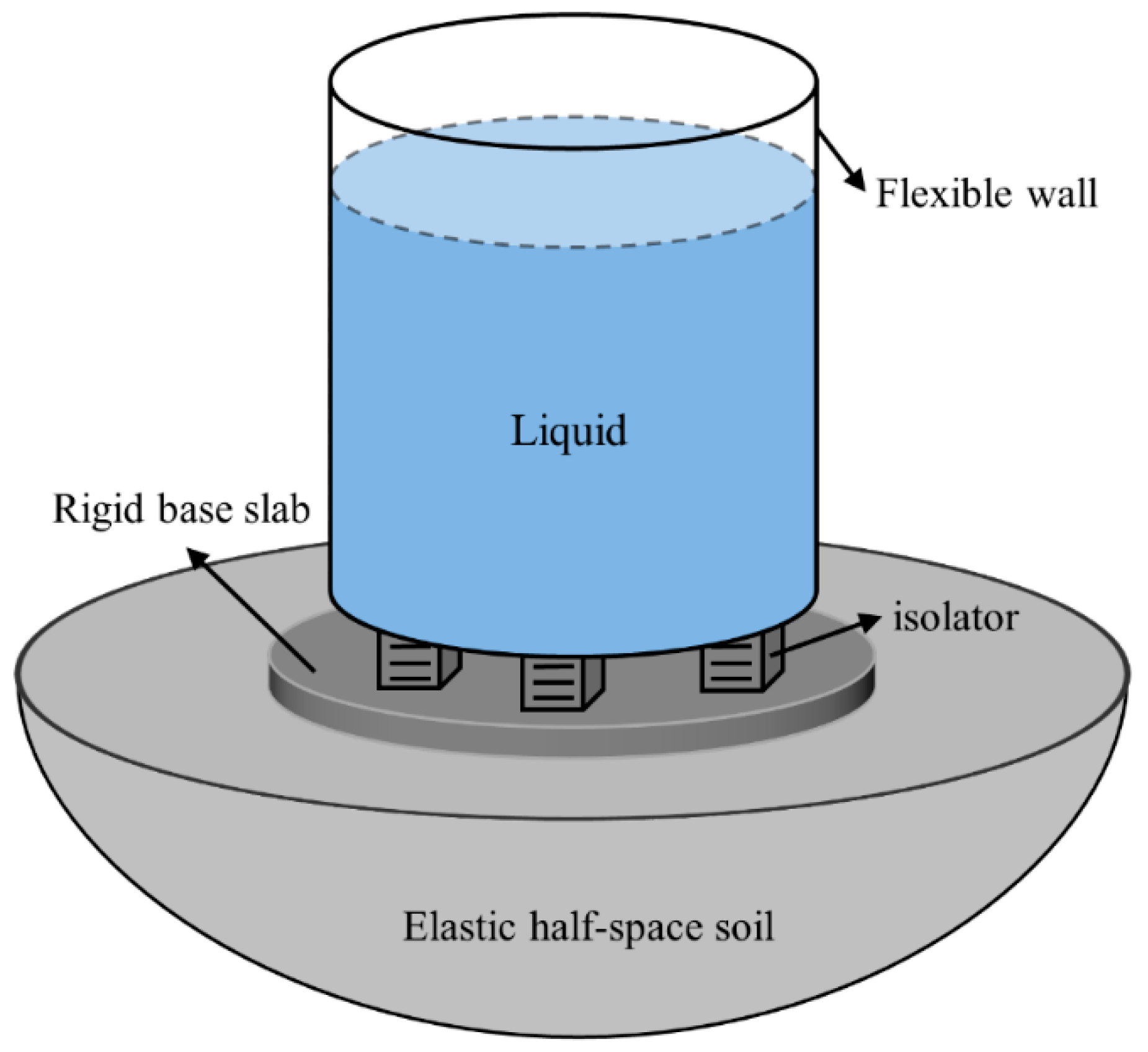
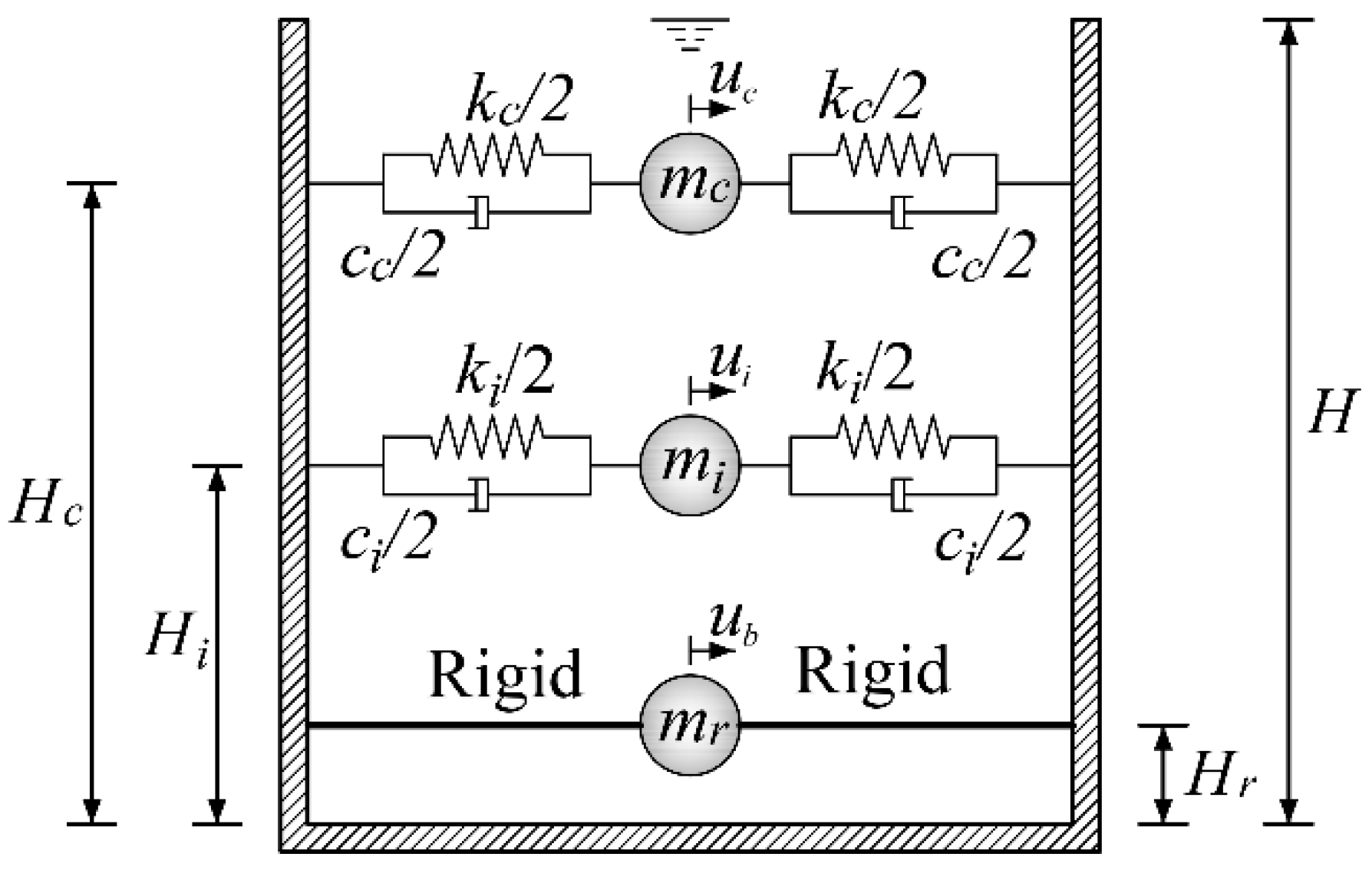
2. Mathematical Model of the Soil–Tank–Liquid System
2.1. Tank–Liquid Interaction
2.2. Soil–Foundation Dynamic Interaction
2.3. Soil–Tank Coupling System with the Base Isolator
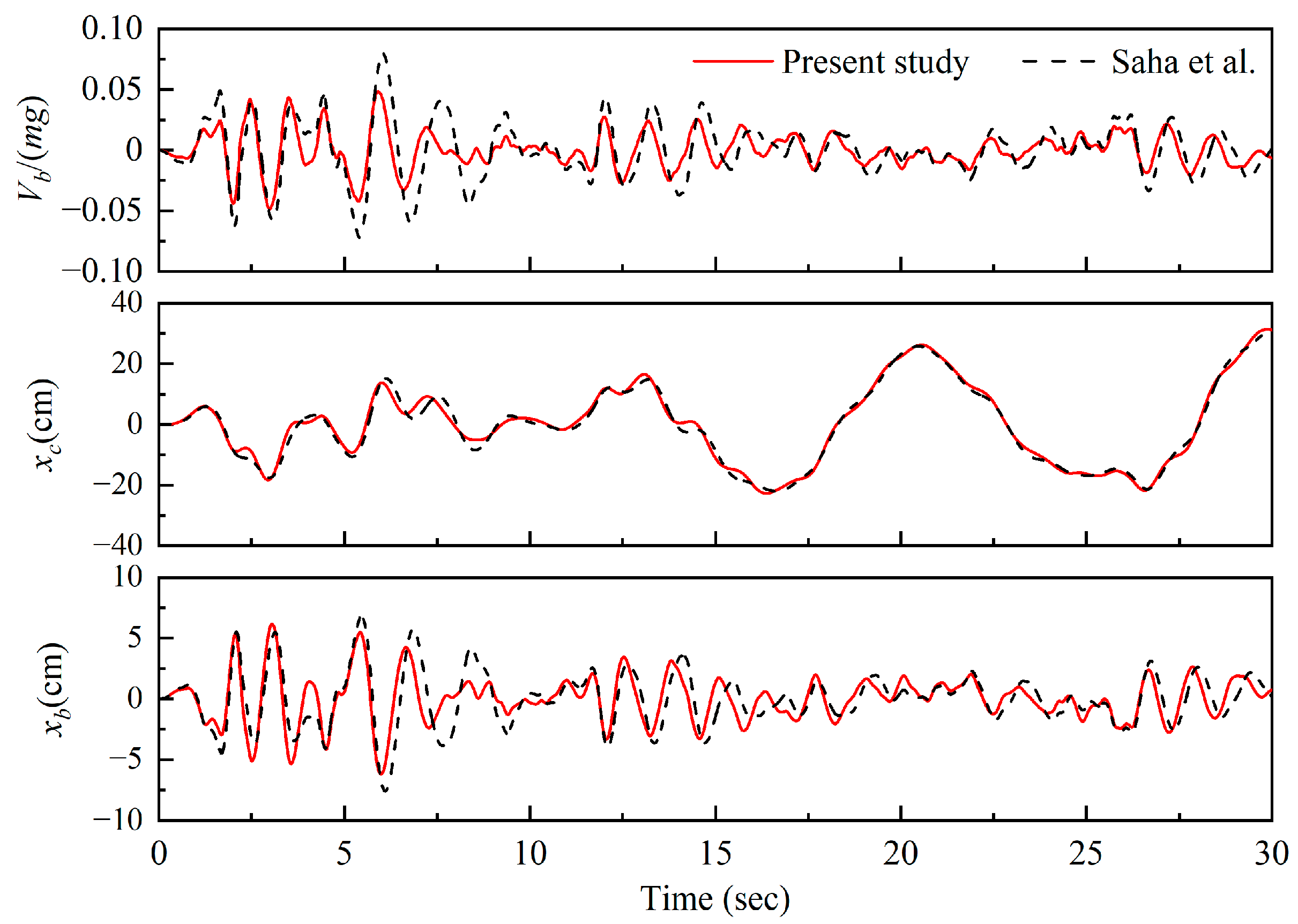
3. Model Verification
4. Parameter Analysis and Results
4.1. Effectiveness of Base Isolation
4.2. Effect of Isolation Period
4.3. Effect of Isolation Damping Ratio
4.4. Effect of Tank Aspect Ratio
4.5. Effect of Soil–Structure Dynamic Interaction
5. Conclusions
- When the base isolation is considered, the base shear and impulsive displacement can be reduced drastically. This result implies that seismic base isolation is an efficient way to reduce the tank responses. Moreover, the isolation system is more effective for the slender tanks in comparison with the broad ones.
- There exists an amplification in the sloshing displacement due to isolation, especially for the slender tanks. Also, the flexibility of the isolator causes the excessive base displacements between the superstructure and the foundation.
- As the isolation period grows, the isolation efficiency also increases. The base displacement, however, is greater in terms of the larger values of the isolation period. With the growth of the isolation damping ratio, the base displacement gradually decreases, whereas the excessive isolation damping ratio causes the increasing base shear and impulsive displacement.
- For the isolated tanks, the effect of the tank aspect ratio on the base shear and impulsive displacement can be negligible. When Vs is less than 250 m/s, there is an amplification of the base shear, sloshing displacement, and base displacement as the shear wave velocity Vs increases. However, the sloshing displacement remains nearly unchanged with the soil becoming flexible.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Zhang, Z.; Xu, J.; Cao, X.; Wang, Y.; Zhu, J.; Yao, L. Nonlinear transient heat transfer analysis of functionally graded material sandwich slabs by incremental differential quadrature element method. Fuhe Cailiao Xuebao/Acta Mater. Compos. Sin. 2024, 41, 6285–6297. [Google Scholar] [CrossRef]
- Al-Yacouby, A.M.; Hao, L.J.; Liew, M.S.; Ratnayake, R.M.C.; Samarakoon, S.M.K. Thin-walled cylindrical shell storage tank under blast impacts: Finite element analysis. Materials 2021, 14, 7100. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Zhou, D.; Wang, J. An equivalent mechanical model for fluid sloshing in a rigid cylindrical tank equipped with a rigid annular baffle. Appl. Math. Model. 2019, 72, 569–587. [Google Scholar] [CrossRef]
- Zhang, Q.; Shui, B.; Zhu, H. Study on sloshing characteristics in a liquid cargo tank under combination excitation. J. Mar. Sci. Eng. 2022, 10, 1100. [Google Scholar] [CrossRef]
- Wang, G.; Wang, T. Effect evaluation of filling medium parameters on operating and mechanical performances of liquid heavy metal heat storage tank. Sustainability 2022, 14, 14551. [Google Scholar] [CrossRef]
- Zhao, Z.; Hu, X.; Zhang, R.; Xie, M.; Liu, S. Advantages and design of inerters for isolated storage tanks incorporating soil conditions. Thin-Walled Struct. 2024, 195, 111356. [Google Scholar] [CrossRef]
- Chaithra, M.; Krishnamoorthy, A.; Avinash, A.R. A review on the modelling techniques of liquid storage tanks considering fluid–structure–soil interaction effects with a focus on the mitigation of seismic effects through base isolation techniques. Sustainability 2023, 15, 11040. [Google Scholar] [CrossRef]
- Jing, W.; Feng, H.; Cheng, X. Dynamic responses of liquid storage tanks caused by wind and earthquake in special environment. Appl. Sci. 2019, 9, 2376. [Google Scholar] [CrossRef]
- Hosseini, S.E.A.; Beskhyroun, S. Dynamic performance investigation of a full-scale unanchored thin-walled steel fluid storage tank via shake table tests. Structures 2024, 70, 107548. [Google Scholar] [CrossRef]
- Haroun, M.A. Vibration studies and tests of liquid storage tanks. Eng. Struct. Dyn. 1983, 11, 179–206. [Google Scholar] [CrossRef]
- Cho, J.R.; Lee, S.Y.; Song, M.S. Dynamic response characteristics of cylindrical baffled liquid storage tank to the baffle number. J. Mech. Sci. Technol. 2019, 33, 5979–5987. [Google Scholar] [CrossRef]
- Baghban, M.H.; Razavi Tosee, S.V.; Valerievich, K.A.; Najafi, L.; Faridmehr, I. Seismic analysis of baffle-reinforced elevated storage tank using finite element method. Buildings 2022, 12, 549. [Google Scholar] [CrossRef]
- Hernandez, D.H.; Larkin, T.; Chouw, N. Shake table investigation of nonlinear soil-structure-fuild interaction of a thin-walled storage tank under earthquake load. Thin-Walled Struct. 2021, 167, 108143. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, S.-H.; Han, S.-W. Nonlinear earthquake responses of unanchored cylindrical liquid storage tanks on flexible soil. Structures 2023, 54, 1465–1490. [Google Scholar] [CrossRef]
- Jing, W.; Shen, J.; Cheng, X.; Yang, W. Seismic responses of a liquid storage tank considering structure-soil-structure interaction. Structures 2022, 45, 2137–2150. [Google Scholar] [CrossRef]
- Jing, W.; Wang, S.; Shen, J.; Song, S. Influence of seismic wave incidence angle on dynamic responses and vibration control of adjacent liquid storage tanks. Int. J. Struct. Stab. Dyn. 2024, 24, 2450254. [Google Scholar] [CrossRef]
- Shan, W.C.; Liu, J.P.; Zhou, J.W. Uplift effect and soil-strucutre interaction on seismic responses of column suppoted steel tanks under multi-dimensional earthquakes. J. Constr. Steel Res. 2025, 226, 109235. [Google Scholar] [CrossRef]
- Haroun, M.A.; Ellaithy, H.M. Model for flexible tanks undergoing rocking. J. Eng. Mech. 1985, 111, 143–157. [Google Scholar] [CrossRef]
- Meng, X.; Li, X.H.; Xu, X.L.; Zhang, J.D.; Zhou, W.L.; Zhou, D. Earthquake Response of Cylindrical Storage Tanks on Elastic Soil. J. Vib. Eng. Technol. 2019, 7, 433–444. [Google Scholar] [CrossRef]
- Sun, Y.; Zhou, D.; Amabili, M.; Wang, J.; Han, H. Liquid sloshing in a rigid cylindrical tank equipped with a rigid annular baffle and on soil foundation. Int. J. Struct. Stab. Dyn. 2020, 20, 2050030. [Google Scholar] [CrossRef]
- Meng, X.; Zhou, D.; Lim, Y.M.; Wang, J.D.; Huo, R.L. Ssismic Response of Rectangular Liquid Container with Dual Horizontal Baffles on Deformable Soil Foundation. J. Earthq. Eng. 2023, 27, 1943–1972. [Google Scholar] [CrossRef]
- Peng, Q.; Wu, H.; Zhang, R.F.; Fang, Q. Numerical simulations of base-isolated LNG storage tanks subjected to large commercial aircraft crash. Thin-Walled Struct. 2021, 163, 107660. [Google Scholar] [CrossRef]
- Kalantari, A.; Nikoomanesh, M.R.; Goudarzi, M.A. Applicability of mass-spring models for seismically isolated liquid storage tanks. J. Earthq. Tsunami. 2019, 13, 1950002. [Google Scholar] [CrossRef]
- Jing, W.; Feng, J.; Wang, S.; Song, S. Failure probability of a liquid storage tank with three-dimensional base-isolation under earthquake action. Structures 2023, 58, 105633. [Google Scholar] [CrossRef]
- Rawat, A.; Matsagar, V.A.; Nagpal, A.K. Numerical study of base-isolated cylindrical liquid storage tanks using coupled acoustic-structural approach. Soil Dyn. Earthq. Eng. 2019, 119, 196–219. [Google Scholar] [CrossRef]
- Zhu, H.P.; Tang, Z.A.; Luo, H. Feasibility analyses of negative-stiffness dampers for seismic performance enhancement of a base-isolated liquid storage tank. Soil Dyn. Earthq. Eng. 2023, 164, 107575. [Google Scholar] [CrossRef]
- Zhang, R.; Weng, D.; Ge, Q. Shaking table experiment on a steel storage tank with multiple friction pendulum bearings. Struct. Eng. Mech. 2014, 52, 875–887. [Google Scholar] [CrossRef]
- Yue, H.; Zhenyun, T.; Zhenbao, L.; Xiuli, D. Seismic performance evaluation of VCFPB isolated storage tank using real-time hybrid simulation. Earthq. Eng. Eng. Vib. 2022, 21, 501–515. [Google Scholar] [CrossRef]
- Yu, Q.-Q.; Wu, J.-Y.; Gu, X.-L.; Zhou, F.-Y. Experimental study on effects of U-shape dampers on earthquake responses of a base-isolated LNG inner tank. Eng. Struct. 2022, 269, 114841. [Google Scholar] [CrossRef]
- Kumar, H.; Saha, S.K. Effects of uncertain soil parameters on seismic responses of fixed base and base-isolated liquid storage tanks. J. Earthq. Eng. 2024, 28, 176–201. [Google Scholar] [CrossRef]
- Cheng, X.; Jing, W.; Chen, J.; Zhang, X. Pounding dynamic responses of sliding base-isolated rectangular liquid-storage structure considering soil-structure interactions. Shock Vib. 2017, 2017, 1–14. [Google Scholar] [CrossRef]
- Kumar, H.; Saha, S.K. Effects of soil-structure interaction on seismic response of fixed base and base isolated liquid storage tanks. J. Earthq. Eng. 2022, 26, 6148–6171. [Google Scholar] [CrossRef]
- Shekari, M.R.; Hekmatzadeh, A.A.; Amiri, S.M. On the nonlinear dynamic analysis of base-isolated three-dimensional rectangular thin-walled steel tanks equipped with vertical baffle. Thin-Walled Struct. 2019, 138, 79–94. [Google Scholar] [CrossRef]
- Shekari, M.R. A coupled BE–FE–BE study for investigating the effect of earthquake frequency content and predominant period on seismic behavior of base-isolated concrete rectangular liquid tanks. J. Fluids Struct. 2018, 77, 19–35. [Google Scholar] [CrossRef]
- Shourestani, S.; Soltani, F.; Ghasemi, M.; Etedali, S. SSI effects on seismic behavior of smart base-isolated structures. Geomech. Eng. 2018, 14, 161–174. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, R.; Liu, X.; Chen, S.; Li, X. Analysis of seismic response of a large-scale isolated LNG tank considering dynamic soil-pile interaction. Structures 2023, 58, 105460. [Google Scholar] [CrossRef]
- Luo, C.; Mu, H.; Wang, H.; Guo, X.; Liu, D.; Feng, H. Study on the seismic mitigation effects of inerter isolated storage tanks. Soil Dyn. Earthq. Eng. 2023, 173, 108140. [Google Scholar] [CrossRef]
- Zhao, M.; Zhou, J. Review of seismic studies of liquid storage tanks. Struct. Eng. Mech. 2018, 65, 557–572. [Google Scholar] [CrossRef]
- Sun, J.; Cui, L.; Li, X.; Wang, Z.; Liu, W.; Lv, Y. Design theory and method of LNG isolation. Earthq. Struct. 2019, 16, 1–9. [Google Scholar] [CrossRef]
- Zhang, H.; Song, C.; Wang, M.; Cheng, Y.; Yue, S.; Wu, C. A geotechnical seismic isolation system based on marine sand cushion for attenuating ground shock effect: Experimental investigation. Soil Dyn. Earthq. Eng. 2023, 168, 107854. [Google Scholar] [CrossRef]
- Kim, N.-S.; Lee, D.-G. Pseudodynamic test for evaluation of seismic performance of base-isolated liquid storage tanks. Eng. Struct. 1995, 17, 198–208. [Google Scholar] [CrossRef]
- Wu, W.-H.; Lee, W.-H. Systematic lumped-parameter models for foundations based on polynomial-fraction approximation. Earthq. Eng. Struct. Dyn. 2002, 31, 1383–1412. [Google Scholar] [CrossRef]
- Jangid, R.S.; Datta, T.K. Seismic behavior of base-isolated buildings: A state-of-the-art-review. Struct. Build. 1995, 110, 186–203. [Google Scholar] [CrossRef]
- Saha, S.K.; Matsagar, V.A.; Jain, A.K. Earthquake response of base-isolated liquid storage tanks for different isolator models. J. Earthq. Tsunami. 2014, 08, 1450013. [Google Scholar] [CrossRef]





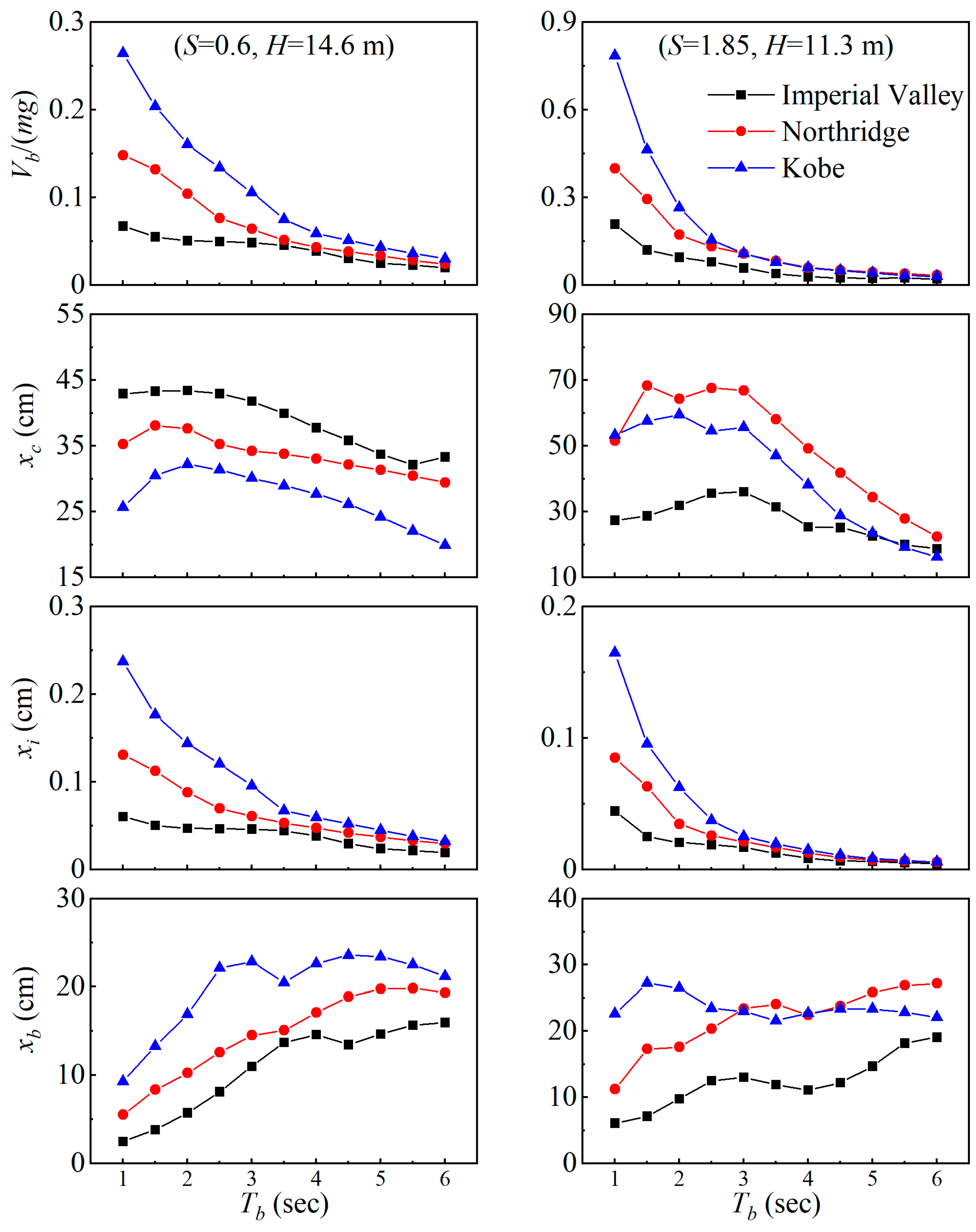


 Imperial Valley;
Imperial Valley;  Northridge;
Northridge;  Kobe).
Kobe).
 Imperial Valley;
Imperial Valley;  Northridge;
Northridge;  Kobe).
Kobe).
| Earthquake | Type of Tank | Non-Isolated Tank | Isolated Tank | ||||
|---|---|---|---|---|---|---|---|
| Vb/mg | xc (cm) | xi (cm) | Vb/mg | xc (cm) | xi (cm) | ||
| Imperial Valley | Broad | 0.167 | 42.4 | 0.130 | 0.051 | 43.5 | 0.047 |
| Slender | 0.401 | 25.7 | 0.077 | 0.095 | 31.9 | 0.021 | |
| Northridge | Broad | 0.209 | 30.0 | 0.169 | 0.104 | 37.6 | 0.088 |
| Slender | 0.637 | 50.0 | 0.133 | 0.173 | 64.4 | 0.035 | |
| Kobe | Broad | 0.423 | 25.9 | 0.338 | 0.161 | 32.2 | 0.144 |
| Slender | 1.249 | 41.5 | 0.251 | 0.266 | 59.5 | 0.063 | |
| Type of Tank | Impulsive Fundamental Period (s) | Convective Fundamental Period (s) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vs = 100 | Vs = 200 | Vs = 300 | Vs = 400 | Vs = 500 | Vs = 700 | Vs = 1000 | Vs = 100 | Vs = 200 | Vs = 300 | Vs = 400 | Vs = 500 | Vs = 700 | Vs = 1000 | |
| Broad tank | 1.58 | 1.35 | 1.30 | 1.29 | 1.28 | 1.27 | 1.27 | 8.38 | 8.32 | 8.31 | 8.31 | 8.30 | 8.30 | 8.30 |
| Slender tank | 1.77 | 1.70 | 1.69 | 1.69 | 1.68 | 1.68 | 1.68 | 3.85 | 3.83 | 3.82 | 3.82 | 3.82 | 3.82 | 3.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Sun, Y.; Wang, C.; Han, H.; Zhou, D. Seismic Response of a Cylindrical Liquid Storage Tank with Elastomeric Bearing Isolations Resting on a Soil Foundation. Infrastructures 2025, 10, 136. https://doi.org/10.3390/infrastructures10060136
Meng X, Sun Y, Wang C, Han H, Zhou D. Seismic Response of a Cylindrical Liquid Storage Tank with Elastomeric Bearing Isolations Resting on a Soil Foundation. Infrastructures. 2025; 10(6):136. https://doi.org/10.3390/infrastructures10060136
Chicago/Turabian StyleMeng, Xun, Ying Sun, Chi Wang, Huixuan Han, and Ding Zhou. 2025. "Seismic Response of a Cylindrical Liquid Storage Tank with Elastomeric Bearing Isolations Resting on a Soil Foundation" Infrastructures 10, no. 6: 136. https://doi.org/10.3390/infrastructures10060136
APA StyleMeng, X., Sun, Y., Wang, C., Han, H., & Zhou, D. (2025). Seismic Response of a Cylindrical Liquid Storage Tank with Elastomeric Bearing Isolations Resting on a Soil Foundation. Infrastructures, 10(6), 136. https://doi.org/10.3390/infrastructures10060136






