Physics-Aware Informer: A Hybrid Framework for Accurate Pavement IRI Prediction in Diverse Climates
Abstract
1. Introduction
2. Methodology
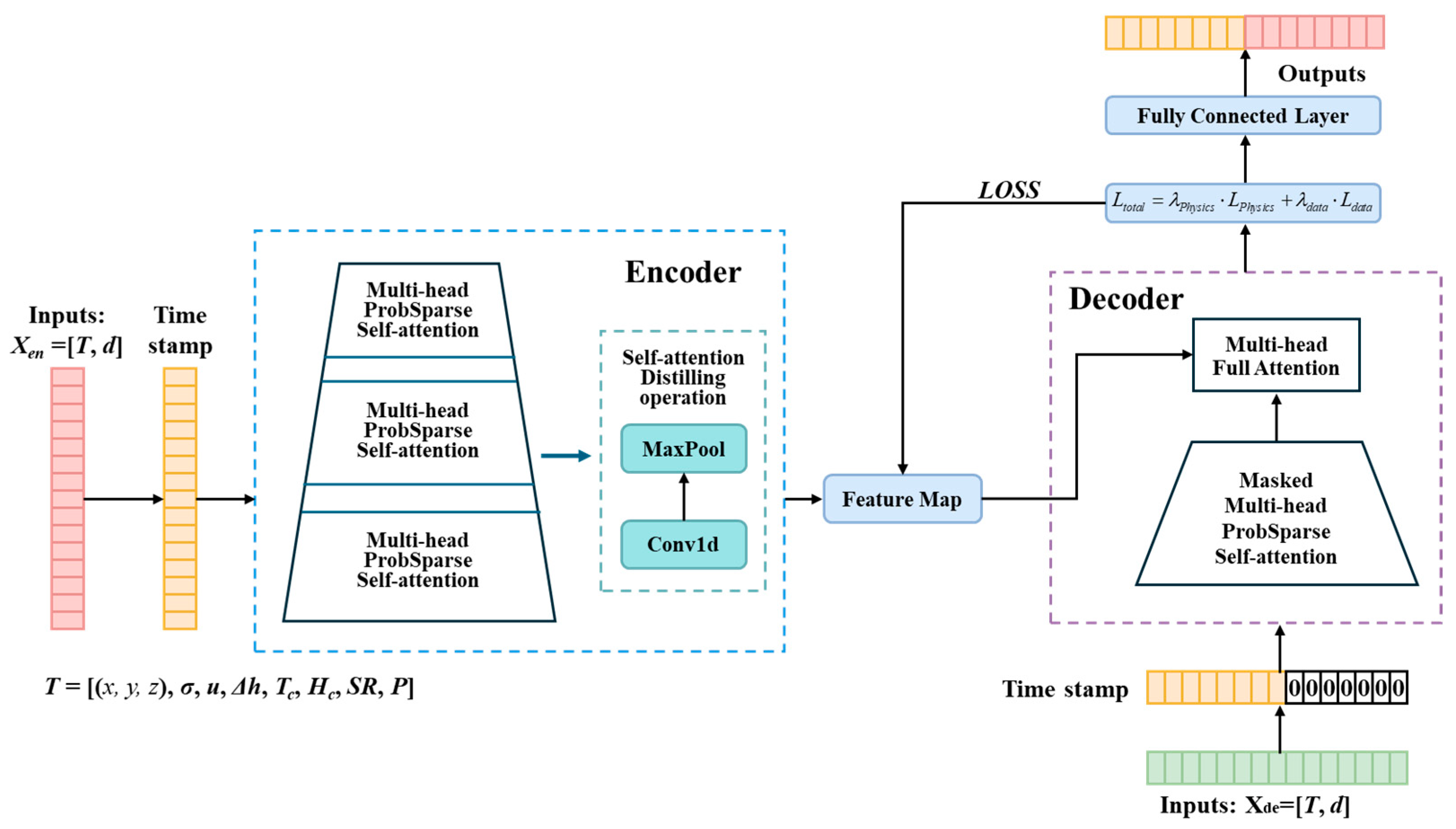
2.1. Overview of the Physics-Aware Informer Model
2.2. Informer Model for Long-Sequence Forecasting
2.2.3. Derivation of the Unified IRI Residual PDE
2.2.4. Integration of Informer with Physical Constraints
3. Experiments
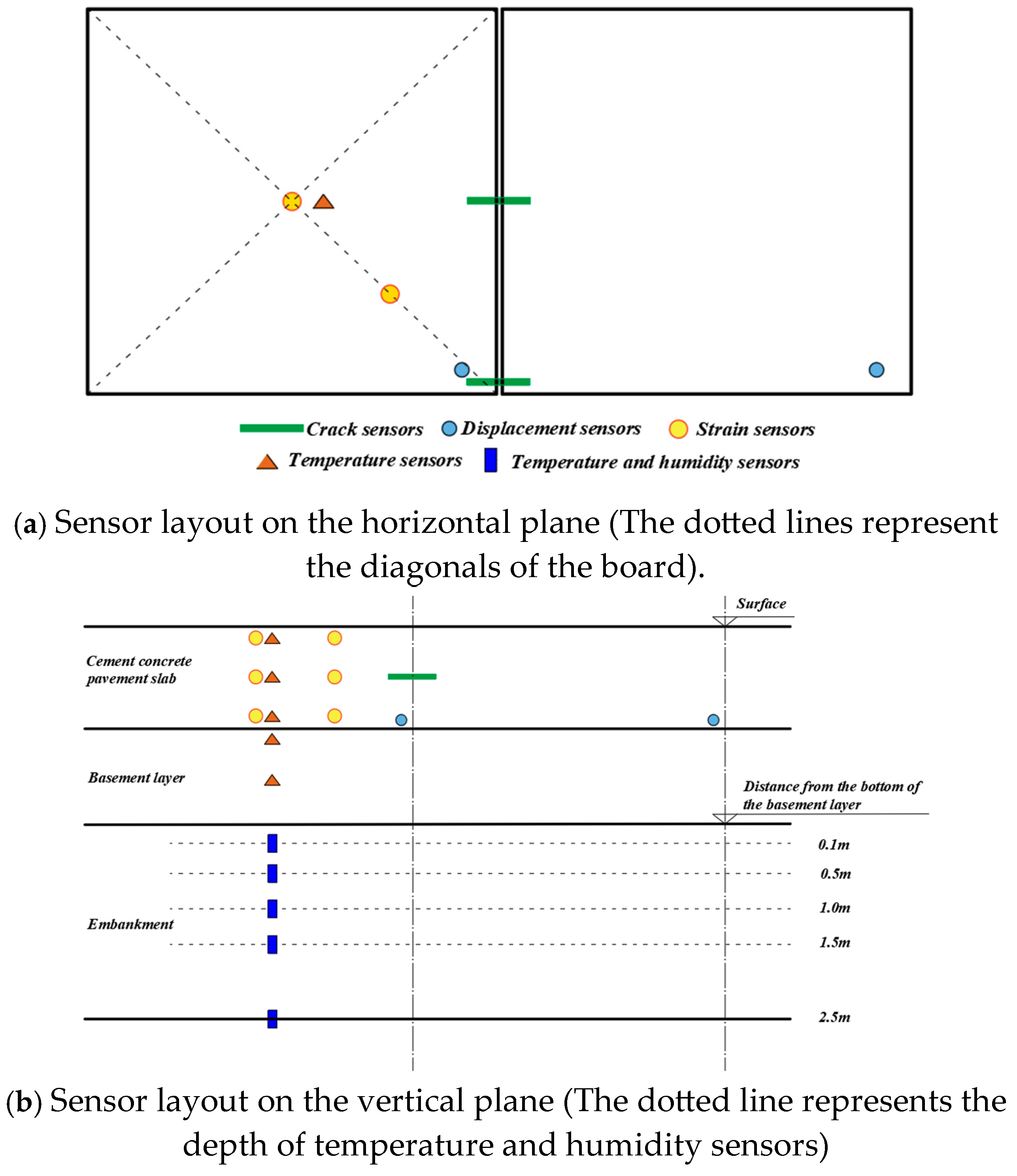
3.1. Data Collection
3.2. Experiment Details
4. Results and Discussion
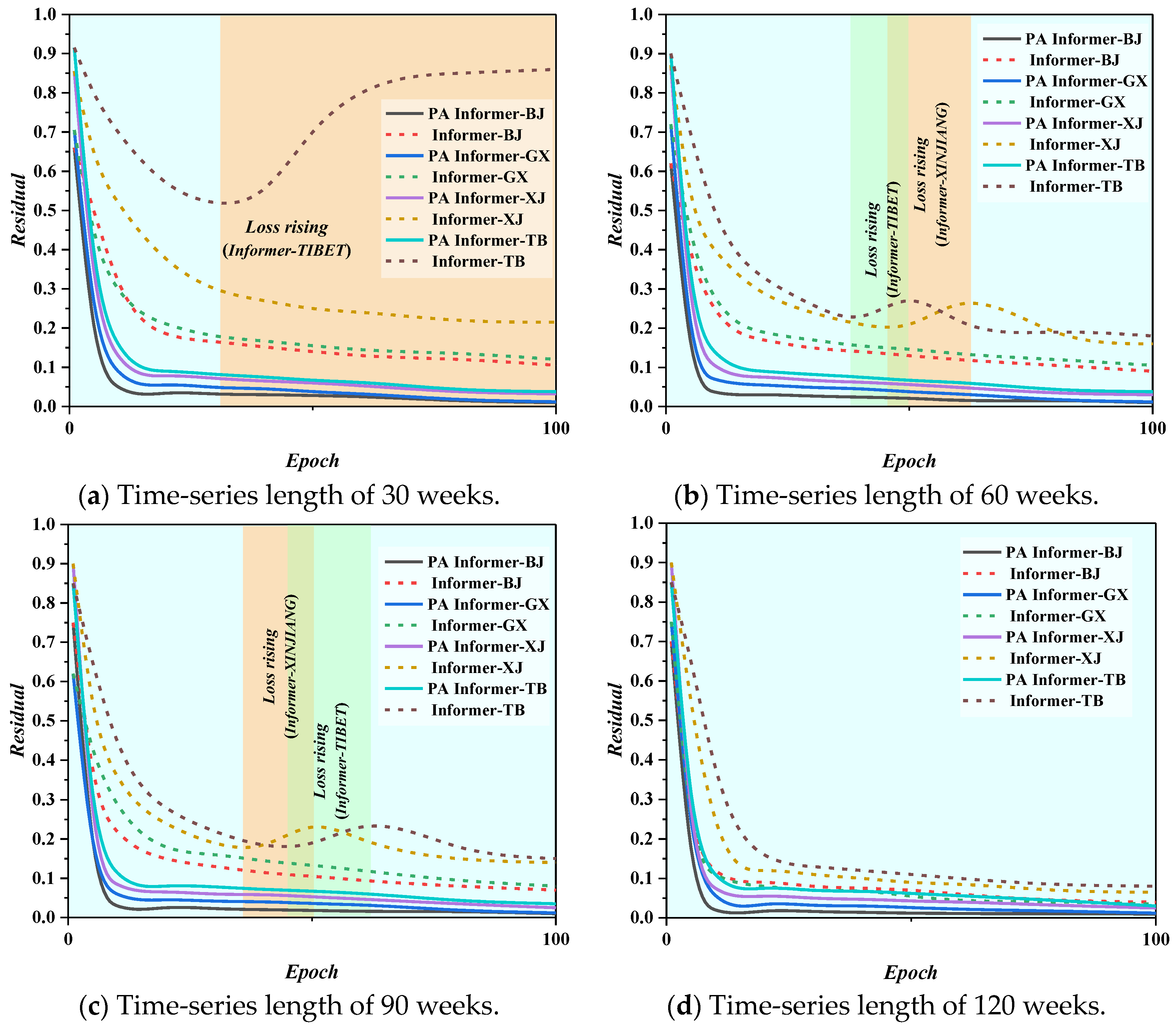
4.1. Hyperparameter Tuning Process
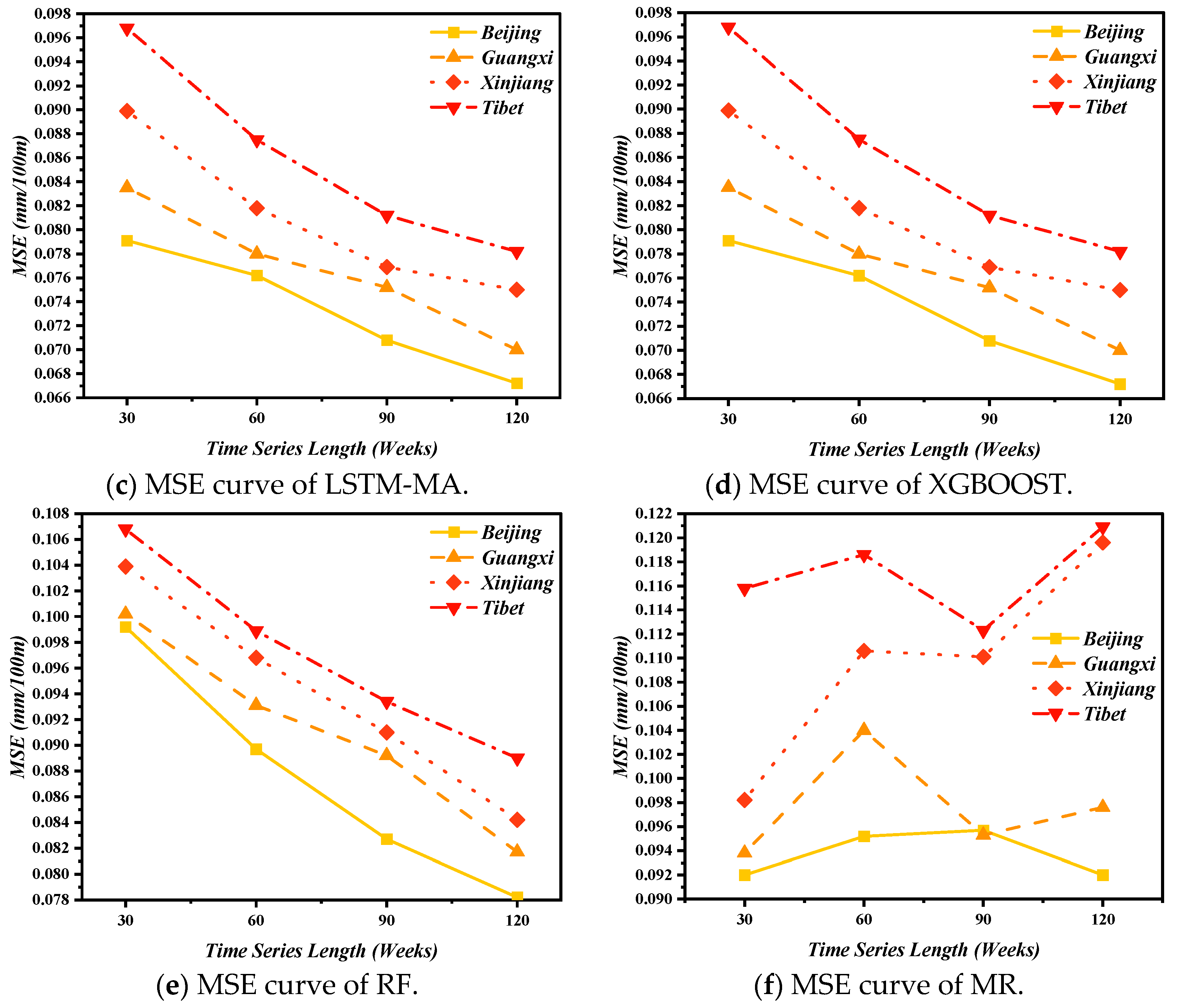
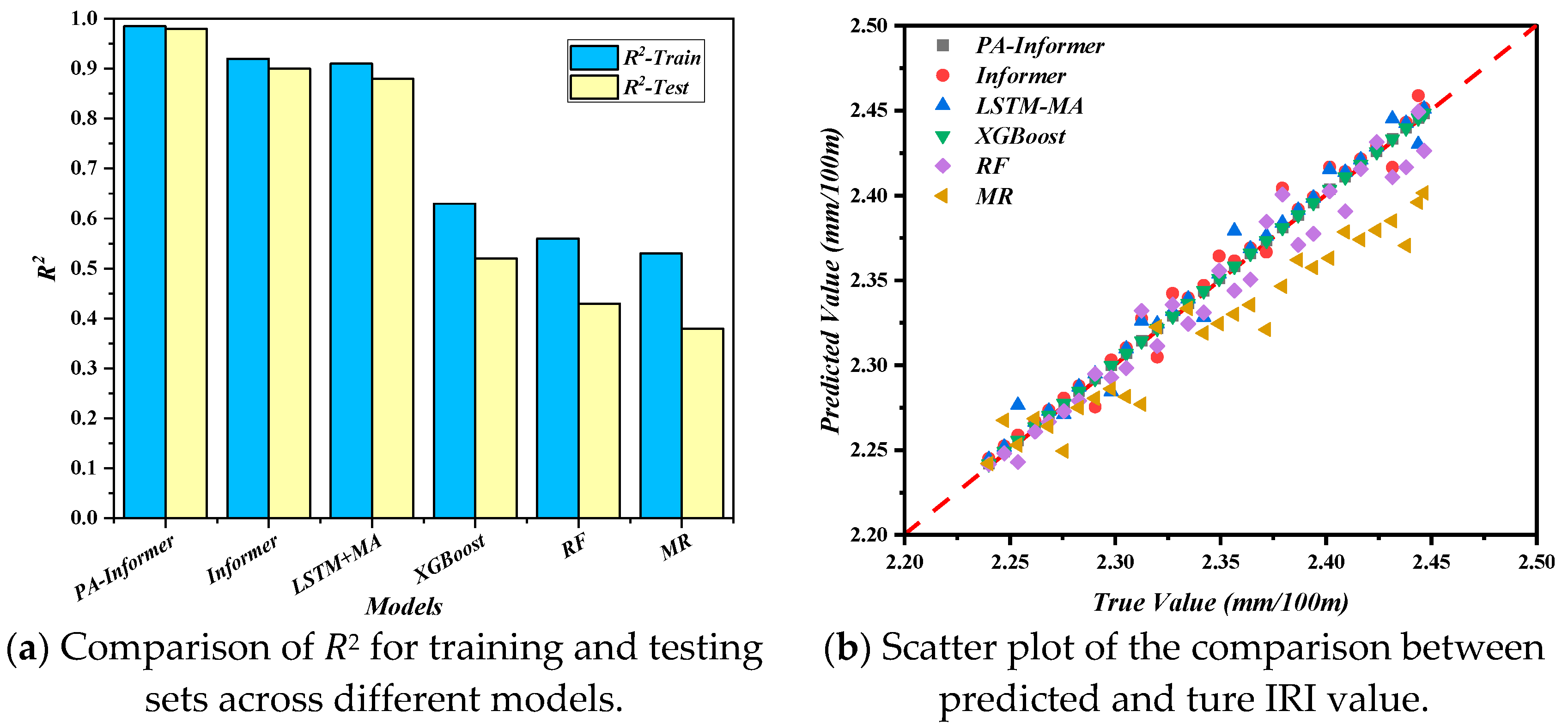
4.2. Prediction Accuracy Evaluation
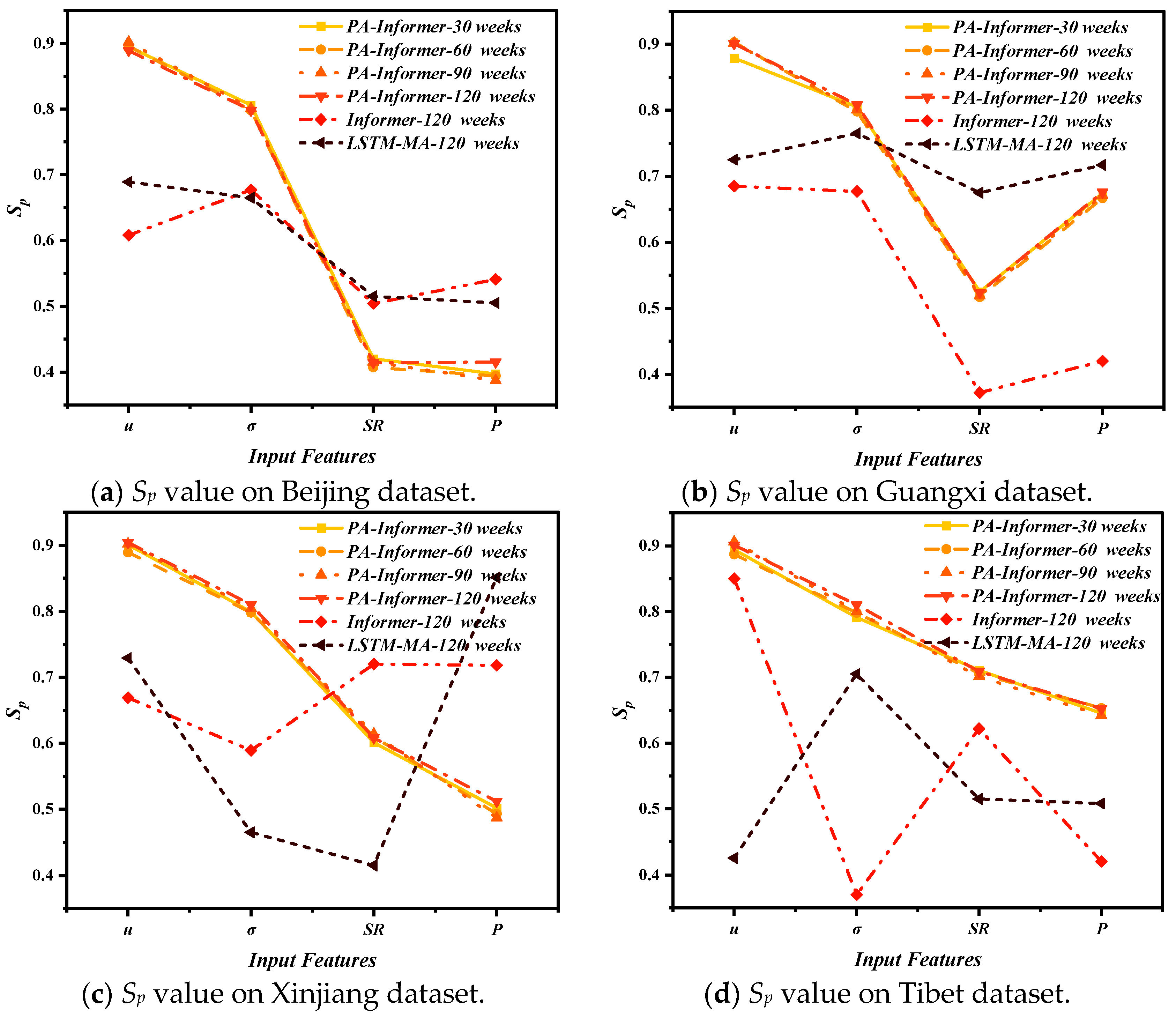
4.3. Sensitivity Analysis
5. Discussion
5.1. Advantages of the PA-Informer Model in Diverse Conditions
5.2. Interpretation of Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, T.; Smith, A.; Zhai, H.; Lu, Y. LSTM+MA: A Time-Series Model for Predicting Pavement IRI. Infrastructures 2025, 10, 10. [Google Scholar] [CrossRef]
- Dalla Rosa, F.; Liu, L.; Gharaibeh, N.G. IRI prediction model for use in network-level pavement management systems. J. Transp. Eng. Part B Pavements 2017, 143, 04017001. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 10606–10615. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Marcelino, P.; de Lurdes Antunes, M.; Gomes, M.C. Machine learning approach for pavement performance prediction. Int. J. Pavement Eng. 2021, 22, 341–354. [Google Scholar] [CrossRef]
- Qin, Y.; Song, D.; Cheng, H.; Cheng, W. A dual-stage attention-based recurrent neural network for time series prediction. arXiv 2017, arXiv:1704.02971. [Google Scholar]
- Deng, F.; Tang, X.; Wu, T. Particle swarm optimization-augmented feedforward networks for pavement rutting prediction. J. Comput. Civ. Eng. 2015, 29, 04014097. [Google Scholar]
- Wang, K.; Huang, Y.; Zhang, Z. Hybrid gray relation analysis and support vector regression for pavement performance prediction. Int. J. Pavement Res. Technol. 2018, 11, 287–294. [Google Scholar]
- Gong, W.; Chen, H.; Zhang, J. Random forest regression for flexible pavement IRI modeling. Transp. Res. Rec. 2019, 2673, 299–309. [Google Scholar]
- Hoang, H.-G.T.; Nguyen, H.-L.; Nguyen, T.-A.; Ly, H.-B. Hybrid machine learning approach for prediction and design optimization of marshall stability in graphene oxide-modified asphalt concrete. Environ. Res. 2025, 285, 122646. [Google Scholar] [CrossRef] [PubMed]
- Damirchilo, B.; Yazdani, R.; Khavarian, M. XGBoost-based pavement performance prediction and handling missing values. Int. J. Pavement Eng. 2020, 21, 456–466. [Google Scholar]
- Song, Y.; Wang, L.; Yin, J. ThunderGBM-based ensemble learning for asphalt pavement IRI prediction. Constr. Build. Mater. 2021, 313, 125421. [Google Scholar]
- Zhou, X.; Li, J.; Fang, S. RNN-based models for asphalt pavement performance prediction using LTPP data. Int. J. Pavement Res. Technol. 2018, 11, 559–567. [Google Scholar]
- Tamagusko, T.; Ferreira, A. Pavement Performance Prediction using Machine Learning: Supervised Learning with Tree-Based Algorithms. Transp. Res. Procedia 2025, 82, 2521–2531. [Google Scholar] [CrossRef]
- Han, Z.; Liu, F.; Zhang, X. Modified RNN for falling weight deflectometer back-calculation. J. Comput. Civ. Eng. 2020, 34, 04020023. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving PDEs. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Toba, A.-L.; Kulkarni, S.; Khallouli, W.; Pennington, T. Long-Term Traffic Prediction Using Deep Learning Long Short-Term Memory. Smart Cities 2025, 8, 126. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Marrero, C.O.; Perdikaris, P.; Tartakovsky, G.D.; Barajas-Solano, D. Physics-informed deep neural networks for learning parameters and constitutive relationships in subsurface flow problems. Water Resour. Res. 2020, 56, e2019WR026731. [Google Scholar] [CrossRef]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A deep learning library for solving differential equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Dai, H.; Liu, Z.; Dai, J.; Liu, Y. An adaptive spatio-temporal attention mechanism for traffic prediction. IEEE Internet Things J. 2021, 8, 11915–11924. [Google Scholar]
- Xu, Z.; Feng, C.; Zhang, L. Physics-enhanced neural networks for multiscale spatiotemporal traffic prediction. Transp. Res. Part C: Emerg. Technol. 2022, 137, 103597. [Google Scholar]
- Sun, L.; Wang, Z.; Zhang, H. Physics-informed deep learning for time-series forecasting in engineering applications. Mech. Syst. Signal Process. 2021, 152, 107377. [Google Scholar]
- Tian, G.; Zhang, C.; Shi, Y.; Li, X. Multi−Wave−Net: A long time series forecasting framework based on multi-scale analysis and multi-channel feature fusion. Expert Sys. With. App. 2024, 251, 124088. [Google Scholar] [CrossRef]
- Child, R.; Gray, S.; Radford, A.; Sutskever, I. Generating long sequences with sparse transformers. arXiv 2019, arXiv:1904.10509. [Google Scholar] [CrossRef]
- Beltagy, I.; Peters, M.E.; Cohan, A. Longformer: The long-document transformer. arXiv 2020, arXiv:2004.05150. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Transformer-XL: Attentive language models beyond a fixed-length context. Proc. Annu. Meet. Assoc. Comput. Linguist. 2019, 2978–2988. [Google Scholar] [CrossRef]
- Sayers, M.W.; Gillespie, T.D.; Paterson, W.D.O. Guidelines for conducting and calibrating road roughness measurements. World Bank Tech. Pap. 1986. Available online: https://hdl.handle.net/2027.42/3133 (accessed on 15 October 2025).
- Sayers, M.W.; Karamihas, S.M. The Little Book of Profiling: Basic Information about Measuring and Interpreting Road Profiles; University of Michigan, Transportation Research Institute: Ann Arbor, MI, USA, 1998. [Google Scholar]
- Chen, Z.; Badrinarayanan, V.; Lee, C.-Y.; Rabinovich, A. GradNorm: Gradient normalization for adaptive loss balancing in deep multitask networks. Proc. Mach. Learn. Res. 2018, 80, 807–815. [Google Scholar]
- Sener, O.; Koltun, V. Multi-task learning as multi-objective optimization. Adv. Neural Inf. Process. Syst. (NeurIPS) 2019, 31, 527–538. [Google Scholar]
- Wang, S.; Teng, Y.; Perdikaris, P.; Karniadakis, G.E. Learning physics-informed neural networks without stacked back-propagation. arXiv 2021, arXiv:2109.13852. [Google Scholar]
- Chatterjee, S.; Singh, B. Durability of concrete in an arid environment: Challenges and remedies. Constr. Build. Mater. 2019, 223, 72–80. [Google Scholar]
- Mehta, P.K.; Monteiro, P.J.M. Concrete: Microstructure, Properties, and Materials; McGraw-Hill Education: Berkshire, UK, 2014. [Google Scholar]
- Vaitkus, A.; Čygas, D.; Laurinavičius, A.; Perveneckas, Z. Analysis and evaluation of asphalt pavement structure damages caused by frost. Balt. J. Road Bridge Eng. 2009, 4, 196–202. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Steel, R.G.D.; Torrie, J.H.; Dickey, D.A. Principles and Procedures of Statistics: A Biometrical Approach; McGraw-Hill Education: Berkshire, UK, 1997. [Google Scholar]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Prechelt, L. Early stopping—But when? In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 1998; pp. 55–69. [Google Scholar]
- Li, N.; Zhang, J.; Peng, Z. Influence of environmental factors on the deterioration of concrete pavements in cold regions. Cold Reg. Sci. Technol. 2012, 83–84, 59–66. [Google Scholar]






| Symbol | Physical Meaning | |
|---|---|---|
| x, y, z | Coordinate | |
| t | Time stamp | |
| σ | Internal stress | |
| u | Horizonal displacement at joints | |
| Height difference at the joint | ||
| L | Length of the road (In this study, L is fixed at 100 m) | |
| Fourth-order elastic stiffness tensor, defined by E and v | ||
| I | Cubic tensor | |
| T | Atmospheric temperature | |
| Tc | Internal temperature of cement concrete | |
| Hc | Internal humidity of cement concrete | |
| α | Thermal expansion coefficient | |
| β | Hygroscopic expansion coefficient | |
| SR | Solar radiation | |
| P | Precipitation | |
| κT | Thermal conductivity | 1.42 W/m·K |
| DH | Moisture diffusion coefficient | 0.068 mm2/s |
| Dataset Types | Typical Environments | Characteristics of Natural Conditions of the Pavements | Provinces |
|---|---|---|---|
| Training set | Arid desert | In the arid desert region, cement concrete pavements face challenges from thermal expansion and contraction due to extreme temperature fluctuations, leading to frequent cracking and joint damage. Sand erosion can abrade the pavement surface, while dust accumulation may reduce skid resistance [32]. | Xinjiang |
| Hot and humid | In humid and rainy regions, excessive moisture infiltrates concrete pavements, causing joint spalling, surface scaling, and subgrade erosion. Persistent water exposure can also lead to damage at joints and cracks, accelerating structural deterioration [33]. | Guangxi | |
| Lightly frozen | Concrete pavements in light ice regions are affected by freeze–thaw cycles, which cause frost heave, cracking, and surface scaling. De-icing chemicals exacerbate surface deterioration and may lead to joint damage, weakening the cement concrete pavement over time [34]. | Beijing | |
| Test set | High-altitude cold region | In Qinghai–Tibet Plateau, the extreme cold and presence of permafrost cause significant frost heave and thaw settlement, leading to uneven surfaces and cracking in concrete pavements. The harsh environment accelerates damage to joints and surface layers, reducing durability [32]. | Tibet |
| Indicators | Formulas |
|---|---|
| MSE | |
| R2 | |
| Sp |
| Hyperparameters | Initial Value | Final Value |
|---|---|---|
| Encoder layers | 3 | 3 |
| Decoder layers | 2 | 2 |
| Token embedding dimension | 5 | 5 |
| Dimension of the hidden layer of feed-forward neutral network | 20 | 20 |
| Learning rate | 0.0001 | 0.001 |
| Learning rate decay | 0.5 | 0.8 |
| Epoch | 100 | 20 |
| Batch size | 32 | 32 |
| λPhysics and λdata | 0.1 and 0.9 | 0.46 and 0.54 |
| 0. 39 and 0.61 | ||
| 0.33 and 0.67 | ||
| 0.21 and 0.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, X.; Zeng, Z.; Yi, F. Physics-Aware Informer: A Hybrid Framework for Accurate Pavement IRI Prediction in Diverse Climates. Infrastructures 2025, 10, 278. https://doi.org/10.3390/infrastructures10100278
Cao X, Zeng Z, Yi F. Physics-Aware Informer: A Hybrid Framework for Accurate Pavement IRI Prediction in Diverse Climates. Infrastructures. 2025; 10(10):278. https://doi.org/10.3390/infrastructures10100278
Chicago/Turabian StyleCao, Xintao, Zhiping Zeng, and Fan Yi. 2025. "Physics-Aware Informer: A Hybrid Framework for Accurate Pavement IRI Prediction in Diverse Climates" Infrastructures 10, no. 10: 278. https://doi.org/10.3390/infrastructures10100278
APA StyleCao, X., Zeng, Z., & Yi, F. (2025). Physics-Aware Informer: A Hybrid Framework for Accurate Pavement IRI Prediction in Diverse Climates. Infrastructures, 10(10), 278. https://doi.org/10.3390/infrastructures10100278





