Dynamic Response and Design Optimization of Box Girder Bridge with Corrugated Steel Webs Subjected to Blast Loads
Abstract
1. Introduction
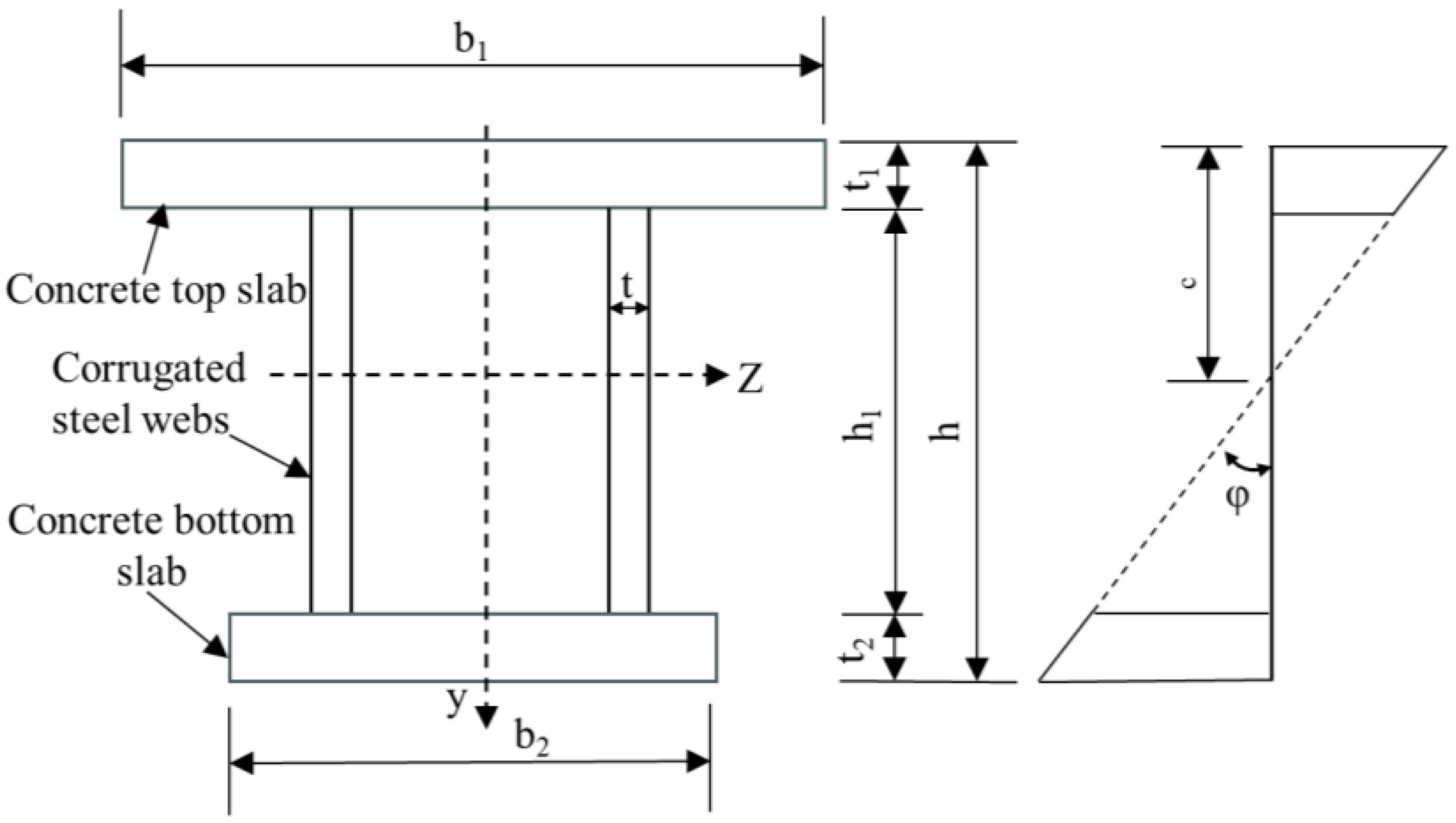
2. Calculation Theory of Box Girder Bridges with CSWs
2.1. Stress Calculation of Box Girder Bridge with CSWs
2.1.1. Bending Normal Stress Calculation
2.1.2. Shearing Stress Calculation
2.2. Deflection Calculation of Box Girder Bridge with CSWs
2.2.1. Deflection Caused by the Bending Deformation
2.2.2. Deflection Caused by the Shearing Deformation
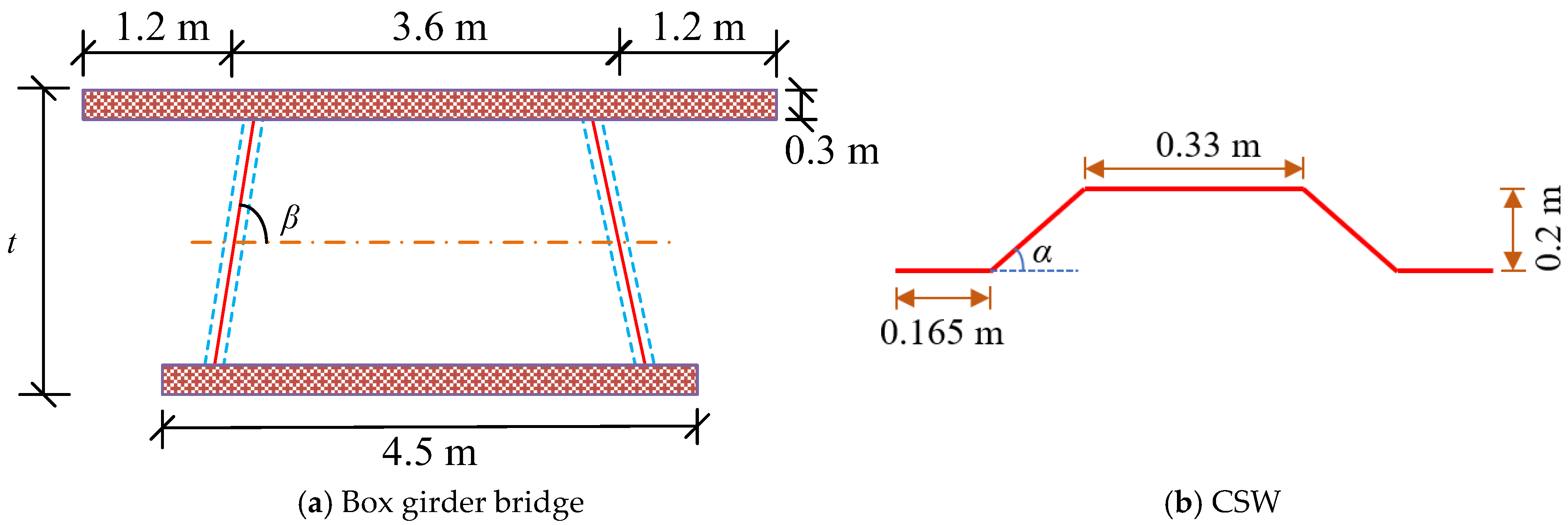
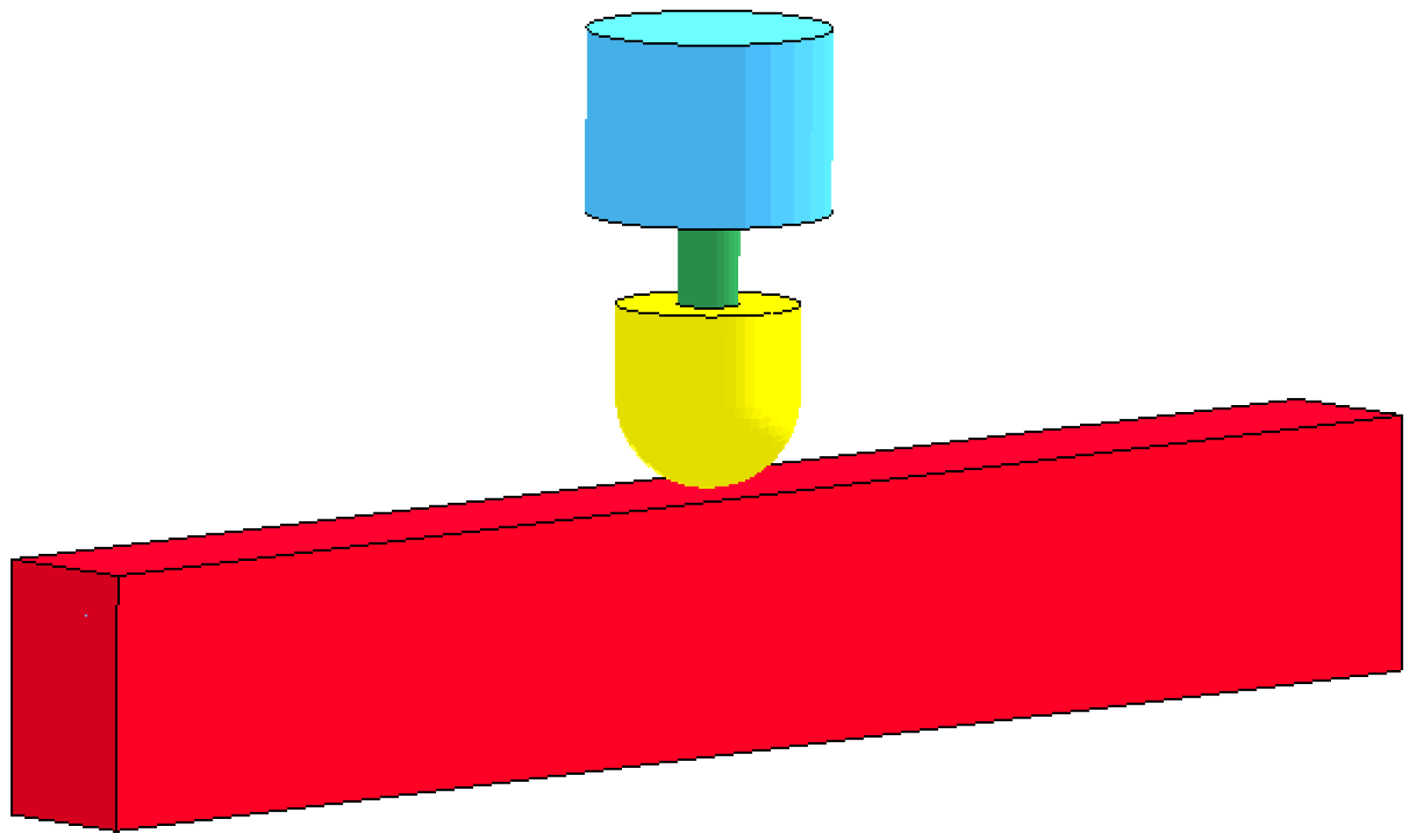
3. Establishment and Calibration of Numerical Models of Box Girder Bridge with CSWs
3.1. Numerical Model of Box Girder Bridge with CSWs
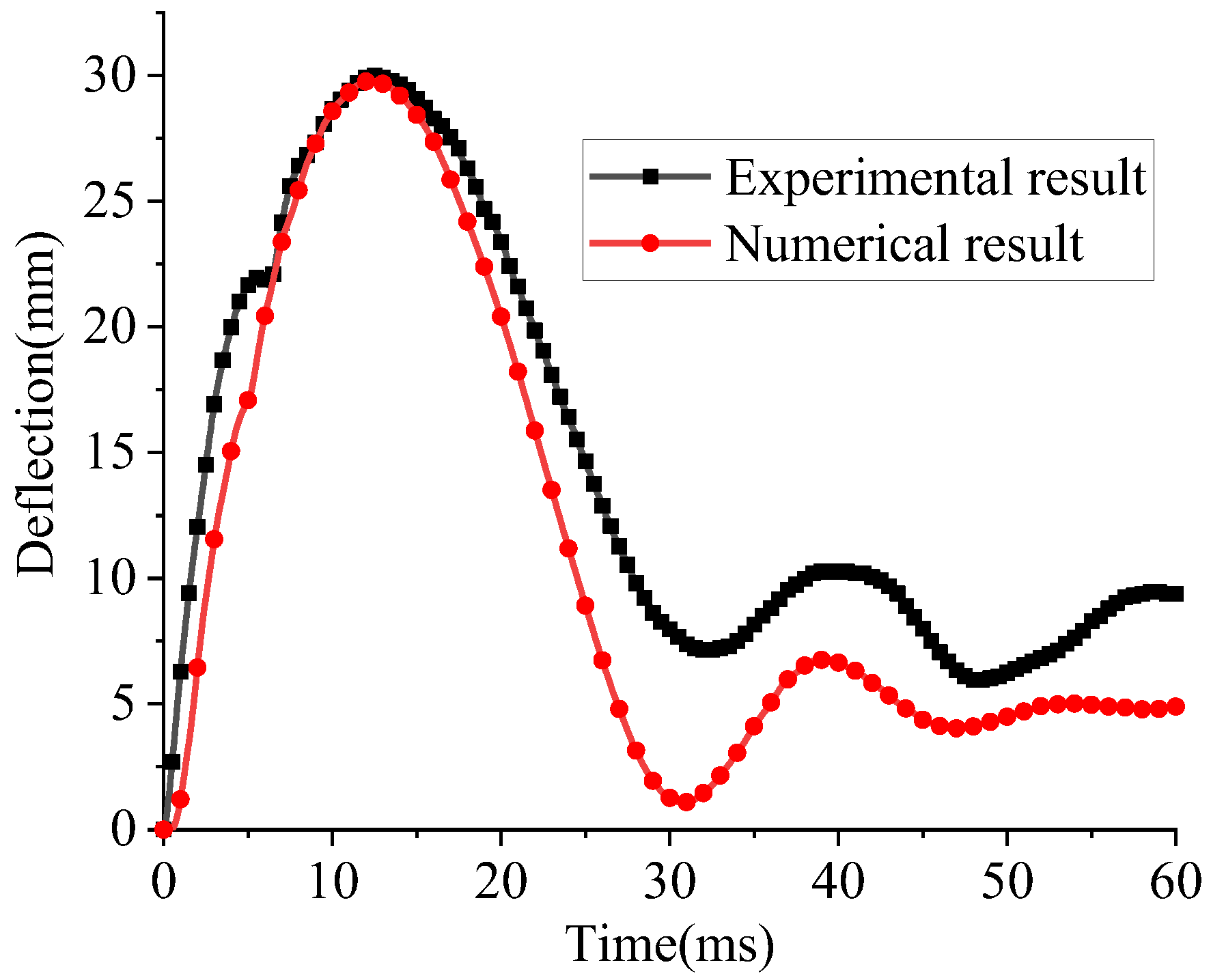
3.2. Calibration of Numerical Model
4. Response of Box Girder Bridge with CSWs Subjected to Blast Load
4.1. Effect of Folding Angle of CSW on the Response of Box Girder Bridge
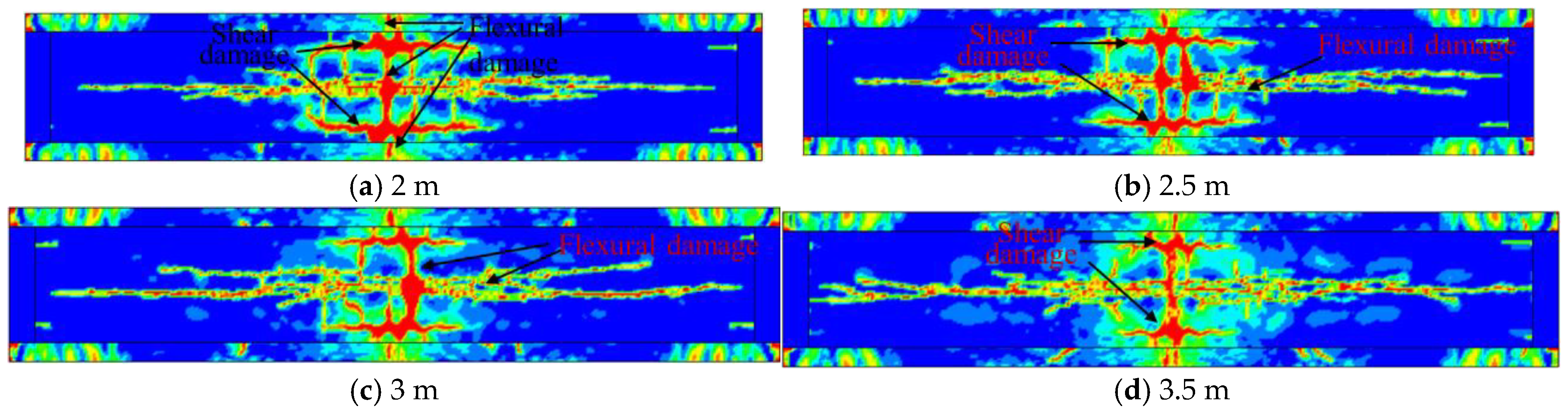
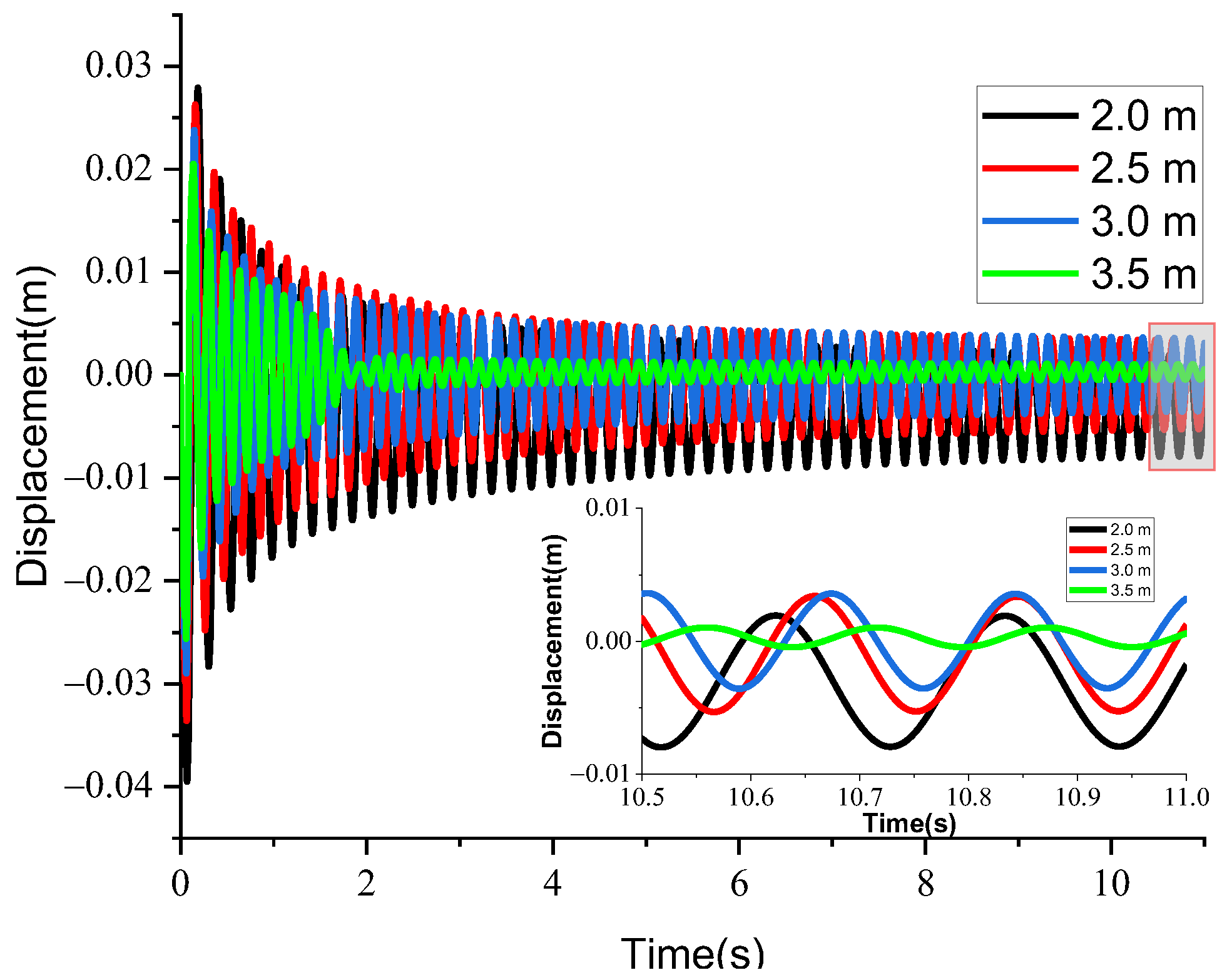
4.2. Effect of Height–Span Ratio on the Response of Bridges with CSWs
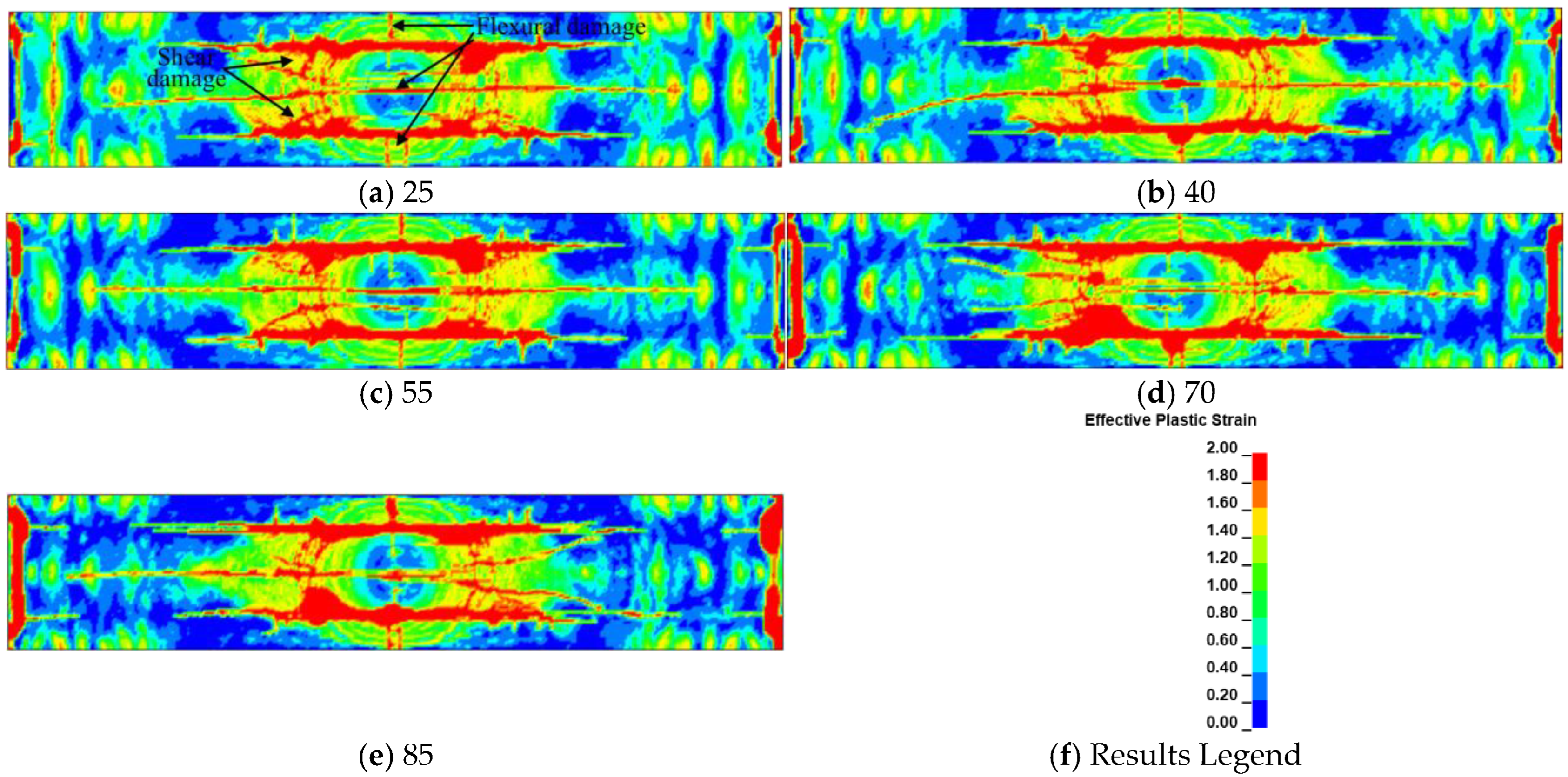
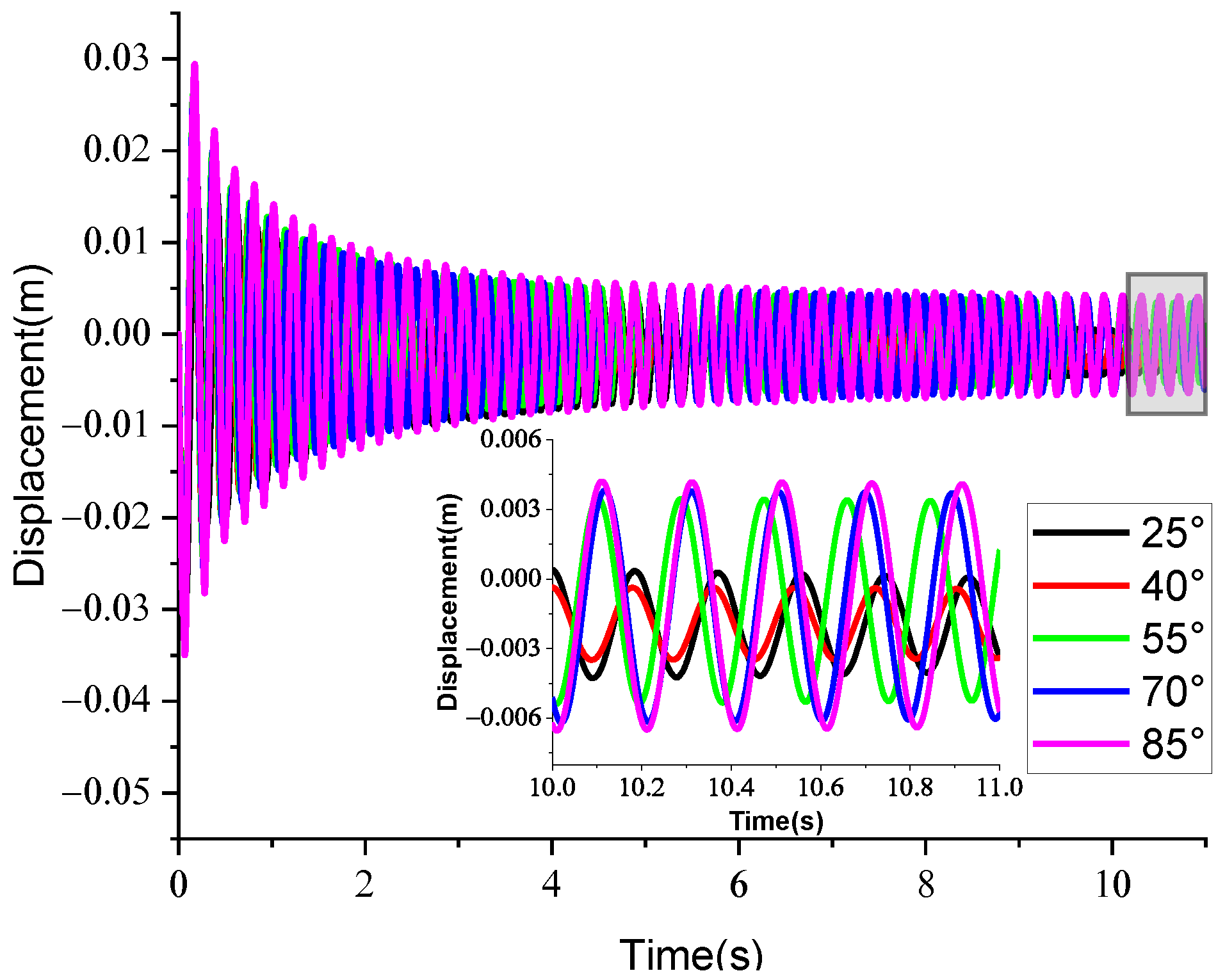
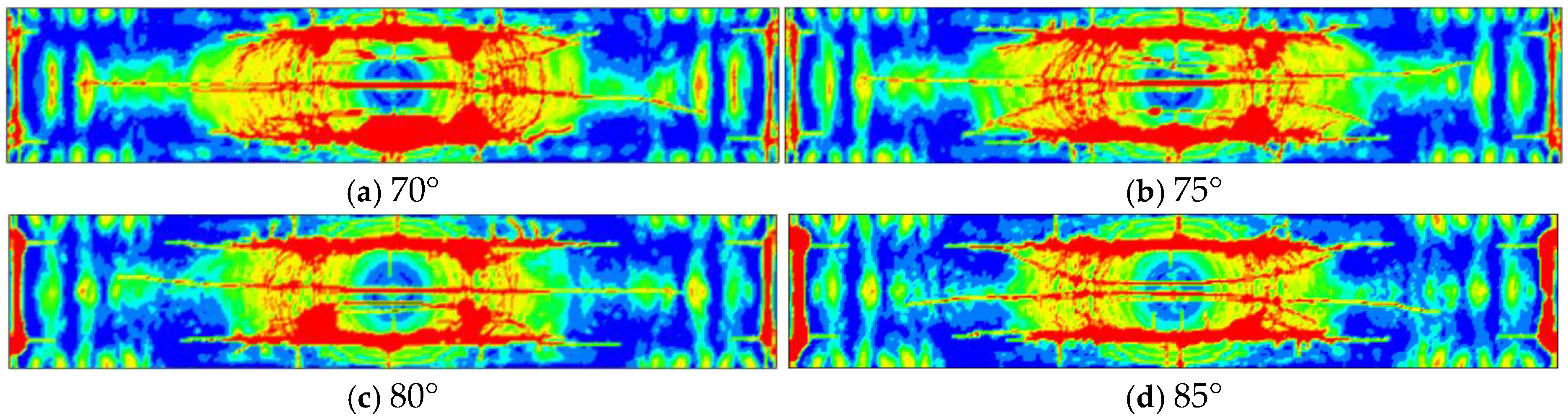
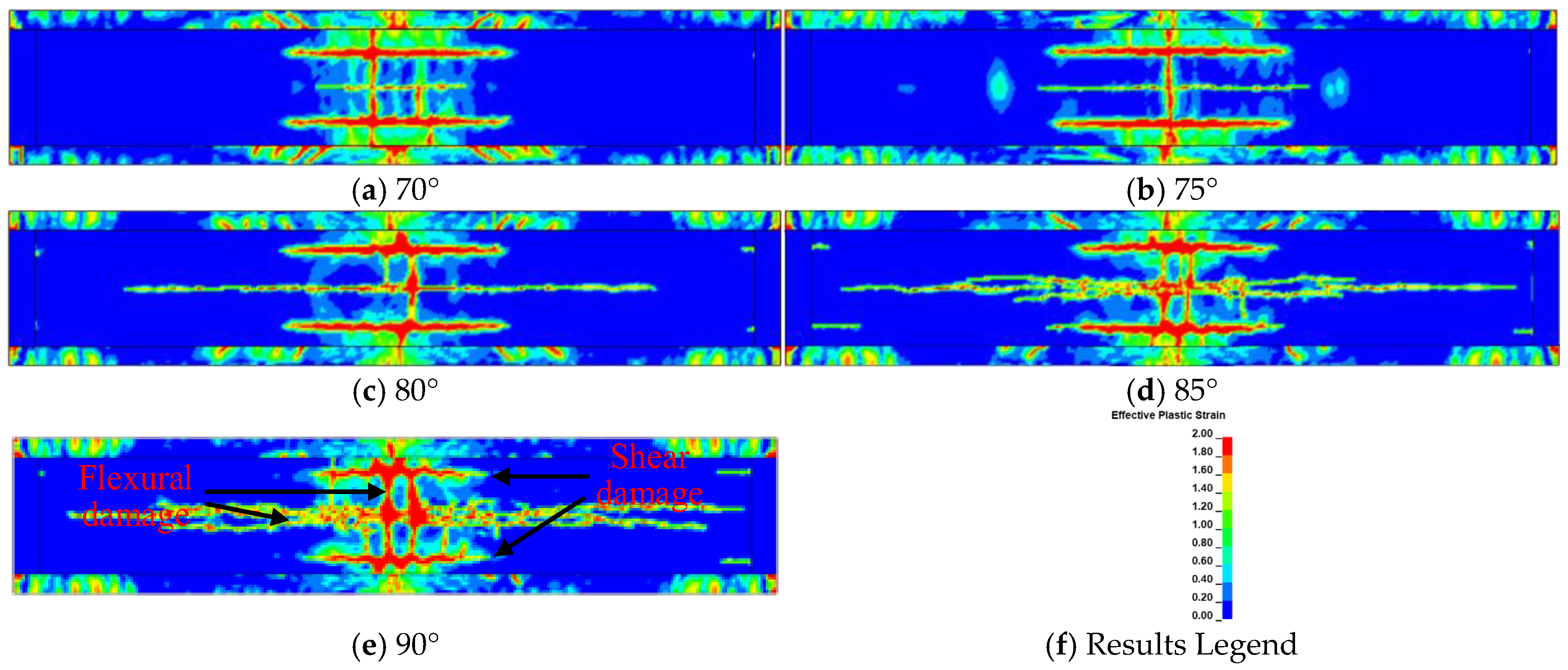
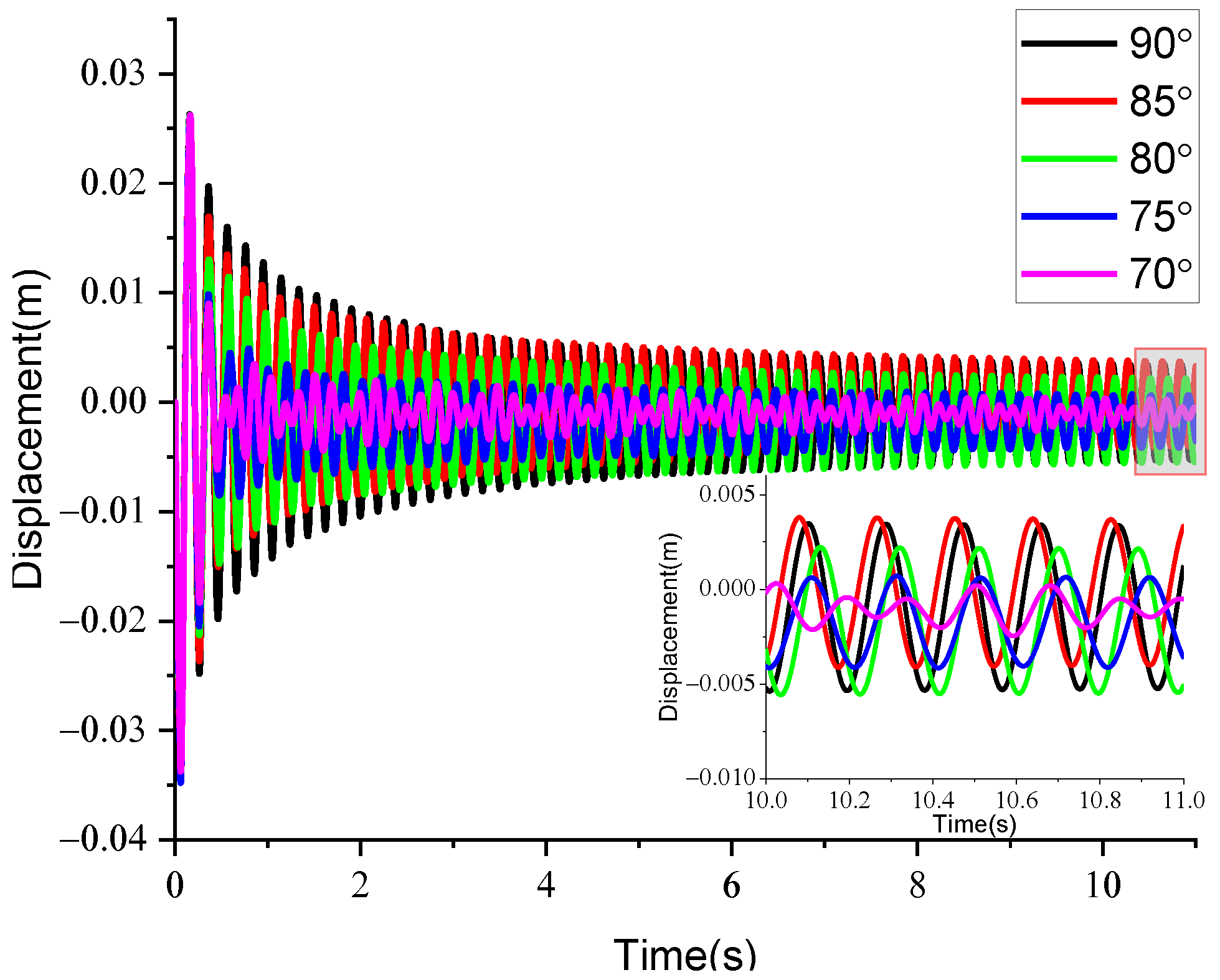
4.3. Effect of Dip Angle on the Response of Bridges with CSWs
5. Discussion
6. Conclusions
- The bridge deck around the CSWs in the middle span of the bridge are severely damaged because of the stress concentration at the intersection of the CSWs and the bridge deck, and the bridge deck is more severely damaged with the increase in folding angle of the CSW. The local stiffness and the shear capacity of the CSW increases with the increase in folding angle. The box girder bridge with a folding angle of 55° has better blast-resistance capacity than bridges composed of other folding angles because the blast-resistance performance of box girder bridges with CSWs is related to the local stiffness of the CSW and the stress concentration at the bridge deck induced by the folding effect of the CSW.
- As the height–span ratio increases, the bending stiffness of the CSW decreases, and the flexural damage around the centerline of the upper deck gradually expands toward to the interface of bridge deck and CSW. The damage area of the bottom deck around the interface of CSW and bridge deck decreases with the increase in CSW height. The shear stiffness of the bridge cross-section decreases as the height–span ratio of the bridge increases. The bottom deck of the bridge is less severely damaged with the increase in height–span ratio. Considering the residual deflection of the bridge bottom deck and the energy absorption capacity of the CSW, the optimal cross-sectional height of the bridge is 3 m.
- The damage degree of the bridge upper deck decreases with the increase in CSW dip angle. The cross-sectional stiffness, the shear capacity, and vertical deformation constraint of the bridge with CSWs increases with the increase in dip angle. Therefore, the flexural damage and shear damage of the bridge bottom deck is more severe with the increase in CSW dip angle. The optimal dip angle of the CSWs for box girder bridges is 85° by comparing the residual deflection at the middle span of the bridge.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Katsimpini, P.S.; Papagiannopoulos, G.; Hatzigeorgiou, G. Nonlinear Analysis of Bridges Considering Soil–Structure Interaction and Travelling Wave Effects Under Combined Train and Near-Fault Seismic Loads. Appl. Sci. 2024, 14, 11688. [Google Scholar] [CrossRef]
- Fathy, E.; Eraky, A.; Mustafa, S.A.; Al-Sallami, A.A. Controlling seismic torsional behavior of skewed bridges to reduce the risk of unseating damage. Structures. Structures 2025, 80, 109874. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, Z.D.; Hu, H.; Guo, Y.Q.; Huang, X.H.; Zhang, Z.W.; Zhang, T.; Xu, C. Experiment, Simulation, and Theoretical Investigation of a New Type of Interlayer Connections Enhanced Viscoelastic Damper. Int. J. Struct. Stab. Dyn. 2025, 25, 2550045. [Google Scholar] [CrossRef]
- Jiang, R.J.; Au, F.T.K.; Xiao, Y.F. Prestressed Concrete Girder Bridges with Corrugated Steel Webs: Review. J. Struct. Eng. 2015, 141, 04014108. [Google Scholar] [CrossRef]
- He, J.; Liu, Y.; Chen, A.; Yoda, T. Mechanical behavior and analysis of composite bridges with corrugated steel webs: State-of-the-art. Int. J. Steel Struct. 2012, 12, 321–338. [Google Scholar] [CrossRef]
- Easley, J.T. Buckling Formulas for Corrugated Metal Shear Diaphragms. J. Struct. Div. 1975, 101, 1403–1417. [Google Scholar] [CrossRef]
- Johnson, R.P.; Cafolla, J.; Bernard, C. Corrugated webs in plate girders for bridges. Struct. Build. 1997, 122, 157–164. [Google Scholar] [CrossRef]
- Driver, R.G.; Abbas, H.H.; Sause, R. Shear Behavior of Corrugated Web Bridge Girders. J. Struct. Eng. 2006, 132, 195–203. [Google Scholar] [CrossRef]
- Hassanein, M.F.; Kharoob, O.F. Shear buckling behavior of tapered bridge girders with steel corrugated webs. Eng. Struct. 2014, 74, 157–169. [Google Scholar] [CrossRef]
- Bergmann, L.; Reissner, E. On the Bending and Torsion of Rectangular Plates with Unequal Bending Stiffness in Two Perpendicular Directions. J. Appl. Mech. 1928, 5, 123–145. [Google Scholar]
- Elgaaly, M.; Seshadri, A.; Rodriquez, R.; Ibrahim, S. Bridge Girders with Corrugated Webs. Transp. Res. Rec. J. Transp. Res. Board 2000, 1696, 162–170. [Google Scholar] [CrossRef]
- Elgaaly, M.; Seshadri, A. Girders with Corrugated Webs under Partial Compressive Edge Loading. J. Struct. Eng. 1997, 123, 783–791. [Google Scholar] [CrossRef]
- Elgaaly, M.; Hamilton, R.W.; Seshadri, A. Shear Strength of Beams with Corrugated Webs. J. Struct. Eng. 1996, 122, 390–398. [Google Scholar] [CrossRef]
- Luo, R.; Edlund, B. Shear capacity of plate girders with trapezoidally corrugated webs. Thin-Walled Struct. 1996, 26, 19–44. [Google Scholar] [CrossRef]
- Luo, R.; Edlund, B. Ultimate strength of girders with trapezoidally corrugated webs under patch loading. Thin-Walled Struct. 1996, 24, 135–156. [Google Scholar] [CrossRef]
- El Metwally, A.; Loov, R.E. Corrugated steel webs for prestressed concrete girders. Mater. Struct. 2003, 36, 127–134. [Google Scholar] [CrossRef]
- Jin, H.; Hao, H.; Hao, Y.; Chen, W. Predicting the response of locally resonant concrete structure under blast load. Constr. Build. Mater. 2020, 252, 118920. [Google Scholar] [CrossRef]
- Jin, H.; Hao, H.; Xu, C.; Huang, Z.; Chen, W. Dynamic response of metaconcrete beam under blast load. Int. J. Struct. Stab. Dyn. 2023, 23, 2350178. [Google Scholar] [CrossRef]
- Jin, H.; Hao, H.; Chen, W.; Xu, C. Effect of enhanced coating layer on the bandgap characteristics and response of metaconcrete. Mech. Adv. Mater. Struct. 2021, 30, 175–188. [Google Scholar] [CrossRef]
- Yang, S.; Liu, Z.; Wang, S.; Zhong, W.; Zhang, R.; Yao, X. Dynamic response and failure analysis for urban bridges under far-field blast loads. Eng. Struct. 2023, 285, 116043. [Google Scholar] [CrossRef]
- Tetougueni, C.D.; Zampieri, P. Structural response of cable-stayed bridge subjected to blast load. Procedia Struct. Integr. 2019, 18, 765–774. [Google Scholar] [CrossRef]
- Pan, Y.; Ventura, C.E.; Cheung, M.M.S. Performance of highway bridges subjected to blast loads. Eng. Struct. 2017, 151, 788–801. [Google Scholar] [CrossRef]
- Vaghefi, M.; Mobaraki, B. Evaluation of the effect of explosion on the concrete bridge deck using LS-DYNA. Int. Rev. Civ. Eng. 2021, 12, 135. [Google Scholar] [CrossRef]
- Gholipour, G.; Billah, A.H.M.M.; Mousavi, A.A. Finite element-based reliability analysis of RC bridge piers subjected to the combination of barge impact and blast loads. Ocean Eng. 2022, 264, 112543. [Google Scholar] [CrossRef]
- Lv, C.; Yan, Q.; Li, L.; Li, S. Field test and probabilistic vulnerability assessment of a reinforced concrete bridge pier subjected to blast loads. Eng. Fail. Anal. 2023, 143, 106802. [Google Scholar] [CrossRef]
- Hashemi, S.K.; Bradford, M.A.; Valipour, H.R. Dynamic response of cable-stayed bridge under blast load. Eng. Struct. 2016, 127, 719–736. [Google Scholar] [CrossRef]
- Yu, S.; Wu, H.; Zhang, G.; Wang, Z.; Yao, J.; Li, H.; Liu, C. Experimental study on anti-shallow-buried-explosion capacity of a corrugated steel-plain concrete composite structure. Int. J. Impact Eng. 2023, 172, 104393. [Google Scholar] [CrossRef]
- Cao, K.; Fu, Q.; Zhang, J.; Tang, C.; Huang, J.; Wang, C.; Bai, W. Effect of corrugated steel angle on the damage characteristics and anti-explosion performance of corrugated steel–concrete composite structures. Struct. Des. Tall Spéc. Build. 2024, 33, e2112. [Google Scholar] [CrossRef]
- Mo, Y.L.; Jeng, C.H.; Chang, Y.S. Torsional behavior of prestressed concrete box-girder bridges with corrugated steel webs. Struct. J. 2000, 97, 849–859. [Google Scholar]
- Abbas, H.H.; Sause, R.; Driver, R.G. Shear Strength and Stability of High Performance Steel Corrugated Web Girders. In Proceedings of the Structural Stability Research Council 2002 Annual Stability Conference, Seattle, DC, USA, 24–27 April 2002. [Google Scholar]
- Zha, S.; Liu, D.; Zhang, J.; Deng, W.; Gu, J. Calculation method for flexural capacity of composite girders with corrugated steel webs. J. Constr. Steel Res. 2024, 214, 108476. [Google Scholar] [CrossRef]
- Cantor, B. Hooke’s Law //The Equations of Materials; Oxford University Press: Oxford, UK, 2020; pp. 207–225. [Google Scholar]
- JTG/T 2231-01—2020; Specifications for Seismic Design of Highway Bridges. China Communications Press: Beijing, China, 2020.
- T/CECS 736-202; Standard for Blast Protection Design of Civil Buildings. China Architecture & Building Press: Beijing, China, 2020.
- Malvar, L.J.; Ross, C.A. Review of strain rate effects for concrete in tension. ACl Mater. J. 1999, 96, 614–616. [Google Scholar]
- CEB; CEBFIP. Model Code 1990; Redwood Books: Wiltshire, UK, 1993. [Google Scholar]
- Malvar, L. Review of Static and Dynamic Properties of Steel Reinforcing Bars. ACI Mater. J. 1998, 95, 609–616. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, W.; Hao, H.; Chen, Z.; Pham, T.M.; Tran, T.T.; Elchalakani, M. Shear behaviour of ambient cured geopolymer concrete beams reinforced with BFRP bars under static and impact loads. Eng. Struct. 2021, 231, 111730. [Google Scholar] [CrossRef]
- Tong, J.-Z.; Yu, C.-Q.; Tong, G.-S.; Xu, S.-L. Experimental study on axial resistant behavior of multi-celled corrugated-plate CFST walls. Eng. Struct. 2023, 295, 116795. [Google Scholar] [CrossRef]
- Yu, C.-Q.; Tong, J.-Z.; Tong, G.-S.; Xu, S.-L.; Chen, M. Axial compressive performance and design of multi-celled corrugated-plate CFST walls. Structures 2023, 57, 105303. [Google Scholar] [CrossRef]
- Lv, L.-J.; Peng, X.-T.; Yang, T.-C. Study on lateral-force resistance performance of cross-slanted corrugated steel plate shear wall. J. Phys. Conf. Ser. 2019, 1168, 022070. [Google Scholar]










| Component | Keyword |
|---|---|
| Concrete deck, cushion plate, end plate | * MAT_072R3 |
| Reinforcement, CSW | * Mat_Piecewise_Linear_Plasticity (Mat_024) |
| Erosion criterion of concrete | * Mat_Add_Erosion (Maximum principal strain: 0.1) |
| Contact condition | Keyword |
| Concrete deck and reinforcement Concrete deck and CSW | * Constrained_Lagrange_in_Solid |
| Concrete deck, end plate, cushion plate | * Automatic_ Surface_to_Surface |
| Material | Parameter | Value |
|---|---|---|
| Concrete (concrete deck, cushion plate, end plate) | Compressive strength (MPa) | 34 |
| Density (kg/m3) | 2300 | |
| Poisson’s ratio | 0.19 | |
| Reinforcement | Elastic modulus (GPa) | 200 |
| Density (kg/m3) | 7800 | |
| Yield stress (MPa) | 300 |
| Displacement | Experimental Result | Numerical Result | Error |
|---|---|---|---|
| Peak displacement (mm) | 30.1 | 29.2 | −3% |
| Residual displacement(mm) | 9.6 | 4.9 | −49% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, C.; Jin, H.; Xu, Y.; He, X.; Zhou, J. Dynamic Response and Design Optimization of Box Girder Bridge with Corrugated Steel Webs Subjected to Blast Loads. Infrastructures 2025, 10, 256. https://doi.org/10.3390/infrastructures10100256
Xie C, Jin H, Xu Y, He X, Zhou J. Dynamic Response and Design Optimization of Box Girder Bridge with Corrugated Steel Webs Subjected to Blast Loads. Infrastructures. 2025; 10(10):256. https://doi.org/10.3390/infrastructures10100256
Chicago/Turabian StyleXie, Changling, Hexin Jin, Yunlong Xu, Xiaopei He, and Junlong Zhou. 2025. "Dynamic Response and Design Optimization of Box Girder Bridge with Corrugated Steel Webs Subjected to Blast Loads" Infrastructures 10, no. 10: 256. https://doi.org/10.3390/infrastructures10100256
APA StyleXie, C., Jin, H., Xu, Y., He, X., & Zhou, J. (2025). Dynamic Response and Design Optimization of Box Girder Bridge with Corrugated Steel Webs Subjected to Blast Loads. Infrastructures, 10(10), 256. https://doi.org/10.3390/infrastructures10100256





