Abstract
In this study, the behavior of the spherical bearing component of the L-100 bridge part (AlfaTech LLC, Perm, Russia) is considered within the framework of a finite element model. The influence of the pattern of the coupling of the antifriction interlayer with the lower steel plate on the operation of the part is examined in terms of ideal contact, full adhesion, and frictional contact. The thickness of the antifriction interlayer varied from 4 to 12 mm. The dependencies of the contact parameters and the stress–strain state on the thickness were determined. Structurally modified polytetrafluoroethylene (PTFE) without AR-200 fillers was considered the material of the antifriction interlayer. The gradual refinement of the behavioral model of the antifriction material to account for structural and relaxation transitions was carried based on a wide range of experimental studies. The elastic–plastic and primary viscoelastic models of material behavior were constructed based on a series of homogeneous deformed-state experiments. The viscoelastic model of material behavior was refined using data from dynamic mechanical analysis over a wide temperature range [−40; +80] °C. In the first approximation, a model of the deformation theory of plasticity with linear elastic volumetric compressibility was identified. As a second approximation, a viscoelasticity model for the Maxwell body was constructed using Prony series. It was established that the viscoelastic model of the material allows for obtaining data on the behavior of the part with an error of no more than 15%. The numerical analog of the construction in an axisymmetric formulation can be used for the predictive analysis of the behavior of the bearing, including when changing the geometric configuration. Recommendations for the numerical modeling of the behavior of antifriction layer materials and the coupling pattern of the bearing elements are given in this work. A spherical bearing with an antifriction interlayer made of Arflon series material is considered for the first time.
1. Introduction
1.1. Research Objectives
This study aimed to create a spherical bearing using relatively simple numerical analogs, taking into account the antifriction interlayer material’s nonlinear behavior. This study includes an analysis of the structural behavior with different element matting patterns, as well as the thickness of the antifriction interlayer. Ensuring efficient operation of bridge bearings is an important task for the sustainable urbanization of territories.
Research tasks include the following:
- The construction of an antifriction interlayer material model that takes into account the nonlinear effects of deformation behavior.
- The influence analysis of the matting pattern of the lower steel plate and the antifriction interlayer in terms of structural behavior.
- The influence analysis of the antifriction interlayer thickness in bearing operation.
- The influence analysis of the material behavioral model for the contact stress–strain state of the bearing.
- The analysis of the bearing behavior with structurally modified polytetrafluoroethylene (PTFE) without an AR-200 filler interlayer.
A digital analog of the bearing will allow us to predict the structural behavior under various conditions with high accuracy. Relatively simple structural models with a relatively small error from the real study object are of particular interest. They are necessary to minimizing the cost of computing resources and time for evaluating engineering solutions. This work aimed to create axisymmetric models of a spherical bearing to analyze the influence of the structural elements’ geometric configuration on the contact stress–strain state.
1.2. Problem Context and Description
The design and construction of bridges is quite a complex process. Social, economic, resource, technical, and geographical factors determine the complexity of bridge structural design [1,2,3]. Building bridges in hard-to-reach areas, such as Arctic territories, mountain gorges, and coastal areas, requires the adaptation of important structural components to extreme conditions. The use of modern materials and the adoption of new design and technological solutions to ensure the long-term trouble-free operation of the structure are also important [1,4]. The high demand for such critical components requires more detailed comprehensive engineering and technical research. Preliminary analysis includes an assessment of materials and existing design solutions [5,6,7]. The final analysis includes the technical diagnostics and monitoring of the structure and its supporting elements [8,9]. Every detail of a bridge is an important component that affects the durability and safety of the structure as a whole.
The bearing is one of the key elements of the bridge [10]. Bearings redistribute the load from the span structures, and they bear dynamic impacts from vehicles and various natural and climatic phenomena [4,11,12]. Bridge bearings have many structural types. But spherical bearings have become widespread due to their high reliability and durability [13,14]. However, now, various factors that affect the stability, strength, and durability of the bearing must be taken into account when designing bridges [15,16,17]. This is because bridges are being built in difficult geographical and climatic conditions with extreme weather events and critical temperature fluctuations. For example, in [18], scientists assessed the impact of spherical steel bearings on train safety under seismic activity. Studies of the wind load on a long-span bridge during typhoons were conducted in order to further accurately assess fatigue damage to structural components [19]. The joint operation of the bearing and the span under complex loading, while also taking into account the means of transport, is of interest [17].
New, innovative designs of spherical bearings are also being developed [20,21,22], enabling increased load limits and fatigue strength. Changes in the geometry of the bearing elements significantly affect the deformation behavior of the structure [23,24]. The geometric parameters of the antifriction interlayer and its position relative to the steel plates have a significant impact on the contact characteristics [25]. Introducing an interlayer with convex and rounded edges allows for a slight increase in stresses and deformations compared to canonical geometry under increased vertical load [26]. Texturing the working surfaces also affects the effective coupling of elements [27,28,29]: it reduces friction, improves wear resistance, and increases the service life of the components. Studying bearing design is important for understanding the behavior of the elements, as well as for optimizing the structure to meet the required operating conditions.
The issues related to spherical bearing materials are also important. The primary influence on bearing performance is exerted by the antifriction interlayer material [25]. Scientists have made significant contributions by improving the physicomechanical and tribological characteristics of these materials [30,31,32]. A wide range of modern polymers and composites are currently available for use as bearing antifriction interlayers [33,34,35]. Polytetrafluoroethylene (PTFE), polyetheretherketone (PEEK), polymethylmethacrylate (PMMA), polyurethane (PU), polyamide (PA), ultra-high-molecular-weight polyethylene (UHMWPE), and composites based on these polymers are considered promising materials for antifriction interlayers [36]. The use of ceramics as sliding surfaces is also being explored [37,38]. Structurally modified PTFEs, both without additives and with nanofillers, manufactured by the Scientific and Production Enterprise Arflon LLC (Moscow, Russia) are also recommended for use as antifriction materials [39]. Arflon materials are characterized by high structural homogeneity, absence of porosity, and a wide range of operating temperatures. The material AR-200 is chemically analogous to PTFE but significantly surpasses it in physical, mechanical, and antifriction properties. In this study, AR-200 is considered as the antifriction interlayer. However, analyzing the behavior of the material within the bearing requires the development of numerical models. The digital model must accurately represent the physicomechanical and thermomechanical properties observed in experimental results. This necessitates a large number of empirical studies, as well as the application of mathematical tools for model development.
The mathematical description of the behavior of antifriction materials is of particular interest. The main research areas include rheology [40], viscoelasticity [41,42], viscoplasticity [43], viscoelastic-plasticity [44,45,46], phase transitions [47,48], etc. The complex nonlinear behavior of modern antifriction materials is important to note, as confirmed by numerous field experiments [49,50,51]. Experimental studies, combined with numerical modeling, make it possible to study the behavior of materials in greater detail. The processes occurring within the structural elements are analyzed, and the stress–strain state of parts and assemblies is evaluated based on key characteristics and parameters. Numerical methods help minimize the volume of experimental research. Numerical analogs of materials enable large-scale structural performance analysis within the framework of digital engineering. The choice of antifriction interlayer material and geometric design configuration can contribute to the optimization of spherical bearings for bridges. Numerical modeling allows for the prediction of structural deformation behavior under various loads, including the contact interaction between elements [52,53,54]. It is crucial to develop digital design models that take into account the nonlinear behavior of antifriction interlayer materials.
As part of the current study, a finite element model of the L-100 spherical bearing (AlfaTech LLC, Perm, Russia) with an antifriction interlayer made from Arflon line material was developed. A gradual refinement of the behavioral model for the antifriction interlayer material was carried out. Commonly used models, both elastic–plastic and viscoelastic, were considered. A high-quality digital analog of the material is essential for creating a spherical bearing model that closely reflects the actual structure. Using the bearing model with a nonlinear material representation of the antifriction interlayer, we investigated the influence of the element coupling pattern and the thickness of the antifriction interlayer on the bearing’s contact interaction parameters. Multifactorial analysis of the structure’s behavior makes it possible to obtain data relevant to designers when developing bearings for specific operating conditions.
2. Materials and Methods
2.1. The Design of the Spherical Bearing
The influence of the thickness of the polymer antifriction interlayer and its coupling pattern with the lower steel plate of the spherical bearing of the bridge span is examined in this study. The geometry of the contact unit of the spherical bearing includes an upper (1) and a lower (2) steel plate, which interact through a spherical antifriction interlayer made of a polymer or composite material (3) (Figure 1).
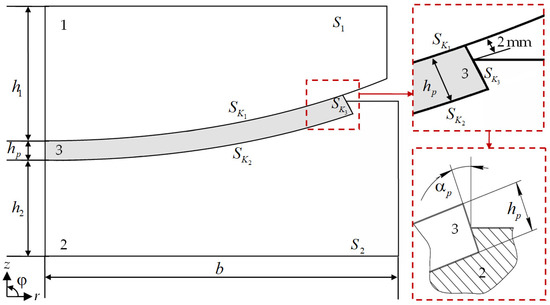
Figure 1.
Calculation scheme of the spherical bearing.
The main geometric parameters of the L-100 bearing (AlfaTech LLC, Perm, Russia) are provided in Table 1. As part of this study, the effect of increasing the antifriction interlayer thickness to 6, 8, 10, and 12 mm on the performance of the structure will be examined. The end face of the antifriction interlayer (3) is partially in contact with the steel structural elements. A 2 mm portion of the interlayer remains free from contact with the lower plate (a protrusion of the antifriction interlayer) to prevent metal-to-metal contact during construction work. The polymer interlayer is press-fitted into the bottom steel plate. The nominal vertical load is 1000 kN.

Table 1.
Main geometric characteristics of the bearing.
A simplified geometry of the antifriction interlayer is considered, excluding the lubricant hole. The problem is analyzed in an axisymmetric formulation using the finite element method in ANSYS Mechanical APDL 2021R2 (Livermore, CA, USA).
A frictional contact is implemented on the contact surface, with a previously unknown distribution pattern of contact status states.
- -
- Sliding
- -
- No contact
- -
- Full attachment (adhesion)
The friction contact corresponds to the polished surface of the steel in the interface area.
On the contact surfaces , three conjugation patterns are implemented:
- An ideal contact, created by modeling a finite element node-to-node grid, which makes it possible to obtain uniform fields of displacements, stresses, and deformations at the interface:
- Full adhesion, which corresponds to the processing of the conjugation surface of the “torn thread” type (3).
- Frictional contact (1)–(3), which includes different statuses with a previously unknown pattern of their distribution over the surface: full adhesion, sliding, and no contact.
Minimal roughness is required for the spherical sliding surface in the interface area between the upper balancer and the antifriction interlayer. This is achieved by using a polished surface on the spherical segment of the balancer. The bed of the balancer (the spherical cutout in the lower steel plate) can be treated in various ways: left unprocessed, given a rough “torn thread”-type surface to maximize adhesion, or polished. The surface treatment pattern can significantly influence the contact parameters and the stress–strain state of the structure. This paper considers the effect of the sliding antifriction interlayer’s coupling pattern with the balancer bed on the performance of the bridge bearing.
2.2. Antifriction Interlayer Material
Structurally modified PTFE without fillers, AR-200 (Scientific and Production Enterprise Arflon LLC, Moscow, Russia), is considered as the material for the antifriction interlayer. The material is produced through compaction and high-temperature physicochemical modification. It features a spherulitic macromolecular structure and is white in color. AR-200 is used in the manufacturing of sliding components.
To develop a material behavioral model, a series of experiments was initially conducted under homogeneous deformation conditions using cylindrical samples measuring 20 × 20 mm. Testing was performed with a Zwick Z100SN5A material testing machine (Zwick Roell AG, Ulm, Germany) and a Multisens extensometer (Zwick Roell AG, Ulm, Germany). The experimental studies were carried out at the Ural Branch of the Russian Academy of Sciences (ICMM UB RAS, Perm, Russia), under the supervision of Dr. A.A. Adamov. The maximum deformation level for the samples was set at 10%, based on the estimated maximum deformation of the bearing’s antifriction interlayer. This limit represents the maximum allowable level for applying small deformation theory. A multi-stage testing program was implemented up to the 10% strain level, including relaxation, unloading, and recovery phases. The traverse movement speed was 3 mm/min. All experimental studies were conducted at room temperature.
The experiment and the processed results of empirical studies are shown in Figure 2.
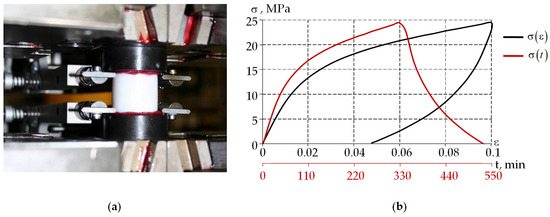
Figure 2.
Experiment on free compression of cylindrical samples: (a) the experiment; (b) the equilibrium experimental curves.
It was established that the material is a viscoplastic, compressible body with nonlinear viscoplastic volumetric compressibility and stress-induced phase transitions.
In the first approximation, a deformation theory of a plasticity model with linear elastic volumetric compressibility was identified (Figure 3a). This model was developed for the case of active loading and did not account for unloading.
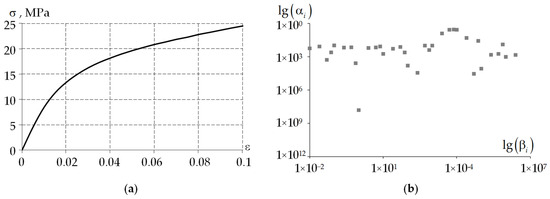
Figure 3.
Material models based on experimental data on the free compression of cylindrical samples: (a) elastic-plasticity; (b) viscoelasticity.
In the second approximation, a viscoelastic model for a Maxwell body was constructed using the Prony series (Figure 3b). The mathematical model was previously described in [55] and is based on the results of a series of experimental studies under uniaxial stress state (USS) conditions.
The dependence of the weighting coefficients on the relaxation times for 34 terms of the Prony series was obtained within the viscoelastic description of the material behavioral model. The empirical constants of the Williams–Landel–Ferry (WLF) temperature–time superposition and , as well as the constant base temperature °K, were also determined. The model parameters correspond to room temperature. However, due to limited experimental data, additional testing is required to fully describe the behavior of AR-200 across a broader range of temperatures and deformation rates.
To further refine the viscoelastic behavioral model, a series of empirical studies was conducted using three-point bending of rectangular specimens. A dynamic mechanical analyzer DMA Q800 (TA Instruments, New Castle, DE, USA) was used (Figure 4). The average dimension of samples was mm (Figure 4). The temperature range of the experiment was [−40; +80] °C. The research was conducted at the plastics laboratory of Perm National Research Polytechnic University (Perm, Russia).

Figure 4.
Experiment on DMA: (a) three-point bend; (b–d) samples.
The dependencies of the storage modulus, loss modulus, and loss tangent (tan δ) on temperature were established (Figure 5). The glass transition temperature 8 °C of the AR-200 was determined. The material exhibited a distinct peak in the loss tangent, which corresponds to the transition region from a glassy to an elastic state near the glass transition temperature.

Figure 5.
Temperature dependencies of the material parameters: (a) the storage modulus; (b) the loss modulus; (c) the loss angle tangent; black lines are the experimental data for a set of samples; red line is the averaged values of the experimental data.
The storage modulus reflects structural changes in the material. A decrease in the storage modulus is observed with increasing temperature, which is associated with material softening and a reduction in the elastic modulus. Changes in the loss modulus are related to relaxation transitions within the material. In the region where the loss modulus increases, the material is in a glassy state. As the temperature continues to rise, the loss modulus decreases, and the material transitions into a highly elastic state.
The results of the DMA experiments formed the basis for a refined model of AR-200 behavior within the framework of viscoelasticity theory, using the temperature–time superposition principle based on the WLF model (Figure 6).
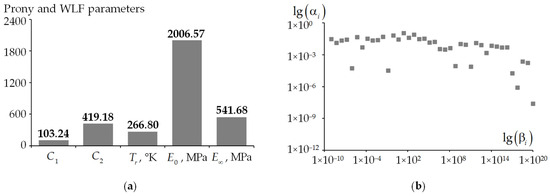
Figure 6.
A viscoelastic Maxwell-type model based on Prony series: (a) Prony and WLF parameters; (b) the dependence of the weighting coefficients on the relaxation time.
The long-term modulus of elasticity at the initial and final moments in time and was determined. The constant reference temperature and the empirical constants of the temperature–time superposition (WLF) and were refined, taking into account a wide temperature range of [−40; +80] °C. For the description of the viscoelastic behavioral model of materials, 40 pairs of coefficients , were defined.
For all AR-200 models, Poisson’s ratio was determined experimentally and was equal to 0.461.
Experimental studies included at least three repetitions to ensure the statistical significance of the results.
Viscoelastic models of the material behavior were constructed using the author’s numerical identification procedure, with an error of less than 5% [55,56].
2.3. The Numerical Model
The numerical implementation of the problem was carried out in the ANSYS Mechanical APDL 2021R2 software package using PLANE182 axisymmetric quadrilateral elements with Lagrangian approximation. Surface-to-surface contact interaction was modeled using the contact element pair CONTA171 and TARGE169. The primary procedures for constructing finite element analogs were based on the Galerkin method, with basic functions selected to have compact support, as per the finite element method. A step-by-step loading algorithm was used, with iterative refinement of the distribution of contact zones, penetration values, and contact forces. The iterative procedure continued until the results of two consecutive iterations produced contact force and penetration values within the specified accuracy.
Frictional contact was modeled using the basic Coulomb friction model, incorporating the condition of critical tangential stress in the contact zone, i.e., exceeding the yield strength of the material beneath the surface (an expanded classical Coulomb friction model). The coefficient of friction was set as a constant value of 0.04, in accordance with manufacturer data for the steel–polymer contact pair used in bridge bearings.
To describe the elastic–plastic behavior of the antifriction interlayer material, the MISO (multilinear isotropic hardening) model was used. For the viscoelastic behavior, the Prony series was employed. The steel structural elements were modeled within the framework of linear elasticity theory, with an elastic modulus of 2 × 1011 and a Poisson’s ratio of 0.3.
Previously, the convergence of the numerical solution with respect to the degree of system discretization was investigated [57]. It was determined that 16 finite elements through the thickness of the interlayer are required for a standard thickness of 4 mm. The finite element mesh in the contact area of the steel plates was aligned with the mesh division of the antifriction interlayer. Beyond the contact area, the mesh size increases gradually (in a gradient manner). Finite element models with antifriction interlayer thicknesses of 4 mm and 12 mm are characterized by approximately 50,000 and 63,000 nodal unknowns, respectively.
3. Results
3.1. Analysis of the Effect of the Interface Pattern of the Antifriction Interlayer with the Lower Steel Plate at an Interlayer Standard Thickness
In the first stage of this study, the effect of the interface pattern between the antifriction interlayer (of standard thickness) and the lower steel plate was assessed. The behavior of the antifriction interlayer material was modeled within an elastic–plastic formulation.
The levels and distribution patterns of the contact parameters on the sliding surface of the spherical balancer , as well as the deformation of the antifriction interlayer near the protrusion, are of particular interest.
The pattern of the contact pressure and contact tangential stress distribution on , obtained by modeling different types of conjugation on , is shown in Figure 7.
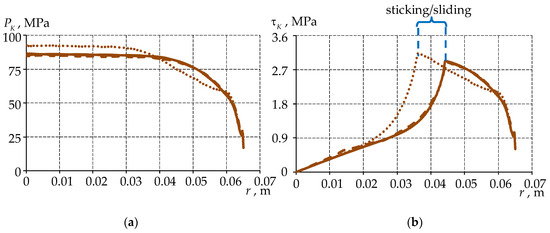
Figure 7.
Contact parameters with different conjugation : (a) contact pressure; (b) contact tangential stress; the solid line is ideal contact; the dashed line is full adhesion; dots are frictional contact.
The contact surfaces did not separate under any coupling pattern , i.e., the “no contact” status did not occur during structural deformation. The interface pattern between the lower steel plate and the antifriction interlayer has the greatest influence on the distribution of zones with different contact statuses . With ideal contact and full adhesion, the transition zone between full adhesion and sliding shifts closer to the edge of the antifriction interlayer. The full adhesion area accounts for 30.97% of the initial contact area with ideal contact and full adhesion , and 16.48% of the initial contact area with frictional contact . The total adhesion area comprises 24.09% of the initial contact area for the frictional contact . The maximum level of contact pressure on the surfaces and is the same for all types of coupling of the antifriction interlayer with the lower steel plate. The maximum level of and at frictional contact is 7–9% higher than at ideal contact and full adhesion. This effect is associated with a decrease in the area of full adhesion at the interface with the spherical balancer (the area of adhesion is almost two times smaller). The maximum levels of and at full adhesion are lower than at ideal contact by 1.41 and 0.84%, respectively.
Plastic flow of the material is observed near the protrusion of the antifriction interlayer. The deformation of the interlayer is overestimated compared to that of the actual structure, due to the fact that the elastic–plastic model does not account for material relaxation. The influence of the element connection pattern on the normal displacements of the antifriction interlayer’s end face is shown in Figure 8.
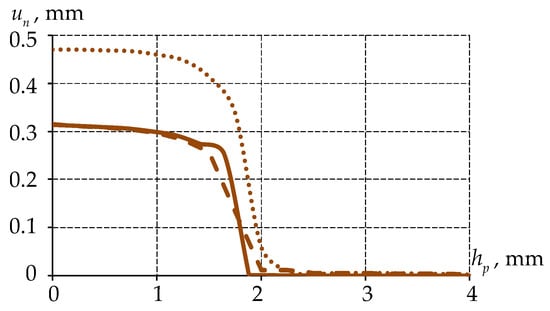
Figure 8.
Distribution of normal displacements along the end of the interlayer at different interfaces : the solid line is ideal contact; the dashed line is full adhesion; the dots are friction contact.
The maximum displacement of the antifriction interlayer is observed near the sliding surface . Under the standard load during indentation by the spherical balancer, the interlayer undergoes significant deformation. In the protrusion zone of the antifriction interlayer, the material enters a state of plastic flow. This deformation can be more accurately modeled by incorporating viscosity into the material behavioral model. Under frictional contact, the antifriction interlayer material can slip relative to the lower steel plate, resulting in a 49.8% increase in the maximum normal displacement. In contrast, the difference in maximum displacement between ideal contact and full adhesion does not exceed 0.1%. The distribution pattern of displacements along the normal direction at the interlayer’s end face shows only minor differences.
The differences in the average values , , and are considered for better clarity (Figure 9). , , and are the mean arithmetic errors of the parameters across the surface. The parameters obtained during ideal contact were selected as the reference values: the model has only one contact surface and requires less computational power to assess changes in the geometry of the structure during engineering surveys.
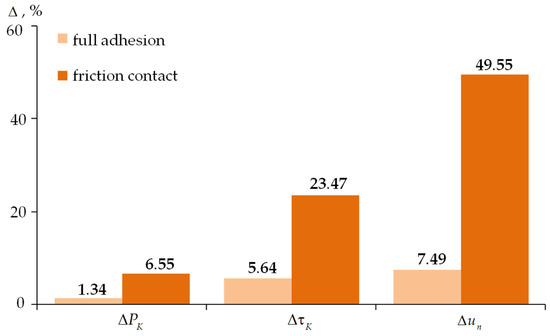
Figure 9.
The arithmetic mean differences in the contact parameters and normal displacement on .
The greatest differences between the solutions are observed in the normal displacement parameter. The difference between frictional contact and ideal contact is approximately 50%, while the difference with full adhesion does not exceed 7.5%. As expected, the smallest differences occur in contact pressure, which is the least sensitive to variations in the numerical implementation parameters. Nevertheless, the difference between frictional contact and ideal contact still exceeds 6.5%. Contact shear stress is more sensitive to contact settings: the difference between full adhesion and ideal contact is 5.64%, whereas for frictional contact, it reaches 23.47%.
Figure 10 shows the isofields of the stress–strain state parameters (intensity of stresses and deformations) of the bearing antifriction interlayer with different contact patterns .
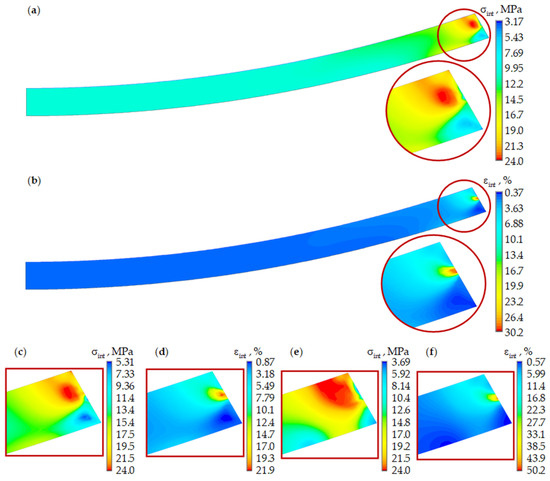
Figure 10.
The parameters of the stress–strain state of the antifriction interlayer: (a,c,e) ; (b,d,f) ; (a,b) ideal contact ; (c,d) full adhesion ; (e,f) frictional contact ; the red circle is the area of the antifriction layer near the edge.
The maximum levels of stress and strain are observed near the edge of the antifriction interlayer, in the protrusion area. The maximum strain level exceeds 10%, and the stress level reaches the peak value from the material’s deformation curve . This is attributed to limitations of the current material model. The maximum area is observed during frictional contact . This occurs because, in this formulation, the antifriction interlayer material undergoes greater deformation due to the possibility of sliding along the contact surfaces. The maximum intensity of deformations is observed near the collar of the spherical cutout of the lower steel plate, where a concentrator forms. To improve accuracy, the material behavioral model should be refined to account for relaxation effects. Implementing full adhesion allows for a more accurate representation of the stress–strain distribution, as it avoids inconsistencies in stress and strain fields between the mating surfaces of the antifriction layer and the bottom plate. The minimum levels of stress and deformation parameters are observed with full adhesion , which demonstrates the effectiveness of processing the contact surface of the lower steel plate using the “torn thread” method.
The “torn thread” surface interaction can be modeled as ideal contact when it is necessary to reduce computational cost. In this case, the differences in the numerical solution for the standard thickness of the antifriction interlayer do not exceed 10%.
This subsection presents the results of analyzing the influence of the conjugation pattern on the stress–strain state of the antifriction interlayer under constant temperature and pressure. However, factors such as temperature, load magnitude, and load periodicity also have a significant impact on the structure’s behavior. These effects are currently being investigated. An increase in temperature leads to a decrease in contact pressure and an increase in both the sliding contact area and contact penetration. This behavior is attributed to the material’s softening under elevated temperatures, caused by structural and phase transitions. Conversely, when the temperature decreases, the opposite effects are observed—associated with the glass transition of the antifriction interlayer material. Similar trends were confirmed by the DMA experimental results.
3.2. Analysis of the Effect of the Thickness of the Bearing Antifriction Interlayer on the Structure’s Behavior
In the second stage of this study, the effect of the antifriction interlayer thickness was assessed under constant protrusion and various coupling patterns between elements.
The distribution patterns of contact parameters and the stress–strain state of the structure do not significantly differ across the different coupling patterns between the antifriction interlayer and the lower steel plate. The influence of interlayer thickness on structural behavior is illustrated using a model with ideal steel–polymer contact .
Subsequently, the effect of interlayer thickness on the maximum parameter levels is analyzed for the different coupling patterns.
3.2.1. Ideal Contact Along the Interface Surfaces of the Antifriction Interlayer with the Lower Steel Plate
The distribution of contact parameters on at different is shown in Figure 11.
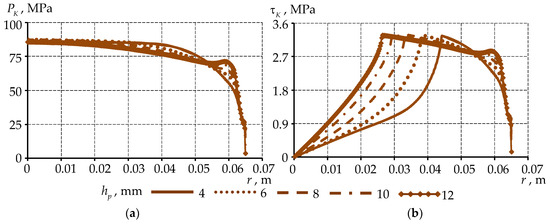
Figure 11.
Distribution of contact parameters on at different : (a) contact pressure; (b) tangential contact stress.
The distribution pattern of contact pressure and tangential contact stress shows only minor differences with changes in the thickness of the antifriction interlayer. As the interlayer thickness increases, there is a tendency for the contact parameters to approach zero near the edge of the interlayer. This effect is associated with increased deformation of the antifriction interlayer material and a larger volume of material exhibiting plastic behavior. When the interlayer thickness > 12 mm or under altered deformation conditions, regions of complete detachment (i.e., loss of contact) may appear. The maximum level of contact parameters changes slightly at ideal contact : an increase in the antifriction interlayer thickness up to 8 mm increases the parameter level by a maximum of 1.2%, followed by a decrease. The maximum tangential contact stress occurs in the transition zone between sticking and sliding contact statuses. A general trend is observed—a decrease in the percentage of the contact area that remains in full adhesion. At the same time, a larger area in the state of adhesion corresponds to a greater volume of material operating under hydrostatic compression, exhibiting primarily elastic properties.
The distributions of the normal end face displacement are shown in Figure 12.
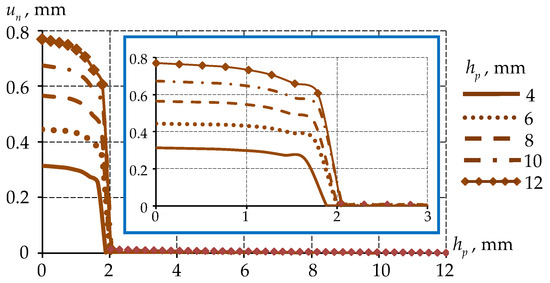
Figure 12.
Distributions of normal displacement along the end of the interlayer at different thicknesses of the antifriction interlayer.
An increase in the thickness of the antifriction interlayer leads to a significant rise in the maximum normal displacement at the surface of the protrusion. Specifically, increasing the thickness from 4 mm to 12 mm results in a more than 2.5-fold increase in the maximum normal displacement. The interlayer thickness is regulated by the Federal Road Agency “Rosavtodor” (Moscow, Russia). Therefore, it is necessary to consider the effect of interlayer thickness across all sizes and configurations of spherical bearings. These structures vary in the radius of curvature of the spherical segment, as previously discussed in [56]. Additionally, different approaches are used to determine the size of the antifriction material protrusion. One potential area for further research is a comprehensive assessment of how the projection geometry influences the overall behavior of the structure. To better capture the deformation behavior of the antifriction interlayer’s end face, it is essential to account for the relaxation properties of the polymer material. This was addressed in subsequent research through the implementation of a viscoelastic material behavioral model.
3.2.2. Comparative Analysis of the Structure’s Behavior at Different Thicknesses and Antifriction Interlayer Interfaces
The next stage of this study focused on analyzing the influence of the coupling pattern between the lower steel plate and the antifriction interlayer across all variants of the bearing’s geometric configuration.
Figure 13 shows the dependencies of the maximum level of contact pressure , tangential contact stress , and normal displacements , as well as the percentage of the surface area , in the state of full adhesion on the antifriction interlayer thickness with different interface patterns .
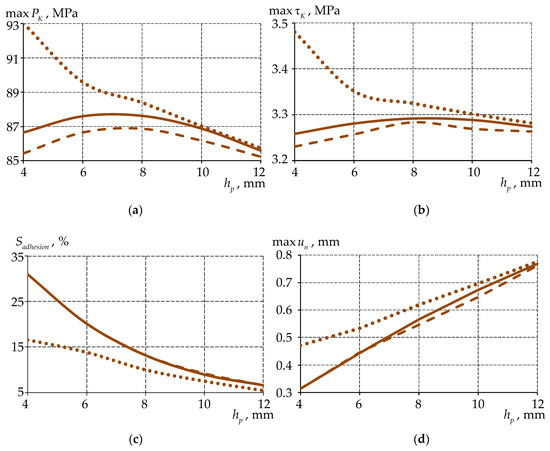
Figure 13.
Dependence of the contact stress–strain state parameters of the antifriction interlayer on : (a) at ; (b) at ; (c) at ; (d) at ; the solid line is ideal contact; the dashed line is full adhesion; the dots are frictional contact.
It can be noted that the spherical bearing deformation at ideal contact and full adhesion has small differences: the field of stress and strain distribution is specified, especially near the antifriction interlayer, as well as contact parameters. The model with a single contact surface (ideal contact on ) can be used to increase the speed of evaluating the deformation behavior of the structure during engineering surveys.
The level of contact parameters at ideal contact and full adhesion is lower than that of a frictional contact with an antifriction interlayer thickness of up to 10 mm. As the antifriction interlayer thickness increases, the differences in the parameters of the contact stress–strain state of the spherical bearing with a different type of interface (surface treatment) with the lower steel plate decrease. With thicknesses of more than 10 mm, the differences are less than 2%.
The percentage of the surface area in the state of full adhesion decreases with increasing thickness of the interlayer. As the sliding area increases, there is a significant rise in the normal displacements at the end face of the interlayer, particularly in the protrusion zone. The “no contact” status between the mating surfaces is not observed on for any of the contact options .
An increase in interlayer thickness leads to a greater volume of material exhibiting nonlinear behavior, which affects the overall performance of the bearing. A larger portion of the interlayer experiences plastic deformation; however, plastic flow does not increase substantially due to the state of all-around compression in the fully adhered contact zones. Nonetheless, the normal displacements at the end face of the interlayer increase by several times—this is considered a negative effect. These results correspond to static loading conditions at constant temperature. Under dynamic, cyclic, or temperature-variable loading, it becomes necessary to use a viscoelastic or viscoelastoplastic material behavioral model for accurate simulation of the bearing’s performance.
3.3. Influence Analysis of the Behavioral Model of the Antifriction Interlayer Material
The influence of the antifriction interlayer material behavioral model on the results of structural deformation needs to be evaluated. This is necessary to minimize the error of the bearing model from the real object. The evaluation of the model was performed with an antifriction interlayer thickness of 4 mm.
A gradual refinement of the material behavioral model was performed to account for structural and relaxation transitions as part of the work. This is necessary to move on to dynamic tasks, including at a wide range of temperatures, to assess the life of the structure and its operation under cyclic and seismic influences.
Three models of behavior are considered:
- The elastic–plastic model of the material behavior is based on experimental data on the free compression of cylindrical samples. The model is implemented only for the case of active loading.
- The viscoelasticity (USS) model is based on data from multi-stage tests for free compression of cylindrical samples to a maximum strain level of 10% with relaxation, unloading, and recovery areas. The model is limited within the range of temperatures close to room temperatures of 22–23 °C. The plasticity of the material and a number of phenomena and effects of the viscoelastic pattern are not taken into account.
- The viscoelasticity (DMA) model is based on the entire set of experimental data, taking into account the DMA study of material behavior over a wide temperature range. The model does not take into account the plasticity of the material.
Figure 14 shows a comparative analysis of the three models of antifriction material behavior within the parameters of the stress–strain state of the elements of the spherical bearing with a standard antifriction interlayer thickness of 4 mm.
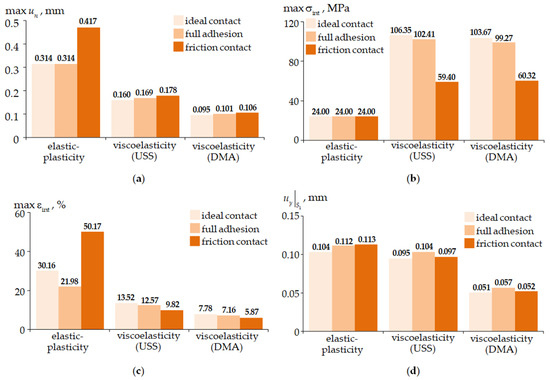
Figure 14.
The parameters of the stress–strain state of the bearing: (a) at ; (b) at ; (c) at ; (d) the settlement of the bearing.
The elastic–plastic behavioral model of the material in the antifriction interlayer has a significant limitation associated with an asymptotic stress level when the deformation level exceeds 10%. Additionally, the model does not account for material relaxation, which can be observed even with iterative loading application. This results in overestimated deformation characteristics at significantly underestimated stress levels. The modeling error of the deformation of the spherical bearing compared to the data from field tests is from 57.7 to 71.9%. The maximum error is observed during frictional contact .
The viscoelasticity (USS) model makes it possible to refine data on the behavior of the antifriction interlayer material. This leads to a significant reduction in the deformation of the antifriction interlayer, while clarifying the level of stresses and deformations of the material. The model makes it possible to effectively describe the multi-stage cyclic deformation of samples [56]. The error in modeling the deformation of the spherical bearing is from 44.1 to 57.4% of the experimental test data. The results of numerical modeling are overestimated. The maximum error is observed at full adhesion .
The viscoelasticity (DMA) model makes it possible to obtain a numerical analog of the spherical bearing, as close as possible to the real design. The error of modeling the deformation of the spherical bearing is from 13.8 to 21.1% of the experimental test data. The minimum error is observed with full adhesion .
The results of experimental tests of the bearing draft contained multi-stage loading with load holding. These effects are not taken into account in the current model of deformation of the bearing. The pattern of the processing of the bottom plate balancer is “torn thread”, which is confirmed by the minimum error of the model with full adhesion to the interface surfaces . The level of settlement of the spherical bearing model with a refined viscoelastic model of polymer material behavior is as close as possible to the actual design. It should be noted that the model is implemented in an axisymmetric formulation and allows one to quickly evaluate engineering solutions for changing the geometric configuration of elements.
The behavioral model of the antifriction interlayer material can be refined after conducting a series of numerical experiments on the dependence of the thermal expansion coefficients on temperature, as well as a series of experiments on uniaxial stress over a wide temperature range. It also requires consideration of the plasticity of the material, which can be carried out when switching to the Anand model.
Comparative Analysis of Viscoelastic and Elastic–Plastic Models of Material Behavior
We will perform a comparative analysis of the bearing behavior in the case of elastic–plastic and viscoelasticity (DMA) models of the behavior of the antifriction interlayer material.
The pattern of the distribution of contact parameters when modeling the antifriction interlayer material behavior within the framework of elastic–plastic and viscoelastic settings is shown in Figure 15.
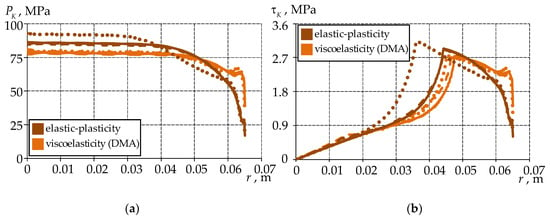
Figure 15.
Comparative analysis of the contact parameters at different conjugation and different models of the antifriction interlayer material behavior: (a) contact pressure; (b) tangential contact stress; the solid line is ideal contact; the dashed line is full adhesion; the dots are frictional contact.
The behavioral model of the antifriction interlayer material does not affect the pattern of the distribution of contact parameters. The viscoelasticity (DMA) model of the antifriction interlayer material shows a decrease in the level of contact parameters compared to elastic-plasticity by 6–8% with ideal contact and full adhesion , and by 13–15% with frictional contact. The percentage area of the contact surface in the state of full adhesion is greater for the viscoelastic material behavior.
Figure 16 shows the normal displacements of the end of the antifriction interlayer when modeling the material behavior in the framework of elastic–plastic and viscoelastic settings.
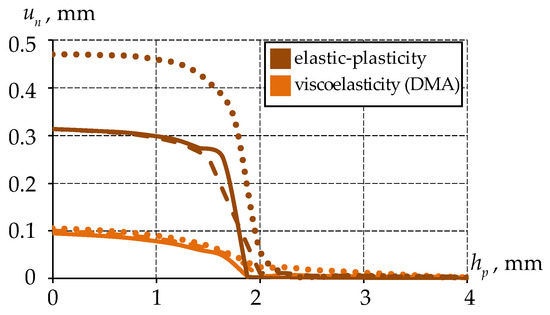
Figure 16.
Comparative analysis of the distribution of displacements along the normal of the end face of the interlayer at different conjugation and different models of behavior of the antifriction interlayer material: the solid line is ideal contact; the dashed line is full adhesion; the dots are frictional contact.
The maximum level of normal displacement of the end of the antifriction interlayer with viscoelastic behavior of the material is 3–5 times lower than with elastic-plasticity.
Figure 17 shows the dependencies of the maximum level of contact pressure , tangential contact stress , and normal displacements , as well as of the bearing draft on the antifriction interlayer thickness in the case of an elastic–plastic and viscoelastic behavioral material model.
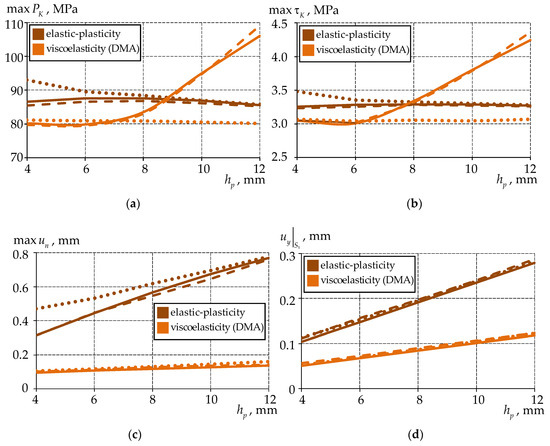
Figure 17.
The dependence of the parameters of the contact stress–strain state of the antifriction interlayer on for elastic–plastic and viscoelastic models of the antifriction interlayer material behavior: (a) at ; (b) at ; (c) at ; (d) settlement of the bearing; the solid line is ideal contact; the dashed line is full adhesion; the dots are frictional contact.
A significant increase in the level of contact pressure and tangential contact stress is observed with ideal contact and full adhesion with an increase in the thickness of the antifriction interlayer in the viscoelastic behavioral material model. These effects are associated with rather harsh deformation conditions of the structure with an increase in the volume of a more malleable material with the possibility of structural and relaxation transitions. The decrease in contact pressure and a small change in the level of tangential contact stress are observed with frictional contact. In general, the contact parameters of the spherical bearing with viscoelastic behavior of the polymer material are lower, with an antifriction interlayer thickness of 10 mm less than that with elastic–plastic behavior.
The deformation of the antifriction material in particular and the spherical bearing as a whole is less with the viscoelastic behavior of the antifriction interlayer than with the elastic–plastic material behavior.
The parameters of the contact stress–strain state of the bearing with a standard thickness of the antifriction interlayer depend little on the coupling pattern.
Of interest is the change in the percentage of the contact surface area in the state of full adhesion, since in this case, hydrostatic compression of the antifriction interlayer is observed, and the material operates within the framework of the theory of elasticity.
Figure 18 shows the dependencies of the percentage of surface area and (for the case of frictional contact along the interface surfaces of the antifriction interlayer and the lower steel plate) in the state of full adhesion on the antifriction interlayer thickness with elastic–plastic and viscoelastic models.
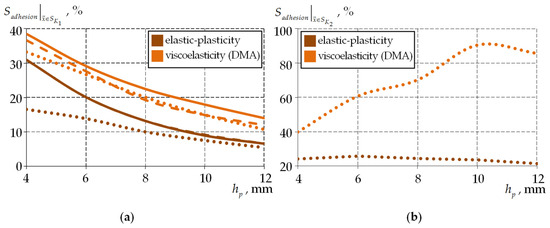
Figure 18.
The percentage of the contact surface area in the state of full adhesion depends on the thickness of the antifriction interlayer: (a) ; (b) ; the solid line is ideal contact; the dashed line is full adhesion; the dots are frictional contact.
The viscoelastic material behavior and its deformation affect the distribution of contact statuses on the sliding surface of the spherical balancer. The percentage of the surface area in the state of full adhesion is greater with the viscoelastic behavior of the antifriction interlayer material. As the thickness increases, the percentage of the surface area in the state of full adhesion decreases with all the considered models of the material behavior.
It can be noted that with an increase in the antifriction interlayer thickness with viscoelastic material behavior on the interface surface in the case of frictional contact, an increase in the percentage of the surface area in the state of full adhesion is observed. This means that with sufficiently large antifriction interlayers, additional surface treatment of the interface of the lower steel plate with a “torn thread” interlayer is not required, thus reducing the time and economic costs of manufacturing the structure. The damping properties will also be improved. This study will be useful in analyzing the contact interaction of the bridge bearing elements under the influence of more complex loads, taking into account the time factor, as well as temperature.
4. Discussion
Spherical bearings are a type of high-load multirotational bridge bearings that compensate for various types of loads from the bridge span and the environment. The effective operation of bearings is related to the gaps between the steel structural elements and the antifriction interlayer thickness [58]. Increasing the antifriction interlayer thickness can reduce the resistance to rotation, internal wear, and damage, and it can also increase the bearing capacity of the structure. However, the restrictions on the antifriction interlayer thickness have not been determined so far. In the current study, the dependencies of the contact parameters and the stress–strain state of the spherical bearings on the antifriction interlayer thickness were determined. These studies were transferred to the manufacturers of bridge bearings and taken into account in engineering methods for calculating the geometric configuration of the structure.
The results of the bearing deformation correlate with data from other studies and the results of field experiments [20,59]. The displacement level of the bearing at 1000 kN is in good agreement with the data of field experiments presented in [20]. The maximum stress level of a standard spherical bearing is also commensurate with the data obtained in our study. The pattern of the stress distribution in the antifriction interlayer corresponds to the results obtained by Deng et al. [59]. The maximum stresses of the antifriction interlayer are also observed near the protrusion. This confirms the possibility of using models in the framework of simulation modeling for a multifactorial analysis of the behavior of structures in statics and dynamics.
Mechanical treatment of the sliding surface can ensure efficient and long-term operation of the bearing [58]. In this case, the influence of the pattern of the surface treatment of the lower steel plate in the area of contact with the antifriction interlayer can also affect the operation of the spherical bearing. As part of this study, it was found that by ensuring full adhesion at the interface, the interface of the antifriction interlayer with the lower steel plate reduced the deformation of the protrusion of the polymer interlayer and the settlement of the structure. At the same time, studies of the behavior of bearings most often consider only one type of coupling of elements [22,59]. Studies often do not take into account the friction on the interface surfaces [59]. Modeling the behavior of the antifriction interlayer material does not take into account the viscoelastic, creep, and plasticity of materials. However, in the framework of field tests, viscous deformation of the antifriction interlayer and plastic flow of materials were observed [58,60]. Nonlinear effects in spherical bearings related to the behavior of materials and the contact state of the elements are complex phenomena and an interesting area of research for understanding the work of the structure [61]. The influence of the coupling pattern of antifriction material and steel structural elements, including taking into account frictional properties, is necessary to evaluate the operation and rationalize the bearings [26]. The current work analyzed, as a first approximation, the influence of the behavioral model of the antifriction interlayer material and the pattern of its interface with steel structural elements. A model of a spherical bearing with viscoelastic behavior of an antifriction material with full adhesion on the interface surfaces of the antifriction interlayer with the lower steel plate made it possible to obtain a discrepancy with experimental data of less than 15%. A comparison with data from experimental studies by other authors shows an error of less than 10% in the model [20]. A large percentage of the difference between the settlement of the model and the experiment is due to the multi-stage experimental program, as well as the limitations of the geometric model of the bearing in the numerical implementation (grooves with lubricant and a flat antifriction interlayer are not taken into account). The model error can be justified by the accepted assumptions on the set of physical, mechanical, and thermal properties of the polymer material: the thermal expansion coefficient and the friction coefficient are constants and do not depend on other characteristics (time, temperature, load value, etc.). This introduces limitations in the application of the constructed models, from the point of view of the quantitative assessment of the parameters of the stress–strain state of the structure.
Let us consider the multi-stage loading of a model with exposure sections, according to a full-scale experiment (Figure 19).
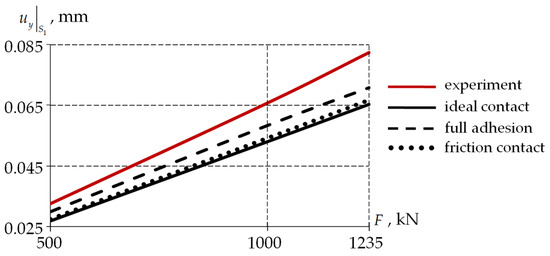
Figure 19.
Settlement of the supporting part during multi-stage loading.
The discrepancy between the results of the numerical simulation and the experiment does not exceed 20% for all variants of the interface of the antifriction interlayer with the lower steel plate of the bearing. The maximum error is observed when modeling an ideal contact . The minimum error of numerical simulation at a nominal load of 1000 kN is observed at full adhesion (~11.37%). This is due to the implementation of the specified type of coupling, due to the equality of the fields of the displacement vector, and due to the components of the stress and strain tensor on the elements’ coupling surfaces. This is not quite “physical” for the considered “steel–polymer” contact. The experiment involved bearings with the character of processing the metal surfaces of the interface of the lower steel plate according to the “torn thread” type, which allows for maximum adhesion to the antifriction interlayer of the material.
5. Conclusions
As part of the first stage of this study, the influence of the coupling pattern on the deformation behavior of spherical bearings of a bridge structure at a standard thickness of the antifriction interlayer was analyzed. Three coupling options were considered: ideal contact, full adhesion, and frictional contact. The behavior of the antifriction interlayer material was modeled within the framework of an elastic–plastic formulation. A number of patterns of the deformation behavior of bridge bearings were established:
- (1)
- The change in the coupling conditions has the greatest effect on the area of full adhesion . In the case of ideal contact and full adhesion , the total adhesion area is 30.97% of the initial contact area, and in the case of frictional contact, it is 16.48% of the initial contact area.
- (2)
- The maximum differences between solutions with the modeling of a contact pair of elements for different types of contact are observed in the normal movement of the end face. The difference between frictional contact and ideal contact is about 50%; full adhesion is no more than 7.5%. Contact pressure: the difference between full adhesion and ideal contact is 5.64%, and for frictional contact is 23.47%.
- (3)
- The effects of plastic flow of the material in the vicinity of the protrusion zone of the antifriction interlayer were observed, which needs to be clarified within the framework of applying the viscoelastic behavioral model in numerical implementation.
A quick qualitative assessment of the characteristics of the stress–strain state of the structure and the parameters of contact interaction in a static formulation of the problem is the main important point of using the elastic–plastic model of material behavior. The “torn thread” conjugation can be modeled as an ideal contact to save computing resources according to the results obtained.
In the second stage of this study, an assessment was made of the effect of the antifriction interlayer thickness at a constant protrusion and the different patterns of the coupling of the elements. The pattern of the distribution of contact pressure and tangential contact stress has small differences when the antifriction interlayer thickness changes. However, an increase in the antifriction interlayer thickness leads to an increase in the maximum level of normal displacement on the surface of the protrusion, which is also confirmed by the results obtained when changing the pattern of the interface. This effect is associated with a decrease in the surface area in the state of full adhesion.
An assessment of the influence of the behavioral patterns of the antifriction interlayer material on the results of structural deformation was performed to form a model of the spherical bearing that is closest to reality. The MISO model was used to describe the elastic–plastic behavior of the antifriction interlayer material, and the Prony series was used for viscoelastic behavior. The viscoelastic material behavior and its deformation affect the distribution of contact statuses on the sliding surface of the spherical balancer. The percentage of the surface area in the state of full adhesion is greater with the viscoelastic behavior of the antifriction interlayer material. The percentage of the surface area in the state of full adhesion decreases with all the considered models of the behavior of the antifriction interlayer material as the thickness increases. The viscoelastic behavioral model of the antifriction material makes it possible to minimize the deviation of the numerical model of the bearing from the actual structure. This proves the necessity of using modern numerical models to describe the behavior of materials in engineering practice.
Several directions are being considered for further development of the work:
- -
- The consideration of the experimentally obtained friction properties of the steel–polymer pair in the analysis of the deformation behavior of the structure;
- -
- The analysis of the effects of cyclic and seismic loads, including temperature and time considerations;
- -
- The transition to a viscoelastic–plastic model of antifriction material behavior.
Author Contributions
Conceptualization, A.A.K., Y.O.N., and A.P.B.; methodology, A.A.K.; software, A.A.K., Y.O.N., Y.S.K., and A.P.B.; validation, A.A.K.; writing—original draft preparation, A.A.K., Y.S.K., and Y.O.N.; writing—review and editing, Y.S.K. and A.P.B.; visualization, A.A.K., Y.S.K., Y.O.N., and A.P.B.; funding acquisition, Y.O.N. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Russian Science Foundation grant no. 25-29-00470, https://rscf.ru/project/25-29-00470/ (accessed on 30 August 2025).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gonzalez, A.; Wiener, M.; Valdez salas, B.; Mungaray, A. Bridges: Structures and Materials, Ancient and Modern. In Infrastructure Management and Construction; IntechOpen: London, UK, 2020. [Google Scholar] [CrossRef]
- Presta, F.; Gibbens, B.; Turner, J. Sydney Gateway’s Twin Network Arches: A Case Study in Complex Bridge Design and Construction. In Proceedings of the Environmentally Friendly Technologies and Structures: Focusing on Sustainable Approaches, Tokyo, Japan, 18–21 May 2025; pp. 1630–1638. [Google Scholar] [CrossRef]
- Zhao, W.; Yang, B.; Nian, Y. Study on economic design and construction program of steel-hybrid combined girder bridge. Adv. Comput. Eng. Technol. Res. 2024, 1, 52. [Google Scholar] [CrossRef]
- Jalaei, F.; Zhang, J.; Mcneil-Ayuk, N.; McLeod, C. Environmental life cycle assessment (LCA) for design of climate-resilient bridges—A comprehensive review and a case study. Int. J. Constr. Manag. 2024, 25, 99–114. [Google Scholar] [CrossRef]
- D’Amato, M.; Ranaldo, A.; Rosciano, M.; Zona, A.; Morici, M.; Gioiella, L.; Micozzi, F.; Poeta, A.; Quaglini, V.; Cattaneo, S.; et al. The Development and Statistical Analysis of a Material Strength Database of Existing Italian Prestressed Concrete Bridges. Infrastructures 2025, 10, 203. [Google Scholar] [CrossRef]
- Ranaldo, A.; Lo Monaco, A.; Palmiotta, A.; D’Amato, M.; Lippolis, A.; Vacca, V.; Sarno, R. A preliminary investigation on material properties of existing prestressed concrete beams. Procedia Struct. Integr. 2024, 62, 145–152. [Google Scholar] [CrossRef]
- Immanuel, Y.; Rifai, A.I.; Saputra, A.J. Bridge Structural Design Simulation: Case Study of Nongsa Pura Bridge. OPSearch Am. J. Open Res. 2024, 3, 268–276. [Google Scholar] [CrossRef]
- Xiong, C.; Shang, Z.; Wang, M.; Lian, S. Dynamic Monitoring of a Bridge from GNSS-RTK Sensor Using an Improved Hybrid Denoising Method. Sensors 2025, 25, 3723. [Google Scholar] [CrossRef] [PubMed]
- Xi, R.J.; He, Q.Y.; Meng, X.L. Bridge monitoring using multi-GNSS observations with high cutoff elevations: A case study. Measurement 2021, 168, 108303. [Google Scholar] [CrossRef]
- Eggert, H.; Kauschke, W. Structural Bearings; Ernst & Sohn: Berlin, Germany, 2002. [Google Scholar]
- Taghipour, A.; Zakeri, J.; Ghozat, A.; Mosayebi, S. Dynamic Behavior Assessment of a Railway Bridge in Isfahan under Over-Height Vehicle Collision Loads and Proposing Maintenance Strategies to Enhance Its Performance. Int. J. Railw. Res. 2025, 12, 34–39. [Google Scholar] [CrossRef]
- Lin, Z.; Xia, D.; Jiang, Y.; Yuan, Z.; Wang, H.; Lin, L. Experimental and Numerical Investigation of Localized Wind Effects from Terrain Variations at a Coastal Bridge Site. J. Mar. Sci. Eng. 2025, 13, 1223. [Google Scholar] [CrossRef]
- Kang, D.H.; Hyun, J.H. Evaluation of the durability of spherical bridge bearing using polyamide engineering plastic middle plate. J. Korean Soc. Urban Railw. 2021, 9, 1021–1031. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Y.; Ju, J. Study on the mechanical properties of a type of spherical bearing. J. Theor. Appl. Mech. 2021, 59, 539–550. [Google Scholar] [CrossRef]
- Borisov, A.I.; Gnatyuk, G.A. Assessment of transport accessibility of the Arctic regions of the Republic of Sakha (Yakutia). Transp. Res. Procedia 2022, 61, 289–293. [Google Scholar] [CrossRef]
- Abarca, A.; Monteiro, R.; O’Reilly, G.J. Seismic risk prioritisation schemes for reinforced concrete bridge portfolios. Struct. Infrastruct. Eng. 2023, 21, 49–69. [Google Scholar] [CrossRef]
- Zhang, P.; Zhao, H.; Shao, Z.; Jiang, L.; Hu, H.; Zeng, Y.; Xiang, P. A rapid analysis framework for seismic response prediction and running safety assessment of train-bridge coupled systems. Soil Dyn. Earthq. Eng. 2024, 177, 108386. [Google Scholar] [CrossRef]
- Wei, B.; Chen, M.; Jiang, L.; Li, C.; Chen, Y.; Lu, A.; Yang, Z.; Li, S. The influence of spherical bridge bearings on train running safety during earthquakes considering train-track–bridge interaction and soil specification. Arch. Civ. Mech. Eng. 2025, 25, 143. [Google Scholar] [CrossRef]
- Ye, X.W.; Xia, P.S.; Su, Y.H.; Chen, B. Analysis and probabilistic modeling of wind characteristics of an arch bridge using structural health monitoring data during typhoons. Struct. Eng. Mech. Int. J. 2017, 63, 809–824. [Google Scholar] [CrossRef]
- Yan, L.; Gou, X.Y.; Zhang, X.; Jiang, Y.; Ran, X.W.; Zhang, P. Experimental and Numerical Investigations on the Spherical Steel Bearing Capacity of New Anti-Separation Design. KSCE J. Civ. Eng. 2024, 28, 889–903. [Google Scholar] [CrossRef]
- Ding, M.; Li, C.X.; Liang, Z.M.; Ju, J.S. Research on the Failure Characteristics of a Spherical Bearing. Strength Mater. 2022, 54, 536–544. [Google Scholar] [CrossRef]
- Shi, X.; Liu, Z.; Guo, T.; Cai, C.S.; Jiang, C. Investigation on contact stress calculation method of spherical hinge structures for swivel construction. Structures 2024, 69, 107290. [Google Scholar] [CrossRef]
- Lin, S.-C. Friction and Lubrication of Sliding Bearings. Lubricants 2023, 11, 226. [Google Scholar] [CrossRef]
- Gajewski, M.D.; Miecznikowski, M. Assessment of the Suitability of Elastomeric Bearings Modeling Using the Hyperelasticity and the Finite Element Method. Materials 2021, 14, 7665. [Google Scholar] [CrossRef] [PubMed]
- Adamov, A.A.; Kamenskikh, A.A.; Pankova, A.P.; Strukova, V.I. Comparative Analysis of the Work of Bridge Spherical Bearing at Different Antifriction Layer Locations. Lubricants 2022, 10, 207. [Google Scholar] [CrossRef]
- Han, O.; Kwark, J.-W.; Lee, J.-W.; Han, W.-J. Analytical Study on the Frictional Behavior of Sliding Surfaces Depending on Ceramic Friction Materials. Appl. Sci. 2023, 13, 234. [Google Scholar] [CrossRef]
- Hu, Q.; Pei, Q.; Li, P. Reducing the Friction Coefficient of Heavy-Load Spherical Bearings in Bridges Using Surface Texturing—A Numerical Study. Lubricants 2025, 13, 180. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Wang, W.; Qin, L.; Dong, G. Surface texture design and its tribological application. J. Mech. Eng. 2019, 55, 85–93. [Google Scholar] [CrossRef]
- Lu, P.; Wood, R.J. Tribological performance of surface texturing in mechanical applications—A review. Surf. Topogr. Metrol. Prop. 2020, 8, 043001. [Google Scholar] [CrossRef]
- Wang, H.; Sun, A.; Qi, X.; Dong, Y.; Fan, B. Experimental and analytical investigations on tribological properties of PTFE/AP composites. Polymers 2021, 13, 4295. [Google Scholar] [CrossRef]
- Deshwal, D.; Belgamwar, S.U.; Bekinal, S.I.; Doddamani, M. Role of reinforcement on the tribological properties of polytetrafluoroethylene composites: A comprehensive review. Polym. Compos. 2024, 45, 14475–14497. [Google Scholar] [CrossRef]
- Berladir, K.; Antosz, K.; Ivanov, V.; Mitaľová, Z. Machine Learning-Driven Prediction of Composite Materials Properties Based on Experimental Testing Data. Polymers 2025, 17, 694. [Google Scholar] [CrossRef]
- Yi, X.; Du, S.; Zhang, L. Composite Materials Engineering, Volume 1: Fundamentals of Composite Materials; Springer: Singapore, 2018. [Google Scholar] [CrossRef]
- Wang, Q.J.; Chung, Y.W. Antifriction Materials and Composites; Springer: Boston, MA, USA, 2013. [Google Scholar] [CrossRef]
- Lin, Z.; Zhang, K.; Ye, J.; Li, X.; Zhao, X.; Qu, T.; Liu, Q.; Gao, B. The effects of filler type on the friction and wear performance of PEEK and PTFE composites under hybrid wear conditions. Wear 2022, 490–491, 204178. [Google Scholar] [CrossRef]
- Abdul, S.M. Recent Advances in UHMWPE/UHMWPE Nanocomposite/UHMWPE Hybrid Nanocomposite Polymer Coatings for Tribological Applications: A Comprehensive Review. Polymers 2021, 13, 608. [Google Scholar] [CrossRef]
- Park, J.-H.; Lee, J.-W. Friction Behavior of Ceramic Materials for the Development of Bridge-Bearing Friction Materials. Appl. Sci. 2025, 15, 152. [Google Scholar] [CrossRef]
- Park, J.H.; Lee, J.W.; Kwark, J.W.; Han, W.J.; Han, O. Characteristics of Friction Behavior of Ceramic Friction Materials according to Surface Materials. J. Korean Recycl. Constr. Resour. Inst. 2023, 11, 535–541. [Google Scholar]
- Bokhoeva, L.A.; Rogov, V.E.; Chermoshentseva, A.S. Antifriction fluoroplastic materials for sliding layers in bridge supports. Mag. Civ. Eng. 2024, 17, 13104. [Google Scholar] [CrossRef]
- Lenk, R.S. Polymer Rheology; Springer Science & Business Media: Dordrecht, The Netherlands, 2012. [Google Scholar] [CrossRef]
- Kraus, M.; Niederwald, M.; Siebert, G.; Keuser, M. Rheological modelling of linear viscoelastic materials for strengthening in bridge engineering. In Proceedings of the 11th German Japanese Bridge Symposium, Osaka, Japan, 30–31 August 2016; pp. 30–31. [Google Scholar]
- Nguyen, T.Q.; Nguyen, T.T.; Nguyen, P.T. Nguyen Analysis of vibration characteristics of bridge spans based on the viscoelastic material model: Investigating the relationship between material properties and dynamic parameters. Structures 2025, 7, 108788. [Google Scholar] [CrossRef]
- Wang, D. Modelling the Contact Behaviour in the Presence of Viscoelasticity. Ph.D. Thesis, University of Leeds, Leeds, UK, 2025. [Google Scholar]
- Doh, J.; Hur, S.H.; Lee, J. Viscoplastic parameter identification of temperature-dependent mechanical behavior of modified polyphenylene oxide polymers. Polym. Eng. Sci. 2019, 59, E200–E211. [Google Scholar] [CrossRef]
- Liu, E.; Wu, J.; Li, H.; Liu, H.; Xiao, G.; Shen, Q.; Kong, L.; Lin, J. Research on viscoelastic behavior of semi-crystalline polymers using instrumented indentation. Polym. Sci. 2021, 59, 1795. [Google Scholar] [CrossRef]
- Alam, M.I.; Khan, D.; Mittal, Y.; Kumar, S. Effect of crack tip shape on near-tip deformation and fields in plastically compressible solids. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 441. [Google Scholar] [CrossRef]
- Persson, B.N.J. Sliding Friction: Physical Principles and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Li, Y.; Guo, W.; Huang, X.; Chen, Z.; Gao, Y. Friction Characteristics and Lubrication Properties of Spherical Hinge Structure of Swivel Bridge. Lubricants 2024, 12, 130. [Google Scholar] [CrossRef]
- Adamov, A.A.; Keller, I.E.; Ivanov, Y.N.; Utev, N.V. Basic Tests and Identification of a Model of Viscoelastic Behavior of Elastomers under Finite Deformations. Mech. Solids 2024, 59, 3831–3843. [Google Scholar] [CrossRef]
- Ilyin, S.O. Structural Rheology in the Development and Study of Complex Polymer Materials. Polymers 2024, 16, 2458. [Google Scholar] [CrossRef]
- Adamov, A.A.; Kamenskikh, A.A. The Deformation Behavior of Modern Antifriction Polymer Materials in the Elements of Transport and Logistics Systems with Frictional Contact. In Digital Science 2019. DSIC 2019. Advances in Intelligent Systems and Computing; Antipova, T., Rocha, Á., Eds.; Springer: Cham, Switzerland, 2020; Volume 1114. [Google Scholar] [CrossRef]
- Chen, W.W.; Wang, Q.J. Thermomechanical analysis of elastoplastic bodies in a sliding spherical contact and the effects of sliding speed, heat partition, and thermal softening. J. Tribol. 2008, 130, 041402. [Google Scholar] [CrossRef]
- Fang, X.; Zhang, C.; Chen, X.; Wang, Y.; Tan, Y. A new universal approximate model for conformal contact and non-conformal contact of spherical surfaces. Acta Mech. 2015, 226, 1657–1672. [Google Scholar] [CrossRef]
- Tao, L.; Wang, Q.; Qi, Z.; Wu, H.; Zhu, H.; Huang, J. Analysis of the Rolling Interface Contact Characteristics in Mixed Lubrication Based on Gaussian Distribution Theory. Materials 2023, 16, 5220. [Google Scholar] [CrossRef]
- Nosov, Y.O.; Kamenskikh, A.A. Experimental Study of the Rheology of Grease by the Example of CIATIM-221 and Identification of Its Behavior Model. Lubricants 2023, 11, 295. [Google Scholar] [CrossRef]
- Kamenskikh, A.A.; Nosov, Y.O.; Bogdanova, A.P. The Study Influence Analysis of the Mathematical Model Choice for Describing Polymer Behavior. Polymers 2023, 15, 3630. [Google Scholar] [CrossRef]
- Kamenskih, A.A.; Trufanov, N.A. Regularities interaction of elements contact spherical unit with the antifrictional polymeric interlayer. J. Frict. Wear 2015, 36, 170–176. [Google Scholar] [CrossRef]
- Roeder, C.W.; Stanton, J.F.; Campbell, T.I. Rotation of High Load Multirotational Bridge Bearings. J. Struct. Eng. 1995, 121, 747–756. [Google Scholar] [CrossRef]
- Deng, N.; He, M.; Gu, N.; Liang, H. Design and Performance Research of a New Type of Spherical Force-Measuring Bearing of Bridges Based on Button Type Microsensor. KSCE J. Civ. Eng. 2024, 28, 5066–5076. [Google Scholar] [CrossRef]
- Adamov, A.A.; Keller, I.E.; Petukhov, D.S.; Kuzminykh, V.S.; Patrakov, I.M.; Grakovich, P.N.; Shilko, I.S. Evaluation of the Performance of PTFE-Composites as Antifriction Layers in Supporting Parts with a Spherical Segment. J. Frict. Wear 2023, 44, 127–134. [Google Scholar] [CrossRef]
- Zhao, L.; Sun, X.; Wu, Z.; Chen, Y.; Liu, J.; Wang, Y. Nonlinear Static Analysis of Spherical Hinges in Horizontal Construction of Bridges. Buildings 2024, 14, 3726. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).