Calibration and Validation of a PEM Fuel Cell Hybrid Powertrain Model for Energy Management System Design
Abstract
1. Introduction
2. Fuel Cell and Battery Hybrid Vehicle Modeling
2.1. Fuel Cell System
2.1.1. Stack Voltage Model
2.1.2. Calibration of Stack Voltage Model
2.1.3. Compressor Model
2.1.4. Calibration of Compressor Model
- Use the reference load to obtain the nominal mass flow rate of the compressor ;
- Input in the FC model to collect the corresponding pressure ratio;
- Calculate compressor power with and pressure ratio, assuming ;
- Obtain the compressor motor parameters from a map incorporating vs. ;
- Create a new compressor map with pressure ratio, and .
2.2. Battery Pack
2.3. Electric Drive
2.4. Vehicle Dynamic System
2.5. Longitudinal Vehicle Controller
2.6. Energy Management Strategy
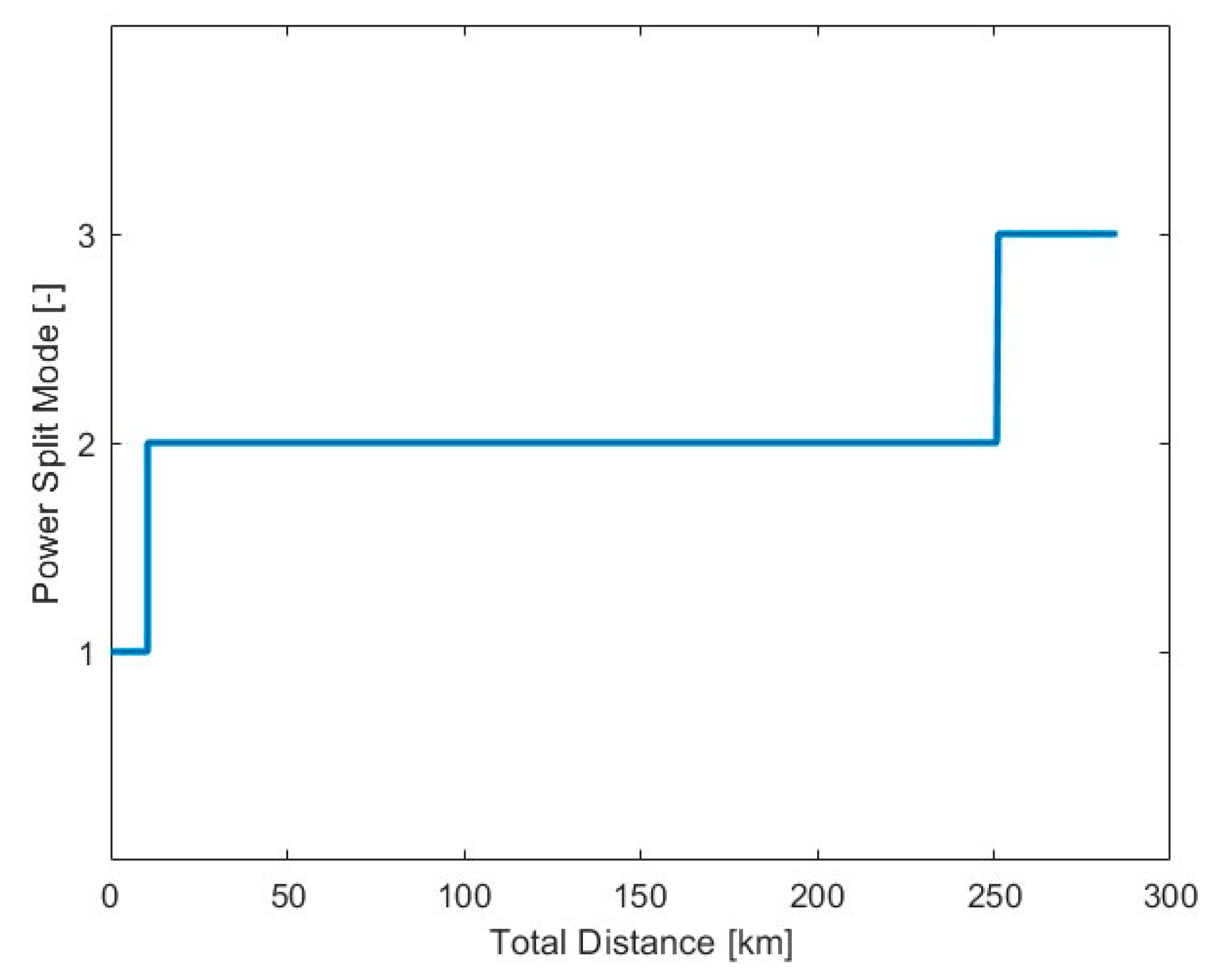
- Battery Depleting Mode: To prevent overcharging in a battery system, when the SoC level is higher than 85%, the system relies primarily on the battery to meet power demands. This strategy aims to prevent overcharging the battery:
- Battery Sustaining Mode: When the SoC falls below 80%, without risking overcharge, Baseline A enters battery sustaining mode. The 80–85% window is implemented to avoid oscillations during mode transitions. In this phase, the fuel cell output is adjusted in real time to meet power demands, while additional energy is used to recharge the battery, maintaining SoC and improving overall efficiency.
- Pure Electric Mode: As hydrogen depletes, the fuel cell shuts down and the vehicle enters pure electric mode, relying solely on the battery for propulsion.
3. Simulation Results
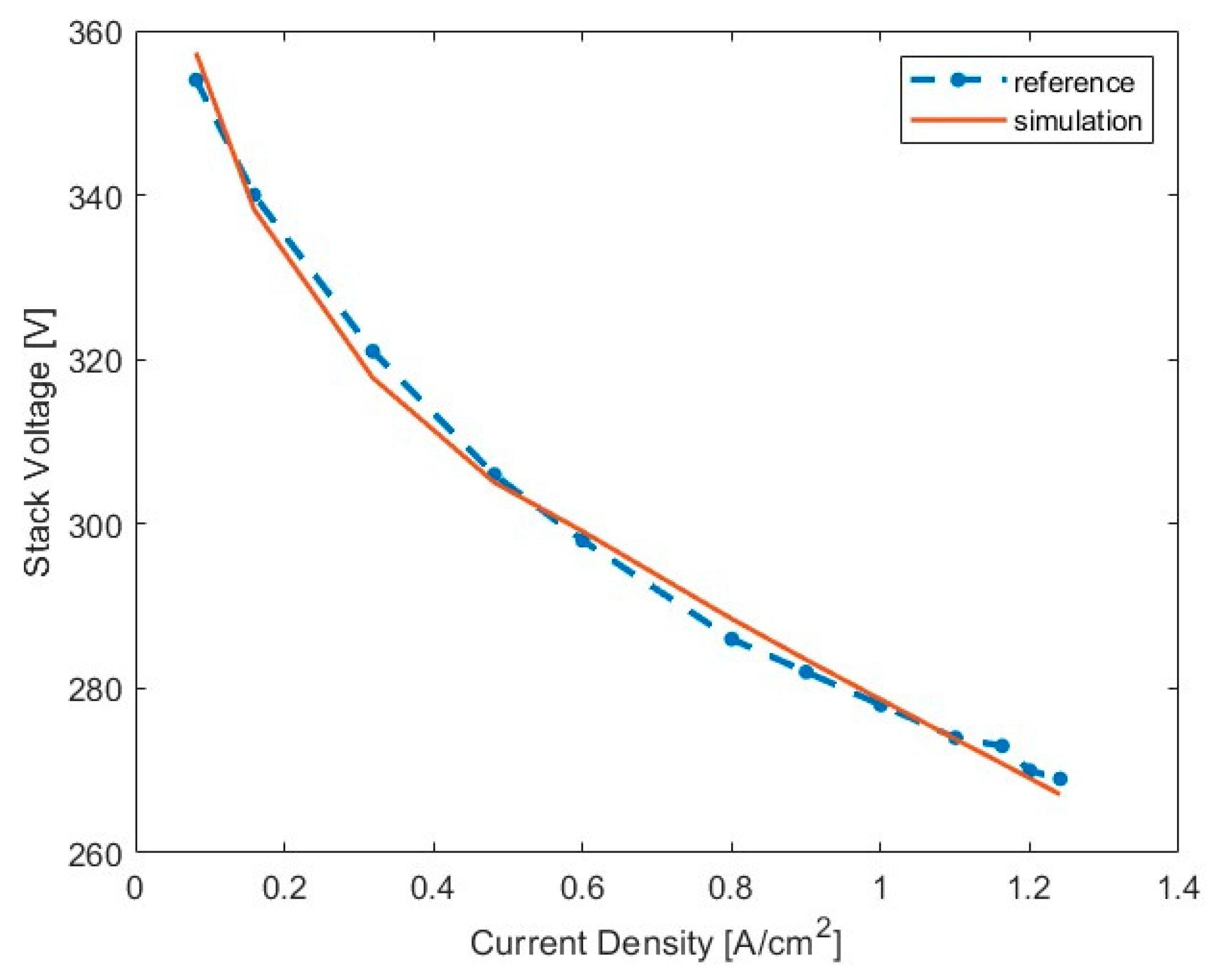
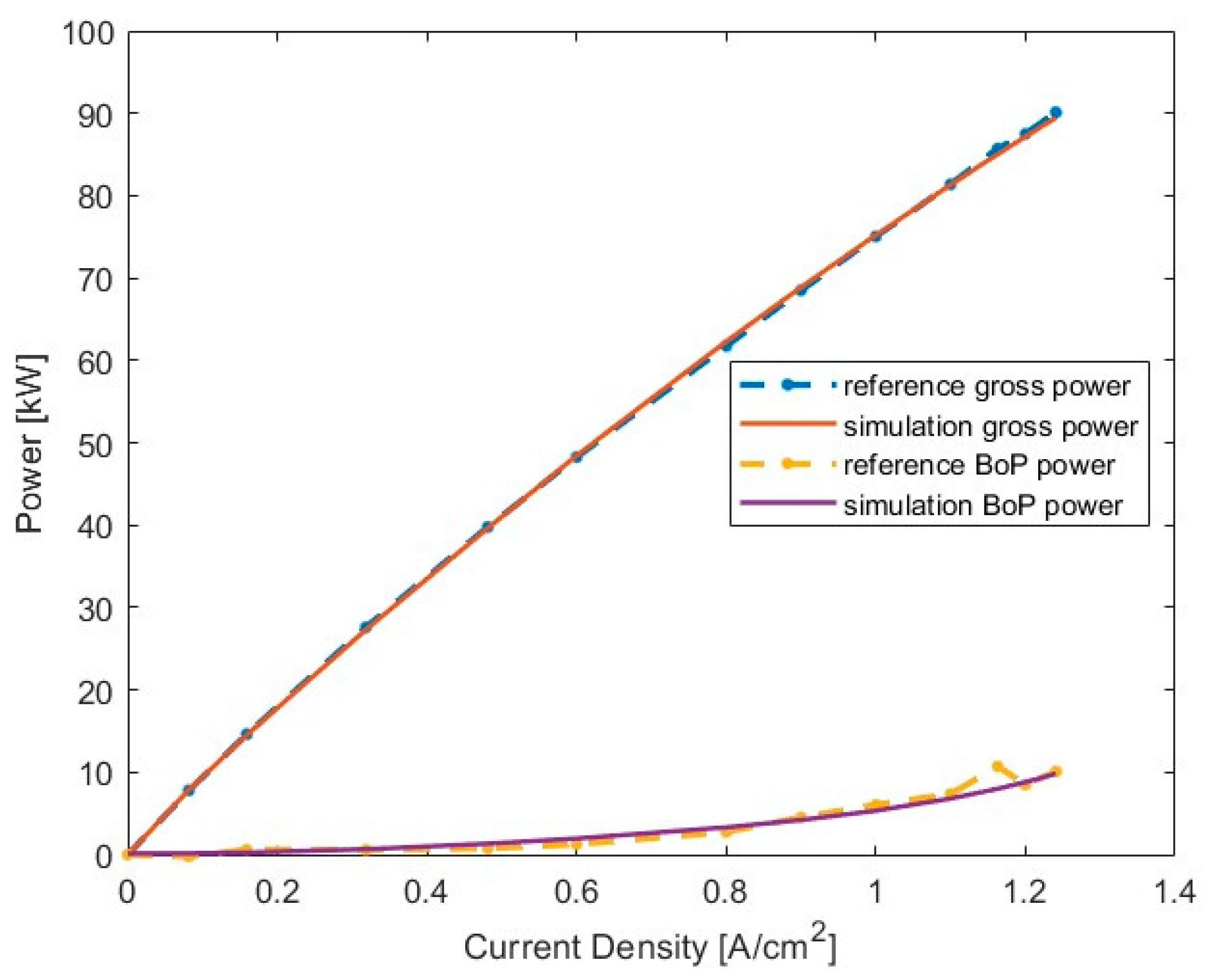
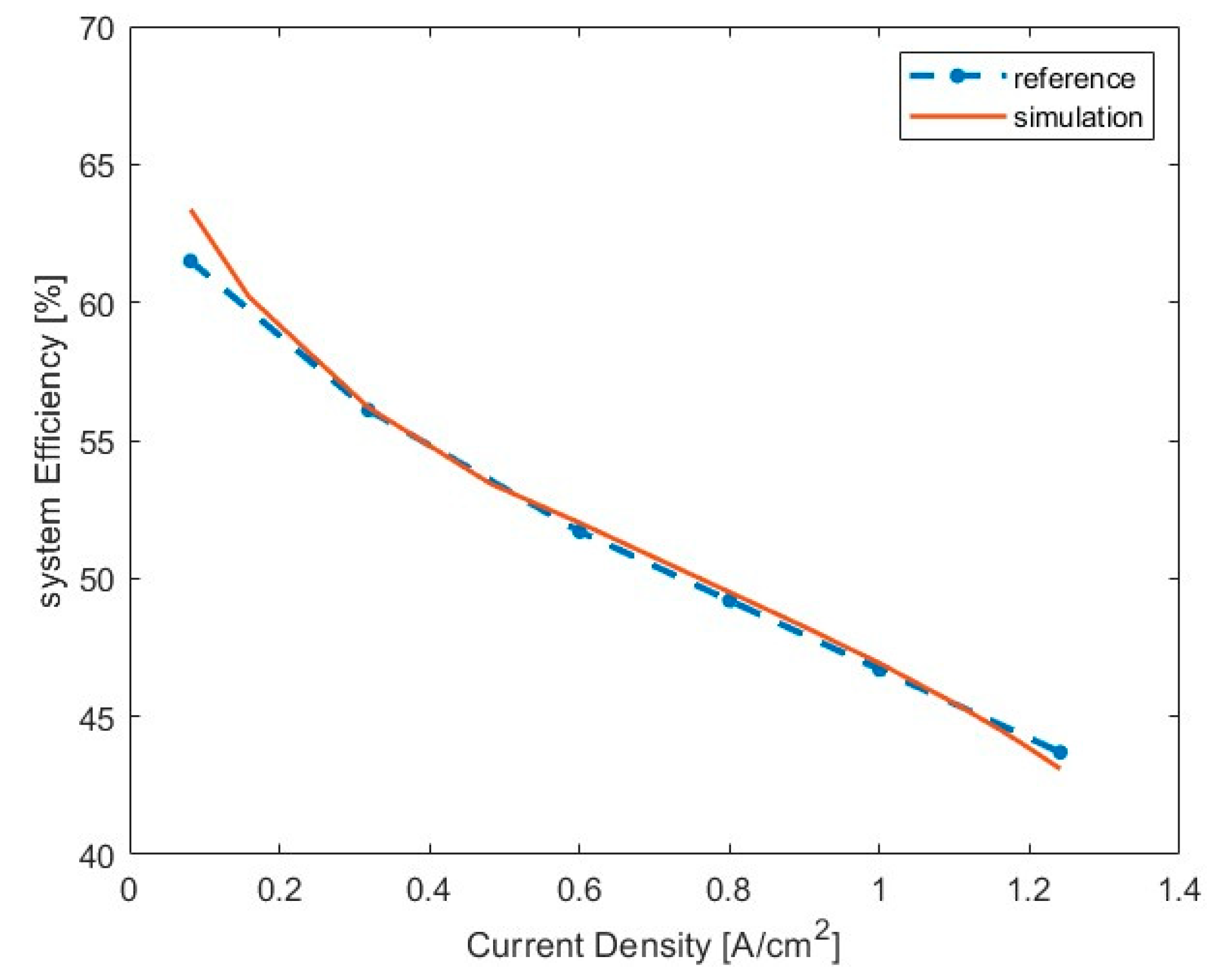
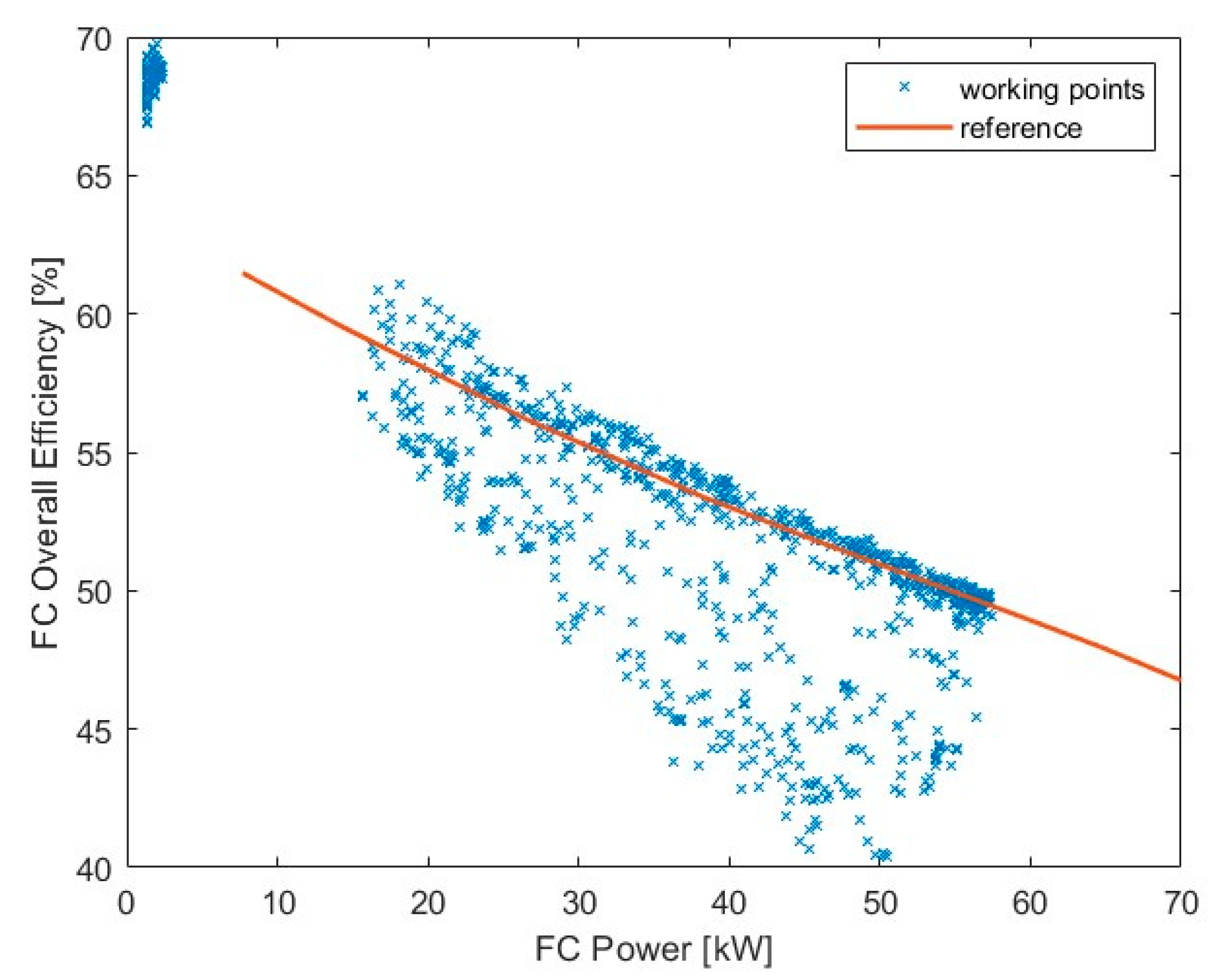
3.1. Calibration Results
3.2. Drive Cycle Simulation
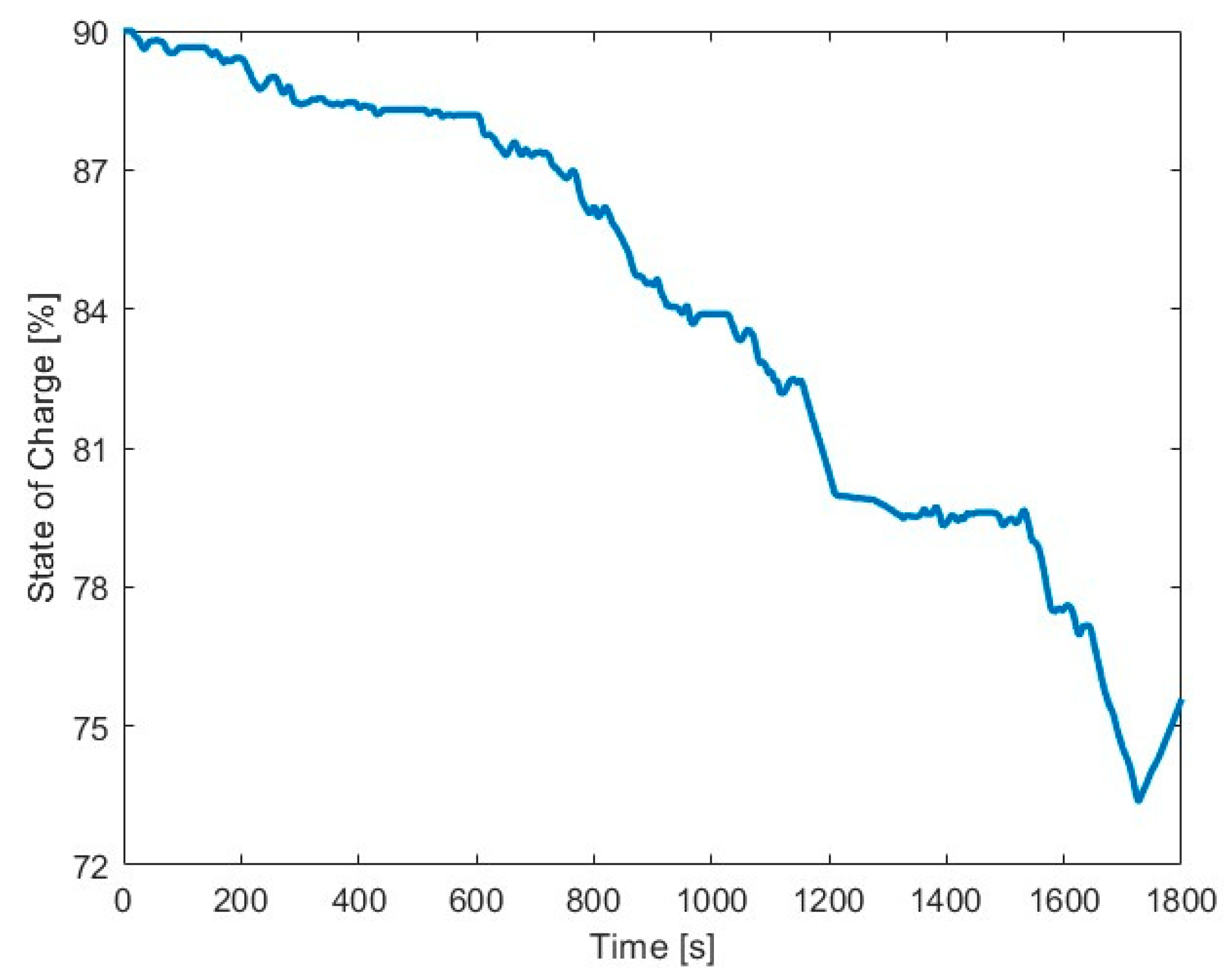
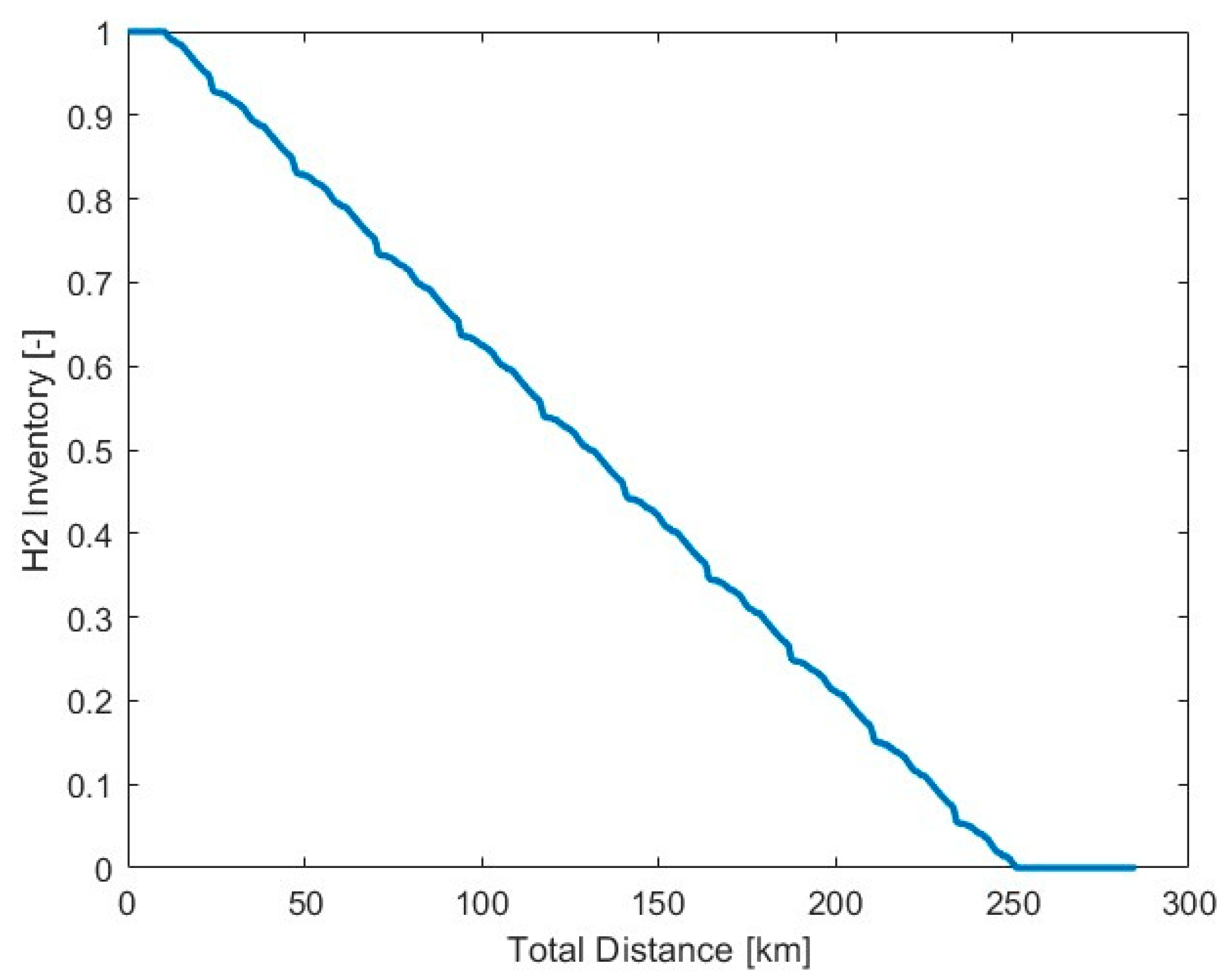
3.2.1. Battery Depleting Mode
3.2.2. Battery Sustaining Model
3.2.3. Repetitive Drive Cycles
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BEV | Battery Electric Vehicle |
| BoP | Balance of Plant |
| EMS | Energy Management Strategies |
| FC | Fuel Cell |
| FCEV | Fuel Cell Electric Vehicle |
| FCS | Fuel Cell Stack |
| ICE | Internal Combustion Engine |
| LCV | Light Commercial Vehicle |
| LHV | Lower Heating Value |
| PCU | Powertrain Control Unit |
| PEM | Proton Exchange Membrane |
| RRSME | Relative Root Square Mean Error |
| SoC | State of Charge |
| SoH2 | State of Hydrogen |
| VDS | Vehicle Dynamic System |
| WLTP | Worldwide Harmonized Light vehicles Test Procedure |
References
- Larminie, J.; Dicks, A.; McDonald, M.S. Fuel Cell Systems Explained; John Wiley and Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Mench, M.M. Fuel Cell Engines; John Wiley and Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Darvishi, Y.; Hassan-Beygi, S.R.; Zarafshan, P.; Hooshyari, K.; Malaga-Toboła, U.; Gancarz, M. Numerical modeling and evaluation of pem used for fuel cell vehicles. Materials 2021, 14, 7907. [Google Scholar] [CrossRef]
- Omran, A.; Lucchesi, A.; Smith, D.; Alaswad, A.; Amiri, A.; Wilberforce, T.; Sodré, J.R.; Olabi, A. Mathematical model of a proton-exchange membrane (PEM) fuel cell. Int. J. Thermofluids 2021, 11, 100110. [Google Scholar] [CrossRef]
- Chugh, S.; Chaudhari, C.; Sonkar, K.; Sharma, A.; Kapur, G.S.; Ramakumar, S.S.V. Experimental and modelling studies of low temperature PEMFC performance. Int. J. Hydrogen Energy 2020, 45, 8866–8874. [Google Scholar] [CrossRef]
- Hou, Y.; Yin, C.; Sheng, X.; Xu, D.; Chen, J.; Tang, H. Automotive fuel cell performance degradation prediction using Multi-Agent Cooperative Advantage Actor-Critic model. Energy 2025, 318, 134899. [Google Scholar] [CrossRef]
- Pukrushpan, J.T.; Peng, H.; Stefanopoulou, A.G. Control-oriented modeling and analysis for automotive fuel cell systems. J. Dyn. Syst. Meas. Control. Trans. 2024, 126, 14–25. [Google Scholar] [CrossRef]
- Chen, J.; He, H.; Wang, Y.-X.; Quan, S.; Zhang, Z.; Wei, Z.; Han, R. Research on energy management strategy for fuel cell hybrid electric vehicles based on improved dynamic programming and air supply optimization. Energy 2024, 300, 131567. [Google Scholar] [CrossRef]
- Fandi, G.; Novák, J.; Chyský, J.; Šrom, J. Review and modeling on hydrogen fuel cells electric vehicle (HFCEV), in comparison with battery electrical vehicle (BEV) using MATLAB environment. Case study: Postal car. Energy Convers. Manag. X 2024, 24, 100684. [Google Scholar] [CrossRef]
- Knöri, T.; Schulze, M. Spatially resolved current density measurements and real-time modelling as a tool for the determination of local operating conditions in polymer electrolyte fuel cells. J. Power Sources 2009, 193, 308–314. [Google Scholar] [CrossRef]
- Verducci, F.; Grimaldi, A.; Colombo, E.; Casalegno, A.; Baricci, A. Dynamic modeling of polymer electrolyte membrane fuel cells under real-world automotive driving cycle with experimental validation on segmented single cell. Renew Energy 2024, 234, 121194. [Google Scholar] [CrossRef]
- Sarmiento-Carnevali, M.; Serra, M.; Batlle, C. Distributed parameter model simulation tool for PEM fuel cells. Int. J. Hydrogen Energy 2014, 39, 4044–4052. [Google Scholar] [CrossRef]
- Han, J.; Woo, J.; Kim, Y.; Yu, S. Fuel cell/battery power supply system operational strategy to secure the durability of commercial hydrogen vehicles. Energy Convers. Manag. 2023, 288, 117163. [Google Scholar] [CrossRef]
- Sun, W.; Liu, H.; Han, M.; Sun, K.; Bai, S.; Li, G. A Novel Method for the Application of the ECMS (Equivalent Consumption Minimization Strategy) to Reduce Hydrogen Consumption in Fuel Cell Hybrid Electric Vehicles. Fluid Dyn. Mater. Process. 2022, 18, 867–882. [Google Scholar] [CrossRef]
- Silva-Vera, E.; Valdez-Resendiz, J.E.; Alejo-Reyes, A.; Rumbo-Morales, J.Y.; Rosas-Caro, J.C.; Sanchez, V.M. Data-driven modeling of proton-exchange membrane fuel cell stacks. Int. J. Hydrogen Energy 2025, 141, 1050–1060. [Google Scholar] [CrossRef]
- Kahveci, E.E.; Taymaz, I. Hydrogen PEMFC stack performance analysis through experimental study of operating parameters by using response surface methodology (RSM). Int. J. Hydrogen Energy 2022, 47, 12293–12303. [Google Scholar] [CrossRef]
- Sahu, I.P.; Krishna, G.; Biswas, M.; Das, M.K. Performance study of PEM fuel cell under different loading conditions. Energy Procedia 2014, 54, 468–478. [Google Scholar] [CrossRef]
- Pukrushpan, J.T. Modeling and Control of Fuel Cell Systems and Fuel Processors; University of Michigan: Ann Arbor, MI, USA, 2003. [Google Scholar]
- Grano, E.; Lazek, T.; Carello, M. A numerical Methodology for Induction Motor Control: Lookup Tables Generation and Steady-State Performance Analysis. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 2024. [Google Scholar] [CrossRef]
- Grano, E.; Bianco, E.; De Carvalho Pinheiro, H.; Carello, M. MTPA and flux weakening control of electric motors: A numerical approach. In Proceedings of the 2023 IEEE International Conference on Environment and Electrical Engineering and 2023 IEEE Industrial and Commercial Power Systems Europe, EEEIC/I and CPS Europe, Madrid, Spain, 6–9 June 2023; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2023. [Google Scholar] [CrossRef]
- de Carvalho Pinheiro, H. PerfECT Design Tool: Electric Vehicle Modelling and Experimental Validation. World Electr. Veh. J. 2023, 14, 337. [Google Scholar] [CrossRef]
- Grano, E.; de Carvalho Pinheiro, H.; Carello, M. A novel electric drive description to bridge the gap between energetic and equivalent-circuit models. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2025, 09544070251330340. [Google Scholar] [CrossRef]
- Eisner, M.K.; Zhou, Z.; Formanski, V.; Kennel, R.M. Improving the air supply and hydrogen dilution control of a fuel cell electric vehicle with explicit model predictive control. Int. J. Hydrogen Energy 2024, 52, 1236–1247. [Google Scholar] [CrossRef]
- Xu, C.; Yang, J.; Chen, K.; Ma, G.; Wang, Y.; Li, Z.; Zhou, Z.; Wu, Z.; Che, S.; Ding, C.; et al. CoSe2-Modified multidimensional porous carbon frameworks as high-Performance anode for fast-Charging sodium-Ion batteries. Chem. Eng. J. 2024, 497, 154875. [Google Scholar] [CrossRef]
- Mazzeo, F.; Di Napoli, L.; Carello, M. Assessing Open Circuit Voltage Losses in PEMFCs: A New Methodological Approach. Energies 2024, 17, 2785. [Google Scholar] [CrossRef]
- Nguyen, T.V.; White, R.E. A Water and Heat Management Model for Proton-Exchange-Membrane Fuel Cells. J. Electrochem. Soc. 1993, 140, 2178–2186. [Google Scholar] [CrossRef]
- Guzzella, L. Vehicle Propulsion Systems: Introduction to Modeling and Optimization, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Singla, M.K.; Gupta, J.; Singh, B.; Nijhawan, P.; Abdelaziz, A.Y.; El-Shahat, A. Parameter Estimation of Fuel Cells Using a Hybrid Optimization Algorithm. Sustainability 2023, 15, 6676. [Google Scholar] [CrossRef]
- Mei, J.; Meng, X.; Tang, X.; Li, H.; Hasanien, H.; Alharbi, M.; Dong, Z.; Shen, J.; Sun, C.; Fan, F.; et al. An Accurate Parameter Estimation Method of the Voltage Model for Proton Exchange Membrane Fuel Cells. Energies 2024, 17, 2917. [Google Scholar] [CrossRef]
- Nafion Membrane, Chemours Nafion, Proton Exchange Membrane. Available online: https://www.nafion.com/en/products/sulfonic-membranes (accessed on 30 July 2025).
- Guzzella, L.; Sciarretta, A. Vehicle Propulsion Systems: Introduction to Modeling and Optimization; Springer: Berlin/Heidelberg, Germany, 2013; Volume 9783642359132, pp. 1–409. [Google Scholar] [CrossRef]
- Moraal, P.; Kolmanovsky, I. Turbocharger modeling for automotive control applications. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 1999. [Google Scholar] [CrossRef]
- Cunningham, J.M.; Hoffman, M.A.; Moore, R.M.; Friedman, D.J. Requirements for a Flexible and Realistic Air Supply Model for Incorporation into a Fuel Cell Vehicle (FCV) System Simulation. In SAE Transactions; SAE International: Warrendale, PA, USA, 1999. [Google Scholar] [CrossRef]
- Wang, C.; Nehrir, M.H.; Shaw, S.R. Dynamic models and model validation for PEM fuel cells using electrical circuits. IEEE Trans. Energy Convers. 2005, 20, 442–451. [Google Scholar] [CrossRef]
- Mazzeo, F.; Graziano, E.; Bodoardo, S.; Papurello, D. Calibration methodology of static, dynamic and ageing parameters of an electrochemical model for a Li-ion cell based on an experimental approach. Renew Energy 2025, 246, 122793. [Google Scholar] [CrossRef]
- Natarajan, N.; Panday, A.; Duddu, S.; Singh, T.T.; Kesavan, D.; Annabathula, S. Electrochemical & Equivalent Circuit Modelling and Validation of Lithium-Ion Cell in GT-AutoLion. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 2022. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, X.; Wang, Z.; Sun, F.; Dorrell, D.G. A review of supercapacitor modeling, estimation, and applications: A control/management perspective. Renew. Sustain. Energy Rev. 2018, 81, 1868–1878. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Fan, J. Evaluation of Lithium-Ion Battery Equivalent Circuit Models for State of Charge Estimation by an Experimental Approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, C.; Dai, B.; Li, Z. Dynamic Simulation of Permanent Magnet Synchronous Motor (PMSM) Electric Vehicle Based on Simulink. Energies 2022, 15, 1134. [Google Scholar] [CrossRef]
- Hasoun, M. (PDF) A Comparative Study of Direct Torque Control and Field Oriented Control for Permanent Magnet Synchronous Motor Drives. Available online: https://www.researchgate.net/publication/319043511_A_Comparative_Study_of_Direct_Torque_Control_and_Field_Oriented_Control_for_Permanent_Magnet_Synchronous_Motor_drives (accessed on 26 May 2025).
- Han, S.; Zhang, F.; Xi, J. A real-time energy management strategy based on energy prediction for parallel hybrid electric vehicles. IEEE Access 2018, 6, 70313–70323. [Google Scholar] [CrossRef]
- Gu, J.; Ouyang, M.; Li, J. Vehicle Dynamic Simulation for Efficiency Optimization of Four-wheel Independent Driven Electric Vehicle. World Electr. Veh. J. 2010, 4, 319–324. [Google Scholar] [CrossRef]
- Yu, G. New Rotational Dynamics- Inertia-Torque Principle and the Force Moment the Character of Statics. J. Appl. Comput. Math. 2015, 4, 319–324. [Google Scholar] [CrossRef]
- Zhao, J. Integrated Longitudinal Vehicle Dynamics Control with Tire/Road Friction Estimation. Available online: https://fid-move.de/en/search/id/BLCP:CN600050884?cHash=cf7443cde723534b4ce3f10fb530d445 (accessed on 27 May 2025).
- Olson, B.J.; Shaw, S.W.; Stépán, G. Stability and bifurcation of longitudinal vehicle braking. Nonlinear Dyn 2005, 40, 339–365. [Google Scholar] [CrossRef]
- Wang, Y.; Deng, Y.; Wang, H.; Zuo, Z. Model predictive control-based longitudinal control for autonomous electric vehicle with changing mass. Asian J. Control. 2023, 25, 1297–1309. [Google Scholar] [CrossRef]
- Musa, A.; Miretti, F.; Misul, D. MPC-Based Cooperative Longitudinal Control for Vehicle Strings in a Realistic Driving Environment. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 2023. [Google Scholar] [CrossRef]
- Jiang, X.; Xing, H.; Chen, S. Longitudinal motion control of autonomous vehicle based on feedforward-fuzzy PI. In Proceedings of the 4th International Conference on Information Science, Electrical, and Automation Engineering (ISEAE 2022), online, 25–27 March 2022; Volume 2257, pp. 1129–1135. [Google Scholar] [CrossRef]
- Xiong, L.; Yang, X.; Zhuo, G.; Leng, B.; Zhang, R. Review on Motion Control of Autonomous Vehicles. Jixie Gongcheng Xuebao/J. Mech. Eng. 2020, 56, 127–143. [Google Scholar] [CrossRef]
- Singh, S. Longitudinal Velocity Control of Autonomous Ground Vehicle using PID and PI Controller. Int. J. Res. Appl. Sci. Eng. Technol. 2021, 9, 504–510. [Google Scholar] [CrossRef]
- Serrao, L.; Onori, S.; Rizzoni, G. ECMS as a realization of pontryagin’s minimum principle for HEV control. In Proceedings of the American Control Conference, Denver, CO, USA, 8–10 July 2009; pp. 3964–3969. [Google Scholar] [CrossRef]
- Madkaikar, S.; Kini, C.R.; Nayak, S.Y. Energy Management Approach for Charge Sustaining Hybrid Electric Vehicle. J. Eng. Sci. Technol. 2021, 16, 4121–4137. [Google Scholar]
- Shi, D.; Xu, H.; Wang, S.; Hu, J.; Chen, L.; Yin, C. Deep reinforcement learning based adaptive energy management for plug-in hybrid electric vehicle with double deep Q-network. Energy 2024, 305, 132402. [Google Scholar] [CrossRef]
- Demirci, O.; Taskin, S.; Schaltz, E.; Demirci, B.A. Review of battery state estimation methods for electric vehicles-Part I: SOC estimation. J. Energy Storage 2024, 87, 111435. [Google Scholar] [CrossRef]
- Di Napoli, L.; Mazzeo, F. Health and Condition Monitoring Tool for Real-Time and on-Board Diagnosis of PEM Fuel Cell in Heavy Duty Vehicles. In SAE Technical Paper; SAE International: Warrendale, PA, USA, 2025. [Google Scholar] [CrossRef]
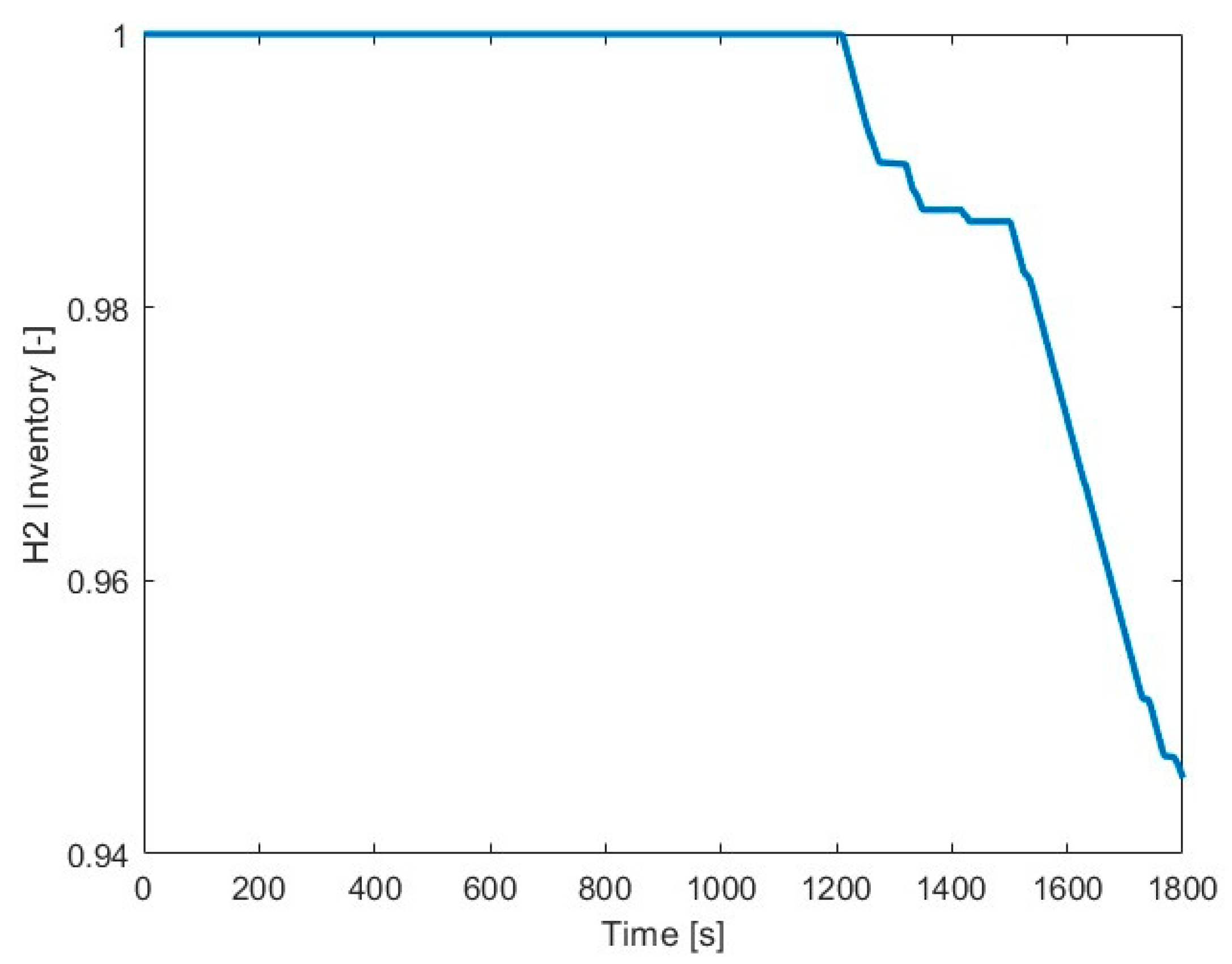

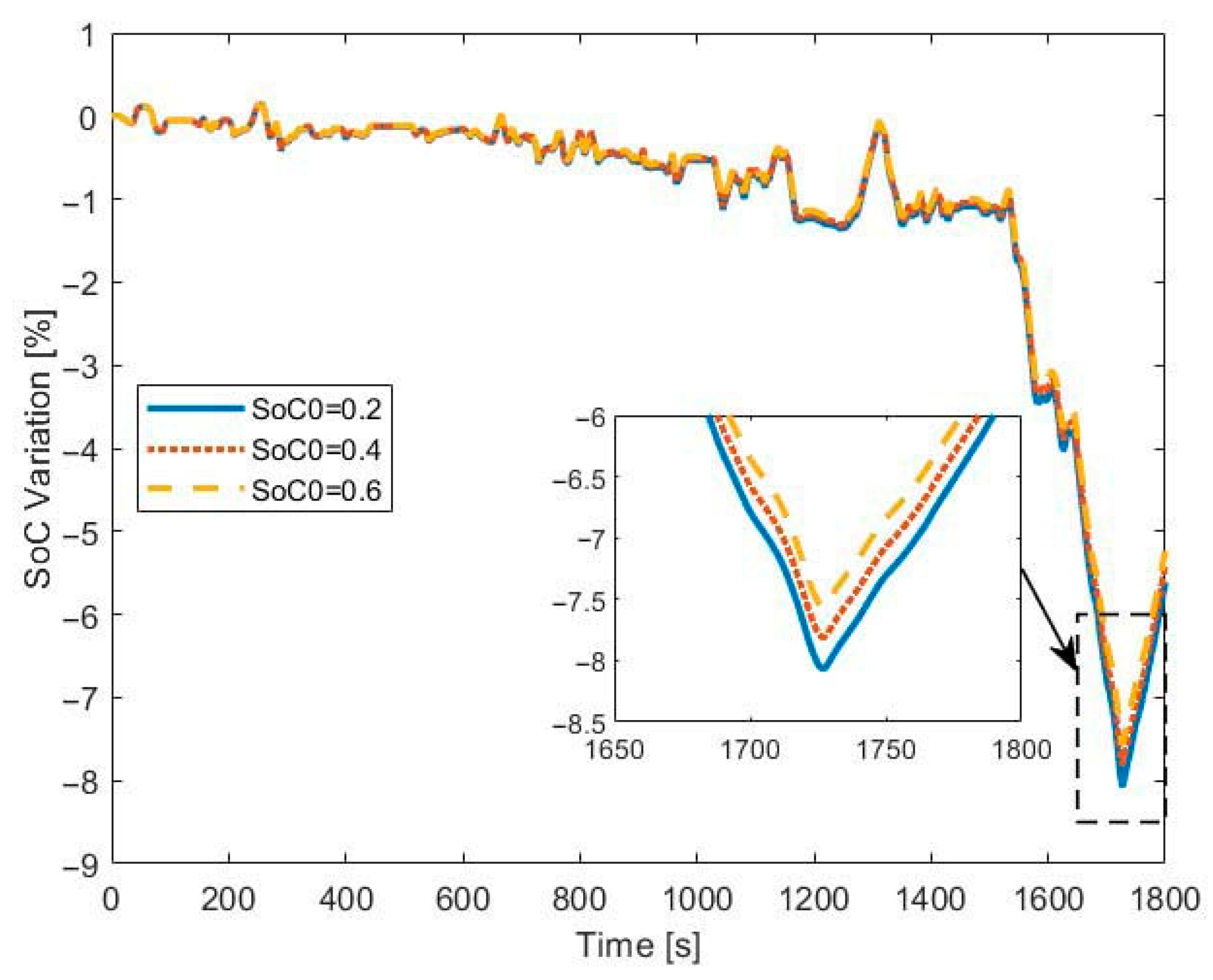

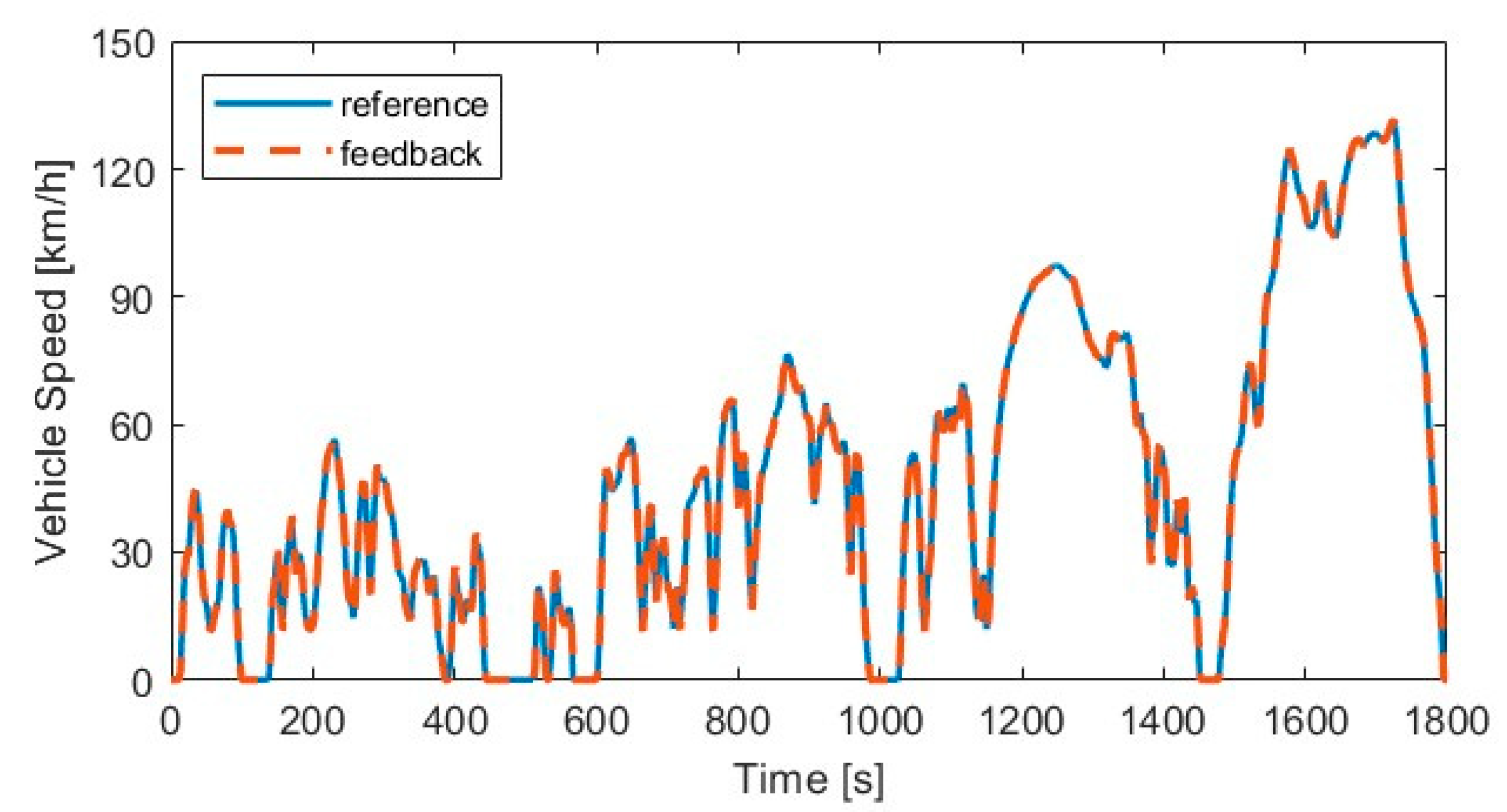
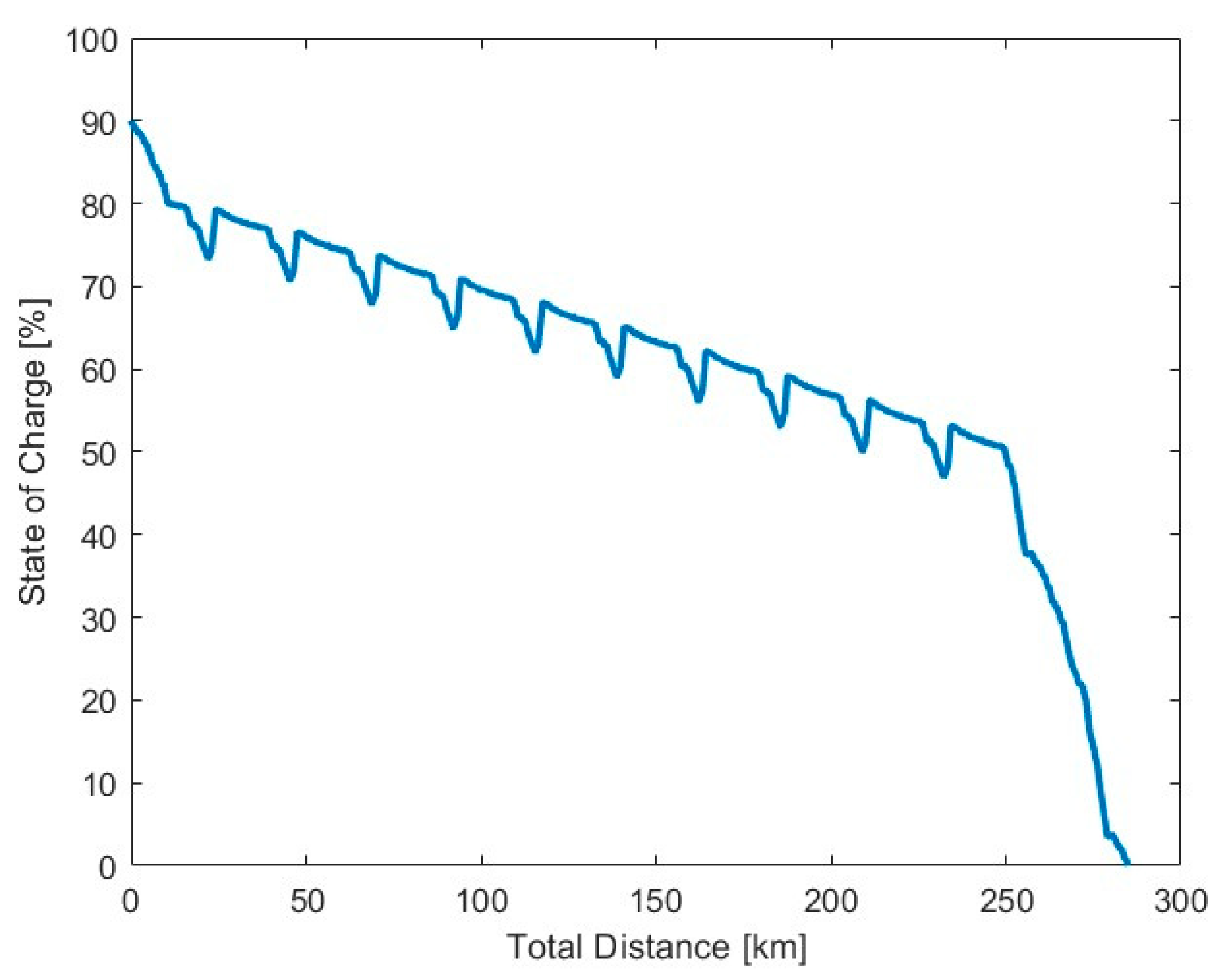
| Parameter | Range | Influence * |
|---|---|---|
| [V] | 0.03–0.15 [2] | Positive to Activation loss |
| around 0.5 [1] | Negative to Activation loss | |
| [μm] | 20–50 [30] | Positive to Ohmic loss |
| 2.0–3.0 [31] | Negative to Concentration loss |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| −8.110 × 10−7 | 2.556 | ||
| 5.588 × 10−6 | −1.298 × 10−8 | ||
| 3.508 × 10−6 | −1.298 × 10−8 | ||
| 2.676 × 10−7 | 0.215 | ||
| 4.821 × 10−4 | 0.799 | ||
| 8.889 × 10−4 | 81.190 | ||
| 0.111 | −1.449 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Grano, E.; Mazzeo, F.; de Carvalho Pinheiro, H.; Carello, M. Calibration and Validation of a PEM Fuel Cell Hybrid Powertrain Model for Energy Management System Design. Designs 2025, 9, 94. https://doi.org/10.3390/designs9040094
Guo Z, Grano E, Mazzeo F, de Carvalho Pinheiro H, Carello M. Calibration and Validation of a PEM Fuel Cell Hybrid Powertrain Model for Energy Management System Design. Designs. 2025; 9(4):94. https://doi.org/10.3390/designs9040094
Chicago/Turabian StyleGuo, Zihao, Elia Grano, Francesco Mazzeo, Henrique de Carvalho Pinheiro, and Massimiliana Carello. 2025. "Calibration and Validation of a PEM Fuel Cell Hybrid Powertrain Model for Energy Management System Design" Designs 9, no. 4: 94. https://doi.org/10.3390/designs9040094
APA StyleGuo, Z., Grano, E., Mazzeo, F., de Carvalho Pinheiro, H., & Carello, M. (2025). Calibration and Validation of a PEM Fuel Cell Hybrid Powertrain Model for Energy Management System Design. Designs, 9(4), 94. https://doi.org/10.3390/designs9040094





