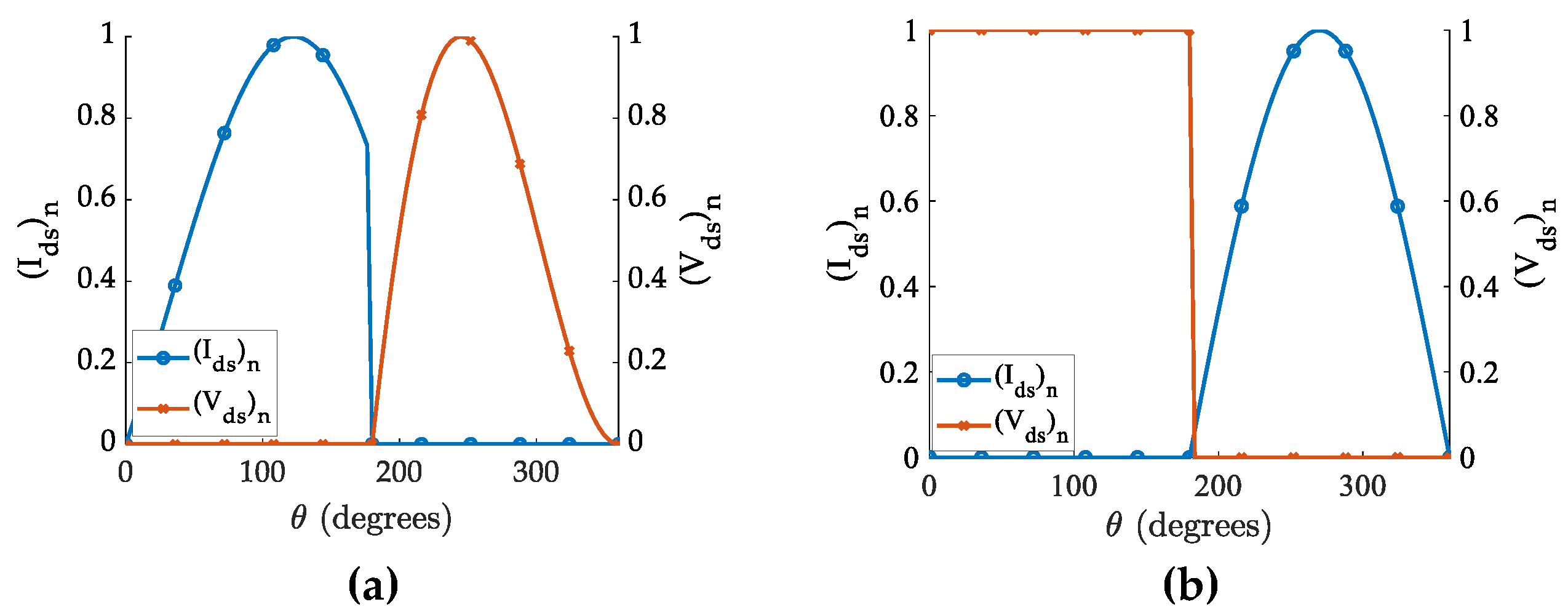Alternative Categorization of Radio Frequency Power Amplifier for Generalized Design Insights

Abstract

In recent years, advancements in semiconductor technologies have significantly transformed Radio Frequency Power Amplifiers (RFPAs), enhancing their efficiency, size, and performance. Despite these advancements, the design of RFPAs remains intrinsically linked to the specific applications for which they are intended. What proves effective in one context, such as communication technologies, may not be equally suitable in others, such as scientific instruments. This discrepancy highlights the lack of a systematic approach to RFPA design that can be applied across different applications. This paper delves into the fundamental concepts of RFPA design, adopting a comprehensive perspective. It further introduces an alternative categorization of RFPAs, thereby providing a generalized design approach.

1. Introduction

Power amplifiers are crucial, but they are also the most power-hungry elements of any radio frequency (RF) chain. They play a pivotal role in amplifying electrical signals into the desired output power, which is essential for driving a wide spectrum of applications, ranging from our everyday microwave ovens to the vast world of wireless connectivity.

The efficiency of a power amplifier is of utmost importance. This metric quantifies the ratio between the RF power generated, with respect to the DC power supplied. Achieving high efficiency in power amplifiers is critical for minimizing energy loss, minimizing heat losses, and ensuring optimal operation of devices and networks while preserving the quality/information of the input signal.

While there have been significant advancements in RFPA (Radio Frequency Power Amplifier) technology [1,2,3], it is important to emphasize that RFPA design significantly depends on the specific application. This is why the design of RFPAs is still currently a critical area for research and development.

An extensive overview of RFPAs, as presented by Raab et al. [4], offers valuable insights into its diverse classes and architectures, showcasing various approaches. Similarly, Lohmeyer et al. conducted a comparative analysis of solid-state power amplifiers (SSPAs) and traveling wave tube amplifiers (TWTAs) within the context of satellite applications [5]. Furthermore, extensive reviews of semiconductor technologies for the design of RFPAs have been discussed in detail by Pengelly et al. [6] and Hamza et al. [7]. Employing a system-level approach, Banu et al. [8] presented a comprehensive theory of RFPA design without considering the specific details of the implementation. Oncu et al. provided valuable perspectives on the design requirements and optimization strategies for RF power amplifiers specifically developed for satellite communication systems [9].

However, despite these valuable contributions, it is evident that a generalized theory for analyzing and designing RFPAs that need to incorporate a series of system requirements is yet to be developed. Moreover, most existing work centers its focus on the trade-off between efficiency and linearity, as reported by Lavrador et al. [10]. While a thorough review of various techniques used to improve linearity and efficiency is presented by Singh et al. [11], it also falls short of offering a comprehensive framework for selecting the optimal combination of design factors and making well-informed decisions.

To address these problems adequately, the classification of RFPAs in a systematic manner is of utmost importance. While the practice of categorizing RFPAs using Classes is a well-established tradition in the field, it has also caused some uncertainty and discussions among engineers and researchers [12]. RFPAs are commonly classified based on their operational characteristics and functionality. However, this traditional classification can be ambiguous and misleading as the term “operating class” encompasses various features. These include bias point selection (Class A, AB, B, or C), matching network topologies (Tuned Load, Class F, etc.), or the operating conditions of the active device (Class E, Class S, etc.). Nonetheless, simply relying on the Class taxonomy may not be sufficient when designing an RFPA for a specific application. On the other hand, systems engineering has evolved as a transdisciplinary field to provide elegant solutions to complex problems [13]. Systems engineers must be able to define the objectives initially and, through consideration of all factors and possibilities, ultimately achieve these objectives while understanding the relationships between them [14]. This work addresses the missing link by simplifying and enabling the creation of elegant solutions for RFPA design using simplified concepts, thereby exploring the relationships. On the other hand, systems engineering has evolved as a transdisciplinary field to provide elegant solutions to complex problems [13]. Systems engineers must be able to define the objectives initially and, through the consideration of all factors and possibilities, ultimately achieve these objectives while understanding the relationships between them [14]. This work addresses the missing link by simplifying and enabling the creation of elegant solutions for RFPA design using simplified concepts, thereby exploring the relationships.

This work first introduces the basic terminology of RFPAs, and then an alternative categorization of RFPAs that organizes various design techniques by time, frequency, and space in an abstract and unified manner. It then presents a design methodology that can be incorporated into flow chart, referred to as vertical and horizontal flow. This flow diagram facilitates analysis, verification, and validation throughout the development of RFPAs.

2. RFPA Fundamentals

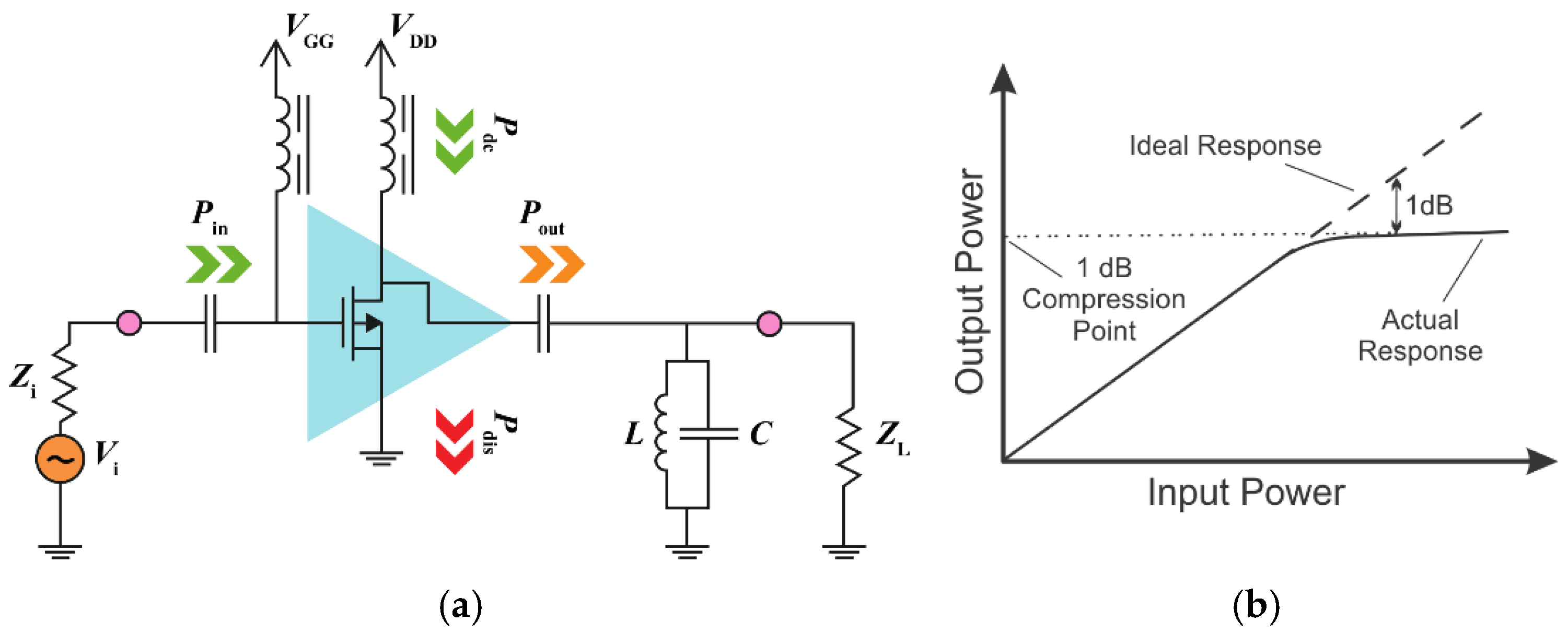
The efficiency of an RFPA, as its central performance metric, quantifies how effectively the amplifier converts the input power into useful output power while minimizing losses, and is defined as the ratio of net output power P_out and the total supplied power P_dc. The basic block diagram of an amplifier is shown in Figure 1a, wherein the circular pink dots represent matching network topology.

Here, P_in is the input RF power, P_out is the output RF power delivered to load Z_L, P_DC is the DC power supplied, P_diss is the dissipated power in the device, and Z_L is the ideal load that needs to be connected to realize maximum efficiency. A detailed description of it is presented by Cripps in [15]. The fundamental relation between these quantities arises due to conservation laws: P_in + P_DC = P_out + P_diss. In this context, it is also useful to consider the gain G, the efficiency η, and the power added efficiency η_add, which are given by Equations (1)–(3), respectively [16].

$$G={\displaystyle \frac{P_{out}}{P_{in}}}$$

(1)

$$\eta ={\displaystyle \frac{P_{out}}{P_{DC}}}$$

(2)

$${\eta }_{add}={\displaystyle \frac{P_{out}-P_{in}}{P_{DC}}}=\eta \left(1-{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$G$}\right.}\right)$$

(3)

The typical performance of an RFPA is characterized as a function of the input drive, with an example being shown in Figure 1b. In practical RF power amplifiers, the relation between the input power and output power is non-linear after a certain threshold. As the input power increases, the output power eventually reaches a point where it saturates instead of increasing further. This point is known as the compression point, P_in,1dB, as shown in Figure 1b. At this point, the input power level drops by 1 dB, and the corresponding efficiency is usually measured at this point.

3. Alternative Categorization

The classification technique proposed in this work is based on the analysis of three pillars: time, frequency, and space. To mathematically represent the relation between these parameters with the efficiency of an RFPA, as defined in Equation (2), one can expand it into Equation (4) [17].

$$\eta ={\displaystyle \frac{P_{out}}{P_{DC}}}={\displaystyle \frac{P_{out,fo}}{P_{diss}+\sum _{h=2}^{\infty }{P}_{out,hf}+P_{out,df} }}$$

(4)

Here, the subscript f_o is defined as follows: $f_o=1/t_o$, where t_o is the fundamental period. $P_{out,fo}$ is the total output power delivered to the load at that fundamental frequency. $P_{diss}$ is the dissipated power in the device which can be related to time. $\sum _{h=2}^{\infty }{P}_{out,hf}$ is the power lost into the harmonics due to the inherent non-linearity of the device, which is related to frequency, and finally $P_{out,df}$ is the maximum power that can delivered to the load efficiently at a design frequency which is related to space in this paper.

The foundation of this categorization draws inspiration from the field of category theory [18], which is a branch of abstract mathematics dedicated to studying mathematical structures and their intricate relationships.

In this context, time, frequency, and space are the objects within this categorical framework, and their relations are described by morphisms. These can simply be thought of as functions subject to certain additional axioms, as their compositions describe the cascade effect of modifying, for instance, the time waveform, on the frequency domain or, indirectly, the space domain. Additionally, the concept of identity in category theory applies here, with the physical meaning of a certain unique transformation in time domain that leaves morphisms acting from time to frequency/space invariant.

Considering one factor at a time allows for the evaluation of efficiency in isolation for each of these critical parameters. However, it is essential to recognize that the interplay and combination between all these elements is inevitable, which can be seen in any practical RFPA design. As will be seen, this categorization may suggest techniques and design approaches that address known problems encountered in RFPA design, such as non-linearity and limited bandwidth, efficiency, or gain.

3.1. Time

A thorough analysis of the term $P_{diss}$, which is related to the time domain waveform of voltage and current, is presented in this subsection. It refers to the dissipated power loss at the RFPA due to the simultaneous presence of voltage and current at the same time.

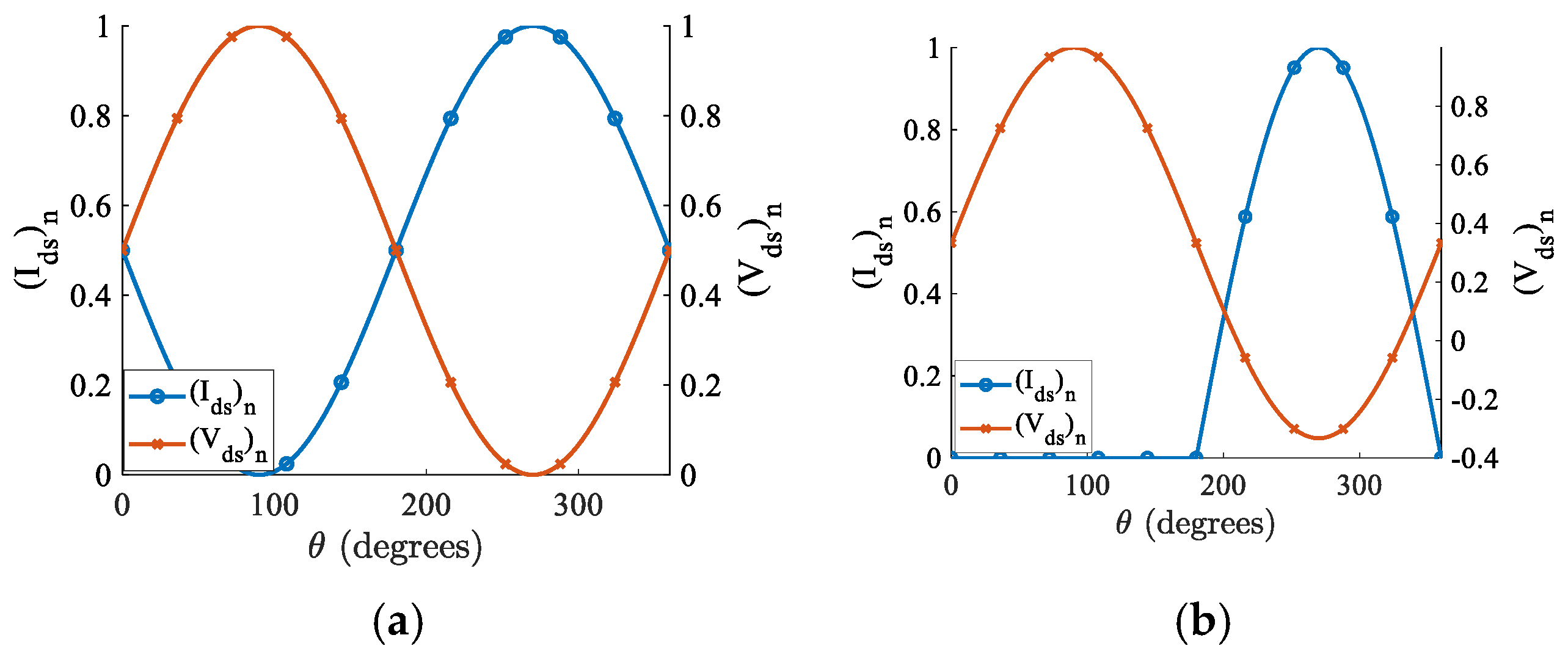
In this context, the active device of the RFPA will be referred to as a transistor, without any loss of generality. The period when the RFPA is active, meaning that both the current and voltage time domain waveforms exist simultaneously in the device, is measured using the conduction angle, $\theta =\omega t$. This conduction angle, which is a function of time and angular frequency and is represented in degrees, is referred to as time in this work.

Figure 2 presents the normalized voltage and current waveforms at the drain of the RFPA. In Figure 2a, the device conducts the entirety of a full cycle with a conduction angle of 360°, leading to high-power dissipation. In contrast, in Figure 2b, the device only conducts for half the period. These variations in power dissipation through the time domain waveform drive the exploration of ways to optimize the RFPA’s efficiency. By strategically imposing a non-overlapping condition, as given by Equation (5), precise control over the device’s operation is achieved.

$${\displaystyle \frac{1}{t_o}}{\int }_0^{t_o}{V}_{ds}\left(t\right)·I_{ds}\left(t\right)=0$$

(5)

By engineering the timing and duty cycle of the voltage and current waveforms on the transistor, the RFPA can be designed in such a way as to eliminate any wasteful power dissipation. In fact, within the field of RFPA design, more advanced classes of waveforms can be employed, as shown in Figure 3. Class E amplifiers, which are also known as switch-mode amplifiers, are one such example. They operate by rapidly switching between on and off states, reducing power dissipation. On the other hand, Class F amplifiers, known as current-mode amplifiers, focus on shaping the voltage waveform to enhance efficiency. These classes of waveforms employ techniques to ensure non-overlapping conditions between the current and voltage waveforms, aiming to achieve theoretical efficiencies of 100%.

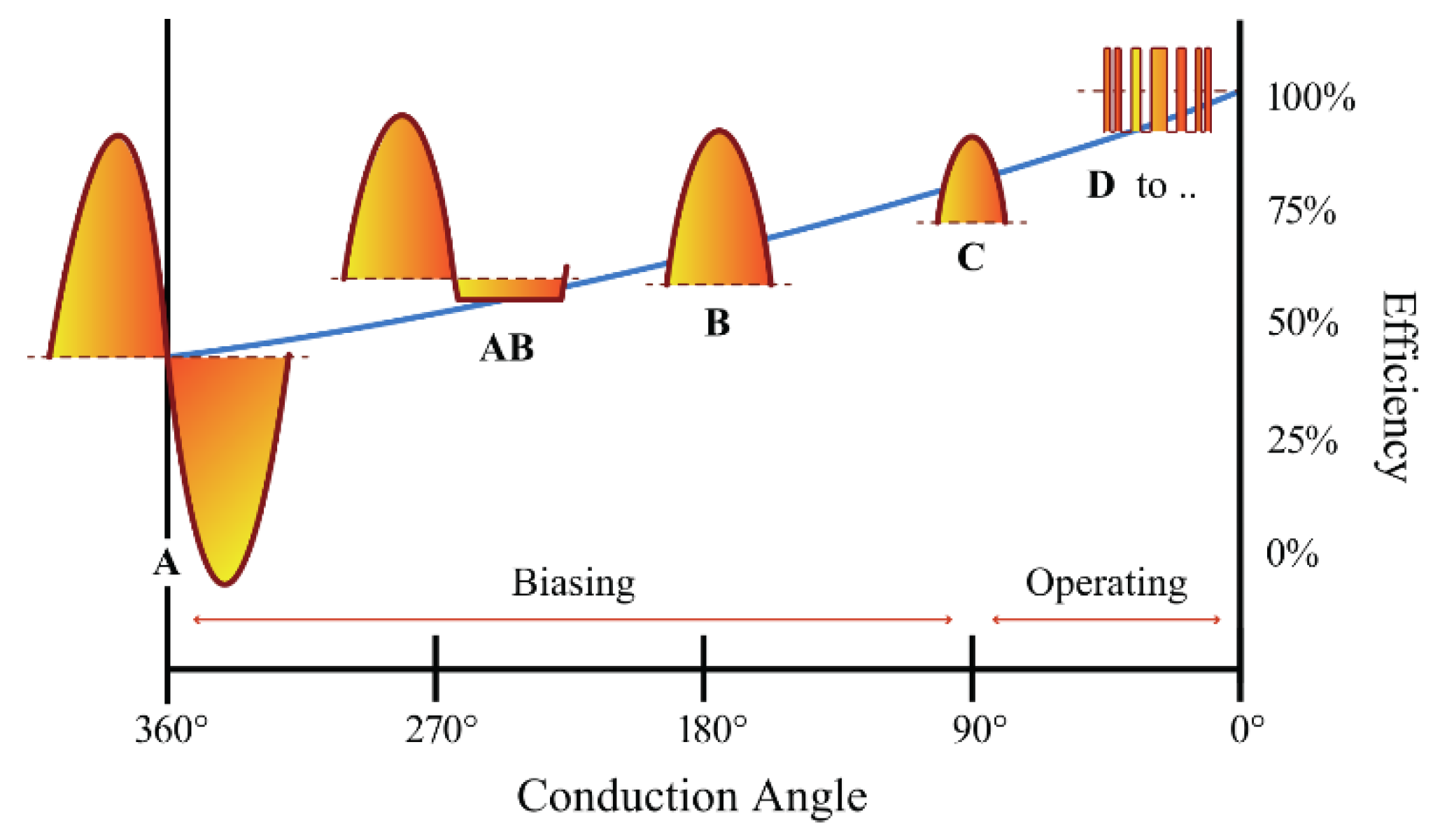
Efficiency can be expressed in terms of the conduction angle θ, as shown in Equation (6), wherein ${\left(v_f\right)}_{max}$ represents the maximum output voltage at the fundamental design frequency, and $V_{DD}$ is the supplied voltage [19]. The theoretical efficiency achievable as a function of this conduction angle is shown Figure 4. Maximum efficiency can be achieved by choosing an appropriate design for the biasing and load networks, ensuring as little overlap as possible between the two waveforms during the operation of the RFPA.

$$\eta ={\displaystyle \frac{\theta -sin\theta cos\theta }{sin\theta -\theta cos\theta }}\left({\displaystyle \frac{{\left(v_f\right)}_{max} }{V_{DD}}}\right)$$

(6)

These findings highlight how crucial it is to carefully consider voltage and current waveforms to achieve highly efficient RFPA. By implementing the non-overlapping condition and carefully engineering the waveforms, remarkable reductions in energy losses can be achieved, thereby enhancing the overall performance of the system. That is why RFPA design is often referred to as waveform engineering [21].

In general, the time domain voltage and current waveform can be approximated as Equations (7) and (8), respectively [22].

$$V_{ds}\left(\theta \right)\approx \left(1-\alpha cos\theta -\beta cos2\theta -\gamma cos3\theta \right)\left(1-\delta sin\theta \right)$$

(7)

$$I_{ds}\left(\theta \right)\approx \left(1+wcos\theta +xcos2\theta +ycos3\theta \right)\left(1-zsin\theta \right)$$

(8)

The parameters $\alpha$ = [1, √2 or 2∕√3], $\beta$ = [0 or 1/2], $\gamma$ = [0 or 1∕(3√3)], and $\delta$ = [−1 to 1] define their time domain voltage waveforms. Meanwhile, the parameters w = [1, √2 or 2∕√3], x = [0 or 1/2], y = [0 or 1∕(3√3)], and z = [−1 to 1] describe the current waveforms.

By substituting different values for these parameters, it becomes possible to derive diverse solution sets for overlapping as well as non-overlapping waveforms, which is fundamental to RFPA design. These sets of solutions can be thought of as the time domain design parameters. For example, when one sets $\alpha =1$, $\delta \in \left[-\mathrm{1,1}\right]$, and all the other parameters to 0 in Equation (7), the Class J/B continuum can be obtained [23]. Some of these waveforms are shown in Figure 5. A more generalized voltage and current waveform can be expressed as a function of $\theta$ in the following way:

$$V_{ds}\left(\theta \right)=a_o+\sum _{n=1}^N{a}_{n}cos\left(n\theta \right)+\sum _{n=1}^N{b}_{n}sin\left(n\theta \right)$$

(9)

$$I_{ds}\left(\theta \right)=c_o+\sum _{n=1}^N{c}_{n}cos\left(n\theta \right)+\sum _{n=1}^N{d}_{n}sin\left(n\theta \right)$$

(10)

Here, $a_o$ and $c_o$ represent the drain dc supply voltage and drain dc supply current, respectively, imposed by the biasing conditions, while $a_n$, $b_n$, $c_n$, and $d_n$ are harmonic coefficients that could theoretically take an infinite number of values, but practical design considerations are expected to limit them. While the set of possible waveforms is diverse, one could simply partition it into the subset of overlapping waveforms and the subset of non-overlapping ones.

3.2. Frequency

Frequency has a direct relation with the bandwidth of an RFPA. The bandwidth of an RFPA refers to the frequency range in which the amplifier can work efficiently. In this context, the analysis of the frequency domain becomes relevant. The term $\sum _{n=2}^{\mathrm{\infty }}{P}_{out,hf}$ in Equation (4) governs the harmonic efficiency of the RFPA and it is obtained by summing over the output power at frequencies which are integer multiples of the fundamental.

However, considering only three harmonics [24] is typically sufficient for designing RFPAs in all practical cases. Based on the voltage and current equations presented in Equations (9) and (10), the fundamental and harmonic components of voltage and current are determined though Fourier integrals, resulting in the following frequency representation of voltage and current:

$$V_n=U_n-j{V}_n$$

(11)

$$I_n=W_n-j{X}_n$$

(12)

With n = 1, 2,…, N. The load impedance at the fundamental as well as at the harmonic frequencies is given by Equation (13):

$$Z_n=-{\displaystyle \frac{V_n}{I_n}}=-{\displaystyle \frac{U_n-j{V}_n}{W_n-j{X}_n}}$$

(13)

High efficiency in RFPAs is often achieved through techniques that optimize the amplifier’s performance at a specific frequency or within a narrow frequency range, employing resonant circuits that maximize power transfer at a particular frequency. Consider, for example, the Class B amplifier, which requires an L-C resonant tank to short all harmonics, ensuring that the output network favors efficiency over bandwidth. While these methods are effective in enhancing efficiency, they naturally restrict the amplifier’s bandwidth because the optimizations are frequency specific.

On the other hand, expanding the bandwidth of an RFPA involves design considerations that can compromise efficiency or linearity. For instance, broadband design techniques, like using non-resonant or wideband matching networks and employing feedback mechanisms, allow the amplifier to operate over a wider range of frequencies. However, these approaches tend to introduce losses or require compromises in the load impedance seen by the transistor at different frequencies, which can reduce the overall efficiency of the amplifier.

These arguments point to a key limitation of RFPAs, namely their limited performance outside the narrow frequency band for which they were originally designed. In this paper, the primary methods to address these issues can be further sub-categorized into two approaches: the step approach and the continuous approach.

3.2.1. Step Approach

The procedure starts by designing the load network for optimal performance at a specific frequency. As a result, the bandwidth of the RFPA is initially limited, so tuning elements [25] need to be incorporated into the load network to mitigate this problem. These elements allow for dynamic adjustments to the load impedance, effectively broadening the RFPA’s operating frequency range.

Tuning elements like varactors [26] or PIN-based diodes offer continuous impedance control, making them ideal for wideband tuning. A capacitor or inductor bank also provides these discrete steps of impedance adjustments, allowing for broader frequency coverage. Alternatively, RF switches [27] have also been used to switch between pre-designed load networks, enabling the RFPA to operate a wide frequency range. However, one must realize that implementing such a design always comes at the cost of a more complex system.

3.2.2. Continuous Approach

The other method of widening the bandwidth of an RFPA is more analytical but does not require any additional control circuity, thereby reducing the overall complexity of the system. The continuous class, initially introduced by Cripps et al. [28], laid the theoretical foundation for the design of broadband RFPAs. Among those, the continuous F [29,30], continuous AB [31], and continuous X [32] amplifiers have gained recognition for their ability to operate efficiently over a wide frequency range.

The mixed-mode design concept, which was initially introduced by Kee et al. [33], was primarily utilized to achieve highly efficient designs. However, as the notion of broadband performance gained prominence, it evolved into the concept of Continuous Class E (CCE) [34,35].

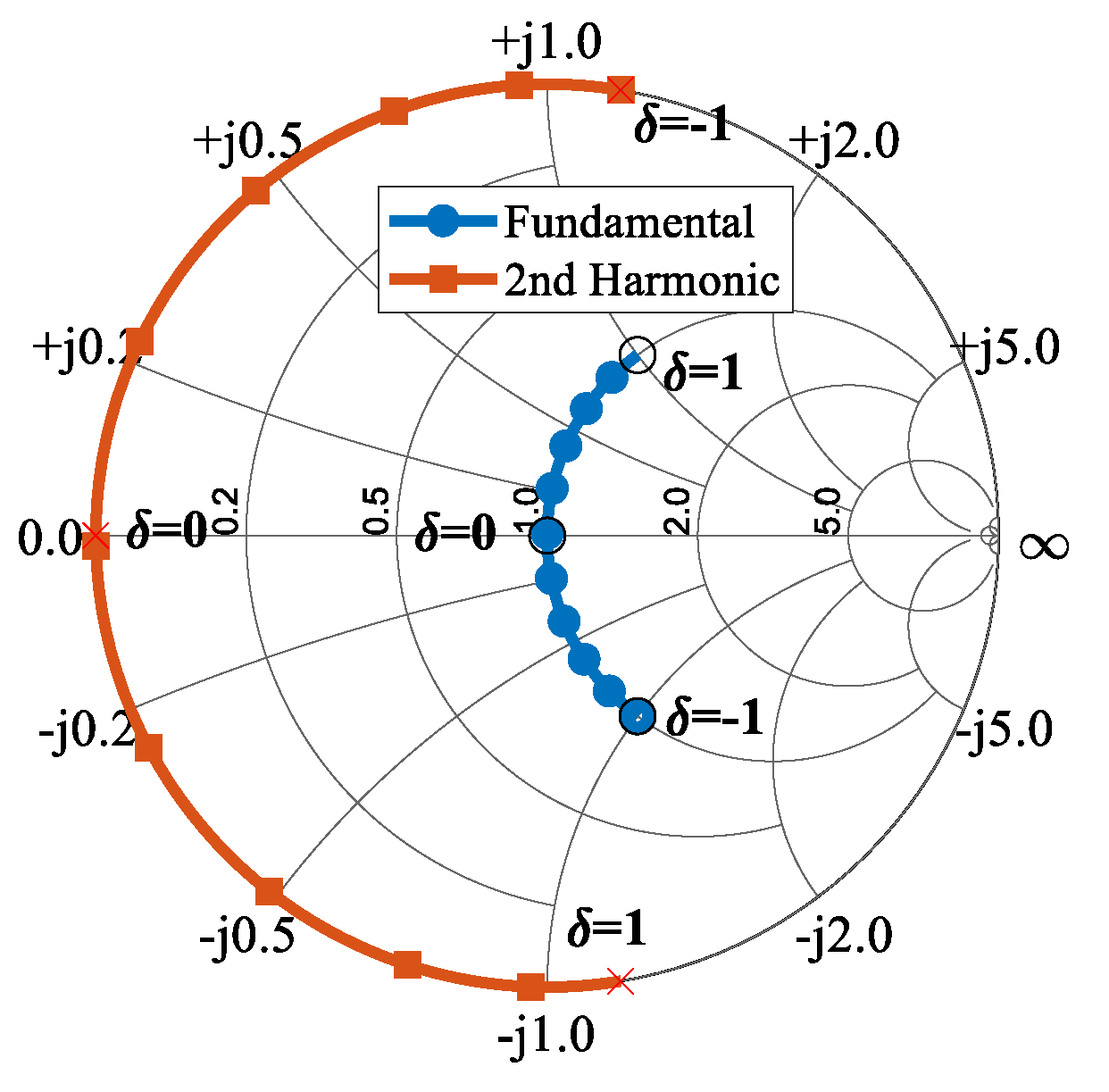
By analyzing the waveforms in the Fourier domain and evaluating harmonic impedances, designers can extend the accessibility of load terminations, thereby enhancing efficiency across a broad spectrum of frequencies. The load trajectory for the fundamental and the second harmonic for class J/B continuum is illustrated on the Smith chart in Figure 6. The corresponding time domain waveform was previously presented in Figure 5. This method involves calculating the trajectory of the load network using Equation (13).

Based on this trajectory, a single load network is then synthesized to satisfy the calculated matching condition. This load network could also be generated by employing hit and trial methods using standard electronic design tools, but it lacks the guarantee of convergence. To ensure a more reliable implementation, two standard techniques have been widely applied: the analytical technique [36] and the real frequency technique (RFT) [37].

The analytical method involves determining the load network’s parameters using filter theory [38]. As it is based on established circuit models and theory, the analytical approach provides a systematic way of designing the load network and ensures good performance and convergence [39].

RFT uses network parameters directly in the frequency domain to synthesize the load network [40,41]. By utilizing actual frequency domain measurements, this approach offers a more accurate representation of the load network’s behavior and impedance characteristics. It is considered a powerful and practical method for synthesizing the load network either through analysis [42] or by using source pull or load pull/source pull measurements [43] and achieving the desired wideband amplifier performance.

Despite the various design techniques available, striking a balance between high efficiency and large bandwidth in RFPAs remains a significant challenge. This difficulty arises due to the inherent trade-offs between these two objectives in amplifier design. Achieving both high efficiency and large bandwidth requires innovative design strategies that carefully balance these conflicting objectives. This might involve hybrid approaches that combine elements of both step and continuous methodologies.

3.3. Space

Finally, considering the power levels at which the RFPA operates efficiently is essential in practical design. In ideal cases when $P_{diss}+\sum _{h=2}^{\infty }{P}_{out,hf}=0$ in Equation (4), efficiency can be expressed as Equation (10).

$$\eta ={\displaystyle \frac{P_{out,fo}}{P_{out,df}}}$$

(14)

Here, $P_{out,fo}$ is the total output power delivered to the load and $P_{out,df}$ is the maximum output power that can be delivered efficiently to the load for the RFPA designed at that level. In this context, the term space refers to the deviation in input/output power levels from the optimal power levels required for efficiently operating the RFPA.

The input/output characteristics of RFPAs are inherently non-linear, displaying linear behavior only at low input drive levels before reaching saturation beyond a certain threshold, as illustrated in Figure 1b. To achieve the best trade-off between efficiency and linearity, the RFPA is operated at its saturation point, denoted as P_in,1dB, where the corresponding output power is P_out,1dB.

In Equation (14), P_out,1dB can be referred to as $P_{out,df}$ without loss of generality. In a similar manner, the efficiency vs. the output power, $P_{out,fo}$, follows a similar trend.

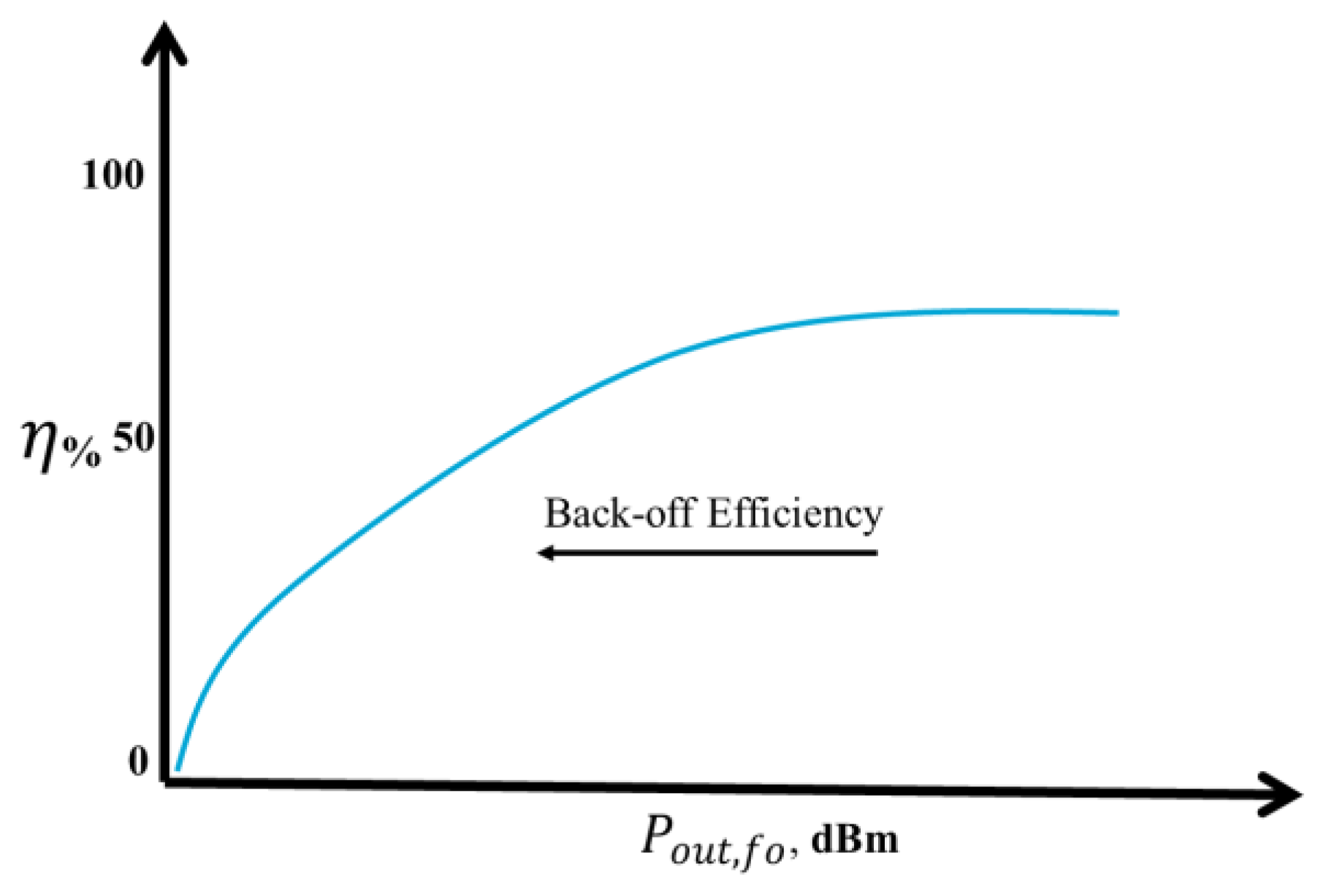
The term efficiency at back-off power is used to describe the efficiency levels of the RFPA when it operates at reduced power levels. In cases involving communication, especially where modulation plays a crucial role, one important metric to consider is the Peak-to-Average Power Ratio (PAPR). As shown in Figure 7, the efficiency of the amplifier decreases significantly below the nominal output power level.

Effective solutions to address these limitations have been developed, with approaches such as supply modulation and load modulation becoming popular, as discussed in Cripps [44] and Arvind et al. [45]. Thus, in an abstract manner, the domain of design space can be sub-categorized into two key subsets: supply modulation and load modulation.

Envelope Tracking is one example of supply modulation technique, while Doherty–Chireix design provides an example of a load modulation technique [45]. Moreover, tunable load networks have also been used by Gamal et al. [46] to deal with the efficiency at the back-off level.

3.4. Category Theory and RFPA

Incorporating the principles of category theory [47] into the analysis of RFPA designs brings a structured approach to examining the interconnections between time, frequency, and space. As pointed out by Henri Poincaré, “Mathematics is the art of giving same name to different objects” [48]. The application of category theory provides a unique lens through which the complexity of RFPA can be unraveled, focusing on three primary analytical dimensions. Further mathematical details about the implications of category theory in RFPA design are outlined in the Appendix A, where an important distinction between the nature of the relations among these three factors (time, frequency, and space) is also emphasized.

For instance, time is represented by the abstract symbol A. Similarly, frequency can be represented by B and design space as C. This abstraction helps to simplify by transforming the complicated RFPA design into a conceptual space where decisions about power, efficiency, linearity, and other critical factors are made. In this context, the morphism functions or mappings between these domains receive specific interpretations relevant to RFPA design and analysis. For example:

i.

A morphism, $f:\mathit{A}\to \mathit{B}$, illustrates the transformations of the signal from the time domain to the frequency domain, similar to calculating the Fourier coefficients to find the ideal impedance conditions required to achieve optimum efficiency levels.

ii.

An identity morphism, $f:\mathit{A}\to \mathit{A}$, highlights the invariant properties within the time domain, such as in case of a Class J/B continuum, where the variation in a certain parameters results in a wide varies of waveforms.

iii.

The composite morphism, $g\circ f:\mathit{A}\to \mathit{C}$, represents the transition across time to space, which describes the process of optimizing the signal parameters to achieve the maximum possible efficiency across varied power and frequency levels.

Translating category theory concepts into practical methodologies within RFPA design not only enriches the existing literature but also paves the way for innovative strategies. At the physical level, the morphisms defined within the context of category theory translate into the techniques that have been developed and documented in the RFPA literature, as well as potential methodologies that could emerge in the future. Such a structured approach provides clarity and coherence in understanding the intricate dynamics of RFPA systems.

Furthermore, this categorization reveals another remarkable advantage: the ability to predict the existence of inverse classes [49] or explore the concept of load modulation in Doherty power amplifiers, as reported by Fishler et al. [50]. This means that potential design solutions or optimizations can be anticipated without the need to delve into extensive and time-consuming design procedures.

4. Generalized Design Approach

Designing RFPAs must always be guided by system requirements and the specific needs of the application, while also considering several inherent trade-offs. Thus, one can imagine a structured modeling procedure that begins with system requirements and encompasses design, analysis, verification and, finally, validation [51]. Figure 8 illustrates this systematic approach, incorporating checkpoints at various stages, which is crucial for ensuring accuracy and efficiency.

Categorizing these various techniques and architectures serves as a stepping stone for the subsequent design phases. The main objective in systems engineering [52,53] is to identify the critical system requirements, namely the frequency and power, along with the time domain description of the signal. For instance, considering whether the signal will have modulation, like in communication systems, or if it will be a pure tone, such as when driving scientific instruments [54,55], is crucial from a systems engineering perspective.

An abstract approach, driven by system requirements, becomes necessary to avoid the unnecessary optimization of design parameters which may not ultimately prove useful or lead to impractical solutions. To simplify the design process of an RFPA, it can be divided into two modules: the horizontal flow, which involves a deep and thorough mathematical analysis followed by simulations, and the vertical flow, where technological tools play a critical role. The flows encompass steps that are purely analytical in nature, requiring the iterative improvement of the topology, and decision-making steps, leading to the final implementation of the RFPA.

4.1. Horizontal Flow

From a designer’s perspective, comprehensively understanding the design process not only requires the standard specifications (efficiency, bandwidth, and gain), but also additional considerations [56]. The process of analyzing and ultimately selecting the proper architecture through mathematical analysis is referred to as horizontal flow in this context.

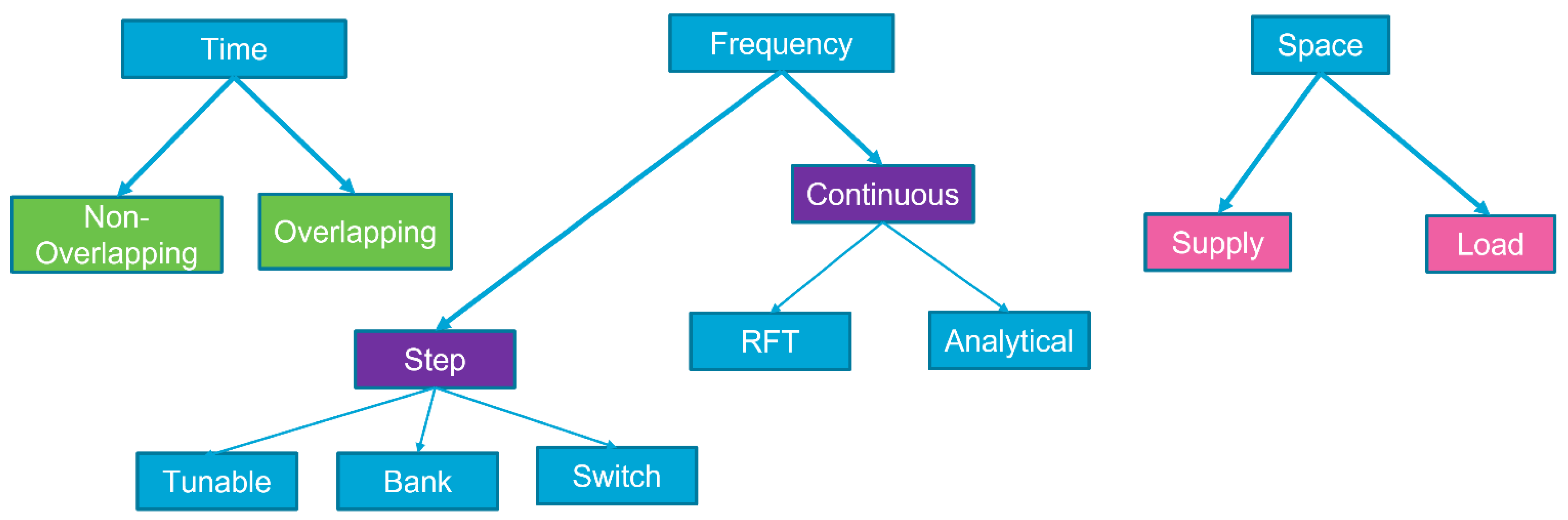
The alternative categorization presented in this work, which is depicted as a tree diagram in Figure 9, offers a new perspective on design principles. To include simplified design insights, any RFPA can be referred to by its time domain waveform, whether it is designed for a range of frequencies or for back-off efficiency levels referred to as space. The union between frequency and space indicates that it can represent either the frequency, the space, or a combination of both.

The tree diagram depicts that on an abstract level, the design of an RFPA is the result of time, coupled with frequency, and space. Here, frequency plays an important role in the bandwidth efficiency trade-off, whereas space plays an important role in the linearity efficiency trade-off. An overview of the cited works categorized using this viewpoint is given in

Table 1. Overview of viewpoint categorization domain proposed in this work with corresponding cited references.

Category Domain	Category Type	Sub-Category Type	Class/Technique	Typical Efficiency	References
Time	Amplifier Class	Overlapping	Class A	25–30%	[4,12]
		Overlapping	Class B	~78.5%	[4,12]
		Overlapping	Class C	~85%	[4,12]
		Non-Overlapping (ZVS)	Class E	60–85%	[4,19,24]
		Non-Overlapping (Harmonic Tuned)	Class F	70–85%	[4,22,44]
		Overlapping	Class J/B Continuum	65–80%	[23,28]
		Non-Overlapping	Continuous Class E	65–75%	[34,35]
		Non-Overlapping	Continuous Class F	65–75%	[29,30]
		Overlapping	Continuous Class AB	55–65%	[31]
		Non-Overlapping	Continuous Class X	60–70%	[32]
Frequency	Design Approach	Step Approach	Tunable Matching (e.g., varactors, banks)	60–75%	[25,26,27]
		Continuous Approach	Class J, F, X, AB, E continuum	60–75%	[28,29,30,31,32,34,35]
	Design Technique	Analytical Design	Filter-based Matching Network	Class-dependent	[36,38,39]
		Real Frequency Technique	Impedance Trajectory Synthesis	Class-dependent	[37,41,43]
Space	Amplifier Class	Load Modulation	Doherty	50–70% at back-off	[44,45]
		Load Modulation	Chireix	~70% at back-off	[45]
		Supply Modulation	Envelope Tracking (ET)	~70% at back-off	[44,45]
		Load Modulation	Adaptive/Tunable Load Matching	60–75%	[46]

.

This flow serves as a valuable guide. The interplay of these three categories for the design of efficient RFPA begins with the selection of required waveforms—either overlapping or non-overlapping. Then, for a wide bandwidth, a step or continuous mode of operation can be used. Lastly, to optimize RFPA efficiency at the back-off level, the load modulation technique, or supply modulation, can be used. With the system requirements clearly defined, the necessary frequency and power specifications can be pinpointed.

4.2. Vertical Flow

The appropriate hardware, which in turn provides the necessary computer models for simulating, verifying, and ultimately manufacturing the final RFPA design, is referred as vertical flow. These models encompass various components like capacitors, inductors, usually the S-parameter files, and non-linear models of the transistors, enabling a comprehensive and effective design process. While the design of an RFPA shares a common approach, the fabrication/physical realization of it can be carried out in two ways.

COTS-based involves the use of readily available Commercial Off-The-Shelf (COTS) components [57,58]. During setup, discrete electronic components, such as transistors, capacitors, and inductors, are combined to construct the power amplifier. This approach offers flexibility and ease of customization but may involve more manual assembly and tuning. It is a practical choice when specific performance requirements need to be met or when cost-effectiveness is a priority.

Chip-based is an integrated implementation that is adopted often in the form of Monolithic Microwave Integrated Circuits (MMICs) or Radio Frequency Integrated Circuits (RFICs) [59]. Here, the entire power amplifier circuit is integrated into a single chip or substrate. This approach streamlines manufacturing, reduces component count, and typically results in smaller form factors. MMICs and RFICs are designed to operate at microwave and radio frequencies, making them well-suited for RFPA applications. They offer advantages in terms of size, consistency, and performance but have limitations in terms of customization and power-handling capabilities.

In essence, the choice between these implementations depends on the specific requirements of the RFPA, including factors such as performance goals, cost constraints, and the desired level of integration. It is essential to consider these options carefully to design RFPAs that meet the intended application’s needs effectively.

On a similar note, while exploring RFPA design, particularly in the medium frequency (MF: 0.3 MHz–3 MHz), high frequency (HF: 3 MHz to 30 MHz), or very high frequency (VHF: 30 MHz to 300 MHz) bands, the practical option often narrows down to utilizing lumped/COTS components. This is because the traditional transmission line becomes impractically large at relatively low frequencies.

In the same context, the choice of transistor type also depends on the specific application. For example, silicon-based BJT (bipolar junction transistor) power transistors do not require negative voltages for biasing, whereas GaN (gallium nitride)-based transistors typically do. If a system lacks a source for generating negative voltages, it is essential to explore designs based on transistors that rely solely on positive voltages. This once again highlights the importance of tailoring the design to meet the specific needs of the application.

4.3. Systems Engineering and Practical Implementation

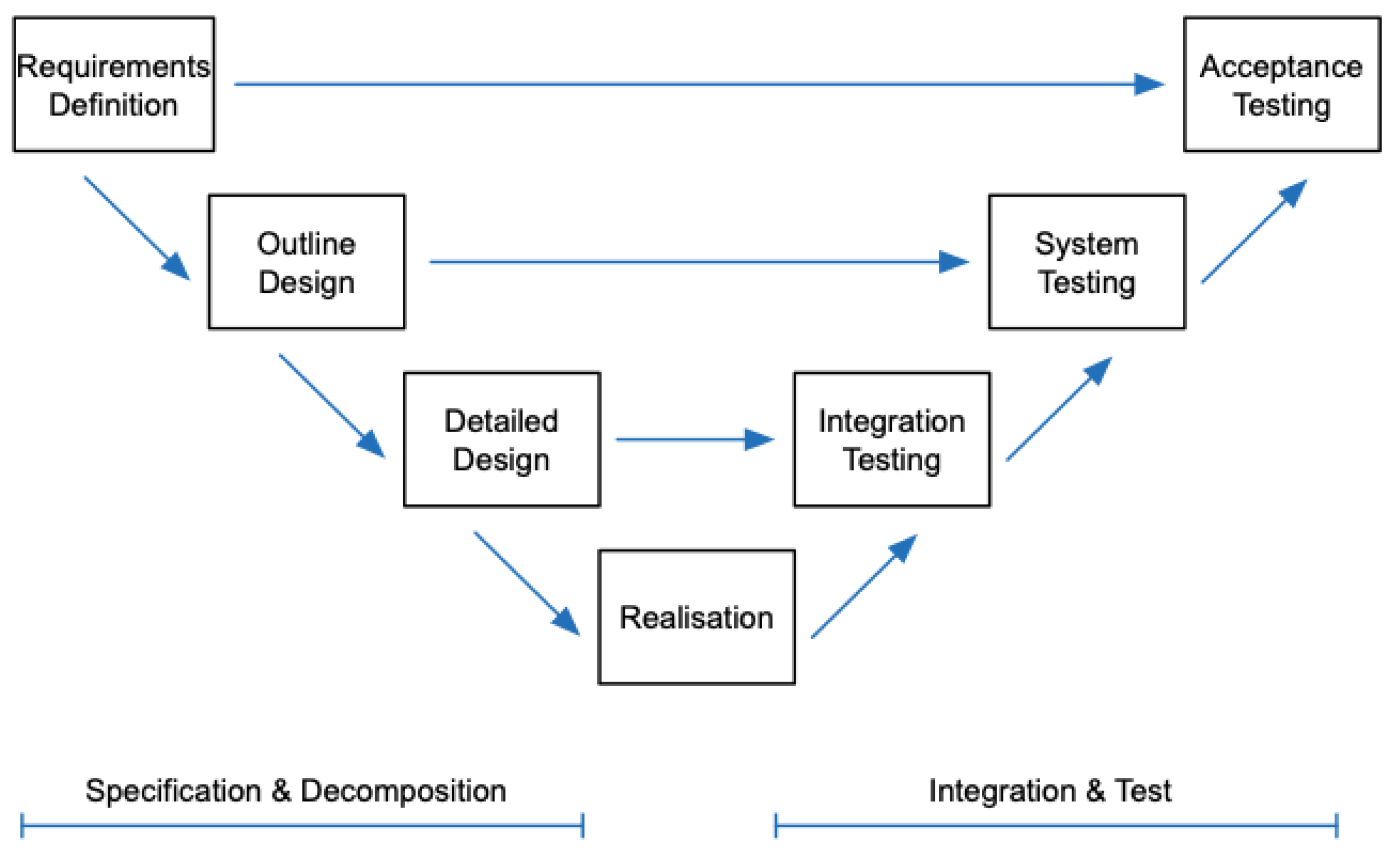
The generalized design flow, as introduced in this paper, shares conceptual alignment with the V-model, which is also known as the verification and validation model used in MBSE [51], where the left leg (horizontal flow) represents domain-specific modeling and architecture analysis, while the right leg (vertical flow) covers implementation, verification, and integration. The horizontal flow of the proposed method incorporates rigorous mathematical modeling and waveform synthesis, corresponding to requirement definition and functional decomposition in the V-model shown in Figure 10. The vertical flow—covering practical realization using components, EM simulation, and system integration—maps to the implementation and verification stages of MBSE.

In addition, this structure aligns with SysML-based MBSE, where system requirements, parametric constraints, and functional behaviors are modeled hierarchically and traced throughout the design flow [52]. Though this work does not employ SysML notation explicitly, the time–frequency–space categories lend themselves well to a SysML modeling framework, enabling traceability between RF performance goals (e.g., linearity, PAPR efficiency) and their respective design components.

4.3.1. Toolchains and Design Procedures

To enable the practical application of this design methodology, specific simulation and prototyping tools are aligned with each phase of the flow. System Modeling and Abstraction: MATLAB/Simulink and RF System Toolbox for top-level link budgets, modulation format simulations, and system trade-off analysis can be used. SysML-based platforms such as Cameo Systems Modeler or IBM Rhapsody can be used for documenting design intent, requirement hierarchies, and performance links.

Analytical and Circuit-Level Design (Horizontal Flow): Keysight ADS and PathWave can be used for harmonic balance, waveform engineering, and load pull optimization [28,33]. MATLAB Symbolic Toolbox and custom Python scripts can be used for analytical derivation of voltage and current waveforms (e.g., Class E/F, J/B continuum) [22,23].

EM Simulation and Realization (Vertical Flow): CST Studio Suite and Ansys HFSS can be used for simulating matching networks, bond wires, and packaging effects in 3D [41]. Non-linear device simulation using Cadence SpectreRF or LTspice can be used for transient validation. Prototyping and Validation: Hardware-in-the-loop (HIL) testbeds using NI LabVIEW, PXI systems, or custom SDR platforms can be used to validate performance under real-time operating scenarios [57]. Load pull systems and vector network analyzers (VNAs) can be used for the empirical validation of impedance trajectories and performance envelopes.

4.3.2. Verification and Traceability

Verification and traceability are critical in system-level RF design. In our framework, each domain—time, frequency, and space—is linked to measurable system-level goals, for example. A communication system may require high efficiency at high PAPR, which maps to optimize back-off efficiency via load/supply modulation (space domain) [44,45].

A wideband radar requires consistent performance across frequencies, directly influencing harmonic termination strategies and continuous-mode waveform design (frequency domain) [28,29]. A scientific instrument that relies on ultra-linear signal reproduction may prioritize precise waveform shaping (time domain) [15,21]. These mappings establish traceable design flows from high-level system specifications to circuit-level implementation, promoting design clarity, modularity, and verifiability within a system engineering framework.

5. Conclusions and Future Work

This paper presents an alternative viewpoint of RFPA design, consolidating established techniques and the literature while introducing a novel categorization approach grounded in category theory. The proposed time–frequency–space framework abstracts the key performance domains—waveform engineering, bandwidth optimization, and power-level adaptability. By distinguishing between analytical (horizontal) and implementation (vertical) phases, this methodology supports systematic trade-off analysis among efficiency, bandwidth, and linearity, tailored to specific application requirements. The integration of a systems engineering perspective ensures traceability from system-level specifications to component-level implementation, enhancing the adaptability and performance of RFPAs across diverse domains such as communication, radar, and instrumentation.

While this paper serves as a viewpoint article, aiming to highlight foundational ideas and conceptual structures, it also opens avenues for deeper inquiry into the practical implications of these theoretical insights. In particular, the scalability of proposed frameworks and the integration of category-theoretic principles present both challenges and opportunities when translated into machine learning applications. The trade-offs inherent in such an integration—between abstraction and implementation, expressiveness and tractability—require careful evaluation. These considerations are especially pertinent when adapting the theory to domain-specific use cases. Future work will aim to address these challenges by developing concrete methodologies that bridge the gap between abstract categorical structures and real-world machine learning architectures, potentially enabling more robust, interpretable, and transferable models.