A Systematic Evaluation of Design Freedoms and Restrictions of Lattice Structures Used as Interlock Bonds

Abstract

Additive manufacturing provides new possibilities in product design compared to traditional manufacturing processes. Particularly additive material extrusion offers the freedom to combine multiple materials in a single component without additional steps. However, combining multiple materials often leads to reduced adhesion, which can hinder the creation of high-strength designs. This issue can be largely mitigated using the geometric freedom of additive manufacturing to produce interlocking structures. This publication investigates the use of lattice structures as interlocking bonds in multi-material applications. The aim is to aid the design of suitable lattice structures by collecting geometric freedoms of lattices, application requirements, and manufacturing constraints, for this information to be used in suitable designs in the future. Initially, the general design freedoms of lattice structures are compiled and explained. Subsequently, these design freedoms are narrowed down based on the specific requirements for interlocking bonds and the limitations imposed by geometry and material combinations during manufacturing. The publication concludes with design recommendations that can be used as the basis for interlock bonds. Suitable lattice designs should aim for high interconnectivity, interconnected porosity, and a high number of similar strut structures, all the while maintaining low dimensions in the interface direction.

1. Introduction

Additive manufacturing (AM) offers significant potential for product design, enabling new design freedoms and introducing new material possibilities, especially in multi-material manufacturing. Among the various AM technologies, additive material extrusion (MEX) stands out for its vast potential to produce multi-material components without additional process steps, thanks to the feasibility of combining different materials within a single layer. However, adhesion at the multi-material interface is typically low, posing challenges for product developers and manufacturers [1,2,3].

Despite this, the geometric and material flexibility of AM can often mitigate these issues. For example, in cases of poor adhesion, interlocking structures can be implemented to change the failure mode from adhesive failure at the interface to cohesive failure within the structure, significantly increasing the maximum load capacity [4,5,6,7,8,9,10,11,12]. This approach makes it easier to utilize material combinations with low adhesion. When using flexible materials, the requirements for such interlocks are more severe, as they tend to require three-dimensional interlocks to prevent extraction of the two interlock halves without breaking.

One example of well-suited 3D interlocks for this task is interlocking lattice structures. These structures have been shown to significantly increase bonding strength in multi-material applications or in adhesive bonds [7,8,9]. However, to fully utilize the potential of interlocking lattice structures for such bonding purposes, it is crucial to understand their design freedoms thoroughly, as their mechanical behavior is highly dependent on their geometric design. Therefore, this publication aims to examine and collect the various design freedoms of interlocking structures on a theoretical basis to aid their application in combining materials with poor adhesive properties into load-bearing structures. The aim is to narrow the vast design space of lattice structures down to a manageable size. This information may then be used to more effectively design interlocking structures for a larger spectrum of applications and broaden the prevalence and practical applications of multi-material AM.

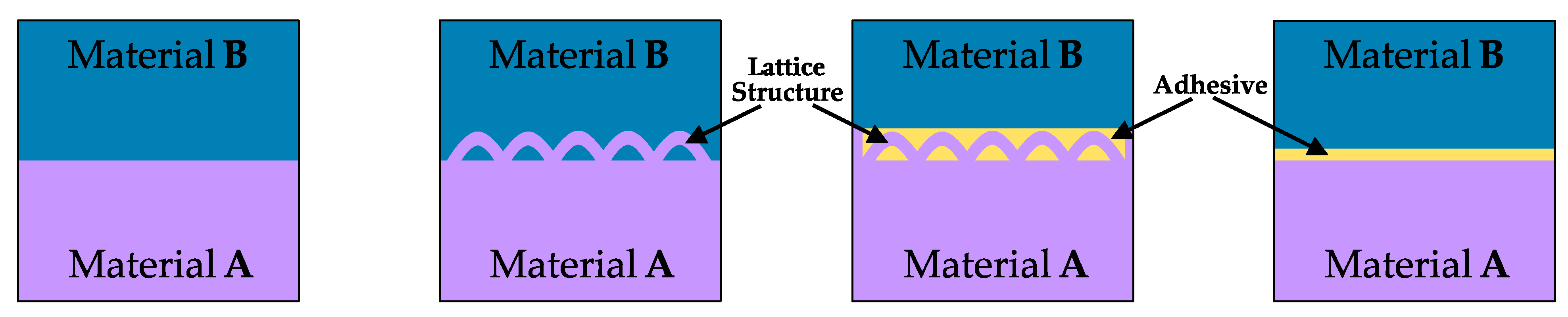
Interlocking bonds can be used for different applications in which low adhesion poses a problem, as depicted in Figure 1. On the one hand, true multi-material additive manufacturing can produce such structures in a single process step. On the other hand, injecting material into the structure in a second step can result in a similar interlocking structure that has been shown to increase bonding strength in adhesive bonding [9]. This publication will mainly focus on the former option of combining two or more materials in a single 3D print, especially regarding combining soft and hard materials.

2. Fundamentals and State of the Art

First, this section will briefly explain additive material as the used manufacturing process, as well as current applications of interlock bonds in MEX components.

2.1. Multi-Material Material Extrusion

Material extrusion (MEX, also known as FFF or FDM) is an additive manufacturing (AM) process that fabricates parts layer by layer by heating and plastifying thermoplastic polymer pre-product. Manufacturing costs of all AM processes are independent of the geometric complexity of the part, and mechanical properties are highly anisotropic due to the layer-by-layer process. By alternating between different extruders or by purging the nozzle with different materials during MEX fabrication, it is possible to combine various materials within the same part and even within the same layer. This capability allows for the manufacturing of multi-material parts without additional processing steps [13].

Using materials with varying properties such as hardness, temperature resistance, or electrical conductivity can be used as an effective means for function integration [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. However, the mechanical properties of multi-material parts produced through this method depend significantly on the adhesive forces forming at the interface. These forces are influenced not only by the materials used but also by the process parameters during printing [38,39,40,41,42,43,44,45,46,47].

2.2. Interlocking Bonding Using Additive Manufacturing

Interlock bonding has been successfully utilized for increasing bonding strength in different applications [4,5,6,7,8,9,10,11,12]. These applications can be categorized into interlocks based on undercuts and complete three-dimensional interlocks. The former typically only shows undercuts in a single direction and can be separated if a single bonding partner deforms [4]. The latter, on the other hand, can never be separated without one partner breaking due to the two sides of the bond being topologically interlinked [7,8,9]. Three-dimensional interlocks are especially useful if the difference in the strength of the two bonding partners is high since the deformation of one partner is to be expected, which could cause undercut-based interlocks to separate.

Lattice structures are one example of such completely interlocking structures. They consist of a regular repeating pattern of unit cells made of plates or struts that typically offer a high performance-to-weight ratio [48,49] and high energy absorption [50,51]. They also provide a high degree of design freedom, enabling the creation of graded structures with finely tuned mechanical behavior [52,53]. Due to their high geometric complexity, these structures are exclusively manufactured using AM technologies. Due to the aforementioned interlocking, they hold significant potential for use in combination with multi-material AM in the form of mechanical locks.

By leveraging the design freedom of AM, these interlocking structures can achieve a high degree of complexity and can surpass conventional methods of enhancing adhesion, such as plasma treatment [9]. However, the behavior of these structures is not well understood, as they exhibit strong anisotropic behavior and often approach the resolution limits of manufacturing machines.

3. Influences on Composite Strength of Interlock Bonds

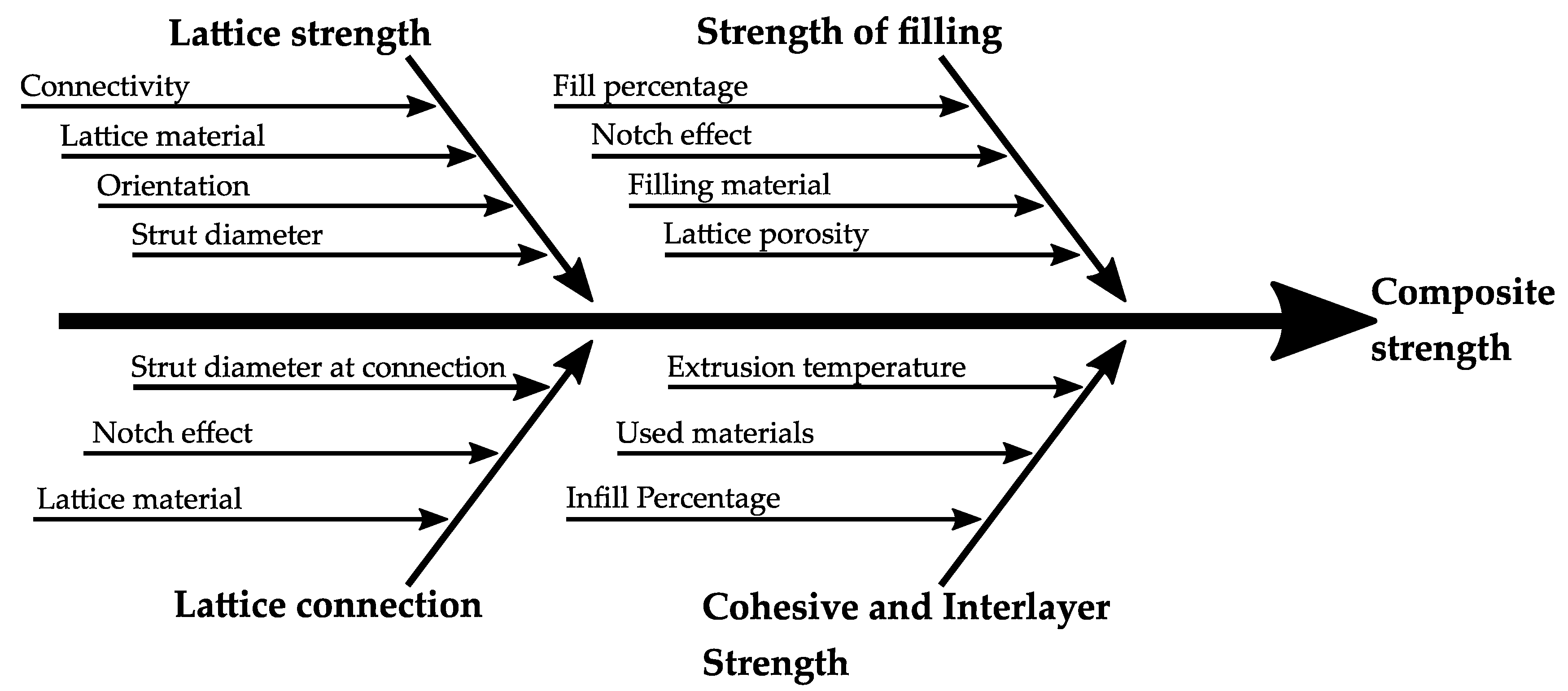
The composite strength of an interlocking bond primarily depends on the weakest part of the bond since the composite will fail if any part of the bond fails. As shown in Figure 2, four main factors contribute to the resulting composite strength, though only three can be influenced by design choices.

Starting from either side of the interlock bond, the cohesive strength in the areas outside of the interlock is determined by interlayer bonding. Failure outside of the bond cannot be meaningfully influenced by the lattice design but can be affected by proper process parameters that influence interlayer bonding, such as extrusion temperature. If failure occurs outside of the multi-material interface (i.e., in the area where only a single material is present), it indicates that the interlock bond withstood more force than the rest of the component could handle. This means that further improving the strength of the interlocking bond would not benefit this particular application since failure would once again occur at the weakest point of the component, i.e., the same position in the single-material area.

The next possible failure point is the fill of the lattice, which consists of a second material manufactured with MEX. Since the fill and the lattice intertwine in three dimensions, adhesive failure cannot cause separation of the interlocking structure without additional cohesive failure in the fill. While strong deformation can cause adhesive failure in the interlocking structures, forces can still be transmitted through the mechanical interlock in that case. Hence, to maximize composite strength, the fill’s strength needs to be maximized by reducing stresses within it. This can be achieved by increasing the cross-sectional area, increasing the fill volume, reducing the notch effect at the interfaces between fill and lattice, and ensuring complete fill without defects or air bubbles.

Another possibility is failure that occurs in the lattice or its connection to the rest of the second substrate. Although lattice strength can be increased by increasing connectivity or rod diameter, this would decrease the fill’s strength by reducing its occupied volume. Hence, a design conflict exists where the optimal composite strength results from balancing lattice strength with fill strength.

The last potential failure point is the connection between the lattice and the rest of the first substrate or correspondingly between the fill structure and the second structure. If the lattice strength, fill strength, and adhesive strength at the substrate are sufficiently high, the connections to the substrates will fail. This can be prevented by increasing the strut diameter at the connections (or correspondingly increasing the pore size at the top) or reducing the notch effect at these locations, again encountering the same design conflict as before.

It becomes clear that, apart from material combination, the design of the lattice is the most important factor contributing to the strength of an interlocking bond. To design structures well suited for the application, it is essential to have knowledge of all design levers and apply them appropriately.

4. Design Freedoms of Interlocking Lattices

To make an informed decision regarding geometries that can be used for interlock design, it is essential to systematically evaluate the design freedoms offered by lattice structures first. This evaluation is conducted for all possible lattice structures in the following section. The identified design freedoms of lattice structures are subsequently refined in later sections, considering manufacturability in relation to MEX and the practicality of interlocking bond applications.

4.1. Cell Structure

When evaluating the use of lattice structures as interlock bonds, it is important to first consider the advantages of different types of cell structures. While technically, only periodically repeating structures form ‘real’ lattices, stochastic and quasiperiodic structures share many properties with periodic lattices and hence should be considered alongside them.

The geometric freedoms of periodic lattice structures are best assessed based on the Bravais lattices based on crystallography. They describe all possible arrangements of points that can be repeated infinitely in 3-dimensional space. When connected to a lattice graph, these points create all possible arrangements of strut-based lattice structures. Each lattice mathematically consists of periodic lattice points, which are described by t(u, v, w) = u × a + v × b + w × c with u, v, w being integers and a, b, c, being the basis vectors of the lattice, repeat infinitely. All possible lattices can be categorized into 14 Bravais lattices according to their symmetry, which in turn can be sorted into 7 lattice systems. Each lattice point in these lattices is identical with regards to symmetry to each other lattice point. Hence, the addition of face- or body-centers restricts the possible geometry of the lattice, as shown in Figure 3 [54,55].

To create physical lattice structures from those mathematical lattice types, the cells must be populated with structural components based on the same or a higher symmetrical class. Besides symmetry, the behavior of lattice structures depends heavily on the geometry of the repeated unit cell. To maintain lattice symmetry, this cell geometry must follow the same symmetrical restrictions as the corresponding lattice type, lest the symmetry collapses into a less symmetrical Bravais lattice. Due to the periodic nature of lattices, the origin point can be chosen arbitrarily; however, to simplify the discourse, we will assume that the cell geometry goes through the origin. Due to symmetry, each other lattice point within the unit cell must be part of the cell geometry as well.

Furthermore, to create only a single lattice, we will assume that the geometry of the unit cell is one connected volume structure. This means that once the cell geometry is repeated ad infinitum, all other lattice points are also part of the emerging space-filling structure. The same holds for equivalent cell edges or cell faces–all equivalent points remain equivalent no matter their placement in the lattice. For example, if a point on one face of a cubic face-centered lattice Figure 3(cF) is part of the structure, all points at the same spot on all cubic faces as well as all corners also must be part of the lattice and are completely indistinguishable from each other. Additionally, since all structures inside of the cell must be connected to the lattice structure in some way, they must also be connected to the origin. This means that no matter the lattice type, all corner points are connected to the lattice, and all points inside a unit cell are connected.

4.2. Cell Type

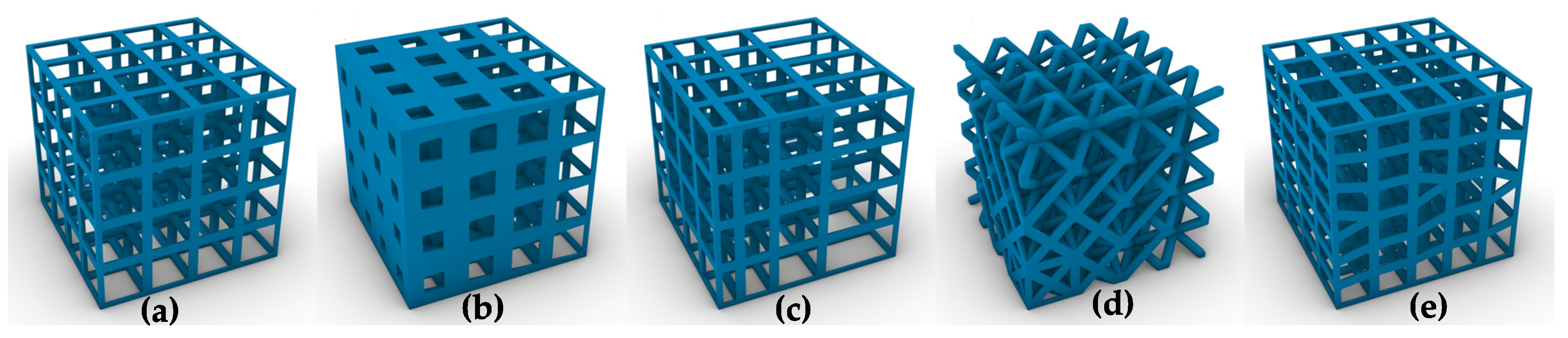
Based on these restrictions, three different types of lattice structures are possible. If the emerging lattice graph is populated by linear struts as interconnections, the forming lattice will be called “1D-based”, while “2D-based” lattices form if the interconnection is implemented through shell structures. More complex structures based on volumes will be called “3D-based”. Examples of these three types are depicted in Figure 4.

Applications of these types are radically different. Since the emerging lattice based on these structures behaves differently, a possible use case must be taken into account when choosing between the three. One-dimensional-based lattices have large areas of interconnected empty space. In addition, their interconnectivity can easily be tailored, which affects mechanical behaviors like rigidity. Two-dimensional-based lattices can form more than one separate area of interconnected empty space or many non-connected pores. However, the structure is usually strongly interconnected, which makes tailoring the mechanical behavior more difficult. Three-dimensional-based lattices have the least design restrictions and, hence, can form a wide variety of structures with hugely different behaviors. Hence, no simple statement can be made in regard to these structures. However, many cases of 3D structures can show similar designs as 1D or 2D-based cells. The structure shown in Figure 4c, for example, can either be thought of as a cube with a sphere-shaped hole or as a cubic strut-based lattice with peculiar node and strut shapes, and hence is similar to a 1D-based cell. Therefore, the structure depicted in Figure 4c. is expected to behave similarly to a simple cubic lattice consisting of cylindrical struts due to similar interconnectivity and pore configuration.

Due to the nature of their unit cells not being filled, lattice structures inherently exhibit some degree of porosity. In an ideal lattice structure devoid of boundary effects, the porosity of both the lattice structure and the unit cell are identical, being solely determined by the unit cell’s geometry. This porosity can vary based on the elements constituting the unit cell. For example, line-based unit cells typically exhibit open porosity in all directions (except in cases where lines fuse due to their thickness). Conversely, shell and volume-based cells can display a range from fully closed to fully open pores, as illustrated in Figure 5.

Unit cells that resemble extrusion elements, such as honeycombs or the structure shown in Figure 5b, generally exhibit porosity in only one direction. When these extrusion-based elements are oriented differently but remain unconnected, the result is multiple unidirectional porosities that are also not interconnected. By interconnecting these one-dimensional structures, it is possible to achieve porosities in one, two, or multiple directions with shell or volume-based cells.

The porosity of the structure, whether open or closed, is crucial for many applications as it influences the mechanical behavior and stress distribution within the lattice structure, as well as its permeability. This permeability is particularly important for applications requiring infiltration, and hence, open porosity is a key requirement for creating interlock bonds.

4.3. Structural Rigidity

The mechanical behavior of strut-based lattice structures is largely influenced by their interconnectivity. The stiffness of these structures is determined by the number of connections (struts) and points (nodes), which can be calculated using the Maxwell criterion. This criterion is represented by the equation [57,58]:

M = s − 3n + 6

where s stands for the number of struts and n represents the number of nodes.

If the Maxwell number (M) is less than zero, it indicates that the system of struts has more degrees of freedom than constraints, resulting in flexible or under-stiff behavior. Conversely, if M equals zero, the structure has an equal number of constraints and degrees of freedom, making it just-stiff, with rigid behavior and no internal stresses. When M is greater than zero, the network is considered over-determined and behaves in an over-stiff manner.

Under-stiff structures show high compliance and tend to be weak, exhibiting bending-dominated behavior due to their excess degrees of freedom. However, since interlock bonding demands high stiffness and low weight, under-stiff lattices cannot be used. Furthermore, the higher the strength-to-weight ratio, the less volume the lattice takes up within the bonding zone. Consequently, more volume is taken up by the interlocking fill structure, increasing its strength and, therefore, the strength of the whole bond. Just-stiff and over-stiff structures, on the other hand, have very low compliance and high strength because of their limited degrees of freedom, resulting in stretch-dominated behavior. Over-stiff structures, in particular, further reduce compliance due to strut redundancy, making them desirable for many lattice structure applications.

When determining their strength regarding the Maxwell criterion, lattices always need to be considered whole, as neighboring cells usually have a stiffening effect on each other. Hence, a single unit cell may have a Maxwell number less than zero and thus be considered under-stiff, even though the structure may turn out to be over-stiff once the criterion is applied to the periodic lattice as a whole. For instance, a cubic unit cell with eight corner nodes and the corresponding edge struts, along with a single body diagonal strut, as shown in Figure 6, may appear under-stiff with a Maxwell number of −5.

However, when considering that each node and strut is part of multiple unit cells within the lattice structure, the mechanical properties become reliant on the quantity and configuration of these unit cells within the lattice. In an infinite arrangement, each corner node is part of eight distinct unit cells, while each edge is part of four unit cells. Similarly, structures located on the faces of the unit cell are shared between two adjacent unit cells, whereas those contained within the cell are not shared at all. Through normalizing, the number of struts and nodes can be adjusted to new values, denoted as s₀ and n₀, representing the effective count of struts and nodes within each cell, considering all surrounding cells.

Therefore, for a significantly large number of unit cells (N), the Maxwell criterion can be modified to:

M = N × s₀ – N × 3n₀ + 6

To determine whether a structure is over-stiff or under-stiff, only the sign of the Maxwell number (positive or negative) is relevant. Hence, both sides of the equation can be divided by N. As the number of unit cells increases, the constant term approaches zero, and consequently, the equation simplifies to (with M’ = M/N):

M′ = s₀ − 3n₀

Using this equation, sufficiently large lattices can be categorized by only considering the unit cell. This way, seemingly under-stiff unit cells can be shown to combine into an over-stiff lattice structure when considering the interconnection and arrangement of multiple unit cells.

4.4. Orientation

To enhance stiffness, not only the number and types of struts but also their orientation and placement are crucial factors. Struts exhibit greater resistance to tensile and compressive loads than to bending, making it advantageous to orient them such that the angle between the struts and the load direction is minimized. The simplest method to achieve this is by rotating the lattice, although other strategies are also viable. In cubic lattices, all edges form right angles with each other, while face diagonals and body diagonals form angles of 45° and 35.3° with the cubic faces, respectively. By distorting the unit cell, these directions can be adjusted to better suit specific applications, as the selection of unit vectors determines the angles and orientation.

Based on the Bravais lattices, the least restricted unit cell shape without right angles or equal-length sides is a parallelepiped. By aligning the three unit vectors with the primary load directions, the displacement of the struts can be minimized. Additionally, parallelepiped cells can be individually distorted, provided their corners still align with neighboring unit cells. Although the resulting structure technically no longer qualifies as a lattice (due to the loss of long-range order), it retains many lattice-like characteristics due to its repeating nature. An example of this distorted structure is illustrated in Figure 7c.

4.5. Density Gradients

To enhance lattice stiffness, controlling the density along the load path is crucial, as stiffness and toughness are primarily influenced by density. Several methods exist to modify cell density: altering strut or shell diameters, adjusting cell size, introducing displacements, or changing the unit cell by modifying the number of struts. These density gradient methods are illustrated in Figure 7.

4.5.1. Strut Diameter and Shell Thickness

The simplest way to adjust lattice density is by changing the strut or shell diameter, as shown in Figure 7b. For cells with low density, where overlapping volume is negligible, lattice density is proportional to shell thickness for shell-based structures and the square of the strut diameter for line-based structures. As overlap increases, the relationship becomes more complex, with the density approaching 100%.

4.5.2. Cell Size

Density can also be adjusted by changing the cell dimensions while keeping the strut or shell thickness constant, as shown in Figure 7c. If parallelepiped cell angles remain constant, cells in each row along the x-vector must have the same y- and z-dimensions. For large, non-overlapping cells, density is inversely proportional to the cell dimension or, equivalently, to the cube of the side length if all side lengths scale equally. When cell size decreases and overlap becomes significant, the density behavior changes, approaching a fixed value based on lattice geometry. This relationship results in a linear correlation when cell size is expressed as the number of cells in a fixed volume. When cell dimensions change equally in all directions, the relationship for strut-based cells becomes quadratic.

As explained above, distorting cell dimensions also changes the angles within the unit cell and might, therefore, affect mechanical behavior in an unintended way.

4.5.3. Unit Cell Modification

Lattice density can also be adjusted by adding or removing struts or shells from the unit cell, as can be seen in Figure 7d. The resulting density varies based on element type, orientation, and thickness. In low-density cells with minimal overlap, the volume fraction is roughly proportional to the sum of strut lengths or shell areas. While the lower bound for density is reached once no more struts can be removed without disconnecting cell corners, density can still be increased by adding shell elements or curved lines even when all connections between lattice points are present. Although modifying the unit cell in this way is less efficient for density adjustment than changing diameter or cell size, it can be beneficial for specific applications, such as reinforcing areas under load, without significantly increasing overall structure weight.

4.5.4. Displacements

Lattice structures can incorporate dislocations similar to real-world crystals, as shown in Figure 7e. Adding half-planes with non-parallelepiped cells at their edges allows for incremental changes in the number of cells within a given volume. However, these wedge-shaped added cells must fit neighboring cells, causing surrounding cells to warp to maintain spatial continuity. This once again changes the angles within the distorted cells. Adding displacements increases cell number while dimensions stay constant, similarly affecting density as described for cell size changes.

4.6. Combination of Methods or Lattices

All methods of altering density are independent and can be applied simultaneously, offering a vast design space for using lattice structures in technical applications. Optimizing a component’s density distribution can be implemented using one or more of these methods.

While this publication focuses on using lattice structures as a basis for interlock bonds, other applications of lattice structures, especially when combined with gradients, are also possible. Gradients allow for fine-tuning of mechanical properties, enabling adjustments to structures for various load cases. By combining several load-specific gradients in different directions, multiple load cases can be considered during the design process, as illustrated below.

Furthermore, different lattices can be combined using Boolean operations while ensuring proper orientation of the relevant struts, as described above. Each partial lattice can then have gradients applied to it separately, guaranteeing proper load transmission for each specific load case, as depicted in Figure 8.

5. Restrictions of Interlocking Lattices Manufactured with MEX

The following section will narrow down the design freedoms stated above based on the specific requirements for interlocking bonds and the limitations imposed by geometry and material combinations during manufacturing. The goal is to arrive at a set of rules that, when met, should provide a good fit for the design of interlock bonds.

5.1. Restrictions in Regard to Function

The implementation of lattice structures as interlock bonds imposes several design constraints, primarily stemming from the required mechanical behavior of the bonds. To minimize the volume needed for the interlock, the strength of the bonds should be maximized, with energy absorption being a secondary consideration. This necessitates a specific design of lattice structures in regard to the freedoms discussed above.

5.1.1. Cell Structure and Orientation

To minimize the volume taken up by the interlock bond, the cell structure should ideally have minimal height. Preferably, a single layer of cells or even half-cells should be used so that the volume occupied by the bond is minimal. As the interlock forms in this very first layer, it is assumed that every additional layer has a decreasing contribution to the bonding strength or even reduces strength by increasing the number of possible failure points. The latter is expected to be especially relevant when the two interlocking materials have very similar strengths.

The symmetry of the cells should ideally follow the symmetry of the load cases. Depending on the load type, different symmetries can be reasonable. Since tensile or compression loads put almost equal stress over the whole cross-sectional area of the bond, a bond optimized for such loads should show a high level of symmetry in the xy-direction and avoid areas of stress concentration. Shear loads in adhesive bonds, on the other hand, form a parabolic stress distribution in the z-direction with a peak at the overlap [59]. However, the case presents more complex interlock bonds since the paths the forces take are likely influenced by the geometry of the lattice. Lastly, peel loads will always apply a line load to the lattice. To avoid load peaks, ideally the lattice should avoid sudden geometric changes perpendicular to the line direction. This is impossible, however, as each strut or wall constitutes such a change. Hence, a steady number of small changes should be preferred. This means a larger number of struts and a lattice with no unit vectors along the line load direction are desirable.

To increase strut count while maintaining porosity, the cells should be as small as possible in the xy-direction. Subsequently, the forces transmitted through each strut are lower, and failure of a single strut has less effect, reducing the chance of cascading failure.

5.1.2. Cell Type

Ideally, unit cells for interlock bonds should exhibit interconnected porosity in three dimensions, as this is the only way to form non-separable undercut areas of two materials with highly different Young’s moduli. Line-based unit cells are particularly advantageous for interlock bonds because they are straightforward to design and predict, and they form three-dimensional interlocks in almost all cases.

Furthermore, the bonds should possess high strength in multiple directions and load cases, indicating the need for a symmetric design. Additionally, eliminating certain failure modes is crucial to enhancing the bonding strength to the greatest extent possible. Uniformity of stresses is the most crucial factor, as failure of only a single strut leads to overburdening of the surrounding structures and cascading failure. Hence, the lattice should be as uniform as possible to distribute stresses as evenly as possible. This means that different types of struts should be avoided, and the lattice should consist of only a single type of strut (horizontal edges, vertical edges, face diagonals, or body diagonals). This also means that, in most cases, gradients are not worthwhile.

5.1.3. Dimensioning and Pore Size

In an interlock bond, the weaker partner determines the overall bond strength. Moreover, enhancing the lattice strength by adjusting its dimensions typically reduces the strength of the interlock partner, and vice versa, as the available volume changes. Consequently, lattice dimensions should be selected in such a way as to ensure that its strength matches that of the interlocking structure, maximizing the overall bond strength. Since the strength of both partners is influenced by the mechanical properties of the materials used, no straightforward conclusion can be drawn without knowledge of the materials. Therefore, the final choice of dimensions must be validated through experiments or simulations. Since the interlock forms through pores inside the lattice, pore size is a crucial factor, especially in cases where the interlock forms not through layered manufacturing but through injection. In cases of high-viscosity materials being injected, larger pores are expected to have a positive impact, as they likely can achieve more complete filling.

5.1.4. Structural Rigidity

Complex stress states, and anisotropic behavior within the lattice should be avoided, as they result in stress concentration in certain struts, which can lead to cascading failures when the critical stress of one strut type is exceeded, therefore overloading the remaining struts. Therefore, it is advantageous to include only a single type of strut in the interlock bond if possible.

For interlock bonds, stretch-dominated behavior is a desirable trait since the strength of the bending-dominated lattice is lower. Structural rigidity criteria dictate that the behavior of lattices is significantly influenced by their interconnectivity and the strut-to-node ratio. Using only a single layer of cells (explanation above) inherently results in low interconnectivity, making the Maxwell criterion the only pertinent guideline for designing rigid interlocking structures. Given that bonding areas are typically extensive, requiring lattice structures to encompass a substantial number of cells, the constant term in Maxwell’s equation becomes negligible. Thus, a strut-to-node ratio of at least 3:1 should be maintained.

To achieve this, it is necessary to prioritize certain strut types over others, as the overall number of struts must be minimized to achieve large pore sizes, and certain strut directions yield higher connectivity. Consequently, only strut types with high connectivity should be selected. Among all possible options, edge struts exhibit the lowest strut-to-vertex ratio of 2:1 and should, therefore, be excluded from interlock bonding structures. Furthermore, the anisotropic behavior of edge struts can lead to premature failure under load, resulting in cascading failures that must be avoided. Most importantly, vertical struts show no undercut and, therefore, are useless for creating interlocks. Hence, their inclusion does not sufficiently enhance structural strength to a degree that warrants the reduced space available for the interlock partner.

Similarly, face diagonal struts should also be avoided, though with slightly less urgency, for analogous reasons. Including a single diagonal into the face of the cubic structure increases the number of struts while not affecting the number of nodes, therefore increasing interconnectivity; however, adding second diagonals into the same cubic face requires an additional node at the face center and does not further increase lattice connectivity while introducing additional failure points. While a cubic structure with no diagonals has a normalized Maxwell number of M’ = 0 (i.e., behaves just-stiff when the structure is infinite), a cubic structure with a single diagonal on each face has a normalized Maxwell number of M’ = 3 (i.e., is stiff) while a structure with two diagonals on each cubic face also has a normalized Maxwell number of M’ = 3. Although horizontal face diagonals provide a large undercut area, they typically require a second row of vertices, which contradicts the requirement of a single layer of struts. Body diagonals exhibit the highest connectivity, making them the preferred choice for interlock bonds. Including a single body diagonal once again adds struts without requiring additional nodes, increasing interconnectivity and making it a safe choice. Furthermore, adding more body diagonals into the structure never decreases interconnectivity, even if an additional node is required. A structure with a single body diagonal has a normalized Maxwell number of M’ = 1. Structures with two, three, or four body diagonals result in values of M’ = 1, M’ = 3, and M’ = 5, respectively, making all of them over-stiff. Experimental results demonstrate that structures composed exclusively of body diagonals exhibit excellent mechanical performance and provide sufficient undercut area to ensure robust interlock bond strength [60]. Although specific use cases may require additional struts, body diagonals should be prioritized and included in almost every lattice designed for interlock bonding applications.

5.1.5. Gradients

While gradients exhibit significant potential for tailoring the mechanical behavior of lattice structures to specific load conditions, interlock bonds are not expected to benefit from density gradients. In these scenarios, density gradients cause local weakening in one portion of the interlock while simultaneously strengthening the other. Because the composite strength is determined by the weakest element of the interlock, the presence of density gradients ultimately results in a reduction in overall composite strength for these types of loads. In most cases, the formation of cracks in the weakened portion seems to be the limiting factor and uniform stress distribution overall shows better results [7,8].

5.1.6. Lattice Base and Top

If the lattice and filling are strong enough, failure will move out from the lattice to the base or the top. To avoid failure due to crack formation at the base of the lattice, all struts of walls should be well-rounded to avoid a notch effect. Similarly, the top of the lattice can lead to crack formation in the interlock partner. Hence, the top of the lattice should show curvature as well (typically at nodes connecting several struts). This is especially important, as notches will occur between layers in any case due to layer-by-layer manufacturing.

5.2. Manufacturing Restrictions in Regards to Geometry

Restrictions regarding the manufacturability of lattice structures are dependent on the utilized manufacturing process and manufacturing machine. These restrictions can predominantly be expressed as dimensional restrictions that are multiples of line width or layer height. The academic literature provides extensive guidance regarding design for additive manufacturing. Due to the relationship between manufacturing machine and design restrictions it is impossible to exhaustively list all restrictions. Hence, the following is not a comprehensive list but provides a brief overview of relevant design restrictions for lattice structures manufactured by MEX. Interested readers should refer to relevant literature for detailed design rules [61,62,63,64,65,66,67].

5.2.1. External Radius of Single-Curved Elements

The external radius should be large enough so that each layer of a component is built up from a contour with an inscribed grid (r_a ≥ 1.5 mm) [61] (rule 12).

5.2.2. Internal Radius of Single-Curved Elements

The internal radius should be sufficiently large to prevent the inner sides of the elements from closing (r_i ≥ 0.3 mm) [61] (rule 13).

5.2.3. Length of Single-Curved Elements

The length of unsupported single-curved elements should be short enough to prevent deformation or excessive vibration. The critical length depends on the overhang angle. (l ≤ 10 × r_a (for α = 45°) or l ≤ 20 × r_a (for α = 90°)) [61] (rule 13).

5.2.4. Firmly Bonded Element Transitions

Edges should be rounded with a radius corresponding to the outer/inner radius of simply curved elements (r_k = r_a ≥ 1.5 mm or r_k = r_i ≥ 0.3 mmrk = r_i ≥ 0.3 mm) [61] (rule 30).

5.2.5. Surface Angles

The surface angle of downward-facing surfaces should be large enough to avoid the need for solid support structures (α ≥ 35°) [61] (rule 52).

5.3. Manufacturing Restrictions in Regards to Material

Different materials exhibit different demands in regard to a variety of process parameters. These different requirements further restrict the possible designs of multi-material lattice structures. Once again, a non-comprehensive list shall provide an overview of relevant material-dependent restrictions.

5.3.1. Build Chamber or Build Plate Temperature

To reduce warping some materials are usually processed using a heated build plate or build chamber. This might pose a problem in multi-material prints when the required build chamber temperature of one material exceeds the heat deflection temperature or even the decomposition temperature of the second material. In such a case, designs need to take into account that lowering the build chamber temperature can increase warping. Hence, designs need to be more resilient against thermal stresses, e.g., by increasing corner radii, etc.

Similar problems might arise when different build plate temperatures are required for the different materials. However, this restriction is typically confined to only the first couple of layers that experience the temperature of the build plate.

5.3.2. Interface Adhesion

Two materials used in the same MEX process can form two different types of interfaces based on the orientation of the interface.

Vertical interfaces form when different materials are used in the same layer. Since lines of molten material are usually placed onto an existing layer (or onto the build plate in the case of the first layer) they mainly stick to already structures consisting of the same material located underneath. Since adhesion is high in such cases, the moving nozzle does not exert enough force to pull the extruded structure off, and consequently, it stays in place.

However, if two different materials are used in consecutive layers right on top of one another, the adhesion at the material interface becomes crucial. The interface can only be manufactured if adhesion is strong enough to keep the extruded structures in place. Even if geometric structures like mechanical interlocks can stop adhesive failure from occurring, such structures only form through the addition of more than one layer and hence serve no benefit in the interface layer. While additional measures are possible, like plasma treatment or the inclusion of a layer consisting of a third material to promote adhesion, they require special equipment (i.e., a plasma nozzle integrated into the manufacturing process or special printers capable of using three or more materials). In practice, these solutions are rarely applicable, and in most cases, insufficient adhesion results in an incompatible material combination.

As a result, the minimal requirement for the formation of interlock bonds is adhesion sufficient to survive the manufacturing process for at least a couple of layers. Once the interlock has formed, forces are mainly transmitted via mechanical interlocking, and adhesion becomes irrelevant.

6. Recommendation for Lattice Design for Interlock Bonding

Based on the restrictions listed above, factors for good lattice design can be stated, and the design space of lattices for mechanical interlock bonding can be reduced to a manageable size.

Since the number of different strut types is to be reduced, connectivity should be as high as possible to achieve stretch-dominated behavior. Body diagonal struts are well suited for this task, but other strut types are applicable as well, as long as the interconnectivity of the resulting lattice is high.

The number of struts in z-direction should be minimal to reduce the number of failure points. Hence, ideally, a single layer of struts is used. The base and top of this lattice should be well-rounded to avoid a notch effect and crack formation.

To produce equal behavior in all directions, each strut should show a similar angle. Hence, a lattice consisting of only a single type of strut with a side ratio close to 1:1 seems like a good option. Minor adjustments might be necessary to avoid incomplete cells (and, therefore, differently behaving struts).

The dimensioning of such lattices highly depends on the manufacturing restrictions resulting from the utilized 3D printer. These restrictions mainly influence cell size and strut diameter.

While smaller cell sizes are beneficial due to the higher number of struts, in the case of MEX, the strut diameter should be larger than 6 times the line width to maintain manufacturability. A typical line width is 0.4 mm, resulting in a minimal strut diameter of 2.4 mm.

While the height of the structure should be kept as low as possible, all strut directions must exceed the minimal overhang angle in order to minimize the low adhesion overlap of different materials. Assuming body diagonal struts are mainly used in the lattice, the ratio of cell height to cell width is important, as it determines the angle of all non-edge struts. The relationship between the overhang angle and the full cell dimensions x, y, and z of body diagonals is given through $\mathit{tan}\alpha ={\displaystyle \frac{z}{\sqrt{x^2+y^2}}}$. For example, assuming a quadratic cell base and a critical overhang angle of 30° (a typical value for MEX machines) results in a minimal cell height of 0.82 times the cell width to ensure manufacturability, see Figure 9.

As mentioned above, the exact dimensioning of such structures depends on the load case and the materials used. Since there are different possibilities to manufacture such lattice structures and form an interlock, the number of possible material combinations is quite high.

Manufacturing of these structures can be accomplished with a variety of AM processes. While the manufacturing restrictions in this publication focus on MEX, adjusting the restrictions according to other processes like powder bed fusion or vat polymerization is easily possible, even while true multi-material manufacturing is significantly more difficult with these processes. This only matters, however, if the interlock is to be formed by multi-material AM.

If an adhesive or a second material is injected into the lattice structure, where it hardens [9,68], producing such structures is by no means restricted to AM processes with multi-material capability.

7. Conclusions and Future Prospects

Additive manufacturing, particularly through additive material extrusion, offers unprecedented flexibility in product design by enabling the integration of multiple materials into a single component without requiring additional steps. Even though interlocking lattice structures can address the challenge of reduced adhesion between different materials, such geometries are rarely used for this purpose. This may be partially due to the large design space, which makes creating well-suited structures difficult.

For this reason, this study has collected the geometric freedoms inherent in lattice structures and additive manufacturing, taking into account the specific requirements and constraints of multi-material applications. The approach involved narrowing down the general design freedoms of lattice structures to address the unique challenges of interlocking bonds and the limitations imposed by both geometric considerations and material combinations during the manufacturing process.

The result is a small number of guidelines that can aid the design process of interlocking lattices as interfaces in multi-material structures and provide a foundational framework for the design of suitable lattice structures in multi-material additive manufacturing.

Suitable lattice designs should have large pores interconnected in three dimensions, high lattice interconnectivity, and a high number of similar structures while maintaining low dimensions in the interface direction. While this still allows for a large number of designs to be used in the application of interlock bonds, these restrictions severely restrict the solution space of possible designs and can help future designers produce suitable geometries. In strut-based lattices, a single layer of cubic body diagonal struts can meet these restrictions, for example.

While the exact design of such structures depends on the restrictions of the used manufacturing machine as well as the moduli and strengths of the used materials, conventional design guidelines for MEX and geometric considerations of the lattice (e.g., porosity vs. modulus-ratio, strut angle vs. maximum overhang angle, strut diameter vs. extrusion width, etc.) can be used to further restrict the design space and generate suitable geometries.

Hence, this work can aid future research and practical applications by enabling designers to leverage the full potential of additive manufacturing to create robust, high-performance multi-material components.