Energy-Efficient Hybrid Wireless Power Transfer Technique for Relay-Based IIoT Applications
Abstract
1. Introduction
1.1. Literature Review
1.2. Motivation and Contribution
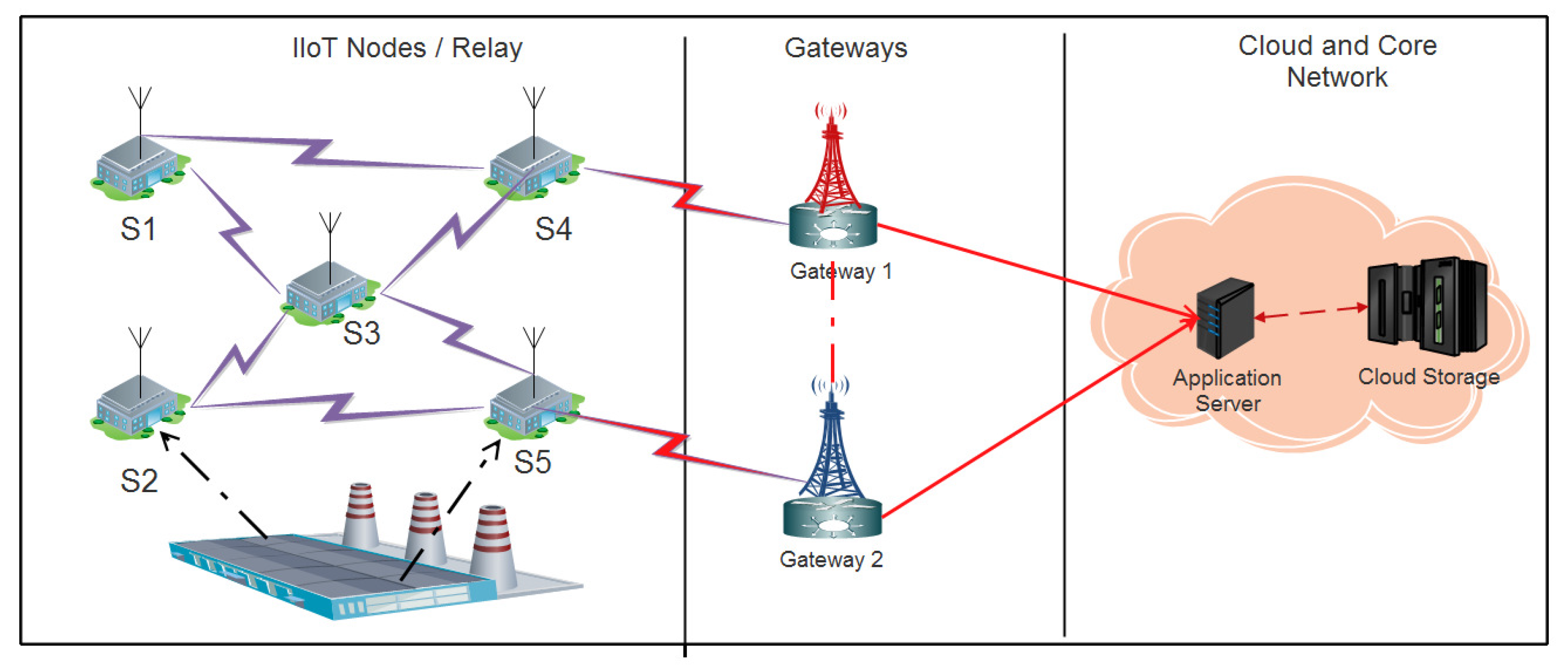
- Present a relay-based network to enhance coverage and capacity in an Industrial IoT network.
- Proposed a hybrid wireless power transfer (HWPT) scheme for IIoT network, where the relay may choose the optimal WPT method for each channel realization.
- Developing mathematical models for hybrid relay-based communication channels tailored for IIoT applications.
- Demonstrating how the proposed H-WPT scheme selects the optimum relay and power source in a decentralized manner using instantaneous channel gain, thus avoiding the significant energy waste associated with centralized control methods.
2. System and Network Models
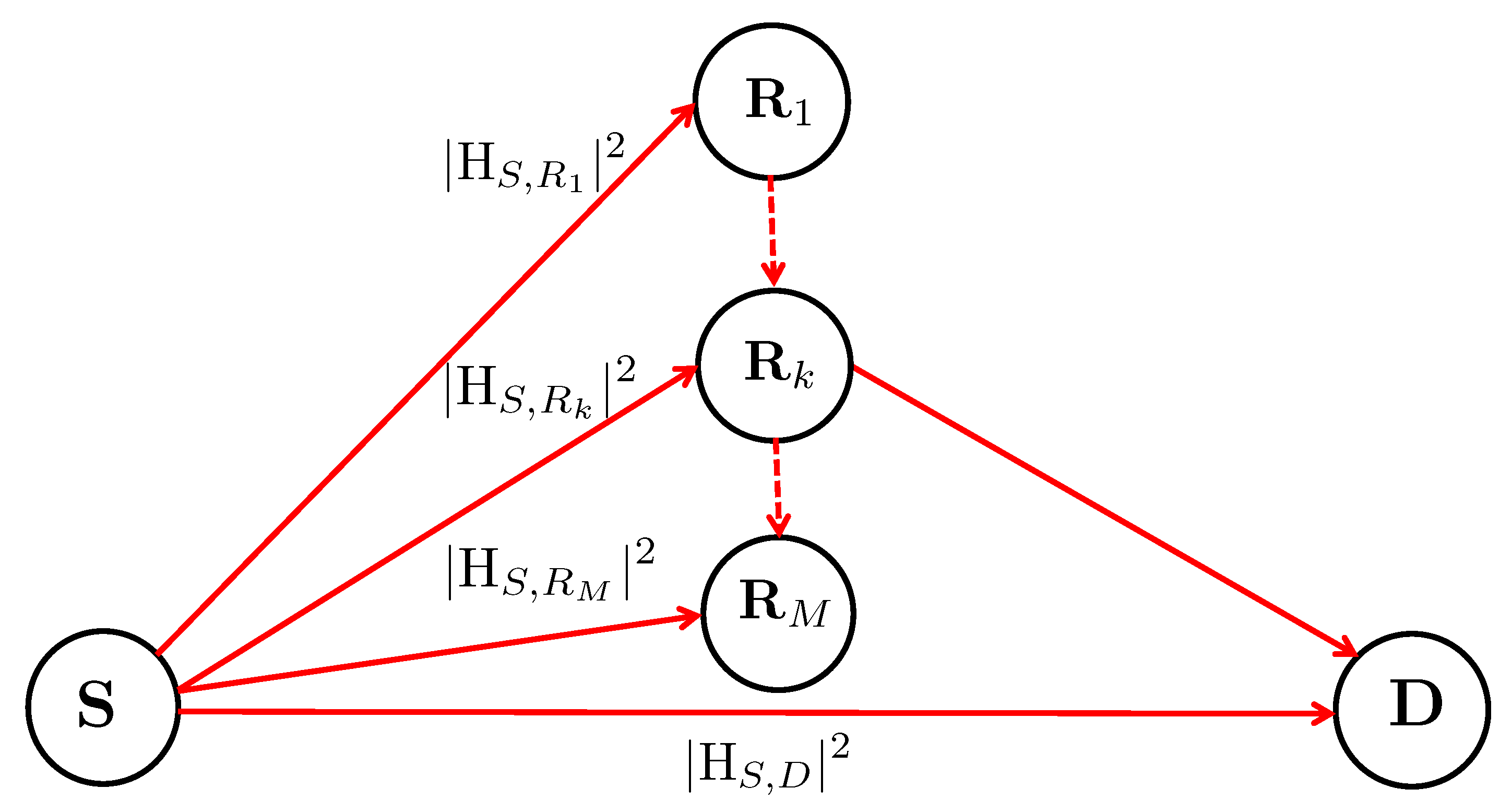
2.1. Relay Network Model
2.2. Channel Model
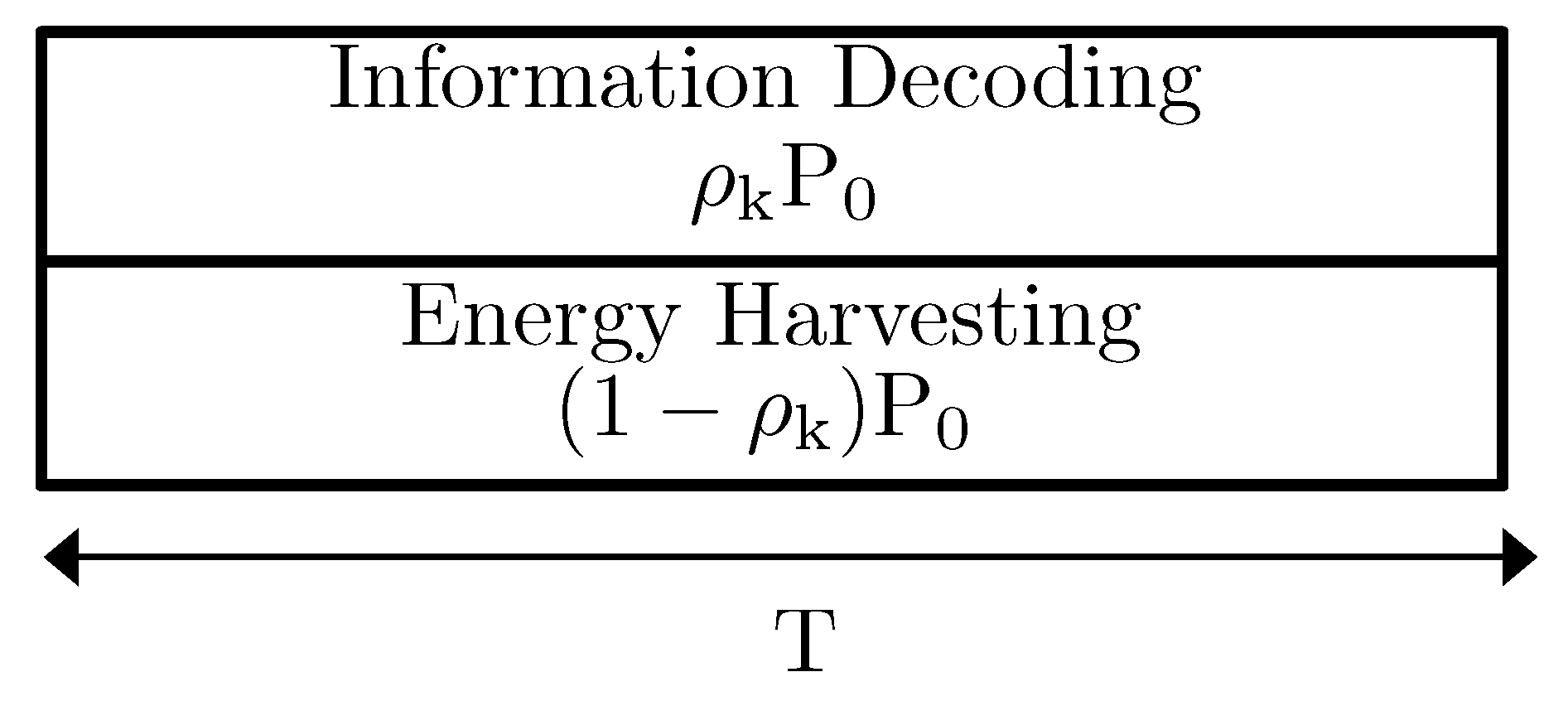
2.3. SWIPT Receiver
3. Performance Analysis
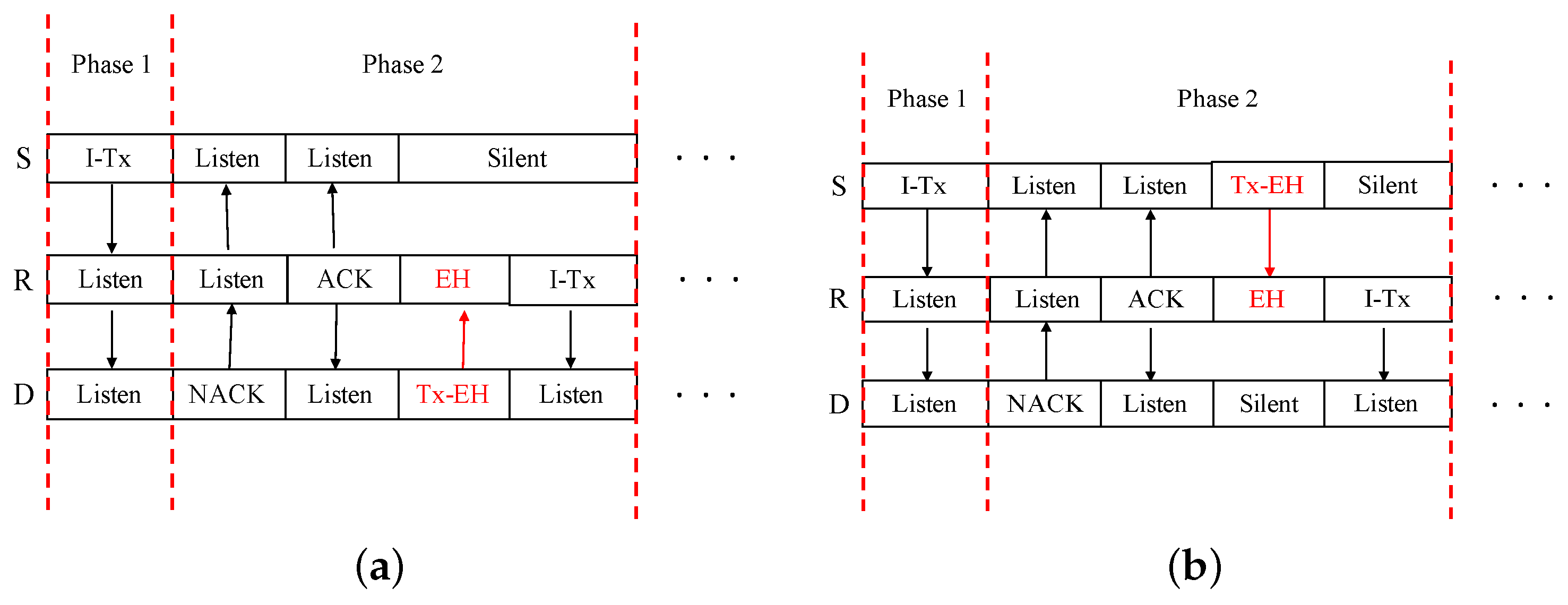
3.1. DWPT Schemes
3.2. S-WPT Scheme
3.3. Hybrid Scheme
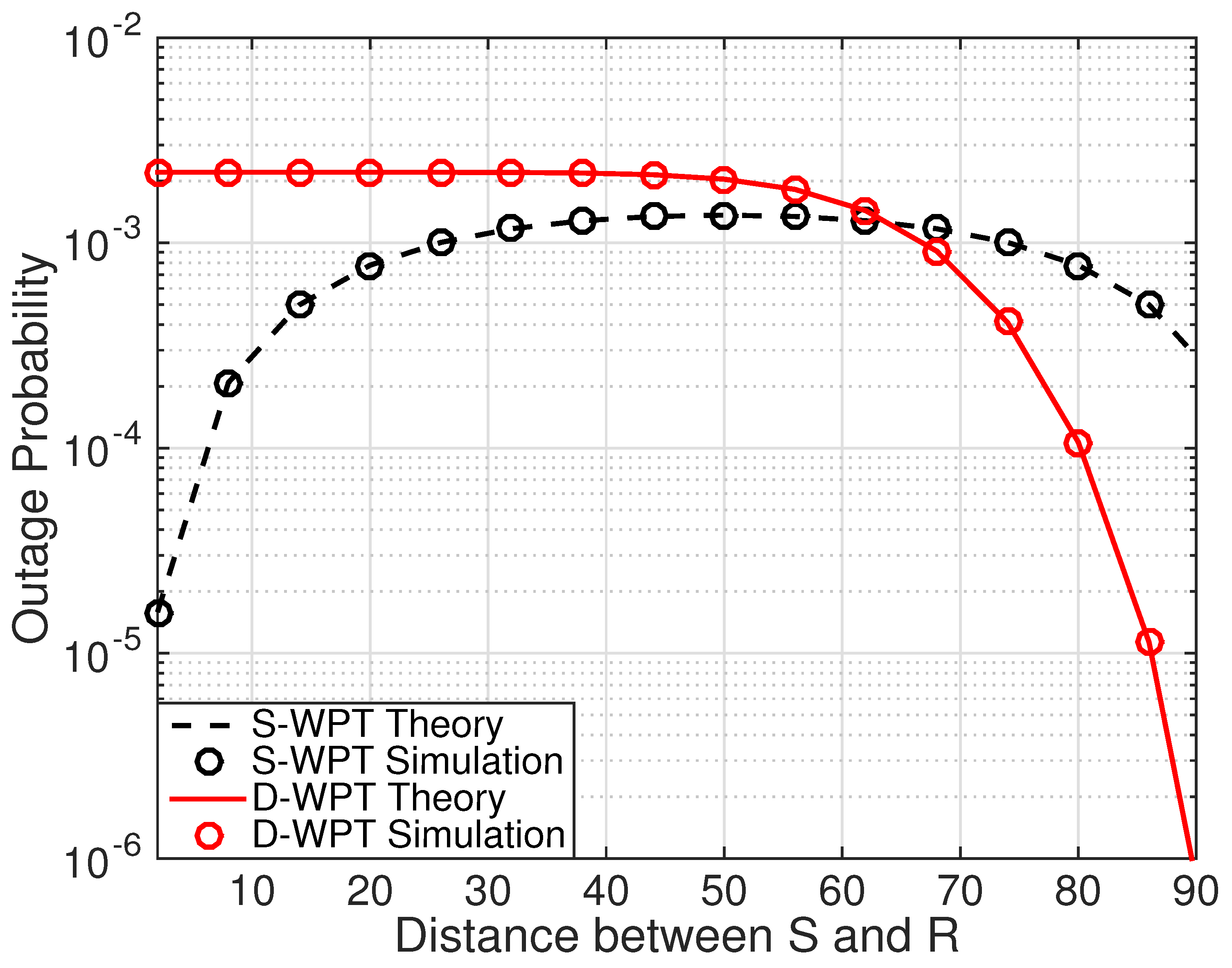
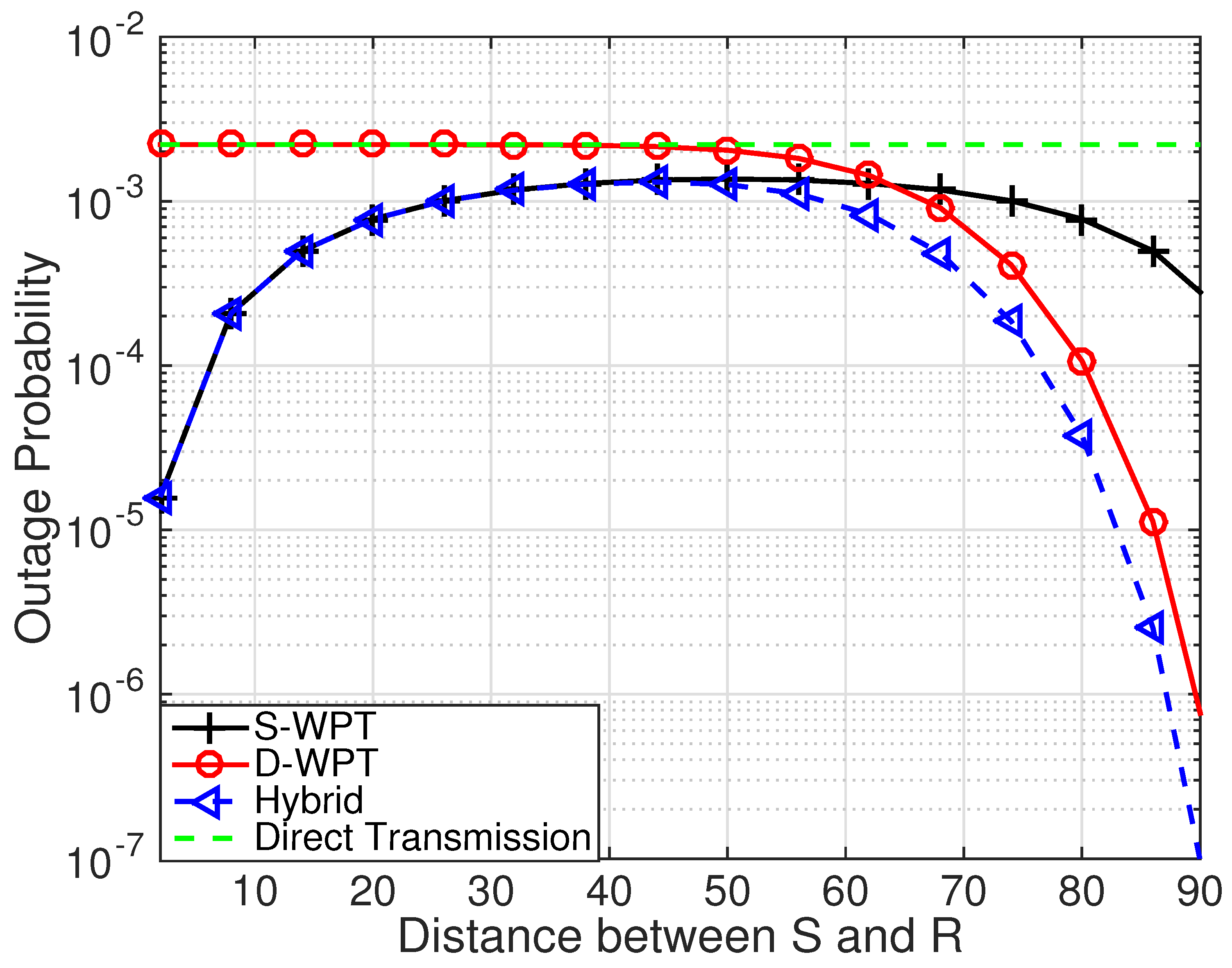
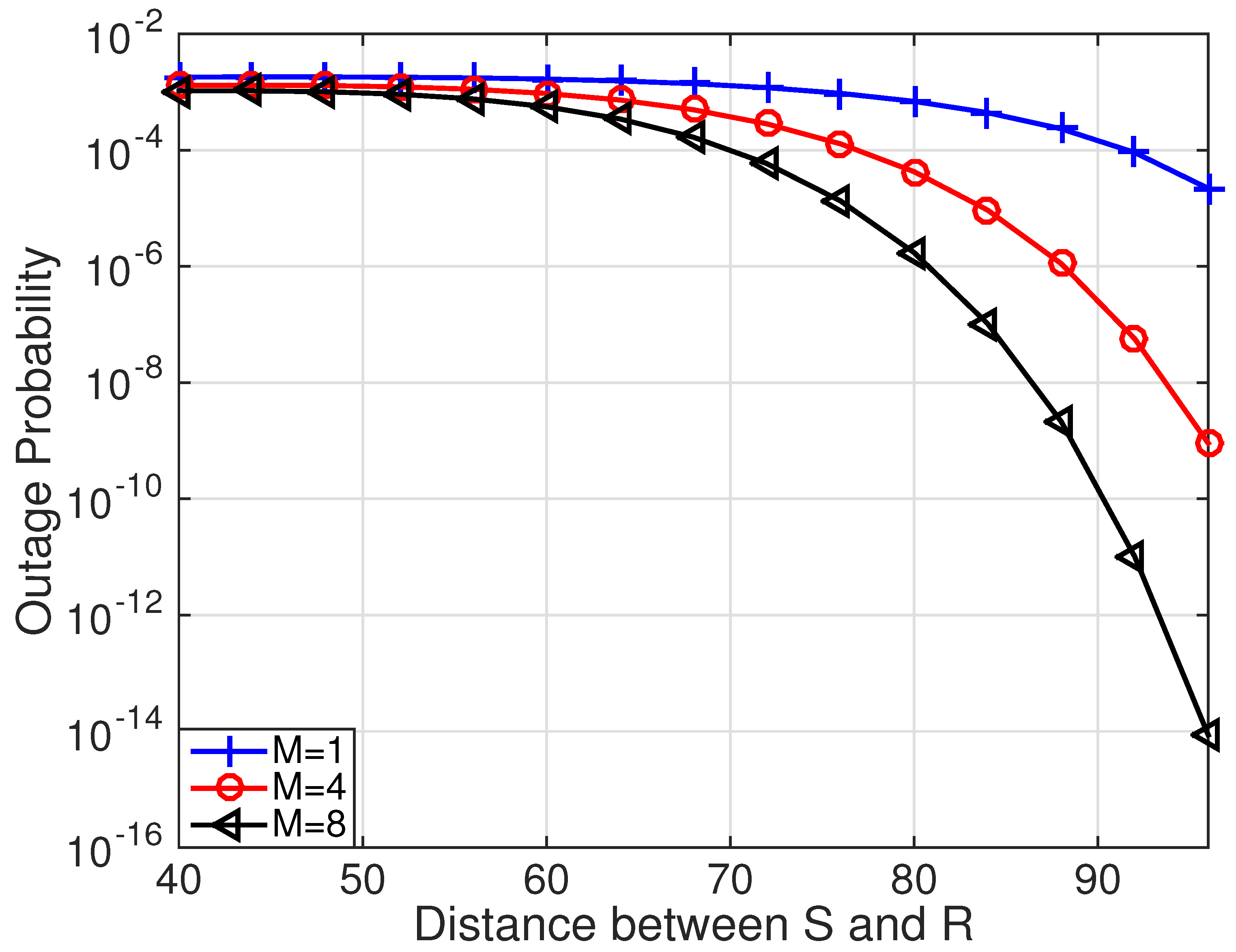
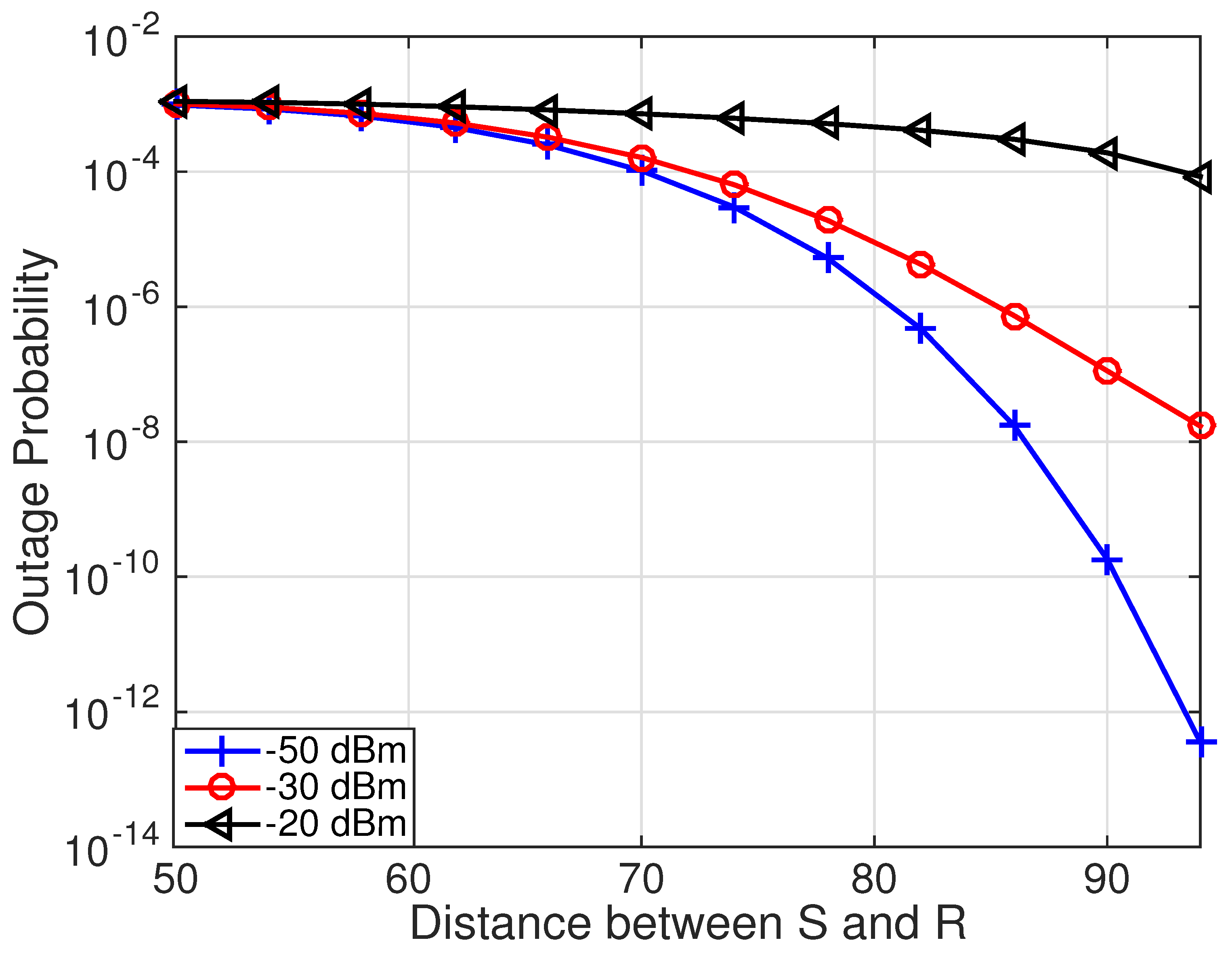
4. Numerical Results and Discussion
4.1. Analytical and Numerical Analysis
4.2. Comparison with Hybrid Approach
4.3. Effect of Relay Nodes
4.4. Effect of Power Consumed by Relay to Broadcast ACK
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols | Definition |
| S and D | Source and destination nodes |
| Relay node | |
| Channel gain between S and D | |
| Additive white Gaussian noise | |
| P | Received signal power over a channel |
| Average signal power sent by a transmitting node over a time period T | |
| Noise level over a channel | |
| Power-splitting ratio | |
| Achievable data rate between S and | |
| Minimum signal strength required to collect energy over a split channel | |
| Signal to noise ratio over a split channel | |
| Gain of the channel | |
| m | Path loss exponent |
| Conversion efficiency | |
| Waiting time required by to receive an ACK or NACK message |
References
- Chi, H.R.; Wu, C.K.; Huang, N.F.; Tsang, K.F.; Radwan, A. A Survey of Network Automation for Industrial Internet-of-Things Toward Industry 5.0. IEEE Trans. Ind. Inform. 2023, 19, 2065–2077. [Google Scholar] [CrossRef]
- Chen, Y.; Lyu, B.; Yang, Z.; Li, F. Wireless-Powered Relays Assisted Batteryless IoT Networks Empowered by Energy Beamforming. Inst. Electron. Inf. Commun. Eng. 2023, 106, 164–168. [Google Scholar] [CrossRef]
- Varshney, L.R. Transporting information and energy simultaneously. In Proceedings of the IEEE International Symposium on Information Theory, Toronto, ON, Canada, 6–11 July 2008; pp. 1612–1616. [Google Scholar]
- Grover, P.; Sahai, A. Shannon meets tesla: Wireless information and power transfer. In Proceedings of the IEEE International Symposium on Information Theory, Austin, TX, USA, 13–18 June 2010; pp. 2363–2367. [Google Scholar] [CrossRef]
- Fouladgar, A.M.; Simeone, O. On the transfer of information and energy in multi-user systems. IEEE Commun. Lett. 2012, 16, 1733–1736. [Google Scholar] [CrossRef]
- Choi, K.W.; Hwang, S.I.; Aziz, A.A.; Jang, H.H.; Kim, J.S.; Kang, D.S.; Kim, D.I. Simultaneous wireless information and power transfer (SWIPT) for Internet of Things: Novel receiver design and experimental validation. IEEE Internet Things J. 2020, 7, 2996–3012. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, R.; Chua, K.C. Wireless Information Transfer with Opportunistic Energy Harvesting. IEEE Trans. Wirel. Commun. 2013, 12, 288–300. [Google Scholar] [CrossRef]
- Zhang, R.; Ho, C.K. MIMO Broadcasting for Simultaneous Wireless Information and Power Transfer. IEEE Trans. Wirel. Commun. 2013, 12, 1989–2001. [Google Scholar] [CrossRef]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Relaying Protocols for Wireless Energy-Harvesting and Information Processing. IEEE Trans. Inf. Theory 2013, 12, 3622–3636. [Google Scholar] [CrossRef]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Throughput and ergodic capacity of wireless energy harvesting based DF relaying network. In Proceedings of the 2014 IEEE International Conference on Communications, ICC 2014, Sydney, Australia, 10–14 June 2014; pp. 4066–4071. [Google Scholar] [CrossRef]
- Gu, Y.; Sonia, A. Interference Aided Energy Harvesting in Decode-and-Forward Relaying Systems. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014; pp. 5389–5393. [Google Scholar]
- Gu, Y.; Sonia, A.; Aïssa, S. RF-Based Energy Harvesting in Decode-and-Forward Relaying Systems: Ergodic and Outage Capacities. IEEE Trans. Wirel. Commun. 2015, 14, 6425–6434. [Google Scholar] [CrossRef]
- Liu, Y. Wireless Information and Power Transfer for Multirelay-Assisted Cooperative Communication. IEEE Commun. Lett. 2016, 20, 784–787. [Google Scholar] [CrossRef]
- Do, N.T.; Bao, V.N.Q.; An, B. Outage Performance Analysis of Relay Selection Schemes in Wireless Energy Harvesting Cooperative Networks over Non-Identical Rayleigh Fading Channels. Sensors 2016, 16, 295. [Google Scholar] [CrossRef]
- Mao, M.; Cao, N.; Chen, Y.; Zhou, Y. Multi-Hop Relaying Using Energy Harvesting. IEEE Wirel. Commun. Lett. 2015, 4, 565–568. [Google Scholar] [CrossRef]
- Singh, V.; Ochiai, H. Performance analysis of the clustering-based multihop wireless energy harvesting sensor networks over symmetric and asymmetric fading channels. Int. J. Distrib. Sens. Netw. 2017, 13, 12. [Google Scholar] [CrossRef][Green Version]
- Do, D.T. Optimal Throughput under Time Power Switching Based Relaying Protocol in Energy Harvesting Cooperative Networks. Mobile Inf. Syst. 2015, 2015, 8. [Google Scholar] [CrossRef]
- Atapattu, S.; Evans, J. Optimal energy harvesting protocols for wireless relay networks. IEEE Trans. Wirel. Commun. 2016, 15, 5789–5803. [Google Scholar] [CrossRef]
- Tao, R.; Salem, A.; Hamdi, K. Adaptive Relaying Protocol for Wireless Power Transfer and Information Processing. IEEE Commun. Lett. 2016, 20, 2027–2030. [Google Scholar] [CrossRef]
- Huang, Y.; Clerckx, B. Joint Wireless Information and Power Transfer for an Autonomous Multiple Antenna Relay System. IEEE Commun. Lett. 2015, 19, 1113–1116. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Y. Wireless Power Transfer Strategies for Cooperative Relay System to Maximize Information Throughput. IEEE Access 2017, 5, 2573–2582. [Google Scholar] [CrossRef]
- Lyu, B.; Hoang, D.T. Optimal time scheduling in relay assisted batteryless IoT networks. IEEE Wirel. Commun. Lett. 2020, 9, 706–710. [Google Scholar] [CrossRef]
- Jung, H.; Lee, B. Wireless Power and Bidirectional Data Transfer System for IoT and Mobile Devices. IEEE Trans. Ind. Electron. 2022, 69, 11832–11836. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Elkashlan, M.; Duong, T.Q.; Nallanathan, A. Two-way relaying networks with wireless power transfer: Policies design and throughput analysis. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014. [Google Scholar] [CrossRef]
- Raghunathan, V.; Ganeriwal, S.; Srivastava, M. Emerging Techniques for Long Lived. IEEE Commun. Mag. 2006, 44, 108–114. [Google Scholar] [CrossRef]
- Singh, V.; Ochiai, H. An Efficient Time Switching Protocol with Adaptive Power Splitting for Wireless Energy Harvesting Relay Networks. In Proceedings of the 2017 IEEE 85th Vehicular Technology Conference (VTC Spring), Sydney, Australia, 4–7 June 2017. [Google Scholar] [CrossRef]
- Proakis, J.G.; Salehi, M. Digital Communications, 5th ed.; McGrawhill: New York, NY, USA, 2008. [Google Scholar]
- Singh, V.; Ochiai, H. Throughput Improvement by Cluster-Based Multihop Wireless Networks with Energy Harvesting Relays. In Proceedings of the IEEE Topical Conference on Wireless Sensors and Sensor Networks (WiSNet), Phoenix, AZ, USA, 15–18 January 2017; pp. 61–64. [Google Scholar]
- Ding, Z.; Krikidis, I.; Sharif, B.; Poor, H.V. Wireless information and power transfer in cooperative networks with spatially random relays. IEEE Trans. Wirel. Commun. 2014, 13, 4440–4453. [Google Scholar] [CrossRef]
- Tannious, R.; Nosratinia, A. Spectrally-efficient relay selection with limited feedback. IEEE J. Sel. Areas Commun. 2008, 26, 1419–1428. [Google Scholar] [CrossRef]
- Bletsas, A.; Khisti, A.; Reed, D.P.; Lippman, A. A Simple Cooperative Diversity Method Based on Network Path Selection. IEEE J. Sel. Areas Commun. 2006, 24, 659–672. [Google Scholar] [CrossRef]
| Variables | Numerical Value |
|---|---|
| Relay node count | |
| Spatial separation between | m |
| Distance between | |
| Target transmission rate | bit per channel use |
| Propagation factor | |
| Power conversion efficiency | |
| Source power | dBm |
| ACK signaling power of relay | dBm |
| Power of noise | dBm with |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, V.; Kumar, R.; Mahapatra, B.; Srinivasan, C.R. Energy-Efficient Hybrid Wireless Power Transfer Technique for Relay-Based IIoT Applications. Designs 2024, 8, 84. https://doi.org/10.3390/designs8050084
Singh V, Kumar R, Mahapatra B, Srinivasan CR. Energy-Efficient Hybrid Wireless Power Transfer Technique for Relay-Based IIoT Applications. Designs. 2024; 8(5):84. https://doi.org/10.3390/designs8050084
Chicago/Turabian StyleSingh, Vikash, Roshan Kumar, Byomakesh Mahapatra, and Chrompet Ramesh Srinivasan. 2024. "Energy-Efficient Hybrid Wireless Power Transfer Technique for Relay-Based IIoT Applications" Designs 8, no. 5: 84. https://doi.org/10.3390/designs8050084
APA StyleSingh, V., Kumar, R., Mahapatra, B., & Srinivasan, C. R. (2024). Energy-Efficient Hybrid Wireless Power Transfer Technique for Relay-Based IIoT Applications. Designs, 8(5), 84. https://doi.org/10.3390/designs8050084








