Wood- and Cable-Based Variable Tilt Stilt-Mounted Solar Photovoltaic Racking System
Abstract
1. Introduction
2. Materials and Methods
2.1. Selection of Wood and Wire Rope
2.2. Dimensional and Mechanical Characteristics of Wooden Members and Cables
2.3. PV Racking Design Parameters
2.4. Main Design
2.4.1. T-Shaped Wood and Cable Design
2.4.2. Cantilevered Carport Wood and Cable Design
2.5. Bill of Materials (BOM)
2.6. Load Calculations
2.7. PV System Simulations
2.8. Variables
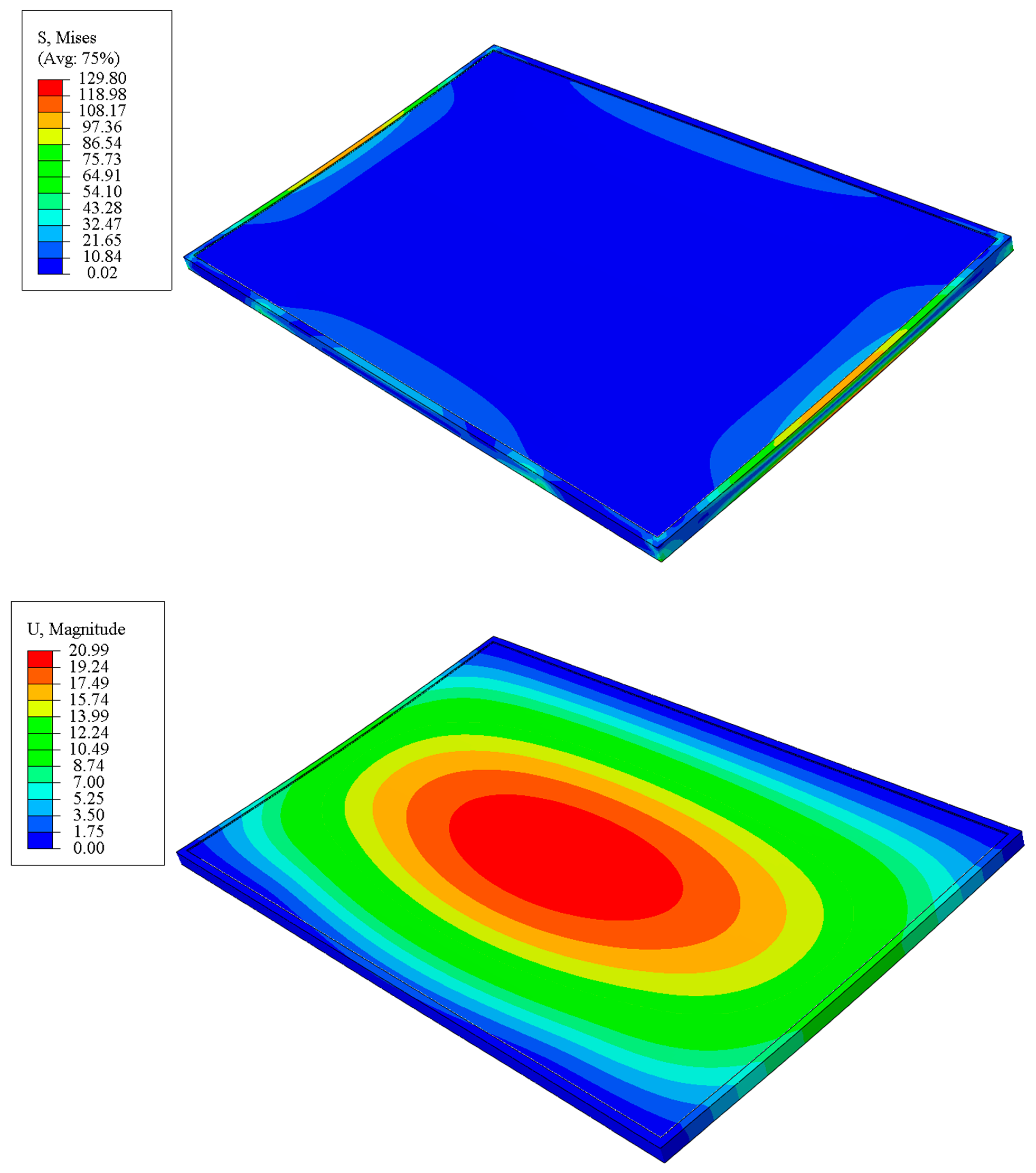
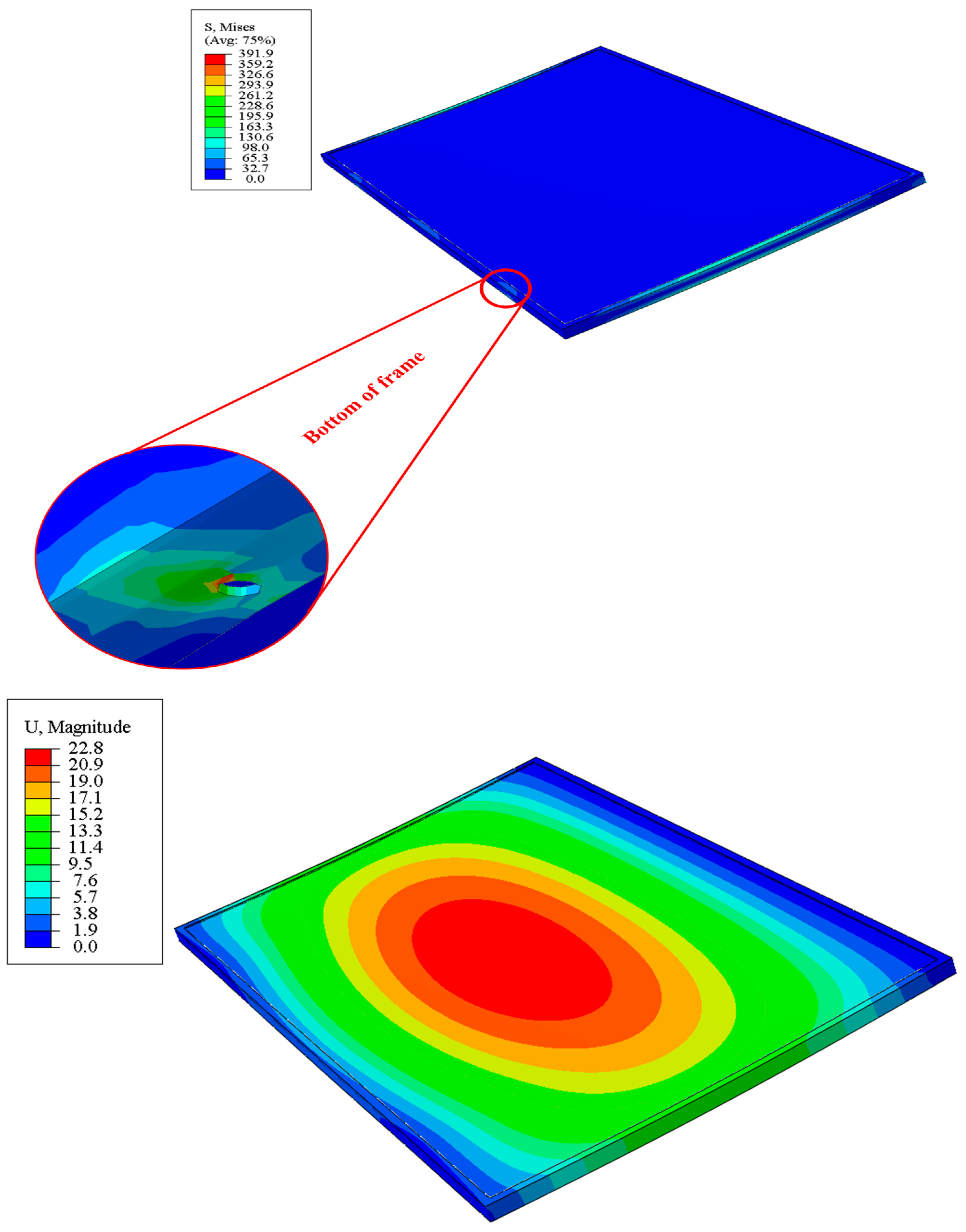
2.9. Finite Element Analysis (FEA)
3. Results
3.1. Loads
3.1.1. Snow Loads
3.1.2. Wind Loads
3.1.3. Dead Load
3.1.4. Load Combination
3.2. Wooden Members Structural Capacity
3.3. Structural Analysis
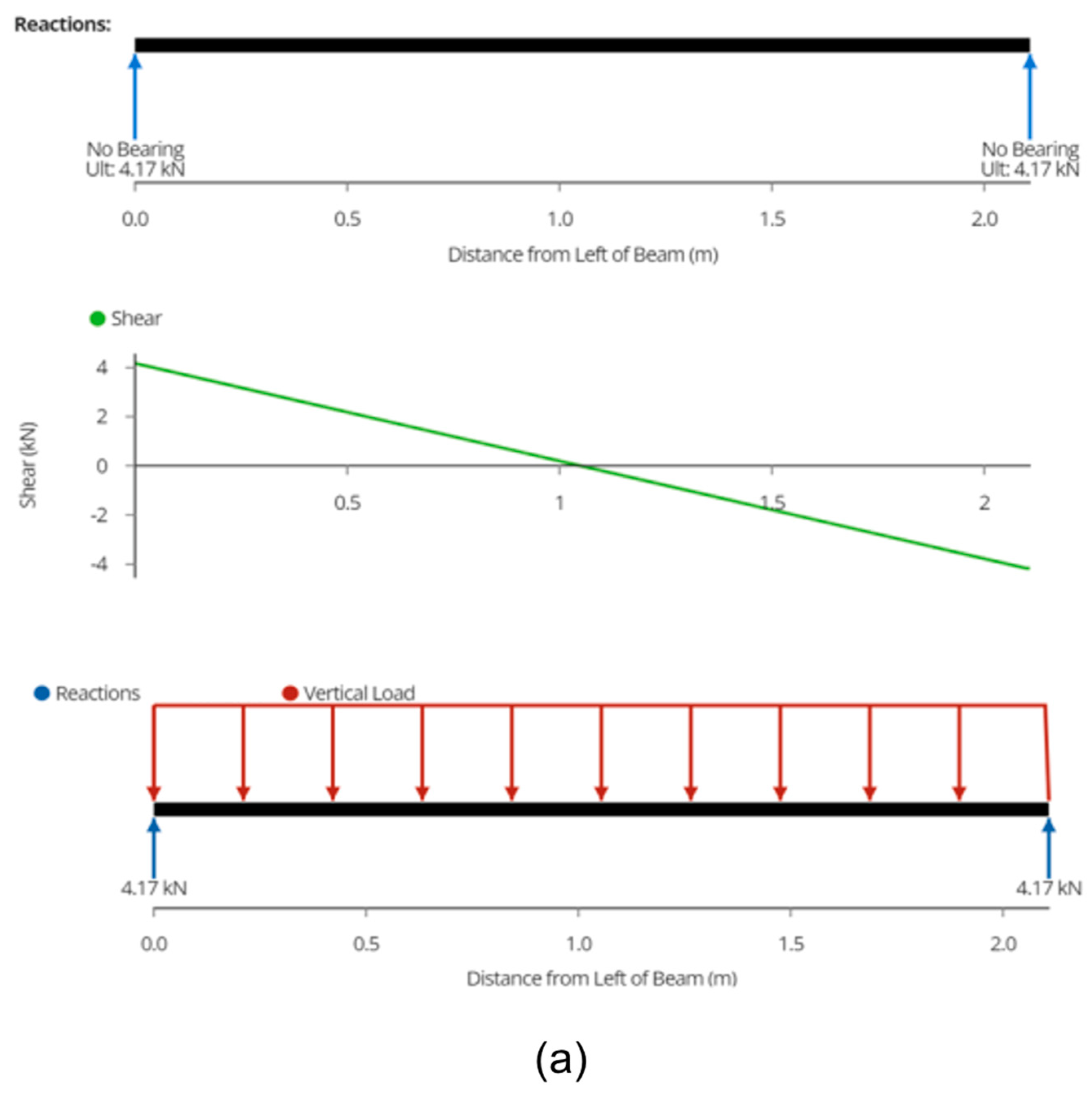
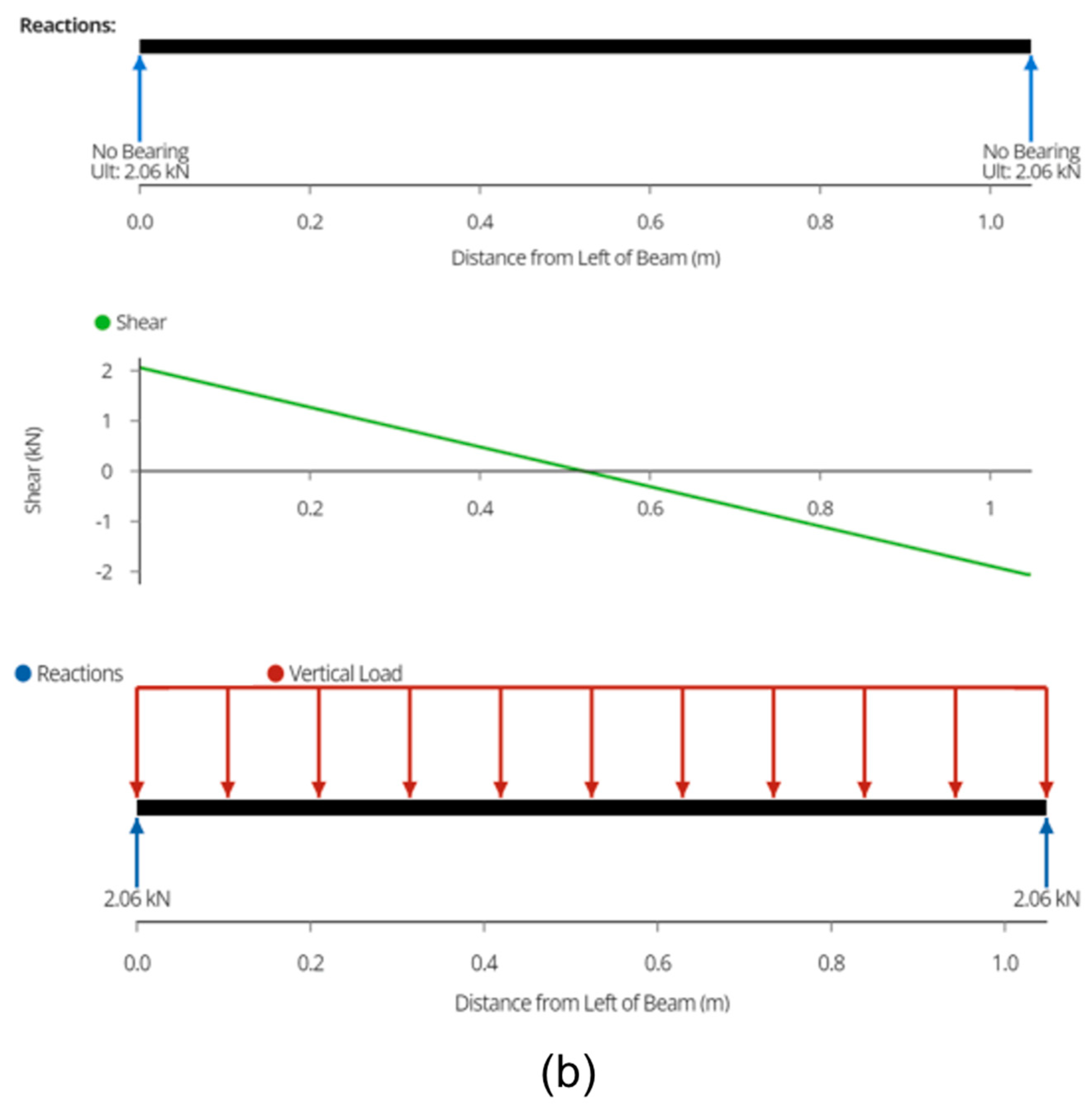
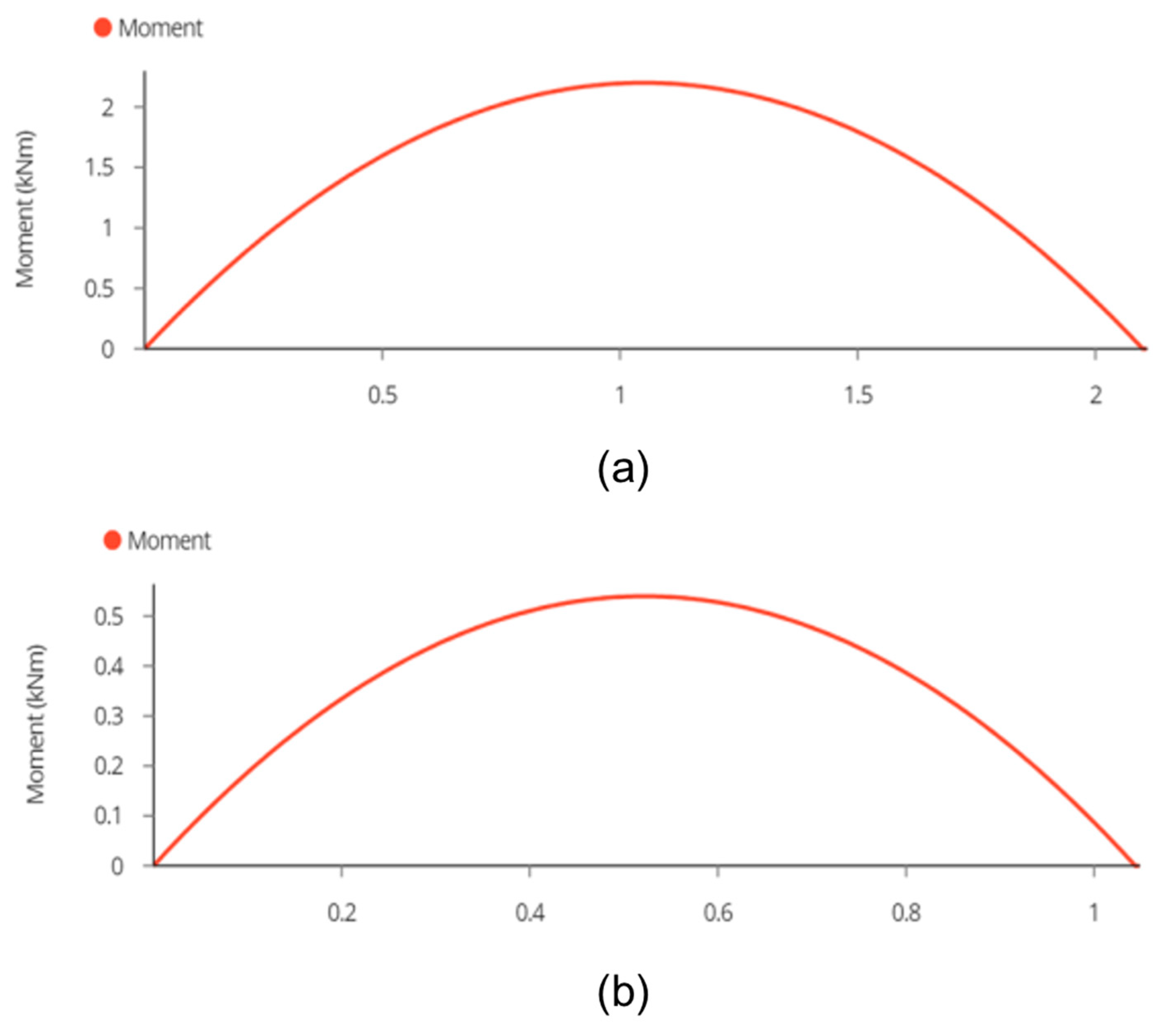
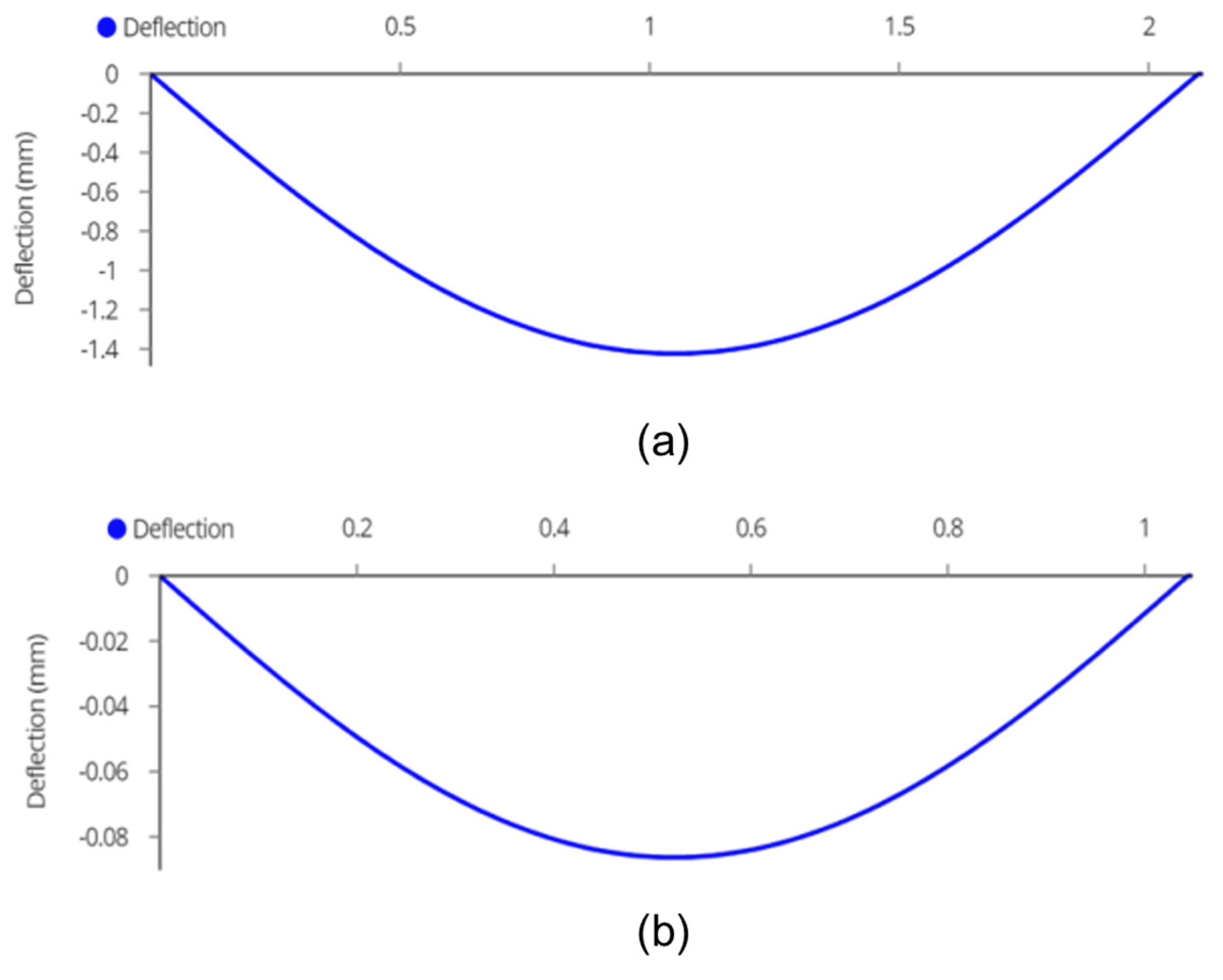
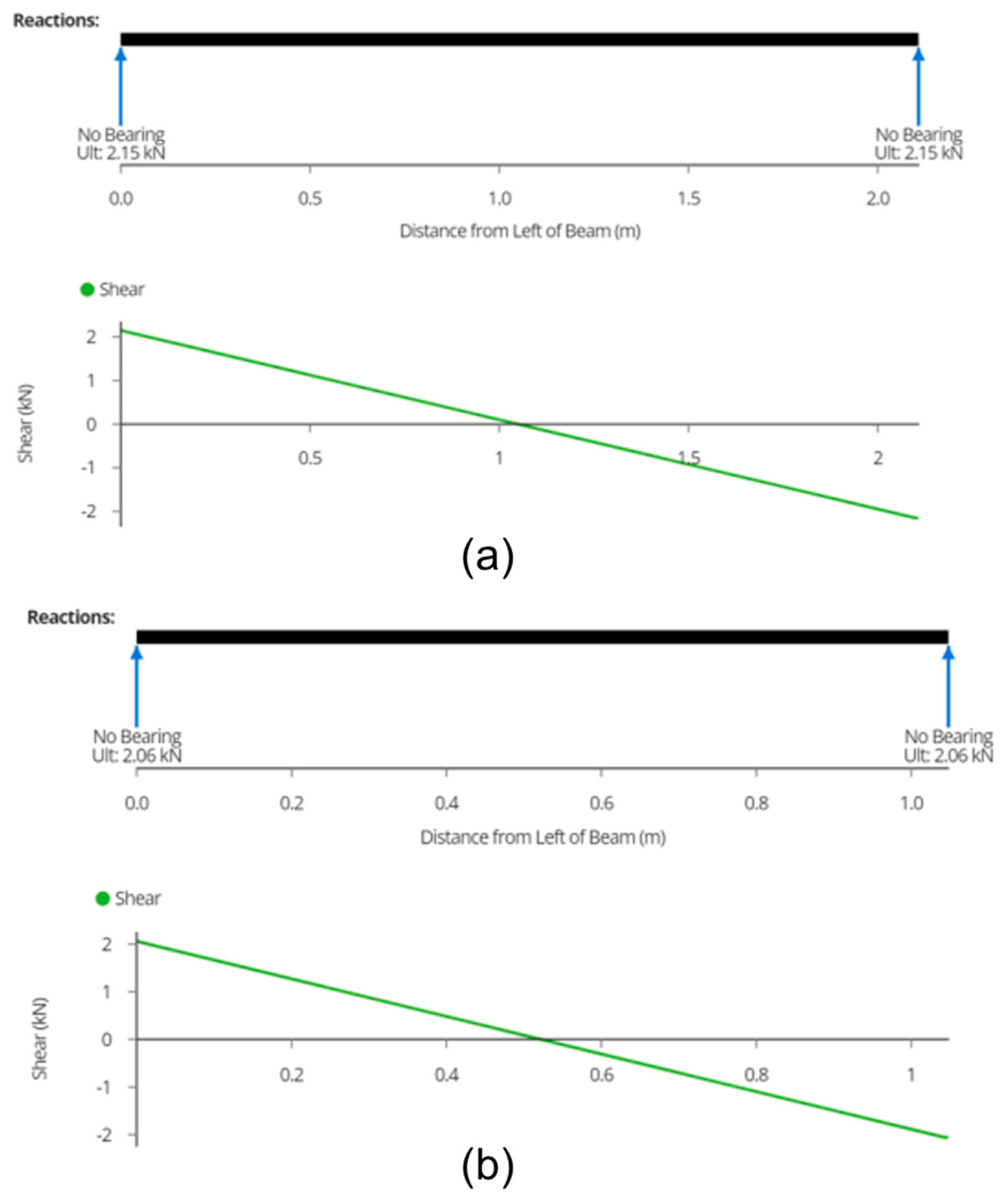
3.3.1. Joist
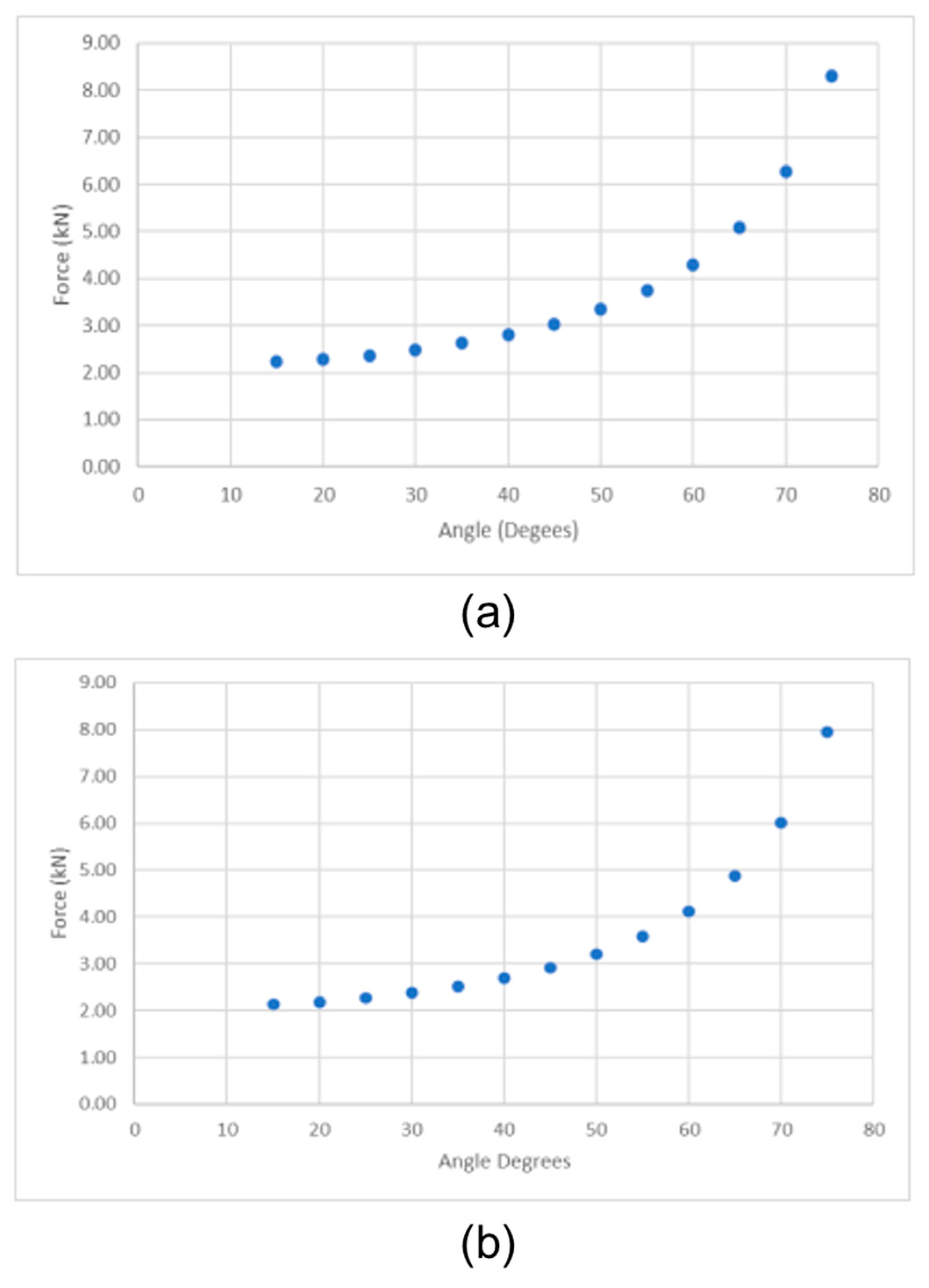
3.3.2. Wire Rope
3.3.3. Posts
4. Discussion
4.1. Wooden Racking Economics
4.2. Agrivoltaics
4.3. Wood Price Sensitivity
4.4. Permits and Certification
4.5. Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Design Analysis Assumptions
Appendix B. Load Calculations
Appendix B.1. Snow Loads
| Factor | Value |
|---|---|
| Importance Factor (Is) | 1.15 |
| Snow Load Factor (Ss) | 1.90 |
| Basic Roof Snow Load Factor (Cb) | 0.80 |
| Wind Exposure Factor (Cw) | 0.75 |
| Slope Factor (Cs) | 1.00, 0.67, 0.33 and 0 |
| Accumulation Factor (Ca) | 1.00 |
| Associated Rain Load (Sr) | 0.40 |
Appendix B.2. Wind Load
- p is the specified external wind pressure in kPa;
- pi is the specified internal wind pressure in kPa.
| Factor | Value |
|---|---|
| Wind Importance Factor (Iw) | 1.15 |
| Reference Velocity Pressure (q) | 0.47 |
| Exposure Factor (Ce) | 0.90 |
| Topographic Factor (Ct) | 1.00 |
| External Pressure Coefficient and Gust Effect Factor ‘Cp.Cg’ | −2.00 |
| Exposure Factor for Internal Pressure (Cei) | 0.90 |
| Internal Gust Effect Factor (Cgi) | 2.00 |
| Internal Pressure Coefficient (Cpi) | −0.70 |
Appendix B.3. Dead Load
Appendix B.4. Load Combinations
Appendix B.5. Wooden Members Structural Capacity
- The resisting bending moment (Mr) must equal or exceed the maximum applied bending moment (Mmax).
- The resisting shear force (Vr) must equal or exceed the maximum applied shear force (Vmax).
- The resisting tensile force (Tr) must equal or exceed the maximum applied tensile force (Tmax).
- The resisting compressive force (Cr) must equal or exceed the maximum applied compressive force (Cmax).
Appendix B.6. Structural Analysis for T-Shaped Racking
Appendix C. Truss Analysis
Appendix C.1. Calculations for 2-Panel T-Shaped Design
Appendix C.1.1. Point A
−2.14 + FABcos(75) = 0
FAB = 8.30 kN
Appendix C.1.2. Point B
2FABcos(75) + 4.18 = FCOL
FCOL = 8.48 kN
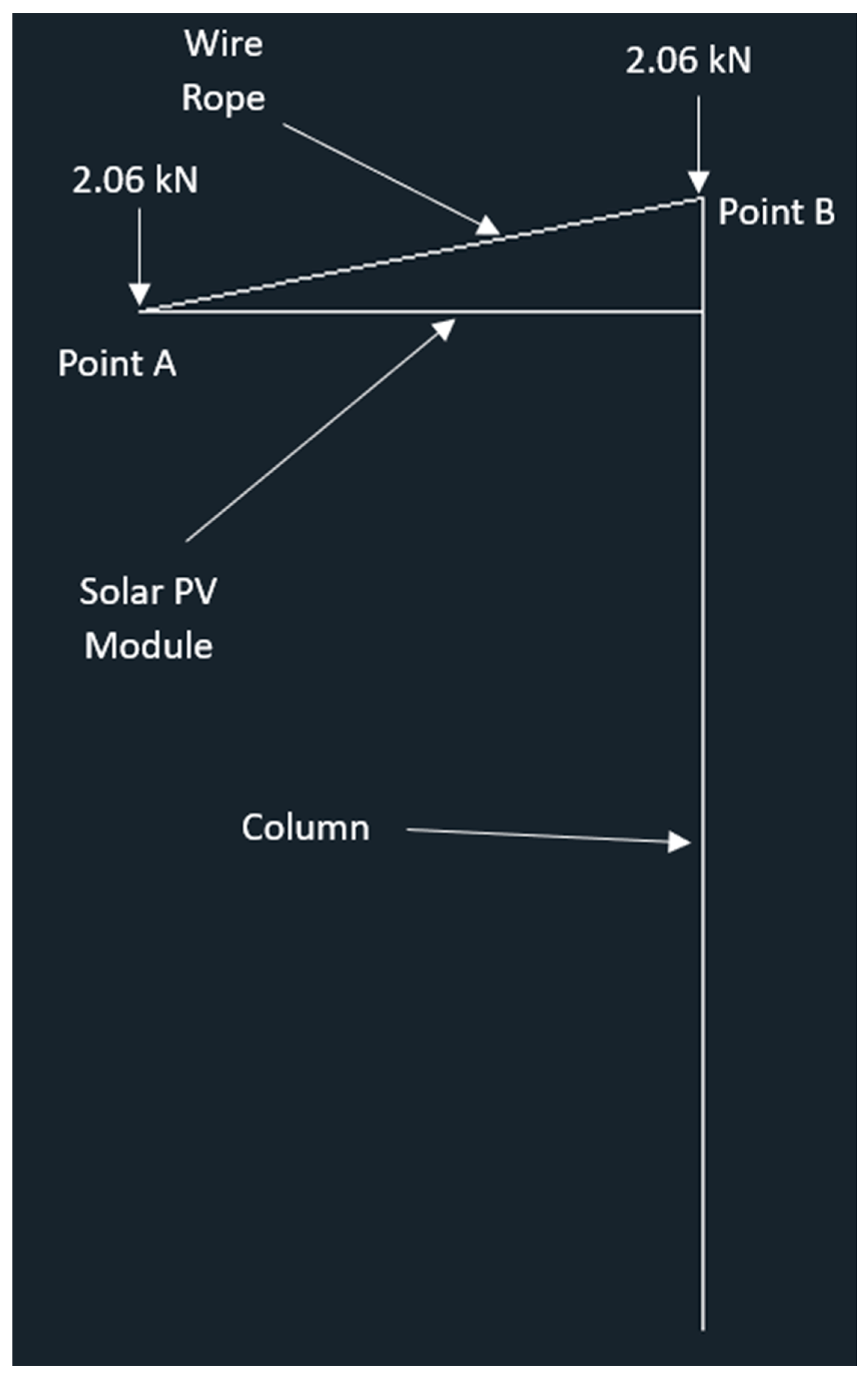
Appendix C.2. Calculations for Cantilever Carport Design
Appendix C.2.1. Point A
−2.06 + FABcos(75) = 0
FAB = 7.95 kN
Appendix C.2.2. Point B
2FABcos(75) + 2.06 = FCOL
FCOL = 6.18 kN
References
- Lu, Y.; Yi, F.; Yu, S.; Feng, Y.; Wang, Y. Pathways to Sustainable Deployment of Solar Photovoltaic Policies in 20 Leading Countries Using a Qualitative Comparative Analysis. Sustainability 2022, 14, 5858. [Google Scholar] [CrossRef]
- Fu, R.; Feldman, D.J.; Margolis, R.M. US Solar Photovoltaic System Cost Benchmark: Q1 2018; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2018.
- Matasci, S. Solar Panel Cost: Avg. Solar Panel Prices by State in 2019: EnergySage. Sol. News EnergySage 2019, 5. Available online: https://www.energysage.com/local-data/solar-panel-cost/ (accessed on 18 October 2023).
- Tsuma, M.; Kibaara, S. A Review of Levelized Cost of Electricity for Photovoltaic Systems Combining with Their Environmental Impacts. In Proceedings of the Sustainable Research and Innovation Conference, Juja, Kenya, 12 November 2022; College of Engineering and Technology at Jomo Kenyatta University of Agriculture and Technology. pp. 220–225. [Google Scholar]
- Dudley, D. Renewable Energy Will Be Consistently Cheaper Than Fossil Fuels By 2020. Forbes 2019. Available online: https://www.forbes.com/sites/dominicdudley/2018/01/13/renewable-energy-cost-effective-fossil-fuels-2020/?sh=189264e74ff2 (accessed on 18 October 2023).
- Solar Industry Research Data. Available online: https://www.seia.org/solar-industry-research-data (accessed on 18 October 2023).
- Vaughan, A. Time to Shine: Solar Power Is Fastest-Growing Source of New Energy. Guardian 2017, 4. Available online: https://www.theguardian.com/environment/2017/oct/04/solar-power-renewables-international-energy-agency (accessed on 18 October 2023).
- Barbose, G.L.; Darghouth, N.R.; LaCommare, K.H.; Millstein, D.; Rand, J. Tracking the Sun: Installed Price Trends for Distributed Photovoltaic Systems in the United States-2018 Edition 2018; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2018.
- IEA Solar PV—Renewables 2020—Analysis. Available online: https://www.iea.org/reports/renewables-2020/solar-pv (accessed on 18 October 2023).
- Levin, T.; Thomas, V.M. Can Developing Countries Leapfrog the Centralized Electrification Paradigm? Energy Sustain. Dev. 2016, 31, 97–107. [Google Scholar] [CrossRef]
- Lang, T.; Ammann, D.; Girod, B. Profitability in Absence of Subsidies: A Techno-Economic Analysis of Rooftop Photovoltaic Self-Consumption in Residential and Commercial Buildings. Renew. Energy 2016, 87, 77–87. [Google Scholar] [CrossRef]
- Hayibo, K.S.; Pearce, J.M. A Review of the Value of Solar Methodology with a Case Study of the U.S. VOS. Renew. Sustain. Energy Rev. 2021, 137, 110599. [Google Scholar] [CrossRef]
- Pitt, D.; Michaud, G. Assessing the Value of Distributed Solar Energy Generation. Curr. Sustain. Renew. Energy Rep. 2015, 2, 105–113. [Google Scholar] [CrossRef]
- Agenbroad, J.; Carlin, K.; Ernst, K.; Doig, S. Minigrids in the Money: Six Ways to Reduce Minigrid Costs by 60% for Rural Electrification; Rocky Mountain Institute: Basalt, CO, USA, 2018. [Google Scholar]
- Szabó, S.; Pinedo Pascua, I.; Puig, D.; Moner-Girona, M.; Negre, M.; Huld, T.; Mulugetta, Y.; Kougias, I.; Szabó, L.; Kammen, D. Mapping of Affordability Levels for Photovoltaic-Based Electricity Generation in the Solar Belt of Sub-Saharan Africa, East Asia and South Asia. Sci. Rep. 2021, 11, 3226. [Google Scholar] [CrossRef]
- Awan, A.B. Optimization and Techno-Economic Assessment of Rooftop Photovoltaic System. J. Renew. Sustain. Energy 2019, 11, 033501. [Google Scholar] [CrossRef]
- Wang, P.; Yu, P.; Huang, L.; Zhang, Y. An Integrated Technical, Economic, and Environmental Framework for Evaluating the Rooftop Photovoltaic Potential of Old Residential Buildings. J. Environ. Manag. 2022, 317, 115296. [Google Scholar] [CrossRef]
- Renewables International, 2013. Photovoltaics after Grid Parity Plug-and-Play PV: The Controversy 2013. Renewables 2013. Available online: http://www.renewablesinternational.net/plug-and-play-pv-the-controversy/150/452/72715/ (accessed on 18 October 2023).
- Barbose, G.; Darghouth, N.; Millstein, D.; Cates, S.; DiSanti, N.; Widiss, R. Tracking the Sun IX: The Installed Price of Residential and Non-Residential Photovoltaic Systems in the United States; LBL Publications: Berkeley, CA, USA, 2016. Available online: https://escholarship.org/uc/item/9s90c8c6 (accessed on 18 October 2023).
- Khan, M.T.A.; Norris, G.; Chattopadhyay, R.; Husain, I.; Bhattacharya, S. Autoinspection and Permitting With a PV Utility Interface (PUI) for Residential Plug-and-Play Solar Photovoltaic Unit. IEEE Trans. Ind. Appl. 2017, 53, 1337–1346. [Google Scholar] [CrossRef]
- Khan, M.T.A.; Husain, I.; Lubkeman, D. Power Electronic Components and System Installation for Plug-and-Play Residential Solar PV. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition, ECCE, Pittsburgh, PA, USA, 14–18 September 2014; pp. 3272–3278. [Google Scholar]
- Lundstrom, B.R. Plug and Play Solar Power: Simplifying the Integration of Solar Energy in Hybrid Applications; Cooperative Research and Development Final Report. CRADA Number CRD-13-523; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2017.
- Mundada, A.S.; Prehoda, E.W.; Pearce, J.M. U.S. market for solar photovoltaic plug-and-play systems. Renew. Energy 2017, 103, 255–264. [Google Scholar] [CrossRef]
- Fthenakis, V.; Alsema, E. Photovoltaics Energy Payback Times, Greenhouse Gas Emissions and External Costs: 2004–Early 2005 Status. Prog. Photovolt. Res. Appl. 2006, 14, 275–280. [Google Scholar] [CrossRef]
- Feldman, D.; Barbose, G.; Margolis, R.; Bolinger, M.; Chung, D.; Fu, R.; Seel, J.; Davidson, C.; Darghouth, N.; Wiser, R. Photovoltaic System Pricing Trends: Historical, Recent, and Near-Term Projections 2015 Edition; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2015.
- Feldman, D.; Barbose, G.; Margolis, R.; Wiser, R.; Darghout, N.; Goodrich, A. Photovoltaic (PV) Pricing Trends: Historical, Recent, and Near-Term Projections, Sunshot 2012; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2012.
- PVinsights PVinsights. Available online: http://pvinsights.com/ (accessed on 23 August 2023).
- Tamarack Solar Products Tamarack Solar Top of Pole Mounts. Available online: https://www.altestore.com/store/solar-panel-mounts/top-of-pole-mounts-for-solar-panels/tamarack-solar-top-of-pole-mounts-6072-cell-solar-panels-p40745/ (accessed on 29 June 2023).
- TPM3 Pole Mount for Three 60/72 Cell Solar Modules. Available online: https://www.modernoutpost.com/product/tpm3-pole-mount-for-three-60-72-cell-solar-modules/ (accessed on 23 August 2023).
- Precedence Research Agrivoltaics Market Is Expected to Increase at a 12.15% of CAGR by 2030. Available online: https://www.precedenceresearch.com/press-release/agrivoltaics-market (accessed on 23 August 2023).
- International Energy Agency Solar. Available online: https://www.iea.org/energy-system/renewables/solar-pv (accessed on 23 August 2023).
- Dupraz, C.; Marrou, H.; Talbot, G.; Dufour, L.; Nogier, A.; Ferard, Y. Combining Solar Photovoltaic Panels and Food Crops for Optimising Land Use: Towards New Agrivoltaic Schemes. Renew. Energy 2011, 36, 2725–2732. [Google Scholar] [CrossRef]
- Guerin, T.F. Impacts and Opportunities from Large-Scale Solar Photovoltaic (PV) Electricity Generation on Agricultural Production. Environ. Qual. Manag. 2019, 28, 7–14. [Google Scholar] [CrossRef]
- Valle, B.; Simonneau, T.; Sourd, F.; Pechier, P.; Hamard, P.; Frisson, T.; Ryckewaert, M.; Christophe, A. Increasing the Total Productivity of a Land by Combining Mobile Photovoltaic Panels and Food Crops. Appl. Energy 2017, 206, 1495–1507. [Google Scholar] [CrossRef]
- Mavani, D.D.; Chauhan, P.M.; Joshi, V. Beauty of Agrivoltaic System Regarding Double Utilization of Same Piece of Land for Generation of Electricity & Food Production. Int. J. Sci. Eng. Res. 2019, 10, 118–148. [Google Scholar]
- Sekiyama, T.; Nagashima, A. Solar Sharing for Both Food and Clean Energy Production: Performance of Agrivoltaic Systems for Corn, A Typical Shade-Intolerant Crop. Environments 2019, 6, 65. [Google Scholar] [CrossRef]
- Agostini, A.; Colauzzi, M.; Amaducci, S. Innovative Agrivoltaic Systems to Produce Sustainable Energy: An Economic and Environmental Assessment. Appl. Energy 2021, 281, 116102. [Google Scholar] [CrossRef]
- Daniels, T.L. The Development of Utility-Scale Solar Projects on US Agricultural Land: Opportunities and Obstacles. Socio-Ecol. Pract. Res. 2023, 5, 205–213. [Google Scholar] [CrossRef]
- Wittbrodt, B.; Laureto, J.; Tymrak, B.; Pearce, J.M. Distributed Manufacturing with 3-D Printing: A Case Study of Recreational Vehicle Solar Photovoltaic Mounting Systems. J. Frugal Innov. 2015, 1, 1. [Google Scholar] [CrossRef]
- Wittbrodt, B.T.; Pearce, J.M. Total U.S. Cost Evaluation of Low-Weight Tension-Based Photovoltaic Flat-Roof Mounted Racking. Sol. Energy 2015, 117, 89–98. [Google Scholar] [CrossRef]
- Wittbrodt, B.; Pearce, J.M. 3-D Printing Solar Photovoltaic Racking in Developing World. Energy Sustain. Dev. 2017, 36, 1–5. [Google Scholar] [CrossRef]
- Arefeen, S.; Dallas, T. Low-Cost Racking for Solar Photovoltaic Systems with Renewable Tensegrity Structures. Sol. Energy 2021, 224, 798–807. [Google Scholar] [CrossRef]
- Pearce, J.M.; Meldrum, J.; Osborne, N. Design of Post-Consumer Modification of Standard Solar Modules to Form Large-Area Building-Integrated Photovoltaic Roof Slates. Designs 2017, 1, 9. [Google Scholar] [CrossRef]
- Vandewetering, N.; Hayibo, K.S.; Pearce, J.M. Impacts of Location on Designs and Economics of DIY Low-Cost Fixed-Tilt Open Source Wood Solar Photovoltaic Racking. Designs 2022, 6, 41. [Google Scholar] [CrossRef]
- Vandewetering, N.; Hayibo, K.S.; Pearce, J.M. Open-Source Design and Economics of Manual Variable-Tilt Angle DIY Wood-Based Solar Photovoltaic Racking System. Designs 2022, 6, 54. [Google Scholar] [CrossRef]
- Vandewetering, N.; Hayibo, K.S.; Pearce, J.M. Open-Source Vertical Swinging Wood-Based Solar Photovoltaic Racking Systems. Designs 2023, 7, 34. [Google Scholar] [CrossRef]
- Masna, S.; Morse, S.M.; Hayibo, K.S.; Pearce, J.M. The Potential for Fencing to Be Used as Low-Cost Solar Photovoltaic Racking. Sol. Energy 2023, 253, 30–46. [Google Scholar] [CrossRef]
- Mayville, P.; Patil, N.V.; Pearce, J.M. Distributed Manufacturing of after Market Flexible Floating Photovoltaic Modules. Sustain. Energy Technol. Assess. 2020, 42, 100830. [Google Scholar] [CrossRef]
- Jamil, U.; Vandewetering, N.; Pearce, J.M. Solar Photovoltaic Wood Racking Mechanical Design for Trellis-Based Agrivoltaics. PLoS ONE 2023, 18, e0294682. [Google Scholar] [CrossRef] [PubMed]
- Franz, J.; Morse, S.; Pearce, J.M. Low-Cost Pole and Wire Photovoltaic Racking. Energy Sustain. Dev. 2022, 68, 501–511. [Google Scholar] [CrossRef]
- Lehmann, S. Sustainable Construction for Urban Infill Development Using Engineered Massive Wood Panel Systems. Sustainability 2012, 4, 2707–2742. [Google Scholar] [CrossRef]
- We Explain Why Wood Is Eco Friendly and a Sustainable Material. Available online: https://www.wooduchoose.com/ (accessed on 18 October 2023).
- ItTakesAForest #ItTakesAForest. Available online: https://ittakesaforest.ca/people-products/wood-making-our-lives-better/ (accessed on 18 October 2023).
- Circular Ecology. Embodied Carbon Footprint Database; Circular Ecology: Worcester, UK, 2023; Available online: https://circularecology.com/embodied-carbon-footprint-database.html (accessed on 18 October 2023).
- Rana, S.; Vandewetering, N.; Powell, J.; Ariza, J.Á.; Pearce, J.M. Geographical Dependence of Open Hardware Optimization: Case Study of Solar Photovoltaic Racking. Technologies 2023, 11, 62. [Google Scholar] [CrossRef]
- Galvanized Aircraft Cable 7x19, 1/4 in. x 200 Feet. Available online: https://www.bestmaterials.com/detail.aspx?ID=25064 (accessed on 18 October 2023).
- Heliene 144HC M6 Bifacial Module 144 Half-Cut Monocrystalline 440W–460W (HSPE-144HC-M6-Bifacial-Rev.05.Pdf) 2022. Available online: https://heliene.com/144hc-m6-monofacial-module/ (accessed on 18 October 2023).
- Molin, E.; Stridh, B.; Molin, A.; Wäckelgård, E. Experimental Yield Study of Bifacial PV Modules in Nordic Conditions. IEEE J. Photovolt. 2018, 8, 1457–1463. [Google Scholar] [CrossRef]
- Riedel-Lyngskær, N.; Ribaconka, M.; Pó, M.; Thorseth, A.; Thorsteinsson, S.; Dam-Hansen, C.; Jakobsen, M.L. The Effect of Spectral Albedo in Bifacial Photovoltaic Performance. Sol. Energy 2022, 231, 921–935. [Google Scholar] [CrossRef]
- Hayibo, K.S. Monofacial vs Bifacial Solar Photovoltaic Systems in Snowy Environments. Renew. Energy 2022, 193, 657–668. [Google Scholar] [CrossRef]
- Russell, A.C.J.; Valdivia, C.E.; Haysom, J.E.; Hinzer, K. Impact of Snow Depth on Single-Axis Tracked Bifacial Photovoltaic System Performance. In Proceedings of the 2022 IEEE 49th Photovoltaics Specialists Conference (PVSC), Philadelphia, PA, USA, 5–10 June 2022; pp. 1–4. [Google Scholar]
- Heidari, N.; Gwamuri, J.; Townsend, T.; Pearce, J.M. Impact of Snow and Ground Interference on Photovoltaic Electric System Performance. IEEE J. Photovolt. 2015, 5, 1680–1685. [Google Scholar] [CrossRef]
- Rigging Canada 3/8″ x 500 Galvanized Aircraft Cable. Available online: https://riggingcanada.ca/store/wire-rope-and-aircraft-cable/aircraft-cable/aircraft-cable-7x19-galvanized/38-x-500-galvanized-aircraft-cable/ (accessed on 18 October 2023).
- Sadat, S.A.; Vandewetering, N.; Pearce, J.M. Mechanical and Economic Analysis of Conventional Aluminum Photovoltaic Module Frames, Frames with Side Holes, and Open-Source Downward-Fastened Frames for Non-Traditional Racking. J. Sol. Energy Eng. 2023, 146, 025001. [Google Scholar] [CrossRef]
- Beinert, A.J.; Romer, P.; Heinrich, M.; Mittag, M.; Aktaa, J.; Neuhaus, D.H. The Effect of Cell and Module Dimensions on Thermomechanical Stress in PV Modules. IEEE J. Photovolt. 2020, 10, 70–77. [Google Scholar] [CrossRef]
- Tummalieh, A.; Beinert, A.J.; Reichel, C.; Mittag, M.; Neuhaus, H. Holistic Design Improvement of the PV Module Frame: Mechanical, Optoelectrical, Cost, and Life Cycle Analysis. Prog. Photovolt. Res. Appl. 2022, 30, 1012–1022. [Google Scholar] [CrossRef]
- CanmetENERGY/Housing, Buildings and Communities National Resources Canada Solar Ready Guidelines. 2013. Available online: https://natural-resources.canada.ca/energy-efficiency/data-research-insights-energy-ef/housing-innovation/solar-ready-guidelines/5141 (accessed on 18 June 2023).
- 2018 NDS. Available online: https://awc.org/publications/2018-nds/ (accessed on 18 June 2023).
- Greentech Renewables Solar PV Racking Options—Comparison Chart|Greentech Renewables. Available online: https://www.greentechrenewables.com/article/solar-pv-racking-options-comparison-chart (accessed on 1 November 2023).
- Vandewetering, N.; Hayibo, K.S.; Pearce, J.M. Open-Source Photovoltaic—Electrical Vehicle Carport Designs. Technologies 2022, 10, 114. [Google Scholar] [CrossRef]
- MarketWatch 2023 Guide to Solar Carports: Are They Worth It? Available online: https://www.marketwatch.com/guides/solar/solar-carport/ (accessed on 6 November 2023).
- SunWatts Solar Carport Mount. Available online: https://sunwatts.com/carport-mounts/ (accessed on 6 November 2023).
- Feldman, D.; Ramasamy, V.; Fu, R.; Ramdas, A.; Desai, J.; Margolis, R. U.S. Solar Photovoltaic System and Energy Storage Cost Benchmark (Q1 2020); National Renewable Energy Lab. (NREL): Golden, CO, USA, 2021.
- Wüstenhagen, R.; Wolsink, M.; Bürer, M.J. Social Acceptance of Renewable Energy Innovation: An Introduction to the Concept. Energy Policy 2007, 35, 2683–2691. [Google Scholar] [CrossRef]
- Batel, S.; Devine-Wright, P.; Tangeland, T. Social Acceptance of Low Carbon Energy and Associated Infrastructures: A Critical Discussion. Energy Policy 2013, 58, 1–5. [Google Scholar] [CrossRef]
- Calvert, K.; Mabee, W. More Solar Farms or More Bioenergy Crops? Mapping and Assessing Potential Land-Use Conflicts among Renewable Energy Technologies in Eastern Ontario, Canada. Appl. Geogr. 2015, 56, 209–221. [Google Scholar] [CrossRef]
- Sovacool, B.K. Exploring and Contextualizing Public Opposition to Renewable Electricity in the United States. Sustainability 2009, 1, 702–721. [Google Scholar] [CrossRef]
- Sovacool, B.K.; Lakshmi Ratan, P. Conceptualizing the Acceptance of Wind and Solar Electricity. Renew. Sustain. Energy Rev. 2012, 16, 5268–5279. [Google Scholar] [CrossRef]
- Dias, L.; Gouveia, J.P.; Lourenço, P.; Seixas, J. Interplay between the Potential of Photovoltaic Systems and Agricultural Land Use. Land Use Policy 2019, 81, 725–735. [Google Scholar] [CrossRef]
- Pearce, J.M. Agrivoltaics in Ontario Canada: Promise and Policy. Sustainability 2022, 14, 3037. [Google Scholar] [CrossRef]
- Jamil, U.; Hickey, T.; Pearce, J.M. Solar Energy Modelling and Proposed Crops for Different Types of Agrivoltaics Systems. Available SSRN 4579628 2023. [Google Scholar] [CrossRef]
- Singh, K.; Mishra, S.; Kumar, M.N. A Review on Power Management and Power Quality for Islanded PV Microgrid in Smart Village. Indian J. Sci. Technol. 2017, 10, 1–4. [Google Scholar] [CrossRef]
- Saleh, M.S.; Althaibani, A.; Esa, Y.; Mhandi, Y.; Mohamed, A.A. Impact of Clustering Microgrids on Their Stability and Re-Silience during Blackouts. In Proceedings of the 2015 International Conference on Smart Grid and Clean Energy Technologies, ICSGCE, Offenburg, Germany, 20–23 October 2015; pp. 195–200. [Google Scholar]
- Record Volatility Presides Over the Lumber Market. Available online: http://www.contractlumber.com/blog/2021/9/3/record-volatility-presides-over-the-lumber-market (accessed on 13 November 2023).
- JuliaSeth Pressure Treated Lumber Prices 2015 vs. 2021. r/halifax. 2021. Available online: https://www.reddit.com/r/halifax/comments/mp2cl0/pressure_treated_lumber_prices_2015_vs_2021/ (accessed on 18 October 2023).
- What Is Driving Price Volatility in the Wood Products Industry? Fastmarkets. 2022. Available online: https://www.fastmarkets.com/insights/price-volatility-drivers-in-wood-products-industry/ (accessed on 18 October 2023).
- Municipal Climate Change Action Center Solar Friendly Municipalities—Permit Taxes 2019. Available online: https://mccac.ca/wp-content/uploads/SolarFriendlyMunicipalities-PermitTaxes.pdf (accessed on 18 October 2023).
- Toronto, C. of Solar Permitting & Regulations. Available online: https://www.toronto.ca/services-payments/water-environment/net-zero-homes-buildings/solar-to/solar/ (accessed on 27 November 2023).
- Solar Panels. Available online: https://www.waterloo.ca/en/living/solar-panels.aspx (accessed on 27 November 2023).
- Building Permits|City of London. Available online: https://london.ca/living-london/building-renovating/building-permits (accessed on 29 November 2023).
- Weisser, D. A Guide to Life-Cycle Greenhouse Gas (GHG) Emissions from Electric Supply Technologies. Energy 2007, 32, 1543–1559. [Google Scholar] [CrossRef]
- Muteri, V.; Cellura, M.; Curto, D.; Franzitta, V.; Longo, S.; Mistretta, M.; Parisi, M.L. Review on Life Cycle Assessment of Solar Photovoltaic Panels. Energies 2020, 13, 252. [Google Scholar] [CrossRef]
- Kim, J.; Rabelo, M.; Padi, S.P.; Yousuf, H.; Cho, E.-C.; Yi, J. A Review of the Degradation of Photovoltaic Modules for Life Expectancy. Energies 2021, 14, 4278. [Google Scholar] [CrossRef]
- Aghaei, M.; Fairbrother, A.; Gok, A.; Ahmad, S.; Kazim, S.; Lobato, K.; Oreski, G.; Reinders, A.; Schmitz, J.; Theelen, M.; et al. Review of Degradation and Failure Phenomena in Photovoltaic Modules. Renew. Sustain. Energy Rev. 2022, 159, 112160. [Google Scholar] [CrossRef]
- Joist Hangers and End Moments—Structural Engineering General Discussion—Eng-Tips. Available online: https://www.eng-tips.com/viewthread.cfm?qid=339938 (accessed on 27 August 2023).
- National Research Council Canada, National Building Code of Canada 2020. 2022. Available online: https://nrc.canada.ca/en/certifications-evaluations-standards/codes-canada/codes-canada-publications/national-building-code-canada-2020 (accessed on 18 October 2023).
- Dead Loads. Available online: https://www.designingbuildings.co.uk/wiki/Dead_loads (accessed on 18 June 2023).
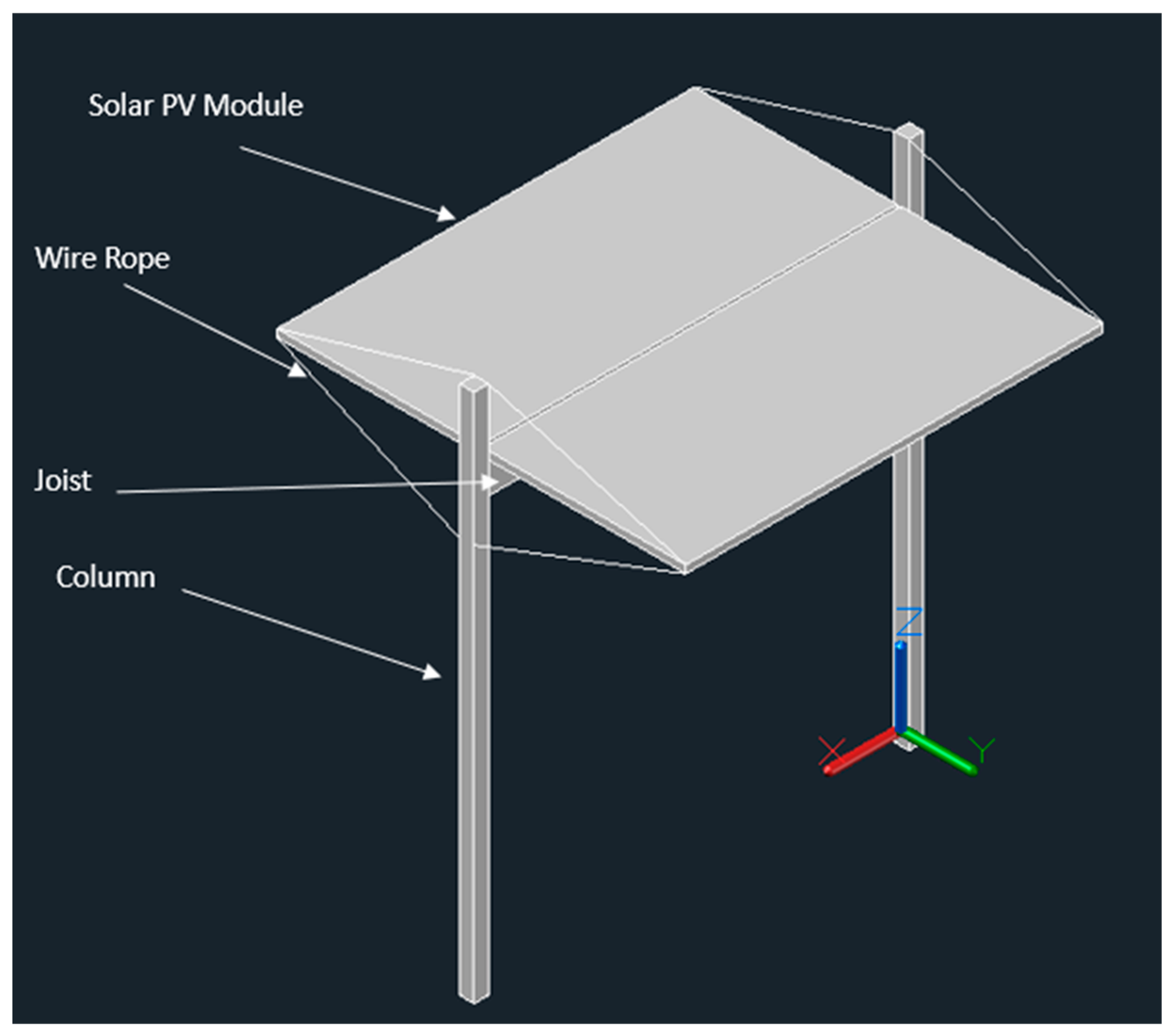
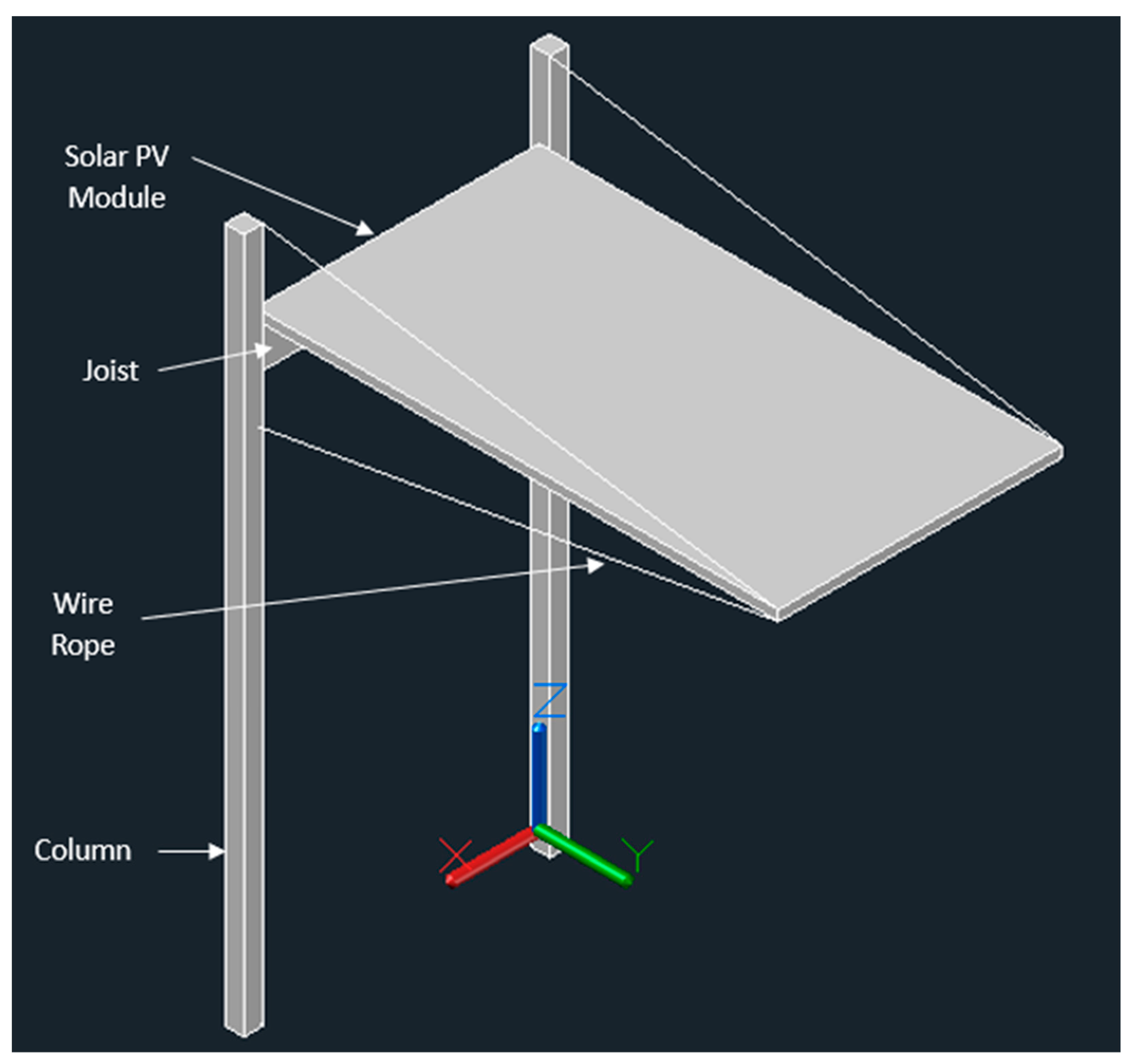
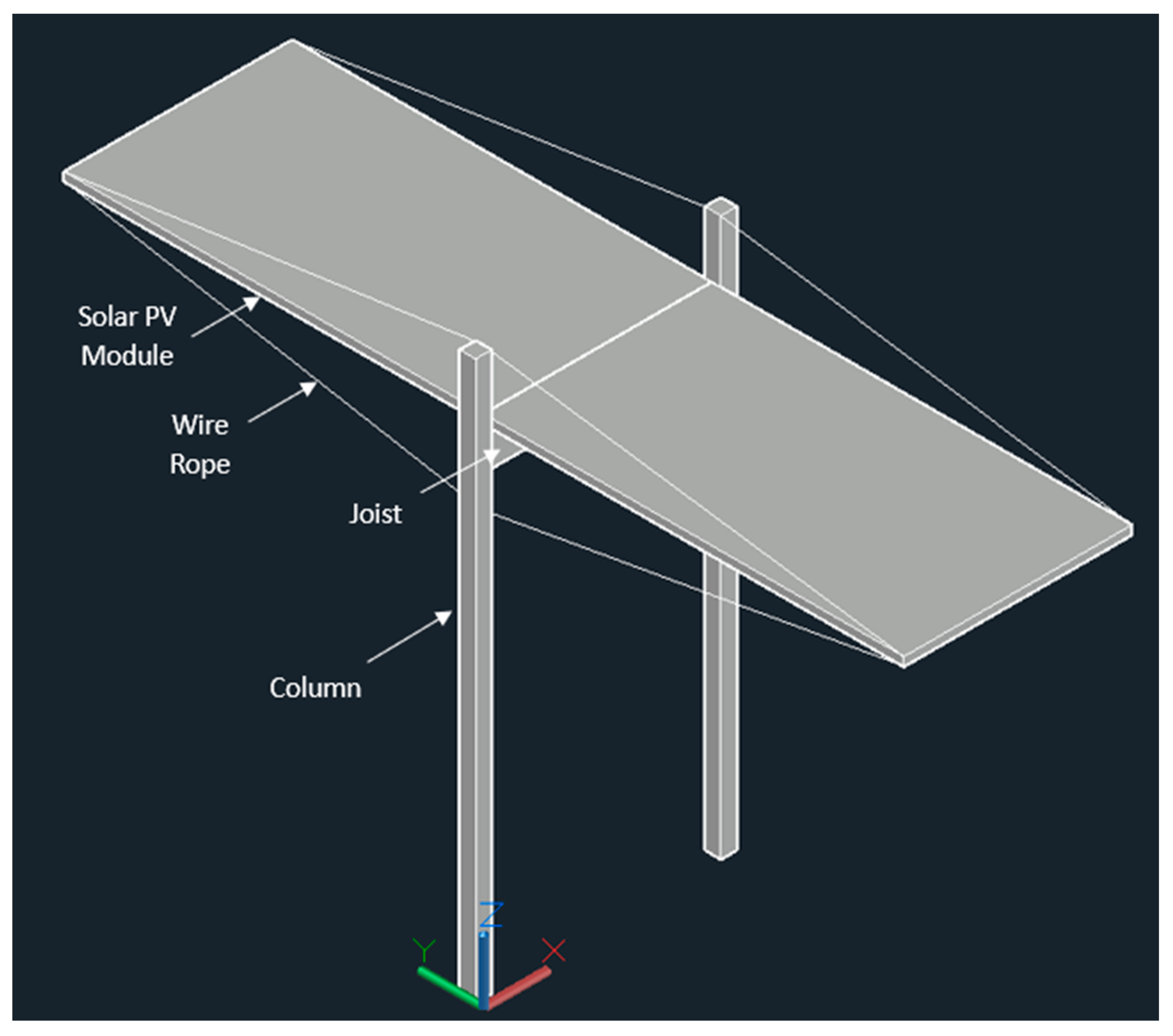


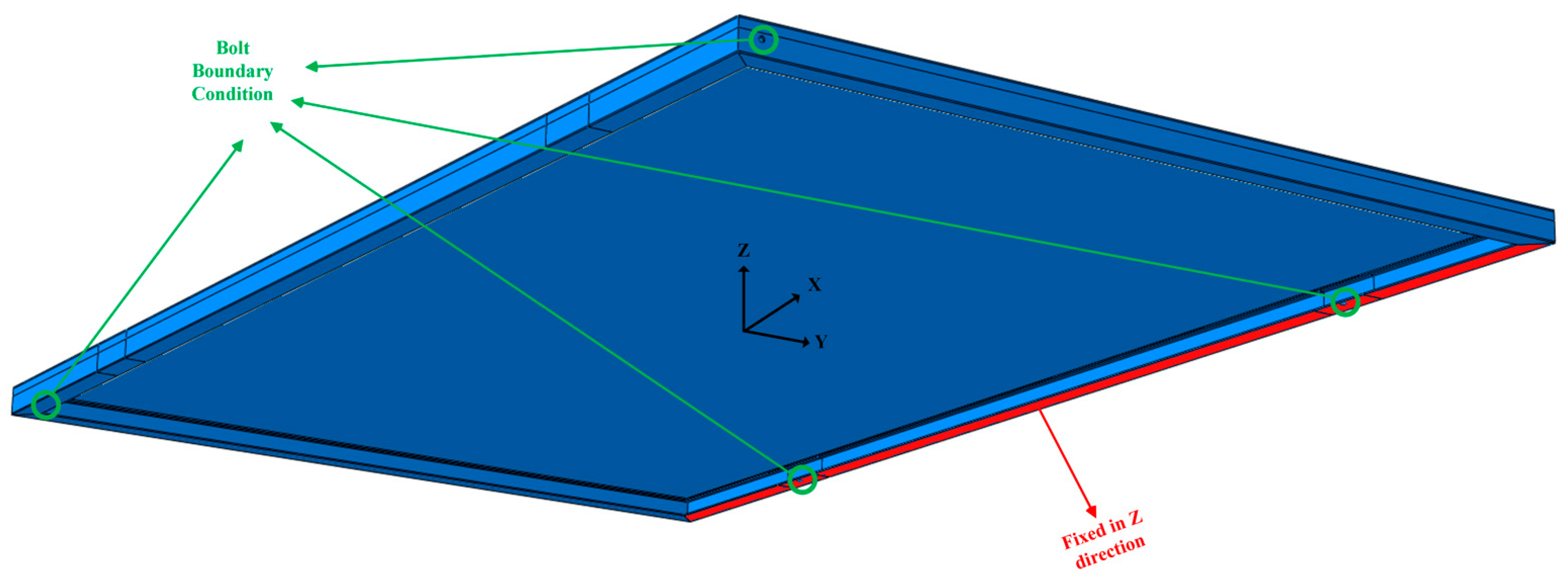





| Lumber | Lumber Breadth ‘b’ (m) | Lumber Height ‘h’ (m) | Area ‘A’ (m2) A = bh | Moment of Inertia ‘I’ (m4) I = bh3/12 | First Moment of Area ‘Q’ (m3) Q = hA/8 |
|---|---|---|---|---|---|
| 2 × 12 | 0.038 | 0.286 | 0.010868 | 7.4079 × 10−5 | 3.8853 × 10−4 |
| 2 × 4 | 0.038 | 0.089 | 0.003382 | 2.2324 × 10−6 | 3.7624 × 10−5 |
| 2 × 6 | 0.038 | 0.140 | 0.005320 | 8.6893 × 10−6 | 9.3100 × 10−5 |
| 2 × 8 | 0.038 | 0.184 | 0.006992 | 1.9726 × 10−5 | 1.6081 × 10−4 |
| 2 × 10 | 0.038 | 0.235 | 0.008930 | 4.1096 × 10−5 | 2.6232 × 10−4 |
| 6 × 6 | 0.140 | 0.140 | 0.019600 | 3.2013 × 10−5 | 3.4300 × 10−4 |
| Diameter—Inches (m) | Breaking Strength—lbs. (N) | Approx. Wt./1000 ft | Workload Limit—lbs. (N) |
|---|---|---|---|
| 1/16 (0.0016) | 480 (2135) | 0.75 | 96 (427) |
| 3/32 (0.0024) | 1000 (4448) | 16.5 | 200 (890) |
| 1/8 (0.0032) | 2000 (8896) | 29 | 400 (1779) |
| 5/32 (0.0040) | 2800 (12,455) | 45 | 560 (2491) |
| 3/16 (0.0048) | 4200 (18,682) | 65 | 840 (3736) |
| 7/32 (0.0056) | 5600 (24,910) | 86 | 1120 (4982) |
| 1/4 (0.0064) | 7000 (31,138) | 110 | 1400 (6228) |
| 5/16 (0.0079) | 9800 (43,592) | 173 | 1960 (8718) |
| 3/8 (0.0095) | 14,400 (64,054) | 243 | 2880 (1281) |
| Member Name | Piece 1 | Cost per Piece (CAD) 2 | Quantity | Cost (CAD) |
|---|---|---|---|---|
| Joists | 2 × 12 × 8 | 35.00 | 1 | 35.00 |
| Posts | 6 × 6 × 10 | 52 | 2 | 104.00 |
| Joist to Post Connection | 2 × 4 Fence Bracket | 0.43 | 2 | 0.86 |
| 7 × 19 PVC Coated and Galvanized Aircraft Cable | 3/8” | 55.44 | 1 | 55.44 |
| Connections | 2-1/2” Brown Deck Screws | 2.61 | 1 | 2.61 |
| Cable Clamp | 5/16” Wire Rope Clip—Zinc Plated | 1.99 | 16 | 31.84 |
| Turnbuckle | 9-3/8 Turnbuckle | 6.94 | 4 | 27.76 |
| Hooks | 4-3/8 Hooks | 5.22 | 8 | 41.76 |
| Washers | 1/4 Washers | 1.90 | 1 | 1.90 |
| Eye Bolts | 1/4 × 2 Eye Bolts | 1.72 | 8 | 13.76 |
| Hinges | Light duty (2”) | 2.69 | 4 | 10.76 |
| Nut and Bolt | 1/4 inch | 2.78 | 1 | 2.78 |
| Metal fixture | 2” | 8.49 | 1 | 8.49 |
| Total Cost with No Concrete | 336.95 | |||
| Concrete for Posts | 30 MPa Quikrete concrete | 6.38 | 10 bags | 63.80 |
| Total Cost: | 400.75 |
| Member Name | Piece 1 | Cost per Piece (CAD) 2 | Quantity | Cost (CAD) |
|---|---|---|---|---|
| Joists | 2 × 6 × 8 | 12.78 | 1 | 12.78 |
| Posts | 8 × 8 × 10 | 125.33 | 2 | 250.66 |
| Joist to Post Connection | 2 × 4 Fence Bracket | 0.43 | 2 | 0.86 |
| 7 × 19 PVC Coated and Galvanized Aircraft Cable | 3/8” | 55.44 | 1 | 55.44 |
| Connections | 2-1/2” Brown Deck Screws | 2.61 | 1 | 2.61 |
| Cable Clamp | 5/16” Wire Rope Clip—Zinc Plated | 1.99 | 8 | 15.92 |
| Turnbuckle | 9-3/8 Turnbuckle | 6.94 | 2 | 13.88 |
| Hooks | 4-3/8 Hooks | 5.22 | 4 | 20.88 |
| Washers | 1/4 Washers | 1.90 | 1 | 1.90 |
| Eye Bolts | 1/4 × 2 Eye Bolts | 1.72 | 4 | 6.88 |
| Hinges | Light duty (2”) | 2.69 | 2 | 5.38 |
| Nut and Bolt | 1/4 inch | 2.78 | 1 | 2.78 |
| Metal Fixture | 2” | 8.49 | 1 | 8.49 |
| Total Cost with No Concrete | 398.45 | |||
| Concrete for Posts | 30 MPa Quikrete concrete | 6.38 | 10 bags | 63.80 |
| Total Cost: | 462.25 |
| Member Name | Piece 1 | Cost per Piece (CAD) 2 | Quantity | Cost (CAD) |
|---|---|---|---|---|
| Joists | 2 × 12 × 8 | 35.00 | 1 | 35.00 |
| Posts | 8 × 8 × 10 | 125.33 | 2 | 250.66 |
| Joist to Post Connection | 2 × 4 Fence Bracket | 0.43 | 2 | 0.86 |
| 7 × 19 PVC Coated and Galvanized Aircraft Cable | 3/8” | 110.88 | 1 | 110.88 |
| Connections | 2-1/2” Brown Deck Screws | 2.61 | 1 | 2.61 |
| Cable Clamp | 5/16” Wire Rope Clip—Zinc Plated | 1.99 | 16 | 31.84 |
| Turnbuckle | 9-3/8 Turnbuckle | 6.94 | 4 | 27.76 |
| Hooks | 4-3/8 Hooks | 5.22 | 8 | 41.76 |
| Washers | 1/4 Washers | 1.90 | 1 | 1.90 |
| Eye Bolts | 1/4 × 2 Eye Bolts | 1.72 | 8 | 13.76 |
| Metal Fixture | 2” | 8.49 | 1 | 8.49 |
| Nut and Bolt | 1/4 inch | 2.78 | 1 | 2.78 |
| Hinges | Light duty (2”) | 2.69 | 4 | 10.76 |
| Total Cost with No Concrete | 539.05 | |||
| Concrete for Posts | 30 MPa Quikrete concrete | 6.38 | 10 bags | 63.80 |
| Total Cost: | 602.85 |
| Material | Thickness [mm] | Density [tonne/mm3] | Young’s Modulus [MPa] | Poisson’s Ratio [64,66] | Strength [MPa] | Number of Elements | |
|---|---|---|---|---|---|---|---|
| Frame | Aluminum (Alloy 6063 [64]) | 1.80 | 2.70 × 10−9 | 70,000 | 0.33 | 214 yield 241 tensile | 15,980 |
| Sealing | Rubber (Polyurethane elastomer [64]) | 2.00 | 6.70 × 10−11 | 7.40 | 0.30 | 0.0814–103 | 3654 |
| Laminate | Glass (soda-lime glass [64]) | 3.2 0 | 2.50 × 10−9 | 70,000 | 0.20 | Compressive Strength = 274 | 64,288 |
| Solar cells (Czochralski silicon [64]) | 0.18 | 2.329 × 10−9 | 112,400 | 0.28 | Compressive Strength = 120 | ||
| Encapsulation (ethylene vinyl acetate [64]) | 0.45 | 9.6 × 10−10 | T-dep. | 0.40 | 3.4–10 | ||
| Back sheet (TPT [64]) | 0.22 | 2.52 × 10−9 | 3500 | 0.29 | Break stress = 132 | ||
| Load Combination | Load [kPa] (up to 15°) | Load [kPa] (30°) | Load [kPa] (up to 45°) | Load [kPa] (60°) |
|---|---|---|---|---|
| 0.9D + 1.4W − 0.5S | −2.99 | −2.77 | −2.56 | −2.33 |
| 1.25D + 1.5S − 0.4W | 3.62 | 2.96 | 2.31 | 1.65 |
| Factor | Value (MPa) |
|---|---|
| fb | 6.03 |
| fv | 0.93 |
| ft | 3.10 |
| fc | 7.93 |
| E | 9652.66 |
| Emin | 3516.33 |
| Factor | Value |
|---|---|
| CD | 1.15 |
| CT | 1.00 |
| CM | 1.00, 0.97 and 0.90 |
| CL | 0.64. 0.76 |
| Cfu | 1.2 |
| Ci | 1, 0.8 and 0.95 |
| Cr | 1.00 |
| CF | 1.10 |
| CP | 0.29 |
| Factored Capacities | Value (MPa) |
|---|---|
| fb * | 4.68 |
| fv * | 0.83 |
| ft * | 3.14 |
| fc * | 2.94 |
| E * | 8253.03 |
| Emin * | 3006.46 |
| Lumber | Resisting Bending Moment ‘Mr’ (kN-m) | Resisting Shear Force ‘Vr’ (kN) | Resisting Tensile Force ‘Tr’ (kN) | Resisting Compressive Force ‘Cr’ (kN) |
|---|---|---|---|---|
| 2 × 4 | 0.23 | 1.87 | 10.62 | 9.97 |
| 2 × 6 | 0.58 | 2.95 | 16.70 | 15.69 |
| 2 × 8 | 1.00 | 3.87 | 21.95 | 20.62 |
| 2 × 10 | 1.64 | 4.94 | 28.04 | 26.34 |
| 4 × 10 | 3.27 | 9.89 | 56.08 | 52.67 |
| 2 × 12 | 2.42 | 6.02 | 34.12 | 32.05 |
| 4 × 4 | 0.55 | 4.39 | 24.87 | 23.36 |
| 6 × 6 | 2.14 | 10.85 | 61.54 | 57.80 |
| Racking System | Cost (CAD) | Cost (CAD/Watt) |
|---|---|---|
| Fixed Racking Configuration [44] | 426 (389) | 0.35 (0.32) * |
| Variable Tilt Racking Configuration [45] | 438 (406) | 0.36 (0.34) * |
| Vertical Wood Racking Configuration [46] | 371 (300) | 0.15 (0.13) * |
| T-shaped Racking Configuration (2-module Design) | 397 | 0.43 |
| T-shaped Racking Configuration (4-module Design) | 1155 | 0.63 |
| Sloped Racking Configuration | 372 | 0.40 |
| Inverse Y Racking Configuration | 427 | 0.46 |
| Fixed Racking Configuration (Modified to 1.8 m with 6 × 6 columns) | 526 | 0.44 |
| Variable Tilt Racking Configuration (Modified to 1.8 m with 6 × 6 columns) | 598 | 0.50 |
| Cantilever Carport Racking Configuration (one module) | 471 | 1.00 |
| Cantilever Carport Racking Configuration (two modules) | 612 | 0.66 |
| Variable tilt Wood and Wire Rope T-shaped Configuration | 410 | 0.44 |
| Country | Price [CAD] 1 | Source 2 |
|---|---|---|
| Canada | 7.69 | The Home Depot, London, Canada |
| USA | 6.62 | The Home Depot, Detroit, USA |
| United Kingdom | 5.84 | B&Q, London, UK |
| Netherlands | 16.04 | Woodvision, Kampen, The Netherlands |
| Australia | 13.29 | Australian Treated Pine Pty Ltd., Melborne, Australia |
| Brazil | 12.13 | Fremade Madeiras, São Paulo, Brazil |
| India | 12.45 | IndiaMart, Uttar Pradesh, India |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamil, U.; Vandewetering, N.; Sadat, S.A.; Pearce, J.M. Wood- and Cable-Based Variable Tilt Stilt-Mounted Solar Photovoltaic Racking System. Designs 2024, 8, 6. https://doi.org/10.3390/designs8010006
Jamil U, Vandewetering N, Sadat SA, Pearce JM. Wood- and Cable-Based Variable Tilt Stilt-Mounted Solar Photovoltaic Racking System. Designs. 2024; 8(1):6. https://doi.org/10.3390/designs8010006
Chicago/Turabian StyleJamil, Uzair, Nicholas Vandewetering, Seyyed Ali Sadat, and Joshua M. Pearce. 2024. "Wood- and Cable-Based Variable Tilt Stilt-Mounted Solar Photovoltaic Racking System" Designs 8, no. 1: 6. https://doi.org/10.3390/designs8010006
APA StyleJamil, U., Vandewetering, N., Sadat, S. A., & Pearce, J. M. (2024). Wood- and Cable-Based Variable Tilt Stilt-Mounted Solar Photovoltaic Racking System. Designs, 8(1), 6. https://doi.org/10.3390/designs8010006










