Active Vibration Control of Timoshenko Sigmoid Functionally Graded Porous Composite Beam with Distributed Piezoelectric Sensor/Actuator in a Thermal Environment
Abstract
1. Introduction
2. Mathematical Modeling
3. Finite Element Formulation
4. Piezoelectric Constitutive Equations
5. Dynamic Equation and State Space Model
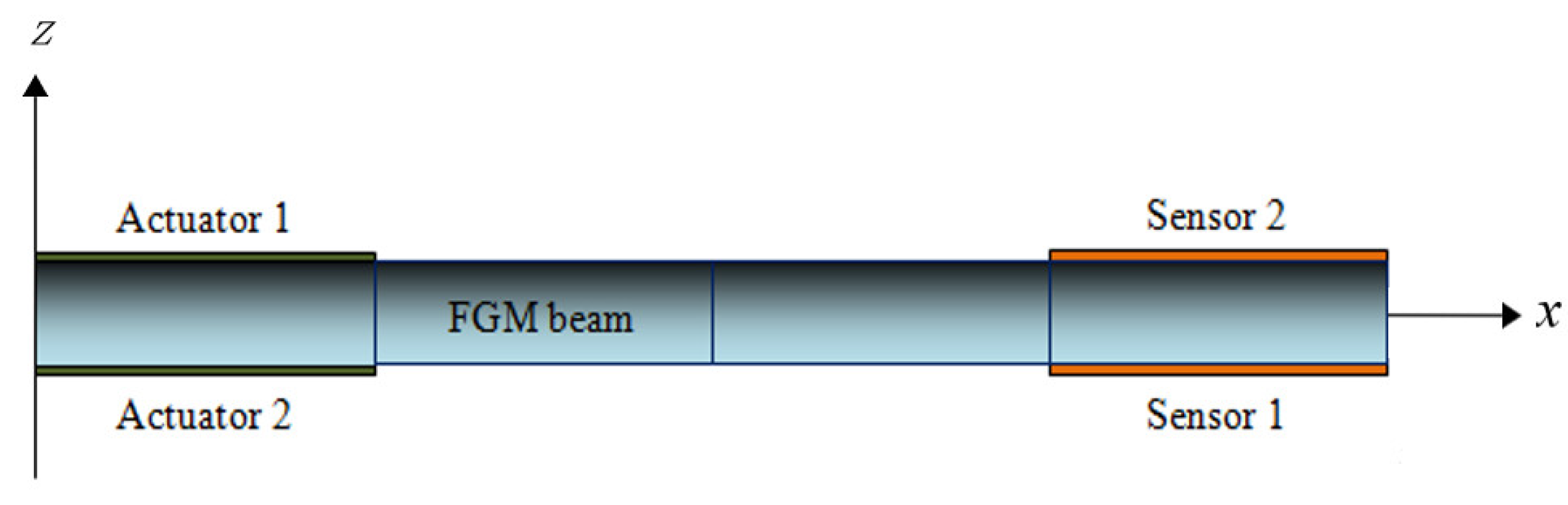
6. Validation Study
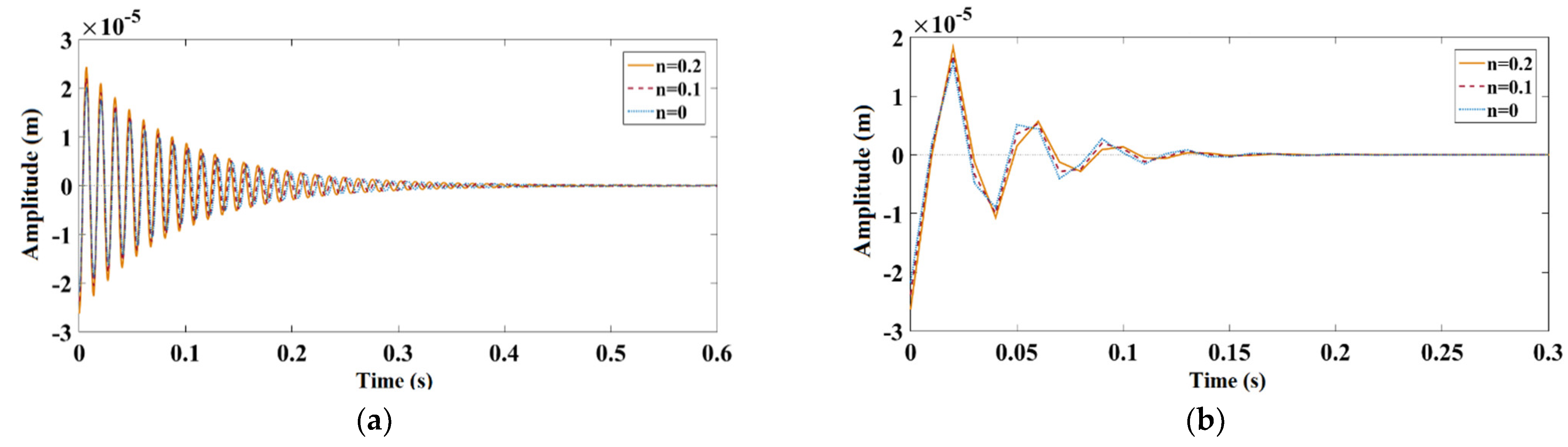
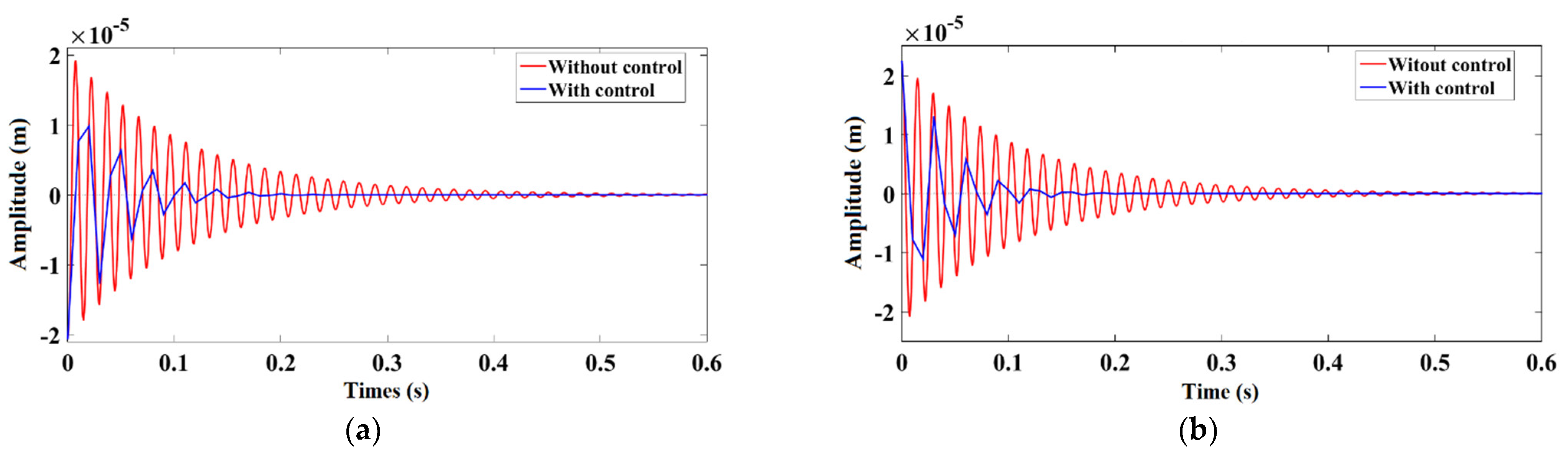
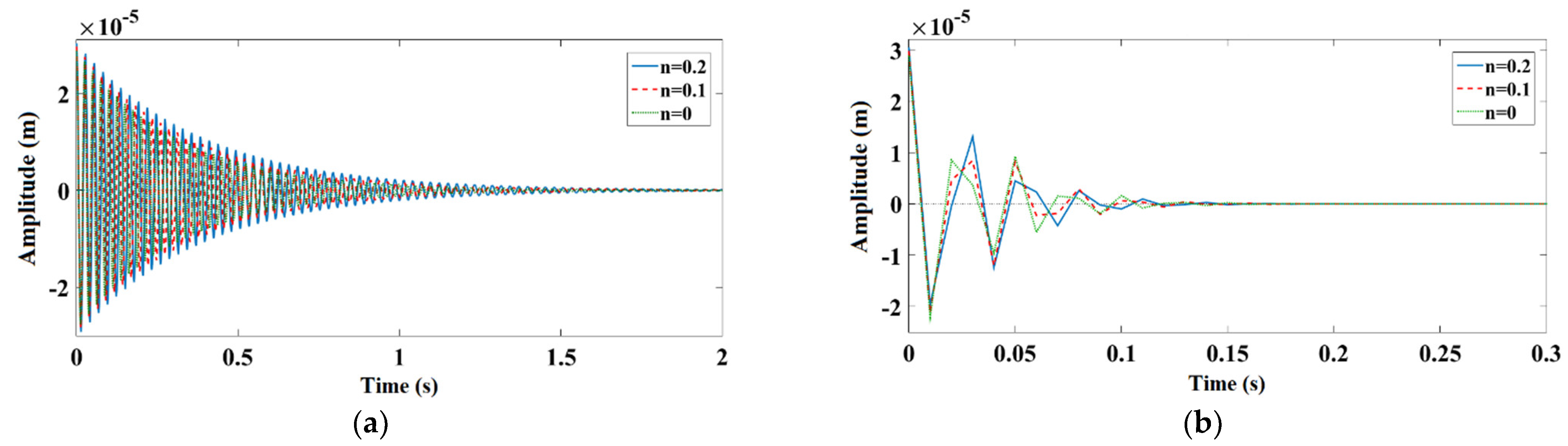
7. Results and Discussions
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B

References
- Bouhedma, S.; Hu, S.; Schütz, A.; Lange, F.; Bechtold, T.; Ouali, M.; Hohlfeld, D. Analysis and Characterization of Optimized Dual-Frequency Vibration Energy Harvesters for Low-Power Industrial Applications. Micromachines 2022, 13, 1078. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Liu, L.; Wang, P.; Liu, Y.; Wei, X.; Xu, Q.; Sun, H. Modeling and Analysis of Radial Electromagnetic Force and Vibration Characteristics Based on Deflection Dual-Stator Switched Reluctance Generator. Micromachines 2022, 13, 1494. [Google Scholar] [CrossRef] [PubMed]
- Beards, C.E. Structural Vibration: Analysis and Damping, 1st ed.; Arnold: London, UK, 1996. [Google Scholar]
- Li, Z.; Su, Z.; Zhao, L.; Han, H.; Guo, Z.; Zhao, Y.; Sun, H. Design and Locomotion Study of Stick-Slip Piezoelectric Actuator Using Two-Stage Flexible Hinge Structure. Micromachines 2021, 12, 154. [Google Scholar] [CrossRef] [PubMed]
- Čeponis, A.; Mažeika, D.; Makutėnienė, D. Development of a Novel 2-DOF Rotary–Linear Piezoelectric Actuator Operating under Hybrid Bending–Radial Vibration Mode. Micromachines 2021, 12, 728. [Google Scholar] [CrossRef] [PubMed]
- Qin, Y.; Zhang, Y.; Duan, H.; Han, J. High-Bandwidth Hysteresis Compensation of Piezoelectric Actuators via Multilayer Feedforward Neural Network Based Inverse Hysteresis Modeling. Micromachines 2021, 12, 1325. [Google Scholar] [CrossRef]
- Wang, W.; Wang, J.; Wang, R.; Chen, Z.; Han, F.; Lu, K.; Ju, B. Modeling and Compensation of Dynamic Hysteresis with Force-Voltage Coupling for Piezoelectric Actuators. Micromachines 2021, 12, 1366. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.; Yan, P.; Li, H. Finite Element Modeling and Test of Piezo Disk with Local Ring Electrodes for Micro Displacement. Micromachines 2022, 13, 951. [Google Scholar] [CrossRef]
- Sanbi, M.; Saadani, R.; Sbai, K.; Rahmoune, M. Thermoelastic and pyroelectric couplings effects on dynamics and active control of smart piezolaminated beam modeled by finite element method. Smart Mater. Res. 2014, 2014, 145087. [Google Scholar] [CrossRef]
- Bendine, K.; Boukhoulda, F.B.; Nouari, M.; Satla, Z. Active vibration control of functionally graded beams with piezoelectric layers based on higher order shear deformation theory. Earthq. Eng. Eng. Vib. 2016, 15, 611–620. [Google Scholar] [CrossRef]
- El Harti, K.; Sanbi, M.; Rahmoune, M.; Saadani, R.; Agounoun, R.; Bentaleb, M.; Rahmoune, M. Active vibration control of sandwich FGM beam with piezoelectric sensor/actuator. Int. J. Appl. Eng. Res 2017, 12, 9338–9345. [Google Scholar]
- Panda, R.K.; Nayak, B.; Sarangi, S.K. Active vibration control of smart functionally graded beams. Procedia Eng. 2016, 144, 551–559. [Google Scholar] [CrossRef]
- Mahamood, R.M.; Akinlabi, E.T. Functionally Graded Materials, Series ed.; Carlos, P., Ed.; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Niino, M.; Hirai, T.; Watanabe, R. Functionally gradient materials. In pursuit of super heat resisting materials for spacecraft. J. Jpn. Soc. Compos. Mater. 1987, 13, 257–264. [Google Scholar] [CrossRef]
- Huang, X.L.; Dong, L.; Wei, G.Z.; Zhong, D.Y. Nonlinear free and forced vibrations of porous sigmoid functionally graded plates on nonlinear elastic foundations. Compos. Struct. 2019, 228, 111326. [Google Scholar] [CrossRef]
- Zhu, J.; Lai, Z.; Yin, Z.; Jeon, J.; Lee, S. Fabrication of ZrO2–NiCr functionally graded material by powder metallurgy. Mater. Chem. Phys. 2001, 68, 130–135. [Google Scholar] [CrossRef]
- Hong, J.; Wang, S.; Qiu, X.; Zhang, G. Bending and Wave Propagation Analysis of Magneto-Electro-Elastic Functionally Graded Porous Microbeams. Crystals 2022, 12, 732. [Google Scholar] [CrossRef]
- Hong, J.; Wang, S.; Zhang, G.; Mi, C. On the Bending and Vibration Analysis of Functionally Graded Magneto-Electro-Elastic Timoshenko Microbeams. Crystals 2021, 11, 1206. [Google Scholar] [CrossRef]
- Yang, Z.X.; He, X.T.; Peng, D.D.; Sun, J.Y. Free damping vibration of piezoelectric cantilever beams: A biparametric perturbation solution and its experimental verification. Appl. Sci. 2019, 10, 215. [Google Scholar] [CrossRef]
- Jing, H.X.; He, X.T.; Du, D.W.; Peng, D.D.; Sun, J.Y. Vibration analysis of piezoelectric cantilever beams with bimodular functionally-graded properties. Appl. Sci. 2020, 10, 5557. [Google Scholar] [CrossRef]
- Sharma, P. Vibration analysis of FGP actuator due to longitudinal piezoelectric coupling coefficient. AIP Conf. Proc. 2020, 2220, 130072. [Google Scholar]
- Zhang, M.; Zhou, Z. Bending and Vibration Analysis of Flexoelectric Beam Structure on Linear Elastic Substrates. Micromachines 2022, 13, 915. [Google Scholar] [CrossRef]
- Doroushi, A.; Eslami, M.R.; Komeili, A. Vibration analysis and transient response of an FGPM beam under thermo-electro-mechanical loads using higher-order shear deformation theory. J. Intell. Mater. Syst. Struct. 2011, 22, 231–243. [Google Scholar] [CrossRef]
- Kang, X.; Zhang, D.G.; Jiang, M. Size effect on dynamic characteristics of piezoelectric micromachined ultrasonic transducers. J. Appl. Sci. Eng. 2013, 16, 353–362. [Google Scholar]
- Njim, E.K.; Bakhy, S.H.; Al-Waily, M. Analytical and numerical investigation of buckling behavior of functionally graded sandwich plate with porous core. J. Appl. Sci. Eng. 2021, 25, 339–347. [Google Scholar]
- Redddy, B.S.; Kumar, J.S.; Reddy, C.E.; Reddy, V.K. Free vibration behaviour of functionally graded plates using higher-order shear deformation theory. J. Appl. Sci. Eng. 2014, 17, 231–241. [Google Scholar]
- El Harti, K.; Rahmoune, M.; Sanbi, M.; Saadani, R.; Bentaleb, M.; Rahmoune, M. Finite element model of vibration control for an exponential functionally graded Timoshenko beam with distributed piezoelectric sensor/actuator. Actuators 2019, 8, 19. [Google Scholar] [CrossRef]
- Maruani, J.; Bruant, I.; Pablo, F.; Gallimard, L. A numerical efficiency study on the active vibration control for a FGPM beam. Compos. Struct. 2017, 182, 478–486. [Google Scholar] [CrossRef]
- Li, L.; Liao, W.H.; Zhang, D.; Zhang, Y. Vibration control and analysis of a rotating flexible FGM beam with a lumped mass in temperature field. Compos. Struct. 2019, 208, 244–260. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Hashemi, M. Vibration analysis of non-uniform imperfect functionally graded beams with porosities in thermal environment. J. Mech. 2017, 33, 739–757. [Google Scholar] [CrossRef]
- Esen, I.; Abdelrahman, A.A.; Eltaher, M.A. On vibration of sigmoid/symmetric functionally graded nonlocal strain gradient nanobeams under moving load. International. J. Mech. Mater. Des. 2021, 17, 721–742. [Google Scholar]
- Esen, I.; Eltaher, M.A.; Abdelrahman, A.A. Vibration response of symmetric and sigmoid functionally graded beam rested on elastic foundation under moving point mass. Mech. Based Des. Struct. Mach. 2021, 1–25. [Google Scholar] [CrossRef]
- Bodaghi, M.; Damanpack, A.R.; Aghdam, M.M.; Shakeri, M. Non-linear active control of FG beams in thermal environments subjected to blast loads with integrated FGP sensor/actuator layers. Compos. Struct. 2012, 94, 3612–3623. [Google Scholar] [CrossRef]
- Kumar, P.; Harsha, S.P. Static and vibration response analysis of sigmoid function-based functionally graded piezoelectric non-uniform porous plate. J. Intell. Mater. Syst. Struct. 2022, 33, 2197–2227. [Google Scholar] [CrossRef]
- El Harti, K.; Rahmoune, M.; Sanbi, M.; Saadani, R.; Bentaleb, M.; Rahmoune, M. Dynamic control of Euler Bernoulli FG porous beam under thermal loading with bonded piezoelectric materials. Ferroelectrics 2020, 558, 104–116. [Google Scholar] [CrossRef]
- El Harti, K.; Sanbi, M.; Saadani, R.; Bentaleb, M.; Rahmoune, M. Dynamic analysis and active control of distributed piezothermoelastic FGM composite beam with porosities modeled by the finite element method. Compos. Mech. Comput. Appl. Int. J. 2021, 12, 57–74. [Google Scholar] [CrossRef]
- Yan, Y.; Liu, B.; Xing, Y.; Carrera, E.; Pagani, A. Free vibration analysis of variable stiffness composite laminated beams and plates by novel hierarchical differential quadrature finite elements. Compos. Struct. 2021, 274, 114364. [Google Scholar] [CrossRef]
- Kabir, H.; Aghdam, M.M. A robust Bézier based solution for nonlinear vibration and post-buckling of random checkerboard graphene nano-platelets reinforced composite beams. Compos. Struct. 2019, 212, 184–198. [Google Scholar] [CrossRef]
- Sharma, P. Vibration analysis of FGPM beam: A review. Mater. Today Proc. 2021, 44, 1384–1390. [Google Scholar] [CrossRef]
- Shivashankar, P.; Gopalakrishnan, S. Review on the use of piezoelectric materials for active vibration, noise, and flow control. Smart Mater. Struct. 2020, 29, 053001. [Google Scholar] [CrossRef]
- Arshid, E.; Khorshidvand, A.R. Free vibration analysis of saturated porous FG circular plates integrated with piezoelectric actuators via differential quadrature method. Thin-Walled Struct. 2018, 125, 220–233. [Google Scholar] [CrossRef]
- Friedman, Z.; Kosmatka, J.B. An improved two-node Timoshenko beam finite element. Comput. Struct. 1993, 47, 473–481. [Google Scholar] [CrossRef]
- Eisenberger, M.; Abramovich, H. Shape control of non-symmetric piezolaminated composite beams. Compos. Struct. 1997, 38, 565–571. [Google Scholar] [CrossRef]
- Cowper, G.R. The shear coefficient in Timoshenko’s beam theory. ASME J. App. Mech. 1996, 33, 335–340. [Google Scholar] [CrossRef]
- Aldraihem, O.J.; Wetherhold, R.C.; Singh, T. Distributed control of laminated beams: Timoshenko theory vs. Euler-Bernoulli theory. J. Intell. Mater. Syst. Struct. 1997, 8, 149–157. [Google Scholar] [CrossRef]
- Anjanappa, M.; Bi, J. Magnetostrictive mini actuators for smart structures applications. Int. J. Smart Mater. Struct. 1994, 3, 383–390. [Google Scholar] [CrossRef]
- Heidary, F.; Reza Eslami, M. Dynamic analysis of distributed piezothermoelastic composite plate using first-order shear deformation theory. J. Therm. Stress. 2004, 27, 587–605. [Google Scholar] [CrossRef]
- Debard, Y. Méthode des Eléments Finis: Poutre Soumise à un Effort Normal; Mans: Le Mans, France, 2011. [Google Scholar]
- Boyere, E. Modélisation de l’Amortissement en Dynamique. 2011. Clé: R5.05.04: 2011. Available online: https://www.code-aster.org/V2/doc/v10/fr/man_r/r5/r5.05.04.pdf (accessed on 7 September 2018).
- Lou, J.; Liao, J.; Wei, Y.; Yang, Y.; Li, G. Experimental identification and vibration control of a piezoelectric flexible manipulator using optimal multi-poles placement control. Appl. Sci. 2017, 7, 309. [Google Scholar] [CrossRef]
| Experimental Results Reference [19] | Theoretical Results Reference [20] | Our Work | Relative Errors (%) |
|---|---|---|---|
| 123.25 | 123.20 | 113.80 | 7.67/7.63 |
| Properties (Units) | FGM | Sensor | Actuator |
|---|---|---|---|
| Length (m) | |||
| Width (m) | |||
| Thickness (m) | |||
| Density | |||
| Young’s modulus (G·Pa) | |||
| Piezoelectric stress constant (Vm/N) | - | ||
| Piezoelectric strain constant (m/V) | - |
| k | 0.2 | 0.5 | 1 | 2 | 5 |
|---|---|---|---|---|---|
| n | |||||
| 0 | 76.8 | 72.7 | 67.5 | 60.8 | 52 |
| 0.1 | 77.8 | 73.4 | 67.7 | 60.1 | 49.8 |
| 0.2 | 79 | 74.3 | 67.9 | 59.2 | 46.9 |
| ΔT = 5 [K] | |||||
| 0 | 76.7 | 72.6 | 67.3 | 60.5 | 51.7 |
| 0.1 | 77.7 | 73.3 | 67.5 | 49.8 | 49.5 |
| 0.2 | 78.9 | 74.2 | 67.7 | 58.9 | 46.6 |
| k | 0.2 | 0.5 | 1 | 2 | 5 |
|---|---|---|---|---|---|
| n | |||||
| 0 | 76.6 | 72.5 | 67.3 | 60.6 | 51.8 |
| 0.1 | 77.6 | 73.2 | 67.5 | 59.9 | 49.6 |
| 0.2 | 78.8 | 74 | 67.7 | 59 | 46.7 |
| ΔT = 5 [K] | |||||
| 0 | 76.5 | 72.4 | 67.1 | 60.3 | 51.5 |
| 0.1 | 77.5 | 73.1 | 67.3 | 59.6 | 49.3 |
| 0.2 | 78.7 | 73.9 | 67.5 | 58.7 | 46.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Harti, K.; Saadani, R.; Rahmoune, M. Active Vibration Control of Timoshenko Sigmoid Functionally Graded Porous Composite Beam with Distributed Piezoelectric Sensor/Actuator in a Thermal Environment. Designs 2023, 7, 2. https://doi.org/10.3390/designs7010002
El Harti K, Saadani R, Rahmoune M. Active Vibration Control of Timoshenko Sigmoid Functionally Graded Porous Composite Beam with Distributed Piezoelectric Sensor/Actuator in a Thermal Environment. Designs. 2023; 7(1):2. https://doi.org/10.3390/designs7010002
Chicago/Turabian StyleEl Harti, Khalid, Rachid Saadani, and Miloud Rahmoune. 2023. "Active Vibration Control of Timoshenko Sigmoid Functionally Graded Porous Composite Beam with Distributed Piezoelectric Sensor/Actuator in a Thermal Environment" Designs 7, no. 1: 2. https://doi.org/10.3390/designs7010002
APA StyleEl Harti, K., Saadani, R., & Rahmoune, M. (2023). Active Vibration Control of Timoshenko Sigmoid Functionally Graded Porous Composite Beam with Distributed Piezoelectric Sensor/Actuator in a Thermal Environment. Designs, 7(1), 2. https://doi.org/10.3390/designs7010002







