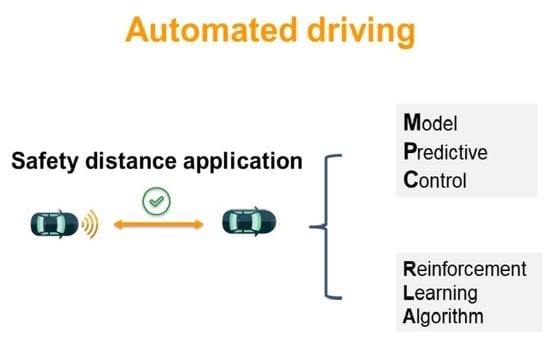
Design and Implementation of Reinforcement Learning for Automated Driving Compared to Classical MPC Control
Abstract
1. Introduction
2. Materials and Methods
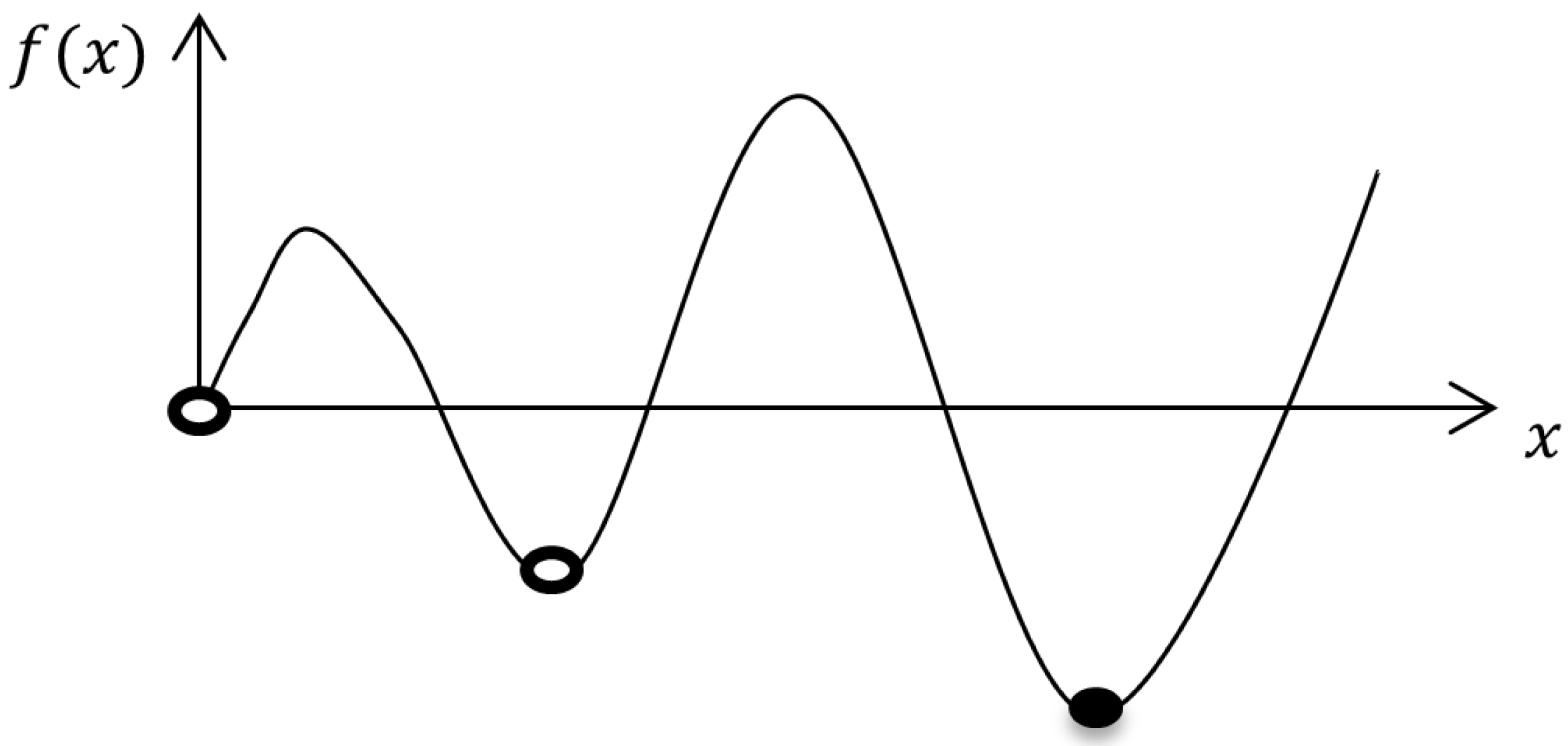
2.1. General Optimization Problem
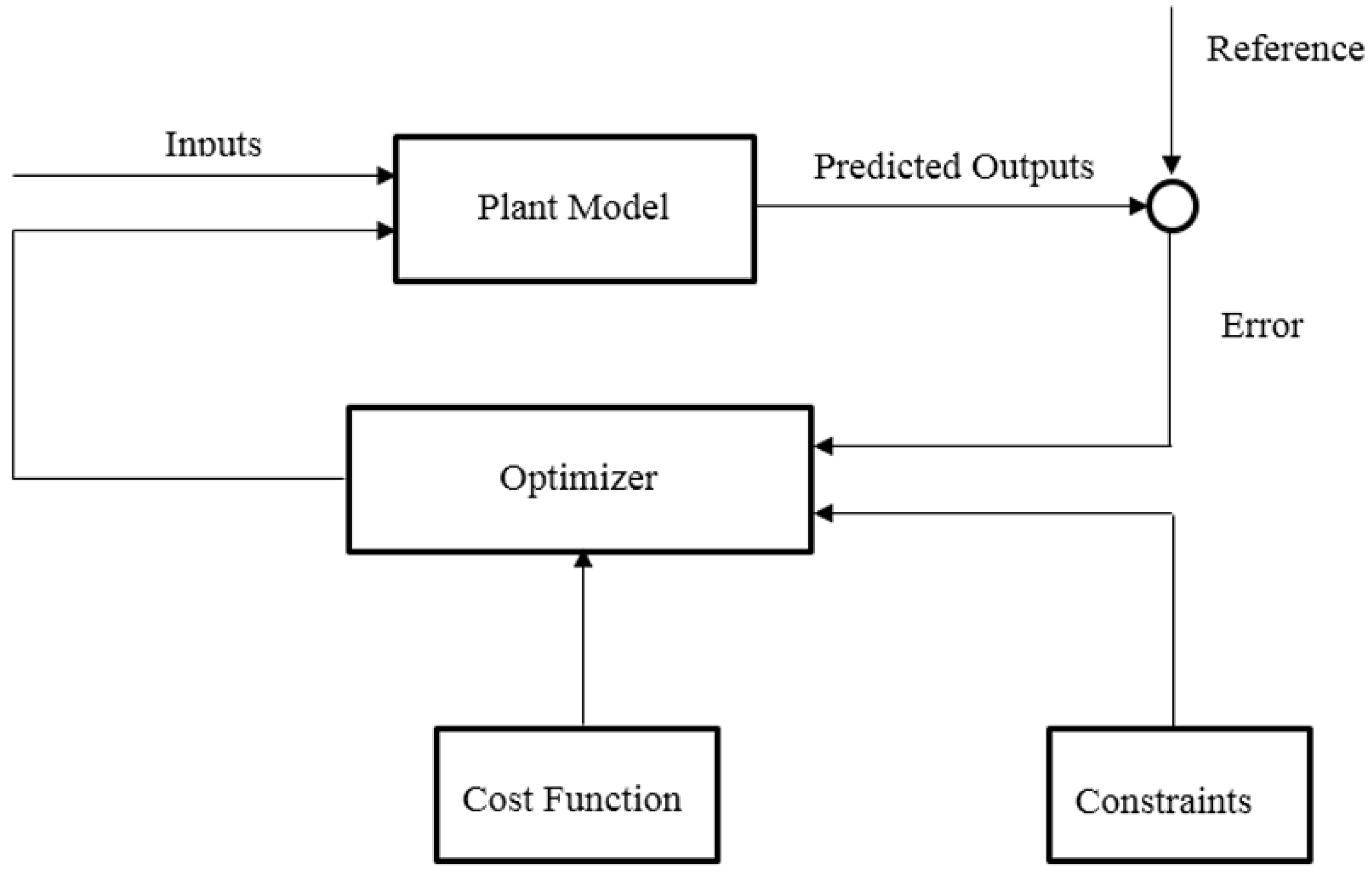
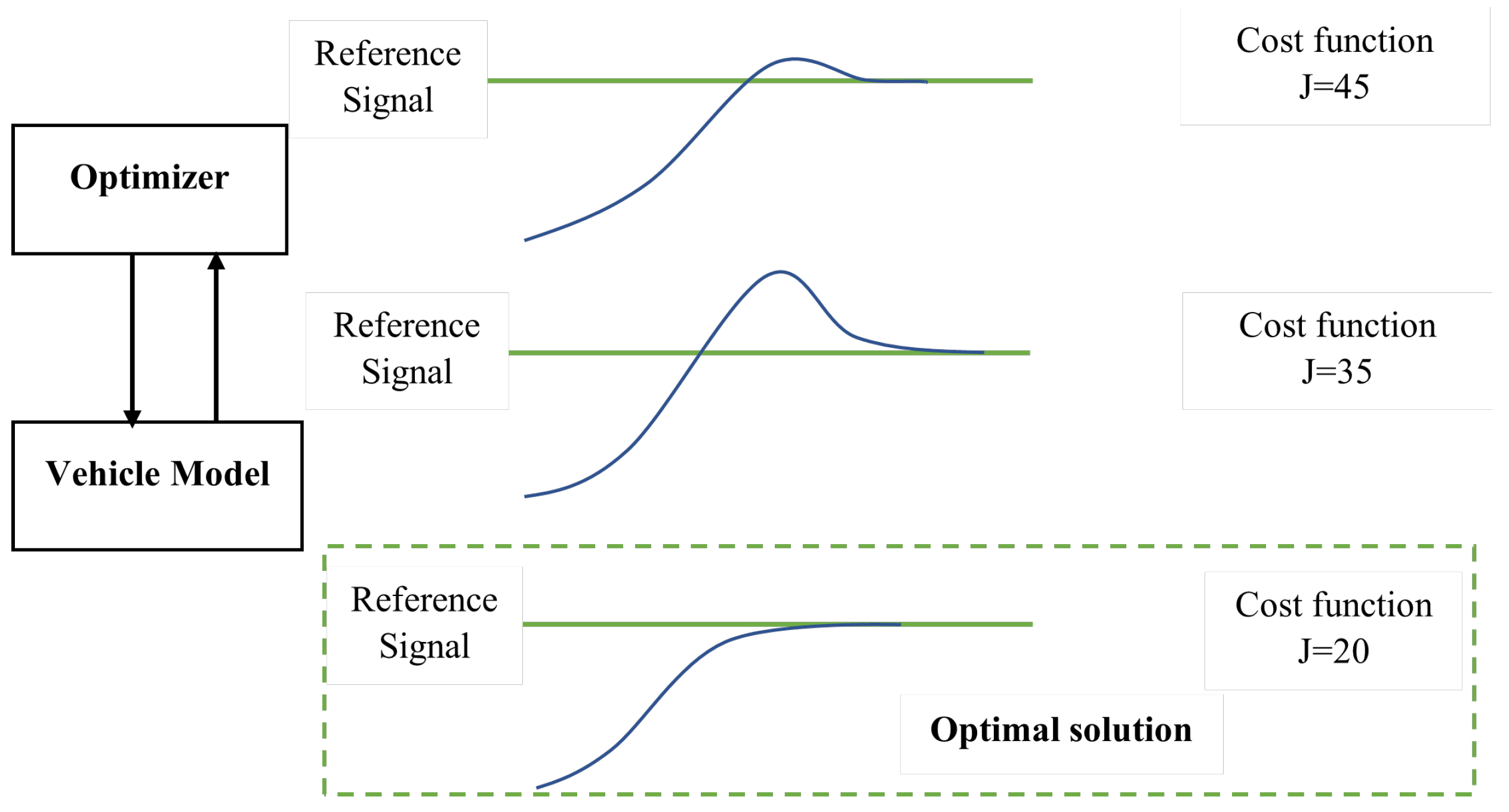
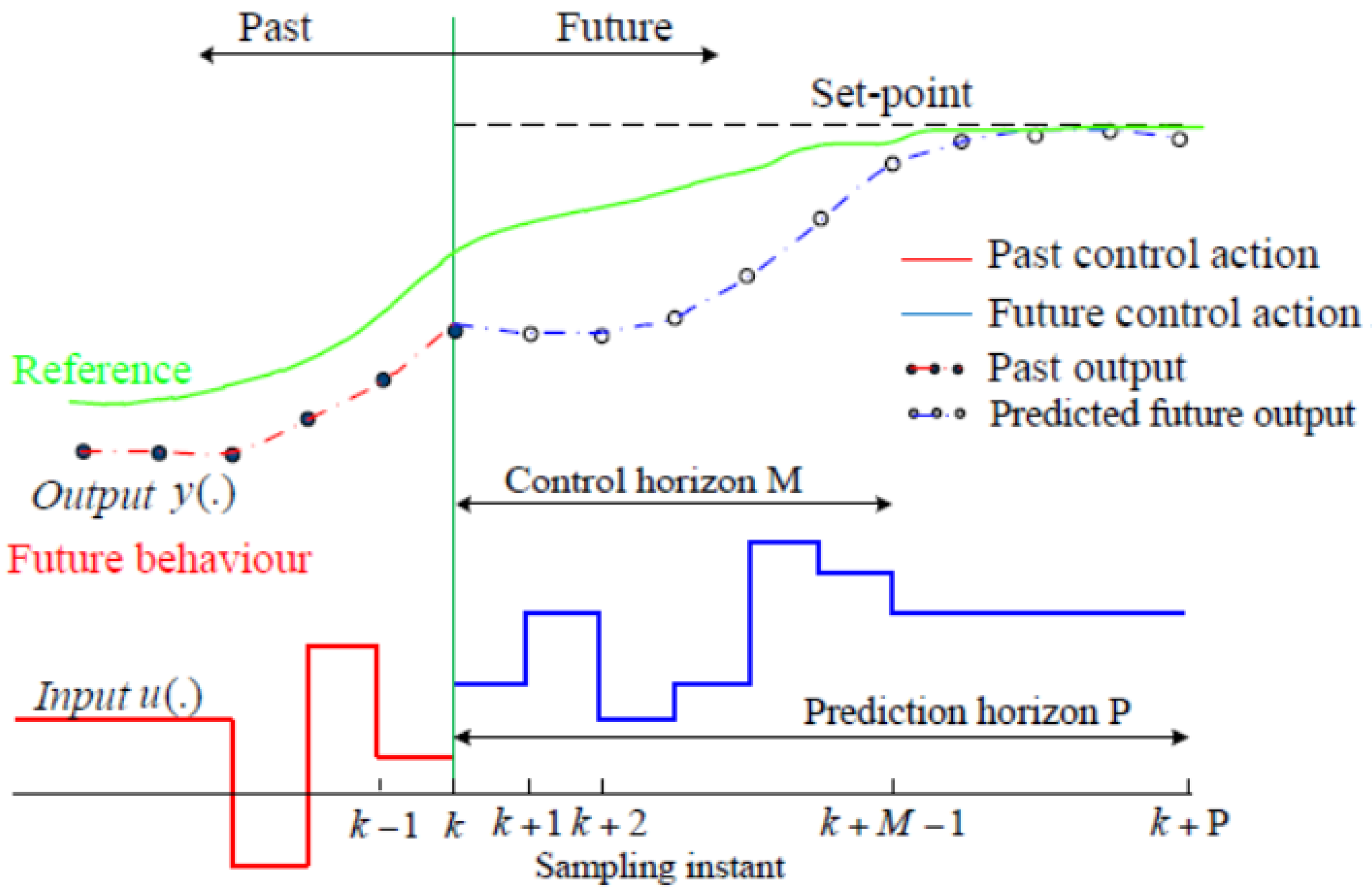
2.2. Model Predictive Controller
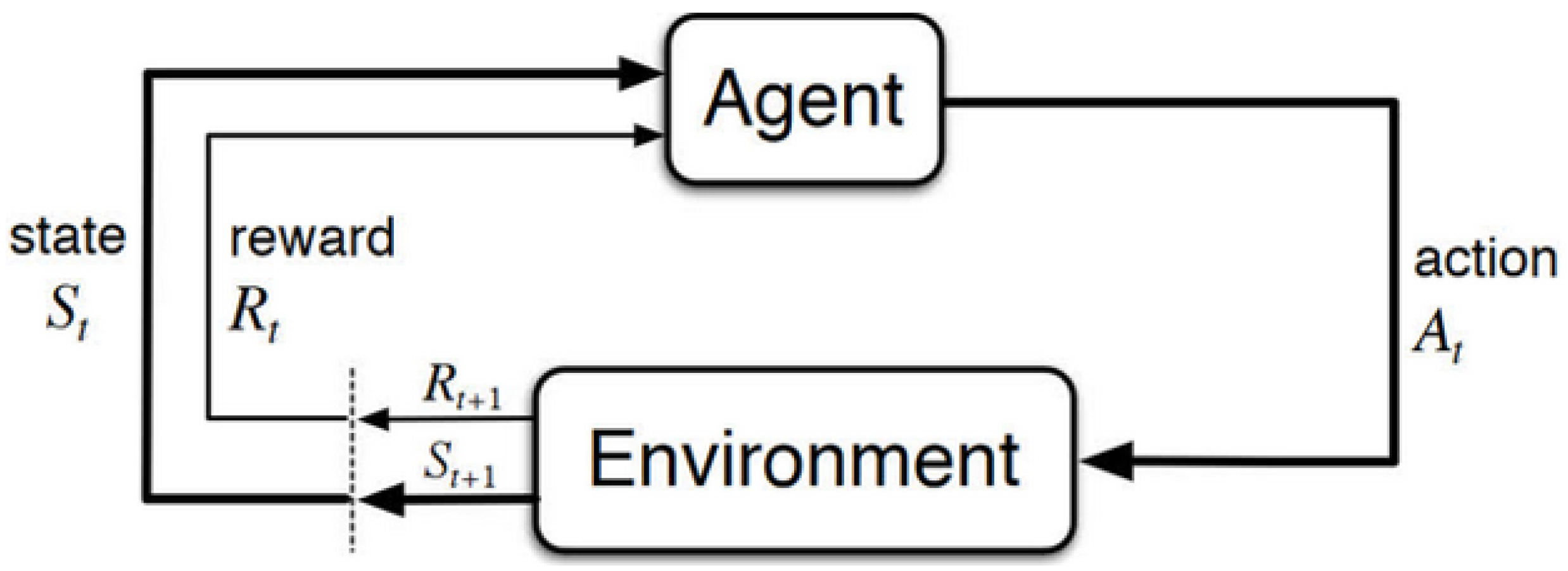
2.3. Reinforcement Learning
2.4. Design of the Controllers Models
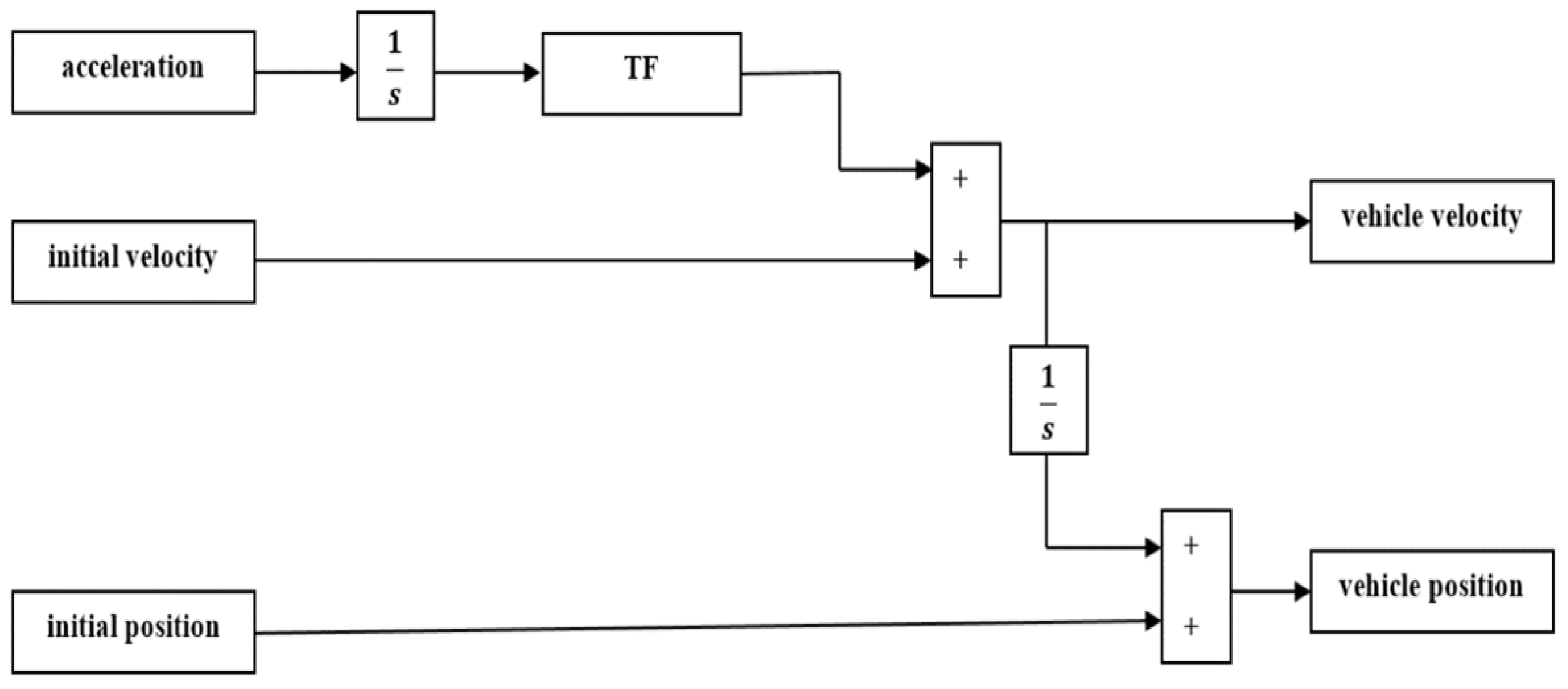
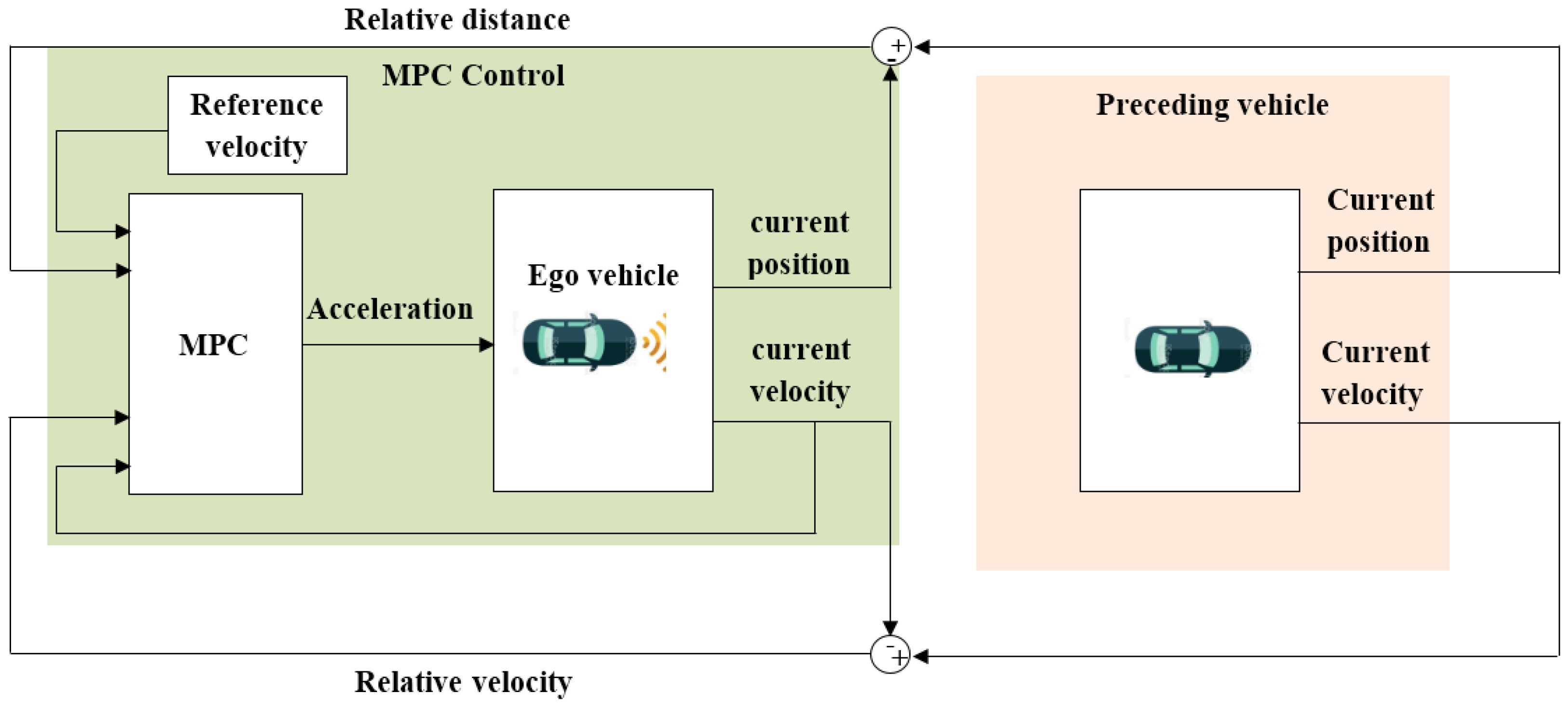
2.4.1. Design of the MPC Controller
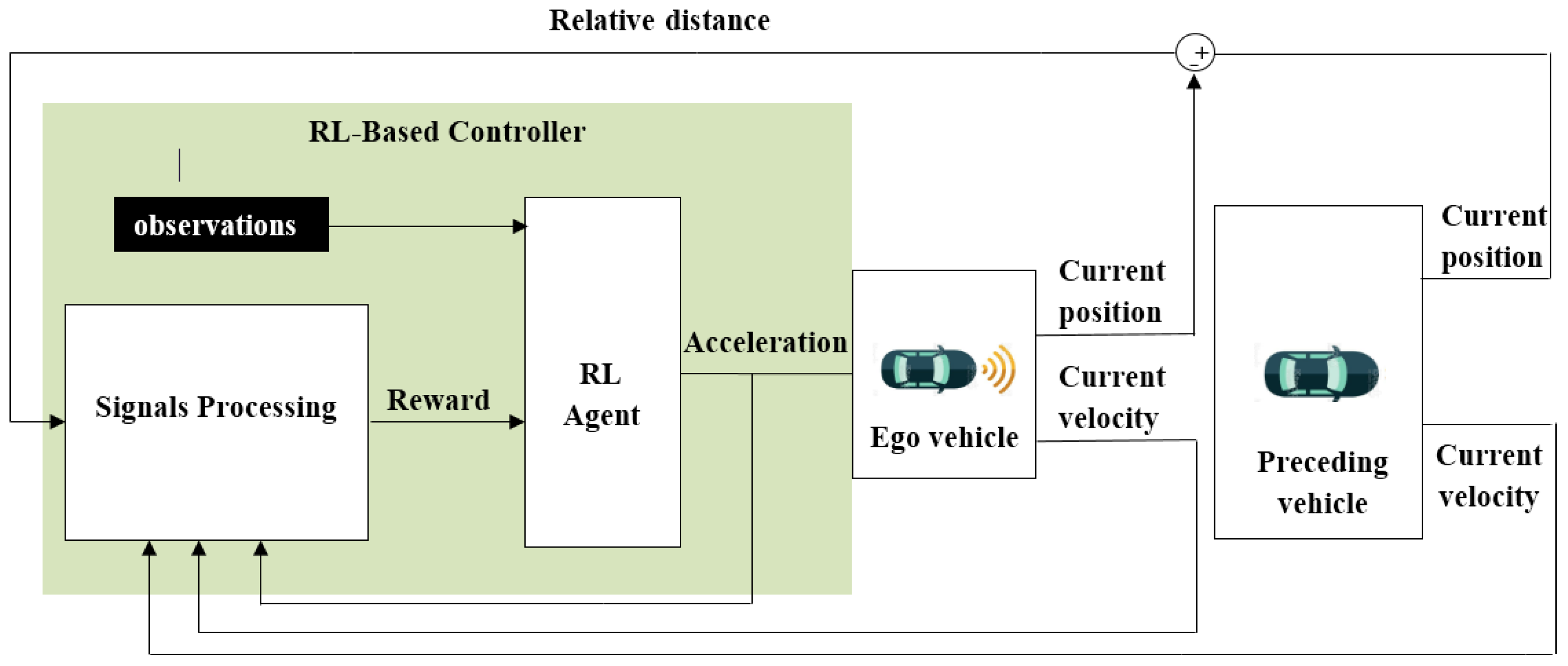
2.4.2. Designing and Training the Reinforcement-Learning-Based Controller
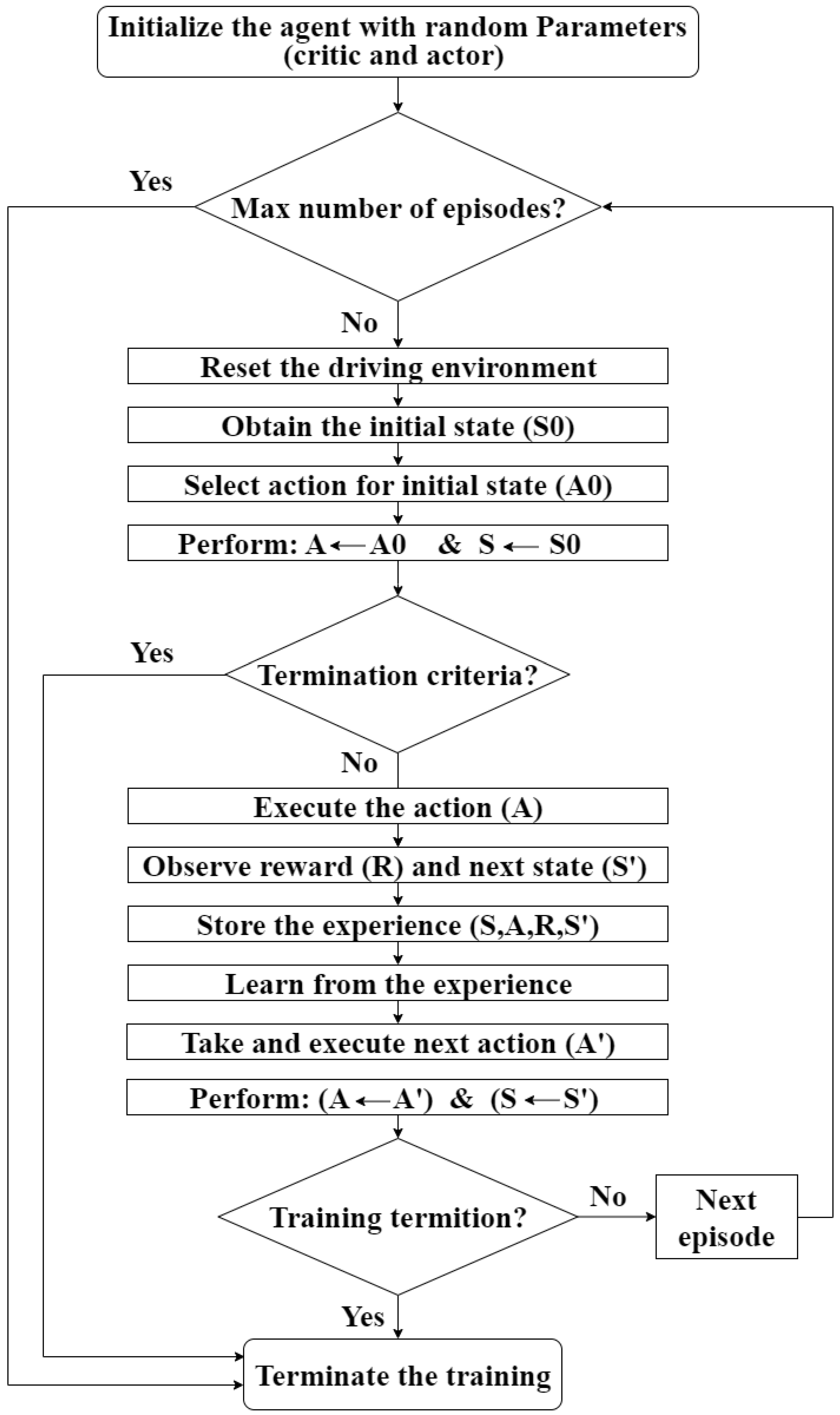
2.4.3. Training Algorithm
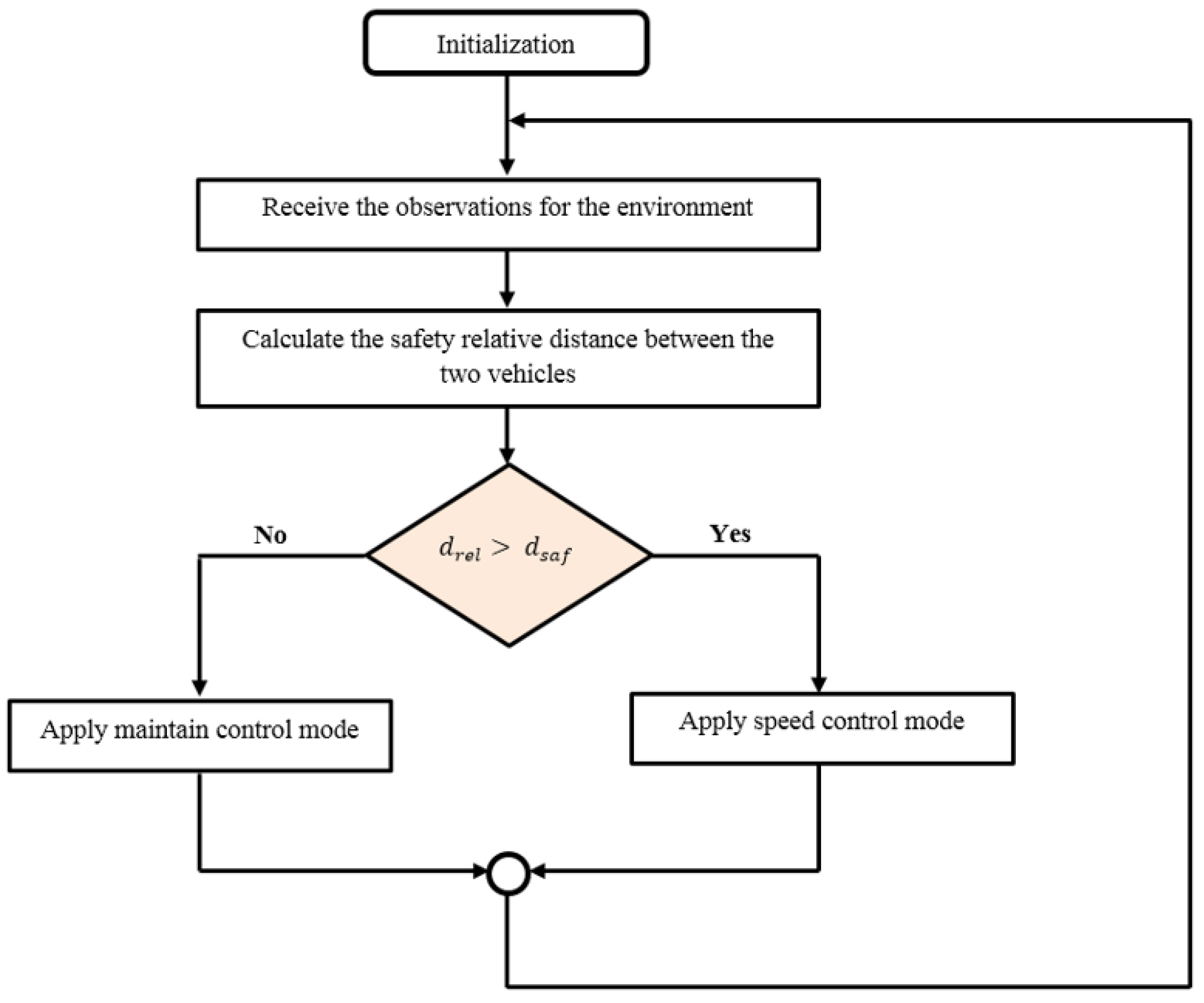
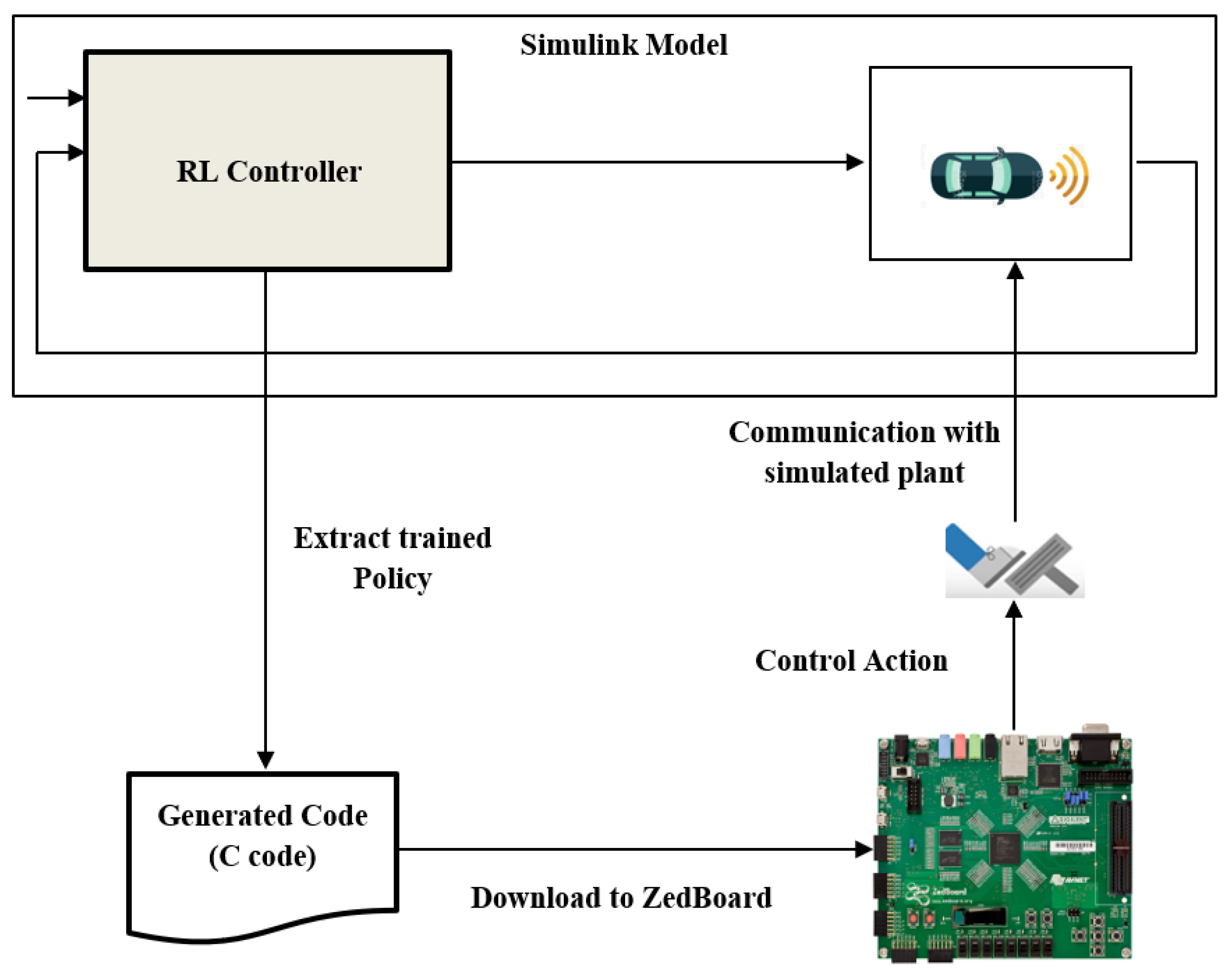
2.4.4. SOC Implementations and Verification of RL Model
3. Results and Discussion
3.1. MATLAB Simulink
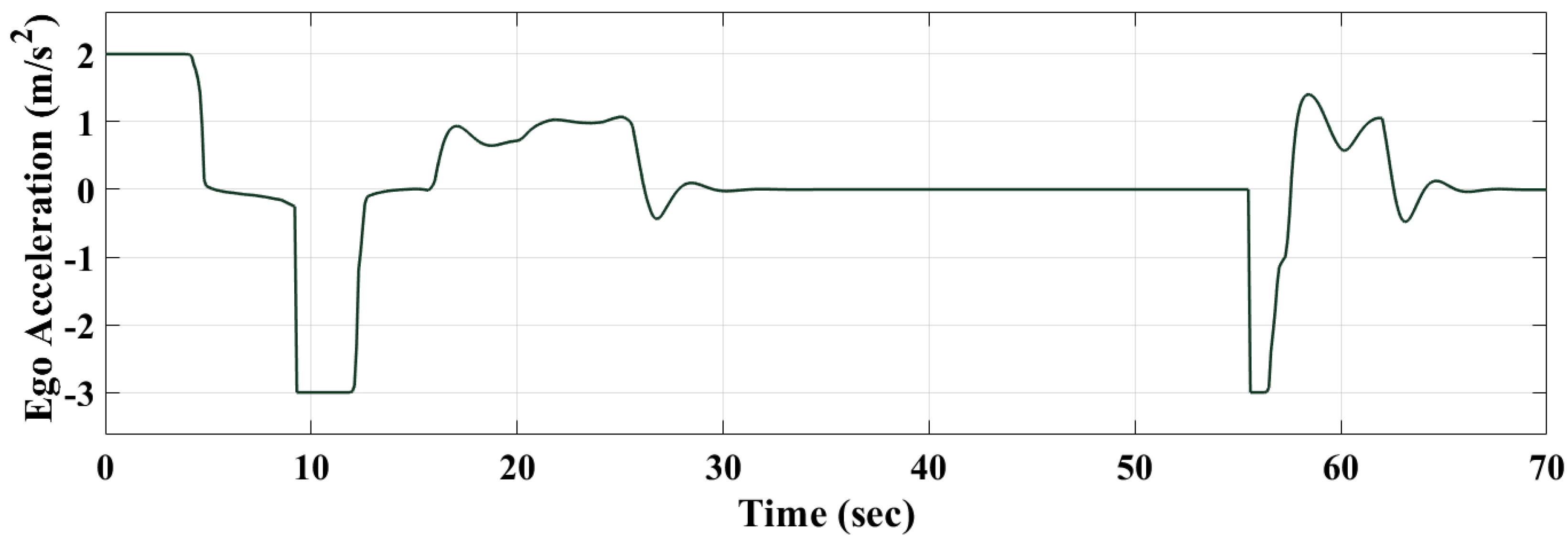
3.1.1. MPC Controller
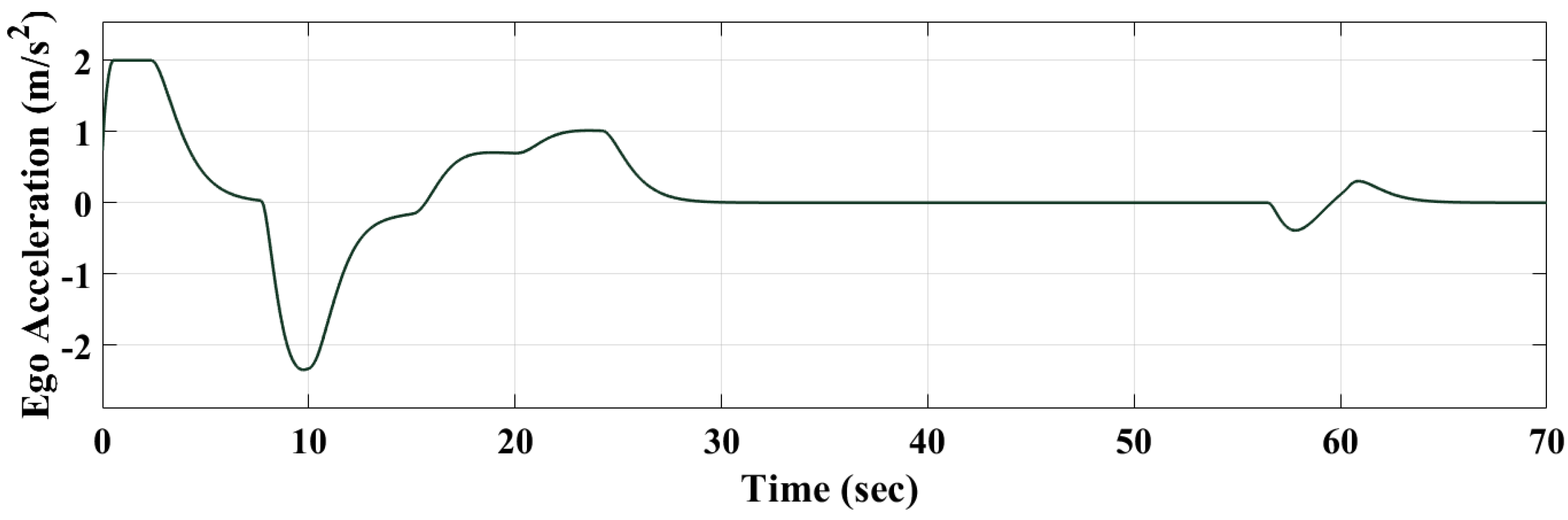
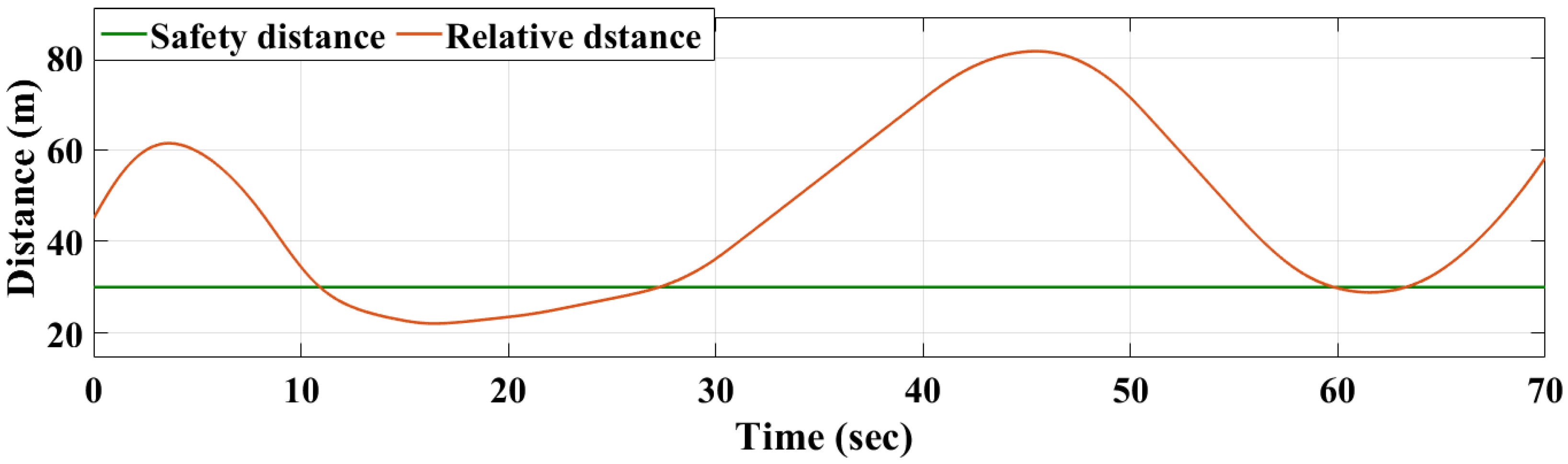
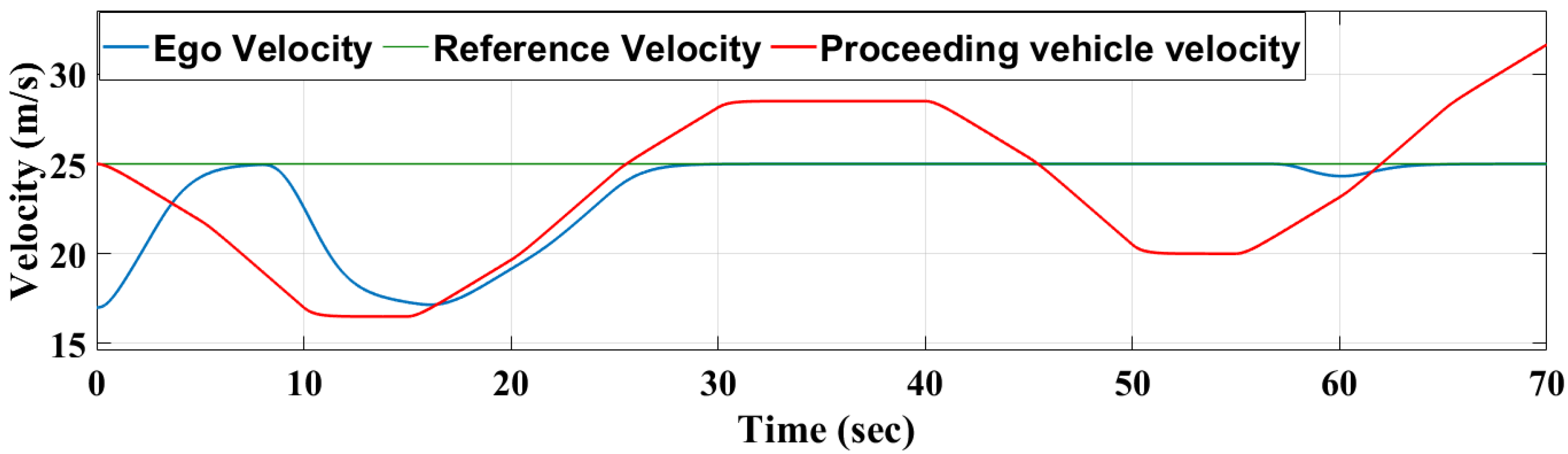
3.1.2. Reinforcement-Learning Control Model
3.1.3. Performance Comparison
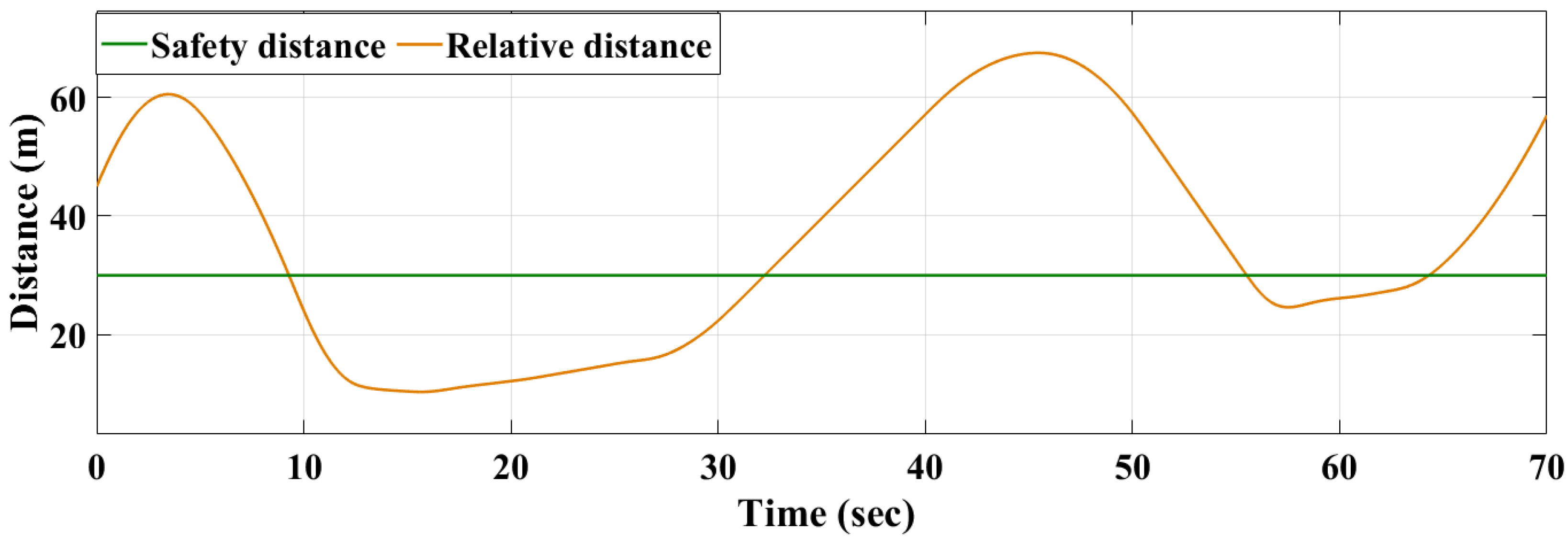
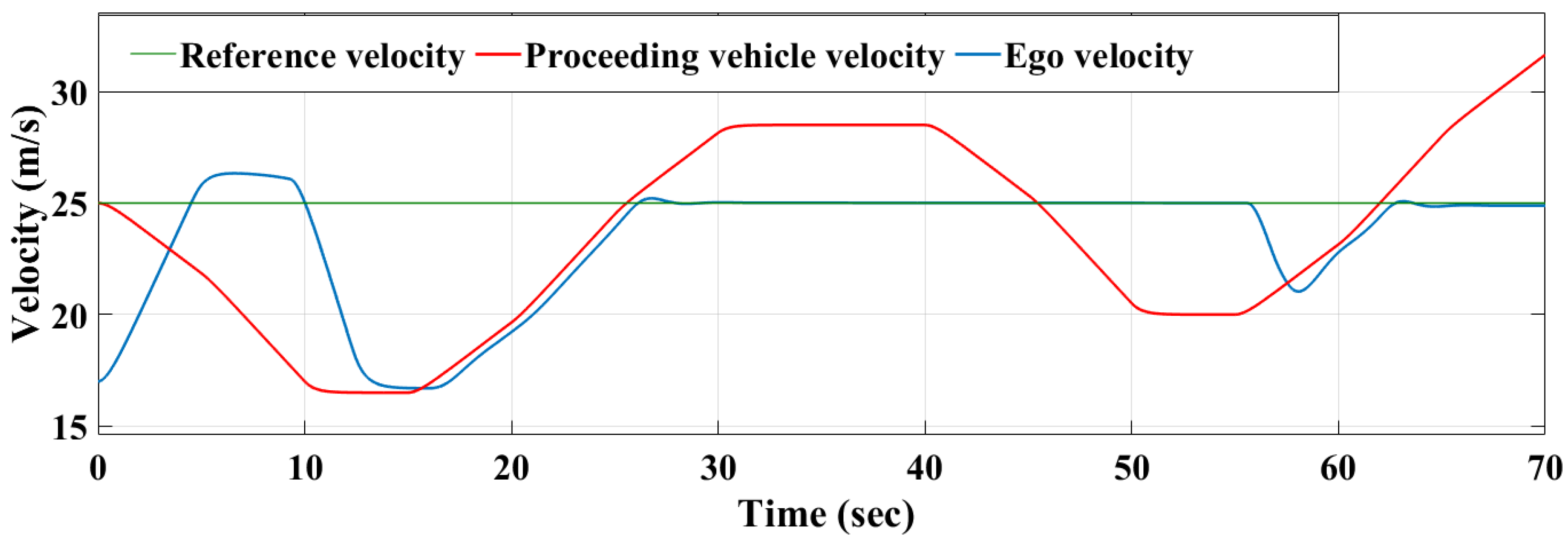
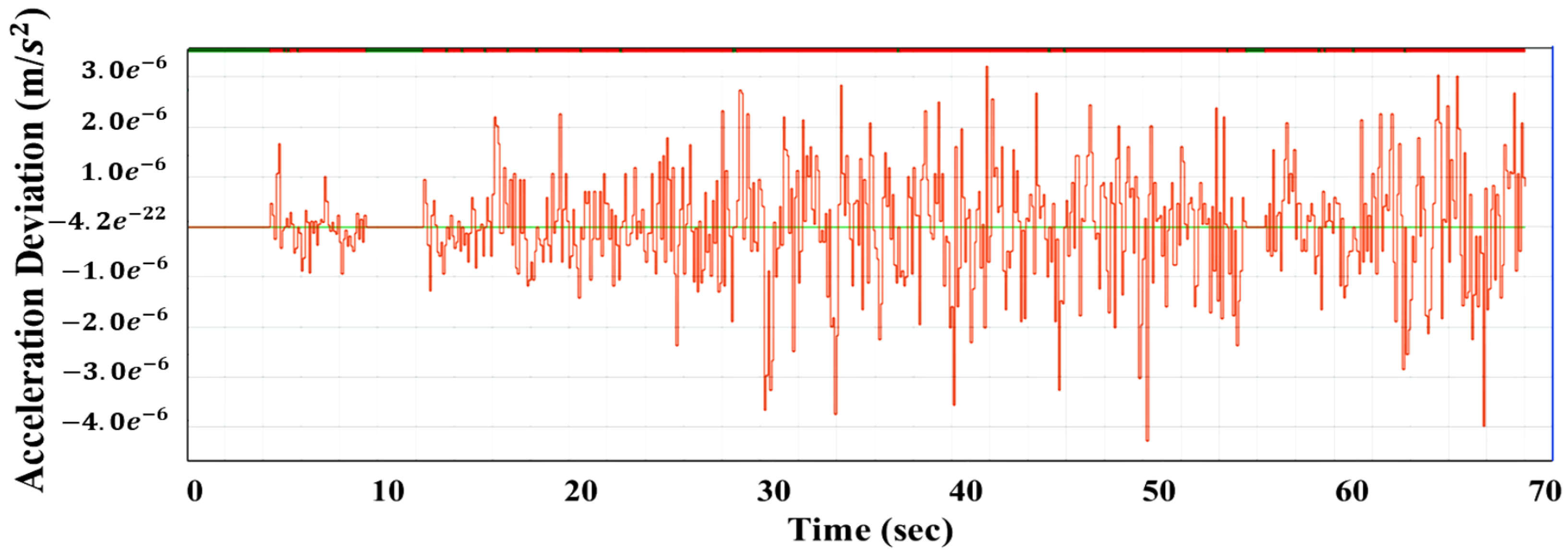
3.2. RL-Model on SOC
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
Abbreviations
| ACC | Adaptive Cruise Control |
| RL | Reinforcement Learning |
| ADAS | Advanced Driver Assistance Systems |
| CACC | Cooperative Adaptive Cruise Control |
| DQN | Deep Q-Learning |
| FPGA | Field-Programmable Gate Array |
| LTL | Linear Temporal Logic |
| MDP | Markov Decision Process |
| MIMO | Multi-Input-Multi-Output |
| MPC | Model Predictive Control |
| QP | Quadratic Problem |
| SOC | System-on-Chip |
References
- Magdici, S.; Althoff, M. Adaptive cruise control with safety guarantees for autonomous vehicles. IFAC 2017, 10, 5774–5781. [Google Scholar] [CrossRef]
- Ziebinski, A.; Cupek, R.; Grzechca, D.; Chruszczyk, L. Review of advanced driver assistance systems (ADAS). In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2017; Volume 1906. [Google Scholar]
- Ioannou, P.; Wang, Y.; Chang, H. Integrated Roadway/Adaptive Cruise Control System: Safety, Performance, Environmental and Near Term Deployment Considerations; California PATH Research Report UCB-ITS-PRR, California PATH Program, Institute of Transportation Studies, University of California: Berkeley, CA, USA, 2007. [Google Scholar]
- Xiao, L.; Gao, F. A comprehensive review of the development of adaptive cruise control systems. Veh. Syst. Dyn. 2010, 48, 1167–1192. [Google Scholar] [CrossRef]
- ISO 15622; Intelligent Transport Systems—Adaptive Cruise Control Systems—Performance Requirements and Test Procedures. ISO: Geneva, Switzerland, 2010. Available online: https://www.iso.org/standard/71515.html (accessed on 20 November 2022).
- Moon, S.; Moon, I.; Yi, K. Design, tuning, and evaluation of a full-range adaptive cruise control system with collision avoidance. Control Eng. Pract. 2009, 17, 442–455. [Google Scholar] [CrossRef]
- Rieger, G.; Scheef, J.; Becker, H.; Stanzel, M.; Zobel, R. Active safety systems change accident environment of vehicles significantly-a challenge for vehicle design. In Proceedings of the 19th International Technical Conference on the Enhanced Safety of Vehicles (ESV), Washington, DC, USA, 6–9 June 2005. [Google Scholar]
- Nilsson, P.; Hussien, O.; Chen, Y.; Balkan, A.; Rungger, M.; Ames, A.; Grizzle, J.; Ozay, N.; Peng, H.; Tabuada, P. Preliminary results on correct-by-construction control software synthesis for adaptive cruise control. In Proceedings of the IEEE Conference on Decision and Control, Piscataway, NJ, USA, 15 December 2014; pp. 816–823. [Google Scholar]
- Ames, A.D.; Grizzle, J.W.; Tabuada, P. Control barrier function based quadratic programs with application to adaptive cruise control. In Proceedings of the IEEE 53rd Annual Conference on Decision and Control, Los Angeles, CA, USA, 15 December 2014; pp. 6271–6278. [Google Scholar]
- Diehl, M.; Ferreau, H.J.; Haverbeke, N. Efficient Numerical Methods for Nonlinear MPC and Moving Horizon Estimation. In Nonlinear Model Predictive Control. Lecture Notes in Control and Information Sciences; Springer: Berlin, Germany, 2009; Volume 384, pp. 391–417. [Google Scholar]
- Stanger, T.; del Re, L.; Stanger, T.; del Re, L. A model predictive cooperative adaptive cruise control approach. In Proceedings of the American Control Conference, Washington, DC, USA, 17–19 June 2013. [Google Scholar]
- Bageshwar, V.L.; Garrard, W.L.; Rajamani, R. Model predictive control of transitional maneuvers for adaptive cruise control vehicles. IEEE Trans. Veh. Technol. 2004, 53, 1573–1585. [Google Scholar] [CrossRef]
- Dey, K.C.; Yan, L.; Wang, X.; Wang, Y.; Shen, H.; Chowdhury, M.; Yu, L.; Qiu, C.; Soundararaj, V. A Review of Communication, Driver Characteristics, and Controls Aspects of Cooperative Adaptive Cruise Control (CACC). IEEE Trans. Intell. Transp. Syst. 2016, 17, 491–509. [Google Scholar] [CrossRef]
- Corona, D.; Lazar, M.; De Schutter, B. A hybrid MPC approach to the design of a Smart adaptive cruise controller. In Proceedings of the IEEE International Symposium on Computer Aided Control System Design, San Francisco, CA, USA, 13–15 April 2009. [Google Scholar]
- Wei, S.; Zou, Y.; Zhang, T.; Zhang, X.; Wang, W. Design and Experimental Validation of a Cooperative Adaptive Cruise Control System Based on Supervised Reinforcement Learning. Appl. Sci. 2018, 8, 1014. [Google Scholar] [CrossRef]
- Kianfar, R.; Augusto, B.; Ebadighajari, A.; Hakeem, U.; Nilsson, J.; Raza, A.; Papanastasiou, S. Design and Experimental Validation of a Cooperative Driving System in the Grand Cooperative Driving Challenge. IEEE Trans. Intell. Transp. Syst. 2012, 13, 994–1007. [Google Scholar] [CrossRef]
- Pfeiffer, M.; Schaeuble, M.; Nieto, J.; Siegwart, R.; Cadena, C. From perception to decision: A data-driven approach to end-to-end motion planning for autonomous ground robots. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1527–1533. [Google Scholar]
- Lamouik, I.; Yahyaouy, A.; Sabri, M.A. Deep neural network dynamic traffic routing system for vehicle. In Proceedings of the 2018 International Conference on Intelligent Systems and Computer Vision (ISCV), Fez, Morocco, 2–4 April 2018. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Amari, S. The Handbook of Brain Theory and Neural Networks; MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Ernst, D.; Glavic, M.; Capitanescu, F.; Wehenkel, L. Reinforcement learning versus model predictive control: A comparison on a power system problem. IEEE Trans. Syst. Man Cyb. 2008, 39, 517–529. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; McPhee, J.; Azad, N.L. Comparison of deep reinforcement learning and model predictive control for adaptive cruise control. IEEE Trans. Intell. Veh. 2020, 6, 221–231. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G.; Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Xu, X.; Zuo, L.; Huang, Z. Reinforcement learning algorithms with function approximation: Recent advance and applications. Inf. Sci. 2014, 216, 1–31. [Google Scholar] [CrossRef]
- Huang, Z.; Xu, X.; He, H.; Tan, J.; Sun, Z. Parameterized Batch Reinforcement Learning for Longitudinal Control of Autonomous Land Vehicles. IEEE Trans. Syst. Man. Cybern. Syst 2019, 49, 730–741. [Google Scholar] [CrossRef]
- Liu, T.; Zou, Y.; Liu, D.X.; Sun, F.C. Reinforcement Learning of Adaptive Energy Management With Transition Probability for a Hybrid Electric Tracked Vehicle. IEEE Trans. Ind. Electron. 2015, 62, 7837–7846. [Google Scholar] [CrossRef]
- Desjardins, C.; Chaib-Draa, B. Cooperative adaptive cruise control: A reinforcement learning approach. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1248–1260. [Google Scholar] [CrossRef]
- Isele, D.; Rahimi, R.; Cosgun, A.; Subramanian, K.; Fujimura, K. Navigating occluded intersections with autonomous vehicles using deep reinforcement learning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 2034–2039. [Google Scholar]
- Li, C.; Czarnecki, K. Urban driving with multi-objective deep reinforcement learning. Proc. Int. Jt. Conf. Auton. Agents Multiagent Syst. AAMAS 2019, 1, 359–367. [Google Scholar]
- Vajedi, M.; Azad, N.L. Ecological adaptive cruise controller for plug-in hybrid electric vehicles using nonlinear model predictive control. IEEE Trans. Intell Transp. Syst. 2015, 10, 113–122. [Google Scholar] [CrossRef]
- Lee, J.; Balakrishnan, A.; Gaurav, A.; Czarnecki, K.; Sedwards, S. W ise M ove: A Framework to Investigate Safe Deep Reinforcement Learning for Autonomous Driving. In Proceedings of the 16th International Conference on Quantitative Evaluation of Systems, Glasgow, UK, 10–12 September 2019. [Google Scholar]
- Venter, G. Review of Optimization Techniques; John Wiley & Sons Ltd.: Chichester, UK, 2010. [Google Scholar] [CrossRef]
- Reda, A.; Bouzid, A.; Vásárhelyi, J. Model Predictive Control for Automated Vehicle Steering. Acta Polytech. Hung. 2020, 17, 163–182. [Google Scholar] [CrossRef]
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming; John Wiley & Sons: New York, NY, USA, 2014. [Google Scholar]
- Howard, R.A. Dynamic Programming and Markov Processes; MIT Press: Cambridge, MA, USA, 1960. [Google Scholar]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep reinforcement learning: A brief survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2022, arXiv:1509.02971. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Jesus, C., Jr.; Bottega, J.A.; Cuadros, M.A.S.L.; Gamarra, D.F.T. Deep deterministic policy gradient for navigation of mobile robots in simulated environments. In Proceedings of the 2019 19th International Conference on Advanced Robotics (ICAR), Belo Horizonte, Brazil, 2–6 December 2019; pp. 362–367. [Google Scholar]
- Sallab, A.E.; Abdou, M.; Perot, E.; Yogamani, S. End-to-End Deep Reinforcement Learning for Lane Keeping Assist. arXiv 2022. Available online: https://arxiv.org/abs/1612.04340 (accessed on 7 November 2022).



| Signal Type | Parameter | Unit | Description |
|---|---|---|---|
Measured outputs (MO) | m/s | Longitudinal velocity of the ego vehicle | |
| m | The relative distance between the proceeding and the ego vehicles | ||
| Measured disturbance (MD) | m/s | Longitudinal velocity of the proceeding vehicle | |
| Manipulated variable (MV) | m/s | acceleration\deceleration | |
| References | m/s | reference velocity in speed mode | |
| m | The reference safety distance |
| MPC Controller Parameters | |
|---|---|
| Sample time () | 0.1 s |
| Prediction horizon (P) | 30 |
| Control horizon (M) | 3 |
| Control Action Constraints | |
| Acceleration | [−3, 3] m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reda, A.; Vásárhelyi, J. Design and Implementation of Reinforcement Learning for Automated Driving Compared to Classical MPC Control. Designs 2023, 7, 18. https://doi.org/10.3390/designs7010018
Reda A, Vásárhelyi J. Design and Implementation of Reinforcement Learning for Automated Driving Compared to Classical MPC Control. Designs. 2023; 7(1):18. https://doi.org/10.3390/designs7010018
Chicago/Turabian StyleReda, Ahmad, and József Vásárhelyi. 2023. "Design and Implementation of Reinforcement Learning for Automated Driving Compared to Classical MPC Control" Designs 7, no. 1: 18. https://doi.org/10.3390/designs7010018
APA StyleReda, A., & Vásárhelyi, J. (2023). Design and Implementation of Reinforcement Learning for Automated Driving Compared to Classical MPC Control. Designs, 7(1), 18. https://doi.org/10.3390/designs7010018