Effect of the Inlet Boundary Conditions on the Flow over Complex Terrain Using Large Eddy Simulation
Abstract
1. Introduction
2. Numerical Method
3. Overview of Inflow Boundary Condition Methods
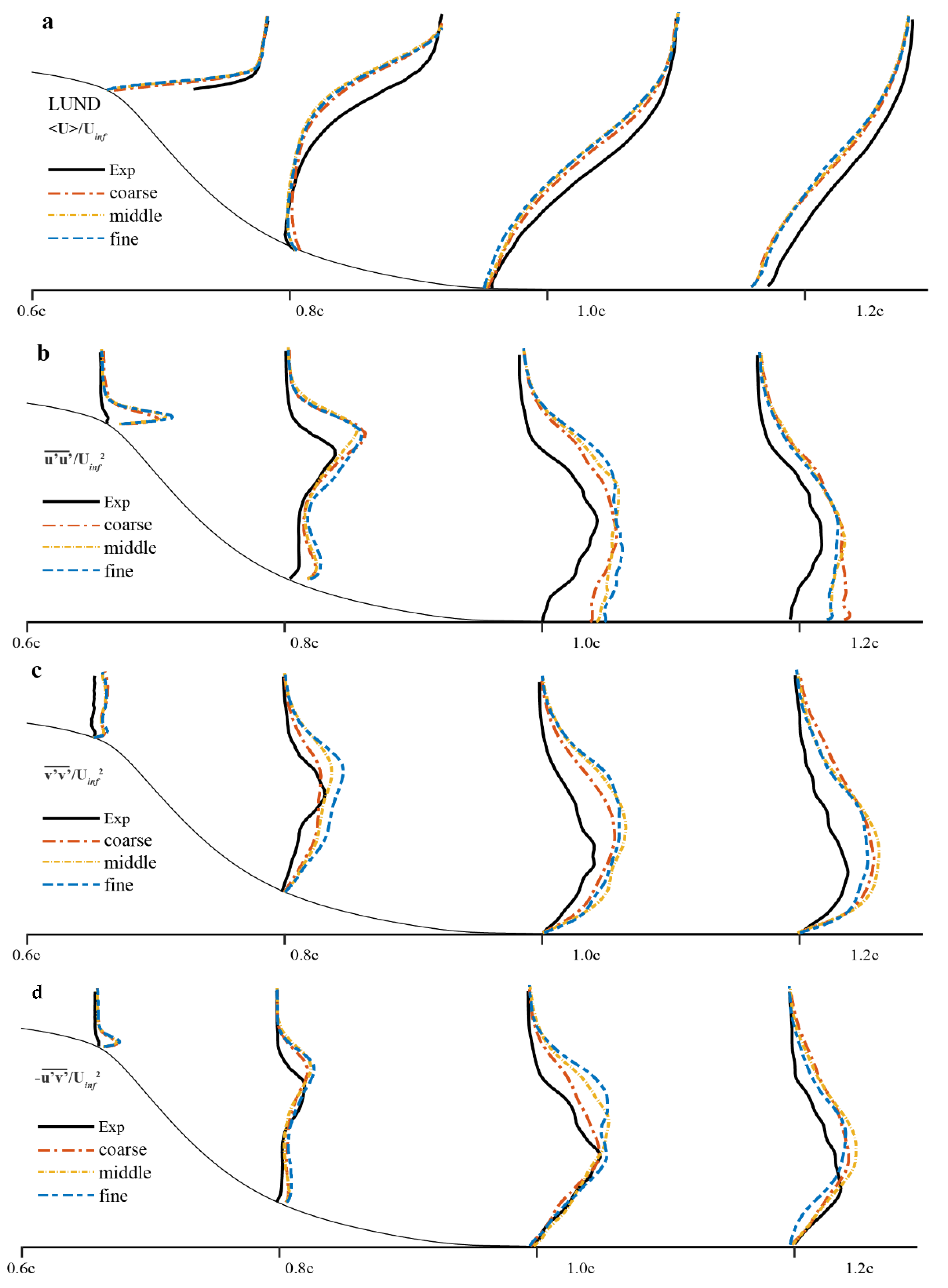
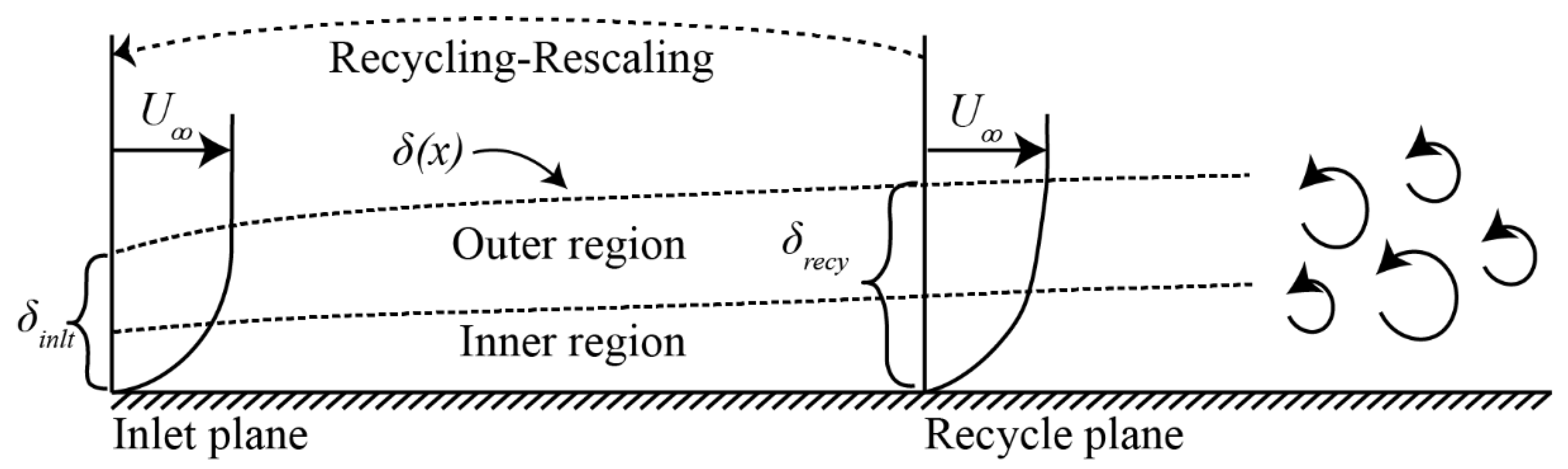
3.1. Recycling and Rescaling Method (Lund)
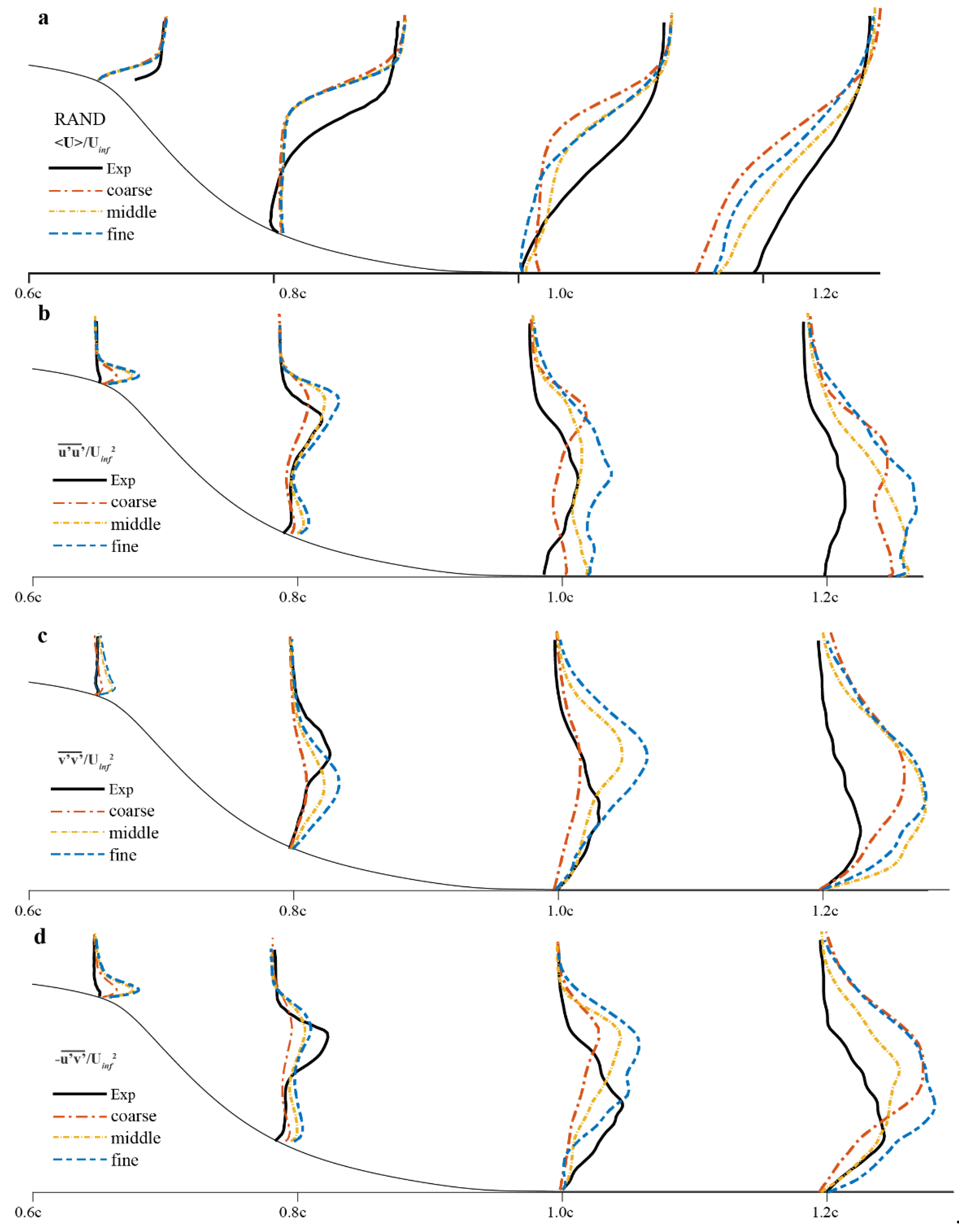
3.2. Random Method (RAND)
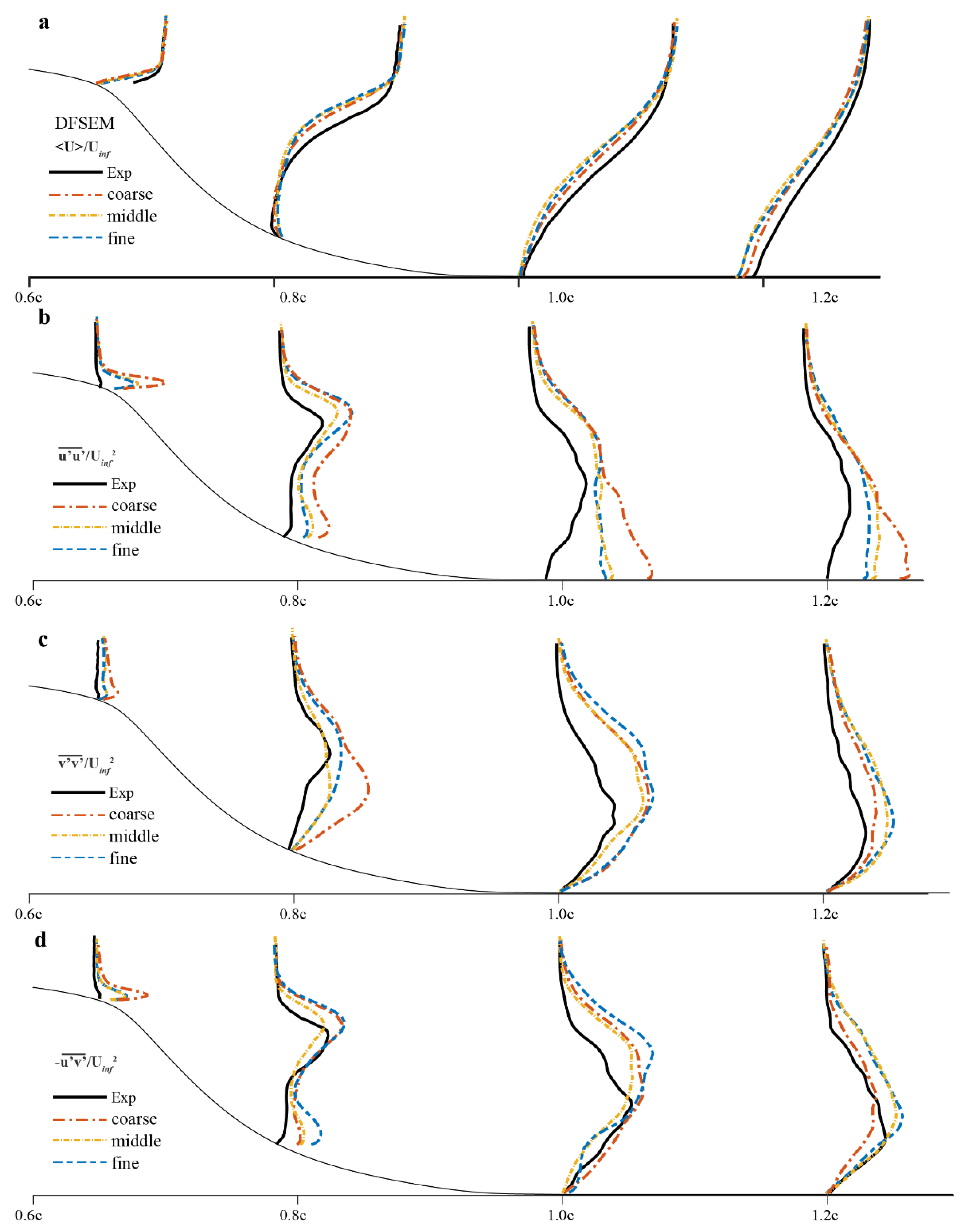
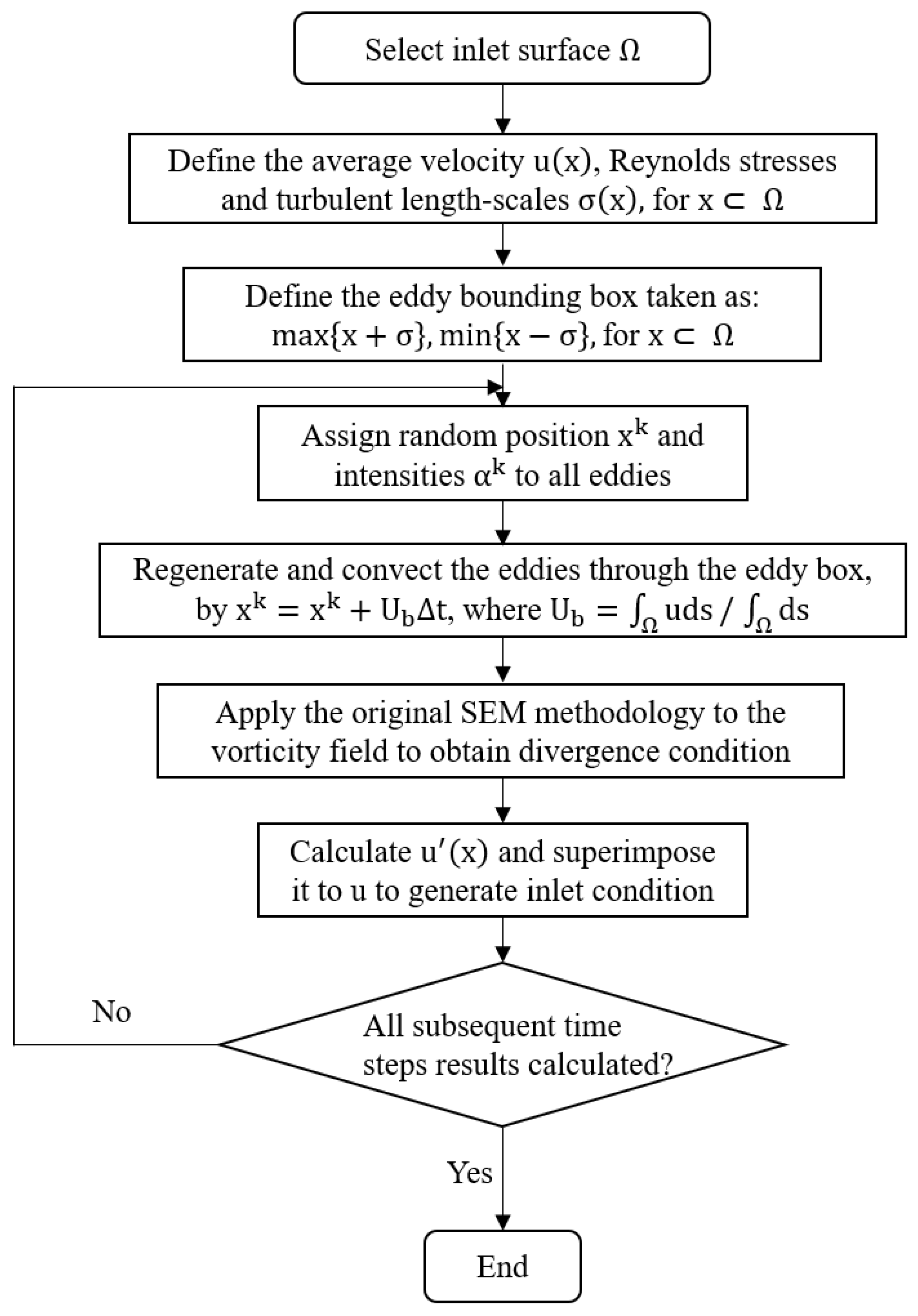
3.3. Divergence Free Synthetic Eddies Method (DFSEM)
4. Numerical Setup
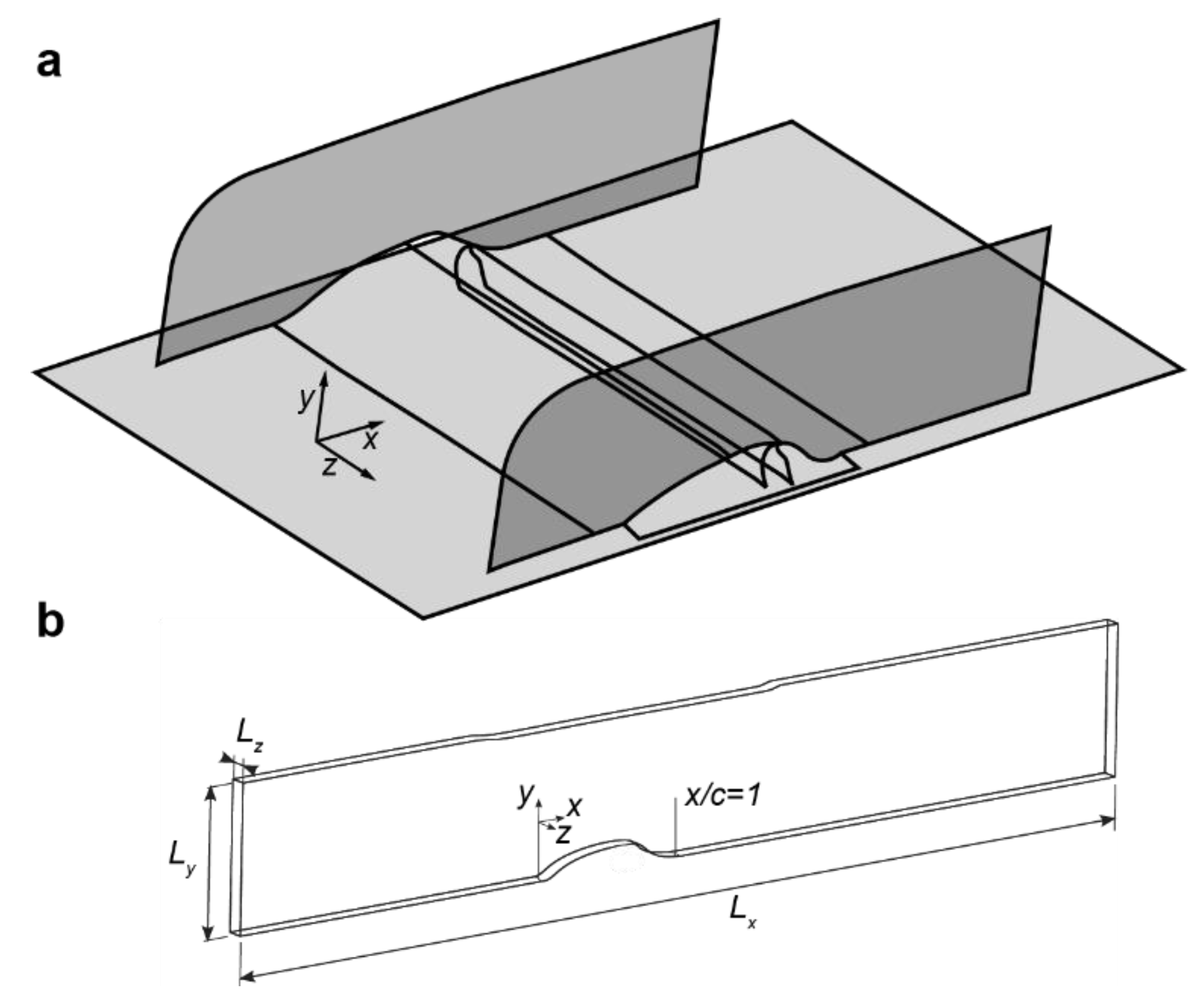
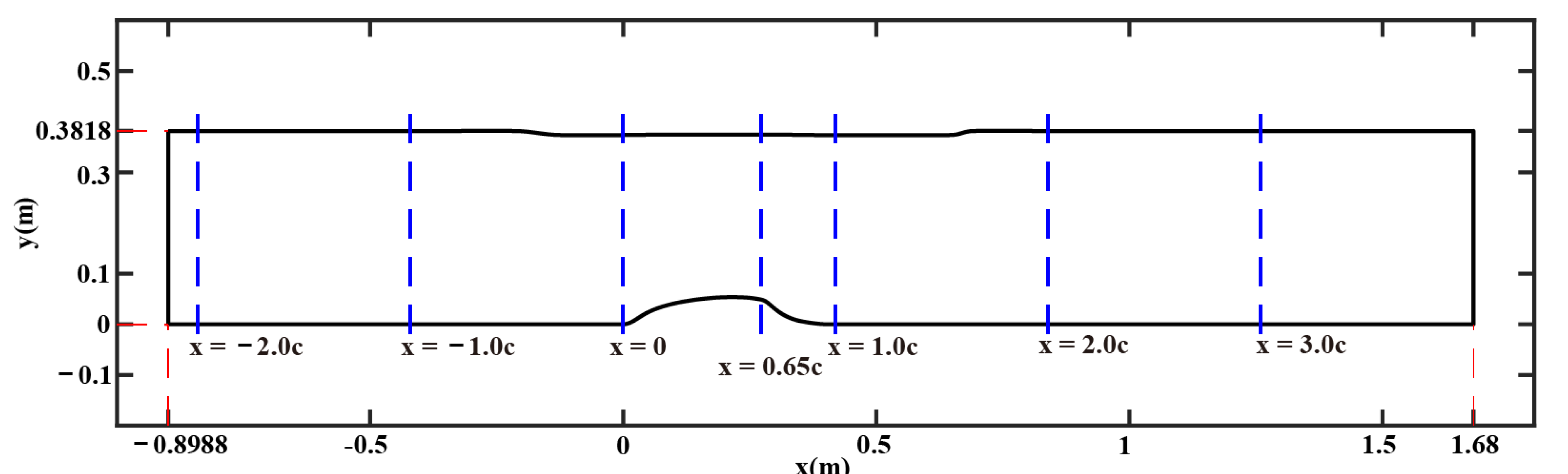
4.1. Hump Model
4.2. Different IBCs Used in the Simulation
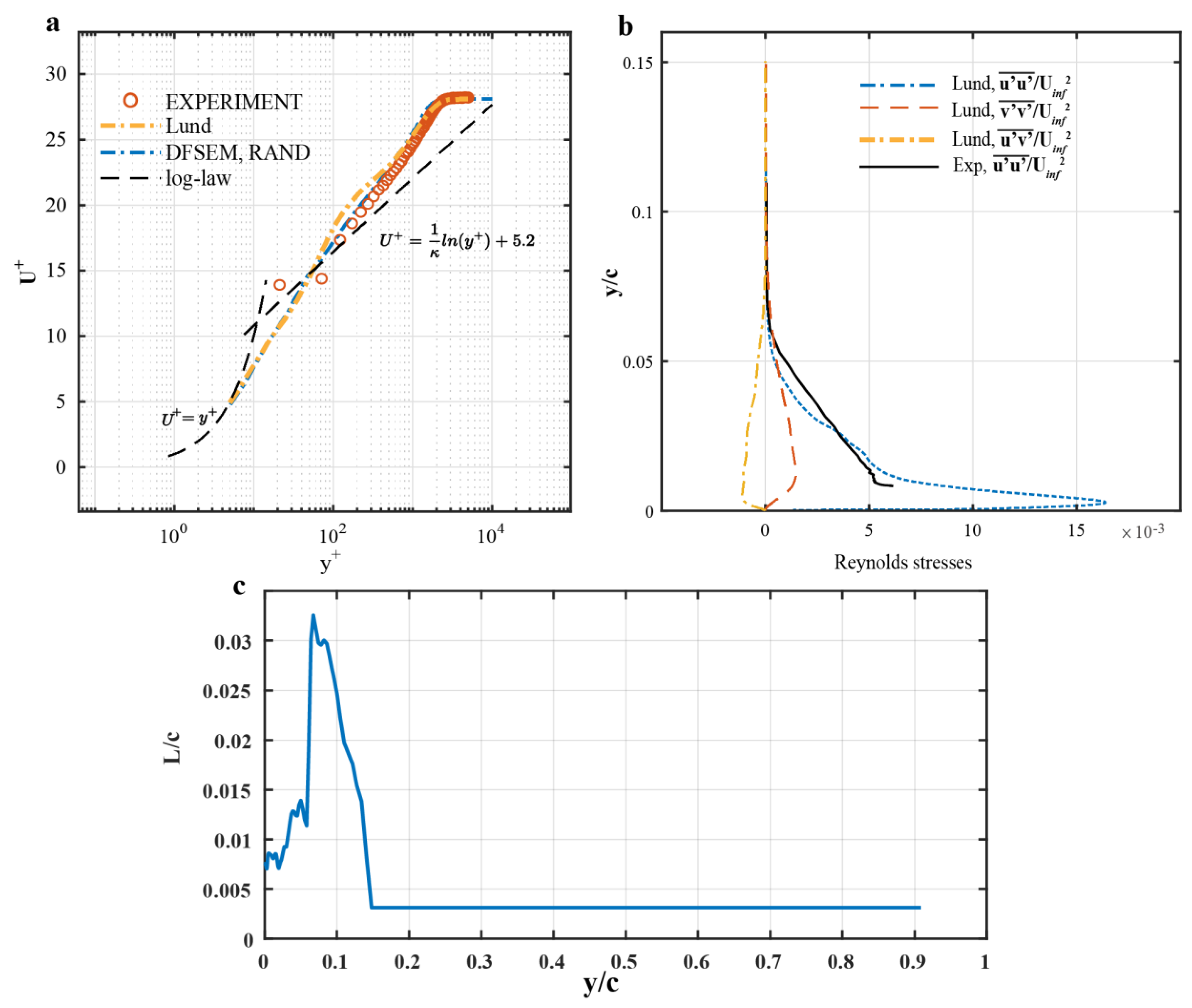
4.3. Inlet Profiles Validation of Different Simulation Methods
5. Results
5.1. Mesh Sensitivity
5.2. Global Velocity Field
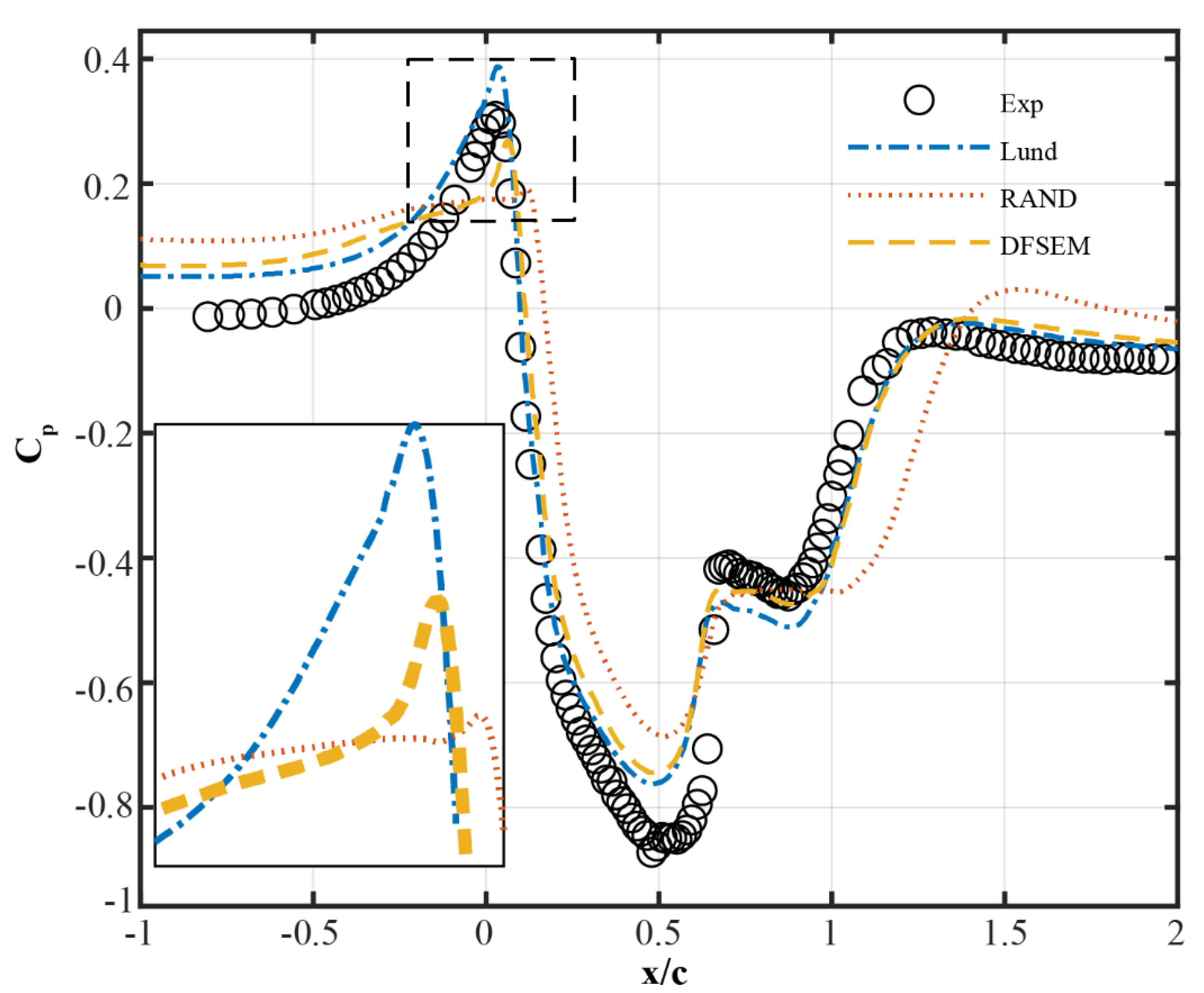
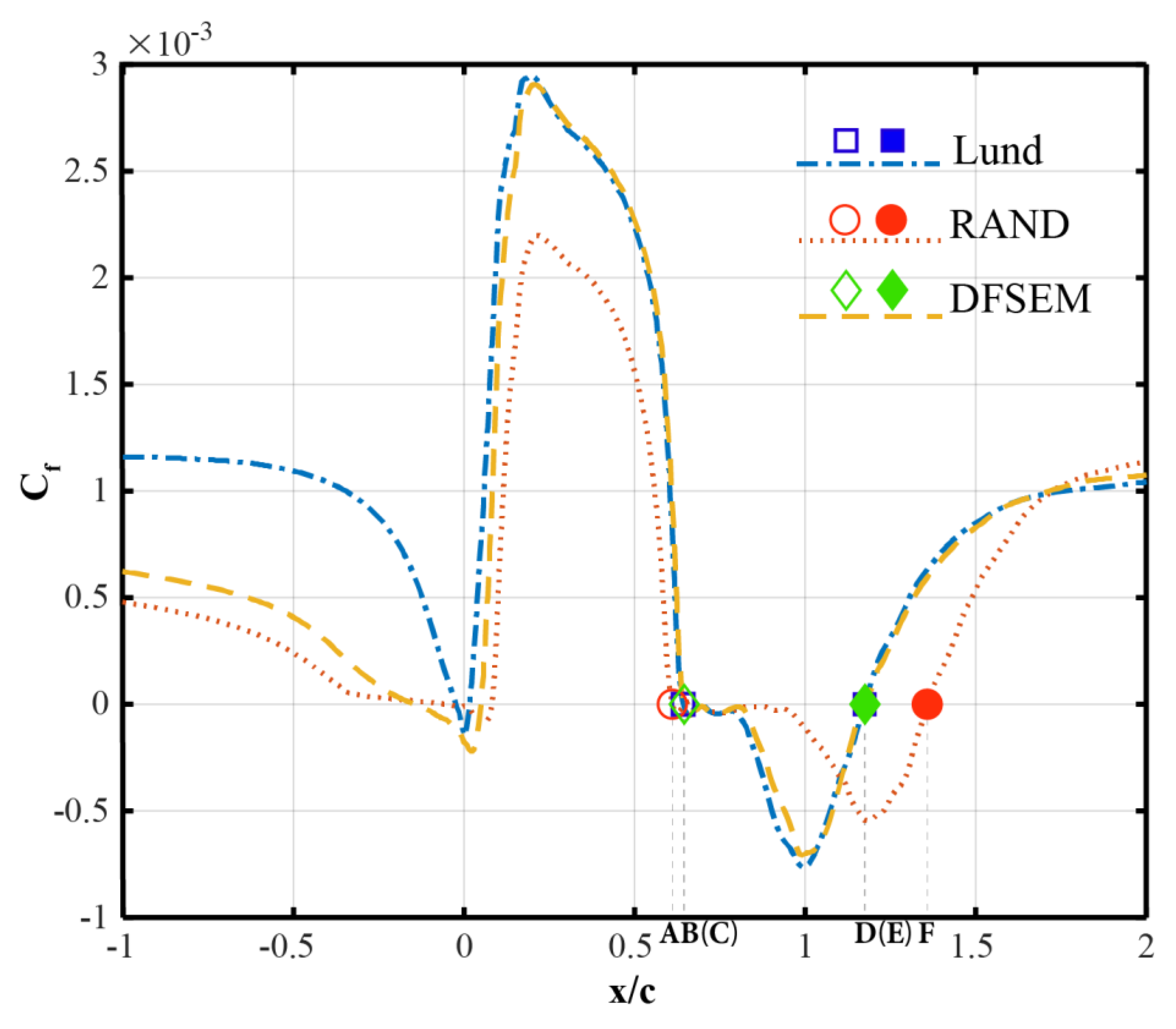
5.3. Flow Separation and Reattachment (Pressure Coefficient and Friction Coefficient)
5.4. Quantifications of the Turbulent Properties before the Hump
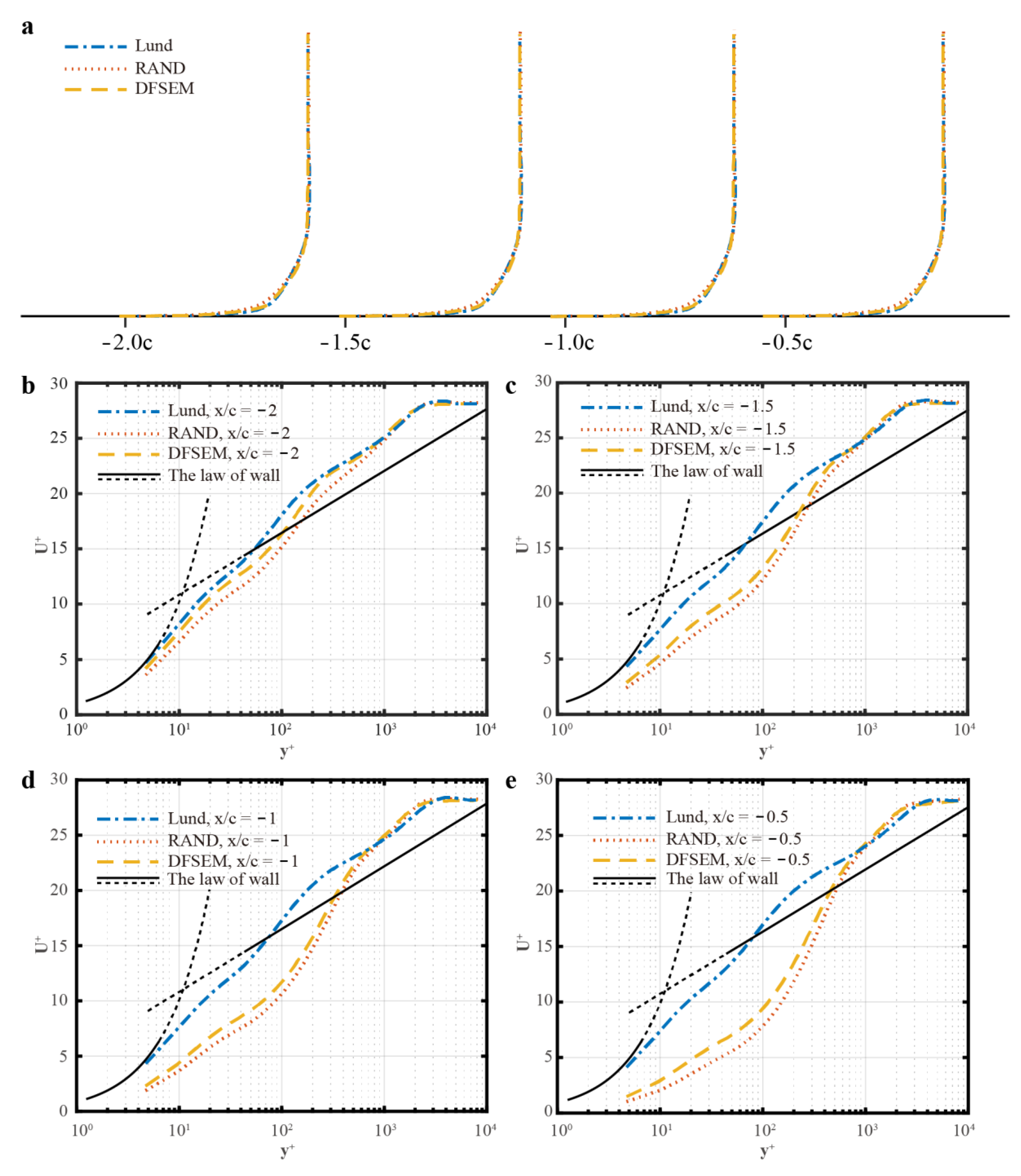
5.4.1. Time-Averaged Velocity Profiles before the Hump
5.4.2. Reynolds Stress Profiles before the Hump
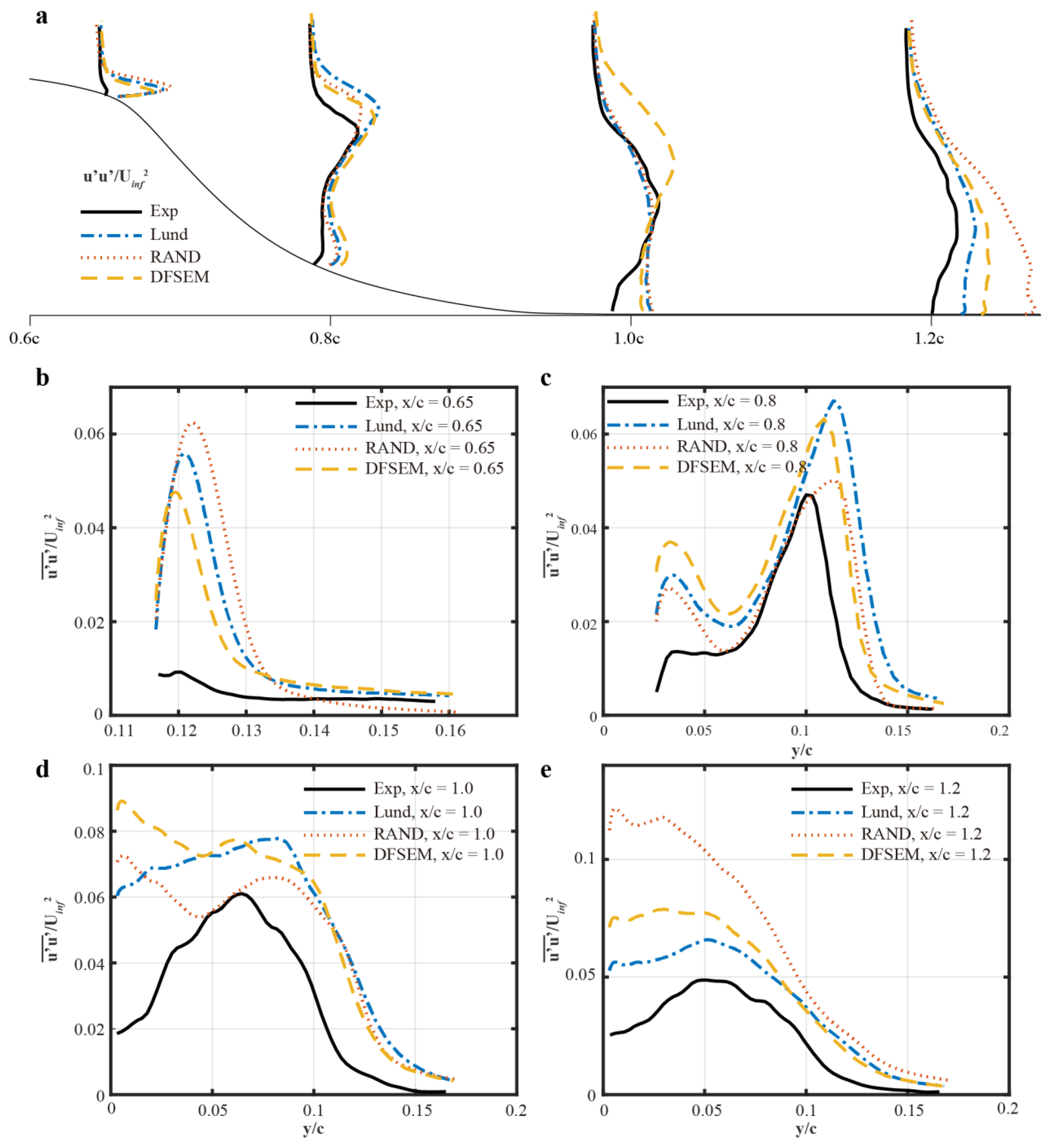
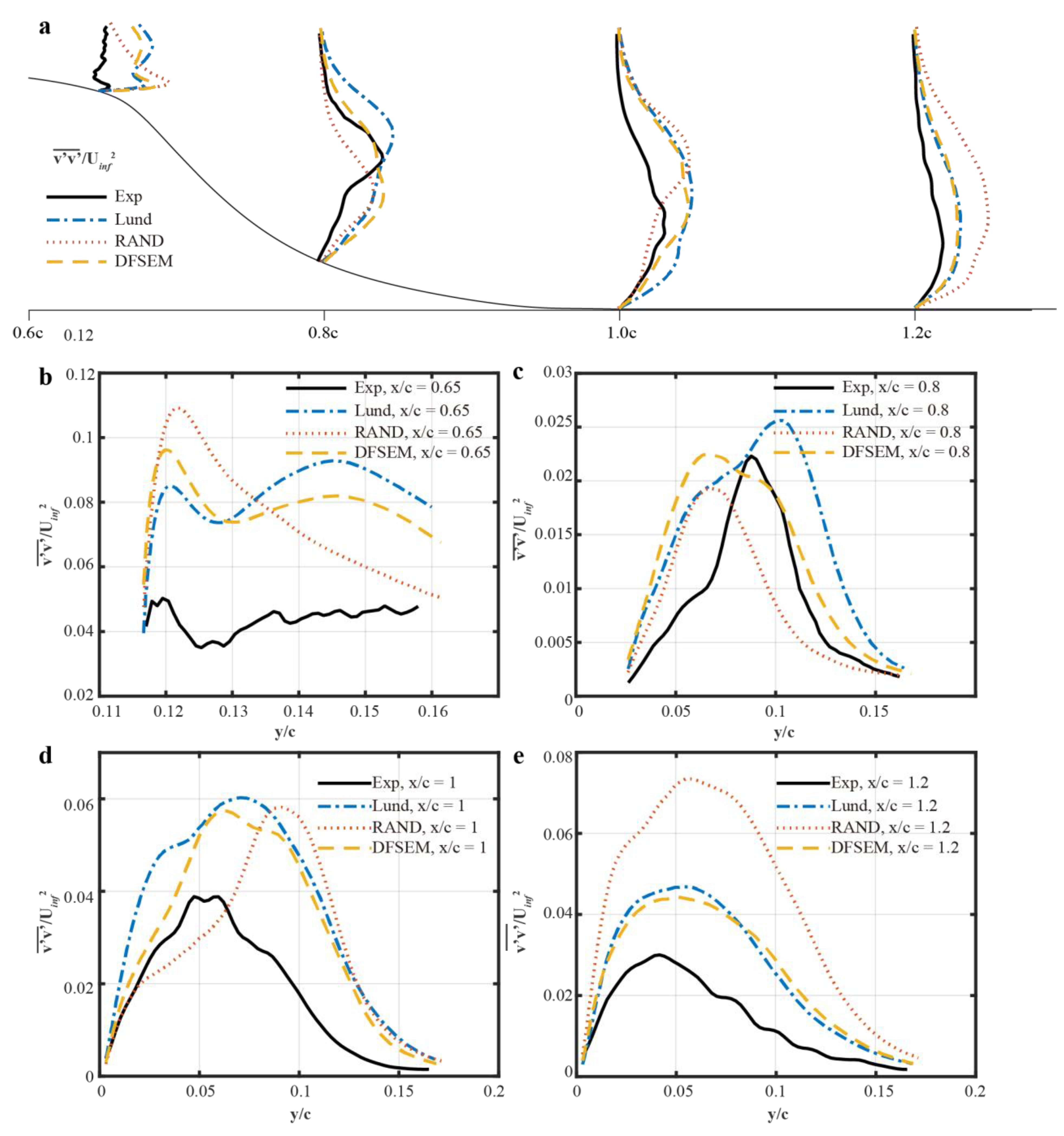
5.5. Quantifications of the Turbulent Properties over the Hump
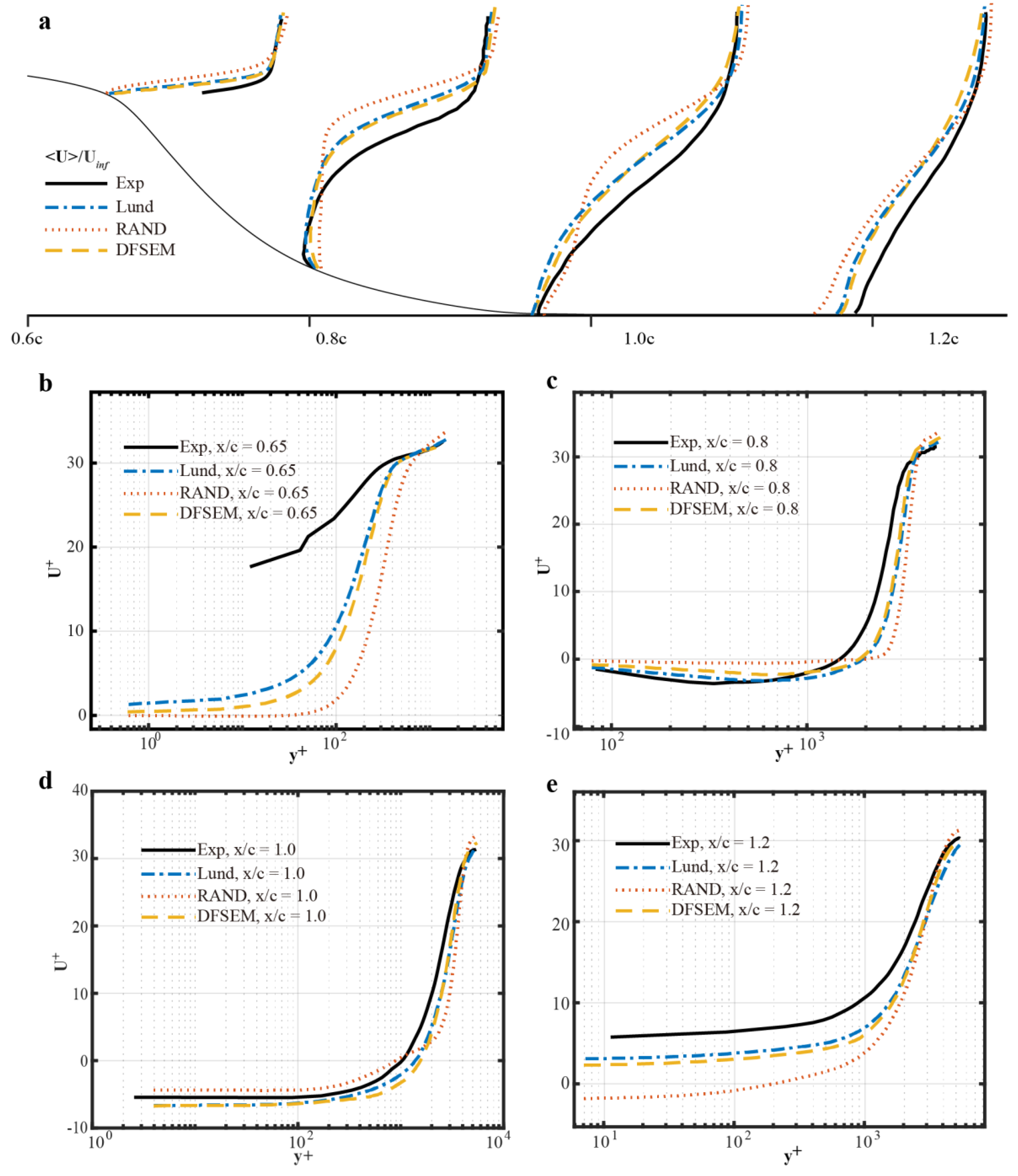
5.5.1. Time-Averaged Velocity Profiles over the Hump
5.5.2. Reynolds Stress Profiles over the Hump
6. Conclusions and Further Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| P | pressure |
| velocity | |
| filtered velocity | |
| wall shear stress | |
| friction velocity defined by | |
| stress tensor | |
| filtered rate-of-strain tensor | |
| turbulent viscosity | |
| Smagorinsky coefficient | |
| sub-grid length | |
| damping function | |
| non-dimensional near wall distance defined by | |
| the production rate | |
| U | mean velocity |
| free stream velocity | |
| average in the spanwise direction | |
| the ratio of friction velocity at the inlet plane to the friction velocity at the recycle plane | |
| boundary layer thickness | |
| Displacement thickness | |
| non-dimensional wall distance defined by | |
| weighting function | |
| momentum thickness | |
| Reynolds number based on momentum thickness | |
| computational time step | |
| T | characteristic time scale of the averaging interval |
| weighting average factor | |
| Reynolds stress tensor | |
| suitable shape function | |
| random numbers with zero average | |
| L | length of the channel with a hump |
| Subscripts | |
| inlt | at the inlet plane in Lund method |
| recy | at the recycle plane in Lund method |
| turbulent length scale in DFSEM | |
| Superscripts | |
| inner | inner region in the boundary layer |
| outer | outer region in the boundary layer |
| ‘ | root mean square of fluctuating value |
Appendix A
References
- Bechmann, A.; Sørensen, N.N.; Johansen, J. Atmospheric flow over terrain using hybrid RANS/LES. Eur. Wind Energy Conf. Exhib. 2007, 1, 107–113. [Google Scholar]
- Quon, E.W.; Ghate, A.S.; Lele, S.K. Enrichment methods for inflow turbulence generation in the atmospheric boundary layer. J. Phys. Conf. Ser. 2018, 1037, 072054. [Google Scholar] [CrossRef]
- Druilhet, A.; Durand, P. Experimental investigation of atmospheric boundary layer turbulence. Atmos. Res. 1997, 43, 345–388. [Google Scholar] [CrossRef]
- Immer, M.C. Time-Resolved Measurement and Simulation of Local Scale Turbulent Urban Flow; ETH-Zürich: Zürich, Switzerland, 2016. [Google Scholar] [CrossRef]
- Bou-Zeid, E.; Meneveau, C.; Parlange, M.B. Large-eddy simulation of neutral atmospheric boundary layer flow over heterogeneous surfaces: Blending height and effective surface roughness. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Krishnan, V.; Squires, K.; Forsythe, J. Prediction of Separated Flow Characteristics over a Hump Using RANS and DES. In Proceedings of the 2nd AIAA Flow Control Conference, Portland, OR, USA, 28 June 2004–1 July 2004; Volume 44. [Google Scholar]
- Pope, S.B. Turbulent Flows. Meas. Sci. Technol. 2001, 12, 2020–2021. [Google Scholar] [CrossRef]
- Tabor, G.; Baba-Ahmadi, M. Inlet conditions for large eddy simulation: A review. Comput. Fluids 2010, 39, 553–567. [Google Scholar] [CrossRef]
- Castro, H.G.; Paz, R.R. A time and space correlated turbulence synthesis method for Large Eddy Simulations. J. Comput. Phys. 2013, 235, 742–763. [Google Scholar] [CrossRef]
- Wu, X.; Moin, P. Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 2009, 630, 5–41. [Google Scholar] [CrossRef]
- Wu, X. Inflow Turbulence Generation Methods. Annu. Rev. Fluid Mech. 2017, 49, 23–49. [Google Scholar] [CrossRef]
- Lund, T.S.; Wu, X.; Squires, K.D. Generation of Turbulent Inflow Data for Spatially-Developing Boundary Layer Simulations. J. Comput. Phys. 1998, 140, 233–258. [Google Scholar] [CrossRef]
- Moin, P.; Mahesh, K. DIRECT NUMERICAL SIMULATION: A Tool in Turbulence Research. Annu. Rev. Fluid Mech. 1998, 30, 539–578. [Google Scholar] [CrossRef]
- Keating, A.; Piomelli, U.; Balaras, E.; Kaltenbach, H.-J. A priori and a posteriori tests of inflow conditions for large-eddy simulation. Phys. Fluids 2004, 16, 4696–4712. [Google Scholar] [CrossRef]
- Araya, G.; Castillo, L.; Meneveau, C.; Jansen, K. A dynamic multi-scale approach for turbulent inflow boundary conditions in spatially developing flows. J. Fluid Mech. 2011, 670, 581–605. [Google Scholar] [CrossRef]
- Kim, Y. Wind Turbine Aerodynamics in Freestream Turbulence. PhD Thesis, University of Southampton, Southampton, UK, 2013. [Google Scholar]
- Klein, M.; Sadiki, A.; Janicka, J. A digital filter based generation of inflow data for spatially developing direct numerical or large eddy simulations. J. Comput. Phys. 2003, 186, 652–665. [Google Scholar] [CrossRef]
- Tolias, I.; Koutsourakis, N.; Hertwig, D.; Efthimiou, G.; Venetsanos, A.; Bartzis, J. Large Eddy Simulation study on the structure of turbulent flow in a complex city. J. Wind. Eng. Ind. Aerodyn. 2018, 177, 101–116. [Google Scholar] [CrossRef]
- Smirnov, A.; Shi, S.; Celik, I. Random Flow Generation Technique for Large Eddy Simulations and Particle-Dynamics Modeling. J. Fluids Eng. 2001, 123, 359–371. [Google Scholar] [CrossRef]
- Kraichnan, R.H. Diffusion by a Random Velocity Field. Phys. Fluids 2010, 13, 22–31. [Google Scholar] [CrossRef]
- Huang, S.H.; Li, Q.S.; Wu, J.R. Journal of Wind Engineering A general inflow turbulence generator for large eddy simulation. J. Wind Eng. Ind. Aerodyn. 2010, 98, 600–617. [Google Scholar] [CrossRef]
- Jarrin, N.; Benhamadouche, S.; Laurence, D.; Prosser, R. A synthetic-eddy-method for generating inflow conditions for large-eddy simulations. Int. J. Heat Fluid Flow 2006, 27, 585–593. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, H.; Huang, Q.; Xue, H.; Lin, K. A multi-scale synthetic eddy method for generating inflow data for LES. Comput. Fluids 2017, 156, 103–112. [Google Scholar] [CrossRef]
- Poletto, R.; Craft, T.; Revell, A. A New Divergence Free Synthetic Eddy Method for the Reproduction of Inlet Flow Conditions for LES. Flow Turbul. Combust. 2013, 91, 519–539. [Google Scholar] [CrossRef]
- Xie, Z.-T.; Castro, I.P. Efficient Generation of Inflow Conditions for Large Eddy Simulation of Street-Scale Flows. Flow Turbul. Combust. 2008, 81, 449–470. [Google Scholar] [CrossRef]
- Aliabadi, A.A.; Veriotes, N.; Pedro, G. A Very Large-Eddy Simulation (VLES) model for the investigation of the neutral atmospheric boundary layer. J. Wind. Eng. Ind. Aerodyn. 2018, 183, 152–171. [Google Scholar] [CrossRef]
- Fröhlich, J.; Mellen, C.P.; Rodi, W.; Temmerman, L.; Leschziner, M.A. Highly resolved large-eddy simulation of separated flow in a channel with streamwise periodic constrictions. J. Fluid Mech. 2005, 526, 19–66. [Google Scholar] [CrossRef]
- Lamberti, G.; García-Sánchez, C.; Sousa, J.; Gorlé, C. Optimizing turbulent inflow conditions for large-eddy simulations of the atmospheric boundary layer. J. Wind Eng. Ind. Aerodyn. 2018, 177, 32–44. [Google Scholar] [CrossRef]
- Yang, Q.; Zhou, T.; Yan, B.; Van Phuc, P.; Hu, W. LES study of turbulent flow fields over hilly terrains—Comparisons of inflow turbulence generation methods and SGS models. J. Wind. Eng. Ind. Aerodyn. 2020, 204, 104230. [Google Scholar] [CrossRef]
- Montorfano, A.; Piscaglia, F.; Ferrari, G. Inlet boundary conditions for incompressible LES: A comparative study. Math. Comput. Model. 2013, 57, 1640–1647. [Google Scholar] [CrossRef]
- Šarić, S.; Jakirlić, S.; Tropea, C. A periodically perturbed backward-facing step flow by means of LES, des and T-RANS: An example of flow separation control. J. Fluids Eng. Trans. ASME 2005, 127, 879–887. [Google Scholar] [CrossRef]
- Vasaturo, R.; Kalkman, I.; Blocken, B.; van Wesemael, P. Large eddy simulation of the neutral atmospheric boundary layer: Performance evaluation of three inflow methods for terrains with different roughness. J. Wind. Eng. Ind. Aerodyn. 2018, 173, 241–261. [Google Scholar] [CrossRef]
- Skote, M.; Wallin, S. Near-wall damping in model predictions of separated flows. Int. J. Comut. Fluid Dyn. 2016, 30, 218–230. [Google Scholar] [CrossRef]
- OpenFOAM-v2006. Turbulent Inlet Boundary Condition Based on Pseudo-Random Numbers and a Given Spatiotemporal-Invariant Mean Field. Available online: https://www.openfoam.com/documentation/guides/latest/api/classFoam_1_1turbulentInletFvPatchField.html (accessed on 30 January 2021).
- Turbulence Modeling Resource. Available online: https://turbmodels.larc.nasa.gov/nasahump_grids_workshop.html (accessed on 30 January 2021).
- Classic Collection All Cases No.83. Available online: http://cfd.mace.manchester.ac.uk/ercoftac/index.html (accessed on 30 January 2021).
- Spalding, D.B. A single formula for the ‘law of the wall. J. Appl. Mech. Trans. ASME 1960, 28, 455–458. [Google Scholar] [CrossRef]
- Azevedo, R.; Roja-Solórzano, L.R.; Leal, J.B. Turbulent structures, integral length scale and turbulent kinetic energy (TKE) dissipation rate in compound channel flow. Flow Meas. Instrum. 2017, 57, 10–19. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Wray, A.; Moin, P. Eddies, Streams, and Convergence Zones in Turbulent Flows. 1988. Available online: https://ntrs.nasa.gov/citations/19890015184 (accessed on 30 January 2021).
- Asgari, E.; Tadjfar, M. Assessment of four inflow conditions on large-eddy simulation of a gently curved backward-facing step. J. Turbul. 2016, 18, 61–86. [Google Scholar] [CrossRef]

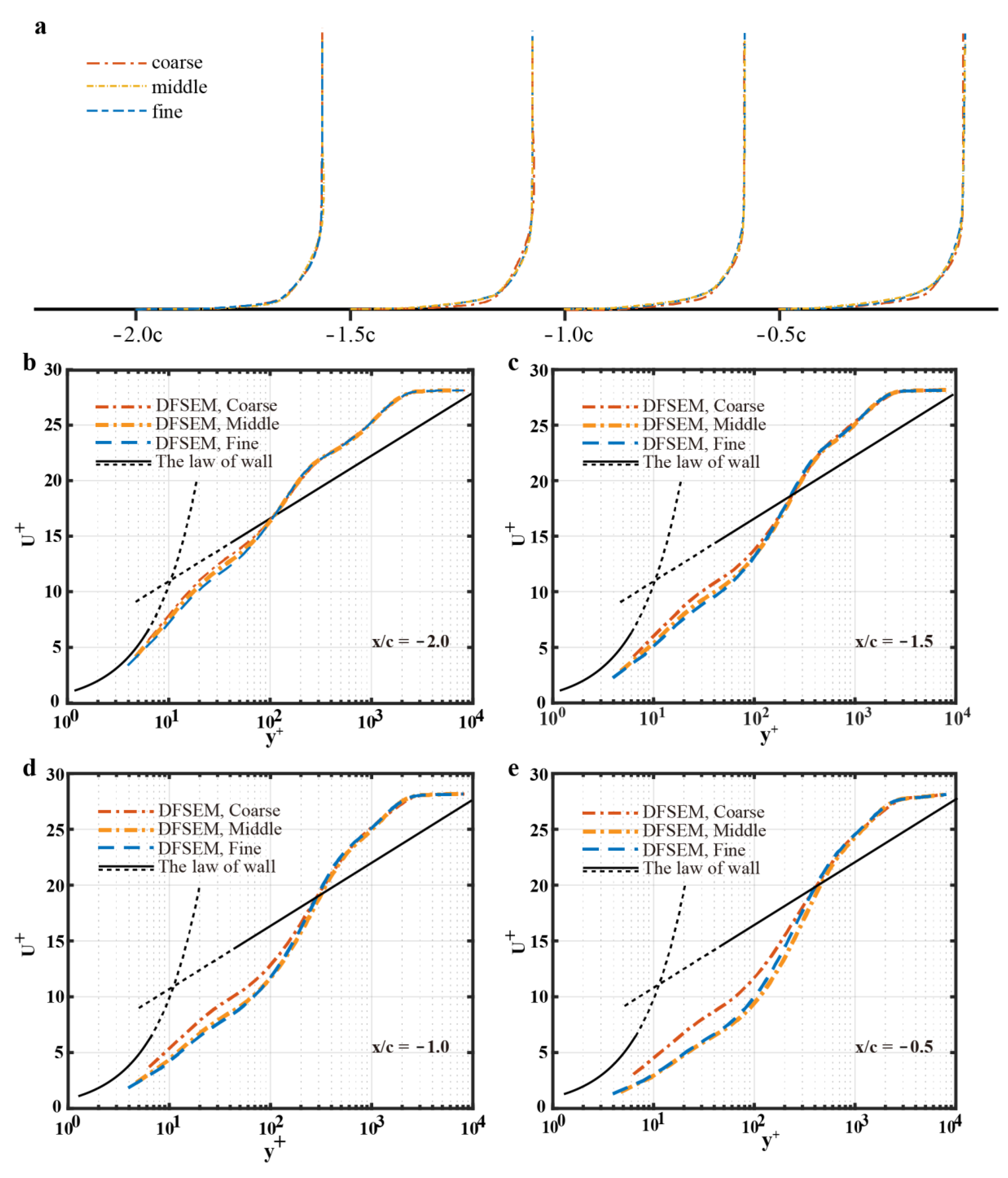
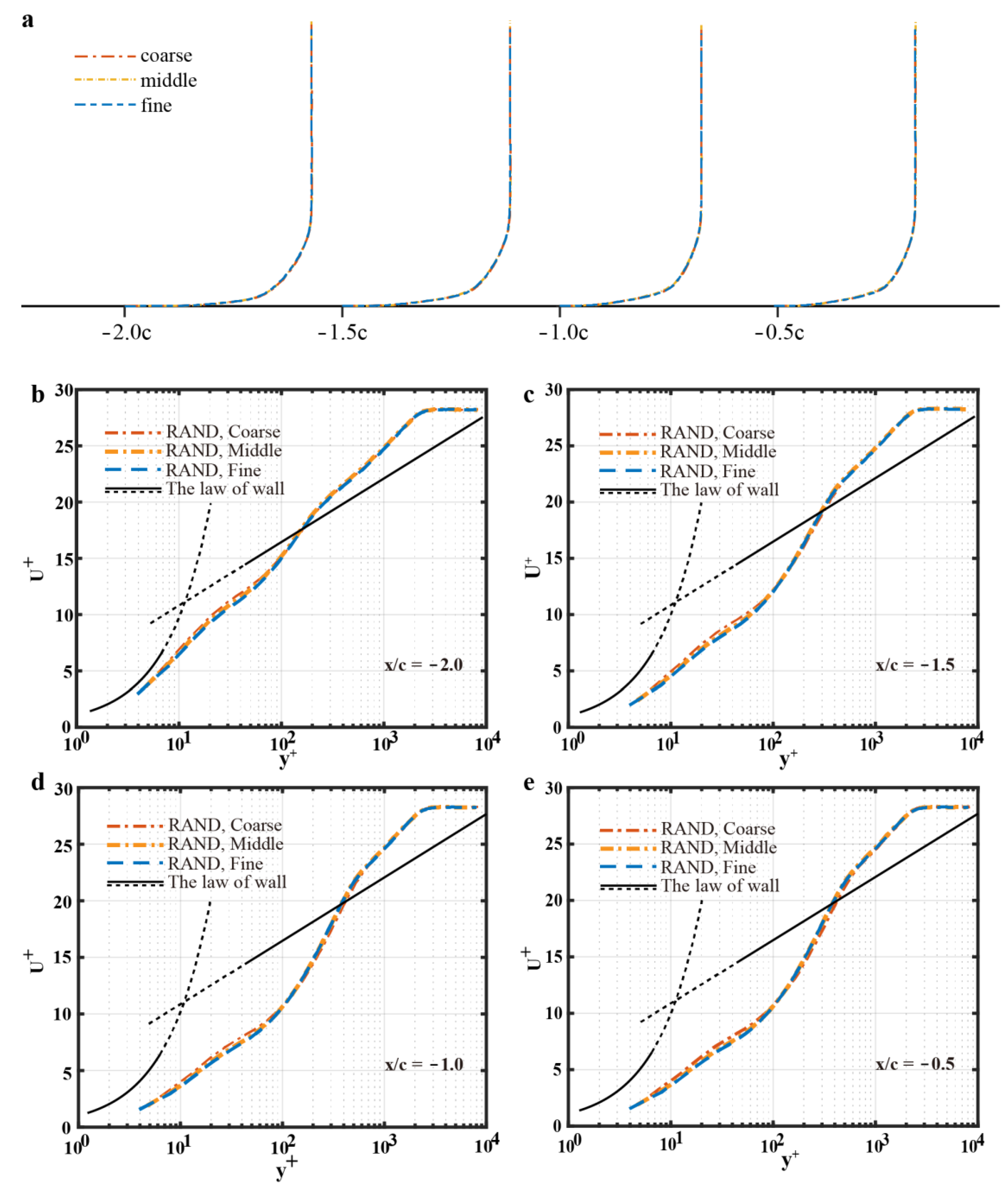
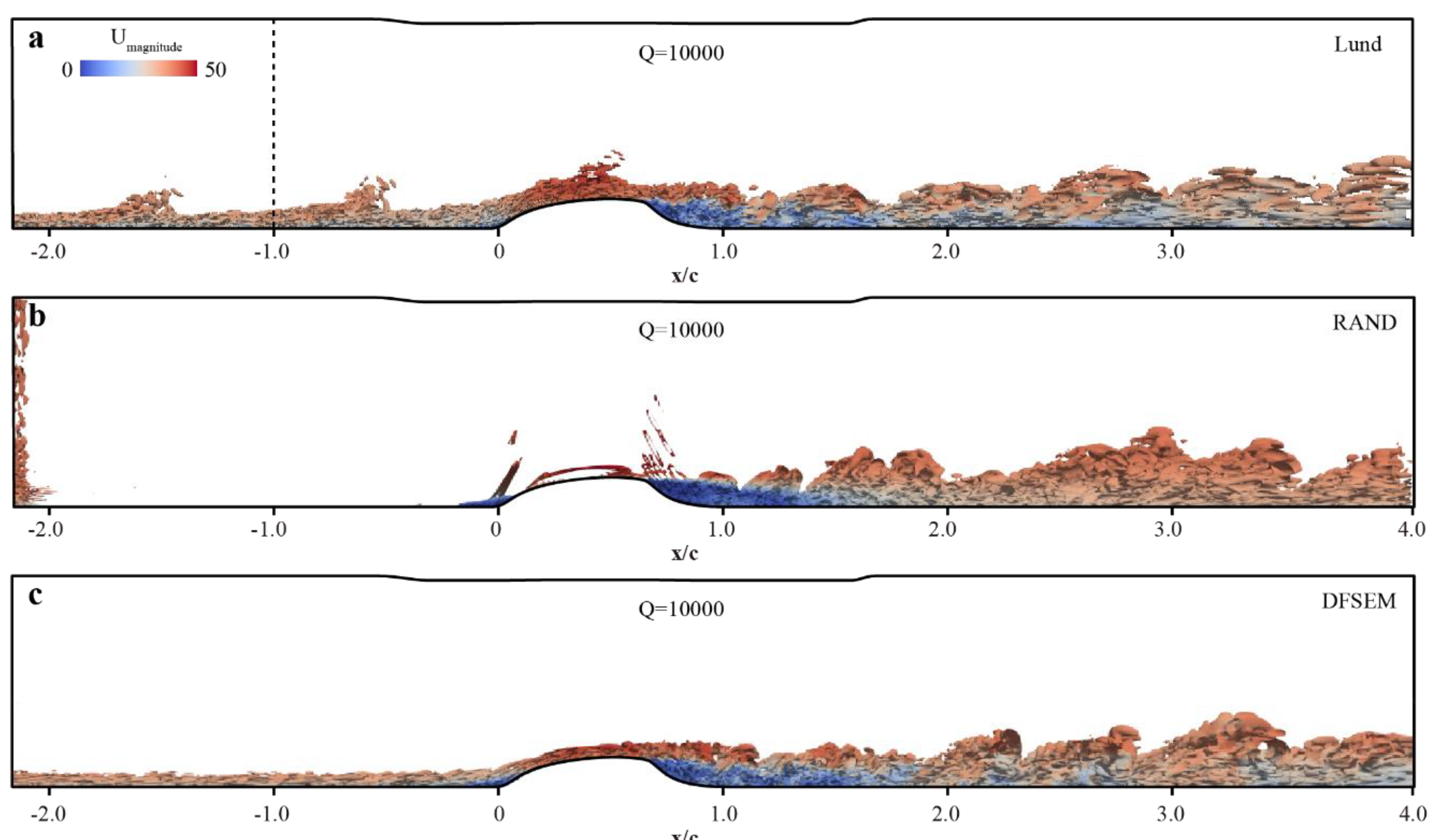
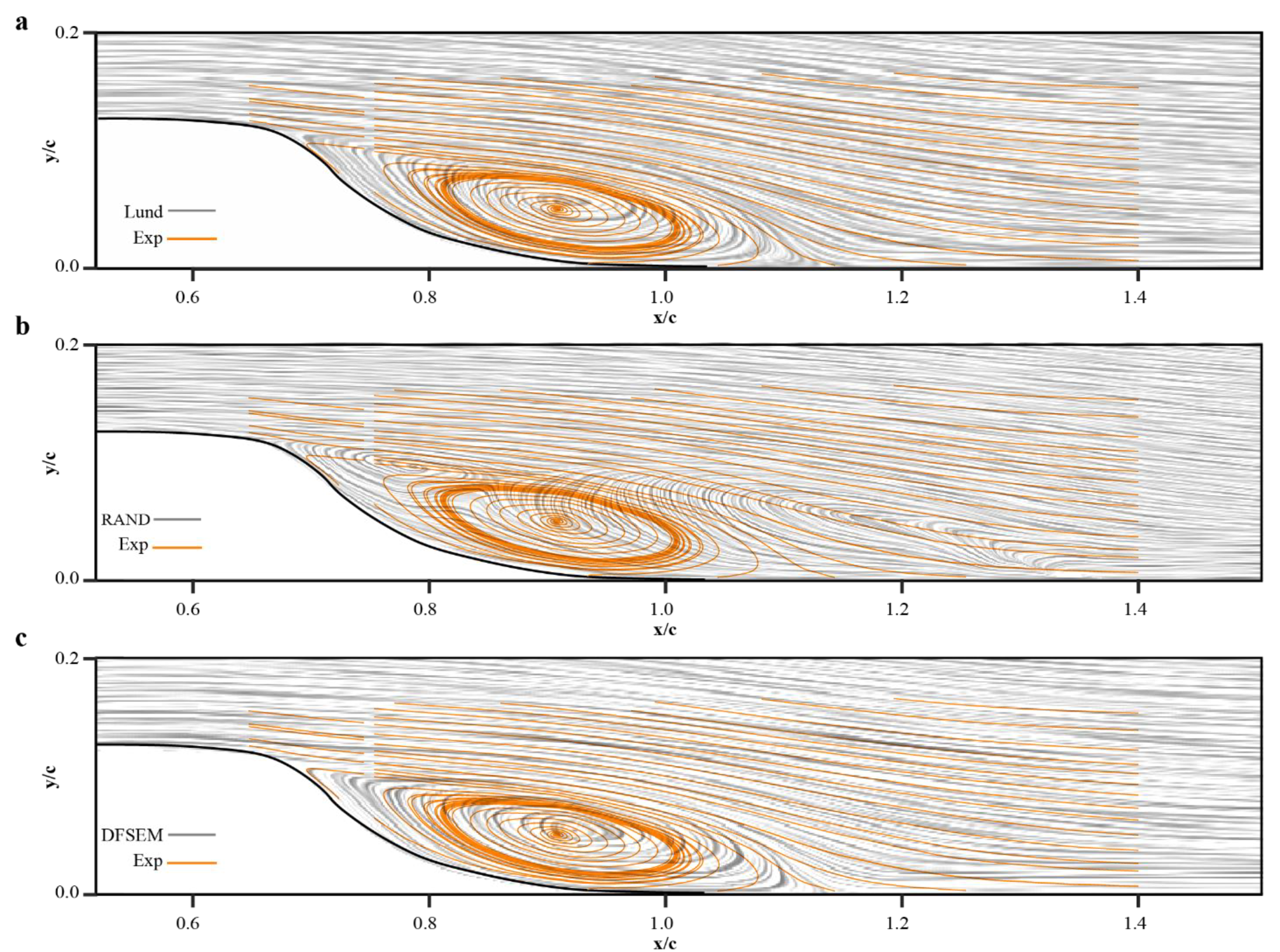


| Mean Velocity | Specified Thicknesses | Reynold Stresses | Turbulent Length Scales | |
|---|---|---|---|---|
| Random | X | — | — | — |
| Lund | X | X | — | — |
| DFSEM | X | — | X | X |
| Density | Mesh Size (x, y, z) | |||
|---|---|---|---|---|
| Coarse | 929 | 6.35 | 125.06 | |
| Middle | 658 | 4.76 | 101.61 | |
| Fine | 619 | 3.18 | 77.42 |
| Exp | Lund | DFSEM | RAND | |
|---|---|---|---|---|
| Separation point (x/c) | 0.648 | 0.642 | 0.645 | 0.610 |
| Rel. diff to Exp (%) | — | 0.93 | 0.46 | 5.86 |
| Re-attach. Point (x/c) | 1.11 | 1.174 | 1.175 | 1.358 |
| Rel. diff to Exp (%) | — | 5.77 | 5.86 | 22.34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Vita, G.; Fraga, B.; Wang, J.; Hemida, H. Effect of the Inlet Boundary Conditions on the Flow over Complex Terrain Using Large Eddy Simulation. Designs 2021, 5, 34. https://doi.org/10.3390/designs5020034
Wang Y, Vita G, Fraga B, Wang J, Hemida H. Effect of the Inlet Boundary Conditions on the Flow over Complex Terrain Using Large Eddy Simulation. Designs. 2021; 5(2):34. https://doi.org/10.3390/designs5020034
Chicago/Turabian StyleWang, Yi, Giulio Vita, Bruño Fraga, Jianchun Wang, and Hassan Hemida. 2021. "Effect of the Inlet Boundary Conditions on the Flow over Complex Terrain Using Large Eddy Simulation" Designs 5, no. 2: 34. https://doi.org/10.3390/designs5020034
APA StyleWang, Y., Vita, G., Fraga, B., Wang, J., & Hemida, H. (2021). Effect of the Inlet Boundary Conditions on the Flow over Complex Terrain Using Large Eddy Simulation. Designs, 5(2), 34. https://doi.org/10.3390/designs5020034









