1. Introduction
In a wide range of engineering applications, the measurement of displacements and deformations plays an important role [
1]. Due to limitations of invasive methods for strain estimations, there exists a strong motivation for the development of contactless measurement techniques. Optical-based strain measurement systems are of particular importance in the measurement systems area as they offer a potential, non-invasive, high throughput strain measurement system [
2,
3,
4]. Therefore, over the past decade, several different systems for measuring optical displacement have been developed [
5,
6]. Digital Image Correlation (DIC) gained a lot of popularity, not only because of its simplicity and accuracy [
2] but also because of its reliability and wide range of applications [
7]. Since this method was first published by Peters and Ranson [
8] in the early 1980s, the DIC method has been continuously improved by different researchers [
6,
9,
10], while the basic principle remained the same. Firstly, accurately time-resolved images of a specimen undergoing deformation are acquired. The subsequent analysis is conducted between image pairs separated over time where one of the images is considered as the reference state while the other represents the deformed state of the specimen. Finally, pairs of images are compared by dividing the reference image into sub-images and searching for the same sub-image in the image of the deformed state [
11]. The local displacement is determined by estimating the inter-image positions of the sub-image pairs.
The method of dividing the image into sub-images, searching between images and processing procedures has undergone many changes and improvements over the years in order to develop accurate methods for use in various fields of technology [
12,
13]. However, one of the main disadvantages of DIC is its high computational load and relatively slow image processing time, which imposes significant limitations on the frame rate of image acquisition, and post-processing of images.
Here, we tested the most common computational strategies used in DIC and evaluated their performance under serial and parallel computational implementation in MATLAB. MATLAB is a computing environment commonly used by engineers, researchers and economists [
14]. The main reason for choosing MATLAB for computing DIC algorithms is because MATLAB allows user to implement and test user-defined algorithms [
15]. It has a large database of built-in algorithms which user can inherit and use them based on the problem requirement [
16]. Besides the built-in database, external libraries can also be used by importing them into the MATLAB interface. It is also possible to perform extensive data analysis and visualization using MATLAB [
17].
MATLAB comes with many powerful sets of tools and functions that make it relatively easy to use higher-level functionality and integrate complex functions into self-developed programs. The DIC procedure adapted by MATLAB distorts the shape of the initial image from a rectangular to an arbitrary shape while converging [
18]. However, MATLAB is slower than other programming languages and has limited control over low-level functions such as memory management [
18,
19]. However, due to its widespread use, we decided to focus on MATLAB.
We sought to combine the integer and subpixel displacement DIC methods in such a way that they are ahead of each other. A modular program was developed to investigate the advantages and disadvantages of different computational methods and their combinations. These methods were tested, compared, and improved until the most efficient and optimized combination of methods was found. Two different approaches to parallelization have been adopted: On the one hand, sub-image parallelization in which sub-images are processed in parallel and, on the other hand, image parallelization in which pairs of entire images are processed in parallel. In addition to quantifying the impact of these approaches to high-level parallelization, the impact of hardware settings on the overall performance of DIC computations was also evaluated.
2. Theoretical Background
The main idea of DIC is to determine displacements between two states of an object of interest by comparing two images of this object in the two different states; a reference image such as a sample in an undeformed state and a target image such as a sample in a deformed state. For this purpose two functions, one represents the grey level in the reference image
f(
x,
y) and the other for the target image
g(
x*,
y*) at the positions [
x,
y] and [
x*,
y*], respectively defined. The reference image is divided into several rectangular sub-images. Each sub-image has a specific grey level distribution that is compared to a sub-image of the same size within the target image. This comparison is performed using correlation coefficients, which provide a measure of similarity [
20].
The strategy of DIC methods can be roughly divided into two steps: First, the integer-pixel displacement search, which determines the displacement of a sub-image as an integer value. Second, a sub-pixel displacement search algorithm capable of determining sub-pixel displacements [
21]. However, in order to reduce computational time generally, the integer-pixel search is performed to provide initial guesses to initiate the sub-pixel displacement algorithm [
20].
2.1. Integer Pixel Displacement
The integer pixel displacement can be determined by a variety of algorithms. The progression of the algorithms varies in many ways, such as: (a) Grid method: It calculates the value of the correlation coefficient from the initial point (
x,
y), which corresponds to calculation point of the reference image, to the grid points in the direction from the inside to outside until a point is obtained, where the value of the correlation coefficient is higher than the established correlation coefficient threshold. (b) Peak search method: It considers the reference point at a starting point, finds a point that has the same
x (
y) coordinate, which is the starting point, and has the highest correlation coefficient value. Then considers the newly found point as a starting point and finds another point that has the same
y (
x) coordinate and has the greatest value of the correlation coefficient with a recently found point. This method is repeated for a further time step [
21]. But all these methods ultimately can calculate the correlation coefficient. Currently, a zero-normalized cross-correlation coefficient, as presented in Equation (1), is commonly used [
20].
Here,
f(
x,
y) and
g(
x*,
y*) represent the grey levels at a certain position in reference and target image, while
and
represent the average grey levels of the sub-images with a size of (2M + 1) × (2M + 1) pixels, where M represents the number of rows in the image [
20]. This correlation coefficient C of a point
p = (
x,
y)
T reaches its maximum if the grey level distributions of both sub-images are equal [
22]. This implies that the displacement is determined by determining the position at which the correlation coefficient is maximal.
With this knowledge, the displacement can be determined using a simple but time-consuming Brute Force Search (BFS) algorithm to allocate the position with the highest correlation coefficient. A brute force search algorithm evaluates all possible positions and determines the position with the highest correlation coefficient [
3].
Another smarter approach is particle swarm optimization. In this optimization strategy, particles are initialized randomly at position
p = (
x1,
x2) with velocity
v = (
v1,
v2). Through iteration with different generations “
t” of the particle “
i” an optimal solution is found. The next generation is determined according to:
where
d represents the
x and
y directions.
c1 and
c2 are predefined acceleration coefficients which influence cognitive (e.g., local) optimization behavior and social (e.g., global) optimization behavior, respectively. The parameters
r1 and
r2 are independent random values between zero and one.
Each particle has a correlation coefficient and a history with one best position
pbest at which it has perceived its maximal correlation coefficient
cbest so far. One particle has perceived the highest correlation coefficient c
best of the whole swarm at the global best position
gbest. The generation dependent weight factor
w is calculated according to:
With the maximum number of generations Gmax.
According to Wu, et al. [
3], a maximum of five generations and a correlation coefficient of 0.75 are enough for efficient DIC calculations. Since these algorithms must be used in real-time, small deformations between two consecutive images can be assumed. Therefore, the integer-pixel search algorithm looks for the target sub-image in an area of 25 pixels around the reference sub-image.
2.2. Sub-Pixel Displacement
Limiting the displacements of the sub-image to an integer value leads to an accuracy of ±0.5 pixels. To further improve the accuracy, an interpolation approach has been introduced to determine the displacement of the sub-image between the two states to sub-pixel values [
23]. In this approach, it is assumed that a grey level of a pixel is equal to the grey level at its center. The most basic approach, bilinear interpolation, to determine the grey level at an arbitrary position
G (
x*,
y*) is as follows:
G (
x*,
y*) denotes the grey level distribution at an arbitrary sub-pixel position (
x*,
y*), while
x’ and
y’ denote the distance along the
x and
y-axis from the next integer pixel position to (
x*,
y*), and
a00,
a01,
a10 and
a11 are the coefficients of the bilinear interpolation function. Utilizing a linear equation system, those coefficients can be determined by the grey levels of surrounding integer pixel positions. Besides this simple bilinear approach, other methods such as bicubic interpolation [
24,
25] or higher-order spline interpolation [
26] have been used as well. Generally, the higher the approaches’ order the higher the accuracy at the expense of computational effort [
2].
Unfortunately, bilinear interpolation just gives grey levels at certain positions within four pixels. To find the position with the highest correlation also a search algorithm is required. Besides the well-known Newton–Raphson (NR) algorithm, a more efficient Inverse-Compositional Gauss–Newton (IC-GN) approach is commonly used [
27]. The IC-GN algorithm uses an affine warp function together with an interpolation approach to backwardly calculate the position of the reference sub-image. In contrast to the NR algorithm, in the IC-GN several parameters can be pre-computed and there is no need to update them at every iteration. A detailed explanation can be found in a publication by Pan, Li and Tong [
28]. Finally, usage of look-up tables for calculation results required multiple attempts to reduce the computational effort further [
28].
2.3. Parallel Computation
Parallel computation is one of the most used methods to reduce computational time. Therefore, it plays an important role in the development of new programs and the optimization of old ones and significant research concerning this topic is ongoing [
29,
30]. Despite its advances and benefits, parallel computation also has its own challenges and is a very complex area with some restrictions and limitations [
30]. Nonetheless, some studies have been published, concerning parallel computing in DIC, either for CPU computation [
23,
27], GPU computation [
30] or a combination of both [
31].
Parallel computing divides one main task into several subtasks which are performed simultaneously. Unfortunately, this is only possible if the subtasks can be processed separately. In DIC, the search for the target sub-images position of different reference sub-images can be processed in parallel in some approaches since they are completely independent of each other. Additionally, whole pairs of the reference image and target image can be processed simultaneously on different workers. Parallel computing can be used for both integer-pixel displacement and sub-pixel displacement search algorithms.
Due to the vastness and complexity of the parallel computation procedures, this study was limited to discussing the same in general terms, while evaluation of the various DIC algorithms and the significance of parallel computing will be done on MATLAB, one of the most commonly used platforms for evaluating DIC algorithms.
Parallel computation splits up one task to perform it on several workers simultaneously. To do this, it is necessary to process data and information in such a way that it is correctly distributed and transmitted to the assigned worker. Because the GPU is attached to the CPU via a PCI express bus, data transfer is slower than for standard CPU usage [
32,
33]. Thus, the computation speed is severely limited by the required amount of data transfer. According to Xinxing Shao et al. [
27] in a study, it is possible to use a pixel selection strategy to further improve the parallel computing efficiency of the DIC and it also allows user to run the real-time analysis.
CPU Parallel Computation in MATLAB
In addition, parallel computing on the GPU, MATLAB offers the ability to execute tasks in parallel on different processors [
19]. To enable parallel computing, MATLAB creates a parallel computing pool from different multicore processors and processes various independent tasks in parallel [
19].
MATLAB provides the user with two different possibilities to execute computing scripts in CPU parallel computation [
34]. On the one hand, the “parfor” loop function, which works similar to a standard “for” loop but executes its command section in parallel. On the other hand, the “parfeval” function, which allows asynchronous sub-function call and processing on a different worker without stopping the main function to wait for any results of the called sub-function [
19].
While CPU parallel processing may seem beneficial, data transfer also has a bottleneck. For parallel computing on a CPU, this is not as critical as for parallel computing on a GPU, but it is still an important factor that must be taken into account [
19]. MATLAB creates a copy of the variable for each worker and passes it to the worker. In a situation where each worker has to process a large amount of data, it takes a significant amount of time to copy and transfer them. Therefore, it is possible that the benefits of parallel computing diminish due to the time spent organizing and transferring data.
3. Tests and Comparisons
Here, we developed a standalone DIC program that uses a combination of different DIC methods including leveraging the benefits of parallel computing to perform DIC analyses as efficiently as possible. The most commonly used and most efficient algorithms were programmed in MATLAB as shown in
Table 1. The modified algorithm from reference [
35] was also tested and evaluated. The testing platform we developed is modular such that it is possible to choose any combination of mathematical search algorithms. To evaluate the performance of different parallelization approaches, two different ways of parallelizing the image evaluation—parallel image processing and parallel sub-image processing—were implemented. All methods and approaches to parallelization were implemented completely independently, which allowed for optimizing the program structure for each module.
Two standard DIC search algorithms, the brute force search algorithm and the Newton–Raphson method, were implemented as reference methods. Additionally, one of the two particle swarm optimization algorithms implemented here was modified so that the gradient descent search algorithm—the star search algorithm was integrated into the particle swarm optimization algorithm. Furthermore, two versions of the inverse-compositional Gauss–Newton method were implemented. One variation was completely implemented by the authors and another one taken from a publication by Baker and Matthews [
35], which was then integrated into the developed software. The two implementations of the inverse-compositional Gauss–Newton algorithm differ in detail as to the overall program structure and usage of higher-level MATLAB functions.
Finally, the accuracy and efficiency of combinations of different methods were tested on two different sets of test data. The first dataset consisted of 204 images of a rectangular specimen undergoing deformation due to tensile forces, taken in the RMIT Materials Laboratory. The second set consisted of 11 images showing different states of a deformation process taken from Blaber, et al. [
34]. A sample of three consecutive images of each of the two datasets is presented in
Figure 1. The histogram of three consecutive images in dataset 1 can be found in
Figure A1,
Figure A2 and
Figure A3 (see
Appendix A).
There are three approaches to choosing a reference image. The simplest approach is a single reference image approach, which uses an image at the beginning of a series with an undeformed test piece before any displacement or force is applied. The motion or displacement of the interrogation points is then tracked over time by correlating subsequent images in the series with the original reference image [
36].
In some cases, the DIC pattern may change significantly during the test, such that the DIC pattern of the deformed sample cannot be correlated back to the undeformed reference image. In this situation, incremental correlation can be used, in which each image is correlated with a previous image instead of correlating with the initial reference image. Incremental correlation gives incremental displacement between each image. The total displacements from the original reference image of the undeformed test piece are calculated by summing the incremental displacements. However, the disadvantage of increasing the correlation is that the errors in the overall offsets also add up, thus the errors usually increase with the number of images in the increasing correlation sequence [
36].
As a trade-off between using a single reference image of an undeformed sample and increasing correlation, a series of images can be divided into sub-series, and the images in each sub-series are correlated back to the image at the beginning of that sub-series. This type of approach is called a partitioned correlation [
36].
In this study, to evaluate the performance of the different approaches in choosing the reference image, the reference image was updated after every evaluation to maximize workload and with the assumption that sequential images in real-time applications only have small displacements. Hence, each evaluated pair of images consists of two consecutive images. Consequently, there were no large displacements between two images. However, the accuracy of the various methods was verified for constant reference images, resulting in large displacements between the two images. All methods were implemented such that they had a guaranteed accuracy of 0.1 pixels, with results usually having an error below 0.05 pixels [
37]. The subset size used was 31 × 31 pixel
2 with a sampling size of 15 pixels. The results were 1.06 million data points for dataset 1 and 200,000 data points for dataset 2. All tests were performed with two different hardware settings, giving directly comparable results as well as providing information on the impact of the system being used. The two used computer systems are listed in
Table 2.
Computer 1 used two workers per core, while Computer 2 used one worker per core. Nonetheless, both were working with four workers. To minimize the influence of any external factors, like high network utilization, all tests were carried out several times at different days and different times. All results presented are the average of several test runs. Test runs with long calculation times were performed 25 times, since the influence of external short-term factors was reduced by the longest simulation time. Medium to very short simulations were repeated 100, 250 or 1000 times to decrease the influence of short duration factors according to the overall simulation period.
4. Results
4.1. Evaluating Result Correctness
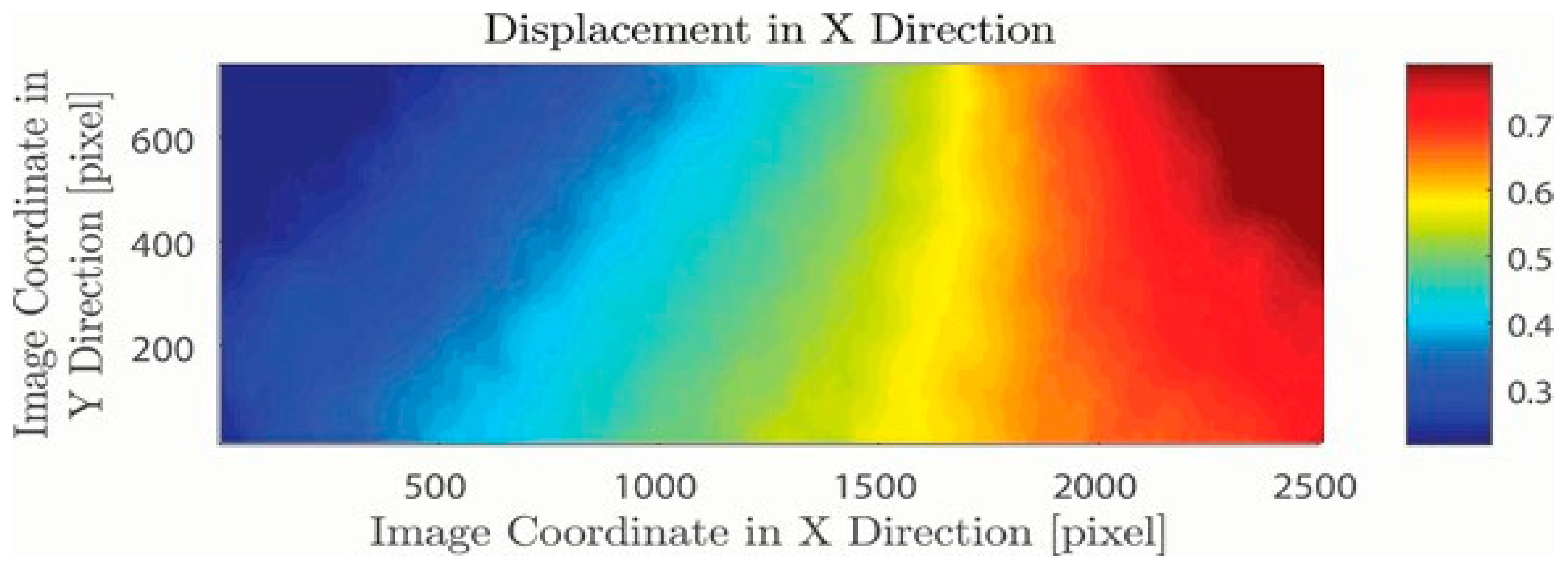
The displacement between the first and the twenty-second image of dataset 1 in the X direction is represented in
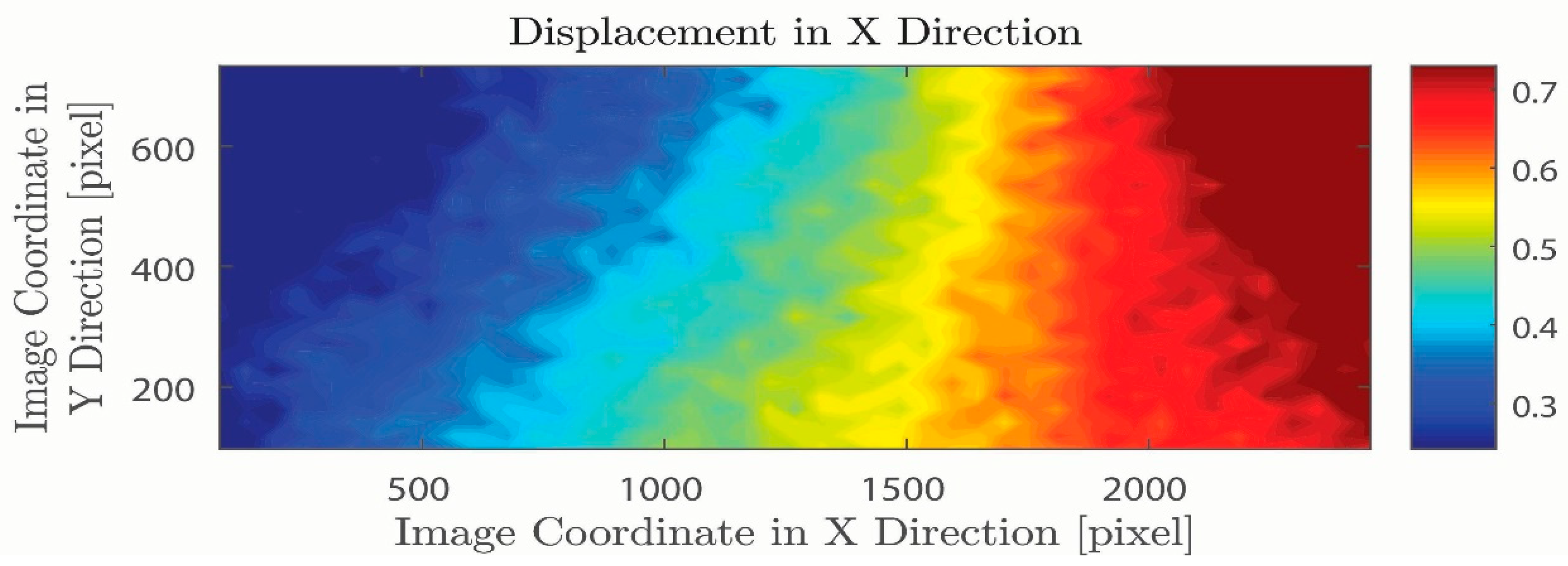
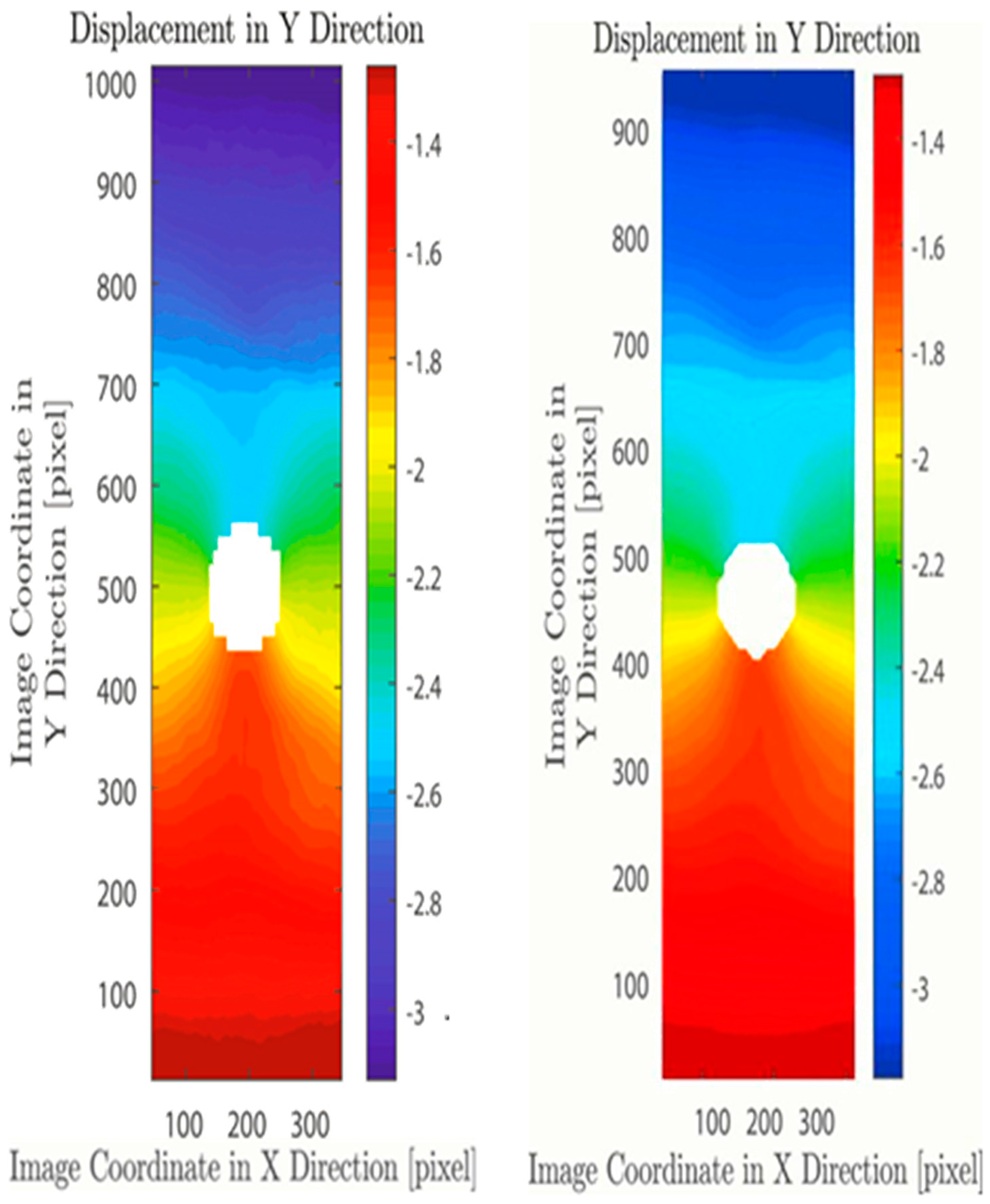
Figure 2, it was determined by using the author’s program. The results of our test platform were validated by comparing it with the results from NCORR by Blaber et al. [
34], as shown in
Figure 3 and
Figure 4. Comparison of the results obtained by a program of the authors and NCORR shows clear similarities. The visualization of the author’s results is slightly different from the visualization of NCORR. Examining the X and Y axes shows that the same section is displayed; investigation of the legend explains the slight differences in the color distribution between the analysis images. This offset in the results could be due to the DIC settings used, especially the subset size. This led to faster convergence, but resulted in the maximum number of upper legends in the author’s program approximately 0.05 higher than lower legends compared to the reference image.
4.2. Evaluating Integer Pixel Routines
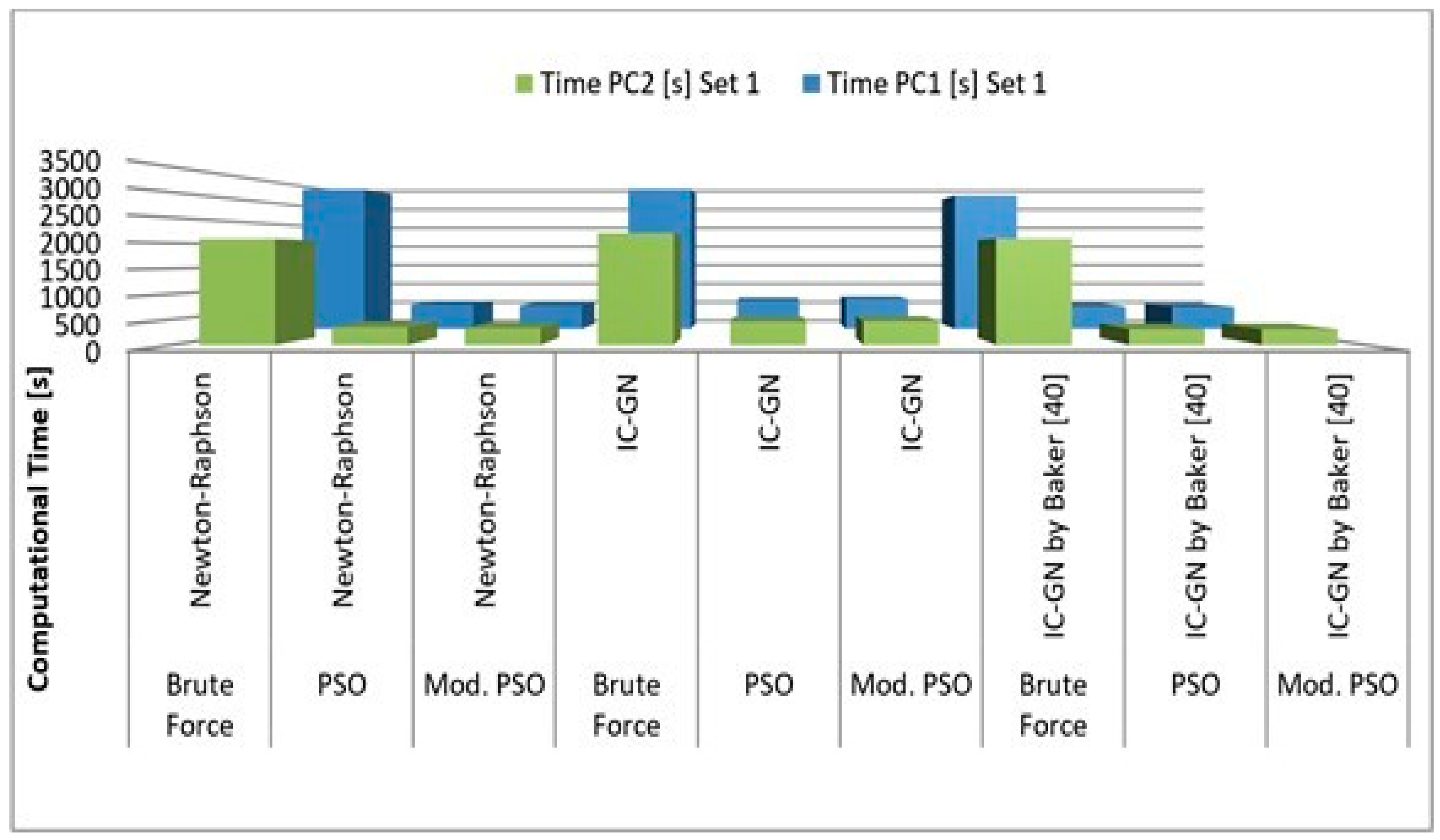
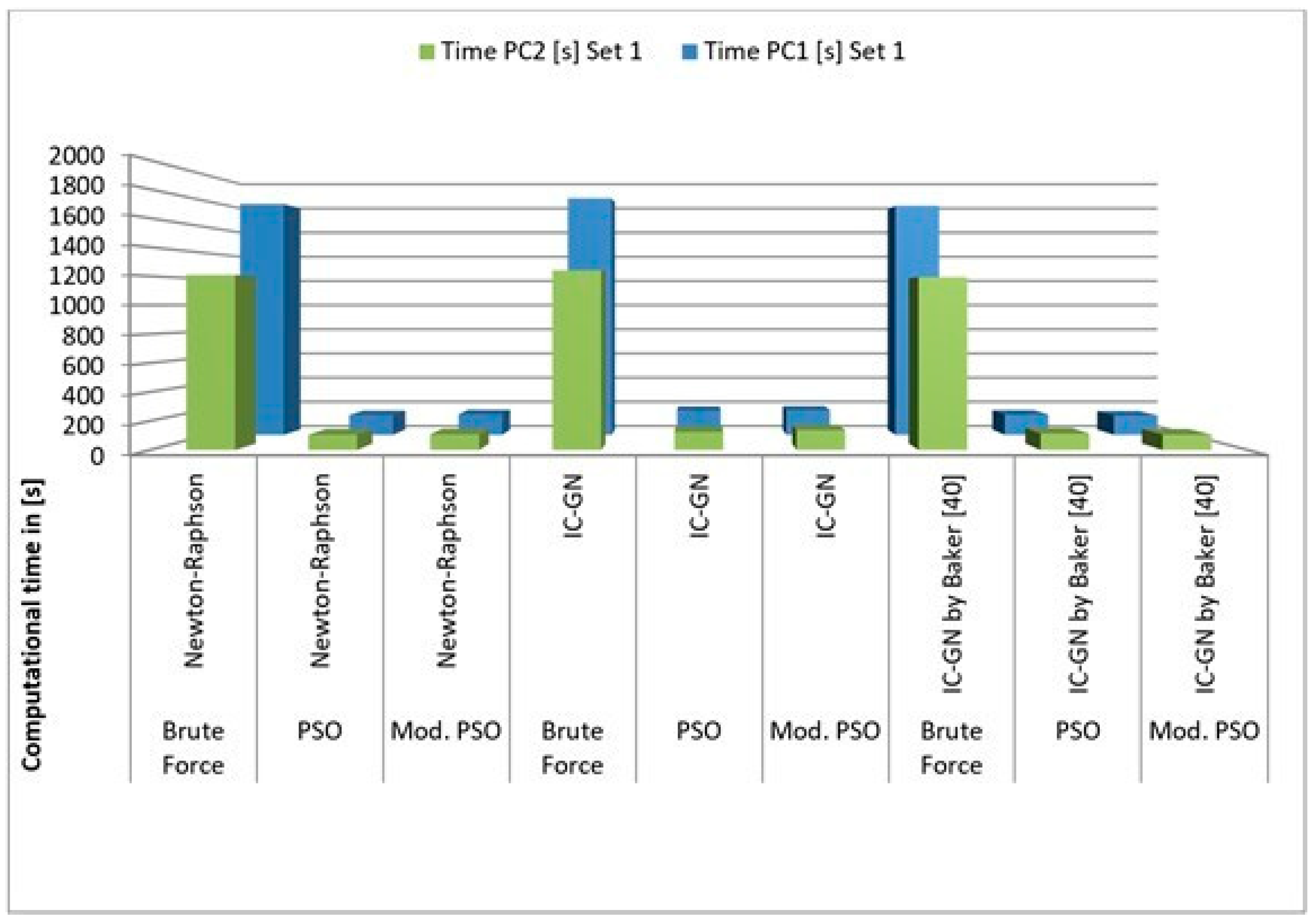
As seen in
Table 3 below, the processing time between the two different datasets is different for the two hardware settings. A representation of
Table 3 in the form of a diagram can be found in
Figure A4 (see
Appendix A). The relative time difference between the two different datasets in serial computation, for analyses conducted on PC 1, is significantly higher if the brute force search algorithm is used. For example, the analysis of dataset 1 is around 30 times longer than the analysis of dataset 2 if the particle swarm optimization and the Newton–Raphson Method are used. If the brute force search algorithm is used, instead of the particle swarm optimization, the ratio of the processing time of dataset 1 to dataset 2 increases to 50. However, the ratio between the time required to analyze dataset 1 to the time required to analyze dataset 2 remains constant on PC 2, regardless of the chosen integer pixel search algorithm. The reason for using two completely different sized datasets is to have data read/overhead time considered for various cases. The time required to load one image is independent of the number of data points [
38]. For example, images of dataset 1 have 5300 data points per image; images of dataset 2 have 1000 data points per image. Bringing this information together shows that t_new for dataset 1 is less than half of t_new of dataset 2 for PC 2, while t_new for dataset one is less than a quarter of data 2 for PC 1.
Typically, all computations processed in serial and conducted on the computer with the better hardware setting (PC 2) were 30%–70% faster than the same analysis conducted on the computer with inferior hardware properties (PC 1). The time difference between PC 1 and PC 2 for the brute force search-based analyses is lower than for the other analyses. For the integer pixel search algorithms in serial computation (
Table 3), all combinations relying on the brute force search algorithm are much slower than the other computations. Moreover, both particle swarm optimization, as well as the modified particle swarm optimization, performed nominally equally on both computers. If the modified particle swarm optimization is used in combination with the Newton–Raphson method, the whole computation is around 5% faster than the standard particle swarm optimization in combination with the Newton–Raphson method. However, a combination of modified particle swarm optimization with the IC-GN algorithm by Baker et al. [
35] is only 2% faster than the standard particle swarm optimization combined with the same IC-GN algorithm. The combination of the IC-GN algorithm implemented by the author and the modified particle swarm optimization algorithm is even slower than a combination with the standard particle swarm optimization.
4.3. Evaluating Sub-Pixel Routines
Comparing the sub-pixel search algorithms in serial computation (see
Table 3), nearly all computations which use the Newton–Raphson method are the fastest if compared to analyses using the same integer-pixel search algorithm. The only exceptions are the combination of the two Particle Swarm Optimizations (PSOs) and IC-GN by Baker et al. [
35] for PC 2 and dataset 2, where both combinations with the IC-GN algorithm by Baker et al. [
35] are slightly faster than the Newton–Raphson algorithm. Furthermore, the IC-GN algorithm published by Baker et al. [
35] is always faster than the IC-GN algorithm implemented by the author. The performance difference for the IC-GN algorithm by Baker et al. [
35] to the algorithm implemented by the authors is small if the brute force search algorithm is used as an integer-pixel search. If the standard particle swarm optimization is used, this difference increases and is maximal if the modified PSO is used. Even though PSO is easy to operate and has a high convergence rate, it does a poor job of balancing exploration and the accuracy of the algorithm is low. To improve the performance of the PSO algorithm, the Particle Swarm Optimization Research Toolbox in MATLAB was used, and several parameters related to various crossover operations, to obtain promising particle guiding patterns and search capabilities, are dynamically adjusted [
39]. This modification was done to obtain better accuracy and faster convergence.
The time required for each image varies significantly depending on methods, hardware settings and even based on image sets. The longest time needed to analyze one pair of images in serial computation was with the brute force search algorithm combined with the IC-GN method by the author, conducted on PC 1 with images of dataset 1, where it took in average of 16.5 s per image pair. This corresponds to a processing frame rate of 0.06 Hz. On the other hand, the shortest time required to analyze one pair of images in serial computation was with the modified particle swarm optimization and the IC-GN by Baker et al. [
35], conducted on PC 2 with dataset 2. In this analysis, 0.71 s were required on average to analyze one image pair which equals a frame rate of 1.4 Hz.
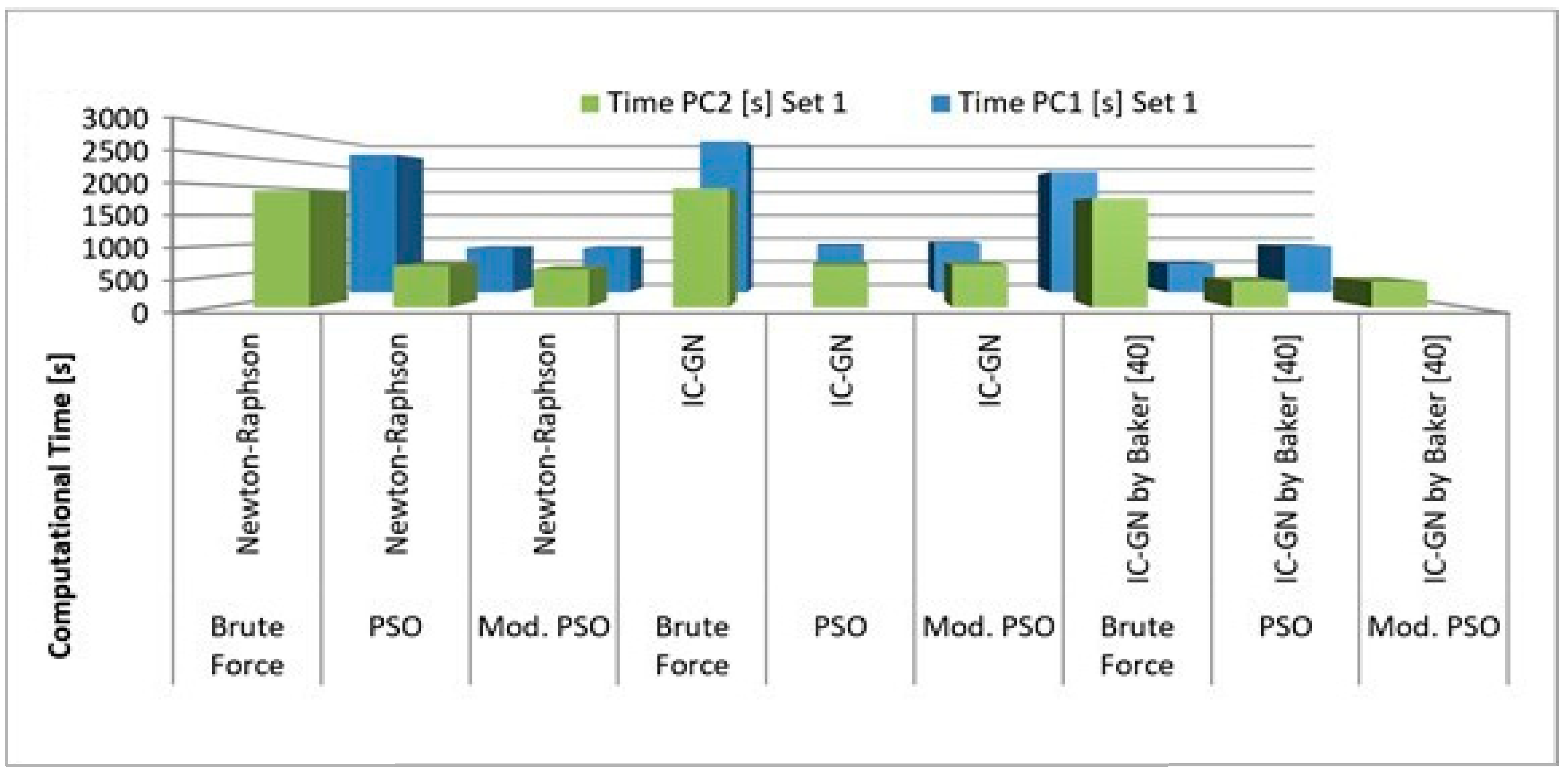
As seen in
Table 4, the time differences between the two different datasets are different for the two hardware settings. A visualization of
Table 4 can be found in
Figure A5 (see
Appendix A). All computations conducted on the computer with the better hardware setting (PC 2) are 30%–200% faster than the same analysis conducted on the computer with inferior hardware setting (PC 1), if processed in sub-image parallel computation. The time difference between PC 1 and PC 2 tends to be smaller for the brute force-based analyses than for the other analyses. Additionally, the influence of hardware settings is stronger for dataset 2 than for dataset 1. Furthermore, the time it takes to analyze two different datasets is more different on PC 2. The difference is small if the brute force search algorithm is used; however, the difference is larger if the particle swarm optimization or the modified particle swarm optimization are used.
4.4. Significance of Parallel Computation
Looking at
Table 4, all the combinations relying on the brute force search algorithm are much slower than the other computations. The brute force search-based computations are between three to five times slower than the other algorithms. Moreover, both the particle swarm optimization as well as the modified particle swarm optimization perform more or less the same. In combination with the Newton–Raphson method, the modification is around 5% faster than the standard particle swarm optimization.
In the case of sub-pixel search algorithms in parallel sub-image computation, in
Table 4, computations using the IC-GN algorithm implemented by the authors are always slower than any of the other two. The time required per image is different between the methods, hardware settings and even image sets. The longest time required to analyze one pair of images in the parallel computation of sub-images was performed using the IC-GN brute force search algorithm performed by the author, on PC 1 with images of dataset 1, where it took an average of 14.47 s per image pair. This equals a frame rate of 0.07 Hz. The least time required to analyze one image pair in parallel sub-image computation was with the Modified particle swarm optimization and the IC-GN by Baker et al. [
35] conducted on PC 2 with dataset 2. In this analysis, 0.66 s were required on average to analyze one image pair which equals a frame rate of 1.5 Hz.
As seen in
Table 5, the time differences between the two different datasets are different for the two hardware settings. A visualization of
Table 5 is shown in
Figure A6 (see
Appendix A). All computations conducted on the computer with the better hardware setting (PC 2) are 40%–100% faster than the same analyses conducted on the computer with inferior hardware setting (PC 1), if they are processed in image parallel computation. The time difference between PC 1 and PC 2 tends to be smaller for brute force search algorithm-based analysis than for other analyses if dataset 2 is analyzed; however, there is not such an influence for dataset 1. Additionally, the influence of the hardware set is stronger for dataset 2 than for dataset 1. In addition, the impact of dataset hardware is stronger for dataset 2 than dataset 1. Additionally, the time it takes to analyze two different datasets is more different on PC 2. The difference is small if the brute force search algorithm is used but big for the other two search algorithms. For example, the analysis of Set 1 took 43 times longer than the analysis of Set 2, with a combination of PSO and NR algorithm on PC 1, while the same analysis took 80 times longer for Set 1 than for Set 2 on PC 2.
Regarding the integer pixel search algorithms in parallel image computation (see
Table 5), all combinations relying on the brute force search algorithm are much slower than the other computations. Computing with the brute force search algorithm is three to four times slower than other algorithms. Moreover, the particle swarm optimization as well as the modified particle swarm optimization performed in the same order of magnitude. A combination of the Newton–Raphson method and modified particle swarm optimization is 5% faster than a combination of the Newton–Raphson method and standard particle swarm optimization. A combination of the modified particle swarm optimization and the IC-GN algorithm by the authors performs equally well with the combination of the standard particle swarm optimization and the same IC-GN algorithm. However, if the IC-GN algorithm published by Baker et al. [
35] is used instead, the variations in performance cannot be generalized, which can be seen in
Table 5.
For the sub-pixel search algorithms in parallel image computation (see
Table 5), it can be seen that computations which use the Newton–Raphson method are faster than computations using the IC-GN algorithm implemented by the author, while computations relying on the IC-GN algorithm published by Baker et al. [
35] are faster. Furthermore, the inverse-compositional Gauss–Newton (IC-GN) algorithm published by Baker et al. [
35] is always faster than the IC-GN algorithm as implemented by the author. The most time required to analyze one image pair in parallel image computation was with the brute force search algorithm combined with IC-GN method by the author, conducted on PC 1 with images of dataset 1, where it took in average of 8.98 s per image pair. On the other hand, the least time required to analyze one image pair in parallel image computation was with the modified particle swarm optimization and the Newton–Raphson method, conducted on PC 2 with dataset 2. In this analysis, 0.29 s were required, on average, to analyze one image pair, which equals a frame rate of 3.5 Hz. The same frame rate could be achieved with a combination of the modified particle swarm optimization and the Newton–Raphson method, as well as with the modified particle swarm optimization and the IC-GN by Baker et al. [
35].
Comparing
Table 3,
Table 4 and
Table 5 shows that the parallel computation of images is more efficient since it is two to three times faster than serial computation. Furthermore, it is remarkable that the time difference is smaller for method combinations relying on the brute force search algorithm. Finally, parallel sub-pixel calculation does not necessarily improve the computational speed of a serial computation. Comparing
Table 3 and
Table 4 shows that parallel sub-image computation is inferior to serial computation in most cases. The parallelization is only beneficial if the brute force search algorithm is used as an integer pixel search algorithm. In general, the larger images of dataset 2 benefits in parallel computation more than the smaller images of dataset 1.
The performance is evaluated for the entire process, not just for the image analysis itself. This includes the program initiation, loading of the images and displaying of results. All computational times presented in
Table 3,
Table 4 and
Table 5 represent the time required from starting the program to presenting the results of the last pairs of images. This is in contradiction with most of the literature, which deal only with image pair analysis and do not address the effects of pre-processing and post-processing at all.
5. Discussion
5.1. Hardware Profile and Influence of Dataset Properties
All analysis executed on PC 2 is faster than the same analyses conducted on PC 1. The reason for this outcome is due to differences in the processor in use between the two computers. PC 1 has a 3.4 GHz Quad-Core CPU, while PC 1 just has a 2.4 GHz Dual Core CPU. Therefore, PC 2 is 1.4 times better in terms of frequency than PC 1. This relationship is also observed in terms of analysis time. However, other factors, such as cache size and data bus speed, also have an impact. The data transfer rate between image storage place and CPU is also a limiting factor. For PC 1 this is most likely the Ethernet connection that connects the system to the central server. This Ethernet connection has a data transfer rate of 1 GBit/s. Additionally, several other data must also be transmitted over this Ethernet connection. Therefore, the whole bandwidth is not available for the program itself. PC 2 has to read the images from its SATA SSD, which has a reading speed of 4.16 GBit/s. It is assumed that no other data transfers are in progress while DIC is running; therefore, the entire band rate is available for the program. These two factors affect the time it takes to read one pair of images and directly result in degraded performance on PC 1. Techniques such as double buffering are not considered. It is assumed that the program always uses the most current image of a live video stream as a target image, with the previously used target image as a new reference image. This is to avoid queuing raw images if the camera is receiving images faster than the software is processing them.
The improvements between the two different computer settings decrease with increasing data traffic. This is explained by the rising portion of data handling time in the total computation time with increasing data traffic. It can be assumed that the data transfer rate between different worker processes is approximately the same for different computers and; therefore, the time required to transfer a certain amount of data is the same for the higher-level hardware settings and for the inferior one. The processing times also differ between the two different datasets. The influence of the brute force search algorithm is stronger for dataset 1 than for dataset 2 when comparing this integer pixel search algorithm with others. The brute force search algorithm determines the correlation coefficient distribution for the whole image. Therefore, the computational time of one sub-image is directly related to the image size. Both particle swarm optimizations work always with a fixed number of particles and generations. Therefore, the computational time of those two algorithms is not directly related to the image size itself. In conclusion, the computation time increases with increasing image size for brute force search, while it remains constant for the two variations of the particle swarm optimization. Of course, this is only true if you choose a constant number of sub-images is chosen.
5.2. Integer Pixel Search
For the integer-pixel search algorithms, the brute force search algorithm is generally the most inefficient algorithm. This was ruled out because this very simple algorithm determines the correlation coefficient for each possible sub-pixel position, which is much more computationally expensive than the two particle swarm optimizations. This is explained by the following calculation. Assuming images have a size of 500 × 1000 pixels and the sub-sets have a size of 31 × 31 pixels, this gives a total of 970 × 470 = 455,900 possible sub-set positions within one image. Consequently, for the brute force search algorithm, 455,900 correlation coefficients must be determined per reference sub-image. Contrary, both particle swarm optimizations use a total number of 50 particles over a maximum of five iterations. In the standard particle swarm optimization, the correlation coefficient of each particle for each iteration step is determined, resulting in a maximal 250 evaluations of the correlation coefficient. For the modified particle swarm optimization, the correlation coefficient of the particle, as well as the four surrounding pixels, is determined, which results in a theoretical total of a maximal 1250 evaluations of the correlation coefficient. Both algorithms use look-up tables to reduce the computational burden if different particles move to the same position. Additionally, the modified particle swarm optimization converges faster which, on average, results in fewer iteration steps. Besides the determination of the correlation coefficients for the different positions, all three methods determine the maximal found correlation coefficients. However, this can be considered less computationally intense compared to the determination of the correlation coefficient itself. By simply comparing the number of calculated correlation coefficients of different methods, it becomes apparent that the brute force search algorithm requires much more computational power than the two particle swarm optimizations [
40].
Unfortunately, the case is not that clear for the standard Particle Swarm Optimization (PSO) and the modified version. The significant difference between those two methods is that the standard version only takes the correlation coefficient at the particles own position into account while the modified version additionally takes also the correlation coefficients at the surrounding pixels into account. This leads to a faster convergence, because more information is considered while updating the particle positions. This also increases the total computational effort per iteration step. Because the particle swarm optimization stops if a sufficiently high correlation coefficient of 0.995 is found, the number of used generations is lower for the modified particle swarm optimization than for the standard version. With regards to the results obtained during the tests carried out and presented in
Table 3,
Table 4 and
Table 5, it can be stated that the modified PSO version performs, in general, at least equally as well as the standard version. Therefore, using a modified version of PSO instead of the standard version may be beneficial as it converges faster [
41]. Shi and Eberhart [
42] modified the standard PSO algorithm by introducing inertial weights
ω, and achieved a balance between global and local search. The reported results show a linear decrease in the
ω while solving the algorithm, which ultimately increased the convergence rate.
5.3. Sub-Pixel Search
A version of the inverse-compositional Gauss–Newton algorithm as published by Baker et al. [
35] is around 2%–3% more efficient than the version implemented by the authors. There can be many reasons for such a discrepancy, and they are described in detail in the specific implemented code. One major difference between the two versions is the data flow to sub-functions. The version published by Baker et al. [
35] uses fewer sub-functions than the version implemented by the author. Otherwise, the amount of data passed by the author’s implementation is lower per sub-function call than the amount of data passed in the version proposed by Baker et al. [
35].
The performance comparison between the Newton–Raphson method and the inverse-compositional Gauss–Newton algorithm by Baker et al. [
35] cannot be generalized and, apparently, both algorithms perform similarly, as can be seen in
Table 3,
Table 4 and
Table 5.
Among all the tests carried out within the framework of this study, sometimes, the IC-GN algorithm by Baker et al. [
35] is faster and sometimes there is no difference. This is somewhat in conflict with theoretical predictions and most of the modern literature, which indicates that the IC-GN algorithm is superior to the Newton–Raphson algorithm [
28]. The implementation of the IC-GN algorithm into the program was more complex compared to the NR algorithm. The fact that MATLAB generally uses call by value functionality strongly increases the time required to shift data from different sub-functions. Every time a sub-function is called, a copy of the data, which has to be transferred between caller function and called function, is created. This drastically increases the computation time. Because the data flow is more complex for both IC-GN versions, than for the NR algorithm, MATLAB requires more time to copy values and allocate memory. This reduces the advantages of IC-GN over the NR algorithm. However, the IC-GN algorithm has the advantage of reducing the computation time by an iteration step. If the number of iterations is small, this advantage is negligible. The overall impact of this is difficult to measure theoretically. Though there is no real evidence that one algorithm is more efficient than the other (except for the IC-GN by the author), a slight connection to the datasets supports the premise that the reason for the worse performance, than theoretically expected, is mainly connected to the data flow and the small number of iterations.
5.4. Parallel Computation
Concerning the different types of computing, the tests performed show that the parallel computation of images is much more efficient than the sequential and parallel computation of sub-images; compare
Table 3,
Table 4 and
Table 5. Parallel image computation solves the same task as in serial computation. In both cases, the worker solves one image completely on its own. In serial computation, a single worker analyses all image pairs, while in parallel image computation, several workers are working on different image pairs at the same time. Nonetheless, the data must be organized and distributed to the workers, which is more complex in the case of parallel image computation, creating an additional workload for this computational type. However, this load is small compared to the analysis itself. Otherwise, parallel sub-image computation differs more from the serial computation. In parallel sub-image computation, the different workers have to solve different sub-sets of the same image pair. To do so, all workers need both the target as well as the reference image. Consequently, this increases the data flow, because every worker needs every image pair and slows down the computation. Assuming four number of workers, which is the case for both hardware settings used in this study, this results in a four times larger amount of data for sub-image parallel computation than for image parallel computation. Therefore, the overall efficiency of sub-image parallel computation is lower than parallel image computation. Nonetheless, all workers are working on the same image pair in sub-image parallel computation. This means that the time between starting the analysis of a particular pair of images and determining the final displacement result is shorter than with image parallel computation.
5.5. GPU Accelerated Technique
Recent developments utilize Graphics Processing Units (GPUs)-based image correlation implementations [
43]. By running computing DIC at different points of interest simultaneously, processing can be significantly accelerated by orders of magnitude [
31]. For parallel processing using the GPU in MATLAB, NVIDIA’s CUDA (Compute Unified Device Architecture) GPU computing technology is utilized [
33]. CUDA is a programming technique developed by NVIDIA which shifts program parts to the GPU [
44]. The CUDA technology is included in MATLAB as simple to use as a toolkit. MATLAB introduced a new data type called “gpuArray”. This data type is similar to a regular array, but additionally includes information that all tasks associated with this array must be performed on the GPU. More than 100 MATLAB functions support this data type and, using CUDA technology, transfer the computational task to the GPU if they are executed with a gpuArray [
32]. The bottleneck of this technology lies within the data transfer. For each computational task, all the necessary data must be transferred from the CPU to the GPU before it can be processed [
45]. Afterwards, any results must be transferred back from the GPU to the CPU. In GPU-based image processing systems, it is also possible to get user-specified feedback from the applications on a real-time basis.
According to Conrad et al. [
37], the GPU-based DIC system is capable of measuring total strain at the speed up to 850 Hz and the strain fields overcome parallel computing limitations. This is enabled by combining a fast camera with path-independent and marker-free image correlation on the GPU, and it is highly limited with the capability of GPU used and dependent on the size of the image. By implementing a DIC algorithm that is capable of running in parallel computing methods, multi-core CPU and GPU allow threads to run concurrently, resulting in the increase of computing speed depending on the simultaneous cores supported by the device [
40]. In the case of both CPU and GPU resources being available, it is wise to use both. The heterogeneous parallel computing on the CPU and GPU can result in further speed improvements over GPU alone. This advantage in acceleration can be achieved by highlighting points of interest (POIs) on both the CPU and GPU and processing them on these two platforms simultaneously [
46]. However, this article focuses only on executing DIC algorithms using two different types of CPU hardware. For further research, comparison between the parallel computing using CPU with and without GPU acceleration can be considered.
6. Conclusions
The analysis of the different mathematical search algorithms shows that there are significant differences in computation times between the tested methods and combinations, despite similar accuracy. It is clear that the combination of implemented methods can reduce the computational time of standard digital image correlation without compromising accuracy. Additionally, the tests performed show that real-time analysis with high frame rates, implemented using CPU processing, requires computational resources that are available only in high-performance computing systems; or are possible only at the expense of a significant reduction in accuracy. However, real-time analysis with a slow frame rate, lower accuracy or a reduced number of evaluated data points is possible in MATLAB with nominally average computing systems—analysis frequencies up to 3.5 Hz are possible with a standard Intel i7 Quad-Core CPU.
The fastest computation can be achieved by a combination of a modified particle swarm optimization, in which a downhill star search algorithm is integrated into the particle swarm optimization search algorithm, as an integer pixel search algorithm. To increase the accuracy to sub-pixel level, Newton–Raphson Search algorithm is best suited when a relatively low accuracy of 0.1 pixels is required.
The computational time is least if image pairs are processed in parallel. Parallelization of smaller tasks, as in sub-image parallel computation, leads to an increase in computation time than in serial processing. The time it takes to process the additional data traffic is longer than the reduction in time by parallelizing the tasks. However, the conducted tests show that the type of parallelization has a direct relation with the computation time, as far as this study is concerned computation time is reduced to up to 55%, even on a computer with a standard quad-core processor. Finally, the tests show that theoretically superior methods can perform worse than other methods due to some practical implementation disadvantages of these methods. Our results also highlight the necessity to explore alternative computing approaches such as GPU-based parallel computing to reduce the evaluation time further.
Author Contributions
Conceptualization, A.T., A.M. and S.R.; Data curation, A.T. and A.M.; Formal analysis, A.T. and A.M.; Investigation, A.T. and A.M.; Methodology, A.T. and A.M.; Project administration, S.R.; Software, A.T. and A.M.; Supervision, S.R.; Validation, A.M. and S.R.; Writing—original draft, A.T., A.M.; Writing—review & editing, A.T., A.M. and S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by AOARD Grant: FA23861914066.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Symbol and Abbreviation | Description |
| MATLAB | Matrix Laboratory |
| f | Grey level in the reference image |
| g | Grey level in the deformed image |
| (x, y) | Denotes the position in the reference image |
| (x*, y*) | Denotes the position in the deformed image |
| Hz | Hertz |
| C | Correlation coefficient |
| v | Velocity |
| d | Direction of the search |
| r | Independent random values |
| ω | inertial weights |
| M | Number of rows in an image |
| N | Number of columns in an image |
| w | Weight factor |
| G | Grey level distribution at an arbitrary sub-pixel |
| a | Coefficients of the bilinear interpolation function |
| t | Time |
| i | Iterations |
| GBit/s | GigaBits per second |
| CPU | Central processing unit |
| GPU | Graphics processing unit |
| CUDA | Compute unified device architecture |
Appendix A
Figure A1.
Histogram of dataset.
Figure A1.
Histogram of dataset.
Figure A2.
Histogram of dataset.
Figure A2.
Histogram of dataset.
Figure A3.
Histogram of dataset.
Figure A3.
Histogram of dataset.
Figure A4.
Overview of the Total Computational Time of dataset 1 in serial computation.
Figure A4.
Overview of the Total Computational Time of dataset 1 in serial computation.
Figure A5.
Overview of the total computational time of dataset 1 in parallel sub-image computation.
Figure A5.
Overview of the total computational time of dataset 1 in parallel sub-image computation.
Figure A6.
Overview of the total computational time of dataset 1 in image parallel computation.
Figure A6.
Overview of the total computational time of dataset 1 in image parallel computation.
References
- Hild, F.; Roux, S. Digital Image Correlation: From Displacement Measurement to Identification of Elastic Properties—A Review. Strain 2006, 42, 69–80. [Google Scholar] [CrossRef]
- Yoneyama, S. Basic principle of digital image correlation for in-plane displacement and strain measurement. Adv. Compos. Mater. 2016, 25, 105–123. [Google Scholar] [CrossRef]
- Wu, R.; Kong, C.; Li, K.; Zhang, D. Real-Time Digital Image Correlation for Dynamic Strain Measurement. Exp. Mech. 2016, 56, 833–843. [Google Scholar] [CrossRef]
- Zhong, F.Q.; Indurkar, P.P.; Quan, C.G. Three-dimensional digital image correlation with improved efficiency and accuracy. Measurement 2018, 128, 23–33. [Google Scholar] [CrossRef]
- Brown, G.M.; Chen, F.; Song, M. Overview of three-dimensional shape measurement using optical methods. Opt. Eng. 2000, 39, 10–22. [Google Scholar] [CrossRef]
- Vendroux, G.; Knauss, W.G. Submicron deformation field measurements: Part 2. Improved digital image correlation. Exp. Mech. 1998, 38, 86–92. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20. [Google Scholar] [CrossRef]
- Peters, W.H.; Ranson, W.F. Digital Imaging Techniques in Experimental Stress Analysis. Opt. Eng. 1982, 21, 213427. [Google Scholar] [CrossRef]
- Mudassar, A.A.; Butt, S. Improved Digital Image Correlation method. Opt. Lasers Eng. 2016, 87, 156–167. [Google Scholar] [CrossRef]
- Simončič, S.; Podržaj, P. An Improved Digital Image Correlation Calculation in the Case of Substantial Lighting Variation. Exp. Mech. 2017, 57, 743–753. [Google Scholar] [CrossRef]
- Pan, B. Digital image correlation for surface deformation measurement: Historical developments, recent advances and future goals. Meas. Sci. Technol. 2018, 29, 082001. [Google Scholar] [CrossRef]
- Yoneyama, S.; Murasawa, G. Digital image correlation. In Experimental Mechanics; Freire, J.F., Ed.; Encyclopedia of Life Support System (EOLSS) Publishers: Oxford, UK, 2009. [Google Scholar]
- Beyerer, J.; Leon, F.P.; Frese, C. Machine Vision: Automated Visual Inspection: Theory, Practice and Applications; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Jiang, Z.; Gao, Y.; Liu, J. A lid approach for predicting wave induced motions of trimaran in regular waves. Brodogradnja 2019, 70, 171–185. [Google Scholar] [CrossRef]
- Gil, P. Short Project-Based Learning with MATLAB Applications to Support the Learning of Video-Image Processing. J. Sci. Educ. Technol. 2017, 26, 508–518. [Google Scholar] [CrossRef]
- Jaton, F. We get the algorithms of our ground truths: Designing referential databases in digital image processing. Soc. Stud. Sci. 2017, 47, 811–840. [Google Scholar] [CrossRef] [PubMed]
- Solav, D.; Moerman, K.M.; Jaeger, A.M.; Genovese, K.; Herr, H.M. MultiDIC: An Open-Source Toolbox for Multi-View 3D Digital Image Correlation. IEEE Access 2018, 6, 30520–30535. [Google Scholar] [CrossRef]
- Cheng, J.A.; Grossman, M.; Mckercher, T. Professional CUDA C Programming; John Wiley & Sons, Inc.: Indianapolis, IN, USA, 2014; ISBN 978-1-118-73927-3. [Google Scholar]
- Kim, P. Convolutional neural network. In MATLAB Deep Learning; Springer, Apress: Berkeley, CA, USA, 2017. [Google Scholar] [CrossRef]
- Pan, B.; Xie, H.M.; Xu, B.Q.; Dai, F.L. Performance of sub-pixel registration algorithms in digital image correlation. Meas. Sci. Technol. 2006, 17, 1615–1621. [Google Scholar] [CrossRef]
- Lin, Y.; Lan, Z. Sub-Pixel Displacement Measurement in Digital Image Correlation Using Particle Swarm Optimization. In Proceedings of the ICINA-International Conference on Information, Networking and Automation, Kunming, China, 18–19 October 2010. [Google Scholar] [CrossRef]
- Rafael, C.G.; Richard, E.W.; Steven, L.E. Digital Image Processing Using MATLAB, 2nd ed.; Gatesmark: Knoxville, TN, USA, 2008; ISBN 978-09-8208-540-0. [Google Scholar]
- Chu, T.C.; Ranson, W.F.; Sutton, M.A. Applications of digital-image-correlation techniques to experimental mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Bruck, H.A.; McNeill, S.R.; Sutton, M.A.; Peters, W.H. Digital image correlation using Newton-Raphson method of partial differential correction. Exp. Mech. 1989, 29, 261–267. [Google Scholar] [CrossRef]
- Pan, B.; Wu, D.; Wang, Z. Internal displacement and strain measurement using digital volume correlation: A least-squares framework. Meas. Sci. Technol. 2012, 23. [Google Scholar] [CrossRef]
- Bornert, M.; Doumalin, P.; Dupré, J.-C.; Poilâne, C.; Robert, L.; Toussaint, E.; Wattrisse, B. Assessment of Digital Image Correlation Measurement Accuracy in the Ultimate Error Regime: Improved Models of Systematic and Random Errors. Exp. Mech. 2017, 58, 33–48. [Google Scholar] [CrossRef]
- Shao, X.; Dai, X.; He, X. Noise robustness and parallel computation of the inverse compositional Gauss–Newton algorithm in digital image correlation. Opt. Lasers Eng. 2015, 71, 9–19. [Google Scholar] [CrossRef]
- Pan, B.; Li, K.; Tong, W. Fast, Robust and Accurate Digital Image Correlation Calculation without Redundant Computations. Exp. Mech. 2013, 53, 1277–1289. [Google Scholar] [CrossRef]
- Asanovic, K.; Bodik, R.; Demmel, J.; Keaveny, T.; Keutzer, K.; Kubiatowicz, J.; Morgan, N.; Patterson, D.; Sen, K.; Wawrzynek, J.; et al. A view of the parallel computing landscape. Commun. ACM 2009, 52, 56–67. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, T.; Jiang, Z.; Kemao, Q.; Liu, Y.; Liu, Z.; Tang, L.; Dong, S. High accuracy digital image correlation powered by GPU-based parallel computing. Opt. Lasers Eng. 2015, 69, 7–12. [Google Scholar] [CrossRef]
- Gates, M.; Heath, M.T.; Lambros, J. High-performance hybrid CPU and GPU parallel algorithm for digital volume correlation. Int. J. High Perform. Comput. Appl. 2014, 29, 92–106. [Google Scholar] [CrossRef]
- NVIDIA. CUDA Developer Zone. 2017. Available online: https://developer.nvidia.com/cuda-zone (accessed on 19 March 2019).
- NVIDIA. CUDA C Best Practices Guide. Available online: http://docs.nvidia.com/cuda/cuda-c-best-practices-guide/index.html (accessed on 19 March 2019).
- Blaber, J.; Adair, B.S.; Antoniou, A. Ncorr: Open-Source 2D Digital Image Correlation Matlab Software. Exp. Mech. 2015, 55, 1105–1122. [Google Scholar] [CrossRef]
- Baker, S.; Matthews, I. Lucas-Kanade 20 Years On: A Unifying Framework. Int. J. Comput. Vis. 2004, 56, 221–255. [Google Scholar] [CrossRef]
- Bigger, R.; Blaysat, B.; Boo, C.; Grewer, M.; Hu, J.; Jones, A.; Klein, M.; Raghavan, K.; Reu, P.; Schmidt, T.; et al. A Good Practices Guide for Digital Image Correlation; International Digital Image Correlation Society: Hangzhou, China, 2018. [Google Scholar] [CrossRef]
- Conrad, F.; Blug, A.; Kerl, J.; Fehrenbach, J.; Regina, D.; Bertz, A.; Kontermann, C.; Carl, D.; Oechsner, M. GPU-based digital image correlation system for uniaxial and biaxial crack growth investigations. Procedia Struct. Integr. 2020, 28, 2195–2205. [Google Scholar] [CrossRef]
- Sutton, M.A.; Matta, F.; Rizos, D.; Ghorbani, R.; Rajan, S.; Mollenhauer, D.H.; Schreier, H.W.; Lasprilla, A.O. Recent Progress in Digital Image Correlation: Background and Developments since the 2013 W M Murray Lecture. Exp. Mech. 2016, 57, 1–30. [Google Scholar] [CrossRef]
- Wang, T.; Kemao, Q.; Seah, H.S.; Lin, F. A flexible heterogeneous real-time digital image correlation system. Opt. Lasers Eng. 2018, 110, 7–17. [Google Scholar] [CrossRef]
- Wang, C.; Song, W. A modified particle swarm optimization algorithm based on velocity updating mechanism. Ain Shams Eng. J. 2019, 10, 847–866. [Google Scholar] [CrossRef]
- Yao, J.; Han, D. Improved Barebones Particle Swarm Optimization with Neighborhood Search and Its Application on Ship Design. Math. Probl. Eng. 2013, 2013, 175848. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. Modified Particle Swarm Optimizer. In Proceedings of the IEEE Conference on Evolutionary Computation, ICEC, Anchorage, AK, USA, 4–9 May 1998. [Google Scholar] [CrossRef]
- Balit, Y.; Charkaluk, E.; Constantinescu, A. Digital image correlation for microstructural analysis of deformation pattern in additively manufactured 316L thin walls. Addit. Manuf. 2020, 31, 100862. [Google Scholar] [CrossRef]
- Shao, X.; Zhong, F.; Huang, W.; Dai, X.; Chen, Z.; He, X. Digital image correlation with improved efficiency by pixel selection. Appl. Opt. 2020, 59, 3389–3398. [Google Scholar] [CrossRef]
- Blug, A.; Regina, D.J.; Eckmann, S.; Senn, M.; Bertz, A.; Carl, D.; Eberl, C. Real-Time GPU-Based Digital Image Correlation Sensor for Marker-Free Strain-Controlled Fatigue Testing. Appl. Sci. 2019, 9, 2025. [Google Scholar] [CrossRef]
- Yang, J.; Huang, J.; Jiang, Z.; Dong, S.; Tang, L.; Liu, Y.; Liu, Z.; Zhou, L. 3D SIFT aided path independent digital volume correlation and its GPU acceleration. Opt. Lasers Eng. 2021, 136, 106323. [Google Scholar] [CrossRef]
- Tyagi, V. Understanding Digital Image Processing; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).