Probability Study on the Thermal Stress Distribution in Thick HK40 Stainless Steel Pipe Using Finite Element Method
Abstract
:1. Introduction
2. Analytical Solution
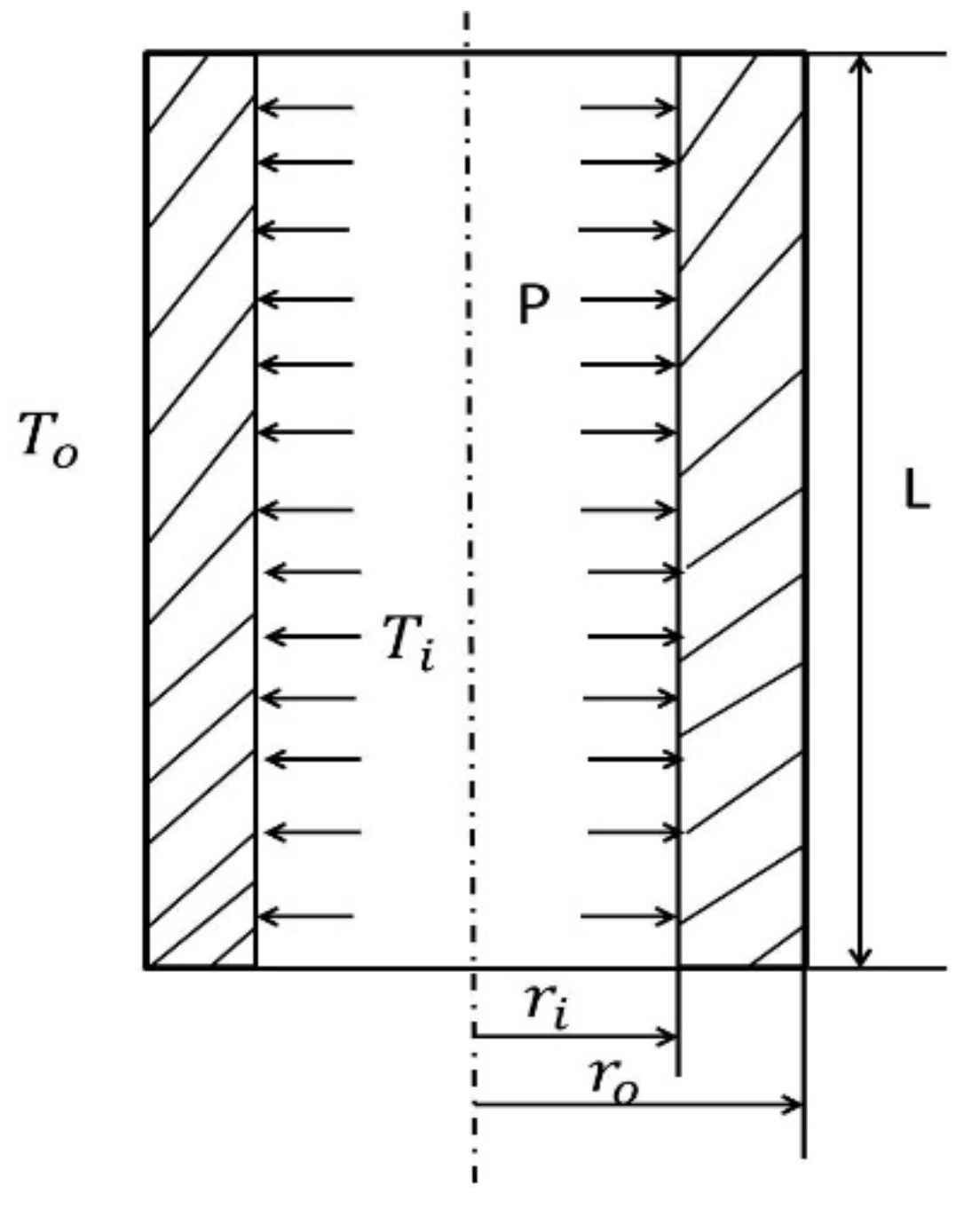
The Stresses for Thick-Walled Cylinder Pipe under Internal Pressure (P) and Thermal Gradient ()
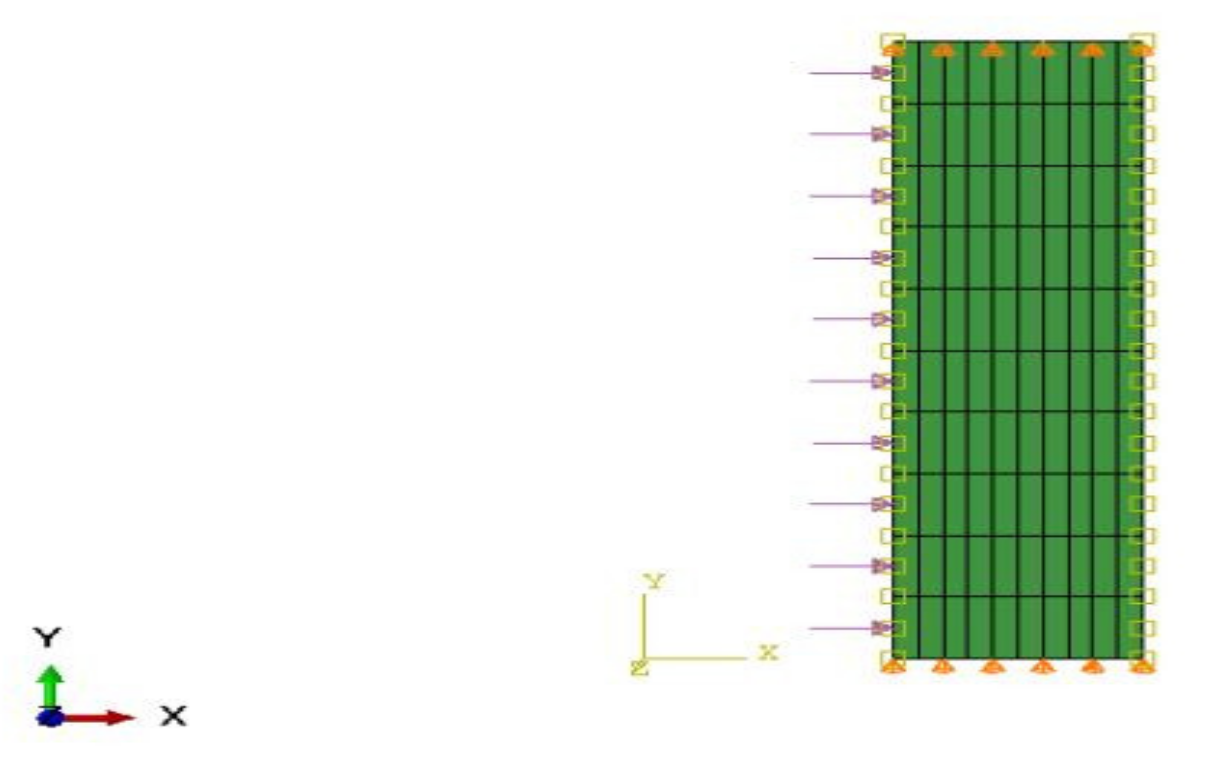
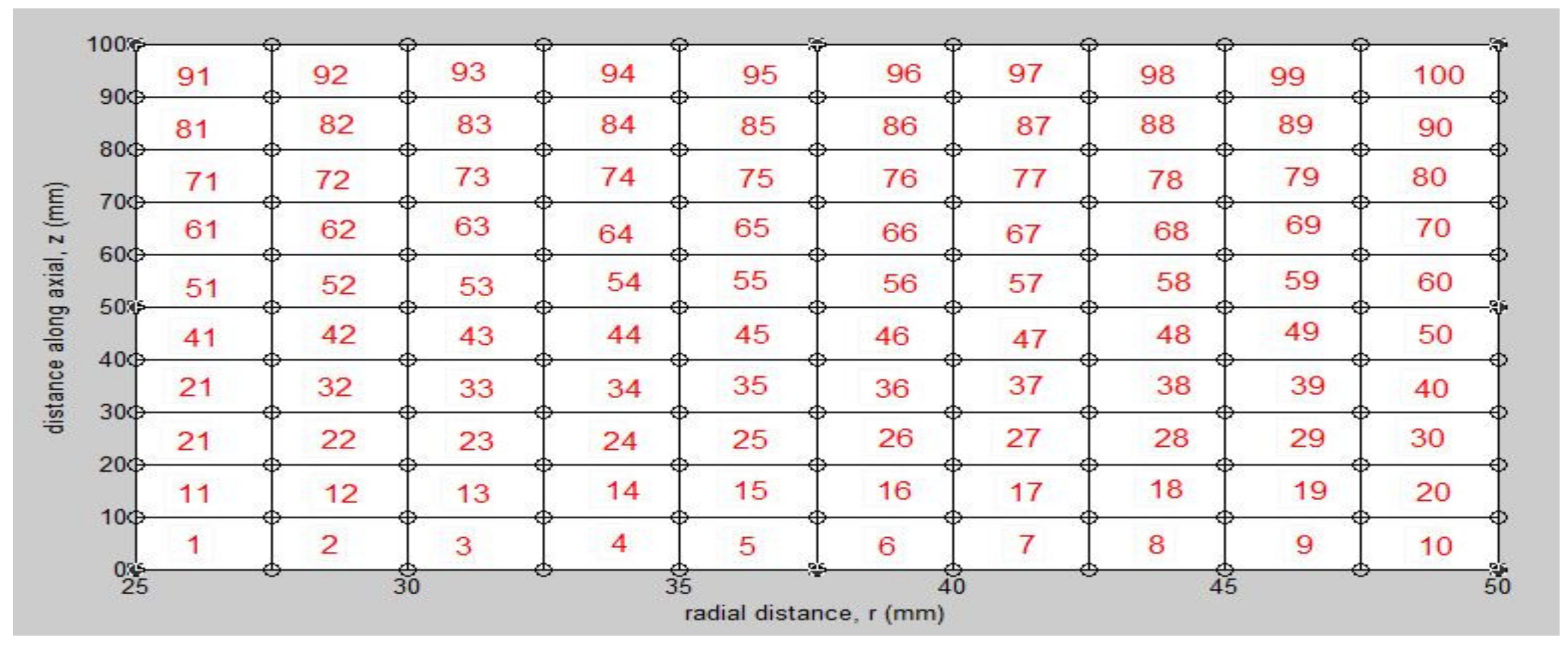
3. Axisymmetric Finite Element Analysis Using ABAQUS Software
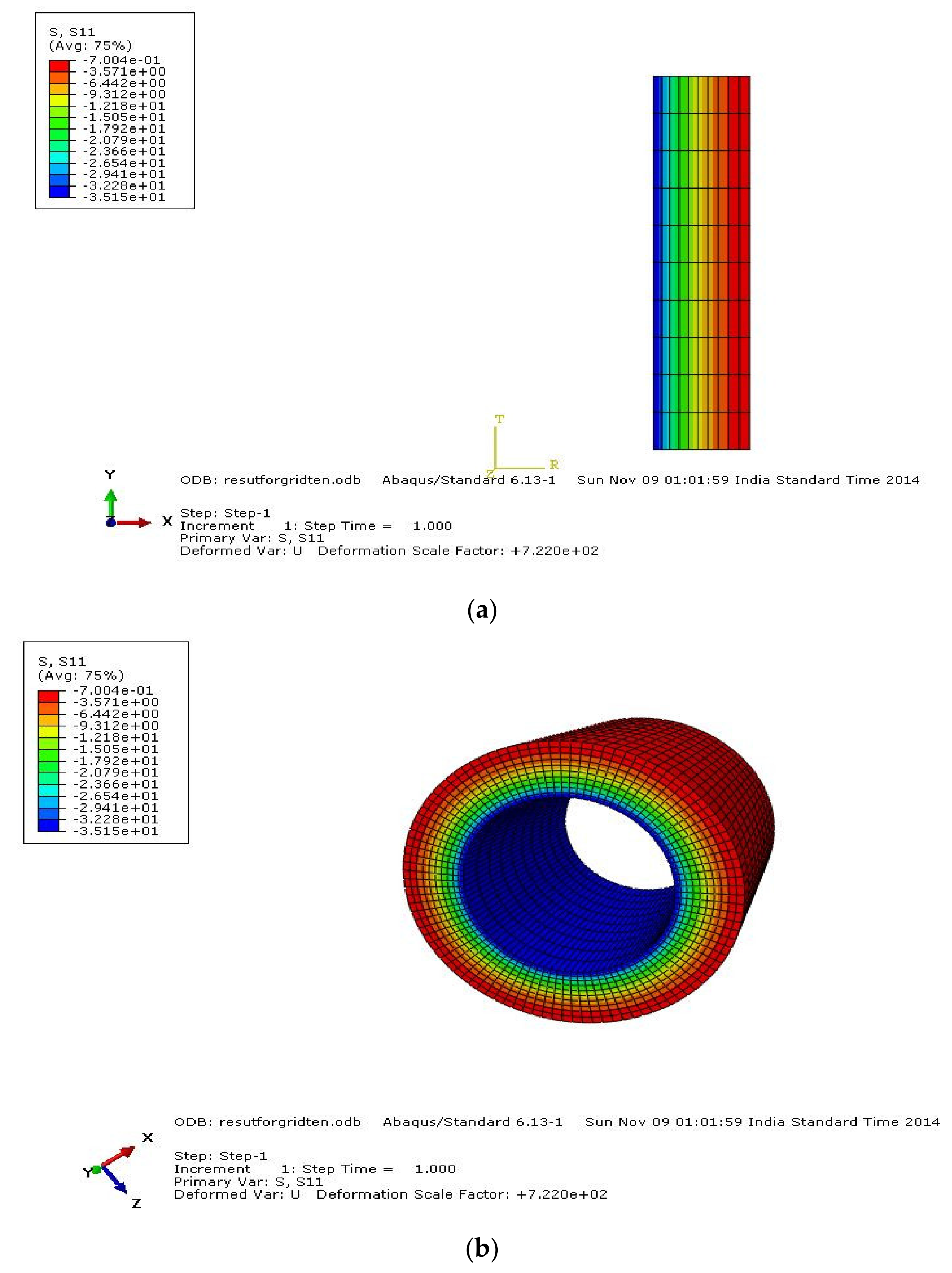
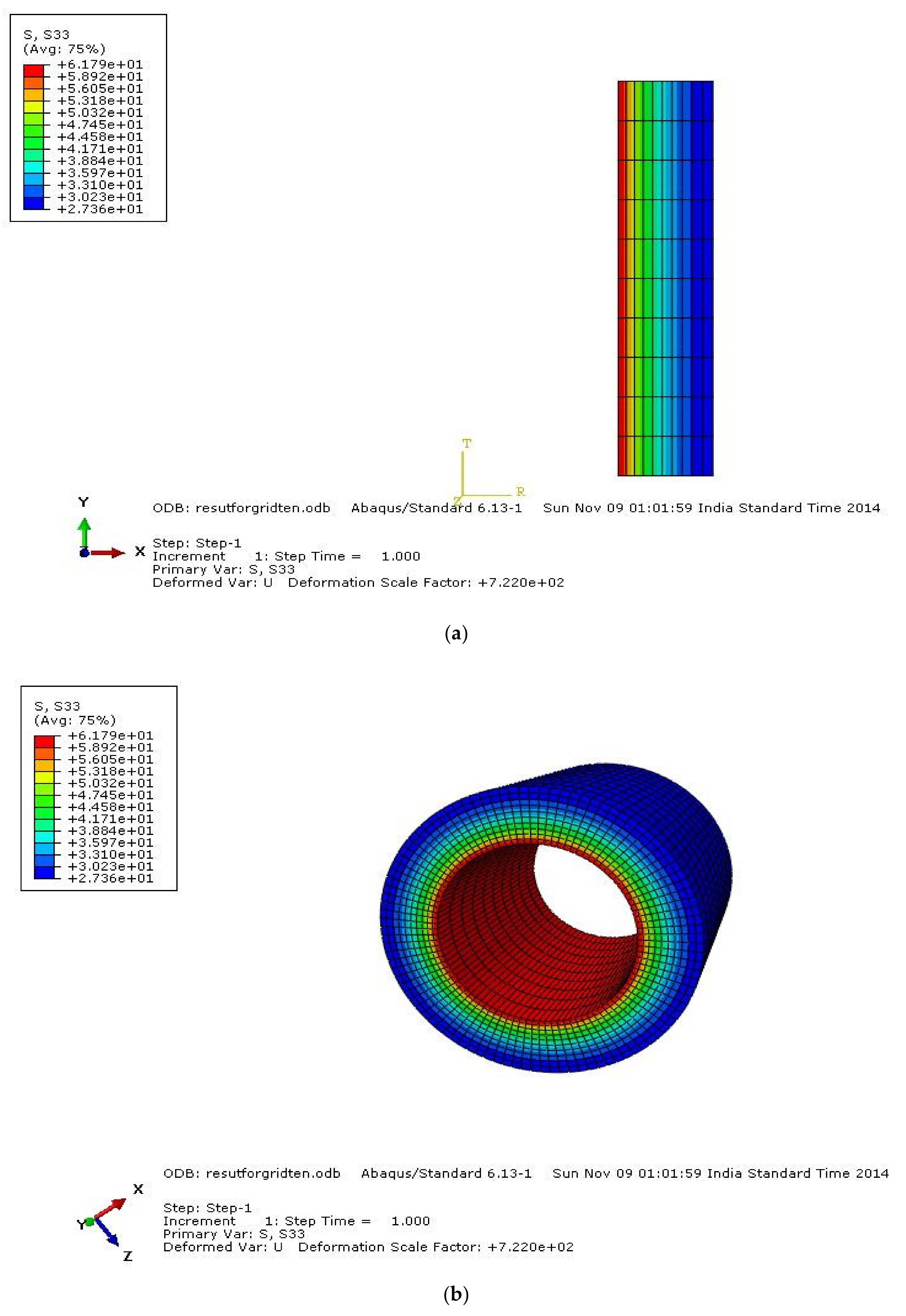
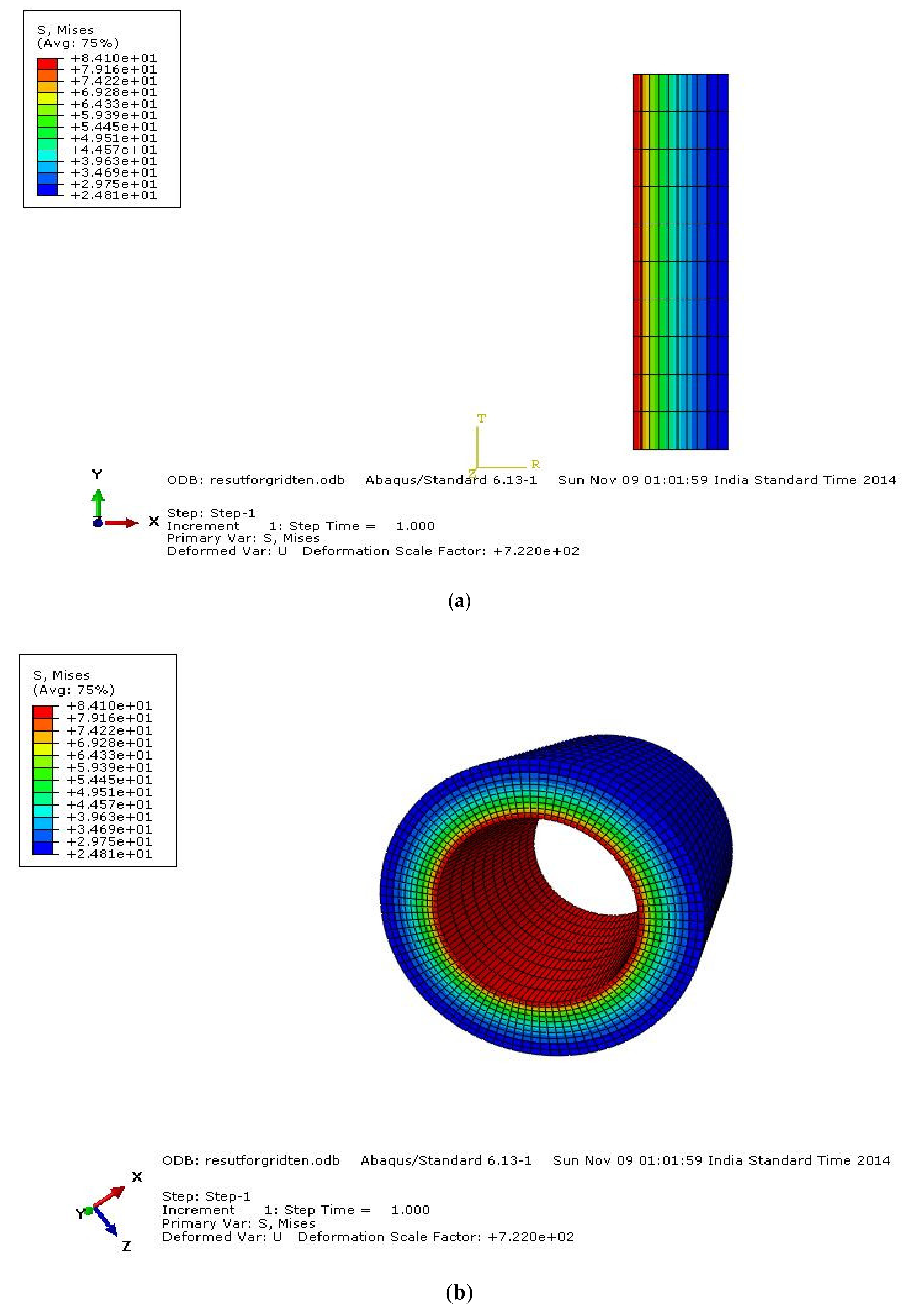
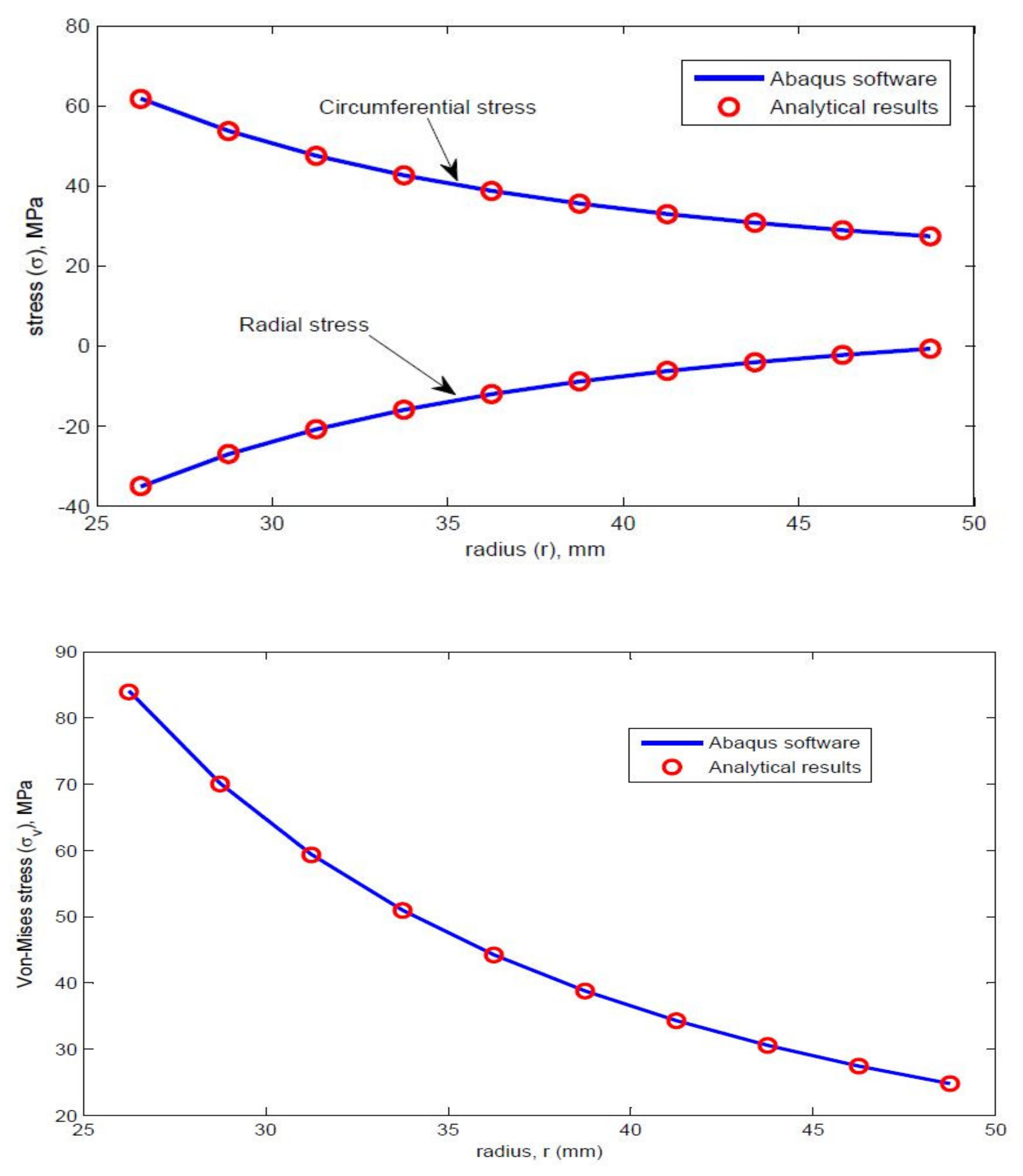
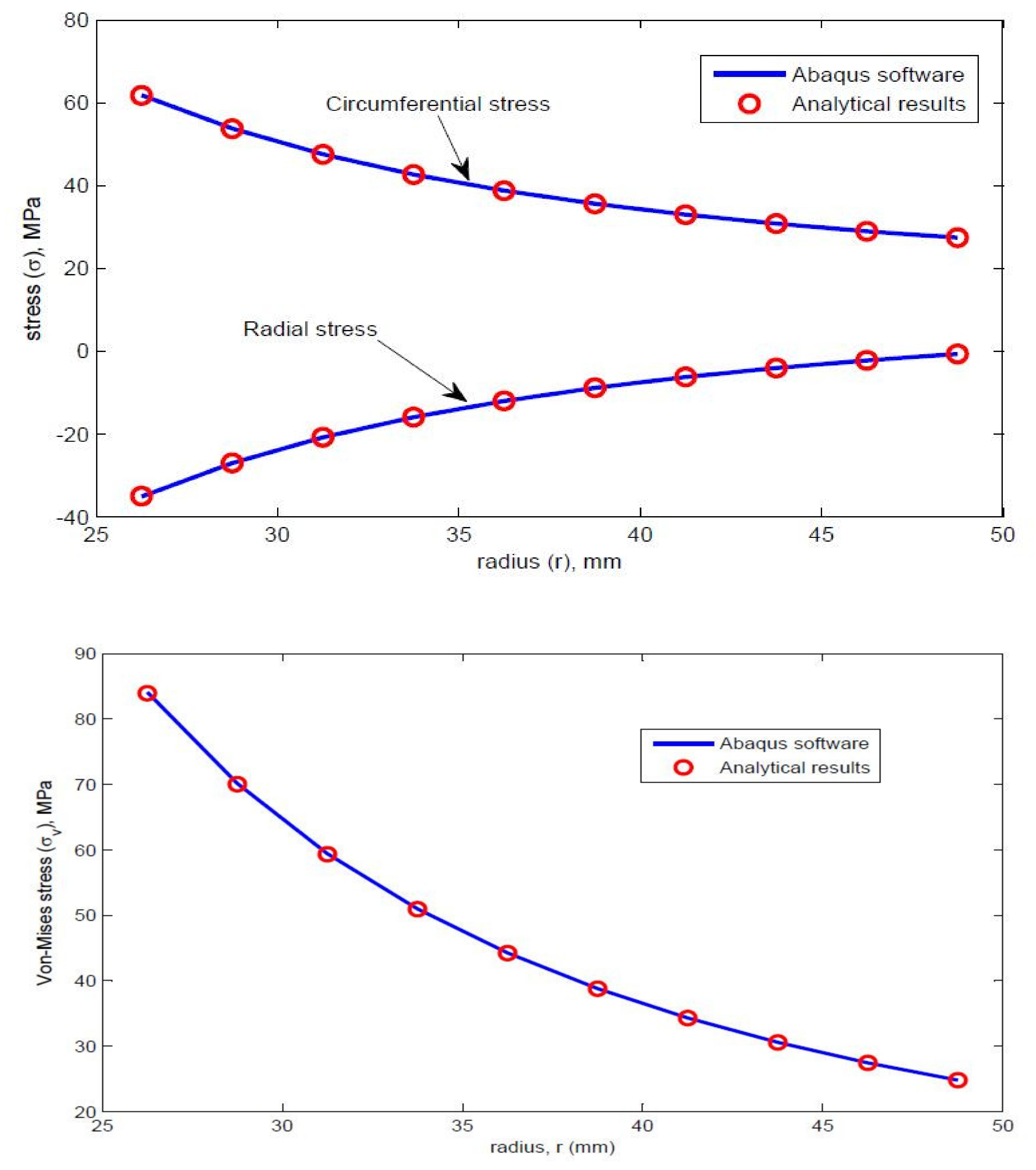
3.1. Comparison of Analytical and FEA using ABAQUS
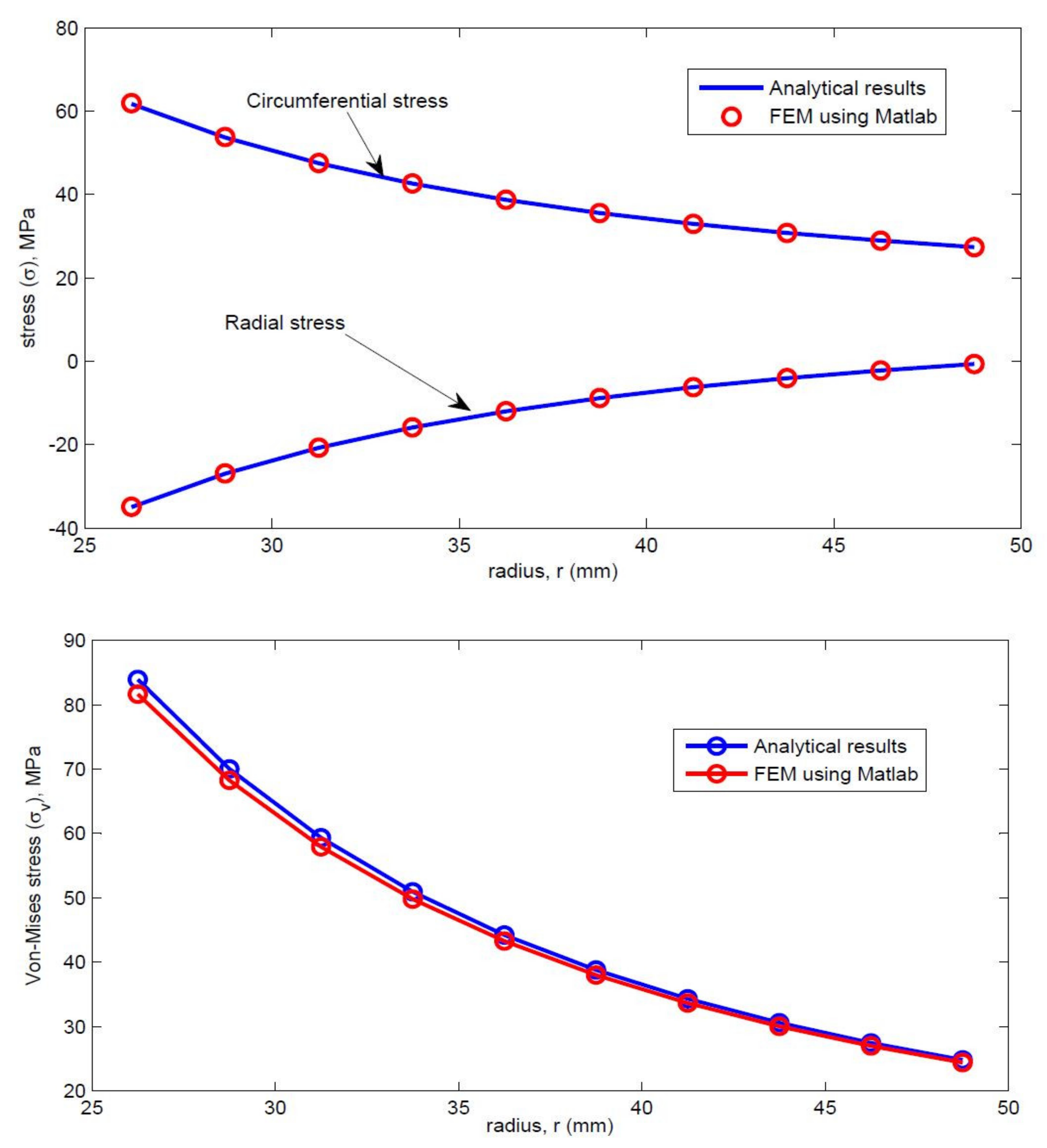
3.2. Comparison of Analytical Results and FEA Results Using Abaqus and FEM Using MATLAB
4. Probabilistic Study
4.1. Monte Carlo Simulation
4.2. Distributed Structural Parameters
4.3. Lognormal Distribution
4.4. Input Distribution
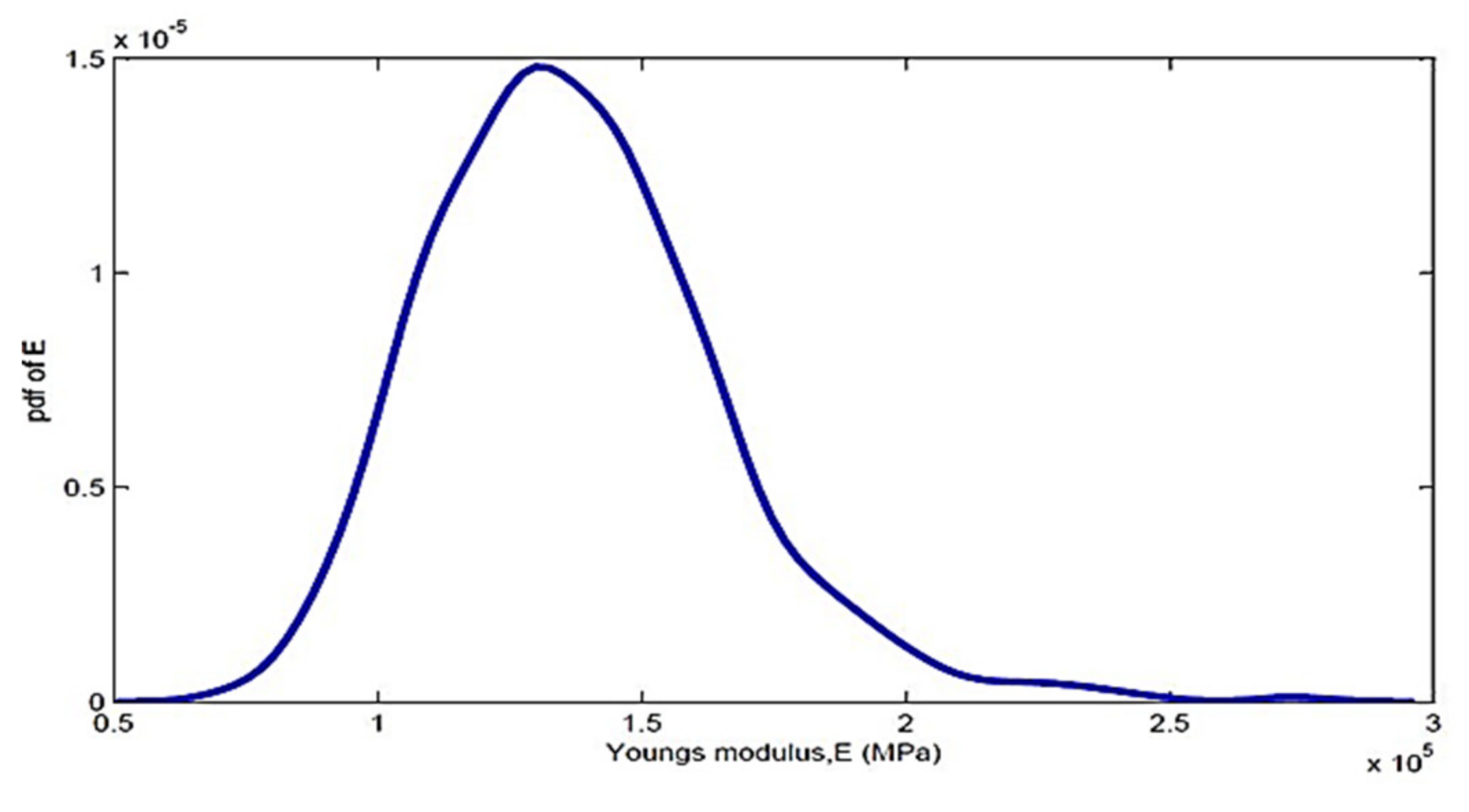
4.4.1. Due to Variability in Material Property
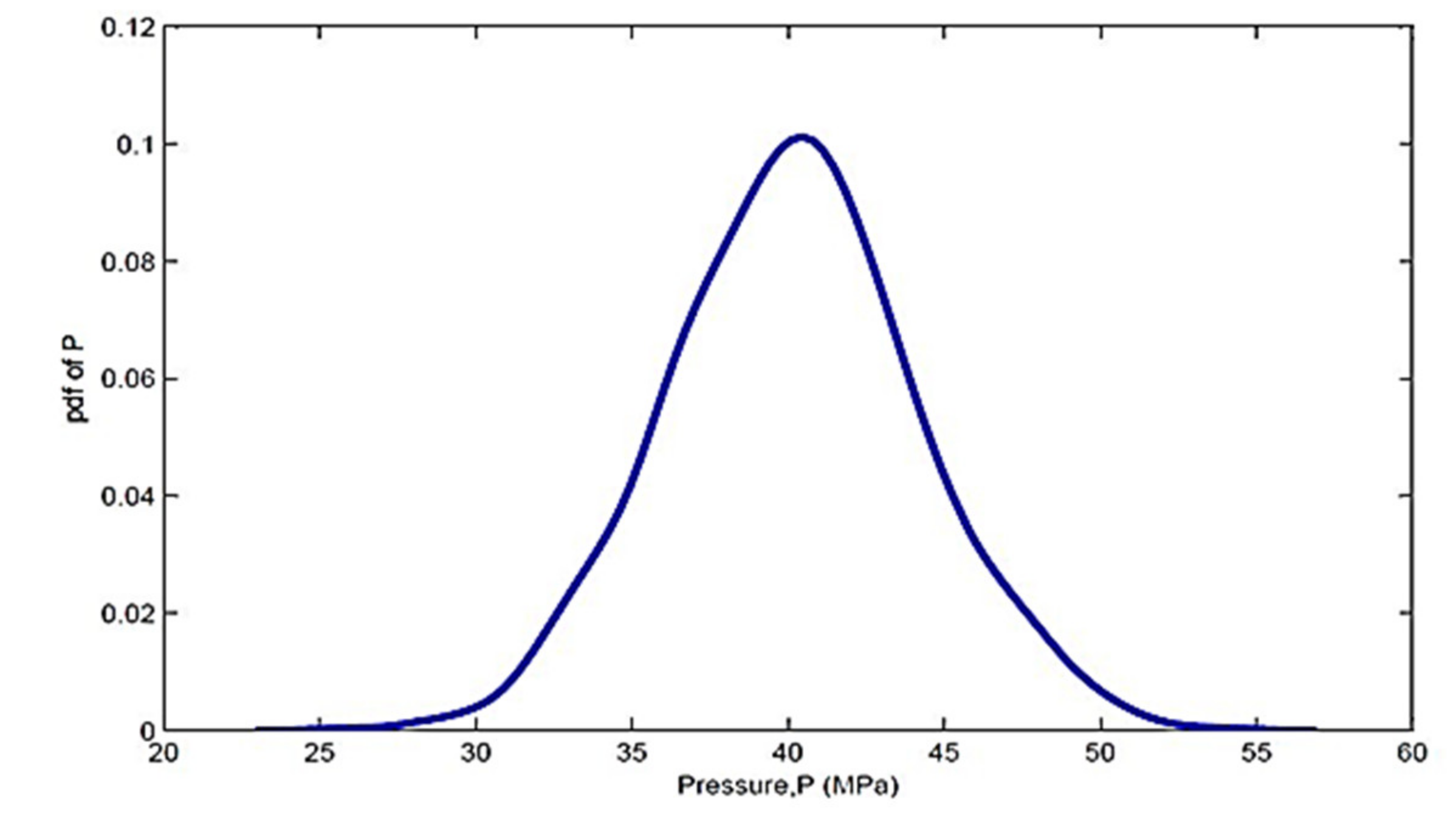
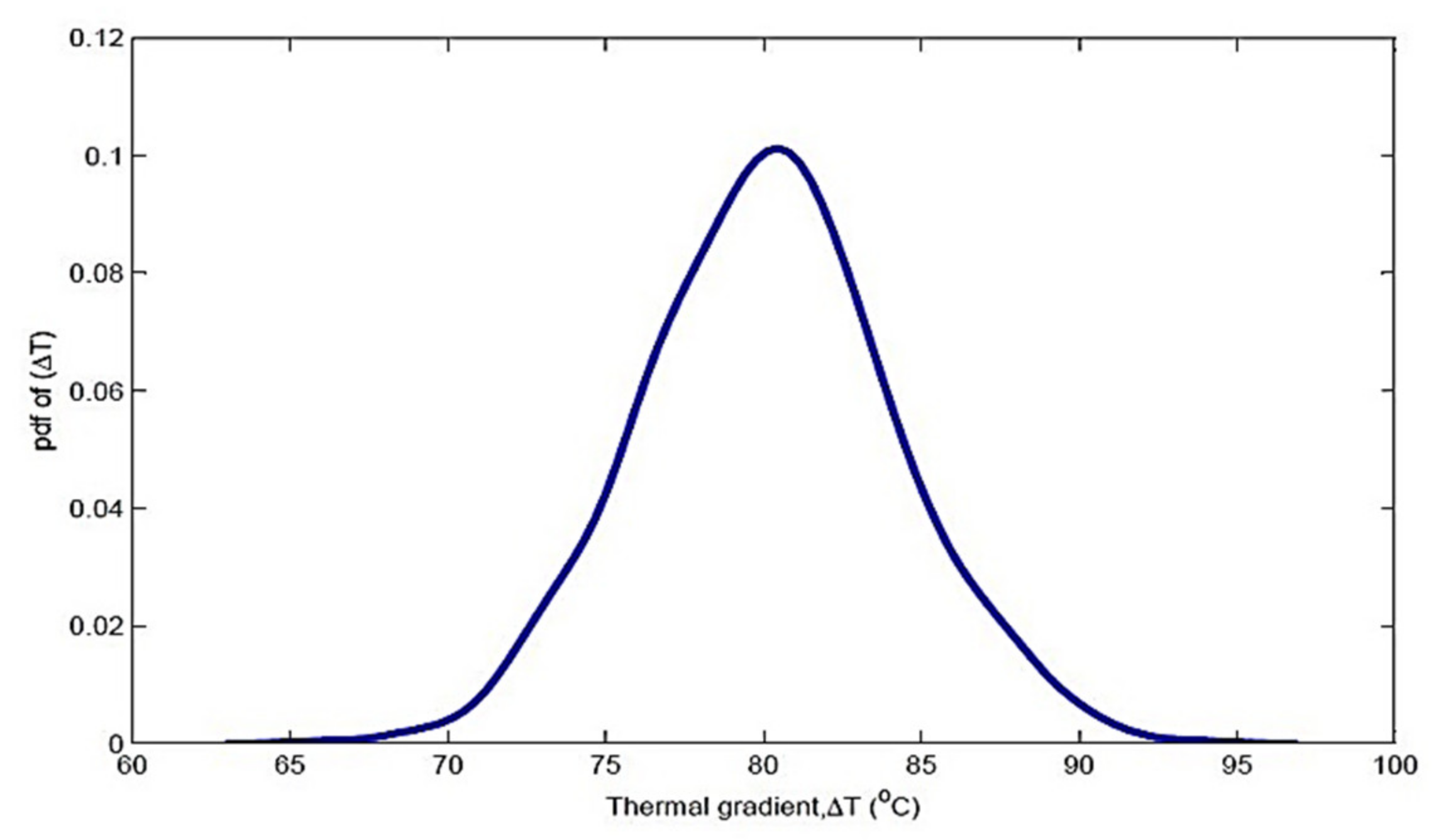
4.4.2. Due to Load Variability
Normal Distribution
Normal Distribution for Pressure
5. Probabilistic Finite Element Formulation
6. Derivation of Stiffness Matrix
Material Specifications
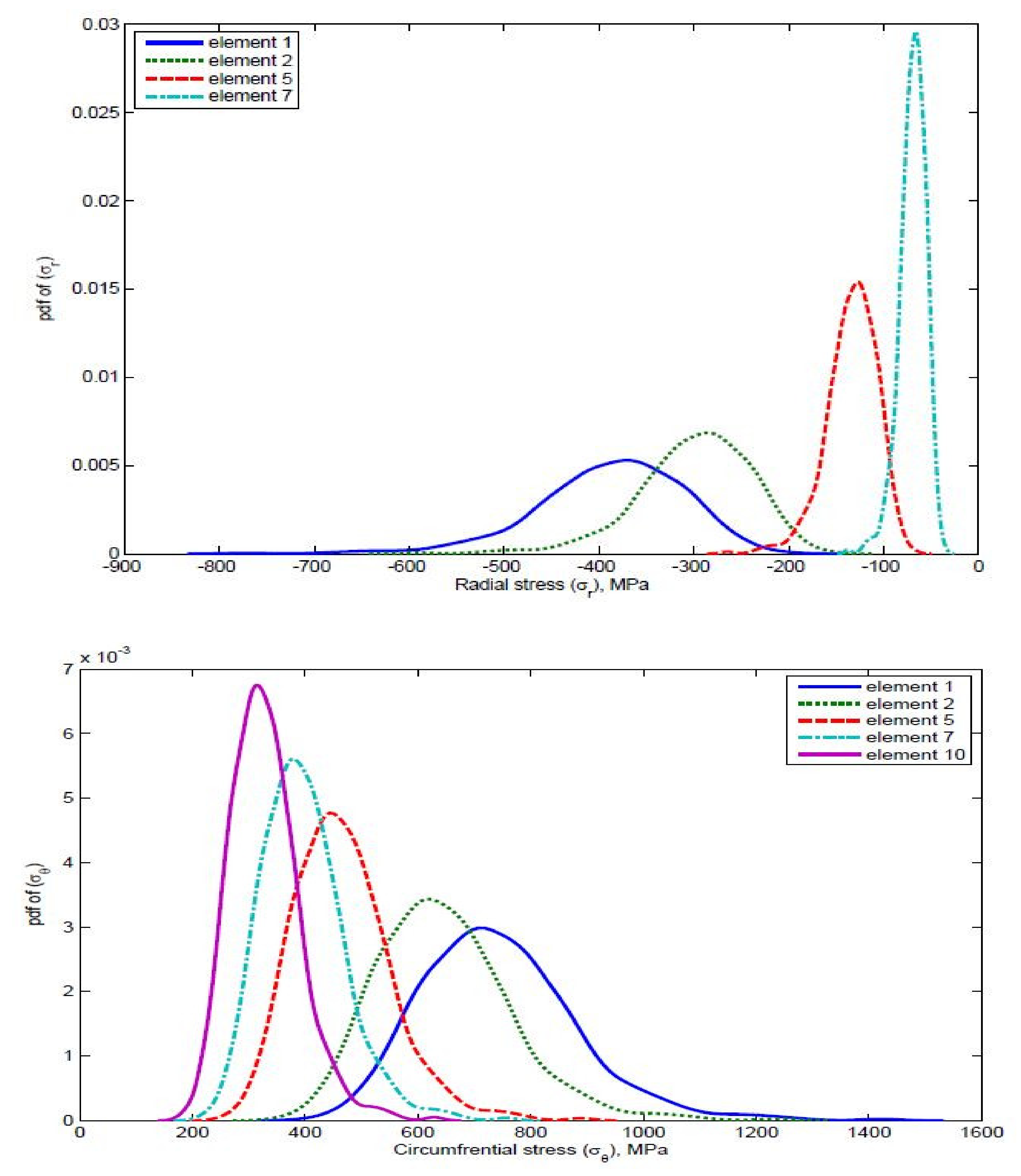
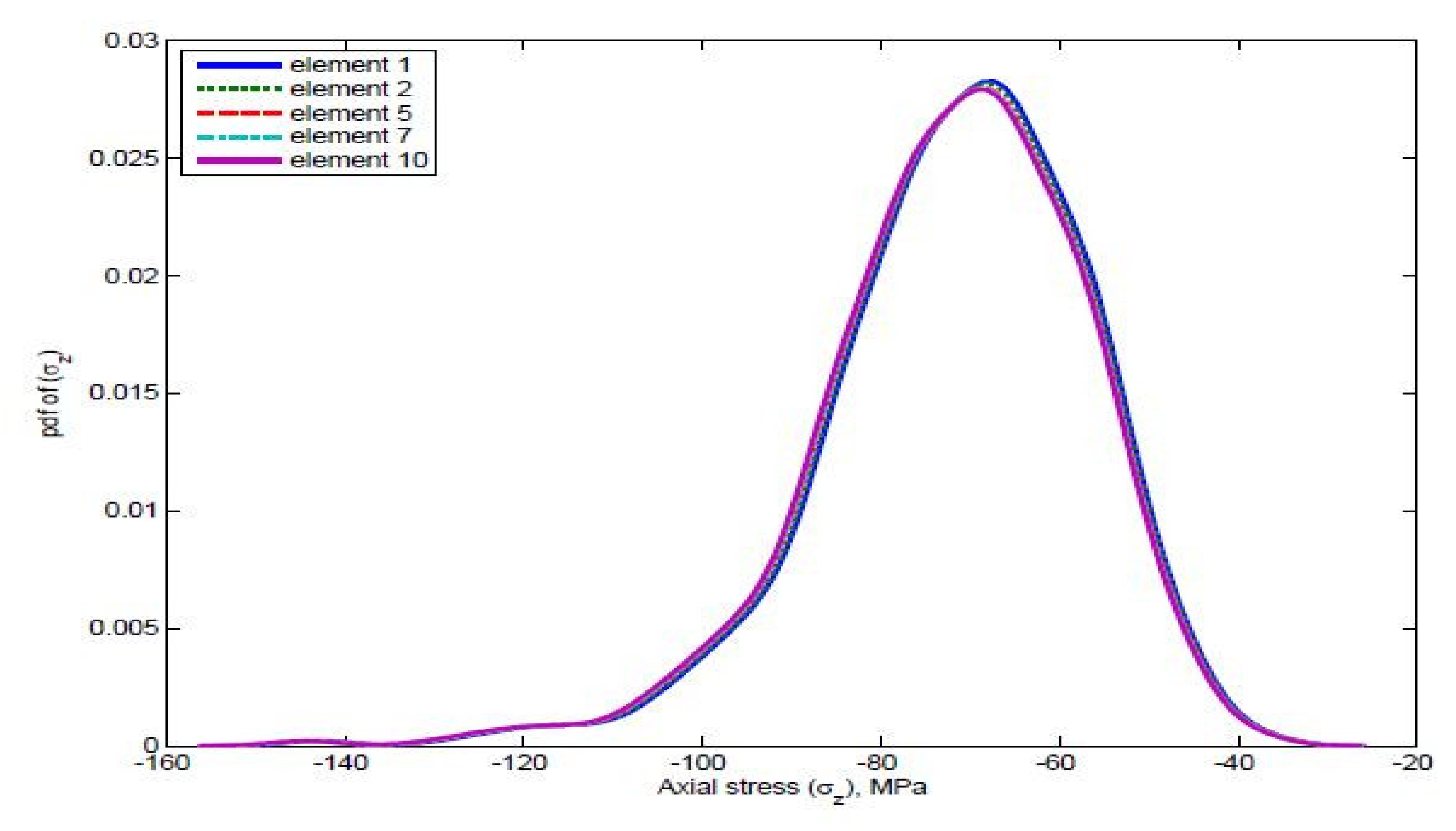
7. Probabilistic Study: Output Distribution
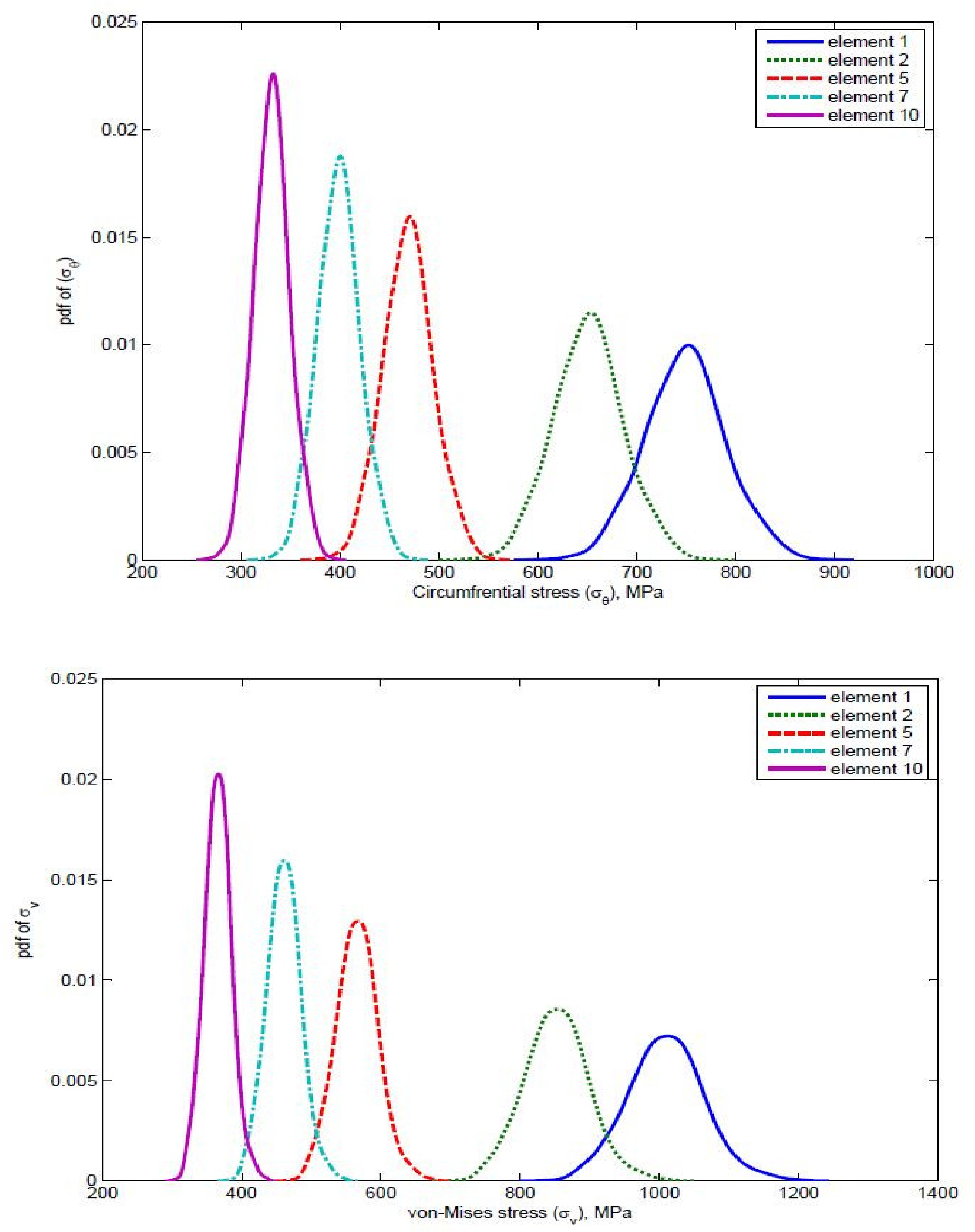
7.1. Output Distribution Due to Material Variability
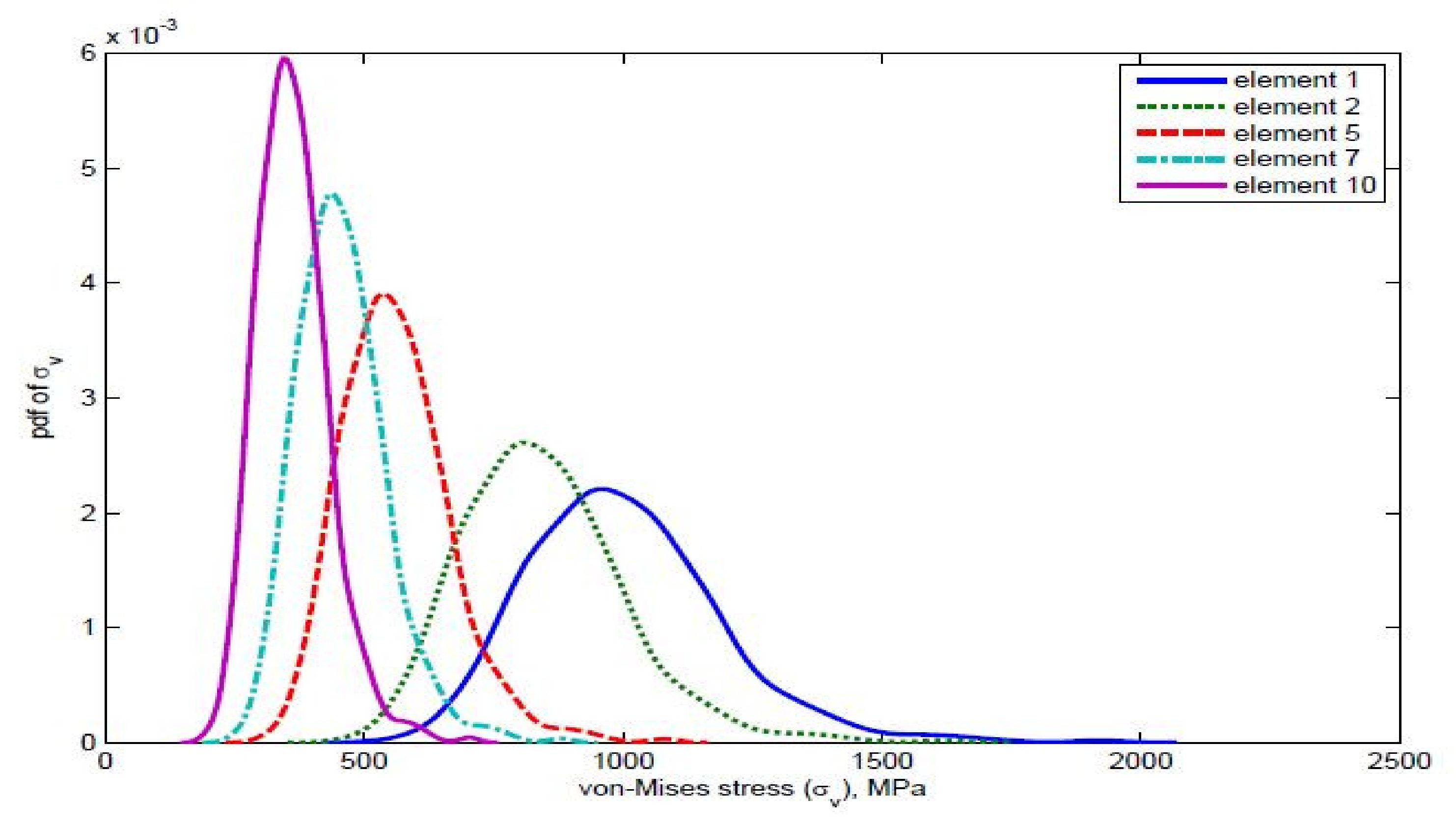
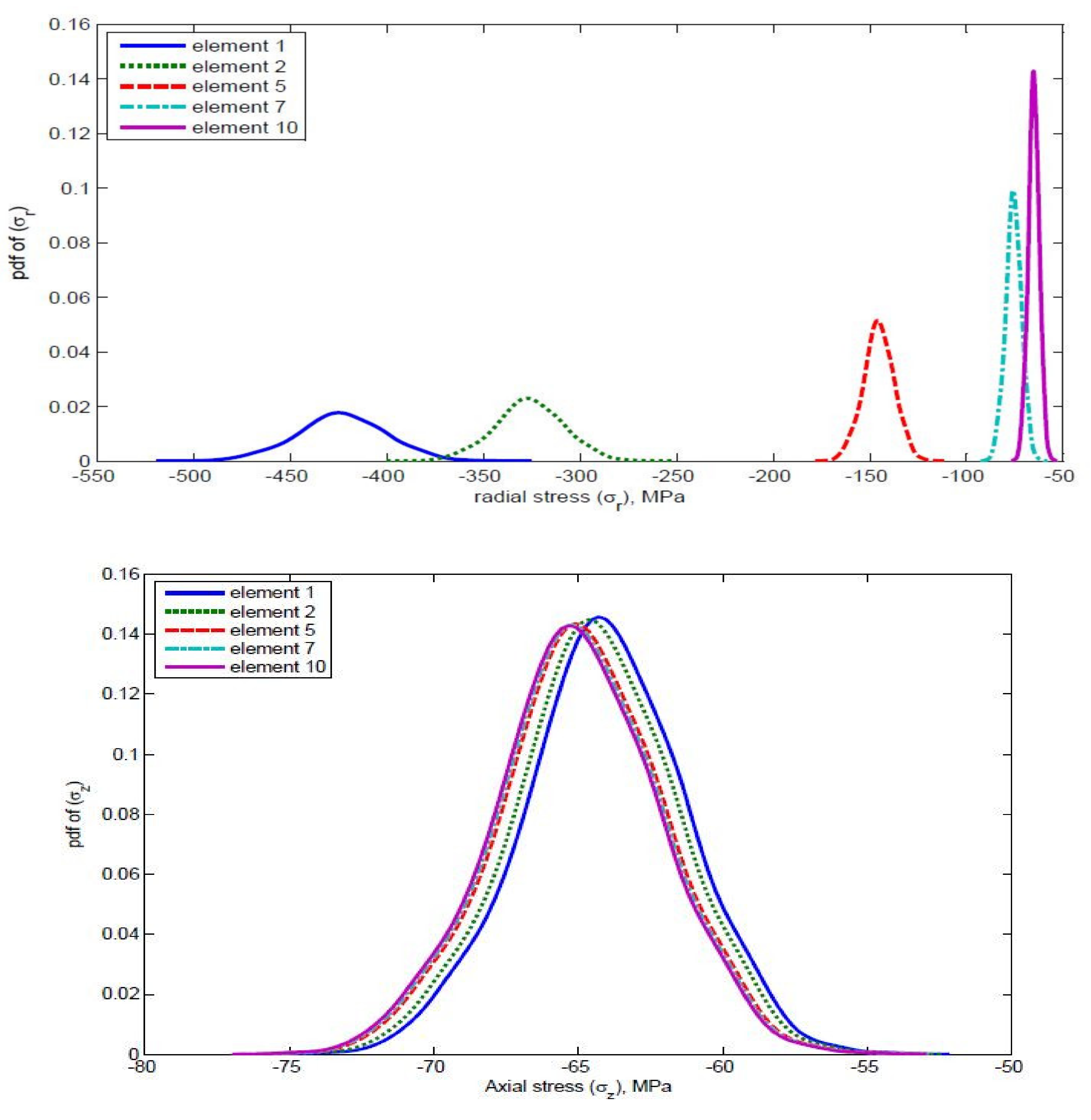
7.2. Output Distribution Due to Both Material and Load Variability
8. Probability of Failure of Von Mises Stress with Respect to Yield Strength
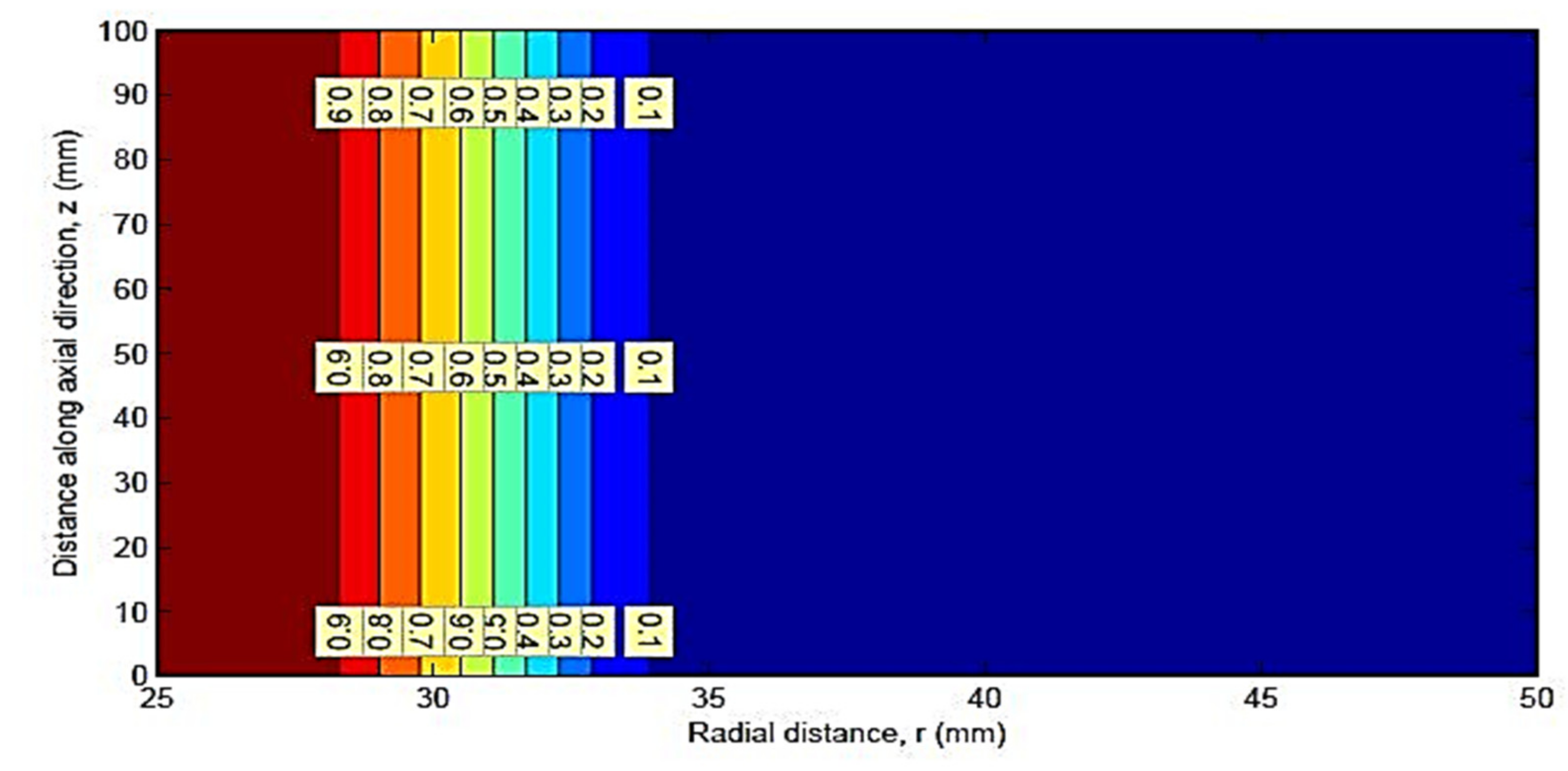
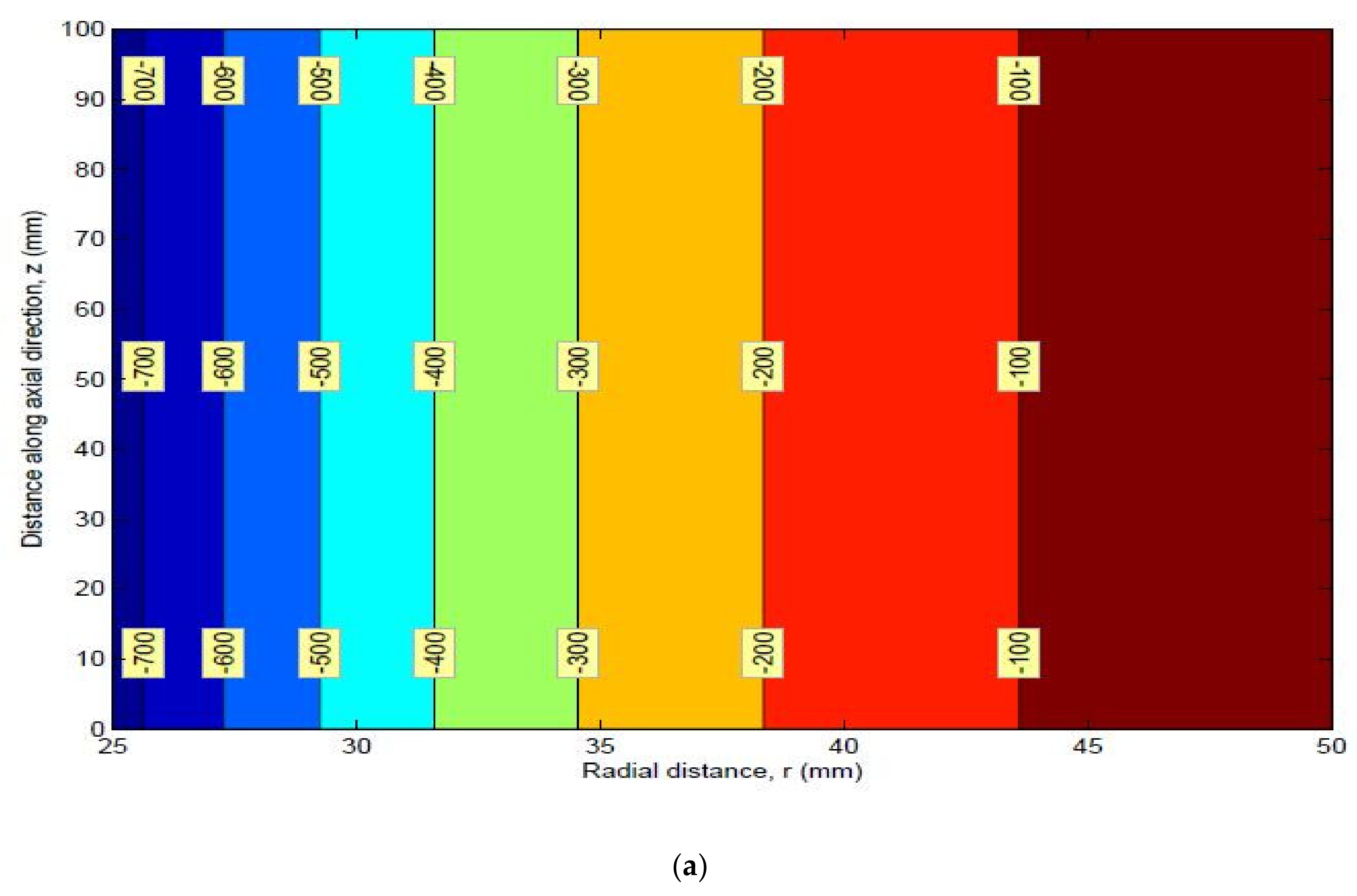
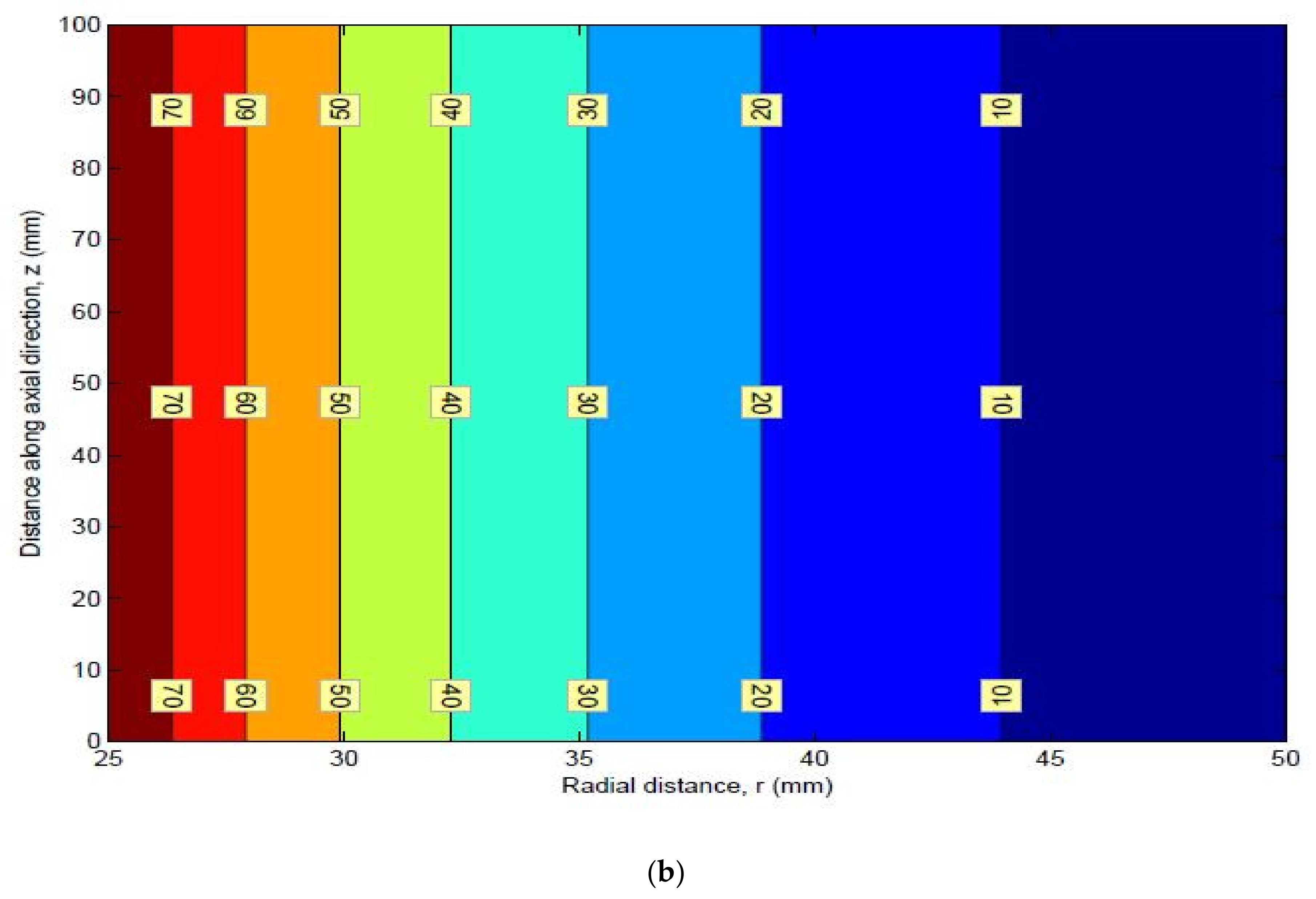
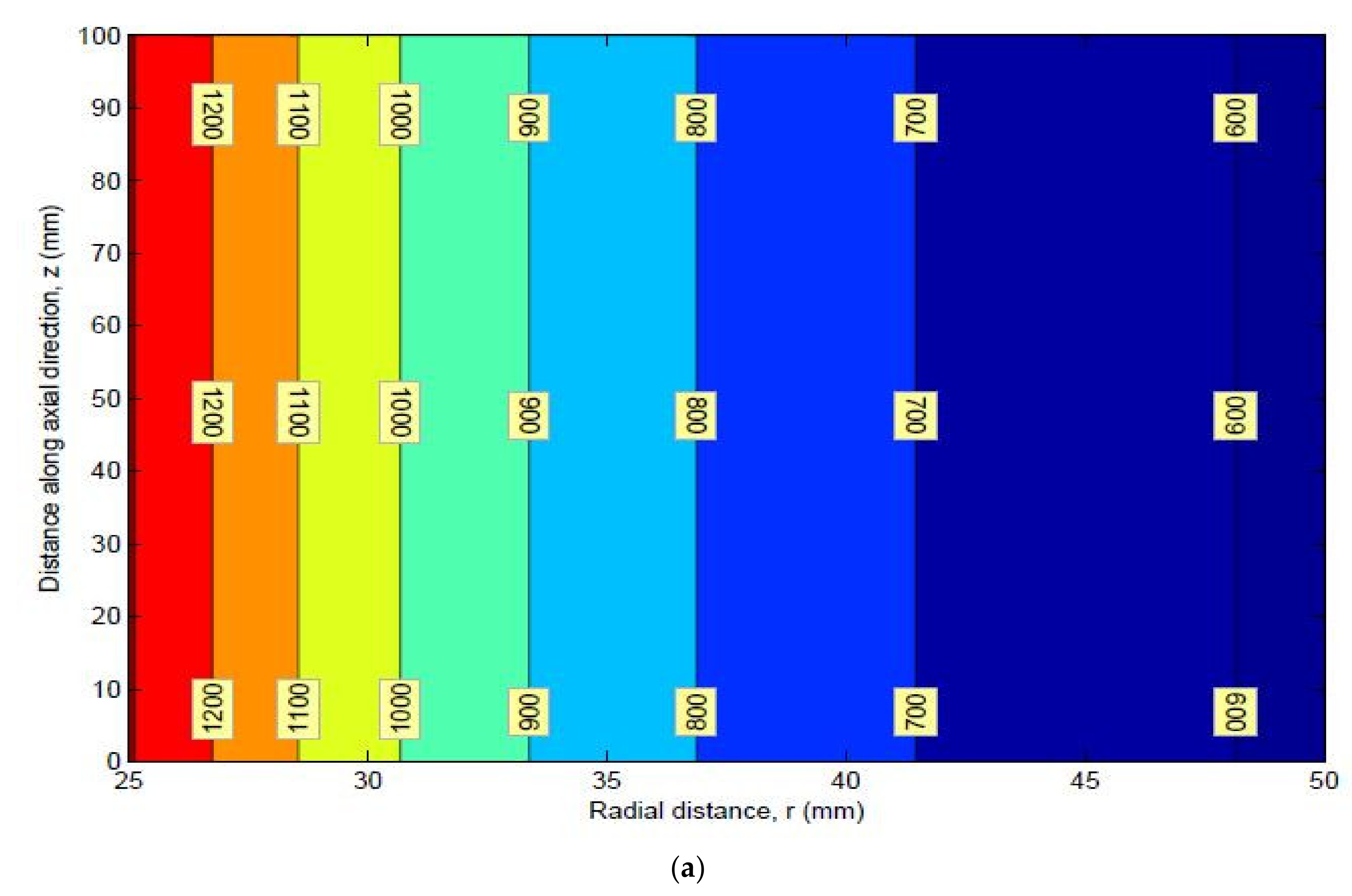
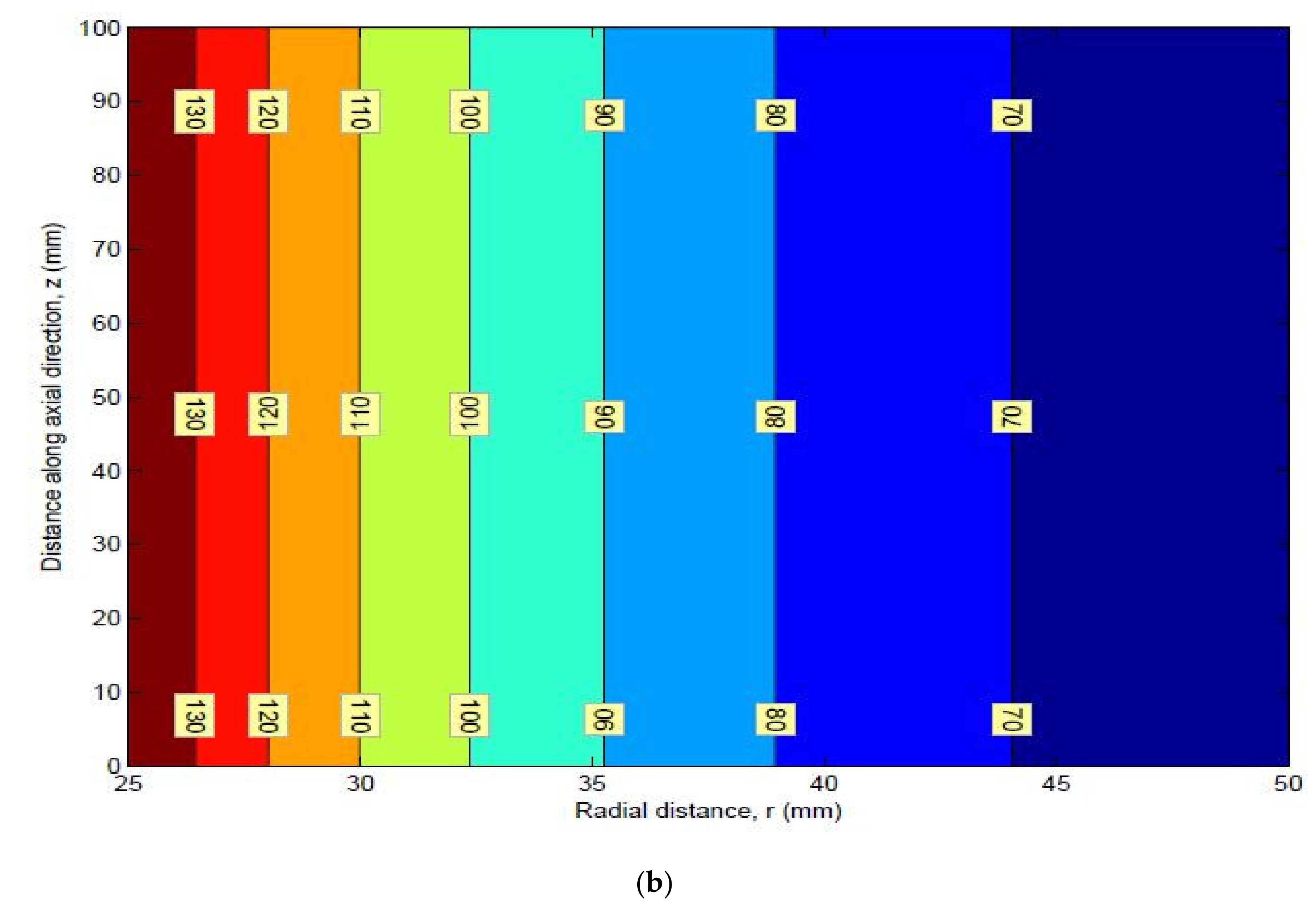
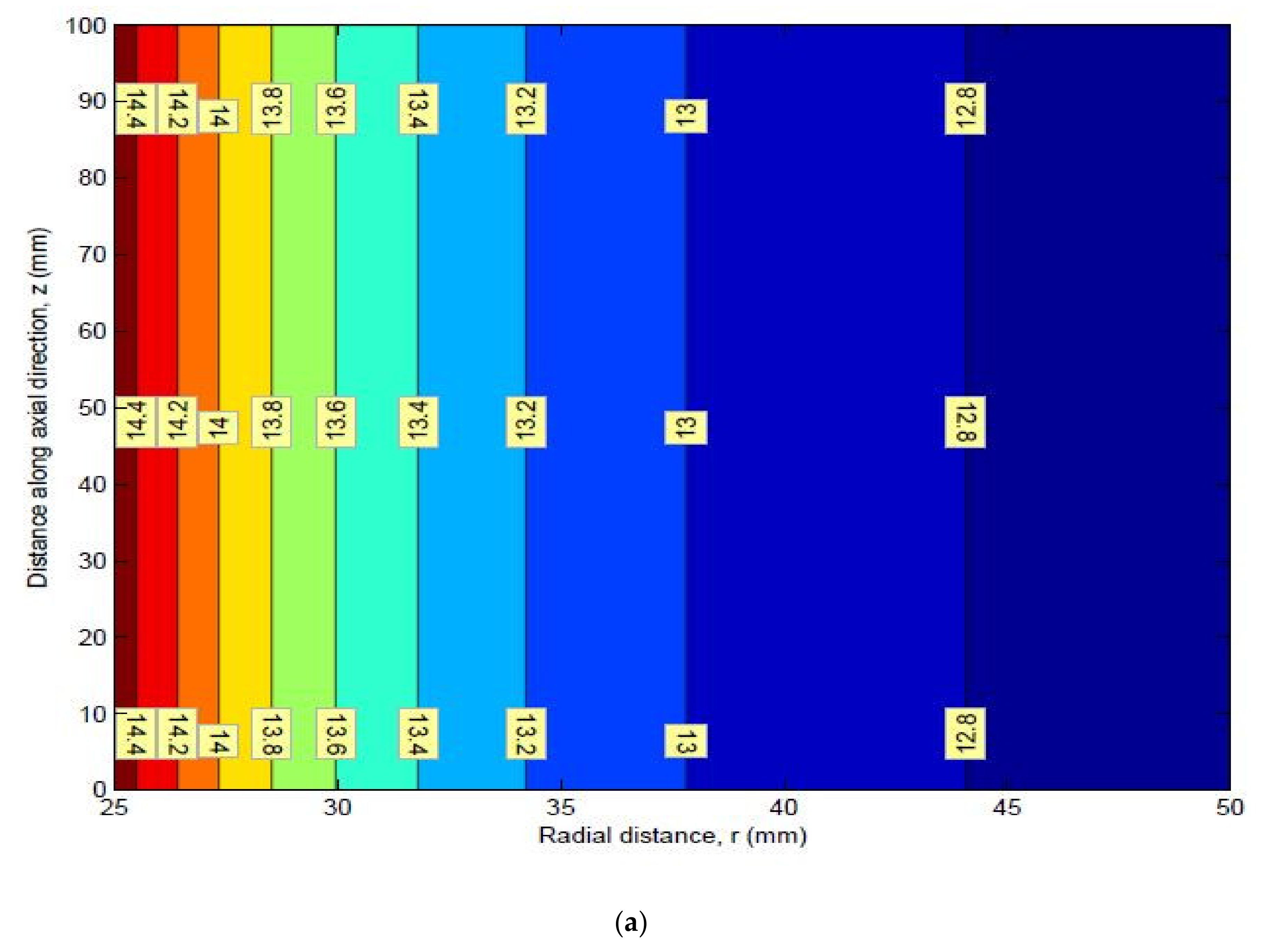
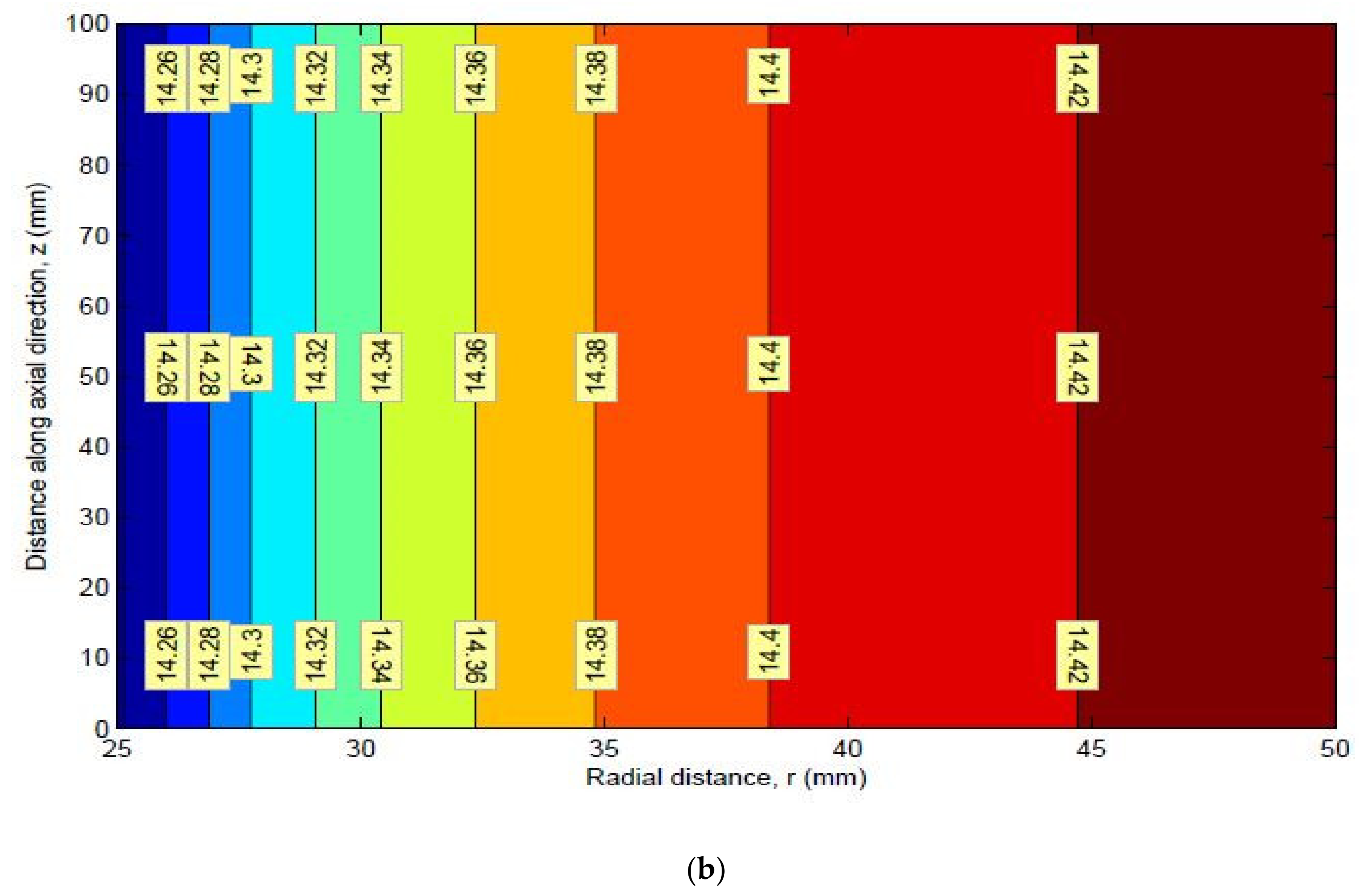
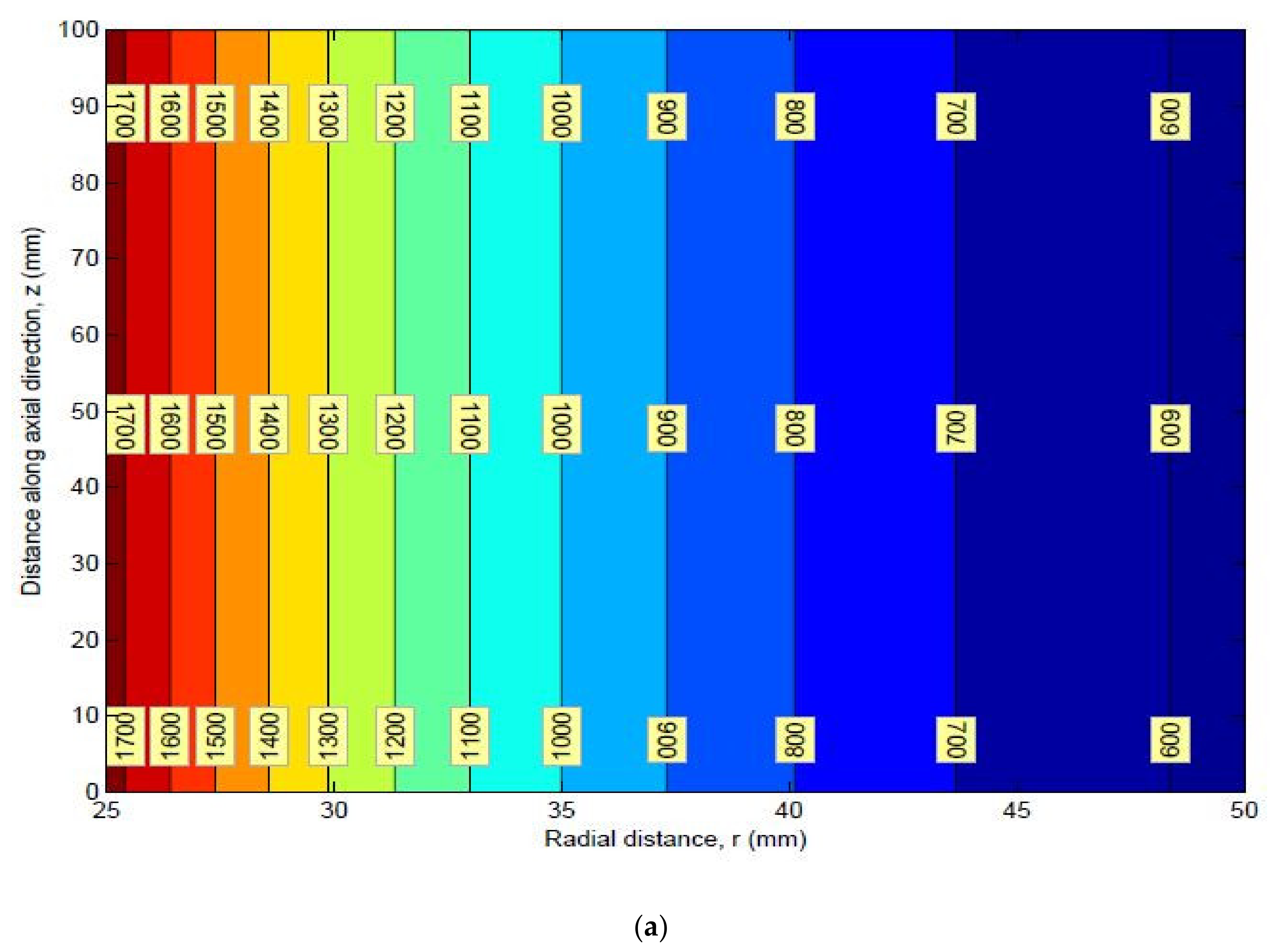
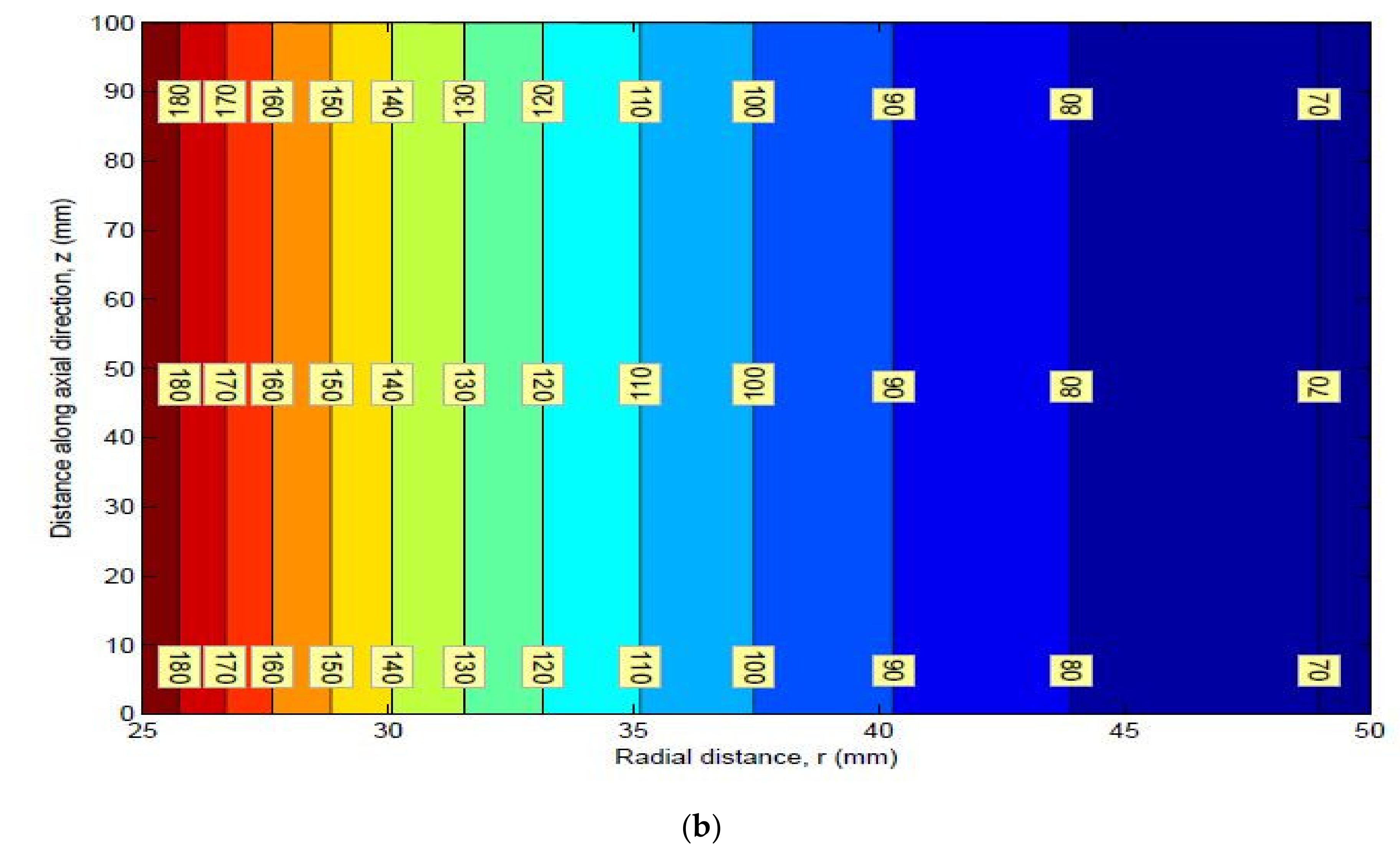
9. Stress Contours
Mean Stress Contours for HK40 Material
10. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
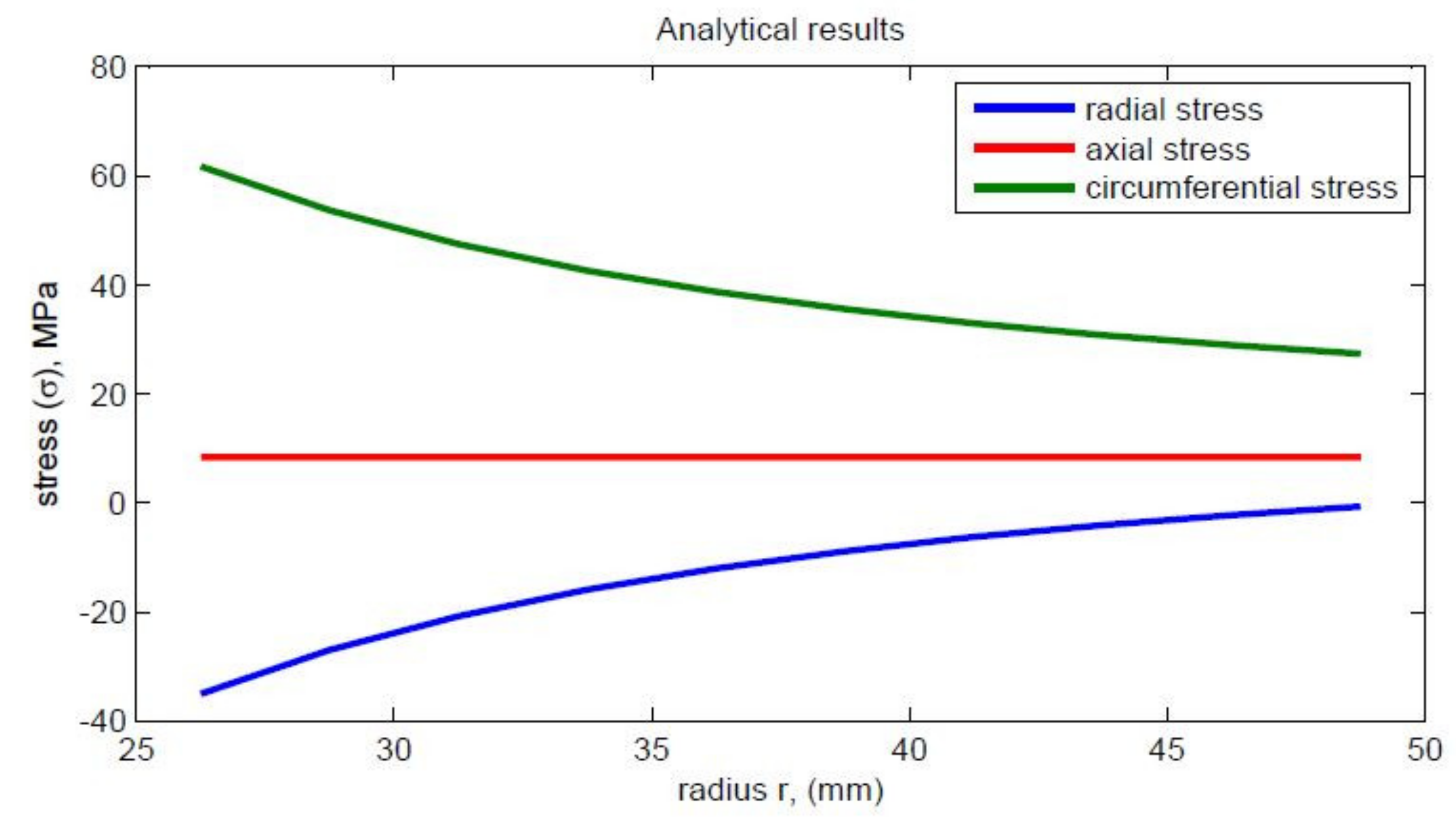
| Radial stress | |
| Thermal gradient | |
| Axial stress | |
| Circumferential stress | |
| Hoop stress induced by pressure | |
| Axial stress induced by pressure | |
| Radial stress induced by pressure | |
| Outer radius (mm) | |
| Inner radius (mm) | |
| a | Ratio of outer to inner radius |
| Poisson’s ratio | |
| r | Radius at any position of tube wall (mm) |
| E | Elastic modulus of material (MPa) |
| Thermal expansion coefficient of material |
References
- Zhou, C.; Tu, S. A Stochastic Computation model for the Creep damage of furnace tube. Int. J. Press. Vessel. Pip. 2001, 78, 617–625. [Google Scholar] [CrossRef]
- Rehman, S.M.; Rao, C.S. Vibration buckling and fracture analysis of a cracked cylindrical shell. Int. J. Des. Eng. 2017, 7, 33–53. [Google Scholar]
- Taye, C. Creep Analysis of boiler tubes by FEM. J. EEA 2005, 22, 1–3. [Google Scholar]
- Chakraborty, S.; Ganguly, S.; Chacko, E.Z.; Ajmani, S.K.; Talukdar, P. Estimation of surface heat flux in continuous casting mould with limited measurement of temperature. Int. J. Therm. Sci. 2017, 118, 435–447. [Google Scholar]
- Guthrie, R.I.L.; Isac, M.; Kim, J.S.; Tavares, R.P. Measurements, simulations and analyses of instantaneous heat fluxes from solidifying steels to the surfaces of twin roll casters and of aluminum to plasma-coated metal substrates. Metall. Mater. Trans. B 2000, 31, 1031–1047. [Google Scholar] [CrossRef]
- Wikstrӧm, P.; Blasiak, W.; Berntsson, F. Estimation of the transient surface temperature and heat flux of a steel slab using an inverse method. Appl. Therm. Eng. 2007, 27, 2463–2472. [Google Scholar] [CrossRef]
- Altenbach, H.; Naumenko, K.; Gorash, Y. Numerical Benchmarks for Creep-Damage Modeling; WILEY-VCH: Berlin, Germany, 2007. [Google Scholar]
- Ibe, O. Fundamentals of Applied probability and Random Processes; Academic Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Prime, M.B.; De Wald, A.T. The contour method. In Practical Residual Stress Measurement Methods; Schajer, G.S., Ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2013. [Google Scholar]
- Yao, X. Non-Linear Finite Element Analysis of Tubular Joints. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 1989. [Google Scholar]
- Oclon, P.; Taler, J. Mixed finite volume and finite element formulation: Linear quadraliteral elements. In Encyclopedia of Thermal Stresses; Hetnarski, R., Ed.; Springer: Berlin, Germany, 20 Circumferential; pp. 3086–3095.
- Ghasemi, A.R.; Kazemian, A.; Moradi, M. Analytical and Numerical Investigation of FGM Pressure vessel Reinforced by Laminated Composite Materials. J. Solid Mech. 2014, 6, 43–53. [Google Scholar]
- Kroese, D.P.; Taimre, T.; Botev, Z.I. Handbook of Monte Carlo Methods; Wiley-Blackwell: Hoboken, NJ, USA, 2011. [Google Scholar]
- Bradford, R. Application of Probabilistic Assessments to the Lifetime Management of Nuclear Boilers in the Creep Regime. In Proceedings of the SMiRT-23, Manchester, UK, 10–14 August 2015. [Google Scholar]

| Radius (mm) | Radial Stress (σr) (MPa) | Circumferential Stress (σθ) (MPa) | Axial Stress (σz) (MPa) | Von Mises Stress (σv) (MPa) |
|---|---|---|---|---|
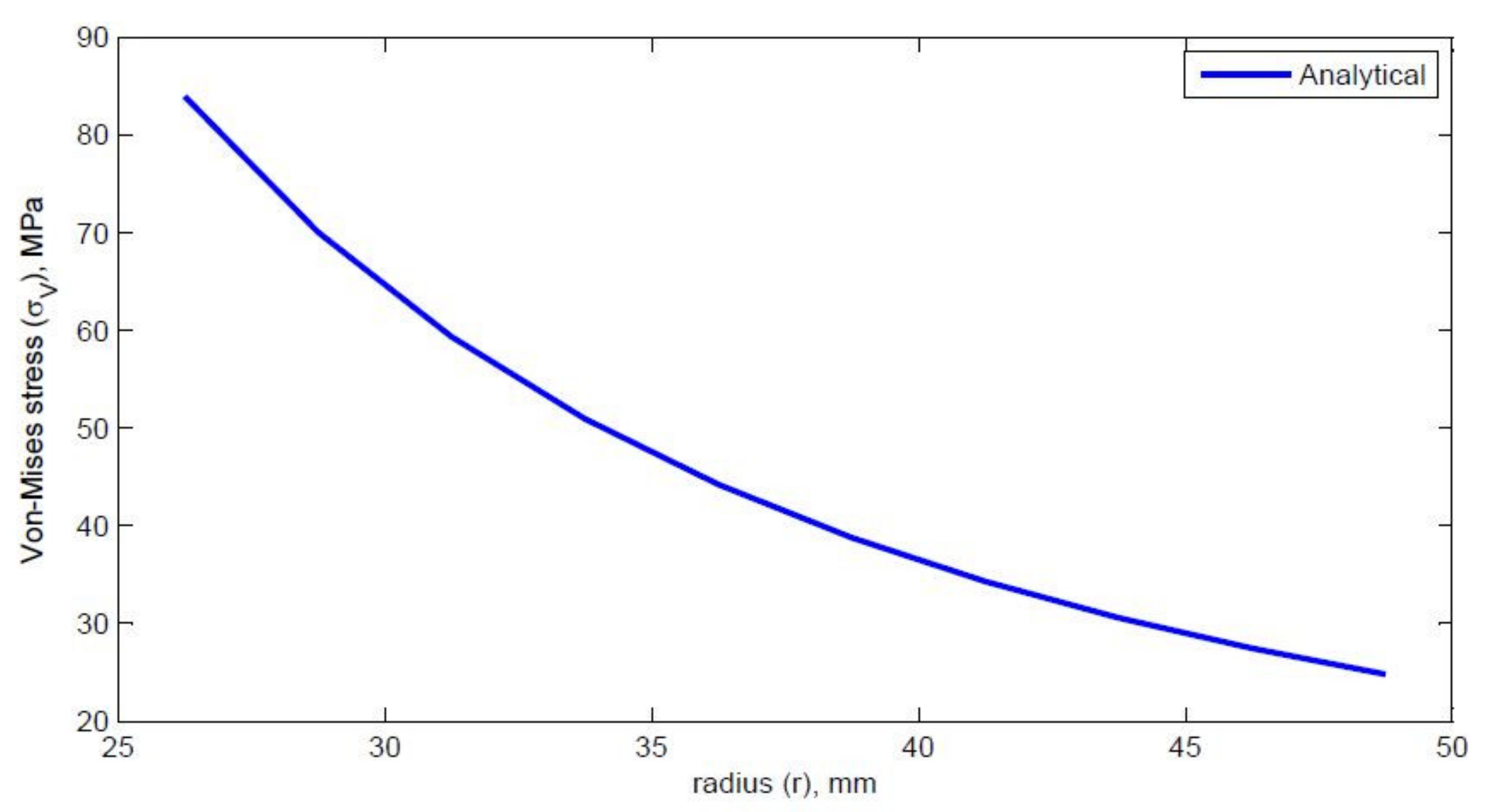
| 26.25 | −35.04 | 61.70 | 8.34 | 83.93 |
| 28.75 | −26.99 | 53.66 | 8.34 | 70.02 |
| 31.25 | −20.80 | 47.46 | 8.34 | 59.33 |
| 33.75 | −15.93 | 42.59 | 8.34 | 50.93 |
| 36.25 | −12.03 | 38.70 | 8.34 | 44.21 |
| 38.75 | −8.86 | 35.53 | 8.34 | 38.77 |
| 41.25 | −6.25 | 32.92 | 8.34 | 34.29 |
| 43.75 | −4.08 | 30.74 | 8.34 | 30.57 |
| 46.25 | −2.24 | 28.91 | 8.34 | 27.44 |
| 48.75 | −0.69 | 27.35 | 8.34 | 24.80 |
| Radius (mm) | Analytical Results | FEA Using ABAQUS | ||||
|---|---|---|---|---|---|---|
| 26.2500 | −35.0416 | 61.7082 | 83.9361 | −35.1470 | 61.7910 | 84.0936 |
| 28.7500 | −26.9943 | 53.6610 | 70.0273 | −27.0669 | 53.7178 | 70.1337 |
| 31.2500 | −20.8000 | 47.4667 | 59.3306 | −20.8515 | 47.5068 | 59.4038 |
| 33.7500 | −15.9305 | 42.5972 | 50.9312 | −15.9679 | 42.6262 | 50.9821 |
| 36.2500 | −12.0333 | 38.7000 | 44.2184 | −12.0611 | 38.7214 | 44.2537 |
| 38.7500 | −8.8658 | 35.5324 | 38.7720 | −8.8868 | 35.5485 | 38.7961 |
| 41.2500 | −6.2565 | 32.9232 | 34.2951 | −6.2727 | 32.9354 | 34.3109 |
| 43.7500 | −4.0816 | 30.7483 | 30.5730 | −4.0942 | 30.7578 | 30.5825 |
| 46.2500 | −2.2498 | 28.9165 | 27.4476 | −2.2597 | 28.9239 | 27.4520 |
| 48.7500 | −0.6925 | 27.3592 | 24.8000 | −0.7004 | 27.3650 | 24.8004 |
| Radius (mm) | Analytical Results | FEM Using MATLAB | ||||
|---|---|---|---|---|---|---|
| 26.250 | −35.041 | 61.708 | 83.936 | −34.950 | 61.883 | 81.636 |
| 28.750 | −26.994 | 53.661 | 70.027 | −26.926 | 53.768 | 68.244 |
| 31.250 | −20.800 | 47.466 | 59.330 | −20.748 | 47.532 | 57.917 |
| 33.750 | −15.930 | 42.597 | 50.931 | −15.890 | 42.635 | 49.789 |
| 36.250 | −12.033 | 38.700 | 44.218 | −12.002 | 38.720 | 43.280 |
| 38.750 | −8.865 | 35.532 | 38.772 | −8.841 | 35.540 | 37.990 |
| 41.250 | −6.256 | 32.923 | 34.295 | −6.237 | 32.923 | 33.636 |
| 43.750 | −4.081 | 30.748 | 30.573 | −4.067 | 30.742 | 30.010 |
| 46.250 | −2.249 | 28.916 | 27.447 | −2.238 | 28.906 | 26.963 |
| 48.750 | −0.692 | 27.359 | 24.800 | −0.684 | 27.346 | 24.378 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bobba, S.; Abrar, S.; Rehman, S.M. Probability Study on the Thermal Stress Distribution in Thick HK40 Stainless Steel Pipe Using Finite Element Method. Designs 2019, 3, 9. https://doi.org/10.3390/designs3010009
Bobba S, Abrar S, Rehman SM. Probability Study on the Thermal Stress Distribution in Thick HK40 Stainless Steel Pipe Using Finite Element Method. Designs. 2019; 3(1):9. https://doi.org/10.3390/designs3010009
Chicago/Turabian StyleBobba, Sujith, Shaik Abrar, and Shaik Mujeebur Rehman. 2019. "Probability Study on the Thermal Stress Distribution in Thick HK40 Stainless Steel Pipe Using Finite Element Method" Designs 3, no. 1: 9. https://doi.org/10.3390/designs3010009
APA StyleBobba, S., Abrar, S., & Rehman, S. M. (2019). Probability Study on the Thermal Stress Distribution in Thick HK40 Stainless Steel Pipe Using Finite Element Method. Designs, 3(1), 9. https://doi.org/10.3390/designs3010009





