Optimum Redesign of an Agricultural Water Bowser
Abstract
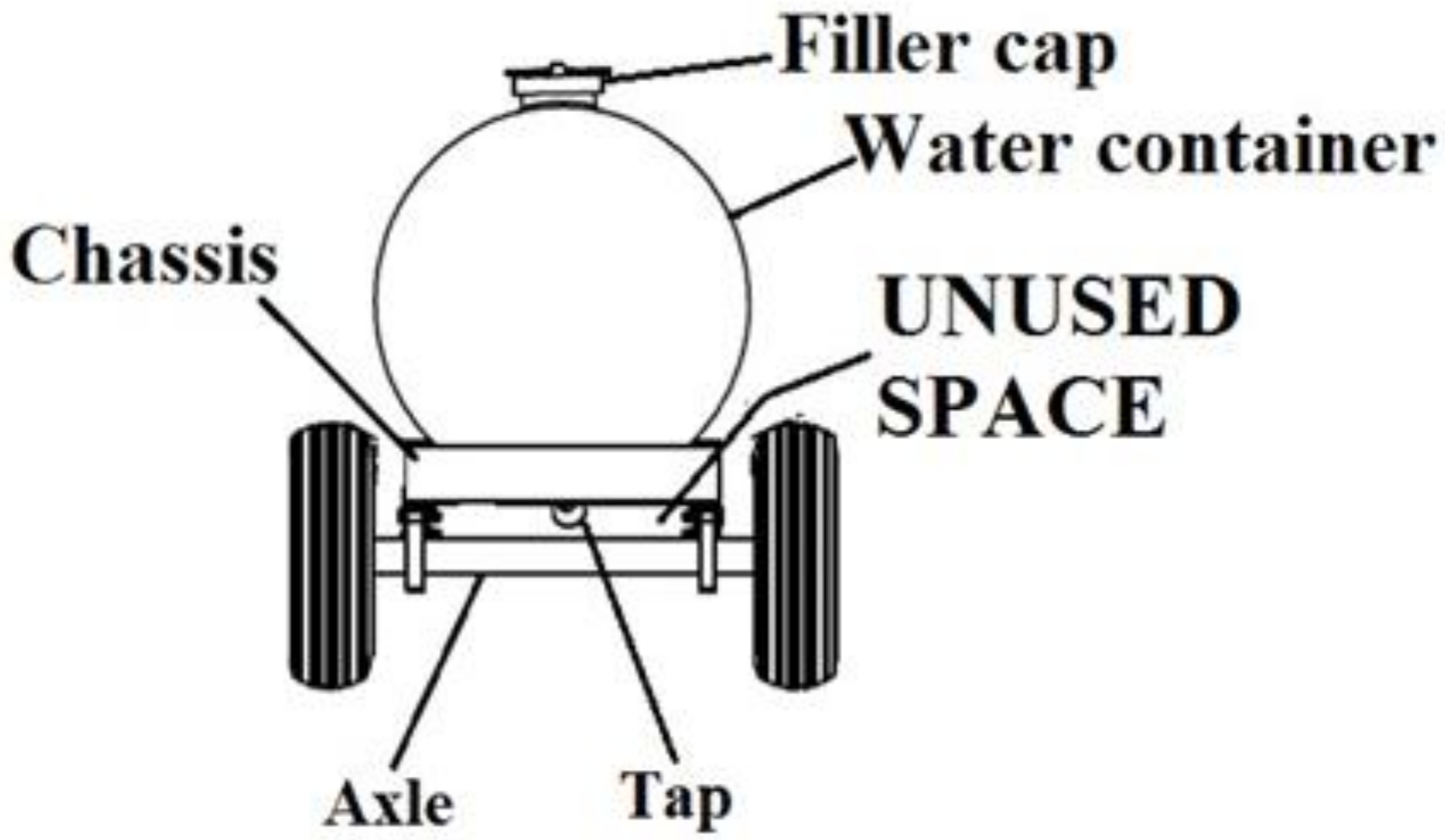
1. Introduction
1.1. Chassis
- C-shaped: The C-rails are the most common type and are used in almost every vehicle. A flat piece of steel is rolled on both sides to form a C-shaped beam.
- Boxed: It is made by welding two similar C-rails together or by bending a flat piece of steel into four sides and then welding where both ends meet.
- Hat: It has a “U” geometry and is not frequently used due to its low strength.
- I-shaped: The I-rails are used on all types of trucks as the cross members in structures.
1.2. Axle
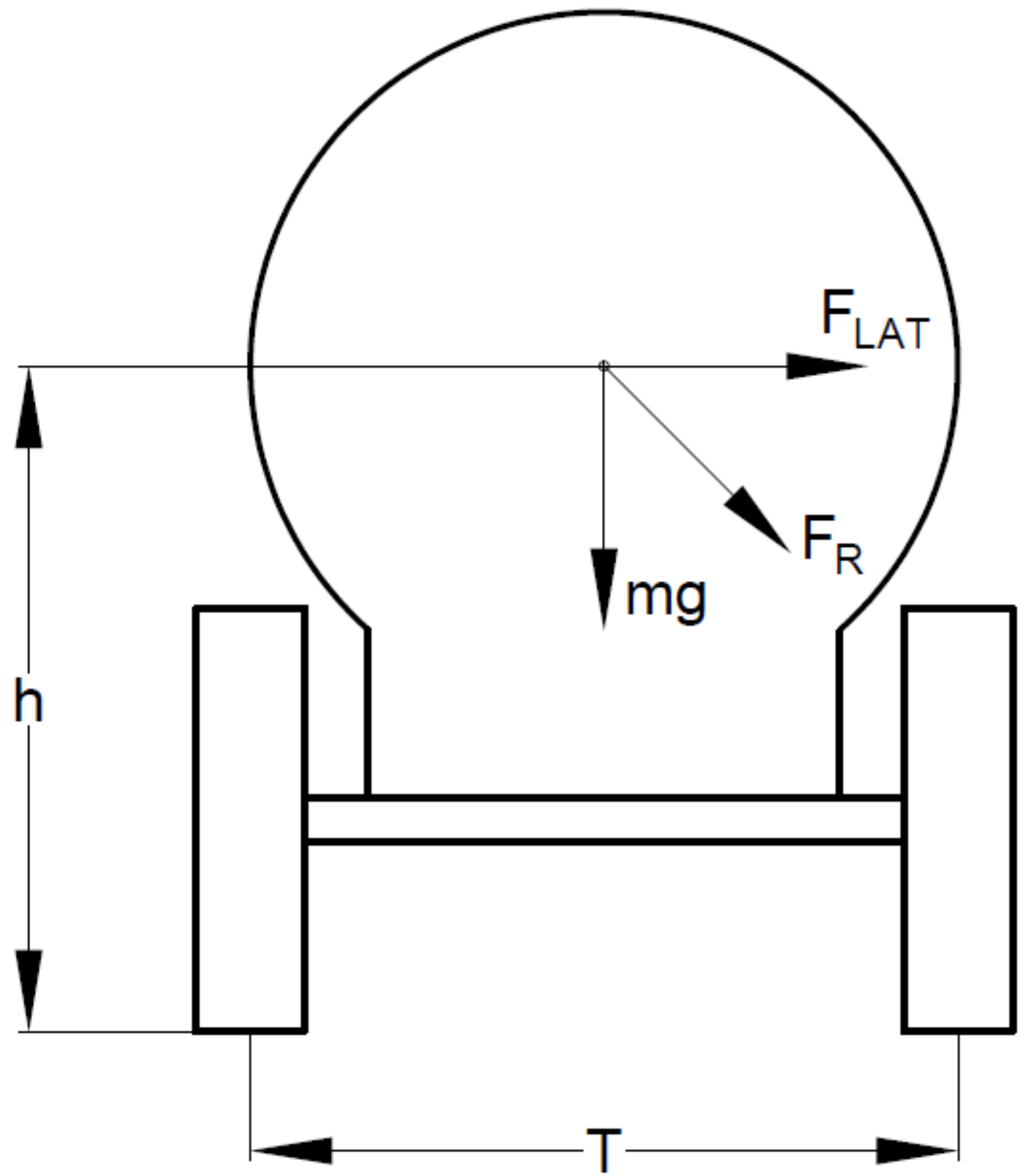
1.3. Vehicle Rollover Stability
1.4. Liquid Sloshing in Road Tankers
1.5. Material
1.6. Tank Design Standards
1.6.1. CFR 49 (Code Federal Regulation)
1.6.2. ADR (Agreement Dangerous Road)
1.6.3. Economic Commission of Europe Regulation No. 111
2. Materials and Methods
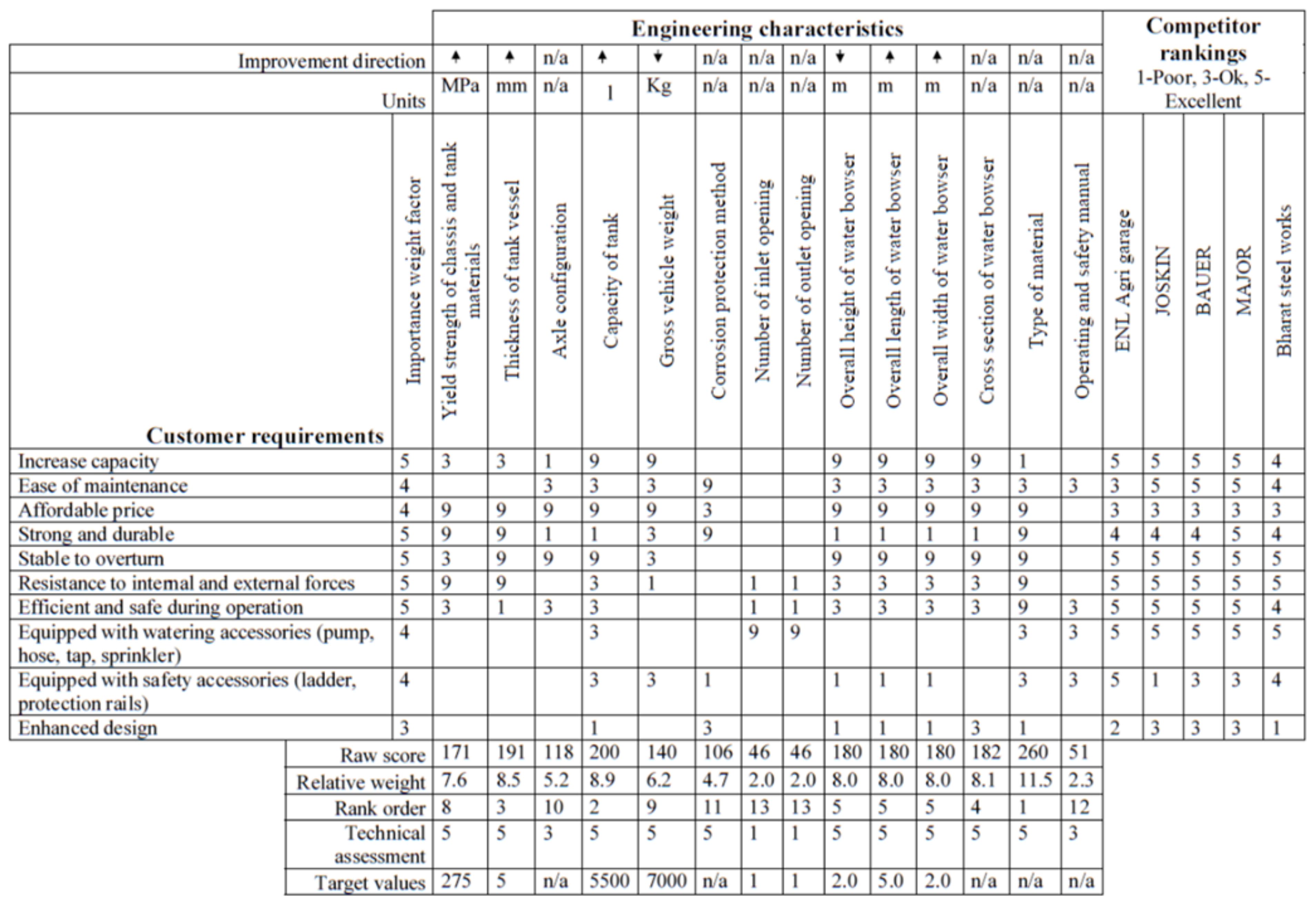
2.1. House of Quality
2.2. Concept Development and Selection
2.3. Detailed Design
2.3.1. Tank Shell
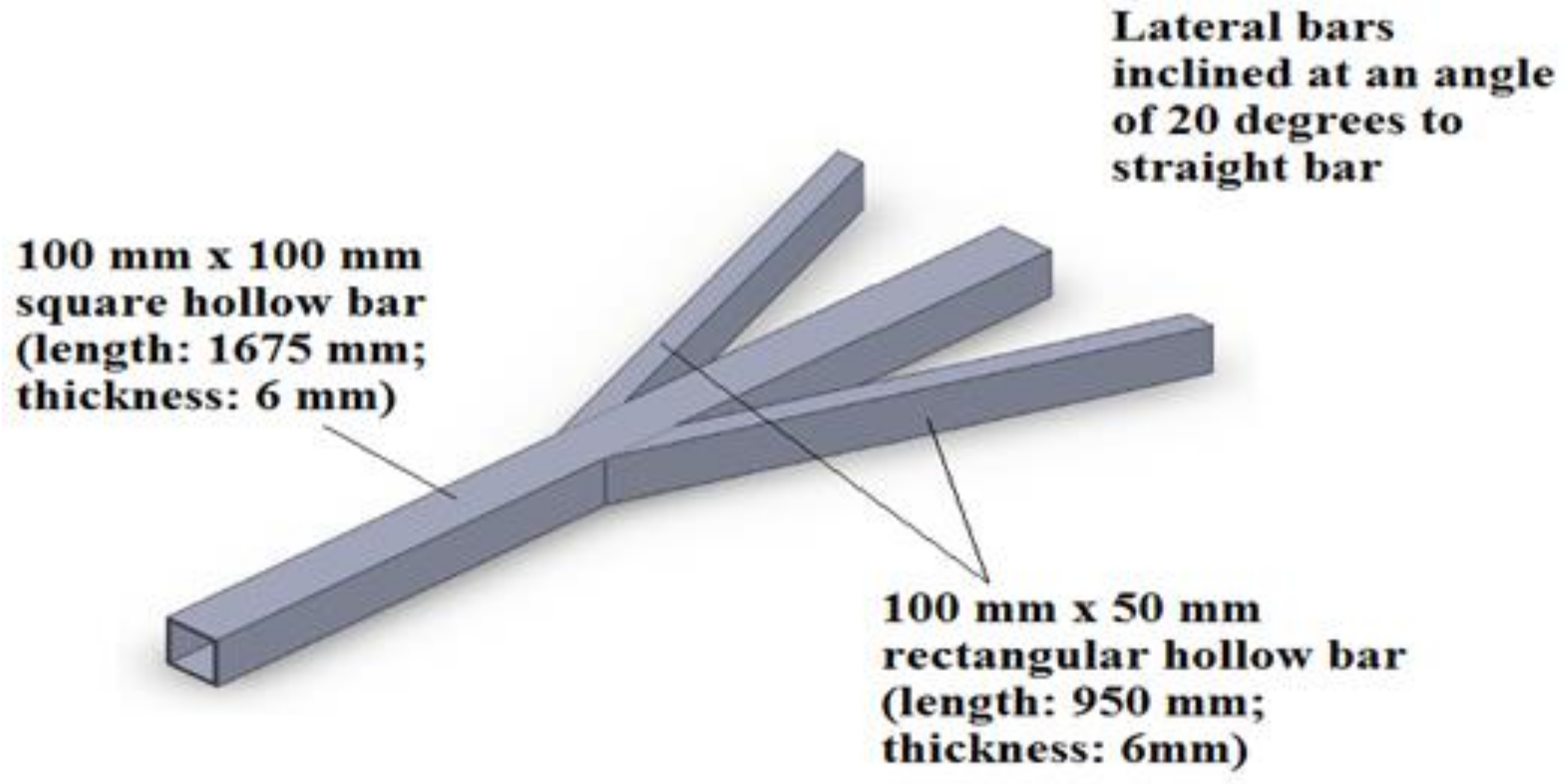
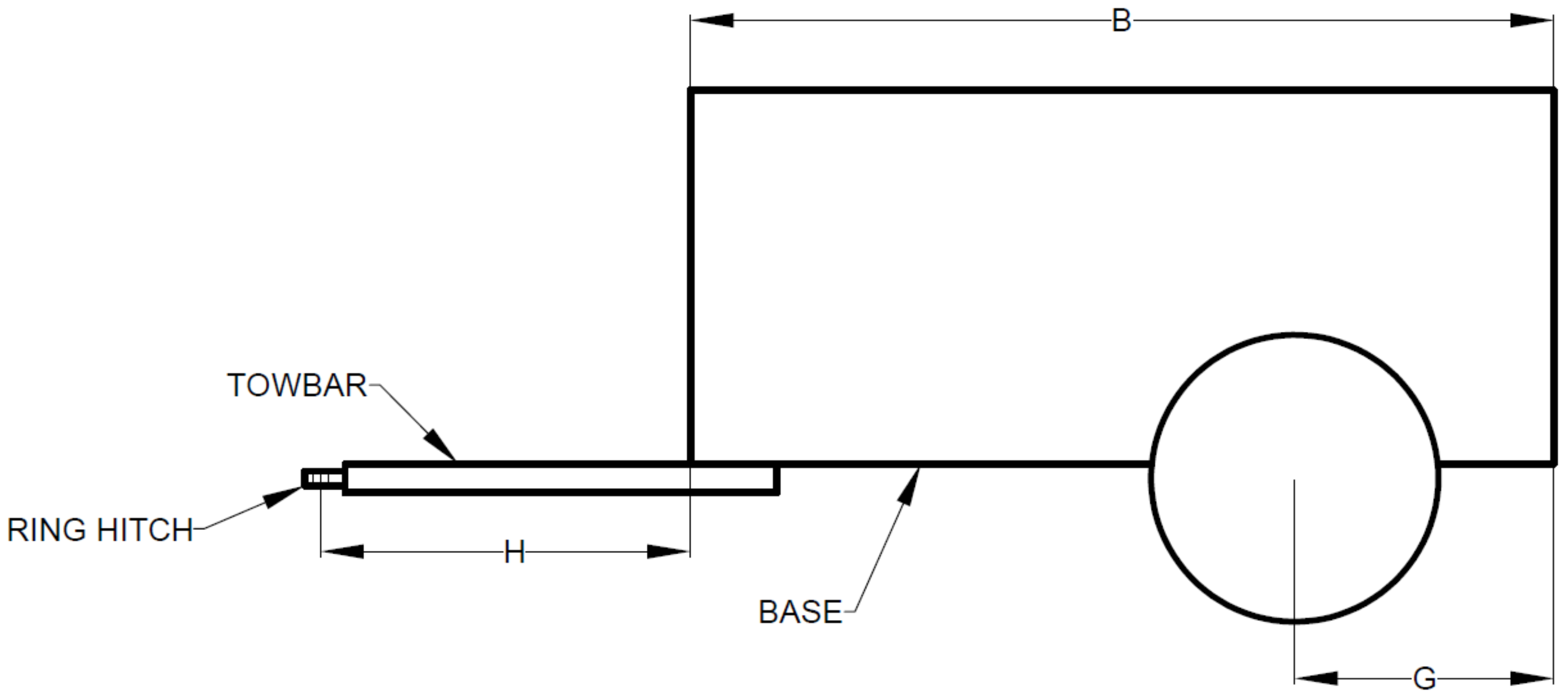
2.3.2. Drawbar
2.3.3. Ring Hitch
2.3.4. Axle Position
2.3.5. Tire
2.3.6. Baffles
2.3.7. Suspension
2.3.8. Safety
2.3.9. Degree of Filling
2.3.10. Water Load and Discharge
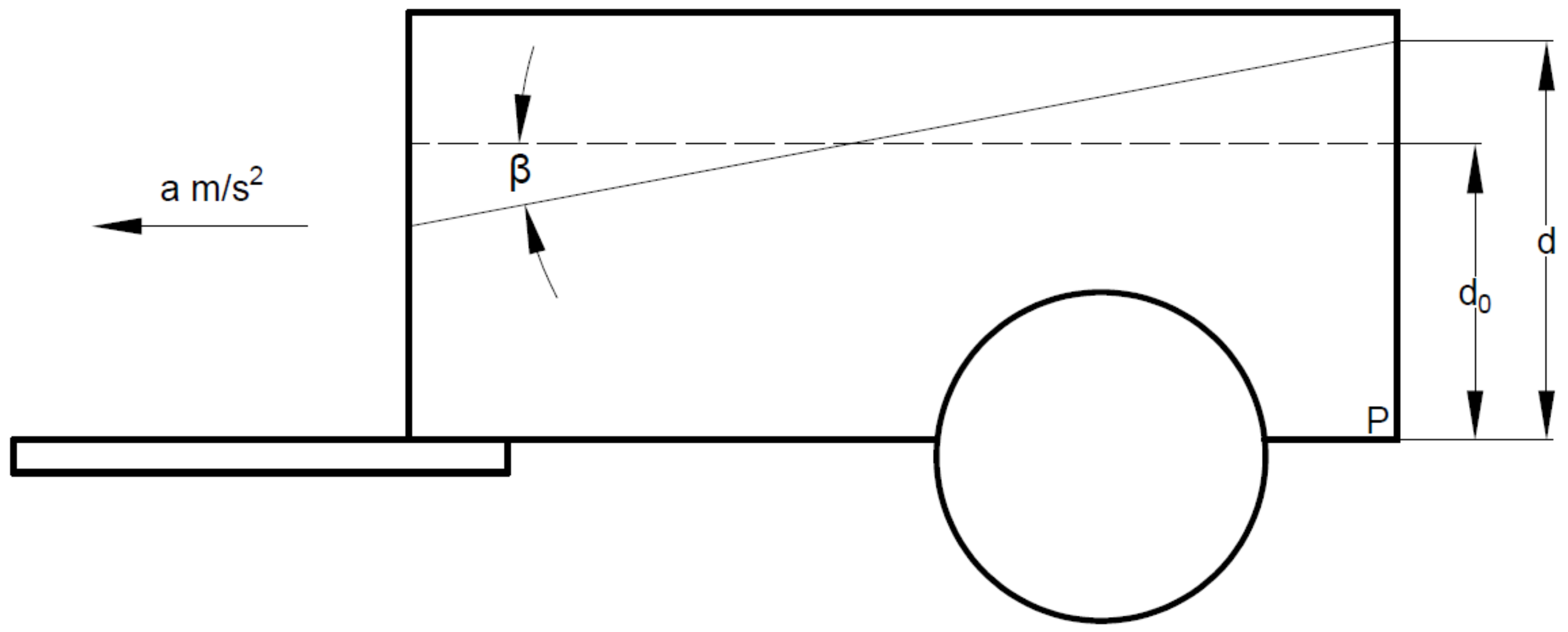
2.3.11. Calculation of Forces
- In the direction of travel and vertically downwards—twice the total mass (2 m)
- At right angles to the direction of travel and vertically upwards—the total mass (m)
2.4. Finite Element Analysis
2.4.1. Modeling
2.4.2. Fixtures
2.4.3. Loads
2.4.4. Meshing
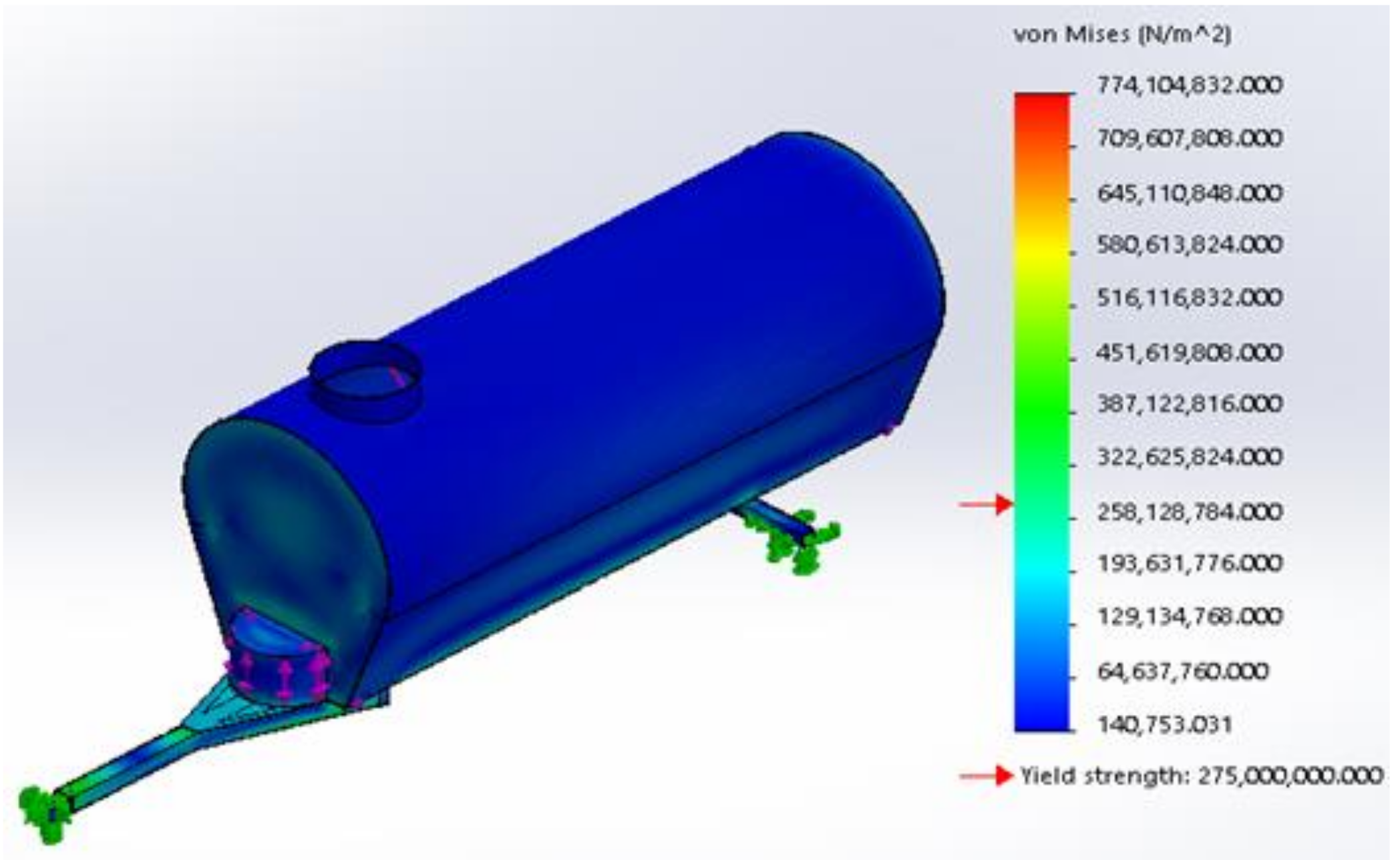
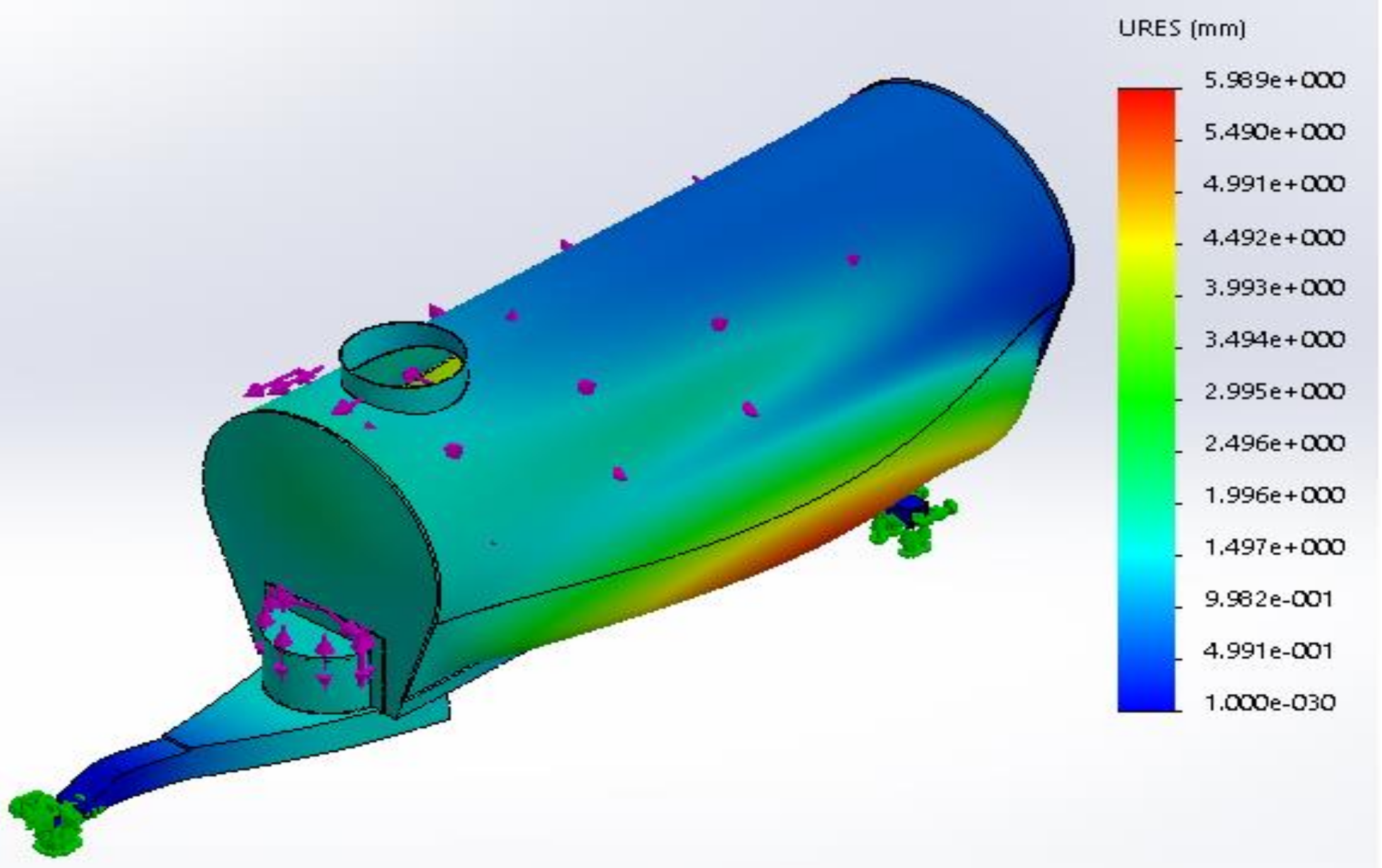
3. Results
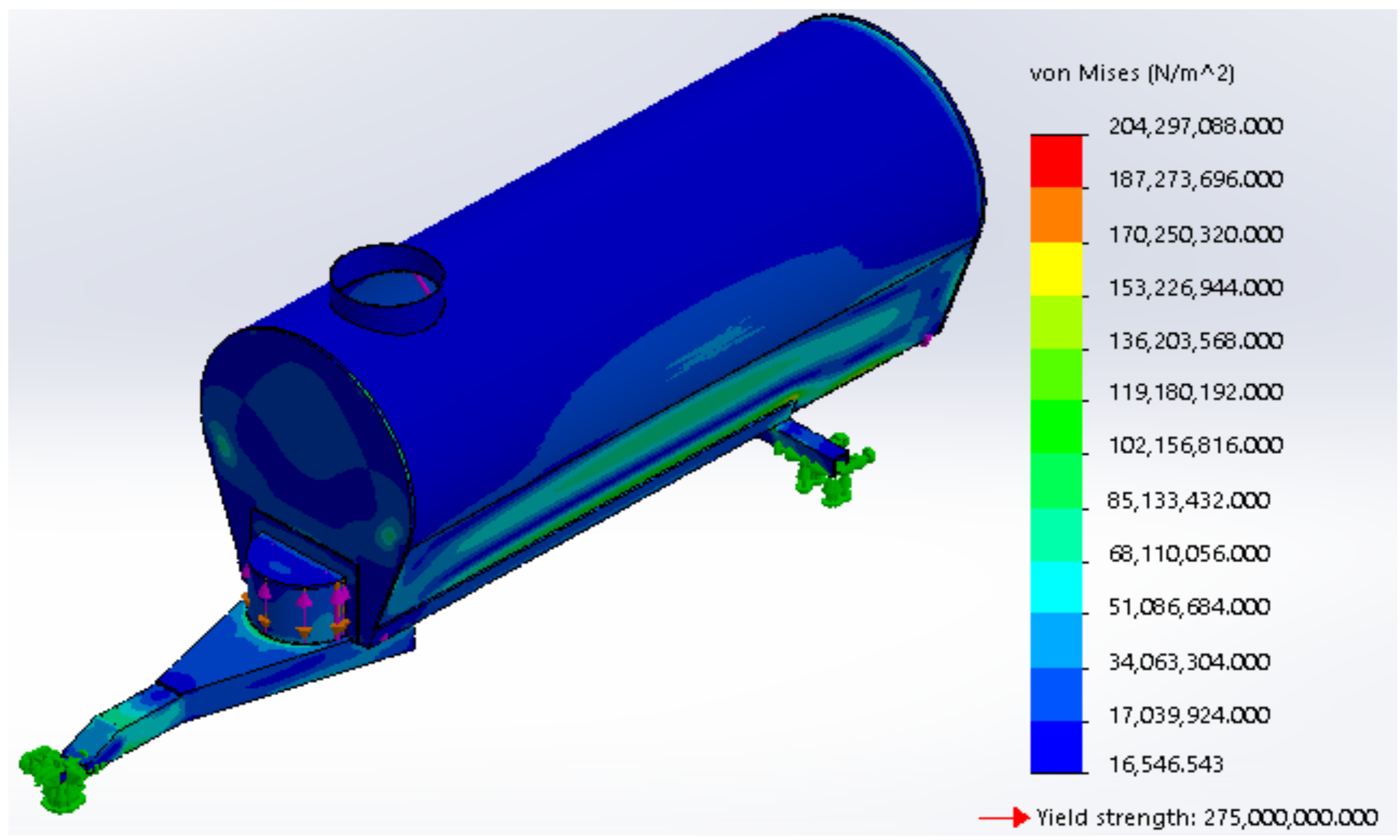
- The thickness of the front and back metal sheets was changed from 6 mm to 20 mm.
- The bottom edge on the sides of the bowser, running from the front to the axle, was stiffened using plates of 12 mm thickness.
- A 120 mm × 120 mm × 10 mm square hollow bar was used for the axle, instead of 100 mm × 80 mm × 6 mm.
- The front part of the drawbar was modified so as to reduce the high stress concentration at the hitch.
- Larger square hollow sections were used for the drawbar.
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Rajasekar, K.; Saravan, R. Literature Review on Chassis Design of On-Road Heavy Vehicles. Int. J. Innov. Sci. Eng. Technol. 2014, 1, 428–433. [Google Scholar]
- Patel, H.; Panchal, K.; Jadav, C. Structural Analysis of Truck Chassis Frame and Design Optimization for Weight Reduction. Int. J. Eng. Adv. Technol. 2013, 2, 665–668. [Google Scholar]
- Ganesan, S.; Panneerselvam, K. Vibration reduction in conventional vehicles by increasing the stiffness on the chassis frame. ARPN J. Eng. Appl. Sci. 2015, 10, 3384–3390. [Google Scholar]
- European Alumimium. Aluminium Automotive Manual. Available online: https://www.european-aluminium.eu/media/1555/aam-applications-chassis-suspension-0-introduction.pdf (accessed on 13 October 2015).
- Gosavi, A.; Shrivastava, A.; Sinha, A. Structural Analysis of Six Axle Trailer Frame Design and Modification for Weight Reduction. Int. J. Emerg. Technol. Adv. Eng. 2014, 4, 523–531. [Google Scholar]
- Dhande, K.; Ulhe, P. Design and Analsysis of Front Axle of Heavy Commercial Vehicle. Int. J. Sci. Technol. Manag. 2014, 3, 114–122. [Google Scholar]
- Thapa, S.B. Trailer Axles - Types and Features. Available online: http://www.selfgrowth.com/articles/trailer-axles-types-and-features (accessed on 13 October 2015).
- Leaf Spring Axles Versus Torsion Axles—Enclosed Cargo Trailers—Trailers 123. 2018. Available online: http://trailers123.com/leaf-spring-axles-versus-torsion-axles (accessed on 13 October 2015).
- Gillespie, T. Fundamentals of Vehicle Dynamics; SAE International: Warrendale, PA, USA, 1992. [Google Scholar]
- Chondros, T.; Michalos, G.; Michaelides, P.; Fainekos, E. An approximate method for the evaluation of the roll stiffness of road tankers. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2007, 221, 1499–1512. [Google Scholar] [CrossRef]
- Winkler, C.; Blower, D.; Chalasani, R.; Ervin, R. Rollover of Heavy Commercial Vehicles; Society of Automotive Engineers: Warrendale, PA, USA, 1999. [Google Scholar]
- Solmaz, S.; Corless, M.; Shorten, R. A methodology for the design of robust rollover prevention controllers for automotive vehicles with active steering. Int. J. Control 2007, 80, 1763–1779. [Google Scholar] [CrossRef]
- Gillespie, T.; Ervin, R. Comparative Study of Vehicle Roll Stability. Phase V. Final Report; University of Michigan, Transportation Research Institute: Ann Arbor, MI, USA, 1983. [Google Scholar]
- Takabatake, D.; Sawada, S.; Yoneyama, N.; Miura, M. Sloshing Reduction Effect of Splitting Wall in Cylindrical Tank. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Ibrahim, R. Liquid Sloshing Dynamics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Azadi, S.; Jafari, A.; Samadian, M. Roll dynamic response of an articulated vehicle carrying liquids. Int. J. Automot. Eng. 2013, 3, 508–522. [Google Scholar]
- Kang, N.; Liu, K. Influence of baffle position on liquid sloshing during braking and turning of a tank truck. J. Zhejiang Univ. Sci. A 2010, 11, 317–324. [Google Scholar] [CrossRef]
- Kandasamy, T. An Analysis of Baffles Designs for Limiting Fluid Slosh in Partly Filled Tank Trucks. Open Transp. J. 2010, 4, 23–32. [Google Scholar] [CrossRef]
- Akyildiz, H. A numerical study of the effects of the vertical baffle on liquid sloshing in two-dimensional rectangular tank. J. Sound Vib. 2012, 331, 41–52. [Google Scholar] [CrossRef]
- Roscommonequipmentcenter.com. Rustproofing Treatments for Steel Water Tanks. 2018. Available online: http://www.roscommonequipmentcenter.com/Project%2011_Rustproofing%20Treatments%20for%20Steel%20Water%20Tanks.pdf (accessed on 23 August 2015).
- U.S. Government. Code of Federal Regulations—Title 49—Transportation; Office of the Federal Register National Archives and Records Administration: Washington, DC, USA, 2012.
- Economic Commission for Europe Inland Transport Committee. European Agreement Concerning the International Carriage of Dangerous Goods by Road (ADR); United Nations Publication: New York, NU, USA, 2016. [Google Scholar]
- Economic Commission for Europe of the United Nations (UN/ECE). Regulation No 111—Uniform Provisions Concerning the Approval of Tank Vehicles of Categories N and O with Regard to Rollover Stability; The Publications Office of the European Union: Luxembourg City, Luxembourg, 2002. [Google Scholar]
- Kutz, M. Environmentally Conscious Mechanical Design; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- BS EN 10025-1:2004. In Hot Rolled Products of Structural Steels. General Technical Delivery Conditions; British Standards Instutitions: London, UK, 2004.
- IS 11270:1985. In Technical Requirements for Ring-Type Hitches for Agricultural Trailers; Bureau of Indian Standards: New Delhi, India, 1985.
- IS 8213:2000. In Agricultural Tractor Trailer—Specification; Bureau of Indian Standards: New Delhi, India, 2000.
- Pillai, N. Principles of Fluid Mechanics and Fluid Machines; Universities Press: Hyderabad, India, 2009. [Google Scholar]
- Meyer, S.; Stahlberg, M.; Schal, S. Braking Deceleration and Starting Acceleration of Modern Agricultural Tractors and Combine Harvester; EVU Conference: Prague, Czech Republic, 2010. [Google Scholar]
- Divergence and Convergence for Simulation Results. 2018. Available online: https://www.3dvision.com/blog/entry/2011/04/22/divergence-and-convergence-for-simulation-results.html (accessed on 31 January 2016).




| Criteria | Weight (%) | Concepts | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Reduced cost (amount of material) | 20 | D | S | − | − | − | − |
| High volume | 25 | A | + | + | + | + | + |
| Ease of manufacturing | 20 | T | + | − | + | − | − |
| Low center of gravity | 20 | U | + | + | + | + | + |
| Ease of maintenance | 5 | M | + | − | + | − | − |
| Safer (fewer sharp edges) | 10 | − | S | S | S | − | S |
| ∑+ | n.a | 70 | 45 | 70 | 45 | 45 | |
| ∑− | n.a | 0 | 45 | 20 | 55 | 45 | |
| ∑S | n.a | 30 | 10 | 10 | 0 | 10 | |
| Criteria | Weight (%) | Concepts | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Reduced cost (amount of material) | 20 | S | D | − | − | − | − |
| High volume | 25 | − | A | + | + | + | + |
| Ease of manufacturing | 20 | − | T | − | − | − | − |
| Low center of gravity | 20 | − | U | + | + | + | + |
| Ease of maintenance | 5 | − | M | − | S | − | − |
| Safer (fewer sharp edges) | 10 | S | − | S | S | − | S |
| ∑+ | 0 | n.a | 45 | 45 | 45 | 45 | |
| ∑− | 70 | n.a | 45 | 40 | 55 | 45 | |
| ∑S | 30 | n.a | 10 | 15 | 0 | 10 | |
| Yield Strength (Re)/MPa | Tensile Strength (Rm)/MPa | Elongation after Fracture (A)/% |
|---|---|---|
| 275 | 410 | 23 |
| Mesh Number | Mesh Size (mm) | Maximum Stress (MPa) | Variation in Stress (%) |
|---|---|---|---|
| 1 | 50 | 151 | - |
| 2 | 40 | 193 | 27.8 |
| 3 | 30 | 240 | 17.1 |
| 4 | 25 | 251 | 4.6 |
| 5 | 20 | 275 | 9.6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seechurn, Y.; Boodhun, R. Optimum Redesign of an Agricultural Water Bowser. Designs 2018, 2, 45. https://doi.org/10.3390/designs2040045
Seechurn Y, Boodhun R. Optimum Redesign of an Agricultural Water Bowser. Designs. 2018; 2(4):45. https://doi.org/10.3390/designs2040045
Chicago/Turabian StyleSeechurn, Yashwantraj, and Ritish Boodhun. 2018. "Optimum Redesign of an Agricultural Water Bowser" Designs 2, no. 4: 45. https://doi.org/10.3390/designs2040045
APA StyleSeechurn, Y., & Boodhun, R. (2018). Optimum Redesign of an Agricultural Water Bowser. Designs, 2(4), 45. https://doi.org/10.3390/designs2040045





