Influencing Parameters on Tire–Pavement Interaction Noise: Review, Experiments, and Design Considerations
Abstract
1. Introduction
2. Driver Influence Parameters
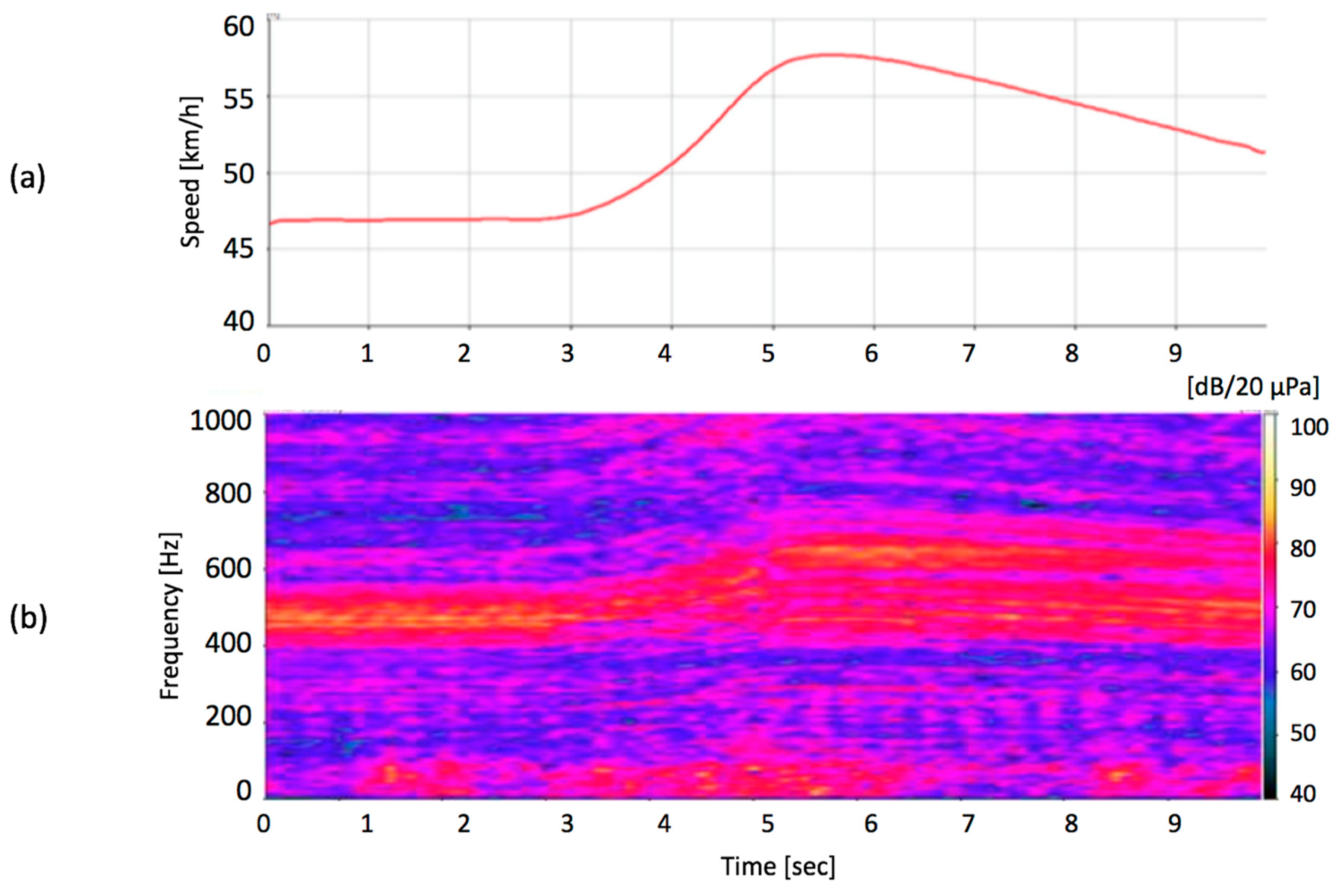
2.1. Speed
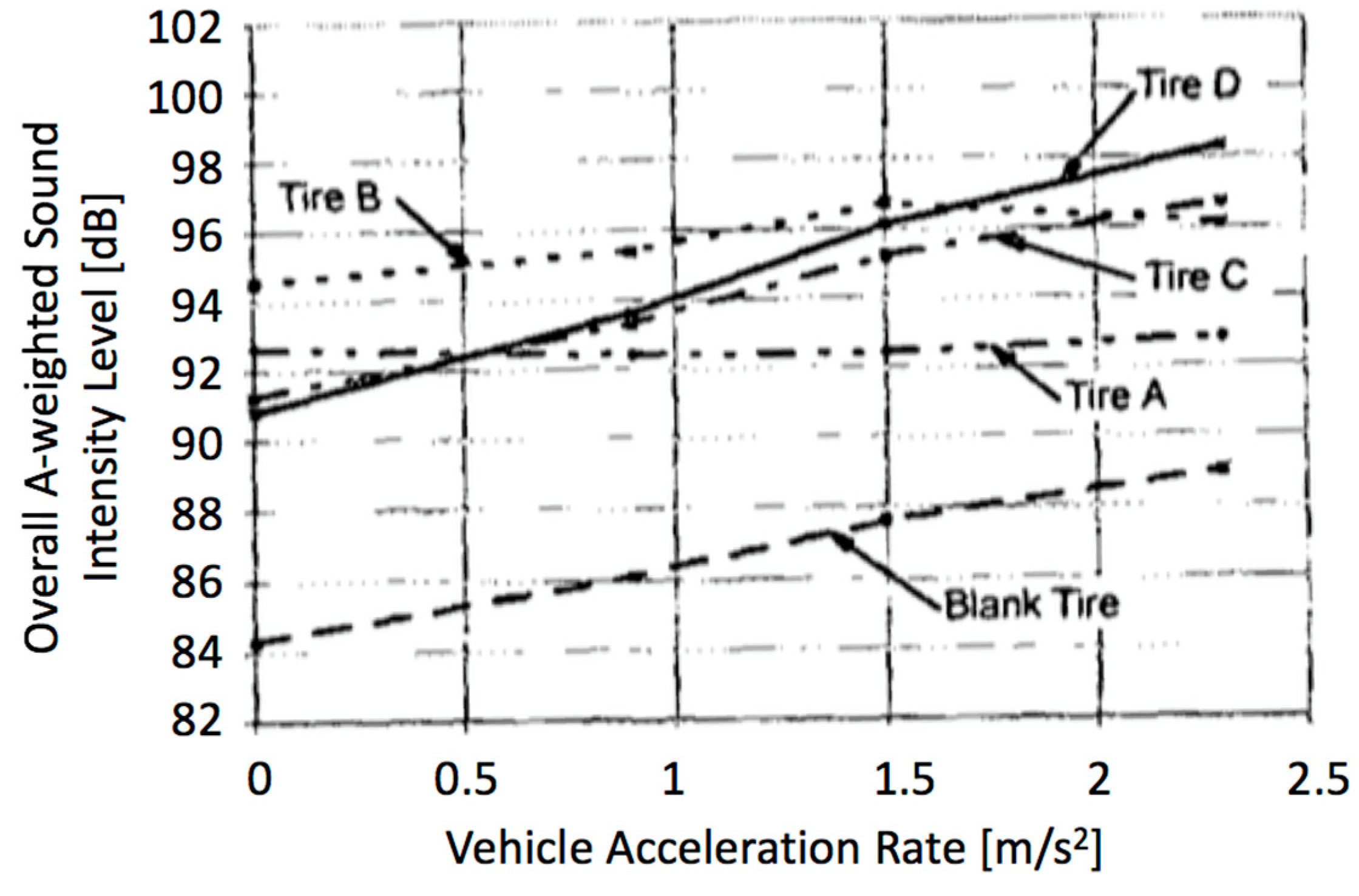
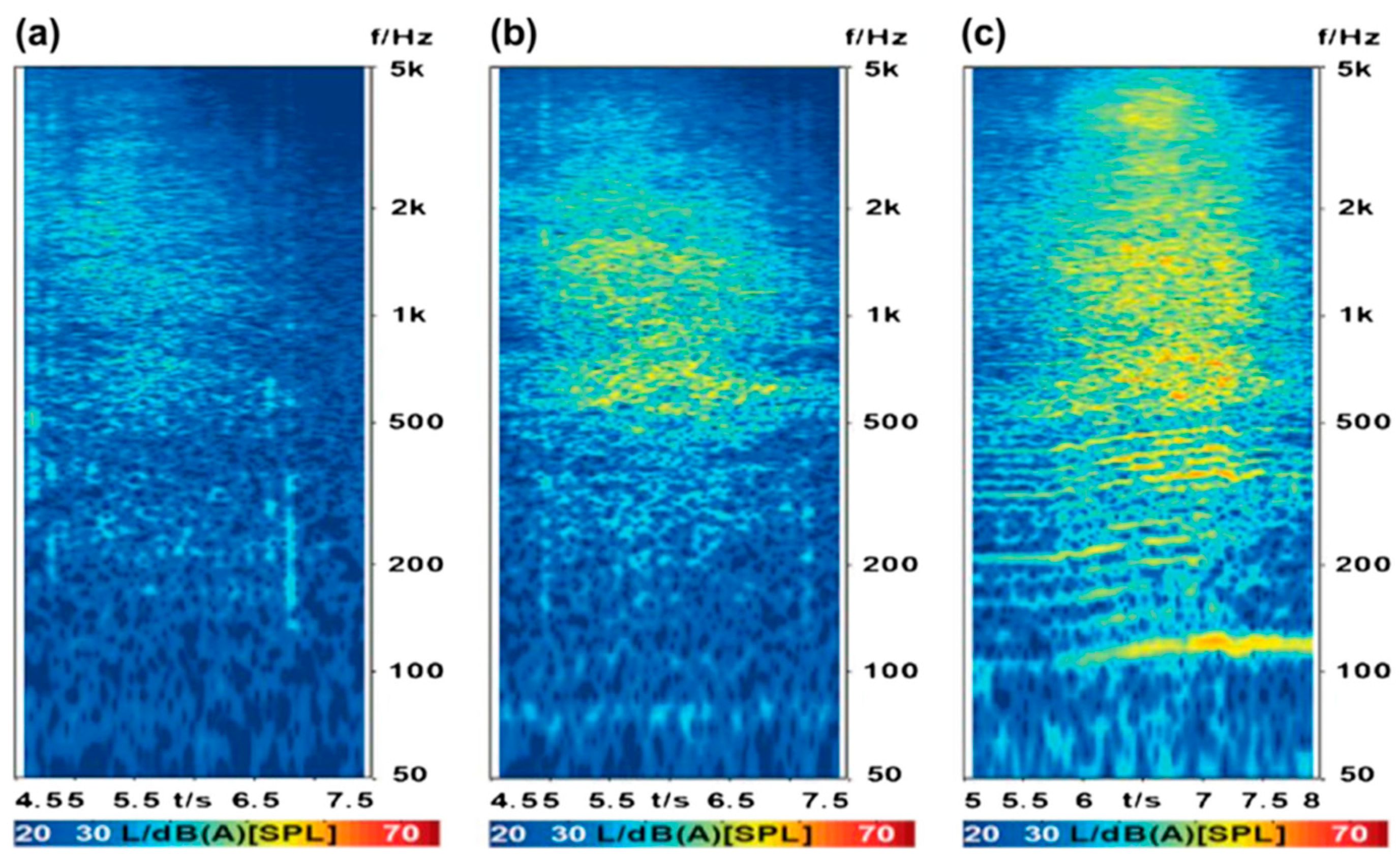
2.2. Longitudinal Force/Slip
2.3. Lateral Force/Slip
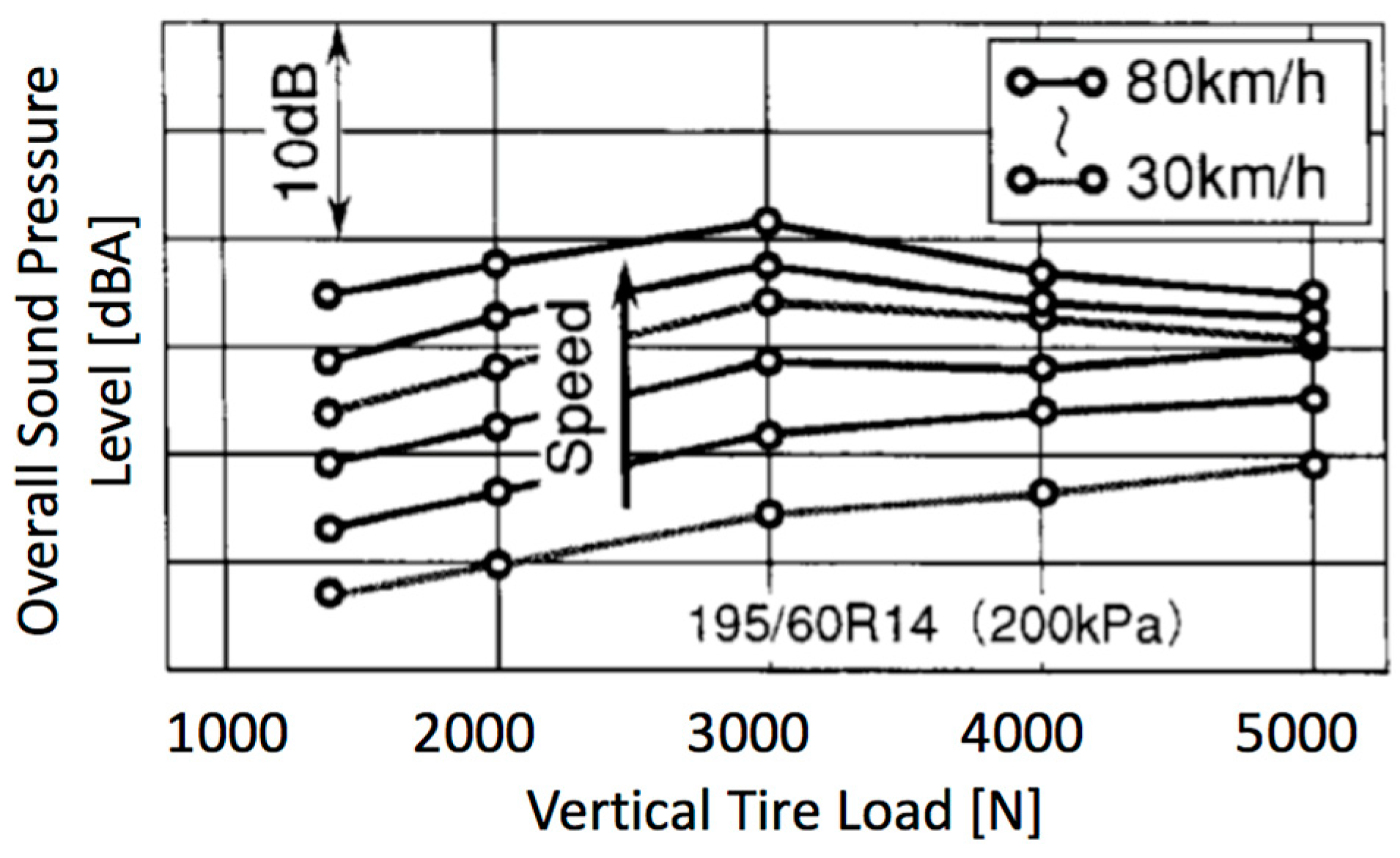
2.4. Tire Load
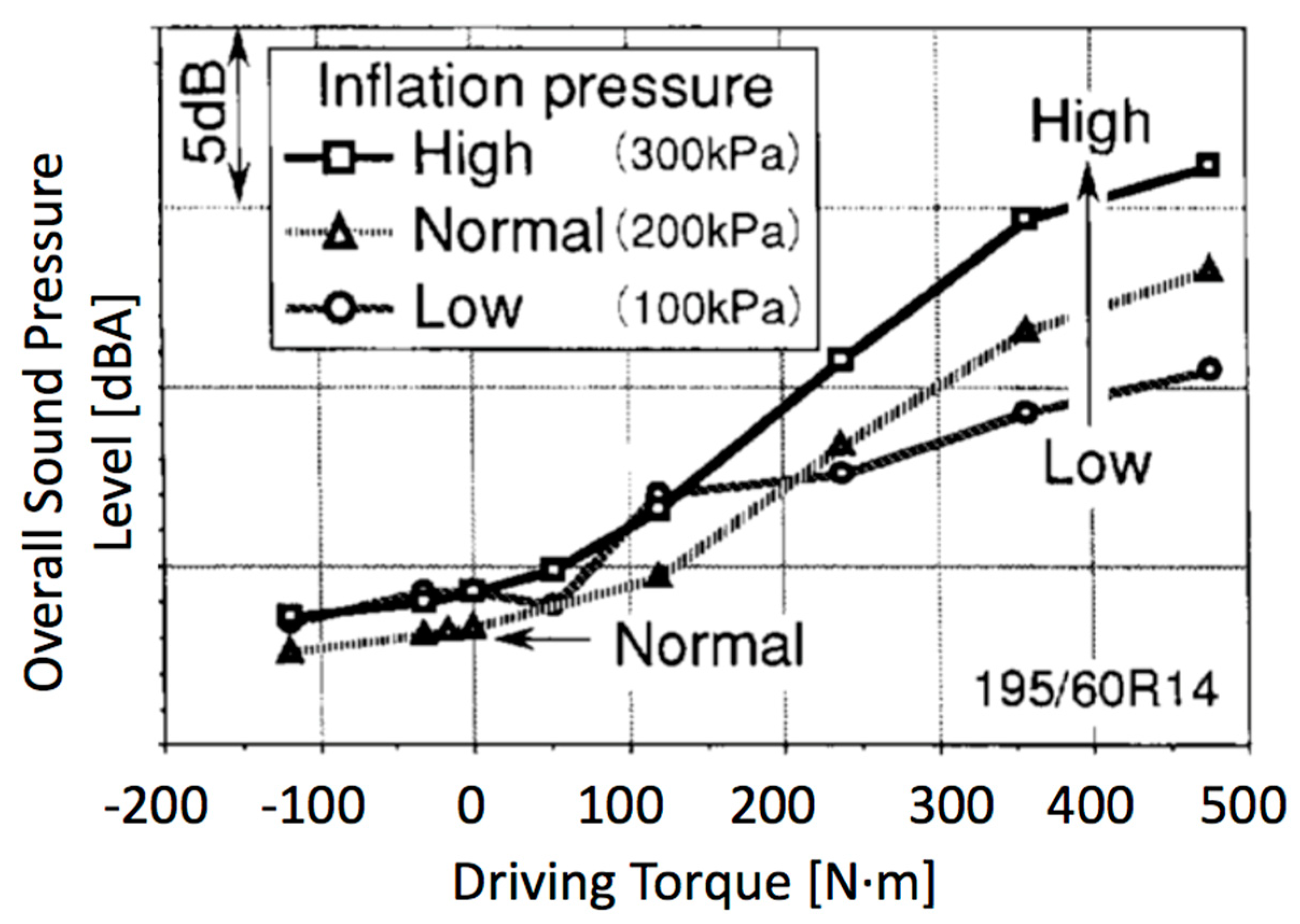
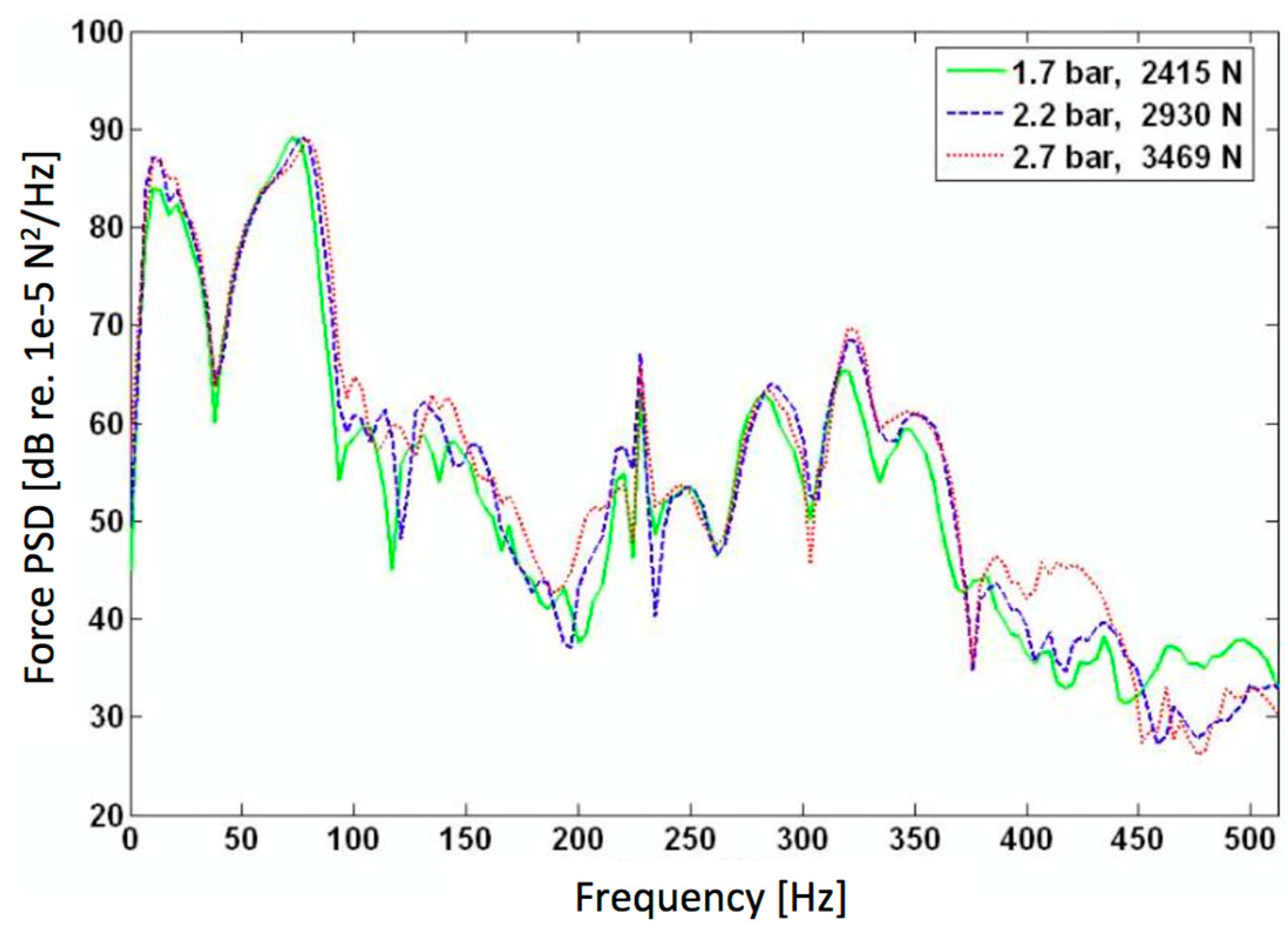
2.5. Inflation Pressure
2.6. Tire Camber Angle
3. Tire Related Parameters
3.1. Tire Type/Construction
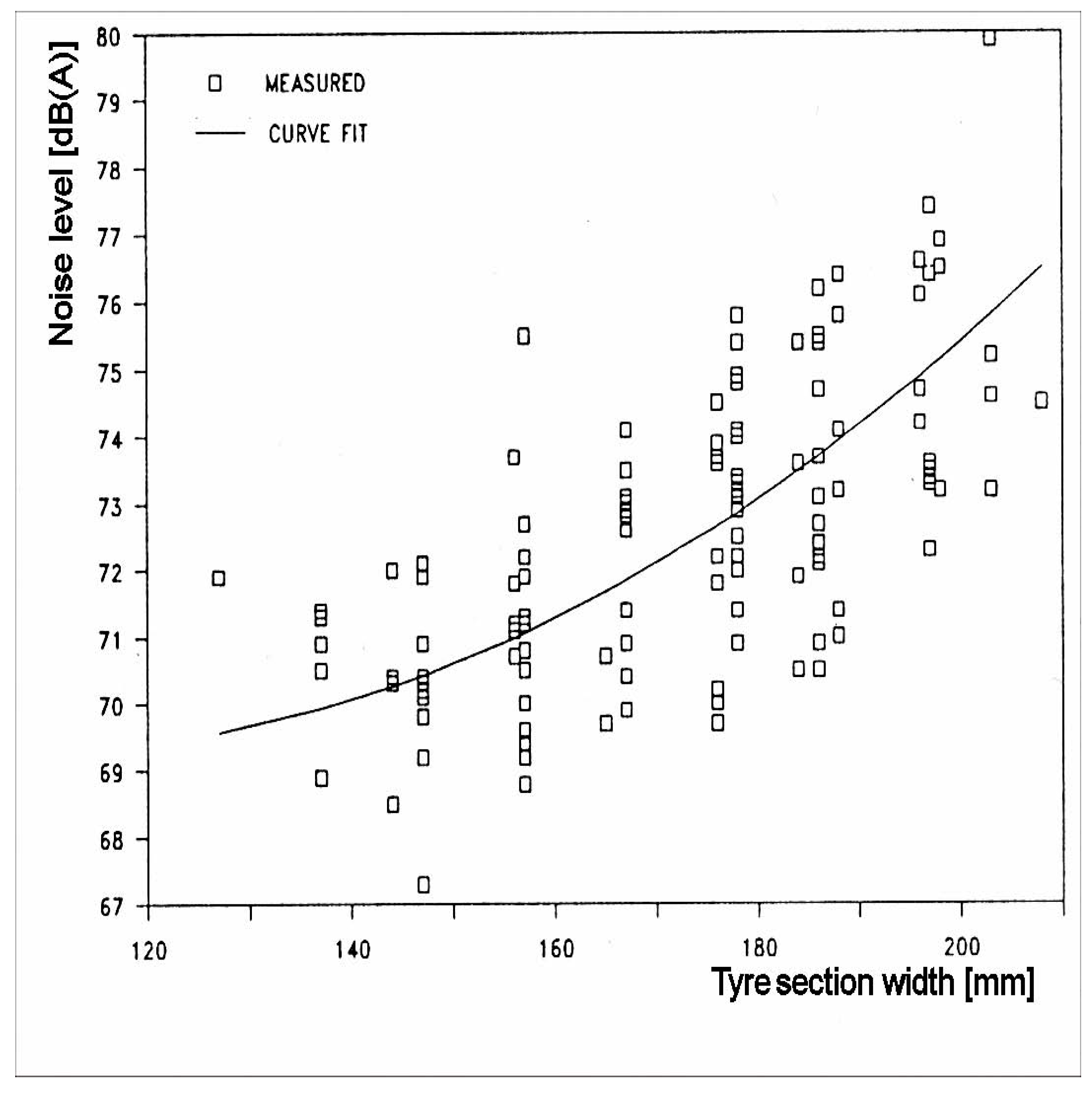
3.2. Tire Size
3.3. Belt Stiffness
3.4. Damping (Loss Factor)
3.5. Non-Uniformity
3.6. Rubber Hardness
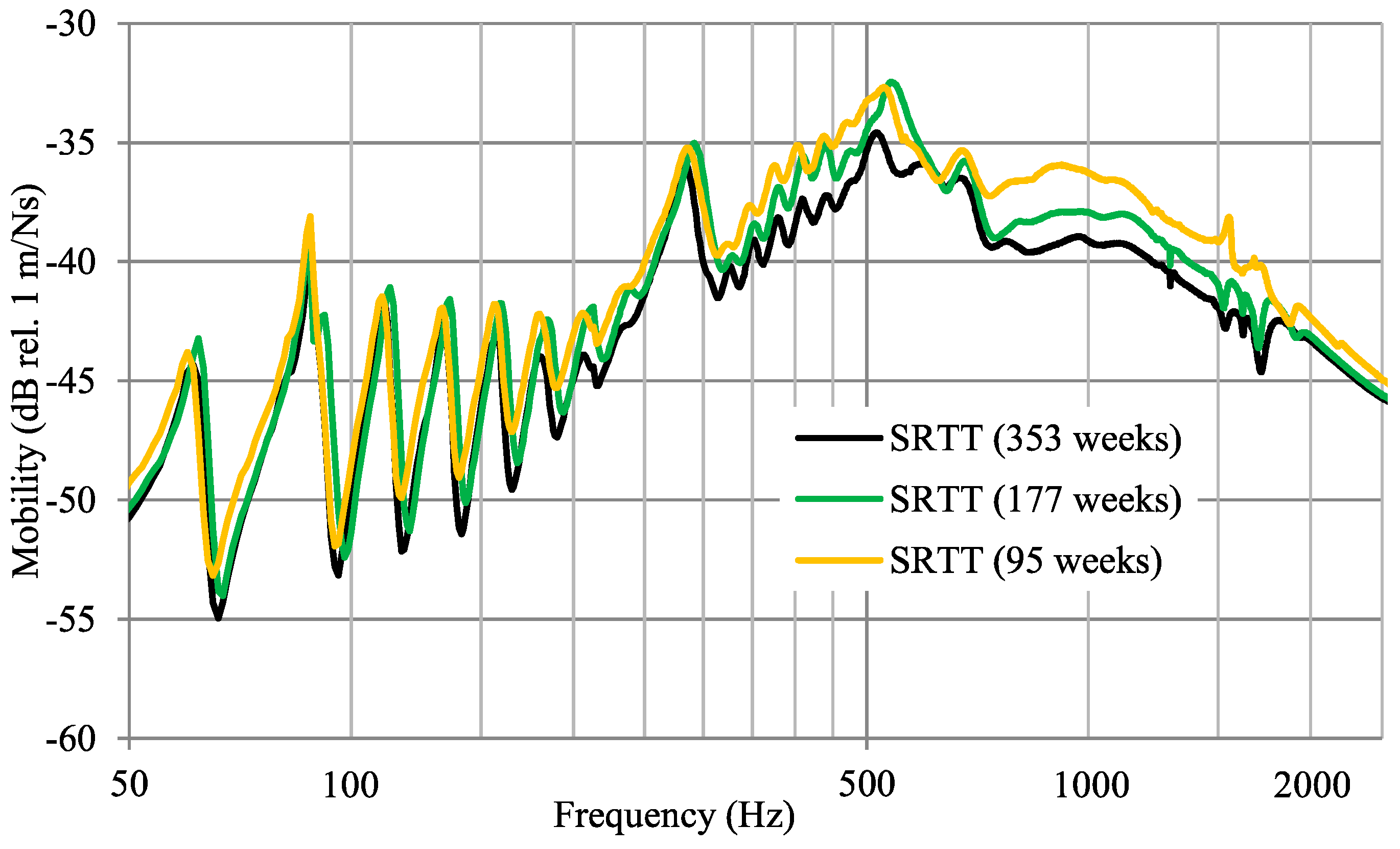
3.7. Wear/Aging
3.8. Retreaded
3.9. Studded
3.10. Tread Porosity
3.11. Tire Cavity Content
3.12. Rolling Resistance
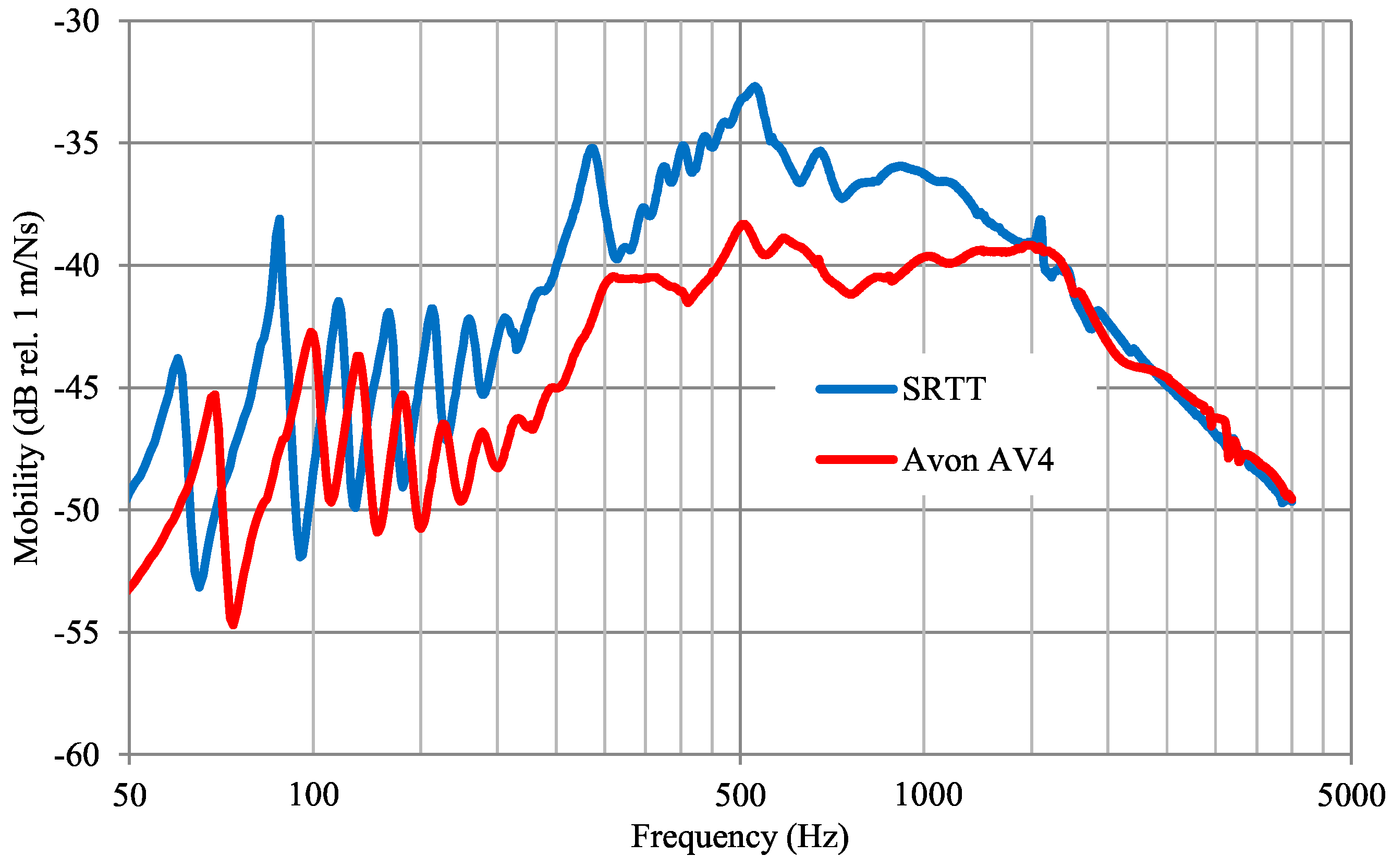
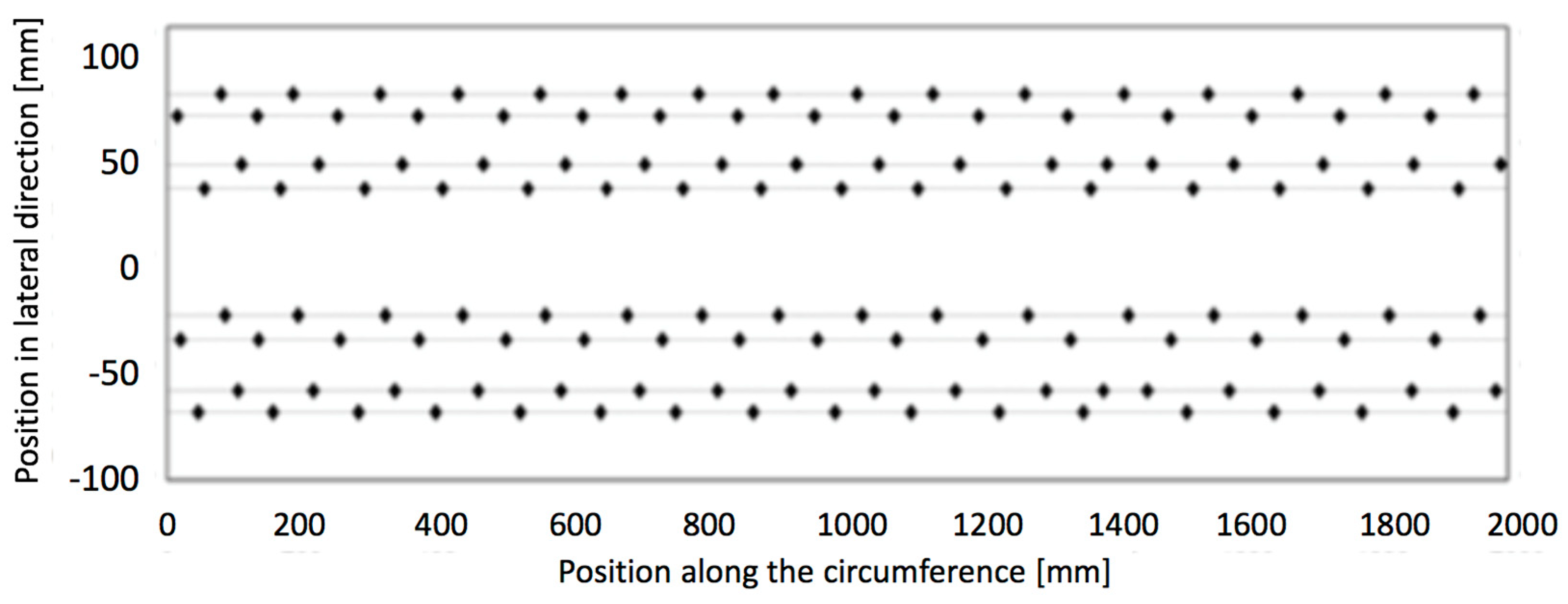
3.13. Reference Tire
4. Tread Pattern Parameters
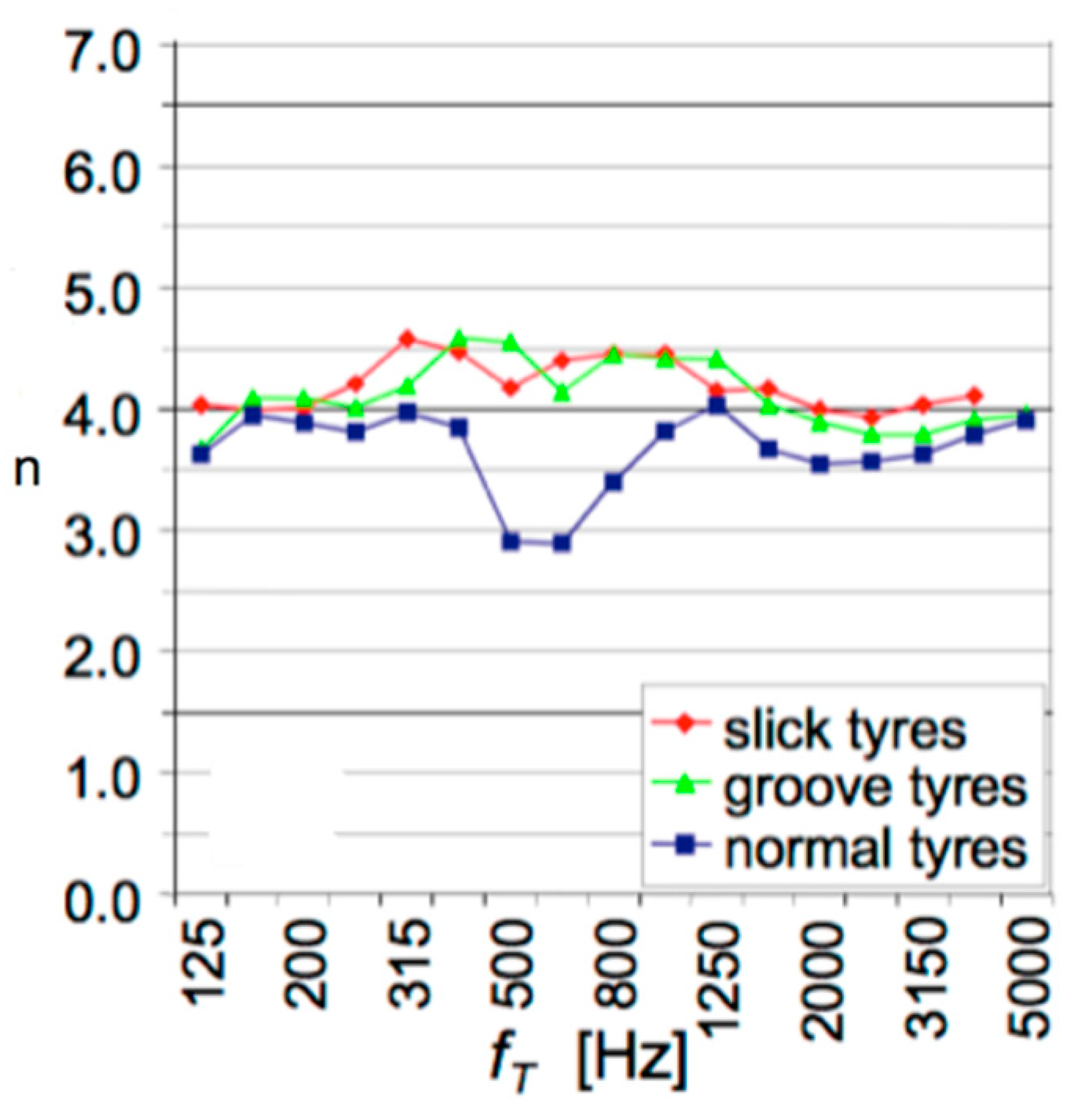
4.1. Randomization
4.2. Rotation Direction/Side Asymmetry
4.3. Ventilation
4.4. Tread Segment
5. Pavement Related Parameters
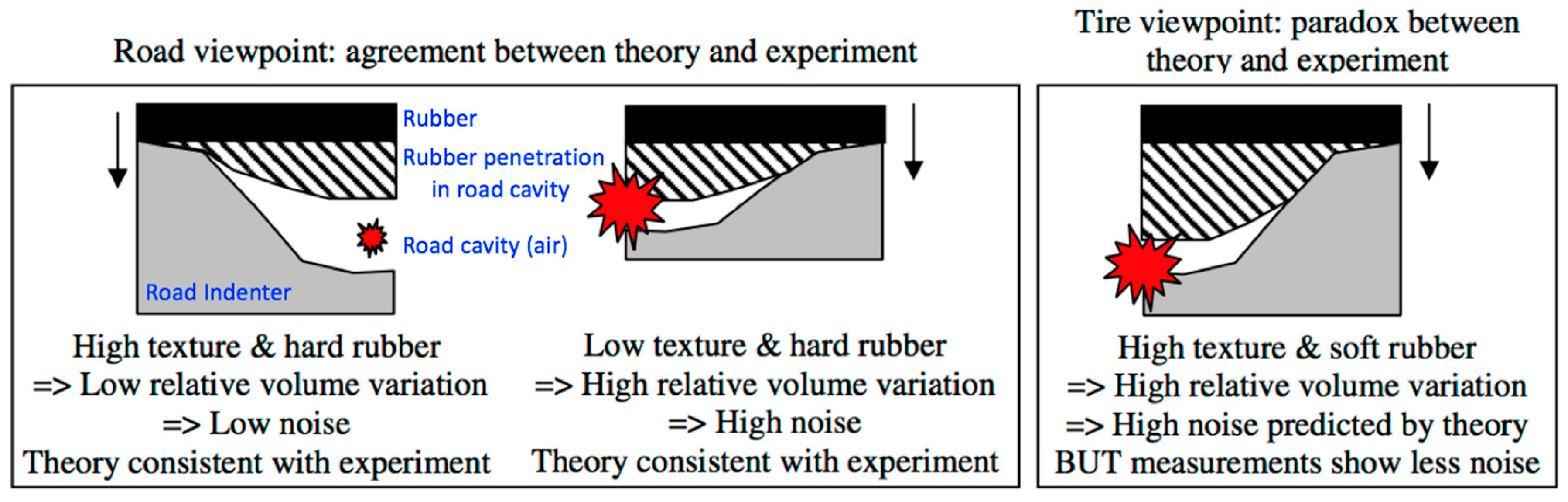
5.1. Texture
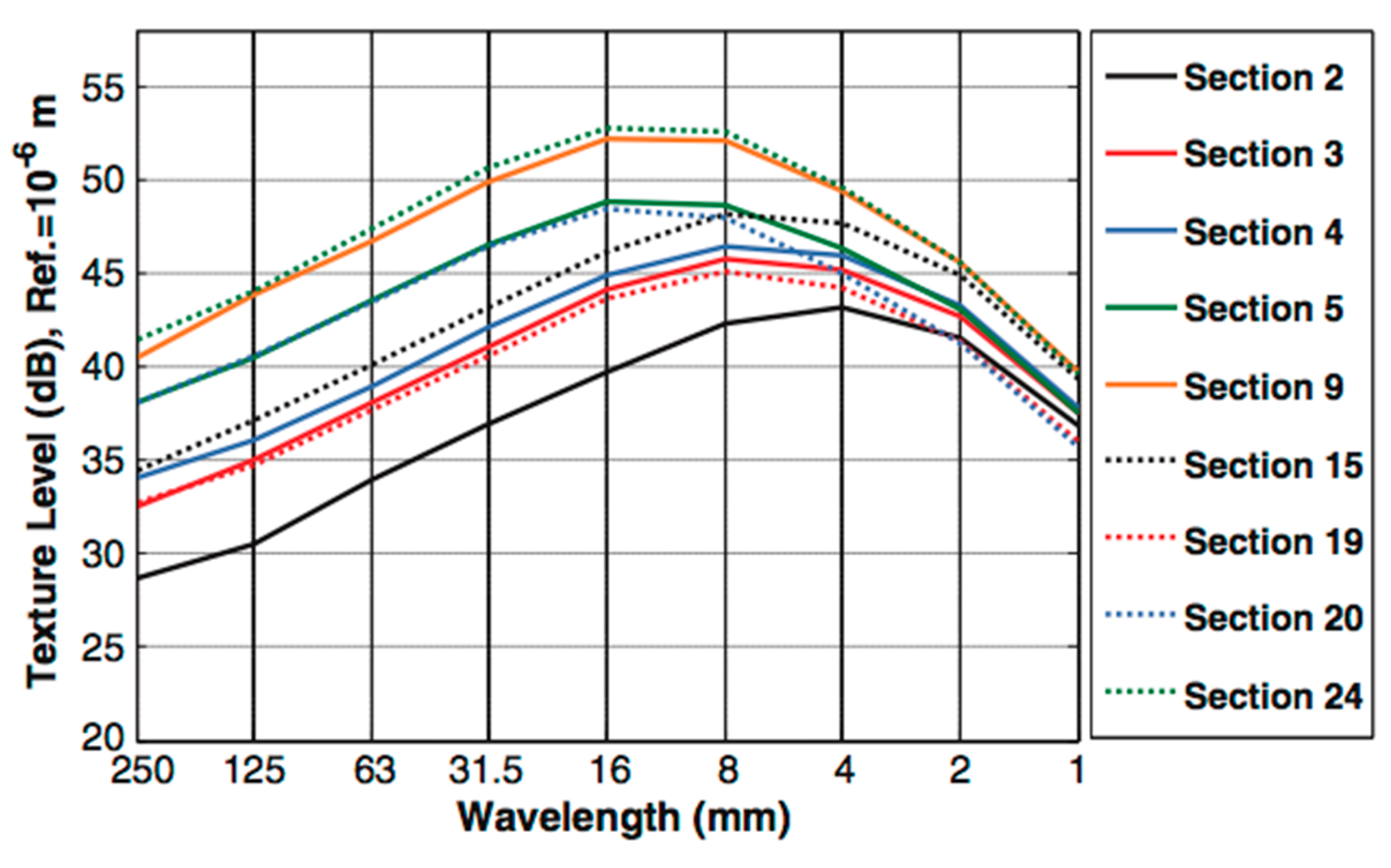
5.1.1. Micro-Texture (below 0.5 mm)
5.1.2. Macro-Texture (0.5–50 mm)
5.1.3. Mega-Texture (50–500 mm)
5.1.4. Unevenness (0.5–50 m)
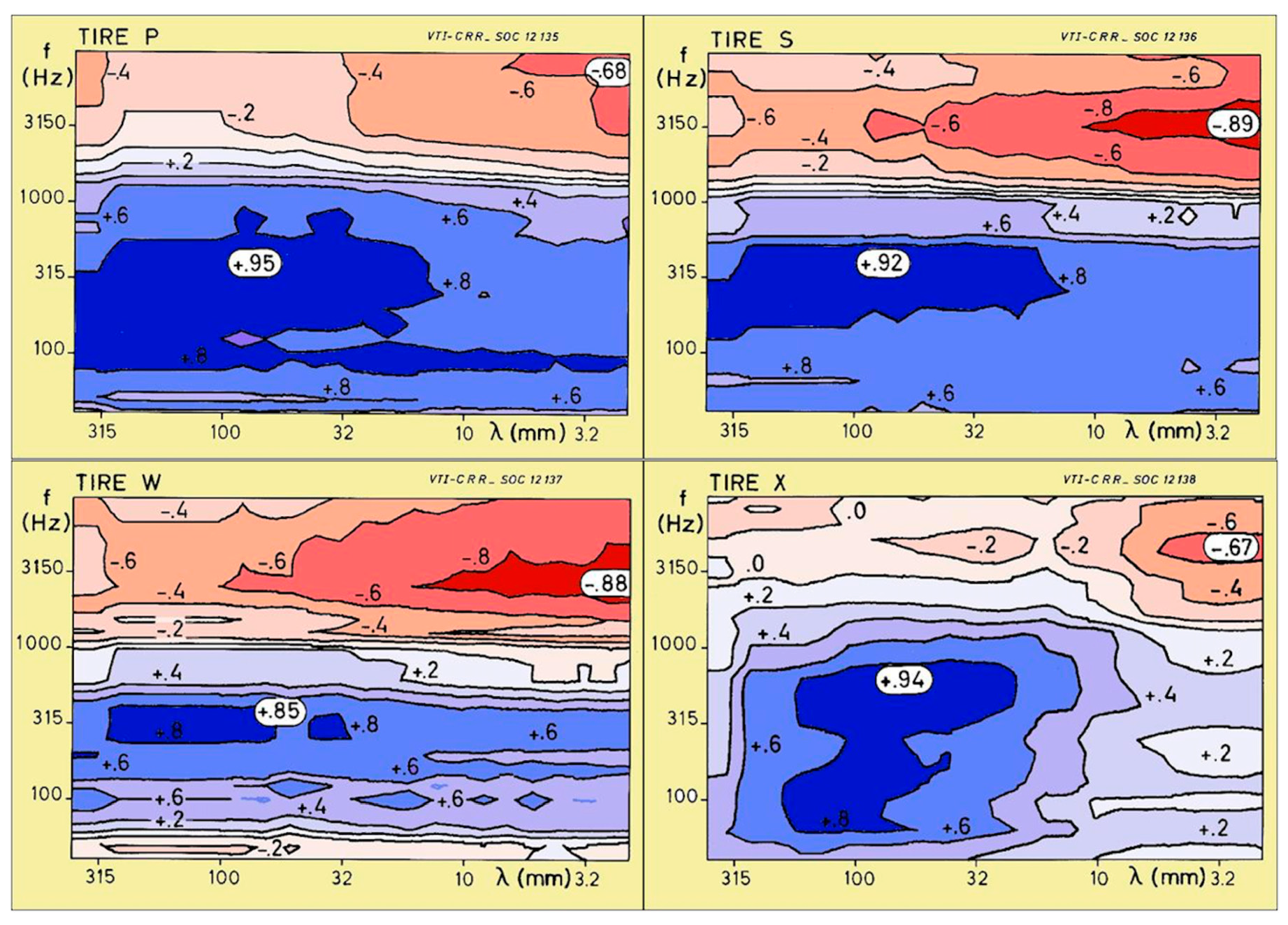
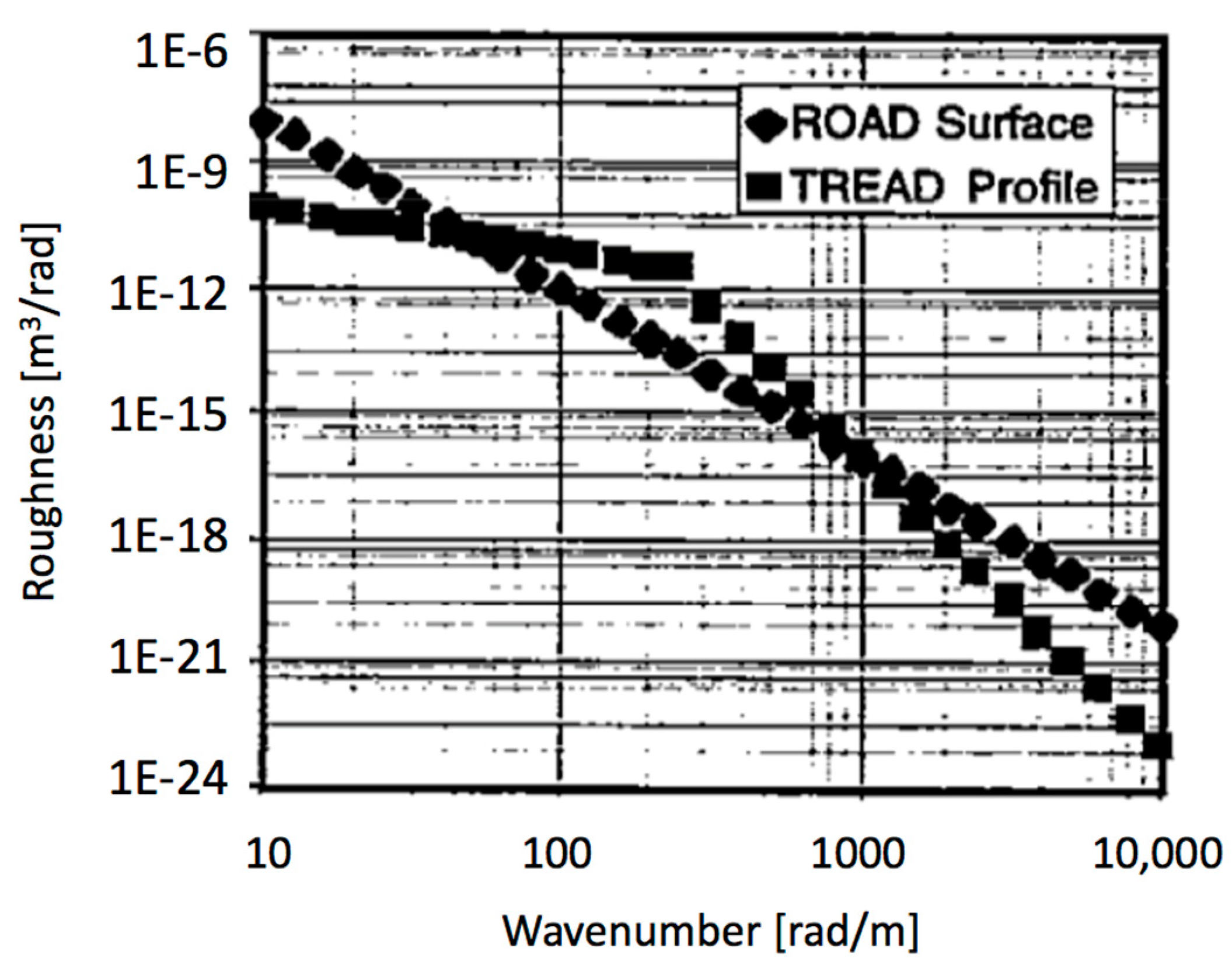
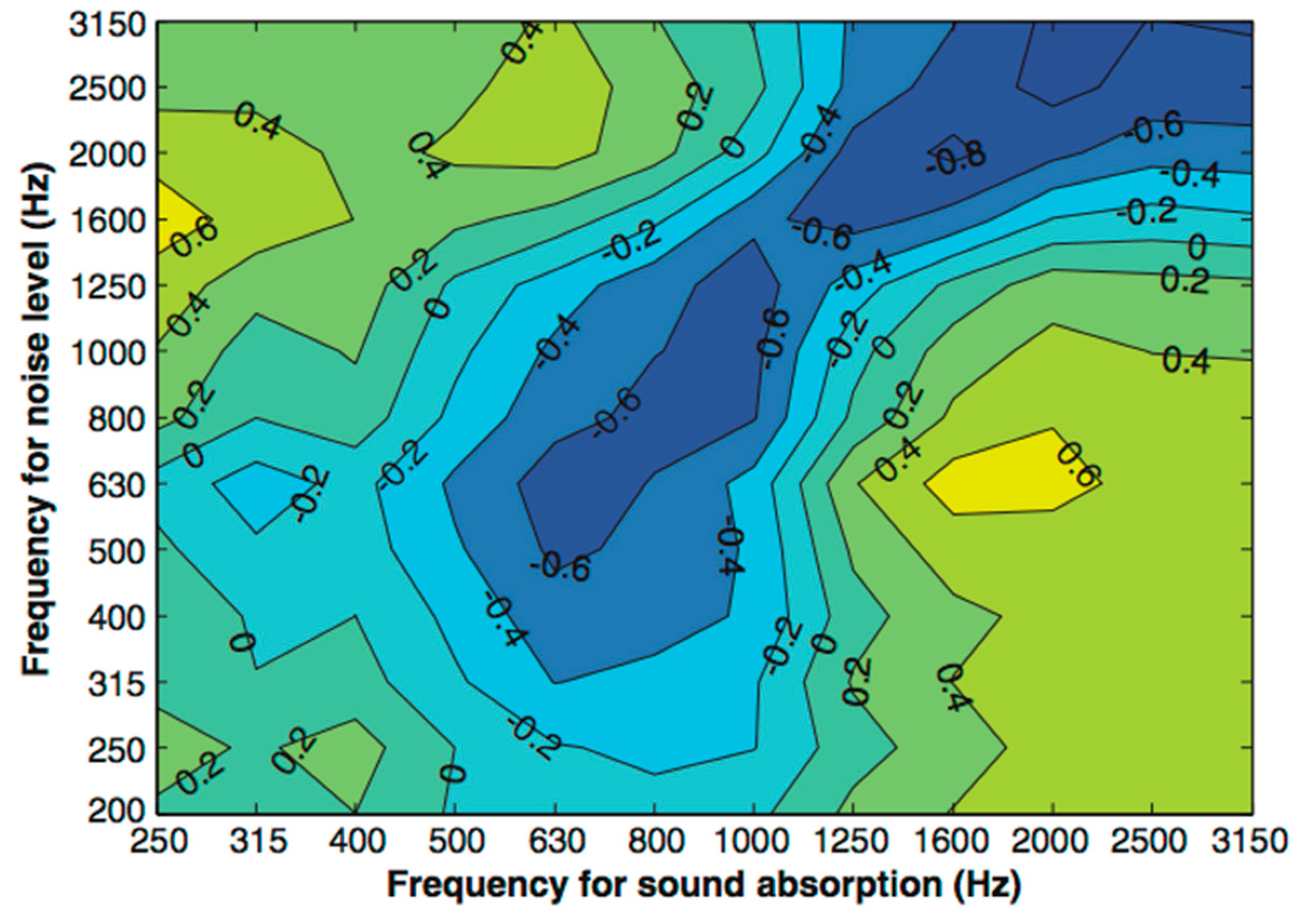
5.2. MPD/MTD/Texture
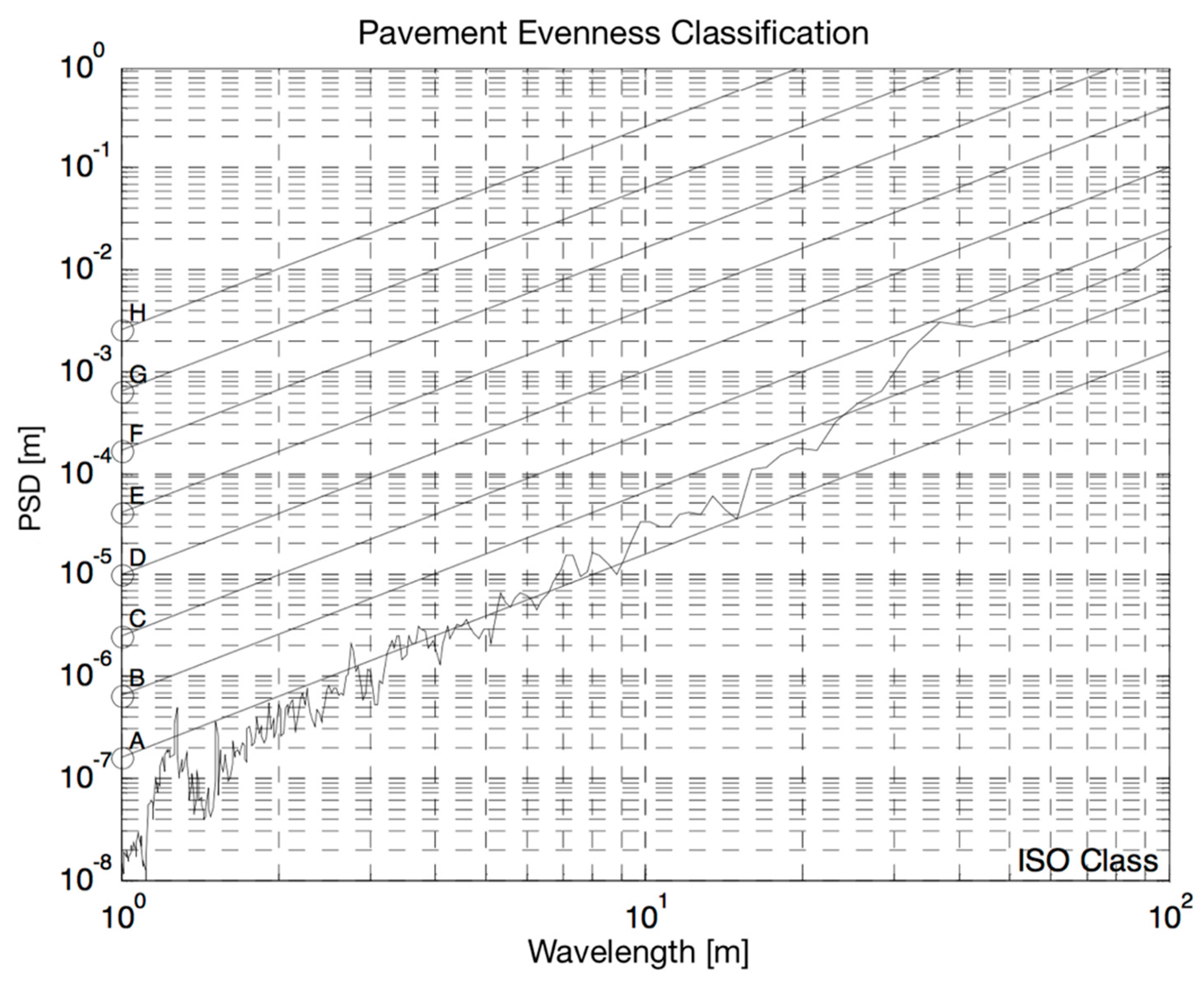
5.3. International Roughness Index (IRI)
5.4. Positive versus Negative Texture
5.5. Transverse Texture
5.6. Anisotropic Texture
5.7. Joints
5.8. Porosity (Air Void Content)
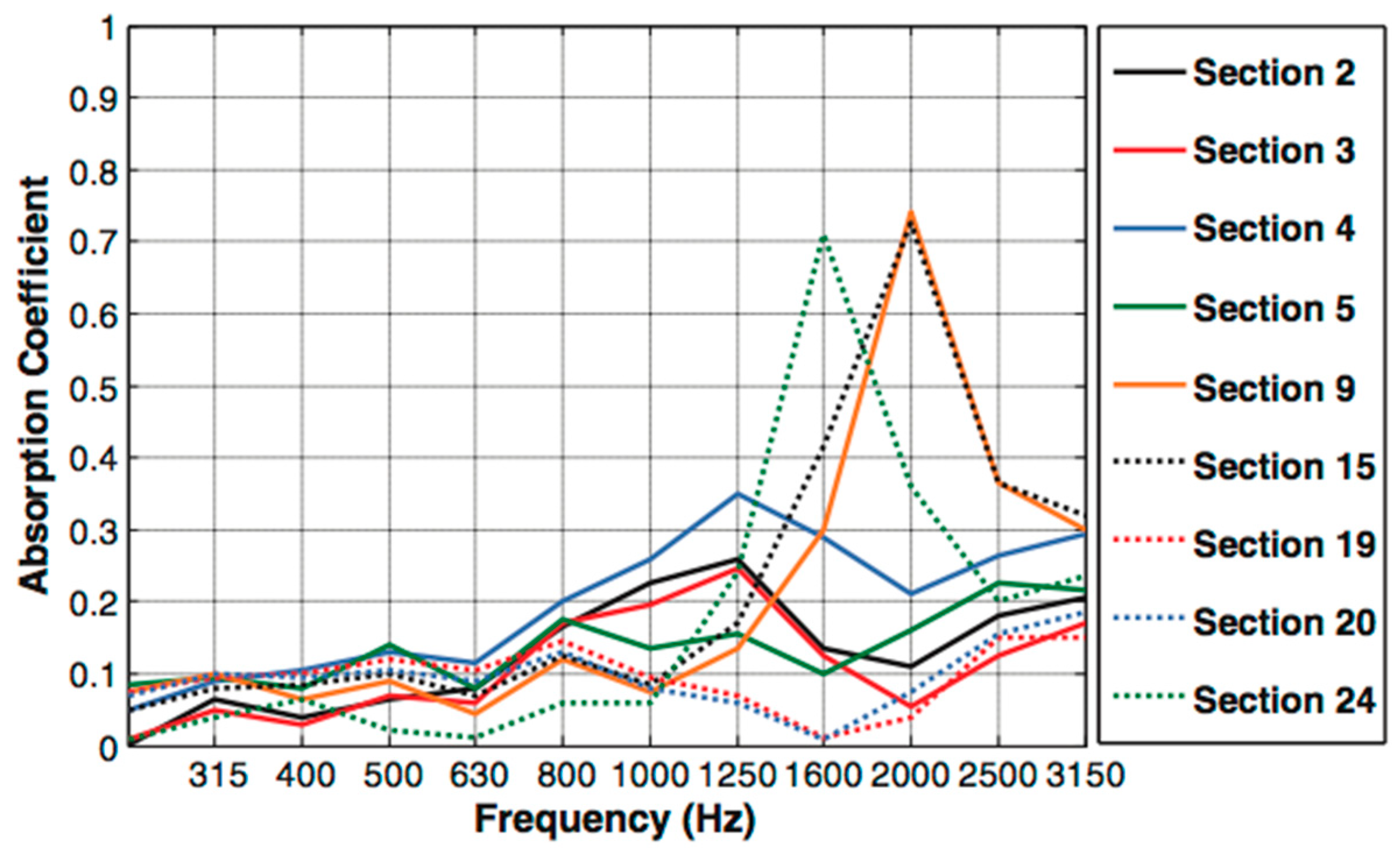
5.9. Sound Absorption
5.10. Airflow Resistance
5.11. Thickness of Layer
5.12. Stiffness (Mechanical Impedance)
5.13. Normal Adhesion
5.14. Tangential Friction
5.15. Wear/Age
5.16. Surface Rating (SR)
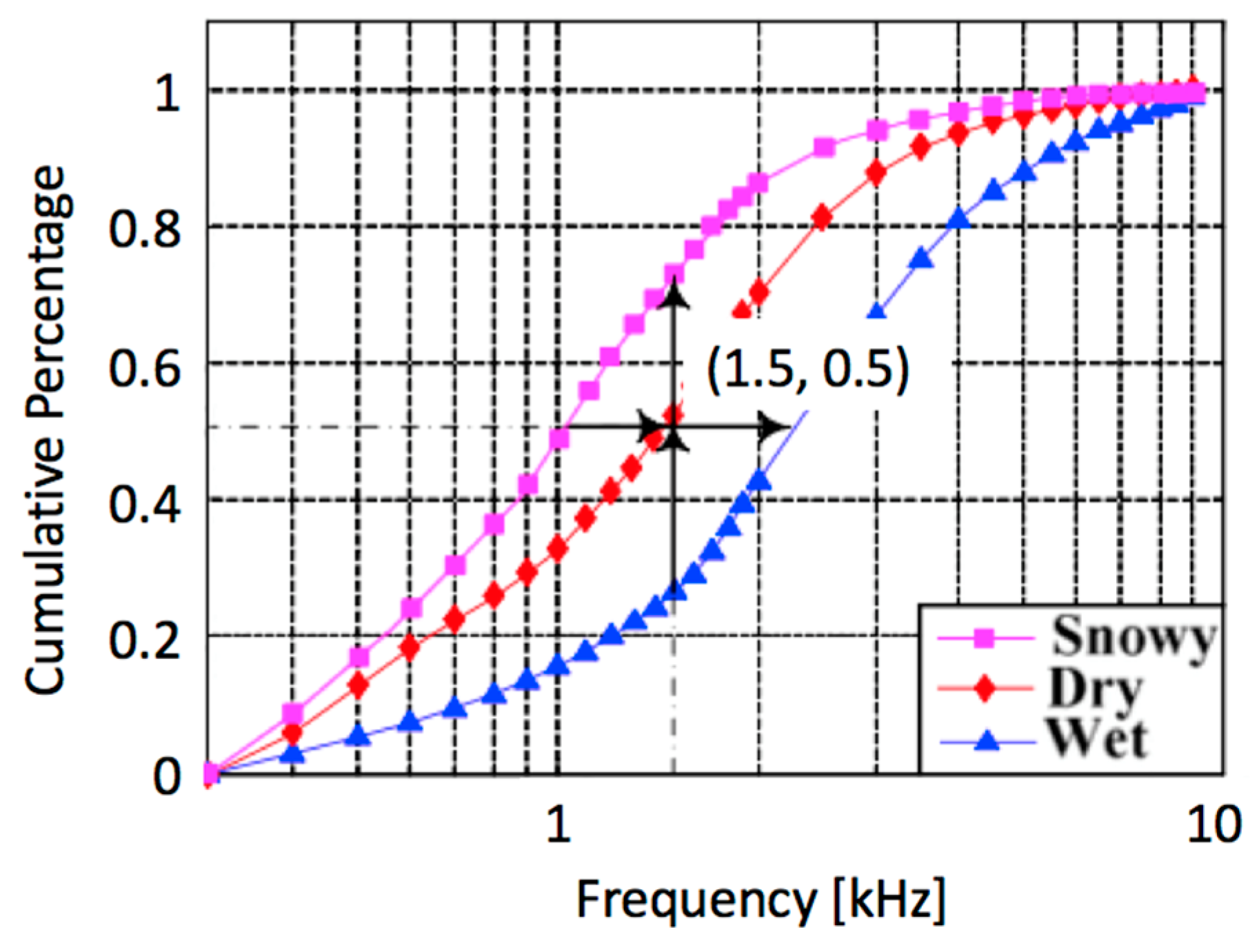
5.17. Wetness
5.18. Mixture Parameters/Materials
5.19. Reference Pavement
6. Environmental Parameters
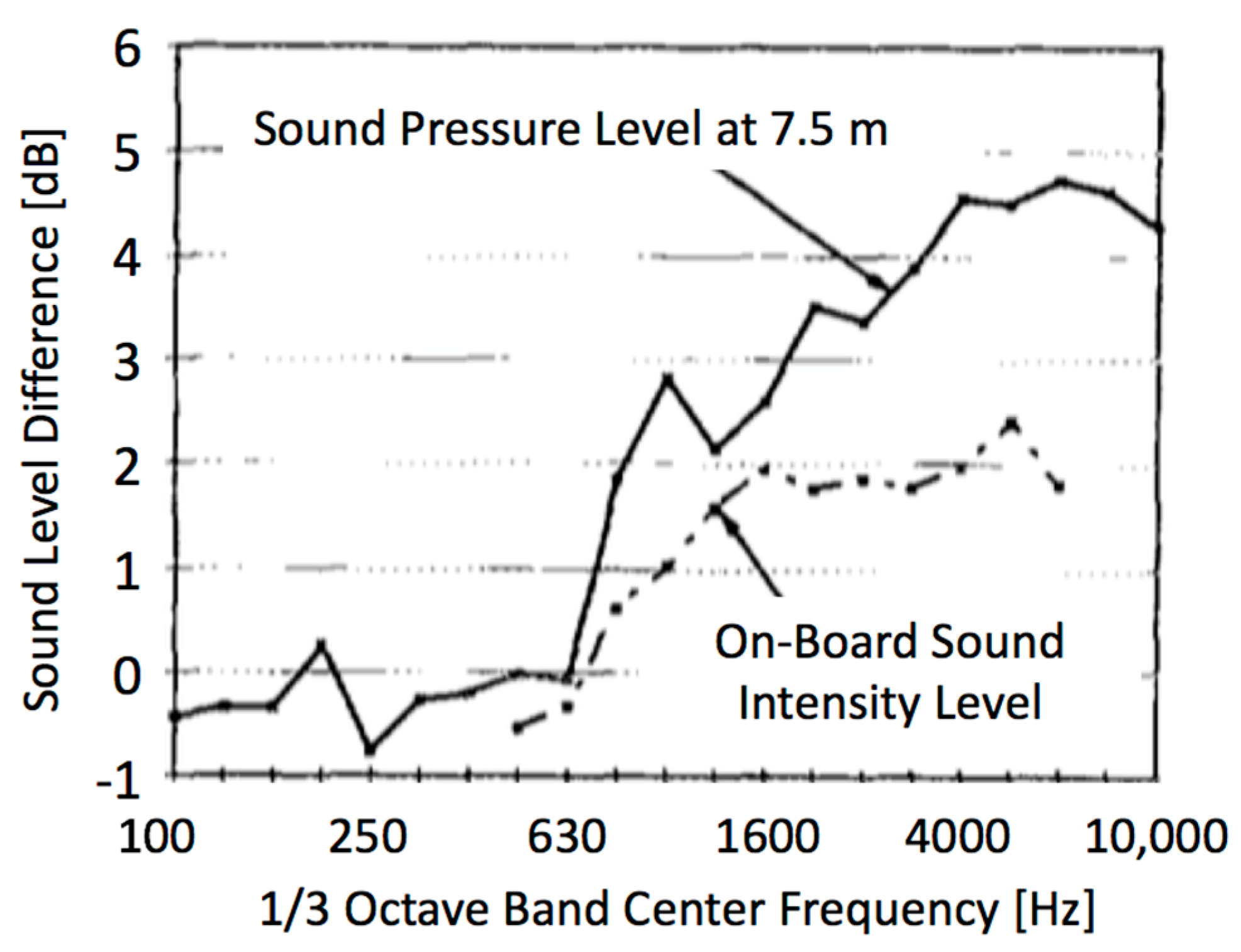
6.1. Temperature
6.2. Air Humidity
6.3. Wind
7. Summary
8. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Sandberg, U.; Ejsmont, J.A. Tyre/Road Noise Reference Book; INFORMEX: Kisa, Sweden; Harg, Sweden, 2002; ISBN 9789163126109, 9163126109. [Google Scholar]
- Li, T.; Burdisso, R.; Sandu, C. Literature review of models on tire-pavement interaction noise. J. Sound Vib. 2018, 420, 357–445. [Google Scholar] [CrossRef]
- Li, T. A state-of-the-art review of measurement techniques on tire–pavement interaction noise. Meas. J. Int. Meas. Confed. 2018, 128, 325–351. [Google Scholar] [CrossRef]
- Li, T. Literature Review of Tire-Pavement Interaction Noise and Reduction Approaches. J. Vibroeng. 2018, 20, 2424–2452. [Google Scholar] [CrossRef]
- Syamkumar, A.; Aditya, K.; Chowdary, V. Development of mode-wise noise prediction models for the noise generated due to tyre-pavement surface interaction. Adv. Mater. Res. 2013, 723, 50–57. [Google Scholar] [CrossRef]
- Sorenson, S.; Jorro, S. Effect of exterior absorption on heavy vehicle tire/surface noise at highway speeds. In Proceedings of the 41st International Congress and Exposition on Noise Control Engineering 2012, INTER-NOISE 2012, New York, NY, USA, 19–22 August 2012; Volume 2, pp. 889–900. [Google Scholar]
- Buckers, C.; Stockert, U. Quiet Road Traffic 3—Interdisciplinary approach to reduce the noise emission at the source. In Proceedings of the European Conference on Noise Control, Prague, Czech Republic, 10–13 June 2012; pp. 984–991. [Google Scholar]
- Biermann, J.-W.; Viehofer, J. Development of cars specified for tire-road noise measurement. In Proceedings of the 41st International Congress and Exposition on Noise Control Engineering 2012, INTER-NOISE 2012, New York, NY, USA, 19–22 August 2012; Volume 11, pp. 9230–9241. [Google Scholar]
- Kim, H. A Study of Wheel Guards for Reduction of High Frequency Road-Noise. SAE Int. J. Passeng. Cars Mech. Syst. 2015, 8, 46–51. [Google Scholar] [CrossRef]
- Li, T.; Feng, J.; Burdisso, R.; Sandu, C. The Effects of Speed on Tire-Pavement Interaction Noise (Tread-Pattern-Related Noise and Non-Tread-Pattern-Related Noise). In Proceedings of the 35th Annual Meeting and Conference on Tire Science and Technology, Akron, OH, USA, 13–14 September 2016. [Google Scholar]
- Sandberg, U. Tyre / road noise—Myths and realities. In Proceedings of the 2001 International Congress and Exhibition on Noise Control Engineering, The Hague, The Netherlands, 27–30 August 2001. [Google Scholar]
- Dare, T.; Bernhard, R. Accelerometer Measurements of Tire Tread Vibrations and Implications to Wheel-Slap Noise. Tire Sci. Technol. 2013, 41, 109–126. [Google Scholar]
- Beckenbauer, T.; Kuijpers, A. Prediction of pass-by levels depending on road surface parameters by means of a hybrid model. In Proceedings of the Inter-Noise, The Hague, The Netherlands, 27–30 August 2001; pp. 2528–2533. [Google Scholar]
- Kuijpers, A.; van Blokland, G. Tyre/road noise models in the last two decades: A critical evaluation. In Proceedings of the Inter-Noise, The Hague, The Netherlands, 27–30 August 2001; p. 2494. [Google Scholar]
- Mogrovejo, D.E.; Flintsch, G.W.; de León Izeppi, E.D.; McGhee, K.K. Effect of Air Temperature and Vehicle Speed on Tire/Pavement Noise Measured with On-Board Sound Intensity Methodology. In Proceedings of the 92nd Annual Meeting on Transportation Research Board (TRB), Washington, DC, USA, 13–17 January 2013. [Google Scholar]
- Ejsmont, J.A. Tire/Road Noise: Comparison of Road and Laboratory Measurements and Influence of Some Tire Parameters on Generation of Sound; VTI Rapport nr 244A; Statens Väg-och Trafikinstitut: Linköping, Sweden, 1982; 47p. [Google Scholar]
- Anderson, D.G.; Landers, S.P. On-board passenger tire sound generation study road versus lab wheel. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 1976. [Google Scholar]
- Nilsson, N.-A. On generating mechanisms for external tire noise. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 1976. [Google Scholar]
- Anonymous. Truck Tire Noise; Rubber Manufacturers Association (RMA): Washington, DC, USA, 1971. [Google Scholar]
- Corcoran, D.A. Effects of operating parameters on truck tire sounds. In SAE Special Publication; SAE SP-373, Paper 720925; SAE International: Warrendale, PA, USA, 1972. [Google Scholar]
- Walker, J.C.; Williams, A.R. The improvement of noise and traction due to road/tire interaction. In Proceedings of the International Tire Noise Conference 1979, Stockholm, Sweden, 29–31 August 1979. [Google Scholar]
- Tetlow, D. Truck Tire Noise—An Initial Survey of Tire Noise Variables; Report; General Motors Proving Ground: Milford, MI, USA, 1968. [Google Scholar]
- Hamet, J.-F. Measurement of power and directivity of tire/road surface noise. In Proceedings of the INTER-NOISE 88, Avignon, France, 30 August–1 September 1988. [Google Scholar]
- Köhler, E.; Liedl, W. Grenzen der Beeinflussungdes Reifenabrollgerausches bei nasser Fahrbahn. In Entwicklungslinien in Kraftfahrzeu-technik und Strassenverkehr, Forschungsbilanz; TUV Rheinland: Cologne, Germany, 1981. [Google Scholar]
- Steven, H.; Pauls, H. Entwicklung Eines Messverfahrens für das Reifen-Fahrbahn-Geräusch; Report from FIGE; FIGE: Herzogenrath, Germany, 1990. [Google Scholar]
- Ivannikov, A.; Haberkorn, U.; Langenberg, H. Einflussgrössen auf Riefen/Fahrbahn-Geräusche eines LKW bei unterschiedlichen Fahrbedingunen; FAT Schriftenreihe Nr. 158; Forschungsvereinigung Automobiltechnik e.v. (FAT): Berlin, Germany, 1998. [Google Scholar]
- Steven, H.; Küppers, D.; van Blokland, G.J.; van Houten, M.H.; van Loon, R. International Validation Test for the Close Proximity (CPX) Method; TÜV: Albstadt, Germany, 2000. [Google Scholar]
- Ho, K.-Y.; Hung, W.-T.; Ng, C.-F.; Lam, Y.-K.; Leung, R.; Kam, E. The effects of road surface and tyre deterioration on tyre/road noise emission. Appl. Acoust. 2013, 74, 921–925. [Google Scholar] [CrossRef]
- Lopez Arteaga, I. Green’s functions for a loaded rolling tyre. Int. J. Solids Struct. 2011, 48, 3462–3470. [Google Scholar] [CrossRef]
- Kim, Y.J.; Bolton, J.S. Effects of rotation on the dynamics of a circular cylindrical shell with application to tire vibration. J. Sound Vib. 2004, 275, 605–621. [Google Scholar] [CrossRef]
- Huang, S.C.; Soedel, W. Effects of coriolis acceleration on the free and forced in-plane vibrations of rotating rings on elastic foundation. J. Sound Vib. 1987, 115, 253–274. [Google Scholar] [CrossRef]
- Huang, S.C.; Soedel, W. Effects of Coriolis acceleration on the forced vibration of rotating cylindrical shells. J. Appl. Mech. 1988, 55, 231–233. [Google Scholar] [CrossRef]
- Schuhmacher, A. Blind Source Separation Applied to Indoor Vehicle Pass-By Measurements. SAE Int. J. Passeng. Cars Mech. Syst. 2015, 8, 1034–1041. [Google Scholar] [CrossRef]
- Ulrich, S. Rollgeräuschmessungen der Bundesanstalt für Strassenwesen an Strassen mit unterschiedlichen Decken und an einem Innentrommelprüfstand (Rolling Noise Measurements of the Federal Highway Research Institute on Roads with Different Ceilings and an Indoor Drum); Mitteilung Nr. 57; Institut für Strassen- und Eisenbahn- und Felsbau and der E.T.H.: Zürich, Switzerland, 1984; p. 207. [Google Scholar]
- Donavan, P.R. Tire-Pavement Interaction Noise Measurement under Vehicle Operating Conditions of Cruise and Acceleration. In Proceedings of the Noise and Vibration Conference, Traverse City, MI, USA, 10–13 May 1993; Society of Automotive Engineers: Warrendale, PA, USA, 1993. [Google Scholar]
- Iwao, K.; Yamazaki, I. A study on the mechanism of tire/road noise. JSAE Rev. 1996, 17, 139–144. [Google Scholar] [CrossRef]
- ISO. Measurement of Noise Emitted by Accelerating Road Vehicles—Engineering Method—Part 1: M and N Categories; ISO 362-1; ISO: Geneva, Switzerland, 2015. [Google Scholar]
- Moore, D.B. The Revised ISO 362 Standard for Vehicle Exterior Noise Measurement. Sound Vib. 2006, 40, 19–23. [Google Scholar]
- Donavan, P.R. Assessment of tire/pavement interaction noise under vehicle passby test conditions using sound intensity measurement methods. J. Acoust. Soc. Am. 1998, 103, 2919. [Google Scholar] [CrossRef]
- Yamazaki, S.; Fujikawa, T.; Hosegawa, A.; Ogasawara, S. Indoor test procedure for evaluation of tire treadwear and influence of suspension alignment. Tire Sci. Technol. 1989, 17, 236–273. [Google Scholar] [CrossRef]
- Ejsmont, J.A. Tire/road noise and rolling resistance - is there a trade-off? In Proceedings of the International Tire/Road Noise Conference 1990, Gothenburg, Sweden, 8–10 August 1990; pp. 439–452. [Google Scholar]
- Donavan, P.R. Quantification of Noise Mechanisms for a Straight-Ribbed, HCR Bias-Ply Truck Tire; Report No. EM-547; General Motors Research Laboratories: Warren, MI, USA, 1982. [Google Scholar]
- Senda, T.; Nakai, M.; Yokoi, M.; Chiba, Y. Tire squeal. Bull. Jpn. Soc. Mech. Eng. (Japan) 1984, 27, 2016–2023. [Google Scholar] [CrossRef]
- Trivisonno, N.M.; Beatty, J.R.; Miller, R.F. Origin of tire squeal—2. Rubber Chem. Technol. 1968, 41, 953–976. [Google Scholar] [CrossRef]
- Reiter, W.F.; Eberhardt, A.C. Experimental investigation of truck tire noise generated through tire vibration. In Proceedings of the INTER-NOISE 74, Washington, DC, USA, 30 September–2 October 1974; p. 467. [Google Scholar]
- Dare, T.P. Generation Mechanisms of Tire-Pavement Noise. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2012. [Google Scholar]
- Taryma, J.A.E.S. Halas Opon Samochodow Osobowych Poruszajacych Sie Posuchych Nawierzchniach Asfaltowych I Betonowych (Tire Noise of Cars Moving on the Dry Surfaces of Asphalt and Concrete). Ph.D Thesis, Technical University of Gdansk, Gdansk, Poland, 1982. (In Polish). [Google Scholar]
- Leasure, W.A., Jr.; Bender, E.K. Tire-road interaction noise. J. Acoust. Soc. Am. 1975, 58, 39–50. [Google Scholar] [CrossRef]
- Sandberg, U.; Kropp, W.; Larsson, K. The multi-coincidence peak around 1kHz in tyre/road noise spectra. Acta Acust. United Acust. 2003, 89, S84. [Google Scholar]
- Tong, G.; Wang, Q.; Yang, K.; Wang, X.C. An experiment investigation to the radial tire noise. Adv. Mater. Res. 2013, 694–697, 361–365. [Google Scholar] [CrossRef]
- Leasure, W.A.; Corley, D.M.; Flynn, D.R.; Forrer, J.S. Truck Noise—I. Peak A-Weighted Sound Levels Due to Truck Tires; Report No. OST/TST-72-1; National Bureau of Standards, Building Research Division: Washington, DC, USA, 1972. [Google Scholar]
- Kilmer, R.D. Test Procedures for Future Tire Noise Regulations. In Proceedings of the P-70, SAE Highway Tire Noise Symposium, San Francisco, CA, USA, 10–12 November 1976; Society of Automotive Engineers: Warrendale, PA, USA, 1976. 6p. [Google Scholar]
- Kilmer, R.D.; Cadoff, M.A.; Mathews, D.E.; Shoemaker, C.O. Effects of Load, Inflation Pressure and Tire Deflection on Truck Tire Noise Levels; DOT-HS-803 874; US Department of Transportation: Washington, DC, USA, 1979; 49p. [Google Scholar]
- Underwood, M.C.P. THe Origins of Tire Noise; University of Southampton, Institute of Sound and Vibration Research: Southampton, UK, 1980. [Google Scholar]
- Nelson, P.M.; Underwood, M.C.P.; Nelson, P.M. Lorry Tire Noise. In Proceedings of the Vehicle Noise and Vibration, London, UK, 5–7 June 1984; 50p. [Google Scholar]
- Walker, J.C. Noise Generated at the Tire-Road Interface. Ph.D. Thesis, TD 1292, Dunlop Ltd., Birmingham, UK, 1981. [Google Scholar]
- Köllman, A. Ermittlung des Standes der Technik hinsichtlich der Geräuschemission von PKW-Reifen; Research Report 105 05 144; FIGE GmbH: Herzogenrath, Germany, 1993. [Google Scholar]
- Wolf, A.; Schuh, B.-M.; Krauss, O. Erfassung des Wissenstandes über Reifen/Fahrbahngeräusche beim Nutzfahrzeug; FAT Schriftenreihe Nr. 97; Forschungsvereinigung Automobiltechnik e.v. (FAT): Frankfurt, Germany, 1992. [Google Scholar]
- Von Meier, A.; van Bloklan, G.J.; Descornet, G. The influence of texture and sound absorption on the noise of porous road surfaces. In Proceedings of the of the Second International Symposium of Road Surface Characteristics, Technical University of Berlin, Berlin, Germany, 23–26 June 1992. [Google Scholar]
- Heckl, M. Tire noise generation. Wear 1986, 113, 157–170. [Google Scholar] [CrossRef]
- Bharadwaja, B.V.S.S.; Siva, P.N. A Numerical Study on the Influencing Parameters of Tire-acoustic Cavity. Appl. Mech. Mater. 2013, 459, 390–395. [Google Scholar] [CrossRef]
- Beniguel, J.F.; Le Pen, D. Tire-alone criterion for structure borne road noise performance. In Proceedings of the International Conference on Noise and Vibration Engineering 2012 (ISMA 2012), Leuven, Belgium, 17–19 September 2012; Volum 2, pp. 1527–1539. [Google Scholar]
- Kropp, W.; Larsson, K.; Wullens, F.; Andersson, P.; Becot, F.-X.; Beckenbauer, T. The modeling of tyre/road noise—A quasi three-dimensional model. In Proceedings of the INTER-NOISE 01, The Hague, Holland, 27–30 August 2001; p. 2322. [Google Scholar]
- Keltie, R.F. Analytical model of the truck tire vibration sound mechanism. J. Acoust. Soc. Am. 1982, 71, 359. [Google Scholar] [CrossRef]
- Tong, G.; Jin, X.; Tian, W.; Yang, K. Simulation on factors affecting radial tire noise. J. Converg. Inf. Technol. (Korea) 2013, 8, 209–216. [Google Scholar]
- Bolton, J.S.; Song, H.J.; Kim, Y.K.; Kang, Y.J. Wave number decomposition approach to the analysis of tire vibration. In Proceedings of the National Conference on Noise Control Engineering, Ypsilanti, MI, USA, 5–8 April 1998; pp. 97–102. [Google Scholar]
- Bremner, P.; Huff, J.; Bolton, J.S. A model study of how tire construction and materials affect vibration-radiated noise. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 1997. [Google Scholar]
- Samuels, S. Recent Australian Tyre/Road Noise Research. In Proceedings of the International Tire Noise Conference; STU-Information No. 168-1980. NUTEK: Stockholm, Sweden, 1979; pp. 1–25. [Google Scholar]
- Muthukrishnan, M. Effects of material properties on tire noise. In SAE Technical Papers; SAE International: Detroit, MI, USA, 1990. [Google Scholar]
- Kostial, P.; Jancikova, Z.; Bakosova, D.; Valicek, J.; Harnicarova, M.; Spicka, I.; Kotial, P.; Bakoova, D.; Picka, I. Artificial Neural Networks Application in Modal Analysis of Tires. Meas. Sci. Rev. 2013, 13, 273–278. [Google Scholar] [CrossRef]
- Anonymous. Foreign Research in TIre Noise; Office of Noise Abatement and Control, U.S., Environmental Protection Agency: Washington, DC, USA, 1980. [Google Scholar]
- Kindt, P.; De Coninck, F.; Sas, P.; Desmet, W. Analysis of tire/road noise caused by road impact excitations. In SAE Technical Papers; SAE International: St. Charles, IL, USA, 2007. [Google Scholar]
- Kindt, P.; De Coninck, F.; Sas, P.; Desmet, W. Experimental modal analysis of radial tires under different boundary conditions. In Proceedings of the 13th International Congress on Sound and Vibration 2006, ICSV 2006, Vienna, Austria, 2–6 July 2006; Volume 6, pp. 5111–5118. [Google Scholar]
- Wozniak, R.; Taryma, S.; Mioduszewski, P. Tire camber angle influence on tire-pavement noise. Noise Control Eng. J. 2015, 63, 216–224. [Google Scholar] [CrossRef]
- Reinink, H.F.; de Graaff, D.F.; Peeters, A.A.A.; Peeters, H.M. Tyre/Road Noise Measurements of Truck Tyres; Report No. M+P.DWW.03.7.1 (5 February 2005); M+P Raadgevende ingenieurs B.V.: Vught, The Netherlands, 2005. [Google Scholar]
- Sandberg, U.; Ejsmont, J.A. Noise emission, friction and rolling resistance of car tiressummary of an experimental study. In Proceedings of the NOISE-CON 2000, Newport Beach, CA, USA, 3–8 December 2000. [Google Scholar]
- Takahashi, M.; Iimura, K.; Hidaka, Y.; Tachibana, H. Sound power levels of road vehicles measured using a reverberant tunnel—Statistical analysis. In Proceedings of the INTER-NOISE 95, Newport Beach, CA, USA, 10–12 July 1995; pp. 207–210. [Google Scholar]
- Mioduszewski, P. Vehicle noise simulation—Computer program. In Proceedings of the EURO/NOISE ‘95 Symposium, Lyon, France, 21–23 March 1995. [Google Scholar]
- Chang, L. Numerical method of evaluating noise from vibrating tyre. Appl. Mech. Mater. 2012, 105–107, 719–722. [Google Scholar] [CrossRef]
- VTI. Effects of Winter Tyres—State of the Art IN SWEDISH; VTI Rapport 543; Swedish National Road and Transport Research Institute: Linköping, Sweden, 2006. [Google Scholar]
- Tanizaki, T.; Ueda, K.; Murabe, T.; Nomura, H.; Kamakura, T. Discrimination between summer and winter tires using tire/road noises emitted by running vehicles. IEEJ Trans. Ind. Appl. 2013, 133, 558–565. [Google Scholar] [CrossRef]
- Bekke, D.; Wijnant, Y.; Weegerink, T.; De Boer, A. Tire-road noise: An experimental study of tire and road design parameters. In Proceedings of the 42nd International Congress and Exposition on Noise Control Engineering 2013, INTER-NOISE 2013: Noise Control for Quality of Life, Innsbruck, Austria, 15–18 September 2013; Volume 1, pp. 173–180. [Google Scholar]
- Seamenn, E.U. Development of low noise tyres in EU project SILENCE. In Proceedings of the Paris Acoustics, Paris, France, 29 June–4 July 2008. [Google Scholar]
- Bernhard, R.J.; Thornton, W.D.; Baumann, J. Effects of Varying the Tire Cap Ply, Sidewall Filler Height and Pavement Surface Texture on Tire/Pavement Noise Generation; SQDH 2003-1, Final Report; Purdue University: West Lafayette, IN, USA, 2003; p. 90. [Google Scholar]
- El-Gindy, M.; Lewis, H.L.; Lewis, A.S. Development of a tire/pavement contact-stress model based on an artificial neural network. In American Society of Mechanical Engineers, Design Engineering Division (Publication) DE; ASME: New York, NY, USA, 1999; Volume 101, pp. 25–34. [Google Scholar]
- Moore, D.F. The Friction of Pneumatic Tires; Elsevier: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Aboutorabi, H.M.R.; Kung, L. Application of Coupled Structural Acoustic Analysis and Sensitivity Calculations to a Tire Noise Problem. Tire Sci. Technol. 2012, 40, 25–41. [Google Scholar] [CrossRef]
- Staadt, R.L. Truck Noise Control; SAE Publ. SP-386; Society of Automotive Engineers: New York, NY, USA, 1974. [Google Scholar]
- Fong, S. Tyre noise predictions from computed road surface texture induced contact pressure. In Proceedings of the INTER-NOISE 98, Christchurch, New Zealand, 16–18 November 1998; pp. 137–140. [Google Scholar]
- Pei, X.; Wang, G.; Zhou, H.; Zhao, F.; Yang, J. Influence of tread structure design parameters on tire vibration noise. In Proceedings of the SAE-China Congress 2015: Selected Papers; Society of Automotive Engineers: New York, NY, USA, 2015; Volume 364, pp. 325–338. [Google Scholar]
- Saemann, E.-U.; Dimitri, G.; Kindt, P. Tire Requirements for Pavement Surface Characteristics. In Proceedings of the 7th Symposium on Pavement Surface Characteristics: SURF 2012, Norfolk, VA, USA, 19–22 September 2012; pp. 1–33. [Google Scholar]
- Kumar, A.; Tandon, A.; Paul, S.; Singla, A.; Kumar, S.; Vijay, P.; Bhangale, U.D. Influence of Tyre’s Dimensional Characteristics on Tyre-Pavement Noise Emission. Phys. Rev. Res. Int. 2011, 1, 124–137. [Google Scholar]
- Sandberg, U.; Ejsmont, J. Tire/road noise—A subject of international concern. In Proceedings of the INTER-NOISE 88, Avignon, France, 30 August–1 September 1988; p. 1309. [Google Scholar]
- Yang, J.S.; Fwa, T.F.; Ong, G.P.; Chew, C.H. Finite-element analysis of effect of wide-base tire on tire-pavement noise. Adv. Mater. Res. 2013, 723, 105–112. [Google Scholar] [CrossRef]
- Storeheier, S.A.; Sandberg, U. Vehicle Related Parameters Affecting Tyre/Road Noise. In Proceedings of the International Tire/Road Noise Conference, Gothenburg, Sweden, 8–10 August 1990; STU-Information No. 794-1990. NUTEK: Stockholm, Sweden, 1990. [Google Scholar]
- Mohamed, Z.; Wang, X. A study of tyre cavity resonance and noise reduction using inner trim. Mech. Syst. Signal Process. 2015, 50–51, 498–509. [Google Scholar] [CrossRef]
- Tanaka, Y.; Horikawa, S.; Murata, S. An evaluation method for measuring SPL and mode shape of tire cavity resonance by using multi-microphone system. Appl. Acoust. 2016, 105, 171–178. [Google Scholar] [CrossRef]
- Kropp, W.; Larsson, K.; Barrelet, S. The influence of belt and tread band stiffness on the tyre noise generation mechanisms. In Proceedings of the International Congress on Acoustics (ICA) 1998, Seattle, WA, USA, 20–26 June 1998. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 1986; Volume 7, ISBN 978-0-7506-2633-0. [Google Scholar]
- O’Boy, D.J.; Dowling, A.P. Tyre/road interaction noise-Numerical noise prediction of a patterned tyre on a rough road surface. J. Sound Vib. 2009, 323, 270–291. [Google Scholar] [CrossRef]
- Watanabe, T.; Tomita, N.; Kishinami, S.; Yamaguchi, H.; Konishi, S.; Kawana, A. Noise generation mechanism of cross-bar tyres and countermeasures against it. Int. J. Veh. Des. 1988, 9, 641–653. [Google Scholar]
- Plotkin, K.J.; Stusnick, E. A Unified Set of Models for Tire/Road Noise Generation; Report: WR-81-26; Environmental Protection Agency, Office of Noise Abatement and Control: Arlington, VA, USA, 1981; 63p. [Google Scholar]
- Doan, V.Q. Influence of tire construction and tire mold profile on coast-by noise. In Tire Technology International 1996, The Annual Review of Tire Materials and Tire Manufacturing Technology; UKi Media & Events: Dorking, Surrey, United Kingdom, 1996. [Google Scholar]
- Eberhardt, A.C. Investigations of the truck tire vibration sound mechanisms. In Proceedings of the International Tire Noise Conference, Stockholm, Sweden, 29–31 August 1979. [Google Scholar]
- Sandberg, U.; Ejsmont, J.A. Influence of tyre rubber hardness on tyre/road noise emission. In Turkish Acoustical Society—36th International Congress and Exhibition on Noise Control Engineering, INTER-NOISE 2007 ISTANBUL, Istanbul, Turkey, 28–31 August 2007; Curran Associates, Inc.: Red Hook, NY, USA, 2007; Volume 1, pp. 394–403. [Google Scholar]
- ISO. Plastics and Ebonite—Determination of Indentation Hardness by Means of a Durometer (Shore Hardness); ISO 868; ISO: Geneva, Switzerland, 2003. [Google Scholar]
- ASTM. Standard Test Method for Rubber Property—Durometer Hardness; ASTM D2240-05(2010); ASTM: West Conshohocken, PA, USA, 2005. [Google Scholar]
- Oddershede, J.; Kragh, J. Changes in noise levels from Standard Reference Test Tyres due to increasing tyre tread hardness. In Proceedings of the Forum Acusticum, FA, Krakow, Poland, 7–12 September 2014. [Google Scholar]
- Wullens, F.; Kropp, W. Influence of the local stiffness of the rubber layer of the tire on the generation of tire/road noise. In Proceedings of the ICA 2001, Rome, Italy, 2–7 September 2001. [Google Scholar]
- Wullens, F. Towards an Optimisation of Tire/Road Parameters for Noise Reduction. Master’s Thesis, Report F 02-01. Department of Applied Acoustics, Chalmers University of Technology, Gothenburg, Sweden, 2002. [Google Scholar]
- Saemann, E.U. Contribution of the tyre to further lowering tyre/road noise. In Proceedings of the ParisAcoustics’08, Paris, France, 29 June–4 July 2008. [Google Scholar]
- Ishige, T.; Furusho, H.; Aoki, Y.; Kawanage, K. Adaptive slip control using a brake torque sensor. In Proceedings of the 9th International Symposium on Advanced Vehicle Control, Kobe, Japan, 6–9 October 2008; Volume 1, pp. 417–422. [Google Scholar]
- Rochoux, D.; Biesse, F. Tire/road noise, the tire vibration as the main noise source from road texture. In Proceedings of the 39th International Congress on Noise Control Engineering 2010, INTER-NOISE 2010, Lisbon, Portugal, 13–16 June 2010; Volume 5, pp. 3597–3606. [Google Scholar]
- Swieczko-Zurek, B.; Ejsmont, J.; Mioduszewski, P.; Ronowski, G.; Taryma, S. The effect of tire aging on acoustic performance of CPX reference tires. In Proceedings of the 44th International Congress and Exposition on Noise Control Engineering, INTER-NOISE 2015, San Francisco, CA, USA, 9–12 August 2015. [Google Scholar]
- Buhlmann, E.; Schulze, S.; Ziegler, T. Ageing of the new CPX reference tyres during a measurement season. In Proceedings of the 42nd International Congress and Exposition on Noise Control Engineering 2013, INTER-NOISE 2013: Noise Control for Quality of Life, Innsbruck, Austria, 15–18 September 2013; Volume 1, pp. 369–376. [Google Scholar]
- Schubert, S.; Mannel, M.; Ertsey, M.; Hoever, C. Influence of the tyre impedance on CPX level used to evaluate tyre/road noise. In Proceedings of the INTER-NOISE 2016—45th International Congress and Exposition on Noise Control Engineering: Towards a Quieter Future, Hamburg, Germany, 21–24 August 2016; pp. 4945–4954. [Google Scholar]
- Langwieder, K.; Lehnerer, P.; Richlowski, W.; Schneider, D.; Stankowitz, W. Die Ergebnisse des Reifen Check und deren Bedeutung für die Verkehrssicherheit (The Results of the Tire Check and ist Significance for Traffic Safety); VDI-Berichte Nr. 1632, 2001; VDI: Düsseldorf, Germany, 2001. [Google Scholar]
- Gothié, M. Information presented at the meeting of PIARC/C1 in Copenhagen, Denmark, September 2001; World Road Association (PIARC): La Défense, France, 2001. [Google Scholar]
- Gothié, M. Presentation at the meeting of PIARC/C1 in Rome, Italy, 05; World Road Association (PIARC): La Défense, France, 2005. [Google Scholar]
- Li, T.; Burdisso, R.; Sandu, C. The Effect of Rubber Hardness and Tire Size on Tire-Pavement Interaction Noise. In Proceedings of the 36th Annual Meeting and Conference on Tire Science and Technology, Akron, OH, USA, 12–13 September 2017. [Google Scholar]
- ETRTO. ETRTO Recommendations 2002; The European Tire and Rim Technical Organization (ETRTO): Brussels, Belgium, 2002. [Google Scholar]
- Thiriez, K.; Subramanian, R. Tire Pressure Special Study: Tread Depth Analysis; DOT HS 809 359; National Center for Statistics and Analysis: Washington, DC, USA, 2001. [Google Scholar]
- Walker, J.C.; Major, D.J. Noise generated at the tire-road interface. In Proceedings of the Annual Conference Stress Analysis Group of Institute of Physics, University of Aston, Birmingham, UK, 2–4 January1974. [Google Scholar]
- Walker, J.C. Noise from the tire-road interface with heavy commercial vehicles. Trans. Eng. 1975, 68, 11–12. [Google Scholar]
- Flanagan, W. Recent studies give unified picture of tire noise. J. Autom. Eng. 1972, 80, 15–19. [Google Scholar]
- Hillquist, R.K.; Carpenter, P.C. A Basic Study of Automobile Tire Noise; GM Engineering Publication 5269; General Motors: Milford, MI, USA, 1973. [Google Scholar]
- Tetlow, D. Truck Tire Noise. Sound Vib. 1971, 5, 17–23. [Google Scholar]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Tong, G.; Wang, Q.; Yang, K.; Wang, L. Simulation on the radial tire wear noise. Appl. Mech. Mater. 2014, 488, 1121–1124. [Google Scholar] [CrossRef]
- FEHRL (Forum of European National Highway Research Laboratories). Tyre/Road Noise; FEHRL Final Report SI2.408210; FEHRL: Woluwe-Saint-Lambert, Belgium, 2001. [Google Scholar]
- Sandberg, U. Survey of noise emission from truck tires. In Proceedings of the Inter-Noise 91, Sydney, Australia, 2–4 December 1991. [Google Scholar]
- Sandberg, U. Noise emissions of road vehicles effect of regulations: Final Report 01-1. Noise News Int. 2001, 9, 147–203. [Google Scholar] [CrossRef]
- Johnsson, R.; Nykänen, A. Stud Noise Auralization. Int. J. Passeng. Cars Mech. Syst. 2013, 6, 1577–1585. [Google Scholar] [CrossRef]
- Nilsson, N.-A. Principles in the control of external tire/road noise. In Proceedings of the INTER-NOISE 82, San Francisco, CA, USA, 17–19 May 1982; p. 123. [Google Scholar]
- Sandberg, U.; Kalman, B.; Williams, A.R. The porous tread tire—The quietest pneumatic tire measured so far? In Proceedings of the International Congress on Noise Control Engineering 2005, INTERNOISE 2005, Rio de Janeiro, Brazil, 7–10 August 2005; Volume 5, pp. 3996–4005. [Google Scholar]
- Pottinger, M.G.; Marshall, K.D.; Lawther, J.M.; Thrasher, D.B. Review Of Tire/Pavement Interaction Induced Noise And Vibration. In ASTM Special Technical Publication; BFGoodrich Co: Brecksville, OH, USA, 1986; pp. 183–287. [Google Scholar]
- Wang, X.; Mohamed, Z.; Ren, H.; Liang, X.; Shu, H. A study of tyre, cavity and rim coupling resonance induced noise. Int. J. Veh. Noise Vib. 2014, 10, 25–50. [Google Scholar] [CrossRef]
- Ejsmont, J.; Ronowski, G.; Taryma, S.; Mioduszewski, P.; Sobieszczyk, S.; Swieczko-Zurek, B. Relations between tire/road noise and tire rolling resistance on different road pavements. In Proceedings of the 41st International Congress and Exposition on Noise Control Engineering 2012, INTER-NOISE 2012, New York, NY, USA, 19–22 August 2012; Volume 11, pp. 9476–9485. [Google Scholar]
- Stenschke, R.; Vietzke, P. Noise and use characteristics of modern car tyres (State of the art). In Proceedings of the 7th International Congress on Sound and Vibration, Garmisch-Partenkirchen, Germany, 4–7 July 2000. [Google Scholar]
- Hoever, C.; Kropp, W. A simulation-based parameter study of car tyre rolling losses and sound generation. In Proceedings of the European Conference on Noise Control, Prague, Czech Republic, 10–13 June 2012; pp. 926–931. [Google Scholar]
- ISO. Passenger Car, Truck, Bus and Motorcycle Tyres—Methods of Measuring Rolling Resistance; ISO 18164; ISO: Geneva, Switzerland, 2005. [Google Scholar]
- ISO. Passenger Car Tyres—Methods of Measuring Rolling Resistance; ISO 8767; ISO: Geneva, Switzerland, 1992. [Google Scholar]
- ISO. Truck and bus Tyres—Methods of Measuring Rolling Resistance; ISO 9948; ISO: Geneva, Switzerland, 1992. [Google Scholar]
- ISO. Motorcycle Tyres—Method of Measuring Rolling Resistance; ISO 13327; ISO: Geneva, Switzerland, 1998. [Google Scholar]
- ISO. Acoustics—Specification of Test Tracks for Measuring Noise Emitted by Road Vehicles and Their Tyres; ISO 10844; ISO: Geneva, Switzerland, 2014. [Google Scholar]
- Rasmussen, R. Measuring and modeling tire-pavement noise on various concrete pavement textures. Noise Control Eng. J. 2009, 57, 139–147. [Google Scholar] [CrossRef]
- ASTM. Standard Specification for P225/60R16 97S Radial Standard Reference Test Tire; ASTM F2493; ASTM: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Ruhala, R.J. A Study of Tire/Pavement Interaction Noise Using Near-Field Acoustical Holography. Ph.D. Thesis, Pennsylvania State University, State College, PA, USA, 1999. [Google Scholar]
- Donavan, P.R.; Lodico, D. Parameters affecting the noise performance of ASTM standard reference test tires. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 2013; Volume 4. [Google Scholar]
- Pope, J.; Reynolds, W.C. Tire noise generation: The roles of tire and road. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 1976. [Google Scholar]
- Li, T.; Feng, J.; Burdisso, R.; Sandu, C. The effects of tread pattern on tire pavement interaction noise. In Proceedings of the INTER-NOISE 2016—45th International Congress and Exposition on Noise Control Engineering: Towards a Quieter Future, Hamburg, Germany, 21–24 August 2016. [Google Scholar]
- Li, T.; Burdisso, R.; Sandu, C. An Artificial Neural Network Model to Predict Tread Pattern-Related Tire Noise. In Proceedings of the SAE 2017 Noise and Vibration Conference and Exhibition, Grand Rapids, MI, USA, 12–15 June 2017. SAE Technical Paper 2017-01-1904. [Google Scholar]
- Cao, P.; Yan, X.; Xiao, W.; Chen, L. A prediction model to coupling noise of tire tread patterns and road texture. In Proceedings of the 8th International Conference of Chinese Logistics and Transportation Professionals—Logistics: The Emerging Frontiers of Transportation and Development in China, Chengdu, China, 8–10 October 2008; American Society of Civil Engineers: Chengdu, China, 2008; pp. 2332–2338. [Google Scholar]
- Alt, N.; Wolff, K.; Eisele, G.; Pichot, F. Fahrzeug Außen Geräuschsimulation (Vehicle exterior noise simulation). Automob. Z. 2006, 108, 832–836. [Google Scholar] [CrossRef]
- Braun, M.E.; Walsh, S.J.; Horner, J.L.; Chuter, R. Noise source characteristics in the ISO 362 vehicle pass-by noise test: Literature review. Appl. Acoust. 2013, 74, 1241–1265. [Google Scholar] [CrossRef]
- Hanson, D.I.; James, C.R.S.; Ne Smith, C. Tire/Pavement Noise Study; NCAT Report 04–02; NCAT: Greensboro, NC, USA, 2004; 49p. [Google Scholar]
- Yong, C.; Wang, X.; Li, J.; Huang, Z. GA-BP Neural Network Based Tire Noise Prediction. Adv. Mater. Res. 2012, 443–444, 65–70. [Google Scholar]
- Ge, J.; Fan, J.; Gu, Q.; Qian, R.; Youming, L. Design method and application of low noise tire. In Proceedings of the Symposium of International Rubber Conference 2004, Beijing, China, 21–25 September 2004. [Google Scholar]
- Saemann, E.-U. Reducing tire/road rolling noise. Presented at the Conference Intelligent Tire Technology, Frankfurt, Germany, 29–30 November 2005. PowerPoint Presentation by Dr Saemann of NVH Engineering, Continental Tyres, Hanover, Germany. [Google Scholar]
- Xie, K.-J. Method of Developing Tread Pattern. U.S. Patent US6514366 B1, 4 February 2003. [Google Scholar]
- Oswald, L.J. Identifying the noise mechanisms of a single element of a tire tread pattern. In Proceedings of the National Conference on Noise Control Engineering: Applied Noise Control Technology, BT—Proceedings—NOISE-CON 81, Raleigh, NC, USA, 4–6 June 1981; pp. 53–56. [Google Scholar]
- Oswald, L.J.; Arambages, A. The noise mechanisms of cross groove tire tread pattern elements. In BT—Surface Vehicle Noise and Vibration Conference Proceedings; Proceedings—Society of Automotive Engineers; SAE, GM Research Lab, Engineering, Mechanics Dep: Warren, MI, USA, 1985. [Google Scholar]
- Chiu, J.-T.; Tu, F.-Y. Application of a pattern recognition technique to the prediction of tire noise. J. Sound Vib. 2015, 350, 30–40. [Google Scholar] [CrossRef]
- Liljegren, K. Visual and Acoustic tyre Tread Design. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2008. [Google Scholar]
- Williams, T.A. Tire tread pattern noise reduction through the application of pitch sequencing. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 1995. [Google Scholar]
- Bandel, P.; Bergomi, R.; Monguzzi, C. Low Noise Sequence of Tread Elements for Vehicle Tires and Related Generation Method. U.S. Patent US5371685, 16 January 1994. [Google Scholar]
- ISO. Acoustics—Description, Measurement and Assessment of Environmental Noise—Part 2: Determination of Environmental Noise Levels; ISO 1996-2; ISO: Geneva, Switzerland, 2007. [Google Scholar]
- Ewart, E.S. Pneumatic Tire. U.S. Patent 1935. [Google Scholar]
- Varterasian, J.H. Quieting noise mathematically its application to snow tires. In BT—Mid-Year Meeting, May 19, 1969–May 23, 1969; SAE Technical Papers; SAE International, Research Labs., General Motors Corp: Warrendale, PA, USA, 1969. [Google Scholar]
- Buddenhagen, F.E. Tire Casing with Noiseless Tread. U.S. Patent US2612928, 7 October 1952. [Google Scholar]
- Landers, S.P. Spreading Noise Generated by load Supporting Elements. U.S. Patent US4327792, 4 May 1982. [Google Scholar]
- Williams, T.A. Tire Pitch Sequencing for Reduced Tire Tread Noise. U.S. Patent US5314551, 24 May 1994. [Google Scholar]
- Wei, Y.; Feng, Q.; Wang, H.; Kaliske, M. A hybrid numerical-experimental analysis for tire air-pumping noise with application to pattern optimization. Noise Control Eng. J. 2016, 64, 56–63. [Google Scholar] [CrossRef]
- Michelin. Michelin Primacy 3 ST Tyres—Lasts Longer & Maximum Safety on Wet Roads. 2016. Available online: http://www.michelin.in/IN/en/tyres/products/primacy-3-st.html (accessed on 10 October 2018).
- Dong, Y.; Tan, Y.; Liu, H.; Yang, L. Noise performance of drainage asphalt pavement. Int. J. Pavement Res. Technol. 2010, 2, 280–283. [Google Scholar]
- Oshino, Y.; Mikami, T.; Ohnishi, H.; Tachibana, H. Investigation into road vehicle noise reduction by drainage asphalt pavement. J. Acoust. Soc. Jpn. 1999, 20, 75–84. [Google Scholar] [CrossRef]
- Wang, G.-L.; Zhou, H.-C.; Yang, J.; Liang, C.; Jin, L. Influence of Bionic Non-smooth Surface on Water Flow in Antiskid Tire Tread Pattern. J. Donghua Univ. Engl. Ed. 2013, 30, 336–342. [Google Scholar]
- Zhou, H. Investigate into Influence of Tire tread Pattern on Noise and Hydroplaning and Synchronously Improving Methods. Ph.D. Thesis, Jiangsu University, Zhejiang, China, 2013; pp. 1–178. [Google Scholar]
- Ejsmont, J.A.; Sandberg, U.; Taryma, S. Influence of tread pattern on tire/road noise. In Passenger Car Meeting, October 1, 1984–October 4, 1984; SAE Technical Papers; Technical University of Gdansk, PolandSwedish Road and Traffic Research Institute, SAE International: Linkoeping, Sweden, 1984; 9p. [Google Scholar]
- Ih, J.-G.; Oey, A. Effect of patterns on wave propagation and sound radiation over the tire surface. In Proceedings of the 41st International Congress and Exposition on Noise Control Engineering 2012, INTER-NOISE 2012, New York, NY, USA, 19–22 August 2012; Volume 2, pp. 1436–1441. [Google Scholar]
- Domenichini, L.; Fracassa, A.; La Torre, F.; Loprencipe, G.; Ranzo, A.; Scalamandrè, A. Relationship between road surface characteristics and noise emission. In Proceedings of the First International Colloquium on Vehicle Tyre Road Interaction, Rome, Italy, 28 May 1999; Paper 99.03. pp. 1–22. [Google Scholar]
- NZ Transport Agency. Guide to State Highway Road Surface Noise; NZ Transport Agency: Wellington, New Zealand, 2014. [Google Scholar]
- Donavan, P.R. Comparative measurements of tire/pavement noise in Europe and the United States. Noise News Int. 2005, 13, 46–53. [Google Scholar] [CrossRef]
- Mcghee, K. Virginia Quiet Pavement Study. In Proceedings of the 7th Symposium on Pavement Surface Characteristics, Presentation at SURF 2012, Norfolk, VA, USA, 19–22 September 2012. [Google Scholar]
- Sandberg, U.; Ejsmont, J.A.; Gustavsson, E. Tire/Road Noise on Rubberized Asphalt and Cement Concrete Surfaces in Sweden; Swedish National Road and Transport Research Institute: Linköping, Sweden, 1990; 60p. [Google Scholar]
- Li, M.; Molenaar, A.; van de Ven, M.; Huurman, R.; van Keulen, W. New Approach for Modelling Tyre/Road Noise. In Proceedings of the Inter-Noise 2009, Ottawa, ON, Canada, 23–26 August 2009. [Google Scholar]
- Klein, P.; Cesbron, J. A 3D envelopment procedure for tyre belt radiated noise level prediction. In Proceedings of the INTER-NOISE 2016—45th International Congress and Exposition on Noise Control Engineering: Towards a Quieter Future, Hamburg, Germany, 21–24 August 2016; pp. 2230–2241. [Google Scholar]
- Li, T. Tire-Pavement Interaction Noise (TPIN) Modeling Using Artificial Neural Network (ANN). Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2017. [Google Scholar]
- ISO. Characterization of Pavement Texture by Use of Surface Profiles—Part 1: Determination of Mean Profile Depth; ISO 13473-1; ISO: Geneva, Switzerland, 1997. [Google Scholar]
- Huschek, S. Characterization of pavement surface texture and its influence on tire/road noise. In Proceedings of the Third International Symposium on Pavement Surface Characteristics, Christchurch, New Zealand, 3–4 September 1996. [Google Scholar]
- Wayson, R.L. NCHRP Synthesis 268—Relationship between Pavement Surface Texture and Highway Traffic Noise; Transportation Research Board, National Academy Press: Washington, DC, USA, 1998; 94p. [Google Scholar]
- Thrasher, D.B.; Miller, R.F.; Bauman, R.G. Effect of pavement texture on tire/pavement interaction noise. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 1976. [Google Scholar]
- Li, M.; van Keulen, W.; Ceylan, H.; Tang, G.; van de Ven, M.; Molenaar, A. Influence of Road Surface Characteristics on Tire-Road Noise for Thin-Layer Surfacings. J. Transp. Eng. 2015, 141, 04015024. [Google Scholar] [CrossRef]
- Biermann, J.; von Estorff, O.; Petersen, S.; Schmidt, H. Computational model to investigate the sound radiation from rolling tires. Tire Sci. Technol. 2007, 35, 209–225. [Google Scholar] [CrossRef]
- Hamet, J.-F.; Klein, P. Road texture and tire noise. In Proceedings of the Inter-Noise 2000, Nice, France, 27–30 August 2000; pp. 178–183. [Google Scholar]
- Hanson, D.I.; Waller, B. Evaluation Of The Noise Characteristics Of Minnesota Pavements; Minnesota Department of Transportation: Saint Paulc, MN, USA, 2005. [Google Scholar]
- Pinnington, R.J. A particle-envelope surface model for road–tyre interaction. Int. J. Solids Struct. 2012, 49, 546–555. [Google Scholar] [CrossRef]
- Pinnington, R.J. Tyre-road contact using a particle-envelope surface model. J. Sound Vib. 2013, 332, 7055–7075. [Google Scholar] [CrossRef]
- He, D.-C.; Wang, L. Texture features based on texture spectrum. Pattern Recognit. 1991, 24, 391–399. [Google Scholar] [CrossRef]
- Lee, Y.G.; Lee, J.H.; Hsueh, Y.C. Texture classification using fuzzy uncertainty texture spectrum. Neurocomputing 1998, 20, 115–122. [Google Scholar] [CrossRef]
- Wang, L.; He, D.-C. Texture classification using texture spectrum. Pattern Recognit. 1990, 23, 905–910. [Google Scholar] [CrossRef]
- ISO. Characterization of Pavement Texture by Use of Surface Profiles—Part 4: Spectral Analysis of Surface Profiles; ISO/TS 13473-4; ISO: Geneva, Switzerland, 2008. [Google Scholar]
- ISO. Characterization of Pavement Texture by Use of Surface Profiles—Part 3: Specification and Classification of Profilometers; ISO 13473-3; ISO: Geneva, Switzerland, 2002. [Google Scholar]
- Dubois, G.; Cesbron, J.; Yin, H.P.; Anfosso-Ledee, F.; Duhamel, D. Statistical estimation of low frequency tyre/road noise from numerical contact forces. Appl. Acoust. 2013, 74, 1085–1093. [Google Scholar] [CrossRef]
- ASTM. Standard Test Method for Measuring Pavement Macrotexture Properties Using the Circular Track Meter; ASTM E2157; ASTM: West Conshohocken, PA, USA, 2009. [Google Scholar]
- Hamet, J.-F.; Klein, P. Use of a rolling model for the study of correlation between road texture and tire noise. In Proceedings of the 2001 International Congress and Exhibition on Noise Control Engineering, The Hague, The Netherlands, 28–30 August 2001. [Google Scholar]
- McDaniel, R.; Shah, A.; Dare, T.; Bernhard, R. Hot Mix Asphalt Surface Characteristics Related to Ride, Texture, Friction, Noise and Durability; Purdue University: St. Paul, MN, USA, 2014. [Google Scholar]
- Dare, T.; Bernhard, R. Predicting tire-pavement noise on longitudinally ground pavements using a nonlinear model. In Proceedings of the 38th International Congress and Exposition on Noise Control Engineering 2009, INTER-NOISE 2009, Ottawa, ON, Canada, 23–26 August 2009; Volume 1, pp. 405–415. [Google Scholar]
- Sandberg, U.; Ejsmont, J.A. Texturing of cement concrete pavements to reduce traffic noise. Noise Control Eng. J. 1998, 46, 231. [Google Scholar] [CrossRef]
- Rasmussen, R.; Karamihas, S.; Mun, E.; Chang, G. Relating pavement texture to tire-pavement noise. In Proceedings of the 35th International Congress and Exposition on Noise Control Engineering, INTER-NOISE 2006, Institute of Noise Control Engineering of the USA, Honolulu, HI, USA, 3–6 December 2006; Volume 1, pp. 422–431. [Google Scholar]
- FHWA. Technical Advisory T 5040.36—Surface Texture for Asphalt and Concrete Pavements; FHWA: Washington, DC, USA, 2005. [Google Scholar]
- Henry, J.J. Evaluation of Pavement Friction Characteristics; Transportation Research Board: Washington, DC, USA, 2000; Volume 291. [Google Scholar]
- Flintsch, G.W.; de Leon, E.; McGhee, K.; Al-Qadi, I. Pavement Surface Macrotexture Measurement and Application. Transp. Res. Rec. J. Transp. Res. Board 2003, 1860, 168–177. [Google Scholar] [CrossRef]
- ASTM. Standard Test Method for Measuring Pavement Macrotexture Depth Using a Volumetric Technique; ASTM E965; ASTM: West Conshohocken, PA, USA, 2006. [Google Scholar]
- ASTM. Standard Practice for Calculating Pavement Macrotexture Mean Profile Depth; ASTM E1845; ASTM: West Conshohocken, PA, USA, 2009. [Google Scholar]
- ISO. Characterization of Pavement Texture by Use of Surface Profiles—Part 5: Determination of Megatexture; ISO 13473-5; ISO: Geneva, Switzerland, 2009. [Google Scholar]
- ISO. Mechanical Vibration—Road Surface Profiles—Reporting of Measured Data; ISO 8608; ISO: Geneva, Switzerland, 1995. [Google Scholar]
- Barbosa, R.S. Vehicle dynamic response due to pavement roughness. J. Braz. Soc. Mech. Sci. Eng. 2011, 33, 302–307. [Google Scholar]
- Stroup-Gardiner, M.; Brown, E.R. Segregation in Hot-Mix Asphalt Pavements; Report No. 441; Transportation Research Board: Washington, DC, USA, 2000. [Google Scholar]
- Zhang, Y.; McDaniel, J.G.; Wang, M.L. Pavement macrotexture estimation using principal component analysis of tire/road noise. Proc. SPIE Int. Soc. Opt. Eng. 2014, 9063, 90630K. [Google Scholar]
- Saykin, V.V. Pavement Macrotexture Monitoring through Sound Generated by the Tire-Pavement Interaction. Master’s Thesis, Northeastern University, Boston, MA, USA, 2011. [Google Scholar]
- Reyes, C.H.; Harvey, J. A method for predicting sound intensity noise levels using laboratory pavement cores. In Proceedings of the Noise-Con 2011, Portland, OR, USA, 25–27 July 2011; pp. 522–534. [Google Scholar]
- Kohler, E. OBSI Testing. In Proceedings of the Presentation at Pavement Evaluation 2010, Roanoke, VA, USA, 25–27 October 2010. [Google Scholar]
- ASTM. Standard Practice for Computing International Roughness Index of Roads from Longitudinal Profile Measurements; ASTM E1926; ASTM: West Conshohocken, PA, USA, 2008. [Google Scholar]
- ASTM. Standard Test Method for Measuring Road Roughness by Static Level Method; ASTM E1364; ASTM: West Conshohocken, PA, USA, 2012. [Google Scholar]
- Sayers, M.W.; Gillespie, T.D.; Paterson, W.D. Guidelines for the Conduct and Calibration of Road Roughness Measurement; World Bank Technical Paper No. 46; The World Bank: Washington, DC, USA, 1986. [Google Scholar]
- ASME. Surface Texture (Surface Roughness, Waviness, and Lay); ASME B46.1; ASME: New York; NY, USA, 2009. [Google Scholar]
- Wullens, F.; Kropp, W.; Jean, P. Quasi-3D versus 3D contact modelling for tyre/road interaction. In Proceedings of the INTER-NOISE 04, Prague, Czech Republic, 22–25 August 2004; p. 3318. [Google Scholar]
- Rasmussen, R.O.; Garber, S.I.; Fick, G.J.; Ferragut, T.R.; Wiegand, P.D. How to Reduce Tire-Pavement Noise- Interim Better Practices; Federal Highway Administration: Washington, DC, USA, 2008. [Google Scholar]
- Kane, A. Concrete Pavement Joints; FHWA Technical Advisory T 5040.30; Federal Highway Administration: Washington, DC, USA, 1990. [Google Scholar]
- Donavan, P. Influence of PCC Surface Texture and Joint Slap on Tire/Pavement Noise Generation. In Proceedings of the Noise-Con 2004, Baltimore, MD, USA, 12–14 July 2004; pp. 251–262. [Google Scholar]
- Meiarashi, S.; Gagarin, N.; Coppage, T. Effect of transverse tines/grooves spacing on tire/pavement noise from aspect of annoyance caused by wailing. In Proceedings of the Inter-Noise 98, Christchurch, New Zealand, 16–18 November 1998; pp. 203–208. [Google Scholar]
- Dare, T.; Bernhard, R.; Thornton, W. Effects of contraction joint width, fill condition, faulting and beveling on wheel-slap noise. Noise Control Eng. J. 2011, 59, 228–233. [Google Scholar] [CrossRef]
- Dare, T.; Bernhard, R. Noise generation in contraction joints in Portland cement concrete. In Proceedings of the 24th National Conference on Noise Control Engineering 2010, Noise-Con 10, Held Jointly with the 159th Meeting of the Acoustical Society of America, Baltimore, MD, USA, 19–21 April 2010; Volume 1, pp. 561–572. [Google Scholar]
- Marriner, D.; Wakefield, C. Modular expansion joint noise in B.C. In Proceedings of the 40th International Congress and Exposition on Noise Control Engineering 2011, INTER-NOISE 2011, Osaka, Japan, 4–7 September 2011; Volume 1, pp. 763–768. [Google Scholar]
- Behzad, M.; Hodaei, M.; Alimohammadi, I. Experimental and numerical investigation of the effect of a speed bump on car noise emission level. Appl. Acoust. 2007, 68, 1346–1356. [Google Scholar] [CrossRef]
- Sexton, T. Controlling expansion joint noise on the Tacoma narrows bridge in Washington State, USA. In Proceedings of the 40th International Congress and Exposition on Noise Control Engineering 2011, INTER-NOISE 2011, Osaka, Japan, 4–7 September 2011; Volume 1, pp. 734–739. [Google Scholar]
- Glaeser, K.-P.; Schwalbe, G.; Zoller, M. Mitigation the noise emissions of vehicles travelling over bridge expansion joints. In Proceedings of the 40th International Congress and Exposition on Noise Control Engineering 2011, INTER-NOISE 2011, Osaka, Japan, 4–7 September 2011; Volume 1, pp. 753–762. [Google Scholar]
- Wakefield, C.W.; Marriner, D.E. Analysis and control of bridge expansion joint croaking noise. Can. Acoust. Acoust. Can. 2011, 39, 138–139. [Google Scholar]
- Tournour, M.A.; Cuschieri, J.M. Contribution to the overall noise level of the vibration of an open grid bridge deck. In Proceedings of the National Conference on Noise Control Engineering, Fort Lauderdale, FL, USA, 1–4 May 1994; pp. 105–110. [Google Scholar]
- Cuschieri, J.M.; Gregory, S.; Tournour, M. Open grid bridge noise from grid and tire vibrations. J. Sound Vib. 1996, 190, 317–343. [Google Scholar] [CrossRef]
- Meggers, D.A. Effectiveness of Polymer Bridge Deck Overlays in Highway Noise Reduction; Report Number KS-15-11; Kansas. Dept. of Transportation: Topeka, KS, USA, 2016. [Google Scholar]
- Payne, A.R.; Scott, J.R. Engineering Design with Rubber; Interscience Publishers Inc.: New York, NY, USA, 1960. [Google Scholar]
- Donavan, P.R. Effect of porous pavement on wayside traffic noise levels. Trans. Res. Rec. 2014, 2403, 28–36. [Google Scholar] [CrossRef]
- Bérengier, M.C.; Stinson, M.R.; Daigle, G.A.; Hamet, J.F. Porous road pavements: Acoustical characterization and propagation effects. J. Acoust. Soc. Am. 1997, 101, 155. [Google Scholar] [CrossRef]
- ASTM. Standard Test Method for Effective Porosity and Effective Air Voids of Compacted Bituminous Paving Mixture Samples; ASTM D7063/D7063M; ASTM: West Conshohocken, PA, USA, 2011. [Google Scholar]
- AASHTO. Theoretical Maximum Specific Gravity and Density of Hot Mix Asphalt (HMA); AASHTO T 209; AASHTO: Washington, DC, USA, 2011. [Google Scholar]
- AASHTO. Bulk Specific Gravity and Density of Compacted Hot Mix Asphalt (HMA) Using Automatic Vacuum Sealing Method; AASHTO T 331; AASHTO: Washington, DC, USA, 2010. [Google Scholar]
- Ongel, A.; Harvey, J. Pavement characteristics affecting the frequency content of tire/pavement noise. Noise Control Eng. J. 2010, 58, 563–571. [Google Scholar] [CrossRef]
- Neithalath, N.; Weiss, J.; Olek, J. Reducing the Noise Generated in Concrete Pavements through Modification of the Surface Characteristics; R&D Serial No. 2878; Portland Cement Association: Skokie, IN, USA, 2005; 71p. [Google Scholar]
- De Roo, F.; Gerretsen, E. TRIAS—Tyre road interaction acoustic simulation model. In Proceedings of the 29th International Congress and Exhibition on Noise Control Engineering, InterNoise 2000, Nice, France, 27–30 August 2000; Volume 4, pp. 2488–2496. [Google Scholar]
- Olek, J.; Weiss, W.J.; Neithalath, N.; Marolf, A.; Sell, E.; Thornton, W.D. Development of Quiet and Durable Porous Portland Cement Concrete Paving Materials; University Transportation Centers Program, Report: SQDH-2003-5; Department of Transportation: Washington, DC, USA, 2003; 181p. [Google Scholar]
- ISO. Acoustics—Determination of Sound Absorption Coefficient and Impedance in Impedance Tubes—Part 1: Method Using Standing Wave Ratio; ISO 10534-1; ISO: Geneva, Switzerland, 1996. [Google Scholar]
- ISO. Acoustics—Determination of Sound Absorption Coefficient and Impedance in Impedance Tubes—Part 2: Transfer-Function Method; ISO 10534-2; ISO: Geneva, Switzerland, 1998. [Google Scholar]
- ASTM. Standard Test Method for Impedance and Absorption of Acoustical Materials Using a Tube, Two Microphones and a Digital Frequency Analysis System; ASTM E1050; ASTM: West Conshohocken, PA, USA, 2012. [Google Scholar]
- ISO. Acoustics—Measurement of Sound Absorption Properties of Road Surfaces In Situ—Part 1: Extended Surface Method; ISO 13472-1; ISO: Geneva, Switzerland, 2002. [Google Scholar]
- ISO. Acoustics—Measurement of Sound Absorption Properties of road Surfaces In Situ—Part 2: Spot Method for Reflective Surfaces; ISO 13472-2; ISO: Geneva, Switzerland, 2010. [Google Scholar]
- Rasmussen, R.O.; Bernhard, R.J.; Sandberg, U.; Mun, E.P. The Little Book of Quieter Pavements; Report No. FHWA-IF-08-004; The Transtec Group: Austin, TX, USA, 2007. [Google Scholar]
- ISO. Acoustics—Materials for Acoustical Applications—Determination of Airflow Resistance; ISO 9053; ISO: Geneva, Switzerland, 1991. [Google Scholar]
- ANSI/ASA. American National Standard Method for Determining the Acoustic Impedance of Ground Surfaces; ANSI/ASA S1.18; ASA: Melville, NY, USA, 2010. [Google Scholar]
- Ren, R.; Gao, C. Improved porous noise reducing asphalt mixture design method. Int. J. Pavement Res. Technol. 2009, 2, 275–279. [Google Scholar]
- Mogrovejo, D.E.; Flintsch, G.W.; De Leon Izeppi, E.D.; McGhee, K.K.; Burdisso, R.A. Short-term effect of pavement surface aging on tire-pavement noise measured with onboard sound intensity methodology. Transp. Res. Rec. 2014, 17–27. [Google Scholar] [CrossRef]
- Berge, T.; Storeheier, S.A. Low noise pavements in a Nordic climate. Results from a four year project in Norway. In Proceedings of the Inter-Noise 2009, Ottawa, ON, Canada, 23–26 August 2009; p. 1936. [Google Scholar]
- Li, M.; Molenaar, A.A.A.; van de Ven, M.F.C.; van Keulen, W. Mechanical impedance measurement on thin layer surface with impedance hammer device. J. Test. Eval. 2012, 40, 860–865. [Google Scholar] [CrossRef]
- Sandberg, U.; Goubert, L. PERSUADE—A European project for exceptional noise reduction by means of poroelastic road surfaces. In Proceedings of the 40th International Congress and Exposition on Noise Control Engineering 2011, INTER-NOISE 2011, Osaka, Japan, 4–7 September 2011; Volume 1, pp. 673–683. [Google Scholar]
- Storeheier, S.A. Preliminary Investigation on a Poroelastic Material Used as a Low Noise Road Surface; SINTEF Foundation Ofscient and Industrial Research; Norwegian Institute of Technology: Trondheim, Norway, 1987; 41p. [Google Scholar]
- Nilsson, N.-A.; Sylwan, O. New vibro-acoustical measurement tools for characterization of poroelastic road surfaces with respect to tire/road noise. In Proceedings of the Tenth International Congress on Sound and Vibration, Stockholm, Sweden, 7–10 July 2003; pp. 4343–4350. [Google Scholar]
- Sandberg, U.; Goubert, L. Poroelastic road surface (PERS): A review of 30 years of R&D work. In Proceedings of the Inter-Noise 2011, Osaka, Japan, 4–7 September 2011. [Google Scholar]
- Swieczko-Zurek, B. Biological hazards in low noise, poroelastic road surfaces. In Proceedings of the 20th International Congress on Sound and Vibration 2013, ICSV 2013, Bangkok, Thailand, 7–11 July 2013; Volume 4, pp. 2813–2818. [Google Scholar]
- Bilawchuk, S. Tire noise assessment of asphalt rubber crumb pavement. Can. Acoust. 2005, 33, 37–41. [Google Scholar]
- Ponniah, J.; Tabib, S.; Lane, B.; Raymond, C. Evaluation of the effectiveness of different mix types to reduce noise level at the tire/pavement interface. In Proceedings of the 2010 Annual Conference and Exhibition of the Transportation Association of Canada: Adjusting to New Realities, TAC/ATC 2010, Halifax, NS, Canada, 26–29 September 2010. [Google Scholar]
- Beckenbauer, T. Akustische Eigenschaften von Fahrbahnoberflaechen. Strasse+Autobahn 2001, 54, 553–561. [Google Scholar]
- Stenschke, R. Activities of the German Federal Environmental Agency to reduce tire/road noise. In Proceedings of the International Tire/Road Noise Conference 1990, Gothenburg, Sweden, 8–10 August 1990. [Google Scholar]
- Liao, G.; Heitzman, M.; West, R.; Wang, S.; Ai, C. Temperature Effects on the Correlations between Tire-Pavement Noises and Pavement Surface Characteristics. New Front. Road Airpt. Eng. 2015, 219–232. [Google Scholar]
- AASHTO. Standard Method of Test for Determining Dynamic Modulus of Hot-Mix Asphalt Concrete Mixtures; AASHTO T 342; AASHTO: Washington, DC, USA, 2011. [Google Scholar]
- Rao, C.; Von Quintus, H.L. Determination of In Place Elastic Layer Modulus–Selection and Demonstration of Backcalculation Methodology and Practice: Phase I Interim Report, Long Term Pavement Performance Program; Federal Highway Administration: Washington, DC, USA, 2012. [Google Scholar]
- ASTM. Standard Test Method for Measuring the P-Wave Speed and the Thickness of Concrete Plates Using the Impact-Echo Method; ASTM C1383; ASTM: West Conshohocken, PA, USA, 2010. [Google Scholar]
- Biligiri, K.P. Effect of pavement materials’ damping properties on tyre/road noise characteristics. Constr. Build. Mater. 2013, 49, 223–232. [Google Scholar] [CrossRef]
- Oshino, Y.; Mikami, T.; Tachibana, H. Study of road surface indices for the assessment of tire/road noise. In Proceedings of the Inter-Noise 2001, The Haag, The Netherlands, 28–30 August 2001. [Google Scholar]
- ASTM. Standard Test Method for Skid Resistance of Paved Surfaces Using a Full-Scale Tire; ASTM E274/E274M; ASTM: West Conshohocken, PA, USA, 2011. [Google Scholar]
- ASTM. Standard Specification for Standard Rib Tire for Pavement Skid-Resistance Tests; ASTM E501; ASTM: West Conshohocken, PA, USA, 2008. [Google Scholar]
- ASTM. Standard Specification for Standard Smooth Tire for Pavement Skid-Resistance Tests; ASTM E524; ASTM: West Conshohocken, PA, USA, 2008. [Google Scholar]
- ASTM. Standard Test Method for Measuring Paved Surface Frictional Properties Using the Dynamic Friction Tester; ASTM E1911; ASTM: West Conshohocken, PA, USA, 2009. [Google Scholar]
- ASTM. Standard Practice for Calculating International Friction Index of a Pavement Surface; ASTM E1960; ASTM: West Conshohocken, PA, USA, 2011. [Google Scholar]
- ASTM. Standard Test Method for Measuring Surface Frictional Properties Using the British Pendulum Tester; ASTM E303; ASTM: West Conshohocken, PA, USA, 2013. [Google Scholar]
- Khaki, A.M.; Forouhid, A.E.; Zare, M. Comparison of the noise level and the skid resistance of asphalt pavement mixtures on road surface. J. Meas. Eng. 2015, 3, 71–76. [Google Scholar]
- McDaniel, R.S.; Kowalski, K.J.; Shah, A.; Olek, J.; Bernhard, R.J. Long-Term Performance of a Porous Friction Course; FHWA/IN/JTRP-2009/22, Joint Transportation Research Program; Indiana Department of Transportation and Purdue University: West Lafayette, IN, USA, 2010. [Google Scholar]
- Kowalski, K.J.; McDaniel, R.S.; Olek, J. Identification of Laboratory Technique to Optimize Superpave HMA Surface Friction Characteristics; FHWA/IN/JTRP-2010/06, Joint Transportation Research Program; Indiana Department of Transportation and Purdue University: West Lafayette, IN, USA, 2010. [Google Scholar]
- Paje, S.E.; Bueno, M.; Teran, F.; Vinuela, U. Monitoring road surfaces by close proximity noise of the tire/road interaction. J. Acoust. Soc. Am. 2007, 122, 2636–2641. [Google Scholar] [CrossRef] [PubMed]
- Ng, W.K.; Ng, P.S.; Hung, W.T. Measurement of tyre/road surface noise with close-proximity method in Hong Kong. In Proceedings of the INTER-NOISE 09, Ottawa, ON, Canada, 23–26 August 2009; p. 1178. [Google Scholar]
- Chalupnik, J.D. Predicting Roadside Noise Levels from Near Field Trailer Measurements. In Proceedings of the Noise-Con 1996, Bellevue, WA, USA, 29 September–2 October 1996; Volume 1, pp. 61–66. [Google Scholar]
- Dare, T.; Wulf, T.; Thornton, W.; Bernhard, R.J. Acoustical Effects of Grinding and Grooving on Portland Cement Concrete Pavements; Technical Report; The Institute for Safe, Quiet and Durable Highways: West Lafayette, IN, USA, 2009. [Google Scholar]
- Bendsten, H.; Kohler, E.; Lu, Q. Acoustic Aging of Asphalt Pavements—A California Danish Comparison; Report 171; Road Directate, Danish Road Institute: Roskilde, Denmark, 2009. [Google Scholar]
- Anderson, K.W.; Uhlmeyer, J.S.; Sexton, T.; Russell, M.; Weston, J. Evaluation of Long-Term Pavement Performance and Noise Characteristics of the Next Generation Concrete Surface: Final Report; Washington (State) Dept. of Transportation, WA-RD 767.2; Washington (State) Dept. of Transportatio: Olympia, WA, USA, 2014; 52p. [Google Scholar]
- Hencken, J.; Haas, E.; Bennert, T. Using Tire/Pavement Interface Noise Results to Define Statistically Similar Bituminous Pavements in Massachusetts. In Proceedings of the Presented at 7th Symposium on Pavement Surface Characteristics: SURF 2012, Norfolk, VA, USA, 19–22 September 2012. [Google Scholar]
- Kay, R.K. Pavement Surface Condition Rating Manual; Washington State Department of Transportation Report; Washington State Department of Transportation: Olympia, WA, USA, 1992. [Google Scholar]
- MNDOT. MnDOT Distress Identification Manual; Report; Minnesota Department of Transportation, Office of Materials and Road Research: St. Paul, MN, USA, 2003. [Google Scholar]
- Miller, J.S.; Bellinger, W.Y. Distress Identification Manual for the Long-Term Pavement Performance Program; FHWA Report No. FHWA-RD-03-031; FHWA: Washington, DC, USA, 2003. [Google Scholar]
- Boullosa, R.R.; Lopez, A.P. Tra. Noise Control Eng. J. 1987, 29, 54. [Google Scholar] [CrossRef]
- Descornet, G. Vehicle noise emission on wet road surfaces. In Proceedings of the INTER-NOISE 00, Nice, France, 27–30 August 2000; p. 4968. [Google Scholar]
- Bergmann, M. Noise generation by tire vibrations. In Proceedings of the INTER- NOISE 80, Miami, FL, USA, 8–10 December 1980; p. 239. [Google Scholar]
- Kongrattanaprasert, W.; Nomura, H.; Kamamura, T.; Ueda, K. Automatic detection of road surface states from tire noise using neural network analysis. IEEJ Trans. Ind. Appl. 2010, 130, 920–925. [Google Scholar] [CrossRef]
- Kocak, S.; Kutay, M.E. Relationship between Material Characteristics of Asphalt Mixtures and Highway Noise. In TRB 91st Annual Meeting Compendium of Papers; Compendium of Papers, Paper No. 12–4309; National Research Council: Washington, DC, USA, 2012. [Google Scholar]
- Biligiri, K.P. Asphalt Mixtures’ Properties Indicative of Tire/Pavement Noise. Ph.D. Thesis, Arizona State University, Tempe, AZ, USA, 2008. [Google Scholar]
- Sohaney, R.; Rasmussen, R.; Seybert, A.; Donavan, P. New ISO test track specification for measuring tire and vehicle noise. Sound Vib. 2012, 46, 9–14. [Google Scholar]
- Moore, D. Revised ISO 10844 Test Surface: Technical Principles. SAE Int. J. Passeng. Cars Mech. Syst. 2011, 4, 1126–1131. [Google Scholar] [CrossRef]
- Van Blokland, G.; Van Leeuwen, M. Efficiency of the combined application of silent tyres and silent road surfaces. In Proceedings of the 39th International Congress on Noise Control Engineering 2010, INTER-NOISE 2010, Lisbon, Portugal, 13–16 June 2010; Volume 5, pp. 3469–3478. [Google Scholar]
- Sandberg, U. Semi-generic temperature corrections for tyre/road noise. In Proceedings of the INTER-NOISE 04, Prague, Czech Republic, 22–25 August 2004; p. 3302. [Google Scholar]
- Kuijpers, A.H.W.M. Further Analysis of the Sperenberg Data—Towards a Better Understanding of the Processes Influencing Tire/Road Noise; Report No. M+P.MVM.99.3.1 rev. 1; MP Consulting Engineers: Hertogenbosch, The Netherlands, 2001. [Google Scholar]
- Konishi, S.; Fujino, T.; Tomita, N.; Sakamoto, M. Temperature effect on tire/road noise. In Proceedings of the International Conference on Noise Control Engineering, Newport Beach, CA, USA, 10–12 July 1995; Volume 1, p. 147. [Google Scholar]
- Anfosso-LédéE, F.; Pichaud, Y. Temperature effect on tyre-road noise. Appl. Acoust. 2007, 68, 1–16. [Google Scholar] [CrossRef]
- Nilsson, N.-A.; Bennerhult, O.; Soderqvist, S. External tire/road noise: its generation and reduction. In Proceedings of the Inter-Noise 80. Noise Control for the 80’s. Proceedings of the 1980 International Conference on Noise Control Engineering; Miami, FL, USA, 8–10 December 1980, pp. 245–252.
- EEC. Tyre Noise: Legal Requirements; EC Directive (2001/43/EC); United Nations Economic Commission for Europe: Geneva, Switzerland, 2001. [Google Scholar]
- SAE. Sound Level Of Highway Truck Tires. SAE J. 2014, 57. [Google Scholar] [CrossRef]
- AASHTO. Standard Method of Test for Measurement of Tire/Pavement Noise Using the On-Board Sound Intensity (OBSI) Method; AASHTO TP 76; AASHTO: Washington, DC, USA, 2013. [Google Scholar]
- Jabben, J. Temperature effects on road traffic noise measurements. In Proceedings of the 40th International Congress and Exposition on Noise Control Engineering 2011, INTER-NOISE 2011, Osaka, Japan, 4–7 September 2011; Volume 1, pp. 552–556. [Google Scholar]
- Bae, A.; Stoffels, S.M.; Lee, S.W. Observed Effects of Subgrade Moisture on Longitudinal Profile. In TRB 85th Annual Meeting Compendium of Papers CD-ROM; Paper No. 06-2312; National Research Council: Washington, DC, USA, 2006. [Google Scholar]
- Donavan, P.R. Investigations of the influence of lower frequency aerodynamic noise on interior cruise and exterior pass-By sound levels. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 2012; Volume 5. [Google Scholar]
- Cantrell, D. Airborne Tire Noise Generation—The Effects of Axle Weight, Tire Inflation Pressure, and Suspension Alignment; Noise & Vibration Laboratory, General Motors Proving Ground: São Paulo, Brazil, 1988. [Google Scholar]
- Graham, W.R. Influence of tire geometry on the horn effect. In Proceedings of the 41st International Congress and Exposition on Noise Control Engineering 2012, INTER-NOISE 2012, New York, NY, USA, 19–22 August 2012; Volume 8, pp. 6995–7008. [Google Scholar]
- Oldenettel, H.; Koster, H.J. Test procedure for the quantification of rolling tire belt vibrations. Veh. Syst. Dyn. 1997, 27, 37–49. [Google Scholar] [CrossRef]
- Hung, W.-T.; Lam, Y.-K.; Ng, C.-F.; Leung, R.C.-K. The impacts of tyre hardness and tread depth on tyre/road noise. In Proceedings of the 20th International Congress on Sound and Vibration 2013, ICSV 2013, Bangkok, Thailand, 7–11 July 2013; Volume 4, pp. 2846–2852. [Google Scholar]
- Thrasher, D.B. Effect of tread wear on tire/pavement interaction noise. In Proceedings of the Inter-Noise 80. Noise Control for the 80’s. Proceedings of the 1980 International Conference on Noise Control Engineering, Miami, FL, USA, 8–10 December 1980; pp. 277–280. [Google Scholar]
- Spelman, R.H. Truck tires—Effects of design and construction on wear and noise. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 1963. [Google Scholar]
- Sandberg, U.; Glaeser, K.-P. Effect of tyre wear on noise emission and rolling resistance. In Proceedings of the INTER-NOISE 08, Shanghai, China, 26–29 October 2008; p. 4066. [Google Scholar]
- Raabe, R.C.; Burche, I. Retreaded truck tire noise tests. In BT—Truck Meeting, November 4, 1974–November 7, 1974; SAE Technical Papers; Bandag, Inc.: Muscatine, IA, USA, 1974. [Google Scholar]
- Hasebe, M. Experimental study of the noise generated by a passenger automobile equipped with studded and regular snow tyres. Appl. Acoust. 1984, 17, 247–254. [Google Scholar] [CrossRef]
- AASHTO. Effects of Studded Tires; TRB/NCHRP/SYN-32; Transportation Research Board: Washington, DC, USA, Federal Highway Administration: Washington, DC, USA; American Association of State Highway and Transportation Officials: Washington, DC, USA; 1975; 58p. [Google Scholar]
- Liu, Y.; Li, T.; Liu, Y.; Su, Y. Optimize the Structure Parameters of Tread Pattern Based on the Fuzzy Genetic Arithmetic. In Proceedings of the 2010 International Conference on Measuring Technology and Mechatronics Automation (ICMTMA 2010), Piscataway, NJ, USA, 13–14 March 2010; Volume 2, pp. 860–863. [Google Scholar]
- Sandberg, U.; Mioduszewski, P. Gaining extra noise reduction and lower rolling resistance by grinding a porous asphalt pavement. In Proceedings of the 41st International Congress and Exposition on Noise Control Engineering 2012, INTER-NOISE 2012, New York, NY, USA, 19–22 August 2012; Volume 8, pp. 6958–6969. [Google Scholar]
- Van Blokland, G.-J.; Von Meier, A. Reducing tyre/road noise with porous road surfaces and the effect of tyre choice. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 1993. [Google Scholar]
- Sachakamol, P.; Dai, L. Impact of porous pavement characteristics on tire/pavement noise emission from ARC roads. In Proceedings of the 17th International Congress on Sound and Vibration 2010, ICSV 2010, Cairo, Egypt, 18–22 July 2010; Volume 4, pp. 2464–2473. [Google Scholar]
- Crocker, M.J.; Hanson, D.; Li, Z.; Karjatkar, R.; Vissamraju, K.S. Measurement of acoustical and mechanical properties of porous road surfaces and tire and road noise. Transp. Res. Rec. 2004, 1891, 16–22. [Google Scholar] [CrossRef]
- Rochat, J.L.; Donavan, P.; Seybert, A.; Dare, T. Pavement sound absorption measurements in the U.S. In Proceedings of the 41st International Congress and Exposition on Noise Control Engineering 2012, INTER-NOISE 2012, New York, NY, USA, 19–22 August 2012; Volume 3, pp. 2612–2626. [Google Scholar]
- Seybert, A.F.; Han, J. Measurement of pavement absorption using ISO 13472-2. In Proceedings of the European Conference on Noise Control, Paris, France, 29 June–4 July 2008; pp. 4907–4911. [Google Scholar]
- Hubelt, J.; Bartolomaeus, W.; Wellner, F. On the correlation between motor vehicle noise levels and in situ measurement data of airflow resistance, water permeability and sound absorption coefficient of open porous asphalts. In Proceedings of the 35th International Congress and Exposition on Noise Control Engineering, INTER-NOISE 2006, Institute of Noise Control Engineering of the USA, Honolulu, HI, USA, 3–6 December 2006; Volume 2, pp. 1119–1123. [Google Scholar]
- Altreuther, B.; Beckenbauer, T. Dynamic measurement of air flow resistance. In Proceedings of the EURONOISE 2006—The 6th European Conference on Noise Control: Advanced Solutions for Noise Control, Tampere, Finland, 30 May–1 June 2006; 6p. [Google Scholar]





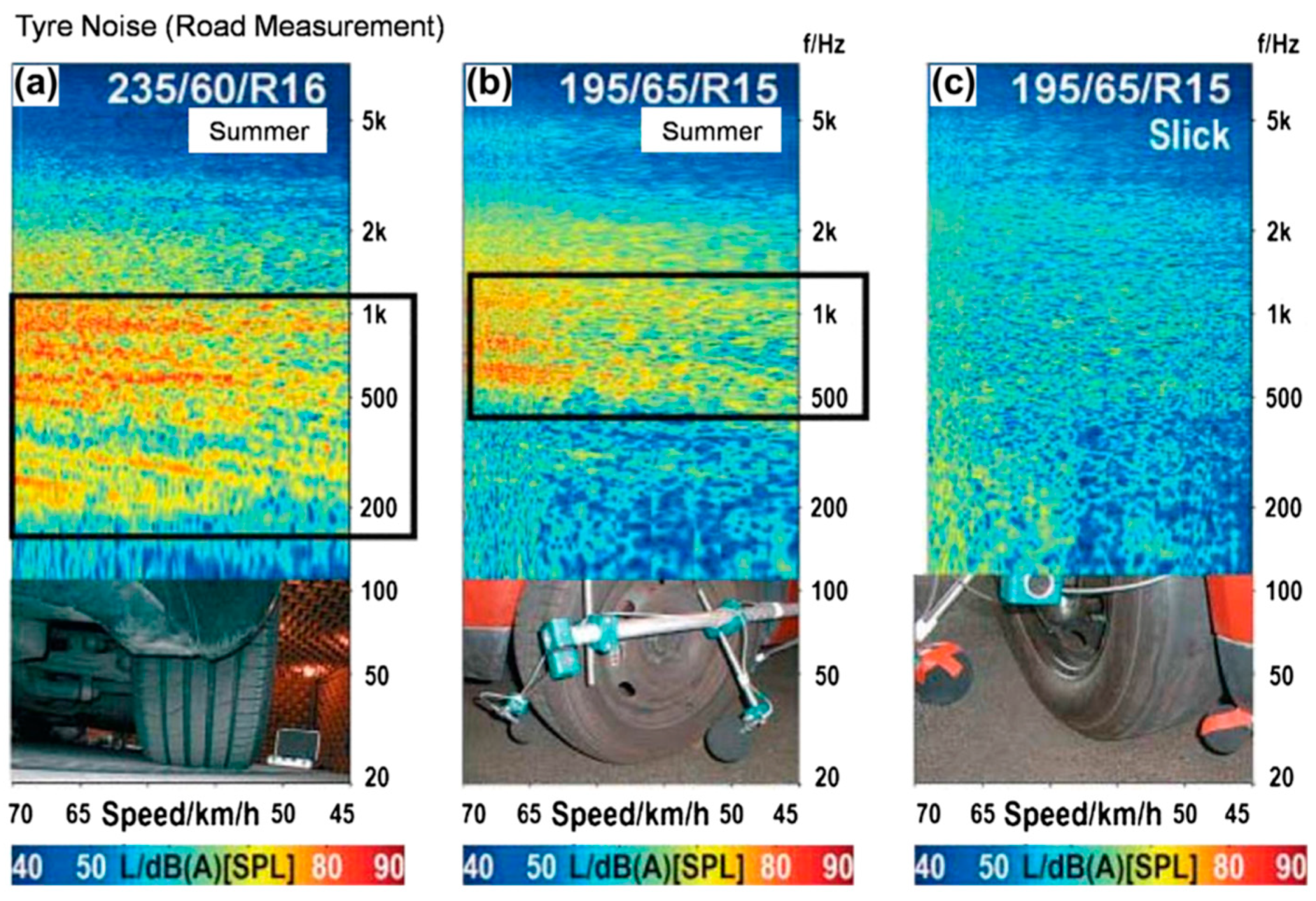
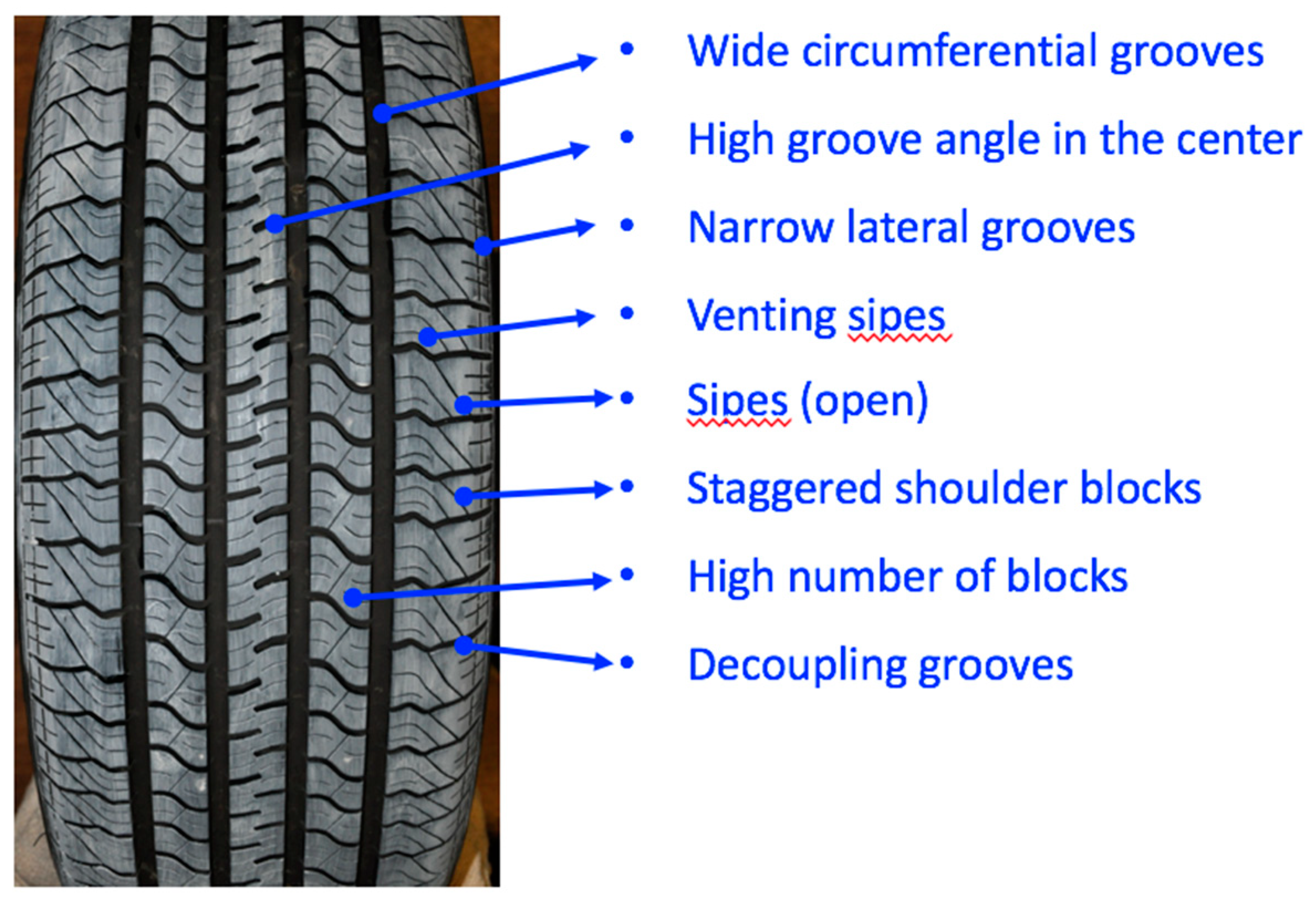
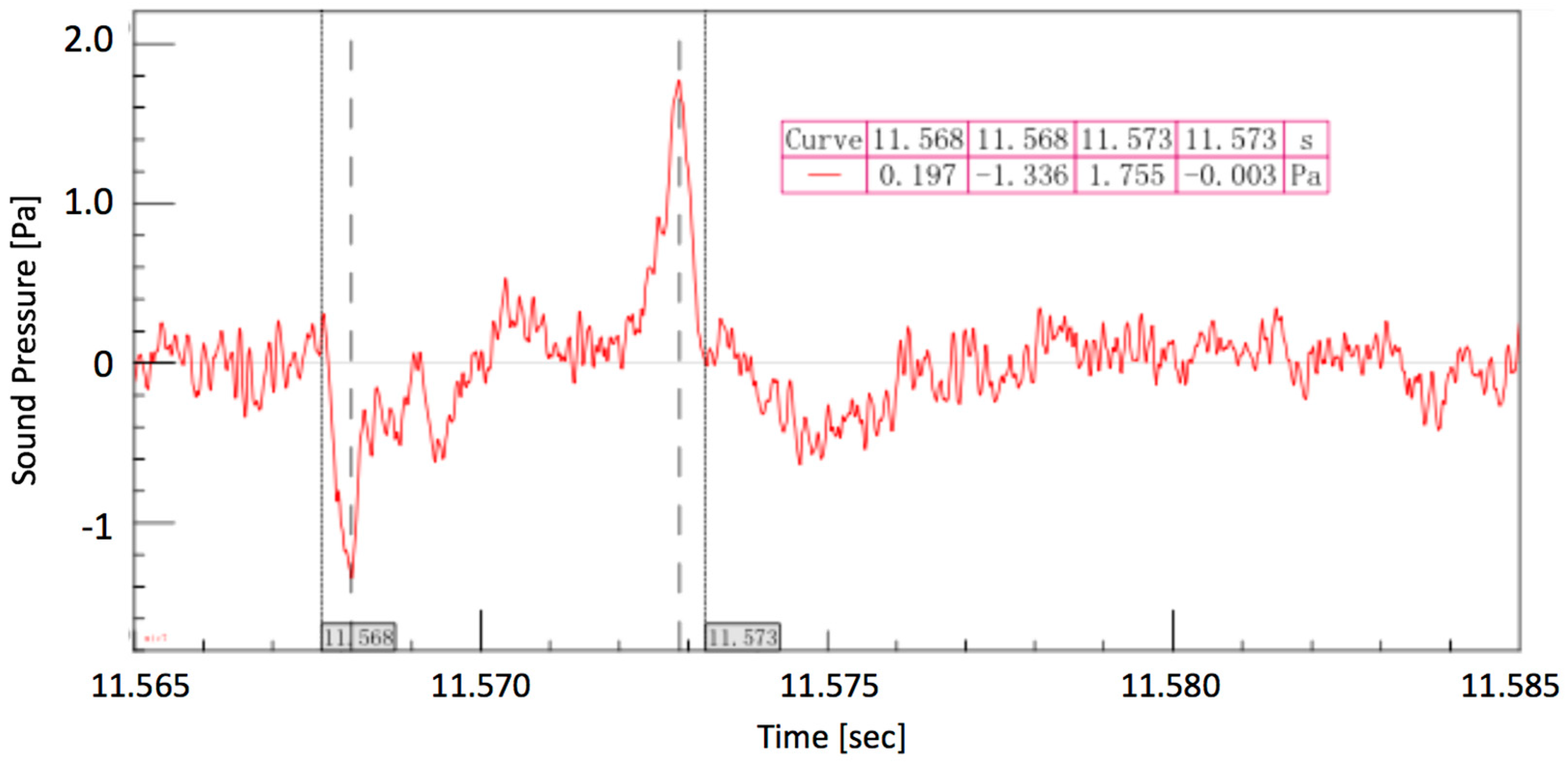
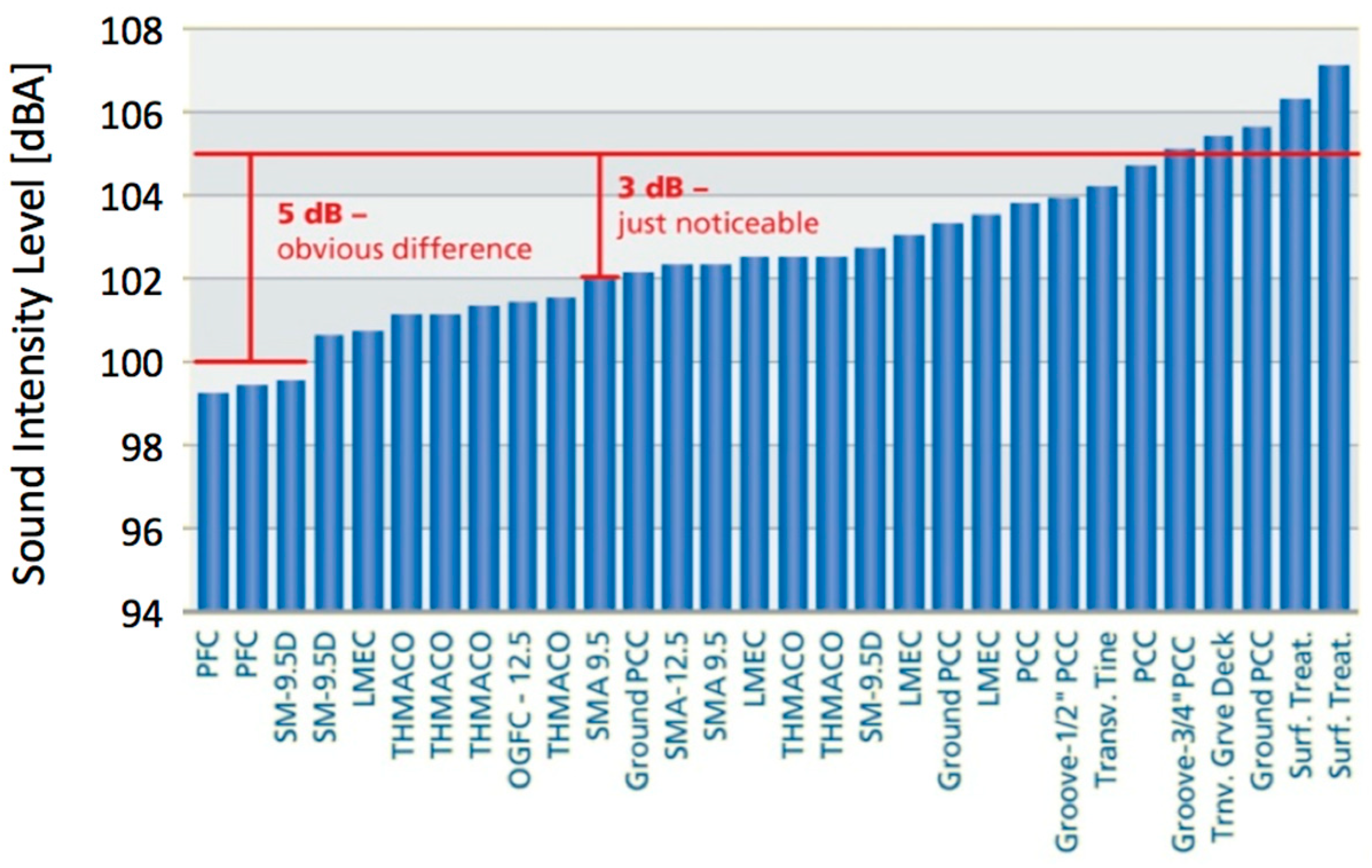
| Parameters | Potential Noise Variation [dB] | |
|---|---|---|
| Speed | 25 | |
| Pavement | 10 | |
| Tire | 10 | |
| Studs in Tire | 8 | |
| Load and Inflation | 5 | |
| Road Condition | 5 | |
| Temperature | 4 | |
| Wheel Torque | 3 | |
| Category | Cars | Trucks |
| Due to Vehicles | 7 | 12 |
| Due to Pavements | 9 | 6 |
| TPIN Mechanism | Speed Exponent |
|---|---|
| Tread Impact | 2.0–3.0 |
| Texture Impact | 3.0–3.5 |
| Stick/Slip (Friction) | 3.0–5.0 |
| Stick/Snap | 3.0–5.0 |
| Air Pumping | 4.0–5.0 |
| Air Turbulence | 5.0–6.0 |
| Pipe Resonance | 0.0 |
| Helmholtz Resonance | 0.0 |
| Reference | Author | Year | A | B | Method | Notes |
|---|---|---|---|---|---|---|
| [16] | Ejsmont | 1982 | =98.2 − 1.95B | 27–46 | CPX and DR | Passenger car tires |
| [17] | Landers | 1976 | N/A | 40 | CPX | Passenger car tires |
| [18] | Nilsson | 1976 | =77 − 1.95B | 14–32 | CB | Incl. wet road |
| [19] | Anonymous | 1971 | 24.1 | 30.5 | CB | Truck, rib |
| 9.3 | 41.6 | Truck, lug | ||||
| [20] | Corcoran | 1972 | N/A | 40 | CB | Truck tires |
| [21] | Walker and Williams | 1979 | N/A | 30–40 | CB | Passenger car tires |
| 33 | Truck tires | |||||
| [22] | Tetlow | 1968 | N/A | 36.5 | CB | Truck, rib |
| 30 | Truck, lug | |||||
| 20 | Wet road | |||||
| [23] | Hamet | 1988 | N/A | 26–41 | CB | Car tires; power levels |
| [24] | Köhler and Liedl | 1981 | N/A | 30–45 | CB | Dry road |
| 20–40 | Wet road | |||||
| [25] | Steven and Pauls | 1990 | 26.2 | 32.9 | CPX | Porous AC 0/5 |
| 27.3 | 33.5 | Porous AC 0/8 | ||||
| 23.4 | 37.3 | ISO-S | ||||
| 24.4 | 36.9 | SMA 0/5 | ||||
| 24.6 | 37.2 | Surface dressing | ||||
| 21.9 | 39.9 | PCC | ||||
| 27.9 | 35.5 | AC 0/11 | ||||
| 27.1 | 36.7 | Asphalt 0/11 | ||||
| [26] | Ivannikov et al. | 1998 | 7.1 | 37.6 | CB | Average of 10 truck tires, ISO surface |
| 11.8 | 36.3 | Average of 10 truck tires, SMA surface | ||||
| 10.7 | 36.8 | Average of 10 truck tires, porous surface | ||||
| [27] | Steven et al. | 2000 | 30.6 | 34.9 | CPX | AC 0/16 with chippings spread on surface |
| 33.5 | 33 | SMA 0/4 | ||||
| 34.2 | 32.6 | SMA 0/6 | ||||
| 30.4 | 34.9 | SMA 0/8 | ||||
| 27.8 | 37 | Surface dressing 5/8 | ||||
| 39.5 | 29.2 | Porous AC 6/16 | ||||
| 37.1 | 29 | Porous AC 4/8+11/16 double layer | ||||
| 34.4 | 29.2 | Porous AC 2/4+11/16 double layer | ||||
| 38.9 | 30.9 | Gussasphalt 0/11+2/5+5/8 | ||||
| 20.3 | 42 | Cement concrete transversely brushed | ||||
| 32.7 | 34.2 | Cement concrete with epoxy-durop 3/4 | ||||
| 24.3 | 37.8 | Cement concrete burlap drag | ||||
| 27.6 | 36.9 | Cement concrete exposed aggregate |
| Reference | Author | Year | Results (Increase per Doubling of Load) | Tire | ||
|---|---|---|---|---|---|---|
| [19] | Anon | 1971 | 5 dBA | Cross-ply truck tires with lugged pattern | ||
| Some tenths of 1 dBA | Cross-ply truck tires with rib pattern | |||||
| [51] | Leasure et al. | 1972 | 3–6 dBA | Cross-bar and pocket tread truck tires | ||
| 0–2.5 dBA | Ribbed truck tires | |||||
| [52] | Kilmer | 1976 | 2–3 dBA | Cross-ply truck tires with crossbar pattern | ||
| Negligible | Cross-ply truck tires with ribbed pattern | |||||
| [53] | Kilmer | 1979 | 5 dBA | Cross-ply truck tires with crossbar pattern | ||
| 1 dBA | Cross-ply truck tires with ribbed pattern | |||||
| [54,55] | Underwood | 1980 | 6.5 dBA | Cross-ply truck tires with crossbar pattern | ||
| 1984 | 0.5 dBA | Cross-ply truck tires with ribbed pattern | ||||
| [56] | Walker | 1981 | Does not change appreciably | Cross-ply truck tires | ||
| [57] | Köllman | 1993 | 2.4 dBA | More than 100 car tires | ||
| [58] | Wolf et al. | 1992 | 1–1.5 dBA | Trucks and buses | ||
| 5 dBA | Traction truck tires | |||||
| 4.4 dBA | Ribbed truck tires | |||||
| [59] | von Meier | 1992 | 3.8 dBA between 70% and 100% max load | Traction truck tires | ||
| 1.2 dBA between 70% and 100% max load | Ribbed truck tires | |||||
| [1] | Sandberg and Ejsmont | 2003 | ISO Surface (Smooth) | GRB-R Surface (Rough) | ||
| Slick Tire | 2.4 dBA | 0.5 dBA | ||||
| Summer Tire | 1.4 dBA | −0.1 dBA | ||||
| Winter Tire | 1.4 dBA | 0.9 dBA | ||||
| Average | 1.7 dBA | 0.4 dBA | ||||
| Relation with TPIN (↑↗•↘ ↓) | Relation with Rolling Resistance (↑↗•↘ ↓) | |
|---|---|---|
| Speed | ↑ | ↗ |
| Tire Load | ↗ | ↑ |
| Inflation Pressure | • | ↓ |
| Rubber Hardness | ↗ | ↘ |
| Wear/Aging | ↗ | ↘ |
| Studded | ↑ | ↗ |
| Surface Rating (IRI) | • | ↗ |
| Porosity | ↓ | • |
| Stiffness (Impedance) | ↗ | N/A |
| MTD/MPD/Texture | ↑ | ↗ |
| Wetness | ↑ | ↑ |
| Element Number | Element Length [inch] |
|---|---|
| 1 | 1.152 |
| 2 | 1.224 |
| 3 | 1.297 |
| 4 | 1.368 |
| 5 | 1.439 |
| 6 | 1.513 |
| 7 | 1.584 |
| 8 | 1.655 |
| 9 | 1.727 |
| Changes in Tread Pattern | A-Weighted SPL | Low to Mid Frequency (Tread Impact) | Mid to High Frequency (Air Resonance) | Highest Frequency (4–16 kHz) | ||
|---|---|---|---|---|---|---|
 | Randomization | Tread randomization | ↓ | ↓ | • | • |
 | Introduction of an “offset” between left and right side of the tread or introduction of asynchronous randomization | ↓ | ↓ | ↓ | • | |
 | Elimination of grooves that coincide with the contour of the tire footprint | ↓ | ↓ | • | • | |
 | Ventilation | Ventilation of air pockets | ↓ | • | ↓ | ↓ |
 | Addition of circumferential grooves to a transverse groove pattern | ↓ | • | ↓ | ↓ | |
 | Addition of “mirror Image” grooves | • | • | • | ↓ | |
 | Addition of lamellae | ↓• | ↓ | • | • | |
 | Tread Segment | Increasedo of groove width 2 → 9 mm 9 → 12 mm | ↑ ↓ | ↑ ↓ | ↑ • | ↓ ↓ |
 | Increase of groove angle (relative to lateral axis) ([161,162]) 0 → 20° 20 → 90° | ↓ • | ↓ ↓ | ↓ • | • • | |
| Dry Handling | Dry Braking | Track Performance | Noise and Comfort | Wet Performance | Regular Wear | Rolling Resistance | Mileage | |
|---|---|---|---|---|---|---|---|---|
| Priority (A is highest) | A | A | A | B | B | B | C | C |
| Large Shoulder Groove Angle | ↓ | ↓ | ↑ | ↑ | ↑ | • | ↑ | • |
| Large Number of Sipes | ↓ | ↓ | ↑ | ↑ | • | ↓ | ↓ | ↓ |
| Large Shifts | • | • | ↑ | ↑ | • | ↑ | ↑ | • |
| Randomization | • | • | • | ↑ | • | ↓ | • | ↓ |
| Wide Blocks | ↑ | ↑ | ↑ | ↑ | ↓ | • | ↓ | ↓ |
| Large Part Horizontal Void | ↑ | ↑ | ↓ | ↓ | ↓ | • | ↓ | ↓ |
| Category | Type | Meaning | Illustration |
|---|---|---|---|
| Randomization | Constant Pitch | All segments are of the same length (no randomization) |  |
| Synchronous | Segments differ in length, but the order of their placement is the same on the left and right side |  | |
| Asynchronous | Segment differ in length and their order is different on left and right side of the tire |  | |
| Symmetry | Symmetric | Segments on the left side of the tire are identical to segments on the right side (but there is an offset in this case) |  |
| Asymmetric | Segments on the left side have different pattern in relation to right side |  | |
| Directivity | Bi-directional | Segments on the left side of the tire are rotated 180° in relation to segments on the right side |  |
| Directional | Segments on the right side are mirror images of the segments on the left side. Other special properties possible, for example tilted lamellae. |  |
| No. | Reference | Tread Pattern Harmonic Spectrum Distribution | Notes |
|---|---|---|---|
| 1 | Mono-space sequence | 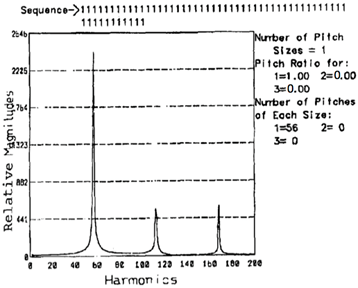 | A mono-space sequence would actually be very noisy. A good example of the sound made would be a car going over a metal bridge grating. |
| 2 | Ewart, 1935 [168] (US Patent 2006197) | 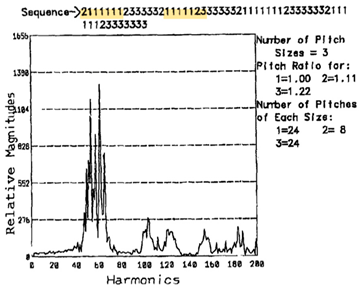 | A pitch sequence typically provides an improvement if it can lower the overall magnitude and spread the Fourier spectrum over a broader bandwidth. Mr. Ewart’s basic approach is relatively simple. The tire is divided into 8 main sections that are each separated by a small 7-degree section. The main sections are composed of pitch lengths of the same sizes arranged so that the main sections have different lengths. The sequence is further constrained to vary from small to medium to large pitches and back down. This basic concept of cycling from small to medium to large and back down is still in use today, 60 years later (1995). |
| 3 | Buddenhagen, 1952 [170] (US Patent 2612928) |  | Mr. Buddenhagen again used a division of the tire into 8 segments. In this technique, each segment comprises 45 degrees of the tire circumference. Each segment is however made up of different pitch lengths. There are 2 “A” segments made up of eight large pitches, 4 “B” segments made up of ten medium segments and 2 “C” segments made up of twelve small pitches. |
| 4 | Landers, 1982 [171] (US Patent 4327792) |  | Mr. Landers makes a major change in the pitch sequencing process by breaking the segments into groupings of the same size pitch that in turn make up segments of the tire circumference that are different sizes. |
| 5 | Williams, 1994 [172] (US Patent 5314551) | 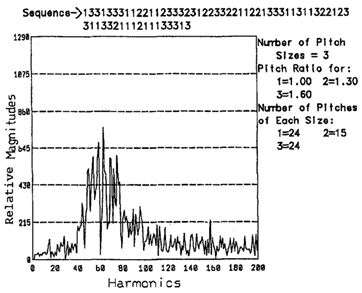 | One of the primary departures of this technique from the previous examples is the consistency of the previous techniques to always progress from a small pitch to a medium and then to a large before progressing back down to a small. The General Tire patent in fact encourages going directly from a small pitch to a large pitch. The patent defines any change between two pitches as a transition. The patent claims that the best frequency distribution is obtained when between 15 to 30 percent of the total transitions between pitches are between a small and a large pitch. |
| Pavement Type | Sub-Type | Illustration |
|---|---|---|
| Traditional | Gravel |  |
| Chipseal |  | |
| Asphalt Concrete (AC) | Single Coat Seal |  |
| Reseal |  | |
| Two-coat Seal |  | |
| Racked-in Seal |  | |
| Sandwich Seal |  | |
| Slurry Seal | 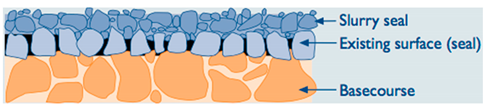 | |
| Cape Seal | 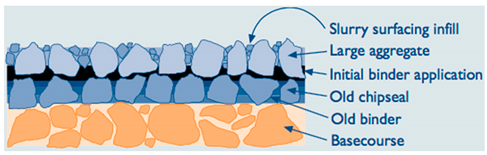 | |
| Asphaltic Concrete | 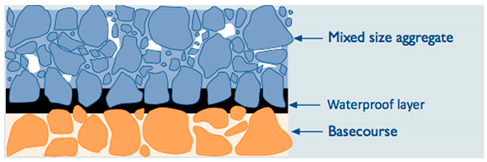 | |
| Open Graded Porous Asphalt (OGPA) | 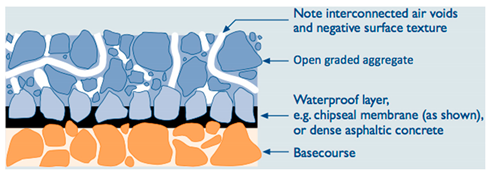 | |
| Stone Mastic Asphalt (SMA) | 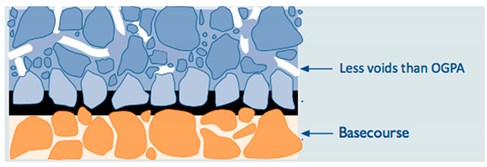 | |
| Macadam | 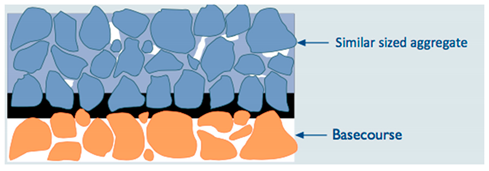 | |
| Cement Concrete (CC) | Transvers Grooves |  |
| Longitudinal Grooves |  | |
| Artificial Turf Drag |  | |
| Burlap Drag |  | |
| Diamond Grinding |  | |
| Exposed Aggregate |  |
| Micro-Texture | Macro-Texture | Mega-Texture | Unevenness | Topographical Undulations | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Wavelength | <0.5 mm | 0.5–50 mm | 50–500 mm | 0.5–50 m | >50 m | |||||
| Road Roughness | ↑ | ↑ | ↑ | ↑ | ↑ | |||||
| Rolling Resistance | ↑ | ↑ | ↑ | ↑ | ||||||
| Tire Road Friction | ↑ | ↑ | ↑ | ↑ | ↓ | ↓ | ||||
| Adhesion | ↓ | ↓ | ||||||||
| Drainage | ↑ | ↑ | ||||||||
| Water Skid Resistance | ↑ | ↑ | ↑ | ↑ | ||||||
| Ride Comfort | ↓ | ↓ | ↓ | |||||||
| Optical Property | • | • | ||||||||
| Road Hold | ↑ | ↑ | ↑ | |||||||
| Splash and Spray | ↓ | ↓ | ||||||||
| Dynamic Loads | ↑ | ↑ | ↑ | |||||||
| Tire Wear | ↑ | ↑ | ||||||||
| Vehicle Wear | ↑ | ↑ | ||||||||
| TPIN | ↑ | ↑ | ||||||||
| Interior Noise | ↑ | ↑ | ||||||||
| Pavement Texture | Macro-Texture (Roughness/Smoothness) | Micro-Texture (Harshness/Polishedness) | Dominant Mechanism |
|---|---|---|---|
 | High (rough) | High (harsh) | Impact and stick/slip |
 | High (rough) | Low (polished) | Impact |
 | Low (smooth) | High (harsh) | Stick/slip |
 | Low (smooth) | Low (polished) | Stick/snap |
| Temperature Coefficient | Dense Asphalt | Porous Asphalt (Porosity > 10%) | Cement Concrete |
|---|---|---|---|
| αair (ref. Tair) [dBA/°C] | −0.10 | −0.06 | −0.03 |
| αpavement (ref. Tpavement) [dBA/°C] | −0.06 | −0.04 | −0.02 |
| αtire (ref. Ttire) [dBA/°C] | −0.09 | −0.05 | −0.03 |
| No. | Parameter | Pertinent Frequency [Hz] | Relation (↑↓) | Potential Noise Variation [dB] | Measurement Equipment | Relevant Mechanism | References |
|---|---|---|---|---|---|---|---|
| 1 | Speed | 250–8000 | ↑ | 25 | Speedometer, wheel/axle-mounted encoder, GPS | Various: impact, air pumping | [5,11,12] |
| 2 | Longitudinal Force/Slip | 800–1600 | ↑ | 10 | Accelerometer | Stick/slip | [35,36,37,38] |
| 3 | Lateral Force/Slip | 1000–8000 | ↑ | 7 | Accelerometer, gyroscope | Stick/slip | [1,43,44] |
| 4 | Tire Load | 800–1600 | ↑ | 2 | Dynamometer | Impact, air pumping | [51,52,53,54,55,56,57,58,59] |
| 5 | Inflation Pressure | 1600–3200 | Complex | 1 | Tire pressure gauge/sensor | Impact, air pumping | [53,319] |
| 6 | Tire Camber Angle | 1000–3000 | ↓ | 5 | Protractor | Impact, stick/slip | [74] |
| No. | Parameter | Pertinent Frequency [Hz] | Relation (↑↓) | Potential Noise Variation [dB] | Measurement Equipment | Relevant Mechanism | References |
|---|---|---|---|---|---|---|---|
| 1 | Tire Type/Construction | N/A | Complex | 3 | N/A | Various | [80,81,82,83,84] |
| 2 | Tire Width | 500–1000 | ↑ | 3 | Measure tape | Various | [94,320] |
| 3 | Tire Diameter | N/A | ↓ | 1 | Measure tape | Impact, horn | [92,96,320] |
| 4 | Belt Stiffness | 500–8000 | ↓ | 2 | Loading test rig with bar | Tire resonance | [16,98,321] |
| 5 | Damping (Loss Factor) | 250–500 | ↓ | 1 | N/A | Tire resonance | [64] |
| 6 | Non-uniformity | 20–200 | ↑ | 1 | Wheel balancing machines | Tire resonance | [16,26] |
| 7 | Rubber Hardness | 1000–3000 | ↑ | 3 | Durometer | Stick/slip | [105,322] |
| 8 | Wear/Aging | 1000–3000 | ↑ (then ↓) | 5 | N/A | Various | [129,323,324,325] |
| 9 | Retreaded | 500 and 2000–3000 | Complex | 2 | N/A | Impact | [130,131,326] |
| 10 | Studded | 400–3000 and above 5000 | ↑ | 6 | N/A | Impact, stick/slip | [327,328] |
| 11 | Tread Porosity | N/A | ↓ | 7 | N/A | Air pumping, horn effect | [134,135] |
| 12 | Tire Cavity Content | 400–1100 | Complex (↓) | 2 | N/A | Cavity resonance | [66,136,137] |
| 13 | Rolling Resistance | N/A | ↑ (Weak correlation) | 0 | Dynamometer drum: ISO 18164 [141] | N/A | [76,138,139,140] |
| No. | Parameter | Pertinent Frequency [Hz] | Relation (↑↓) | Potential Noise Variation [dB] | Measurement Equipment | Relevant Mechanism | References |
|---|---|---|---|---|---|---|---|
| 1 | Randomization | 600–1000 | ↓ | 0 or marginal | N/A | Tread impact | [1,179] |
| Elimination of Groove Footprint Coinciding | 800–1000 | ↓ | N/A | N/A | Tread impact | [1,179] | |
| Offset between Left and Right Side | N/A | ↓ | 5 | Caliper | Tread impact | [1,179,329] | |
| 2 | Rotation Direction / Side Asymmetry | N/A | ↑ | 3 | N/A | Various | [1,179] |
| 3 | Ventilation | 800–1000 and 1600–4000 | ↓ | 2 | N/A | Air pumping, air resonance | [1,130,179] |
| 4 | Addition of Mirror Image Grooves | Above 4000 | ↓ | 0 | N/A | Air pumping, air resonance | [1,179] |
| Addition of Lamellae | 800–1000 | ↓ | N/A | N/A | Air pumping, air resonance | [1,179] | |
| Groove Width | 800–2000 | ↑ 9 mm ↓ | N/A | Caliper | Air pumping | [1,130,179] | |
| Groove Angle (Relative to Lateral) | 800–2000 | ↓ | N/A | Protractor | Tread impact | [1,130,179] |
| No. | Parameter | Pertinent Frequency [Hz] | Relation (↑↓) | Potential Noise Variation [dB] | Measurement Equipment | Relevant Mechanism | References |
|---|---|---|---|---|---|---|---|
| 1 | Micro-texture (below 0.5 mm) | 2000–4000 | ↓ | N/A but Marginal | Laser profiler: ISO 13473 [203]; Circular Track Meter (CTM): ASTM E2157 [205] for macro-texture only | Stick/slip, stick/snap | [208,209] |
| Macro-texture (0.5–50 mm) | 100–1000 and 2000–4000 | ↓ and (10 mm) ↑ | N/A but Significant | Texture impact, air pumping | [207,210,211] | ||
| Mega-texture (50–500 mm) | 100–1000 | ↑ | N/A but Significant | Texture impact | [211,216] | ||
| Unevenness (500–800 mm) | N/A | ↑ | 4 | N/A | [181] | ||
| Unevenness (10–50 m) | 200–1500 | ↓ | 1 | ||||
| 2 | MPD/MTD/ Texture | N/A | Complex | 10 | Sand patch method: ASTM E965 [214], ASTM E1845 [215] and ISO 13473-1 [189] | Same as macro-texture | [221] |
| 3 | International Roughness Index (IRI) | Same as unevenness | Same as unevenness | Same as unevenness | Profilometer: ASTM E1926 [224] and ASTM E1364 [225] | Same as unevenness | [223] |
| 4 | Positive versus Negative Texture | N/A | ↑ | N/A | Laser profiler | Texture impact, air pumping | [13] |
| 5 | Transverse Texture | N/A | ↑ | N/A | Laser profiler | Texture impact | [228] |
| 6 | Anisotropic Texture | N/A | ↑ | N/A | Laser profiler | Texture impact, air pumping | [229] |
| 7 | Joints | 800–1000 | ↑ | 3 | Laser profiler | Texture impact, air pumping | [12,231,233,234,235,236] |
| 8 | Porosity | 500–1600 and 3000 | ↓ | 7 | Pavement core sample: ASTM D7063/D7063M [246] | Various | [330,331,332,333] |
| 9 | Sound Absorption | Similar to Porosity | Similar to Porosity | Similar to Porosity | Impedance tube: ISO 10534-1 [253] and ISO 13472-1 [256] | Pavement Absorption | [59,334,335] |
| 10 | Airflow Resistance | N/A | ↑ | N/A | Impedance tube: ISO 9053 [259] and ANSI/ASA S1.18 [260] | Air pumping, air resonance | [222,336,337] |
| 11 | Thickness of Layer | 500–1600 | ↓ | 5 | Measure tape | Acoustic and mechanical impedance | [1] |
| 12 | Stiffness (Mechanical Impedance) | 800–1250 | ↑ | 1 | Impact hammer device: AASHTO T 342 [275] | Vibration Transfer | [265,266,267,268,269] |
| 13 | Normal Adhesion | 2000–4000 | ↑ | 1 | N/A | Stick/snap | [1] |
| 14 | Tangential Friction | 2500–6300 | ↑ | 0 | Dynamic Friction Tester (DFT): ASTM E1911 [283] | Stick/slip | [76] |
| 15 | Wear/Age | 1000–4000 | ↑ | 2 | N/A | Impact, absorption | [250,262,290,293] |
| 16 | Surface Rating (SR) | N/A | ↓ | N/A | N/A | Impact | [296,297] |
| 17 | Wetness | Above 1000 Hz | ↑ | 3 | N/A | Water splash effect | [5,299,300] |
| 18 | Mixture Parameters/Materials | N/A | Complex | Significant | N/A | Various | [303,304] |
| No. | Parameter | Pertinent Frequency [Hz] | Relation (↑↓) | Potential Noise Variation [dB] | Measurement Equipment | Relevant Mechanism | References |
|---|---|---|---|---|---|---|---|
| 1 | Temperature | 1000–4000 | ↓ | 3 | Thermometer | Impact | [310,311] |
| 2 | Air Humidity | N/A | ↓ | 1 | Air humidity meter | Sound propagation | [317] |
| 3 | Wind | 300 and 2000 | ↑ | N/A | Wind meter | Air Turbulence | [5,318] |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T. Influencing Parameters on Tire–Pavement Interaction Noise: Review, Experiments, and Design Considerations. Designs 2018, 2, 38. https://doi.org/10.3390/designs2040038
Li T. Influencing Parameters on Tire–Pavement Interaction Noise: Review, Experiments, and Design Considerations. Designs. 2018; 2(4):38. https://doi.org/10.3390/designs2040038
Chicago/Turabian StyleLi, Tan. 2018. "Influencing Parameters on Tire–Pavement Interaction Noise: Review, Experiments, and Design Considerations" Designs 2, no. 4: 38. https://doi.org/10.3390/designs2040038
APA StyleLi, T. (2018). Influencing Parameters on Tire–Pavement Interaction Noise: Review, Experiments, and Design Considerations. Designs, 2(4), 38. https://doi.org/10.3390/designs2040038





